Convergence and stability of the Milstein scheme for stochastic differential equations with piecewise continuous arguments

Abstract

This work develops the Milstein scheme for commutative stochastic differential equations with piecewise continuous arguments (SDEPCAs), which can be viewed as stochastic differential equations with time-dependent and piecewise continuous delay. As far as we know, although there have been several papers investigating the convergence and stability for different numerical methods on SDEPCAs, all of these methods are Euler-type methods and the convergence orders do not exceed 1/2. Accordingly, we first construct the Milstein scheme for SDEPCAs in this work and then show its convergence order can reach 1. Moreover, we prove that the Milstein method can preserve the stability of SDEPCAs. In the last section, we provide several numerical examples to verify the theoretical results.

1 Introduction

Differential equations with piecewise continuous arguments (EPCAs) are well used in control theory and some biomedical models ([1,2,3,4]). A typical EPCA is of the form

$$\begin{aligned} x'(t)=f(t,x(t),x(h(t))), \end{aligned}$$

where the argument h(t) has intervals of constancy. A potential application of EPCAs is the stabilization of hybrid control systems with feedback delay [1]. In recent years, some scholars further developed the theory of stabilization for hybrid stochastic differential equations by feedback control based on discrete-time state observations ([5, 6]), and this theory is actually based on the stability of the hybrid stochastic differential equation with piecewise continuous arguments (SDEPCA)

$$\begin{aligned} \text {d}x(t)=(f(x(t),r(t),t)+u(x([t/\tau ]\tau ),r(t),t))\text {d}t+g(x(t),r(t),t)\text {d}\omega (t). \end{aligned}$$

Therefore, the properties of SDEPCAs have received more and more consideration.

However, most of SDEPCAs do not have explicit solutions; hence, it is extremely important to solve them by numerical methods. Moreover, in order to achieve the required accuracy in many real-world problems, the development of higher-order numerical methods is necessary. But to our knowledge, the numerical methods currently developed for global Lipschitz continuous or highly nonlinear SDEPCAs are all Euler or Euler-type methods (such as the split-step theta method, the tamed Euler method, the truncated Euler method), and the convergence orders of all of these methods do not exceed one-half (see, e.g., [7,8,9,10,11,12]). Therefore, the main aim of this work is to construct a higher-order numerical scheme for SDEPCAs.

The Milstein scheme is a well-known numerical scheme for stochastic ordinary differential equations (SODEs) with a strong order of convergence one ([13,14,15,16,17,18,19]). Several scholars have further derived and analyzed the Milstein scheme for stochastic delay differential equations (SDDEs) [20,21,22,23,24,25,26,27,28,29]. However, most of these papers only consider the stochastic differential equations with constant delay [20,21,22,23,24,25,26,27,28], while an SDEPCA can be viewed as a stochastic differential equation with time-dependent delay, and the delay function is piecewise continuous and not differentiable. Therefore, it is worthwhile to construct the Milstein scheme for SDEPCAs.

In this work, we construct the Milstein scheme for SDEPCAs following the approach used by Kloeden et al. for SODEs [14] and SDDEs [29] and prove that the Milstein solution also converges strongly with order one to the exact solution of commutative SDEPCAs. It is worth mentioning that the Milstein scheme constructed in this paper contains only the derivatives of the coefficients f and $g_j$ to the first component, which is different from the ones derived in the existing publications.

Moreover, whether the numerical method can preserve the stability of the exact solution is also an important criterion for the goodness of the numerical method [30,31,32,33]. Therefore, we also consider the stability of the Milstein method in this paper. The rest of this work is arranged as follows. Some basic lemmas and preliminaries are introduced in the second section. The Milstein scheme is developed, and its uniform boundedness in p-th moment is obtained in Sect. 3. Then, the strong convergence order of the Milstein method is proved in Sect. 4. The mean square exponential stability of the Milstein method is given in Sect. 5. Finally, several illustrative examples are given.

2 Notations and preliminaries

Throughout this paper, unless otherwise specified, we will use the following notations. $\vert x\vert$ denotes the Euclidean vector norm, and $\langle x,y\rangle$ denotes the inner product of vectors x, y. If A is a vector or matrix, its transpose is denoted by $A^\text {T}$. If A is a matrix, its trace norm is denoted by $\vert A\vert =\sqrt{{{\,\textrm{trace}\,}}(A^\text {T}A)}$. For two real numbers a and b, we will use $a\vee b$ and $a\wedge b$ for the $\max \left\{ a,b\right\}$ and $\min \left\{ a,b\right\}$, respectively. $\mathbb {N}:=\{0,1,2,\dots ,\}$. $[\cdot ]$ denotes the greatest-integer function.

Moreover, let $(\Omega ,\mathcal {F},\left\{ \mathcal {F}_t\right\} _{t\ge 0},\mathbb {P})$ be a complete probability space with a filtration $\left\{ \mathcal {F}_t\right\} _{t\ge 0}$ satisfying the usual conditions (i.e., it is right continuous and $\mathcal {F}_0$ contains all $\mathbb {P}$-null sets), and let $\mathbb {E}$ denote the expectation corresponding to $\mathbb {P}$. Denote by $\mathcal {L}^p([0,T];\mathbb {R}^n)$ the family of all $\mathbb {R}^n$-valued, $\mathcal {F}_t$-adapted processes $\left\{ f(t)\right\} _{0\le t\le T}$ such that $\int _0^T\vert f(t)\vert ^p dt<\infty ,$ a.s. Denote by $\mathcal {L}^p([0,\infty );\mathbb {R}^n)$ the family of process $\left\{ f(t)\right\} _{t\ge 0}$ such that for every $T>0$, $\left\{ f(t)\right\} _{0\le t\le T}\in \mathcal {L}^p([0,T];\mathbb {R}^n).$

Let $B(t)=(B^1(t),\dots ,B^d(t))^\text {T}$ is a d-dimensional Brownian motion defined on the probability space $(\Omega ,\mathcal {F},\left\{ \mathcal {F}_t\right\} _{t\ge 0},\mathbb {P})$; we consider the following SDEPCA:

$$\begin{aligned} \text {d}x(t)=f(x(t),x([t]))\text {d}t+\sum _{j=1}^d g_j(x(t),x([t]))\text {d}B^j(t) \end{aligned}$$

(1)

on $t\ge 0$ with initial data $x(0)=x_0\in \mathbb {R}^n$, where $x(t)=(x_1(t),x_2(t),\dots ,x_n(t))^\text {T}\in \mathbb {R}^n$, $f:\mathbb {R}^n\times \mathbb {R}^n\rightarrow \mathbb {R}^n$, $g_j:\mathbb {R}^n\times \mathbb {R}^n\rightarrow \mathbb {R}^{n}$, $j=1,2,\dots ,d$. The definition of the exact solution for (1) is as follows.

Definition 1

[34] An $\mathbb {R}^n$-valued stochastic process $\left\{ x(t),t\ge 0\right\}$ is called a solution of (1) on $[0,\infty ),$ if it has the following properties:

• $\left\{ x(t),t\ge 0\right\}$ is continuous and $\mathcal {F}_t$-adapted;

• $\left\{ f(x(t),x([t]))\right\} \in \mathcal {L}^1([0,\infty );\mathbb {R}^n)$ and $\left\{ g_j(x(t),x([t]))\right\} \in \mathcal {L}^2([0,\infty );\mathbb {R}^{n})$;

• (1) is satisfied on each interval $[n,n+1)\subset [0,\infty )$ with integral end points almost surely.

A solution $\left\{ x(t),t\ge 0\right\}$ is said to be unique if any other solution $\left\{ \bar{x}(t),t\ge 0\right\}$ is indistinguishable from $\left\{ x(t),t\ge 0\right\}$, that is,

$$\begin{aligned} \mathbb {P}\left\{ x(t)=\bar{x}(t)\ \text {for\, all}\ t\ge 0\right\} =1. \end{aligned}$$

We assume that the coefficients of (1) satisfy the following conditions.

Assumption 2.1

Suppose f(x, y) and $g_j(x,y)$ are continuously twice differentiable in $x\in \mathbb {R}^n$ with derivatives bounded as follows: for constant $M>0$

$$\begin{aligned} \left| \frac{\partial f(x,y)}{\partial x_k}\right| \vee \left| \frac{\partial g_j(x,y)}{\partial x_k}\right| \vee \left| \frac{\partial ^2 f(x,y)}{\partial x_k\partial x_i}\right| \vee \left| \frac{\partial ^2 g_j(x,y)}{\partial x_k\partial x_i}\right| \le M \end{aligned}$$

holds for all $x, y\in \mathbb {R}^n$, $k,i=1,2,\dots n$, and $j=1,2,\dots , d$, where

$$\begin{aligned} \frac{\partial f(x,y)}{\partial x_k}=&\left( \frac{\partial f_1(x,y)}{\partial x_k},\frac{\partial f_2(x,y)}{\partial x_k},\cdots ,\frac{\partial f_n(x,y)}{\partial x_k}\right) ^\text {T},\\ \frac{\partial g_j(x,y)}{\partial x_k}=&\left( \frac{\partial g_{1j}(x,y)}{\partial x_k},\frac{\partial g_{2j}(x,y)}{\partial x_k},\cdots ,\frac{\partial g_{nj}(x,y)}{\partial x_k}\right) ^\text {T},\\ \frac{\partial ^2 f(x,y)}{\partial x_k\partial x_i}=&\frac{\partial }{\partial x_i}\left( \frac{\partial f(x,y)}{\partial x_k}\right) =\left( \frac{\partial ^2 f_1(x,y)}{\partial x_k\partial x_i},\cdots ,\frac{\partial ^2 f_n(x,y)}{\partial x_k\partial x_i}\right) ^\text {T},\\ \frac{\partial ^2 g_j(x,y)}{\partial x_k\partial x_i}=&\frac{\partial }{\partial x_i}\left( \frac{\partial g_j(x,y)}{\partial x_k}\right) =\left( \frac{\partial ^2 g_{1j}(x,y)}{\partial x_k\partial x_i},\cdots ,\frac{\partial ^2 g_{nj}(x,y)}{\partial x_k\partial x_i}\right) ^\text {T}. \end{aligned}$$

Remark 1

Under Assumption 2.1, for all $x,y,\bar{x}\in \mathbb {R}^n$,

$$\begin{aligned} \vert f(x,y)-f(\bar{x},y)\vert \vee \vert g_j(x,y)-g_j(\bar{x},y)\vert \le \bar{M}\vert x-\bar{x}\vert , \end{aligned}$$

(2)

where $\bar{M}=\sqrt{n}M$.

Proof

For any $x,y,\bar{x}\in \mathbb {R}^n$, according to the mean value theorem of vector-valued function (see [35]), we have

$$\begin{aligned} \vert f(x,y)-f(\bar{x},y)\vert =&\left| \frac{\partial f(\bar{x}+\theta (x-\bar{x}),y)}{\partial x}\right| \vert x-\bar{x}\vert \\ =&\sqrt{\sum _{k=1}^n\left| \frac{\partial f(\bar{x}+\theta (x-\bar{x}),y)}{\partial x_k}\right| ^2}\vert x-\bar{x}\vert \\ \le&\sqrt{n}M\vert x-\bar{x}\vert , \end{aligned}$$

where $\theta \in (0,1)$, $\frac{\partial f(x,y)}{\partial x}:=\left( \frac{\partial f_l(x,y)}{\partial x_k}\right) _{l,k},~l,k=1,2,\dots ,n$. In the same way, we can also get

$$\begin{aligned} \vert g_j(x,y)-g_j(\bar{x},y)\vert \le \sqrt{n}M\vert x-\bar{x}\vert . \end{aligned}$$

The proof is completed. $\square$

Assumption 2.2

There exists a positive constant L such that

$$\begin{aligned} \vert f(x, y)-f(x,\bar{y})\vert \vee \vert g_j(x,y)-g_j(x,\bar{y})\vert \le L\vert y-\bar{y}\vert \end{aligned}$$

(3)

for all $x, y,\bar{y}\in \mathbb {R}^n$.

Remark 2

Under Assumptions 2.1 and 2.2, there exist a constant $\bar{L}>0$ such that f and $g_j, j=1,\dots , d$ satisfy the following linear growth condition:

$$\begin{aligned} \vert f(x,y)\vert \vee \vert g_j(x,y)\vert \le \bar{L}(1+\vert x\vert +\vert y\vert ) \end{aligned}$$

(4)

for all $x,y\in \mathbb {R}^n$.

Proof

By (2) and (3), using the fundamental inequality $\vert a+b\vert \le \vert a\vert +\vert b\vert$, one can obtain

$$\begin{aligned} \vert f(x,y)\vert \le&\vert f(x,y)-f(0,y)\vert +\vert f(0,y)-f(0,0)\vert +\vert f(0,0)\vert \\ \le&\bar{M}\vert x-0\vert +L\vert y-0\vert +\vert f(0,0)\vert \\ \le&(\bar{M}+L+\vert f(0,0)\vert )(1+\vert x\vert +\vert y\vert ). \end{aligned}$$

Similarly, it can also be proved that

$$\begin{aligned} \vert g_j(x,y)\vert \le (\bar{M}+L+\vert g_j(0,0)\vert )(1+\vert x\vert +\vert y\vert ). \end{aligned}$$

Let $\bar{L}=\bar{M}+L+\vert f(0,0)\vert +\sum _{j=1}^d\vert g_j(0,0)\vert$; the proof is completed. $\square$

Based on Theorem 1 in [36], one can obtain the existence and uniqueness of the exact solution for (1) on the interval $[n,n+1), \forall n\in \mathbb {N}$, then the following existence and uniqueness of the solution holds on the whole time interval $[0,\infty )$ according to the continuity. For more details, one can also see Theorem 3.1 in [34]. Moreover, the proof of the following boundedness can be found in [37].

Lemma 2.3

Under Assumptions 2.1 and 2.2, there is a unique global solution x(t) to (1) on $t\ge 0$ with initial data $x(0)=x_0$. Moreover, for any $p\ge 2$, there is a positive constant C such that

$$\begin{aligned} \mathbb {E}\sup _{t\in [0,T]}\vert x(t)\vert ^p<C,~\forall T>0. \end{aligned}$$

Lemma 2.4

[15, 38] Let $Z_1,\dots ,Z_N:\Omega \rightarrow \mathbb {R}, N\in \mathbb {N}$ be $\mathcal {F}/\mathcal {B}(\mathbb {R})$-measurable mapping with $\mathbb {E}\vert Z_n\vert ^p\le \infty$ for all $n=1,2,\dots ,N$ and with $\mathbb {E}(Z_{n+1}\vert Z_1,\dots ,Z_n)=0$ for all $n=1,2,\dots ,N-1$. Then,

$$\begin{aligned} \Vert Z_1+\cdots +Z_n\Vert _{L^p}\le C_p(\Vert Z_1\Vert ^2_{L^p}+\cdots +\Vert Z_n\Vert ^2_{L^p})^{\frac{1}{2}}, \end{aligned}$$

for every $p\in [2,\infty )$, where $\Vert \cdot \Vert _{L^p}:=(\mathbb {E}\vert \cdot \vert ^p)^{1/p}$, $C_p$ is a constant depend on p but independent of n.

3 The Milstein scheme

Let us now define the Milstein scheme for (1). Set $\Delta =1/m$ be a given step size with integer $m\ge 1$, and let the grid points $t_k$ be defined by $t_k=k\Delta (k=0,1,\dots )$. For $x,y\in \mathbb {R}^n, j,r=1,2,\dots , d$, define

$$\begin{aligned}&L^jg_r(x,y)=\sum _{i=1}^n g_{ij}(x,y)\frac{\partial g_r(x,y)}{\partial x_i},\\&I_{rj}(k)=\int _{t_{k}}^{t_{k+1}}\int _{t_{k}}^u \text {d}B^r(v)\text {d}B^j(u). \end{aligned}$$

In this work, we only consider the SDEPCAs with diffusion coefficients $g_j$ satisfies the so-called commutativity condition $L^{j}g_r(x,y)=L^{r}g_j(x,y), j\ne r$.

Since for arbitrary $k\in \mathbb {N}$, there always exist $s\in \mathbb {N}$ and $l=0,1,2,\dots ,m-1$ such that $k=sm+l$, the discrete Milstein solution $X_{sm+l}\approx x(t_{sm+l})$ is defined by

$$\begin{aligned} X_{sm+l+1}= & {} X_{sm+l}+ f\left( X_{sm+l},X_{sm}\right) \Delta +\sum _{j=1}^dg_j\left( X_{sm+l},X_{sm}\right) \Delta B^j_{sm+l}\nonumber \\{} & {} +\sum _{j,r=1}^d L^j g_r(X_{sm+l},X_{sm}) I_{rj}(sm+l), \end{aligned}$$

(5)

where $X_0=x(0)=x_0$, $\Delta B^j_{sm+l}=B^j(t_{sm+l+1})-B^j(t_{sm+l})$. Due to $I_{rj}(k)+I_{jr}(k)=\Delta B^j_k\Delta B^r_k$ for $r\ne j$, (5) can also be written as

$$\begin{aligned} X_{sm+l+1}= & {} X_{sm+l}+ f\left( X_{sm+l},X_{sm}\right) \Delta +\sum _{j=1}^dg_j\left( X_{sm+l},X_{sm}\right) \Delta B^j_{sm+l}\nonumber \\{} & {} +\frac{1}{2}\sum _{j,r=1}^d L^j g_r(X_{sm+l},X_{sm})\Delta B^j_{sm+l}\Delta B^r_{sm+l}-\frac{1}{2}\sum _{j=1}^d L^j g_j(X_{sm+l},X_{sm})\Delta . \end{aligned}$$

(6)

Let

$$\begin{aligned} \bar{X}(t)=\sum _{sm+l=0}^{\infty }X_{sm+l}I_{[t_{sm+l},t_{sm+l+1})}(t), ~t\ge 0, \end{aligned}$$

(7)

The continuous version of scheme (5) is given by

$$\begin{aligned} X(t)= & {} X_0+\int _{0}^t f(\bar{X}(u),\bar{X}([u])) \text {d}u+\sum _{j=1}^d \int _{0}^t g_j(\bar{X}(u),\bar{X}([u])) \text {d}B^j(u) \nonumber \\{} & {} +\sum _{j,r=1}^d \int _{0}^t L^jg_r(\bar{X}(u),\bar{X}([u]))\Delta B^r(u)\text {d}B^j(u), \end{aligned}$$

(8)

where $\Delta B^r(u)=B^r(u)-B^r([u/\Delta ]\Delta )$. It can be verified that $X(t_{sm+l})=\bar{X}(t_{sm+l})=X_{sm+l}$.

Throughout this paper, let C be a generic constant that varies from one place to another and depends on p, but independent of $\Delta$.

Theorem 3.1

Let Assumptions 2.1 and 2.2 hold. Then, for any $\Delta \in (0,1]$ and $p\ge 2$, the Milstein scheme (5) has the following property:

$$\begin{aligned} \sup _{0\le t_{sm+l}\le T}\mathbb {E}\vert X_{sm+l}\vert ^p\le C, ~\forall T>0. \end{aligned}$$

Proof

For any $T>0, t_{sm+l+1}\in [0,T], s\in \mathbb {N}, l=0,1,\cdots , m-1$, according to (8), one has

$$\begin{aligned} X_{sm+l+1}=&X(t_{sm+l+1})\\ =&X(t_{sm})+\int _{t_{sm}}^{t_{sm+l+1}} f(\bar{X}(u),\bar{X}([u])) \text {d}u+\sum _{j=1}^d \int _{t_{sm}}^{t_{sm+l+1}} g_j(\bar{X}(u),\bar{X}([u])) \text {d}B^j(u)\\&+\sum _{j,r=1}^d \int _{t_{sm}}^{t_{sm+l+1}} L^jg_r(\bar{X}(u),\bar{X}([u]))\Delta B^r(u)\text {d}B^j(u). \end{aligned}$$

By the inequality $(\sum _{i=1}^n\vert a_i\vert )^p\le n^{p-1}\vert a_i\vert ^p, p\ge 1$, we have

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^p\le{} & {} 4^{p-1}\mathbb {E}\vert X_{sm}\vert ^p+4^{p-1}\mathbb {E}\left| \int _{t_{sm}}^{t_{sm+l+1}} f(\bar{X}(u),\bar{X}([u])) \text {d}u\right| ^p \nonumber \\{} & {} +(4d)^{p-1}\sum _{j=1}^d\mathbb {E}\left| \int _{t_{sm}}^{t_{sm+l+1}} g_j(\bar{X}(u),\bar{X}([u])) \text {d}B^j(u)\right| ^p \nonumber \\{} & {} +(4dr)^{p-1}\sum _{j,r=1}^d\mathbb {E}\left| \int _{t_{sm}}^{t_{sm+l+1}} L^jg_r(\bar{X}(u),\bar{X}([u]))\Delta B^r(u)\text {d}B^j(u)\right| ^p. \end{aligned}$$

(9)

According to Hölder’s inequality and the Burkholder-Davis-Gundy (B-D-G) inequality, we can deduce that

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^p\le{} & {} C\mathbb {E}\vert X_{sm}\vert ^p+C((l+1)\Delta )^{p-1}\mathbb {E}\int _{t_{sm}}^{t_{sm+l+1}}\left| f(\bar{X}(u),\bar{X}([u])) \right| ^p\text {d}u \nonumber \\{} & {} +C((l+1)\Delta )^{\frac{p-2}{2}}\sum _{j=1}^d\mathbb {E}\int _{t_{sm}}^{t_{sm+l+1}}\left| g_j(\bar{X}(u),\bar{X}([u])) \right| ^p\text {d}u \nonumber \\{} & {} +C((l+1)\Delta )^{\frac{p-2}{2}}\sum _{j,r=1}^d\mathbb {E}\int _{t_{sm}}^{t_{sm+l+1}}\left| L^jg_r(\bar{X}(u),\bar{X}([u]))\Delta B^r(u)\right| ^p\text {d}u \nonumber \\ \le{} & {} C\mathbb {E}\vert X_{sm}\vert ^p+C\sum _{i=0}^l\mathbb {E}\int _{t_{sm+i}}^{t_{sm+i+1}}\left| f(X_{sm+i},X_{sm}) \right| ^p\text {d}u \nonumber \\{} & {} +C\sum _{j=1}^d\sum _{i=0}^l\mathbb {E}\int _{t_{sm+i}}^{t_{sm+i+1}}\left| g_j(X_{sm+i},X_{sm}) \right| ^p\text {d}u \nonumber \\{} & {} +C\sum _{j,r=1}^d\sum _{i=0}^l\mathbb {E}\int _{t_{sm+i}}^{t_{sm+i+1}}\left| L^jg_r(X_{sm+i},X_{sm})\Delta B^r(u)\right| ^p\text {d}u \nonumber \\ \le{} & {} C\mathbb {E}\vert X_{sm}\vert ^p+C\Delta \sum _{i=0}^l\mathbb {E}\left| f(X_{sm+i},X_{sm}) \right| ^p+C\Delta \sum _{j=1}^d\sum _{i=0}^l\mathbb {E}\left| g_j(X_{sm+i},X_{sm}) \right| ^p \nonumber \\{} & {} +C\sum _{j,r=1}^d\sum _{i=0}^l\mathbb {E}\vert L^jg_r(X_{sm+i},X_{sm})\vert ^p\int _{t_{sm+i}}^{t_{sm+i+1}}\mathbb {E}\left| \int _{t_{sm+i}}^u\text {d}B^r(v)\right| ^p\text {d}u, \end{aligned}$$

(10)

in the last inequality we use the fact that $L^jg_r(X_{sm+i},X_{sm})$ is $\mathcal {F}_{t_{sm+i}}$-measurable, while $\Delta B^r(u)=B^r(u)-B^r(t_{sm+i})$ is $\mathcal {F}_{t_{sm+i}}$-independent. Applying the B-D-G inequality again, together with (4), we can arrive at

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^p\le{} & {} C\mathbb {E}\vert X_{sm}\vert ^p+C\Delta \left( l+1+\sum _{i=0}^l\mathbb {E}\vert X_{sm+i}\vert ^p+(l+1)\mathbb {E}\vert X_{sm}\vert ^p\right) \nonumber \\{} & {} +C\sum _{j,r=1}^d\sum _{i=0}^l\mathbb {E}\vert L^jg_r(X_{sm+i},X_{sm})\vert ^p\int _{t_{sm+i}}^{t_{sm+i+1}} \Delta ^{\frac{p}{2}}\text {d}u\nonumber \\ \le{} & {} C\mathbb {E}\vert X_{sm}\vert ^p+C+C\Delta \sum _{i=0}^l\mathbb {E}\vert X_{sm+i}\vert ^p+C\mathbb {E}\vert X_{sm}\vert ^p\nonumber \\{} & {} +C\Delta ^{\frac{p}{2}+1}\sum _{j,r=1}^d\sum _{i=0}^l\mathbb {E}\left| \sum _{k=1}^ng_{kj}(X_{sm+i},X_{sm})\frac{\partial g_r(X_{sm+i},X_{sm})}{\partial x_k}\right| ^p. \end{aligned}$$

(11)

According to Assumption 2.1 and (4), one can obtain

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^p\le{} & {} C\mathbb {E}\vert X_{sm}\vert ^p+C+C\Delta \sum _{i=0}^l\mathbb {E}\vert X_{sm+i}\vert ^p \nonumber \\{} & {} +CdM^pn^{p-1}\Delta ^{\frac{p}{2}+1}\sum _{j=1}^d\sum _{i=0}^l\sum _{k=1}^n\mathbb {E}\left| g_{kj}(X_{sm+i},X_{sm})\right| ^p \nonumber \\ \le{} & {} C\mathbb {E}\vert X_{sm}\vert ^p+C+C\Delta \sum _{i=0}^l\mathbb {E}\vert X_{sm+i}\vert ^p \nonumber \\{} & {} +Cd^2M^pn^{p}L\Delta ^{\frac{p}{2}+1}\left( l+1+\sum _{i=0}^l\mathbb {E}\vert X_{sm+i}\vert ^p+(l+1)\mathbb {E}\vert X_{sm}\vert ^p\right) \nonumber \\ \le{} & {} C\mathbb {E}\vert X_{sm}\vert ^p+C+C\Delta \sum _{i=0}^l\mathbb {E}\vert X_{sm+i}\vert ^p. \end{aligned}$$

(12)

By the discrete Gronwall inequality, we have

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^p\le C(1+\mathbb {E}\vert X_{sm}\vert ^p)e^{C(l+1)\Delta }, \end{aligned}$$

hence

$$\begin{aligned} 1+\mathbb {E}\vert X_{sm+l+1}\vert ^p\le C(1+\mathbb {E}\vert X_{sm}\vert ^p). \end{aligned}$$

In particular, take $l=m-1$, it is easy to see that

$$\begin{aligned} 1+\mathbb {E}\vert X_{(s+1)m}\vert ^p\le C(1+\mathbb {E}\vert X_{sm}\vert ^p). \end{aligned}$$

Then,

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^p\le C(1+\mathbb {E}\vert X_{sm}\vert ^p)\le C^2(1+\mathbb {E}\vert X_{(s-1)m}\vert ^p)\le \cdots \le C^{s+1}(1+\vert X_0\vert ^p). \end{aligned}$$

Consequently, for any $T>0, t_{sm+l}\in [0,T]$, one can deduce that

$$\begin{aligned} \mathbb {E}\vert X_{sm+l}\vert ^p\le C^{[T]+1}(1+\vert X_0\vert ^p)\le C. \end{aligned}$$

The proof is completed. $\square$

Lemma 3.2

Let Assumptions 2.1 and 2.2 hold. Then, for any $T>0, \Delta \in (0,1]$ and $p\ge 2$,

$$\begin{aligned} \sup _{0\le t\le T}\mathbb {E}\vert X(t)-\bar{X}(t)\vert ^p\le C\Delta ^{p/2},\quad \sup _{0\le t\le T}\mathbb {E}\vert X(t)\vert ^p\le C. \end{aligned}$$

Proof

For any $t\in [0,T]$, there are always $s\in \mathbb {N}$ and $l=0,1,\dots ,m-1$ such that $t\in [t_{sm+l},t_{sm+l+1})$, by (7) and (8), one has

$$\begin{aligned} \mathbb {E}\vert X(t)-\bar{X}(t)\vert ^p\le&3^{p-1}\mathbb {E}\left| \int _{t_{sm+l}}^t f(X_{sm+l},X_{sm}) \text {d}u\right| ^p\\&+3^{p-1}\mathbb {E}\left| \sum _{j=1}^d \int _{t_{sm+l}}^t g_j(X_{sm+l},X_{sm}) \text {d}B^j(u)\right| ^p\\&+3^{p-1}\mathbb {E}\left| \sum _{j,r=1}^d \int _{t_{sm+l}}^t L^jg_r(X_{sm+l},X_{sm})\Delta B^r(u)\text {d}B^j(u)\right| ^p. \end{aligned}$$

Similar to the process of (9)-(12), applying Hölder’s inequality, the B-D-G inequality, Assumption 2.1, (4), and Theorem 3.1, one can arrive at

$$\begin{aligned} \mathbb {E}\vert X(t)-\bar{X}(t)\vert ^p\le&C\Delta ^{p}\mathbb {E}\left| f(X_{sm+l},X_{sm}) \right| ^p+C\Delta ^{\frac{p}{2}}\sum _{j=1}^d\mathbb {E} \left| g_j(X_{sm+l},X_{sm}) \right| ^p\\&+C\Delta ^{\frac{p-2}{2}}\sum _{j,r=1}^d\mathbb {E}\vert L^jg_r(X_{sm+l},X_{sm})\vert ^p\int _{t_{sm+l}}^t\mathbb {E}\left| \int _{t_{sm+l}}^u \text {d}B^r(v)\right| ^p\text {d}u\\ \le&C\Delta ^{p}(1+\mathbb {E}\vert X_{sm+l}\vert ^p+\mathbb {E}\vert X_{sm}\vert ^p) +C\Delta ^{\frac{p}{2}}(1+\mathbb {E}\vert X_{sm+l}\vert ^p+\mathbb {E}\vert X_{sm}\vert ^p) \\&+C\Delta ^{p}\sum _{j,r=1}^d\mathbb {E}\left| \sum _{k=1}^ng_{kj}(X_{sm+l},X_{sm})\frac{\partial g_r(X_{sm+l},X_{sm})}{\partial x_k}\right| ^p\\ \le&C\Delta ^{\frac{p}{2}}(1+\mathbb {E}\vert X_{sm+l}\vert ^p+\mathbb {E}\vert X_{sm}\vert ^p) +C\Delta ^{p}\sum _{j,r=1}^d\sum _{k=1}^n\mathbb {E}\left| g_{kj}(X_{sm+l},X_{sm})\right| ^p\\ \le&C\Delta ^{\frac{p}{2}}(1+\mathbb {E}\vert X_{sm+l}\vert ^p+\mathbb {E}\vert X_{sm}\vert ^p) \\ \le&C\Delta ^{\frac{p}{2}}. \end{aligned}$$

Moreover, it is easy to see that

$$\begin{aligned} \mathbb {E}\vert X(t)\vert ^p\le 2^{p-1}\mathbb {E}\vert \bar{X}(t)\vert ^p+2^{p-1}\mathbb {E}\vert X(t)-\bar{X}(t)\vert ^p\le 2^{p-1}\sup _{0\le t_{sm+l}\le T}\mathbb {E}\vert X_{sm+l}\vert ^p+C\Delta ^{\frac{p}{2}}\le C. \end{aligned}$$

$\square$

4 Strong convergence rate of the Milstein scheme

In the following, we sometimes use the notation $(\Phi )_i$ to denote the i-th component of $\Phi \in \mathbb {R}^n$. Let $\varphi :\mathbb {R}^n\times \mathbb {R}^n\rightarrow \mathbb {R}^n$ be twice differentiable with respect to the first component, then according to the Taylor formula,

$$\begin{aligned} \varphi (x,y)-\varphi (\bar{x},y)=\sum _{i=1}^n\frac{\partial \varphi (\bar{x},y)}{\partial x_i}(x-\bar{x})_i+R(\varphi )(x-\bar{x}) \end{aligned}$$

for $x,y,\bar{x}\in \mathbb {R}^n$, where

$$\begin{aligned} R(\varphi )(x-\bar{x})=\frac{1}{2}\sum _{i,j=1}^n\frac{\partial ^2\varphi (\bar{x}+\theta (x-\bar{x}),y)}{\partial x_i\partial x_j}(x-\bar{x})_i(x-\bar{x})_j, \end{aligned}$$

with $\theta \in (0,1)$. Note that $X([t])=\bar{X}([t])$ for all $t\ge 0$, hence

$$\begin{aligned} \varphi (X(t),X([t]))-\varphi (\bar{X}(t),\bar{X}([t]))=\sum _{i=1}^n\frac{\partial \varphi (\bar{X}(t),\bar{X}([t]))}{\partial x_i}(X(t)-\bar{X}(t))_i+R(\varphi )(X(t)-\bar{X}(t)) \end{aligned}$$

(13)

with

$$\begin{aligned} R(\varphi )(X(t)-\bar{X}(t))=\frac{1}{2}\sum _{i,j=1}^n\frac{\partial ^2\varphi (\bar{X}(t)+\theta (X(t)-\bar{X}(t)),\bar{X}([t]))}{\partial x_i\partial x_j}(X(t)-\bar{X}(t))_i(X(t)-\bar{X}(t))_j. \end{aligned}$$

Applying (7) and (8), let $\kappa (t)=[t/\Delta ]\Delta$, one has

$$\begin{aligned} (X(t)-\bar{X}(t))_i=&\int _{\kappa (t)}^t f_i(\bar{X}(u),\bar{X}([u])) \text {d}u+\sum _{k=1}^d\int _{\kappa (t)}^t g_{ik}(\bar{X}(u),\bar{X}([u])) \text {d}B^k(u)\\&+\sum _{k,r=1}^d \int _{\kappa (t)}^t \left( L^kg_r(\bar{X}(u),\bar{X}([u]))\right) _i\Delta B^r(u)\text {d}B^k(u). \end{aligned}$$

Define

$$\begin{aligned}{} & {} \bar{R}(\varphi )(X(t)-\bar{X}(t)):=R(\varphi )(X(t)-\bar{X}(t))+\sum _{i=1}^n\frac{\partial \varphi (\bar{X}(t),\bar{X}([t]))}{\partial x_i} \int _{\kappa (t)}^t f_i(\bar{X}(u),\bar{X}([u])) \text {d}u \nonumber \\{} & {} +\sum _{i=1}^n\frac{\partial \varphi (\bar{X}(t),\bar{X}([t]))}{\partial x_i}\sum _{k,r=1}^d \int _{\kappa (t)}^t \left( L^kg_r(\bar{X}(u),\bar{X}([u]))\right) _i\Delta B^r(u)\text {d}B^k(u), \end{aligned}$$

(14)

which gives

$$\begin{aligned}{} & {} \varphi (X(t),X([t]))-\varphi (\bar{X}(t),\bar{X}([t])) \nonumber \\{} & {} \quad =\sum _{i=1}^n\frac{\partial \varphi (\bar{X}(t),\bar{X}([t]))}{\partial x_i}\sum _{k=1}^d\int _{\kappa (t)}^t g_{ik}(\bar{X}(u),\bar{X}([u])) \text {d}B^k(u)\nonumber \\{} & {} \quad +\bar{R}(\varphi )(X(t)-\bar{X}(t)). \end{aligned}$$

(15)

Lemma 4.1

Let Assumptions 2.1 and 2.2 hold. Then, for any $T>0, \Delta \in (0,1]$, and $p\ge 2$,

$$\begin{aligned} \mathbb {E}\vert R(\varphi )(X(t)-\bar{X}(t))\vert ^p\vee \mathbb {E}\vert \bar{R}(\varphi )(X(t)-\bar{X}(t))\vert ^p\le C\Delta ^{p},~\forall t\in [0,T] \end{aligned}$$

for $\varphi =f, g_j$, $j=1,2,\dots ,d$.

Proof

Take $\varphi =f$, for any $t\in [0,T]$, using Hölder’s inequality, one has

$$\begin{aligned}&\mathbb {E}\vert R(f)(X(t)-\bar{X}(t))\vert ^p\\ =&\mathbb {E}\bigg \vert \frac{1}{2} \sum _{i,r=1}^n \frac{\partial ^2 f(\bar{X}(t)+\theta (X(t)-\bar{X}(t)),\bar{X}([t]))}{\partial x_i\partial x_r}(X(t)-\bar{X}(t))_i(X(t)-\bar{X}(t))_r\bigg \vert ^p\\ \le&n^{2(p-1)}\sum _{i,r=1}^n\mathbb {E}\bigg \vert \frac{\partial ^2 f(\bar{X}(t)+\theta (X(t)-\bar{X}(t)),\bar{X}([t]))}{\partial x_i\partial x_r}(X(t)-\bar{X}(t))_i(X(t)-\bar{X}(t))_r\bigg \vert ^p\\ \le&n^{2(p-1)}\sum _{i,r=1}^n\left( \mathbb {E}\bigg \vert \frac{\partial ^2 f(\bar{X}(t)+\theta (X(t)-\bar{X}(t)),\bar{X}([t]))}{\partial x_i\partial x_r}\bigg \vert ^{2p}\right) ^{1/2}\\&\times \left( \mathbb {E}\vert (X(t)-\bar{X}(t))_i\vert ^{4p}\right) ^{1/4}\left( \mathbb {E}\vert (X(t)-\bar{X}(t))_r\vert ^{4p}\right) ^{1/4}.\\ \end{aligned}$$

By Assumption 2.1 and Lemma 3.2, one can obtain that

$$\begin{aligned} \mathbb {E}\vert R(f)(X(t)-\bar{X}(t))\vert ^p\le n^{2p}M^p\left( \mathbb {E}\vert X(t)-\bar{X}(t)\vert ^{4p}\right) ^{1/2}\le C\Delta ^p. \end{aligned}$$

(16)

Moreover, recall that for any $t\in [0,T]$, there always exist $s\in \mathbb {N}$ and $l=0,1,\dots ,m-1$ such that $t\in [t_{sm+l},t_{sm+l+1})$, which gives $\kappa (t)=t_{sm+l}$, hence

$$\begin{aligned}{} & {} \mathbb {E}\vert \bar{R}(f)(X(t)-\bar{X}(t))\vert ^p \nonumber \\\le & {} 3^{p-1}\mathbb {E}\vert R(f)(X(t)-\bar{X}(t))\vert ^p+3^{p-1}\mathbb {E}\left| \sum _{i=1}^n\frac{\partial f(\bar{X}(t),\bar{X}([t]))}{\partial x_i} \int _{t_{sm+l}}^t f_i(\bar{X}(u),\bar{X}([u])) \text {d}u\right| ^p \nonumber \\{} & {} +3^{p-1}\mathbb {E}\left| \sum _{i=1}^n\frac{\partial f(\bar{X}(t),\bar{X}([t]))}{\partial x_i}\sum _{k,r=1}^d \int _{t_{sm+l}}^t \left( L^kg_r(\bar{X}(u),\bar{X}([u]))\right) _i\Delta B^r(u)\text {d}B^k(u)\right| ^p \nonumber \\= & {} 3^{p-1}\mathbb {E}\vert R(f)(X(t)-\bar{X}(t))\vert ^p+3^{p-1}\mathbb {E}\left| \sum _{i=1}^n\frac{\partial f(X_{sm+l},X_{sm})}{\partial x_i} \int _{t_{sm+l}}^t f_i(X_{sm+l},X_{sm}) \text {d}u\right| ^p \nonumber \\{} & {} +3^{p-1}\mathbb {E}\left| \sum _{i=1}^n\frac{\partial f(X_{sm+l},X_{sm})}{\partial x_i}\sum _{k,r=1}^d \int _{t_{sm+l}}^t \left( L^kg_r(X_{sm+l},X_{sm})\right) _i\Delta B^r(u)\text {d}B^k(u)\right| ^p. \end{aligned}$$

(17)

Using Assumption 2.1, Hölder’s inequality, (4) and Theorem 3.1, one can deduce that

$$\begin{aligned}{} & {} \mathbb {E}\left| \sum _{i=1}^n\frac{\partial f(X_{sm+l},X_{sm})}{\partial x_i} \int _{t_{sm+l}}^t f_i(X_{sm+l},X_{sm}) \text {d}u\right| ^p \nonumber \\ \le{} & {} n^{p-1}\sum _{i=1}^n\mathbb {E}\left| \frac{\partial f(X_{sm+l},X_{sm})}{\partial x_i} \int _{t_{sm+l}}^t f_i(X_{sm+l},X_{sm}) \text {d}u\right| ^p \nonumber \\ \le{} & {} n^{p-1}M^p\sum _{i=1}^n\mathbb {E}\left| \int _{t_{sm+l}}^t f_i(X_{sm+l},X_{sm}) \text {d}u\right| ^p \nonumber \\ \le{} & {} n^{p-1}M^p\Delta ^{p-1}\sum _{i=1}^n\mathbb {E}\int _{t_{sm+l}}^t \left| f_i(X_{sm+l},X_{sm})\right| ^p \text {d}u \nonumber \\ \le{} & {} C\Delta ^{p-1}\int _{t_{sm+l}}^t (1+\mathbb {E}\vert X_{sm+l}\vert ^p+\mathbb {E}\vert X_{sm}\vert ^p)\text {d}u \nonumber \\ \le{} & {} C\Delta ^{p}. \end{aligned}$$

(18)

Similarly, applying Assumption 2.1 and the B-D-G inequality, it yields

$$\begin{aligned}{} & {} \mathbb {E}\left| \sum _{i=1}^n\frac{\partial f(X_{sm+l},X_{sm})}{\partial x_i}\sum _{k,r=1}^d \int _{t_{sm+l}}^t \left( L^kg_r(X_{sm+l},X_{sm})\right) _i\Delta B^r(u)\text {d}B^k(u)\right| ^p \nonumber \\ \le{} & {} n^{p-1}d^{2(p-1)}M^p\sum _{i=1}^n\sum _{k,r=1}^d\mathbb {E}\left| \int _{t_{sm+l}}^t \left( L^kg_r(X_{sm+l},X_{sm})\right) _i\Delta B^r(u)\text {d}B^k(u)\right| ^p\nonumber \\ \le{} & {} n^{p-1}d^{2(p-1)}M^p\sum _{i=1}^n\sum _{k,r=1}^d C\Delta ^{\frac{p-2}{2}}\mathbb {E}\int _{t_{sm+l}}^t \left| \left( L^kg_r(X_{sm+l},X_{sm})\right) _i\Delta B^r(u) \right| ^p\text {d}u\nonumber \\ \le{} & {} C\Delta ^{\frac{p-2}{2}}\sum _{i=1}^n\sum _{k,r=1}^d \int _{t_{sm+l}}^t \mathbb {E}\left| \left( L^kg_r(X_{sm+l},X_{sm})\right) _i\right| ^{p}\mathbb {E}\left| \int _{t_{sm+l}}^u\text {d}B^r(v) \right| ^{p}\text {d}u. \end{aligned}$$

(19)

According to the definition of $L^kg_r(X_{sm+l},X_{sm})$, using Assumptions 2.1, 2.2, and Theorem 3.1, we can know that

$$\begin{aligned} \mathbb {E}\left| \left( L^kg_r(X_{sm+l},X_{sm})\right) _i\right| ^{p}\le{} & {} \left( \mathbb {E}\left| L^kg_r(X_{sm+l},X_{sm})\right| ^{2p}\right) ^{1/2} \nonumber \\ \le{} & {} \left( \mathbb {E}\left| \sum _{i=1}^n g_{ik}(X_{sm+l},X_{sm})\frac{\partial g_r(X_{sm+l},X_{sm})}{\partial x_i}\right| ^{2p}\right) ^{1/2} \nonumber \\ \end{aligned}$$

$$\begin{aligned} \le{} & {} n^{\frac{2p-1}{2}}M^p\left( \sum _{i=1}^n\mathbb {E}\left| g_{ik}(X_{sm+l},X_{sm})\right| ^{2p}\right) ^{1/2} \nonumber \\ \le{} & {} C\left( 1+\mathbb {E}\vert X_{sm+l}\vert ^{2p}+\mathbb {E}\vert X_{sm}\vert ^{2p}\right) ^{1/2} \nonumber \\ \le{} & {} C. \end{aligned}$$

(20)

Substituting (20) into (19), with the help of B-D-G inequality again, we can obtain that

$$\begin{aligned}{} & {} \mathbb {E}\left| \sum _{i=1}^n\frac{\partial f(X_{sm+l},X_{sm})}{\partial x_i}\sum _{k,r=1}^d \int _{t_{sm+l}}^t \left( L^kg_r(X_{sm+l},X_{sm})\right) _i\Delta B^r(u)\text {d}B^k(u)\right| ^p \nonumber \\ \le{} & {} C\Delta ^{\frac{p-2}{2}}\sum _{r=1}^d \int _{t_{sm+l}}^t \mathbb {E}\left| \int _{t_{sm+l}}^u\text {d}B^r(v) \right| ^{p}\text {d}u \nonumber \\ \le{} & {} C\Delta ^p. \end{aligned}$$

(21)

Combining (16), (17), (18), and (21) yields

$$\begin{aligned} \mathbb {E}\vert \bar{R}(f)(X(t)-\bar{X}(t))\vert ^p\le C\Delta ^p,\quad \forall t\in [0,T]. \end{aligned}$$

Repeating the process above, we can also prove

$$\begin{aligned} \mathbb {E}\vert R(g_j)(X(t)-\bar{X}(t))\vert ^p\vee \mathbb {E}\vert \bar{R}(g_j)(X(t)-\bar{X}(t))\vert ^p\le C\Delta ^p,\quad \forall t\in [0,T] \end{aligned}$$

for all $j=1,2,\dots ,d$. $\square$

Theorem 4.2

Let Assumptions 2.1 and 2.2 hold. Then, for any $\Delta \in (0,1]$ and $p>0$,

$$\begin{aligned} \mathbb {E}\sup _{0\le t\le T}\vert x(t)-X(t)\vert ^p\le C\Delta ^{p},~\forall T>0. \end{aligned}$$

Proof

For any $t\in [0,T]$ and $p\ge 2$, according to (1) and (8), using Itô’s formula, we can arrive at

$$\begin{aligned} \vert x(t)-X(t)\vert ^p\le&\int _0^t p\vert x(u)-X(u)\vert ^{p-2}\left( (x(u)-X(u))^TF(u)+\frac{p-1}{2}\sum _{j=1}^d\vert G_j(u)\vert ^2\right) \text {d}u\\&+\sum _{j=1}^d \int _0^t p\vert x(u)-X(u)\vert ^{p-2}(x(u)-X(u))^TG_j(u)\text {d}B^j(u), \end{aligned}$$

where

$$\begin{aligned} F(u)=f(x(u),x([u]))-f(\bar{X}(u),\bar{X}([u])), \end{aligned}$$

$$\begin{aligned} G_j(u)=g_j(x(u),x([u]))-g_j(\bar{X}(u),\bar{X}([u]))-\sum _{r=1}^{d}L^jg_r(\bar{X}(u),\bar{X}([u]))\Delta B^r(u). \end{aligned}$$

Then, for any $T_1\in [0,T]$,

$$\begin{aligned} \mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^p\le \sum _{i=1}^6 A_i, \end{aligned}$$

(22)

where

$$\begin{aligned} A_1=&p\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\left( x(t)-X(t)\right) ^\text {T}\left( f(x(t),x([t]))-f(X(t),X([t]))\right) \text {d}t,\\ A_2=&p\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\left( x(t)-X(t)\right) ^\text {T}\left( f(X(t),X([t]))-f(\bar{X}(t),\bar{X}([t]))\right) \text {d}t,\\ A_3=&p(p-1)\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\sum _{j=1}^d \vert g_j(x(t),x([t]))-g_j(X(t),X([t]))\vert ^2\text {d}t,\\ A_4=&p(p-1)\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\sum _{j=1}^d \Bigg \vert g_j(X(t),X([t]))-g_j(\bar{X}(t),\bar{X}([t]))\\&-\sum _{r=1}^{d}L^jg_r(\bar{X}(t),\bar{X}([t]))\Delta B^r(t)\Bigg \vert ^2\text {d}t,\\ A_5=&p\sum _{j=1}^d\mathbb {E}\sup _{0\le t\le T_1}\int _0^t \vert x(u)-X(u)\vert ^{p-2}\left( x(u)-X(u)\right) ^\text {T}\\&\times \left( g_j(x(u),x([u]))-g_j(X(u),X([u]))\right) \text {d}B^j(u),\\ A_6=&p\sum _{j=1}^d\mathbb {E}\sup _{0\le t\le T_1}\int _0^t \vert x(u)-X(u)\vert ^{p-2}\left( x(u)-X(u)\right) ^\text {T}\\&\times \bigg (g_j(X(u),X([u]))-g_j(\bar{X}(u),\bar{X}([u]))-\sum _{r=1}^{d}L^jg_r(\bar{X}(u),\bar{X}([u]))\Delta B^r(u)\bigg )\text {d}B^j(u). \end{aligned}$$

Applying Young’s inequality, (2) and (3), it is easy to get that

$$\begin{aligned} A_1\le{} & {} p\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-1}\left| f(x(t),x([t]))-f(X(t),X([t]))\right| \text {d}t \nonumber \\ \le{} & {} (p-1)\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p}\text {d}t+ \mathbb {E}\int _0^{T_1}\left| f(x(t),x([t]))-f(X(t),X([t]))\right| ^p\text {d}t \nonumber \\ \le{} & {} C\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p}\text {d}t+C\mathbb {E}\int _0^{T_1} \vert x([t])-X([t])\vert ^{p}\text {d}t \nonumber \\ \le{} & {} C\int _0^{T_1} \left( \mathbb {E}\sup _{0\le u\le t}\vert x(u)-X(u)\vert ^{p}\right) \text {d}t. \end{aligned}$$

(23)

Similarly, we can also get

$$\begin{aligned} A_3= & {} p(p-1)\sum _{j=1}^d\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2} \vert g_j(x(t),x([t]))-g_j(X(t),X([t]))\vert ^2\text {d}t \nonumber \\\le & {} (p-1)(p-2)\sum _{j=1}^d\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p}\text {d}t \nonumber \\{} & {} + 2(p-1)\sum _{j=1}^d\mathbb {E}\int _0^{T_1}\left| g_j(x(t),x([t]))-g_j(X(t),X([t]))\right| ^p\text {d}t \nonumber \\\le & {} C\int _0^{T_1} \left( \mathbb {E}\sup _{0\le u\le t}\vert x(u)-X(u)\vert ^{p}\right) \text {d}t. \end{aligned}$$

(24)

Next, we give an estimation for $A_4$. According to (15), we have

$$\begin{aligned}&g_j(X(t),X([t]))-g_j(\bar{X}(t),\bar{X}([t]))\\&=\sum _{i=1}^n\frac{\partial g_j(\bar{X}(t),\bar{X}([t]))}{\partial x_i}\sum _{k=1}^d\int _{\kappa (t)}^t g_{ik}(\bar{X}(u),\bar{X}([u])) \text {d}B^k(u)+\bar{R}(g_j)(X(t)-\bar{X}(t)). \end{aligned}$$

Recall that $L^{j}g_k(x,y)=L^{k}g_j(x,y)$, we have

$$\begin{aligned}{} & {} \sum _{i=1}^n\frac{\partial g_j(\bar{X}(t),\bar{X}([t]))}{\partial x_i}\sum _{k=1}^d\int _{\kappa (t)}^tg_{ik}(\bar{X}(u),\bar{X}([u])) \text {d}B^k(u) \nonumber \\= & {} \sum _{k=1}^d \sum _{i=1}^ng_{ik}(\bar{X}(t),\bar{X}([t]))\frac{\partial g_j(\bar{X}(t),\bar{X}([t]))}{\partial x_i} \int _{\kappa (t)}^t\text {d}B^k(u) \nonumber \\= & {} \sum _{k=1}^d L^k g_j(\bar{X}(t),\bar{X}([t]))\int _{\kappa (t)}^t\text {d}B^k(u)\nonumber \\= & {} \sum _{k=1}^d L^j g_k(\bar{X}(t),\bar{X}([t]))\Delta B^k(t). \end{aligned}$$

(25)

Hence,

$$\begin{aligned} g_j(X(t),X([t]))- & {} g_j(\bar{X}(t),\bar{X}([t]))=\sum _{k=1}^d L^j g_k(\bar{X}(t),\bar{X}([t]))\Delta B^k(t)\nonumber \\+ & {} \bar{R}(g_j)(X(t)-\bar{X}(t)), \end{aligned}$$

(26)

and then

$$\begin{aligned} A_4= & {} p(p-1)\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\sum _{j=1}^d \left| \bar{R}(g_j)(X(t)-\bar{X}(t))\right| ^2\text {d}t \nonumber \\\le & {} (p-1)(p-2)\sum _{j=1}^d\mathbb {E}\int _0^{T_1}\vert x(t)-X(t)\vert ^{p}\text {d}t+2(p-1)\sum _{j=1}^d\mathbb {E}\int _0^{T_1}\left| \bar{R}(g_j)(X(t)-\bar{X}(t))\right| ^p\text {d}t \nonumber \\\le & {} C\mathbb {E}\int _0^{T_1}\vert x(t)-X(t)\vert ^{p}\text {d}t+C\int _0^{T_1}\mathbb {E}\left| \bar{R}(g_j)(X(t)-\bar{X}(t))\right| ^p\text {d}t \nonumber \\\le & {} C\int _0^{T_1}\left( \mathbb {E}\sup _{0\le u\le t}\vert x(u)-X(u)\vert ^{p}\right) \text {d}t+C\Delta ^p. \end{aligned}$$

(27)

Using the B-D-G inequality, fundamental inequality $2ab\le a^2+b^2$, (2), and (3), one sees that

$$\begin{aligned} A_5\le{} & {} C\sum _{j=1}^d\mathbb {E}\left( \int _0^{T_1} \vert x(t)-X(t)\vert ^{2p-2}\vert g_j(x(t),x([t]))-g_j(X(t),X([t]))\vert ^2\text {d}t\right) ^{\frac{1}{2}} \nonumber \\ \le{} & {} C\sum _{j=1}^d\mathbb {E}\left( \sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\vert g_j(x(t),x([t]))-g_j(X(t),X([t]))\vert ^2\text {d}t\right) ^{\frac{1}{2}}\nonumber \\ \le{} & {} \frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}\nonumber \\+ & {} C\sum _{j=1}^d\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\vert g_j(x(t),x([t]))-g_j(X(t),X([t]))\vert ^2\text {d}t \nonumber \\ \le{} & {} \frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p}\text {d}t\nonumber \\+ & {} C\sum _{j=1}^d\mathbb {E}\int _0^{T_1}\vert g_j(x(t),x([t]))-g_j(X(t),X([t]))\vert ^p\text {d}t\nonumber \\ \le{} & {} \frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\int _0^{T_1}\left( \sup _{0\le u\le t}\mathbb {E} \vert x(u)-X(u)\vert ^{p}\right) \text {d}t. \end{aligned}$$

(28)

Applying the B-D-G inequality again, with the help of (26) and Lemma 4.1, it can be derived that

$$\begin{aligned} A_6\le{} & {} p\sum _{j=1}^d\mathbb {E}\sup _{0\le t\le T_1}\int _0^t \vert x(u)-X(u)\vert ^{p-1}\vert \bar{R}(g_j)(X(u)-\bar{X}(u))\vert \text {d}B^j(u) \nonumber \\ \le{} & {} C\sum _{j=1}^d\mathbb {E}\left( \int _0^{T_1}\vert x(t)-X(t)\vert ^{2p-2}\vert \bar{R}(g_j)(X(t)-\bar{X}(t))\vert ^2\text {d}t\right) ^{\frac{1}{2}}\nonumber \\ \le{} & {} C\sum _{j=1}^d\mathbb {E}\left( \sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}\int _0^{T_1}\vert x(t)-X(t)\vert ^{p-2}\vert \bar{R}(g_j)(X(t)-\bar{X}(t))\vert ^2\text {d}t\right) ^{\frac{1}{2}}\nonumber \\ \end{aligned}$$

$$\begin{aligned} \le{} & {} \frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\sum _{j=1}^d\mathbb {E}\int _0^{T_1}\vert x(t)-X(t)\vert ^{p-2}\vert \bar{R}(g_j)(X(t)-\bar{X}(t))\vert ^2\text {d}t\nonumber \\ \le{} & {} \frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\mathbb {E}\int _0^{T_1}\vert x(t)-X(t)\vert ^{p}\text {d}t\nonumber \\{} & {} +C\sum _{j=1}^d\int _0^{T_1}\mathbb {E}\vert \bar{R}(g_j)(X(t)-\bar{X}(t))\vert ^p\text {d}t\nonumber \\ \le{} & {} \frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\int _0^{T_1}\left( \mathbb {E}\sup _{0\le u\le t}\vert x(u)-X(u)\vert ^{p}\right) \text {d}t+C\Delta ^p. \end{aligned}$$

(29)

In the following, we give an estimation for $A_2$. According to (15),

$$\begin{aligned} f(X(t),X([t]))-f(\bar{X}(t),\bar{X}([t]))=\phi (\bar{X}(t),\bar{X}([t]))+\bar{R}(f)(X(t)-\bar{X}(t)), \end{aligned}$$

where

$$\begin{aligned} \phi (\bar{X}(t),\bar{X}([t])):=\sum _{i=1}^n\frac{\partial f(\bar{X}(t),\bar{X}([t]))}{\partial x_i}\sum _{k=1}^d\int _{\kappa (t)}^t g_{ik}(\bar{X}(u),\bar{X}([u])) \text {d}B^k(u). \end{aligned}$$

Using Hölder’s inequality and Lemma 4.1, one has

$$\begin{aligned} A_2= & {} p\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\left( x(t)-X(t)\right) ^\text {T}\left( f(X(t),X([t]))-f(\bar{X}(t),\bar{X}([t]))\right) \text {d}t \nonumber \\\le & {} B+p\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-1}\vert \bar{R}(f)(X(t)-\bar{X}(t))\vert \text {d}t \nonumber \\\le & {} B+(p-1)\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^p\text {d}t+\int _0^{T_1}\mathbb {E}\vert \bar{R}(f)(X(t)-\bar{X}(t))\vert ^p\text {d}t \nonumber \\\le & {} B+(p-1)\int _0^{T_1} \left( \mathbb {E}\sup _{0\le u\le t}\vert x(u)-X(u)\vert ^p\right) \text {d}t+C\Delta ^p, \end{aligned}$$

(30)

where

$$\begin{aligned} B= p\mathbb {E}\int _0^{T_1} \vert x(t)-X(t)\vert ^{p-2}\left( x(t)-X(t)\right) ^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t. \end{aligned}$$

According to the Young inequality, it is easy to arrive at

$$\begin{aligned} B\le&p\mathbb {E}\left( \sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p-2}\int _0^{T_1} \left( x(t)-X(t)\right) ^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right) \\ \le&\frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\mathbb {E}\left( \int _0^{T_1} \left( x(t)-X(t)\right) ^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right) ^{\frac{p}{2}}. \end{aligned}$$

Taking the difference between (1) and (8), one has

$$\begin{aligned}&x(t)-X(t)\\ =&x(\kappa (t))-X(\kappa (t))+\int _{\kappa (t)}^t (f(x(u),x([u]))-f(\bar{X}(u),\bar{X}([u])))\text {d}u\\&+\sum _{j=1}^d\int _{\kappa (t)}^t \left( g_j(x(u),x([u]))-g_j(\bar{X}(u),\bar{X}([u]))-\sum _{r=1}^d L^jg_r(\bar{X}(u),\bar{X}([u]))\Delta B^r(u)\right) \text {d}B_j(u), \end{aligned}$$

where $\kappa (t)=[t/\Delta ]\Delta$, then

$$\begin{aligned} B\le \frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+\sum _{i=1}^5B_i \end{aligned}$$

(31)

with

$$\begin{aligned} B_1 =&C\mathbb {E}\left( \int _0^{T_1} (x(\kappa (t))-X(\kappa (t)))^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right) ^{\frac{p}{2}},\\ B_2 =&C\mathbb {E}\left\{ \int _0^{T_1} \left( \int _{\kappa (t)}^t (f(x(u),x([u]))-f(X(u),X([u])))\text {d}u\right) ^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right\} ^{\frac{p}{2}},\\ B_3 =&C\mathbb {E}\left\{ \int _0^{T_1} \left( \int _{\kappa (t)}^t (f(X(u),X([u]))-f(\bar{X}(u),\bar{X}([u])))\text {d}u\right) ^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right\} ^{\frac{p}{2}}, \\ B_4 =&C\mathbb {E}\left\{ \int _0^{T_1} \left( \sum _{j=1}^d\int _{\kappa (t)}^t \left( g_j(x(u),x([u]))-g_j(X(u),X([u]))\right) \text {d}B_j(u)\right) ^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right\} ^{\frac{p}{2}},\\ B_5 =&C\mathbb {E}\Bigg \{\int _0^{T_1} \bigg (\sum _{j=1}^d\int _{\kappa (t)}^t \Big (g_j(X(u),X([u]))-g_j(\bar{X}(u),\bar{X}([u]))\\&\qquad \qquad \qquad \qquad \qquad -\sum _{r=1}^d L^jg_r(\bar{X}(u),\bar{X}([u]))\Delta B^r(u)\Big )\text {d}B_j(u)\bigg )^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\Bigg \}^{\frac{p}{2}}.\\ \end{aligned}$$

Let $N=[T_1/\Delta ]$,

$$\begin{aligned} B_1=&\underbrace{C\mathbb {E}\left( \sum _{sm+l=0}^{N-1}\int _{t_{sm+l}}^{t_{sm+l+1}} (x(\kappa (t))-X(\kappa (t)))^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right) ^{\frac{p}{2}}}_{B_{11}}\\&+\underbrace{C\mathbb {E}\left( \int _{\kappa (T_1)}^{T_1} (x(\kappa (t))-X(\kappa (t)))^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right) ^{\frac{p}{2}}}_{B_{12}}. \end{aligned}$$

Set

$$\begin{aligned} Z_{sm+l+1}=\int _{t_{sm+l}}^{t_{sm+l+1}} (x(\kappa (t))-X(\kappa (t)))^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t,~sm+l+1=1,\dots ,N, \end{aligned}$$

it is easy to know that $\mathbb {E}(Z_{sm+l+2}\vert Z_1,Z_2,\dots ,Z_{sm+l+1})=0$ for all $sm+l+1=1,\dots ,N-1$, then for $p\ge 4$, by Lemma 2.4, we have

$$\begin{aligned} B_{11}\le&C\left| \sum _{sm+l=0}^{N-1}Z_{sm+l+1}\right| _{L^{p/2}}^{\frac{p}{2}}\le C\left( C_p\left( \sum _{sm+l=0}^{N-1}\vert Z_{sm+l+1}\vert _{L^{p/2}}^2\right) ^{\frac{1}{2}}\right) ^{\frac{p}{2}}\\ \le&CN^{\frac{p}{4}-1} \sum _{sm+l=0}^{N-1}\mathbb {E}\vert Z_{sm+l+1}\vert ^{\frac{p}{2}}\\ =&CN^{\frac{p}{4}-1} \sum _{sm+l=0}^{N-1}\mathbb {E}\left| \int _{t_{sm+l}}^{t_{sm+l+1}} (x(\kappa (t))-X(\kappa (t)))^\text {T}\phi (\bar{X}(t),\bar{X}([t]))\text {d}t\right| ^{\frac{p}{2}}\\ \le&CT_1^{\frac{p}{4}-1}\Delta ^{\frac{p}{4}}\sum _{sm+l=0}^{N-1}\mathbb {E}\int _{t_{sm+l}}^{t_{sm+l+1}} \vert x(\kappa (t))-X(\kappa (t))\vert ^{\frac{p}{2}}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t\\ \le&C\mathbb {E}\int _{0}^{T_1} \vert x(\kappa (t))-X(\kappa (t))\vert ^{\frac{p}{2}}\left( \Delta ^{\frac{p}{4}}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\right) \text {d}t\\ \le&C\mathbb {E}\int _{0}^{T_1} \vert x(\kappa (t))-X(\kappa (t))\vert ^{p}\text {d}t+C\Delta ^{\frac{p}{2}}\int _{0}^{T_1} \mathbb {E}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{p}\text {d}t. \end{aligned}$$

Applying Assumption 2.1, the fundamental inequality $(\sum _{i=1}^n a_i)^p\le n^{p-1}\sum _{i=1}^na_i^p$, (4) and Lemma 3.2, for any $t\in [0,T_1]$,

$$\begin{aligned} \mathbb {E}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{p}= & {} \mathbb {E}\left| \sum _{i=1}^n\frac{\partial f(\bar{X}(t),\bar{X}([t]))}{\partial x_i}\sum _{k=1}^d\int _{\kappa (t)}^t g_{ik}(\bar{X}(u),\bar{X}([u])) \text {d}B^k(u)\right| ^p \nonumber \\\le & {} M^p(nd)^{p-1}\sum _{i=1}^n\sum _{k=1}^d\mathbb {E}\left( \vert g_{ik}(\bar{X}(t),\bar{X}([t]))\vert ^{p}\left| \int _{\kappa (t)}^t\text {d}B^k(u)\right| ^p\right) \nonumber \\\le & {} M^pn^pd^{p-1}\sum _{k=1}^d\left( \mathbb {E}\vert g_k(\bar{X}(t),\bar{X}([t]))\vert ^{2p}\right) ^{\frac{1}{2}}\left( \mathbb {E}\left| \int _{\kappa (t)}^t\text {d}B^k(u)\right| ^{2p}\right) ^{\frac{1}{2}}\nonumber \\\le & {} C\left( 1+\mathbb {E}\vert \bar{X}(t)\vert ^{2p}+\mathbb {E}\vert \bar{X}([t]))\vert ^{2p}\right) ^{\frac{1}{2}}\left( \mathbb {E}\left| \int _{\kappa (t)}^t\text {d}B^k(u)\right| ^{2p}\right) ^{\frac{1}{2}}\nonumber \\\le & {} C\Delta ^{\frac{p}{2}}\left( 1+\sup _{0\le u\le t}\mathbb {E}\vert X(u)\vert ^{2p}\right) ^{\frac{1}{2}} \nonumber \\\le & {} C\Delta ^{\frac{p}{2}}. \end{aligned}$$

(32)

Hence,

$$\begin{aligned} B_{11}\le C\int _{0}^{T_1}\left( \mathbb {E} \sup _{0\le u\le t}\vert x(u)-X(u)\vert ^{p}\right) \text {d}t+C\Delta ^{p}. \end{aligned}$$

According to Hölder’s inequality, we can get that

$$\begin{aligned} B_{12}\le&C\Delta ^{\frac{p}{2}-1}\mathbb {E}\int _{\kappa (T_1)}^{T_1} \vert x(\kappa (T_1))-X(\kappa (T_1))\vert ^{\frac{p}{2}}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t\\ \le&\mathbb {E}\left( \vert x(\kappa (T_1))-X(\kappa (T_1))\vert ^{\frac{p}{2}}\cdot C\Delta ^{\frac{p}{2}-1}\int _{\kappa (T_1)}^{T_1} \vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t\right) \\ \le&\frac{1}{8}\mathbb {E}\vert x(\kappa (T_1))-X(\kappa (T_1))\vert ^{p}+C\Delta ^{p-2}\mathbb {E}\left( \int _{\kappa (T_1)}^{T_1} \vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t\right) ^2\\ \le&\frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\Delta ^{p-1}\int _{\kappa (T_1)}^{T_1} \mathbb {E}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{p}\text {d}t\\ \le&\frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\Delta ^{p}. \end{aligned}$$

Therefore, one can obtain

$$\begin{aligned} B_1\le B_{11}+B_{12}\le \frac{1}{8}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\Delta ^{p}+C\int _{0}^{T_1}\left( \mathbb {E} \sup _{0\le u\le t}\vert x(u)-X(u)\vert ^{p}\right) \text {d}t. \end{aligned}$$

(33)

Using Hölder’s inequality and (32), together with (2)-(3), one can arrive at

$$\begin{aligned} B_2\le{} & {} C\mathbb {E}\int _0^{T_1} \left| \int _{\kappa (t)}^t (f(x(u),x([u]))-f(X(u),X([u])))\text {d}u\right| ^{\frac{p}{2}}\left| \phi (\bar{X}(t),\bar{X}([t]))\right| ^{\frac{p}{2}}\text {d}t \nonumber \\ \le{} & {} C\int _0^{T_1} \left( \mathbb {E}\left| \int _{\kappa (t)}^t (f(x(u),x([u]))-f(X(u),X([u])))\text {d}u\right| ^{p}\right) ^{\frac{1}{2}}\left( \mathbb {E}\left| \phi (\bar{X}(t),\bar{X}([t]))\right| ^{p}\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{\frac{p}{4}}\int _0^{T_1} \left( \mathbb {E}\left| \int _{\kappa (t)}^t (f(x(u),x([u]))-f(X(u),X([u])))\text {d}u\right| ^{p}\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{\frac{p}{4}}\int _0^{T_1} \left( \Delta ^{p-1}\mathbb {E}\int _{\kappa (t)}^t (\vert x(u)-X(u)\vert ^p+\vert x([u])-X([u])\vert ^{p})\text {d}u\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{\frac{p}{4}}\int _0^{T_1} \left( \Delta ^{p}\mathbb {E} \sup _{0\le u\le t}\vert x(u)-X(u)\vert ^p\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{p}+C\int _0^{T_1} \left( \mathbb {E} \sup _{0\le u\le t}\vert x(u)-X(u)\vert ^p\right) \text {d}t. \end{aligned}$$

(34)

Similarly,

$$\begin{aligned} B_3\le&C\mathbb {E}\int _0^{T_1} \left| \int _{\kappa (t)}^t (f(X(u),X([u]))-f(\bar{X}(u),\bar{X}([u])))\text {d}u\right| ^{\frac{p}{2}}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t\\ \le&C\Delta ^{\frac{p}{2}-1}\mathbb {E}\int _0^{T_1} \left( \int _{\kappa (t)}^t \left| f(X(u),X([u]))-f(\bar{X}(u),\bar{X}([u]))\right| ^{\frac{p}{2}}\text {d}u\right) \vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t\\ \le&C\Delta ^{\frac{p}{2}-1}\mathbb {E}\int _0^{T_1} \left( \int _{\kappa (t)}^t \left| X(u)-\bar{X}(u)\right| ^{\frac{p}{2}}\text {d}u\right) \vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t\\ \le&C\Delta ^{\frac{p}{2}-1}\int _0^{T_1} \left\{ \mathbb {E}\left( \int _{\kappa (t)}^t \left| X(u)-\bar{X}(u)\right| ^{\frac{p}{2}}\text {d}u\right) ^2\right\} ^{\frac{1}{2}}\left\{ \mathbb {E}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^p\right\} ^{\frac{1}{2}}\text {d}t\\ \le&C\Delta ^{\frac{3p-2}{4}}\int _0^{T_1} \left\{ \int _{\kappa (t)}^t \mathbb {E}\left| X(u)-\bar{X}(u)\right| ^p\text {d}u\right\} ^{\frac{1}{2}}\text {d}t.\\ \end{aligned}$$

It follows from Lemma 3.2 that

$$\begin{aligned} B_3\le C\Delta ^{\frac{3p-2}{4}}\int _0^{T_1} \Delta ^{\frac{p+2}{4}}\text {d}t\le C\Delta ^p. \end{aligned}$$

(35)

Using Hölder’s inequality and the B-D-G inequality again, with the help of (32), yields

$$\begin{aligned} B_4\le{} & {} C\mathbb {E}\int _0^{T_1} \left| \sum _{j=1}^d\int _{\kappa (t)}^t \left( g_j(x(u),x([u]))-g_j(X(u),X([u]))\right) \text {d}B(u)\right| ^{\frac{p}{2}}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t \nonumber \\ \le{} & {} C\sum _{j=1}^d\int _0^{T_1}\left( \mathbb {E}\left| \int _{\kappa (t)}^t \left( g_j(x(u),x([u]))-g_j(X(u),X([u]))\right) \text {d}B(u)\right| ^p\right) ^{\frac{1}{2}}\nonumber \\{} & {} \times \left( \mathbb {E}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^p\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{\frac{p}{4}}\sum _{j=1}^d\int _0^{T_1}\left( \Delta ^{\frac{p-2}{2}}\mathbb {E}\int _{\kappa (t)}^t \left| g_j(x(u),x([u]))-g_j(X(u),X([u]))\right| ^p\text {d}u\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{\frac{p-1}{2}}\int _0^{T_1}\left( \mathbb {E}\int _{\kappa (t)}^t (\vert x(u)-X(u)\vert ^p+\vert x([u])-X([u]))\vert ^p)\text {d}u\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{\frac{p}{2}}\int _0^{T_1} \left( \mathbb {E}\sup _{0\le u\le t}\vert x(u)-X(u)\vert ^p\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{p}+C\int _0^{T_1}\left( \mathbb {E}\sup _{0\le u\le t}\vert x(u)-X(u)\vert ^p\right) \text {d}t. \end{aligned}$$

(36)

By (26), (32) and Lemma 4.1, we have

$$\begin{aligned} B_5\le{} & {} C\mathbb {E}\int _0^{T_1} \left| \sum _{j=1}^d\int _{\kappa (t)}^t \bar{R}(g_j)(X(t)-\bar{X}(t))\text {d}B_j(u)\right| ^{\frac{p}{2}}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^{\frac{p}{2}}\text {d}t \nonumber \\ \le{} & {} C\sum _{j=1}^d\int _0^{T_1} \left( \mathbb {E}\left| \int _{\kappa (t)}^t \bar{R}(g_j)(X(t)-\bar{X}(t))\text {d}B_j(u)\right| ^{p}\right) ^{\frac{1}{2}} \left( \mathbb {E}\vert \phi (\bar{X}(t),\bar{X}([t]))\vert ^p\right) ^{\frac{1}{2}}\text {d}t \nonumber \\ \le{} & {} C\Delta ^{\frac{p}{4}}\sum _{j=1}^d\int _0^{T_1} \left( \Delta ^{\frac{p-2}{2}}\int _{\kappa (t)}^t \mathbb {E}\left| \bar{R}(g_j)(X(t)-\bar{X}(t))\right| ^{p}\text {d}u\right) ^{\frac{1}{2}} \text {d}t \nonumber \\ \le{} & {} C\Delta ^p. \end{aligned}$$

(37)

Combining (31) and (33)–(37), it yields

$$\begin{aligned} B\le \frac{1}{4}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\Delta ^{p}+C\int _{0}^{T_1}\left( \mathbb {E} \sup _{0\le u\le t}\vert x(u)-X(u)\vert ^{p}\right) \text {d}t. \end{aligned}$$

Substituting this into (30), one has

$$\begin{aligned} A_2\le \frac{1}{4}\mathbb {E}\sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}+C\Delta ^{p}+C\int _{0}^{T_1}\left( \mathbb {E} \sup _{0\le u\le t}\vert x(u)-X(u)\vert ^{p}\right) \text {d}t. \end{aligned}$$

(38)

Combining (22)–(24),(27)–(29), and (38), we have

$$\begin{aligned} \mathbb {E} \sup _{0\le t\le T_1}\vert x(t)-X(t)\vert ^{p}\le C\Delta ^{p}+C\int _0^{T_1}\left( \mathbb {E}\sup _{0\le u\le t}\vert x(u)-X(u)\vert ^p\right) \text {d}t,~\forall T_1\in [0,T]. \end{aligned}$$

Consequently, it can be deduced from the Gronwall inequality that

$$\begin{aligned} \mathbb {E} \sup _{0\le t\le T}\vert x(t)-X(t)\vert ^{p}\le C\Delta ^{p}e^{CT}\le C\Delta ^{p}, ~p\ge 4. \end{aligned}$$

Furthermore, for any $q\in (0,4)$, by Hölder’s inequality,

$$\begin{aligned} \mathbb {E} \sup _{0\le t\le T}\vert x(t)-X(t)\vert ^{q}=&\mathbb {E} \left( \sup _{0\le t\le T}\vert x(t)-X(t)\vert \right) ^{q}\\ \le&\left( \mathbb {E} \sup _{0\le t\le T}\vert x(t)-X(t)\vert ^{p}\right) ^{\frac{q}{p}}\\ \le&C\Delta ^{q}. \end{aligned}$$

The proof is completed. $\square$

5 Stability analysis of the Milstein method

In this section, we investigate the exponential stability of the Milstein method for (1). Throughout this section, we shall assume that (1) has a unique global solution for any given initial data $x_0$. Firstly, we suppose that $f(0,0)=0$ and $g_j(0,0)=0, j=1,\dots ,d$ and give the following two definitions of stability.

Definition 2

The SDEPCA (1) is said to be exponentially stable in mean square if there exist positive constants $\lambda$ and $H_1$ such that for any given initial value $x_0\in \mathbb {R}^n$,

$$\begin{aligned} \mathbb {E}\vert x(t)\vert ^2\le H_1\vert x_0 \vert ^2e^{-\lambda t},\quad \forall t\ge 0. \end{aligned}$$

Definition 3

For a given step-size $\Delta >0$, the Milstein method is said to be exponentially stable in mean square if there exist positive constants $\gamma$ and $H_2$ such that for any given initial value $x_0\in \mathbb {R}^n$,

$$\begin{aligned} \mathbb {E}\vert X_{k}\vert ^2\le H_2\vert x_0 \vert ^2e^{-\gamma k\Delta } \end{aligned}$$

for all $k\in \mathbb {N}$.

Remark 3

Under Assumptions 2.1, 2.2, and $f(0,0)=g_j(0,0)=0$, similar to the Remark 2, it follows

$$\begin{aligned} \vert f(x,y)\vert \vee \vert g_j(x,y)\vert \le \tilde{L}(\vert x\vert +\vert y\vert ) \end{aligned}$$

(39)

for all $x, y\in \mathbb {R}^n$, where $\tilde{L}=\bar{M}+L$, $\bar{M}$, and L are defined in Assumptions 2.1 and 2.2.

Let $g=(g_1,g_2,\dots ,g_d)$, we assume the following condition holds to obtain the stability.

Assumption 5.1

Assume that there are positive constants $\lambda _1>\lambda _2>0$ such that

$$\begin{aligned}\langle x,f(x,y)\rangle +\frac{1}{2}\vert g(x,y)\vert ^2\le -\lambda _1\vert x\vert ^2+\lambda _2\vert y\vert ^2,\quad \forall x, y\in \mathbb {R}^n. \end{aligned}$$

By Theorem 4.1 in [7], we can obtain the exponentially stability in the mean square of (1).

Theorem 5.2

Let Assumption 5.1 holds. Then, (1) is exponentially stable in mean square, i.e.,

$$\begin{aligned} \mathbb {E}\vert x(t)\vert ^2\le H_1\vert x_0 \vert ^2e^{-\lambda t},\quad \forall t\ge 0, \end{aligned}$$

where $\lambda =-\log r(1)$ and $H_1=r(1)^{-1}$ with $r(1)=\frac{\lambda _2}{\lambda _1}+(1-\frac{\lambda _2}{\lambda _1})e^{-2\lambda _1}$.

To obtain the stability of the Milstein method, we introduce the following lemmas (for details of the proofs, see [7]).

Lemma 5.3

Let $z_{sm+l}$ be a sequence of numbers, $s,m\in \mathbb {N}, l=0,1,\dots ,m-1$. If there are constants $\alpha>\beta >0$ such that $1-\alpha \Delta >0$ and

$$\begin{aligned} z_{sm+l+1}\le (1-\alpha \Delta )z_{sm+l}+\beta \Delta z_{sm}, \end{aligned}$$

then

$$\begin{aligned} z_{sm+l+1}\le \left( \frac{\beta }{\alpha }+\left( 1-\frac{\beta }{\alpha }\right) e^{-\alpha (l+1)\Delta }\right) z_{sm}. \end{aligned}$$

Lemma 5.4

Assume that $\alpha ,\beta$ are two positive constants. If $\alpha >\beta$, then for all $t\ge 0$, we have

$$\begin{aligned} 0< \frac{\beta }{\alpha }+\left( 1-\frac{\beta }{\alpha }\right) e^{-\alpha t}<1. \end{aligned}$$

Let $K=nd^2(d^2+2)M^2\tilde{L}^2+2\tilde{L}^2$, $\alpha =2\lambda _1-K\Delta$, $\beta =2\lambda _2+K\Delta$, $\Gamma (m)=\frac{\beta }{\alpha }+\left( 1-\frac{\beta }{\alpha }\right) e^{-\alpha }$, where M and $\tilde{L}$ are defined in Assumptions 2.1 and Remark 3, respectively. Then, we obtain the exponential stability of the Milstein method.

Theorem 5.5

Let Assumptions 2.1, 2.2, and 5.1 hold. Then, for any step-size $0<\Delta <\bar{\Delta }\wedge 1$, the Milstein scheme (5) is exponentially stable in mean square, i.e.,

$$\begin{aligned} \mathbb {E}\vert X_{k}\vert ^2\le H_2\vert x_0 \vert ^2e^{-\gamma k\Delta } \end{aligned}$$

for all $k\in \mathbb {N}$, where $H_2=\frac{1}{\Gamma (m)}$, $\gamma =-\log \Gamma (m)$,

$$\begin{aligned} \bar{\Delta }={\left\{ \begin{array}{ll} \frac{\lambda _1-\lambda _2}{K}, &{}~\text {if}~ \lambda _1^2\le K, \\ \left( \frac{\lambda _1-\lambda _2}{K}\right) \wedge \left( \frac{\lambda _1-\sqrt{\lambda _1^2-K}}{K}\right) ,&{}~\text {otherwise}. \end{array}\right. } \end{aligned}$$

Moreover, $\lim _{\Delta \rightarrow 0}\gamma =\lambda$, where $\lambda$ is defined in Theorem 5.2.

Proof

For any $s\in \mathbb {N}, l=0,1,\dots ,m-1$, according to (6), using Assumption 5.1,

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^2 =&\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert f\left( X_{sm+l},X_{sm}\right) \vert ^2\Delta ^2+\mathbb {E}\vert g\left( X_{sm+l},X_{sm}\right) \Delta B_{sm+l}\vert ^2 \nonumber \\&+\mathbb {E}\vert H_{sm+l}\vert ^2+2\mathbb {E}\langle X_{sm+l},f\left( X_{sm+l},X_{sm}\right) \Delta \rangle \nonumber \\&+2\mathbb {E}\langle X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta ,g\left( X_{sm+l},X_{sm}\right) \Delta B_{sm+l}\rangle \nonumber \\&+2\mathbb {E}\langle X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta +g\left( X_{sm+l},X_{sm}\right) \Delta B_{sm+l},H_{sm+l}\rangle , \end{aligned}$$

(40)

where

$$\begin{aligned} H_{sm+l}=&\frac{1}{2}\sum _{j,r=1}^d L^j g_r(X_{sm+l},X_{sm})\Delta B^j_{sm+l}\Delta B^r_{sm+l}-\frac{1}{2}\sum _{j.=1}^d L^j g_j(X_{sm+l},X_{sm})\Delta \\ =&\frac{1}{2}\sum _{j,r=1, j\ne r}^d L^j g_r(X_{sm+l},X_{sm})\Delta B^j_{sm+l}\Delta B^r_{sm+l}\\&+\frac{1}{2}\sum _{j=1}^d L^j g_j(X_{sm+l},X_{sm})\left( (\Delta B_{sm+l}^j)^2-\Delta \right) . \end{aligned}$$

Note that $L^j g_r(X_{sm+l},X_{sm})$ is $\mathcal {F}_{t_{sm+l}}$-measurable, $\Delta B_{sm+l}^j$ and $\Delta B_{sm+l}^r$ are $\mathcal {F}_{t_{sm+l}}$-independent; moreover, $\Delta B_{sm+l}^j$ and $\Delta B_{sm+l}^r$ are independent, and using the fundamental inequality, we can arrive at

$$\begin{aligned} \mathbb {E}\vert H_{sm+l}\vert ^2\le&\frac{d^2}{2}\sum _{j,r=1, j\ne r}^d\mathbb {E}\left| L^j g_r(X_{sm+l},X_{sm})\Delta B^j_{sm+l}\Delta B^r_{sm+l}\right| ^2\\&+\frac{d}{2}\sum _{j=1}^d\mathbb {E}\left| L^j g_j(X_{sm+l},X_{sm})\left( (\Delta B_{sm+l}^j)^2-\Delta \right) \right| ^2\\ \le&\frac{d^2}{2}\sum _{j,r=1, j\ne r}^d\mathbb {E}\vert L^j g_r(X_{sm+l},X_{sm})\vert ^2\mathbb {E}\vert \Delta B^j_{sm+l}\vert ^2 \mathbb {E}\vert \Delta B^r_{sm+l}\vert ^2\\&+\frac{d}{2}\sum _{j=1}^d\mathbb {E}\vert L^j g_j(X_{sm+l},X_{sm})\vert ^2\mathbb {E}\vert (\Delta B_{sm+l}^j)^2-\Delta \vert ^2.\\ \end{aligned}$$

Recall the definition of $L^j g_r(x,y)$, using Assumption 2.1 and (39), we have

$$\begin{aligned} \mathbb {E}\vert L^j g_r(X_{sm+l},X_{sm})\vert ^2 =&\mathbb {E}\left| \sum _{i=1}^n g_{ij}(X_{sm+l},X_{sm})\frac{\partial g_r(X_{sm+l},X_{sm})}{\partial x_i}\right| ^2\\ \le&nM^2 \mathbb {E}\left| g_{j}(X_{sm+l},X_{sm})\right| ^2\\ \le&2nM^2\tilde{L}^2(\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2) . \end{aligned}$$

Hence,

$$\begin{aligned} \mathbb {E}\vert H_{sm+l}\vert ^2\le{} & {} nd^2M^2\tilde{L}^2\sum _{j,r=1, j\ne r}^d(\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2)\mathbb {E}\vert \Delta B^j_{sm+l}\vert ^2 \mathbb {E}\vert \Delta B^r_{sm+l}\vert ^2 \nonumber \\{} & {} +ndM^2\tilde{L}^2\sum _{j=1}^d (\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2)\mathbb {E}\vert (\Delta B_{sm+l}^j)^2-\Delta \vert ^2 \nonumber \\ \le{} & {} nd^4M^2\tilde{L}^2(\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2)\Delta ^2 \nonumber \\{} & {} +ndM^2\tilde{L}^2\sum _{j=1}^d (\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2)(\mathbb {E}\vert \Delta B_{sm+l}^j\vert ^4+\Delta ^2-2\Delta \mathbb {E}\vert \Delta B_{sm+l}^j\vert ^2) \nonumber \\ \le{} & {} nd^2(d^2+2)M^2\tilde{L}^2(\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2)\Delta ^2. \end{aligned}$$

(41)

In addition, using the independence again, one has

$$\begin{aligned}{} & {} \mathbb {E}\langle X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta ,H_{sm+l}\rangle \nonumber \\= & {} \frac{1}{2}\mathbb {E}\left\langle X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta ,\sum _{j,r=1, j\ne r}^d L^j g_r(X_{sm+l},X_{sm})\Delta B^j_{sm+l}\Delta B^r_{sm+l}\right\rangle \nonumber \\{} & {} +\frac{1}{2}\mathbb {E}\left\langle X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta ,\sum _{j=1}^d L^j g_j(X_{sm+l},X_{sm})\left( (\Delta B_{sm+l}^j)^2-\Delta \right) \right\rangle \nonumber \\= & {} \frac{1}{2}\sum _{j,r=1, j\ne r}^d\mathbb {E}\left\{ \left( X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta \right) ^\text {T} L^j g_r(X_{sm+l},X_{sm})\Delta B^j_{sm+l}\Delta B^r_{sm+l}\right\} \nonumber \\{} & {} +\frac{1}{2}\sum _{j=1}^d \mathbb {E}\left\{ \left( X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta \right) ^\text {T}L^j g_j(X_{sm+l},X_{sm})(\Delta B_{sm+l}^j)^2\right\} \nonumber \\{} & {} -\frac{1}{2}\sum _{j=1}^d \mathbb {E}\left\{ \left( X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta \right) ^\text {T}L^j g_j(X_{sm+l},X_{sm})\Delta \right\} \nonumber \\= & {} 0. \end{aligned}$$

(42)

Similarly,

$$\begin{aligned}{} & {} \mathbb {E}\langle g\left( X_{sm+l},X_{sm}\right) \Delta B_{sm+l},H_{sm+l}\rangle \nonumber \\= & {} \frac{1}{2}\mathbb {E}\left\{ \left( \sum _{k=1}^d g_k\left( X_{sm+l},X_{sm}\right) \Delta B^k_{sm+l}\right) ^\text {T}\sum _{j,r=1, j\ne r}^d L^j g_r(X_{sm+l},X_{sm})\Delta B^j_{sm+l}\Delta B^r_{sm+l}\right\} \nonumber \\{} & {} +\frac{1}{2}\mathbb {E}\left\{ \left( \sum _{k=1}^d g_k\left( X_{sm+l},X_{sm}\right) \Delta B^k_{sm+l}\right) ^\text {T}\sum _{j=1}^d L^j g_j(X_{sm+l},X_{sm})\left( (\Delta B_{sm+l}^j)^2-\Delta \right) \right\} \nonumber \\= & {} \frac{1}{2}\mathbb {E}\left\{ \sum _{k,j,r=1, k\ne j\ne r}^d g_k\left( X_{sm+l},X_{sm}\right) ^\text {T}L^j g_r(X_{sm+l},X_{sm})\Delta B^k_{sm+l}\Delta B^j_{sm+l}\Delta B^r_{sm+l}\right\} \nonumber \\{} & {} +\frac{1}{2}\mathbb {E}\left\{ \sum _{j,r=1, j\ne r}^dg_j(X_{sm+l},X_{sm})^\text {T} L^j g_r(X_{sm+l},X_{sm})(\Delta B^j_{sm+l})^2\Delta B^r_{sm+l}\right\} \nonumber \\{} & {} +\frac{1}{2}\mathbb {E}\left\{ \sum _{j,r=1, j\ne r}^dg_r(X_{sm+l},X_{sm})^\text {T} L^j g_r(X_{sm+l},X_{sm})\Delta B^j_{sm+l}(\Delta B^r_{sm+l})^2\right\} \nonumber \\{} & {} +\frac{1}{2}\mathbb {E}\left\{ \sum _{k,j=1}^d g_k\left( X_{sm+l},X_{sm}\right) ^\text {T}L^j g_j(X_{sm+l},X_{sm})\left( (\Delta B_{sm+l}^j)^2-\Delta \right) \Delta B^k_{sm+l}\right\} \nonumber \\= & {} 0. \end{aligned}$$

(43)

Moreover, it is easy to know that

$$\begin{aligned} \mathbb {E}\langle X_{sm+l}+f\left( X_{sm+l},X_{sm}\right) \Delta ,g\left( X_{sm+l},X_{sm}\right) \Delta B_{sm+l}\rangle =0. \end{aligned}$$

(44)

Substituting (41)–(44) into (40), using (39) and Assumption 5.1, one can obtain that

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^2=&\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert f\left( X_{sm+l},X_{sm}\right) \vert ^2\Delta ^2+\mathbb {E}\vert g\left( X_{sm+l},X_{sm}\right) \Delta B_{sm+l}\vert ^2\\&+nd^2(d^2+2)M^2\tilde{L}^2(\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2)\Delta ^2\\&+2\mathbb {E}\langle X_{sm+l},f\left( X_{sm+l},X_{sm}\right) \Delta \rangle \\ =&\mathbb {E}\vert X_{sm+l}\vert ^2+\left( nd^2(d^2+2)M^2\tilde{L}^2+2\tilde{L}^2\right) (\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2)\Delta ^2\\&+2\Delta \mathbb {E}\left( \langle X_{sm+l},f\left( X_{sm+l},X_{sm}\right) \rangle +\frac{1}{2}\vert g\left( X_{sm+l},X_{sm}\right) \vert ^2\right) \\ \le&\mathbb {E}\vert X_{sm+l}\vert ^2+K(\mathbb {E}\vert X_{sm+l}\vert ^2+\mathbb {E}\vert X_{sm}\vert ^2)\Delta ^2-2\lambda _1\mathbb {E}\vert X_{sm+l}\vert ^2\Delta +2\lambda _2\mathbb {E}\vert X_{sm}\vert ^2\Delta \\&=(1-\alpha \Delta )\mathbb {E}\vert X_{sm+l}\vert ^2+\beta \Delta \mathbb {E}\vert X_{sm}\vert ^2. \end{aligned}$$

Since $\Delta <\bar{\Delta }$, we have $\alpha>\beta >0$ and $1-\alpha \Delta >0$, by Lemma 5.3, yields

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^2\le \Gamma (l+1) \mathbb {E}\vert X_{sm}\vert ^2. \end{aligned}$$

where $\Gamma (l+1)=\left( \frac{\beta }{\alpha }+\left( 1-\frac{\beta }{\alpha }\right) e^{-\alpha (l+1)\Delta }\right)$. In particular, if $l=m-1$, it follows

$$\begin{aligned} \mathbb {E}\vert X_{(s+1)m}\vert ^2\le \Gamma (m)\mathbb {E}\vert X_{sm}\vert ^2. \end{aligned}$$

Therefore

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^2\le&\Gamma (l+1) \mathbb {E}\vert X_{sm}\vert ^2\\ \le&\Gamma (l+1)\Gamma (m) \mathbb {E}\vert X_{(s-1)m}\vert ^2\\ \vdots \\ \le&\Gamma (l+1)\Gamma (m)^s \vert x_0\vert ^2.\\ \end{aligned}$$

According to Lemma 5.4, we know that $\Gamma (l+1)\in (0,1)$ for all $l=0,1,\dots ,m-1$. Hence,

$$\begin{aligned} \mathbb {E}\vert X_{sm+l+1}\vert ^2\le&\frac{\Gamma (l+1)}{\Gamma (m)^{(l+1)\Delta }}e^{(sm+l+1)\Delta \log \Gamma (m)} \vert x_0\vert ^2\\ \le&\frac{1}{\Gamma (m)}e^{(sm+l+1)\Delta \log \Gamma (m)} \vert x_0\vert ^2. \end{aligned}$$

Let $H_2=\frac{1}{\Gamma (m)}>1$, $\gamma =-\log \Gamma (m)>0$, we can get that

$$\begin{aligned} \mathbb {E}\vert X_{k}\vert ^2\le H_2 e^{-\gamma k\Delta } \vert x_0\vert ^2,\quad \forall k\in \mathbb {N}. \end{aligned}$$

Furthermore,

$$\begin{aligned} \lim _{\Delta \rightarrow 0}\gamma&=- \lim _{\Delta \rightarrow 0}\log \Gamma (m)\\ =&- \lim _{\Delta \rightarrow 0}\log \left( \frac{\beta }{\alpha }+\left( 1-\frac{\beta }{\alpha }\right) e^{-\alpha }\right) \\ =&- \log \left( \frac{\lambda _2}{\lambda _1}+\left( 1-\frac{\lambda _2}{\lambda _1}\right) e^{-2\lambda _1}\right) \\ =&\lambda . \end{aligned}$$

The proof is completed. $\square$

6 Numerical examples

In this section, two numerical examples are given to show the convergence rate obtained in the previous section.

Example 1

In this example, we consider the scalar SDEPCA

$$\begin{aligned} \text {d}x(t)=2x([t])\text {d}t-x(t)\text {d}B(t) \end{aligned}$$

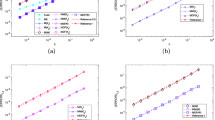
on $t\ge 0$ with the initial value $x_0=1$, B(t) is a scalar Brownian motion. We generate 3000 different Brownian paths. Let $T=1$, Fig. 1 depicts p-th moment errors $\mathbb {E}\vert x(1)-X_{m}\vert ^p$ as a function of the step size $\Delta$ in log-log plot, where we use the numerical solutions produced by Euler and Milstein methods with step sizes $2^{-3},2^{-4},2^{-5},2^{-6}$, and $2^{-7}$. The simulation using the Euler scheme with step size $\Delta = 2^{-16}$ is regarded as the “true solution.” It can be seen from Fig. 1 that the convergence order of the Euler method is around $\frac{1}{2}$, while the convergence order of the Milstein method is close to 1.

Fig. 1

Log-log plot of errors against step sizes (left: $p=2$; right: $p=4$)

Example 2

In the following, we consider the 2-dim SDEPCA

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {d}x_1(t)=(-x_1(t)+\frac{1}{2}x_2(t)+\sin (x_1([t])))\text {d}t+(x_1(t)+x_2([t])+\cos (x_2([t])))\text {d}B(t),\\ \text {d}x_2(t)=(\frac{1}{2}x_1(t)-x_2(t)+\cos (x_1([t])))\text {d}t+(\sin (x_1(t))+x_2([t]))\text {d}B(t) \end{array}\right. } \end{aligned}$$

on $t\ge 0$ with the initial value $x_0=(1,2)^\text {T}$. We use the numerical solution of the Euler method with step-size $\Delta = 2^{-15}$ as the “exact solution,” and the step sizes for numerical solutions are taken to be $2^{-4},2^{-5},2^{-7},2^{-8}$, and $2^{-9}$. The convergence rates for Euler and Milstein methods are shown in Fig. 2.

Fig. 2

Log-log plot of errors against step sizes (left: $T=3,p=1$; right: $T=2,p=2$)

Example 3

In this example, we consider the stability of the Milstein method for the following scalar SDEPCA

$$\begin{aligned} \text {d}x(t)=(-x(t)+\frac{1}{4}x([t]))\text {d}t+\frac{1}{2}x(t)\text {d}B(t) \end{aligned}$$

(45)

on $t\ge 0$ with the initial value $x_0=10$. It is easy to get that $n=d=1, M=1, L=\frac{1}{4}$, hence $\tilde{L}=M+L=\frac{5}{4}$ and $K=\frac{125}{16}$. On the other hand, we can obtain that $\lambda _1=\frac{3}{4}$, $\lambda _2=\frac{1}{8}$ by Assumption 5.1. Since $\lambda _1^2=\frac{9}{16}<K$, according to Theorem 5.5, $\bar{\Delta }=\frac{\lambda _1-\lambda _2}{K}=\frac{2}{25}$. Therefore, we choose three step sizes $\Delta =2^{-4}, 2^{-5}$, and $2^{-6}$ to show the stability of the Milstein method. The mean square stability of the numerical solutions can be observed from Fig. 3.

Fig. 3

The mean square stability of the Milstein solutions for (45)