Abstract
The notation of Moore-Penrose inverse of matrices has been extended from matrix space to even-order tensor space with Einstein product. In this paper, we give the numerical study on the Moore-Penrose inverse of tensors via the Einstein product. More precisely, we transform the calculation of Moore-Penrose inverse of tensors via the Einstein product into solving a class of tensor equations via the Einstein product. Then, by means of the conjugate gradient method, we obtain the approximate Moore-Penrose inverse of tensors via the Einstein product. Finally, we report some numerical examples to show the efficiency of the proposed methods and testify the conclusion suggested in this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background and motivation
Tensor is a multidimensional array, which is exactly the higher order generalization of matrix. Research on tensors has been very active recently [5, 6, 9, 16, 21] as tensors have a lot of applications in many different fields, such as graph analysis, computer vision, signal processing, data mining, human motion recognition, and chemometrics; one can see [4, 7, 8, 10, 11, 31, 33] and the references cited therein. Tensor models are employed in numerous disciplines addressing the problem of finding the multilinear structure in multiway data sets. Especially, multilinear systems model many phenomena in mechanics, physics, Markov process, control theory, partial differential equations, and engineering problems [13,14,15, 17,18,19,20, 32], such as the radiation transfer equation, high-dimensional Possion equation, Einstein gravitational field equation, and piezoelectric effect equation.
A lot of works have been done on tensors for the past four decades. However, there are few research works on the theory and applications of the generalized inverse of tensors. In 2016, Sun et al. [32] first introduced a generalized inverse called the Moore-Penrose inverse of an even-order tensor via the Einstein product, and a concrete representation for the Moore-Penrose inverse was given by using the singular value decomposition (SVD) of a tensor. Then, the authors obtained the minimum-norm least-squares solution of some multilinear systems by means of the Moore-Penrose inverse of tensors. Behera and Mishra [3] continued the same study and proposed some different types of generalized inverses of tensors. Different from the work in [3, 32], Jin et al. [24] defined a Moore-Penrose inverse of higher order tensors by using the t-product constructed in [27]. They proved that the Moore-Penrose inverse of an arbitrary tensor exists and is unique by using the technique of fast Fourier transform. They also presented some properties of the Moore-Penrose inverse of tensors and established some representations of {1}-inverses, {1, 3}-inverses and {1, 4}-inverses of tensors.
In [3], Behera and Mishra proposed two open problems. The first one is about the reverse-order law for the Moore-Penrose inverse of tensors and the second one is about full rank factorization of tensors. In 2018, Panigrahy et al. [28] answered the first problem for even-order tensors. Again, Panigrahy and Mishra [29] added more results to the same theory but for arbitrary order tensors. In the same year, Liang and Zheng [25] solved the other problem and proposed the full rank decomposition of tensors by introducing a new kind of tensor rank, which gives a novel representation of the Moore-Penrose inverse of tensors. They also obtained several formulae related to the Moore-Penrose inverse of tensors and their {i, j, k}-inverses.
In 2017, Ji and Wei [22] studied another extension of the Moore-Penrose inverse of an even-order tensor, called weighted Moore-Penrose inverse, and established the relation between the minimum-norm least-squares solution of a multilinear system and the weighted Moore-Penrose inverse of tensors. Behera et al. [2] further studied the weighted Moore-Penrose inverse of tensors and proposed a few identities involving the weighted Moore-Penrose inverse of tensors. They also obtained some necessary and sufficient conditions of the reverse-order law for the weighted Moore-Penrose inverse of arbitrary-order tensors. In 2018, Panigrahy and Mishra [30] improved the definition of Moore-Penrose inverse of an even-order tensor to a tensor of any order, which is called product Moore-Penrose inverse. A necessary and sufficient condition for the coincidence of the Moore-Penrose inverse and the product Moore-Penrose inverse is also proposed. At the same year, Ji and Wei [23] extended the notion of Drazin inverse of a square matrix to an even-order square tensor, and obtained an expression for the Drazin inverse through the core-nilpotent decomposition for a tensor of even-order. As an application, the Drazin inverse solution of the singular linear tensor equation \(\mathcal {A}\ast _{N} \mathcal {X} = {\mathscr{B}}\) has been included. Ma et al. [26] derived some representations of tensor expressions involving the Moore-Penrose inverse and investigated the perturbation theory for the Moore-Penrose inverse of tensors via the Einstein product.
Since the Moore-Penrose inverse of tensors plays an important role in solving multilinear systems [3, 24, 32], it needs to further study this subject. The definitions of Moore-Penrose inverse are based on the singular value decomposition (SVD) of tensors, t-product of tensors, and full rank decomposition of tensors. All the existing works mainly analyze the properties of the Moore-Penrose inverse of tensors from an analytical perspective. The research work about the algorithm for computing the Moore-Penrose inverse of tensors is relatively rare. Although Jin et al. [24] established an algorithm for computing the Moore-Penrose inverse of a tensor by using the technique of fast Fourier transform and inverse fast Fourier transform of a matrix, the algorithm involves matrix computation. Naturally, a question arises: Does there exists an iterative algorithm, which involves only tensor computation, for computing the Moore-Penrose inverse of tensors?
In this paper, we will answer this question. This study can lead to the enhancement of the computation of Moore-Penrose inverse of tensors along with solutions of multilinear structure in multidimensional systems. In this regard, we reformulate the calculation of Moore-Penrose inverse of real tensors as the solution of linear tensor equation or equations. For the linear tensor equation or equations, we apply the conjugate gradient method to find the solution.
The main contribution of this paper is as follows:
-
to give the new equivalent characterization of Moore-Penrose inverse of tensors via the Einstein product.
-
to present two numerical methods to obtain the Moore-Penrose inverse of tensors via the Einstein product.
1.2 Outline
This paper is organized as follows. In the next subsection, we present some notations and definitions which will be useful for proving the main results in Sections 2 and 3. In Section 2, we first transform the computation of {1,3}-inverse and {1,4}-inverse of a tensor \(\mathcal {A}\) into solving a class of tensor equations with one variable. Then, we develop the conjugate gradient method for the solution of tensor equation in order to obtain \(\mathcal {A}^{(1,4)}\) and \(\mathcal {A}^{(1,3)}\). Meanwhile, we give the convergence analysis and prove the finite termination property of the proposed method. By means of the numerical results of {1,4}-inverse \(\mathcal {A}^{(1,4)}\) and {1,3}-inverse \(\mathcal {A}^{(1,3)}\), and the relationship \(\mathcal {A}^{\dagger }=\mathcal {A}^{(1,4)}\ast _{N} \mathcal {A}\ast _{M} \mathcal {A}^{(1,3)}\), we obtain the unique Moore-Penrose inverse \(\mathcal {A}^{\dagger }\). In Section 3, we first derive an important property of the Moore-Penrose inverse of tensors. Based on the property of the Moore-Penrose inverse of tensors, we transform the computation of Moore-Penrose inverse of tensors into solving a class of tensor equations with two variables. Then, we present the conjugate gradient method to solve the tensor equation and give the convergence analysis. Numerical examples of the proposed algorithm are shown and analyzed in Section 4. The paper ends up with some concluding remarks in Section 5.
1.3 Notations and definitions
For a positive integer N, let [N] = {1,⋯ , N}. An order N tensor \(\mathcal {A}=(a_{i_{1}{\cdots } i_{N}})_{1\leq i_{j}\leq I_{j}} (j=1,\cdots ,N)\) is a multidimensional array with I1I2⋯IN entries. Let \(\mathbb {C}^{I_{1}\times \cdots \times I_{N}}\) and \(\mathbb {R}^{I_{1}\times \cdots \times I_{N}}\) be the sets of the order N dimension I1 ×⋯ × IN tensors over the complex number field \(\mathbb {C}\) and the real number field \(\mathbb {R}\), respectively. Here I1, I2, ⋯, IN are dimensions of the first, second, ⋯, N th way, respectively. The order of a tensor is the number of dimensions. A first-order tensor is a vector while a second-order tensor is a matrix. Higher-order tensors are tensors of order three or higher. Each entry of \(\mathcal {A}\) is denoted by \(a_{i_{1}{\cdots } i_{N}}\). For N = 3, \(\mathcal {A}\in \mathbb {C}^{I_{1}\times I_{2}\times I_{3}}\) is a third-order tensor, and \(a_{i_{1}i_{2}i_{3}}\) denotes the entry of that tensor.
For a tensor \(\mathcal {A}=(a_{i_{1}{\cdots } i_{N}j_{1}{\cdots } j_{M}})\in \mathbb {C}^{I_{1}\times \cdots \times I_{N} \times J_{1}\times \cdots \times J_{M}}\), let \({\mathscr{B}}=(b_{i_{1}\cdots i_{M}j_{1}{\cdots } j_{N}}) \in \mathbb {C}^{J_{1}\times \cdots \times J_{M} \times I_{1}\times \cdots \times I_{N}}\) be the conjugate transpose of \(\mathcal {A}\), where \(b_{i_{1}\cdots i_{M}j_{1}{\cdots } j_{N}}=\overline {a}_{j_{1}{\cdots } j_{N}i_{1}{\cdots } i_{M}}\). The tensor \({\mathscr{B}}\) is denoted by \(\mathcal {A}^{H}\). When \(b_{i_{1}{\cdots } i_{M}j_{1}\cdots j_{N}}=a_{j_{1}{\cdots } j_{N}i_{1}{\cdots } i_{M}}\), the tensor \({\mathscr{B}}\) is called the transpose of \(\mathcal {A}\), denoted by \(\mathcal {A}^{T}\). We say a tensor \(\mathcal {D}=(d_{i_{1}{\cdots } i_{N}j_{1}{\cdots } j_{N}})\in \mathbb {C}^{I_{1}\times \cdots \times I_{N} \times I_{1}\times \cdots \times I_{N}}\) is a diagonal tensor if \(d_{i_{1}\cdots i_{N}j_{1}{\cdots } j_{N}}=0\) in the case that the indices i1⋯iN are different from j1⋯jN. The unit tensor \(\mathcal {I}\) is the one with all entries being zero except for the diagonal entries \(d_{i_{1}{\cdots } i_{N}i_{1}{\cdots } i_{N}}=1\). The zero tensor \(\mathcal {O}\) is the one with all entries being zero. The trace of a tensor \(\mathcal {A}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N} \times I_{1}\times \cdots \times I_{N}}\) is \(\text {tr}(\mathcal {A})={\sum }_{i_{1}{\cdots } i_{N}}a_{i_{1}{\cdots } i_{N}i_{1}\cdots i_{N}}\) [4]. A few more notations and definitions are introduced below.
Let \(\mathcal {A}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N}\times K_{1}\times \cdots \times K_{N}}\) and \({\mathscr{B}}\in \mathbb {C}^{K_{1}\times \cdots \times K_{N}\times J_{1}\times \cdots \times J_{M}}\); the Einstein product [4] of tensors \(\mathcal {A}\) and \({\mathscr{B}}\) is defined by the operation ∗N via
It is obvious that \(\mathcal {A}\ast _{N}{\mathscr{B}}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}\) and the associative law of this tensor product are true. By (1.1), if \({\mathscr{B}}\in \mathbb {C}^{K_{1}\times \cdots \times K_{N}}\), then
where \(\mathcal {A}\ast _{N}{\mathscr{B}}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N}}\). This product is used in the study of the theory of relativity and in the area of continuum mechanics [17]. We comment here that the Einstein product ∗1 reduces to the standard matrix multiplication as:
for \(A\in \mathbb {C}^{m\times n}\) and \(B\in \mathbb {C}^{n\times l}\). We also know that when \(\mathcal {A}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N}}\) and \({\mathscr{B}}\) is a vector \(b=(b_{i_{N}})\in \mathbb {C}^{I_{N}}\), the Einstein product is defined by the operation ×1 via
where \(\mathcal {A}\times _{1}{\mathscr{B}}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N-1}}\).
Lemma 1.1
[32] Let \(\mathcal {A}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N}\times K_{1}\times \cdots \times K_{N}}\) and \({\mathscr{B}}\in \mathbb {R}^{K_{1}\times \cdots \times K_{N}\times J_{1}\times \cdots \times J_{M}}\). Then \((\mathrm {1}) (\mathcal {A}\ast _{N}{\mathscr{B}})^{H}={\mathscr{B}}^{H}\ast _{N}\mathcal {A}^{H}\); \((\mathrm {2}) (\mathcal {I}_{N}\ast _{N}{\mathscr{B}})={\mathscr{B}}\) and \(({\mathscr{B}}\ast _{M}\mathcal {I}_{M})={\mathscr{B}}\), where the unit tensors \(\mathcal {I}_{N}\in \mathbb {C}^{K_{1}\times \cdots \times K_{N}\times K_{1}\times \cdots \times K_{N}}\) and \(\mathcal {I}_{M}\in \mathbb {C}^{J_{1}\times \cdots \times J_{M}\times J_{1}\times \cdots \times J_{M}}\).
Definition 1.2
[4] Let \(\mathcal {A},{\mathscr{B}}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N} \times J_{1}\times \cdots \times J_{M}}\). The inner product of two tensors \(\mathcal {A}\) and \({\mathscr{B}}\) is defined by:
For a tensor \(\mathcal {A}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N} \times I_{1}\times \cdots \times I_{N}}\), the tensor norm induced by this inner product is Frobenius norm \(\|\mathcal {A}\|=({\sum }_{i_{1}{\cdots } i_{N}j_{1}{\cdots } j_{N}}|a_{i_{1}{\cdots } i_{N}j_{1}{\cdots } j_{N}}|^{2})^{\frac {1}{2}}\). Wang and Xu [34] derived the symmetric property of this inner product as follows.
Lemma 1.3
[34] Let \(\mathcal {A},{\mathscr{B}}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N} \times J_{1}\times \cdots \times J_{M}}\). Then
In addition, it follows from the definition of the inner product and the properties of the tensor trace that for any \(\mathcal {A},{\mathscr{B}}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N} \times J_{1}\times \cdots \times J_{M}}\) and any scalar \(\alpha \in \mathbb {C}\),
-
(1)
linearity in the first argument:
$$ \langle\alpha\mathcal{A},\mathcal{B}\rangle=\alpha\langle\mathcal{A},\mathcal{B}\rangle,~\langle\mathcal{A}+\mathcal{C},\mathcal{B}\rangle=\langle\mathcal{A},\mathcal{B}\rangle+\langle\mathcal{C},\mathcal{B}\rangle, $$ -
(2)
positive definiteness: \(\langle \mathcal {A},\mathcal {A}\rangle >0\) for all nonzero tensor \(\mathcal {A}\).
And, for two tensors \(\mathcal {X},\mathcal {Y}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N} \times J_{1}\times \cdots \times J_{M}}\), by simple calculations, we obtain
Lemma 1.4
[12] Let \(\mathcal {A}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{N}}\) and \({\mathscr{B}}\in \mathbb {R}^{K_{1}\times \cdots \times K_{M}\times L_{1}\times \cdots \times L_{M}}\). Then for any \(\mathcal {X}\in \mathbb {R}^{J_{1}\times \cdots \times J_{N}\times K_{1}\times \cdots \times K_{M}}\) and \(\mathcal {Y}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times L_{1}\times \cdots \times L_{M}}\), we have
Lemma 1.5
Let \(\mathcal {D}\in \mathbb {R}^{J_{1}\times \cdots \times J_{N}\times I_{1}\times \cdots \times I_{N}} \) and \(\mathcal {C}\in \mathbb {R}^{L_{1}\times \cdots \times L_{M}\times K_{1}\times \cdots \times K_{M}}\). Then for any \(\mathcal {X}\in \mathbb {R}^{J_{1}\times \cdots \times J_{N} \times K_{1}\times \cdots \times K_{M}}\) and \(\mathcal {Y}\in \mathbb {R}^{L_{1}\times \cdots \times L_{M}\times I_{1}\times \cdots \times I_{N}}\), we have
Proof
The result can be established by using an argument similar to the one used in Lemma 1.4. □
For a tensor \(\mathcal {A}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N}\times I_{1}\times \cdots \times I_{N}}\), if there exists a tensor \({\mathscr{B}}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N}\times I_{1} \times \cdots \times I_{N}}\) such that \(\mathcal {A}\ast _{N}{\mathscr{B}} = {\mathscr{B}}\ast _{N}\mathcal {A} = \mathcal {I}\), then \(\mathcal {A}\) is said to be invertible and \({\mathscr{B}}\) is called the inverse of \(\mathcal {A}\) and denoted by \(\mathcal {A}^{-1}\) [4]. For a general tensor \(\mathcal {A}\) in \(\mathbb {C}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}\), its inverse may not exist. But it is shown in [25] that there exists a unique Moore-Penrose inverse \(\mathcal {X}\) in \(\mathbb {C}^{J_{1}\times \cdots \times J_{M}\times I_{1}\times \cdots \times I_{N}}\). The definition of the Moore-Penrose inverse of tensors in \(\mathbb {C}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}\) via the Einstein product is as follows.
Definition 1.6
[25] Let \(\mathcal {A}\in \mathbb {C}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}\). The tensor \(\mathcal {X}\) in \(\mathbb {C}^{J_{1}\times \cdots \times J_{M} \times I_{1}\times \cdots \times I_{N}}\) satisfied
is called the Moore-Penrose inverse of \(\mathcal {A}\), denoted by \(\mathcal {A}^{\dagger }\).
Particularly, if a tensor \(\mathcal {X}\) satisfies tensor equations (i), (j), ⋯, (k) in (1.3), it is called an {i, j,⋯ , k}-inverse of \(\mathcal {A}\), denoted by \(\mathcal {A}^{(i,j,\cdots ,k)}\). The set of {i, j,⋯ , k}-inverses of a tensor \(\mathcal {A}\) is denoted by \(\mathcal {A}\{i, j,\cdots , k\}\).
Clearly, we have \(\mathcal {A}^{\dagger }=\mathcal {A}^{-1}=\mathcal {A}^{(i,j,\cdots ,k)}\) if \(\mathcal {A}\) is invertible. Especially, if M = N, it reduces to the Moore-Penrose inverse defined in [32].
2 Reformulation as tensor equations with one variable
In [3], Behera and Mishra studied the properties of the generalized inverse of tensors and obtained the following results.
Lemma 2.1
[3, Theorem 2.32.] Let \(\mathcal {A}\in \mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{N}}\). Then
Similar to Lemma 2.1, we are easy to see the following fact. For completeness, we give a detailed proof.
Proposition 2.2
Let \(\mathcal {A}\in \mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\). Then
Proof
Let \(\mathcal {X}=\mathcal {A}^{(1,4)}\ast _{N} \mathcal {A}\ast _{M} \mathcal {A}^{(1,3)}\). Then
and
Since
it follows that
By some calculations, we know
Therefore, we conclude that
Hence, \(\mathcal {X}=\mathcal {A}^{\dagger }\), which completes the proof. □
Let
Then the computation of {1,3}-inverse in \(\mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\) becomes the following tensor equations
If
then the computation of {1,4}-inverse in \(\mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\) becomes the tensor equations (2.2). In other words, the computation of {1,3}-inverse of a tensor can be transformed into finding the solution of tensor equations (2.2) with the coefficient tensors given in (2.1), and the computation of {1,4}-inverse of a tensor can be transformed into finding the solution of tensor equations (2.2) with the coefficient tensors given in (2.3). Once the {1,4}-inverse and {1,3}-inverse of a tensor \(\mathcal {A}\) are obtained, it follows from Proposition 2.2 that the unique Moore-Penrose inverse of \(\mathcal {A}\) equals to \(\mathcal {A}^{\dagger }=\mathcal {A}^{(1,4)}\ast _{N} \mathcal {A}\ast _{M} \mathcal {A}^{(1,3)}\).
For the tensor equations (2.2), we apply the tensor form of the conjugate gradient method to find the solution, which is described as in Algorithm 2.3.
Algorithm 2.3 (Conjugate gradient method with tensor form for solving (2.2))
-
Step 0 Input appropriate dimensionality tensors \(\mathcal {A}_{1}, {\mathscr{B}}_{1}, \mathcal {F}_{1}\!\in \!\mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\), \(\mathcal {C}_{1}\in \mathbb {R}^{I_{1}\times {\cdots } \times I_{N} \times I_{1}\times \cdots \times I_{N}}\), \(\mathcal {D}_{1}\in \mathbb {R}^{J_{1}\times {\cdots } \times J_{M}\times J_{1}\times \cdots \times J_{M}}\), \(\mathcal {A}_{2}\in \mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}} \), \({\mathscr{B}}_{2}, \mathcal {C}_{2}, \mathcal {F}_{2}\in \mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times I_{1}\times \cdots \times I_{N}}\) and \(\mathcal {D}_{2} \in \mathbb {R}^{J_{1}\times {\cdots } \times J_{M}\times I_{1}\times \cdots \times I_{N}}\) in (2.2). Choose the initial tensor \(\mathcal {X}_{0}\in \mathbb {R}^{J_{1}\times {\cdots } \times J_{M}\times I_{1}\times \cdots \times I_{N}}\).
-
Step 1 Compute
$$ \begin{array}{@{}rcl@{}} \mathcal{R}_{0}^{(1)}\!& = &\mathcal{F}_{1}-\mathcal{A}_{1}\ast_{M}\mathcal{X}_{0}\ast_{N}\mathcal{B}_{1} -\mathcal{C}_{1}\ast_{N}\mathcal{X}_{0}^{T}\ast_{M}\mathcal{D}_{1}, ~\mathcal{R}_{0}^{(2)}\\ & = &\mathcal{F}_{2}- \mathcal{A}_{2}\ast_{M}\mathcal{X}_{0}\ast_{N}\mathcal{B}_{2} -\mathcal{C}_{2}\ast_{N}\mathcal{X}_{0}^{T}\ast_{M}\mathcal{D}_{2}, \end{array} $$and
$$ \begin{array}{@{}rcl@{}} \widetilde{\mathcal{R}}_{0}&=&\mathcal{A}_{1}^{T}\ast_{N}\mathcal{R}_{0}^{(1)}\ast_{M}\mathcal{B}_{1}^{T} +\mathcal{A}_{2}^{T}\ast_{M}\mathcal{R}_{0}^{(2)}\ast_{N}\mathcal{B}_{2}^{T} +\mathcal{D}_{1}\ast_{M}(\mathcal{R}_{0}^{(1)})^{T}\ast_{N}\mathcal{C}_{1}\\ &&+\mathcal{D}_{2}\ast_{M}(\mathcal{R}_{0}^{(2)})^{T}\ast_{M}\mathcal{C}_{2}. \end{array} $$Set \(\mathcal {Q}_{0}=\widetilde {\mathcal {R}}_{0}\) and k = 0.
-
Step 2 If \(\|\mathcal {R}_{k}^{(1)}\|^{2}+\|\mathcal {R}_{k}^{(2)}\|^{2}=0\), stop. Otherwise, go to step 3.
-
Step 3 Update the sequence
$$ \mathcal{X}_{k+1}=\mathcal{X}_{k}+\alpha_{k} \mathcal{Q}_{k}. $$(2.4)where
$$ \alpha_{k}=\frac{\|\mathcal{R}_{k}^{(1)}\|^{2}+\|\mathcal{R}_{k}^{(2)}\|^{2}}{\|\mathcal{Q}_{k}\|^{2}}. $$(2.5) -
Step 4 Compute
$$ \begin{array}{l} \mathcal{R}_{k+1}^{(1)}=\mathcal{F}_{1}-\mathcal{A}_{1}\ast_{M}\mathcal{X}_{k+1}\ast_{N}\mathcal{B}_{1} -\mathcal{C}_{1}\ast_{N}\mathcal{X}_{k+1}^{T}\ast_{M}\mathcal{D}_{1},\\ \mathcal{R}_{k+1}^{(2)}=\mathcal{F}_{2}- \mathcal{A}_{2}\ast_{M}\mathcal{X}_{k+1}\ast_{N}\mathcal{B}_{2} -\mathcal{C}_{2}\ast_{N}\mathcal{X}_{k+1}^{T}\ast_{M}\mathcal{D}_{2} \end{array} $$(2.6)and
$$ \begin{array}{@{}rcl@{}} \widetilde{\mathcal{R}}_{k+1}& = &\mathcal{A}_{1}^{T}\!\ast_{N}\!\mathcal{R}_{k+1}^{(1)}\!\ast_{M}\!\mathcal{B}_{1}^{T} +\mathcal{A}_{2}^{T}\!\ast_{M}\!\mathcal{R}_{k+1}^{(2)}\!\ast_{M}\!\mathcal{B}_{2}^{T} +\mathcal{D}_{1}\!\ast_{M}\!(\mathcal{R}_{k+1}^{(1)})^{T}\!\ast_{N}\!\mathcal{C}_{1}\\ &&+\mathcal{D}_{2}\!\ast_{M}\!(\mathcal{R}_{k+1}^{(2)})^{T}\!\ast_{M}\!\mathcal{C}_{2}. \end{array} $$(2.7) -
Step 5 Update the sequences
$$ \mathcal{Q}_{k+1}=\widetilde{\mathcal{R}}_{k+1}+\beta_{k} \mathcal{Q}_{k}, $$(2.8)where:
$$ \beta_{k}=\frac{\|\mathcal{R}_{k+1}^{(1)}\|^{2}+\|\mathcal{R}_{k+1}^{(2)}\|^{2}} {\|\mathcal{R}_{k}^{(1)}\|^{2}+\|\mathcal{R}_{k}^{(2)}\|^{2}}. $$(2.9) -
Step 6 Set k := k + 1, return to step 2.
In what follows, we give the convergence analysis of Algorithm 2.3.
Lemma 2.4
Let \(\{\mathcal {R}_{k}^{(1)}\}\), \(\{\mathcal {R}_{k}^{(2)}\}\), \(\{\widetilde {\mathcal {R}}_{k}\}\) and \(\{\mathcal {Q}_{k}\}\) be generated by Algorithm 2.3. Then
Proof
By the relations (2.4) and (2.6), we immediately have
Similarly, we obtain
It then follows from the relations (2.11), (2.12) and Lemmas 1.4 and 1.5 that
which completes the proof.□
Lemma 2.5
Let \(\{\mathcal {R}_{k}^{(1)}\}\), \(\{\mathcal {R}_{k}^{(2)}\}\) and \(\{\mathcal {Q}_{k}\}\) be generated by Algorithm 2.3. Then
Proof
First, we prove that
This will be shown by induction on k. For k = 1, by Lemma 2.4, the definition of α0 and the fact \(\mathcal {Q}_{0}=\widetilde {\mathcal {R}}_{0}\), we obtain
Meanwhile, by Lemmas 1.3 and 2.4, the relation (2.8) and the definitions of α0 and β0, we get
Therefore, the relation (2.14) is true for k = 1. Assume now that the relation (2.14) is true for some k. Then for k + 1, it follows from Lemma 2.4, the relation (2.8), the definition of αk and the induction principle that
Meanwhile, according to Lemmas 1.3 and 2.4, the relation (2.8) and the definitions of αk and βk, we get
In addition, by Lemma 2.4, the relation (2.8), the definition of αk, and the induction principle, for j = 0,1,2,⋯ , k − 1, we obtain
Meanwhile, according to Lemmas 1.3 and 2.4, the relation (2.8), and the induction principle, for j = 0,1,2,⋯ , k − 1, we get
So the relation (2.14) is true for k + 1. By the induction principle, the relation (2.14) is true for all 0 ≤ j < i ≤ k. For j > i, by Lemma 1.3, one has
which completes the proof.□
Lemma 2.6
Let \(\{\mathcal {R}_{k}^{(1)}\}\), \(\{\mathcal {R}_{k}^{(2)}\}\) and \(\{\mathcal {Q}_{k}\}\) be generated by Algorithm 2.3. If \(\overline {\mathcal {X}}\) is a solution of the tensor equations (2.2), then
Proof
This will be shown by induction on k. For k = 0, by Algorithm 2.3 and Lemma 1.5, we have
Therefore, the relation (2.15) is true for k = 0. Assume now that the relation (2.15) is true for some k. Then for k + 1, it follows from the relation (2.4), the definition of αk, and the induction principle that
Hence
which completes the proof.□
Theorem 2.7
For any initial tensor \(\mathcal {X}_{0}\), the solution of the tensor equations (2.2) can be derived in at most IJ + I2 iterative steps by Algorithm 2.3.
Proof
If there exists some i0(0 ≤ i0 ≤ IJ + I2 − 1) such that \(\|\mathcal {R}_{i_{0}}^{(1)}\|^{2}+\|\mathcal {R}_{i_{0}}^{(2)}\|^{2}=0\), then \(\mathcal {X}_{i_{0}}\) is the solution of the tensor equations (2.2). If \(\|\mathcal {R}_{k}^{(1)}\|^{2}+\|\mathcal {R}_{k}^{(2)}\|^{2}\neq 0(k=0,1,\cdots ,IJ+I^{2}-1)\), by Lemma 2.6, we know \(\mathcal {Q}_{k}\neq \mathcal {O}(k=0,1,\cdots ,IJ+I^{2}-1)\). Then \(\mathcal {X}_{IJ+I^{2}}\) and \(\mathcal {Q}_{IJ+I^{2}}\) can be generated by Algorithm 2.3. By Lemma 2.5, we know that \(\langle \mathcal {R}_{i}^{(1)},\mathcal {R}_{j}^{(1)}\rangle + \langle \mathcal {R}_{i}^{(2)},\mathcal {R}_{j}^{(2)}\rangle =0\) and \(\langle \mathcal {Q}_{i}, \mathcal {Q}_{j}\rangle =0\) for all i, j = 0,1,2,⋯ , IJ + I2 − 1, and i≠j. So the tensor sequence of \(\left (\mathcal {R}_{0}^{(1)}, \mathcal {R}_{0}^{(2)}\right )\), ⋯, \(\left (\mathcal {R}_{IJ + I^{2} - 1}^{(1)} ,\mathcal {R}_{IJ + I^{2} - 1}^{(2)}\right )\) is an orthogonal basis of the linear space \( \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}} \times \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times I_{1}\times \cdots \times I_{N}}\). Since \(\left (\mathcal {R}_{IJ+I^{2}}^{(1)}, \mathcal {R}_{IJ+I^{2}}^{(2)}\right )\!\in \!\mathbb {R}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}\times \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times I_{1}\times \cdots \times I_{N}}\) and \(\langle \mathcal {R}_{IJ+I^{2}}^{(1)},\mathcal {R}_{k}^{(1)}\rangle + \langle \mathcal {R}_{IJ+I^{2}}^{(2)},\mathcal {R}_{k}^{(2)}\rangle =0\) for k = 0,1,⋯ , IJ + I2 − 1, we have \(\mathcal {R}_{IJ+I^{2}}^{(1)}=\mathcal {O}\) and \(\mathcal {R}_{IJ+I^{2}}^{(2)}=\mathcal {O}\), which completes the proof.□
3 Reformulation as tensor equations with two variables
In order to obtain the main result of this section, we first introduce the following lemma.
Lemma 3.1
Let \(\mathcal {A}\in \mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\). If \(\mathcal {A}^{H}\ast _{N}\mathcal {A}=\mathcal {O}\), then \(\mathcal {A}=\mathcal {O}\).
Proof
Let \(\mathcal {A}=(a_{i_{1}{\cdots } i_{N}j_{1}{\cdots } j_{M}})\in \mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\) and \(\mathcal {A}^{H} = (b_{j_{1}{\cdots } j_{M}i_{1}{\cdots } i_{N}})\in \mathbb {C}^{J_{1}\times {\cdots } \times J_{M}\times I_{1}\times \cdots \times I_{N}}\), where \(b_{j_{1}\cdots j_{M}i_{1}{\cdots } i_{N}}= \bar {a}_{i_{1}{\cdots } i_{N}j_{1}{\cdots } j_{M}}\). Then, for any given j1 ∈ J1, ⋯, jM ∈ JM, we have
Since \(\mathcal {A}^{H}\ast _{N}\mathcal {A}=\mathcal {O}\), it follows that \(a_{i_{1}{\cdots } i_{N}j_{1}{\cdots } j_{M}}=0\) for all i1 ∈ I1, ⋯, iN ∈ IN, j1 ∈ J1, ⋯, jM ∈ JM. Hence \(\mathcal {A}=\mathcal {O}\). The proof is completed.□
Theorem 3.2
Let \(\mathcal {A}\!\in \!\mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\). If there exist \(\mathcal {X}\!\in \!\mathbb {C}^{J_{1}\times {\cdots } \times J_{M}\times I_{1}\times \cdots \times I_{N}}\), \(\mathcal {U}\in \mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times I_{1}\times \cdots \times I_{N}}\) and \(\mathcal {V}\in \mathbb {C}^{J_{1}\times {\cdots } \times J_{M}\times J_{1}\times \cdots \times J_{M}}\) satisfying
then \(\mathcal {X}\) is unique and \(\mathcal {X}=\mathcal {A}^{\dagger }\).
Proof
According to the Moore-Penrose equation (1.3), we have
Denote \(\mathcal {U}=(\mathcal {A}^{\dagger })^{H}\ast _{M}\mathcal {A}^{\dagger }\in \mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times I_{1}\times \cdots \times I_{N}}\) and \(\mathcal {V}=\mathcal {A}^{\dagger }\ast _{N}(\mathcal {A}^{\dagger })^{H}\in \mathbb {C}^{J_{1}\times {\cdots } \times J_{M}\times J_{1}\times \cdots \times J_{M}}\). By the relation (3.2), it is easy to see that \(\mathcal {A}^{\dagger }\) satisfies (3.1).
Now, we show that there exists a unique \(\mathcal {X}\) satisfying (3.1). Suppose not, there exists \(\mathcal {X}_{1}\in \mathbb {C}^{J_{1}\times {\cdots } \times J_{M}\times I_{1} \times \cdots \times I_{N}}\) such that \(\mathcal {X}_{1}\neq \mathcal {X}\) and
where \(\mathcal {U}_{1}\in \mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times I_{1}\times \cdots \times I_{N}}\) and \(\mathcal {V}_{1}\in \mathbb {C}^{J_{1}\times {\cdots } \times J_{M}\times J_{1}\times \cdots \times J_{M}}\). Let
It then follows from (3.1), (3.3), and (3.4) that
By some calculations, we immediately have
which, together with Lemma 3.1, yields that \(\mathcal {X}_{2}\ast _{N}\mathcal {A} =\mathcal {O}\). Meanwhile, we find
which, together with Lemma 3.1, yields that \(\mathcal {X}_{2}=\mathcal {O}\). According to the relation (3.4), it follows that \(\mathcal {X}=\mathcal {X}_{1}\). This obtains a contradiction. Hence, we conclude that there exists a unique \(\mathcal {X}\) satisfying (3.1) and \(\mathcal {X}=\mathcal {A}^{\dagger }\). The proof is completed.□
Corollary 3.3
Let \(\mathcal {A}\!\in \!\mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\). If there exist \(\mathcal {X}\!\in \!\mathbb {C}^{J_{1}\times {\cdots } \times J_{M}\times I_{1}\times \cdots \times I_{N}}\) and \(\mathcal {Y}\in \mathbb {C}^{I_{1}\times {\cdots } \times I_{N}\times J_{1} \times \cdots \times J_{M}}\) satisfying
then \(\mathcal {X}=\mathcal {A}^{\dagger }\).
Proof
Let \(\mathcal {U}=\mathcal {Y}\ast _{M}\mathcal {A}^{H}\) and \(\mathcal {V}=\mathcal {A}^{H}\ast _{N}\mathcal {Y}\). Then, by (3.5), we have
It then follows from Theorem 3.2 that \(\mathcal {X}=\mathcal {A}^{\dagger }\). The proof is completed.□
Let
By Corollary 3.3, the computation of Moore-Penrose inverse of tensors in \(\mathbb {R}^{I_{1}\times {\cdots } \times I_{N} \times J_{1}\times \cdots \times J_{M}}\) becomes the following tensor equations with two variables
For the tensor equations (3.7), we apply the tensor form of the conjugate gradient method to find the solution, which is described as in Algorithm 3.4.
Algorithm 3.4 (Conjugate gradient method with tensor form for solving (3.7))
-
Step 0 Input appropriate dimensionality tensors \(\mathcal {A}_{1}\), \({\mathscr{B}}_{1}\), \(\mathcal {C}_{1}\), \(\mathcal {D}_{1}\), \(\mathcal {F}_{1}\) and \(\mathcal {A}_{2} \), \({\mathscr{B}}_{2}\), \(\mathcal {C}_{2}\), \(\mathcal {D}_{2}\), \(\mathcal {F}_{2}\) in (2.2). Choose the initial tensors \(\mathcal {X}_{0}\in \mathbb {R}^{J_{1}\times {\cdots } \times J_{M}\times I_{1}\times \cdots \times I_{N}}\) and \(\mathcal {Y}_{0}\in \mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\).
-
Step 1 Compute
$$ \begin{array}{@{}rcl@{}} \mathcal{R}_{0}^{(1)}& = &\mathcal{F}_{1}-\mathcal{A}_{1}\!\ast_{M}\!\mathcal{X}_{0}\!\ast_{N}\!\mathcal{B}_{1} -\mathcal{C}_{1}\!\ast_{N}\!\mathcal{Y}_{0}\!\ast_{M}\!\mathcal{D}_{1},\\ \mathcal{R}_{0}^{(2)}& = &\mathcal{F}_{2}- \mathcal{A}_{2}\!\ast_{M}\!\mathcal{X}_{0}\!\ast_{N}\!\mathcal{B}_{2} -\mathcal{C}_{2}\!\ast_{N}\!\mathcal{Y}_{0}\!\ast_{M}\!\mathcal{D}_{2}, \end{array} $$and
$$ \begin{array}{@{}rcl@{}} \widetilde{\mathcal{R}}_{0}^{(1)}& = &\mathcal{A}_{1}^{T}\!\ast_{N}\!\mathcal{R}_{0}^{(1)}\!\ast_{M}\!\mathcal{B}_{1}^{T} +\mathcal{A}_{2}^{T}\!\ast_{M}\!\mathcal{R}_{0}^{(2)}\ast_{N}\mathcal{B}_{2}^{T},\\ \widetilde{\mathcal{R}}_{0}^{(2)}& = &\mathcal{C}_{1}^{T}\!\ast_{N}\!\mathcal{R}_{0}^{(1)}\!\ast_{M}\!\mathcal{D}_{1}^{T} +\mathcal{C}_{2}^{T}\!\ast_{M}\!\mathcal{R}_{0}^{(2)}\ast_{N}\mathcal{D}_{2}^{T}. \end{array} $$Set \(\mathcal {P}_{0}=\widetilde {\mathcal {R}}_{0}^{(1)}\), \(\mathcal {Q}_{0}=\widetilde {\mathcal {R}}_{0}^{(2)}\) and k = 0.
-
Step 2 If \(\|\mathcal {R}_{k}^{(1)}\|^{2}+\|\mathcal {R}_{k}^{(2)}\|^{2}=0\), stop. Otherwise, go to step 3.
-
Step 3 Update the sequences
$$ \mathcal{X}_{k+1}=\mathcal{X}_{k}+\alpha_{k} \mathcal{P}_{k},~\mathcal{Y}_{k+1}=\mathcal{Y}_{k}+\alpha_{k} \mathcal{Q}_{k}, $$(3.8)where
$$ \alpha_{k}=\frac{\|\mathcal{R}_{k}^{(1)}\|^{2}+\|\mathcal{R}_{k}^{(2)}\|^{2}} {\|\mathcal{P}_{k}\|^{2}+\|\mathcal{Q}_{k}\|^{2}}. $$(3.9) -
Step 4 Compute
$$ \mathcal{R}_{k+1}^{(1)} = \mathcal{F}_{1} - \mathcal{A}_{1}\ast_{M}\mathcal{X}_{k+1} \ast_{N}\mathcal{B}_{1} - \mathcal{C}_{1}\ast_{N}\mathcal{Y}_{k+1}\ast_{M}\mathcal{D}_{1}, $$$$ ~\mathcal{R}_{k+1}^{(2)} = \mathcal{F}_{2} - \mathcal{A}_{2}\ast_{M}\mathcal{X}_{k+1}\ast_{N}\mathcal{B}_{2} - \mathcal{C}_{2}\ast_{N}\mathcal{Y}_{k+1}\ast_{M}\mathcal{D}_{2}, $$$$ \widetilde{\mathcal{R}}_{k+1}^{(1)}=\mathcal{A}_{1}^{T}\ast_{N}\mathcal{R}_{k+1}^{(1)}\ast_{M}\mathcal{B}_{1}^{T} +\mathcal{A}_{2}^{T}\ast_{M}\mathcal{R}_{k+1}^{(2)}\ast_{N}\mathcal{B}_{2}^{T}, $$$$ \widetilde{\mathcal{R}}_{k+1}^{(2)}=\mathcal{C}_{1}^{T}\ast_{N}\mathcal{R}_{k+1}^{(1)}\ast_{M} \mathcal{D}_{1}^{T} +\mathcal{C}_{2}^{T}\ast_{M}\mathcal{R}_{k+1}^{(2)}\ast_{N}\mathcal{D}_{2}^{T}. $$ -
Step 5 Update the sequences
$$ \mathcal{P}_{k+1}=\widetilde{\mathcal{R}}_{k+1}^{(1)}+\beta_{k} \mathcal{P}_{k},~ \mathcal{Q}_{k+1}=\widetilde{\mathcal{R}}_{k+1}^{(2)}+\beta_{k} \mathcal{Q}_{k}, $$(3.10)where
$$ \beta_{k}=\frac{\|\mathcal{R}_{k+1}^{(1)}\|^{2}+\|\mathcal{R}_{k+1}^{(2)}\|^{2}} {\|\mathcal{R}_{k}^{(1)}\|^{2}+\|\mathcal{R}_{k}^{(2)}\|^{2}}. $$(3.11) -
Step 6 Set k := k + 1, return to step 2.
Lemma 3.5
Let \(\{\mathcal {R}_{k}^{(1)}\}\), \(\{\mathcal {R}_{k}^{(2)}\}\), \(\{\widetilde {\mathcal {R}}_{k}^{(1)}\}\), \(\{\widetilde {\mathcal {R}}_{k}^{(2)}\}\), \(\{\mathcal {P}_{k}\}\) and \(\{\mathcal {Q}_{k}\}\) be generated by Algorithm 3.4. Then
Proof
By step 4 of Algorithm 3.4 and the relation (3.8), we immediately have
Similarly, we obtain
It then follows from the relations (3.12), (3.13) and Lemma 1.4 that
which completes the proof.□
Lemma 3.6
Let \(\{\mathcal {R}_{k}^{(1)}\}\), \(\{\mathcal {R}_{k}^{(2)}\}\), \(\{\mathcal {P}_{k}\}\) and \(\{\mathcal {Q}_{k}\}\) be generated by Algorithm 3.4. Then
Proof
First, we prove that
This will be shown by induction on k. For k = 1, by Lemma 3.5, the fact \(\mathcal {P}_{0}=\widetilde {\mathcal {R}}_{0}^{(1)}\) and \(\mathcal {Q}_{0}=\widetilde {\mathcal {R}}_{0}^{(2)}\) and the definition of α0, we obtain
Meanwhile, by Lemmas 1.3 and 3.5 and the relations (3.9)–(3.11), we get
Therefore, the relation (3.14) is true for k = 1. Assume now that the relation (3.14) is true for some k. Then for k + 1, it follows from Lemma 3.5, the relations (3.9) and (3.10), and the induction principle that
Meanwhile, according to Lemmas 1.3 and 3.5, the relation (3.10), and the definitions of αk and βk, it follows that
In addition, by Lemma 3.5, the relation (3.10), the definition of αk, and the induction principle, for j = 0,1,2,⋯ , k − 1, we obtain
Meanwhile, according to Lemma 3.5, the relation (3.10) and the induction principle, for j = 0,1,2,⋯ , k − 1, we get
So the relation (3.14) is true for k + 1. By the induction principle, the relation (3.14) is true for all 0 ≤ j < i ≤ k. For j > i, by Lemma 1.3, it follows that
and
which completes the proof.□
Lemma 3.7
Let \((\mathcal {X},\mathcal {Y})\in \mathbb {R}^{J_{1}\times {\cdots } \times J_{M}\times I_{1}\times \cdots \times I_{N}}\times \mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\) be a solution of the tensor equations (3.7). Then for any initial tensors \(\mathcal {X}_{0}\in \mathbb {R}^{J_{1}\times {\cdots } \times J_{M}\times I_{1} \times \cdots \times I_{N}}\) and \(\mathcal {Y}_{0}\in \mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\), we have
where the sequences \(\{\mathcal {X}_{k}\}\), \(\{\mathcal {Y}_{k}\}\), \(\{\mathcal {P}_{k}\}\), \(\{\mathcal {Q}_{k}\}\), \(\{\mathcal {R}_{k}^{(1)}\}\) and \(\{\mathcal {R}_{k}^{(2)}\}\) are generated by Algorithm 3.4.
Proof
This will be shown by induction on k. For k = 0, by Lemmas 1.4 and 1.5, it follows that
Therefore, the relation (3.15) is true for k = 0. Assume now that the relation (3.15) is true for some k. Then for k + 1, by the relation (3.8), the definition of αk, and the induction principle, we have
Hence
which completes the proof.□
Theorem 3.8
For any initial tensors \(\mathcal {X}_{0}\in \mathbb {R}^{J_{1}\times {\cdots } \times J_{M}\times I_{1}\times \cdots \times I_{N}}\) and \(\mathcal {Y}_{0}\in \mathbb {R}^{I_{1}\times {\cdots } \times I_{N}\times J_{1}\times \cdots \times J_{M}}\), the solution of the tensor equations (3.7) can be derived in at most 2IJ iterative steps by Algorithm 3.4.
Proof
If there exists some i0(0 ≤ i0 ≤ 2IJ − 1) such that \(\|\mathcal {R}_{i_{0}}^{(1)}\|^{2}+\|\mathcal {R}_{i_{0}}^{(2)}\|^{2}=0\), then \(\left (\mathcal {X}_{i_{0}},\mathcal {Y}_{i_{0}}\right )\) is a solution of the tensor equations (3.7). If \(\|\mathcal {R}_{k}^{(1)}\|^{2}+\|\mathcal {R}_{k}^{(2)}\|^{2}\neq 0(k=0,1,\cdots ,2IJ-1)\), by Lemma 3.7, we know \(\left (\mathcal {P}_{k},\mathcal {Q}_{k}\right )\neq \left (\mathcal {O}, \mathcal {O}\right )\in \mathbb {R}^{J_{1}\times \cdots \times J_{M}\times I_{1} \times \cdots \times I_{N}}\times \mathbb {R}^{I_{1} \times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}(k=0,1,\cdots ,2IJ-1)\). Then \(\left (\mathcal {X}_{2IJ}, \mathcal {Y}_{2IJ}\right )\) and \(\left (\mathcal {P}_{2IJ},\mathcal {Q}_{2IJ}\right )\) can be generated by Algorithm 3.4. By Lemma 3.6, we know that \(\langle \mathcal {R}_{i}^{(1)},\mathcal {R}_{j}^{(1)}\rangle + \langle \mathcal {R}_{i}^{(2)},\mathcal {R}_{j}^{(2)}\rangle =0\) and \(\langle \mathcal {P}_{i}, \mathcal {P}_{j}\rangle +\langle \mathcal {Q}_{i}, \mathcal {Q}_{j}\rangle =0\) for all i, j = 0,1,2,⋯, 2IJ − 1, and i≠j. So the tensor sequence of \(\left (\mathcal {R}_{0}^{(1)}, \mathcal {R}_{0}^{(2)}\right ), \cdots , \left (\mathcal {R}_{2IJ-1}^{(1)} ,\mathcal {R}_{2IJ-1}^{(2)}\right )\) is an orthogonal basis of the linear space \( \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}\times \mathbb {R}^{J_{1}\times \cdots \times J_{M}\times I_{1}\times \cdots \times I_{N}}\). Since \(\left (\mathcal {R}_{2IJ}^{(1)}, \mathcal {R}_{2IJ}^{(2)}\right )\in \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}\times \mathbb {R}^{J_{1}\times \cdots \times J_{M}\times I_{1}\times \cdots \times I_{N}}\) and \(\langle \mathcal {R}_{2IJ}^{(1)},\mathcal {R}_{k}^{(1)}\rangle + \langle \mathcal {R}_{2IJ}^{(2)},\mathcal {R}_{k}^{(2)}\rangle =0\) for k = 0,1,⋯ ,2IJ − 1, we have \(\mathcal {R}_{2IJ}^{(1)}=\mathcal {O}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times J_{1}\times \cdots \times J_{M}}\) and \(\mathcal {R}_{2IJ}^{(2)}=\mathcal {O}\in \mathbb {R}^{J_{1}\times \cdots \times J_{M}\times I_{1}\times \cdots \times I_{N}}\). The proof is completed.□
4 Numerical experiments
In this section, we give some numerical examples to show the performance of our proposed iterative algorithms. All of the tests are implemented in MATLAB R2015a with the machine precision 10− 16 on a personal computer (Intel (R) Core (TM)i7-5500U), where the CPU is 2.40 GHz and the memory is 8.0 GB. All the implementations are based on the functions from the MATLAB Tensor Toolbox developed by Bader and Kolda [1]. For example, we illustrate how to use the Einstein product in Matlab tensor toolbox. For tensors \(\mathcal {A}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N}\times K_{1}\times \cdots \times K_{N}}\) and
\({\mathscr{B}}\in \mathbb {R}^{K_{1}\times \cdots \times K_{N}\times J_{1}\times \cdots \times J_{M}}\), the Einstein product \(\mathcal {A}\ast _{N}{\mathscr{B}}\) can be implemented by using the tensor command “ttt”. More concretely
In this section, we first verify the validity of the proposed numerical algorithm. Second, we demonstrate the accuracy of the proposed numerical algorithm.
4.1 Validity of the proposed method
Example 1
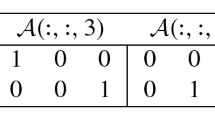
In this example, we use Maltab function tenrand([m n p q]) to generate the tensor \(\mathcal {A}\). Such as, we take m = 4, n = 6 and p = q = 5, and we let the tensor \(\mathcal {A}\) as follows.
In this example, we test the numerical performance of Algorithm 2.3. By using Algorithm 2.3, after 367 and 374 iterative steps, we obtain \(\mathcal {A}^{\{1,4\}}\) and \(\mathcal {A}^{\{1,3\}}\), respectively. According to Lemma 2.1, we know \(\mathcal {A}^{\dagger }=\mathcal {A}^{(1,4)}\ast _{N} \mathcal {A}\ast _{N} \mathcal {A}^{(1,3)}\). Hence, we obtain the Moore-Penrose inverse \(\mathcal {A}^{\dagger }\) as follows.
At this case, the residuals of tensor equations (1), (2), (3), and (4) in (1.3) (see Definition 1.6) are 8.3508e − 07, 4.5770e − 07, 1.1107e − 06, and 1.0290e − 06, respectively. This confirms that \(\mathcal {A}^{\dagger }\) is indeed the numerical result of the Moore-Penrose inverse of \(\mathcal {A}\). Hence, the Moore-Penrose inverse of a tensor can be obtained by Algorithm 2.3 effectively.
Example 2
In this example, we use Maltab function tenrand([m n p q]) to generate the tensor \(\mathcal {A}\). Such as, we take m = 4, n = 3, p = 5 and q = 4, and we let the tensor \(\mathcal {A}\) as follows.
In this example, we test the numerical performance of Algorithm 3.4. The stopping criterion is considered as the k th iteration satisfies:
where ε = 10− 6. After 89 iterative steps, we obtain the Moore-Penrose inverse of \(\mathcal {A}\) as follows.
At this case, the residuals of tensor equations (1), (2), (3), and (4) in (1.3) (see Definition 1.6) are 3.9308e − 07, 1.1978e − 07, 2.5707e − 07, and 4.9847e − 07, respectively. This indicates that \(\mathcal {A}^{\dagger }\) is indeed the Moore-Penrose inverse of \(\mathcal {A}\). Hence, Algorithm 3.4 can calculate the Moore-Penrose inverse effectively.
4.2 Accuracy of numerical solutions
If a good approximation to the Moore-Penrose inverse \(\mathcal {A}^{\dagger }\) of a tensor \(\mathcal {A}\) is known in advance by using another method, then we can perform Algorithm 3.4 in order to obtain solutions of high accuracy.
Let ϕ be a map which satisfying
where \(\text {ivec}(\mathbf {i},\mathbb {I})=i_{1}+\sum \limits _{r=2}^{N}(i_{r}-1)\prod \limits _{u=1}^{r-1}I_{u}\) and \(\text {ivec}(\mathbf {j},\mathbb {J})=j_{1}+\sum \limits _{s=2}^{M}(j_{s}-1)\prod \limits _{v=1}^{s-1}J_{v}\). Let \(\mathcal {A}\in \mathbb {R}^{I_{1}\times \cdots \times I_{N} \times J_{1}\times \cdots \times J_{M}}\). Assume that the SVD of \(\phi (\mathcal {A})\) satisfies \(\phi (\mathcal {A})=\mathbf {U}\mathbf {S}\mathbf {V}^{H}\). According to [4, 25], the SVD of \(\mathcal {A}\) is
where \(\mathcal {U}=\phi ^{-1}(\mathbf {U})\), \(\mathcal {S}=\phi ^{-1}(\mathbf {S})\) and \(\mathcal {V}=\phi ^{-1}(\mathbf {V})\). Then, by Theorem 3.4 of [25], the Moore-Penrose inverse of \(\mathcal {A}\) exists uniquely and satisfies
in which \(\mathcal {S}^{\dagger }=(\mathcal {S}^{\dagger }_{j_{1}{\cdots } j_{M}i_{1}{\cdots } i_{N}})\in \mathbb {R}^{J_{1}\times \cdots \times J_{M}\times I_{1}\times \cdots \times I_{N}}\) is defined by
Hence, we only need the “reshape” command and the singular value decomposition of \(\phi (\mathcal {A})\) to obtain the Moore Penrose inverse of a tensor \(\mathcal {A}\).
By applying MATLAB’s svd function to the matrix \(\phi (\mathcal {A})\) and using the “reshape” command, we obtain the Moore-Penrose inverse of \(\mathcal {A}\), denoted by \(\mathcal {A}^{\dagger }_{\text {svd}}\). We can perform Algorithm 3.4 with the initial tensor \(\mathcal {X}_{0}=\mathcal {A}^{\dagger }_{\text {svd}}\) and \(\mathcal {Y}_{0}\) being arbitrary in order to obtain a more accurate Moore-Penrose inverse \(\mathcal {A}^{\dagger }_{\text {new}}\). To see the degree of accuracy, we compare the mean of the Fronenius norms
and
If Algorithm 3.4 gives a more accurate Moore-Penrose inverse of tensor \(\mathcal {A}\), the following inequality is expected to hold
Our as many as 200 experiments with randomly chosen tensor \(\mathcal {A}=100*\text {tenrand}([4 3~5~3])-50\) show that (4.2) holds for all 200 tensors of \(\mathcal {A}\). This means that Algorithm 3.4 enhances the accuracy of the Moore-Penrose inverse obtained by MATLAB’s svd function. In other words, Algorithm 3.4 always generates the Moore-Penrose inverse of high accuracy in the end.
5 Concluding remarks
The aim of this paper is to give the numerical study on the Moore-Penrose inverse of tensors via the Einstein product. For this purpose, we first transform the calculation of {1,4}-inverse of a tensor \(\mathcal {A}\) (\(\mathcal {A}^{\{1,4\}}\)) and the {1,3}-inverse of a tensor \(\mathcal {A}\) (\(\mathcal {A}^{\{1,3\}}\)) into finding the solution of a class of tensor equations via the Einstein product with one variable. Then, by the known property \(\mathcal {A}^{\dagger }=\mathcal {A}^{(1,4)}\ast _{N} \mathcal {A}\ast _{N} \mathcal {A}^{(1,3)}\) (see [3, Theorem 2.32]), we obtain the Moore-Penrose inverse \(\mathcal {A}^{\dagger }\). Unlike the above method, we derive the equivalent characterization of the Moore-Penrose inverse of tensors. Then, we solve the tensor equations via the Einstein product with two variables by means of the conjugate gradient method. In this way, we implement the numerical calculation of the Moore-Penrose inverse of tensors via the Einstein product.
References
Bader, B.W., Kolda, T.G., et al.: MATLAB Tensor Toolbox Version 2.5, 2012. http://www.sandia.gov/tgkolda/TensorToolbox/
Behera, R., Maji, S., Mohapatra, R.N.: Weighted Moore-Penrose inverses of arbitrary order tensors. Comput. Appl. Math. 39, 284 (2020)
Behera, R., Mishra, D.: Further results on generalized inverses of tensors via the Einstein product. Linear Multilinear Algebra 65, 1662–1682 (2017)
Brazell, M., Li, N., Navasca, C., Tamon, C.: Solving multilinear systems via tensor inversion. SIAM J. Matrix Anal. Appl. 34, 542–570 (2013)
Bu, C., Zhang, X., Zhou, J., Wang, W., Wei, Y.: The inverse, rank and product of tensors. Linear Algebra Appl. 446, 269–280 (2014)
Bu, C., Zhou, J., Wei, Y.: E-cospectral hypergraphs and some hypergraphs determined by their spectra. Linear Algebra Appl. 459, 397–403 (2014)
Burdick, D.S., Tu, X.M., McGown, L.B., Millican, D.W.: Resolution of multicomponent fluorescent mixtures by analysis of the excitation-emission frequency array. J. Chemom. 4, 15–28 (1990)
Cooper, J., Dutle, A.: Spectra of uniform hypergraphs. Linear Algebra Appl. 436, 3268–3292 (2012)
Ding, W., Wei, Y.: Fast Hankel tensor-vector product and its application to exponential data fitting. Numer. Linear Algebra Appl. 22, 814–832 (2015)
Eldén, L.: Matrix Methods in Data Mining and Pattern Recognition. SIAM, Philadelphia (2007)
Hu, S., Qi, L.: Algebraic connectivity of an even uniform hypergraph. J. Comb. Optim. 24, 564–579 (2012)
Huang, B.H., Ma, C.F.: An iterative algorithm to solve the generalized Sylvester tensor equations. Linear Multilinear Algebra 68, 1175–1200 (2020)
Huang, B.H., Xie, Y.J., Ma, C.F.: Krylov subspace methods to solve a class of tensor equations via the Einstein product. Numer. Linear Algebra Appl. 26, e2254 (2019)
Huang, B.H., Ma, C.F.: Global least squares methods based on tensor form to solve a class of generalized Sylvester tensor equations. Appl. Math. Comput. 369, 124892 (2020)
Huang, B.H., Li, W.: Numerical subspace algorithms for solving the tensor equations involving Einstein product. Numer. Linear Algebra Appl (2020). https://doi.org/10.1002/nla.2351
Kolda, T., Bader, B.: Tensor decompositions and applications. SIAM Rev. 51, 455–500 (2009)
Lai, W.M., Rubin, D., Krempl, E.: Introduction to Continuum Mechanics. Butterworth Heinemann, Oxford (2009)
Li, B.W., Tian, S., Sun, Y.S., Hu, Z.M.: Schur-decomposition for 3D matrix equations and its applications in solving radiative discrete ordinates equations discretized by Chebyshev collocation spectral method. J. Comput. Phys. 229, 1198–1212 (2010)
Li, B.W., Sun, Y.S., Zhang, D.W.: Chebyshev collocation spectral methods for coupled radiation and conduction in a concentric spherical participating medium. ASME J. Heat Transfer. 131, 062701–062709 (2009)
Li, W., Ng, M.: On the limiting probability distribution of a transition probability tensor. Linear Multilinear Algebra 62, 362–385 (2014)
Li, Z., Ling, C., Wang, Y., Yang, Q.: Some advances in tensor analysis and polynomial optimization. Oper. Res. Trans. 18, 134–148 (2014)
Ji, J., Wei, Y.: Weighted Moore-Penrose inverses and fundamental theorem of even-order tensors with Einstein product. Front. Math. China 12, 1319–1337 (2017)
Ji, J., Wei, Y.: The Drazin inverse of an even-order tensor and its application to singular tensor equations. Comput. Math. Appl. 75, 3402–3413 (2018)
Jin, H., Bai, M., Bentez, J., Liu, X.: The generalized inverses of tensors and an application to linear models. Comput. Math. Appl. 74, 385–397 (2017)
Liang, M., Zheng, B.: Further results on Moore-Penrose inverses of tensors with application to tensor nearness problems. Comput. Math. Appl. 77, 1282–1293 (2019)
Ma, H.F., Li, N., Stanimirović, P.S., Katsikis, V.N.: Perturbation theory for Moore-Penrose inverse of tensor via Einstein product. Comput. Appl. Math. 38, 111 (2019)
Martin, C.D., Shafer, R., LaRue, B.: An order-p tensor factorization with applications in imaging. SIAM J. Sci. Comput. 35, 474–490 (2013)
Panigrahy, K., Behera, R., Mishra, D.: Reverse-order law for the Moore-Penrose inverses of tensors. Linear Multilinear Algebra 68, 246–264 (2020)
Panigrahy, K., Mishra, D.: On reverse-order law of tensors and its application to additive results on Moore–Penrose inverse. RACSAM 184, 114 (2020)
Panigrahy, K., Mishra, D.: Extension of Moore-Penrose inverse of tensor via Einstein product. Linear Multilinear Algebra (2020) https://doi.org/10.1080/03081087.2020.1748848
Smilde, A., Bro, R., Geladi, P.: Multi-Way Analysis: Applications in the Chemical Sciences. Wiley, West Sussex (2004)
Sun, L., Zheng, B., Bu, C., Wei, Y.: Moore-Penrose inverse of tensors via Einstein product. Linear Multilinear Algebra 64, 686–698 (2016)
Vlasic, D., Brand, M., Pfister, H., Popovic, J.: Face transfer with multilinear models. ACM Trans. Graph. 24, 426–433 (2005)
Wang, Q.W., Xu, X.: Iterative algorithms for solving some tensor equations. Linear Multilinear Algebra 67, 1325–1349 (2019)
Funding
This research is supported by China Postdoctoral Science Foundation (Grant No. 2019M660203) and National Natural Science Foundation of China (Grant Nos. 12001211, 12071159, 61976053)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Huang, B. Numerical study on Moore-Penrose inverse of tensors via Einstein product. Numer Algor 87, 1767–1797 (2021). https://doi.org/10.1007/s11075-021-01074-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-021-01074-0