Nonlinear dynamic response and bifurcation of variable thickness sandwich conical shell with internal resonance

Abstract

This paper explores the nonlinear dynamic responses and bifurcations of the truncated sandwich simply supported porous conical shell with varying thickness under 1:1 internal resonance. Two skins with carbon fiber and a core with porous aluminum foam, which has an exponentially variable thickness along the generator and various porosity distribution types along the core thickness, make up the sandwich shell structure with varying stiffness. The porous shell structure is affected by a combination of the in-plane load, transverse excitation, thermal stress and aerodynamic force, which is formulated by employing first-order piston theory with a modified term for curvature. By way of FSDT, von-Karman geometrical formulations, Hamilton’s principle and Galerkin procedure, the nonlinear dynamic formulations in ordinary differential form for the variable stiffness porous sandwich shell structure are identified. The averaged equations in polar and Cartesian coordinate forms for the sandwich structure under the combined circumstance of 1:1 internal resonance, first-order main resonance and 1/2 subharmonic resonance are determined by multiple-scale technique. The frequency-amplitude and force–amplitude characteristic curves, phase portraits, time history and bifurcation diagrams are exhibited by numerical simulation. The impacts of the damping coefficient, detuning parameters, temperature increment, transverse and in-plane excitations on the nonlinear dynamics and bifurcation behaviors of variable thickness sandwich porous conical shell are demonstrated.

1 Introduction

As an important part of the carrier rocket, the fairing is designed to protect the satellite and other payloads from harmful environments such as aerodynamic forces, aerodynamic heating and acoustic vibration, so special materials that have excellent mechanical properties are required. Porous metal foam materials have a large pore size and specific surface area, which give them lightweight, high temperature resistant and energy absorption properties. Corresponding to special locations and sizes of the pores, the porous metal foam can produce continuously varying physical properties along the thickness [1,2,3]. As observed in Fig. 1, the rocket structure’s top fairing component can be reduced to a combined model of a truncated conical shell and a negligibly small top shell. The sandwich structure, which is made of two high-strength skins and a lightweight core, is particularly suitable for the airfoils of high-speed vehicles and segments subject to extreme aerodynamic forces and heating, such as the fairing shells of carrier rockets [4, 5]. The variable thickness fairing shells can enhance structural stiffness, eliminate stress concentration, and reduce centrifugal stress and structural mass [6, 7]. The fairing shells are constantly exposed to complicated forces, such as thermal stresses aerodynamic pressure, in-plane and transverse forces, leading to complex nonlinear dynamic behaviors. Specifically, the nonlinear internal resonance behaviors can lead to increased structural vibration, increased noise, and even damage and breakage [8,9,10]. Therefore, it is essential and remarkable to explore the nonlinear dynamics of the variable thickness truncated porous sandwich conical shell under complicated forces and internal resonance.

Fig. 1

The model of a rocket structure with faring component

Recently, sandwich structures with porous metal foam material have gained considerable interest from practical applications and theoretical research due to their superior mechanical performance. Zhu et al. [11] examined the natural vibration behaviors of sandwich skew plates composed of two pure metal skins and a porous metal foam core. Using the isogeometric method and modified Riks approach, the various buckling characteristics of porous metal sandwich skew plates exposed to compressive forces were found by Sengar et al. [12]. Zhou et al. [13] discussed the effects of the impact location, metal foam core’s thickness and distribution on the impact characteristic of sandwich square plates, and optimized the geometric pathways by analytical formulation. Xin et al. [14] presented a Navier solution for obtaining natural vibration frequencies and modes of porous metal foam sandwich thick beam. Xiao et al. [15] proposed a novel lightweight porous mental foam-filled corrugated sandwich structure, which had outstanding load-bearing and heat transfer properties. The impact characteristics of sandwich beams made of aluminum foam porous core and mild steel surface sheet with various thickness distributions were tested by Guo et al. [16]. Keleshteri et al. [17] determined the fundamental frequencies and the related buckling loads of the functionally graded porous sandwich cylindrical panels through the Navier approach. Grag et al. [18, 19] researched the vibration and static properties of metal foam sandwich beams and plates, and examined the impact of boundary condition, geometry, and porosity parameters on sandwich beam behavior. Zhang et al. [20] examined analytically and numerically the plastic characteristic of a porous sandwich rectangular tube under clamped support and transverse load.

It can be noted that numerous researchers have explored the dynamic response characteristics of the variable thickness structures. Tornabene et al. [21,22,23] adopted the higher-order ESL method and GDQ approach for determining modal and natural frequency of doubly-cured anisotropic shell structures with varying geometry, thickness and boundary. The vibration behavior analysis of varying thickness orthotropic plates with various boundaries, and geometric and material parameters was performed by Song et al. [24] providing a novel generalized analytical approach. By utilizing the classical thin shell framework and Rayleigh–Ritz technique, a porous cantilever variable thickness plate was modeled by Hao et al. [25] to discover the free vibration behavior of the spinning twisted plate. Liu et al. [26] provided a meshless generalized finite difference technique to examine the bending characteristics of thin plates with varying thickness and different boundaries. A novel shear deformation plate theory with trigonometric functions for obtaining natural frequencies of FGM two-directional varying thickness plates was established by Hoang et al. [27]. Kumar et al. [28] explored the impact of porosity parameter, foundation and varying thickness on the vibration behaviors of an exponential FGM plate placed on an orthotropic elastic foundation. Foroutan et al. [29] employed the approach of fourth-order P–T and multiple scales to determine the resonant characteristic and nonlinear vibration behavior of varying thickness toroidal FGM shell structures subject to external loads. Cao et al. [30] examined the nonlinear vibration of the arches with varying thickness and cross-sectional shapes by utilizing the differential quadrature procedure and direct iteration approach. Sofiyev et al. [31,32,33,34] utilized the Galerkin technique and Runge–Kutta procedure to analyze the dynamic buckling characteristics of the conical shell with varying thickness and FGM, and explored a novel expression about modified Young’s moduli considering the vacancies and scale effects.

Furthermore, a large number of literature and research focused on the internal resonance behaviors of rings, tubes, beams, plates and shells under complex loads. Casalotti et al. [35] conducted research on 1:2 and 1:3 internal resonance responses of a thin tube subject to external force, and found potential energy exchange from the local modes to the global modes. Wu et al. [36] utilized the Galerkin procedure and approximate multiple-scale technique to explore numerically the nonlinear dynamics of a flexible beam-ring configuration with 1:1 internal resonance. The nonlinear internal resonant characteristics of a cantilevered thin shell were analyzed by Qiu et al. [37] utilizing the Galerkin technique and asymptotic perturbation method. Khaniki et al. [38] adopted a novel strategy for nonlinear forced vibration investigation of nanoplates with nonlocal strain gradients, whose specifically combined parameters can cause different internal resonant behaviors. Employing the modified Lindstedt Poincare method, Ding et al. [39, 40] explored the impacts of initial geometric defect, GPLs and pore parameters on the nonlinear resonance responses of grapheme platelets reinforced metal foam (GPLRMF) cylindrical and doubly curved shells with geometric defect. Additionally, Ding et al. [41, 42] also used the methods of variable amplitudes (MVA) and multiple scales to nonlinear forced vibration and resonance responses of axially traveling GPLRMF shell structures. The nonlinear vibration responses of GPLRMF conical shells with 1:1 internal resonance were investigated by Saboori et al. [43] adopting the Galerkin procedure, perturbation and multiple-scale analysis. Based on the HSDT, Galerkin method and MVA, Zhang et al. [44] analyzed the principal and internal coupled resonance characteristics of rotating GPLRMF cylindrical shells, and found the multiple jumping behavior and bifurcation phenomenon of the coupled resonance. Employing FSDT, Galerkin procedure and multi-scale technique, Sofiyev et al. [45,46,47,48] investigated the nonlinear forced vibration behaviors including primary resonance of carbon nanotubes reinforced double-curved shells and laminated plates, and discussed the influences of CNT distribution patterns, nonlinearity and external force on the forced vibration frequencies, and also examined the effects of transverse shear deformations, geometric and material parameters on natural frequencies of truncated FGM sandwich conical shell.

However, rare researchers have reported the modeling and nonlinear internal resonance analysis of the porous metal foam sandwich truncated variable thickness conical shell subject to complicated loads. In this work, the nonlinear internal resonant responses of varying thickness porous truncated sandwich simply supported conical shell subject to the thermal stress, supersonic aerodynamic force, transverse and in-plane loads. The sandwich structure is made of multi-layer carbon fiber skins and an aluminum foam core with exponentially varying thickness. The porous foam’s porosity distribution schemes have five various patterns containing Pattern-V, Pattern-Λ, Pattern-U, Pattern-X and Pattern-O. Utilizing the FSDT, von-Karman geometrical formulations, Hamilton’s principle, Galerkin technique and introducing dimensionless parameters, the dimensionless 2DOF nonlinear ordinary differential dynamic formulations for the porous sandwich shell structure with variable stiffness are determined. The multiple-scale technique is employed for the perturbation investigation to obtain the averaged formulations under 1:1 internal resonance. The characteristics of the frequency-amplitude responses, force–amplitude curves, bifurcations, periodic and chaotic behaviors are analyzed by numerical calculations. The impacts of the detuning parameters, damping coefficient, temperature increment, transverse and in-plane loads on the nonlinear dynamic responses and bifurcation performances of the variable stiffness truncated porous shell structure with 1:1 internal resonance, first-order main resonance and 1/2 subharmonic resonance are examined.

2 Nonlinear dynamic formulations

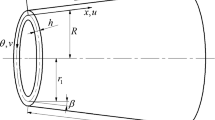
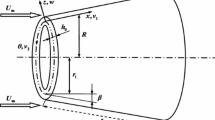
Figure 2 depicts the geometric model of a truncated variable stiffness conical shell, which has varying total thickness $h$ along the length $L$, semi-vertical angle $\beta$, minimal mid-surface radius $r_{1}$ and maximal mid-plane radius $r_{2}$. Furthermore, the averaged radius at any position along the generatrix is presented as $R = r_{1} + x\sin \beta$. Consider a coordinate system $\left( {x,\theta ,z} \right)$ that has an origin positioned at the top of the middle plane of the variable thickness structure, and assume that the sandwich conical shell has $N$ layers with a cross-ply lamination order of $\left( {0/90} \right)_{s}$.

Fig. 2

Geometric description of truncated variable stiffness sandwich conical shell

Moreover, the sandwich structure is composed of two skins with an identical number of carbon fiber layers and thickness $h_{f}$, as well as a middle aluminum foam core layer with a varying thickness $h_{c}$ along the generatrix, which can take the following expression of [49]

$$ h_{c} \left( x \right) = h_{2} \left[ {1 - \left( {\frac{{h_{1} }}{{h_{2} }}} \right)\left( {1 - \frac{x}{L}} \right)} \right]^{{N_{x} }} $$

(1)

where $N_{x}$ implies the thickness function’s exponent, whereas $h_{{1}}$ and $h_{{2}}$ independently symbolize the maximal and minimal thickness of the middle porous core along the $x$ direction. The largest and smallest thicknesses are positioned at the top and bottom of the sandwich structure to minimize the centrifugal stress during rapid rotation, separately.

As presented in Fig. 2, the sandwich varying thickness structure is subjected to the supersonic flow $U_{\infty }$, uniformly distributed transverse excitation $F\cos {(}\Omega_{1} T_{0} {)}$ and in-plane excitation $p_{1} \cos (\Omega_{2} T_{0} )$. By utilizing the first-order piston framework, the aerodynamic load $P_{a}$ created by supersonic flow is vertical to the longitudinal direction of the sandwich structure and can be described as [50]

$$ P_{a} = - \frac{{\gamma_{a} p_{\infty } M_{a}^{2} }}{{\sqrt {M_{a}^{2} - 1} }}\left[ {w_{,x} + \left( {\frac{{M_{a}^{2} - 2}}{{M_{a}^{2} - 1}}} \right)\frac{1}{{M_{a} a_{\infty } }}\dot{w} - \frac{1}{{2R\sqrt {M_{a}^{2} - 1} }}w} \right] $$

(2)

where $M_{a}$, $\gamma_{a}$, $p_{\infty }$ and $a_{\infty }$ signify the Mach number, adiabatic index, free flow static pressure and sound velocity, individually. The related transverse displacement, aerodynamic damping, and modified term for curvature are determined by the three terms of the above formulation, independently.

Five distinct middle aluminum porous foam’s porosity distribution patterns, including Pattern-V, Pattern-Λ, Pattern-U, Pattern-X and Pattern-O, along with the relative mass density, Young’s modulus and sketch, are displayed in Table 1 [1,2,3, 51]. The pores in Pattern-V and Pattern-Λ types have continuous and monotonous variation through the exterior surface to the interior surface, as opposed to the uniform pores in Pattern-U distribution. Additionally, the pores in Pattern-X and Pattern-O types are dispersed constantly through the mid-surface to the interior and exterior layers of the variable thickness sandwich conical shell.

Table 1 Porosity distribution types of aluminum foam

As displayed in Table 1, the $E_{max}$ and $\rho_{max}$ individually indicate the highest Young’s modulus and mass density, while $N_{c}$ and $\rho_{c}$ symbolize the coefficients of porosity and mass density for all porous distribution. In particular, $\lambda$ and $\rho_{c}^{*}$ refer to the parameters for the pores of Pattern-U distribution. Their formulations are expressed as

$$ \rho_{c} = 1 - \sqrt {1 - N_{c} } $$

(3a)

$$ \lambda = \frac{1}{{N_{c} }}\left( {1 - \left( {1 - \frac{{2\rho_{c} }}{\pi }} \right)^{2} } \right) $$

(3b)

$$ \rho_{c}^{ * } = \frac{{1 - \sqrt {1 - N_{c} } }}{\lambda } $$

(3c)

Within the framework of FSDT, the three displacements of the variable thickness sandwich structure can be expressed as

$$ u\left( {x,\theta ,z} \right) = u_{0} \left( {x,\theta } \right) + z\phi_{x} \left( {x,\theta } \right) $$

(4a)

$$ v\left( {x,\theta ,z} \right) = v_{0} \left( {x,\theta } \right) + z\phi_{\theta } \left( {x,\theta } \right) $$

(4b)

$$ w\left( {x,\theta ,z} \right) = w_{0} \left( {x,\theta } \right) $$

(4c)

in which $u_{0}$, $v_{0}$ and $w_{0}$ independently demonstrate the mid-plane displacements of arbitrary position, while $\phi_{x}$ and $\phi_{\theta }$ symbolize the mid-surface normal rotations around circumferential and longitudinal axis, separately.

Through the combination of the von-Karman geometric nonlinear formulations with displacements in Eq. (4a–c), the nonlinear strains are defined as

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{\left( 0 \right)} } \\ {\varepsilon_{\theta }^{\left( 0 \right)} } \\ {\gamma_{x\theta }^{\left( 0 \right)} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{\left( 1 \right)} } \\ {\varepsilon_{\theta }^{\left( 1 \right)} } \\ {\gamma_{x\theta }^{\left( 1 \right)} } \\ \end{array} } \right\}, \left\{ {\begin{array}{*{20}c} {\gamma_{\theta z} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\phi_{\theta } + \frac{1}{R}\left( {\frac{{\partial w_{0} }}{\partial \theta } - v_{0} \cos \beta } \right)} \\ {\phi_{x} + \frac{{\partial w_{0} }}{\partial x}} \\ \end{array} } \right\} $$

(5)

where

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{\left( 0 \right)} } \\ {\varepsilon_{\theta }^{\left( 0 \right)} } \\ {\gamma_{x\theta }^{\left( 0 \right)} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \\ {\frac{1}{R}\left( {u_{0} \sin \beta + w_{0} \cos \beta + \frac{{\partial v_{0} }}{\partial \theta }} \right) + \frac{1}{2}\frac{1}{{R^{2} }}\left( {\frac{{\partial w_{0} }}{\partial \theta }} \right)^{2} } \\ {\frac{{\partial v_{0} }}{\partial x} + \frac{1}{R}\left( {\frac{{\partial u_{0} }}{\partial \theta } - v_{0} \sin \beta + \frac{{\partial w_{0} }}{\partial x}\frac{{\partial w_{0} }}{\partial \theta }} \right)} \\ \end{array} } \right\} $$

(6a)

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{\left( 1 \right)} } \\ {\varepsilon_{\theta }^{\left( 1 \right)} } \\ {\gamma_{x\theta }^{\left( 1 \right)} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \phi_{x} }}{\partial x}} \\ {\frac{1}{R}\left( {\frac{{\partial \phi_{\theta } }}{\partial \theta } + \phi_{x} \sin \beta } \right)} \\ {\frac{{\partial \phi_{\theta } }}{\partial x} + \frac{1}{R}\left( {\frac{{\partial \phi_{x} }}{\partial \theta } - \phi_{\theta } \sin \beta } \right)} \\ \end{array} } \right\} $$

(6b)

By utilizing generalized Hooke’s law and accounting for the heating stress impact, every layer’s constitutive relationships of the porous sandwich structure with varying thickness are prescribed as [52]

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\sigma_{x\theta } } \\ {\sigma_{\theta z} } \\ {\sigma_{xz} } \\ \end{array} } \right\}^{\left( k \right)} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & 0 & 0 & 0 \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & 0 & 0 & 0 \\ 0 & 0 & {\overline{Q}_{66} } & 0 & 0 \\ 0 & 0 & 0 & {\overline{Q}_{44} } & 0 \\ 0 & 0 & 0 & 0 & {\overline{Q}_{55} } \\ \end{array} } \right]^{\left( k \right)} \left\{ {\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\gamma_{x\theta } } \\ {\gamma_{\theta z} } \\ {\gamma_{xz} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\alpha_{x} } \\ {\alpha_{\theta } } \\ {2\alpha_{x\theta } } \\ 0 \\ 0 \\ \end{array} } \right\}\Delta T\left( z \right)} \right\}^{\left( k \right)} $$

(7)

where $k$ represents every layer’s number, $\Delta T$ stands for the linear temperature increment as opposed to a specified temperature, and $\overline{Q}_{ij}$ $\left( {i,j = 1,2,4,5,6} \right)$ imply the converted stiffness factors. Moreover, $\alpha_{x}$, $\alpha_{\theta }$ and $\alpha_{x\theta }$ denote the converted heating expansion factors.

Due to the properties of isotropic material, the middle porous aluminum foam layer has identical thermal expansion factors $\alpha$ along $x$ and $\theta$ directions, while the shear component $\alpha_{x\theta }$ is zero. Additionally, the converted thermal expansion factors of two carbon fiber skins can be identified through

$$ \alpha_{x} = \alpha_{1} \cos^{2} \gamma + \alpha_{2} \sin^{2} \gamma $$

(8a)

$$ \alpha_{\theta } = \alpha_{1} \sin^{2} \gamma + \alpha_{2} \cos^{2} \gamma $$

(8b)

$$ \alpha_{x\theta } = \left( {\alpha_{1} - \alpha_{2} } \right)\sin \gamma \cos \gamma $$

(8c)

where $\alpha_{{1}}$ and $\alpha_{2}$ denote the factors of heating expansion along the $x_{1}$ and $x_{2}$ directions of the skins, separately.

The aluminum foam core layer’s stiffness coefficients $\overline{Q}_{ij}$ concerning various porosity distribution schemes are formulated as the Eq. (9). While for the two orthotropic skins made of carbon fiber, the converted stiffness factors $\overline{Q}_{ij}$ are determined by the Eq. (10a, b).

$$ \overline{Q}_{11} = \frac{{E_{T} \left( z \right)}}{{1 - \nu^{2} }},\;\overline{Q}_{12} = \frac{{\nu E_{T} \left( z \right)}}{{1 - \nu^{2} }},\;\overline{Q}_{22} = \overline{Q}_{11} ,\;\overline{Q}_{44} = \frac{{E_{T} \left( z \right)}}{{2\left( {1 + \nu } \right)}},\overline{Q}_{55} = \overline{Q}_{66} = \overline{Q}_{44} $$

(9)

$$ \left\{ {\begin{array}{*{20}c} {\overline{Q}_{11} } \\ {\overline{Q}_{12} } \\ {\overline{Q}_{22} } \\ {\overline{Q}_{66} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {C^{4} } & {2C^{2} S^{2} } & {S^{4} } & {4C^{2} S^{2} } \\ {C^{2} S^{2} } & {C^{4} + S^{4} } & {C^{2} S^{2} } & { - 4C^{2} S^{2} } \\ {S^{4} } & {2C^{2} S^{2} } & {C^{4} } & {4C^{2} S^{2} } \\ {C^{2} S^{2} } & { - 2C^{2} S^{2} } & {C^{2} S^{2} } & {\left( {C^{2} - S^{2} } \right)^{2} } \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} {Q_{11} } \\ {Q_{12} } \\ {Q_{22} } \\ {Q_{66} } \\ \end{array} } \right\} $$

(10a)

$$ \left\{ {\begin{array}{*{20}c} {\overline{Q}_{44} } \\ {\overline{Q}_{55} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {C^{2} } & {S^{2} } \\ {S^{2} } & {C^{2} } \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} {Q_{44} } \\ {Q_{55} } \\ \end{array} } \right\},\;C = \cos \gamma ,\;S = \sin \gamma $$

(10b)

in which subscript $T$, $\nu$ and $\gamma$ sequentially demonstrate the type of porosity pattern, Poisson’s ratio and stacking angle between adjacent layers of the varying thickness sandwich structure. Whereas the stiffness factors $Q_{ij}$ of the middle porous layers are calculated according to the engineering constants, as below

$$ Q_{11} = \frac{{E_{1} }}{{1 - \nu_{12} \nu_{21} }},\;Q_{12} = \frac{{\nu_{12} E_{1} }}{{1 - \nu_{12} \nu_{21} }},\;Q_{22} = \frac{{E_{2} }}{{1 - \nu_{12} \nu_{21} }},\;Q_{66} = G_{12} ,\;Q_{44} = G_{23} ,\;Q_{55} = G_{13} $$

(11)

By replacing the above strain–displacement and constitutive relations to energy terms of the shell and then applying Hamilton’s principle, the nonlinear dynamic formulations in following partial differential form for the porous sandwich truncated conical shell are eventually determined as [8,9,10, 53]

$$ N_{xx,x} + \frac{1}{R}N_{xx} \sin \beta + \frac{1}{R}N_{x\theta ,\theta } - \frac{1}{R}N_{\theta \theta } \sin \beta = I_{0} \ddot{u}_{0} + I_{1} \ddot{\phi }_{x} $$

(12a)

$$ N_{x\theta ,x} + \frac{2}{R}N_{x\theta } \sin \beta + \frac{1}{R}N_{\theta \theta ,\theta } + \frac{1}{R}Q_{\theta } \cos \beta = I_{0} \ddot{v}_{0} + I_{1} \ddot{\phi }_{\theta } $$

(12b)

$$ \begin{aligned} Q_{x,x} + & \frac{1}{R}Q_{x} \sin \beta + \frac{1}{R}Q_{\theta ,\theta } + N_{xx,x} \frac{{\partial w_{0} }}{\partial x} + N_{xx} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{R}N_{xx} \frac{{\partial w_{0} }}{\partial x}\sin \beta + \frac{1}{R}N_{x\theta ,x} \frac{{\partial w_{0} }}{\partial \theta } \\ + & \frac{1}{R}N_{x\theta ,\theta } \frac{{\partial w_{0} }}{\partial x} + \frac{2}{R}N_{x\theta} \frac{{\partial^{2} w_{0} }}{\partial x\partial \theta } - \frac{1}{R}N_{\theta \theta } \cos \beta + \frac{1}{{R^{2} }}N_{\theta \theta ,\theta } \frac{{\partial w_{0} }}{\partial \theta } + \frac{1}{{R^{2} }}N_{\theta \theta } \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }} \\ + & F_{1} \cos \left( {\Omega_{1} t} \right) - p_{1} \cos \left( {\Omega_{2} t} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + P_{a} - \kappa \dot{w}_{0} = I_{0} \ddot{w}_{0} \\ \end{aligned} $$

(12c)

$$ M_{xx,x} + \frac{1}{R}M_{xx} \sin \beta + \frac{1}{R}M_{x\theta ,\theta } - \frac{1}{R}M_{\theta \theta } \sin \beta - Q_{x} = I_{1} \ddot{u}_{0} + I_{2} \ddot{\phi }_{x} $$

(12d)

$$ M_{x\theta ,x} + \frac{2}{R}M_{x\theta } \sin \beta + \frac{1}{R}M_{\theta \theta ,\theta } - Q_{\theta } = I_{1} \ddot{v}_{0} + I_{2} \ddot{\phi }_{\theta } $$

(12e)

in which one dot and two dot superscript sequentially demonstrate the first-order and second-order derivative of the relative time, and $\kappa$ signifies the damping factor of the sandwich structure. All the inertia components for the variable stiffness sandwich shell structure can be extracted by Eq. (13), while the in-plane and shear components of moment resultants and stress resultants, which consider the impact of the thermal stress, are prescribed as Eq. (14).

$$ I_{i} = \sum\limits_{k = 1}^{N} {\int_{zk}^{{z_{k + 1} }} {z^{i} \rho^{(k)} } dz} ,\;\left( {i = 0,1,2} \right) $$

(13)

$$ \left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{\theta \theta } } \\ {N_{x\theta } } \\ {M_{xx} } \\ {M_{\theta \theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 \\ {A_{12} } & {A_{22} } & 0 & {B_{12} } & {B_{22} } & 0 \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 \\ {B_{12} } & {B_{22} } & 0 & {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {B_{66} } & 0 & 0 & {D_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{x}^{\left( 0 \right)} } \\ {\varepsilon_{\theta }^{\left( 0 \right)} } \\ {\gamma_{x\theta }^{\left( 0 \right)} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\varepsilon_{x}^{\left( 1 \right)} } \\ {\varepsilon_{\theta }^{\left( 1 \right)} } \\ {\gamma_{x\theta }^{\left( 1 \right)} } \\ \end{array} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {N_{xx}^{T} } \\ {N_{\theta \theta }^{T} } \\ {N_{x\theta }^{T} } \\ {M_{xx}^{T} } \\ {M_{\theta \theta }^{T} } \\ {M_{x\theta }^{T} } \\ \end{array} } \right\} $$

$$ \left\{ {\begin{array}{*{20}c} {Q_{x} } \\ {Q_{\theta } } \\ \end{array} } \right\} = K\left[ {\begin{array}{*{20}c} {A_{55} } & 0 \\ 0 & {A_{44} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{\theta z} } \\ \end{array} } \right\} $$

(14)

where $K$ expresses the shear correction component and is approximately defined as $5/6$. All the stiffness components in the above formulations can be achieved by Eqs. (15a,b), and the in-plane thermal moment resultants and stress resultants for the porous structure are identified as Eq. (16).

$$ \left( {A_{ij} ,B_{ij} ,D_{ij} } \right) = \sum\limits_{k = 1}^{N} {\int_{{z_{k} }}^{{z_{k + 1} }} {\overline{Q}_{ij}^{\left( k \right)} } \left( {1,z,z^{2} } \right)dz} ,\;\left( {i,j = 1,2,6} \right) $$

(15a)

$$ A_{ij} = \sum\limits_{k = 1}^{N} {\int_{{Z_{k} }}^{{Z_{k + 1} }} {\overline{Q}_{ij}^{(k)} (1,z,z^{2} )dz} } ,\;(i,j = 4,5) $$

(15b)

$$ \left( {\left\{ \begin{gathered} N_{xx}^{T} \\ N_{\theta \theta }^{T} \\ N_{x\theta }^{T} \\ \end{gathered} \right\},\left\{ \begin{gathered} M_{xx}^{T} \\ M_{\theta \theta }^{T} \\ M_{x\theta }^{T} \\ \end{gathered} \right\}} \right) = \sum\limits_{k = 1}^{N} {\int_{{z_{k} }}^{{z_{k + 1} }} {\left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & 0 \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & 0 \\ 0 & 0 & {\overline{Q}_{66} } \\ \end{array} } \right]}^{\left( k \right)} \left\{ \begin{gathered} \alpha_{x} \\ \alpha_{\theta } \\ 2\alpha_{x\theta } \\ \end{gathered} \right\}^{\left( k \right)} \left( {\Delta T,\Delta Tz} \right)dz} $$

(16)

Introducing the abovementioned Eqs. (13)–(16) into Eqs. (12a–e), the simplified nonlinear dynamic equations in the form of five generalized displacements for the sandwich structure with variable thickness can be formulated as

$$ L_{11} u_{0} + L_{12} v_{0} + L_{13} w_{0} + L_{14} \phi_{x} + L_{15} \phi_{\theta } + L_{16} + N_{1} = I_{0} \ddot{u}_{0} + I_{1} \ddot{\phi }_{x} $$

(17a)

$$ L_{21} u_{0} + L_{22} v_{0} + L_{23} w_{0} + L_{24} \phi_{x} + L_{25} \phi_{\theta } + L_{26} + N_{2} = I_{0} \ddot{v}_{0} + I_{1} \ddot{\phi }_{\theta } $$

(17b)

$$ \begin{aligned} L_{{31}} u_{0} + & L_{{32}} v_{0} + \left( {L_{{33}} + L_{{37}} p_{1} } \right)w_{0} + L_{{34}} \phi _{x} + L_{{35}} \phi _{\theta } \\ + & L_{{36}} + N_{3} + F_{1} \cos \left( {\Omega _{1} t} \right) + P_{a} - \kappa \dot{w}_{0} = I_{0} \ddot{w}_{0} \\ \end{aligned} $$

(17c)

$$ L_{41} u_{0} + L_{42} v_{0} + L_{43} w_{0} + L_{44} \phi_{x} + L_{45} \phi_{\theta } + L_{46} + N_{4} = I_{1} \ddot{u}_{0} + I_{2} \ddot{\phi }_{x} $$

(17d)

$$ L_{51} u_{0} + L_{52} v_{0} + L_{53} w_{0} + L_{54} \phi_{x} + L_{55} \phi_{\theta } + L_{56} + N_{5} = I_{1} \ddot{v}_{0} + I_{2} \ddot{\phi }_{\theta } $$

(17e)

where $L_{ij}$ and $N_{i}$ imply the linear and nonlinear symbols in partial differential form, and their explicit formulations are mentioned in the earlier research [54, 55]. Moreover,

$$ L_{37} = - \cos \left( {\Omega_{2} t} \right)d_{11} $$

(18)

The boundary condition is assumed as simply supported at two ends of the porous varying thickness structure and illustrated as [56, 57]

$$ N_{xx} = M_{xx} = v_{0} = w_{0} = \phi_{\theta } = 0\;{\text{at}}\;x = {\text{0 and }}x = L $$

(19)

The displacements and transverse excitation functions of the varying thickness structure are developed by utilizing the double trigonometric series to meet the aforementioned boundary condition, as below [58]

$$ u_{0} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {u_{mn} } \left( t \right)\cos \left( {\frac{m\pi x}{L}} \right)\cos \left( {n\theta } \right)} $$

(20a)

$$ v_{0} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {v_{mn} } \left( t \right)\sin \left( {\frac{m\pi x}{L}} \right)\sin \left( {n\theta } \right)} $$

(20b)

$$ w_{0} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {w_{mn} } \left( t \right)\sin \left( {\frac{m\pi x}{L}} \right)\cos \left( {n\theta } \right)} $$

(20c)

$$ \phi_{x} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {\phi_{{x_{mn} }} } \left( t \right)\cos \left( {\frac{m\pi x}{L}} \right)\cos \left( {n\theta } \right)} $$

(20d)

$$ \phi_{\theta } = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {\phi_{{\theta_{mn} }} } \left( t \right)\sin \left( {\frac{m\pi x}{L}} \right)\sin \left( {n\theta } \right)} $$

(20e)

$$ F = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {F_{mn} } \sin \left( {\frac{m\pi x}{L}} \right)\cos \left( {n\theta } \right)} $$

(20f)

in which m and n refer to the full-wave number in generatrix direction and the half-wave number in circumferential direction, separately. Furthermore, $F_{mn}$, $u_{mn} \left( t \right)$, $v_{mn} \left( t \right)$, $w_{mn} \left( t \right)$, $\phi_{{x_{mn} }} \left( t \right)$ and $\phi_{{\theta_{mn} }} \left( t \right)$ individually stand for the amplitudes of transverse excitation and time-related displacement for different modes.

The nonlinear vibrations of the first two modes for the porous sandwich conical shell are much larger than those of other modes, and the weakly nonlinear internal resonance behaviors are taken into consideration. Consequently, we can utilize the first two linear modes to approximately solve the nonlinear dynamic equations of the conical shell with variable thickness [10]. The in-plane and rotational inertia components in Eq. (17a–e) can be overlooked since their effects on the system’s nonlinear vibrations are considerably lower than those of the radial inertia component [59]. It’s feasible to focus on the first two modes of the radial displacement $w_{0}$.

Introducing the abovementioned double series into the simplified nonlinear dynamic Eqs. (17a–e) and utilizing the Galerkin technique, the in-plane and rotational displacements $u_{0}$, $v_{0}$, $\phi_{x}$ and $\phi_{\theta }$ are stated as the functions of radial displacement $w_{0}$. The 2DOF nonlinear dynamic formulations in following ordinary differential form for the varying thickness porous sandwich shell structure are ultimately constructed by introducing the in-plane and rotational displacement functions into Eq. (17c), as below

$$ \ddot{W}_{1} + \mu_{1} \dot{W}_{1} + \omega_{1}^{2} W_{1} + \zeta_{11} W_{1}^{3} + \zeta_{12} W_{1} W_{2}^{2} + \zeta_{13} W_{1} p_{1} \cos \left( {\Omega_{2} t} \right) = \zeta_{14} F_{1} \cos \left( {\Omega_{1} t} \right) $$

(21a)

$$ \ddot{W}_{2} + \mu_{2} \dot{W}_{2} + \omega_{2}^{2} W_{2} + \zeta_{21} W_{2}^{3} + \zeta_{22} W_{1}^{2} W_{2} + \zeta_{23} W_{2} p_{1} \cos \left( {\Omega_{2} t} \right) = \zeta_{24} F_{2} \cos \left( {\Omega_{1} t} \right) $$

(21b)

where $\omega_{{1}}^{{2}} = \zeta_{{{15}}} + \zeta_{{{16}}} p_{\infty }$, $\omega_{{2}}^{{2}} = \zeta_{{{25}}} + \zeta_{{{26}}} p_{\infty }$. $W_{1}$ and $W_{2}$ represent the amplitudes of radial displacement for the first two modes, while $F_{1}$ and $F_{2}$ denote the amplitudes of transverse excitation for the first two modes. To establish the dimensionless dynamic formulations for the porous shell structure with variable stiffness, the above variables and coefficients are converted as

$$ \begin{gathered} \tau = \omega _{1} t,\;W_{1} = q_{1} h_{1} ,\;W_{2} = q_{2} h_{1} ,\;\bar{\Omega }_{1} = \frac{{\Omega _{1} }}{{\omega _{1} }},\;\bar{\Omega }_{2} = \frac{{\Omega _{2} }}{{\omega _{2} }},\; \hfill \\ \bar{\mu }_{1} = \frac{{\mu _{1} }}{{\omega _{1} }},\;\bar{\mu }_{2} = \frac{{\mu _{2} }}{{\omega _{2} }},\;\bar{\omega }_{1} = \frac{{\omega _{1} }}{{\omega _{1} }},\;\bar{\omega }_{2} = \frac{{\omega _{2} }}{{\omega _{1} }},\;\bar{p}_{1} = \frac{{p_{1} }}{{h_{1}^{2} }},\; \hfill \\ \bar{F}_{1} = \frac{{F_{1} }}{{h_{1}^{3} }},\;\bar{F}_{2} = \frac{{F_{2} }}{{h_{1}^{3} }},\;\bar{\zeta }_{{ij}} = \frac{{\zeta _{{ij}} h_{1}^{2} }}{{\omega _{1}^{2} }},\;(i = 1,2,\;j = 1,2,3,4) \hfill \\ \end{gathered} $$

(22)

By applying Eq. (22) into Eqs. (21a, b), the dimensionless nonlinear dynamic formulations for variable thickness porous conical shell structure are ultimately obtained, as follows

$$ \ddot{q}_{1} + \overline{\mu }_{1} \dot{q}_{1} + \overline{\omega }_{1}^{2} q_{1} + \overline{\zeta }_{11} q_{1}^{3} + \overline{\zeta }_{12} q_{1} q_{2}^{2} + \overline{\zeta }_{13} q_{1} \overline{p}_{1} \cos \left( {\overline{\Omega }_{2} t} \right) = \overline{\zeta }_{14} \overline{F}_{1} \cos \left( {\overline{\Omega }_{1} t} \right) $$

(23a)

$$ \ddot{q}_{2} + \overline{\mu }_{2} \dot{q}_{2} + \overline{\omega }_{2}^{2} q_{2} + \overline{\zeta }_{21} q_{2}^{3} + \overline{\zeta }_{22} q_{1}^{2} q_{2} + \overline{\zeta }_{23} q_{2} \overline{p}_{1} \cos \left( {\overline{\Omega }_{2} t} \right) = \overline{\zeta }_{24} \overline{F}_{2} \cos \left( {\overline{\Omega }_{1} t} \right) $$

(23b)

3 Perturbation analysis

In this part, the multiple-scale technique is utilized for the perturbation analysis of sandwich porous structure with varying thickness to overcome the problem of internal resonance [60]. By inputting a small perturbation factor $\varepsilon$, all the transverse displacement-related terms, damping and excitation terms are assumed to be tiny quantities as the following converted form.

$$ q_{i} = \varepsilon ^{{\frac{1}{2}}} \tilde{w}_{i} ,\;\bar{\mu }_{i} = \varepsilon \tilde{\mu }_{i} ,\;\bar{p}_{1} = \varepsilon \tilde{p}_{1} ,\;\bar{F}_{i} = \varepsilon ^{{\frac{3}{2}}} \tilde{F}_{i} ,\;(i = 1,2) $$

(24)

The horizontal and curved bars on the dimensionless parameters are neglected for simplicity, and the dimensionless nonlinear dynamic formulations are rewritten by introducing Eq. (24) into Eqs. (23a,b), as follows

$$ \ddot{w}_{1} + \varepsilon \mu_{1} \dot{w}_{1} + \omega_{1}^{2} w_{1} + \varepsilon \zeta_{11} w_{1}^{3} + \varepsilon \zeta_{12} w_{1} w_{2}^{2} + \varepsilon \zeta_{13} w_{1} p_{1} \cos \left( {\Omega_{2} \tau } \right) = \varepsilon \zeta_{14} F_{1} \cos \left( {\Omega_{1} \tau } \right) $$

(25a)

$$ \ddot{w}_{2} + \varepsilon \mu_{2} \dot{w}_{2} + \omega_{2}^{2} w_{2} + \varepsilon \zeta_{21} w_{2}^{3} + \varepsilon \zeta_{22} w_{1}^{2} w_{2} + \varepsilon \zeta_{23} w_{2} p_{1} \cos \left( {\Omega_{2} \tau } \right) = \varepsilon \zeta_{24} F_{2} \cos \left( {\Omega_{1} \tau } \right) $$

(25b)

Based on the multiple-scale technique, it is supposed that Eqs. (25a, b) has an approximate solution of the following form

$$ w_{1} = x_{10} \left( {T_{0} ,T_{1} } \right) + \varepsilon x_{11} \left( {T_{0} ,T_{1} } \right) + \cdots $$

(26a)

$$ w_{2} = x_{20} \left( {T_{0} ,T_{1} } \right) + \varepsilon x_{21} \left( {T_{0} ,T_{1} } \right) + \cdots $$

(26b)

where $T_{0} = \tau$, $T_{1} = \varepsilon \tau$.

Afterwards, the related differential operators are identified as

$$ \frac{d}{d\tau } = \frac{\partial }{{\partial T_{0} }}\frac{{\partial T_{0} }}{\partial \tau } + \frac{\partial }{{\partial T_{1} }}\frac{{\partial T_{1} }}{\partial \tau } + \cdots = D_{0} + \varepsilon D_{1} + \cdots, $$

(27a)

$$ \frac{{d^{2} }}{{d\tau^{2} }} = \left( {D_{0} + \varepsilon D_{1} + \cdots } \right)^{2} = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \cdots ,$$

(27b)

where $D_{k} = \frac{\partial }{{\partial T_{k} }}$, $\left( {k = 0,1} \right)$.

By applying Eqs. (26a, b)–(27a, b) to Eqs. (25a, b) and making the factors of the identical power about small value $\varepsilon$ in two sides of the equations equal, the formulations are derived as follows.

Order $\varepsilon^{0}$:

$$ D_{{0}}^{{2}} x_{{{10}}} + \omega_{{1}}^{{2}} x_{{{10}}} = 0 $$

(28a)

$$ D_{{0}}^{{2}} x_{{{20}}} + \omega_{{2}}^{{2}} x_{{{20}}} = {0} $$

(28b)

Order $\varepsilon^{1}$:

$$ D_{0}^{2} x_{11} + \omega_{1}^{2} x_{11} = - 2D_{0} D_{1} x_{10} - \mu_{1} D_{0} x_{10} - \zeta_{11} x_{10}^{3} - \zeta_{12} x_{10} x_{20}^{2} - \zeta_{13} p_{1} \cos (\Omega_{2} T_{0} )x_{10} + \zeta_{14} F_{1} \cos (\Omega_{1} T_{0} ) $$

(29a)

$$ D_{0}^{2} x_{21} + \omega_{2}^{2} x_{21} = - 2D_{0} D_{1} x_{20} - \mu_{2} D_{0} x_{20} - \zeta_{21} x_{20}^{3} - \zeta_{22} x_{10}^{2} x_{20} - \zeta_{23} p_{1} \cos (\Omega_{2} T_{0} )x_{20} + \zeta_{24} F_{2} \cos (\Omega_{1} T_{0} ) $$

(29b)

Solving Eqs. (28a, b), the solution in following complex form is prescribed as

$$ x_{{{10}}} = A_{{1}} \left( {T_{{1}} } \right)e^{{i\omega_{{1}} T_{{0}} }} + \overline{A}_{{1}} \left( {T_{{1}} } \right)e^{{ - i\omega_{{1}} T_{{0}} }} $$

(30a)

$$ x_{{{20}}} = A_{{2}} \left( {T_{{1}} } \right)e^{{i\omega_{{2}} T_{{0}} }} + \overline{A}_{{2}} \left( {T_{{1}} } \right)e^{{ - i\omega_{{2}} T_{{0}} }} $$

(30b)

in which $\overline{A}_{{1}}$ and $\overline{A}_{{2}}$ denotes the complex conjugate components of $A_{{1}}$ and $A_{{2}}$.

Introducing Eqs. (30a, b) into Eqs. (29a, b) can obtain

$$ \begin{aligned} D_{0}^{2} x_{{11}} + \omega _{1}^{2} x_{{11}} = & \left( { - 2i\omega _{1} D_{1} A_{1} - i\mu _{1} \omega _{1} A_{1} - 3\zeta _{{11}} A_{1}^{2} \bar{A}_{1} - 2\zeta _{{12}} A_{1} A_{2} \bar{A}_{2} - \frac{1}{2}\zeta _{{13}} A_{1} p_{1} e^{{i\Omega _{2} T_{0} }} } \right)e^{{i\omega _{1} T_{0} }} \\ & - \zeta _{{11}} A_{1}^{3} e^{{3i\omega _{1} T_{0} }} - \zeta _{{12}} A_{1} A_{2}^{2} e^{{i(\omega _{1} + 2\omega _{2} )T_{0} }} - \zeta _{{12}} \bar{A}_{1} A_{2}^{2} e^{{i(2\omega _{2} - \omega _{1} )T_{0} }} \\ & - \frac{1}{2}\zeta _{{13}} \bar{A}_{1} p_{1} e^{{i(\Omega _{2} - \omega _{1} )T_{0} }} + \frac{1}{2}\zeta _{{14}} F_{1} e^{{i\Omega _{1} T_{0} }} + CC \\ \end{aligned} $$

(31a)

$$ \begin{aligned} D_{0}^{2} x_{{21}} + \omega _{2}^{2} x_{{21}} = & \left( { - 2i\omega _{2} D_{1} A_{2} - i\mu _{2} \omega _{2} A_{2} - 3\zeta _{{21}} A_{2}^{2} \bar{A}_{2} - 2\zeta _{{22}} A_{1} \bar{A}_{1} A_{2} - \frac{1}{2}\zeta _{{23}} A_{2} p_{1} e^{{i\Omega _{2} T_{0} }} } \right)e^{{i\omega _{2} T_{0} }} \\ & - \zeta _{{21}} A_{2}^{3} e^{{3i\omega _{2} T_{0} }} - \zeta _{{22}} A_{1}^{2} A_{2} e^{{i(2\omega _{1} + \omega _{2} )T_{0} }} - \zeta _{{22}} A_{1}^{2} \bar{A}_{2} e^{{i(2\omega _{1} - \omega _{2} )T_{0} }} \\ & - \frac{1}{2}\zeta _{{23}} \bar{A}_{2} p_{1} e^{{i(\Omega _{2} - \omega _{2} )T_{0} }} + \frac{1}{2}\zeta _{{24}} F_{2} e^{{i\Omega _{1} T_{0} }} + CC \\ \end{aligned} $$

(31b)

in which $CC$ indicates the complex conjugate components corresponding to previous components.

Considering the circumstance of 1:1 internal resonance, first-order main resonance and 1/2 subharmonic resonance, the transverse force’s frequency is approximately identical to first-order natural frequency for the porous sandwich conical shell with varying thickness, while the in-plane force’s frequency is almost identical to twice first-order natural frequency. As a result, the resonance relationships of the system are stated by adding the detuning parameters $\sigma_{{1}}$ and $\sigma_{{2}}$, as shown below.

$$ \Omega _{1} = \omega _{1} + \varepsilon \sigma _{1} ,\;\omega _{2} = \omega _{1} + \varepsilon \sigma _{2} ,\;\Omega _{2} = 2\Omega _{1} $$

(32)

Introducing Eq. (32) into the right end of Eq. (31a, b) yields the following conditions for eliminating the secular term

$$ 2i\omega _{1} D_{1} A_{1} + i\mu _{1} \omega _{1} A_{1} + 3\zeta _{{11}} A_{1}^{2} \bar{A}_{1} + 2\zeta _{{12}} A_{1} A_{2} \bar{A}_{2} + \frac{1}{2}\zeta _{{13}} \bar{A}_{1} p_{1} e^{{2i\sigma _{1} T_{1} }} + \zeta _{{12}} \bar{A}_{1} A_{2}^{2} e^{{2i\sigma _{2} T_{1} }} - \frac{1}{2}\zeta _{{14}} F_{1} e^{{i\sigma _{1} T_{1} }} = 0 $$

(33a)

$$ 2i\omega _{2} D_{1} A_{2} + i\mu _{2} \omega _{2} A_{2} + 3\zeta _{{21}} A_{2}^{2} \bar{A}_{2} + 2\zeta _{{22}} A_{1} \bar{A}_{1} A_{2} + \frac{1}{2}\zeta _{{23}} \bar{A}_{2} p_{1} e^{{2i(\sigma _{1} - \sigma _{2} )T_{1} }} + \zeta _{{22}} A_{1}^{2} \bar{A}_{2} e^{{ - 2i\sigma _{2} T_{1} }} - \frac{1}{2}\zeta _{{24}} F_{2} e^{{i(\sigma _{1} - \sigma _{2} )T_{1} }} = 0 $$

(33b)

The two amplitudes $A_{{1}}$ and $A_{{2}}$ can be stated as the functions of following polar coordinate form.

$$ A_{1} (T_{1} ) = \frac{1}{2}a_{1} (T_{1} )e^{{i\phi _{1} (T_{1} )}} ,A_{2} (T_{1} ) = \frac{1}{2}a_{2} (T_{1} )e^{{i\phi _{2} (T_{1} )}} $$

(34)

By removing Eq. (34) in Eqs. (33a, b) and dividing the real and imaginary components, the averaged formulations in polar coordinate form for the variable thickness porous sandwich shell structure can be found as follows

$$ \dot{a}_{1} = - \frac{{\mu_{1} a_{1} }}{2} - \frac{{\zeta_{12} a_{1} a_{2}^{2} \sin (2\gamma_{1} )}}{{8\omega_{1} }} - \frac{{\zeta_{13} p_{1} a_{1} \sin (2\gamma_{1} + 2\gamma_{2} )}}{{4\omega_{1} }} + \frac{{\zeta_{14} F_{1} \sin (\gamma_{1} + \gamma_{2} )}}{{2\omega_{1} }} $$

(35a)

$$ \begin{aligned} a_{1} \dot{\gamma }_{1} = & a_{1} \sigma _{1} - a_{2} (\sigma _{1} - \sigma _{2} ) + \frac{{3\zeta _{{21}} a_{2}^{3} }}{{8\omega _{2} }} + \frac{{\zeta _{{22}} a_{1}^{2} a_{2} \cos (2\gamma _{1} )}}{{8\omega _{2} }} + \frac{{\zeta _{{22}} a_{1}^{2} a_{2} }}{{4\omega _{2} }} \\ & + \frac{{\zeta _{{23}} p_{1} a_{2} \cos (2\gamma _{2} )}}{{4\omega _{2} }} - \frac{{\zeta _{{24}} F_{2} \cos (\gamma _{2} )}}{{2\omega _{2} }} - \frac{{3\zeta _{{11}} a_{1}^{3} }}{{8\omega _{1} }} - \frac{{\zeta _{{12}} a_{1} a_{2}^{2} \cos (2\gamma _{1} )}}{{8\omega _{1} }} \\ & - \frac{{\zeta _{{12}} a_{1} a_{2}^{2} }}{{4\omega _{1} }} - \frac{{\zeta _{{13}} p_{1} a_{1} \cos (2\gamma _{1} + 2\gamma _{2} )}}{{4\omega _{1} }} + \frac{{\zeta _{{14}} F_{1} \cos (\gamma _{1} + \gamma _{2} )}}{{2\omega _{1} }} \\ \end{aligned} $$

(35b)

$$ \dot{a}_{2} = - \frac{{\mu_{2} a_{2} }}{2} + \frac{{\zeta_{22} a_{1}^{2} a_{2} \sin (2\gamma_{1} )}}{{8\omega_{2} }} - \frac{{\zeta_{23} p_{1} a_{2} \sin (2\gamma_{2} )}}{{4\omega_{2} }} + \frac{{\zeta_{24} F_{2} \sin (\gamma_{2} )}}{{2\omega_{2} }} $$

(35c)

$$ \begin{aligned} a_{2} \dot{\gamma }_{2} = & a_{2} (\sigma _{1} - \sigma _{2} ) - \frac{{3\zeta _{{21}} a_{2}^{3} }}{{8\omega _{2} }} - \frac{{\zeta _{{22}} a_{1}^{2} a_{2} \cos (2\gamma _{1} )}}{{8\omega _{2} }} \\ & - \frac{{\zeta _{{22}} a_{1}^{2} a_{2} }}{{4\omega _{2} }} - \frac{{\zeta _{{23}} p_{1} a_{2} \cos (2\gamma _{2} )}}{{4\omega _{2} }} + \frac{{\zeta _{{24}} F_{2} \cos (\gamma _{2} )}}{{2\omega _{2} }} \\ \end{aligned} $$

(35d)

where $\gamma_{1} = \sigma_{2} T_{1} - \varphi_{1} + \varphi_{2}$, $\gamma_{2} = \left( {\sigma_{1} - \sigma_{2} } \right)T_{1} - \varphi_{2}$.

The two amplitudes $A_{{1}}$ and $A_{{2}}$ can be also rewritten and defined as the functions of the Cartesian coordinate form, as below

$$ A_{1} = \frac{1}{2}\left( {x_{1} + ix_{2} } \right)e^{{i\lambda_{1} }} ,A_{2} = \frac{1}{2}\left( {x_{3} + ix_{4} } \right)e^{{i\lambda_{2} }} $$

(36)

By applying Eq. (36) in Eqs. (33a, b) and dividing the real and imaginary components, the averaged formulations in Cartesian coordinate form are achieved as

$$ \begin{aligned} \dot{x}_{1} = & \sigma _{1} x_{2} - \frac{1}{2}\mu _{1} x_{1} - \frac{3}{{8\omega _{1} }}\zeta _{{11}} \left( {x_{1}^{2} x_{2} + x_{2}^{3} } \right) \\ & - \frac{1}{{8\omega _{1} }}\zeta _{{12}} \left( {2x_{1} x_{3} x_{4} + 3x_{2} x_{3}^{2} + 5x_{2} x_{4}^{2} } \right) + \frac{1}{{4\omega _{1} }}\zeta _{{13}} p_{1} x_{2} \\ \end{aligned} $$

(37a)

$$ \begin{aligned} \dot{x}_{2} = & - \sigma _{1} x_{1} - \frac{1}{2}\mu _{1} x_{2} + \frac{3}{{8\omega _{1} }}\zeta _{{11}} \left( {x_{1} x_{2}^{2} + x_{1}^{3} } \right) + \frac{1}{{8\omega _{1} }}\zeta _{{12}} \left( {2x_{2} x_{3} x_{4} + 3x_{1} x_{4}^{2} + 5x_{1} x_{3}^{2} } \right) \\ & + \frac{1}{{4\omega _{1} }}\zeta _{{13}} p_{1} x_{1} - \frac{1}{{2\omega _{1} }}\zeta _{{14}} F_{1} \\ \end{aligned} $$

(37b)

$$ \begin{aligned} \dot{x}_{3} = & \left( {\sigma _{1} - \sigma _{2} } \right)x_{4} - \frac{1}{2}\mu _{2} x_{3} - \frac{3}{{8\omega _{2} }}\zeta _{{21}} \left( {x_{3}^{2} x_{4} + x_{4}^{3} } \right) \\ & - \frac{1}{{8\omega _{2} }}\zeta _{{22}} \left( {x_{1}^{2} x_{4} + 2x_{1} x_{2} x_{3} + 3x_{2}^{2} x_{4} } \right) + \frac{1}{{4\omega _{2} }}\zeta _{{23}} p_{1} x_{4} \\ \end{aligned} $$

(37c)

$$ \begin{aligned} \dot{x}_{4} = & \left( {\sigma _{2} - \sigma _{1} } \right)x_{3} - \frac{1}{2}\mu _{2} x_{4} + \frac{3}{{8\omega _{2} }}\zeta _{{21}} \left( {x_{3} x_{4}^{2} + x_{3}^{3} } \right) \\ & + \frac{1}{{8\omega _{2} }}\zeta _{{22}} \left( {x_{2}^{2} x_{3} + 2x_{1} x_{2} x_{4} + 3x_{1}^{2} x_{3} } \right) \\ & + \frac{1}{{4\omega _{2} }}\zeta _{{23}} p_{1} x_{3} - \frac{1}{{2\omega _{2} }}\zeta _{{24}} F_{2} \\ \end{aligned} $$

(37d)

where $\lambda_{1} = \sigma_{1} T_{1}$, $\lambda_{2} = \left( {\sigma_{1} - \sigma_{2} } \right)T_{1}$.

4 Frequency responses and force responses

4.1 Comparative investigation

Before conducting the numerical calculations, it is significant and necessary to confirm the reliability of the strategy applied in this investigation. To accomplish the intended result, the dimensionless natural frequencies of the truncated conical shell under simply supported conditions are identified and formulated as $\overline{\Omega } = \omega r_{2} \sqrt {\left( {1 - \nu^{2} } \right)\rho /E}$. Next, as Table 2 demonstrates, the frequency results are evaluated with those of Lam et al. [61] and Li et al. [62].

Table 2 Comparison of dimensionless natural frequencies $\overline{\Omega }$ for truncated simply supported conical shell ($m = 1$)

The Aluminum without pores is employed as a comparable material of the structure, which is independent of temperature increase and has material attributes of $E = 70\;{\text{GPa}}$, $\rho = 2707\;{\text{kg/m}}^{{3}}$, $v = 0.3$, $\alpha = 2.4 \times 10^{ - 8} \;{\text{m/K}}$. And the specified physical dimensions are considered to be $h_{c} = 0.01$, $h_{c} /r_{2} = 0.01$, $L\sin \beta /r_{2} = 0.25$. Additionally, the generatrix wave number $m$ is specified as 1. Table 2 indicates that the current results exhibit a high degree of consistency with those identified throughout the previous research.

4.2 Frequency characteristics

In this part, the natural frequency parameters are presented to explore the nonlinear vibration characteristics and determine the nonlinear internal resonance conditions of the truncated porous sandwich structure with varying thickness.

The parameters related to material characteristics, geometric shapes and airflow properties are presented in the following investigations. Specifically, the carbon fiber skins’ property parameters are considered to be $E_{1} = 140\;{\text{GPa}}$, $E_{{2}} = {10}\;{\text{GPa}}$, $G_{12} = G_{13} = G_{23} = 7\;{\text{GPa}}$, $v = 0.3$, $\alpha_{1} = - 0.3 \times 10^{ - 6} \;{\text{m/K}}$, $\alpha_{2} = 28 \times 10^{ - 6} \;{\text{m/K}}$, while the physical characteristics of aluminum foam core with five diverse schemes of porosity distribution pattern are stated as $E_{max} = 70\;{\text{GPa}}$, $\rho_{\max } = 2707\;{\text{kg/m}}^{{3}}$, $\nu = 0.3$, $\alpha = {2}{.4} \times {10}^{{ - {8}}} {m/K}$. The dimensionless natural frequencies are defined as $\Omega = \omega r_{2} \sqrt {\left( {1 - \nu^{2} } \right)\rho_{\max } /E_{\max } }$. The sandwich porous shell structure with varying stiffness is simply supported and at $\Delta T = 100^\circ {\text{C}}$, and the structural parameters are $N = 9$, $N_{c} = 0.5$, $N_{x} = 1$, $h_{1} = 0.01$, $h_{2} /h_{1} = 0.5$, $h_{f} /h_{1} = 0.8$, $r_{1} /h_{1} = 400$, $\beta = 30^{ \circ }$ and $\kappa = 0.005$. The airflow properties are expected to be $M_{a} = 3$, $a_{\infty } = 213.36\;{\text{m/s}}$, $\gamma_{a} = 1.4$, $p_{\infty } = 10\;{\text{MPa}}$.

Figure 3 portrays the variation of first two order natural frequencies versus the porous core’s length-to-thickness ratio $L/h_{1}$ for the varying thickness porous conical shell with five distribution schemes of pores. It is obvious that the larger $L/h_{1}$ of the core, the lower the frequency parameters of the various porosity distribution schemes. The largest fundamental frequency parameters of the first two vibration modes belong to the Pattern-Λ distribution due to its higher stiffness, whereas the other four distribution schemes have considerably similar values of natural frequencies. From Fig. 3, it can be also found that the first two fundamental frequencies are quite close to each other for the five styles of pore distribution schemes. It’s worth noting that when the middle layer’s length-to-thickness ratio $L/h_{1} = 100$, the ratio of natural frequencies for first two modes can be considered as 1:1, and the modes of the first two order frequency parameters are $\left( {1,3} \right)$ and $\left( {1,4} \right)$ at this time [46]. As a result, the Pattern-Λ distributed sandwich conical shell structure with varying thickness and $L/h_{1} = 100$ is used for the next numerical simulation.

Fig. 3

Influence of the length-to-thickness ratio of core on first two order frequency parameters for the shell structure with various porosity distribution schemes

4.3 Frequency-amplitude responses

This section revolves around the frequency-amplitude responses of varying thickness sandwich structure under 1:1 internal resonance, first-order main resonance and 1/2 subharmonic resonance. The frequency-amplitude characteristic curves of the varying stiffness sandwich porous shell can be developed by using the MATLAB software to solve the averaged Eq. (35) in polar coordinate form. The impacts of damping coefficient, detuning parameter, temperature increment, transverse and in-plane forces on the resonant frequency-amplitude responses of the sandwich structure with variable stiffness are explored.

Figure 4 depicts the effects of damping coefficient $\mu_{1}$ on the resonant frequency-amplitude response characteristics of first two modes for the Pattern-Λ distributed sandwich shell structure with varying thickness, whose parameters are chosen as $\mu_{2} = 0.3$, $\sigma_{2} = 2$, $F = 100$, $P_{1} = 0$. Figure 4a and b represent the first-order and second-order modal frequency-amplitude curves, respectively. Because of the hardening impact of the cubic nonlinear components in the dynamical formulation, a resonant peak appears on the right side of $\sigma_{1} = 0$, which indicates that the structure has a hardening-spring property. The amplitudes of second-order mode are remarkably smaller than those of first-order mode, revealing that the energy is mainly concentrated in first-order mode. From the results, it is evident that the damping coefficient $\mu_{1}$ has a considerable impact on amplitude reduction. The first-order modal response amplitudes near the resonant region become smaller with increasing the damping coefficient, while the response amplitudes away from resonant region are insensitive to the change of $\mu_{1}$. The stable response amplitudes of the second-order mode are slightly affected by the damping coefficient, while the unstable region decreases as the damping coefficient increases.

Fig. 4

The frequency-amplitude curves of sandwich structure under various damping coefficients $\mu_{1}$, a the first-order resonance, b the second-order resonance

The frequency-amplitude response characteristics of Pattern-Λ distributed porous conical shell with the main resonance of first-order mode and 1:1 internal resonance under three various transverse excitations $F$, which are selected as 0, 4000 and 8000, are presented in Fig. 5. Figure 5a and b individually demonstrate the nonlinear frequency responses of first-order and second-order resonances, where the parameters are $\mu_{1} = 0.04$, $\mu_{2} = 0.3$, $\sigma_{2} = 2$, $P_{1} = 0$. A resonant peak towards the right occurs in both modes, which reflects that the responses of the structure are characterized as stiffness-hardening behavior. With increasing transverse excitation $F$ in two modal resonances, the resonant peak and size of resonant domain rise. Furthermore, when the system is subjected to larger transverse excitation, the nonlinearity and instability of the frequency-amplitude response become stronger owing to the softening effect of transverse force on sandwich shell structure.

Fig. 5

The frequency-amplitude curves of sandwich structure with variable thickness under various transverse excitations $F$, a the first-order resonant response curves, b the second-order resonant response curves

The frequency-amplitude response characteristics of 1:1 internal resonance and 1/2 subharmonic resonance for a truncated porous sandwich conical shell with Pattern-Λ porosity distribution and variable stiffness under three different in-plane excitations $P$ are illustrated in Fig. 6, where the parameters are selected as $\mu_{1} = 0.04$, $\mu_{2} = 0.3$, $\sigma_{2} = 2$ and $F = 100$. The first-order modal resonant responses have clear stiffness hardening effects and concentrate the main energy, as presented in Fig. 6, where the responses of the first-order mode have pronounced peaks towards the right and their amplitude is significantly bigger than those of the second-order mode. The resonant peaks of two modes rise with increasing in-plane force, while the response amplitudes further from the resonant area barely change. As the in-plane excitation rises, the unstable region widens because of the softening effect on the sandwich shell structure.

Fig. 6

The frequency-amplitude curves of sandwich shell structure under various in-plane excitations $P_{1}$, a the first-order resonant responses, b the second-order resonant responses

Figure 7 displays the impacts of detuning parameter $\sigma_{2}$ on 1:1 internal resonant frequency-amplitude response characteristics for the porous sandwich shell structure with varying thickness and Pattern-Λ porosity distribution, where parameters are provided as $\mu_{1} = 0.04$, $\mu_{2} = 0.3$, $F = 100$, $P_{1} = 0$. For the first-order mode, the resonant regions and peak values at $\sigma_{2} = - 2$ and $\sigma_{2} = 2$ are approximately the same, while the smallest region and peak value of resonance belong to $\sigma_{2} = 0$. For the second-order mode, the stable resonant peak value and resonant region are the smallest when $\sigma_{2}$ is equal to 0, and the stable resonant peak values are nearly identical when $\sigma_{2}$ is chosen as − 2 and 2, with the stable peak of resonance at $\sigma_{2} = - 2$ developing the softening-spring characteristic and the stable peak of resonance at $\sigma_{2} = 2$ suffering the hardening-spring property. The appearance of unstable areas is more complicated for the second-order mode, specifically, the unstable resonant peak at $\sigma_{2} = - 2$ presents the stiffness hardening characteristic and is the largest value of the peaks, the unstable resonant peak at $\sigma_{2} = 0$ gives itself a larger resonant peak, while the unstable resonant peak at $\sigma_{2} = 2$ provides the smallest peak value.

Fig. 7

The frequency-amplitude curves of varying thickness porous shell structure under various detuning parameters $\sigma_{2}$, a the first-order resonant curves, b the second-order resonant curves

Under the circumstance of the main resonance of first-order mode and 1:1 internal resonance, the influences of the temperature increment $\Delta T$ on the frequency-amplitude response characteristics of Pattern-Λ distributed porous conical shell with variable stiffness are examined in Fig. 8. The temperature increments are chosen as 100, 300 and 500, while the other parameters are $\mu_{1} = 0.04$, $\mu_{2} = 0.3$, $\sigma_{2} = 2$, $F = 100$ and $P_{1} = 0$. Compared with the second-order mode, the first-order mode has larger amplitudes and more obvious resonant peaks towards the right, which shows that the first-order mode concentrates the main energy and has stronger nonlinearity. It can be found from Fig. 8 that the effects of temperature increment on the resonant amplitude are evident. As the temperature increment $\Delta T$ increases, the resonant peaks and unstable regions of the two modes increase, which indicates that a larger temperature increment will increase the instability of the nonlinear system.

Fig. 8

The frequency-amplitude curves of porous sandwich structure under various temperature increments $\Delta T$, a the first-order resonant curves, b the second-order resonant curves

4.4 Force–amplitude responses

The force–amplitude responses of the porous sandwich structure with variable stiffness under 1:1 internal resonance and first-order main resonance are primarily investigated in this part. Defining the left components of averaged formulations in the form of polar coordinate to zero and utilizing the MATLAB program, the resonant force–amplitude curves of the sandwich shell structure are portrayed to examine the impacts of damping coefficient, temperature increment, in-plane excitation and two detuning parameters.

The force–amplitude curves of Pattern-Λ distributed porous sandwich shell structure with 1:1 internal resonance under various damping coefficients $\mu_{1}$, which are provided as 0.3, 0.6 and 0.9, are exhibited in Fig. 9. From Fig. 9a and b, the nonlinear force characteristic curves of the resonant responses for first-order and second-order modes are separately displayed, in which the parameters are $\mu_{2} = 0.3$, $\sigma_{1} = 0$, $\sigma_{2} = 2$, $P_{1} = 0$. The first-order modal resonant amplitudes are substantially bigger than those of the second-order mode, implying that the energy is essentially captured by the first-order mode. As discovered in Fig. 9, when the damping coefficient rises, the first-order modal response amplitude decreases, while the second-order modal response amplitude increases. The result demonstrates that there is a considerable energy transfer between the first two modes. Furthermore, as transverse excitation increases under the same damping coefficient, the unstable response amplitudes of the second-order and first-order modes appear simultaneously, and the smaller $\mu_{1}$, the earlier the unstable response amplitudes appear in the system.

Fig. 9

The force–amplitude responses of sandwich shell structure under various damping parameters $\mu_{1}$, a the first-order resonant responses, b the second-order resonant responses

Figure 10 exhibits the 1:1 internal resonant force–amplitude response characteristics of variable thickness truncated sandwich shell structure with Pattern-Λ pore distribution under various in-plane excitation $P_{1}$, where parameters are given by $\mu_{1} = \mu_{2} = 0.3$, $\sigma_{1} = 0$, $\sigma_{2} = 2$. Figure 10a and b are the first-order and second-order order modal force–amplitude response curves, individually. The response amplitudes of the second-order mode are shown to be considerably lower than those of the first-order mode, suggesting that although the second-order modal response is more visibly impacted by internal resonance, it contains less energy. For the first-order mode, the structure has a larger resonant response amplitude and faster appearance of the unstable response amplitude as the in-plane excitation $P_{1}$ increases. While for the second-order mode, there are several unstable response amplitude groups and a decrease in resonant amplitude of the structure as the in-plane excitation $P_{1}$ rises. The results illustrate that when the transverse and in-plane forces occur simultaneously, the resonant response of the porous sandwich structure is complicated and unstable.

Fig. 10

The force–amplitude curves of porous shell structure under various in-plane excitations $P_{1}$, a the first-order modal resonance, b the second-order modal resonance

Figure 11 pronounces impacts of detuning parameter $\sigma_{1}$ on the first two modal force–amplitude response characteristics for Pattern-Λ distributed sandwich conical shell under 1:1 internal resonance and main resonance of first-order mode, where parameters are $\mu_{1} = \mu_{2} = 0.3$, $\sigma_{2} = 0$, $P_{1} = 0$. When the transverse excitation $F$ is extremely small, the system at $\sigma_{1} = 0$ has a greater stable response amplitude for the two modes. For the first-order mode, the structure has a higher response amplitude and the unstable resonant response amplitude occurs faster at $\sigma_{1} = 0.1$ as the transverse excitation rises, while the smallest response amplitude belongs to the system with $\sigma_{1} = - 0.1$. While for the second-order mode, as the transverse force $F$ continues to increase, the response amplitude of the system with $\sigma_{1} = 0.1$ becomes the largest, and after the transverse excitation is greater than 2500, the largest response amplitude belongs to the system with $\sigma_{1} = - 0.1$.

Fig. 11

The force–amplitude curves of sandwich shell structure under various detuning parameters $\sigma_{1}$, a the first-order resonant response curves, b the second-order resonant response curves

Figure 12 shows the force–amplitude response characteristics for the Pattern-Λ distributed sandwich shell structure under 1:1 internal resonance for first two modes and different detuning parameters $\sigma_{2}$, and other parameters are provided as $\mu_{1} = \mu_{2} = 0.3$, $\sigma_{1} = 0$, $P_{1} = 0$. For the first-order mode, the system with $\sigma_{2} = - 0.1$ has a larger stabilized response amplitude when the transverse excitation $F$ is extremely small, while the system has a larger response amplitude and a wider unstable response amplitude region when detuning parameter $\sigma_{2}$ and transverse force $F$ increases. For the second-order mode, when $F$ is relatively small, the largest stable resonant response amplitude belongs to the structure with $\sigma_{2} = 0$. Because of the energy exchange between two modes, the second-order modal response amplitude becomes smaller with increasing $\sigma_{2}$ and $F$, but the area of unstable response amplitude occurs at the same time for the two modes.

Fig. 12

The force–amplitude curves of varying thickness shell structure under various detuning parameters $\sigma_{2}$, a the first-order resonant response curves, b the second-order resonant response curves

Figure 13 shows the effects of temperature increment $\Delta T$ on the force–amplitude response characteristics of the variable stiffness sandwich conical shell with Type-Λ porosity distribution in the case of 1:1 internal resonance and main resonance of first-order mode, where the parameters are $\mu_{1} = \mu_{2} = 0.3$, $\sigma_{1} = 0$, $\sigma_{2} = 2$, $P_{1} = 0$. It can be observed from Fig. 13 that as the temperature increment $\Delta T$ increases, the two modes have larger force-response amplitudes and wider unstable regions, which indicates that the instability of the nonlinear system becomes larger. When the transverse excitation $F$ becomes bigger, unstable response amplitudes appear in both modes at the same time, the difference in response amplitudes of the first-order mode between different temperature increments decreases, while the difference in response amplitudes of the second-order mode between different temperature increments increases. This is due to the energy transfer between the two modes. Since the main energy is concentrated in the first-order mode, it can be seen that the response amplitudes of the first-order mode is considerably larger than those of the second-order mode.

Fig. 13

The force–amplitude response curves of porous sandwich conical shell with varying stiffness under various temperature increments $\Delta T$, a the first-order resonant response curves, b the second-order resonant response curves

5 Bifurcation and chaotic dynamics

The bifurcation and chaotic dynamics of Pattern-Λ distributed sandwich truncated shell structure with varying stiffness under 1:1 internal resonance are explored in the present part. The numerical simulation is conducted by adopting the Runge–Kutta algorithm to solve the averaged Eq. (37) in Cartesian coordinate form. The impacts of transverse force, in-plane excitation, and damping parameter on the nonlinear dynamics of the porous sandwich shell structure with variable thickness are analyzed by applying bifurcation diagrams, time history diagrams, two-dimensional and three-dimensional phase portraits. Unless otherwise specified, the default initial position is $\left( { - 0.1, - 0.01, - 0.025, - 0.01} \right)$, and the detuning parameters are $\sigma_{1} = 1.5$, $\sigma_{2} = 0.6$.

The bifurcation diagrams of the Pattern-Λ distributed variable thickness porous sandwich conical shell under 1:1 internal resonance for transverse force $F$ are demonstrated in Fig. 14, where Fig. 14a and b individually represent the bifurcation diagrams for the variations of the first-order and second-order modal amplitudes with the transverse excitation $F$. The in-plane force $P_{1}$ is chosen as 0, and the damping coefficients $\mu_{1}$ and $\mu_{2}$ are equal to $\mu$, which takes the value of 0.01. The transverse excitation $F$ is selected within the range of 1000–8000. It can be mentioned from Fig. 14 that with increasing transverse force $F$, the nonlinear dynamic responses of the structure successively go through chaotic motion, quasi-periodic motion, and finally into periodic motion.

Fig. 14

The bifurcation diagrams of the Pattern-Λ distributed sandwich shell structure versus the transverse excitation $F$, a the variations of $w_{1}$ with $F$, b the variations of $w_{2}$ with $F$

Figures 15, 16 and 17 display the response curves of the Pattern-Λ distributed truncated varying thickness sandwich conical shells at different motion states when the transverse force $F$ is considered to be 2000, 5000 and 8000, respectively. Specifically, (a) and (c) depict the phase portraits on planes $\left( {x_{1} ,x_{2} } \right)$ and $\left( {x_{3} ,x_{4} } \right)$, (b) and (d) portray the first and second order modal time history diagrams on planes $\left( {\tau ,x_{1} } \right)$ and $\left( {\tau ,x_{3} } \right)$, and (e) plots the three-dimensional phase portraits in space $\left( {x_{1} ,x_{2} ,x_{3} } \right)$. As observed in Figs. 15, 16 and 17, the structure experiences chaotic motion as the transverse force is $F = 2000$, quasi-period motion as the transverse force is $F = 5000$, and finally stabilizes at periodic motion as the transverse force is $F = 8000$.

Fig. 15

The chaotic motion of porous truncated sandwich shell structure when $F = 2000$

Fig. 16

The quasi-period motion of varying thickness sandwich structure when $F = 5000$

Fig. 17

The period motion of Pattern-Λ distributed sandwich shell structure when $F = 8000$

Figure 18 depicts the variation of motion state of the Pattern-Λ distributed variable thickness porous sandwich shell structure with in-plane excitation $P_{1}$ under 1: 1 internal resonance. The first-order and second-order modal bifurcation diagrams as the in-plane force $P_{1}$ varies from 2200 to 2900 are portrayed in Fig. 18a and b, in which the damping coefficient $\mu$ is 0.01 and the transverse excitation $F$ is 8000. It can be marked that when the in-plane force rises, the motion state of two amplitudes $w_{1}$ and $w_{2}$ exhibits the phenomenon of alternating periodic motion and quasi-periodic motion. The nonlinear motion responses of the shell structure with Pattern-Λ distribution and variable stiffness are specifically presented as: quasi-period motion → period motion → period-doubling bifurcation → quasi-period motion → period motion → period-doubling bifurcation → quasi-period motion. After the in-plane force exceeds 2800, the amplitude of quasi-periodic motion becomes larger, indicating that the motion of the system is beginning to be chaotic.

Fig. 18

The bifurcation diagrams of varying thickness shell structure versus the in-plane excitation $P_{1}$, a the bifurcation diagram for $w_{1}$ with $P_{1}$, b the bifurcation diagram for $w_{2}$ with $P_{1}$

Matching to the nonlinear vibration responses presented in Figs. 18, 19 and 20 provide the various motion response curves when the in-plane force $P_{1}$ is taken as various values for Pattern-Λ distributed sandwich shell structure with varying thickness. Figure 19 exhibits the periodic motions of the varying thickness sandwich porous structure as the in-plane force is provided as $P_{1} = 2600$, and Fig. 20 indicates the quasi-period motion of the sandwich structure with varying stiffness as the in-plane force is $P_{1} = 2800$.

Fig. 19

The period motion of the varying thickness porous sandwich structure when $P_{1} = 2600$

Fig. 20

The quasi-period motion of the varying stiffness sandwich structure when $P_{1} = 2900$

The bifurcation diagrams for the variation of the amplitudes $w_{1}$ and $w_{2}$ with damping parameter $\mu$ of Pattern-Λ distributed varying thickness conical shell are confirmed in Fig. 21. The damping parameter is selected from 0.06 to 0.14, and the load parameters are $F = 8000$, $P_{1} = 0$. It is noted that with increasing damping parameter $\mu$, the motion state of the two amplitudes $w_{1}$ and $w_{2}$ of the structure is: periodic motion → period-doubling bifurcation → quasi-period motion → periodic motion → period-doubling bifurcation → quasi-period motion, showing the alternating occurrence of periodic motion and quasi-period motion. Figures 22 and 23 describe the periodic motion and quasi-period motion of Pattern-Λ distributed variable thickness porous sandwich shell structure as the damping coefficients are selected as $\mu = 0.065$ and $\mu = 0.09$, individually.

Fig. 21

The bifurcation diagrams of the varying stiffness sandwich structure versus the damping parameter $\mu$, a the first-order bifurcation diagram, b the second-order bifurcation diagram

Fig. 22

The period motion of porous sandwich structure with variable thickness when $\mu = 0.065$

Fig. 23

The quasi-period motion of porous varying stiffness shell structure when $\mu = 0.09$

6 Conclusion

The nonlinear resonant dynamics and bifurcation behaviors of the sandwich porous truncated conical shell with varying stiffness under simply supported boundary and 1:1 internal resonance are examined in this work. The sandwich porous sandwich with varying thickness is made of two skins with carbon fiber and a porous middle core with aluminum foam, which has five various porosity distribution schemes along thickness direction and an exponentially variable thickness along the meridional direction. A complex combination of the in-plane excitation, transverse load, supersonic aerodynamic pressure and thermal stress impacts the sandwich shell structure with varying thickness. By means of FSDT, von-Karman geometrical nonlinear relations and Hamilton's principle, the nonlinear partial differential dynamic formulations are identified for the porous sandwich shell structure. Utilizing Galerkin technique, the 2DOF second-order ordinary differential nonlinear dynamic formulations are ultimately established. The multiple-scale technique is adopted for yielding the 1:1 internal resonant averaged equations in polar and Cartesian coordinate forms for the sandwich porous shell structure. The comparative investigation is adopted to validate the accuracy of current approach. The variation of the first two order natural frequency parameters with length-to-thickness ratio of the core with five porosity distribution schemes are provided to explore the nonlinear vibration behaviors internal resonance conditions for the sandwich porous structure with varying thickness.

The frequency-amplitude and force–amplitude characteristic curves of the porous sandwich shell structure with varying thickness and Pattern-Λ porosity distribution scheme under 1:1 internal resonance and external combined resonance are exhibited by solving the polar coordinate averaged formulations. It’s marked that the energy is mainly concentrated in the first-order mode, whose amplitudes are higher than those the second-order mode. With decreasing damping coefficient and increasing temperature increment, transverse and in-plane excitations, the system has a larger frequency–response resonant peak and performs hardening-spring characteristic. The detuning parameter has complex impact on the first two order frequency-amplitude response characteristics. Moreover, as the damping coefficient increases, and the in-plane excitation and two detuning parameters decrease, the first-order force-response resonant amplitude eventually becomes lower, while the second-order force-response resonant amplitude ultimately rises. As the result indicates, a significant amount of energy is transferred between the first two modes. However, as the temperature increment increases, the force-response resonant amplitudes of the two modes become larger.

The nonlinear dynamic responses and bifurcations of the sandwich Pattern-Λ distributed conical shell with varying stiffness under 1:1 internal resonance are presented. The numerical calculations are performed by applying the Runge–Kutta procedure to solve the Cartesian coordinate averaged formulations and obtain the phase portraits, bifurcation and time history diagrams. With increasing transverse load, the nonlinear resonant motions of the porous sandwich shell structure sequentially experience chaotic motion, quasi-periodic motion, and eventually periodic motion. As the in-plane excitation and damping parameter increases, the motion of the two order modal amplitudes $w_{1}$ and $w_{2}$ indicates the occurrence of alternating periodic motion and quasi-period motion. Additionally, the nonlinear system moves from period motion to quasi-periodic motion through the period-doubling bifurcation.