Nonlinear vibrations and chaotic phenomena of functionally graded material truncated conical shell subject to aerodynamic and in-plane loads under 1:2 internal resonance relation

Abstract

This paper focuses on the nonlinear dynamic responses of a functionally graded material (FGM) truncated conical shell under 1:2 internal resonance relation. The FGM truncated conical shell is subjected to the in-plane load and the aerodynamic load along the meridian direction. According to a power-law distribution, the material properties are assumed to be modified along the thickness direction smoothly and continuously and the material properties are temperature dependent. The aerodynamic load is obtained by the first-order piston theory with the curvature correction term. According to von Karman type nonlinear geometric relations, first-order shear deformation shell theory, Hamilton principle, the nonlinear equations of motion for the FGM truncated conical shell are established. Furthermore, the nonlinear equations of motion are reduced into a system of the ordinary differential equations by utilizing Galerkin procedure. The multiple scales method is used to obtain the averaged equations for the FGM truncated conical shell under the relations of 1:2 internal resonance and 1/2 subharmonic resonance. The frequency–response curves, time history diagrams, phase portraits, Poincare maps and bifurcation diagrams with different parameters are yielded by employing numerical calculations. The influences of exponent of volume fraction, Mach number, damping coefficient and in-plane load on the nonlinear resonance behaviors of the FGM truncated conical shell are investigated. The chaotic and periodic motions of the FGM truncated conical shell have been discussed in detail.

1 Introduction

Functionally graded materials (FGMs) are famous for their excellence thermomechanical performances, and the FGM structures inspired researchers to explore the dynamics which are often used in the high strength or high temperature environments [1, 2]. Because of the continuous and smooth varies of the volume fractions of the constituent materials for the functionally graded materials, the material properties, for example the Young’s modulus, the thermal expansion coefficient and the density, all change continuously. Therefore, the FGM structures can relieve the problems of the interfacial debonding and the stress concentration. It is well known that the conical shell structure is one of the primary structures in many engineering community, for example, aircraft and rocket propulsion system, ship structures, pressure and piping vessels [3, 4]. The FGM conical shells are often subjected to the complex loads, for example aerodynamic load, in-plane load, transverse load and thermal stress, which will result in the complex nonlinear dynamics. Particularly, the occurrence of the nonlinear internal resonance phenomenon can cause the large amplitude vibration, noises, irrecoverable deformations and cracks in practical engineering applications, even the failure of the structures. In the early days, the resonances leaded to the collapse of the 860 m Taksim bridge in the USA. Therefore, it is significant to predict and understand the nonlinear dynamic characteristics of FGM conical shell with internal resonance under complex loads.

Now, much researches have been carried out for the vibration characteristics of FGM conical shells. Javani et al. [5] performed a thermally induced vibration analysis for a functionally graded material conical shell which is considered the uncoupled thermoelasticity assumptions. The effects of the thickness upon the deflections, the semi vertex angle, geometrical nonlinearity, the length and the temperature dependency of the conical shells are investigated. Based on the higher-order shear deformation theory, Ansari et al. [6] investigated the large-amplitude free and forced vibrations of functionally graded carbon nanotube reinforced composite conical shells. Chan et al. [7, 8] investigated the nonlinear dynamic responses and vibrations of truncated eccentrically stiffened functionally graded conical shells and truncated functionally graded conical panels surrounded by the elastic medium in the thermal environment. The influences of elastic foundations, dimensional parameters, inhomogeneous, temperatures and outside stiffeners on the nonlinear vibration and dynamic response of the truncated conical shells are investigated. Dai et al. [9] studied the frequency characteristics of the rotating truncated conical shells by using the Haar wavelet method. The vibration behaviors of a truncated conical sandwich shell that include temperature-dependent homogeneous core and porous behavior in the various thermal conditions are investigated by Rahmani et al. [10].

Song et al. [11] investigated the free vibrations of a truncated conical shell under the inertia force and elastic constraints with the arbitrary boundary conditions. Hao et al. [12, 13] investigated the nonlinear vibration and supersonic flutter of a FGM circular conical panel by using the first order shear deformation theory. Sofiyev [14] provided the review on the buckling and vibration of functionally graded materials, functionally graded sandwich-conical shell, functionally graded layered conical shell and functionally graded conical shell. Jooybar et al. [15] investigated the effects of the geometrical parameters, the thermo environment, and graded index of the materials on free vibration of FGM conical panel by using differential quadrature method. Hao et al. [16] researched on the truncated metal-ceramic graded conical shell on aero-thermo-elastic flutter characteristics subjected to aerodynamic pressure and aerodynamic heating. Using Hamilton’s principle and first-order shear deformation theorem, the equilibrium equations of two joined laminated conical shells were derived by Izadi et al. [17], and the free vibration analyses of the shells were investigated. Zhao et al. [18] presented a spectro-geometric-Ritz solution for the free vibration analyses of conical-cylindrical-spherical shell combinations with the arbitrary boundary conditions.

In the past few years, much researchers have interested in buckling characteristics of the conical shells. Sofiyev et al. [19, 20] studied the dynamic stability of the functionally graded truncated conical shells and the FG orthotropic conical shells by using FSDT. Hoa et al. [21] investigated the nonlinear thermomechanical buckling and postbuckling of the ES-FGM truncated conical shells. The influences of the temperature, the stiffeners, the foundations, the material properties, the geometric dimensions on the stability of shells are given. Based on the classical shell theory, Chan et al. [22] provided a nonlinear static analysis for a truncated functionally graded carbon nanotubes-reinforced composite conical shells subjected to the axial load. Then, Chan et al. [23] studied the nonlinear buckling characteristics of truncated stiffened FGM conical shells subjected to a uniform axial compressive load and resting on the elastic foundation by using first-order shear deformation theory. The buckling analyses of the composite laminated conical shells reinforced with graphene sheets are investigated by Kiani [24]. Jiao et al. [25] proposed a semi-analytical approach to investigate dynamic buckling characteristics of the composite cylindrical shell reinforced by functionally graded carbon nanotubes under the dynamic displacement loads. Talebitooti [26] investigated the buckling of the composite sandwich conical shells subjected to a uniform external lateral pressure based on the first-order shear deformation shell theory.

Dung et al. [27] studied the buckling behaviors of a FGM truncated conical shell, the influences of stiffeners, dimensional parameters and material properties and discussed in detail. Zhao et al. [28] investigated the thermal-mechanical buckling characteristics of a FGM conical panel by using the element-free KP-Ritz method. Pasqua et al. [29] studied the buckling characteristics of the composite conical shell subject to different disturbed loads. According to FSDT, the buckling behaviors of a composite sandwich conical shell subject to uniform external lateral load was given by Talebitooti [30]. Maali et al. [31] studied the buckling behaviors of a thin imperfection conical panel under the simply supported condition. According to the modified Donnell shell theory, Sofiyev et al. [32] investigated the thermo-elastic buckling of a FGM conical shell. The nonlinear temperature increase along the thickness direction was considered by them. Bich et al. [33] studied the linear buckling of the FGM conical panels subject to the external and axial pressures.

The improved double Fourier series has been widely used in vibration analysis of the beam, plate and shell structures under elastic boundary conditions or arbitrary boundary conditions with elastic supported. For example, Shi and Wang et al. [34,35,36,37,38] carried out a lot of researches on the vibration analyses of beam, plate and shell structures under the arbitrary boundary conditions by using the improved double Fourier series. According to an accurate modified Fourier series solution, the free vibration analyses of the truncated conical shells with general elastic boundary conditions were presented by Jin et al. [39]. Dai et al. [40] investigated dynamic behavior of cylindrical shell structures with general boundary condition based on the modified Fourier series method.

Zhang et al. [41,42,43,44] carried out a lot of studies on internal resonance behaviors of composite plate and shell structures, and their research results show that internal resonance has a great influence on the nonlinear vibration of plate and shell structures. Our group has done a lot of research on the shell and plate structures by using the techniques in this paper. For example, we have investigated the nonlinear vibration [3, 4] and nonlinear flutter [12, 16] of the FGM truncated conical shell and the nonlinear internal resonance behaviors of the FGM cylindrical shell [44]. Therefore, the method used in this paper is effective for dealing with the nonlinear dynamics problem of the FGM truncated conical shell.

Up to now, few researches have been carried out the nonlinear resonance behaviors of the FGM truncated conical shell with 1:2 internal resonance. In this paper, the nonlinear dynamics of a FGM truncated conical shell which is subjected to in-plane load and aerodynamic load under 1:2 internal resonance condition are investigated. Based on Hamilton principle, von Karman type nonlinear relations and FSDT, the nonlinear governing equations of motion for the FGM truncated conical shell are established. By using the Galerkin method, the ordinary differential equations of motion along the radial displacement are obtain. The qualification which the 1:2 internal resonance occurs of the FGM truncated conical shell is found. The multiple scales method is used to obtain the averaged equations for the FGM truncated conical shell under the relations of 1:2 internal resonance and 1/2 subharmonic resonance. The frequency-response curves, time history diagrams, phase portraits, Poincare maps and bifurcation diagrams with different parameters are yielded by employing numerical calculations to show the complex nonlinear dynamics and chaotic phenomena of the FGM truncated conical shell. The influences of exponent of volume fraction, Mach number, damping coefficient and in-plane load on the nonlinear resonance behaviors on the nonlinear vibrations of the FGM truncated conical shell are studied. The chaotic and periodic motions of the FGM truncated conical shell have been discussed in detail.

2 Equations of motion

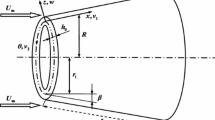
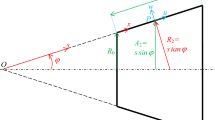
Figure 1 shows the model of a FGM truncated conical shell. The geometric parameters of the FGM truncated conical shell are as follows: semi-vertex angle $\beta$, thickness h, length L and minor inner radius $r_{1}$. The radius of any point along the meridional are computed by $R=r_{1} +x\sin \beta$. The curvilinear coordinate system $\left( {x,\;\theta ,\,z} \right)$ is along the meridional, circumferential and radial directions, respectively, which is located on the mid-surface of the FGM truncated conical shell. It is considered that the FGM truncated conical shell is subjected to the in-plane load and aerodynamic load. The uniformly distributed in-plane load which at the two ends $x=0$ and $x=L$ of the FGM truncated conical shell is represented as $p_{1} \cos \left( {\Omega t} \right)$.

Fig. 1

The model of a FGM truncated conical shell is given

Considering the supersonic flow is parallel to the outside of the FGM truncated conical shell. Based on the first-order piston theory with the curvature correction term, the aerodynamic load $P_\mathrm{a}$ are approximated as [45, 48].

$$\begin{aligned} P_\mathrm{a} =-\frac{\gamma _\mathrm{a} p_{\infty } M_\mathrm{a}^{2} }{\sqrt{M_\mathrm{a}^{2}-1} }\,\left[ {\frac{\partial w}{\partial x}+\left( {1-\frac{1}{M_\mathrm{a}^{2} -1}} \right) \frac{1}{M_\mathrm{a} a_{\infty } }\frac{\partial w}{\partial t}-\frac{w}{2R\sqrt{M_\mathrm{a}^{2} -1} }} \right] , \end{aligned}$$

(1)

where last term is the curvature correction term, $M_\mathrm{a}$, $a_{\infty }$, $p_{\infty }$, $\gamma _\mathrm{a}$ and t are Mach number, free stream velocity of sound, free stream static pressure, adiabatic exponent and time, respectively.

The material properties are regarded as varying continuously and smoothly along the thickness direction z according to a power law distribution. Thus, the outside surface of the FGM truncated conical shell is ceramic rich. At the same time, the internal surface is metal rich. The schematic diagram of the volume fractions of the ceramic and the metal for the FGM truncated conical shell through the thickness direction is given in Fig. 2. The volume fractions of the ceramic and the metal for the truncated FGM conical shell is shown in Fig. 3, and they are written as follows

$$\begin{aligned} V_{c} \left( z \right) =\left( {\frac{2z+h}{2h}} \right) ^{\eta }, V_{m} \left( z \right) =\left( {\frac{h-2z}{2h}} \right) ^{\eta }, \end{aligned}$$

(2)

where V is the volume fraction, the subscripts c and m represent ceramic and metal, respectively, and the superscript $\eta$ is the volume fraction index of the ceramic.

Fig. 2

The schematic diagram of the volume fractions of the ceramic and the metal for the FGM truncated conical shell through the thickness direction is obtained

Fig. 3

The volume fractions of the ceramic through the thickness direction are obtained

The value of the Poisson’s ratio $\upnu$ of the FGM truncated conical shell is regarded as a constant. The other material properties of the FGM truncated conical shell, such as mass density $\rho$, Young’s modulus E and coefficient of the thermal expansion $\alpha$, are determined according to a linear rule of mixture as [49]

$$\begin{aligned} P=P_{c} V_{c} +P_{m} V_{m} , \end{aligned}$$

(3)

The typical temperature-dependent material properties can be expressed as [50]

$$\begin{aligned} P_{i} =P_{0} \left( {P_{-1} T^{-1}+1+P_{1} T+P_{2} T^{2}+P_{3} T^{3}} \right) , i=c\,,\;m, \end{aligned}$$

(4)

where the temperature coefficients $P_{0}$, $P_{-1}$, $P_{1}$, $P_{2}$ and $P_{3}$ are the coefficients of the temperature T expressed in Kelvin. These coefficients are different for different constituent materials.

According to the first-order shear shell deformation theory [51], the displacement fields of the FGM truncated conical shell are assumed as

$$\begin{aligned} u\left( {x,\theta ,z,t} \right)= & {} u_{0} \left( {x,\theta ,t} \right) +z\varphi _{x} \left( {x,\theta ,t} \right) , \end{aligned}$$

(5a)

$$\begin{aligned} v\left( {x,\theta ,z,t} \right)= & {} v_{0} \left( {x,\theta ,t} \right) +z\varphi _{\theta } \left( {x,\theta ,t} \right) , \end{aligned}$$

(5b)

$$\begin{aligned} w\left( {x,\theta ,z,t} \right)= & {} w_{0} \left( {x,\theta ,t} \right) , \end{aligned}$$

(5c)

where u, v and w stand for the displacements of any point in the x, $\theta$ and z directions, respectively, which are the functions of the middle in-plane displacements $u_{0}$, $v_{0}$ and $w_{0}$ of the FGM conical shell and the mid-surface rotations $\varphi _{x}$ and $\varphi _{\theta }$ of the $\theta$ axis and the x axis, respectively.

Using the von Karman geometric nonlinear strain–displacement relationships, the nonlinear strains can be obtained as [52, 53]

$$\begin{aligned} \varepsilon _{x}= & {} \frac{\partial u_{0} }{\partial x}+z\frac{\partial \varphi _{x} }{\partial x}+\frac{1}{2}\left( {\frac{\partial w_{0} }{\partial x}} \right) ^{2}, \end{aligned}$$

(6a)

$$\begin{aligned} \varepsilon _{\theta }= & {} \mathfrak {R}\frac{\partial v_{0} }{\partial \theta }+z\mathfrak {R}\frac{\partial \varphi _{\theta } }{\partial \theta }+\mathfrak {R}w_{0} \cos \beta +\mathfrak {R}\left( {u_{0} +z\varphi _{x} } \right) \sin \beta +\frac{1}{2}\mathfrak {R}^{2}\left( {\frac{\partial w_{0} }{\partial \theta }} \right) ^{2}, \end{aligned}$$

(6b)

$$\begin{aligned} \gamma _{x\theta }= & {} \mathfrak {R}\frac{\partial u_{0} }{\partial \theta }+z\mathfrak {R}\frac{\partial \varphi _{x} }{\partial \theta }-\mathfrak {R}\left( {v_{0} +z\varphi _{\theta } } \right) \sin \beta +\frac{\partial v_{0} }{\partial x}+z\frac{\partial \varphi _{\theta } }{\partial x}+\mathfrak {R}\frac{\partial w_{0} }{\partial x}\frac{\partial w_{0} }{\partial \theta }, \end{aligned}$$

(6c)

$$\begin{aligned} \gamma _{\theta z}= & {} \varphi _{\theta } +\mathfrak {R}\frac{\partial w_{0} }{\partial \theta }-\mathfrak {R}v_{0} \cos \beta , \end{aligned}$$

(6d)

$$\begin{aligned} \gamma _{xz}= & {} \frac{\partial w_{0} }{\partial x}+\varphi _{x} , \end{aligned}$$

(6e)

where $\mathfrak {R}=1/R$, $\varepsilon _{x}$ and $\varepsilon _{\theta }$ stand for principal strains, $\gamma _{x\theta }$, $\gamma _{\theta z}$, and $\gamma _{xz}$ denote shear strains.

The thermal effect on the FGM truncated conical shell is considered. As a result of the viscous aerodynamic heating on the outside surface of the FGM truncated conical shell, the temperature can be calculated as follow [54]

$$\begin{aligned} T_{c} =T_{\infty } +R_{f} \frac{\gamma -1}{2}M_\mathrm{a}^{2} T_{\infty } , \end{aligned}$$

(7)

where $T_{\infty }, T_{c},R_{f}$ and $\gamma$ are the temperature of the incoming flow, the temperature of the outside surface for the FGM truncated conical shell, the steady-state temperature recovery factor and the specific heat ratio, respectively.

The temperature distribution along the radial direction of the FGM truncated conical shell is regarded as polynomial series [55]

$$\begin{aligned} T\left( z \right) =T_{m} +\left( {T_{c} -T_{m} } \right) \varsigma \left( z \right) , \end{aligned}$$

(8)

where the polynomial series $\varsigma \left( z \right)$ is shown

$$\begin{aligned} \varsigma \left( z \right)= & {} \frac{1}{C}\left[ {\left( {\frac{2z+h}{2h}} \right) -\frac{k_{cm} }{k_{m} \left( {\eta +1} \right) }\left( {\frac{2z+h}{2h}} \right) ^{\left( {\eta +1} \right) }+\frac{k_{cm}^{2} }{k_{m}^{2} \left( {2\eta +1} \right) }\left( {\frac{2z+h}{2h}} \right) ^{\left( {2\eta +1} \right) }} \right. \nonumber \\&\left. {-\frac{k_{cm}^{3} }{k_{m}^{3} \left( {3\eta +1} \right) }\left( {\frac{2z+h}{2h}} \right) ^{\left( {3\eta +1} \right) }+\frac{k_{cm}^{4} }{k_{m}^{4} \left( {4\eta +1} \right) }\left( {\frac{2z+h}{2h}} \right) ^{\left( {4\eta +1} \right) }-\frac{k_{cm}^{5} }{k_{m}^{5} \left( {5\eta +1} \right) }\left( {\frac{2z+h}{2h}} \right) ^{\left( {5\eta +1} \right) }} \right] ,\nonumber \\ \end{aligned}$$

(9)

with

$$\begin{aligned} k_{cm} =k_{c} -k_{m} , \end{aligned}$$

(10)

and

$$\begin{aligned} C=1-\frac{k_{cm} }{\left( {\eta +1} \right) k_{m} }+\frac{k_{cm}^{2} }{\left( {2\eta +1} \right) k_{m}^{2} }-\frac{k_{cm}^{3} }{\left( {3\eta +1} \right) k_{m}^{3} }+\frac{k_{cm}^{4} }{\left( {4\eta +1} \right) k_{m}^{4} }-\frac{k_{cm}^{5} }{\left( {5\eta +1} \right) k_{m}^{5} }, \end{aligned}$$

(11)

where $k_{m}$ and $k_{c}$ are the thermal conductivities of the metal and ceramic.

The constitutive relations of FGM truncated conical shell with the thermal stress can be yielded as

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _{x} \\ \sigma _{\theta } \\ \sigma _{x\theta } \\ \sigma _{\theta z} \\ \sigma _{xz} \\ \end{array}} \right\} =\left[ {{\begin{array}{*{20}c} {Q_{11} } &{} {Q_{12} } &{} 0 &{} 0 &{} 0 \\ {Q_{12} } &{} {Q_{22} } &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {Q_{66} } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {Q_{44} } &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {Q_{55} } \\ \end{array} }} \right] \left\{ {\left\{ {\begin{array}{l} \varepsilon _{x} \\ \varepsilon _{\theta } \\ \gamma _{x\theta } \\ \gamma _{\theta z} \\ \gamma _{xz} \\ \end{array}} \right\} -\left\{ {\begin{array}{c} \alpha \\ \alpha \\ 0 \\ 0 \\ 0 \\ \end{array}} \right\} \Delta T} \right\} . \end{aligned}$$

(12)

The temperature variation is regarded as $\Delta T=T\left( z \right) -T_{0}$, and $T_{0}$ represents the reference temperature. The stiffness coefficients $Q_{ij}$ are calculated as follow

$$\begin{aligned} Q_{{11}} =Q_{{22}} =\frac{E}{1-\upnu ^{2}}, Q_{{12}} =\frac{\upnu E}{1-\upnu ^{2}}, Q_{{44}} =Q_{{55}} =Q_{{66}} =\frac{E}{2\left( {1+\upnu } \right) }. \end{aligned}$$

(13)

Based on Hamilton’s principle, the nonlinear partial differential equations of motion for the truncated FGM conical shell are established as

$$\begin{aligned}&N_{xx,x} +\mathfrak {R}N_{x\theta ,\theta } +\mathfrak {R}N_{xx} \sin \beta -\mathfrak {R}N_{\theta \theta } \sin \beta =I_{0} \ddot{{u}}_{0} +I_{1} \ddot{{\varphi }}_{x} , \end{aligned}$$

(14a)

$$\begin{aligned}&N_{x\theta ,x} +\mathfrak {R}N_{\theta \theta ,\theta } +2\mathfrak {R}N_{x\theta } \sin \beta +\mathfrak {R}Q_{\theta } \cos \beta =I_{0} \ddot{{v}}_{0} +I_{1} \ddot{{\varphi }}_{\theta } , \end{aligned}$$

(14b)

$$\begin{aligned}&Q_{x,x} +\mathfrak {R}Q_{\theta ,\theta } +\mathfrak {R}Q_{x} \sin \beta -\mathfrak {R}N_{\theta \theta } \cos \beta +N_{xx,x} \frac{\partial w_{0} }{\partial x}+N_{xx} \frac{\partial ^{2}w_{0} }{\partial x^{2}}+\mathfrak {R}N_{xx} \frac{\partial w_{0} }{\partial x}\sin \beta \nonumber \\&\quad +\mathfrak {R}^{2}N_{\theta \theta ,\theta } \frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}^{2}N_{\theta \theta } \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}+\mathfrak {R}N_{x\theta ,\theta } \frac{\partial w_{0} }{\partial x}+2\mathfrak {R}N_{x\theta ,\theta } \frac{\partial ^{2}w_{0} }{\partial x\partial \theta } \nonumber \\&\quad +\mathfrak {R}N_{x\theta ,x} \frac{\partial w_{0} }{\partial \theta }+P_\mathrm{a} -p_{1} \cos \left( {\Omega t} \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}-\kappa \dot{{w}}_{0} =I_{0} \ddot{{w}}_{0} , \end{aligned}$$

(14c)

$$\begin{aligned}&M_{xx,x} +\mathfrak {R}M_{x\theta ,\theta } -\mathfrak {R}Q_{x} +\mathfrak {R}M_{xx} \sin \beta -\mathfrak {R}M_{\theta \theta } \sin \beta =I_{1} \ddot{{u}}_{0} +I_{2} \ddot{{\varphi }}_{x} , \end{aligned}$$

(14d)

$$\begin{aligned}&M_{x\theta ,x} +\mathfrak {R}M_{\theta \theta ,\theta } -\mathfrak {R}Q_{\theta } +2\mathfrak {R}M_{x\theta } \sin \beta =I_{1} \ddot{{v}}_{0} +I_{2} \ddot{{\varphi }}_{\theta } , \end{aligned}$$

(14e)

where $\mathfrak {R}=1/R$, $\kappa$ represents damping coefficient of the shell, “$^.$” is partial derivative with respect to the time.

All the inertia terms truncated FGM conical shell in the above equations are given

$$\begin{aligned} I_{i} =\int _{-\frac{h}{2}}^{\frac{h}{2}} {z^{i}\rho } \mathrm{d}z, \left( {i=0\,,\;1 ,\,2} \right) . \end{aligned}$$

(15)

The components of the thermal stress and stress resultants are calculated as

$$\begin{aligned} \left\{ {\begin{array}{l} N_{xx} \\ N_{\theta \theta } \\ N_{x\theta } \\ \end{array}} \right\}= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {\left\{ {\left[ A \right] ,\left[ B \right] } \right\} } \left\{ {\begin{array}{l} \varepsilon ^{(0)} \\ \varepsilon ^{(1)} \\ \end{array}} \right\} \mathrm{d}z+\left\{ {\begin{array}{c} N_{xx}^{T} \\ N_{\theta \theta }^{T} \\ 0 \\ \end{array}} \right\} , \end{aligned}$$

(16a)

$$\begin{aligned} \left\{ {\begin{array}{l} M_{xx} \\ M_{\theta \theta } \\ M_{x\theta } \\ \end{array}} \right\}= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {\left\{ {\left[ B \right] ,\left[ D \right] } \right\} } \left\{ {\begin{array}{l} \varepsilon ^{(0)} \\ \varepsilon ^{(1)} \\ \end{array}} \right\} \mathrm{d}z+\left\{ {\begin{array}{c} M_{xx}^{T} \\ M_{\theta \theta }^{T} \\ 0 \\ \end{array}} \right\} , \end{aligned}$$

(16b)

$$\begin{aligned} \left\{ {\begin{array}{l} Q_{x} \\ Q_{\theta } \\ \end{array}} \right\}= & {} K\int _{-\frac{h}{2}}^{\frac{h}{2}} {\left[ A \right] } \left\{ {\begin{array}{l} \gamma _{xz} \\ \gamma _{\theta z} \\ \end{array}} \right\} \mathrm{d}z, \end{aligned}$$

(16c)

$$\begin{aligned} \left( {\left\{ {\begin{array}{c} N_{xx}^{T} \\ N_{\theta \theta }^{T} \\ N_{x\theta }^{T} \\ \end{array}} \right\} ,\left\{ {\begin{array}{c} M_{xx}^{T} \\ M_{\theta \theta }^{T} \\ M_{x\theta }^{T} \\ \end{array}} \right\} } \right)= & {} \int _{z_{k} }^{z_{k+1} } {\left[ {{\begin{array}{*{20}c} {Q_{11} } &{} {Q_{12} } &{} 0 \\ {Q_{12} } &{} {Q_{22} } &{} 0 \\ 0 &{} 0 &{} {Q_{66} } \\ \end{array} }} \right] } \left\{ {\begin{array}{l} \alpha _{x} \\ \alpha _{\theta } \\ \alpha _{x\theta } \\ \end{array}} \right\} \left( {\Delta T,\Delta Tz} \right) \mathrm{d}z, \end{aligned}$$

(16d)

where K is the shear correction coefficient and give it as follows [56]

$$\begin{aligned} K=\frac{5}{\left( {6-\upnu } \right) }. \end{aligned}$$

(17)

The tensile rigidity $A_{ij}$, the bending-tensile coupling rigidity $B_{ij}$, and the bending rigidity $D_{ij}$ of the FGM truncated conical shell can be expressed by

$$\begin{aligned} \left( {A_{ij} ,B_{ij} ,D_{ij} } \right)= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {Q_{ij} \left( {1,z,z^{2}} \right) } \mathrm{d}z,\quad \left( {i,j=1,2,6} \right) , \end{aligned}$$

(18a)

$$\begin{aligned} A_{ij}= & {} \int _{-\frac{h}{2}}^{\frac{h}{2}} {Q_{ij} } \mathrm{d}z,\quad \left( {i,j=4,5} \right) . \end{aligned}$$

(18b)

Using the aforementioned equations, the nonlinear equations of motion in form of generalized displacements for the FGM truncated conical shell are given in the “Appendix A.”

The boundary conditions of the FGM truncated conical shell are considered as the simply supported at the two ends

$$\begin{aligned} x=0\hbox { and }x=L: w_{0} =\;v_{0} =N_{x} =M_{x} =M_{x\theta } =0. \end{aligned}$$

(19)

The displacements $u_{0}$, $v_{0}$, $w_{0}$, $\varphi _{x}$ and $\varphi _{\theta }$ of the FGM truncated conical shell, which satisfy the boundary conditions, are represented in the form of the double Fourier sine series

$$\begin{aligned} u_{0}= & {} \sum \limits _{m=1}^M {\sum \limits _{n=1}^N {u_{mn} \left( t \right) } \cos \left( {\frac{m\pi x}{L}} \right) \cos \left( {n\theta } \right) } , \end{aligned}$$

(20a)

$$\begin{aligned} v_{0}= & {} \sum \limits _{m=1}^M {\sum \limits _{n=1}^N {v_{mn} } \left( t \right) \sin \left( {\frac{m\pi x}{L}} \right) \sin \left( {n\theta } \right) } , \end{aligned}$$

(20b)

$$\begin{aligned} w_{0}= & {} \sum \limits _{n=1}^M {\sum \limits _{m=1}^N {W_{mn} \left( t \right) } \sin \left( {\frac{m\pi x}{L}} \right) \cos \left( {n\theta } \right) } , \end{aligned}$$

(20c)

$$\begin{aligned} \varphi _{x}= & {} \sum \limits _{m=1}^M {\sum \limits _{n=1}^N {\varphi _{xmn} \left( t \right) } \cos \left( {\frac{m\pi x}{L}} \right) \sin \left( {n\theta } \right) } , \end{aligned}$$

(20d)

$$\begin{aligned} \varphi _{\theta }= & {} \sum \limits _{m=1}^M {\sum \limits _{n=1}^N {\varphi _{\theta mn} } \left( t \right) \sin \left( {\frac{m\pi x}{L}} \right) \sin \left( {n\theta } \right) } , \end{aligned}$$

(20e)

where $u_{mn} \left( t \right)$, $v_{mn} \left( t \right)$, $W_{mn} \left( t \right)$, $\varphi _{xmn} (t)$ and $\varphi _{\theta mn} (t)$ are the time-varying terms, m and n are the generatrix half waves number and the circumferential waves number.

Based on the study results of Noseir [57] and Bhimaraddi [58], the influences of the inertia terms in rotation and in-plane on nonlinear vibrations of FGM truncated conical shell are very small comparing to radial inertia term which given in Eq. (18). Thus, the inertia terms of $u_{0}$, $v_{0}$, $\varphi _{x}$ and $\varphi _{\theta }$ can be omitted. Thus, the first two modes of transverse displacement w are very important. Substituting the double Fourier series of Eq. (20) into Eqs. (A1), (A2), (A4) and (A5), Galerkin integration procedure is employed to acquire four constant coefficients of the coupled algebraic equations. Then, the displacements $u_{0}$, $v_{0}$, $\varphi _{x}$ and $\varphi _{\theta }$ with respect to the displacement $w_{0}$ can be derived. Therefore, substituting the expressions about $u_{0}$, $v_{0}$, $\varphi _{x}$ and $\varphi _{\theta }$ into the ordinary differential equation obtained by Eq. (A3), the nonlinear ordinary differential equations of motion for the FGM truncated conical shell are obtained

$$\begin{aligned} \ddot{{W}}_{11} +\mu _{1} \dot{{W}}_{11} +\omega _{1}^{2} W_{11} +\zeta _{11} W_{11}^{3} +\zeta _{12} W_{11}^{2} W_{12} +\zeta _{13} W_{11} W_{12}^{2} +\zeta _{14} W_{12}^{3} +\zeta _{15} W_{11} \left( {p_{1} \cos \Omega t} \right)= & {} 0, \end{aligned}$$

(21a)

$$\begin{aligned} \ddot{{W}}_{12} +\mu _{2} \dot{{W}}_{12} +\omega _{2}^{2} W_{12} +\zeta _{21} W_{12}^{3} +\zeta _{22} W_{11}^{2} W_{12} +\zeta _{23} W_{11} W_{12}^{2} +\zeta _{24} W_{12}^{3} +\zeta _{25} W_{11} \left( {p_{1} \cos \Omega t} \right)= & {} 0, \nonumber \\ \end{aligned}$$

(21b)

In order to get the dimensionless equations of the FGM truncated conical shell, the following transformation of the variables and parameters are introduced

$$\begin{aligned} \tau= & {} \omega _{1} t, W_{11} =q_{1} h, W_{12} =q_{2} h, {\bar{\Omega }}=\frac{\Omega }{\omega _{1} }, {\bar{\mu }}_{1} =\frac{\mu _{1} }{\omega _{1} }, {\bar{\mu }}_{2} =\frac{\mu _{2} }{\omega _{1} },\nonumber \\ {\bar{\omega }}_{1}= & {} \frac{\omega _{1} }{\omega _{1} }, {\bar{\omega }}_{2} =\frac{\omega _{2} }{\omega _{1} }, {\bar{p}}_{1} =\frac{p_{1} }{\omega _{1}^{2} }, {\bar{\zeta }}_{ij} =\frac{\zeta _{ij} h^{2}}{\omega _{1}^{2} }, (i=\;1\,,\;2, j=\;1\,,\;2\,,\;3\,,\,4). \end{aligned}$$

(22)

Thus, the dimensionless equation of the FGM truncated conical shell can be rewritten as

$$\begin{aligned} \ddot{{q}}_{1} +{\bar{\mu }}_{1} \dot{{q}}_{1} +{\bar{\omega }}_{1}^{2} q_{1} +{\bar{\zeta }}_{11} q_{1}^{3} +{\bar{\zeta }}_{12} q_{1}^{2} q_{2} +{\bar{\zeta }}_{13} q_{1} q_{2}^{2} +{\bar{\zeta }}_{14} q_{2}^{3} +{\bar{\zeta }}_{15} q_{1} \left( {{\bar{p}}_{1} \cos {\bar{\Omega }}\tau } \right)= & {} 0, \end{aligned}$$

(23a)

$$\begin{aligned} \ddot{{q}}_{2} +{\bar{\mu }}_{2} \dot{{q}}_{2} +{\bar{\omega }}_{2}^{2} q_{2} +{\bar{\zeta }}_{21} q_{1}^{3} +{\bar{\zeta }}_{22} q_{1}^{2} q_{2} +{\bar{\zeta }}_{23} q_{1} q_{2}^{2} +{\bar{\zeta }}_{24} q_{2}^{3} +{\bar{\zeta }}_{25} q_{1} \left( {{\bar{p}}_{1} \cos {\bar{\Omega }}\tau } \right)= & {} 0, \end{aligned}$$

(23b)

where “$\cdot$” stands for the derivative with respect to the dimensionless time $\tau$.

3 Perturbation analysis

By using the scale method [59], a perturbation analysis is carried out in following study. A small perturbation parameter $\varepsilon$ is introduced to characterize the amplitude of the radial displacement, the loading and the damping of the FGM truncated conical shell

$$\begin{aligned} q_{i} =\varepsilon w_{i} , \tilde{{\mu }}_{i} =\varepsilon ^{2}{\bar{\mu }}_{i} , \tilde{{p}}=\varepsilon ^{2}{\bar{p}}, (i=\;1\,,\;2). \end{aligned}$$

(24)

Substituting Eq. (24) into Eq. (23), the dimensionless system is obtained as follows. For simplicity, the overbars are omitted in the following equations

$$\begin{aligned}&\ddot{{w}}_{1} +\varepsilon \mu _{1} \dot{{w}}_{1} +\omega _{1}^{2} w_{1} +\varepsilon \zeta _{11} w_{1}^{3} +\varepsilon \zeta _{12} w_{1}^{2} w_{2} +\varepsilon \zeta _{13} w_{1} w_{2}^{2} +\varepsilon \zeta _{14} w_{2}^{3}\nonumber \\&\quad +\,\varepsilon \zeta _{15} w_{1} \left( {p_{1} \cos \Omega t} \right) =0, \end{aligned}$$

(25a)

$$\begin{aligned}&\ddot{{w}}_{2} +\varepsilon \mu _{2} \dot{{w}}_{2} +\omega _{2}^{2} w_{2} +\varepsilon \zeta _{21} w_{2}^{3} +\varepsilon \zeta _{22} w_{1}^{2} w_{2} +\varepsilon \zeta _{23} w_{1} w_{2}^{2} +\varepsilon \zeta _{24} w_{2}^{3}\nonumber \\&\quad +\varepsilon \zeta _{25} w_{1} \left( {p_{1} \cos \Omega t} \right) =0. \end{aligned}$$

(25b)

For utilizing the multiple scales method, the approximate solutions of Eq. (25) are assumed as follows

$$\begin{aligned} w_{n} (\tau \,,\;\varepsilon )=x_{n0} (T_{0} ,T_{1} )+\varepsilon x_{n1} (T_{0} ,T_{1} )+\cdots ,\left( {n=1\;,\;2} \right) , \end{aligned}$$

(26)

where $T_{0} =\tau$, $T_{1} =\varepsilon \tau$.

Then, one obtains the following differential operators

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau }= & {} \frac{\partial }{\partial {}{}T_{0} }\frac{\partial \,T_{0} }{\partial \,\tau }+\frac{\partial }{\partial \,T_{1} }\frac{\partial \,T_{1} }{\partial \tau }+\cdots =D_{0} +\varepsilon {}{}D_{1} +\cdots , \end{aligned}$$

(27a)

$$\begin{aligned} \frac{\mathrm{d}^{2}}{\mathrm{d}\tau ^{2}}= & {} \left( {D_{0} +\varepsilon {}D_{1} \cdots } \right) ^{2}=D_{0}^{2} +2\varepsilon {}D_{0} D_{1} +\cdots , \end{aligned}$$

(27b)

where $D_{k} =\frac{\partial }{\partial T_{k} }$, $(k=0\,,\;1\,)$.

The following analyses are focused on the case of 1:2 internal resonant and 1/2 subharmonic resonant relations. Therefore, the resonant relations can be proved as

$$\begin{aligned} 2\omega _{1} =\Omega -\varepsilon \sigma _{1} , \omega _{2} =\Omega -\varepsilon \sigma _{2} , \Omega =2, \end{aligned}$$

(28)

where $\sigma _{1}$ and $\sigma _{2}$ are the detuning parameters.

Substituting Eqs. (26)–(28) into Eq. (25) and equating the coefficients of the same power of $\varepsilon$ yield the following equations

Order $\varepsilon ^{{0}}$

$$\begin{aligned} D_{0}^{2} \,x_{10} +x_{10}= & {} 0, \end{aligned}$$

(29a)

$$\begin{aligned} D_{0}^{2} x_{20} +x_{20}= & {} 0, \end{aligned}$$

(29b)

Order $\varepsilon ^{{1}}$

$$\begin{aligned} D_{0}^{2} x_{11} +\frac{x_{11} }{4}= & {} -2D_{0} D_{1} x_{10} -\mu _{1} D_{0} x_{10} +\frac{\sigma _{1} }{2}x_{10} -\zeta _{11} x_{10}^{3} -\zeta _{12} x_{10}^{2} x_{20}\nonumber \\&-\zeta _{13} x_{10} x_{20}^{2} -\zeta _{14} x_{20}^{3} -\zeta _{15} x_{10} p_{1} \cos \left( \tau \right) , \end{aligned}$$

(30a)

$$\begin{aligned} D_{0}^{2} x_{21} +x_{21}= & {} -2D_{0} D_{1} x_{20} -\mu _{2} D_{0} x_{20} +2\sigma _{2} x_{20} -\zeta _{21} x_{10}^{3} -\zeta _{22} x_{10}^{2} x_{20}\nonumber \\&-\zeta _{23} x_{10} x_{20}^{2} -\zeta _{24} x_{20}^{3} -\zeta _{25} x_{20} p_{1} \cos \left( \tau \right) . \end{aligned}$$

(30b)

The solution of Eq. (29) is represented in the complex form

$$\begin{aligned} x_{10}= & {} A_{1} \left( {T_{1} } \right) \text{ e}^{\frac{i}{2}T_{0} }+{\bar{A}}_{1} \left( {T_{1} } \right) \text{ e}^{-\frac{i}{2}T_{0} }, \end{aligned}$$

(31a)

$$\begin{aligned} x_{20}= & {} A_{2} \left( {T_{1} } \right) \text{ e}^{\frac{i}{2}T_{0} }+{\bar{A}}_{2} \left( {T_{1} } \right) \text{ e}^{-\frac{i}{2}T_{0} }, \end{aligned}$$

(31b)

where ${\bar{A}}_{1}$ and ${\bar{A}}_{2}$ are the complex conjugate parts of $A_{1}$ and $A_{2}$, respectively.

Substituting Eq. (31) into Eq. (30), one yields

$$\begin{aligned} D_{0}^{2} x_{11} +\frac{x_{11} }{4}= & {} \left( {-iD_{1} A_{1} -\frac{\mu _{1} i}{2}A_{1} +\frac{\sigma _{1} }{2}A_{1} -3\zeta _{11} A_{1}^{2} {\bar{A}}_{1} -2\zeta _{12} A_{1} {\bar{A}}_{1} A_{2} } \right. \nonumber \\&\left. {-\frac{1}{2}\zeta _{15} p_{1} {\bar{A}}_{1} } \right) \text{ e}^{\frac{i}{2}T_{0} }+CC+NST, \end{aligned}$$

(32a)

$$\begin{aligned} D_{0}^{2} x_{21} +x_{21}= & {} \left( {-2iD_{1} A_{2} -\mu _{2} iA_{2} +2\sigma _{2} A_{2} -2\zeta _{22} A_{1} {\bar{A}}_{1} A_{2} -3\zeta _{24} A_{2}^{2} {\bar{A}}_{2} } \right. \nonumber \\&\left. {-\frac{1}{2}\zeta _{25} p_{1} {\bar{A}}_{2} } \right) \text{ e}^{iT_{0} }+CC+NST, \end{aligned}$$

(32b)

where CC stand for the complex conjugate terms of the preceding parts and NST stand for the parts which cannot produce the secular terms.

The amplitude functions can be written in polar form as

$$\begin{aligned} A_{1} =\frac{1}{2}a_{1} \text{ e}^{i\varphi _{1} }, A_{2} =\frac{1}{2}a_{2} \text{ e}^{i\varphi _{2} }. \end{aligned}$$

(33)

Substituting Eq. (33) into the parts that producing the secular terms of Eq. (32), the averaged equations in polar form are yielded by separating the real and imaginary parts

$$\begin{aligned} \frac{\mathrm{d}a_{1} }{\mathrm{d}T_{1} }= & {} -\frac{\mu _{1} a_{1} }{2}-\frac{\zeta _{15} p_{1} a_{1} }{2}\sin \left( {2\varphi _{1} } \right) , \end{aligned}$$

(34a)

$$\begin{aligned} a_{1} \frac{\mathrm{d}\varphi _{1} }{\mathrm{d}T_{1} }= & {} -\frac{\sigma _{1} a_{1} }{2}-\frac{\zeta _{15} p_{1} a_{1} }{2}\cos \left( {2\varphi _{1} } \right) +\frac{3\zeta _{11} a_{1}^{3} }{4}++\frac{\zeta _{13} a_{1} a_{2}^{2} }{2}, \end{aligned}$$

(34b)

$$\begin{aligned} \frac{\mathrm{d}a_{2} }{\mathrm{d}T_{1} }= & {} -\frac{\mu _{2} a_{2} }{2}-\frac{\zeta _{25} p_{1} a_{2} }{4}\sin \left( {2\varphi _{2} } \right) , \end{aligned}$$

(34c)

$$\begin{aligned} a_{2} \frac{\mathrm{d}\varphi _{2} }{\mathrm{d}T_{1} }= & {} -\frac{\sigma _{2} a_{2} }{2}-\frac{\zeta _{25} p_{1} a_{2} }{2}\cos \left( {2\varphi _{2} } \right) -\frac{3\zeta _{21} a_{2}^{3} }{8}+\frac{\zeta _{23} a_{1}^{2} a_{2} }{4}. \end{aligned}$$

(34d)

The amplitude functions are also rewritten in the Cartesian form, as following

$$\begin{aligned} A_{1} =x_{1} +ix_{2} , A_{2} =x_{3} +ix_{4} . \end{aligned}$$

(35a)

Substituting Eq. (35) into the parts that producing the secular terms of Eq. (32) and separating the real and imaginary parts, the four-dimensional averaged equations in the form of Cartesian can be obtained as

$$\begin{aligned} \frac{\mathrm{d}x_{1} }{\mathrm{d}T_{1} }= & {} \frac{\sigma _{1} x_{2} }{2}-\frac{\mu _{1} x_{1} }{2}-\frac{\zeta _{15} p_{1} x_{2} }{4}-3\zeta _{11} x_{2}^{3} -3\zeta _{11} x_{1}^{2} x_{2} -2\zeta _{13} x_{2} x_{3}^{2} -2\zeta _{13} x_{2} x_{4}^{2} , \end{aligned}$$

(36a)

$$\begin{aligned} \frac{\mathrm{d}x_{2} }{\mathrm{d}T_{1} }= & {} -\frac{\sigma _{1} x_{1} }{2}-\frac{\mu _{1} x_{2} }{2}-\frac{\zeta _{15} p_{1} x_{1} }{4}+3\zeta _{11} x_{1}^{3} +3\zeta _{11} x_{1} x_{2}^{2} +2\zeta _{13} x_{1} x_{3}^{2} +2\zeta _{13} x_{1} x_{4}^{2} , \end{aligned}$$

(36b)

$$\begin{aligned} \frac{\mathrm{d}x_{3} }{\mathrm{d}T_{1} }= & {} \sigma _{2} x_{4} -\frac{\mu _{2} x_{3} }{2}-\frac{\zeta _{25} p_{1} x_{4} }{4}-\frac{3\zeta _{21} x_{4}^{3} }{2}-\frac{3\zeta _{21} x_{3}^{2} x_{4} }{2}-\zeta _{23} x_{1}^{2} x_{4} -\zeta _{23} x_{2}^{2} x_{4} , \end{aligned}$$

(36c)

$$\begin{aligned} \frac{\mathrm{d}x_{4} }{\mathrm{d}T_{1} }= & {} -\sigma _{2} x_{3} -\frac{\mu _{2} x_{4} }{2}-\frac{\zeta _{25} p_{1} x_{3} }{4}+\frac{3\zeta _{21} x_{3}^{3} }{2}+\frac{3\zeta _{21} x_{3} x_{4}^{2} }{2}+\zeta _{23} x_{1}^{2} x_{3} +\zeta _{23} x_{2}^{2} x_{3} . \end{aligned}$$

(36d)

4 Frequency responses

In this section, a FGM $(\hbox {SUS304/SI}_{\mathrm {3}} \hbox {N}_{\mathrm {4}})$ truncated conical shell are considered, the smaller radius at middle surface $r_{1} =0.8\,\text{ m }$, semi-vertex angle $\beta =30^\circ$ and thickness $h=0.002\,\text{ m }$. The mass densities, Young’s modulus and coefficients of thermal expansion of SUS304 and $\hbox {SI}_{\mathrm {3}} \hbox {N}_{\mathrm {4}}$ are given in Table 1. The airflow characteristics are provided as following: $\alpha _{\infty } =213.3\hbox {6}$ m/s, $\gamma _{\alpha } =1.4$ and $T_{\infty } =233.26\,\hbox {K}$. In Fig. 4, when the ratio of the length to the smaller radius is $L\text{/ }r_{1} =3.76$, it is found that the natural frequency $\omega _{2} =2\omega _{1}$, then, ${\bar{\omega }}_{2} =\omega _{2} /\omega _{1} =2$. When the in-plane load frequency is close to $2\omega _{1}$, there will be the case of 1:2 internal resonant and 1/2 subharmonic resonant relations.

Table 1 The material properties of SUS304, $\hbox {SI}_{\mathrm {3}} \hbox {N}_{\mathrm {4}}$ and $\hbox {ZrO}_{\mathrm {2}}$ are given

Firstly, the mode convergence is studied. The condition which the 1:2 internal resonance occurs of the FGM truncated conical shell is considered. The dimensionless transverse amplitudes of the FGM truncated conical shell at the point (3L/4, 0, 0) with first mode (1, 1), first two modes (1, 1) and (1, 2), first three modes (1, 1), (1, 2) and (2, 1) are calculated in Table 1, respectively, when exponent of volume fraction for the ceramic $\eta =5$ and Mach number $M_\mathrm{a} =3$. It can be seen that the amplitudes of the FGM truncated conical shell with 1:2 internal resonance obtained with the first two modes and the first three modes are nearly the same, and a further increase in the number of components does not greatly influence the results.

Fig. 4

The curve of the ratio of the first two order natural frequencies $\omega _{2} \text{/ }\omega _{1}$ versus the ratio of length to top radius $L\text{/ }r_{1}$ is obtained

Table 2 Comparison of the dimensionless transverse amplitudes of the FGM truncated conical shell at the point (3L/4, 0, 0) for first mode, first two modes and first three modes is given

To evaluate the developed program and present formulation, the dimensionless natural frequencies $(\Omega _{n} =\omega _{n} R\sqrt{\left( {1-\upnu ^{2} } \right) \rho /E} )$ are calculated and are compared to those of Liew [60], Kerboua [61] and Najafov [62] for a pure metal conical shell in Table 3. The geometry relations of the pure metal truncated conical shell are $R/h=100$, $\beta =\pi /6$ and $L=0.25R\sin \beta$. As expected, for the pure metal truncated conical shell, the present results are in good agreement with that in the literatures. Furthermore, the natural frequencies are compared with Pradhan et al. [62] and Shen [63] for the FGM $(\hbox {SUS304/ZrO}_{\mathrm {2}})$ cylindrical shell, as shown in Table 4. The geometric parameters of the cylindrical shell are given: $h=0.002\,\text{ m }$, $R=1\,\text{ m }$ and $L=20\,\text{ m }$. The material properties of the FGM (SUS304/ZrO2) are shown in Table 1. It is illuminated that the present results are agree well with the existing results.

In addition, the validation of the present method has been done by comparing the dimensionless central moments of FGM plate in Table 5 with the value obtained by using the method which is provided by Ref. [51]. The Ti–6Al–4V/Al$_{\mathrm {2}} \hbox {O}_{\mathrm {3}}$ FGM plate has the length $a=0.2$ m, the width $b=0.5$ m and the thickness $h=0.002$ m. One can note that excellent agreement is reached.

Table 3 The comparison of dimensionless natural frequency $\left( {\Omega _{n} =\omega _{n} R\left( L \right) \sqrt{\left( {1-\upnu ^{2} } \right) \rho /E} } \right)$ for truncated pure metal conical shell with Liew [50], Kerboua [51] and Najafov [52] is obtained

Table 4 The comparison of natural frequencies with Pradhan et al. [53] and Shen [54] for thin FGM $(\hbox {SUS304/ZrO}_{\mathrm {2}})$ cylindrical shell is obtained

Table 5 Comparison of the dimensionless central moments ${\bar{M}}_{xx} =M_{xx} /\left( {q_{0} a^{2}} \right)$ and ${\bar{M}}_{yy} =M_{yy} /\left( {q_{0} a^{2}} \right)$ for ${\eta }=0.5$ and 1.0 is given

Fig. 5

The frequency–amplitude response curves of the FGM conical truncated shell with different in-plane loads $p_{1}$ are obtained when $\eta =5$ and $M_\mathrm{a} =2$, a the first-order mode, b the second-order mode

Fig. 6

The frequency–amplitude response curves of the truncated FGM conical shell with different Mach numbers $M_\mathrm{a}$ are obtained when $\eta =5$ and $p_{1} =60$

Fig. 7

The frequency–amplitude response curves of the truncated FGM conical shell with different damping coefficient $\mu _{1}$ are obtained when $\eta =5$ and $p_{1} =60$

Fig. 8

The frequency–amplitude response curves of the FGM truncated conical shell with different exponents of volume fraction $\eta$ are obtained when $M_\mathrm{a} =2$ and $p_{1} =60$

In the following studies, the numerical calculations are used to investigate the nonlinear dynamics of the FGM truncated conical shell subject to aerodynamics and in-plane load. Based on the averaged equation (34), amplitude–frequency responses of the FGM truncated conical shell can be investigated. The left parts of the averaged equation (34) are proposed to zero. Then, using Maple program, the amplitude–frequency and amplitude–force response curves of the FGM truncated conical shell are plotted. By inspecting the maximum real part of the Jacobian matrix of the averaged equation (34), the stabilities of the solutions can be revealed.

Figure 5 depicts the frequency–amplitude response curves of the FGM conical truncated shell with different in-plane loads $p_{1}$. Mach number is selected as 2, and the value of the volume fraction index is 5. Figure 5a and b is the frequency–amplitude response curves of the first-order mode and the second-order mode of the FGM truncated conical shell, respectively. The full line, the dash line and the dot dash line represent the frequency amplitude-response curves with different in-plane loads which are chosen as 60, 80 and 100, respectively. The star represents the stable solutions, and the circle represents the unstable solutions. The upper branch of the frequency–amplitude response curves of the FGM conical truncated shell is stable and the lower branch is unstable. By comparing the three lines which in Fig. 5a and b, it is illustrated that there are hardening-spring characteristics for the two modes of the FGM truncated conical shell. The region of two curves becomes wider when in-plane load increasing for the FGM truncated conical shell. It is observed that the nonlinear resonance characteristics become stronger and amplitudes of the two modes are getting larger when the in-plane excitation increasing. Figure 6 illustrates the effect of Mach number of the FGM truncated conical shell on the frequency–amplitude characteristics. No matter what Mach number is 2 or 3, there are hardening-spring characteristics for the two modes of the FGM truncated conical shell. The region of two curves for $M_\mathrm{a} =3$ is little wider than that for $M_\mathrm{a} =2$. It is due to that with the increase of Mach number, the effects of the aerodynamic heating and the aerodynamic force of the FGM truncated conical shell becoming powerful. Figure 7 plots amplitude–response curves with different damping coefficients $\mu _{1}$ when $M_\mathrm{a} =2$ and $p_{1} =60$. It is shown that with the increase of the damping coefficients, the nonlinear resonance characteristics are getting weaker and amplitudes of two modes become smaller. Figure 8 illustrates the influence of the volume fraction index of the FGM truncated conical shell on the frequency–amplitude responses. It is shown that with the decrease of the volume fraction index, the nonlinear resonance characteristics are stronger and the amplitudes become larger for the two modes of the FGM truncated conical shell.

Fig. 9

The bifurcation diagram of the truncated FGM conical shell for the in-plane load $p_{1}$ is obtained when the exponents of volume fraction for the ceramic $\eta =0.5$ and Mach number $M_\mathrm{a} =2$, a bifurcation diagram of the first-order mode, b bifurcation diagram of the second-order mode

Fig. 10

The period motion of the truncated FGM conical shell exists when $\eta =0.5$, $M_\mathrm{a} =2$ and $p_{1} =60$, a the phase portrait on the plane $(x_{1} \,,\;x_{2} )$, b the time history on the plane$(\tau \,,\;x_{1} )$, c the phase portrait on the plane $(x_{3} \,,\;x_{4} )$, d the time history on the plane $(\tau \,,\;x_{3} )$, (e) the three-dimensional phase portrait in the space $(x_{1} \,,\;x_{2} ,x_{3} )$, f the poincare map on the plane $(x_{1} \,,\;x_{2} )$

5 Periodic and chaotic motions

Based on Eq. (36), the chaotic and periodic motions of the truncated FGM conical shell are investigated. The fourth-order varied-step Runge-Kutta algorithm through the MATLAB software is used to explore the existence of the chaotic and periodic motions for the truncated FGM conical shell. The bifurcation diagrams, time phase portraits, Poincare maps and history diagrams can be plotted to reveal the influences of in-plane load, Mach number, exponent of volume fraction and damping coefficient on the nonlinear vibrations and chaos of the truncated FGM conical shell.

Figure 9 plots the bifurcation diagrams of the first-order and second-order modes of the truncated FGM conical shell versus in-plane load when $p_{1}$ increases from 60 to 100. Mach number is $M_\mathrm{a} =2$, and the exponents of the volume fraction for the ceramic is $\eta =0.5$. It can be observed that there is only the periodic motion for the truncated FGM conical shell. It is due to the fact that the volume index is lower, the volume fraction of ceramic is higher, the stiffness of the FGM truncated conical shell is larger. Figure 10 is the motion responses of the truncated FGM conical shell when in-plane load is 60. The motion responses include the following parts, (a) phase portrait on the plane $(x_{1} \,,\;x_{2} )$, (b) time history on the plane $(\tau \,,\;x_{1} )$, (c) phase portrait on the plane $(x_{3} \,,\;x_{4} )$, (d) time history on the plane $(\tau \,,\;x_{3} )$, (e) three-dimensional phase portrait in space $(x_{1} \,,\;x_{2} ,x_{3} )$, (f) Poincare map on the plane $(x_{1} \,,\;x_{2} )$.

Fig. 11

The bifurcation diagram of the truncated FGM conical shell for the in-plane load $p_{1}$ is obtained when the exponents of volume fraction for the ceramic $\eta =5$ and Mach number $M_\mathrm{a} =2$

Fig. 12

The period motion of the FGM truncated conical shell is given when $\eta =5$, $M_\mathrm{a} =2$ and $p_{1} =60$

Figure 11 illustrates the bifurcation diagrams of the nonlinear vibrations of the truncated FGM conical shell versus in-plane load when $p_{1}$ increases from 60 to 100. The exponent of volume fractions for ceramic is $\eta =5$ and Mach number is $M_\mathrm{a} =2$, respectively. It is illuminated that the motion of the truncated FGM conical shell is: the periodic motion $\rightarrow$ the quasi-period motion $\rightarrow$ the chaotic motion. A multiple periodic bifurcation exists in the periodic region when $p_{1}$ increases from 65 to 78. Figures 12, 13, 14, 15 and 16 prove the different motion responses of the truncated FGM conical shell when in-plane loads are chosen as different values. Figures 12, 13 and 14 are the periodic motions of the FGM truncated conical shell when in-plane load are given as $p_{1} =60$, $p_{1} =75$ and $p_{1} =80$, respectively. Figure 13 is the motion response when the multiple periodic bifurcation exists. Figure 15 depicts quasi-period motion of the FGM truncated conical shell when $p_{1} =92$. Figure 16 indicates the chaotic motion of the FGM truncated conical shell when the in-plane load is selected as 100.

Fig. 13

The period motion of the FGM truncated conical shell is given when $\eta =5$, $M_\mathrm{a} =2$ and $p_{1} =75$

Fig. 14

The period motion of the FGM truncated conical shell is given $\eta =5$, $M_\mathrm{a} =2$ and $p_{1} =80$

Fig. 15

The quasi-period motion of the FGM truncated conical shell is given when $\eta =5$, $M_\mathrm{a} =2$ and $p_{1} =92$

Fig. 16

The chaotic motion of the FGM truncated conical shell is given when $\eta =5$, $M_\mathrm{a} =2$ and $p_{1} =100$

Fig. 17

The bifurcation diagram of the truncated FGM conical shell for in-plane load $p_{1}$ is obtained when exponent of volume fraction for the ceramic $\eta =5$ and Mach number $M_\mathrm{a} =3$

Fig. 18

The period motion of the FGM truncated conical shell is given when $\eta =5$, $M_\mathrm{a} =3$ and $p_{1} =60$

Fig. 19

The quasi-period motion of the FGM truncated conical shell is given when $\eta =5$, $M_\mathrm{a} =3$ and $p_{1} =75$

Fig. 20

The chaotic motion of the FGM truncated conical shell is given when $\eta =5$, $M_\mathrm{a} =3$ and $p_{1} =100$

Figure 17 illustrates the change of the motion responses of the truncated FGM conical shell from periodic motion to chaotic motion. The exponent of the volume fraction for the ceramic is 5 and Mach number is 3. It is shown that when in-plane load increases to 70, the motion of the FGM truncated conical shell changes from periodic motion to quasi-period motion. Then, there is chaotic motion existing when the in-plane load increases to 78. Figures 18, 19 and 20 depict the periodic motion $(p_{1} =60)$, quasi-period motion $(p_{1} =75)$ and chaotic motion $(p_{1} =100)$, respectively, that are corresponding to the motion responses given in Fig. 17. Comparing these graphs with Figs. 11, 12, 13, 14, 15 and 16, it is found that with the increase of Mach number, chaotic motion and quasi-period motion occur in advance. The amplitude when Mach number is $M_\mathrm{a} =3$ is greater than that in the case of $M_\mathrm{a} =2$. It is because of that when Mach number increases, the aerodynamic heating creates higher temperature, and thus, the stiffness of the FGM truncated conical shell decreases. At the same time, the influence of the aerodynamic force on the nonlinear vibrations of the FGM truncated conical shell is greater.

The case of the exponent of the volume fraction $\eta =10$ and Mach number $M_\mathrm{a} =2$ is considered. Figure 21 plots bifurcation diagram of amplitude for the FGM truncated conical shell versus in-plane load when $p_{1}$ increases from 40 to 100. The motion responses of the truncated FGM conical shell are given as: periodic motion $\rightarrow$ quasi-period motion $\rightarrow$ periodic motion $\rightarrow$ quasi-period motion $\rightarrow$ chaotic motion. Figures 22, 23, 24, 25 and 26 depict the different motion responses when the in-plane excitation is chosen as different parameters for the FGM truncated conical shell. Figures 22 and 24 represents the periodic motion of the FGM truncated conical shell, Figs. 23 and 25 indicates the quasi-period motion, Fig. 26 depicts the chaotic motion. By comparing Figs. 9, 17 and 21, it is shown that the chaotic motion yields earlier when the exponent of the volume fraction increases.

Fig. 21

The bifurcation diagram of the truncated FGM conical shell for in-plane load $p_{1}$ is obtained when exponent of volume fraction for the ceramic $\eta =1$ and Mach number $M_\mathrm{a} =2$

Fig. 22

The period motion of the FGM truncated conical shell is given when $\eta =1$, $M_\mathrm{a} =2$ and $p_{1} =40$

Fig. 23

The quasi-period motion of the FGM truncated conical shell is given when $\eta =1$, $M_\mathrm{a} =2$ and $p_{1} =55$

Fig. 24

The period motion of the FGM truncated conical shell is given when $\eta =1$, $M_\mathrm{a} =2$ and $p_{1} =60$

Fig. 25

The quasi-period motion of the FGM truncated conical shell is given when $\eta =1$, $M_\mathrm{a} =2$ and $p_{1} =64$

Fig. 26

The chaotic motion of the FGM truncated conical shell is given when $\eta =1$, $M_\mathrm{a} =2$ and $p_{1} =100$

Fig. 27

The bifurcation diagram of the truncated FGM conical shell for damping coefficient $\mu _{1}$ is obtained when exponent of volume fraction for the ceramic $\eta =5$, in-plane load $p_{1} =100$ and Mach number $M_\mathrm{a} =3$

Figure 27 depicts the bifurcation diagram of the FGM truncated conical shell for the damping coefficient $\mu _{1}$ is obtained when the exponents of volume fraction for the ceramic $\eta =5$, the in-plane load $p_{1} =100$ and Mach number $M_\mathrm{a} =3$. It can be observed that the motions of the FGM truncated conical shell are as follows: chaotic motion $\rightarrow$ quasi-period motion $\rightarrow$ chaotic motion $\rightarrow$ periodic motion. Figure 28 depicts the chaotic motion of the FGM truncated conical shell; Figs. 29 and 31 represents the periodic motion; Fig. 30 indicates the quasi-period motion.

6 Conclusions

In this paper, the nonlinear internal resonance behaviors of a simply supported FGM truncated conical shell with 1:2 internal resonance are investigated. According to a power-law distribution, the material properties are assumed to be modified along the thickness direction smoothly and continuously. The aerodynamic load is derived by using the first-order piston theory that including the curvature correction term. According to von Karman type nonlinear geometric relations, first-order shear deformation theory, Hamilton principle, the nonlinear equations of motion for the FGM truncated conical shell are established. Furthermore, the nonlinear equations of motion are reduced into a system of the ordinary differential equation by utilizing Galerkin procedure. The multiple scales method is used to obtain the averaged equations for the FGM truncated conical shell under the relations of 1:2 internal resonance and 1/2 subharmonic resonance.

The frequency–amplitude responses are investigated by solving the four-dimensional averaged equations. It is found that there are hardening-spring characteristics for the FGM truncated conical shell under the different cases. With the increase in Mach number or in-plane load, the nonlinear resonance characteristics become stronger. When the exponent of volume fraction or the damping coefficient decreases, the nonlinear resonance characteristics of the truncated FGM conical shell gets stronger and the amplitudes of two modes become larger.

Fig. 28

The chaotic motion of the FGM truncated conical shell is given when $\mu _{1} =10$, $\eta =5$, $M_\mathrm{a} =3$ and $p_{1} =100$

Fig. 29

The period motion of the FGM truncated conical shell is given when $\mu _{1} =14.6$, $\eta =5$, $M_\mathrm{a} =3$ and $p_{1} =100$

Fig. 30

The quasi-period motion of the FGM truncated conical shell is given when $\mu _{1} =15$, $\eta =5$, $M_\mathrm{a} =3$ and $p_{1} =100$

Fig. 31

The period motion of the FGM truncated conical shell is given when $\mu _{1} =20$, $\eta =5$, $M_\mathrm{a} =3$ and $p_{1} =100$

The complex nonlinear motion responses of the FGM truncated conical shell have been discussed in detail. It is observed that when in-plane load or damping coefficient increase, the periodic, the quasi-period and the chaotic motions occur for the FGM truncated conical shell. With the increase of the Mach number, the quasi-period motion and the chaotic motion both occur in advance. It is because of that with the increase of Mach number, aerodynamic heating creates higher temperature, and stiffness of the FGM truncated conical shell decreases. At the same time, the influence of the aerodynamic force on the nonlinear motion responses is greater. The chaotic motion yields earlier when the exponent of the volume fraction increases. It is due to that the increasing of the exponent of the volume fraction may cause smaller Young’s modulus and greater thermal expansion coefficient of the FGM truncated conical shell.

Appendix A

Nonlinear equations in form of generalized displacements are listed, as follows

$$\begin{aligned}&A_{11} \frac{\partial ^{2}u_{0} }{\partial x^{2}}+\mathfrak {R}^{2}A_{66} \frac{\partial ^{2}u_{0} }{\partial \theta ^{2}}+\mathfrak {R}A_{11} \frac{\partial u_{0} }{\partial x}\sin \beta -\mathfrak {R}^{2}A_{22} u_{0} \cos ^{2}\beta +\mathfrak {R}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}v_{0} }{\partial x\partial \theta }\nonumber \\&\quad -\mathfrak {R}^{2}\left( {A_{22} +A_{66} } \right) \frac{\partial v_{0} }{\partial \theta }\sin \beta +\mathfrak {R}^{2}A_{66} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }\nonumber \\&\quad +2\mathfrak {R}\left( {A_{11} -A_{12} } \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}\sin \beta -2\mathfrak {R}^{3}\left( {A_{12} -A_{22} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\sin \beta +\mathfrak {R}A_{12} \frac{\partial w_{0} }{\partial x}\cos \beta \nonumber \\&\quad -\mathfrak {R}^{2}A_{22} w_{0} \sin \beta \cos \beta +B_{11} \frac{\partial ^{2}\varphi _{x} }{\partial x^{2}}+\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}\varphi _{x} }{\partial \theta ^{2}}+\mathfrak {R}B_{11} \frac{\partial \varphi _{x} }{\partial x}\sin \beta -\mathfrak {R}^{2}B_{22} \varphi _{x} \sin ^{2}\beta \nonumber \\&\quad -\mathfrak {R}^{2}\left( {B_{22} +B_{66} } \right) \frac{\partial \varphi _{\theta } }{\partial \theta }\sin \beta +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}\varphi _{\theta } }{\partial x\partial \theta }+A_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial x} \nonumber \\&\quad +\mathfrak {R}N_{xx}^{T} \sin \beta -\mathfrak {R}N_{\theta \theta }^{T} \sin \beta =I_{0} \ddot{{u}}_{0} +I_{1} \ddot{{\varphi }}_{x} , \end{aligned}$$

(A1)

$$\begin{aligned}&\mathfrak {R}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}u_{0} }{\partial x\partial \theta }+\mathfrak {R}^{2}\left( {A_{22} +A_{66} } \right) \frac{\partial u_{0} }{\partial \theta }\sin \beta +A_{66} \frac{\partial ^{2}v_{0} }{\partial x^{2}}+\mathfrak {R}^{2}A_{22} \frac{\partial ^{2}v_{0} }{\partial \theta ^{2}}\nonumber \\&\qquad -\mathfrak {R}^{2}\left( {KA_{44} \cos ^{2}\beta +A_{66} \sin ^{2}\beta } \right) v_{0} +\mathfrak {R}A_{66} \frac{\partial w_{0} }{\partial \theta }\frac{\partial ^{2}w_{0} }{\partial x^{2}}+\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial \theta } \nonumber \\&\qquad +\mathfrak {R}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}A_{66} \frac{\partial w_{0} }{\partial \theta }\frac{\partial w_{0} }{\partial x}\sin \beta +\mathfrak {R}^{2}A_{22} \frac{\partial w_{0} }{\partial \theta }\cos \beta \nonumber \\&\qquad +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}\varphi _{x} }{\partial x\partial \theta }+\mathfrak {R}^{2}\left( {B_{22} +B_{66} } \right) \frac{\partial \varphi _{x} }{\partial \theta }\sin \beta +\mathfrak {R}B_{66} \frac{\partial \varphi _{\theta } }{\partial x}\sin \beta +\mathfrak {R}B_{22} \frac{\partial ^{2}\varphi _{\theta } }{\partial \theta ^{2}}\nonumber \\&\qquad +\mathfrak {R}A_{66} \frac{\partial v_{0} }{\partial x}\sin \beta +\mathfrak {R}^{2}KA_{44} \frac{\partial w_{0} }{\partial \theta }\cos \beta +\left( {\mathfrak {R}KA_{44} \cos \beta -\mathfrak {R}^{2}B_{66} \sin ^{2}\beta } \right) \varphi _{\theta }\nonumber \\&\quad =I_{0} \ddot{{v}}_{0} +I_{1} \ddot{{\varphi }}_{\theta } , \end{aligned}$$

(A2)

$$\begin{aligned}&2\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial \varphi _{x} }{\partial \theta }+0.5\mathfrak {R}^{2}A_{11} \left( {\frac{\partial w_{0} }{\partial x}} \right) ^{3}\sin \beta -\mathfrak {R}N_{\theta \theta }^{T} \cos \beta +\mathfrak {R}\left( {B_{11} +B_{22} } \right) \frac{\partial \varphi _{x} }{\partial x}\frac{\partial w_{0} }{\partial x}\nonumber \\&\quad -\mathfrak {R}^{2}A_{66} \frac{\partial v_{0} }{\partial \theta }\frac{\partial w_{0} }{\partial x}\sin \beta -\mathfrak {R}^{3}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}+2\mathfrak {R}^{2}\left( {A_{12} +2A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }\frac{\partial w_{0} }{\partial x}\nonumber \\&\quad -\mathfrak {R}^{2}B_{66} \frac{\partial \varphi _{\theta } }{\partial x}\frac{\partial w_{0} }{\partial x}\sin \beta +A_{11} \frac{\partial ^{2}u_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial x}+B_{11} \frac{\partial ^{2}\varphi _{x} }{\partial x^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}v_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial x}\nonumber \\&\quad +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}\varphi _{\theta } }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}A_{66} \frac{\partial ^{2}u_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}\left( {KA_{55} +N_{xx}^{T} } \right) \frac{\partial w_{0} }{\partial x}\sin \beta \nonumber \\&\quad +\frac{3}{2}A_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\left( {\frac{\partial w_{0} }{\partial x}} \right) ^{2}+0.5\mathfrak {R}^{2}\left( {A_{12} +2A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\left( {\frac{\partial w_{0} }{\partial x}} \right) ^{2}+0.5\mathfrak {R}^{2}A_{12} \left( {\frac{\partial w_{0} }{\partial x}} \right) ^{2}\cos \beta \nonumber \\&\quad +\mathfrak {R}\left( {A_{11} +A_{12} } \right) \frac{\partial w_{0} }{\partial x}\frac{\partial u_{0} }{\partial x}\sin \beta +\mathfrak {R}^{2}A_{12} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial u_{0} }{\partial x}-A_{12} \frac{\partial u_{0} }{\partial x}\cos \beta +A_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial u_{0} }{\partial x}\nonumber \\&2\mathfrak {R}A_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial v_{0} }{\partial x}-\mathfrak {R}^{2}A_{66} \frac{\partial w_{0} }{\partial \theta }\frac{\partial v_{0} }{\partial x}+\mathfrak {R}A_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}w_{0} \cos \beta +\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}w_{0} \cos \beta \nonumber \\&\quad -\mathfrak {R}^{2}A_{22} w_{0} \cos \beta +\mathfrak {R}B_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\varphi _{x} \sin \beta +\mathfrak {R}^{3}B_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\varphi _{x} \sin \beta \nonumber \\&\quad +\left( {\mathfrak {R}KA_{55} -\mathfrak {R}^{2}B_{22} \cos \beta } \right) \varphi _{x} \sin \beta +\mathfrak {R}^{3}B_{66} \frac{\partial w_{0} }{\partial \theta }\varphi _{\theta } \sin ^{2}\beta -\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\varphi _{\theta } \sin \beta \nonumber \\&\quad +\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}u_{0} \sin \beta -\mathfrak {R}^{3}A_{22} u_{0} \sin \beta \cos \beta +\mathfrak {R}^{2}A_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}u_{0} \sin \beta \nonumber \\&\quad +\mathfrak {R}^{3}A_{66} \frac{\partial w_{0} }{\partial \theta }v_{0} \sin ^{2}\beta -2\mathfrak {R}^{2}A_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }v_{0} \sin \beta +\mathfrak {R}^{2}\left( {KA_{44} +N_{\theta \theta }^{T} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\nonumber \\&\quad +\mathfrak {R}^{3}\left( {B_{22} -B_{66} } \right) \frac{\partial \varphi _{x} }{\partial \theta }\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}A_{66} \frac{\partial ^{2}v_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}B_{66} \frac{\partial ^{2}\varphi _{\theta } }{\partial x^{2}}\frac{\partial w_{0} }{\partial \theta }\nonumber \\&\quad +\mathfrak {R}^{2}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}\varphi _{x} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}^{3}A_{66} \frac{\partial ^{2}v_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}^{3}B_{22} \frac{\partial ^{2}\varphi _{\theta } }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial \theta }\nonumber \\&\quad +\left( {KA_{55} +N_{xx}^{T} -p\cos \Omega t} \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}+0.5\mathfrak {R}\left( {A_{12} +2A_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}\left( {\frac{\partial w_{0} }{\partial \theta }} \right) ^{2}\nonumber \\&\quad +0.5\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\left( {\frac{\partial w_{0} }{\partial \theta }} \right) ^{2}+\mathfrak {R}A_{12} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial v_{0} }{\partial \theta }+\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial v_{0} }{\partial \theta }+KA_{55} \frac{\partial \varphi _{x} }{\partial x}\nonumber \\&\quad -\mathfrak {R}^{2}\left( {KA_{44} +A_{22} } \right) \frac{\partial v_{0} }{\partial \theta }\cos \beta +B_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial \varphi _{x} }{\partial x}-\mathfrak {R}B_{12} \frac{\partial \varphi _{x} }{\partial x}\cos \beta +\mathfrak {R}^{2}B_{12} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial \varphi _{x} }{\partial x}\nonumber \\&\quad +2\mathfrak {R}B_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial \varphi _{\theta } }{\partial x}-\mathfrak {R}^{2}B_{66} \frac{\partial w_{0} }{\partial \theta }\frac{\partial \varphi _{\theta } }{\partial x}\sin \beta +\mathfrak {R}^{3}\left( {A_{22} -A_{66} } \right) \frac{\partial w_{0} }{\partial \theta }\frac{\partial u_{0} }{\partial \theta }\sin \beta \nonumber \\&\quad +\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}\varphi _{x} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}\left( {A_{12} +A_{66} } \right) \frac{\partial ^{2}u_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }+0.5\mathfrak {R}^{3}A_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\cos \beta \nonumber \\&\quad +2\mathfrak {R}^{3}A_{66} \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial u_{0} }{\partial \theta }+P_\mathrm{a} -\kappa \dot{{w}}_{0} =I_{0} \ddot{{w}}_{0} , \end{aligned}$$

(A3)

$$\begin{aligned}&B_{11} \frac{\partial ^{2}u_{0} }{\partial x^{2}}+\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}u_{0} }{\partial \theta ^{2}}+\mathfrak {R}B_{11} \frac{\partial u_{0} }{\partial x}\sin \beta -\mathfrak {R}^{2}B_{22} u_{0} \sin ^{2}\beta +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}v_{0} }{\partial x\partial \theta }\nonumber \\&\quad -\mathfrak {R}^{2}\left( {B_{22} +B_{66} } \right) \frac{\partial v_{0} }{\partial \theta }\sin \beta +0.5\mathfrak {R}^{2}\left( {B_{11} -B_{12} } \right) \frac{\partial ^{2}w_{0} }{\partial x^{2}}\sin \beta -\mathfrak {R}^{2}B_{22} w_{0} \sin \beta \cos \beta \nonumber \\&\quad +\mathfrak {R}B_{12} \frac{\partial w_{0} }{\partial x}\cos \beta +B_{11} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial x}+\mathfrak {R}^{2}B_{66} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial x}-KA_{55} \frac{\partial w_{0} }{\partial x}\nonumber \\&\quad -0.5\mathfrak {R}^{2}\left( {B_{12} +B_{22} } \right) \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\sin \beta +\mathfrak {R}^{2}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial \theta }-\left( {KA_{55} +\frac{1}{R^{2}}D_{22} } \right) \varphi _{x}\nonumber \\&\quad +\mathfrak {R}D_{11} \frac{\partial \varphi _{x} }{\partial x}\sin \beta +\mathfrak {R}^{2}D_{66} \frac{\partial ^{2}\varphi _{x} }{\partial \theta ^{2}}+D_{11} \frac{\partial ^{2}\upphi _{x} }{\partial x^{2}}+\mathfrak {R}\left( {D_{12} +D_{66} } \right) \frac{\partial ^{2}\varphi _{x} }{\partial x\partial \theta }\nonumber \\&\quad -\mathfrak {R}^{2}\left( {D_{22} +D_{66} } \right) \frac{\partial \varphi _{\theta } }{\partial \theta }\sin \beta +\mathfrak {R}M_{xx}^{T} \sin \beta -\mathfrak {R}M_{\theta \theta }^{T} \sin \beta =I_{1} \ddot{{u}}_{0} +I_{2} \ddot{{\varphi }}_{x} , \end{aligned}$$

(A4)

$$\begin{aligned}&\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}u_{0} }{\partial x\partial \theta }+\mathfrak {R}^{2}\left( {B_{22} +B_{66} } \right) \frac{\partial u_{0} }{\partial \theta }\sin \beta +B_{66} \frac{\partial ^{2}v_{0} }{\partial x^{2}}+\mathfrak {R}^{2}B_{22} \frac{\partial ^{2}v_{0} }{\partial \theta ^{2}}\nonumber \\&\qquad +\left( {\mathfrak {R}KA_{44} \cos \beta -\mathfrak {R}^{2}B_{66} \sin ^{2}\beta } \right) v_{0} +\mathfrak {R}^{2}B_{66} \frac{\partial w_{0} }{\partial x}\frac{\partial w_{0} }{\partial \theta }\sin \beta \nonumber \\&\qquad +\left( {\mathfrak {R}^{2}B_{22} \cos \beta -\mathfrak {R}KA_{44} } \right) \frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}^{3}B_{22} \frac{\partial ^{2}w_{0} }{\partial \theta ^{2}}\frac{\partial w_{0} }{\partial \theta }+\mathfrak {R}B_{66} \frac{\partial ^{2}w_{0} }{\partial x^{2}}\frac{\partial w_{0} }{\partial \theta }\nonumber \\&\qquad +\mathfrak {R}^{2}\left( {D_{22} +D_{66} } \right) \frac{\partial \varphi _{\theta } }{\partial \theta }+\mathfrak {R}^{2}D_{22} \frac{\partial ^{2}\varphi _{\theta } }{\partial \theta ^{2}}+\mathfrak {R}D_{66} \frac{\partial \varphi _{\theta } }{\partial x}-\left( {KA_{44} +\mathfrak {R}^{2}D_{66} \sin ^{2}\beta } \right) \varphi _{\theta }\nonumber \\&\qquad +\mathfrak {R}B_{66} \frac{\partial v_{0} }{\partial x}\sin \beta +\mathfrak {R}\left( {B_{12} +B_{66} } \right) \frac{\partial ^{2}w_{0} }{\partial x\partial \theta }\frac{\partial w_{0} }{\partial x}+\mathfrak {R}\left( {D_{12} +D_{66} } \right) \frac{\partial ^{2}\varphi _{x} }{\partial x\partial \theta }+D_{66} \frac{\partial ^{2}\varphi _{\theta } }{\partial x^{2}}\nonumber \\&\quad =I_{1} \ddot{{v}}_{0} +I_{2} \ddot{{\varphi }}_{\theta } . \end{aligned}$$

(A5)