1 Introduction

Magnetism has been a subject of intense research [1, 2]. Only a few metallic elements, notably iron, cobalt, nickel and some rare earths, have exhibited the large-scale magnetic effects that result in the commercial materials [3, 4]. There has been certain enhancement on the atomic spin effect in alloys or oxides of some materials containing those elements and some neighboring ions [3, 5]. That enhancement has resulted from the cooperative interaction of a large number (\(10^{13}\)–\(10^{14}\)) of the atomic spins producing a region in which all the atomic spins within it are aligned parallel [3]. Those materials have been called ferromagnetic [3]. Ferromagnetic materials have piqued the interest of researchers due to their applications in the data processing [2, 3], storage [2, 3, 6, 7] and communication [2, 3].

To study certain nonlinear phenomena in optics [8], fluid mechanics [9], Bose–Einstein condensation [10], plasma physics [11], etc., nonlinear evolution equations have been developed. Recently, researchers have concentrated their efforts on some nonlinear evolution equations relevant to the ferromagnetic materials, such as the Lakshmanan–Porsezian–Daniel equation describing the nonlinear spin excitations in one-dimensional isotropic biquadratic Heisenberg ferromagnetic spin with the octupole-dipole interaction [12, 13], a nonlinear Schrödinger-type equation for the magnetization dynamics of a ferromagnetic thin film with the interfacial Dzyaloshinskii–Moriya interaction in the long-wave-length approximation [14], a variable-coefficient modified Kadomtsev–Petviashvili system for certain electromagnetic waves in an isotropic charge-free infinite ferromagnetic thin film with the potential application in magneto-optic recording [15]. Another example has been the Kraenkel–Manna–Merle system for the ultra-short waves in a saturated ferromagnetic material with the zero conductivity in the presence of an external field [16], i.e.,

$$\begin{aligned}&- \nabla \cdot \left( \nabla \cdot {{\textbf {H}}} \right) + \nabla ^2 {{\textbf {H}}} = \frac{\partial ^2}{\partial \tau ^2} \left( {{\textbf {H}}} + {{\textbf {M}}} \right) , \end{aligned}$$
(1a)
$$\begin{aligned}&\frac{\partial }{\partial \tau } {{\textbf {M}}} = - {{\textbf {M}}} \wedge {{\textbf {H}}}_{\text {eff}} + \kappa {{\textbf {M}}} \wedge \frac{\partial }{\partial \tau } \frac{{{\textbf {M}}}}{\rho }, \end{aligned}$$
(1b)

from the Maxwell’s equations with the Landau–Lifshitz–Gilbert equation, where the vectors H and M stand for the dimensionless magnetic induction and magnetization density, respectively, the constants \(\rho \) and \(\kappa \) mean the dimensionless saturation magnetization and Gilbert-damping parameter, respectively, \(\nabla \) represents for the divergence of corresponding vector field and \(\tau \) denotes the normalized time variable.

Via a blend of the coordinate transformations and certain expansion series of the magnetization density and the magnetic induction [17], System (1) has been transformed into the following system [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]:

$$\begin{aligned}&u_{xt} - u v_x + \sigma v_x = 0, \end{aligned}$$
(2a)
$$\begin{aligned}&v_{xt} + u u_x = 0, \end{aligned}$$
(2b)

with the real differentiable functions \(u = u(x,t)\) and \(v = v(x,t)\) standing for the magnetization and the external magnetic field related to the saturated ferromagnetic material, respectively, the parameter \(\sigma \) denoting the damping effect, while the subscripts meaning the partial derivatives with respect to the space variable x and time variable t.

Solitons, one type of the nonlinear waves, have been studied in nonlinear optics [32,33,34], Bose–Einstein condensation [35], fluid mechanics [36, 37] and other fields [38,39,40,41,42]. Researchers’ interests have also been drawn to some other types of the nonlinear waves, including the breathers [43, 44], periodic waves [45, 46] and rouge waves [47]. The Darboux transformation (DT) has been proposed as a method for finding the soliton solutions [48, 49]. The ability to derive some multiple solitons without an iterative approach has been regarded as an advantage of the N-fold DT over the one-fold DT, where N is a positive integer [50, 51]. Other ways for solving the nonlinear evolution equations have been developed, such as the Hirota method [52,53,54,55,56], Riemann–Hilbert approach [57], Bäcklund transformation [58,59,60], similarity reduction [61, 62], Lie symmetry approach [63], Pfaffian technique [64] and so on.

For System (2), Ref. [18] has obtained the corresponding Lax pair as

$$\begin{aligned}&\Phi _x=M \Phi ,\qquad M= \begin{pmatrix} v_x \lambda &{} u_x \lambda \\ u_x \lambda &{} - v_x \lambda \end{pmatrix}, \end{aligned}$$
(3a)
$$\begin{aligned}&\Phi _t = R \Phi , \qquad R= \begin{pmatrix} \frac{1}{4} \lambda ^{-1} &{} - \frac{1}{2} u \\ \frac{1}{2} u &{} -\frac{1}{4} \lambda ^{-1} \end{pmatrix}, \end{aligned}$$
(3b)

under the damping effect coefficient \(\sigma =0\), where \(\Phi =(\phi _{1}, \phi _{2})^T\), \(\phi _{1}\) and \(\phi _{2}\) are the differentiable functions of x and t, spectral parameter \(\lambda \) is a constant, the superscript “T” means the transpose for a vector/matrix. System (2) has been reproduced through the compatibility condition \(M_t-R_x + MR -RM=0\) [18]. Contributions have been seen on System (2): bilinear forms [17]; DT and loop-like soliton excitations [19]; rogue-wave solutions [20, 21]; some soliton solutions [17, 18, 22,23,24,25,26,27]; some analytic solutions [28,29,30] and influence of the damping effects [31].

However, to our knowledge, N-fold DT of System (2) and some solitonic interactions which differ from those in Refs. [17,18,19, 22,23,24,25,26,27] have not been reported. In Sect. 2, we shall determine an N-fold DT of System (2) via Lax Pair (3). In Sect. 3, based on our N-fold DT, we shall derive the three-fold solutions of System (2) when \(N=3\), which can describe the interaction among the three solitons, and the four-fold solutions of System (2) when \(N=4\), which can describe the interaction among the four solitons. In Sect. 4, we shall discuss the solitonic interactions graphically. In Sect. 5, our conclusions will be given.

2 N-fold DT of System (2)

To derive an N-fold DT of System (2) by virtue of Lax Pair (3), we begin by introducing a gauge transformation

$$\begin{aligned} {\widetilde{\Phi }} = D \Phi , \end{aligned}$$
(4)

where D is a reversible matrix and \({\widetilde{\Phi }}\) is required to satisfy

$$\begin{aligned} {\widetilde{\Phi }}_x&= {\widetilde{M}} {\widetilde{\Phi }}, \qquad {\widetilde{M}} = \left( D_{x} + D M \right) D^{-1}, \end{aligned}$$
(5a)
$$\begin{aligned} {\widetilde{\Phi }}_t&= {\widetilde{R}} {\widetilde{\Phi }}, \qquad {\widetilde{R}} = \left( D_{t} + D R \right) D^{-1}, \end{aligned}$$
(5b)

while \({\widetilde{M}}\) and \({\widetilde{R}}\) have the same forms as M and R, respectively, except that the old potentials u, v have been replaced with new ones \({\widetilde{u}}\), \({\widetilde{v}}\), and the superscript “\(-1\)” represents the inverse of a matrix. We assume that the N-fold Darboux matrix D is in the form of a polynomial matrix of \(\lambda \) as follows:

$$\begin{aligned} D= & {} \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix}\nonumber \\= & {} \begin{pmatrix} \lambda ^{-N} + \sum \limits _{n=0}^{N-1}{a^{(n)} \lambda ^{-n} } &{} \sum \limits _{n=0}^{N-1}{b^{(n)} \lambda ^{-n}} \\ \sum \limits _{n=0}^{N-1}{ (-1)^{N-n+1} b^{(n)} \lambda ^{-n}} &{} \lambda ^{-N} + \sum \limits _{n=0}^{N-1}{ (-1)^{N-n} a^{(n)} \lambda ^{-n} } \end{pmatrix}, \nonumber \\ \end{aligned}$$
(6)

where \(a^{(n)}\)’s and \(b^{(n)}\)’s are some to-be-determined functions of x and t. Supposing that \(\lambda _{\imath }\!\)’s (\(\lambda _{\imath } \ne 0\), \(\imath = 1, 2, \ldots , N \)) are the N roots of detD, we have

$$\begin{aligned} \text {det} D = \frac{1}{\lambda ^{2N}} \prod \limits _{\imath =1}^{N} \left( \lambda ^2 - \lambda _{\imath }^2 \right) . \end{aligned}$$
(7)

Thus, we are able to determine \(a_n^{(n)}\)’s and \(b_n^{(n)}\)’s uniquely via the following linear algebraic system:

$$\begin{aligned}&\sum \limits _{n=0}^{N-1}{a^{(n)} \lambda _{\imath }^{-n} } + \delta _{\imath } \sum \limits _{n=0}^{N-1}{b^{(n)} \lambda _{\imath }^{-n}} = -\lambda _{\imath }^{-N}, \end{aligned}$$
(8a)
$$\begin{aligned}&\sum \limits _{n=0}^{N-1}{ (-1)^{N-n+1} b^{(n)} \lambda _{\imath }^{-n}} + \delta _{\imath } \sum \limits _{n=0}^{N-1}{ (-1)^{N-n} a^{(n)} \lambda _{\imath }^{-n} }\nonumber \\&\quad = - \delta _{\imath } \lambda _{\imath }^{-N}, \end{aligned}$$
(8b)

where

$$\begin{aligned} \delta _{\imath } = \frac{\varphi _2 \left( \lambda _{\imath } \right) }{\varphi _1 \left( \lambda _{\imath } \right) }, \end{aligned}$$
(9)

and \(\varphi \left( \lambda \right) = \left( \varphi _{1} \left( \lambda \right) , \varphi _{2} \left( \lambda \right) \right) ^T\) is a solution of Lax Pair (3), while the N parameters \(\lambda _{\imath }\!\)’s (\(\lambda _{\imath } \ne \lambda _{\jmath }, \imath \ne \jmath \)) are suitably chosen so that the determinant of the coefficients for Eqs. (8) is nonzero.

Proposition 1

The matrix \({\widetilde{M}}\) defined via Eq. (5a) has the same form as M, i.e.,

$$\begin{aligned} {\widetilde{M}} = \begin{pmatrix} {\widetilde{v}}_x \lambda &{} {\widetilde{u}}_x \lambda \\ {\widetilde{u}}_x \lambda &{} -{\widetilde{v}}_x \lambda \end{pmatrix}, \end{aligned}$$

where the transformations from the old potential functions u, v into the new ones \({\widetilde{u}}\), \({\widetilde{v}}\) are given by

$$\begin{aligned} {\widetilde{u}}&= u + b^{(N-1)} \end{aligned}$$
(10a)
$$\begin{aligned} {\widetilde{v}}&= v + a^{(N-1)} + \theta \left( t \right) , \end{aligned}$$
(10b)

with \(\theta \left( t \right) \) being a differentiable function of t.

Proof

Let \(D^{-1}=D^{*}/ \text {det} D\) and

$$\begin{aligned} \left( D_x + D M \right) D^{*} = \begin{pmatrix} k_{11} \left( \lambda \right) &{} k_{12} \left( \lambda \right) \\ k_{21} \left( \lambda \right) &{} k_{22} \left( \lambda \right) \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} k_{11} \left( \lambda \right)&= a_x d - b_x c + \left[ u_x \left( bd-ac \right) +v_x \left( ad + bc \right) \right] \lambda , \\ k_{12} \left( \lambda \right)&= a b_x - a_x b + \left[ u_x \left( a^2 -b^2 \right) - 2v_x ab \right] \lambda , \\ k_{21} \left( \lambda \right)&= c_x d - c d_x + \left[ u_x \left( d^2 -c^2 \right) + 2v_x cd \right] \lambda , \\ k_{22} \left( \lambda \right)&= a d_x - b c_x + \left[ u_x \left( ac-bd \right) - v_x \left( ad + bc \right) \right] \lambda , \end{aligned} \nonumber \\ \end{aligned}$$
(11)

and the superscript “\(*\)” denotes the adjoint of a matrix. Making use of Eqs. (3a), (8) and (9), we have

$$\begin{aligned} \begin{aligned}&a_{x} \left( \lambda _{\imath } \right) = - \delta _{\imath ,x} b \left( \lambda _{\imath } \right) - \delta _{\imath } b_x \left( \lambda _{\imath } \right) , \\&c_{x} \left( \lambda _{\imath } \right) = - \delta _{\imath ,x} d \left( \lambda _{\imath } \right) - \delta _{\imath } d_x \left( \lambda _{\imath } \right) , \\&\delta _{\imath ,x} = u_x \lambda _{\imath } - 2 v_x \lambda _{\imath } \delta _{\imath } - u_x \lambda _{\imath } \delta _{\imath }^2. \end{aligned} \end{aligned}$$
(12)

Following that, combining Eqs. (11) with (12) yields

$$\begin{aligned} k_{11} \left( \lambda _{\imath } \right) =k_{12} \left( \lambda _{\imath } \right) =k_{21} \left( \lambda _{\imath } \right) =k_{22} \left( \lambda _{\imath } \right) =0, \end{aligned}$$
(13)

which indicates that \( \lambda _{\imath }\!\)’s are the roots of \(k_{11} \left( \lambda \right) \), \(k_{12} \left( \lambda \right) \), \(k_{21} \left( \lambda \right) \) and \(k_{22} \left( \lambda \right) \).

It should be noted that \(k_{11} \left( \lambda \right) \), \(k_{12} \left( \lambda \right) \), \(k_{21} \left( \lambda \right) \) and \(k_{22} \left( \lambda \right) \) are all the polynomials of \(\lambda \) with order \(-2N+1\). With the help of Eq. (7), it can be verified that there exists a matrix P such that

$$\begin{aligned} \left( D_x + D M \right) D^{*} = \text {det} D \cdot P, \end{aligned}$$
(14)

where

$$\begin{aligned} P = \begin{pmatrix} p_{11}^{(1)} \lambda + p_{11}^{(0)} &{} p_{12}^{(1)} \lambda + p_{12}^{(0)} \\ p_{21}^{(1)} \lambda + p_{21}^{(0)} &{} p_{22}^{(1)} \lambda + p_{22}^{(0)} \end{pmatrix}, \end{aligned}$$

while \(p_{11}^{(1)}\), \(p_{11}^{(0)}\), \(p_{12}^{(1)}\), \(p_{12}^{(0)}\), \(p_{21}^{(1)}\), \(p_{21}^{(0)}\), \(p_{22}^{(1)}\) and \(p_{22}^{(0)}\) are some to-be-determined functions of x and t. In order to determine P, we rewrite Eq. (14) as

$$\begin{aligned} D_x + D M = P D. \end{aligned}$$
(15)

Equating the same powers of \(\lambda \) in Eq. (15) leads to the following results:

$$\begin{aligned} \begin{aligned} p_{11}^{(1)}&=v_x + a_x^{(N-1)} = {\widetilde{v}}_x, \\ p_{12}^{(1)}&=p_{21}^{(1)}=u_x + b_x^{(N-1)} = {\widetilde{u}}_x, \\ p_{22}^{(1)}&=-v_x - a_x^{(N-1)} =- {\widetilde{v}}_x, \\ p_{11}^{(0)}&=p_{12}^{(0)}=p_{21}^{(0)}=p_{22}^{(0)}=0. \end{aligned} \end{aligned}$$
(16)

From Eqs. (5a) and (16), we arrive at the conclusion that \(P={\widetilde{M}}\). The proof is completed.

Proposition 2

The matrix \({\widetilde{R}}\) defined via Eq. (5b) has the same form as R under Transformations (1), i.e.,

$$\begin{aligned} {\widetilde{R}} = \begin{pmatrix} \frac{1}{4} \lambda ^{-1} &{} -\frac{1}{2} {\widetilde{u}} \\ \frac{1}{2} {\widetilde{u}} &{} - \frac{1}{4} \lambda ^{-1} \end{pmatrix}. \end{aligned}$$

Proof

Let

$$\begin{aligned} \left( D_t + D R \right) D^{*} = \begin{pmatrix} l_{11} \left( \lambda \right) &{} l_{12} \left( \lambda \right) \\ l_{21} \left( \lambda \right) &{} l_{22} \left( \lambda \right) \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} l_{11} \left( \lambda \right)&= \frac{1}{4} \left( ad+bc \right) \lambda ^{-1} + \frac{1}{2} u \left( ac + bd \right) + a_t d - b_t c, \\ l_{12} \left( \lambda \right)&= - \frac{1}{2} ab \lambda ^{-1} - \frac{1}{2} u \left( a^2 + b^2 \right) + a b_t -a_t b, \\ l_{21} \left( \lambda \right)&= \frac{1}{2} cd \lambda ^{-1} + \frac{1}{2} u \left( c^2 + d^2 \right) + c_t d -c d_t, \\ l_{22} \left( \lambda \right)&= - \frac{1}{4} \left( ad+bc \right) \lambda ^{-1} - \frac{1}{2} u \left( ac + bd \right) + a d_t - b c_t. \end{aligned} \nonumber \\ \end{aligned}$$
(17)

By virtue of Eqs. (3b), (8) and (9), we have

$$\begin{aligned} \begin{aligned}&a_{t} \left( \lambda _{\imath } \right) = - \delta _{\imath ,t} b \left( \lambda _{\imath } \right) - \delta _{\imath } b_t \left( \lambda _{\imath } \right) , \\&c_{t} \left( \lambda _{\imath } \right) = - \delta _{\imath ,t} d \left( \lambda _{\imath } \right) - \delta _{\imath } d_t \left( \lambda _{\imath } \right) , \\&\delta _{\imath ,t} = \frac{1}{2} u - \frac{1}{2} \lambda _{\imath }^{-1} \delta _{\imath } + \frac{1}{2} u \delta _{\imath }^2. \end{aligned} \end{aligned}$$
(18)

Then, applying Eqs. (17) and (18), we can verify that \( \lambda _{\imath }\!\)’s are the roots of \(l_{11} \left( \lambda \right) \), \(l_{12} \left( \lambda \right) \), \(l_{21} \left( \lambda \right) \) and \(l_{22} \left( \lambda \right) \).

Noting that \(l_{11} \left( \lambda \right) \) and \(l_{22} \left( \lambda \right) \) are the polynomials of \(\lambda \) with order \(-2N-1\), whereas \(l_{12} \left( \lambda \right) \) and \(l_{21} \left( \lambda \right) \) are the polynomials of \(\lambda \) with order \(-2N\). With the help of Eq. (7), it can be verified that there exists a matrix Q such that

$$\begin{aligned} \left( D_t + D R \right) D^{*}= \text {det} D \cdot Q, \end{aligned}$$
(19)

where

$$\begin{aligned} Q = \begin{pmatrix} q_{11}^{(1)} \lambda ^{-1} + q_{11}^{(0)} &{} q_{12}^{(0)} \\ q_{21}^{(0)} &{} q_{22}^{(1)} \lambda ^{-1} + q_{22}^{(0)} \end{pmatrix}, \end{aligned}$$

while \(q_{11}^{(1)}\), \(q_{11}^{(0)} \), \(q_{12}^{(0)}\), \(q_{21}^{(0)}\), \(q_{22}^{(1)}\) and \(q_{22}^{(0)}\) are some to-be-determined functions of x and t. In order to determine Q, we rewrite Eq. (19) as

$$\begin{aligned} D_t + D R = Q D. \end{aligned}$$
(20)

Equating the same powers of \(\lambda \) in Eq. (20), we obtain the following results:

$$\begin{aligned} \begin{aligned} q_{12}^{(0)}&=-\frac{1}{2} u - \frac{1}{2} b^{(N-1)} = - \frac{1}{2} {\widetilde{u}}, \\ q_{21}^{(0)}&=\frac{1}{2} u + \frac{1}{2} b^{(N-1)}=\frac{1}{2} {\widetilde{u}}, \\ q_{11}^{(1)}&=\frac{1}{4}, \qquad q_{22}^{(1)}=-\frac{1}{4}, \qquad q_{11}^{(0)}=q_{22}^{(0)}=0. \end{aligned} \end{aligned}$$
(21)

From Eqs. (5b) and (21), we can see that \(Q={\widetilde{R}}\). The proof is completed.

According to Propositions 1 and 2, Transformations (4) and (1) can transform Lax Pair (3) into Lax Pair (5). Further, we have the following theorem:

Theorem 1

Let u and v be the seed solutions of System (2), \(\varphi \left( \lambda \right) = \left( \varphi _{1} \left( \lambda \right) , \varphi _{2} \left( \lambda \right) \right) ^T\) be the solution of Lax Pair (3), then the N-Fold DT of System (2) is given by Transformation (4) and

$$\begin{aligned} {\widetilde{u}}&= u + b^{(N-1)},\\ {\widetilde{v}}&= v + a^{(N-1)} + \theta \left( t \right) , \end{aligned}$$

where

$$\begin{aligned} a^{(N-1)} = \frac{{\Delta a}^{(N-1)}}{\Delta }, \qquad b^{(N-1)} = \frac{\Delta b^{(N-1)}}{\Delta }, \end{aligned}$$
$$\begin{aligned} \begin{aligned}&\Delta = \begin{vmatrix} 1&\lambda _1^{-1}&\cdots&\lambda _1^{-N+1}&\delta _1&\lambda _1^{-1} \delta _1&\cdots&\lambda _1^{-N+1} \delta _1\\ 1&\lambda _2^{-1}&\cdots&\lambda _2^{-N+1}&\delta _2&\lambda _2^{-1} \delta _2&\cdots&\lambda _2^{-N+1} \delta _2\\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\ddots&\vdots \\ 1&\lambda _N^{-1}&\cdots&\lambda _N^{-N+1}&\delta _N&\lambda _N^{-1} \delta _N&\cdots&\lambda _N^{-N+1} \delta _N\\ (-1)^N \delta _1&(-1)^{N-1} \lambda _1^{-1} \delta _1&\cdots&- \lambda _1^{-N+1} \delta _1&(-1)^{N+1}&(-1)^N \lambda _1^{-1}&\cdots&\lambda _1^{-N+1} \\ (-1)^N \delta _2&(-1)^{N-1} \lambda _2^{-1} \delta _2&\cdots&- \lambda _2^{-N+1} \delta _2&(-1)^{N+1}&(-1)^N \lambda _2^{-1}&\cdots&\lambda _2^{-N+1} \\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\ddots&\vdots \\ (-1)^N \delta _N&(-1)^{N-1} \lambda _N^{-1} \delta _N&\cdots&- \lambda _N^{-N+1} \delta _N&(-1)^{N+1}&(-1)^N \lambda _N^{-1}&\cdots&\lambda _N^{-N+1} \end{vmatrix}, \end{aligned} \end{aligned}$$

\(\Delta a^{(N-1)}\) is produced from \(\Delta \) by replacing its Nth column with \((-\lambda _1^{-N}, -\lambda _2^{-N}, \ldots , -\lambda _N^{-N}, -\lambda _1^{-N} \delta _1, -\lambda _2^{-N} \delta _2, \ldots , -\lambda _N^{-N} \delta _N)^{T} \) and \(\Delta b^{(N-1)}\) is produced from \(\Delta \) by replacing its 2Nth column with \((-\lambda _1^{-N}, -\lambda _2^{-N}, \ldots , -\lambda _N^{-N}, -\lambda _1^{-N} \delta _1, -\lambda _2^{-N} \delta _2, \ldots , -\lambda _N^{-N} \delta _N)^{T} \).

3 Solitonic interactions of System (2)

To obtain some solutions featuring the interactions among the solitons of System (2), we first have to choose the suitable seed solutions. Taking the seed solutions of System (2) as \(u=0\), \(v= \alpha x +\beta (t) \), we derive the following solutions of Lax Pair (3):

$$\begin{aligned} \varphi = \begin{pmatrix} \varphi _{1} \left( \lambda \right) \\ \varphi _{2} \left( \lambda \right) \end{pmatrix}= \begin{pmatrix} e^{ \alpha \lambda x + \frac{1}{4} \lambda ^{-1}t } \\ e^{ - \alpha \lambda x - \frac{1}{4} \lambda ^{-1}t } \end{pmatrix}, \end{aligned}$$
(22)

where \(\alpha \) is a constant and \(\beta (t)\) is a differentiable function of t.

Then, utilizing Theorem 1, we give the three- and four-fold solutions of System (2) as follows:

(I) When \(N=3\), three-fold solutions of System (2) can be expressed as

$$\begin{aligned} {\widetilde{u}} = \frac{\Delta b^{(2)}}{\Delta }, \qquad {\widetilde{v}} = \alpha x + \frac{{\Delta a}^{(2)}}{\Delta } + \theta \left( t \right) , \end{aligned}$$
(23)

where

$$\begin{aligned}&\Delta = \begin{vmatrix} 1&\lambda _1^{-1}&\lambda _1^{-2}&\delta _1&\lambda _1^{-1} \delta _1&\lambda _1^{-2} \delta _1 \\ 1&\lambda _2^{-1}&\lambda _2^{-2}&\delta _2&\lambda _2^{-1} \delta _2&\lambda _2^{-2} \delta _2 \\ 1&\lambda _3^{-1}&\lambda _3^{-2}&\delta _3&\lambda _3^{-1} \delta _3&\lambda _3^{-2} \delta _3 \\ -\delta _1&\lambda _1^{-1} \delta _1&-\lambda _1^{-2} \delta _1&1&-\lambda _1^{-1}&\lambda _1^{-2} \\ -\delta _2&\lambda _2^{-1} \delta _2&-\lambda _2^{-2} \delta _2&1&-\lambda _2^{-1}&\lambda _2^{-2} \\ -\delta _3&\lambda _3^{-1} \delta _3&-\lambda _3^{-2} \delta _3&1&-\lambda _3^{-1}&\lambda _3^{-2} \end{vmatrix},\\&\Delta a^{(2)}= \begin{vmatrix} 1&\lambda _1^{-1}&-\lambda _1^{-3}&\delta _1&\lambda _1^{-1} \delta _1&\lambda _1^{-2} \delta _1 \\ 1&\lambda _2^{-1}&-\lambda _2^{-3}&\delta _2&\lambda _2^{-1} \delta _2&\lambda _2^{-2} \delta _2 \\ 1&\lambda _3^{-1}&-\lambda _3^{-3}&\delta _3&\lambda _3^{-1} \delta _3&\lambda _3^{-2} \delta _3 \\ -\delta _1&\lambda _1^{-1} \delta _1&-\lambda _1^{-3} \delta _1&1&-\lambda _1^{-1}&\lambda _1^{-2} \\ -\delta _2&\lambda _2^{-1} \delta _2&-\lambda _2^{-3} \delta _2&1&-\lambda _2^{-1}&\lambda _2^{-2} \\ -\delta _3&\lambda _3^{-1} \delta _3&-\lambda _3^{-3} \delta _3&1&-\lambda _3^{-1}&\lambda _3^{-2} \end{vmatrix}, \\&\Delta b^{(2)}= \begin{vmatrix} 1&\lambda _1^{-1}&\lambda _1^{-2}&\delta _1&\lambda _1^{-1} \delta _1&-\lambda _1^{-3} \\ 1&\lambda _2^{-1}&\lambda _2^{-2}&\delta _2&\lambda _2^{-1} \delta _2&-\lambda _2^{-3} \\ 1&\lambda _3^{-1}&\lambda _3^{-2}&\delta _3&\lambda _3^{-1} \delta _3&-\lambda _3^{-3} \\ -\delta _1&\lambda _1^{-1} \delta _1&-\lambda _1^{-2} \delta _1&1&-\lambda _1^{-1}&-\lambda _1^{-3} \delta _1 \\ -\delta _2&\lambda _2^{-1} \delta _2&-\lambda _2^{-2} \delta _2&1&-\lambda _2^{-1}&-\lambda _2^{-3} \delta _2 \\ -\delta _3&\lambda _3^{-1} \delta _3&-\lambda _3^{-2} \delta _3&1&-\lambda _3^{-1}&-\lambda _3^{-3} \delta _3 \end{vmatrix}. \end{aligned}$$

(II) When \(N=4\), four-fold solutions of System (2) can be expressed as

$$\begin{aligned} {\widetilde{u}} = \frac{\Delta b^{(3)}}{\Delta }, \qquad {\widetilde{v}} = \alpha x + \frac{{\Delta a}^{(3)}}{\Delta } + \theta \left( t \right) , \end{aligned}$$
(24)

where

$$\begin{aligned}&\Delta = \begin{vmatrix} 1&\quad \lambda _1^{-1}&\quad \lambda _1^{-2}&\quad \lambda _1^{-3}&\quad \delta _1&\quad \lambda _1^{-1} \delta _1&\quad \lambda _1^{-2} \delta _1&\quad \lambda _1^{-3} \delta _1 \\ 1&\quad \lambda _2^{-1}&\quad \lambda _2^{-2}&\quad \lambda _2^{-3}&\quad \delta _2&\quad \lambda _2^{-1} \delta _2&\quad \lambda _2^{-2} \delta _2&\quad \lambda _2^{-3} \delta _2 \\ 1&\quad \lambda _3^{-1}&\quad \lambda _3^{-2}&\quad \lambda _3^{-3}&\quad \delta _3&\quad \lambda _3^{-1} \delta _3&\quad \lambda _3^{-2} \delta _3&\quad \lambda _3^{-3} \delta _3 \\ 1&\quad \lambda _4^{-1}&\quad \lambda _4^{-2}&\quad \lambda _4^{-3}&\quad \delta _4&\quad \lambda _4^{-1} \delta _4&\quad \lambda _4^{-2} \delta _4&\quad \lambda _4^{-3} \delta _4 \\ \delta _1&\quad -\lambda _1^{-1} \delta _1&\quad \lambda _1^{-2} \delta _1&\quad -\lambda _1^{-3} \delta _1&\quad -1&\quad \lambda _1^{-1}&\quad -\lambda _1^{-2}&\quad \lambda _1^{-3} \\ \delta _2&\quad -\lambda _2^{-1} \delta _2&\quad \lambda _2^{-2} \delta _2&\quad -\lambda _2^{-3} \delta _2&\quad -1&\quad \lambda _2^{-1}&\quad -\lambda _2^{-2}&\quad \lambda _2^{-3} \\ \delta _3&\quad -\lambda _3^{-1} \delta _3&\quad \lambda _3^{-2} \delta _3&\quad -\lambda _3^{-3} \delta _3&\quad -1&\quad \lambda _3^{-1}&\quad -\lambda _3^{-2}&\quad \lambda _3^{-3} \\ \delta _4&\quad -\lambda _4^{-1} \delta _4&\quad \lambda _4^{-2} \delta _4&\quad -\lambda _4^{-3} \delta _4&\quad -1&\quad \lambda _4^{-1}&\quad -\lambda _4^{-2}&\quad \lambda _4^{-3} \end{vmatrix},\\&\Delta a^{(3)}= \begin{vmatrix} 1&\quad \lambda _1^{-1}&\quad \lambda _1^{-2}&\quad -\lambda _1^{-4}&\quad \delta _1&\quad \lambda _1^{-1} \delta _1&\quad \lambda _1^{-2} \delta _1&\quad \lambda _1^{-3} \delta _1 \\ 1&\quad \lambda _2^{-1}&\quad \lambda _2^{-2}&\quad -\lambda _2^{-4}&\quad \delta _2&\quad \lambda _2^{-1} \delta _2&\quad \lambda _2^{-2} \delta _2&\quad \lambda _2^{-3} \delta _2 \\ 1&\quad \lambda _3^{-1}&\quad \lambda _3^{-2}&\quad -\lambda _3^{-4}&\quad \delta _3&\quad \lambda _3^{-1} \delta _3&\quad \lambda _3^{-2} \delta _3&\quad \lambda _3^{-3} \delta _3 \\ 1&\quad \lambda _4^{-1}&\quad \lambda _4^{-2}&\quad -\lambda _4^{-4}&\quad \delta _4&\quad \lambda _4^{-1} \delta _4&\quad \lambda _4^{-2} \delta _4&\quad \lambda _4^{-3} \delta _4 \\ \delta _1&\quad -\lambda _1^{-1} \delta _1&\quad \lambda _1^{-2} \delta _1&\quad -\lambda _1^{-4} \delta _1&\quad -1&\quad \lambda _1^{-1}&\quad -\lambda _1^{-2}&\quad \lambda _1^{-3} \\ \delta _2&\quad -\lambda _2^{-1} \delta _2&\quad \lambda _2^{-2} \delta _2&\quad -\lambda _2^{-4} \delta _2&\quad -1&\quad \lambda _2^{-1}&\quad -\lambda _2^{-2}&\quad \lambda _2^{-3} \\ \delta _3&\quad -\lambda _3^{-1} \delta _3&\quad \lambda _3^{-2} \delta _3&\quad -\lambda _3^{-4} \delta _3&\quad -1&\quad \lambda _3^{-1}&\quad -\lambda _3^{-2}&\quad \lambda _3^{-3} \\ \delta _4&\quad -\lambda _4^{-1} \delta _4&\quad \lambda _4^{-2} \delta _4&\quad -\lambda _4^{-4} \delta _4&\quad -1&\quad \lambda _4^{-1}&\quad -\lambda _4^{-2}&\quad \lambda _4^{-3} \end{vmatrix}, \\&\Delta b^{(3)}= \begin{vmatrix} 1&\quad \lambda _1^{-1}&\quad \lambda _1^{-2}&\quad \lambda _1^{-3}&\quad \delta _1&\quad \lambda _1^{-1} \delta _1&\quad \lambda _1^{-2} \delta _1&\quad -\lambda _1^{-4} \\ 1&\quad \lambda _2^{-1}&\quad \lambda _2^{-2}&\quad \lambda _2^{-3}&\quad \delta _2&\quad \lambda _2^{-1} \delta _2&\quad \lambda _2^{-2} \delta _2&\quad -\lambda _2^{-4} \\ 1&\quad \lambda _3^{-1}&\quad \lambda _3^{-2}&\quad \lambda _3^{-3}&\quad \delta _3&\quad \lambda _3^{-1} \delta _3&\quad \lambda _3^{-2} \delta _3&\quad -\lambda _3^{-4} \\ 1&\quad \lambda _4^{-1}&\quad \lambda _4^{-2}&\quad \lambda _4^{-3}&\quad \delta _4&\quad \lambda _4^{-1} \delta _4&\quad \lambda _4^{-2} \delta _4&\quad -\lambda _4^{-4} \\ \delta _1&\quad -\lambda _1^{-1} \delta _1&\quad \lambda _1^{-2} \delta _1&\quad -\lambda _1^{-3} \delta _1&\quad -1&\quad \lambda _1^{-1}&\quad -\lambda _1^{-2}&\quad -\lambda _1^{-4} \delta _1\\ \delta _2&\quad -\lambda _2^{-1} \delta _2&\quad \lambda _2^{-2} \delta _2&\quad -\lambda _2^{-3} \delta _2&\quad -1&\quad \lambda _2^{-1}&\quad -\lambda _2^{-2}&\quad -\lambda _2^{-4} \delta _2 \\ \delta _3&\quad -\lambda _3^{-1} \delta _3&\quad \lambda _3^{-2} \delta _3&\quad -\lambda _3^{-3} \delta _3&\quad -1&\quad \lambda _3^{-1}&\quad -\lambda _3^{-2}&\quad -\lambda _3^{-4} \delta _3 \\ \delta _4&\quad -\lambda _4^{-1} \delta _4&\quad \lambda _4^{-2} \delta _4&\quad -\lambda _4^{-3} \delta _4&\quad -1&\quad \lambda _4^{-1}&\quad -\lambda _4^{-2}&\quad -\lambda _4^{-4} \delta _4 \end{vmatrix}. \end{aligned}$$
Fig. 1
figure 1

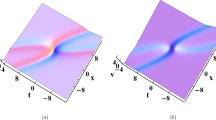
Interaction among the three solitons via Solutions (23) with \(\alpha =\frac{1}{10}\), \(\theta (t)=\text {sin} (\frac{1}{4}t)\), \(\lambda _1=-\frac{3}{2}\), \(\lambda _2=-1\) and \(\lambda _3=-2\)

Full size image
Fig. 2
figure 2

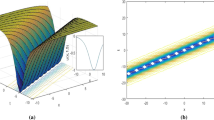
Interaction among the four solitons via Solutions (24) with \(\alpha =\frac{1}{10}\), \(\theta (t)=\text {cos} (\frac{1}{4}t)\), \(\lambda _1=-3\), \(\lambda _2=\frac{3}{2}\), \(\lambda _3=2\) and \(\lambda _4=-1\)

Full size image

4 Discussions

With N-fold DT (4) and (1), we are able to give the N-fold solutions of System (2) via the determinants in Theorem 1. It should be pointed out that the DT constructed in Ref. [19] is a special case of our N-Fold DT (4) and (1) when \(N=1\) or 2. Interactions among the solitons of System (2) can be described via the N-fold solutions with certain parameters. Three-Fold Solutions (23) can describe the interaction among the three solitons with certain parameters, which is different from those in Refs. [17,18,19, 22,23,24,25,26,27]. With respect to u(x, t), the magnetization related to the saturated ferromagnetic material, Fig. 1a shows the interaction among the two bell-shape solitons and one anti-bell-shape soliton. With respect to v(x, t), the external magnetic field related to the saturated ferromagnetic material, Fig. 1b displays the interaction among the three kink-shape solitons. Those solitons interact with one another around \(t = 0\), and then move apart. Amplitudes, velocities and shapes of those solitons remain unchanged after the interaction, indicating that the interaction is elastic. Interaction among the four solitons can be described via Four-Fold Solutions (24) with certain parameters, which is different from those in Refs. [17,18,19, 22,23,24,25,26,27]. With respect to u(x, t), the magnetization related to the saturated ferromagnetic material, as shown in Fig. 2a, we can see the elastic interaction among the two bell-shape solitons and two anti-bell-shape solitons. With respect to v(x, t), the external magnetic field related to the saturated ferromagnetic material, elastic interaction among the four kink-shape solitons is exhibited in Fig. 2b. It can be observed that the amplitudes and shapes of those solitons change nonlinearly in the interaction region and then recover after the interaction.

5 Conclusions

Ferromagnetic-material investigations have been active, with the applications in direct-current power supplies, radios, televisions, high-frequency power supplies, microwave equipments, magnetic recorders, electrodes, sensors, ferrofluids, etc. As for the ultra-short waves in a saturated ferromagnetic material with the zero conductivity in the presence of an external field, with respect to u(x, t), the magnetization related to the saturated ferromagnetic material, and v(x, t), the external magnetic field related to the saturated ferromagnetic material, we have studied the Kraenkel–Manna–Merle system in this paper, i.e., System (2). With Lax Pair (3), we have constructed N-Fold DT (4) and (1) of System (2). By virtue of N-Fold DT (4) and (1) with \(N=3\) and 4, we have derived Three-Fold Solutions (23) and Four-Fold Solutions (24) of System (2), respectively. Via Three-Fold Solutions (23) and Four-Fold Solutions (24), we have given the solitonic interactions which are different from those in Refs. [17,18,19, 22,23,24,25,26,27]. Figure 1a shows the interaction among the two bell-shape solitons and one anti-bell-shape soliton, whereas Fig. 1b displays the interaction among the three kink-shape solitons. Figure 2a exhibits the interaction among the two bell-shape solitons and two anti-bell-shape solitons, and Fig. 2b shows the interaction among the four kink-shape solitons. As we have observed, those interactions are elastic.