Generalized Darboux transformation and solitons for a Kraenkel-Manna-Merle system in a ferromagnetic saturator

Abstract

Ferromagnetic materials are considered to have the applications in data storage, data processing and telecommunication. A Kraenkel-Manna-Merle system, which describes the nonlinear electromagnetic short waves in a ferromagnetic saturator, is investigated in this paper. With respect to the magnetization related to the saturated ferromagnetic material and external magnetic field, a generalized Darboux transformation (GDT) is constructed and utilized to derive the solitons, multi-pole solitons and their interactions. Analytic expressions of the double-pole solitons are offered and analyzed via the asymptotic analysis. Then, amplitudes, characteristic lines, slopes and phase shifts of the asymptotic solitons are presented. With the multiple spectral parameters involved in the GDT, interactions among the solitons and multi-pole solitons are illustrated.

1 Introduction

Recent development of the computer and information technology has accompanied the demands of the massive data and high-density storage [1]. Ferromagnetic materials have been regarded as the ideal storage media in information technology [2, 3]. Ferromagnetic materials, e.g., iron, cobalt, nickel and certain rare-earth metals, have exhibited a spontaneous net magnetization at the atomic level in the absence of an external magnetic field [4]. Furthermore, ferromagnetic materials have been considered to have the applications in data processing and telecommunication [5, 6].

To describe the nonlinear electromagnetic short waves in a ferromagnetic saturator, a Kraenkel-Manna-Merle system has been proposed¹ [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]

$$\begin{aligned} \begin{aligned}&u_{xt}-uv_x+\kappa v_x=0, \\&v_{xt}+uu_x=0, \end{aligned} \end{aligned}$$

(1)

where u and v are two real differentiable functions of x and t, u is related to the component of the magnetization in a certain direction about the saturated ferromagnetic material, v is related to the component of the external magnetic field in a certain direction, $\kappa$ represents the damping effect, and the subscripts denote the partial derivatives with respect to the scaled space variable x and time variable t.

Solitons, a kind of the nonlinear waves, have exhibited the capability of the propagation of the waves without losing the shape for a long distance [24]. Therefore, solitons, which are stable, has been investigated in fluid mechanics [25], fiber optics [26], plasma physics [27], material sciences [28] and other fields [29]. With the development of the advanced large-scale information storage and transmission, solitons have shown the potential applications in ferromagnetic materials [30]. Moreover, other nonlinear waves, e.g., breathers, periodic waves and rogue waves, have also attracted the researchers’ attention [31,32,33,34].

For System (1), the breather solitons, periodic oscillation solitons and multi-pole instantons via the consistent tanh expansion method have been presented [8]; certain dark solitons, bright solitons, singular solitons, combined dark-bright solitons, combined dark-singular solitons, periodic and singular periodic waves via the extended sinh-Gordon equation expansion method have been exhibited [9]; loop-like periodic waves in the Jacobi elliptic functions and solitons in the hyperbolic functions have been investigated [10]; effects of the inhomogeneous exchange and simultaneous damping effects on the magnetic solitons have been explored [11]; loop solitons in the localized multivalued waveguide channels have been offered [12]; certain solitons have been studied via the inverse scattering transform method and Wadati-Konno-Ichikawa scheme [13]; Darboux transformation (DT) and a series of the loop-like soliton structures have been obtained [14]; through the generalized $G' / G$-expansion method, hump-soliton, cusp-soliton, loop-soliton and kink-soliton have been observed [15]; single soliton, complex combo solitons, complex hyperbolic and trigonometric solutions through the extended direct algebraic method have been studied [16]; two types of the soliton twining behaviors have been derived via the bilinear method [17]; two types of the periodically oscillating solitons have been discussed via the Riccati equation mapping method [18]; influences of the damping effect on the solitons in the ferrites materials have been investigated [19, 20]; some novel traveling wave solutions have been presented [21]; certain dark, singular and combo solitons along with periodic solutions have been studied via the modified auxiliary equation method and generalized projective Riccati equations method [22]; oscillation rogue waves via the truncated Painlev$\mathrm{\acute{e}}$ method have been obtained [23].

When $\kappa$ is selected as 0, a Lax pair for System (1) has been obtained as [14, 35]

$$\begin{aligned} \begin{aligned}&\Phi =\begin{pmatrix} \phi _1&\phi _2 \end{pmatrix}^{{\text{T}}},~~\Phi _x=U\Phi ,~~\Phi _t=V\Phi ,\\&U=\lambda \begin{pmatrix} v_x &{} u_x \\ u_x &{} -v_x\end{pmatrix},~~V=\begin{pmatrix} \frac{1}{4\lambda } &{} -\frac{u}{2} \\ \frac{u}{2} &{} -\frac{1}{4\lambda } \end{pmatrix}, \end{aligned} \end{aligned}$$

(2)

where $\phi _1$ and $\phi _2$ are two real differentiable functions of x and t, $\lambda$ is a real spectral parameter, the superscript “T” denotes the transpose of the matrix. From the compatibility condition $U_t-V_x+UV-VU=0$ of Lax Pair (2), System (1) has been obtained [14].

DT method has enabled the users to obtain the solutions with the aid of the Lax pair of certain nonlinear evolution equations [36]. However, one limitation of the DT method has been considered as that each spectral parameter can only be iterated once in the multi-iteration process [36]. Thus, in the N-fold solutions obtained via the DT, each spectral parameter has corresponded to a separate localized wave component, e.g., the soliton, breather and rogue wave, where N is a positive integer [37]. On the basis of Lax Pair (2), N-fold DT and solitons with the straight characteristic lines for System (1) have been offered [35]. However, due to the disturbances and soliton energy dissipations in the ferromagnetic saturator, velocities of the nonlinear waves for System (1) have been considered as changeable under certain conditions [7]. Therefore, we have considered that the localized waves with the changeable velocities have the potential applications in the ferrites.

Multi-pole solitons, also called the degenerate solitons or higher-order solitons, whose characteristic lines are the curves, have been obtained through the generalized Darboux transformation (GDT) method and Hirota method [38,39,40]. Multi-pole solitons have described the interactions of multiple chirped pulses with the same amplitudes and group velocities in an optical fiber [41]. Different from the DT method, GDT method, in which the spectral parameters can be iterated more than once, has enabled us to obtain the localized waves with the changeable velocities [42]. In the GDT method, the kth-order multi-pole solitons have been derived through iterating one spectral parameter k times, which are different from the kth-order solitons obtained via the Darboux transformation (DT) method, where k is a integer and $k\ge 2$ [43].

To our knowledge, GDT, multi-pole solitons and interaction among the solitons and multi-pole solitons for System (1) have not been investigated. In Sect. 2, with symbolic computation [44,45,46,47,48] we will construct a GDT for System (1). In Sect. 3, multi-pole solitons and interaction among the solitons and multi-pole solitons for System (1) will be presented and analyzed. In Sect. 4, our conclusions will be drawn.

2 GDT for System (1)

Based on Lax Pair (2), we firstly construct of an N-fold Darboux transformation for System (1). Motivated by the form of the first-order DT matrix in Refs. [14, 35], we assume the N-fold DT matrix $D^{[N]}$ as the following form

$$\begin{aligned} \begin{aligned}&D^{[N]}=\begin{pmatrix} 1+\sum _{j=1}^{N}a^{(j)}\lambda ^j &{} \sum _{j=1}^{N}b^{(j)}\lambda ^j \\ \sum _{j=1}^{N}(-1)^{j+1}b^{(j)}\lambda ^j &{} 1+\sum _{j=1}^{N}(-1)^{j}a^{(j)}\lambda ^j \end{pmatrix}, \end{aligned} \end{aligned}$$

(3)

where $j=1,~2,~\dots ,~N$, $a^{(j)}$’s and $b^{(j)}$’s are 2N functions of x and t to be determined, and the superscript [N] denotes the Nth-order iteration.

Through the following equations [35]

$$\begin{aligned} \begin{aligned}&\left( D^{[N]}\Phi \right) \big |_{\lambda =\lambda _j}=0, \end{aligned} \end{aligned}$$

(4)

we utilized the Crammer’s Rule and calculate $a^{(1)}$ and $b^{(1)}$ as

$$ \begin{aligned}&a^{(1)}=\frac{\Gamma _1}{\Gamma },~b^{(1)}=\frac{\Gamma _2}{\Gamma },\\&\Gamma =\left|\begin{array}{cccccccc}\lambda _1\phi _{1,1} &{} \lambda _1^2\phi _{1,1} &{} \cdots &{} \lambda _1^N\phi _{1,1} &{} \lambda _1\phi _{2,1} &{} \lambda _1^2\phi _{2,1} &{} \cdots &{} \lambda _1^N\phi _{2,1} \\ (-1)^1\lambda _1\phi _{2,1} &{} (-1)^2\lambda _1^2\phi _{2,1} &{}\cdots &{}(-1)^N\lambda _1^N\phi _{2,1} &{}(-1)^2\lambda _1\phi _{1,1} &{} (-1)^3\lambda _1^2\phi _{1,1} &{}\cdots &{}(-1)^{N+1}\lambda _1^N\phi _{1,1}\\ \lambda _2\phi _{1,2} &{} \lambda _2^2\phi _{1,2} &{} \cdots &{} \lambda _2^N\phi _{1,2} &{} \lambda _2\phi _{2,2} &{} \lambda _2^2\phi _{2,2} &{} \cdots &{} \lambda _2^N\phi _{2,2} \\ (-1)^1\lambda _2\phi _{2,2} &{} (-1)^2\lambda _2^2\phi _{2,2} &{}\cdots &{}(-1)^N\lambda _2^N\phi _{2,2} &{}(-1)^2\lambda _2\phi _{1,2} &{} (-1)^3\lambda _2^2\phi _{1,2} &{}\cdots &{}(-1)^{N+1}\lambda _2^N\phi _{1,2}\\ \vdots &{} \vdots &{}\ddots &{} \vdots &{} \vdots &{} \vdots &{}\ddots &{} \vdots \\ \lambda _N\phi _{1,N} &{} \lambda _N^2\phi _{1,N} &{} \cdots &{} \lambda _N^N\phi _{1,N} &{} \lambda _N\phi _{2,N} &{} \lambda _N^2\phi _{2,N} &{} \cdots &{} \lambda _N^N\phi _{2,N} \\ (-1)^1\lambda _N\phi _{2,N} &{} (-1)^2\lambda _N^2\phi _{2,N} &{}\cdots &{}(-1)^N\lambda _N^N\phi _{2,N} &{}(-1)^2\lambda _N\phi _{1,N} &{} (-1)^3\lambda _N^2\phi _{1,N} &{}\cdots &{}(-1)^{N+1}\lambda _N^N\phi _{1,N}\\ \end{array}\right|,\\&\gamma =\big (-\phi _{1,1},-\phi _{2,1},-\phi _{1,2},-\phi _{2,2},\cdots ,-\phi _{1,N},-\phi _{2,N}\big )^\textrm{T}, \end{aligned} $$

(5)

where $\Gamma _1$ is derived through replacing the first column of $\Gamma$ with $\gamma$, $\Gamma _2$ is derived through replacing the $(N+1)$th column of $\Gamma$ with $\gamma$, $\lambda _j$’s are N different spectral parameters, and $\left( \phi _{1,j}, \phi _{2,j}\right) ^{{\text{T}}}$ is a solution of Lax Pair (2) at $\lambda =\lambda _j$ and the seed solutions u,  v.

Then, an N-fold DT and solutions for System (1) can be expressed as

$$\begin{aligned} \begin{aligned}&\Phi ^{[N]}=D^{[N]}\Phi ,~~\Phi ^{[N]}_x=U^{[N]}\Phi ^{[N]},~~\Phi ^{[N]}_t=V^{[N]}\Phi ^{[N]},\\&U^{[N]}=\lambda \begin{pmatrix} v^{[N]}_x &{} u^{[N]}_x \\ u^{[N]}_x &{} -v^{[N]}_x\end{pmatrix},~~V^{[N]}=\begin{pmatrix} \frac{1}{4\lambda } &{} -\frac{u^{[N]}}{2} \\ \frac{u^{[N]}}{2} &{} -\frac{1}{4\lambda } \end{pmatrix},\\&u^{[N]}=u+b^{(1)},~~v^{[N]}=v+a^{(1)}+f_1(t), \end{aligned} \end{aligned}$$

(6)

where $f_1(t)$ is a differential function of t, u and v are the seed solutions,  $u^{[N]}$ and $v^{[N]}$ are the N-fold solutions, and $U^{[N]}$ and $V^{[N]}$ are the transformed Lax pair matrices.

Next, on the basis of N-Fold DT (6), we will construct a GDT for System (1).

We choose M spectral parameters $\lambda _s$, where M is a positive integer, $M\le N$ and $s=1,2,\dots ,M$. Among the M spectral parameters, each spectral parameter $\lambda _s$ will be iterated $r_s+1$ times, where $r_s$ is a positive integer and $M+\sum _{s=1}^Mr_s=N$. We add a real small parameter perturbation $\epsilon$ to $\lambda _s$, i.e.,

$$\begin{aligned} \begin{aligned} \lambda _s\rightarrow \lambda _s+\epsilon . \end{aligned} \end{aligned}$$

(7)

At this time, the relationships between the potentials $u^{[N]},~v^{[N]}$ and u,  v via the GDT is the same as the relationships in N-Fold DT (6). However, different from Eq. (4), $a^{(j)}$’s and $b^{(j)}$’s are determined via the following equations

$$\begin{aligned} \begin{aligned}&\lim _{\epsilon \rightarrow 0}D^{[N]}\big |_{\lambda =\lambda _s+\epsilon }~\begin{pmatrix} \phi _{1} \\ \phi _{2} \end{pmatrix}\Bigg |_{\lambda =\lambda _s+\epsilon }\epsilon ^{-p_s}=0, \end{aligned} \end{aligned}$$

(8)

where $p_s=0,1,\dots ,r_s$.

Through Eq. (8), $a^{(1)}$ and $b^{(1)}$ are determined as

$$\begin{aligned} \begin{aligned}&u^{[N]}=u+b^{(1)},~~v^{[N]}=v+a^{(1)}+f_1(t),\\&a^{(1)}=\frac{|\Omega _1|}{|\Omega |},~b^{(1)}=\frac{|\Omega _2|}{|\Omega |},\\&\Omega =\lim _{\epsilon \rightarrow 0}\bigg (A_1^{{\text{T}}},\frac{\text{d}}{\text{d}\lambda _{1}}A_1^{{\text{T}}},\cdots ,\frac{\text{d}^{r_1}}{(r_1)!\text{d}\lambda _{1}^{r_1}}A_1^{\text{T}},\cdots , A_m^{\text{T}}, \frac{\text{d}}{\text{d}\lambda _{M}}A_M^{\text{T}},\cdots ,\frac{\text{d}^{r_M}}{(r_M)!\text{d}\lambda _{M}^{r_M}}A_M^{\text{T}} \bigg )^{\text{T}},\\&A_s=\left( A_{s,1},A_{s,2}\right) ,\\&A_{s,1}=\begin{pmatrix}(\lambda _s+\epsilon )\phi _{1}|_{\lambda =\lambda _s+\epsilon } &{} (\lambda _s+\epsilon )^2\phi _{1}|_{\lambda =\lambda _s+\epsilon } &{} \cdots &{} (\lambda _s+\epsilon )^N\phi _{1}|_{\lambda =\lambda _s+\epsilon }\\ (-1)^1(\lambda _s+\epsilon )\phi _{2}|_{\lambda =\lambda _s+\epsilon } &{} (-1)^2(\lambda _s+\epsilon )^2\phi _{2}|_{\lambda =\lambda _s+\epsilon } &{}\cdots &{}(-1)^N(\lambda _s+\epsilon )^N\phi _{2}|_{\lambda =\lambda _s+\epsilon } \end{pmatrix},\\&A_{s,2}=\begin{pmatrix} (\lambda _s+\epsilon )\phi _{2}|_{\lambda =\lambda _s+\epsilon } &{} (\lambda _s+\epsilon )^2\phi _{2}|_{\lambda =\lambda _s+\epsilon } &{} \cdots &{} (\lambda _s+\epsilon )^N\phi _{2}|_{\lambda =\lambda _s+\epsilon }\\ (-1)^2(\lambda _s+\epsilon )\phi _{1}|_{\lambda =\lambda _s+\epsilon } &{} (-1)^3(\lambda _s+\epsilon )^2\phi _{1}|_{\lambda =\lambda _s+\epsilon } &{}\cdots &{}(-1)^{N+1}(\lambda _s+\epsilon )^N\phi _{1}|_{\lambda =\lambda _s+\epsilon } \end{pmatrix},\\ \end{aligned} \end{aligned}$$

(9)

where $\Omega _1$ and $\Omega _2$ can be obtained through replacing the 1st and $(N+1)$th columns of $A_s$ in $\Omega$ with $\left( -\phi _{1}|_{\lambda =\lambda _s+\epsilon },-\phi _{2}|_{\lambda =\lambda _s+\epsilon }\right) ^{\text{T}}$, respectively.

In particular, when $M=N$, i.e., $r_s=0$, each of the N spectral parameters is iterated only once. Under such condition, Solutions (9) are reduced to the solutions in Eq. (5).

In Solutions (9), the value of M represents that Solutions (9) are composed of the M independent nonlinear waves, the value of $r_s$ represents that the order of the nonlinear waves corresponding to $\lambda _s$ is $r_s+1$, and the value of N represents the total order of Solutions (9). In sum, N-Fold DT Matrix (3) and Solutions (9) form an N-Fold GDT for Eq. (1).

3 Solitonic interactions for System (1)

In order to derive certain solitons for System (1), we need to select the seed solutions for System (1). After the calculation, we find that the following seed solutions, i.e., $u=\alpha ,~v=\beta x+f_2(t)$, are the sufficient conditions for obtaining the solitons for System (1). In this section, we set $\alpha =f_2(t)=f_1(t)=0$. However, the following studies can be extended to the cases under $\alpha f_1(t)f_2(t)\ne 0$.

Therefore, eigenfunction $\Phi \left( \lambda _s+\epsilon \right)$ with $\lambda =\lambda _s+\epsilon$ for Lax Pair (2) can be presented as

$$\begin{aligned} \begin{aligned} \Phi \left( \lambda _s+\epsilon \right) =\begin{pmatrix} g_{s} \\ h_{s} \end{pmatrix}=\begin{pmatrix} l_1e^{\beta (\lambda _s+\epsilon )x+\frac{1}{4(\lambda _s+\epsilon )t}} \\ l_2e^{-\beta (\lambda _s+\epsilon )x-\frac{1}{4(\lambda _s+\epsilon )t}} \end{pmatrix}, \\ \end{aligned} \end{aligned}$$

(10)

where $\epsilon$ is a small parameter. Next, we expand eigenfunction $\Phi \left( \lambda _s+\epsilon \right)$ with the small parameter $\epsilon$ as follows:

$$\begin{aligned} \begin{aligned}&\begin{pmatrix} g_{s} \\ h_{s} \end{pmatrix}=\begin{pmatrix} g_{s,0} \\ h_{s,0} \end{pmatrix}+\begin{pmatrix} g_{s,1} \\ h_{s,1} \end{pmatrix}\epsilon +\begin{pmatrix} g_{s,2} \\ h_{s,2} \end{pmatrix}\epsilon ^2+\cdots , \\&\begin{pmatrix} g_{s,0} \\ h_{s,0}\end{pmatrix}=\begin{pmatrix} l_1e^{\beta \lambda _sx+\frac{1}{4\lambda _st}} \\ l_2e^{-\beta \lambda _sx-\frac{1}{4\lambda _st}} \end{pmatrix},~~\begin{pmatrix} g_{s,1} \\ h_{s,1} \end{pmatrix}=\begin{pmatrix} \left( \beta x-\frac{t}{4\lambda _s^2}\right) g_{s,0} \\ \left( \frac{t}{4\lambda _s^2}-\beta x\right) h_{s,0} \end{pmatrix}, \\&\begin{pmatrix} g_{s,2} \\ h_{s,2} \end{pmatrix}=\begin{pmatrix} \left[ \frac{1}{2}\left( \beta x-\frac{t}{4\lambda _s^2}\right) ^2 +\frac{t}{4\lambda _s^3}\right] g_{s,0} \\ \left[ \frac{1}{2}\left( \beta x-\frac{t}{4\lambda _s^2}\right) ^2 -\frac{t}{4\lambda _s^3}\right] h_{s,0} \end{pmatrix}\cdots \\ \end{aligned} \end{aligned}$$

(11)

We find that $g_{s,1},~h_{s,1},~g_{s,2},~h_{s,2}$ and so on are the mixtures of polynomials and exponential functions. Therefore, Solutions (9), which contain both the polynomials and exponential functions, are called the semirational solutions. Through setting the values of N,  M and $r_s$ in Solutions (9), different types of the semirational solutions for System (1) can be obtained. When $r_s\ge 1$, i.e., the complex spectral parameter $\lambda _s$ is iterated more than once, $\lambda _s$ corresponds to the $(r_s+1)$th-order multi-pole solitons in Solutions (9); when $r_s=0$, $\lambda _s$ corresponds to the one soliton in Solutions (9).

3.1 Multi-pole solitons for Eq. (1)

As we set $M=r_1=1,~N=2$ in Solutions (9), with respect to the magnetization related to the saturated ferromagnetic material and external magnetic field, the double-pole solitons solutions for Eq. (1) can be derived as

$$\begin{aligned} \begin{aligned}&u^{[1]}=2l_1l_2\frac{l_1^2(\rho -2\lambda _1)e^\frac{\theta }{2}-l_2^2(\rho +2\lambda _1)e^{-\frac{\theta }{2}}}{\lambda _1^2\left( l_1^4e^\theta +l_2^4e^{-\theta }\right) +l_1^2l_2^2(\rho ^2+2\lambda _1^2)},\\&v^{[1]}=\beta x-2\frac{\lambda _1\left( l_1^4e^\theta -l_2^4e^{-\theta }\right) +2l_1^2l_2^2\rho }{\lambda _1^2\left( l_1^4e^\theta +l_2^4e^{-\theta }\right) +l_1^2l_2^2(\rho ^2+2\lambda _1^2)},\\&\theta =\frac{t}{\lambda _1}+4\beta \lambda _1 x,~\rho =t-4\beta \lambda _1^2x. \end{aligned} \end{aligned}$$

(12)

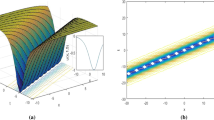
As shown in Fig. 1, the characteristic lines of the double-pole solitons are the curves. We also find that the background plane of $u^{[1]}$ is fixed, while the background plane of $v^{[1]}$ changes from negative to zero and then to positive with the increase of t.

Fig. 1

3D figures of the double-pole solitons: a Component u; b Component v via Solutions (12) with $\lambda _1=1,~\beta =\frac{1}{4}$ and $l_{11}=l_{12}=1$

Since the background of $u^{[1]}$ is fixed while the background plane of $v^{[1]}$ is changing, we take $u^{[1]}$ as an example to analyze the asymptotic properties of Solutions (12). In fact, $u^{[1]}$ and $v^{[1]}$ own the same curve characteristic lines.

Motivated by Refs. [40,41,42], we firstly perform the following asymptotic analysis procedure to investigate the asymptotic behaviors of $u^{[1]}$ in Solutions (12).

We firstly prove that the characteristic lines of $u^{[1]}$ are not the straight lines as follows:

We consider an arbitrary line $L:\frac{t}{\lambda _1}+c_1 x=c_2$, where $c_1$ and $c_2$ are the arbitrary real numbers. Since $\rho =\lambda _1\theta -8\beta \lambda _1^2x,$ $u^{[1]}$ are dependent only on the variables $\theta$ and x. Thus, it is necessary to investigate the behavior of $\theta$ alone L as $|x|\rightarrow \infty$. In view of $\theta -\left( \frac{t}{\lambda _1}+c_1 x\right) =\left( 4\beta \lambda _1 -c_1\right) x$, as $x\rightarrow +\infty$, the value of $\theta$ is

$$\begin{aligned} \begin{aligned} \theta =\left\{ \begin{aligned} -\infty , \quad&c_1>4\beta \lambda _1, \\ O(1) \quad&c_1=4\beta \lambda _1, \\ +\infty , \quad&c_1<4\beta \lambda _1, \\ \end{aligned} \right. \end{aligned} \end{aligned}$$

(13)

and vice versa, where O(1) denotes that the two quantities are of the same order, i.e., the ratio limit of two quantities tends to a nonzero constant.

As shown in Expressions (13), the value of $\theta$ can be $+\infty ,~-\infty$ or O(1) at infinity on the line L. Hence, we can calculate the dominant behaviors of $u^{[1]}$ corresponding to the above three cases of $\theta$ as

$$\begin{aligned}&u^{[1]}=\left\{ \begin{array}{ll}-2\frac{l_1(\rho +2\lambda _1)}{\lambda _1^2l_2}e^{\frac{\theta }{2}},&\quad\theta\rightarrow -\infty ,\\2l_1l_2\frac{\left( l_1^2e^\frac{\theta }{2}-l_2^2e^{-\frac{\theta }{2}}\right) \rho -2\lambda _1 \left( l_1^2e^\frac{\theta }{2}+l_2^2e^{-\frac{\theta }{2}}\right) }{l_1^2l_2^2\rho ^2+\lambda _1^2\left( l_1^4e^\theta +l_2^4e^{-\theta }\right) +2l_1^2l_2^2\lambda _1^2},&\quad\theta=O(1),\\2\frac{l_2(\rho -2\lambda _1)}{\lambda _1^2l_1}e^{-\frac{\theta }{2}},&\quad\theta\rightarrow +\infty .\\ \end{array} \right. \\ \end{aligned}$$

(14)

Easy to know that $e^{\frac{\theta }{2}}\rightarrow 0$ as $\theta \rightarrow -\infty$, $e^{-\frac{\theta }{2}}\rightarrow 0$ as $\theta \rightarrow \infty$, and $l_1^2l_2^2\rho ^2\gg \Big |\left( l_1^2e^\frac{\theta }{2}-l_2^2e^\frac{-\theta }{2}\right) \rho \Big |$ as $\theta =O(1),~x\rightarrow \pm \infty$. That is to say, no matter which of the three cases in Expressions (13), $u^{[1]}$ will approach 0 as $|x|\rightarrow \infty$ alone the line L. In summary, characteristic lines of $u^{[1]}$ are not the straight lines.

Therefore, characteristic lines of $u^{[1]}$ are the curves in the $x-t$ plane. Along the curves to infinity, $e^{\theta }$ and $\rho$ approach infinity. Thus, a balance between $e^{\theta }$ and $\rho$ can be considered as

$$\begin{aligned} \begin{aligned} \frac{\rho }{e^{p\theta }}\sim O(1),~~~~~~~|x|\rightarrow +\infty , \end{aligned} \end{aligned}$$

(15)

where p is a real variable constant depending on the values of $e^{\theta }$ and $\rho$. According to the relationship between p and $\pm \frac{1}{2}$, we classify and obtain the following six dominant behaviors of $u^{[1]}$ as

$$ \begin{aligned} u^{[1]}=\left\{ \begin{array}{ll}\frac{2l_1}{l_2} \frac{e^{\frac{\theta }{2}}}{\rho } ,&\quad p>\frac{1}{2},~\theta \rightarrow \infty ,\\2l_1l_2 \frac{\rho e^{\frac{\theta }{2}} }{ \lambda _1^2l_1^2e^\theta +l_2^2\rho ^2 },&\quad p=\frac{1}{2},~\theta \rightarrow \infty ,\\ \frac{2l_2}{l_1\lambda _1^2} \frac{\rho }{e^{\frac{\theta }{2}}}, &\quad 0<p<\frac{1}{2},~\theta \rightarrow \infty ,\\-\frac{2l_1}{l_2\lambda _1^2} \frac{ \rho }{e^{-\frac{\theta }{2}}},&\quad -\frac{1}{2}<p<0,~\theta \rightarrow -\infty ,\\-2l_1l_2\frac{ \rho e^{-\frac{\theta }{2}} }{\lambda _1^2l_2^2e^{-\theta }+l_1^2\rho ^2},&\quad p=-\frac{1}{2},~\theta \rightarrow -\infty ,\\-\frac{2l_2}{l_1}\frac{ e^{-\frac{\theta }{2}} }{\rho },&\quad p<-\frac{1}{2},~\theta \rightarrow -\infty .\\ \end{array} \right. \\ \end{aligned}$$

(16)

Equations (16) indicate that $u^{[1]}$ behaves as the solitons with the stable amplitudes only when $p=\pm \frac{1}{2}$. Whether $p=\frac{1}{2}$ or $-\frac{1}{2}$, x may approach to $+\infty$ or $-\infty$. Therefore, we assume that $\lambda _1l_1l_2>0$ and $\beta >0$, and then calculate the following four asymptotic solitons as

$$\begin{aligned} \begin{aligned}&u^{[1]}\rightarrow u^{[1]}_{1,+}=\frac{1}{\lambda _1}\text{sech}\left( \frac{\theta }{2}+\text{ln}\frac{\lambda _1l_1}{l_2\rho }\right) ,\\&\quad \rho e^{-\frac{\theta }{2}}=O(1),~\theta \rightarrow +\infty ,~x\rightarrow +\infty ,~\rho>0,\\&u^{[1]}\rightarrow u^{[1]}_{1,-}=\frac{1}{\lambda _1}\text{sech}\left( \frac{\theta }{2}+\text{ln}\frac{-\rho l_1}{\lambda _1l_2}\right) ,\\&\quad \rho e^{\frac{\theta }{2}}=O(1),~\theta \rightarrow -\infty ,~x\rightarrow -\infty ,~\rho<0,\\&u^{[1]}\rightarrow u^{[1]}_{2,+}=-\frac{1}{\lambda _1}\text{sech}\left( \frac{\theta }{2}+\text{ln}\frac{\rho l_1}{\lambda _1l_2}\right) ,\\&\quad \rho e^{\frac{\theta }{2}}=O(1),~\theta \rightarrow -\infty ,~x\rightarrow +\infty ,~\rho >0,\\&u^{[1]}\rightarrow u^{[1]}_{2,-}=-\frac{1}{\lambda _1}\text{sech}\left( \frac{\theta }{2}+\text{ln}\frac{\lambda _1l_1}{-l_2\rho }\right) ,\\&\quad \rho e^{-\frac{\theta }{2}}=O(1),~\theta \rightarrow +\infty ,~x\rightarrow -\infty ,~\rho <0. \end{aligned} \end{aligned}$$

(17)

Similar to the above analysis procedure, we can prove that $v^{[1]}$ in Solutions (12) possesses the same characteristic lines as $u^{[1]}$ in Solutions (12). However, since the background of $v^{[1]}$ is a linear functions of t, i.e., $\beta t$, asymptotic solitons $v^{[1]}_{1,\pm }$ and $v^{[1]}_{2,\pm }$ have no fixed amplitudes.

3D figures and contour figures of $u^{[1]}$ and $v^{[1]}$ via Solutions (12) are shown in Fig. 2.

Fig. 2

a, c 3D figures; b, d Contour figures of the double-pole solitons via Solutions (12) with $\lambda _1=1,~\beta =\frac{1}{4}$ and $l_{11}=l_{12}=1$

Asymptotic Solitons (17) represent the two bright-type solitons $u^{[1]}_{1,\pm }$ and two dark-type solitons $u^{[2]}_{2,\pm }$. From Asymptotic Solitons (17), the following properties of the four asymptotic solitons $u^{[1]}_{1,\pm }$ and $u^{[1]}_{2,\pm }$ are obtained as follows:

(a) Amplitudes:

$$\begin{aligned} \begin{aligned} A(u^{[1]}_{1,\pm })=A(u^{[1]}_{2,\pm })=\frac{1}{|\lambda _1|}. \end{aligned} \end{aligned}$$

(18)

(b) Characteristic lines:

$$\begin{aligned} \begin{aligned}&u^{[1]}_{1,+}:~\lambda _1l_1e^{\frac{\theta }{2}}-l_2\rho =0;~u^{[1]}_{1,-}:~\rho l_1e^{\frac{\theta }{2}}+\lambda _1l_2=0;\\&u^{[1]}_{2,+}:~\rho l_1e^{\frac{\theta }{2}}-\lambda _1l_2=0;~u^{[1]}_{2,-}:~\lambda _1l_1e^{\frac{\theta }{2}}+l_2\rho =0. \end{aligned} \end{aligned}$$

(19)

(c) Slopes:

$$\begin{aligned} \begin{aligned} S(u^{[1]}_{1,\pm })&=\frac{1}{4\lambda _1^2\beta }\frac{2\lambda _1-|\rho |}{2\lambda _1+|\rho |};\\ S(u^{[1]}_{2,\pm })&=\frac{1}{4\lambda _1^2\beta }\frac{2\lambda _1+|\rho |}{2\lambda _1-|\rho |}. \end{aligned} \end{aligned}$$

(20)

(d) Phase shifts $P(\chi )$ between $u^{[1]}_{\chi ,+}$ and $u^{[1]}_{\chi ,-}$ $(\chi =1,~2)$:

$$\begin{aligned} \begin{aligned} P(1)=-P(2)=2~\text{ln}\left| \frac{\lambda _1}{\rho }\right| . \end{aligned} \end{aligned}$$

(21)

The above four asymptotic solitons own the same amplitude. In view of P(1) and P(2) are opposite under the same $|\rho |$, and the value of $S(u^{[1]}_{\chi ,+})$ at $\beta$ is equal to that of $S(u^{[1]}_{\chi ,-})$ at $-\rho$, we can infer that the interaction between $u^{[1]}_{1}$ and $u^{[1]}_{2}$ is elastic.

We have

$$\begin{aligned} \begin{aligned}&S(\theta )=-\frac{1}{4\lambda _1^2\beta }\le S(u^{[1]}_{1,\pm })\le 0;\\&S(u^{[1]}_{2,\pm })\le S(\theta )=-\frac{1}{4\lambda _1^2\beta }.\\ \end{aligned} \end{aligned}$$

(22)

Therefore, asymptotic solitons $u^{[1]}_{1,\pm }$ are located between the two straight lines $L_1:\theta =0$ and $L_2:x=0$, and asymptotic solitons $u^{[1]}_{2,\pm }$ are located outside of the straight line $L_1$, as shown in Fig. 2b.

As we set $M=1,~r_1=2,~N=3$ in Solutions (9), the triple-pole solitons for Eq. (1) are illustrated in Fig. 3; as we set $M=1,~r_1=3,~N=4$ in Solutions (9), the quadruple-pole solitons for Eq. (1) are illustrated in Fig. 4. We summarize a rule about the Nth-order multi-pole solitons for Eq. (1): when N is even, the Nth-order multi-pole solitons consist of $\frac{N}{2}$ bright solitons and $\frac{N}{2}$ dark solitons; when N is odd, the Nth-order multi-pole solitons consist of $\frac{N-1}{2}$ bright solitons and $\frac{N+1}{2}$ dark solitons. Moreover, these bright and dark solitons are arranged alternately.

Fig. 3

3D figures of the triple-pole solitons: a Component u; b Component v via Solutions (9) with $\lambda _1=\frac{2}{3},~\beta =\frac{2}{3}$ and $l_{11}=l_{12}=1$

Fig. 4

3D figures of the quadruple-pole solitons: a Component u; b Component v via Solutions (12) with $\lambda _1=\frac{2}{3},~\beta =\frac{2}{3}$ and $l_{11}=l_{12}=1$

Compared with the solitons in Refs. [8,9,10,11,12,13,14,15,16,17,18,19, 21, 22, 35], the double-pole solitons in Figs. 1 and 2 show the different dynamic characteristics. Curve characteristic lines indicate that the velocities of the solitons are changing with the changes of x and t. Moreover, each branch of $u^{[1]}$ owns the same amplitude.

3.2 Interactions among the solitons and multi-pole solitons for System (1)

As we set $M=1,~r_1=0$ and $N=1$ in Solutions (12), with respect to the magnetization related to the saturated ferromagnetic material and external magnetic field, expressions of the one-soliton solutions are derived as

$$\begin{aligned} \begin{aligned} u^{[1]}&=-\frac{1}{\lambda _1}\text{sech}\left( \frac{\theta }{2}+\text{ln}\frac{l_{11}}{l_{12}}\right) ,\\ v^{[1]}&=\beta x-\frac{l_{11}^2e^\theta -l_{12}^2}{\lambda _1\left( l_{11}^2e^\theta +l_{12}^2\right) },\\ \theta&=\frac{t}{\lambda _1}+4\beta \lambda _1 x. \end{aligned} \end{aligned}$$

(23)

From One-Soliton Solutions (23), we obtain that velocity of the one soliton is $-\frac{1}{4\beta \lambda _1^2}$.

As we set $M=2,~r_1=1,~r_2=0$ and $N=3$ in Solutions (12), the interaction among the one soliton and double-pole solitons is illustrated in Fig. 5. Figures 3 and  5 both contain three soliton components, including two curve-type solitons and one line-type soliton. However, the line-type soliton in Fig. 3 doesn’t have a phase shift before and after the interaction while the line-type soliton in Fig. 5 has a phase shift before and after the interaction. In other words, we can consider that Fig. 3 with an arbitrary line-type soliton is a special case of Fig. 5.

Fig. 5

3D figures of the interaction among the one soliton and double-pole solitons: a Component u; b Component v via Solutions (12) with $\lambda _1=\frac{2}{3},~\lambda _2=-1,~\beta =\frac{2}{3}$ and $l_{11}=l_{12}=l_{21}=l_{22}=1$

As we set $M=2,~r_1=2,~r_2=0$ and $N=4$ in Solutions (12), the interaction among the one soliton and triple-pole solitons are illustrated in Fig. 6. As we set $M=2,~r_1=1,~r_2=1$ and $N=4$ in Solutions (12), the interaction among the two double-pole solitons are illustrated in Fig. 7.

Fig. 6

3D figures of the interaction among the one soliton and triple-pole solitons: a Component u; b Component v via Solutions (12) with $\lambda _1=\frac{2}{3},~\lambda _2=-1,~\beta =\frac{2}{3}$ and $l_{11}=l_{12}=l_{21}=l_{22}=1$

Fig. 7

3D figures of the interaction among the two double-pole solitons: a Component u; b Component v via Solutions (12) with $\lambda _1=\frac{2}{3},~\lambda _2=-1,~\beta =\frac{2}{3}$ and $l_{11}=l_{12}=l_{21}=l_{22}=1$

Compared with those simple situations in Figs. 1, 3, 4, the interaction areas in Figs. 5, 6, 7 appear more disordered, which correspond to the realistic occasions of the electromagnetic wave propagation in a ferromagnetic saturator. In fact, with the increase of M and N, i.e., the total order of Solutions (12) and the number of spectral parameters, solutions of System (1) will be composed of more solitons. Due to the limitation of computing power, we only show up to the fourth-order solutions.

In Figs. 5, 6, 7, all the solitons extend to infinity and maintain their shapes. We find that before and after the interaction, the solitons and multi-pole solitons only have a phase shift while their velocities, amplitudes, shapes, and widths do not change at all. That is to say, interactions among the solitons and multi-pole solitons are elastic. We also find that the one soliton component in Fig. 6 is dark-type, while the one soliton component in Fig. 5 is bright-type.

In Figs. 1, 2, 3, 4, only a peak arises in the multi-pole solitons. However, soliton interactions in Figs. 5, 6, 7 present more peaks and depressions as follows: two depressions in Fig. 5, two peaks and a depression in Fig. 6, and two peaks and two depressions in Fig. 7. Moreover, interaction regions of the fourth-order solitons in Figs. 6, 7 are kinked.

It has been reported that the bound-state solitons appear and exhibit the periodic attractions or repulsions between the adjacent solitons when two or more solitons have the same velocity [43]. However, in Solutions (12), unequal spectral parameters indicate that different solitons have different velocities, thus, bound-state solitons cannot be derived.

4 Conclusions

In this paper, a Kraenkel-Manna-Merle system, i.e., System (1), which describes the nonlinear electromagnetic short waves in a ferromagnetic saturator, has been investigated. On the basis of N-Fold DT (6), a GDT has been constructed and utilized to derive Solutions (12).

Double-pole soliton solutions have been derived as Solutions (12) and have been shown in Fig. 1. Asymptotic analysis on Solutions (12) has given rise to Asymptotic Solitons (17), which lead to Characteristic Lines (19), Slopes (20) and Phase Shifts (21) of $u^{[1]}_{1,\pm }$ and $u^{[1]}_{2,\pm }$. We have found that the four asymptotic solitons $u^{[1]}_{1,\pm }$ and $u^{[1]}_{2,\pm }$ own the same amplitude $|\lambda _1|^{-1}$, the asymptotic solitons $u^{[1]}_{1,\pm }$ are located between the two straight lines $L_1$ and $L_2$, and the asymptotic solitons $u^{[1]}_{2,\pm }$ are located outside of the straight line $L_1$, as shown in Fig. 2. The above conclusions and phenomena on the double-pole solitons have been similar to those analyses in Refs. [40, 42], i.e., System (1) and the generalized nonlinear Schrödinger equations have shown the same multi-pole soliton characteristics.

For Eq. (1), the triple-pole solitons have been shown in Fig. 3; the quadruple-pole solitons have been illustrated in Fig. 4; the interaction among the one soliton and double-pole solitons has been presented in Fig. 5; the interaction among the one soliton and triple-pole solitons has bee shown in Fig. 6; the interaction among the two double-pole solitons has been presented in Fig. 7. We have summarized a rule about the Nth-order multi-pole solitons: when N is even, the Nth-order multi-pole solitons consists of $\frac{N}{2}$ bright solitons and $\frac{N}{2}$ dark solitons; when N is odd, the Nth-order multi-pole solitons consists of $\frac{N-1}{2}$ bright solitons and $\frac{N+1}{2}$ dark solitons. Compared with the normal solitons in Ref. [35], the above multi-pole solitons have only shown changes in propagation velocities while other physical properties such as the wave heights and amplitudes remain unchanged.

In the future, we expect to extend the above asymptotic analysis method to the triple-pole or even N-fold-pole soliton solutions and multi-pole breather solutions, although those discussions must be more complex. It is worth noting that the simultaneous emergence among the multi-pole phenomena and bound states also have potential research spaces.