1 Introduction

Although linear vibration isolator is the most widely used and matured vibration isolator in real engineering, it has inherent shortcomings. That is, it can purely isolate vibration when excited frequency is more than \(\sqrt 2\) times of natural frequency; moreover, the vibration isolation performance at low-frequency band is weak [1]. One way to reduce the initial isolation frequency is to reduce the static stiffness by sacrificing the load capacity [2, 3]. Thus, people try to study a device with high static stiffness, but its dynamic stiffness is low, which means that the vibration isolation frequency is guaranteed, and it can withstand large load [4, 5]. This novel isolation system can support high weight thanks to its high static stiffness; at the same time, the low dynamic stiffness makes it have excellent low-frequency vibration isolation capability.

Since the seminal works of Alsbushov [4], various types of QZS systems have been developed. Liu and coworkers [6,7,8] have extensively studied novel QZS systems whose negative stiffness was offered by two Euler buckled beams or sliding beams, including basic QZS characteristics, ultra-low-frequency nonlinear isolation and imperfection analysis. A low-frequency QZS vibration isolator was designed by Jing et al. [9,10,11,12,13] based on bio-inspired limb-like mechanism. Its basic structure was similar to that of a scissors mechanism, and its excellent vibration isolation abilities were analytically and experimentally verified. Zhou and coauthors [14, 15] and Liu et al. [16] used linear spring to support mass while paralleling a cam–roller–spring structure with negative stiffness to form a QZS system, where the later work used the nonlinear springs in the negative stiffness mechanism. Shaw et al. [17, 18] have designed novel QZS systems using bistable composite plate as negative stiffness structure. QZS vibrators were also designed by using electromagnets or permanent magnets distributed in special locations, whose QZS performances were verified by theoretical and experimental methods [19,20,21,22,23,24,25]. In these kinds of QZS systems, it is noteworthy that the negative stiffness can be actively controlled and adjusted by changing the current. Besides, many others researches have also been conducted to investigate the vibration isolation performances of various QZS systems [26,27,28,29,30,31].

Utilizing oblique springs to supply negative stiffness is a simple way to design QZS systems.

Carrella et al. [32,33,34] used a pair of oblique springs to obtain negative stiffness and then achieved the QZS property by paralleling another positive stiffness coil spring. It was proved that the effect of negative stiffness structure is positive in terms of the force and displacement transmissibility. Lu et al. [35,36,37,38] and Wang et al. [39] have substantially studied two-stage QZS vibration isolation systems, in which the nonlinear negative stiffness was also achieved via oblique springs. Xu et al. [40] designed a QZS system with four oblique springs to generate negative stiffness and one coil spring in parallel to provide positive stiffness, theoretically and experimentally demonstrating that the system had a wider frequency band for effective vibration isolation. Zhao et al. [41] added a group of oblique springs to the traditional three springs QZS system and expanded the range of quasi-zero stiffness by superposition of different stiffness regions. Zhou et al. [42] put forward a kind of dynamic vibration absorber based on oblique spring QZS system; through theoretical and experimental methods, it was confirmed that the proposed vibration absorber has better low-frequency vibration reduction performance when compared with linear vibration absorber. Subsequently, Jing et al. [43] applied a time-delay active control technology in an identical QZS system, showing that the natural frequency was reduced and the vibration isolation effect was significantly improved. Analogously, Yang and Cao [44, 45] have designed a QZS isolator with time-delay active control. They showed that the use of control is equivalent to increasing the damping force, and higher time-delay can reduce the response amplitude.

According to the above works discussed, the QZS system, whose negative stiffness is provided by oblique springs, has one main drawback. That is, the displacement range of QZS is extremely small, and vibration with large amplitude can even be worsened, therefore limiting its application in real engineering. Thus, the main contribution of this study is to attempt to broaden the displacement range of QZS via a semi-active control strategy. In addition, we design a QZS system by using six oblique springs. Static and dynamic analysis are further performed to investigate the QZS performances of the designed system.

This paper is organized as follows. After the introduction, a QZS system with six oblique linear springs’ mechanism and a vertical coil spring is introduced in Sect. 2. In Sect. 3, the dynamic characteristics of the QZS are studied, in which the force–displacement transmissibility and jump phenomena are analyzed and discussed. A semi-active control method based on a feedback displacement control strategy is presented to turn the QZS performance of the proposed system in Sect. 4. The paper is closed with some concluding remarks.

2 Static analysis

2.1 The QZS system

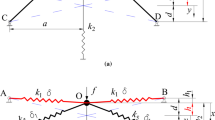
As shown in Fig. 1a, the QZS system is composed of seven linear springs, of which only one vertical coil spring offers positive stiffness for the system, and the other springs provide negative stiffness. The six springs are initially tilted in space, starting from the horizontal plane, marked as an angle θ. The initial length \(L_{0}\) and stiffness \(K\) of the six springs are the same. The upper ends of these springs are gathered at point A with a height of h from the horizontal plane, and the other ends are hinged at point \(B,C,D,E,F\) and G, respectively. The displacement of point A moving vertically downward from equilibrium point O is expressed by Y. As shown in Fig. 1(b), the six hinged points are uniformly distributed by circumference with point O as the center point; the distances from point \(B,C,D,E,F\) and G to point O are marked as a. The coil spring, K1, is installed in parallel with the six oblique springs mechanism on the horizontal plane, and the other point is fixed on a plane parallel to the horizontal plane.

Fig. 1
figure 1

a Schematic representation of six oblique springs’ QZS system; b schematic representation of hinge points distribution of six oblique springs at horizontal level

Full size image

2.2 Analysis of negative stiffness characteristics

As shown in Fig. 2, a vertical downward force, F0, is applied at point A, point A moves downwards, and the six oblique springs are compressed from the initial length L0 to L1. (L0 is smaller than L1.) The displacement of point A is represented by x0, which is calculated from the initial position. The relationship between force F0 and displacement x0 is

$$ F_{0} = 6K(L_{0} - L_{1} )\sin \theta $$
(1)

where \(\sin \theta = (h - x_{0} )/L_{1}\), \(L_{1} = \sqrt {(h - x_{0} )^{2} + a^{2} }\). Let Y0 be the displacement of point A moving vertically downward from equilibrium point O, then Eq. (1) can be rewritten as

$$ F_{0} = 6K(h - x_{0} )\left( {\frac{{L_{0} }}{{\sqrt {a^{2} + (h - x_{0} )^{2} } }} - 1}\right) = 6KY_{0}\left(1 - \frac{{L_{0} }} {{\sqrt {a^{2} + Y_{0}^{2} } }} \right) $$
(2)
Fig. 2
figure 2

Schematic representation of spatial geometric distribution of six oblique springs’ negative stiffness mechanism

Full size image

The non-dimensional form of Eq. (2) is

$$ \hat{F}_{0} = 6\hat{Y}_{0} \left( {1 - \frac{1}{{\sqrt {\hat{a}^{2} + \hat{Y}_{0}^{2} } }}} \right) $$
(3)

where \(\hat{F}_{0} = {{F_{0} } \mathord{\left/ {\vphantom {{F_{0} } {KL}}} \right. \kern-\nulldelimiterspace} {KL}}\), \(\hat{Y}_{0} = {{Y_{0} } \mathord{\left/ {\vphantom {{Y_{0} } {L_{0} }}} \right. \kern-\nulldelimiterspace} {L_{0} }}\), \(\hat{a} = {a \mathord{\left/ {\vphantom {a L}} \right. \kern-\nulldelimiterspace} L}_{0}\)

Therefore, the non-dimensional stiffness is obtained as follows

$$ \hat{K}_{0} = 6\left( {1 - \frac{{\hat{a}^{2} }}{{(\hat{a}^{2} + \hat{Y}_{0}^{2} )^{3/2} }}} \right) $$
(4)

On the basis of above discussion, it can be apparently seen that \(\hat{a}\) determines the state of the negative mechanism. When \(\hat{a} = 1\), the six springs, initially, lie horizontally; while when \(\hat{a} = 0\), they are perpendicular to the horizontal plane in space. Figure 3 and Fig. 4 show the force–displacement and stiffness–displacement relationships for different values of \(\hat{a}\), respectively; both are in the non-dimensional forms. From Fig. 3, it can be clearly found that the six oblique springs’ mechanism has the negative stiffness characteristic around the equilibrium point except when \(\hat{a} = 0\), and the force–displacement curve has a highly nonlinear relationship. In addition, the force becomes larger as \(\hat{a}\) decreases from 1 to 0. Moreover, the nonlinearity of the curve gets stronger by decreasing the value of \(\hat{a}\), except when \(\hat{a}\) equals 0; when \(\hat{a} = 0\), the curve presents linear property before and after the equilibrium point. From Fig. 4, again, it can be seen that the six oblique springs’ mechanism shows negative property near the equilibrium point except for \(\hat{a} = 0\). Additionally, if the value of \(\hat{a}\) is reduced, the minimum value of negative stiffness becomes smaller.

Fig. 3
figure 3

Non-dimensional force–displacement characteristic

Full size image
Fig. 4
figure 4

Non-dimensional stiffness–displacement characteristic

Full size image

Let \(\hat{K}_{0}\) be less than zero, yielding the relationship between the non-dimensional displacement and \(\hat{a}\), which can be defined by Eq. (5). The relationship is also plotted in Fig. 5; the displacement range of the six oblique springs’ mechanism with negative stiffness is directly related to its structural parameters \(\hat{a}\).

$$ \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y} } \right| \le \sqrt {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a}^{2} } $$
(5)
Fig. 5
figure 5

Non-dimensional displacement from the static equilibrium position as a function of \(\hat{a}\)

Full size image

2.3 Analysis of QZS characteristics

From Fig. 1a, putting a downwards force \(F\) on point A, the displacement Y given by

$$ F = K_{1} (Y + h) + 6KY(1 - \frac{L}{{\sqrt {a^{2} + Y^{2} } }}) $$
(6)

Taking the non-dimensional form of Eq. (6) gives

$$ \hat{F} = \hat{Y} + \hat{h} + 6\lambda \hat{Y}\left( {1 - \frac{1}{{\sqrt {\hat{a}^{2} + \hat{Y}^{2} } }}} \right) $$
(7)

where \(\hat{Y} = Y/L\), \(\hat{\user2{h}} = {\varvec{h}}/L\), \(\hat{a} = a/L\), \(\lambda = K/K_{1}\), \(\hat{F} = F/K_{1} L\).

Through the differential calculation of the Eq. (7), the non-dimensional stiffness is as follows

$$ \hat{K} = 1 + 6\lambda \left( {1 - \frac{{\hat{a}^{2} }}{{(\hat{a}^{2} + \hat{Y}^{2} )^{3/2} }}} \right) $$
(8)

The system should satisfy the condition of quasi-zero stiffness, i.e., let Eq. (8) be zero, one gets,

$$ \lambda = \frac{{(\hat{a}^{2} + \hat{Y}^{2} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}{{6(\hat{a}^{2} - (\hat{a}^{2} + \hat{Y}^{2} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} )}} $$
(9)

When the system is in static equilibrium, Eq. (9) degenerates to be

$$ \lambda = \frac{{\hat{a}}}{{6(1 - \hat{a})}} $$
(10)

3 Dynamic behavior of the QZS system

3.1 Approximation of the stiffness of the QZS system

In order to simplify the calculation and facilitate the subsequent analysis, Taylor series is used to expand Eq. (7) and approximately replaced by a cubic polynomial. The results are as follows:

$$ \hat{F}_{1} = \frac{3\lambda }{{\hat{a}^{3} }}\hat{Y}^{3} $$
(11)

Correspondingly, the non-dimensional stiffness is as follows

$$ \hat{K} = \frac{9\lambda }{{\hat{a}^{3} }}\hat{Y}^{2} $$
(12)

The approximate non-dimensional force–displacement curve of the proposed QZS system is plotted in Fig. 6. The approximate non-dimensional stiffness–displacement curve is plotted in Fig. 7. They are compared with the exact curve as well. It can be found that the error between approximate expression and exact expression is sufficiently small, specially near the equilibrium point; thus, it can be concluded that the approximation strategy is reasonable. The error of the non-dimensional stiffness at a specific point of displacement is given as follows:

$$ \varepsilon_{k} = \left[ {1 - \frac{{K_{{{\text{approximate}}}} }}{{K_{{{\text{exact}}}} }}} \right] \times 100\% = \left[ {1 - \frac{{\frac{9\lambda }{{a^{2} }}\hat{Y}^{2} }}{{1 + 6\lambda (1 - \frac{{\hat{a}^{2} }}{{(\hat{a}^{2} + \hat{Y}^{2} )^{3/2} }})}}} \right] \times 100\% $$
(13)
Fig. 6
figure 6

Non-dimensional force–displacement characteristic

Full size image
Fig. 7
figure 7

Non-dimensional stiffness–displacement characteristic

Full size image

3.2 Force–displacement characteristic and jumping phenomena

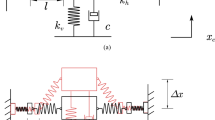
As shown in Fig. 8, linear damping is added to the QZS system. When the system is not loaded, the mass, m, keeps the system exactly in the static equilibrium position. k0 is used to represent the quasi-zero stiffness, and the damping is represented by c. At the top of the system, a simple harmonic excitation \(F = H_{0} \cos (\omega t)\) is applied downward, and the response force at the foundation is marked as F1.

Fig. 8
figure 8

Equivalent model of QZS vibration isolation system

Full size image

In conclusion, QZS system has better quasi-zero performance only when it is close to the static equilibrium position. Before dynamic analysis, the following assumptions should be made:

  1. (1)

    Under the action of excitation F, the QZS system is always close to the static equilibrium position.

  2. (2)

    The force–displacement equation is approximately replaced by Eq. (11).

Based on the above assumptions, the equation of motion can be approximately expressed as

$$ m\ddot{x} + c\dot{x} + \frac{3}{{a^{3} }}LKx^{3} = H_{0} \cos (\omega t) $$
(14)

Its non-dimensional form reads

$$ \ddot{\hat{x}} + 2\xi \dot{\hat{x}} + \mu \hat{x}^{3} = \hat{H}_{0} \cos (\psi \tau ) $$
(15)

where

$$ \omega_{1} = \sqrt {\frac{{k_{1} }}{m}} ,\psi = \frac{\omega }{{\omega_{1} }},\tau = \omega_{1} t,\lambda = \frac{k}{{k_{1} }},\hat{a} = \frac{a}{L},\mu = \frac{3\lambda }{{\hat{a}^{3} }},\xi = \frac{c}{{2m\omega_{1} }},\hat{y} = \frac{y}{L},\hat{H}_{0} = \frac{{H_{0} }}{{K_{1} L}} $$

Analyzing Eq. (15), the equation for the motion of the QZS system is a Duffing system with zero linear term. The harmonic balance method [46, 47] will be used to numerically obtain the solution without considering other higher harmonic frequencies. The periodic response can be expressed as \(\hat{x}(\tau ) = H_{1} \cos (\psi \tau + \varphi )\). Inserting the response into Eq. (15) yields the frequency–amplitude characteristic, as

$$ \hat{H}_{0} = \sqrt {\left( {\frac{3}{4}\mu H_{1}^{3} + H_{1} \psi^{2} } \right)^{2} + (2H_{1} \xi \psi )^{2} } $$
(16)

From Eq. (16), the damping ratio \(\xi\), the parameter of system nonlinearity \(\mu\), the amplitude of harmonic excitation force \(\hat{H}_{0}\) and the frequency of excitation \(\psi\) all affect the amplitude of system response \(H_{1}\).

The QZS system has jumping phenomena, that is, the jump frequency is the excitation frequency, the response amplitude of the system will suddenly decrease significantly. On the contrary, the phenomenon for the jump-up frequency is just the opposite. By expanding Eq. (16) and merging the same terms, the equation for parameters \(\psi^{2}\) is obtained as follows

$$ H_{1}^{2} \psi^{4} + (4\xi^{2} H_{1}^{2} - \frac{3}{2}\mu H_{1}^{4} )\psi^{2} + \frac{9}{16}\mu^{2} H_{1}^{6} - \hat{H}_{0}^{2} = 0 $$
(17)

Solving Eq. (17) gives

$$ \psi_{1.2} = \frac{1}{2}\sqrt {3\mu H_{1}^{2} - 8\xi^{2} \pm \frac{4}{{H_{1} }}\sqrt { - 3\mu \xi^{2} H_{1}^{4} + 4\xi^{4} H_{1}^{2} + \hat{H}_{0}^{2} } } $$
(18)

When parameter \(\psi_{1} = \psi_{2}\) and damping ratio \(\xi < < 1\), the maximal amplitude of the system response is given by

$$ H_{1\max } = \sqrt {\frac{{2\xi^{3} + \sqrt {4\xi^{6} + 3\mu \hat{H}_{0}^{2} } }}{3\mu \xi }} $$
(19)

Substituting Eq. (19) into Eq. (18), one gets the jump-down frequency, as

$$ \psi_{x} = \frac{1}{{\sqrt {2\xi } }}\sqrt {\sqrt {\xi^{6} + \frac{3}{4}\mu \hat{H}_{0}^{2} } - 3\xi^{3} } $$
(20)

Given \(4\xi^{6} < < 3\mu \hat{H}_{0}^{2}\), Eq. (20) can be further approximated as

$$ \psi_{x} \approx \left( {\frac{{3\mu H_{0}^{2} }}{{16\xi^{2} }}} \right)^{1/4} $$
(21)

When the damping ratio \(\xi = 0\) and solving the equation \({{d\psi } \mathord{\left/ {\vphantom {{d\psi } {dH_{1} }}} \right. \kern-\nulldelimiterspace} {dH_{1} }} = 0\), the approximate expression of the corresponding amplitude for the jump-up frequency can be obtained as follows

$$H_{1s}\approx\left({\frac{{2\hat{H}_{0} }}{3\mu }} \right)^{{{1\mathord{\left/ {\vphantom {1 3}}\right. \kern-\nulldelimiterspace} 3}}}$$
(22)

By substituting Eq. (22) into Eq. (18), the jump-up frequency is calculated as

$$\psi_{{\varvec{s}}} \approx\left( {\frac{{9\hat{H}_{0} \sqrt \mu }}{4}}\right)^{{{1 \mathord{\left/{\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}}$$
(23)

Based on the above analysis, the jump frequency of the system is affected by the nonlinearity parameter \(\mu\), the damping ratio \(\xi\) and the amplitude of harmonic excitation force \(\hat{H}_{0}\). We will further qualify the influences of these parameters by numerical simulation analysis.

The relationship between the jump frequency and the nonlinearity parameter \(\mu\) is shown in Fig. 9 with other parameters fixed as \(\xi = 0.02\) and \(\hat{H}_{0} = 0.2\). It can be found that both jump-up frequency and jump-down frequency increase with the increase in the nonlinearity parameter \(\mu\), with the former being much smaller than the latter. Note that the effective vibration isolation frequency range widens by decreasing the jump-down frequency, meaning that reducing the value of the nonlinearity parameter \(\mu\) can make the vibration isolation ability better.

Fig. 9
figure 9

The effect of nonlinearity parameter \(\mu\) on the jump frequency for parameter settings of \(\xi = 0.02\) and \(\hat{H}_{0} = 0.2\)

Full size image

We also plot the curve that describes the relationship between the system jump frequency and the amplitude of harmonic excitation force \(\hat{H}_{0}\) as shown in Fig. 10; other parameters are kept as \(\mu = 5\) and \(\xi = 0.02\). It can be found that the influence is similar to that of the nonlinearity parameter \(\mu\).

Fig. 10
figure 10

The effect of amplitude of harmonic excitation force \(\hat{H}_{0}\) on the jump frequency for parameter settings of \(\mu = 5\) and \(\xi = 0.02\)

Full size image

The relationship between the system jump frequency and damping ratio \(\xi\) is shown in Fig. 11 by keeping other parameters as \(\mu = 5\) and \(\hat{H}_{0} = 0.2\). Obviously, the jump-down frequency decreases by enlarging the damping ratio \(\xi\). When \(\xi\) reaches the critical damping ratio \(\xi_{{\text{c}}}\), the jumping interval becomes zero, i.e., the two jump frequencies are equal, and there are no longer jumping phenomena. The critical damping ratio is expressed by \(\xi_{{\text{c}}}\) as follows:

$$ \xi_{c} = \left( {\frac{{9\hat{H}_{0} \sqrt \mu }}{4}} \right)^{1/3} \left[ { - \frac{1}{2} + \frac{1}{{12\left( {\frac{1}{108} + \frac{{i\sqrt[{}]{23}}}{216}} \right)^{1/3} }} + \left( {\frac{1}{108} + \frac{{i\sqrt[{}]{23}}}{216}} \right)^{1/3} } \right]^{1/2} $$
(24)
Fig. 11
figure 11

The effect of damping ratio \(\xi\) on the jump frequency for parameter settings of \(\mu = 5\) and \(\hat{H}_{0} = 0.2\)

Full size image

3.3 Force transmissibility

For the system presented in Fig. 8, the force transferred to the foundation is given by

$$ \hat{F}_{1} = 2\xi \dot{\hat{x}} + \mu \hat{x}^{3} $$
(25)

Using the harmonic balance method and neglecting the higher harmonics, the magnitude of the force can be reformulated as

$$ \overline{\hat{F}}_{1} = \sqrt {\left( {\frac{3}{4}\mu H_{1}^{3} } \right)^{2} + ( - 2\xi \psi H_{1} )^{2} } $$
(26)

Then, the force transmissibility is given by

$$ \eta = \frac{{\overline{\hat{F}}_{1} }}{{\hat{H}_{0} }} = \frac{{\sqrt {\left( {\frac{3}{4}\mu H_{1}^{3} } \right)^{2} + \left( { - 2\xi \psi H_{1} } \right)^{2} } }}{{\hat{H}_{0} }} $$
(27)

The force transmissibility is determined by four parameters; they are the amplitude of harmonic excitation force \(\hat{H}_{0}\), the damping ratio \(\xi\), the nonlinearity parameter \(\mu\) and the frequency \(\psi\). The force transmissibility is plotted in Fig. 12 for three values of the damping ratio \(\xi\), i.e., \(\xi { = }0.05\), 0.2 and 0.5. The other parameters are \(\mu = 3\) and \(\hat{H}_{0} = 0.05\). The transmissibility for the linear system is also presented for comparison purpose. Note that the linear system only consists of one positive spring. It is obvious that the maximum amplitude of the transmissibility of two systems both decreases with an increase in damping ratio. Finally, the jumping phenomena of QZS system will disappear because the damping ratio has increased to a certain value. The effective isolation frequency range of linear system is not affected by the change of damping. Nonetheless, for the QZS systems, when the damping ratio is small, i.e., \(\xi { = }0.05\), it is obvious that the transmission curve is bent to the right hand side, and the initial effective isolation frequency is the jump-down frequency. When \(\xi { = }0.2\), the initial isolation frequency is obviously reduced and the jumping phenomena is disappeared. Finally, it can be said that compared with the two systems, the QZS system is more susceptible to damping, but its low-frequency vibration isolation ability is superior.

Fig. 12
figure 12

Magnitude of the force transmissibility for different values of \(\xi\): 0.05, 0.2 and 0.5

Full size image

The force transmissibility is plotted in Fig. 13 for \(\xi = 0.05\),\(\hat{H}_{0} = 0.5\) and three values of the nonlinearity parameter \(\mu\), i.e., \(\mu { = }0.05\), 0.5 and 1. When \(\mu { = }5\), the transmission curve is obviously bent to the right hand side. When the nonlinearity parameter decreases to be 1, the bending degree of the transmission curve does not change and not obviously move to the left, but the peak value of the response decreases. Further reducing the nonlinearity parameter to \(\mu { = 0}{\text{.5}}\), the transfer curve changes according to the same law. It is shown that the jump-down frequency becomes smaller with the decrease in the nonlinearity parameter \(\mu\), which also means that the frequency range of vibration that can be isolated becomes larger.

Fig. 13
figure 13

Magnitude of the force transmissibility for different values of \(\mu\): 0.5, 1 and 5

Full size image

Figure 14 shows that the jump frequency tends larger as the amplitude of harmonic excitation force \(\hat{H}_{0}\) increases where the parameters are \(\xi = 0.05\) and \(\mu = 3\). When the amplitude of harmonic excitation force is small, i.e., \(\hat{H}_{0} { = 0}{\text{.05}}\), it is obvious that the bending degree of the transmission curve does not change. However, compared with the amplitude of harmonic excitation force, for \(\hat{H}_{0} { = 0}{\text{.5}}\), the curve moves more clearly to the left. This means that the initial isolation frequency is relatively low for harmonic excitation force with smaller amplitude.

Fig. 14
figure 14

Magnitude of the force transmissibility for different values of \(\hat{H}_{0}\): 0.05, 0.5 and 1

Full size image

4 Semi-active control for the proposed QZS system

For the system presented in Fig. 8, the non-dimensional stiffness and displacement characteristic are shown in Fig. 15, where the values of \(\hat{a}\) are different and \(\lambda = 1\). It can be confirmed from the diagram that the stiffness characteristics of the system are affected by \(\hat{a}\). When \(\hat{a}{ = 1}\), the non-dimensional stiffness \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K}\) varies with displacement but remains positive stiffness all the time. For \(\hat{a}{ = }{6 \mathord{\left/ {\vphantom {6 7}} \right. \kern-\nulldelimiterspace} 7}\), the zero stiffness of the system appears only at one point, that is, the static equilibrium position. It's positive at all other displacements, and the value of positive stiffness is proportional to the displacement. For \(\hat{a}{ = }{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-\nulldelimiterspace} 7}\), zero stiffness appears at two positions, and the stiffness remains negative between the two zero stiffness points. However, the negative stiffness is not stable, so it is necessary to avoid this situation.

Fig. 15
figure 15

Non-dimensional stiffness of the QZS system when \(\lambda = 1\) and different values of \(\hat{a}\): 6/7, 5/7 and 1

Full size image

Combined with the above analysis, it can be found that by adjusting the values of \(\hat{a}\), the non-dimensional stiffness remaining zero in a certain displacement range can be achieved. Combined with the non-dimensional stiffness expressed in Eq. (8), when the \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K}\) remains zero, the relationship between \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y}\) and parameter \(\hat{a}\) is given by

$$\hat{Y} = \pm \sqrt {\left({\frac{6\lambda }{{1 + 6\lambda }}\hat{a}^{2}}\right)^{{{2\mathord{\left/{\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}-\hat{a}^{2}}$$
(28)

When \(\lambda = 1\), \( {6 \mathord{\left/ {\vphantom {6 7}} \right. \kern-\nulldelimiterspace} 7}\hat{a}^{{2}{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} - \hat{a}^{2} \ge 0\) should be satisfied in Eq. (28). Therefore, the range of parameter \(\hat{a}\) can be obtained as follows:

$$ 0 \le \hat{a} \le \frac{6}{7} $$
(29)

The relationship between \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y}\) and parameter \(\hat{a}\) given by Eq. (28) is plotted in Fig. 16 for \(\lambda = 1\). It can be seen that, when the displacement of the isolated mass changes, two different spring inclination angles can be found to correspond to the displacement, thus keeping the stiffness of the system to be zero.

Fig. 16
figure 16

The relationship between non-dimensional displacement \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Y}\) and parameter \(\hat{a}\) for Eq. (28) when \(\lambda = 1\)

Full size image

Based on this feature, a semi-active control method for the proposed QZS system based on a feedback displacement control strategy is proposed, as shown in Fig. 17. A displacement sensor is mounted on the mass of vibration isolation to detect the displacement deviating from the initial position when vibration occurs. The specific control flow is shown in Fig. 18. The feedback displacement is transmitted to the controller, which can adjust the distance between one end of the oblique springs and the center of the system, thereby leading to the alteration of the inclination angle of the springs. Finally, under the semi-active control strategy, the stiffness remains zero in a certain displacement range.

Fig. 17
figure 17

Schematic diagram of QZS with semi-active control method based on a feedback displacement control strategy

Full size image
Fig. 18
figure 18

Schematic diagram of semi-active control method

Full size image

The first half of the curve in Fig. 16 is taken as the process that the inclination angle of the springs varies with the displacement. This means that when the displacement changes from zero to approximately equal to 0.33, the \(\hat{a}\) decreases from about 0.86 to roundly 0.47. At the same time, the displacement sensor has a certain accuracy, so the feedback displacement is a finite number of numerical values with deterministic accuracy. Finally, the non-dimensional stiffness characteristics of the active stiffness QZS system are shown in Fig. 19. From Fig. 19, the non-dimensional displacement of the system is approximately in the range of − 0.33 to 0.33, and the non-dimensional stiffness of the QZS system remains zero. Beyond this displacement range, the stiffness is always positive because the six oblique springs’ structure no longer has negative stiffness characteristics.

Fig. 19
figure 19

Non-dimensional stiffness of the QZS system with semi-active control method

Full size image

Using the parameters shown in Table 1, the prototype model of semi-active QZS system is established in ADAMS, as shown in Fig. 20. At this time, the system is in equilibrium. One end of the six oblique springs is connected with the vibration isolation platform, and the other end is connected to the end of six vertical rods. The vertical rods can move along the direction of the circumference radius under the action of the controller and then adjust the inclination angle of the six oblique springs.

Table 1 The design parameters of the QZS system
Full size table
Fig. 20
figure 20

Virtual prototype model of semi-active QZS system

Full size image

The accuracy of the model needs to be verified. When the mass of the isolation platform is set to zero, the vertical spring is in the natural state, and the vertical rods maintain the initial position. The vertical force of the vibration isolation platform is obtained by applying displacement excitation on the platform, as shown in Fig. 21. Obviously, the system exhibits zero stiffness, so the virtual prototype model is qualitatively verified.

Fig. 21
figure 21

Time–force curve of virtual prototype model

Full size image

Considering the dimension of the system, Eq. (28) is approximately simplified. The governing equation between the displacement regulated by the controller and the vibration response amplitude of the isolation platform can be obtained:

$$ \Delta x = 0.8\varepsilon \Delta y $$
(30)

where \(\Delta x\) is the displacement regulated by the controller, \(\Delta y\) is the vibration amplitude of the vibration isolation platform measured by the sensor and \(\varepsilon\) is the adjustment coefficient, which is related to vibration excitation and frequency.

In the ADAMS model of equilibrium state, considering the effective control interval of semi-active control, the vibration excitation applied to the base of the system is \(Y = 10sin(2t)\).

Firstly, the simulation response curve of QZS system without semi-active control is obtained, as shown in Fig. 22. From Fig. 22, the response amplitude is far higher than the excitation amplitude, which worsens the vibration and does not have vibration isolation performance. Secondly, the semi-active control is started and the adjustment coefficient is set to 0.1. As shown in Fig. 22, the steady-state response amplitude is about 3 mm, only about one third of the excitation amplitude, which means that the QZS system under semi-active control can overcome the vibration deterioration problem under large amplitude excitation and maintain excellent vibration isolation performance.

Fig. 22
figure 22

Comparison of excitation signal and vibration isolation system response

Full size image

5 Conclusion

In this study, we have designed and analyzed a QZS system with an oblique linear spring structure. Its jumping phenomena and force–displacement transmissibility were investigated by the harmonic balance method. Moreover, based on the characteristic that the dynamic stiffness of the system is directly related to the initial inclination angle of the springs, a semi-active control method of displacement feedback control strategy is proposed. Finally, a virtual prototype simulation model of the QZS system is established. The essential results provide a new idea for semi-active control of the QZS system. The theoretical and simulation analysis results demonstrate that: (a) Increasing the damping of the proposed QZS system can improve its transmission characteristics. The vibration isolation effect is better for the vibration with lower excitation amplitude. Compared with the linear system, the proposed QZS system has a better vibration isolation effect, especially in the low-frequency band. (b) The numerical results show that under the semi-active control strategy, the zero stiffness range has been broadened from a single equilibrium point to a large displacement range, i.e., the non-dimensional displacement is about -0.33 to 0.33. (c) Combined with ADAMS simulation results, under the semi-active control strategy, the system still maintains a good vibration isolation performance for large amplitude vibration, indicating that expanding the zero stiffness–displacement range of the proposed QZS system can improve the vibration isolation ability of the system for large amplitude vibration.

Further research will explore the impact of delay on the control effect of the system and propose a control algorithm for the delay.