Force transmissibility of a two-stage vibration isolation system with quasi-zero stiffness

Abstract

A quasi-zero stiffness (QZS) vibration isolator outperforms other passive control strategies in vibration attenuation especially in a low-frequency band, but it also has an intrinsic limitation of low roll-off rate in the effective frequency range of vibration isolation. To overcome this limitation, a two-stage QZS vibration isolation system (VIS) is proposed, in which the QZS feature is realized by combining a vertical liner spring with two parallel cam–roller–spring mechanisms. Considering a possible disengagement between the cam and the roller under large amplitude vibration, a piecewise nonlinear dynamical model is developed and approximately solved by the averaging method. The analytical solutions for amplitude–frequency relationship and force transmissibility are derived. The results reveal that the two-stage QZS VIS has both advantages of low-frequency vibration isolation and high roll-off rate. It is also found that the second resonance can be eliminated when heavy damping is present in the upper stage, and hence, a broader effective frequency range of isolation can be achieved. High intermediate mass and soft vertical springs in the lower stage are also found to result in high-quality isolation performance.

1 Introduction

As well known, for a single-stage linear vibration isolation system (VIS), there is a trade-off between isolation efficiency and static deflection. An ideal passive isolator should possess large static stiffness to support the weight of a structure whose vibration should be contained and at the same time have low-dynamic stiffness to achieve outstanding vibration isolation effectiveness. A type of isolators, made from a negative stiffness mechanism in parallel with a spring suspension, can achieve a high-static-low-dynamic (HSLD) stiffness characteristic. When the positive stiffness is entirely counteracted by the negative stiffness mechanism at the static equilibrium position, a so-called quasi-zero stiffness (QZS) isolator is produced.

The design and analysis of QZS VIS have been well documented in the monograph by Alabuzhev [1] and in comprehensive reviews by Ibrahim [2] and Liu et al. [3], respectively. Carrella et al. [4, 5] studied the static and dynamic characteristics of a QZS isolator constructed by connecting a vertical spring in parallel with two geometrically symmetric oblique springs, which indicated that a QZS isolator outperformed the corresponding linear one under excitations whose amplitudes are smaller than some critical values. Hao and Cao [6] focused on frequency responses of primary, sub/super-harmonic and chaotic behaviour of a QZS VIS based on the SD oscillator [7] without truncating for QZS isolation mechanism. Le and Ahn [8] studied the displacement transmissibility of a QZS isolator consisting of coil springs, and their results showed that adding a negative stiffness mechanism notably improved the isolation performance. To prevent oblique springs from possible buckling, Lan et al. [9] proposed specific planar springs instead of oblique coil springs for their QZS isolator [4, 8]. Xu et al. [10] constructed prototypes of QZS isolators by connecting a vertical coil spring with four oblique coil springs and then carried out experimental tests. The superior vibration isolation effectiveness of the QZS isolators was confirmed, especially for low-frequency excitations. Platus [11] proposed a compact QZS isolator using a laterally loaded flexural beam as the negative stiffness element to cancel the stiffness of the spring suspension, and thereby producing an ultra-low resonant frequency of the VIS. Liu et al. [12] developed a QZS mechanism from buckled Euler beams, and then, Huang Liu et al. [13] studied the effect of system imperfections on the dynamic response of this kind of vibration isolation system. Shaw et al. [14] built an apparatus of a QZS isolator implemented by connecting linear springs in parallel with a bi-stable composite plate. Sun et al. [15] proposed an isolation platform with a multi-layer scissor-like truss structure to achieve QZS property and further analysed the nonlinear characteristics of stiffness and damping by considering friction and inertia of the links [16]. Robertson et al. [17] presented a QZS isolator by using magnetic levitation. Xu et al. [18] proposed a QZS isolator consisting of horizontal magnetic springs and vertical coil springs. Wu et al [19] also developed a magnetic spring with negative stiffness to counteract the positive stiffness of the system to seek excellent isolation performance. For torsional vibration isolation in a shaft system, Zhou et al. [20] developed an isolator with torsional QZS characteristic. For vibration control of a rotor, Abbasi et al. [21] carried out design optimization of a suspension with HSLD stiffness.

However, the intrinsic limitation of both the linear and nonlinear single-stage VISs is that the force transmissibility decreases at a rate of $1/{\omega ^{2}}$ in the effective frequency range of vibration isolation [22], where $\omega$ is the excitation frequency. To overcome this limitation, an intermediate mass and stiffness are inserted into the single-layer system to construct a two-stage VIS, which has a high transmissibility roll-off rate up to $1/{\omega ^{4}}$ [22]. Nevertheless, there exist two peak values of transmissibility at the two natural frequencies of the linear two-stage system. Thus, such an isolator would most likely give rise to an increase in resonance effect in low-frequency vibration isolation. Like a single-stage VIS, a small stiffness is needed to reduce the natural frequencies, but this results in a large static deflection. Hence, the mechanism with negative stiffness was incorporated into the linear two-stage VIS to achieve excellent vibration isolation performance and at the same time to ensure small static deflection [23].

A two-stage QZS VIS with cam–roller–spring mechanism (CRSM) is proposed in this paper. The QZS properties in both stages are achieved by connecting a vertical spring in parallel with CRSMs, each of which consists of a pair of cam and roller and a horizontal spring. The CRSMs can provide negative stiffness in the vertical direction, which is utilized to counteract the positive stiffness of the vertical spring and hence obtain the QZS property, which was validated by theoretical analysis and experimental test in a previous work by the main authors of this paper [24]. The cam is always in contact with the roller when the displacement amplitude of the mass is lower than a certain value, determined by geometrical dimensions of the roller and the cam, but it disengages from the roller in the case of large displacement. Therefore, the force–displacement relationship can be expressed completely by a piecewise linear–nonlinear function. Further, the piecewise linear–nonlinear dynamic model of the two-stage QZS VIS is established, and then, its approximate solutions are determined by the averaging method [25] to obtain the amplitude–frequency (A-F) relationship. Base on those results, the vibration isolation performance is evaluated analytically in terms of the force transmissibility. It is worth noting that, to analytically achieve fundamental responses of the two-stage QZS VIS, the following approximations are made: (1) the force–displacement expression is approximated by its third-order Taylor’s expansion at the equilibrium position; (2) only the primary resonance (or the first approximation) is considered when we calculate the fundamental responses.

The paper is organized as follows. Section 2 presents the model of the two-stage QZS VIS and static characteristics. In Sect. 3, the piecewise linear–nonlinear dynamic model is established, and the A-F relationship is obtained analytically. The dynamic behaviour and vibration isolation performance are analysed in Sects. 4 and 5, respectively. Finally, Sect. 6 draws some conclusions of this work.

2 Stiffness characteristics of the two-stage QZS VIS

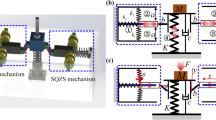
Consider a two-stage VIS with quasi-zero stiffness in Fig. 1. It is developed based on the design concept of QZS isolators in a previous work of the main authors of this paper [24]. For the sake of brevity, the detailed working principle of a QZS isolator is not given in the present paper, which can be found in [24]. $m_1$ is the suspended mass, and $m_2$ is the mass of the intermediate stage. $k_{v1}$ and $k_{v2}$ denote stiffness of the upper vertical spring and the lower one, respectively, and $k_{h1}$ and $k_{h2}$ represent stiffness of the upper horizontal spring and the lower one, respectively. The roller with radius $r_1$ connected with the horizontal spring can not only roll against the cam but also move along the horizontal direction, while the semicircular cam with radius $r_2$ fixed on the mass support is designed to just move along the vertical direction. The cam keeps contact with the roller when the displacement is less than a critical value, but disengagement occurs when the displacement is larger than the critical value. The VIS is initially in the static equilibrium position without external excitations as shown in Fig. 1. At that position, the centres of semicircular cam and roller are required to lie on the same horizontal line. The vertical and horizontal springs in the upper stage are compressed by deflections of $\Delta X_1 ={m_1 g}/{k_{v1} }$ and $\delta _1$, respectively. At the same time, the vertical and horizontal springs in the lower stage are compressed by deflections of $\Delta X_2 ={\left( {m_1 +m_2 } \right) g}/{k_{v2} }$ and $\delta _2$, respectively. Friction between a roller and a cam is very small and thus is neglected.

Fig. 1

Schematic of the two-stage QZS VIS under a harmonic excitation. 1 cam, 2 roller, 3 slider

When the suspended mass (upper stage) and the intermediate mass (lower stage) oscillate vertically about the static equilibrium position, the centres of semicircular cam deviate from their static equilibrium positions. The absolute displacements of the suspended mass and the intermediate stage are designated by $x_1$ and $x_2$, respectively. The upper stage is mounted on the intermediate stage, and the relative displacement of the upper stage is given by $x_1 -x_2$. The cam–roller–spring mechanisms in both stages act as a negative stiffness in the vertical direction, which can counteract the positive stiffness of vertical springs and hence reduce stiffness of the whole VIS. At the equilibrium positions, when the negative stiffness is equal to the positive stiffness of vertical spring, the stiffness for both stages is zero, which is the so-called zero stiffness condition.

To carry out the static analysis of the upper stage, the intermediate mass is assumed to be fixed, and thus, $x_{2}=0$. A quasi-static force $f_1$ is applied at the suspended mass, leading to a vertical displacement $\Delta x_1$ relative to the intermediate mass from the static equilibrium position, as shown in Fig. 2. In this figure, $f_v$ and $f_h$ denote the restoring forces of vertical and horizontal coil springs, respectively, and $f_c$ represents the contact force between the cam and the roller. When $\left| {\Delta x_1 } \right| \le x_d =\sqrt{r_2 \left( {2r_1 +r_2 } \right) }$, the roller always keeps contact with the cam. Nevertheless, when $\left| {\Delta x_1 } \right| >x_d$, the roller disengages from the cam and moves along the vertical wall of the support. Thus, the relationship between the applied force and the displacement can be represented as a piecewise linear–nonlinear function. It is noted that the restoring force of the system is equal to the applied force, but in the opposite direction.

Fig. 2

Schematic diagram of a static analysis of the support and the roller in the upper stage, and three typical relative positions between the cam and the roller: b contact, c critical position, d disengagement

The static force–displacement relationship for the upper stage can be given by

$$\begin{aligned}&f_1 (\Delta x_1 )\nonumber \\&\quad =\left\{ {{\begin{array}{ll} k_{v1} \Delta x_1 -2k_{h1} \Delta x_1\\ \left[ {1+\frac{\delta _1 -\left( {r_1 +r_2 } \right) }{\sqrt{\left( {r_1 +r_2 } \right) ^{2}-\Delta x_1^2 }}} \right] &{} \quad \left| {\Delta x_1} \right| <x_d \\ k_{v1} \Delta x_1 &{}\quad \left| {\Delta x_1 } \right| \ge x_d \\ \end{array} }} \right. \end{aligned}$$

(1)

Using $\Delta \bar{x}_1 ={\Delta x_1 }/{\left( {r_1 +r_2 } \right) }$ and $\bar{f}_1 ={f_1 }/{\left[ {k_{v1} \left( {r_1 +r_2 } \right) } \right] }$, Eq. (1) can be rewritten in the non-dimensional form:

$$\begin{aligned} \bar{f}_1 \left( {\Delta \bar{x}_1 } \right) =\left\{ \begin{array}{ll} \Delta \bar{x}_1 -2\beta _1 \Delta \bar{x}_1\\ \left[ {1+\frac{\bar{\delta }_1 -1}{\sqrt{1-\Delta \bar{x}_1^{2}}}} \right] &{} \quad \left| {\Delta \bar{x}_1 } \right| <\bar{x}_d \\ \Delta \bar{x}_1 &{}\quad \left| {\Delta \bar{x}_1 } \right| \ge \bar{x}_d\\ \end{array} \right. \end{aligned}$$

(2)

where $\bar{\delta }_1 ={\delta _1 }/{\left( {r_1 +r_2 } \right) }$ and $\beta _1 =k_{h1} /k_{v1}$. To design a QZS isolator, the assumption that the mass oscillates about the equilibrium position with small amplitude, i.e. $\left| {\Delta x_1 } \right| <x_d$, is employed. The non-dimensional stiffness of the system can be obtained by differentiating the first expression of Eq. (2) with respect to the non-dimensional displacement and this yields

$$\begin{aligned} \bar{K}_1 =1-2\beta _1 \left[ {1+\frac{\bar{\delta }_1 -1}{\left( {1-\Delta \bar{x}_1^{2}} \right) ^{\frac{3}{2}}}} \right] \end{aligned}$$

(3)

As expected, there is a unique relationship between parameter $\beta _1$ and $\bar{\delta }_1$, resulting in zero stiffness characteristics at the static equilibrium position, which can be obtained by setting $\bar{K}_1 \left( {\Delta \bar{x}_1 =0} \right) =0$, which leads to

$$\begin{aligned} \bar{\delta }_{\mathrm{QZS}1} =\frac{1}{2\beta _1 } \end{aligned}$$

(4)

By substituting Eq. (4) into the first expression of Eq. (2), the force–displacement relationship of the upper stage with QZS characteristic can be given by

$$\begin{aligned} \bar{f}_{\mathrm{QZS}1} \left( {\Delta \bar{x}_1 } \right) {=}\Delta \bar{x}_1 \left[ {1-\frac{1}{\bar{\delta }_{\mathrm{QZS}1} }\left( {1{+}\frac{\bar{\delta }_{\mathrm{QZS}1} {-}1}{\sqrt{1-\Delta \bar{x}_1^2 }}} \right) } \right] \nonumber \\ \end{aligned}$$

(5)

Then, considering the disengagement between the roller and the cam, the complete expression of the restoring force of the upper stage can be given by

$$\begin{aligned}&\bar{f}_{\mathrm{QZS}1} \left( {\Delta \bar{x}_1 } \right) \nonumber \\&\quad =\left\{ \begin{array}{ll} \Delta \bar{x}_1 \left[ {1{-}\frac{1}{\bar{\delta }_{\mathrm{QZS}1} }\left( {1{+}\frac{\bar{\delta }_{\mathrm{QZS}1} {-}1}{\sqrt{1-\Delta \bar{x}_1^2 }}} \right) } \right] &{}\quad \left| {\Delta \bar{x}_1 } \right| <\bar{x}_d \\ \Delta \bar{x}_1 &{}\quad \left| {\Delta \bar{x}_1 } \right| \ge \bar{x}_d \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(6)

where $\bar{x}_d ={\sqrt{r_2 \left( {2r_1 +r_2 } \right) }}/{\left( {r_1 +r_2 } \right) }$. In order to simplify the subsequent dynamic analysis, the first expression of Eq. (6) is approximated by its third-order Taylor’s expansion at the equilibrium position

$$\begin{aligned} \bar{f}_{\mathrm{QZS}1}^a \left( {\bar{x}_1 } \right) =\left\{ \begin{array}{ll} \gamma _1 \Delta \bar{x}_1^3 &{}\quad \left| {\Delta \bar{x}_1 } \right| <\bar{x}_d \\ \Delta \bar{x}_1 &{}\quad \left| {\Delta \bar{x}_1 } \right| \ge \bar{x}_d \\ \end{array} \right. \end{aligned}$$

(7)

where $\gamma _1 =\left( {1-\bar{\delta }_{\mathrm{QZS}1} } \right) /\left( {2\bar{\delta }_{\mathrm{QZS}1} } \right)$.

The exact force–displacement relationship is depicted in Fig. 3, which is compared with the approximate one. It can be seen that the expression of the restoring force is a discontinuous function, i.e. the value of the restoring force undergoes a jump at the critical position $\left| {\Delta \bar{x}_1 } \right| =\bar{x}_d$. As expected, the exact but complex expression of the restoring force can be replaced by the approximate one in the subsequent dynamic analysis, which is verified in Sect. 4.

Fig. 3

Exact force–displacement relationship (hollow cycle) compared with the approximate one (asterisk) when $\bar{\delta }_{\mathrm{QZS}1} =0.9$

By utilizing the same method for static analysis of the upper stage, and on the assumption that there is no relative displacement between the two stages, the complete expression of the restoring force of the lower stage is given by

$$\begin{aligned}&f_2 (\Delta x_2 )\nonumber \\&\quad =\left\{ {{\begin{array}{ll} k_{v2} \Delta x_2 -2k_{h2} \Delta x_2\\ \left[ {1+\frac{\delta _2 -\left( {r_1 +r_2 } \right) }{\sqrt{\left( {r_1 +r_2 } \right) ^{2}-\Delta x_2^2 }}} \right] &{}\quad \left| {\Delta x_2 } \right| <x_d \\ k_{v2} \Delta x_2 &{}\quad \left| {\Delta x_2 } \right| \ge x_d \\ \end{array}}} \right. \end{aligned}$$

(8)

where $f_2 (\Delta x_2 )$ is a static force applied on the intermediate mass $m_2$. Using $\Delta \bar{x}_2 ={\Delta x_2 }/{\left( {r_1 +r_2 } \right) }$ and $\bar{f}_2 ={f_2 }/{\left[ {k_{v1} \left( {r_1 +r_2 } \right) } \right] }$, the above can be rewritten as non-dimensional form

$$\begin{aligned}&\bar{f}_2 \left( {\Delta \bar{x}_2} \right) \nonumber \\&\quad =\left\{ {\begin{array}{ll} \eta \Delta \bar{x}_2 {-}2\beta _2 \Delta \bar{x}_2 \left[ {1{+}\frac{\bar{\delta }_2 -1}{\sqrt{1{-}\Delta \bar{x}_2^{2}}}} \right] &{} \quad \left| {\Delta \bar{x}_2 } \right| <\bar{x}_d \\ \eta \Delta \bar{x}_2 &{}\quad \left| {\Delta \bar{x}_2 } \right| \ge \bar{x}_d \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(9)

where $\bar{\delta }_2 ={\delta _2 }/{\left( {r_1 +r_2 } \right) }$, $\beta _2 =k_{h2} /k_{v1}$, $\eta ={k_{v2} }/{k_{v1} }$. The zero stiffness condition of the lower stage at the static equilibrium position is given by

$$\begin{aligned} \bar{\delta }_{\mathrm{QZS}2} =\frac{\eta }{2\beta _2 } \end{aligned}$$

(10)

By substituting Eq. (10) into the first expression of Eq. (9), the complete force–displacement relationship of the lower stage with QZS characteristic can be given by

$$\begin{aligned}&\bar{f}_{\mathrm{QZS}2} \left( {\Delta \bar{x}_2 } \right) \nonumber \\&\quad =\left\{ {{\begin{array}{ll} \left[ {1-\frac{1}{\bar{\delta }_{\mathrm{QZS}2} }\left( {1+\frac{\bar{\delta }_{\mathrm{QZS}2} -1}{\sqrt{1-\Delta \bar{x}_2^2 }}} \right) } \right] \eta \Delta \bar{x}_2 &{}\quad \left| {\Delta \bar{x}_2 } \right| <\bar{x}_d \\ \eta \Delta \bar{x}_2 &{}\quad \left| {\Delta \bar{x}_2 } \right| \ge \bar{x}_d \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(11)

The first expression of Eq. (11) can be also approximated to a cubic function by using a third-order Taylor series expansion at $\Delta \bar{x}_2 =0$. Hence, the force–displacement relationship in the lower stage can be approximately given by

$$\begin{aligned} \bar{f}_{\mathrm{QZS}2}^a \left( {\Delta \bar{x}_2 } \right) =\left\{ {{\begin{array}{ll} \eta \gamma _2 \Delta \bar{x}_2^3 &{}\quad \left| {\Delta \bar{x}_2 } \right| <\bar{x}_d \\ \eta \Delta \bar{x}_2 &{} \quad \left| {\Delta \bar{x}_2 } \right| \ge \bar{x}_d \\ \end{array} }} \right. \end{aligned}$$

(12)

where $\gamma _2 =\left( {1-\bar{\delta }_{\mathrm{QZS}2} } \right) /\left( {2\bar{\delta }_{\mathrm{QZS}2} } \right)$.

Table 1 Control parameters of the system

3 Approximate analytical solutions for two-stage QZS VIS

Considering the influence of damping, two linear viscous dampers are added in parallel with the vertical springs in both stages, respectively. Note that damping in horizontal springs is neglected. The equations of motion for the two-stage VIS under harmonic force excitation applied on the suspended mass $m_1$ are given by

$$\begin{aligned} \left\{ {{\begin{array}{l} m_1 \ddot{x}_1 +c_1 (\dot{x}_1 -\dot{x}_2 )+f_1 \left( {x_1 -x_2 } \right) =F\cos (\omega t) \\ m_2 \ddot{x}_2 -c_1 (\dot{x}_1 -\dot{x}_2 )\\ +c_2 \dot{x}_2 -f_1 \left( {x_1 -x_2 } \right) +f_2 \left( {x_2 } \right) =0 \\ \end{array} }} \right. \end{aligned}$$

(13)

where F is the excitation amplitude, $c_1$ and $c_2$ are the damping coefficients of the upper stage and lower stage, respectively, and $f_1 \left( {x_1 -x_2 } \right)$ and $f_2 \left( {x_2 } \right)$ are the restoring force defined by Eqs. (1) and (8), respectively. Recall that $x_1$ and $x_2$ denote absolute displacements of the suspended mass and the intermediate mass, respectively. For the two-stage QZS VIS, substituting Eqs. (4) and (10) into Eq. (13), the equations of motion can be written in the non-dimensional form as

$$\begin{aligned} \left\{ {{\begin{array}{l} \bar{x}^{\prime \prime }_1 +2\zeta _1 \left( {\bar{x}^{\prime }_1 -\bar{x}^{\prime }_2} \right) +\bar{f}_{\mathrm{QZS}1} \left( {\bar{x}_1 -\bar{x}_2 } \right) \\ \quad =\bar{F}\cos (\Omega \tau ) \\ \mu \bar{{{x}^{\prime \prime }}}_2 -2\zeta _1 \left( {\bar{{{x}^{\prime }}}_1 -\bar{{{x}^{\prime }}}_2 } \right) +2\mu \zeta _2 \bar{{{x}^{\prime }}}_2 \\ \quad -\bar{f}_{\mathrm{QZS}1} \left( {\bar{x}_1 -\bar{x}_2 } \right) \\ \quad +\bar{f}_{\mathrm{QZS}2} \left( {\bar{x}_2 } \right) =0 \\ \end{array} }} \right. \end{aligned}$$

(14)

where

$$\begin{aligned} \tau= & {} \omega _n t,\;\Omega =\frac{\omega }{\omega _n },\;\omega _n \!=\!\sqrt{\frac{k_{v1} }{m_1 }},\;\bar{F}=\frac{F}{k_{v1} \left( {r_1 +r_2 } \right) },\nonumber \\ \mu= & {} \frac{m_2 }{m_1 },\;\zeta _1 =\frac{c_1 }{2m_1 \omega _n },\;\zeta _2 =\frac{c_2 }{2m_2 \omega _n } \end{aligned}$$

(15)

and $\left( \right) ^{\prime }$ denotes differentiation with respect to $\tau$. In addition, $\bar{f}_{\mathrm{QZS}1} \left( {\bar{x}_1 -\bar{x}_2 } \right)$ and $\bar{f}_{\mathrm{QZS}2} \left( {\bar{x}_2 } \right)$ are defined by Eqs. (6) and (11). As mentioned previously, restoring forces can be simplified to be cubic functions. The dynamic equations, therefore, can be approximately given by

$$\begin{aligned} \left\{ {{\begin{array}{l} \bar{x}^{\prime \prime }_1 +2\zeta _1 \left( {\bar{{{x}^{\prime }}}_1 -\bar{{{x}^{\prime }}}_2 } \right) +\bar{f}_{\mathrm{QZS}1}^a \left( {\bar{x}_1 -\bar{x}_2 } \right) \\ =\bar{F}\cos (\Omega \tau ) \\ \mu \bar{{{x}^{\prime \prime }}}_2 -2\zeta _1 \left( {\bar{{{x}^{\prime }}}_1 -\bar{{{x}^{\prime }}}_2 } \right) +2\mu \zeta _2 \bar{{{x}^{\prime }}}_2 \\ -\bar{f}_{\mathrm{QZS}1}^a \left( {\bar{x}_1 -\bar{x}_2 } \right) \\ \quad +\bar{f}_{\mathrm{QZS}2}^a \left( {\bar{x}_2 } \right) =0 \\ \end{array} }} \right. \end{aligned}$$

(16)

where $\bar{f}_{\mathrm{QZS}1}^a \left( {\bar{x}_1 -\bar{x}_2 } \right)$ and $\bar{f}_{\mathrm{QZS}2}^a \left( {\bar{x}_2 } \right)$ are defined by Eqs. (7) and (12), respectively. Furthermore, the matrix form of Eq. (16) can be given by

$$\begin{aligned} \bar{\mathbf{M}}\bar{\mathbf{x}}^{\prime \prime }+\bar{\mathbf{C}}\bar{\mathbf{x}}^{\prime }+\bar{\mathbf{K}}\bar{\mathbf{x}}=\bar{\mathbf{f}} \end{aligned}$$

(17)

where $\bar{\mathbf{x}}=\left[ {{\begin{array}{c} {\bar{x}_1 } \\ {\bar{x}_2 } \\ \end{array} }} \right]$,    $\bar{\mathbf{M}}=\left[ {{\begin{array}{cc} 1&{} 0 \\ 0&{} \mu \\ \end{array} }} \right]$,    $\bar{\mathbf{C}}=\left[ {{\begin{array}{cc} {2\zeta _1 }&{} {-2\zeta _1 } \\ {-2\zeta _1 }&{} {2\zeta _1 +2\mu \zeta _2 } \\ \end{array} }} \right]$,    $\bar{\mathbf{K}}=\left[ {{\begin{array}{cc} 0&{} 0 \\ 0&{} 0 \\ \end{array} }} \right]$ and $\bar{\mathbf{f}}=\left[ {{\begin{array}{c} {\bar{F}\cos (\Omega \tau )-\bar{f}_{\mathrm{QZS}1}^a \left( {\bar{x}_1 -\bar{x}_2 } \right) } \\ {\bar{f}_{\mathrm{QZS}1}^a \left( {\bar{x}_1 -\bar{x}_2 } \right) -\bar{f}_{\mathrm{QZS}2}^a \left( {\bar{x}_2 } \right) } \\ \end{array} }} \right]$.

To make a better understanding of this two-stage vibration isolation system, the control parameters, which have significant effects on the dynamic response and vibration isolation performance, are summarized in Table 1.

Due to the piecewise nonlinear characteristics, the fundamental response solution of the dynamic equations will be obtained by using the averaging method [25]. For the derivate linear system of the nonlinear system represented by Eq. (17), the steady state responses can be given by

$$\begin{aligned} \begin{array}{l} \bar{\mathbf{x}}\left( \tau \right) =\mathbf{u}\cos \phi +\mathbf{v}\sin \phi \\ \bar{\mathbf{x}}^{\prime }\left( \tau \right) =-\mathbf{u}\Omega \sin \phi +\mathbf{v}\Omega \cos \phi \\ \end{array} \end{aligned}$$

(18)

where $\mathbf{u}=\left[ {u_1,u_2 } \right] ^{\mathbf{T}},\mathbf{v}=\left[ {v_1,v_2 } \right] ^{\mathbf{T}}$ are constant and $\phi =\Omega \tau$. However, for the original nonlinear system, the solution of Eq. (17) can be still expressed in the form of Eq. (18) provided that $\mathbf{u}$ and $\mathbf{v}$ are functions of $\tau$ rather than constants.

Differentiating the first formula of Eq. (18) with respect to the time $\tau$ yields

$$\begin{aligned} \bar{\mathbf{x}}^{\prime }\left( \tau \right)= & {} \mathbf{u}^{\prime }\left( \tau \right) \cos \phi -\mathbf{u}\left( \tau \right) \Omega \sin \phi +\mathbf{v}^{\prime }\left( \tau \right) \sin \phi \nonumber \\&+\,\mathbf{v}\left( \tau \right) \Omega \cos \phi \end{aligned}$$

(19)

Comparing the second formula of Eqs. (18) and (19), it can be found that

$$\begin{aligned} \mathbf{u}^{\prime }\left( \tau \right) \cos \phi +\mathbf{v}^{\prime }\left( \tau \right) \sin \phi =0 \end{aligned}$$

(20)

Differentiating the second formula of Eq. (18), we obtain

$$\begin{aligned} \bar{\mathbf{x}}^{\prime \prime }\left( \tau \right)= & {} -\,\mathbf{u}^{\prime }\left( \tau \right) \Omega \sin \phi -\mathbf{u}\left( \tau \right) \Omega ^{2}\cos \phi \nonumber \\&+\,\mathbf{v}^{\prime }\left( \tau \right) \Omega \cos \phi -\mathbf{v}\left( \tau \right) \Omega ^{2}\sin \phi \end{aligned}$$

(21)

Substituting the expressions about $\bar{\mathbf{x}}^{\prime \prime }\left( \tau \right)$, $\bar{\mathbf{x}}^{\prime }\left( \tau \right)$ and $\bar{\mathbf{x}}\left( \tau \right)$ into Eq. (17), the following equation is obtained

$$\begin{aligned}&\left( \bar{\mathbf{M}}{} \mathbf{v}^{\prime }\Omega -\bar{\mathbf{M}}\mathbf{u}\Omega ^{2}+\bar{\mathbf{C}}{} \mathbf{v}\Omega +\bar{\mathbf{K}}{} \mathbf{u} \right) \cos \phi \nonumber \\&\qquad -\left( {\bar{\mathbf{M}}{} \mathbf{u}^{\prime }}\Omega +\bar{\mathbf{M}}{} \mathbf{v}\Omega ^{2}+\bar{\mathbf{C}}{} \mathbf{u}\Omega -\bar{\mathbf{K}}{} \mathbf{v} \right) \sin \phi =\bar{\mathbf{f}}\nonumber \\ \end{aligned}$$

(22)

Then, the result of adding Eq. (20) multiplied by $\bar{\mathbf{M}}\Omega \cos \phi$ and Eq. (22) multiplied by $-\sin \phi$ is given by

$$\begin{aligned} \bar{\mathbf{M}}{} \mathbf{u}^{\prime }\Omega= & {} \left[ {\left( \bar{\mathbf{K}}-\bar{\mathbf{M}}\Omega ^{2} \right) \mathbf{v-}\Omega \bar{\mathbf{C}}\mathbf{u}} \right] \sin ^{2}\phi \nonumber \\&+\,\left[ \left( {\bar{\mathbf{K}}-\bar{\mathbf{M}}\Omega ^{2}} \right) \mathbf{u}+\Omega \bar{\mathbf{C}}{} \mathbf{v} \right] \sin \phi \cos \phi \nonumber \\&-\,\bar{\mathbf{f}}\sin \phi \end{aligned}$$

(23)

Similarly, the result of adding Eq. (20) multiplied by $\bar{\mathbf{M}}\Omega \sin \phi$ and Eq. (22) multiplied by $\cos \phi$ is given by

$$\begin{aligned} \bar{\mathbf{M}}{v}^{\prime }\Omega= & {} -\left[ {\left( \bar{\mathbf{K}}-\bar{\mathbf{M}}\Omega ^{2} \right) \mathbf{u}+\Omega \bar{\mathbf{C}}\mathbf{v}} \right] \cos ^{2}\phi \nonumber \\&-\left[ {\left( \bar{\mathbf{K}}-\bar{\mathbf{M}}\Omega ^{2} \right) \mathbf{v}-\Omega \bar{\mathbf{C}}{} \mathbf{u}} \right] \sin \phi \cos \phi \nonumber \\&+\,\bar{\mathbf{f}}\cos \phi \end{aligned}$$

(24)

Then, integrating the resultant equations of (23) and (24) with respect to $\tau$ from 0 to $2\pi$ and taking the average value, one obtains

$$\begin{aligned} \left\{ {{\begin{array}{l} \bar{\mathbf{M}}{} \mathbf{u}^{\prime }\Omega =\frac{1}{2}\left( {\bar{\mathbf{K}}-\bar{\mathbf{M}}\Omega ^{2}} \right) \mathbf{v}-\frac{1}{2}\bar{\mathbf{C}}{} \mathbf{u}\Omega +\frac{1}{2}{} \mathbf{q}_1 \\ \bar{\mathbf{M}}{} \mathbf{v}^{\prime }\Omega =-\frac{1}{2}\left( {\bar{\mathbf{K}}-\bar{\mathbf{M}}\Omega ^{2}} \right) \mathbf{u}-\frac{1}{2}\bar{\mathbf{C}}{} \mathbf{v}\Omega +\frac{1}{2}{} \mathbf{q}_2 \\ \end{array} }} \right. \end{aligned}$$

(25)

where $\mathbf{q}_m =\left[ {q_{m1},q_{m2} } \right] ^{\mathbf{T}}\;\left( {m=1,2} \right)$,    $\mathbf{q}_1 =-\frac{1}{\pi }\int _0^{2\pi } {\bar{\mathbf{f}}\sin \phi } \hbox {d}\phi$,    $\mathbf{q}_2 =\frac{1}{\pi }\int _0^{2\pi } {\bar{\mathbf{f}}\cos \phi } \hbox {d}\phi$, and the elements of $\mathbf{q}_m$ are given by

$$\begin{aligned} q_{11}= & {} \left\{ {{\begin{array}{ll} \frac{3}{4}\gamma _1 \left( {v_1 -v_2 } \right) A_{12}^2 &{} \quad A_{12} <\bar{x}_d \\ \\ \frac{\gamma _1 }{\pi }A_{12}^3 \left\{ {\sin \varphi _{F1} \left[ {\frac{3}{8}\left( {2\pi +4\psi _0 } \right) +\sin 2\psi _0 +\frac{1}{8}\sin 4\psi _0 } \right] } \right\} &{} \\ \quad +\frac{A_{12} }{\pi }\left[ {\sin \varphi _{F1} \left( {-2\psi _0 -\sin 2\psi _0 } \right) } \right] &{} \quad A_{12} \ge \bar{x}_d \\ \end{array} }} \right. \end{aligned}$$

(26)

$$\begin{aligned} q_{21}= & {} \left\{ {{\begin{array}{ll} \bar{F}-\frac{3}{4}\gamma _1 \left( {u_1 -u_2 } \right) A_{12}^2 &{} \quad A_{12} <\bar{x}_d \\ \\ \bar{F}-\frac{\gamma _1 }{\pi }A_{12}^3 \left\{ {\cos \varphi _{F1} \left[ {\frac{3}{8}\left( {2\pi +4\psi _0 } \right) +\sin 2\psi _0 +\frac{1}{8}\sin 4\psi _0 } \right] } \right\} &{}\\ \quad -\frac{A_{12} }{\pi }\left[ {\cos \varphi _{F1} \left( {-2\psi _0 -\sin 2\psi _0 } \right) } \right] &{} \quad A_{12} \ge \bar{x}_d \\ \end{array} }} \right. \end{aligned}$$

(27)

$$\begin{aligned} q_{12}= & {} \left\{ {{\begin{array}{ll} \frac{3}{4}\eta \gamma _2 v_2 A_2^2 -q_{11} &{} A_2 <\bar{x}_d \\ \\ \eta \frac{\gamma _2 }{\pi }A_2^3 \left\{ {\sin \varphi _{F2} \left[ {\frac{3}{8}\left( {2\pi +4\Phi _0 } \right) +\sin 2\Phi _0 +\frac{1}{8}\sin 4\Phi _0 } \right] } \right\} &{} \\ \quad +\eta \frac{A_2 }{\pi }\left[ {\sin \varphi _{F2} \left( {-2\Phi _0 -\sin 2\Phi _0 } \right) } \right] -q_{11} &{}\quad A_2 \ge \bar{x}_d \\ \end{array} }} \right. \end{aligned}$$

(28)

$$\begin{aligned} q_{22}= & {} \left\{ {{\begin{array}{ll} -\frac{3}{4}\eta \gamma _2 u_2 A_2^2 -q_{21} +\bar{F}&{}\quad A_2 <\bar{x}_d \\ \\ \quad -\eta \frac{\gamma _2 }{\pi }A_2^3 \left\{ {\cos \varphi _{F2} \left[ {\frac{3}{8}\left( {2\pi +4\Phi _0 } \right) +\sin 2\Phi _0 +\frac{1}{8}\sin 4\Phi _0 } \right] } \right\} \\ -\eta \frac{A_2 }{\pi }\left[ {\cos \varphi _{F2} \left( {-2\Phi _0 -\sin 2\Phi _0 } \right) } \right] -q_{21} +\bar{F} &{}\quad A_2 \ge \bar{x}_d \\ \end{array} }} \right. \end{aligned}$$

(29)

where $A_{12} =\sqrt{\left( {u_1 -u_2 } \right) ^{2}+\left( {v_1 -v_2 } \right) ^{2}}$, $A_2 =\sqrt{u_2^2 +v_2^2 }$, and

$$\begin{aligned}&\sin \varphi _{F1} =\frac{v_1 -v_2 }{\sqrt{\left( {u_1 -u_2 } \right) ^{2}+\left( {v_1 -v_2 } \right) ^{2}}},\nonumber \\&\sin \varphi _{F2} =\frac{v_2 }{\sqrt{u_2^2 +v_2^2 }} \nonumber \\&\cos \psi _0 =\frac{\bar{x}_d }{\sqrt{\left( {u_1 -u_2 } \right) ^{2}+\left( {v_1 -v_2 } \right) ^{2}}},\nonumber \\&\cos \Phi _0 =\frac{\bar{x}_d }{\sqrt{u_2^2 +v_2^2 }} \end{aligned}$$

(30)

Steady-state vibration occurs when

$$\begin{aligned} \mathbf{u}^{\prime }=\mathbf{v}^{\prime }=0 \end{aligned}$$

(31)

Substituting conditions (31) into Eq. (25), a set of coupled nonlinear algebraic equations for $\mathbf{u}$ and $\mathbf{v}$ is obtained

$$\begin{aligned} \left\{ {{\begin{array}{l} {\left( \bar{\mathbf{K}}-\bar{\mathbf{M}}\Omega ^{2} \right) \mathbf{v}-\bar{\mathbf{C}}{} \mathbf{u}\Omega +\mathbf{q}_1 =0} \\ {\left( {\bar{\mathbf{K}}-\bar{\mathbf{M}}\Omega ^{2}} \right) \mathbf{u} +\bar{\mathbf{C}}{} \mathbf{v}\Omega -\mathbf{q}_2 =0} \\ \end{array} }} \right. \end{aligned}$$

(32)

It is reminded that $\mathbf{q}_1 =\left[ {q_{11},q_{12} } \right] ^{\mathbf{T}}$ and $\mathbf{q}_2 =\left[ {q_{21},q_{22}} \right] ^{\mathbf{T}}$. The response amplitudes of the intermediate mass and the suspended mass are denoted as $A_2$ (already given previously under Eq. (29)) and $A_1$ (given below), respectively

$$\begin{aligned} A_1 =\sqrt{u_1^2 +v_1^2 } \end{aligned}$$

(33)

Therefore, the response amplitudes can be found by solving the amplitude–frequency (A-F) Eq. (32), and then, vibration isolation performances can be evaluated by force transmissibility. Note that considering the disengagement between the roller and the cam, the amplitude–frequency functions, i.e. Eq. (32), are usually cannot be solved analytically, and thus, the explicit relationship between the response and control parameters is difficult to be described. Therefore, these equations are solved by means of the least squares method embedded into the function fsolve of the commercial software MATLAB$^{\circledR }$. And then the effects of control parameters on the response are demonstrated by parametric analysis.

4 Dynamics of the two-stage QZS VIS

The displacement A-F responses of the intermediate mass are predicted by analytical method based on the approximate restoring force, i.e. Eq. (16), as shown in Fig. 4, which is compared with numerical solutions, when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\bar{F}=0.5$, $\mu =1.5$, $\eta =2$, $\zeta _1 =\zeta _2 =0.1$, $\bar{x}_d =0.943$. For each selected frequency of excitation, the solution of amplitude is determined by numerically solving Eq. (32), as depicted in Fig. 4, in which the solid lines represent stable solutions, and dashed lines unstable ones. The numerical solutions of Eqs. (14) and (16) are obtained by using a Runge–Kutta method with fourth-order accuracy, which is embedded into the function ode45 of MATLAB$^{\circledR }$ with adaptive variable step size automatically chosen by the algorithm, as also depicted in Fig. 4, where markers ‘o’ and ‘*’ denote numerical solutions of Eqs. (14) and (16), respectively. Finally, it is worth noting that the numerical solutions are obtained by using both upward and downward frequency sweep.

Fig. 4

Displacement A-F responses of the two-stage QZS VIS. Solid lines and dash line denote stable and unstable analytical solutions (AS) of Eq. (16), respectively, and ‘o’ and ‘*’ denote numerical solutions of Eqs. (14) and (16), respectively, when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\bar{F}=0.5$, $\mu =1.5$, $\eta =2$, $\zeta _1 =\zeta _2 =0.1$

It can be observed that there exists a good agreement between analytical solutions and numerical ones, although differences occur at low frequencies due to involvement of more than one frequency component. In other words, in low-frequency range, the response is complicated, such as sub/super-harmonic, quasi-periodic or even chaotic. However, the analytical response is obtained under the approximation that it only has one harmonic component at the frequency of excitation. For example, when $\Omega =0.3$, the time histories and magnitude spectra of displacement responses of the intermediate mass are depicted in Fig. 5a, b, respectively, which demonstrates that there exist several super-harmonic components besides the one at the excitation frequency. In contrast, in high-frequency range, the response mostly has one harmonic component with the frequency identical to that of excitation, as shown in Fig. 5c, d when $\Omega =1.5$, and thus, the analytical response excellently matches with the numerical one.

Fig. 5

Displacement responses of the intermediate mass. a Time histories and b magnitude spectra when $\Omega =0.3$; c time histories and d magnitude spectra when $\Omega =1.5$

Furthermore, the good agreement also can be attributed to that when displacement amplitude $A_2$ is on the lower branch, the amplitude is well below $\bar{x}_d$, and the restoring force can be approximated by a cubic function effectively. Moreover, when the amplitude is on the upper branch, it is above $\bar{x}_d$, and the approximate expression of the restoring force is identical to the exact one. Therefore, the dynamic model with approximate restoring force can be utilized to predict the fundamental responses effectively. Also shown is the solution structure for the immediate mass. Obviously, there are two resonance curves bent rightwards. With the increase in excitation frequency $\Omega$, a jump down could happen depending on which solution branch the system state lies on. The bottom branch represents a weak oscillation state.

4.1 Effects of excitation amplitude

As shown in Fig. 6, the displacement A-F responses are considerably influenced by the excitation amplitude. When the excitation amplitude is small, such as $\bar{F}=0.03$, displacement amplitudes on the resonance branch are close to $\bar{x}_d$. The maximum amplitude rises as the excitation amplitude increases. Moreover, large excitations, such as $\bar{F}=0.1$, will induce resonance at the frequency equal to the first resonance frequency of the corresponding two-stage linear system. Note that the corresponding linear system is constructed by removing the roller–cam–spring mechanisms from the QZS system. In addition, the jump-down frequency also increases with the enlargement of the excitation amplitude, which will undermine the low-frequency vibration isolation performance.

Also shown is that displacement amplitudes at very low-excitation frequencies increase noticeably as the excitation amplitude increases until disengagement between the cam and roller occurs (Fig. 6a, b). However, when the excitation amplitude is large enough to induce disengagement, displacement amplitudes at very low frequencies increase slightly as the excitation amplitude increases (Fig. 6c, d). This can be attributed to the fact that the stiffness of the QZS isolator increases dramatically due to the disengagement, as shown in Fig. 3.

Fig. 6

Influence of exciting amplitude on A-F response, when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\mu =1.5$, $\eta =2$, $\zeta _1 =\zeta _2 =0.01$, where dot dash line represents $A_2 =\bar{x}_d$. a $\bar{F}=0.03$; b $\bar{F}=0.05$; c $\bar{F}=0.1$; and d $\bar{F}=0.125$

4.2 Effects of damping

The effects of damping on A-F response are shown in Fig. 7. It can be seen that the resonance is extremely sensitive to damping. Comparing Fig. 7a with b reveals that high damping in the both stages can lower resonances and even completely eliminate resonances. A comparison between Fig. 7c, d shows that large damping in the upper stage can eliminate the second resonance, and large damping in the lower stage can suppress the first resonance. Therefore, a reasonable amount of damping can effectively decrease the jump-down frequencies and reduce the displacement amplitude, which is beneficial to performance of two-stage QZS VIS.

Fig. 7

Influence of damping on A-F response, when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\mu =1.5$, $\eta =2$, $\bar{F}=0.1$, where dot dash line represents $A_2 =\bar{x}_d$. a $\zeta _1 =0.01$, $\zeta _2 =0.01$; b $\zeta _1 =0.2$, $\zeta _2 =0.2$; c $\zeta _1 =0.01$, $\zeta _2 =0.1$; and d $\zeta _1 =0.1$, $\zeta _2 =0.01$

5 Force transmissibility of the two-stage QZS VIS

Assuming that the response is dominated by the fundamental harmonic response, the force transmitted to the base can be given by

$$\begin{aligned} \bar{f}_T \left( \tau \right) \!=\!\left\{ \!\begin{array}{ll} -2\mu \zeta _2 \Omega A_2 \sin \Omega \tau +\eta \gamma _2 A_2^3 \cos ^{3}\Omega \tau &{} \\ \quad \approx -2\mu \zeta _2 \Omega A_2 \sin \Omega \tau \!+\!\frac{3}{4}\eta \gamma _2 A_2^3 \cos \Omega \tau &{}\quad A_2 \!<\!\bar{x}_d \\ -2\mu \zeta _2 \Omega A_2 \sin \Omega \tau +\eta A_2 \cos \Omega \tau &{}\quad A_2 \ge \bar{x}_d \\ \end{array}\right. \nonumber \\ \end{aligned}$$

(34)

Therefore, the analytical force transmissibility, defined as the ratio of the amplitude of the transmitted force to that of the excitation, can be written in the form of decibel as

$$\begin{aligned} T=\left\{ {{\begin{array}{ll} 20\log _{10} \left( {\sqrt{\frac{{9\eta ^{2}\gamma ^{2}A_2^6 }/{16}+\left( {2\mu \zeta _2 \Omega } \right) ^{2}A_2^2 }{\bar{F}^{2}}}} \right) &{}\quad A_2 <\bar{x}_d \\ 20\log _{10} \left( {\sqrt{\frac{\eta ^{2}A_2^2 +\left( {2\mu \zeta _2 \Omega } \right) ^{2}A_2^2 }{\bar{F}^{2}}}} \right) &{} \quad A_2 \ge \bar{x}_d \\ \end{array} }} \right. \end{aligned}$$

(35)

It should be noted that both the expressions of transmitted force and force transmissibility are discontinuous, due to the discontinuousness of the restoring force at $\left| {\bar{x}_2 } \right| =\bar{x}_d$, as defined in Sect. 2.

The analytical force transmissibility will be verified by the numerical solutions. Under excitations with different amplitudes, the system will experience complicated dynamical behaviour, such as sub/super-harmonic motion, quasi-periodic motion and chaotic motion. Generally, for those types of motions, the numerical force transmissibility cannot be explicitly represented by the ratio of the amplitude of the transmitted force to that of the excitation; however, it can be evaluated in the statistical form, which is defined as the ratio of the root mean square (RMS) of response to that of the excitation [26, 27], i.e.

$$\begin{aligned} {T}^{\prime }=20\log _{10} \left( {\frac{\hbox {RMS}\left[ {\bar{f}_T \left( {\tau _i } \right) } \right] }{\hbox {RMS}\left[ {\bar{f}\left( {\tau _i } \right) } \right] }} \right) \end{aligned}$$

(36)

where $\bar{f}_T \left( {\tau _i } \right)$ and $\bar{f}\left( {\tau _i } \right)$ are time histories of the transmitted force and excitation, respectively, which can be given by

$$\begin{aligned} \bar{f}_T \left( {\tau _i } \right)= & {} 2\mu \zeta _2 \bar{x}^{\prime }_2 \left( {\tau _i } \right) +\bar{f}_{\mathrm{QZS}2} \left[ {\bar{x}_2 \left( {\tau _i } \right) } \right] \nonumber \\ \bar{f}\left( {\tau _i } \right)= & {} \bar{F}\cos (\Omega \tau _i ) \end{aligned}$$

(37)

where $\bar{x}_2 \left( {\tau _i } \right)$ and $\bar{x}^{\prime }_2 \left( {\tau _i } \right)$ are displacement and velocity time histories of the intermediate mass, respectively, obtained by numerically solving Eq. (17).

Figure 8 shows the analytical and numerical force transmissibility of the two-stage QZS VIS, compared with the corresponding two-stage linear system. The analytical results of Eq. (35) are obtained by using approximate expressions of the restoring force, but numerical solutions of Eq. (36) by using exact ones. It is observed that there is a good agreement between the analytical results and numerical ones, especially on the lower branch. The discontinuity of analytical results can be attributed to the fact that the expression of the force transmissibility, i.e. Eq. (34), is discontinuous.

The two-stage QZS VIS is compared with the corresponding linear system to evaluate its performance. It can be seen from Fig. 8 that the first jump-down frequency is almost equal to the first natural frequency of the linear system $(\Omega =0.737)$. The second peak on the transmissibility curve does not occur at the frequency greater than the second natural frequency of the linear system. The effective frequency range of vibration isolation is broadened and force transmissibility is reduced significantly at high frequencies compared with the linear system. Furthermore, the transmissibility decreases notably after the second jump-down frequency. Therefore, the two-stage QZS VIS outperforms its linear counterpart, and it has advantages both in low-frequency isolation and high roll-off rate.

Fig. 8

Force transmissibility of the two-stage QZS VIS. Solid line and dashed line denote stable and unstable analytical results, respectively, and solid dots denote numerical results, when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\mu =1.5$, $\eta =2$, $\bar{F}=0.1$, and dot-dashed line represents the linear VIS

5.1 Effects of mass ratio on force transmissibility

Mass ratio of the intermediate mass $m_2$ to the suspended mass $m_1$ is one of the most concerns in parameter design of the two-stage VIS [22]. Figure 9 shows the influence of the mass ratio $\mu$ on the force transmissibility. It can be seen that increasing the mass ratio has two effects. The transmissibility of the first peak reduces, whereas that of the second peak increases. Both the frequencies of the first peak and the second one are reduced to lower values. Therefore, increasing the mass ratio can reasonably improve vibration isolation performance, which implies that the intermediate mass should be sufficiently large for the two-stage QZS VIS.

Fig. 9

Effect of the mass ratio $\mu$ on the transmissibility of the two-stage QZS isolator when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\eta =2$, $\zeta _1 =\zeta _2 =0.01$, $\bar{F}=0.1$. Solid line $\mu =1$; dashed line $\mu =1.5$; and dashed-dotted line $\mu =2.5$

Fig. 10

Effect of the stiffness ratio $\eta$ on the transmissibility of the two-stage QZS isolator when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\mu =1.5$, $\zeta _1 =\zeta _2 =0.01$, $\bar{F}=0.1$. Solid line $\eta =3$; dashed line $\eta =2$; and dashed-dotted line $\eta =1$

Fig. 11

Influence of exciting amplitude on the transmissibility, when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\mu =1.5$, $\eta =2$, $\zeta _1 =\zeta _2 =0.01$. a $\bar{F}=0.03$; b $\bar{F}=0.05$; c $\bar{F}=0.1$; and d $\bar{F}=0.125$. Solid line QZS VIS; dashed-dotted line linear VIS

5.2 Effects of stiffness ratio of the vertical springs

The effects of stiffness ratio $\eta ={k_{v2} }/{k_{v1} }$ on force transmissibility are shown in Fig. 10. It can be seen that the first jump-down frequency and the first peak transmissibility increase as the stiffness ratio $\eta$ increases. In addition, the transmissibility on the second resonance branch also increases as the stiffness ratio $\eta$ increases, which is detrimental to vibration isolation performance. Therefore, reducing the stiffness ratio $\eta$ can shift the beginning vibration isolation frequency to a lower one, which suggests that a softer vertical spring should be used to support the lower stage.

Fig. 12

Influence of damping on the transmissibility, when $\bar{\delta }_{\mathrm{QZS}1} =\bar{\delta }_{\mathrm{QZS}2} =0.9$, $\mu =1.5$, $\eta =2$, $\bar{F}=0.1$. a $\zeta _1 =0.01$, $\zeta _2 =0.01$; b $\zeta _1 =0.2$, $\zeta _2 =0.2$; c $\zeta _1 =0.01$, $\zeta _2 =0.1$; and d $\zeta _1 =0.1$, $\zeta _2 =0.01$. Solid line QZS VIS; dashed-dotted line linear VIS

5.3 Effects of excitation amplitude

The effects of excitation amplitude on the force transmissibility are illustrated in Fig. 11. It is found that the second peak on the transmissibility curve does not occur at the frequency greater than the second natural frequency of the linear system no matter how large the excitation amplitude is. The first resonance occurs at the first natural frequency $(\Omega =0.737)$ of the linear system, when the excitation amplitude is large. The first jump-down frequency increases as the excitation amplitude increases, but it does not exceed 0.737. At low frequencies, the upper branch of force transmissibility curve rises as the excitation amplitude decreases, but in the effective frequency range of vibration isolation the force transmissibility is hardly influenced by the excitation amplitude.

5.4 Effects of damping

The impact of damping on the force transmissibility is illustrated in Fig. 12. The transmissibility of the system with light damping in both stages, as shown in Fig. 12a, is compared with the system processing heavy damping in both stages, as illustrated in Fig. 12b. It can be observed that heavy damping in both stages can reduce the first jump-down frequency, suppress resonance, lower force transmissibility peak and broaden effective frequency range. However, heavy damping leads to an increase in the force transmissibility at high frequencies and hence degrades the vibration isolation performance. Therefore, as a trade-off, a reasonable level of damping is required to suppress resonance and simultaneously ensure high vibration isolation effectiveness.

By comparing Fig. 12c with d, it can be seen that heavy damping had better be set up on the upper stage rather than on the lower stage, because the second resonance can be completely eliminated when heavier damping is located on the upper stage (Fig. 12d). This finding can guide the design on the allocation of damping in the two-stage QZS VIS.

6 Conclusions

The use of quasi-zero stiffness in a two-stage vibration isolation system to improve its performance was studied. The QZS property was achieved by developing a cam–roller–spring mechanism with negative stiffness to counteract the positive stiffness of a vertical coil spring. Considering possible disengagement between the cam and roller at large amplitudes, a piecewise nonlinear dynamic model of the VIS was established. The equation of motion was approximately solved by using the averaging method, and then, the resultant coupled nonlinear algebraic equations of the periodic steady-state vibration were solved. The A-F curve was plotted which severely bends to the right due to the strong nonlinearity. The force transmissibility was analysed to evaluate the performance of vibration isolation. The effects on force transmissibility of mass ratio, vertical spring stiffness ratio, excitation amplitude and damping were discussed.

It was found that mass ratio and stiffness ratio influence vibration isolation mainly at low frequencies. Force transmissibility can be reduced by increasing the mass ratio and decreasing the vertical spring stiffness ratio, which implies that the intermediate mass should be large enough and a softer vertical spring should be located on the lower stage. Increasing damping in both stages shortens the resonance branch and even eliminates it, but degrades isolation performance at high frequencies. Therefore, as a trade-off, a reasonable level of damping is required to suppress resonance and simultaneously ensure high vibration isolation efficiency. High damping on the upper stage is preferred to eliminate the second resonance and hence to broaden the effective frequency range of vibration isolation. Furthermore, it is a significant observation that no matter how large the excitation amplitude is, the resonance frequencies will never exceed the natural frequencies of the corresponding linear system, which outperforms other QZS mechanisms.