1 Introduction

Nonlinear waves are universal in many fields such as fluids, plasma, optics, finance. A number of nonlinear partial differential equations have been established to model various nonlinear waves. Many effective methods have been established to explore exact solutions to describe different waves, for instance, the inverse scattering transform [1], the symmetry approaches [2], the Hirota bilinear method [3] and various feasible transformations [4, 5] including the Bäcklund transformation and the Darboux transformation. It is noticed that localized excitations in (1 + 1)- and (2 + 1)-dimensions have been discussed a lot, ranging from a line-soliton, solitoff, kink and anti-kink to an exponentially decaying dromion, algebraically decaying lump, time-periodic breather, spatially periodic breather, rogue wave and even a multi-valued folded solitary wave. By contrast, nonlinear localized waves in (3 + 1)-dimensions are relatively less considered.

The method of variable separation is known as one of the fundamental and effective methods for solving linear partial differential equations. Many efforts have been made to develop nonlinear versions of the linear variable separation method to find variable separation solutions for nonlinear partial differential equations. For instance, from the viewpoint of geometry, it was proposed that a solution of an evolution equation is separable if and only if it is a curve in the \((k+1)\)-parameter space of characteristic fields [6]. The generalized conditional symmetry approach was used to study the separation of variables of quasilinear diffusion equations with nonlinear source, and a complete list of canonical forms was obtained for such equations admitting the functionally separable solutions [7]. By means of the symmetry constraints, a systematic variable separation approach has been established [8], although the independent variables of a reduced field have not been totally separated. As it was applicable only for integrable models with Lax pairs, the method was later extended to any models no matter whether they possess Lax pairs or not [9]. In order to totally separate the independent variables, the multilinear variable separation approach (MLVSA) and two types of generalizations were first proposed to deal with (2 + 1)-dimensional integrable systems [10, 11]. It is shown effective to obtain variable separation solutions of nonlinear systems both integrable and not. However, no arbitrary function with fewer variables exists for nonintegrable systems, and thus it is impossible to describe abundant localized waves. Therefore, it is more meaningful to apply the MLVSA to integrable systems in the sense that they have Lax pairs, infinitely many symmetries and conservation laws and so on. The most essential starting point for the MLVSA is that it must have an auto-Bäcklund transformation with an arbitrary nonconstant seed solution. Lately, we have applied the MLVSA to a (3 + 1)-dimensional Boiti–Leon–Manna–Pempinelli equation, yielding a new kind of variable separation solution with an arbitrary seed solution evolved in the potential fields, and thus, different from the previous results, the seed solution also plays a role in the wave interactions with different background waves for the potential filed [12].

Recently, soliton molecules have attracted much attention for their continuous discoveries in nonlinear optical experiments [13,14,15,16]. As a special type of nonlinear excitations, soliton molecules have also been demonstrated in other physical systems, such as in dipolar Bose–Einstein condensates and so on [17]. Soliton molecules come along from some fundamental solitons acting as “atoms” [18]. It has been mathematically revealed that a soliton molecule can be generated from an exact two-soliton solution [19]. A new mechanism, the velocity resonant, has been proposed to find soliton molecules [20], and then many nonlinear systems have been found to be able to excite soliton molecules [21,22,23,24,25,26,27]. Hinted by this scheme, we found interesting dromion molecules from a dromion lattice based on the multilinear variable separation solution [12].

In this paper, we focus on finding new variable separation solutions and novel nonlinear localized excitations, particularly soliton molecules, for the following (3 + 1)-dimensional nonlinear evolution equation

$$\begin{aligned}&3u_{xz}-2u_{yt}-u_{xxxy}+2(uu_y)_x\nonumber \\&\quad +\,2(u_{x}\partial ^{-1}_xu_y)_x=0, \end{aligned}$$
(1)

with \(\partial _x^{-1}\) denoting the integration with respect to the variable x, which was first introduced to illustrate that it can be decomposed into three (1 + 1)-dimensional AKNS equations with the help of a direct way and the nonlinearization of a Lax pair [28]. Simultaneously, algebraic-geometrical solutions expressed explicitly in terms of the Riemann theta functions were obtained. Later on, many solutions of Eq. (1) have been obtained including the N-soliton solutions, complexions, positons, negatons, rogue waves, breathers and so on [29,30,31,32,33,34,35,36,37,38]. Particularly, based on the decomposition approach, the antidark soliton solution on a finite background was constructed for Eq. (1) via the Darboux transformation together with the limit technique; then, under the velocity resonant mechanism, the antidark soliton molecules were found [23].

The paper is organized as follows. In Sect. 2, a new variable separation solution with two arbitrary variable separated functions is obtained for Eq. (1), from which various nonlinear excitations and wave interactions on different wave backgrounds can be explored. In Sect. 3, three different restrictions are imposed on the arbitrary variable separated functions, and thus three types of nonlinear excitations, namely, the dromions, lumps and ring solitons, are obtained. In particular, when a pair of dromions, lumps or ring solitons have the same velocity, then they can be resonant to soliton molecules. Elastic interactions between a dromion and a dromion molecule, between a lump and a lump molecule, between two lump molecules, between a ring soliton and a ring soliton molecule are graphically illustrated, respectively. The last section is devoted to discussion and summary.

2 Variable separation solutions

In order to apply the multilinear variable separation approach, we first introduce the following auto-Bäcklund transformation

$$\begin{aligned} u=-3(\ln f)_{xx}+u_0+u_1, \end{aligned}$$
(2)

where \(u_0\equiv u_0(z,t), u_1 \equiv u_1(x,t)\) are arbitrary functions of the indicated arguments. It is straightforward to verify that \(u=u_0+u_1\) satisfies Eq. (1), and u determined by Eq. (2) is also a solution of (1) if f satisfies the bilinear equation

$$\begin{aligned}&(6D_{y}D_{t}-9D_{z}D_{x}+3D_x^{3}D_y-6(u_0+u_1)D_xD_y \nonumber \\&\quad + 2h_1x+2h_0)f \cdot f=0, \end{aligned}$$
(3)

obtained by substituting (2) into (1), where \(h_0\) and \(h_1\) are two arbitrary functions of (y, z, t), and \(D_i (i=x, y, z, t)\) is the well-known Hirota’s bilinear operator defined as [4]

$$\begin{aligned}&D_{x}^{m}D_{y}^{n}D_{z}^{r}D_{t}^{s} f \cdot f \\&\quad =(\partial _x-\partial _{x'})^{m}(\partial _y-\partial _{y'})^{n} (\partial _z-\partial _{z'})^{r}(\partial _t-\partial _{t'})^{s}\\&\qquad f(x, y, z, t)\cdot f(x', y', z', t')|_{x'=x, y'=y, z'=z, t'=t}. \end{aligned}$$

It is noted that some results from Eq. (3) with \(u_0=u_1=h_0=h_1=0\) have been obtained in recent years. For instance, a bilinear Bäcklund transformation was derived, from which soliton and stationary rational solutions for Eq. (1) were obtained [34]. The classical Hirota’s bilinear method requiring f be the linear composition of some exponential functions of the traveling wave variables \(\xi _{i}=k_{i1}x+k_{i2}y+k_{i3} t+k_{i4}\) with constants \(k_{ij}~(j=1,2,3,4)\) was used to get N-soliton solutions [33]. Taking some proper constraints on these constants \(k_{ij}\), breathers and rogue waves were produced accordingly [35]. Besides, more assumptions can be made on f to produce different wave excitations and interactions, for example, taking f as some polynomials of the variables x, y, z, t leads to rational and rogue wave solutions [36], and if some exponential functions were simultaneously introduced, then different interactions between lumps and other solitons were obtained [37]. Combined with the KP hierarchy reduction method, semi-rational solutions were derived to describe fission and fusion collision of high-order lumps and line solitons [38] .

Here, we aim to find new nonlinear variable separation solutions of nonlinear system (1) by assuming the expansion function f is fixed as

$$\begin{aligned} f=a_0+a_{1}r+a_{2}s+a_{3}rs, \end{aligned}$$
(4)

where \(a_0, a_1, a_2\) and \(a_3\) are constants, and \(r\equiv r(x,t)\) and \(s\equiv s(y,z)\) are functions of the indicated variables. The substitution of (4) into (3) leads to

$$\begin{aligned}&(a_0a_3-a_1a_2)(s_yr_{xxx}\nonumber \\&+2s_yr_t+3s_zr_x-2(u_0+u_1)s_y)=0, \end{aligned}$$
(5)

with \(h_0\) and \(h_1\) fixed as zero. It is not difficult to find that if requiring \(a_0a_3-a_1a_2\ne 0\) and \(u_0=h(t)-3g'(z)/2\) with two arbitrary functions g and h of the indicated arguments, Eq. (5) can be separated into two variable separated equations

$$\begin{aligned}&2r_t+r_{xxx}-2(u_1+h(t))r_x=C, \end{aligned}$$
(6)
$$\begin{aligned}&s_z-g'(z)s_y=C, \end{aligned}$$
(7)

where the separation constant C can be set zero without the loss of generality. Solving Eqs. (6) and (7) gives

$$\begin{aligned} u_{1}=\frac{2r_t+r_{xxx}}{2r_x}-h(t),\qquad s=s(y+g(z)). \end{aligned}$$
(8)

Consequently, we obtain a new multilinear variable separation solution (MLVSS) of (1) as

$$\begin{aligned} u= & {} \frac{2r_t+r_{xxx}}{2r_x}-\frac{3}{2}g'(z)-\frac{3(a_1+a_3s)r_{xx}}{a_0+a_1r+a_2s+a_3rs} \nonumber \\&+\frac{3(a_1+a_3s)^2r_x^2}{(a_0+a_1r+a_2s+a_3rs)^2}, \end{aligned}$$
(9)

where g is an arbitrary function of z, r is an arbitrary function of (x, t), and s is an arbitrary function of \((y+g)\).

It is remarkable that the arbitrary functions in MLVSS (9) can be utilized to construct abundant nonlinear excitations. It is worthy of stressing that the first two terms in (9) are responsible for different background waves, and thus one might be able to observe the interplay between the background waves and various excited waves determined by the last two terms in (9). Furthermore, it is emphasized that for this particular model, the potential of the field U,

$$\begin{aligned} U\equiv u_y= & {} \frac{ 6(a_0 a_3-a_1 a_2) (a_3 s+a_1) s_yr^2_x}{(a_3 r s+a_1 r+a_2 s+a_0)^3} \nonumber \\&-\frac{3 (a_0 a_3-a_1 a_2) s_yr_{xx}}{(a_3 r s+a_1 r+a_2 s+a_0)^2}, \end{aligned}$$
(10)

cannot be expressed in the universal form applicable for a number of integrable systems [10,11,12].

3 Nonlinear excitations and their interactions

It is well known that dromions, lumps, compactons, foldons and many other localized excitations can be explained by a MLVSS [10, 11]. In fact, more various wave interactions can be explored for the sake of the arbitrary functions in MLVSS (9) (or Eq. 10). In this section, we are fully concentrated on constructing soliton molecules made of different “atoms” including dromions, lumps and ring solitons, and then investigating their interactions.

3.1 Dromions, dromion molecules and their interactions

To look for dromion excitations for the potential field \(U(\equiv u_y)\) given by (10), the variable separated functions r and s are restricted as

$$\begin{aligned} r= & {} c+\sum _{i=1}^{N}\exp [\omega _i-(k_ix+v_i t+b_i)^2], \quad \nonumber \\ s= & {} C+\exp [\Omega -(K_1 y+{{\,\mathrm{sech}\,}}(L_1 z))^2], \end{aligned}$$
(11)

where \(k_i,~v_i,~b_i,~\omega _i,~K_1,~L_1,~c,~C\) and \(\Omega \) are arbitrary constants. In order to make it easier to graphically display diverse wave interactions, we take \(z=5\). In this reduced space-time \(\{x, y, t\}\), the potential quantity U determined by (10) with (11) can describe diverse dromion behaviors, and the arbitrary constants \(v_i\) and \(\omega _i\) determine the velocities and shapes of the dromions, respectively. Below gives three representative cases about the basic dromion–dromion interaction, new dromion molecules and a dromion–dromion molecule interaction.

Case 1. Dromion–dromion interaction. Two dromions can be obtained by taking \(a_0=N=\omega _2=2,~c=\omega _1=v_1=-v_2=3, ~a_1=a_2=K_1=L_1=k_1=k_2=1, ~a_{3}= C=\Omega =0\) and \(b_1=-b_2=5\). They travel in the opposite directions along the x-axis, and fully collide at time \(t=-5/3\), determined from the general formula for the interaction time

$$\begin{aligned} t= \frac{b_1 k_1 - b_2 k_2}{k_1 v_2-v_1 k_2}. \end{aligned}$$
(12)

Case 2. Dromion molecules. It is known that two dromions can be resonant to form a dromion molecule when their velocities are of the same, inherited from the velocity resonant mechanism. If the velocities of two dromions in the above case are replaced by \(v_1=v_2=3\), then they are bounded to be a dromion molecule, moving steadily along the x-axis, as displayed in Fig. 1. It is clearly observed that the dromion molecule is asymmetric, due to different three-dimensional structures of two dromion “atoms.” Actually, the shapes of dromions are determined by the parameters \(\omega _i\) and their center distances are calculated by \( \vert b_1-b_2 \vert \) along the x-axis. Consequently, taking \(\omega _1=\omega _2\) results in the generation of a symmetric dromion molecule.

Fig. 1
figure 1

An asymmetrical dromion molecule: a 3D plot at time \(t=0\); b density plot at time \(t=0\); and c time evolution from \(t=-1\) to \(t=1\)

Full size image

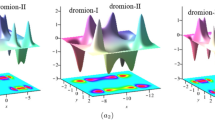
Case 3. Dromion–dromion molecule interactions. It is noted that various soliton molecules consisting of different numbers of either symmetric or asymmetric dromions can be produced by utilizing Eq. (11) for that it acts as a building block of N dromions with different \(b_i\) and \(v_i\). Therefore, it is feasible to investigate nonlinear interactions between dromions and dromion molecules. Here, we consider the simplest example with \( N=3\) for a dromion and a symmetric dromion molecule. The related parameters are taken as \(c=\omega _3=v_1=-v_2=-v_3 = b_3= 3\) \(K_1=L_1=k_1=k_2=k_3=1\), \(\omega _1=\omega _2=2\), \(C=\Omega =0\) and \(b_1=-b_2=5\). In this particular setting, an independent dromion interacts with the dromion “atoms” of a symmetric dromion molecule one by one at time \(t_1=-5/3\) and \(t_2=-1/3\), which is calculated from general interaction time (12) and

$$\begin{aligned} t_2= \frac{b_1 k_1 - b_3 k_3}{k_1 v_3-v_1 k_3}, \end{aligned}$$
(13)

respectively. It is also graphically demonstrated in Fig. 2 that after the collision, the dromion and the dromion molecule remain their shapes and velocities; consequently, they have experienced a completely elastic interaction.

Fig. 2
figure 2

An elastic interaction between a dromion and a symmetrical dromion molecule at times a \(t=-4\), b \(t=-1\) and c \(t=2\), respectively

Full size image

3.2 Lumps, lump molecules and their interactions

Now we suppose r and s in the form of

$$\begin{aligned} r= & {} c+\sum _{i=1}^{N} \frac{h_i}{\omega _i-(k_ix+v_i t+b_i)^2}, \quad \nonumber \\ s= & {} C+\sum _{i=1}^{M} \frac{H_i}{\Omega _i-(K_i y+V_i z+B_i)^2}, \end{aligned}$$
(14)

where \(c,~C,~k_i,~v_i,~b_i,~h_i,~\omega _i,~K_i,~V_i,~B_i,~H_i \) and \(\Omega _i\) are arbitrary constants to observe nonlinear wave patterns of lumps and lump molecules. Under this assumption, the potential field U given by Eq. (10) with (14) describes an \( N \times M\) lump lattice, and then by adjusting the velocities and shapes of its lumps, lump molecules with different numbers of symmetric and asymmetric lumps could be generated. Hereafter, \(z=a_3=2\) and \(a_0=a_1=a_2=1\) are fixed to display lump molecule–lump molecule and lump–lump molecule interactions.

Case 1. Lump molecules. In the case of \(N=M=2\), a lump lattice is constructed by \(2 \times 2\) lumps, namely, four lumps are situated in two rows and two columns. Take the parameters as \(c=-v_1=k_1=k_2=h_1=K_1=K_2=V_1=V_2=1\), \(h_2=v_2=3\), \(b_1=-b_2=\omega _1=\omega _2= C=H_1=H_2=5\), \(-B_1=B_2=8\) and \(\Omega _1=\Omega _2=1/5\). Hence, two lumps in each column are identical and bounded to form a symmetric lump molecule. The center distance between two lump “atoms” is 16 given by \(\vert B_1 - B_2 \vert \) along the y axis. These two symmetric lump molecules move along the x axis, fully interact each other at time \(t=2.5\) determined by Eq. (12), and the interaction is shown completely elastic. If the values of \(h_1\) and \(\Omega _1\) are replaced by \(h_1=3\) and \(\Omega _1=1\), then two asymmetric lump molecules come in being, move in the opposite directions along the x-axis and also interact fully elastically at \(t=2.5\), as exhibited in Fig. 3.

Fig. 3
figure 3

An elastic interaction between two asymmetrical lump molecules at time a \(t=-2\), b \(t=2.5\) and c \(t=7\), respectively

Full size image

Case 2. Lump–lump molecule interactions. Here a simplest interaction is considered between a lump and a symmetric lump molecule by setting \(N=3\) and \(M=1\). More complicated interactions can be explored by introducing more lumps and lump molecules. Figure 4 displays an elastic interaction between a lump and a symmetric lump molecule under the parameters \(c=h_1=\omega _3=v_2=v_3=b_3=3\), \(K_1=V_1=k_1=k_2=k_3=h_2=h_3=-v_1=1\), \(C=\omega _1=\omega _2=\omega _3=H_1=b_1=-b_2=5\), \(B_1=-8\) and \(\Omega =1/5\). It is seen that the lump interacts with two lump “atoms” one by one at time \(t=2.5\) and \(t=0.5\) decided by Eqs. (12) and (13), respectively.

Fig. 4
figure 4

An elastic interaction between a lump and a symmetrical lump molecule at time a \(t=-3\), b \(t=2\) and c \(t=7\), respectively

Full size image

3.3 Ring solitons, ring soliton molecules and their interactions

In some special situations, one can have a typical wave solution with its value nonzero only on a closed curve and decaying exponentially away from it, which is named a ring soliton and exists in many (2 + 1)-dimensional integrable systems [10]. Here it is discovered that similar ring solitons exist in the reduced (3 + 1)-dimensional setting and ring soliton molecules can also be excited. The variable separated functions r and s in the following form

$$\begin{aligned} r= & {} c+\sum _{i=1}^{N}\exp [\omega _i-(k_i x+ v_i t+b_i)^2], \quad \nonumber \\ s= & {} C+\sum _{i=1}^{M}\cosh [\Omega _i+(K_i y+ V_i z+B_i)^2], \end{aligned}$$
(15)

with arbitrary constants c, C, \(k_i\), \(v_i\), \(b_i\), \(h_i\), \(\omega _i\), \(K_i\), \(V_i\), \(B_i\), \(H_i\) and \(\Omega _i\) can be used to build up ring solitons for the potential field U with \(a_0=2\), \(a_3=0\), \(a_1=a_2=1\) in the reduced space-time \(\{x,y,t\}\) by setting \(z=0\). The values of \(v_i/k_i\) and \(V_i/K_i\) give the velocities, \(v_i, V_i, b_i\) and \(B_i\) decide the center, \(\omega _i\) and \(\Omega _i\) determine the radius (and thus the amplitudes) of the ring solitons, respectively. Below demonstrates a ring soliton, and the interaction between a ring soliton and a ring soliton molecule.

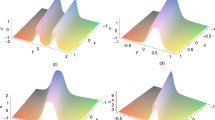
Case 1. Ring solitons. Let us take \(N=M=1\) to show a ring soliton in detail with the parameters fixed as \(c=C=-K_1=k_1=V_1=-v_1=\Omega _1=1\), \(\omega _1=10\) and \(B_1=b_1=5\). In this case, a novel crossed saddle-type ring soliton is constructed as shown in Fig. 5a. It is not difficult to verify that the potential field U decays exponentially away from the circle \((x+5)^2+(y+5)^2=9\), namely, the ring soliton has its center at \((-5,-5)\) and a radius 3 at time \(t=0\), as displayed in Fig. 5b. The wave pattern for the corresponding original field u is exhibited in Fig. 5c, which illustrates that u captures a salient feature of a ring soliton situated on a parabolic like wave background, as a result of the interplay between the excited wave and the wave background.

Fig. 5
figure 5

A novel ring-type soliton at time \(t=0\), a the potential field U, b density plot of U and c the original field u

Full size image

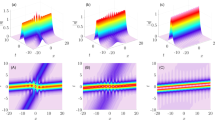
Case 2. Ring soliton–ring soliton molecule interactions. Under the parameters \(N=3\), \(M=c=C=k_1=k_2=k_3=K_1=V_1=-v_1=-v_2=v_3=\Omega _1=1\), \(\omega _1=\omega _2=10\), \(\omega _3=15\) and \(b_1=-b_2=-b_3=B_1=5\), the potential field U describes an interaction between a ring soliton and a symmetric ring soliton molecule, as shown in Fig. 6. The symmetric ring soliton molecule is constituted by two small ring solitons in the same shape and velocity. The two “atoms” have the same radius 3 and their centers are located at \((t - 5,-5)\) and \((t +5,-5)\), respectively, while the big ring soliton has the radius \(\sqrt{14}\) and its center at \((-t +5,-5)\). It is observed that the interaction is elastic as they all restore their structures and velocities after the big ring soliton interacts with two “atom” ring solitons one by one at time \(t=0\) and 5, respectively.

Fig. 6
figure 6

An elastic interaction between a symmetrical ring soliton molecule and a ring soliton at time a \(t=-6\), b \(t=3\) and c \(t=12\), respectively

Full size image

If \(\omega _2\) is set as 15 instead of 10, then one obtains an asymmetric ring soliton molecule for the potential field U, which interacts elastically with the ring soliton in Fig. 7a–c. The related nonlinear excitations for the original field u are plotted in Fig. 7d–f accordingly.

Fig. 7
figure 7

An elastic interaction between an asymmetric ring soliton molecule and a ring soliton at time a, d \( t=-8\), b, e \(t=2\) and c, f \(t=12\) for the potential field U (upper) and the original field u (lower), respectively

Full size image

4 Summary and discussion

In summary, with the help of the multi-linear variable separation approach, we have obtained a new variable separation solution for a (3 + 1)-dimensional nonlinear evolution equation. Three types of selections have been made for the arbitrary variable separated functions to describe different excitations including the N-dromion solution, \(N\times M\) lump lattice and \(N\times M\) ring soliton lattice. Following the velocity resonant mechanism, soliton molecules can be produced by adjusting the velocities of some dromions, lumps and ring solitons.

In detail, soliton molecules with two “atoms” are discussed, which are the dromion molecule, lump molecule and ring soliton molecule. It is graphically demonstrated that these soliton molecules can be symmetric or asymmetric, depending on their “atom” solitons are of the same or not. It is also revealed that interactions between the dromion molecule and the dromion, between the lump molecule and the lump, between two lump molecules, between the ring soliton molecule and the ring soliton are all completely elastic. In addition, it is shown that in a special situation, the original field u can share a similar nonlinear excitation for the potential field U except for an extra parabolic-like wave background.

As is known, soliton molecules have been observed in different physical experiments. Due to various wave structures of solitons, the structures of soliton molecules can also be very diverse. It is hoped that the findings in this work really enrich the types of soliton molecules. In addition, soliton molecules possessing other structures can also be explored in this mathematical setting. However, the physical background of these soliton molecules is still unclear and also the mechanism of their appearance, which deserve further investigations.