Antidark solitons and soliton molecules in a (3 + 1)-dimensional nonlinear evolution equation

Abstract

We investigate a (3 + 1)-dimensional nonlinear evolution equation which is a higher-dimensional generalization of the Korteweg–de Vries equation. On the basis of the decomposition approach, the N-antidark soliton solution on a finite background is constructed by using the Darboux transformation together with the limit technique. The asymptotic analysis for the N-antidark soliton solution is performed, and the collision between multiple antidark solitons is proved to be elastic. Under the velocity resonant mechanism, the antidark soliton molecules on the (x, t), (y, t), (y, z) and (t, z) planes are found instead of the (x, y) and (x, z) planes. Based on the three- and the four-antidark soliton solutions, the elastic collision between a soliton molecule and a common soliton and the elastic collision between two soliton molecules are analytically demonstrated, respectively. These results may be useful for the study of soliton molecules in hydrodynamics and nonlinear optics.

1 Introduction

Soliton molecules, bound states of solitons, have been drastically studied to a certain extent due to their significant applications in a variety of contexts including optics [1,2,3,4] and Bose–Einstein condensates [5, 6], to name a few. In 2017, Herink et al. track the formation of stable soliton molecules and reveal rapid internal motions for diverse bound states in a femtosecond laser oscillator of real-time access to multipulse interactions [3]. In 2018, Liu et al. observe the entire buildup process of soliton molecules to explore the complex soliton interaction dynamics in a mode-locked laser [4]. In 2019, Zakharov et al. demonstrate the experimental observation of shaped breathing soliton molecules in a standard single-mode fiber [7].

The formation of soliton molecules has always been an important task to exhibit the bound states of solitons analogous to molecules in numerous fields of physics from theoretical and experimental perspectives. More recently, Lou et al. have developed the velocity resonant mechanism to obtain soliton molecules in many integrable systems such as the defocusing Hirota equation [8], the fifth-order Korteweg–de Vries (KdV) equation [9] and the Sharma–Tasso–Olver–Burgers equation [10]. Intricate soliton molecules such as dark molecule, kink–kink molecule, kink–breather molecule and breather–breather molecule have been found. Furthermore, Li et al. have studied soliton molecules in the complex modified KdV equation [11], the (2 + 1)-dimensional Sawada–Kotera equation [12] and the (2 + 1)-dimensional B-type Kadomtsev–Petviashvili equation [13].

Concerning the realistic physical environment, one should not confine the soliton molecule investigations to (1 + 1)-dimensional and (2 + 1)-dimensional models, although the findings of integrable models in higher dimensions are not an easy work. As a matter of fact, the oceanic rogue waves, solitons and lumps are (2 + 1)-dimensional phenomena [14,15,16,17,18,19,20] and in ultrafast optics and fluids the more complex multidimensional dynamics should be considered [21,22,23,24,25,26,27,28,29,30,31]. Therefore, the extension of soliton molecules in higher-dimensional descriptions such as the (3 + 1)-dimensional equations is essential. In this paper, we consider a (3 + 1)-dimensional nonlinear evolution equation ((3 + 1)D NEE):

$$\begin{aligned} 3w_{xz}+(2w_{t}-w_{xxx}-2ww_{x})_{y}-2(w_{x}\partial _{x}^{-1}w_{y})_{x}=0,\nonumber \\ \end{aligned}$$

(1)

where $w=w(x,y,t,z)$ is a real function, the subscripts denote the partial derivatives and $\partial ^{-1}_{x}$ is defined by $(\partial ^{-1}_{x}f)(x)=\int _{-\infty }^{x}f(s)ds$. It is easy to find that in terms of a simple scale transformation $w\rightarrow u$, $t\rightarrow -6\sqrt{3}T$, $x\rightarrow \sqrt{3}X$, the center part of Eq. (1) can become the standard KdV equation $u_{T}+u_{XXX}+6uu_{X}=0.$ Consequently, Eq. (1) can be viewed as a (3 + 1)-dimensional generalization of the KdV equation and has potential applications in hydrodynamics, nonlinear optics, and so on.

The (3 + 1)D NEE (1) was first proposed by Geng when studying algebraic–geometrical solutions for multidimensional nonlinear evolution equations [32]. As pointed out by Geng, Eq. (1) can be decomposed into three (1 + 1)-dimensional AKNS equations, i.e., the nonlinear Schrödinger (NLS) equation, the complex modified KdV (cmKdV) equation and the Lakshmanan–Porsezian–Daniel (LPD) equation, and hence justifies its physical application in turn. In the past few years, finding exact solutions for the (3 + 1)D NEE (1) has attracted considerable attention, and its soliton solutions, lump solutions and various types of interactional solutions on the zero background have been constructed via Hirota’s bilinear method [33,34,35]. Particularly, Wazwaz has derived the multiple-soliton solutions and multiple singular soliton solutions for Eq. (1) through the simplified Hirota’s bilinear method [36]. Additionally, Wang et al. [37] have recently studied its rational solutions that have been shown to exhibit doubly localized lumps and line rogue waves on a finite background by utilizing the Darboux transformation (DT) method. Note that in our previous work [37], the construction of rational solutions for Eq. (1) is based on the fact that Eq. (1) is decomposed into three (1 + 1)-dimensional AKNS equations with the focusing case, while for the defocusing case, to our knowledge, has not been considered by any authors. Based on this point of view, our paper aims to investigate antidark solitons and soliton molecules in Eq. (1) on a finite background instead of zero background [33,34,35,36] through the DT method [38,39,40,41,42] and limit technique [43,44,45,46,47,48,49,50,51,52].

The paper can be arranged as follows. In Sect. 2, based on the decomposition approach [32, 53, 54], we firstly decompose Eq. (1) into the NLS equation, the cmKdV equation and the LPD equation with the defocusing case. Then, we introduce a quartet Lax pair and construct the N-fold DT for the linear eigenvalue problem. In Sect. 3, we derive the N-antidark soliton solution represented in a compact determinant form as well as Hirota’s bilinear N-soliton solution form [55]. The asymptotic behavior [56,57,58] for the N-antidark soliton solution is discussed, and the property of elastic collision between multiple antidark solitons is preserved. In Sect. 4, under the velocity resonant mechanism, we demonstrate that the soliton molecules can exist on the (x, t), (y, t), (y, z) and (t, z) planes rather than the (x, y) and (x, z) planes. The elastic collision between a soliton molecule and a common soliton and the elastic collision between two soliton molecules are analytically shown with the help of the three- and the four-antidark soliton solutions, respectively. Finally, we give our conclusion.

2 Decomposition and Darboux transformation

In this section, we shall decompose the (3 + 1)D NEE (1) into the NLS equation, the mKdV equation and the LPD equation with the defocusing case. To this end, we consider the first three members of the AKNS hierarchy:

$$\begin{aligned}&\mathrm{i}q_{y}+\dfrac{1}{2}q_{xx}-q^2r=0,\ \mathrm{i}r_{y}-\dfrac{1}{2}r_{xx}+r^2q=0, \end{aligned}$$

(2)

$$\begin{aligned}&q_t+q_{xxx}-6qrq_x=0,\ r_t+r_{xxx}-6qrr_x=0, \end{aligned}$$

(3)

and

$$\begin{aligned}&\mathrm{i}q_{z}+\dfrac{1}{2}(q_{xxxx}-8qrq_{xx}\nonumber \\&\quad +\,6q^3r^2-4q_{x}r_xq-6rq_x^2-2q^2r_{xx})=0,\nonumber \\&\mathrm{i}r_{z}-\dfrac{1}{2}(r_{xxxx}-8qrr_{xx}+6r^3q^2\nonumber \\&\quad -\,4q_{x}r_xr-6qr_x^2-2r^2q_{xx})=0. \end{aligned}$$

(4)

It is not difficult to verify that Eqs. (2)–(4) are compatible since the flows determined by them can commute. We thus have the following proposition.

Proposition 1

Let (q, r) be a compatible solution of Eqs. (2)–(4), then the constraint

$$\begin{aligned} w=-3qr \end{aligned}$$

(5)

solves the (3 + 1)D NEE (1).

Proof

In terms of Eqs. (2)–(4), one obtains

$$\begin{aligned} w_{y}= & {} -\dfrac{3}{2}\mathrm{i}(rq_{xx}-qr_{xx}),\ \partial _{x}^{-1}w_{y}\\&=-\dfrac{3}{2}\mathrm{i}(rq_{x}-qr_{x}),\\ w_{xxxy}= & {} -\dfrac{3}{2}\mathrm{i}(rq_{xxxx}-qr_{xxxx})_{x}\\&-\,3\mathrm{i}(r_{x}q_{xxx}-q_{x}r_{xxx})_{x},\\ w_{t}= & {} 3(qr_{xxx}+rq_{xxx})-2w^2w_{x},\ w_{x}\partial _{x}^{-1}w_{y}\\&=\dfrac{9}{2}\mathrm{i}(r^{2}q_{x}^2-q^2r_x^2),\\ w_{ty}= & {} -\dfrac{3}{2}\mathrm{i}(qr_{xxxx}-rq_{xxxx})_{x}\\&-\,\dfrac{3}{2}\mathrm{i}(q_{xxx}r_{x}-r_{xxx}q_{x})_{x} -2(w\partial _{x}^{-1}w_{y})_{xx},\\ w_{zx}= & {} -\dfrac{3}{2}\mathrm{i}(rq_{xxxx}-qr_{xxxx})_{x}\\&+\,\,2(ww_{y}+w_{x}\partial _{x}^{-1}w_{y})_{x}, \end{aligned}$$

which lead to the (3 + 1)D NEE (1). $\square$

Next, we show that Eqs. (2)–(4) are completely integrable and can be cast into a quartet Lax pair

$$\begin{aligned} \varPhi _{x}&=U\varPhi ,\ U=\left( \begin{array}{cc} -\mathrm{i}\lambda &{} q \\ r &{} \mathrm{i}\lambda \\ \end{array} \right) , \end{aligned}$$

(6)

$$\begin{aligned} \varPhi _{y}&=V^{(1)}\varPhi ,\ V^{(1)}=\left( \begin{array}{cc} -\mathrm{i}\lambda ^2-\dfrac{\mathrm{i}}{2}qr &{} \lambda q+\dfrac{\mathrm{i}}{2}q_{x}\\ \lambda r-\dfrac{\mathrm{i}}{2}r_{x} &{} \mathrm{i}\lambda ^2+\dfrac{\mathrm{i}}{2}qr \\ \end{array} \right) , \end{aligned}$$

(7)

$$\begin{aligned} \varPhi _{t}&=V^{(2)}\varPhi ,\ V^{(2)}=\left( \begin{array}{cc} V^{(2)}_{11} &{} V^{(2)}_{12} \\ V^{(2)}_{21} &{} -V^{(2)}_{11} \\ \end{array} \right) , \end{aligned}$$

(8)

$$\begin{aligned} \varPhi _{z}&=V^{(3)}\varPhi ,\ V^{(3)}=\left( \begin{array}{cc} V^{(3)}_{11} &{} V^{(3)}_{12} \\ V^{(3)}_{21} &{} -V^{(3)}_{11} \\ \end{array} \right) , \end{aligned}$$

(9)

where $\varPhi =(\psi ,\varphi )^{T}$ is the eigenfunction, $\lambda$ is the spectral parameter and

$$\begin{aligned}&V^{(2)}_{11}=-4\mathrm{i}\lambda ^3-2\mathrm{i}\lambda qr+rq_x-qr_x,\\&V^{(2)}_{12}=4\lambda ^2q+2\mathrm{i}\lambda q_{x}+2q^2r-q_{xx},\\&V^{(2)}_{21}=4\lambda ^2r-2\mathrm{i}\lambda r_{x}+2r^2q-r_{xx},\\&V^{(3)}_{11}=4\mathrm{i}\lambda ^4+2\mathrm{i}\lambda ^2qr-\lambda (r q_{x}-qr_{x})\\&\qquad \qquad +\dfrac{\mathrm{i}}{2}(3q^2r^2 -qr_{xx}-rq_{xx}+q_{x}r_{x}),\\&V^{(3)}_{12}=-4\lambda ^3q-2\mathrm{i}\lambda ^2q_{x}+\lambda (q_{xx}-2q^2r)\\&\qquad \qquad +\dfrac{\mathrm{i}}{2}(q_{xxx}-6qrq_{x}),\\&V^{(3)}_{21}=-4\lambda ^3r+2\mathrm{i}\lambda ^2r_{x}+\lambda (r_{xx}-2r^2q)\\&\qquad \qquad -\dfrac{\mathrm{i}}{2}(r_{xxx}-6qrr_{x}). \end{aligned}$$

The compatible conditions of this linear eigenvalue problem, i.e., $U_{t_{m}}-V^{(m)}_{x}+UV^{(m)}-V^{(m)}U=0$ ($t_{m}=y,t,z,m=1,2,3$), can reproduce Eqs. (2)–(4), respectively. In view of Eq. (5), we know that there are two kinds of decomposition for Eq. (1), namely $w=3|q|^2$ the focusing reduction of the linear eigenvalue problem

$$\begin{aligned} r=-q^{*},\ U^{\dag }(\lambda )=-U(\lambda ^{*}),\ V^{(j)\dag }(\lambda )=-V^{(j)}(\lambda ^{*}),\nonumber \\ \end{aligned}$$

(10)

and $w=-3|q|^2$ the defocusing reduction of the linear eigenvalue problem

$$\begin{aligned} r=q^{*},\ U^{\dag }(\lambda )= & {} -\varLambda U(\lambda ^{*})\varLambda ,\ V^{(j)\dag }(\lambda )\nonumber \\= & {} -\varLambda V^{(j)}(\lambda ^{*})\varLambda , \end{aligned}$$

(11)

where $\varLambda =\mathrm{diag}(1,-1),\ j=1,2,3$. Noteworthily, the focusing case has been considered in our recent work [37] and the rational solutions for Eq. (1) have been investigated. In this paper, we discuss the defocusing case and concentrate on the antidark solitons and soliton molecules in Eq. (1).

At this point, assuming that $\varPhi _i$ ($i=1,2,\ldots ,N$) are N solutions for the linear eigenvalue problem (6)–(9) with the symmetry reduction (11) at $q=q[0]$ and $\lambda =\lambda _i$, then the N-fold DT takes the form

$$\begin{aligned} T[N]=\sum _{j=1}^{N}\dfrac{T_j}{\lambda -\lambda _{j}^{*}}=I-XM^{-1}(\lambda -D)^{-1}X^{\dag }\varLambda ,\nonumber \\ \end{aligned}$$

(12)

where

$$\begin{aligned} X= & {} (\varPhi _1,\varPhi _2,\ldots ,\varPhi _N),\ D=\mathrm{diag}(\lambda _1^{*},\lambda _2^{*},\cdots ,\lambda _N^{*}),\\ M= & {} \left( \begin{array}{cccc} \dfrac{\varPhi _{1}^{\dag }\varPhi _{1}}{\lambda _{1}-\lambda _{1}^{*}} &{} \dfrac{\varPhi _{1}^{\dag }\varPhi _{2}}{\lambda _{2}-\lambda _{1}^{*}} &{} \cdots &{} \dfrac{\varPhi _{1}^{\dag }\varPhi _{N}}{\lambda _{N}-\lambda _{1}^{*}} \\ \dfrac{\varPhi _{2}^{\dag }\varPhi _{1}}{\lambda _{1}-\lambda _{2}^{*}} &{} \dfrac{\varPhi _{2}^{\dag }\varPhi _{2}}{\lambda _{2}-\lambda _{2}^{*}} &{} \cdots &{} \dfrac{\varPhi _{2}^{\dag }\varPhi _{N}}{\lambda _{N}-\lambda _{2}^{*}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \dfrac{\varPhi _{N}^{\dag }\varPhi _{1}}{\lambda _{1}-\lambda _{N}^{*}} &{} \dfrac{\varPhi _{N}^{\dag }\varPhi _{2}}{\lambda _{2}-\lambda _{N}^{*}} &{} \cdots &{} \dfrac{\varPhi _{N}^{\dag }\varPhi _{N}}{\lambda _{N}-\lambda _{N}^{*}} \\ \end{array} \right) . \end{aligned}$$

Then, by applying

$$\begin{aligned}&T[N]_{x}+T[N]U=U[N]T[N],\ U[N]=U(\lambda ,q[N]),\\&T[N]_{y}+T[N]V^{(1)}=V^{(1)}[N]T[N],\\&V^{(1)}[N]=V^{(1)}(\lambda ,q[N]),\\&T[N]_{t}+T[N]V^{(2)}=V^{(2)}[N]T[N],\\&V^{(2)}[N]=V^{(2)}(\lambda ,q[N]),\\&T[N]_{z}+T[N]V^{(3)}=V^{(3)}[N]T[N],\\&V^{(3)}[N]=V^{(3)}(\lambda ,q[N]), \end{aligned}$$

we have

$$\begin{aligned} q[N]=q[0]+2\mathrm{i}\sum _{j=1}^{N}T_{j}^{[12]}, \end{aligned}$$

and

$$\begin{aligned} |q[N]|^2=|q[0]|^2+\mathrm{i}\dfrac{\partial }{\partial x}\sum _{j=1}^{N}\left( T_{j}^{[11]}-T_{j}^{[22]}\right) . \end{aligned}$$

Additionally, using

$$\begin{aligned} \left( \dfrac{\varPhi _{i}^{\dag }\varPhi _{j}}{\lambda _{j}-\lambda _{i}^{*}}\right) _{x}=-\mathrm{i}\varPhi _{i}^{\dag }\varPhi _{j}, \end{aligned}$$

one obtains the new potential expressed in a compact determinant form

$$\begin{aligned} q[N]=q[0]-2\mathrm{i}\dfrac{\det (M_1)}{\det (M)}, \end{aligned}$$

(13)

where

$$\begin{aligned} M_{1}=\left( \begin{array}{ccccc} \dfrac{\varPhi _{1}^{\dag }\varPhi _{1}}{\lambda _{1}-\lambda _{1}^{*}} &{} \dfrac{\varPhi _{1}^{\dag }\varPhi _{2}}{\lambda _{2}-\lambda _{1}^{*}} &{} \cdots &{} \dfrac{\varPhi _{1}^{\dag }\varPhi _{N}}{\lambda _{N}-\lambda _{1}^{*}} &{} \varphi _{1}^{*}\\ \dfrac{\varPhi _{2}^{\dag }\varPhi _{1}}{\lambda _{1}-\lambda _{2}^{*}} &{} \dfrac{\varPhi _{2}^{\dag }\varPhi _{2}}{\lambda _{2}-\lambda _{2}^{*}} &{} \cdots &{} \dfrac{\varPhi _{2}^{\dag }\varPhi _{N}}{\lambda _{N}-\lambda _{2}^{*}} &{} \varphi _{2}^{*}\\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ \dfrac{\varPhi _{N}^{\dag }\varPhi _{1}}{\lambda _{1}-\lambda _{N}^{*}} &{} \dfrac{\varPhi _{N}^{\dag }\varPhi _{2}}{\lambda _{2}-\lambda _{N}^{*}} &{} \cdots &{} \dfrac{\varPhi _{N}^{\dag }\varPhi _{N}}{\lambda _{N}-\lambda _{N}^{*}} &{} \varphi _{N}^{*}\\ \psi _{1}&{} \psi _{2} &{}\cdots &{}\psi _{N} &{}0 \end{array} \right) , \end{aligned}$$

and its intensity

$$\begin{aligned} |q[N]|^2=|q[0]|^2-\dfrac{\partial ^2}{\partial x^2}\ln \det (M). \end{aligned}$$

(14)

3 Antidark solitons and elastic collisions

For our studies, we start from the general plane-wave solution of Eqs. (2)–(4), that is,

$$\begin{aligned} q[0]=c\mathrm{e}^{\mathrm{i}\theta },\ \theta =ax+by+dt+ez, \end{aligned}$$

(15)

where c and a are real constants and stand for the background and frequency of the complex field envelope q, respectively, and b, d, e are wave numbers such that

$$\begin{aligned} b=-\dfrac{1}{2}a^2-c^2,\ d=a^3+6ac^2,\ e=\dfrac{1}{2}a^4+6a^2c^2+3c^4. \end{aligned}$$

Substituting Eq. (15) and $\lambda =\lambda _j$ ($j=1,2,\cdots ,N$) into the quartet Lax pair (6)–(9), we can arrive at the fundamental solution

$$\begin{aligned} \varPhi _{j}=\left( \begin{array}{cc} 1 &{} 1 \\ \dfrac{2\mathrm{i}c}{\chi _j+a} &{} \dfrac{2\mathrm{i}c}{\chi _j^{*}+a} \\ \end{array} \right) \left( \begin{array}{c} \mathrm{e}^{\mathrm{i}\omega _j}\\ \alpha _{j}(\lambda _j^{*}-\lambda _j)\mathrm{e}^{\mathrm{i}\omega _j^{*}} \\ \end{array} \right) , \end{aligned}$$

where $\alpha _j$ is an arbitrary complex constant,

$$\begin{aligned} \begin{array}{l} \chi _j=2\lambda _j+\sqrt{(2\lambda _j+a)^2-4c^2},\\ \chi _j^{*}=2\lambda _j-\sqrt{(2\lambda _j+a)^2-4c^2}, \end{array} \end{aligned}$$

and

$$\begin{aligned} \omega _j=\left( \lambda _j-\dfrac{1}{2}\chi _j\right) (x-\nu _{j1}y-\nu _{j2}t-\nu _{j3}z), \end{aligned}$$

with

$$\begin{aligned} \begin{array}{l} \nu _{j1}=-\left( \lambda _j-\dfrac{1}{2}a\right) ,\ \nu _{j2}=-(4\lambda ^2-2a\lambda +2c^2+a^2),\\ \nu _{j3}=4\lambda ^3-2a\lambda ^2+(a^2+2c^2)\lambda -\dfrac{1}{2}a(a^2+6c^2). \end{array} \end{aligned}$$

Here,

$$\begin{aligned} \mathrm{Im}(\chi _j)=\sqrt{-(2\lambda _j+a)^2+4c^2}>0, \end{aligned}$$

such that

$$\begin{aligned} -c-\dfrac{1}{2}a<\lambda _j<c-\dfrac{1}{2}a,\ \lambda _j\in {\mathbb {R}}. \end{aligned}$$

(16)

On account of the N-fold DT and the limit $\lambda _j^{*}\rightarrow \lambda _j$, we can derive the N-dark soliton solution of Eqs. (2)–(4), as

$$\begin{aligned} q[N]=ce^{\mathrm{i}\theta }\left[ 1-2\mathrm{i}\dfrac{\det (\widehat{M_{1}})}{\det (\widehat{M})}\right] , \end{aligned}$$

(17)

where

with

$$\begin{aligned} \beta _j=-\mathrm{Im}(\chi _j)\mathrm{Im}\left[ \alpha _j^{*}\left( 1-\dfrac{4c^2}{(\chi _j+a)^2}\right) \right] >0, \end{aligned}$$

and

$$\begin{aligned} \mathrm{Im}(\omega _j)= & {} m_{j}(x-\nu _{j1}y-\nu _{j2}t-\nu _{j3}z), \\ m_j= & {} -\dfrac{1}{2}\mathrm{Im}(\chi _j)<0. \end{aligned}$$

At this time, returning to Eq. (5) with the symmetry reduction $r=q^{*}$ and Eq. (14), we can present the N-antidark soliton solution for Eq. (1), namely

$$\begin{aligned} w[N]=-3\left[ c^2-\dfrac{\partial ^2}{\partial x^2}\ln \det (\widehat{M})\right] . \end{aligned}$$

(18)

Explicitly, for $N=1$ in the above formula, we can get the one-antidark soliton solution

$$\begin{aligned} w[1]=-3\left[ c^2-m_1^2\mathrm{sech}^2(K_1)\right] , \end{aligned}$$

where

$$\begin{aligned} K_1=m_{1}(x-\nu _{11}y-\nu _{12}t-\nu _{13}z)+\dfrac{1}{2}\ln \beta _1. \end{aligned}$$

It can be computed that the maximum amplitude of w[1] is

$$\begin{aligned} w[1]_\mathrm{max}=-3(c^2-m_1^2)=-\dfrac{3}{4}(2\lambda _1+a)^2, \end{aligned}$$

(19)

and it is localized at the line

$$\begin{aligned} x-\nu _{11}y-\nu _{12}t-\nu _{13}z=-\dfrac{\ln \beta _1}{2m_1}. \end{aligned}$$

In addition, we find $w[1]\rightarrow -3c^2$ for $x\rightarrow \pm \infty$, which implies that the antidark soliton propagates on a finite background instead of the zero background.

Fig. 1

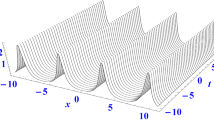
Collision of two antidark solitons in Eq. (20). The parameters are $c=1,a=\frac{1}{2},\lambda _1=0,\lambda _2=\frac{1}{3},\chi _1=\frac{\mathrm{i}}{2}\sqrt{15}, \chi _2=\frac{2}{3}+\frac{\mathrm{i}}{6}\sqrt{95},\beta _1=\frac{1}{10{,}000},\beta _2=10{,}000$

To proceed, the two-antidark soliton solution can be explicitly written as

$$\begin{aligned} w[2]= & {} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_1}+\mathrm{e}^{-2K_2}\right. \nonumber \\&\left. \quad +e^{-2(K_1+K_2+A_{12})}\big ]\right) , \end{aligned}$$

(20)

where

$$\begin{aligned} A_{12}= & {} \ln \dfrac{|\chi _1-\chi _2^{*}|}{|\chi _1-\chi _2|},\\ K_l= & {} m_{l}(x-\nu _{l1}y-\nu _{l2}t-\nu _{l3}z)+\dfrac{1}{2}\ln \beta _l,\ l=1,2. \end{aligned}$$

Following the standard asymptotic analysis process, we have:

• (i) If $K_1=m_{1}(x-\nu _{11}y-\nu _{12}t-\nu _{13}z)+\frac{1}{2}\ln \beta _1=\mathrm{constant}$,

  $$\begin{aligned} w[2]\rightarrow \left\{ \begin{array}{l} -3\left[ c^2-m_1^2\mathrm{sech}^2(K_1)\right] ,\quad K_2\rightarrow +\infty ,\\ -3\left[ c^2-m_1^2\mathrm{sech}^2(K_1+A_{12})\right] ,\ K_2\rightarrow -\infty . \end{array} \right. \end{aligned}$$

• (ii) If $K_2=m_{2}(x-\nu _{21}y-\nu _{22}t-\nu _{23}z)+\frac{1}{2}\ln \beta _2=\mathrm{constant}$,

  $$\begin{aligned} w[2]\rightarrow \left\{ \begin{array}{l} -3\left[ c^2-m_2^2\mathrm{sech}^2(K_2+A_{12})\right] ,\ K_1\rightarrow -\infty ,\\ -3\left[ c^2-m_2^2\mathrm{sech}^2(K_2)\right] ,\quad K_1\rightarrow +\infty . \end{array} \right. \end{aligned}$$

  We exhibit in Fig. 1 the collision of two antidark solitons on the (x, y), (x, t), (x, z), (y, t), (y, z) and (t, z) planes. It is shown that the collision is elastic since the amplitude, velocity and shape of each soliton are unchanged after the collision except for a phase difference which is given by $A_{12}=\ln \frac{|\chi _1-\chi _2^{*}|}{|\chi _1-\chi _2|}$.

Fig. 2

Collision of three antidark solitons in Eq. (21). The parameters are $c=1,a=\frac{1}{2},\lambda _1=0,\lambda _2=\frac{1}{3}, \lambda _3=\frac{1}{2},\chi _1=\frac{\mathrm{i}}{2}\sqrt{15}, \chi _2=\frac{2}{3}+\frac{\mathrm{i}}{6}\sqrt{95},\chi _3=1+\frac{\mathrm{i}}{2}\sqrt{7}, \beta _1=\frac{1}{10{,}000},\beta _2=10{,}000,\beta _3=20{,}000$

Furthermore, the explicit three-antidark soliton solution is found to be

$$\begin{aligned}&w[3]=-3\bigg (c^2-\dfrac{\partial ^2}{\partial x^2} \ln \big [1+\mathrm{e}^{-2K_1}+\mathrm{e}^{-2K_2}+\mathrm{e}^{-2K_3}\nonumber \\&\qquad \qquad +e^{-2(K_1+K_2+A_{12})}+\mathrm{e}^{-2(K_1+K_3+A_{13})}\nonumber \\&\qquad \qquad +\mathrm{e}^{-2(K_2+K_3+A_{23})}+\mathrm{e}^{-2(K_1+K_2+K_3+A_{12}+A_{13}+A_{23})}\big ]\bigg ),\nonumber \\ \end{aligned}$$

(21)

where

$$\begin{aligned} A_{jl}= & {} \ln \dfrac{|\chi _j-\chi _l^{*}|}{|\chi _j-\chi _l|},\\ K_l= & {} m_{l}(x-\nu _{l1}y-\nu _{l2}t-\nu _{l3}z)+\dfrac{1}{2}\ln \beta _l,\\&j<l=1,2,3. \end{aligned}$$

Similarly, we have the following asymptotic behaviors:

• (i) If $K_1=m_{1}(x-\nu _{11}y-\nu _{12}t-\nu _{13}z)+\frac{1}{2}\ln \beta _1=\mathrm{constant}$,

  $$\begin{aligned} w[3]\rightarrow \left\{ \begin{array}{l} -3\left[ c^2-m_1^2\mathrm{sech}^2(K_1)\right] ,\quad K_2\rightarrow +\infty ,\ K_3\rightarrow +\infty ,\\ -3\left[ c^2-m_1^2\mathrm{sech}^2(K_1+A_{12}+A_{13})\right] ,\ K_2\rightarrow -\infty ,\ K_3\rightarrow -\infty . \end{array} \right. \end{aligned}$$

• (ii) If $K_2=m_{2}(x-\nu _{21}y-\nu _{22}t-\nu _{23}z)+\frac{1}{2}\ln \beta _2=\mathrm{constant}$,

  $$\begin{aligned} w[3]\rightarrow \left\{ \begin{array}{l} -3\left[ c^2-m_2^2\mathrm{sech}^2(K_2+A_{23})\right] ,\ K_1\rightarrow +\infty ,\ K_3\rightarrow -\infty ,\\ -3\left[ c^2-m_2^2\mathrm{sech}^2(K_2+A_{12})\right] ,\ K_1\rightarrow -\infty ,\ K_3\rightarrow +\infty . \end{array} \right. \end{aligned}$$

• (iii) If $K_3=m_{3}(x-\nu _{31}y-\nu _{32}t-\nu _{33}z)+\frac{1}{2}\ln \beta _3=\mathrm{constant}$,

  $$\begin{aligned} w[3]\rightarrow \left\{ \begin{array}{l} -3\left[ c^2-m_3^2\mathrm{sech}^2(K_3+A_{13}+A_{23})\right] ,\ K_1\rightarrow -\infty ,\ K_2\rightarrow -\infty ,\\ -3\left[ c^2-m_3^2\mathrm{sech}^2(K_3)\right] ,\quad K_1\rightarrow +\infty ,\ K_2\rightarrow +\infty . \end{array} \right. \end{aligned}$$

  The elastic collision property of three antidark solitons is kept, as seen in Fig. 2.

Next, by calculating the determinant of the $N\times N$ Cauchy-type matrix in Eq. (18), we can put forward the N-antidark soliton solution for Eq. (1) in Hirota’s bilinear N-soliton solution form

$$\begin{aligned} w[N]= & {} -3\bigg (c^2-\dfrac{\partial ^2}{\partial x^2} \displaystyle \ln \nonumber \\&\bigg [\sum _{\mu =0,1}\mathrm{e}^{-2(\sum _{j=1}^{N}\mu _jK_j+\sum _{1\le j<l}^{N}\mu _j\mu _lA_{jl})} \bigg ]\bigg ),\nonumber \\ \end{aligned}$$

(22)

where

$$\begin{aligned} A_{jl}= & {} \ln \dfrac{|\chi _j-\chi _l^{*}|}{|\chi _j-\chi _l|},\ K_l=m_{l}(x-\nu _{l1}y-\nu _{l2}t\\&\quad -\nu _{l3}z)+\dfrac{1}{2}\ln \beta _l,\ j<l=1,2,\cdots ,N. \end{aligned}$$

The detailed derivation for the above formula is given in Appendix. Further, we make the asymptotic analysis for the N-antidark soliton solution by assuming $K_k=m_{k}(x-\nu _{k1}y-\nu _{k2}t-\nu _{k3}z)+\frac{1}{2}\ln \beta _k=\mathrm{constant}$ ($1\le k\le N$), we conclude that

$$\begin{aligned} w[N]\rightarrow \left\{ \begin{array}{l} -3\left[ c^2-m_k^2\mathrm{sech}^2(K_k+\varDelta _{k}^{-})\right] ,\ K_i\rightarrow +\infty ,\ K_j\rightarrow -\infty \\ -3\left[ c^2-m_k^2\mathrm{sech}^2(K_k)+\varDelta _{k}^{+}\right] ,K_i\rightarrow -\infty ,\ K_j\rightarrow +\infty \end{array} \right. ,\ 1\le i<k<j\le N, \end{aligned}$$

where

$$\begin{aligned} \varDelta _{k}^{-}=\left\{ \begin{array}{l} \displaystyle \ln \prod _{l=k+1}^{n}\dfrac{\left| \chi _k-\chi _l^{*}\right| }{\left| \chi _k-\chi _l\right| }, \ 1\le k\le N-1,\\ 0,\quad k=N, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \varDelta _{k}^{+}=\left\{ \begin{array}{l} 0,\quad k=1,\\ \displaystyle \ln \prod _{l=1}^{k-1}\dfrac{\left| \chi _k-\chi _l^{*}\right| }{\left| \chi _k-\chi _l\right| },\ 2\le k\le N. \end{array}\right. \end{aligned}$$

4 Antidark soliton molecules

In this section, we utilize the velocity resonant method to discuss the possible formation of antidark soliton molecules on the (x, y), (x, t), (x, z), (y, t), (y, z) and (t, z) planes. We first consider the resonant condition on each plane.

• (i) On the (x, y) plane, the resonant condition is $\nu _{11}=\nu _{21}$ and we have

  $$\begin{aligned} \lambda _2=\lambda _1. \end{aligned}$$

  (23)

• (ii) On the (x, t) plane, the resonant condition is $\nu _{12}=\nu _{22}$ and we obtain

  $$\begin{aligned} \lambda _2=\dfrac{1}{2}(a-2\lambda _1). \end{aligned}$$

  (24)

• (iii) On the (x, z) plane, the resonant condition is $\nu _{13}=\nu _{23}$ and it holds that

  $$\begin{aligned} \lambda _2=\dfrac{1}{4}(a-2\lambda _1) \pm \dfrac{1}{2}\sqrt{-3\left( \lambda _1-\dfrac{1}{6}a\right) ^2-\dfrac{2}{3}a^2-2c^2}.\nonumber \\ \end{aligned}$$

  (25)

• (iv) On the (y, t) plane, the resonant condition is $\dfrac{\nu _{11}}{\nu _{21}}=\dfrac{\nu _{12}}{\nu _{22}}$ and it follows that

  $$\begin{aligned} \lambda _2=\dfrac{a\lambda _1+c^2}{2\lambda _1-a}. \end{aligned}$$

  (26)

• (v) On the (y, z) plane, the resonant condition is $\dfrac{\nu _{11}}{\nu _{21}}=\dfrac{\nu _{13}}{\nu _{23}}$ and it yields

  $$\begin{aligned} \lambda _2= & {} \dfrac{1}{4}(a-2\lambda _1) \pm \dfrac{1}{4} \nonumber \\&\sqrt{\dfrac{-8\lambda _1^3-4a\lambda _1^2+2a^2\lambda _1+a^3+16ac^2}{a-2\lambda _1}}.\nonumber \\ \end{aligned}$$

  (27)

• (vi) On the (t, z) plane, the resonant condition is $\dfrac{\nu _{12}}{\nu _{22}}=\dfrac{\nu _{13}}{\nu _{23}}$ and it implies

  $$\begin{aligned} \lambda _2= & {} \dfrac{1}{2(4\lambda _1^2-2a\lambda _1+2c^2+a^2)}\nonumber \\&(2a\lambda _1^2-a^2\lambda _1-2ac^2\pm \sqrt{\upsilon }), \end{aligned}$$

  (28)

  where

  $$\begin{aligned} \upsilon= & {} -(12 a^2+32 c^2) \lambda _1^4+4a(a^2-4 c^2)\lambda _1^3\nonumber \\&-\,(3a^4+32c^4)\lambda _1^2 -8ac^2(a^2+c^2)\lambda _1\\&+\,\,2c^2(a^4+2a^2c^2-4c^4). \end{aligned}$$

  From Eqs. (23) and (25), one can find that it is impossible to choose two different real spectral parameters to yield the resonant conditions, and hence the antidark soliton molecules on the (x, y) and (x, z) planes cannot be formed. Nevertheless, the antidark soliton molecules on the (x, t), (y, t), (y, z) and (t, z) planes can be obtained as long as Eqs. (24), (26), (27) and (28) are satisfied, respectively.

Meanwhile, we would like to say that the interesting collision between a soliton molecule (SM) and a common soliton (S) is also elastic, which can be proved by the other asymptotic analysis of w[3]:

• (i) If $K_1,K_2=\mathrm{constant}$,

  $$\begin{aligned} w[3]_\mathrm{SM+S}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_1}+\mathrm{e}^{-2K_2}+e^{-2(K_1+K_2+A_{12})}\big ]\right) ,\ K_3\rightarrow +\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\widetilde{K}_1}+\mathrm{e}^{-2\widetilde{K}_2}+e^{-2(\widetilde{K}_1+\widetilde{K}_2+A_{12})}\big ]\right) ,\ K_3\rightarrow -\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \widetilde{K}_1=K_1+A_{13},\ \widetilde{K}_2=K_2+A_{23}. \end{aligned}$$

• (ii) If $K_1,K_3=\mathrm{constant}$,

  $$\begin{aligned} w[3]_\mathrm{SM+S}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\widehat{K}_1}+\mathrm{e}^{-2\widehat{K}_3}+e^{-2(\widehat{K}_1+\widehat{K}_3+A_{13})}\big ]\right) ,\ K_2\rightarrow -\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_1}+\mathrm{e}^{-2K_3}+e^{-2(K_1+K_3+A_{13})}\big ]\right) ,\ K_2\rightarrow +\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \widehat{K}_1=K_1+A_{12},\ \widehat{K}_3=K_3+A_{23}. \end{aligned}$$

• (iii) If $K_2,K_3=\mathrm{constant}$,

  $$\begin{aligned} w[3]_\mathrm{SM+S}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_2}+\mathrm{e}^{-2K_3}+e^{-2(K_2+K_3+A_{23})}\big ]\right) ,\ K_1\rightarrow +\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\bar{K}_2}+\mathrm{e}^{-2\bar{K}_3}+e^{-2(\bar{K}_2+\bar{K}_3+A_{23})}\big ]\right) ,\ K_1\rightarrow -\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \bar{K}_2=K_1+A_{12},\ \bar{K}_3=K_3+A_{13}. \end{aligned}$$

  The antidark soliton molecule and the elastic collision between a soliton molecule and a common soliton on the (x, t), (y, t), (y, z) and (t, z) planes can be presented by choosing adequate parameters, as seen in Figs. 3, 4, 5 and 6.

Fig. 3

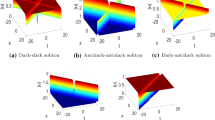
a Antidark soliton molecule in Eq. (20) and b collision between an soliton molecule and a common soliton in Eq. (21) on the (x, t) plane. The parameters are $c=1,a=\frac{1}{2},\lambda _1=0,\lambda _2=\frac{1}{4}, \lambda _3=\frac{1}{2},\chi _1=\frac{\mathrm{i}}{2}\sqrt{15}, \chi _2=\frac{1}{2}+\mathrm{i}\sqrt{3},\chi _3=1+\frac{\mathrm{i}}{2}\sqrt{7}, \beta _1=\frac{1}{10{,}000},\beta _2=10{,}000,\beta _3=20{,}000$

Fig. 4

a Antidark soliton molecule in Eq. (20) and b collision between an soliton molecule and a single soliton in Eq. (21) on the (y, t) plane. The parameters are $c=1,a=\frac{1}{2},\lambda _1=-1,\lambda _2=-\frac{1}{5}, \lambda _3=\frac{1}{2},\chi _1=-2+\frac{\mathrm{i}}{2}\sqrt{7}, \chi _2=-\frac{2}{5}+\frac{\mathrm{i}}{10}\sqrt{399},\chi _3=1+\frac{\mathrm{i}}{2}\sqrt{7}, \beta _1=\frac{1}{10{,}000},\beta _2=10{,}000,\beta _3=20{,}000$

Fig. 5

a Antidark soliton molecule in Eq. (20) and b collision between an soliton molecule and a single soliton in Eq. (21) on the (y, z) plane. The parameters are $c=1,a=\frac{1}{2},\lambda _1=-1,\lambda _2=\frac{5}{8}-\frac{\sqrt{545}}{40},\lambda _3=\frac{1}{2}, \chi _1=-2+\frac{\mathrm{i}}{2}\sqrt{7},\chi _2=-\frac{\sqrt{545}}{20}+\frac{5}{4} +\frac{\mathrm{i}}{20}\sqrt{-170+70\sqrt{545}},\chi _3=1+\frac{\mathrm{i}}{2}\sqrt{7}, \beta _1=\frac{1}{10{,}000},\beta _2=10{,}000,\beta _3=20{,}000$

Fig. 6

a Antidark soliton molecule in Eq. (20) and b collision between an soliton molecule and a single soliton in Eq. (21) on the (t, z) plane. The parameters are $c=1,a=2,\lambda _1=-\frac{1}{4},\lambda _2=-\frac{11}{58}-\frac{5}{58}\sqrt{35},\lambda _3=-\frac{3}{2}, \chi _1=-\frac{1}{2}+\frac{\mathrm{i}}{2}\sqrt{7}, \chi _2=-\frac{5}{29}\sqrt{35}-\frac{11}{29}+\frac{\mathrm{i}}{29}\sqrt{280+470\sqrt{35}}, \chi _3=-3+\mathrm{i}\sqrt{3},\beta _1=\frac{1}{10{,}000},\beta _2=10{,}000,\beta _3=20{,}000$

Finally, we discuss the elastic collision of two antidark soliton molecules based on the four-antidark soliton solution. By use of the asymptotic analysis, we have:

• (i) If $K_1,K_2=\mathrm{constant}$,

  $$\begin{aligned} w[4]_\mathrm{SM+SM}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_1}+\mathrm{e}^{-2K_2}+e^{-2(K_1+K_2+A_{12})}\big ]\right) ,\ K_3,K_4\rightarrow +\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\widetilde{\widehat{K}}_1}+\mathrm{e}^{-2\widetilde{\widehat{K}}_2}+e^{-2(\widetilde{\widehat{K}}_1 +\widetilde{\widehat{K}}_2+A_{12})}\big ]\right) ,\ K_3,K_4\rightarrow -\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \widetilde{\widehat{K}}_1=K_1+A_{13}+A_{14},\ \widetilde{\widehat{K}}_2=K_2+A_{23}+A_{24}. \end{aligned}$$

• (ii) If $K_1,K_3=\mathrm{constant}$,

  $$\begin{aligned} w[4]_\mathrm{SM+SM}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\widetilde{\widehat{K}}_1} +\mathrm{e}^{-2\widetilde{\widehat{K}}_3}+e^{-2(\widetilde{\overline{K}}_1 +\widetilde{\overline{K}}_3+A_{13})}\big ]\right) ,\ K_2,K_4\rightarrow -\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_1}+\mathrm{e}^{-2K_3}+e^{-2(K_1+K_3+A_{13})}\big ]\right) ,\ K_2,K_4\rightarrow +\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \widetilde{\bar{K}}_1=K_1+A_{12}+A_{14},\ \widetilde{\bar{K}}_3=K_3+A_{23}+A_{34}. \end{aligned}$$

• (iii) If $K_1,K_4=\mathrm{constant}$,

  $$\begin{aligned} w[4]_\mathrm{SM+SM}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_1}+\mathrm{e}^{-2K_4}+e^{-2(K_1+K_4+A_{14})}\big ]\right) ,\ K_2,K_3\rightarrow +\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\widehat{\widetilde{K}}_1} +\mathrm{e}^{-2\widehat{\widetilde{K}}_4}+e^{-2(\widehat{\widetilde{K}}_1 +\widehat{\widetilde{K}}_4+A_{14})}\big ]\right) ,\ K_2,K_3\rightarrow -\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \widehat{\widetilde{K}}_1=K_1+A_{12}+A_{13},\ \widehat{\widetilde{K}}_4=K_4+A_{24}+A_{34}. \end{aligned}$$

• (iv) If $K_2,K_3=\mathrm{constant}$,

  $$\begin{aligned} w[4]_\mathrm{SM+SM}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\widehat{\widetilde{K}}_2} +\mathrm{e}^{-2\widehat{\widetilde{K}}_3}+e^{-2(\widehat{\widetilde{K}}_2 +\widehat{\widetilde{K}}_3+A_{23})}\big ]\right) ,\ K_1,K_4\rightarrow -\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_2}+\mathrm{e}^{-2K_3}+e^{-2(K_2+K_3+A_{23})}\big ]\right) ,\ K_1,K_4\rightarrow +\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \widehat{\bar{K}}_2=K_2+A_{12}+A_{24},\ \widehat{\bar{K}}_3=K_3+A_{13}+A_{34}. \end{aligned}$$

  (v) If $K_2,K_4=\mathrm{constant}$,

  $$\begin{aligned} w[4]_\mathrm{SM+SM}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_2}+\mathrm{e}^{-2K_4}+e^{-2(K_2+K_4+A_{24})}\big ]\right) ,\ K_1,K_3\rightarrow +\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\bar{\widetilde{K}}_2} +\mathrm{e}^{-2\bar{\widetilde{K}}_3}+e^{-2(\bar{\widetilde{K}}_2 +\bar{\widetilde{K}}_4+A_{24})}\big ]\right) ,\ K_1,K_3\rightarrow -\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \bar{\widetilde{K}}_2=K_2+A_{12}+A_{23},\ \bar{\widetilde{K}}_4=K_4+A_{14}+A_{34}. \end{aligned}$$

• (vi) If $K_3,K_4=\mathrm{constant}$,

  $$\begin{aligned} w[4]_\mathrm{SM+SM}\rightarrow \left\{ \begin{array}{l} -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2\bar{\widehat{K}}_3} +\mathrm{e}^{-2\bar{\widehat{K}}_4}+e^{-2(\bar{\widehat{K}}_3 +\bar{\widehat{K}}_4+A_{34})}\big ]\right) ,\ K_1,K_2\rightarrow -\infty ,\\ -3\left( c^2-\dfrac{\partial ^2}{\partial x^2}\ln \big [1+\mathrm{e}^{-2K_3}+\mathrm{e}^{-2K_4}+e^{-2(K_3+K_4+A_{34})}\big ]\right) ,\ K_1,K_2\rightarrow +\infty , \end{array} \right. \end{aligned}$$

  where

  $$\begin{aligned} \bar{\widehat{K}}_3=K_3+A_{13}+A_{23},\ \bar{\widehat{K}}_4=K_4+A_{14}+A_{24}. \end{aligned}$$

  For illustration, we display in Fig. 7(a) and 7(b) the collisions of two antidark soliton molecules on the (x, t) and (y, t) planes, respectively. The collisions on the (x, t) and (y, t) planes can be similarly presented, and here we omit exhibiting them.

Fig. 7

a, b Collision of two antidark soliton molecules in Eq. (22) for $N=4$ on the (x, t) and (y, t) planes. The parameters are a $c=1,a=\frac{1}{2},\lambda _1=0,\lambda _2=\frac{1}{4},\lambda _3=\frac{1}{3},\lambda _4=\frac{7}{12}, \chi _1=\frac{\mathrm{i}}{2}\sqrt{15},\chi _2=\frac{1}{2}+\mathrm{i}\sqrt{3},\chi _3=-\frac{2}{3}+\frac{\mathrm{i}}{6}\sqrt{143}, \chi _4=\frac{7}{6}+\frac{\mathrm{i}}{3}\sqrt{11}$; b $c=1,a=\frac{1}{2},\lambda _1=-1,\lambda _2=-\frac{1}{5},\lambda _3=-\frac{1}{3},\lambda _4=-\frac{5}{7}, \chi _1=-2+\frac{\mathrm{i}}{2}\sqrt{7},\chi _2=-\frac{2}{5}+\frac{\mathrm{i}}{10}\sqrt{399}, \chi _3=-\frac{2}{3}+\frac{\mathrm{i}}{6}\sqrt{143},\chi _4=-\frac{10}{7}+\frac{\mathrm{i}}{14}\sqrt{615}$. The other parameters are $\beta _1=\frac{1}{10{,}000},\beta _2=10{,}000,\beta _3=20{,}000,\beta _4=\frac{1}{20{,}000}$

5 Conclusion

In summary, based on a quartet lax pair, we have constructed the N-antidark soliton solution represented in a compact determinant form as well as the equivalent Hirota’s bilinear N-soliton solution form for the (3+1)D NEE (1) by the N-fold DT along with the limit technique. The (3+1)D model, as a higher-dimensional generalization of the KdV equation, is decomposed to three integrable (1+1)D equations, i.e., the NLS equation, the cmKdV equation and the LPD equation. The two- and the three-antidark soliton solutions on the (x, y), (x, t), (x, z), (y, t), (y, z) and (t, z) planes have been graphically exhibited. The asymptotic analysis has been rigorously performed for the N-antidark soliton solution. Moreover, by virtue of the velocity resonant method, we have found that the soliton molecule that has two antidark solitons propagating with the same velocities can be formed on the (x, t), (y, t), (y, z) and t, z planes, while on the (x, y) and (x, z) planes it cannot be obtained. In addition, the elastic collision between a soliton molecule and a common soliton has been demonstrated by the asymptotic analysis method. Lastly, we have graphically and analytically discussed the elastic collision of two antidark soliton molecules on the basis of the four-antidark soliton solution. We hope these results may help understand the soliton molecule dynamics in fields ranging from hydrodynamics to nonlinear optics, and so on.

Appendix: The derivation of Eq. (22)

Proof

Considering the following $N\times N$ determinant with respect to $\zeta$

$$\begin{aligned} g(\zeta )=\det \left( \dfrac{\beta _{j}}{\chi _l-\chi _{j}^{*}}\delta _{jl}\zeta +\dfrac{1}{\chi _l-\chi _j^{*}} \mathrm{e}^{\mathrm{i}(\theta _l-\theta _{j}^{*})} \right) _{1\le j,l\le N}, \end{aligned}$$

we have the expansion

$$\begin{aligned} g(\zeta )=\left( \prod _{i=1}^{N}\dfrac{\beta _i}{\chi _i-\chi _i^{*}}\right) (\zeta ^N+a_1\zeta ^{N-1}+\cdots +a_N). \end{aligned}$$

Then, one can compute that

$$\begin{aligned} a_N= & {} g(0)/\left( \prod _{i=1}^{N}\dfrac{\beta _i}{\chi _i-\chi _i^{*}}\right) \\= & {} \det \left( \dfrac{1}{\chi _l-\chi _j^{*}} \mathrm{e}^{\mathrm{i}(\theta _l-\theta _{j}^{*})} \right) /\left( \prod _{i=1}^{N}\dfrac{\beta _i}{\chi _i-\chi _i^{*}}\right) . \end{aligned}$$

In terms of the determinant of the following Cauchy matrix

$$\begin{aligned} \det \left( \dfrac{1}{\chi _l-\chi _j^{*}}\right) =\prod _{i=1}^{N}\dfrac{1}{\chi _i-\chi _i^{*}}\prod _{1\le j<l}^{N}\dfrac{|\chi _j-\chi _l|^2}{|\chi _j-\chi _l^{*}|^2}, \end{aligned}$$

one obtains

$$\begin{aligned} a_N= & {} \mathrm{e}^{\mathrm{i}(\theta _1-\theta _1^{*})+\mathrm{i}(\theta _2-\theta _2^{*})+\cdots +\mathrm{i}(\theta _N-\theta _N^{*})}\dfrac{1}{\beta _1\beta _2\cdots \beta _N}\\&\prod _{1\le j<l}^{N} \dfrac{|\chi _j-\chi _l|^2}{|\chi _j-\chi _l^{*}|^2} \\= & {} \mathrm{e}^{-2(\sum _{j=1}^{N}K_j+\sum _{1\le j<l}^{N}\mu _j\mu _lA_{jl}) }. \end{aligned}$$

Furthermore, we can calculate that

$$\begin{aligned} \begin{array}{l} a_{N-1}= g'(0)/\left( \prod _{i=1}^{N}\dfrac{\beta _i}{\chi _i-\chi _i^{*}}\right) \\ =\displaystyle \mathrm{e}^{\mathrm{i}(\theta _2-\theta _2^{*})+\mathrm{i}(\theta _3-\theta _3^{*})+\cdots +\mathrm{i}(\theta _N-\theta _N^{*})}\dfrac{1}{\beta _2\beta _3\cdots \beta _N}\\ \prod _{2\le j<l}^{N}\dfrac{|\chi _j-\chi _l|^2}{|\chi _j-\chi _l^{*}|^2}\\ \displaystyle \qquad \qquad +\mathrm{e}^{\mathrm{i}(\theta _1-\theta _1^{*})+\mathrm{i}(\theta _3-\theta _3^{*})+\cdots +\mathrm{i}(\theta _N-\theta _N^{*})}\dfrac{1}{\beta _1\beta _3\cdots \beta _N}\\ \qquad \prod _{ {{\begin{array}{c} 1\le j<l,\\ j\ne 2\\ \end{array}}}}^{N}\dfrac{|\chi _j-\chi _l|^2}{|\chi _j-\chi _l^{*}|^2}+\cdots \\ \qquad \qquad \displaystyle +\mathrm{e}^{\mathrm{i}(\theta _1-\theta _1^{*})+\mathrm{i}(\theta _2-\theta _2^{*})+\cdots +\mathrm{i}(\theta _{N-1}-\theta _{N-1}^{*})}\\ \dfrac{1}{\beta _1\beta _2\cdots \beta _{N-1}}\prod _{1\le j<l}^{N-1}\dfrac{|\chi _j-\chi _l|^2}{|\chi _j-\chi _l^{*}|^2}. \end{array} \end{aligned}$$

Continuing the above process by following

$$\begin{aligned} a_{N-2}= & {} \dfrac{1}{2!}g''(0)/\left( \prod _{i=1}^{N}\dfrac{\beta _i}{\chi _i-\chi _i^{*}}\right) ,\cdots ,\\ a_{1}= & {} \dfrac{1}{(N-1)!}g^{N-1}(0)/\left( \prod _{i=1}^{N}\dfrac{\beta _i}{\chi _i-\chi _i^{*}}\right) , \end{aligned}$$

one can infer that

$$\begin{aligned}&\widehat{M}=g(1)=\det \left( \dfrac{\beta _{j}}{\chi _l-\chi _{j}^{*}}\delta _{jl}+\dfrac{1}{\chi _l-\chi _j^{*}} \mathrm{e}^{\mathrm{i}(\theta _l-\theta _{j}^{*})} \right) \\&\quad = \sum _{\mu =0,1}\mathrm{e}^{-2(\sum _{j=1}^{n}\mu _jK_j+\sum _{1\le j<l}^{n}\mu _j\mu _lA_{jl})}. \end{aligned}$$

$\square$