Color image encryption based on cross 2D hyperchaotic map using combined cycle shift scrambling and selecting diffusion

Abstract

A novel color image encryption algorithm based on a cross 2D hyperchaotic map is proposed in this paper. The cross 2D hyperchaotic map is constructed using one nonlinear function and two chaotic maps with a cross structure. Chaotic behaviors are illustrated using bifurcation diagrams, Lyapunov exponent spectra, phase portraits, etc. In the color image encryption algorithm, the keys are generated using hash function SHA-512 and the information of the plain color image. First, the color plain image is converted to a combined bit-level matrix and permuted by the chaos-based row and column combined cycle shift scrambling method. Then, the scrambled integer matrix is diffused according to the selecting sequence which depends on the chaotic sequence. Last, decompose the diffusion matrix to get the encrypted color image. Simulation experiments and security evaluations show that the algorithm can encrypt the color image effectively and has good security to resist various kinds of attacks.

1 Introduction

In modern society, along as the fast growth of the Internet, big data, artificial intelligence, and 5G communications, a large amount of information has been digitized and transmitted over the network. As an important information carrier, the security of digital images attracts more and more attention. Because color images contain richer information than gray-level images, the related research in encryption of color images has been a hot research topic [1,2,3,4,5,6,7,8,9,10,11].

The method to encrypt image is different from the way to encrypt text because the image has characteristics of massive data volume and highly relevant contents between pixels. Thus, traditional encryption technologies include DES, IDES, and RSA are not any more appropriate for encrypting image. The chaotic system has the features of sensitiveness of control parameters and initial conditions, ergodicity, random-like behavior, and unpredictable orbit. It corresponds to the concepts of key design, confusion, diffusion, and round-robin in cryptography, which makes chaos theory have great potential in the field of cryptography.

In the last decades, many methods of image cryptography are introduced based on chaos theory [12,13,14,15,16,17,18,19,20]. Because of the limitation of computer precision, the dynamical behavior of most low-dimensional chaotic systems degenerates, which leads to the defects of small keyspace and weak security performance. The image encryption algorithms design of using a high-dimensional continuous chaotic system still have the defect that the encrypted image interruptible by known-plaintext attack or selected plaintext attack [21,22,23,24]. Besides, the computational complexity and time consumption of the encryption algorithm are increased.

Compared with chaotic systems, hyperchaotic maps having more than one positive Lyapunov exponent have more complicated and abundant behaviors of dynamics, which enhance the stochasticity and unpredictability of the relevant systems [25]. Therefore, when applied to encryption, the hyperchaotic system can generate larger keyspace and more complex random sequences. Using the hyperchaotic system to design algorithms for encrypting color image will greatly improve the security of the algorithm [26,27,28,29,30,31,32].

How to design an encryption algorithm according to the characteristics of the color image and chaotic system still has a large research value. In the last several years, some new chaotic maps have been applied to image encryption algorithms [33,34,35,36,37]. Some of the new chaotic maps still have defects that trajectory is not distributed in the whole phase space or has no complex dynamic behavior.

Because of the above shortcomings, we design a nonlinear discrete cross 2D hyperchaotic map and propose a color image cryptography technique based on this hyperchaotic map. The 2D hyperchaotic map is constructed using one nonlinear function and two chaotic maps with cross structure. Chaotic behaviors are illustrated using bifurcation diagrams, Lyapunov exponent spectra, phase portraits, etc. The simulation results prove that the cross 2D hyperchaotic map has good chaotic performance. In the color image encryption algorithm, the keys are associated with the plain color image, that is, distinct plain color images produce different keys, thus enhancing security against selected plaintext/ciphertext attacks. The color plain image is converted to a combined bit-level matrix and permuted by the chaos-based row and column combined cycle shift scrambling method. Then, the scrambled integer matrix is diffused according to the selecting sequence which depends on the chaotic sequence. The cipher color image is obtained by decomposed the diffused matrix. The proposed encryption algorithm makes the three color components of the color image influence each other to eliminate the correlations between them. Simulation results show that the algorithm can encrypt the color image effectively and has good security.

The remainder of this paper has been structured in the following ways. Section 2 introduces the model of the nonlinear cross 2D hyperchaotic map. In Sect. 3, we analyze the dynamic behaviors of the proposed cross 2D hyperchaotic map. Section 4 introduces algorithm for encryption and decryption of color images. Section 5 evaluates the results of the experiments and the security of the method. Section 6 provides the conclusion.

2 Cross 2D hyperchaotic map

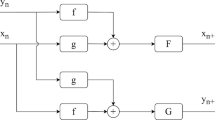
In this paper, a cross 2D hyperchaotic map is proposed, and the structure is shown in Fig. 1. The proposed model has two inputs variables and two cross outputs, which is when input is x_n the output is y_n+1, and when input is y_n the output is x_n+1. Function f is a nonlinear function, functions F and G are two chaotic maps. The + sign indicates the addition of two inputs. The mathematical expression of the model is shown in Eq. (1).

$$ \left\{ \begin{gathered} x_{{n + 1}} = F(f(y_{n} )) \hfill \\ y_{{n + 1}} = G(x_{n} + y_{n} ) \hfill \\ \end{gathered} \right. $$

(1)

Fig. 1

Diagram of Nonlinear cross 2D hyperchaotic map

where F and G can be selected as any one-dimensional chaotic map.

The chaotic map F is chosen as the infinite collapse map [38] defined as

$$ x_{{i + 1}} = \sin \left( {\frac{\alpha }{{x_{i} }}} \right) $$

(2)

where its control parameter $\alpha \ne 0$. And the chaotic map G is chosen as the Sine map in this paper. The Sine map is given as

$$ x_{{i + 1}} = \beta \sin \left( {\pi x_{i} } \right) $$

(3)

where $\beta$ is a control parameter and it has an interval of (0,1]. The nonlinear function f is set to sin function, that is $f(x) = sin(x)$. So the mathematical expression of the modified 2D coupled chaotic map model is set to

$$ \left\{ \begin{gathered} x_{{i + 1}} = \sin \left( {\frac{\alpha }{{\sin (y_{i} )}}} \right) \hfill \\ y_{{i + 1}} = \beta \sin (\pi (x_{i} + y_{i} )) \hfill \\ \end{gathered} \right. $$

(4)

where its control parameter $\alpha \ne 0$, $\beta \in (0,1]$, the initial value $y_{0} \ne 0$.

3 Dynamics analysis of the cross 2D hyperchaotic map

3.1 Bifurcation diagram

The dynamical behaviors of a chaotic system can be evaluated by its bifurcation diagram. A bifurcation diagram shows the changes in the system’s motion state along with the control parameters. The evolution process of the system can be directly observed by the bifurcation diagram. Set the initial conditions $x_{0} = 0.3$and $y_{0} = 0.6$. Fixing $\beta = 1$, when the control parameter $\alpha$ in the range [0.25, 2], the bifurcation diagram is illustrated in Fig. 2a. From Fig. 2a, we can see that the system goes through a periodic state to chaotic orbit. When $0.55 < \alpha \le 2$, the system exhibits chaotic behavior. Fixing $\alpha = 1$ illustrates the bifurcation diagram when control parameter $\beta$ in the range [0.1, 1] in Fig. 2b. The results show that the system exhibits the periodic behavior between (0.34, 0.353), and produces chaotic attractors throughout the remaining range.

Fig. 2

Bifurcation diagrams of the proposed system

3.2 Lyapunov exponent spectrum

The Lyapunov exponent is one of the characteristics used to identify the chaotic characteristics of dynamic systems. For a high-order dynamic system, due to the different directions of the initial separation vector, the exponential divergence rate will be different, so there are multiple Lyapunov exponents. The system has the same number of Lyapunov exponents and order. Consequently, the two-dimensional system with two Lyapunov exponents.

The Lyapunov exponents of the system are two negative numbers, indicating that the system is at a fixed point. The system has a negative and a zero Lyapunov exponent when it is in a periodic orbit. The Lyapunov exponent of the system is one positive and one negative when it is in a chaotic orbit. The Lyapunov exponent of the system is two positive numbers when the system is in hyperchaotic state. Hyperchaotic systems normally possess more sophisticated and abundant dynamic behaviors compared to chaotic systems, which enhances the stochastic and unpredictable nature of the systems.

In the proposed map, the Lyapunov exponents spectrum is shown in Fig. 3a when fixing $\beta = 1$ and varying $\alpha$. It can be seen that when $\alpha \in (1.55,{\text{ }}1.47)$, the largest Lyapunov exponent is positive, so the system is in the chaotic state. When $\alpha \in [1.47,{\text{ }}2]$, the two Lyapunov exponents are both positive, so the system can generate hyperchaotic attractors.

Fig. 3

Lyapunov exponents spectrum

Figure 3b shows the Lyapunov exponents spectrum varying $\beta$ when $\alpha = 1$. We can see that the system exhibits the periodic behavior when $\beta \in (0.34,{\text{ }}0.353)$. There are two positive Lyapunov exponents when $\beta \in [0.25,{\text{ }}0.34] \cup [0.354,{\text{ 0}}{\text{.56}}]$, and the map exhibits the hyperchaotic state. The system is in chaotic attractors in the range of $\beta \in (0.56,{\text{ }}1]$.

It can be seen that there is a one-to-one correspondence between the Lyapunov exponent spectrum and the bifurcation diagrams.

3.3 Attractor phase diagram

A chaotic system with good chaotic performance usually has complex attractors which occupy a large area in the phase diagram. Set the initial conditions $x_{0} = 0.3$ and $y_{0} = 0.6$; the attractor phase diagrams are generated in Fig. 4. The system generates the hyperchaotic attractors as shown in phase diagrams (Fig. 4a and b) when parameters $\alpha = 2$, $\beta = 1$ and $\alpha = 1$, $\beta = 0.5$. When parameters $\alpha = 1$ and $\beta = 1$, the attractor phase diagram is shown in Fig. 4c; the system generates the chaotic attractor. When parameters $\alpha = 1$ and $\beta = 0.35$, the system demonstrates the periodic behavior displayed in Fig. 4d.

Fig. 4

Attractor phase diagrams

3.4 Sensitivity analysis of initial value

A well-performing chaotic system can be extremely sensible to its initial values. A slight difference of initial value can produce a completely diverse chaotic trajectory. In order to analyze the initial sensitivity of the proposed hyperchaotic map, the initial value is varied 10^–16, and the experimental outcomes are shown in Fig. 5. It is observed that the proposed hyperchaotic system has great sensitivity to the initial value.

Fig. 5

Initial value sensitivity

The simulation results indicate that, compared with other two-dimensional chaotic maps, the proposed 2D hyperchaotic map has better chaotic property as shown in Table 1.

Table 1 Chaotic property compared with other 2D chaotic maps

4 Cross 2D hyperchaotic map-based color image encryption and decryption algorithm

Since the proposed cross 2D hyperchaotic map has good chaotic performance, this section proposes a color image cryptographic method based on this hyperchaotic map. Figure 6 displays the flowchart for the proposed encryption scheme, which includes the substitution process and the diffusion process.

Fig. 6

Flowchart of proposed encryption algorithm

4.1 Key generation

Due to the irreversibility and strong security of the hash algorithm, we use it to generate the key of the color image encryption scheme. A 512-bit secret key K is produced by the SHA-512 hash function $K = SHA_{{512}} ({\text{ }})$, in which the input value of this hash function is related to the plain color image to increase the security and able to resist select plaintext/ ciphertext attack. Divide the 512-bit key K into 8-bit blocks, which can be expressed as $K{\text{ = }}k_{1} ,k_{2} ,...,k_{{64}}$. K is processed and grouped in sub-keys as follows:

$$ \left\{ \begin{gathered} K1 = \frac{{k_{1} \oplus k_{2} \oplus ... \oplus k_{{16}} }}{{256}} \hfill \\ K2 = \frac{{k_{{17}} \oplus k_{{18}} \oplus ... \oplus k_{{32}} }}{{256}} \hfill \\ K3 = \frac{{k_{{33}} \oplus k_{{34}} \oplus ... \oplus k_{{48}} }}{{256}} \hfill \\ K4 = \frac{{k_{{49}} \oplus k_{{50}} \oplus ... \oplus k_{{64}} }}{{256}} \hfill \\ \end{gathered} \right.. $$

(5)

4.2 Chaos-based row and column combined cycle shift scrambling

In the scrambling process, average the statistical information of the image by varying the position of the image pixels to make the image energy uniform. A chaos-based row and column combined cycle shift scrambling method is proposed:

Step 1. The image matrix is assumed to be of size M × N, that is M rows and N columns. Set the row vectors PR and column vectors PC. Process rows and columns together, there are M + N vectors.

Step 2. A chaotic sequence X₁ of length M + N, a chaotic sequence X₂ of length M and a chaotic sequence X₃ of length N are selected. The chaotic sequences are further processed by

$$ X_{1} ^{\prime } (i) = \bmod (ceil(X_{1} (i) \times 10^{{15}} ),M + N),\quad {\text{1}} \le i \le M + N $$

(6)

$$ X_{2} ^{\prime } (j) = \bmod (ceil(X_{2} (j) \times 10^{{15}} ),N),\quad {\text{1}} \le j \le M $$

(7)

$$ X_{3} ^{\prime } (k) = \bmod (ceil(X_{3} (k) \times 10^{{15}} ),M),\quad {\text{1}} \le k \le N $$

(8)

where ceil(x) gives back the smallest integer greater than or equal to x, and mod() represents the modular action.

Step 3. Sort the sequence $X_{1} ^{\prime }$, record the transform position TP of each element in the chaotic series, thus the length of vector TP is M + N and the elements of TP are all non-repeating integers between 1 and M + N.

Step 4. Exchange the locations of image elements using row and column combined cycle shift by

$$ \left\{ {\begin{array}{*{20}c} {PR(TP(i)) = circshift(PR(TP(i)),X_{2} ^{\prime } (j)),{\text{ }}j = j + 1} & {TP(i) \le M} \\ {PC(TP(i) - M) = circshift(PC(TP(i) - M),X_{3} ^{\prime } (k)),{\text{ }}k = k + 1} & {TP(i) > M} \\ \end{array} } \right. $$

(9)

where $circshift(A,SHIFTSIZE)$ circularly move the data in array A using the SHIFTSIZE elements. When $TP(i) \le M$, circularly shift the $TP(i)$ th row by $X_{2} ^{\prime } (j)$ elements to the right. When $TP(i) > M$, circularly shift the $TP(i) - M$ th column by $X_{3} ^{\prime } (k)$ elements down.

Take an image matrix with the size of 4 × 4 as an example shown in Fig. 7, where TP = {8, 1, 4, 7, 3, 2, 5, 6}, $X_{2} ^{\prime }$ = {3, 2, 3, 1}, $X_{3} ^{\prime }$ = {2, 0, 1, 3}. It can be seen that the position of every pixel varies only after a single permutation.

Fig. 7

4 × 4 matrix scrambled by row and column combined cycle shift

4.3 Permutation process

Step 1. In general, the size of the color plain image P is assumed to be M × N. And there are three components in the color image: the red (R) part, the green (G) part, and the blue (B) part. Each part pixel’s value in the range of 0 to 255. Hence, one pixel can be converted into 8-bit binary value. Therefore, an M × N size color image P can be expended to three binary image matrixes R_b, G_b, and B_b with size M × 8 N. Combine the R_b, G_b, and B_b matrixes vertically and get a combined image matrix P_b with 3 × M rows, 8 × N columns. Thus, the three color image components can influence each other.

Step 2. Set the permute key $K_{{permute}} = SHA_{{512}} (R,G,B)$, which R, G, and B are all the pixels in each color component of plain image so that different plain images will get a distinct key. Obtain the sub-keys K1, K2, K3, K4 according to Eq. (5), and the chaotic system (4) parameters and initial conditions are given:

$$ \left\{ \begin{gathered} \alpha = \bmod (K1,0.5) + 1 \hfill \\ \beta = \bmod (K2,0.5) + 0.6 \hfill \\ x_{0} = \bmod (K3,1) \hfill \\ y_{0} = \bmod (K4,1) \hfill \\ \end{gathered} \right.. $$

(10)

Step 3. Iterate the chaotic system (4) 3 M + 8 N + k times, the length of the sequence discarded is k for better chaos, where $k = \bmod (sum(R + G + B),100) + 500$, $sum(R + G + B)$ means the sum of all these elements in three components. Get the chaotic sequences $x(i) = \left\{ {x_{1} ,x_{2} ,...,x_{{3M + 8N}} } \right\}$ and $y(i) = \left\{ {y_{1} ,y_{2} ,...,y_{{3M + 8N}} } \right\}$.

Step 4. Use the chaos-based row and column combined cycle shift scrambling method described in Sect. 4.2 to permute the bit-level image matrix P_b with the size of 3 M × 8 N, where the chaotic sequence X₁ = $x(i)$ (i = 1, 2,…, 3 M + 8 N), X₂ = $y(i)$ (i = 1, 2,…, 3 M), X₃ = $y(i)$ (i = 3 M + 1,…, 3 M + 8 N). A permutated bit-level image matrix $P_{b} ^{\prime }$ is generated.

Step 5. Transform $P_{b} ^{\prime }$ to an integer image matrix denoted as $P^{\prime }$ with the size of 3 M × N. The position of pixels is changed as well as the value of the pixels in the permutated image $P^{\prime }$.

4.4 Diffusion process

During the diffusion process, the pixel values of the image are altered so that small differences in a single pixel spread over a maximum number of pixels. The proposed diffusion equation is chosen according to the selecting sequence which depends on the chaotic sequence.

Step 1. Set the diffuse key $K_{{diffuse}} = SHA_{{512}} (P^{\prime } ([i{\text{ }}j{\text{ }}k],:))$, where $P^{\prime } ([i{\text{ }}j{\text{ }}k],:)$ is the ith row, jth row, and kth row of the permutated image matrix $P^{\prime }$. Obtain the sub-keys K1^’, K2^’, K3^’, K4^’ according to Eq. (5), and set the initial conditions and parameters of the chaotic system (4) using Eq. (10).

Step 2. The hyperchaotic map (4) is iterated 3 M × N + k₁ times, where $k_{1} = \bmod (sum(sum(P^{\prime } (:,i:j))),100) + 500$, $P^{\prime } (:,i:j)$ is the ith to jth columns of $P^{\prime }$. Discard the former k values of the chaotic sequences. Get the chaotic series $x^{\prime}(i) = \left\{ {x_{1} ^{\prime } ,x_{2} ^{\prime } ,...,x^{\prime}_{{3M \times N}} } \right\}$ and $y^{\prime}(i) = \left\{ {y_{1} ^{\prime } ,y_{2} ^{\prime } ,...,y^{\prime}_{{3M \times N}} } \right\}$.

Step 3. The selecting sequence $S(i) = \left\{ {s_{1} ,s_{2} ,...,s_{{3M \times N}} } \right\}$ and the diffusion sequence $D(i) = \left\{ {d_{1} ,d_{2} ,...,d_{{3M \times N}} } \right\}$ can be obtained using Eqs. (11) and (12)

$$ S(i) = \bmod (ceil(x^{\prime}(i) \times 10^{{15}} ),3) $$

(11)

$$ D(i) = \bmod (ceil(y^{\prime}(i) \times 10^{{15}} ),256). $$

(12)

Step 4. According to the chaotic-based selecting diffusion equations below, the encrypted combined image pixel matrix $C^{\prime}(i) = \left\{ {c^{\prime}_{1} ,c^{\prime}_{2} ,...,c^{\prime}_{{3M \times N}} } \right\}$ can be acquired out of the diffusion matrix D and the permutation image $P^{\prime }$.

$$ \left\{ \begin{gathered} C^{\prime}(i) = \bmod (P^{\prime}(i) + D(i),256){\text{ }}S(i) = 0 \hfill \\ C^{\prime}(i) = \bmod (P^{\prime}(i) - D(i),256){\text{ }}S(i) = 1 \hfill \\ C^{\prime}(i) = P^{\prime}(i) \oplus D(i){\text{ }}S(i) = 2 \hfill \\ \end{gathered} \right. $$

(13)

where $\oplus$ denotes bit-level XOR operator.

Step 5. Vertical transformation $C^{\prime}$ into the R, G, and B color matrix to get its cipher color image C in size of M × N.

4.5 Decryption algorithm

The decryption method is the reverse of the encryption method using the permute key $K_{{permute}}$ and the diffuse key $K_{{diffuse}}$ provided in the encryption algorithm, which means $K_{{permute}}$ and $K_{{diffuse}}$ should be provided and known in the decryption method.

Step 1. Obtain the cipher image C and convert it to the R, G, and B color components’ matrix. Combine the color matrixes vertically and get a combined encrypted image matrix $C^{\prime }$ with 3 × M rows, N columns.

Step 2. Use the same diffuse key $K_{{diffuse}}$ as the encryption algorithm to obtain the same selecting sequence $S(i)$ and the diffusion sequence $D(i)$.

Step 3. The matrix $C_{D}$ can be attained using the inverse diffusion formula equation below from the diffusion matrix D and the encrypted image matrix $C^{\prime }$.

$$ \left\{ \begin{gathered} C_{D} (i) = \bmod (C^{\prime } (i) - D(i),256){\text{ }}S(i) = 0 \hfill \\ C_{D} (i) = \bmod (C^{\prime } (i) + D(i),256){\text{ }}S(i) = 1 \hfill \\ C_{D} (i) = C^{\prime } (i) \oplus D(i){\text{ }}S(i) = 2 \hfill \\ \end{gathered} \right.. $$

(14)

Step 4. Extended the matrix $C_{D}$ to its binary image matrixes $C_{{Db}}$. Use the same permute key $K_{{permute}}$ as the encryption algorithm to obtain the same chaotic sequences X₁, X₂, and X₃ in the encryption permutation process.

Step 5. The matrix $C_{P}$ can be acquired using the reverse row and column combined cycle shift scrambling Eq. (15) to reverse permute the bit-level image matrix $C_{{Db}}$.

$$ \left\{ \begin{gathered} PR(TP(i)) = circshift(PR(TP(i)), - X_{2} ^{\prime } (j)),{\text{ }}j = j + 1{\text{ }}TP(i) \le M \hfill \\ PC(TP(i) - M) = circshift(PC(TP(i) - M), - X_{3} ^{\prime } (k)),k = k + 1 TP(i) > M \hfill \\ \end{gathered} \right.. $$

(15)

Step 6. Transform $C_{P}$ to an integer image matrix denoted as $C_{I}$ which its size is 3 M × N. Convert $C_{I}$ into the R, G, and B color matrix vertically to obtain the decrypted image.

5 Experimental results and performance analysis

The experimental results and performance of the algorithm are analyzed. To verify the effectiveness of the cryptographic system, a number of images were simulated numerically.

The chosen sample images are the different sizes color images of 256 × 256 House, 500 × 480 Baboon, 512 × 512 Lena, 512 × 512 Peppers, 720 × 576 Barbara, and 768 × 512 Parrots. Figure 8 illustrates the experimental simulation performance of the House, Baboon, Lena, Barbara, and Parrots images. The encrypted images are comparable to the image of noise with no visual leakage of information.

Fig. 8

Encryption and decryption results

5.1 Keyspace analysis

The encryption algorithm with larger keyspace are better able to resist brute-force assaults and have higher degree of security. In this method, the key contains the initial conditions $x_{0}$, $y_{0}$, $x_{0} ^{\prime }$, $y_{0} ^{\prime }$, parameters $\alpha$, $\beta$, $\alpha ^{\prime}$, $\beta ^{\prime}$ and the discard length k, k₁ of the hyperchaotic system in the permutation and diffusion processes. Because the computational precision is 10^–16, the size of the keyspace for one round encryption is $10^{{16 \times 8}} > 2^{{425}}$ which is much bigger than $2^{{100}}$ to guarantee the security according to [39]. So the keyspace is sufficiently large to defend against any violent attack.

5.2 Key sensitivity analysis

For the high-security image encryption algorithm, key sensitivity is an essential feature. A slightly different key used in encryption will generate a radically altered cryptographic image. And minor changes in the key used for decryption will cause decryption failure. The encryption and decryption keys are changed 10^–16 to analyze the key sensitivity of the proposed scheme. Figure 9 displays the experimental performance of the key sensitivity. Any small modification in the encryption key will lead to a totally distinct encrypted image. A minor alteration in a key will produce an entirely different image, and the correct decrypted image will not be available.

Fig. 9

Key sensitivity

5.3 Histogram

The image histogram reveals information about the distribution of pixel values. To prevent statistical analysis attacks from recovering any meaningful message from the histogram of a cryptographic image, the cryptographic image needs to be uniformly distributed. Figure 10 shows the histograms of the plain images and the relevant cryptographic images. As shown in Fig. 10, the histogram allocation of the cryptographic images is uniform, which makes it very hard for any attacker to analyze the cryptographic image through a statistically analysis attack.

Fig. 10

Histogram of different plain images and cipher images

5.4 Correlation of adjacent pixels

The correlation between the neighboring pixels is at a high degree in a plain image, which may reveal the attacker's statistical information. Therefore, encrypted images should minimize the correlation between the adjacent pixels. For each pair, the correction factor is computed using the equation below.

$$ r_{{xy}} = \frac{{\text{cov} (x,y)}}{{\sqrt {D(x)} \sqrt {D(y)} }} $$

(16)

where $E(x) = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {x_{i} }$, $D(x) = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {(x_{i} - E(x))^{2} }$, $\text{cov} (x,y) = \frac{1}{N}\sum\limits_{{i = 1}}^{N} {(x_{i} - E(x))(y_{i} - E(y))}$, x and y are gray-scale values of two neighboring pixels in the image.

The distribution of the correlation between the color components of the original Lena image and the encrypted image in horizontal, vertical, and diagonal adjacent pixels are shown in Fig. 11. The correlation results between the adjacent pixels of the test images are provided in Table 2. From the figure and table, it can be observed that the correlation between neighboring pixels of the encrypted image satisfies zero correlation by effectively encrypt the image, indicating that the encryption method provides promising security.

Fig. 11

Correlation of adjacent pixels of plain image and cipher image

Table 2 Correlation coefficients of plain image and ciphered image

5.5 Information entropy analysis

Information entropy can be applied to quantitatively quantify and calculate the information source’s randomness. The entropy $H(m)$ of a signal source m could be calculated using the following equation:

$$ H(m) = \sum\limits_{{i = 0}}^{{2^{N} - 1}} {p(m_{i} )\log \frac{1}{{p(m_{i} )}}} , $$

(17)

where $p(m_{i} )$ denotes the symbol $m_{i}$’s probability represents the probability of symbol and the entropy is represented in bits. The information entropy is 8 for an ideal completely random image.

Table 3 calculates the information entropy of the encrypted images and compares them with those of other methods. The information entropy of the encrypted image is quite near to the theory value 8, which implies that the information disclosure during encryption is ignorable and that the cryptosystem is secure.

Table 3 The results of information entropy

5.6 Differential attack

A safe image cryptography method is supposed to be extremely sensible to any small changes in the plain image, implying that a single pixel variation in the plain image will result in a totally distinct encrypted image.

The differential attack is tested using the uniform average change intensity (UACI) and the number of pixels change rate (NPCR). The following formulas are used to calculate NPCR and UACI:

$$ {\text{NPCR}} = \frac{{\sum\nolimits_{{ij}} {D(i,j)} }}{{M \times N}} \times 100\% $$

(18)

$$ {\text{UACI}} = \frac{1}{{M \times N}}[\sum\limits_{{i,j}} {\frac{{\left| {C_{1} (i,j) - C_{2} (i,j)} \right|}}{{255}}} ] \times 100\% $$

(19)

where M and N denote the rows and columns of the image, C₁ and C₂ are the encrypted images before and after a pixel change of the plain image, respectively.

We randomly vary the one-bit value of the pixel among any color component, and then evaluate NPCR and UACI in the red, green, and blue components. Table 3 lists the NPCR and UACI performance of this algorithm and compares them with other methods. It can be observed from Table 4 that the NPCR and UACI results are quite near to the theoretical values, and the cryptosystem is effective against both plaintext and differential attacks.

Table 4 NPCR and UACI values (%)

5.7 Noise and data loss attacks

Image data are vulnerable to disturbance and data damage during the transmission process. A highly secure image cryptography algorithm is supposed to be resistant to disturbance and data loss attacks. Different densities of salt and pepper noise are added to the encrypted Lena images. From Fig. 12, it is visible that the decrypted image can be still restored with success and the noise cannot stop us to identify the decrypted image content visually.

Fig. 12

The decryption results with different density noises

The encrypted image of the lost data and the corresponding decrypted image are illustrated in Fig. 13. Results of the experiments show that the more the image is lost, the more unclear the image is decrypted. However, the image can still be decrypted and recognized although the image is half lost. The algorithm is highly robust to noise attacks and information loss attacks.

Fig. 13

Data loss attack

5.8 Running Performance

To satisfy the fast increase in image data capacity, image cryptography methods should be fast and efficient. In the proposed algorithm, all pixels in the three color components can be completely shuffled through one operation of row and column combined cycle shift scrambling. And it requires only a single turn of permutation and diffusion to realize high security. So our proposed algorithm can exhibit rapid encryption speed.

To analyze the calculation complexity of the proposed scheme, assume that the size of the color plain image is M × N. In the permutation process, the time complexity is O(3 M + 8 N). During the diffusion process, the complexity of time is O(M × N × 3). Therefore, the time complexity of the proposed method is O(M × N).

To calculate the properties of this method, MATLAB R2017a with Intel(R) Core (TM) i5-8300H CPU@2.30 GHz and 4.0G RAM on Windows 10 OS were utilized. Table 5 lists the running time of the proposed encrypting images. When encryption and decryption of different color images with different sizes, the program can achieve good running performance within a few seconds.

Table 5 Execution time analysis (seconds)

Table 6 indicates the running time of the proposed algorithm compares with other methods when encrypt and decrypt color images of size 512 × 512. Although the experimental environments are different, our proposed algorithm shows relatively good efficiency compared with the similar environment algorithms. It shows that our proposed algorithm is preferred for real-time applications due to its performance in encryption and decryption speed.

Table 6 Compared with other methods for execution time (seconds)

6 Conclusion

This paper designed a cross 2D hyperchaotic map, which is constructed using one nonlinear function and two chaotic maps with cross structure. Numerous experiments such as bifurcation diagrams, Lyapunov exponent spectra, and phase portraits are carried out to illustrate the complex chaotic behavior of the proposed hyperchaotic system. The simulation outcomes show that this nonlinear crossed two-dimensional hyperchaotic system provides good chaotic performance. In the color image encryption algorithm, the keys are generated using hash function SHA-512 and the information of the plain color image. First, the color plain image is converted to a combined bit-level matrix and permutated by the chaotic-based row and column combined cycle shift scrambling method. Then, the scrambled integer matrix is diffused according to the selecting sequence. The cipher color image is obtained by decomposed the diffused matrix. The proposed encryption algorithm makes the three color components of color image affect one another to eliminate the correlations between them. Through the comparison of encryption performance, this proposed algorithm has been proven to have enough keyspace, a sensitive key, resistance to statistical attacks and differential attacks, and is applicable for real-time implementations.