1 Introduction

In recent years, a variety of chaos-based digital image encryption algorithms have been investigated [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27, 29,30,31, 35, 37,38,39,40]. Spatiotemporal chaotic system is gradually regarded with better properties suitable for image encryption than one-dimensional chaotic system, such as larger parameter space, better randomness and more chaotic sequences [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27, 35, 37,38,39,40]. Then, many researches [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27, 34, 35] are based on the system of coupled map lattices (CML) [26, 27], which enhances the security of the encryption algorithms. Seyedzadeh et al. [13] proposed a novel image encryption algorithm based on the two-dimensional logistic map and the quantum chaotic map, which are independently coupled with nearest-neighboring coupled map lattices. Wang et al. [14] proposed an encryption algorithm for images using CML and DNA sequence operations. However, the CML system is coupled by adjacent lattices, and the parameter \(\mu\) still has periodic windows in the bifurcation diagram of some lattice. Due to the adjacent coupling between lattices, parameters \(\mu \in (3.87,3.925)\) and \(\varepsilon = 0.1\) can only generate local chaotic behavior of the CML system [27], which implies some of the lattices are not in chaotic behavior. The lattice should be selected carefully for image encryption because such space regular coupling of the adjacent coupling in the CML system is a linear coupling in space.

Many studies [15,16,17,18] concentrated on dynamically random links for coupling. Sinha [15] proposed the random coupling of spatiotemporal system which initiated the study of the non-neighborhood coupling in coupled map lattices. Mondal et al. [16] presented the enhancement spatiotemporal regularity by rapidly switched random links. Nag et al. [18] presented the synchronization behavior of delay-coupled chaotic smooth unmoral maps with stochastic switching of links at every time step. However, the chaotic sequences in such systems of randomness-based coupling cannot be reproduced at the second time in the same parameters, which are not suitable for applying in cryptography.

The NCML and MLNCML systems [19, 20] presented nonlinear chaotic map coupling method to achieve the non-neighborhood coupling based on one-dimensional CML. However, a two-dimensional coupled map lattice allows a more precise description of the real nature phenomena than the one-dimensional case. To the best of our knowledge, very little work was done to adapt this coupling to evaluate two-dimensional coupled map lattices. In this paper, we discover the new features of spatiotemporal chaotic systems in spatial mixed coupling with the two-dimensional CML. Furthermore, this system is also evaluated for the feasibility of the image encryption application for its superior features in dynamics.

A variety of image encryption algorithms using bit-level permutation have been investigated, which can change the position and value of a pixel simultaneously [28,29,30,31,32,33, 35, 36]. In [32], Praveenkumar et al. proposed a novel image encryption approach with chaotic sequences which are generated for each bit plane. All pixels of an image are separated into groups of bits by information of different bit planes in Zhu’s scheme [29]. However, the bits in one-bit plane cannot be permuted into other bit planes in these algorithms. Therefore, the statistical information in each bit plane remains unmodified.

In this paper, we employ the two-dimensional spatiotemporal chaotic system which mixed linear–nonlinear coupled map lattices for the diffusion in the image encryption. The two-dimensional mixed system employing the spatial nonlinear coupling can generate better pseudo-random sequences than that employing adjacent coupling. The mixed system also contains the new features such as less periodic windows in bifurcations and larger range of parameters in chaotic dynamics. For the permutation phase, we employ the Arnold cat map for bit-level permutation. Furthermore, the wide range of choices for the initial conditions and control parameters lead to a large key space. The experimental results show the effectiveness of the proposed image encryption algorithm.

The remainder of this paper is organized as follows. In Sect. 2, the proposed spatiotemporal chaotic system based on two-dimensional CML is presented. The proposed image encryption scheme is described in Sect. 3. Simulation results and performance analyses are reported in Sect. 4.

2 The proposed spatiotemporal chaotic system

The proposed spatiotemporal chaotic system based on two-dimensional CML can be represented by

$$\begin{aligned} \begin{aligned} x_{(n+1)}(i,j)&=(1-\varepsilon )f[x_n(i,j)] +(1-\eta )\frac{\varepsilon }{4}\{f[x_n(i-1,j)]\\&\quad +\,f[x_n(i+1,j)]+f[x_n(i,j-1)]+f[x_n(i,j+1)]\}\\&\quad +\,\eta \frac{\varepsilon }{4}\{f[x_n(a,j)]+f[x_n(b,j)]+f[x_n(i,c)]+f[x_n(i,d)]\}, \end{aligned} \end{aligned}$$
(1)

where i, j, a, b, c, d are the lattices \((1\le i,j,a,b,c,d\le L)\), \(\varepsilon\) is the coupling parameter \((0\le \varepsilon \le 1)\), \(\eta\) is the coupling parameter \((0\le \eta \le 1)\), n is the time index \((n=1,2,3...)\) and \(f(x)=\mu x(1-x)\), \(\mu \in (0,4]\). The relations of i, j, a, b, c, d are defined by the Arnold cat map described by

$$\begin{aligned} \left[ \begin{array}{c} a \\ b \end{array} \right] = \left[ \begin{array}{cc} 1 &{} p \\ q &{} pq+1 \end{array} \right] \left[ \begin{array}{c} i+1 \\ i-1 \end{array} \right] ({\text {mod}}\ L), \end{aligned}$$
(2)
$$\begin{aligned} \left[ \begin{array}{c} c \\ d \end{array} \right] = \left[ \begin{array}{cc} 1 &{} p \\ q &{} pq+1 \end{array} \right] \left[ \begin{array}{c} j+1 \\ j-1 \end{array} \right] ({\text {mod}}\ L), \end{aligned}$$
(3)

where p and q are the parameters of Arnold cat map.

The parameters p, q and \(\eta\) make the proposed system into diverse dynamics systems. When selecting \(\eta = 0\), Eq. (1) can be degenerated as the 2DCML system [26] as

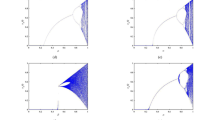
$$\begin{aligned} \begin{aligned} x_{(n+1)}(i,j)&=(1-\varepsilon )f[x_n(i,j)]+\frac{\varepsilon }{4}\{f[x_n(i-1,j)]\\&+f[x_n(i+1,j)]+f[x_n(i,j-1)]+f[x_n(i,j+1)]\}. \end{aligned} \end{aligned}$$
(4)

The bifurcation diagram without periodic windows in the proposed system is the new feature for cryptography. The CML system is regarded as a suitable spatiotemporal chaotic system for cryptography partially because of its less periodic windows than low-dimension chaotic map. Thus, the proposed system is more suitable for cryptography for the same reason. The parameter as a secret key has a larger key space than logistic map or the CML system. Besides, the parameter can be designed as one of the secret keys.

Without loss of generality, the proposed system assigns the same \(L = 100\) as the CML system does [26]. Figure 1b–e indicates that the periodic windows are reduced compared with the 2DCML system in Fig. 1a when increasing the parameter \(\eta\). When increasing the value of \(\eta\), the number of bifurcation points is varying larger and the gaps between bifurcation points are varying closer. Due to the nonlinear coupling leading to the instability of the possible periods of orbits, the times of period doubling bifurcations is misled and unobvious. Therefore, periodic windows are reduced and when increasing the value of the parameter \(\eta\), the nonlinear coupling is strengthened and periodic windows are vanished eventually. The nonlinear coupling decreases the times of period doubling bifurcations, and the proposed system becomes chaotic after a point.

Fig. 1
figure 1

Bifurcation diagrams when \(\mu \in [3.5,4.0]\). a The 2DCML system, b The proposed system \((\eta = 0.3)\), c The proposed system \((\eta = 0.5)\), d The proposed system \((\eta = 0.7)\), e The proposed system \((\eta = 0.9)\)

Full size image

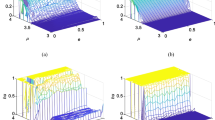
Any system holding chaotic behavior presented at least one positive Lyapunov exponent. The proposed system can be considered as L dimensions dynamics; the Kolmogorov-Sinai entropy density h of the L dimensions dynamics is average of positive Lyapunov exponents [34]. When \(\eta = 0.3\), Fig. 2b shows that there are only two valleys at \(3.6< \mu <3.8\) and \(\varepsilon = 0.1\), \(3.6< \mu <3.8\) and \(\varepsilon = 0.2\) in the proposed system while the 2DCML system has three valleys at \(3.6< \mu <3.8\) and \(\varepsilon = 0.1\), \(3.6< \mu <3.8\) and \(\varepsilon = 0.2\), \(3.6< \mu <3.8\) and \(\varepsilon = 0.6\), which are shown in Fig. 2a. Therefore, the proposed system characterizes stronger chaotic behaviors at the range of \(3.6< \mu <3.8\) and \(\varepsilon = 0.6\) than the 2DCML system. During increasing the value of \(\eta\), Fig. 2b–e indicates that the proposed system has higher Kolmogorov-Sinai entropy density than the 2DCML system [26] and the MLNCML system [19] do, which is shown in Fig. 2a, f.

Fig. 2
figure 2

Kolmogorov-Sinai entropy density for different parameters. a The 2DCML system, b The proposed system \((\eta = 0.3)\), c The proposed system \((\eta = 0.5)\), d The proposed system \((\eta = 0.7)\), e The proposed system \((\eta = 0.9)\), f The MLNCML system

Full size image

Without loss of generality, we focus on the proposed system by assuming a grid of \(L = 64\), \(L\times L = 4096\) as the 2DCML system [26] assigned the same value. When the value of \(\eta\) increases, nonlinear coupling strengthens the diffusions between lattices harder than neighborhood coupling does. The local inhomogeneous trend becomes stronger, and the reactions dominate the system behavior. At the same time, the orderly trend of diffusion is obviously weakened because most of lattices are in chaos and turbulence. Figure 3a indicates that the same parameters \(\mu\) and \(\varepsilon\) which lead the proposed system in fully turbulence can only lead the 2DCML system in defect turbulence pattern shown in Fig. 3b. Therefore, compared with the 2DCML system, the proposed system contains larger range of parameters for this pattern. Figure 4a, b indicates that the proposed system is chaos fully compared with the 2DCML.

Fig. 3
figure 3

Snapshot patterns for the proposed system and 2DCML when \(times = 1000\). a The proposed system \((\mu = 3.93\), \(\eta = 0.3\) and \(\varepsilon = 0.1)\), b The 2DCML system \((\mu = 3.93\) and \(\varepsilon = 0.1)\)

Full size image
Fig. 4
figure 4

Regular behaviors when \(\mu = 3.93\). a The proposed system zoomed \((\mu = 3.93\), \(\eta = 0.3\) and \(\varepsilon = 0.1)\), b The 2DCML system zoomed \((\mu = 3.93\) and \(\varepsilon = 0.1)\)

Full size image

3 The proposed image encryption algorithm

Firstly, the image is permuted by the Arnold cat map for bit-level permutation and then diffused by the chaotic sequences of the proposed system. The permutation and diffusion phases can be encrypted in many rounds for higher security.

3.1 Secret key formulation

The proposed algorithm process utilizes a more than 4000 bit-long secret key. The secret key is composed of: K, \(\mu (\mu \in [3.87, 4])\), \(\varepsilon (\varepsilon \in [0.1, 1])\), \(\eta (\eta \in [0.5, 1])\). The secret key K includes 100 components denoted as \(K =\)\(\{ K(1,1)\), K(1, 2), \(K(1,3)\ldots\), \(K(10,10) \}\) where each component of K(i, j) is a 40-bit-long unit. The secret keys \(\mu\), \(\varepsilon\) and \(\eta\) refer to the parameters \(\mu\), \(\varepsilon\) and \(\eta\) in Eq. (1).

3.2 Permutation phase

Pixel-level confusion can only change the locations of the original pixels. For bit-level permutation, the situation is quite different. A pixel in a grayscale image usually consists of eight bits, but these bits carry different amount of information. For example, if the eight bits among the eight pixels are permuted, \(2^7/255\) of the total information of each pixel is exchanged. In other words, 50.2% of the information of each pixel is changed if the eight bits of the pixels are permuted. Therefore, bit-level permutation not only modifies the pixel values but also exchanges the information of the pixels. A plain image with 256 gray levels can be extended to eight binary images, in which only two values (0 and 1) exist for each pixel [28, 29].

The plain image is firstly extended to bit plane, given by: \(G(x,y) = Pic8Pic7Pic6...Pic1\), where G(x, y) is the value of the pixel at coordinate (x, y) and the number in parentheses indicates the bit index from highest bit 8 to the lowest bit 1. A bit can contain different amounts of information depending on its position in the pixel. The highest eighth bit carries about 50% of the total information of the image. On the other hand, the lower three bits (third, second and first) carry less than 3% of the image information. In order to modify the statistical information in each bit plane, we reorganize binary images to two groups: \(P1=\{Pic8,Pic3,Pic2,Pic1\}\) and \(P2=\{Pic7,Pic6,Pic5,Pic4\}\) in which P1 carries about 13.2% of the image information and P2 carries about 11.8% of the total information of image. After the image is reorganized, the information distribution of the image is more balanced, which is more conducive to the encryption of the image. The binary images of Lena reorganized are shown in Fig. 5.

Fig. 5
figure 5

Binary images reorganized. aP1, bP2

Full size image

In permutation phase, Arnold cat map for bit-level permutations can be chosen in P1 and P2 by

$$\begin{aligned} \left[ \begin{array}{c} x' \\ y' \end{array} \right] = A \left[ \begin{array}{c} x \\ y \end{array} \right] ({\text {mod}}\ N\times 2) = \left[ \begin{array}{cc} 1 &{} v \\ w &{} vw+1 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] ({\text {mod}}\ N\times 2), \end{aligned}$$
(5)

where (x, y) and \((x',y')\) are the original bit position and permuted bit position, and v and w are calculated by

$$\begin{aligned} v &= bin2dec(K(1,1)\oplus K(1,2)\oplus K(1,3)\oplus \cdots \oplus K(5,10)){\text {mod}}\ N, \end{aligned}$$
(6)
$$\begin{aligned} w & = bin2dec(K(6,1)\oplus K(6,2)\oplus K(6,3)\oplus \cdots \oplus K(10,10)){\text {mod}}\ N. \end{aligned}$$
(7)

3.3 Diffusion phase

The proposed system in Eq. (1) is employed for the diffusion phase. The initial values \(x_1(i,j)\) are calculated by

$$\begin{aligned} x_1(i,j) = bin2dec(K(i,j))/2^{40}, \end{aligned}$$
(8)

where (i, j) is lattice index, \((i,j)\in [1,10]\). The system contains 100 initial values, which contributes a large key space of \(2^{4000}\approx 10^{1200}\). In addition, the parameter \(\mu\) in the system can guarantee the whole system in chaotic behaviors when it varies from 3.8 to 4 continuously. However, the parameter \(\mu\) in logistic map has periodic windows and a narrow value range for its corresponding chaotic behavior. The value of \(\mu\) should be assigned very close to 4. Therefore, the system is superior to logistic map in cryptography.

The proposed system has better Lyapunov exponents than the 2DCML system, which indicates that each lattice can generate a chaotic sequence for encryptions when the parameter \(\mu\) varies continuously. The 100 chaotic sequences in the corresponding lattices provide a sufficient amount of pseudo-random series for encryptions. Thus, the diffusion is designed by

$$\begin{aligned} c[m] = \{p[m]+c[m-1]+(x_{\mathrm{step}+m}(i,j)\times 10^{10})\}{\text {mod}}\ 256, \end{aligned}$$
(9)

where m is the pixel sequence which is formed vertically from the upper left corner to the lower right corner, \(m\in [1,N\times N]\). The initial value c[0] is 0; \(x_{\mathrm{step}+m}(i,j)\) is the chaotic sequence of the proposed system where the lattice index is i and j. The unfixed value i and j entirely depends on the secret key of K, which can enhance the sensitivity of the proposed algorithm for K and its security. The value step depends on the sum of pixels about original image, which can resist efficiently the chosen-plaintext attack. The values i, j and step are calculated by

$$\begin{aligned} i= & {} 1+v({\text {mod}}\ 10), \end{aligned}$$
(10)
$$\begin{aligned} j= & {} 1+w({\text {mod}}\ 10), \end{aligned}$$
(11)
$$\begin{aligned} \hbox {step}= & {} 300+{\text {mod}}\ (\text {sum(picture)},100). \end{aligned}$$
(12)

3.4 Encryption algorithm

Input: The secret keys where K is a 4000-bit-long block, \(\mu (\mu \in [3.87,4])\), \(\eta (\eta \in [0.5,1])\), \(c[0](c[0]\in [0,255])\) and \(\varepsilon (\varepsilon \in [0.1,1])\). The source image sp. The number of rounds of encryption.

  • Output: Returns ciphered image c.

  • Step 1. The variables of v and w are calculated in Eqs. (6) and (7) according to K.

  • Step 2. The source image sp is reorganized and arranged into the permuted image p with Eq. (5).

  • Step 3. The initial values \(x_1(i,j)\) are calculated in Eq. (8).

  • Step 4. The 100 chaotic sequences in the proposed spatiotemporal chaotic system are calculated in Eq. (1).

  • Step 5. The permuted image p is encrypted into the ciphered image c in Eqs. (9), (10) (11) and (12) by using the above chaotic sequences. If the current round is not the final round of encryption, the above steps will repeat again. Otherwise, the encryption process completes.

3.5 Decryption algorithm

Input: The secret keys where K is a 4000-bit-long block, \(\mu (\mu \in [3.87,4])\), \(\eta (\eta \in [0.5,1])\), \(c[0](c[0]\in [0,255])\) and \(\varepsilon (\varepsilon \in [0.1,1])\). The ciphered image c. The number of rounds of decryption.

  • Output: Returns the recovery plaintext image sp.

  • Step 1. The initial values \(x_1(i,j)\) are calculated in Eq. (8).

  • Step 2. The 100 chaotic sequences in the proposed spatiotemporal chaotic system are calculated in Eq. (1).

  • Step 3. The variables of v and w are calculated in Eqs. (6) and (7) according to K.

  • Step 4. The permuted image p is decrypted, and the corresponding equation is represented by

    $$\begin{aligned} p[m] = \{c[m]-(x_{\mathrm{step}+m}(i,j)\times 10^{10})-c[m-1]\}{\text {mod}}\ 256. \end{aligned}$$
    (13)

    Step 5. The plaintext image sp is decrypted by employing Arnold cat map. If the current round is not the final round of decryption, the above steps will repeat again. Otherwise, the decryption process completes.

For simulating experiments, we assign \(p = 6\), \(q = 7\), \(\mu = 3.87\), \(\varepsilon = 0.5\), \(\eta = 0.9\). Figure 6 shows the encryption and decryption of images for one round. Figure 6u–x shows the encryption and decryption of a color image of Lena.

In the proposed algorithm, the bit-level permutation and the value step depend on the sum of pixels about original image, which can resist efficiently the chosen-plaintext attack. These features strengthen the cryptosystem security.

Fig. 6
figure 6

Encryption, decryption of images. a Original image of Lena, b permuted image of Lena, c encrypted image of Lena, d decrypted image of Lena, e original image of Baboon, f permuted image of Baboon, g encrypted image of Baboon, h decrypted image of Baboon, i original image of Barb, j permuted image of Barb, k encrypted image of Barb, l decrypted image of Barb, m original image of Hill, n permuted image of Hill, o encrypted image of Hill, p decrypted image of Hill, q original image of Harbor, r permuted image of Harbor, s encrypted image of Harbor, t decrypted image of Harbor. u original color image of Lena, v permuted color image of Lena, w encrypted color image of Lena, x decrypted color image of Lena

Full size image

4 Performance analyses

To evaluate the security of the encryption scheme, we employ the secret key sensitivity, histogram analysis, UACI, NPCR, correlation analysis and information entropy in experiments.

4.1 Key space

The key space should be large enough to make brute force attacks infeasible. Number of control parameters in secret key: secret key K has 4000-bit-long block, \(\mu\) has a precision of \(10^{-2}\) and \(\mu \ge 3.7\), \(\varepsilon\) has a precision of \(10^{-1}\) and \(\eta\) has a precision of \(10^{-1}\). The key space size is more than \(2^{4000}\approx 10^{1200}\). It can be seen that the proposed encryption algorithm is good at resisting brute force attack.

4.2 Key sensitivity

For testing the secret key sensitivity of K, without loss of generality, only the last bit of K(10, 10) is changed. Figure 7 shows the two ciphered images of the Lena image generated from two security keys with only the last bit of K(10, 10) difference.

For testing the secret key sensitivity of \(\mu\), without loss of generality, we assign \(\mu = 3.871\). Figure 8 shows the two ciphered images of the Lena image generated from two security keys with only the \(\mu\) difference.

For testing the secret key sensitivity of \(\eta\), without loss of generality, we assign \(\eta = 0.91\). Figure 9 shows the two ciphered images of the Lena image generated from two security keys with only the \(\eta\) difference.

For testing the secret key sensitivity of \(\varepsilon\), without loss of generality, we assign \(\varepsilon = 0.51\). Figure 10 shows the two ciphered images of the Lena image generated from two security keys with only the \(\varepsilon\) difference.

Fig. 7
figure 7

Key sensitivity of K. a Original Lena image, b ciphered Lena image using original K, c ciphered Lena image using changed K, d difference between (b) and (c)

Full size image
Fig. 8
figure 8

Key sensitivity of \(\mu\). a Original Lena image, b ciphered Lena image using original \(\mu\), c ciphered Lena image using changed \(\mu\), d difference between (b) and (c)

Full size image
Fig. 9
figure 9

Key sensitivity of \(\eta\). a Original Lena image, b ciphered Lena image using original \(\eta\), c ciphered Lena image using changed \(\eta\), d Difference between (b) and (c)

Full size image
Fig. 10
figure 10

Key sensitivity of \(\varepsilon\). a Original Lena image, b ciphered Lena image using original \(\varepsilon\), c ciphered Lena image using changed \(\varepsilon\), d difference between (b) and (c)

Full size image

4.3 Histogram analysis

An ideal encrypted image should have a uniform and completely different histogram against the plain image for preventing the adversary from extracting any meaningful information from the fluctuating histogram of the cipher image.

Figures 11 and 12 show the histograms of the plain images, encrypted images using the proposed algorithm and encrypted images using 2DCML. Variances of histograms are listed in Table 1. The lower value of variances indicates the higher uniformity of ciphered images. In Table 1, the variance value is 637992.5804 for histogram of the plain image Lena, and the variance value is 1053.4431 for histogram of ciphered image Lena using 2DCML, which is greater than the variance 921.3020 for histogram of ciphered image Lena using the proposed algorithm. Therefore, the proposed algorithm is efficient.

Fig. 11
figure 11

Histograms of the plain images and ciphered images. a Histogram of Lena, b histogram of ciphered Lena image using the proposed algorithm, c histogram of ciphered Lena image using 2DCML algorithm, d histogram of Baboon, e histogram of ciphered Baboon image using the proposed algorithm, f histogram of ciphered Baboon image using 2DCML algorithm, g histogram of Barb, h histogram of ciphered Barb image using the proposed algorithm, i histogram of ciphered Barb image using 2DCML algorithm, j histogram of Hill, k histogram of ciphered image Hill using the proposed algorithm, l histogram of ciphered Hill image using 2DCML algorithm, m Histogram of Harbor, n histogram of ciphered Harbor image using the proposed algorithm, o histogram of ciphered Harbor image using 2DCML algorithm

Full size image
Fig. 12
figure 12

Histograms of the color Lena image and ciphered color Lena image. a Histogram of R channel of color Lena, b histogram of R channel of ciphered color Lena image using the proposed algorithm, c histogram of R channel of ciphered color Lena image using 2DCML algorithm, d histogram of G channel of color Lena, e histogram of G channel of ciphered color Lena image using the proposed algorithm, f histogram of G channel of ciphered color Lena image using 2DCML algorithm, g histogram of B channel of color Lena, h histogram of B channel of ciphered color Lena image using the proposed algorithm, i histogram of B channel of ciphered color Lena image using 2DCML algorithm

Full size image

4.4 Differential attack

To test the resistance of the differential attack of the encryption scheme, we employ the UACI (unified average changing intensity) and NPCR (number of pixels change rate), which are defined by

$$\begin{aligned} \text {UACI} = \frac{1}{M\times N}\left[ \sum _{ij}\frac{|c_1(i,j)-c_2(i,j)|}{255}\right] \times 100\%, \end{aligned}$$
(14)
$$\begin{aligned} \left\{ \begin{aligned} D(i,j) & = \left\{ \begin{aligned} 1 & = c_1(i,j)\ne c_2(i,j);\\ 0 &= \hbox {otherwise}, \end{aligned} \right. \\ \text {NPCR} & = \frac{\sum _{ij}D(i,j)}{M\times N}\times 100\%, \\ \end{aligned} \right. \end{aligned}$$
(15)

where \(c_1\) and \(c_2\) are the two ciphered images. Without loss of generality, we select 50 groups’ images for each experimental image, and each group includes two images: One is the original image and the other is the image which changed one randomly selected pixel value by adding 1 in original image. The NPCR and UACI values with one round of encryption are shown as Fig. 13a, b, which are distributed near the ideal value (the horizontal line in Fig. 13). The average values of NPCR and UACI are NPCR = 0.996122681 and UACI = 0.334466780, which are very close to the ideal values. The NPCR and UACI performance compared with other algorithms is listed in Table 2. These comparisons confirm that the proposed algorithm is highly sensitive to a pixel change in plain image.

Table 1 Variances of histograms compared the plain images and ciphered images
Full size table
Fig. 13
figure 13

NPCR and UACI values. a The NPCR values, b The UACI values

Full size image
Table 2 NPCR and UACI performance compared with other algorithms
Full size table
Table 3 Correlation coefficient of images
Full size table
Table 4 Comparison of the correlation coefficients of cipher images
Full size table
Table 5 Information entropy of images
Full size table

4.5 Correlation analysis

The correlation between adjacent pixels in the ciphered image should be significantly reduced, which is a good feature of encryption schemes. To test the correlation of plaintext image and ciphered image, the following procedures are carried out. First, randomly select 2000 pairs of two adjacent pixels from an image. Then, the correlation coefficients of adjacent pixels in vertical, horizontal and diagonal directions are evaluated by

$$\begin{aligned} r_{xy}= & {} \frac{\mathrm{cov}(x,y)}{\sqrt{D(x)}\sqrt{D(y)}}, \end{aligned}$$
(16)
$$\begin{aligned} E(x)= & {} \frac{1}{S}\sum _{i=1}^{S}x_i, \end{aligned}$$
(17)
$$\begin{aligned} D(x)= & {} \frac{1}{S}\sum _{i=1}^{S}(x_i-E(x))^2, \end{aligned}$$
(18)
$$\begin{aligned} {\text {cov}}(x,y) & = \frac{1}{S}\sum _{i=1}^{S}(x_i-E(x))(y_i-E(y)), \end{aligned}$$
(19)

where x and y denote two adjacent pixels and S is the total number of duplets (x, y) obtained from the image. E(x) and D(x) are the expectation and the variance of x, respectively. The calculated correlation coefficients of plaintext images and the corresponding ciphered images from the proposed encryption scheme are listed in Table 3. Comparisons of the correlation coefficients of images are listed in Table 4.

4.6 Information entropy

We calculate the information entropy of the plain images and the corresponding cipher images. The results are listed in Table 5. It is obvious that the entropies of the cipher images are all close to the ideal value 8, which means that the probability of accidental information leakage is very small. Meanwhile, compared with other algorithms [5, 6, 9, 22, 38], information entropy using proposed algorithm is higher. Thus, the proposed algorithm has the desired property of information entropy.

4.7 Computational and complexity analysis

All the tests are implemented in Visual Studio 2010 (Visual C++) with a Windows 7 Professional operating system, and the computer is of an Intel Core 2.5 GHz CPU, 4 GB RAM and 1000 GB hard disk, and some graphs are plotted using MATLAB 2014(a). The image of Lena, the 512\(\times\)512 image with 256 gray levels, is encrypted, respectively, by the proposed algorithm, Zhang’s algorithm [35] and Lian’s algorithm [29, 39] for ten times. The average encryption time is 297.5 (ms), 218.4 (ms) and 336.7(ms), respectively.

For analyses of execution time in permutations, the time-consuming part in computations is the pixel moving operations. Both the proposed algorithm and Zhang’s algorithm need O\((N^2)\) iterations of pixel moving operations. In Lian’s algorithm, except the needed O\((N^2)\) iterations of pixel moving operations, another time-consuming part in computations is O\((N^2)\) iterations of calculations of a sine function, which needs more time than the proposed algorithm.

For analyses of execution time in diffusions, the time-consuming part in computations is the operation of multiplying floating-point numbers. The proposed algorithm needs more time than the Zhang’s algorithm because the proposed algorithm needs O\((L^2 \times N^2)\) iterations of multiplying floating-point numbers, while the Zhang’s algorithm needs O\((L \times N^2)\) iterations of multiplying floating-point numbers. However, the proposed algorithm is more efficient compared with Lian’s algorithm in total time. There is a trade-off between security and processing time. The proposed algorithm offers higher security as highlighted in previous sections, and if we decrease the size of lattices L, the proposed algorithm can run faster.

5 Conclusions

We propose a new image encryption algorithm using two-dimensional spatiotemporal chaos system, which mixed linear–nonlinear coupled map lattices. The system contains the new features such as less periodic windows in bifurcations and larger range of parameters in chaotic dynamics, which is more suitable for cryptography. In addition, the image is permuted by the Arnold cat map for bit-level permutation, which can change the position and value of a pixel simultaneously. A more than 4000-bit-long secret key has been used to generate the initial conditions and parameters of the maps. The algorithm also includes the sum of pixels about original image, which can resist efficiently the chosen-plaintext attack. The numerical results show that the proposed algorithm has superior security and high efficiency for image encryption.