1 Introduction

The control problem of nonlinear stochastic systems is diffusely considered in different fields, such as biological systems, chemical reaction processes, financial systems [1, 2]. And in existing control theories, the time-triggered control (TTC) is an important method for most control problems [3,4,5,6,7]. As we know, the TTC requires the controller to be updated at every moment. This defect of TTC greatly limits its practical applications [8]. Therefore, the method of event-triggered control (ETC) was proposed, which greatly reduces the computational complexity compared with the TTC approach. In ETC, the execution of the control task is determined according to a well-designed event-trigger mechanism, and the input control action is updated only when the triggering condition is violated. Since the property of less computation is required in ETC, it has been widely used to solve consistency problems in different systems, including multi-agent systems [9,10,11], unknown dynamics nonlinear systems [12, 13], switching systems [14, 15], and networked control systems [16, 17].

It has been well acknowledged that nonlinear Itô-type stochastic systems are widely used in various fields, such as biological engineering, finance, nuclear reactors, and physics [18, 19]. The stochastic systems not only supplement the deterministic systems, but also precisely reflect the dynamic characteristics of engineering systems. The existence of stochastic disturbances changes the dynamic characteristics of the original system, reduces the control performance, and even destroys the stability of the stochastic systems. In recent years, many scholars have studied the stability of stochastic systems. The problem of ETC for stochastic nonlinear delay systems with exogenous disturbances was first solved by Zhu in [20]. In [21], the stability analysis and design procedure of ETC for nonlinear stochastic systems with state-dependent noise were studied. For network-based control of linear stochastic systems with state multiplicative noise, the time-delay method and ETC approach were proposed to obtain sufficient conditions for the exponential mean square stability in [22]. However, almost all researches on ETC problems for stochastic systems focus on the design of feedback controller to achieve the control objectives. Different from the traditional control methods, the optimal control not only realizes the control goal but also optimizes the given performance cost function [23]. Optimal control has a very wide scope of applications in practice, such as enterprise planning, satellite launch, and production control. Therefore, it is of great significance to study the event-triggered optimal control (ETOC) of the nonlinear stochastic systems.

As we all know, the solution of optimal control problem usually comes down to the solution of HJB equation. However, the analytical solution of the HJB equation of nonlinear systems is very hard to get [24]. The ADP method that combines dynamic programming, reinforcement learning, and adaptive technology was firstly presented by Werbos in [25]. It provides a novel and effective method for solving the optimal control problem of nonlinear systems. Compared with dynamic programming, the advantage of ADP is suitable for complex nonlinear systems. Moreover, it can effectively solve nonlinear HJB equation and overcome the disaster of dimensionality. A greedy iterative algorithm by ADP was designed to solve the HJB for discrete-time nonlinear optimal control in [26]. For nonlinear polynomial systems, a new global ADP approach was suggested to do with the adaptive optimal control problem [27]. The difference between this method and the known nonlinear ADP method is that it avoids the neural network (NN) approximation and greatly improves computational efficiency.

ADP methods for deterministic nonlinear systems with ETOC have been studied by many scholars and have been well developed [28,29,30,31,32,33,34,35,36]. For discrete-time nonlinear deterministic systems, the ETOC problem was studied in [28], which proposes an adaptive ETOC according to heuristic dynamic programming. In [29], an ETC based on ADP method was suggested to solve the optimal control problem of unknown nonlinear continuous-time systems with input constraints. Dong proposed an ETOC structure and ADP approach for nonlinear systems with control constraints in [32]. According to event-trigger mechanism and ADP approach, a new optimal control method for unknown nonlinear continuous-time systems was proposed in [34]. Guo et al. [36] studied the event-triggered guaranteed cost optimal tracking control problem for a class of uncertain nonlinear system by using ADP approach. However, there is no research for Itô-type stochastic systems with ETOC based on ADP method.

In addition, most works on ETOC problems for nonlinear deterministic systems first need to obtain event-triggered HJB equations and then get approximate solutions by using ADP methods [37,38,39,40]. Noting that the fact that the event-triggered HJB equation is already a kind of approximate of the given equation, the error of the solution is relatively large. Moreover, the optimal performance index in ETOC is bound to degrade to some extent since the use of event-triggered control. Therefore, it is essential to investigate how much performance will decline for the ETC approach. However, there is little research on how the event-trigger scheme affects the optimal performance index. In the works of Dong et al. [32] and Zhu et al. [33], the prespecified cost function (C-F) for the ETOC contains an integral term, and the boundedness of the integral term was not analyzed. Luo et al. [41] proposed a new ETOC method, which guarantees an upper bound for C-F. However, this work does not take into account the impact of stochastic disturbances for system and performance index, which is not in line with practical applications.

Motivated by the above discussions, the problem of ETOC for nonlinear Itô-type stochastic systems is studied utilizing the ADP method in this paper. And the main contributions are as follows.

  1. i)

    ETOC for nonlinear Itô-type stochastic systems is designed for the first time in this paper by using ADP method, which can get the numerical solution of HJB equation. Moreover, it can reduce computational load and savings communication resources.

  2. ii)

    In the existing researches, there is no literature to study the influence of ETOC on the corresponding performance index of Itô-type stochastic optimal control problem. In our work, a new ETOC is presented to ensure the predetermined upper bound of the corresponding performance index for Itô-type stochastic optimal control problem.

  3. iii)

    For ETOC problems, the main purpose of most works is to achieve the numerical solution of the event-triggered HJB equation by applying ADP method [37,38,39,40]. However, considering the fact that the event-triggered HJB equation itself is already a kind of approximate of the original HJB equation. In our work, a new event-triggering scheme is proposed, which can be used to design ETOC directly via the solution of HJB equation and the accuracy of the approximate solution can be improved.

The rest of the paper is introduced as follows. In Sect. 2, we give the problem statements and preliminaries. The ETOC scheme, stability problem, and an upper bound of the C-F are developed in Sect. 3. Section 4 constructs CNN to estimate the optimal value function. The ETOC based on ADP method is analyzed theoretically in Sect. 5. In Sect. 6, examples results are presented to illustrate the application of the proposed method. Section 7 concludes this paper.

2 Problem statements and preliminaries

The notations used in this paper are as follows. \({\mathbb {R}}^{n}\) denotes the n-dimensional Euclidean space and \(\Vert \cdot \Vert \) represent vector norm. The superscript \(\mathrm {T}\) represents the operation of transpose. Denote by \((\varOmega ,{{\mathcal {F}}},\{{\mathcal {F}}_t\}_{t\ge 0},P)\) a complete probability space with a natural filtration \({\{{\mathcal {F}}_t\}}_{t\ge 0}\). \({\mathbb {E}}\{\cdot \}\) denotes the correspondent expectation operator with regard to a given probability measure P. \(\underline{\sigma }(\cdot )\) and \(\overline{\sigma }(\cdot )\) represent the minimum and maximum of singular values. \({\mathcal {X}}\) is a compact set of \({\mathbb {R}}^{n}\). Let \(C^2({\mathcal {X}})\) represent the family of nonnegative functions \({\mathcal {V}}(x)\) and \({\mathcal {Y}}(x)\), which are twice differentiable in \(x\in {\mathcal {X}}\subset {\mathbb {R}}^{n}\). \(\Vert A\Vert ^{2}_{b}=b^{\mathrm{T}}Ab\) for symmetric matrix \( A>(\ge )0\) and real vector b.

Consider the Itô-type nonlinear stochastic systems as

$$\begin{aligned} dx(t) =F(x(t)) dt+{\mathcal {G}}_{1}(x(t)) u(x(t))dt+{\mathcal {G}}_{2}(x(t)) dw(t),\nonumber \\ \end{aligned}$$
(1)

where \(x=\left[ x_{1}, \cdots , x_{n}\right] ^{\mathrm{T}}\in {\mathcal {X}}\subset {\mathbb {R}}^{n}\) represents the system state, the control input \(u(x(t)) \in {\mathbb {R}}^{p}\), and w(t) be a one-dimensional Brownian motion defined on space \((\varOmega ,{{\mathcal {F}}},\{{\mathcal {F}}_t\}_{t\ge 0},P)\). F(x(t)), \({\mathcal {G}}_{1}(x(t))\), and \({\mathcal {G}}_{2}(x(t))\) are Lipschitz continuous on compact set \({\mathcal {X}} \in {\mathbb {R}}^{n}\). Moreover, \(F(0) =0,~{\mathcal {G}}_{1}(0)=0,~{\mathcal {G}}_{2}(0) = 0\).

The cost function of (1) can be written as

$$\begin{aligned}&{\mathcal {J}}(x(t),u(t))\nonumber \\&\quad ={\mathbb {E}}\left\{ \int _{0}^{+\infty } \left( {\mathcal {Q}}(x(t))+u^{\mathrm{T}}(x(t)) {\mathcal {R}} u(x(t))\right) d t\right\} , \end{aligned}$$
(2)

where \({\mathcal {Q}}(x(t))\) is a positive definite function, expressed as a weighting function of state x(t) with \({\mathcal {Q}}(0)=0\), and \({\mathcal {R}} > 0\).

The goal of optimal control problems is to find the optimal value function as

$$\begin{aligned} {\mathcal {V}}^{*}(x(t))=\min _{u(x(t))} {\mathcal {J}}[x(t),~u(x(t))], \end{aligned}$$
(3)

where \({\mathcal {V}}^{*}(x(t))\in C^2({\mathcal {X}})\), \({\mathcal {V}}^{*}(x(t))\ge 0\), and \({\mathcal {V}}^{*}(0)=0\). If the control input u(x(t)) is admissible, then the Hamiltonian of \({\mathcal {V}}^{*}(x(t))\) and u(x(t)) is given as

$$\begin{aligned}&{\mathcal {H}}(x,u(x),{\mathcal {V}}_{x}^{*})\nonumber \\&\quad ={\mathcal {V}}_{x}^{*}F(x)+ {\mathcal {V}}_{x}^{*}{\mathcal {G}}_{1}(x)u(x) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} {\mathcal {V}}_{xx}^{*} {\mathcal {G}}_{2}\nonumber \\&\qquad +{\mathcal {Q}}(x)+u^{\mathrm{T}}(x) {\mathcal {R}} u(x), \end{aligned}$$
(4)

where

$$\begin{aligned} {\mathcal {V}}_{x} \triangleq \left[ \frac{\partial {\mathcal {V}}}{\partial x_{1}} ~\frac{\partial {\mathcal {V}} }{\partial x_{2}}~\cdots ~\frac{\partial {\mathcal {V}}}{\partial x_{n}}\right] , \end{aligned}$$

and

$$\begin{aligned} {\mathcal {V}}_{x x} \triangleq \left[ \frac{\partial ^{2} {\mathcal {V}}}{\partial x_{i} x_{j}}\right] _{n \times n}=\left[ \begin{array}{ccc} \frac{\partial ^{2} {\mathcal {V}}}{\partial x_{1} \partial x_{1}} &{} \cdots &{} \frac{\partial ^{2} {\mathcal {V}}}{\partial x_{1} \partial x_{n}} \\ \vdots &{} \ddots &{} \vdots \\ \frac{\partial ^{2} {\mathcal {V}}}{\partial x_{n} \partial x_{1}} &{} \cdots &{} \frac{\partial ^{2} {\mathcal {V}}}{\partial x_{n} \partial x_{n}} \end{array}\right] . \end{aligned}$$

Based on [42], \({\mathcal {V}}^{*}(x)\) can be achieved through solving HJB equation as

$$\begin{aligned} \min _{u(x)} {\mathcal {H}}\left( x,u(x), {\mathcal {V}}_{x}^{*}\right) =0. \end{aligned}$$
(5)

Therefore, the optimal control is given as

$$\begin{aligned} u^{*}(x)=-\frac{1}{2} {\mathcal {R}}^{-1}(x){\mathcal {G}}_{1}^{\mathrm{T}}(x) {\mathcal {V}}_{x}^{*}, \end{aligned}$$
(6)

and the optimal performance index can be written as

$$\begin{aligned} {\mathcal {J}}^{*}(x_{0})=\min {\mathcal {J}}(x_{0},u)={\mathcal {V}}^{*}(x_{0}). \end{aligned}$$

Substituting (6) into (5), the HJB equation becomes

$$\begin{aligned}&{\mathcal {V}}_{x}^{*}F(x)+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} {\mathcal {V}}_{xx}^{*} {\mathcal {G}}_{2}\nonumber \\&-\frac{1}{4}{\mathcal {V}}_{x}^{*}{\mathcal {G}}_{1}(x){\mathcal {R}}^{-1}(x) {\mathcal {G}}_{1}^{\mathrm{T}}(x)({\mathcal {V}}_{x}^{*})^{\mathrm{T}}+{\mathcal {Q}}(x)=0. \end{aligned}$$
(7)

Remark 1

Noticing that the HJB (7) is a time-triggered HJB equation, the controller is required to stay active at every time instance. Obviously, the time-triggered optimal control (TTOC) has the disadvantage of requiring a heavy computational burden and needs more communication sources. Fortunately, the controller in the ETOC method is updated only when the triggering condition is violated, which can surmount the above shortcomings. In this paper, we will develop a novel ETOC to achieve the approximate solution of (7).

3 Design of ETOC and stability analysis

Let triggering instants set \(\{t_{k}\}\) satisfy \(0=t_{1}<\cdots<t_{k}<\cdots ,\lim _{k\rightarrow \infty }t_{k}=\infty \) and define the sampled state as

$$\begin{aligned} \bar{x}(t)= x\left( t_{k}\right) ,~t\in \left[ t_{k},t_{k+1}\right) ,~k\in {\mathbb {N}}, \end{aligned}$$

where \(t_{k}\) is the triggering instant. Let e(t) represent the error of true state x(t) and sampled state \(\bar{x}(t)\). Then, we have

$$\begin{aligned} e(t)=\bar{x}(t)-x(t),~\text{ for }~\forall ~t\in \left[ t_{k}, t_{k+1}\right) . \end{aligned}$$
(8)

The sampling interval of the ETOC is defined as

$$\begin{aligned} h_{k}\triangleq t_{k+1}-t_{k}. \end{aligned}$$

According to (6), the ETOC has the form

$$\begin{aligned} \mu (\bar{x})=u^{*}(\bar{x})=-\frac{1}{2} {\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(\bar{x})({\mathcal {V}}_{\bar{x}}^{*})^{\mathrm{T}}. \end{aligned}$$
(9)

By system (1), error (8), and ETOC (9), the closed-loop system is written as

$$\begin{aligned}&dx\nonumber \\&\quad =F(x)d t+{\mathcal {G}}_{1}(x) \mu (\bar{x})dt+{\mathcal {G}}_{2}(x)dw\nonumber \\&\quad =F(x)dt-\frac{1}{2} {\mathcal {G}}_{1}(x) {\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(\bar{x}) ({\mathcal {V}}_{\bar{x}}^{*})^{\mathrm{T}} +{\mathcal {G}}_{2}(x)dw\nonumber \\&\quad =F(x)dt-\frac{1}{2} {\mathcal {G}}_{1}(x) {\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}({x+e}) ({\mathcal {V}}_{{x+e}}^{*})^{\mathrm{T}}\nonumber \\&\qquad +{\mathcal {G}}_{2}(x)dw. \end{aligned}$$
(10)

Now, a new event-triggering scheme considered in this paper is

$$\begin{aligned}&{\mathcal {Z}}_{c}(x,\bar{x})\nonumber \\&\quad =(1+c)\left[ {\mathcal {V}}_{x}^{*}F(x)+ {\mathcal {V}}_{x}^{*}{\mathcal {G}}_{1} (x)\mu (\bar{x})+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} {\mathcal {V}}_{xx}^{*} {\mathcal {G}}_{2}\right] \nonumber \\&\qquad +{\mathcal {Q}}(x)+\mu ^{\mathrm{T}}(\bar{x}) {\mathcal {R}} \mu (\bar{x})\nonumber \\&\quad < 0, \end{aligned}$$
(11)

where \(c>0\) is a predetermined constant parameter, which will determine an upper bound of the C-F of (2). The controller will be updated according to the current state when the triggering scheme (11) is violated. Therefore, the next release time instant \(t_{k+1}\) can be updated as

$$\begin{aligned} t_{k+1}=\inf \left\{ t|{\mathcal {Z}}_{c}(x(t),\bar{x}(t)) \geqslant 0, t\geqslant t_{k}\right\} . \end{aligned}$$
(12)

Theorem 1

Closed-loop system (10) with the event-triggered optimal controller \(\mu (\bar{x})\) in (9) and the event-triggering scheme (11) is asymptotically stable in probability and the upper bound can be given for the C-F if \({\mathcal {V}}^{*}(x)\) is a solution of (7).

Proof

Choose \({\mathcal {V}}^{*}(x)\) as the Lyapunov function. According to (11) and (12), we acquire

$$\begin{aligned} {\mathcal {L}}{\mathcal {V}}^{*}&= {\mathcal {V}}_{x}^{*}F(x) +{\mathcal {V}}_{x}^{*}{\mathcal {G}}_{1}(x)\mu (\bar{x}) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} {\mathcal {V}}_{xx}^{*} {\mathcal {G}}_{2}\nonumber \\&=\frac{1}{1+c}\left[ {\mathcal {Z}}_{c}(x,\bar{x})-{\mathcal {Q}}(x) -\mu ^{\mathrm{T}}(\bar{x}){\mathcal {R}}\mu (\bar{x})\right] \nonumber \\&\leqslant -\frac{1}{1+c}\left[ {\mathcal {Q}}(x)+\mu ^{\mathrm{T}}(\bar{x}) {\mathcal {R}} \mu (\bar{x})\right] \nonumber \\&\leqslant 0, \end{aligned}$$
(13)

which implies that (10) is asymptotically stable in probability.

Based on (13), we have

$$\begin{aligned} {\mathcal {Q}}(x)+\mu ^{\mathrm{T}}(\bar{x}) {\mathcal {R}} \mu (\bar{x}) \leqslant -(1+c){\mathcal {L}}{\mathcal {V}}^{*}(x). \end{aligned}$$

Next, it follows from Dynkin formula and (13) with \({\mathcal {V}}(x_{T})>0\) that for any \(T>0\),

$$\begin{aligned}&{\mathbb {E}}\left\{ \int _{0}^{T}\left( {\mathcal {Q}}(x(t))+\mu ^{\mathrm{T}}(x(t)) {\mathcal {R}} \mu (x(t))\right) d t\right\} \\&\quad \leqslant -(1+c){\mathbb {E}}\left\{ \int _{0}^{T}{\mathcal {L}}{\mathcal {V}}^{*} (x(t)) dt\right\} \\&\quad =(1+c){\mathbb {E}}\{{\mathcal {V}}(x_{0})-{\mathcal {V}}(x_{T})\}\\&\quad \le (1+c) {\mathcal {V}}^{*}(x_{0})\\&\quad =(1+c){\mathcal {J}}^{*}(x_{0}). \end{aligned}$$

Letting \(T\rightarrow \infty \), one can obtain

$$\begin{aligned}&{\mathbb {E}}\left\{ \int _{0}^{\infty }\left( {\mathcal {Q}}(x(t)) +\mu ^{\mathrm{T}}(\bar{x}(t)) {\mathcal {R}}\mu (\bar{x}(t))\right) d t\right\} \\&\quad \le (1+c){\mathcal {J}}^{*}(x_{0}). \end{aligned}$$

Accordingly, an upper bound \((1+c){\mathcal {J}}^{*}(x_{0})\) is guaranteed on the cost function \( {\mathcal {J}}(x_{0}, \mu )\). \(\square \)

Corollary 1

For system (10) with the triggering scheme (11) and the triggering time sequence (12), the sampling interval \(h_{k}\) of the ETOC is monotonic non-decreasing. That is, \(h_{k_{1}}\geqslant h_{k_{2}}\), for any \(k_{1} \geqslant k_{2}>0\).

Proof

For \(t\in \left[ 0, h_{k_{2}}\right] \), according to (12), we have

$$\begin{aligned}&{\mathcal {Z}}_{k_{1}}(x, \bar{x})-{\mathcal {Z}}_{k_{2}}(x, \bar{x}) \\&\quad =\left( k_{1}-k_{2}\right) \left[ {\mathcal {V}}_{x}^{*}F(x) +{\mathcal {V}}_{x}^{*}{\mathcal {G}}_{1}(x)\mu (\bar{x}) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} {\mathcal {V}}_{xx}^{*} {\mathcal {G}}_{2}\right] \\&\quad =\frac{k_{1}-k_{2}}{1+k_{2}}\left[ {\mathcal {Z}}_{k_{2}} (x, \bar{x})-{\mathcal {Q}}(x)-\mu ^{\mathrm{T}}(\bar{x}) {\mathcal {R}}\mu (\bar{x}))\right] \\&\quad \leqslant -\frac{k_{1}-k_{2}}{1+k_{2}}\left[ {\mathcal {Q}}(x) +\mu ^{\mathrm{T}}(\bar{x}) {\mathcal {R}} \mu (\bar{x}))\right] \leqslant 0, \end{aligned}$$

one can obtain \({\mathcal {Z}}_{k_{1}}(x, \bar{x})\leqslant {\mathcal {Z}}_{k_{2}}(x, \bar{x})\), then, \(h_{k_{1}}\geqslant h_{k_{2}}\). \(\square \)

Corollary 2

Combining system (10) with triggering scheme (11) and the triggering instant sequence (12). If the parameter \(c = 0\), we can obtain the sampling interval \(h_{k}= 0\) for all k and \({\mathcal {J}}(x_{0},\mu )={\mathcal {J}}^{*}(x_{0})\). Then, the ETOC will degrade into a traditional TTOC.

Proof

According the HJB equation (7), we obtain

$$\begin{aligned} {\mathcal {V}}_{x}^{*}F(x)+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} {\mathcal {V}}_{xx}^{*} {\mathcal {G}}_{2}+{\mathcal {Q}}(x)=(u^{*} (x))^{\mathrm{T}}{\mathcal {R}}u^{*}(x). \end{aligned}$$
(14)

Based on (11), (14) and the condition \(c=0\), we get

$$\begin{aligned}&{\mathcal {Z}}_{c}(x,\bar{x})\nonumber \\&\quad = {\mathcal {V}}_{x}^{*}F(x)+ {\mathcal {V}}_{x}^{*}{\mathcal {G}}_{1} (x)\mu (\bar{x})+0.5{\mathcal {G}}_{2}^{\mathrm{T}} {\mathcal {V}}_{xx}^{*} {\mathcal {G}}_{2}\\&\qquad +{\mathcal {Q}}(x)+(\mu (\bar{x}))^{\mathrm{T}}{\mathcal {R}}\mu (\bar{x})\nonumber \\&\quad =(u^{*}(x))^{\mathrm{T}}{\mathcal {R}}u^{*}(x)-2(u^{*}(x))^{\mathrm{T}}{\mathcal {R}}\mu (\bar{x})\\&\qquad +(\mu (\bar{x}))^{\mathrm{T}}{\mathcal {R}}\mu (\bar{x})\nonumber \\&\quad = \left\| u^{*}(x)-\mu (\bar{x})\right\| _{{\mathcal {R}}}^{2} \ge 0, \end{aligned}$$

one can obtain from (12) that \(t_{k+1}=t_{k}\), that is, \(h_{k}=0\) for all \(k=0,1,2,\cdots \). According to the condition \(c=0\) and Theorem 1, we can obtain \({\mathcal {J}}(x_{0},u)\le {\mathcal {J}}^{*}(x_{0})\). Meanwhile, \({\mathcal {J}}^{*}(x_{0})\) is the minimum performance, i.e, \({\mathcal {J}}(x_{0},u)\ge {\mathcal {J}}^{*}(x_{0})\). Then, we get \({\mathcal {J}}(x_{0},u)={\mathcal {J}}^{*}(x_{0})\). \(\square \)

Remark 2

Based on Corollary 1, we know that a larger c will lead to a larger sampling time, which greatly reduces the computational complexity and saving communication resources. That is, c is a tuning parameter between the TTOC and the ETOC.

Remark 3

It is worth noting that our proposed event-triggered scheme (11) can guarantee that the C-F has an upper bound, and we consider the system and C-F affected by stochastic disturbances. Although the ADP method was used to solve the ETOC problem of continuous systems in [32, 34, 43], the C-F of event-triggered control was not unsolved. In addition, there has been no works to study the influence of ETOC on the C-F of stochastic optimal control problems.

Remark 4

In our work, the proposed ETOC approach only needs to solve the HJB equation (7) directly and does not need the event-triggered HJB equation, which has better practicability. However, the HJB equation of event-triggered was needed in [37, 40], where the value function \({\mathcal {V}}^{*}(x)\) was required to satisfy both the event-triggered HJB equation and original HJB equation. Thus, our work is more practical than those in [37, 40].

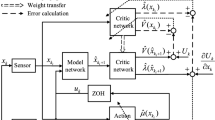
4 Critic neural network design

The \({\mathcal {V}}^{*} (x)\) is estimated by using a CNN. And the structure of NN-based approximate value function as

$$\begin{aligned} {\mathcal {V}}^{*}(x)=\sum _{k=1}^{L} \omega _{k}^{*} m_{k}(x)+\delta (x), \end{aligned}$$
(15)

where \(\omega ^{*} \triangleq \left[ \omega _{1}^{*}, \cdots , \omega _{L}^{*}\right] ^{\mathrm{T}}\) represents the CNN weight vector, \(m_{k}(x) \triangleq \left[ m_{1}(x), \cdots , m_{L}(x)\right] ^{\mathrm{T}}\) is the vector activation function with \(m_{k}(x)\in C^{2}({\mathcal {X}})\) and \(m_{k}(0) = 0\), and \(\delta (x)\) denotes the error of CNN estimation.

Due to the ideal weight \(\omega ^{*}\) is usually not available and difficult to obtain. Therefore, the CNN is applied to approximate \({\mathcal {V}}^{*}(x)\) as

$$\begin{aligned} \hat{{\mathcal {V}}}(x)=\sum _{k=1}^{L} \omega _{k} m_{k}(x)=M_{L}^{\mathrm{T}}(x)\omega . \end{aligned}$$
(16)

Submitting (16) to (9), the ETOC based on ADP is expressed as

$$\begin{aligned} \mu (\bar{x})=-\frac{1}{2} {\mathcal {R}}^{-1}{\mathcal {G}}_{1}^{\mathrm{T}} (\bar{x}) \nabla _{\bar{x}} M_{L}(\bar{x}) \bar{\omega }, \end{aligned}$$
(17)

where \(\nabla _{\bar{x}} M_{L} \triangleq \left[ \frac{\partial M_{L}}{\partial \bar{x}_{1}}~ \frac{\partial M_{L} }{\partial \bar{x}_{2}}~\cdots ~\frac{\partial M_{L}}{\partial \bar{x}_{L}}\right] \), \(\bar{\omega }(t)=\omega \left( t_{k}\right) \), \(\forall t \in \left[ t_{k}, t_{k+1}\right) \), and \({\mathcal {Z}}_{c}(x,\bar{x})\) in the event-triggering scheme (11) is performed with

$$\begin{aligned}&{\mathcal {Z}}_{c}(x,\bar{x})\nonumber \\&\quad =(1+c)[\hat{{\mathcal {V}}}_{x}F(x)+ \hat{{\mathcal {V}}}_{x}{\mathcal {G}}_{1} (x)\mu (\bar{x})+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}}\hat{{\mathcal {V}}}_{xx} {\mathcal {G}}_{2}]\nonumber \\&\qquad +{\mathcal {Q}}(x)+\mu (\bar{x})^{\mathrm{T}}(x) {\mathcal {R}} \mu (\bar{x})\nonumber \\&\quad <~0, \end{aligned}$$
(18)

where \(c>0\) is the predetermined constant that will determine an upper bound of the C-F with the ETOC (17). \(\hat{{\mathcal {V}}}(x)\) is the approximation of \({\mathcal {V}}^{*}(x)\). When the event-triggering scheme (18) is violated, the controller will be updated according to the current state x(t).

The ADP approach is developed to study the CNN weight vector \(\omega \). Motivated by works [34, 41, 44], the following assumption is presented.

Assumption 1

Let \({\mathcal {P}}(x)\in C^{2}({\mathcal {X}})\) and \({\mathcal {P}}(0)=0\) be a Lyapunov function candidate such that

$$\begin{aligned}&\nabla _{x}{\mathcal {P}}(x)F(x)+\nabla _{x}{\mathcal {P}} (x){\mathcal {G}}_{1}(x)u^{*}(x)\\&+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2}{\mathcal {P}} (x)}{\partial x^{2}}{\mathcal {G}}_{2} \leqslant 0, \end{aligned}$$

where

$$\begin{aligned} \nabla _{x}{\mathcal {P}} \triangleq \left[ \frac{\partial {\mathcal {P}}}{\partial x_{1}} ~\frac{\partial {\mathcal {P}} }{\partial x_{2}}~\cdots ~\frac{\partial {\mathcal {P}}}{\partial x_{n}}\right] , \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^{2}{\mathcal {P}}(x)}{\partial x^{2}} \triangleq \left[ \frac{\partial ^{2} {\mathcal {P}}}{\partial x_{i} x_{j}}\right] _{n \times n} =\left[ \begin{array}{ccc} \frac{\partial ^{2} {\mathcal {P}}}{\partial x_{1} \partial x_{1}} &{} \cdots &{} \frac{\partial ^{2} {\mathcal {P}}}{\partial x_{1} \partial x_{n}} \\ \vdots &{} \ddots &{} \vdots \\ \frac{\partial ^{2} {\mathcal {P}}}{\partial x_{n} \partial x_{1}} &{} \cdots &{} \frac{\partial ^{2} {\mathcal {P}}}{\partial x_{n} \partial x_{n}} \end{array}\right] . \end{aligned}$$

Meanwhile, \(\left\| \nabla _{x} {\mathcal {P}}\right\| \leqslant {\mathcal {P}}_{ M}\) with \({\mathcal {P}}_{M}>0.\)

According to (16) and (17), the approximate Hamiltonian has the form

$$\begin{aligned}&\hat{ {\mathcal {H}}}(x,\mu (x),\nabla _{x}\hat{{\mathcal {V}}}(x)) \\&\quad =\omega ^{\mathrm{T}}[\nabla _{x}^{\mathrm{T}}M_{L}(x)F(x)+\nabla _{x}^{\mathrm{T}} M_{L}(x){\mathcal {G}}_{1}(x)\mu (x)]\\&\qquad +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}}I_{n\times n}\otimes \omega ^{\mathrm{T}} \frac{\partial ^{2} M_{L}(x)}{\partial x^{2}} {\mathcal {G}}_{2}\\&\qquad +{\mathcal {Q}}(x) +\mu ^{\mathrm{T}}(x) {\mathcal {R}} \mu (x), \end{aligned}$$

where \(\otimes \) represents the Kronecker product. Since the estimation error in the CNN, the replacement of \({\mathcal {V}}^{*}(x)\) and \(u^{*}(x)\) in (5) with \(\hat{{\mathcal {V}}}(x)\) and \(\mu (x)\) will cause residual error, that is, \(\hat{{\mathcal {V}}}(x)\ne 0\). Therefore, the residual error between \(\hat{{\mathcal {H}}}(x,\mu (x),\nabla _{x} \hat{{\mathcal {V}}}(x))\) and \({\mathcal {H}}(x, u^{*}(x), \nabla _{x}{\mathcal {V}}^{*}(x))\) can be expressed as

$$\begin{aligned} \eta (x, \omega )&\triangleq \hat{ {\mathcal {H}}}\left( x, \mu (x), \nabla _{x} \hat{{\mathcal {V}}}(x)\right) \nonumber \\&\quad -{\mathcal {H}}\left( x, u^{*}(x), \nabla _{x} {\mathcal {V}}^{*}(x)\right) \nonumber \\&= \hat{{\mathcal {H}}}\left( x, \mu (x), \nabla _{x} \hat{{\mathcal {V}}}(x)\right) -0 \nonumber \\&=\hat{ {\mathcal {H}}}\left( x, \mu (x), \nabla _{x} \hat{{\mathcal {V}}}(x)\right) . \end{aligned}$$
(19)

Due to derive the minimum value of \(\eta \), the square residual error has the form

$$\begin{aligned} E(x, \omega ) \triangleq \frac{1}{2} \eta ^{2}(x,\omega ). \end{aligned}$$

Accordingly, the following gradient-descent-like rule is designed as

$$\begin{aligned} \dot{\omega }&=-\gamma \frac{\phi (x)}{1+\phi ^{\mathrm{T}}(x)\phi (x)}\eta (x, w)\nonumber \\&\quad +\frac{k}{2}\nabla _{x}^{\mathrm{T}} M_{L}(x){\mathcal {G}}_{1}(x) {\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(x) \nabla _{x}^{\mathrm{T}} {\mathcal {P}}(x), \end{aligned}$$
(20)

where

$$\begin{aligned} \phi (x)&=\nabla _{x}^{\mathrm{T}}M_{L}(x)F(x)+\nabla _{x}^{\mathrm{T}}M_{L}(x){\mathcal {G}}_{1} (x)\mu (x)\nonumber \\&\quad +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}}\otimes I_{L\times L}\frac{\partial ^{2} M_{L}(x)}{\partial x^{2}} {\mathcal {G}}_{2}, \end{aligned}$$

and

$$\begin{aligned} k \triangleq \left\{ \begin{array}{ll} 0,~\text{ if } &{}\nabla _{x}{\mathcal {P}}(x)F(x)+ \nabla _{x}{\mathcal {P}} (x){\mathcal {G}}_{1}(x)\mu (\bar{x})\\ &{}+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}} (x)}{\partial x^{2}}{\mathcal {G}}_{2}\leqslant 0, \\ 1,~\text{ else }. \end{array}\right. \end{aligned}$$
(21)

Remark 5

Two explanations for (20) are showed as follows.

  1. (1)

    The purpose of the first term in (20) is to minimize the target function E(x, w) via the gradient descent method. Meanwhile, \(1/(1+\phi ^{\mathrm{T}}(x)\phi (x))\) is a normalized processing term, and \(\gamma >0\) is a constant gain.

  2. (2)

    The last term in (20) is added to ensure the stability of system (1). The derivation of this term is as follows. Represent the derivative of \({\mathcal {P}}(x)\) along system trajectory

    $$\begin{aligned} dx=F(x)dt+{\mathcal {G}}_{1}(x)\mu (x)dt+{\mathcal {G}}_{2}(x)dw \end{aligned}$$

    as

    $$\begin{aligned} \varPsi&=\nabla _{x}{\mathcal {P}}(x)F(x)+ \nabla _{x}{\mathcal {P}} (x){\mathcal {G}}_{1}(x)\mu (x)\\&\quad +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2}. \end{aligned}$$

    Applying the gradient descent approach to \(\varPsi \), we have

    $$\begin{aligned} -\frac{\partial \varPsi }{\partial \omega }=\frac{1}{2}\nabla ^{\mathrm{T}}_{x} M_{L}(x){\mathcal {G}}_{1}(x) {\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}} (x) \nabla _{x}^{\mathrm{T}} {\mathcal {P}}(x). \end{aligned}$$

Obviously, it is helpful to prove \(\varPsi < 0\), which can ensure the stability of system (1).

Remark 6

Now, we introduce the implementation principle of the ETOC based on ADP. Utilizing x and \(\bar{x}\) to validation event-triggering scheme (18), and using x in (20) to calculate the CNN weight \(\omega \). The control input (17) will be calculated according to \(\bar{x}\) and \(\bar{\omega }\) when the event-triggering scheme (18) is violated.

5 Theoretical analysis

The system stability and cost function bound are analyzed theoretically in this section. First, the following definition and assumptions are introduced.

Definition 1

[45] For system (10), the trajectory x(t) is SGUUB in p-th moment. For a compact set \({\mathcal {X}} \in R^{n}\) and any \(x(t_{0})=x_{0}\), if there exist constant \(b_{1}>0\) and \(T(b_{1},x_{0})\) satisfying \({\mathbb {E}}[\Vert x(t)\Vert ^{p}]<b_{1}\), \(t>t_{0}+T\).

Define the CNN weights error is \(\hat{\omega }(t) \triangleq \omega (t)-\omega ^{*}\). Then, we have

$$\begin{aligned} \dot{\hat{\omega }}(t)=\dot{\omega }(t). \end{aligned}$$
(22)

Assumption 2

The control input \(u^{*}(x)\) is Lipschitz continuous, that is to say, for every \(x_{1},x_{2}\in {\mathcal {X}}\), there exists \(K>0\) satisfies

$$\begin{aligned} \left\| u^{*}(x_{1})-u^{*}(x_{2})\right\| \le K\left\| x_{1}-x_{2}\right\| . \end{aligned}$$

Assumption 3

Assume that \( K_{1}\Vert x\Vert ^{2} \leqslant {\mathcal {Q}}(x) \leqslant K_{2}\Vert x\Vert ^{2}\), and \(K_{3}\Vert x\Vert \leqslant \left\| u^{*}(x)\right\| \leqslant K_{4}\Vert x\Vert \), where \(K_{1},K_{2},K_{3},K_{4}>0\).

Assumption 4

Assume that

  1. (1)

    F(x) is Lipschitz continuous, that is, for any \(x_{1}, x_{2} \in {\mathcal {X}}\), there exists \(l_{f}>0\) satisfying

    $$\begin{aligned} \left\| F\left( x_{1}\right) -F\left( x_{2}\right) \right\| \leqslant l_{f}\Vert x_{1}-x_{2}\Vert . \end{aligned}$$

    \(F(x),~{\mathcal {G}}_{1}(x)\), and \({\mathcal {G}}_{2}(x)\) are bounded on the compact set \({\mathcal {X}}\), that is, \(\Vert F\Vert \leqslant F_{M}\), \(\Vert {\mathcal {G}}_{1}\Vert \leqslant {\mathcal {G}}_{1M}\), \(\Vert {\mathcal {G}}_{2}\Vert \leqslant {\mathcal {G}}_{2M}\), where \(F_{M},~{\mathcal {G}}_{1M}\), and \({\mathcal {G}}_{2M}>0\);

  2. (2)

    \(\omega ^{*}\) is bounded, that is, \(\Vert \omega ^{*}\Vert \leqslant \omega _{M},\) where \(\omega _{M}>0\);

  3. (3)

    There exists \(M_{M},~d _{M},~and~d_{MM}>0\) such that \(\Vert M_{L}(x)\Vert \leqslant M_{M}\), \(\left\| \nabla _{x} M_{L}(x)\right\| \leqslant d _{M}\), and

    \(\left\| \frac{\partial ^{2}M_{L}(x)}{\partial x^{2}}\right\| \leqslant d_{MM}\) for all \(x\in {\mathcal {X}}\);

  4. (4)

    \(\nabla _{x} \delta (x)\) is Lipschitz continuous, that is, for every \(x_{1}, x_{2} \in {\mathcal {X}}\), there exists \(l_{d \delta }>0\) such that

    $$\begin{aligned} \left\| \nabla _{x} \delta \left( x_{1}\right) -\nabla _{x} \delta \left( x_{2}\right) \right\| \leqslant l_{d \delta }\left\| x_{1}-x_{2}\right\| , \end{aligned}$$

    and there exist \(\delta _{M},~\delta _{d M},~and~\delta _{D M}>0\) such that \(\Vert \delta (x)\Vert \leqslant \delta _{M}\), \(\Vert \nabla _{x}\delta (x)\Vert \leqslant \delta _{dM}\), and \(\left\| \frac{\partial ^{2}\delta (x)}{\partial x^{2}}\right\| \leqslant \delta _{D M}\) for all \(x\in {\mathcal {X}}\);

  5. (5)

    \(\phi (x)\) is bounded on the compact set \({\mathcal {X}}\), that is, \(\phi _{m} \leqslant \phi (x) \leqslant \phi _{M},\) where \(\phi _{m},~\phi _{M}>0\);

Theorem 2

Consider system (1) with control (17) and the event-triggering scheme (11) with (18), and let Assumptions 2–4 hold. Then, the true state x(t), sampled state \(\bar{x}(t)\), and CNN weights error \(\hat{w}(t)\) are SGUUB in probability, if there exist matrices \(Y>0\) and

$$\begin{aligned} \Vert S\Vert \geqslant \bar{D}, \end{aligned}$$
(23)

where

$$\begin{aligned} S= & {} [\Vert x\Vert ,\Vert \bar{x}\Vert , \Vert \hat{w}\Vert ]^{\mathrm{T}},\\ \bar{D}= & {} \frac{\Vert V\Vert +\sqrt{\Vert V\Vert ^{2}(V)+4 U \underline{\sigma }(Y)}}{2 \underline{\sigma }(Y)}, \end{aligned}$$

and U, V, Y are as follows:

$$\begin{aligned} U= & {} \frac{1}{2}\Vert {\mathcal {G}}_{2M}\Vert ^{2}\Vert \delta _{D M}\Vert +\delta _{d M}F_{M}+q_{1}, \\ V= & {} \left[ \begin{array}{c} q_{2} \\ \delta _{dM} {\mathcal {G}}_{1M} K_{4}+q_{2} \\ d_{M} F_{M}-\frac{\gamma \phi _{M}^{2}\omega _{M}}{1+\phi _{M}^{2}} +\frac{1}{2}\Vert {\mathcal {G}}_{2M}\Vert ^{2}\Vert d_{M M}\Vert \end{array}\right] , \\ Y= & {} \left[ \begin{array}{ccc} \frac{K_{1}}{1+c}+\frac{\gamma \phi _{M}\left( K_{1}+K_{3}\right) }{1+\phi _{M}^{2}} &{} 0 &{} 0 \\ 0 &{} \frac{K_{3}^{2}}{1+c} &{} -\frac{d_{M} {\mathcal {G}}_{1M} K_{4}}{2} \\ 0 &{} -\frac{d _{M} {\mathcal {G}}_{1M} K_{4}}{2} &{} \frac{\gamma \phi _{M}^{2}}{1+\phi _{M}^{2}} \end{array}\right] , \end{aligned}$$

where

$$\begin{aligned} q_{1}=\frac{1}{2}{\mathcal {P}}_{M}{\mathcal {G}}_{1M}^{2} \overline{\sigma }^{-1}({\mathcal {R}}) \delta _{M}, ~q_{2} ={\mathcal {P}}_{M}{\mathcal {G}}_{1M}K_{3}. \end{aligned}$$

Proof

Selecting the Lyapunov function condition

$$\begin{aligned} {\mathcal {Y}}(x(t))={\mathcal {V}}^{*}(\bar{x}_{k})+{\mathcal {V}}^{*}(x(t)) +\frac{1}{2}\hat{\omega }^{\mathrm{T}}\hat{\omega }+{\mathcal {P}}(x(t)),\nonumber \\ \end{aligned}$$
(24)

where \({\mathcal {P}}(x(t))\in C^{2}({\mathcal {X}})\) is given in Assumption 1,

\({\mathcal {Y}}(x(t))\in C^{2}({\mathcal {X}})\), and \({\mathcal {Y}}(x(t))\ge 0\) is a positive function due to \({\mathcal {V}}^{*}(\bar{x}_{k})>0\), \({\mathcal {V}}^{*}(x(t))>0\), \({\mathcal {V}}^{*}(0)=0\), \({\mathcal {P}}(x(t))>0\), \({\mathcal {P}}(0)=0\). Since (24) includes both discrete dynamics and continuous dynamics, we analyze the stability analysis under the following two cases.

Case 1 Events are not triggered, that is, \(t\in [t_{k}, t_{k+1})\). For system (10), taking the derivative operation for (24) and using (22), we get

$$\begin{aligned} {\mathcal {L}}{\mathcal {Y}}(x(t))={\mathcal {L}}{\mathcal {V}}^{*} (\bar{x}_{k})+{\mathcal {L}}{\mathcal {V}}^{*}(x(t))+\hat{\omega }^{\mathrm{T}} \dot{\hat{\omega }}+{\mathcal {L}}{\mathcal {P}}(x(t)). \end{aligned}$$

It is worth noting that \(\bar{x}_{k}\) remains invariant on \(t\in [t_{k},t_{k+1})\), thus,

$$\begin{aligned} {\mathcal {L}}{\mathcal {V}}^{*}(\bar{x}_{k})=0. \end{aligned}$$
(25)

From (15), one has

$$\begin{aligned} {\mathcal {V}}^{*}(x)&=M_{L}^{\mathrm{T}}(x) \omega ^{*}+\delta (x) =M_{L}^{\mathrm{T}}(x)(\omega -\hat{\omega })+\delta (x) \nonumber \\&=\hat{{\mathcal {V}}}(x)-M_{L}^{\mathrm{T}}(x) \hat{\omega }+\delta (x). \end{aligned}$$
(26)

It follows from Assumption 2, Assumption 4 and (26) that

$$\begin{aligned} {\mathcal {L}}{\mathcal {V}}^{*}(x)&={\mathcal {V}}_{x}^{*}F(x) +{\mathcal {V}}_{x}^{*}{\mathcal {G}}_{1}(x)\mu (\bar{x}) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} {\mathcal {V}}_{xx}^{*} {\mathcal {G}}_{2} \nonumber \\&=\hat{{\mathcal {V}}}_{x}F(x)+ \hat{{\mathcal {V}}}_{x}{\mathcal {G}}_{1}(x)\mu (\bar{x}) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \hat{{\mathcal {V}}}_{xx} {\mathcal {G}}_{2}\nonumber \\&\quad -\nabla _{x}M_{L}(x)F(x)\hat{\omega }-\nabla _{x}M_{L}(x){\mathcal {G}}_{1}(x) \mu (\bar{x})\hat{\omega }\nonumber \\&\quad -\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}}\frac{\partial ^{2} M_{L}(x) \hat{\omega }}{\partial x^{2}} {\mathcal {G}}_{2}+\nabla _{x}\delta (x)F(x)\nonumber \\&\quad +\nabla _{x}\delta (x){\mathcal {G}}_{1}(x)\mu (\bar{x}) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}}\frac{\partial ^{2} \delta (x)}{\partial x^{2}} {\mathcal {G}}_{2}\nonumber \\&\leqslant -\frac{1}{1+c}\left[ {\mathcal {Q}}(x)+\mu (\bar{x})^{\mathrm{T}} {\mathcal {R}}\mu (\bar{x})\right] \nonumber \\&\quad -\left[ \nabla _{x}M_{L}(x)\hat{\omega }-\nabla _{x} \delta (x)\right] [F(x) +{\mathcal {G}}_{1}(x) \mu (\bar{x})]\nonumber \\&\quad -\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} M_{L}(x)\hat{\omega }}{\partial x^{2}} {\mathcal {G}}_{2}+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} \delta (x)}{\partial x^{2}} {\mathcal {G}}_{2}\nonumber \\&\leqslant -\frac{1}{1+c} \left[ K_{1}\Vert x\Vert ^{2}+K_{3}^{2}\Vert \bar{x}\Vert ^{2}\right] \nonumber \\&\quad +\left( d_{M}\Vert \hat{\omega }\Vert +\delta _{d M}\right) \left( F_{M} +{\mathcal {G}}_{1M} K_{4}\Vert \bar{x}\Vert \right) \nonumber \\&\quad +\frac{1}{2}\Vert {\mathcal {G}}_{2M}\Vert ^{2}\Vert d_{M M}\Vert \Vert \hat{\omega }\Vert +\frac{1}{2}\Vert {\mathcal {G}}_{2M}\Vert ^{2}\Vert \delta _{D M}\Vert . \end{aligned}$$
(27)

The infinitesimal generator of \({\mathcal {P}}(x)\) is written as

$$\begin{aligned} {\mathcal {L}}{\mathcal {P}}(x)&=\nabla _{x}{\mathcal {P}}(x)(F(x) +{\mathcal {G}}_{1}(x)\bar{\mu }(x))+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2}\nonumber \\&= \nabla _{x}{\mathcal {P}}(x)(F(x)+{\mathcal {G}}_{1}(x)\mu (x)) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2}\nonumber \\&\quad +\nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x)\bar{\mu }(x) -\nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x)\mu (x). \end{aligned}$$
(28)

According to (20) and (22), one can obtain

$$\begin{aligned} {\mathcal {L}}{\mathcal {V}}_{\hat{\omega }}(\hat{\omega })&=\hat{\omega }^{\mathrm{T}}\dot{\hat{\omega }} =-\gamma \frac{\hat{\omega }^{\mathrm{T}} \phi (x)}{1+\phi ^{\mathrm{T}} (x)\phi (x)}\eta (x, \omega )\nonumber \\&\quad + \frac{k}{2}\hat{\omega }^{\mathrm{T}}\nabla _{x}^{\mathrm{T}} M_{L} (x){\mathcal {G}}_{1}(x) \mathcal {R}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(x) \nabla _{x}^{\mathrm{T}} {\mathcal {P}}(x). \end{aligned}$$
(29)

From Assumptions 3, 4, and (19), the first term of right side in (29) has the following property:

$$\begin{aligned}&-\gamma \frac{\hat{\omega }^{\mathrm{T}} \phi (x)}{1+\phi ^{\mathrm{T}} (x)\phi (x)}\eta (x, w) \\&\quad =-\gamma \frac{\hat{\omega }^{\mathrm{T}} \phi ^{\mathrm{T}}(x) \phi (x)}{1+\phi ^{\mathrm{T}}(x)\phi (x)}\omega -\gamma \frac{({\mathcal {Q}}(x)+\mu ^{\mathrm{T}}(x) {\mathcal {R}} \mu (x))}{1+\phi ^{\mathrm{T}}(x)\phi (x)}\phi (x)\\&\quad =-\gamma \frac{\hat{\omega }^{\mathrm{T}} \phi ^{\mathrm{T}} (x)\phi (x)}{1+\phi ^{\mathrm{T}}(x)\phi (x)}(\omega ^{*}+\hat{\omega })\\&\qquad -\gamma \frac{({\mathcal {Q}}(x)+\mu ^{\mathrm{T}}(x) {\mathcal {R}} \mu (x))}{1+\phi ^{\mathrm{T}}(x)\phi (x)}\phi (x)\\&\quad \leqslant -\gamma \frac{\phi _{M}^{2}\Vert \hat{\omega } \Vert (\omega _{M}+\Vert \hat{\omega }\Vert )}{1+\phi _{M}^{2}} -\gamma \frac{\phi _{M}(K_{1}+K_{3})\Vert x\Vert ^{2}}{1+\phi _{M}^{2}}. \end{aligned}$$

For k in (21), consider the following two situations:

1) For \(k=0\), one have

$$\begin{aligned}&\nabla _{x}{\mathcal {P}}(x)(F(x)+{\mathcal {G}}_{1}(x)\mu (\bar{x}))\\&\quad +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2}\leqslant 0. \end{aligned}$$

Then, we can get

$$\begin{aligned}&\frac{k}{2}\hat{\omega }^{\mathrm{T}}\nabla _{x}^{\mathrm{T}} M_{L}(x){\mathcal {G}}_{1}(x){\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(x) \nabla _{x}^{\mathrm{T}} {\mathcal {P}}(x)+{\mathcal {L}}{\mathcal {P}}(x)\nonumber \\&\quad \leqslant 0. \end{aligned}$$
(30)

2) For \(k=1\), one have

$$\begin{aligned} \nabla _{x}{\mathcal {P}}(x)(F(x)+{\mathcal {G}}_{1}(x)\mu (\bar{x})) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2}>0. \end{aligned}$$

Then, from (28), one can obtain

$$\begin{aligned}&{\mathcal {L}}{\mathcal {P}}(x)+\frac{k}{2}\hat{\omega }^{\mathrm{T}}\nabla _{x}^{\mathrm{T}} M_{L}(x){\mathcal {G}}_{1}(x) {\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(x) \nabla _{x}^{\mathrm{T}} {\mathcal {P}}(x)\nonumber \\&\quad = \nabla _{x}{\mathcal {P}}(x)F(x)+ \nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x)\mu (x) +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2}\nonumber \nonumber \\&\qquad +\nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x)\mu (\bar{x}) -\nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x)\mu (x)\nonumber \\&\qquad +\frac{1}{2}\hat{\omega }^{\mathrm{T}}\nabla _{x}^{\mathrm{T}} M_{L} (x){\mathcal {G}}_{1}(x){\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}} (x) \nabla _{x}^{\mathrm{T}} {\mathcal {P}}(x) \nonumber \\&\quad =\nabla _{x}{\mathcal {P}}(x)F(x)-\frac{1}{2}{\mathcal {G}}_{1} (x){\mathcal {R}}^{-1}{\mathcal {G}}_{1}^{\mathrm{T}}(x)\nabla _{x}M_{L} (x)(\omega -\hat{\omega }) \nonumber \\&\qquad +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2}+\nabla _{x}{\mathcal {P}} (x){\mathcal {G}}_{1}(x)(\mu (\bar{x})-\mu (x)) \nonumber \\&\quad =\nabla _{x}{\mathcal {P}}(x)F(x)-\frac{1}{2}{\mathcal {G}}_{1} (x){\mathcal {R}}^{-1}{\mathcal {G}}_{1}^{\mathrm{T}}(x)\nabla _{x} ({\mathcal {V}}^{*}(x)-\delta (x)) \nonumber \\&\qquad +\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2}+\nabla _{x} {\mathcal {P}}(x){\mathcal {G}}_{1}(x)(\mu (\bar{x})-\mu (x))\nonumber \\&\quad = \nabla _{x}{\mathcal {P}}(x)F(x)+ \nabla _{x}{\mathcal {P}}(x) {\mathcal {G}}_{1}(x)u^{*}(x)+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \frac{\partial ^{2} {\mathcal {P}}(x)}{\partial x^{2}}{\mathcal {G}}_{2} \nonumber \\&\qquad +\frac{1}{2}\nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x) {\mathcal {R}}^{-1}{\mathcal {G}}_{1}^{\mathrm{T}}(x)\nabla _{x}\delta (x) \nonumber \\&\qquad +\nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x)(\mu (\bar{x})-\mu (x)). \end{aligned}$$
(31)

Based on (30), (31), and Assumptions 2–4, we have

$$\begin{aligned} \nonumber&{\mathcal {L}}{\mathcal {P}}(x)+0.5k \hat{\omega }^{\mathrm{T}}\nabla _{x}^{\mathrm{T}} M_{L}(x) {\mathcal {G}}_{1}(x) {\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(x) \nabla _{x}^{\mathrm{T}} {\mathcal {P}}(x) \nonumber \\&\quad \le \frac{1}{2}\nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x){\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(x)\nabla _{x}\delta (x)\nonumber \\&\qquad +\nabla _{x}{\mathcal {P}}(x){\mathcal {G}}_{1}(x)(\mu (\bar{x})-\mu (x)) \nonumber \\&\quad \le q_{1}+q_{2}(\Vert \bar{x}\Vert +\Vert x\Vert ), \end{aligned}$$
(32)

Combining (30) and (32), we have

$$\begin{aligned}&{\mathcal {L}}{\mathcal {P}}(x)+\frac{k}{2} \hat{\omega }^{\mathrm{T}}\nabla _{x}^{\mathrm{T}} M_{L}(x){\mathcal {G}}_{1}(x) {\mathcal {R}}^{-1} {\mathcal {G}}_{1}^{\mathrm{T}}(x) \nabla _{x}^{\mathrm{T}} {\mathcal {P}}(x) \\&\quad \le \max \{0,q_{1}+q_{2}(\Vert \bar{x}\Vert +\Vert x\Vert )\} \le q_{1}+q_{2}(\Vert \bar{x}\Vert +\Vert x\Vert ). \end{aligned}$$

Next, by (25), (27), (29), and (32), we have

$$\begin{aligned}&{\mathcal {L}}{\mathcal {Y}}(x(t))\nonumber \\&\quad \leqslant -\frac{1}{1+c} \left[ K_{1}\Vert x\Vert ^{2} +K_{3}^{2}\Vert \bar{x}\Vert ^{2}\right] \nonumber \\&\qquad +\left( d_{M}\Vert \hat{\omega }\Vert +\delta _{d M}\right) \left( F_{M}+{\mathcal {G}}_{1M} K_{4}\Vert \bar{x}\Vert \right) \nonumber \\&\qquad +\frac{1}{2}\Vert {\mathcal {G}}_{2M}\Vert ^{2}\Vert d_{M M}\Vert \Vert \hat{\omega }\Vert +\frac{1}{2}\Vert {\mathcal {G}}_{2M}\Vert ^{2}\Vert \delta _{D M}\Vert \nonumber \\&\qquad -\gamma \frac{\phi _{M}^{2}\Vert \hat{\omega }\Vert (\omega _{M} +\Vert \hat{\omega }\Vert )}{1+\phi _{M}^{2}}-\gamma \frac{\phi _{M}(K_{1} +K_{3})\Vert x\Vert ^{2}}{1+\phi _{M}^{2}}\nonumber \\&\qquad + q_{1}+q_{2}(\Vert \bar{x}\Vert +\Vert x\Vert ) \nonumber \\&\quad =-S^{\mathrm{T}} YS+V^{\mathrm{T}} S+U. \end{aligned}$$
(33)

Then, from condition \(Y>0\), we have

$$\begin{aligned} {\mathcal {L}}{\mathcal {Y}}(x(t)) \leqslant -\underline{\sigma }(Y)\Vert S\Vert ^{2}+\Vert V\Vert \Vert S\Vert +U. \end{aligned}$$
(34)

Using condition (23) and doing completing the squares for (34), we get

$$\begin{aligned} {\mathcal {L}}{\mathcal {Y}}(x(t)) \leqslant 0. \end{aligned}$$

By applying \({\mathbb {E}}[{\mathcal {L}}{\mathcal {Y}}(x(t))] \leqslant 0\) and using Dykin formula, one can obtain

$$\begin{aligned} {\mathbb {E}}[{\mathcal {Y}}(x(t))]-{\mathbb {E}}[{\mathcal {Y}}(x_{0})] \le {\mathbb {E}}\int _{0}^{t}{\mathcal {L}}{\mathcal {Y}}(x(s))ds\le 0. \end{aligned}$$

Thus, we get

$$\begin{aligned} {\mathbb {E}}[{\mathcal {Y}}(x(t))]\le {\mathbb {E}}[{\mathcal {Y}}(x_{0})]. \end{aligned}$$

Then, the true state x(t), sampled state \(\bar{x}(t)\), and CNN weights error \(\hat{w}(t)\) are SGUUB in probability.

Case 2 We consider the event-triggered moment \(t=t_{k}\). Consider the difference of the Lyapunov function \({\mathcal {Y}}(x(t_{k}))\) defined in (24) on the event-triggered instant, we get

$$\begin{aligned} \varDelta {\mathcal {Y}}(x(t_{k}))&={\mathcal {Y}}(x(t_{k})) -{\mathcal {Y}}(x(t_{k}^{-})) \nonumber \\&=\varDelta {\mathcal {V}}^{*}(\bar{x}(t_{k}))+\varDelta {\mathcal {V}}^{*}(x(t_{k}))\nonumber \\&\quad +\varDelta {\mathcal {V}}_{\hat{\omega }}(\hat{\omega }(t_{k})) +\varDelta {\mathcal {P}}(x(t_{k})), \end{aligned}$$

where \(x(t_{k}^{-})=\lim \limits _{\alpha \rightarrow 0}x(t_{k-1}-\alpha )\).

From the stability of the flow dynamics, we have that for \(\Vert S\Vert \geqslant \bar{D},\)

$$\begin{aligned}&\varDelta {\mathcal {V}}^{*}\left( x\left( t_{k}\right) \right) \triangleq {\mathcal {V}}^{*}\left( x\left( t_{k}\right) \right) -{\mathcal {V}}^{*}\left( x^{-}\left( t_{k}\right) \right) \le 0,\\&\varDelta {\mathcal {V}}_{\hat{\omega }}(\hat{\omega }(t_{k})) \triangleq {\mathcal {V}}_{\hat{\omega }}(\hat{\omega }(t_{k})) -{\mathcal {V}}_{\hat{\omega }}\left( \hat{\omega }^{-}\left( t_{k}\right) \right) \le 0,\\&\varDelta {\mathcal {P}}\left( x\left( t_{k}\right) \right) \triangleq {\mathcal {P}} \left( x\left( t_{k}\right) \right) -{\mathcal {P}}\left( x^{-}\left( t_{k}\right) \right) \le 0,\\&\varDelta {\mathcal {V}}^{*}\left( \bar{x}\left( t_{k}\right) \right) \triangleq {\mathcal {V}}^{*}\left( \bar{x}\left( t_{k}\right) \right) -{\mathcal {V}}^{*}\left( \bar{x}\left( t_{k-1}\right) \right) \\&\qquad \le -{\mathcal {K}}(\Vert e(t_{k})\Vert ), \end{aligned}$$

where \({\mathcal {K}}(\cdot )\) represents class-\({\mathcal {K}}\) functions in [46]. The strictly increasing property of class-\({\mathcal {K}}\) functions ensures the decrease of \(\varDelta {\mathcal {V}}^{*}\left( \bar{x}\left( t_{k}\right) \right) \).

Therefore, we can get \(\varDelta {\mathcal {Y}}\left( x(t_{k})\right) <0 \text { when }\Vert S\Vert \geqslant \bar{D}\). Finally, one can obtain \({\mathbb {E}}[{\mathcal {Y}}(x(t_{k}))]\le {\mathbb {E}}[{\mathcal {Y}}(x_{0})]\) when \(\Vert S\Vert \geqslant \bar{D}\). Then, the true state x(t), sampled state \(\bar{x}(t)\), and CNN weights error \(\hat{w}(t)\) are SGUUB in probability. \(\square \)

Theorem 3

For system (1) with control input (17), let Assumptions 2–4 hold. Then, an upper bound is given on the cost function \(\bar{{\mathcal {J}}}\left( x_{0}, \mu \right) \).

Proof

For system (1) with control (17), doing derivative operation for \({\mathcal {V}}^{*}(x)\) in (15), we get

$$\begin{aligned} {\mathcal {L}}{\mathcal {V}}^{*}(x)&={\mathcal {L}}\hat{{\mathcal {V}}}(x)+{\mathcal {L}}{\delta }(x)\nonumber \\&=\hat{{\mathcal {V}}}_{x}^{*}F(x)+ \hat{{\mathcal {V}}}_{x}^{*}{\mathcal {G}}_{1} (x)\mu (\bar{x})+\frac{1}{2}{\mathcal {G}}_{2}^{\mathrm{T}} \hat{{\mathcal {V}}}_{xx}^{*} {\mathcal {G}}_{2} +{\mathcal {L}}{\delta }(x)\nonumber \\&=\frac{1}{1+c} \left[ {\mathcal {H}}_{c}(x, \bar{x})-{\mathcal {Q}}(x)-\mu ^{\mathrm{T}} (\bar{x}) {\mathcal {R}} \mu (\bar{x})\right] +{\mathcal {L}}{\delta }(x) \nonumber \\&\leqslant -\frac{1}{1+c}\left[ {\mathcal {Q}}(x)+\mu ^{\mathrm{T}}(\bar{x}){\mathcal {R}} \mu (\bar{x})\right] +{\mathcal {L}}{\delta }(x). \end{aligned}$$

Then, we get

$$\begin{aligned} {\mathcal {Q}}(x)+\mu ^{\mathrm{T}}(\bar{x}){\mathcal {R}} \mu (\bar{x}) \le -(1+c)[{\mathcal {L}}{\mathcal {V}}^{*}(x)+{\mathcal {L}}{\delta }(x)]. \end{aligned}$$

According to the Dynkin formula and condition \(\Vert \delta \Vert \leqslant \delta _{M}\), for any \(T>0\) and \({\mathcal {V}}(x_{T})>0\), one has

$$\begin{aligned}&{\mathbb {E}}\left\{ \int _{0}^{T}\left( {\mathcal {Q}}(x(t)) +\mu ^{\mathrm{T}}(\bar{x}(t)) {\mathcal {R}}\mu (\bar{x}(t))\right) d t\right\} \\&\quad \leqslant -(1+c){\mathbb {E}}\left\{ \int _{0}^{T} [{\mathcal {L}}{\mathcal {V}}^{*}(x(t)) +{\mathcal {L}}{\delta }(x(t))] d t\right\} \\&\quad =(1+c){\mathbb {E}}\left\{ {\mathcal {V}}^{*}(x_{0}) -{\mathcal {V}}^{*}(x_{T})+\delta (x_{0}) -\delta (x_{T}) \right\} \\&\quad \le (1+c) ({\mathcal {V}}^{*}(x_{0})+2\delta _{M})\\&\quad =(1+c)[{\mathcal {J}}^{*}(x_{0})+2\delta _{M}]. \end{aligned}$$

Letting \(T\rightarrow \infty \), we have

$$\begin{aligned} \bar{{\mathcal {J}}}(x_{0},\mu )&={\mathbb {E}}\left\{ \int _{0}^{\infty } \left( {\mathcal {Q}}(x(t))+\mu ^{\mathrm{T}}(\bar{x}(t)) {\mathcal {R}} \mu (\bar{x}(t))\right) d t\right\} \\&\le (1+c)[{\mathcal {J}}^{*}(x_{0})+2\delta _{M}]. \end{aligned}$$

Thus, we can conclude that there exist an upper bound \((1+c)[{\mathcal {J}}^{*}(x_{0})+2\delta _{M}]\) for the real performance index. Furthermore, it can be demonstrated that the upper bound of prespecified C-F will be close to the ideal value when the NN estimation error \(\delta (x) \rightarrow 0\). \(\square \)

Remark 7

Noticing that for deterministic continuous-time systems, there have been many results reported about ETOC based on the ADP method [33, 41]. However, there has been no published paper on the topic for nonlinear Itô-type stochastic systems. Our work is the first attempt to fill the gap of this subject.

Remark 8

It is worth emphasizing that an upper bound of the prespecified C-F can be obtained by the parameter c. Besides, according to Theorem 3, when the estimation error of NN is considered, the upper bound of NN can also be analyzed via ADP. However, in [32, 33], the prespecified C-F for the ETOC contained an integral term, and the boundedness of the integral term was not analyzed.

Remark 9

In our work, the event-triggering scheme (11) is different from those in [38, 39], and the latter ignored the effect of stochastic disturbances. In [38, 39], the main purpose is to achieve the numerical solution of the event-triggered HJB equation by applying ADP method. However, the event-triggered HJB equation is really a kind of approximate of the given HJB equation. It is noteworthy that the event-triggering scheme (11) can utilize the ADP method directly to get original solution of HJB equation. Thus, the error of numerical solution can be reduced.

6 Simulation results

Example 1

In this example, a controlled Van der Pol oscillator of system (1) is expressed as

$$\begin{aligned} dx(t)={\mathcal {A}}(x(t)) dt+&{\mathcal {G}}_{1}(x(t)) u(x(t))dt\nonumber \\&+{\mathcal {G}}_{2}(x(t)) dw(t), \end{aligned}$$
(35)

where

$$\begin{aligned} {\mathcal {A}}(x)=[0.1x_{2}~-x_{1}-\frac{1}{3} x_{2}\left( 1-x_{1}^{2}\right) -0.1x_{1}^{2} x_{2}]^{\mathrm{T}},\nonumber \\ {\mathcal {G}}_{1}(x) =[0~0.2x_{1}]^{\mathrm{T}}, ~~{\mathcal {G}}_{2} (x)=[0~ x_{2}]^{\mathrm{T}}. \end{aligned}$$

The corresponding cost function is given in (2), where \({\mathcal {R}}=1\) and \({\mathcal {Q}}(x)=x^{\mathrm{T}}Ix\) with an identity matrix I. The Lyapunov function candidate \({\mathcal {P}}(x)=\frac{1}{2}(x_{1}^2+x_{2}^2)\) and the initial value \(x(t)=[0.5,-1]^{\mathrm{T}}\). Let the CNN activation function is \(M_{L}(x)=[x_{1}^2, x_{2}^2, x_{1}x_{2}]^{\mathrm{T}}\), and the CNN weight vector \(\omega =[\omega _{1}, \omega _{2}, \omega _{3}]^{\mathrm{T}}\). Let the parameter c of triggering scheme (18) as 0.05.

Fig. 1
figure 1

The state response x(t) and \(\bar{x}(t)\)

Full size image
Fig. 2
figure 2

The ETOC \(\mu (t)\) and TTOC u(t)

Full size image
Fig. 3
figure 3

The trajectories of \(\omega \)

Full size image
Fig. 4
figure 4

Sampling period \(h_{k}\)

Full size image

By means of MATLAB, the simulation figures are shown in Figs. 1–4. Figure 1 shows the response of the state x and \(\bar{x}\), one can obtain that system (35) is asymptotically stable in probability. Meanwhile, it shows that the state x under the TTOC and the ETOC has a similar effect, and ETOC reduces the computing load. Figure 2 shows that the ETOC \(\mu (t)\) and the TTOC u(x). It reflects that the frequency of control updating of ETOC can be greatly reduced. The convergence of the CNN weight \(\omega \) is shown in Fig. 3, which demonstrates that the CNN weight converges to \([0.0467, -1.1023, -0.2016]^{\mathrm{T}}\). Thus, the approximate value function is written as \(\hat{{\mathcal {V}}}(x)=M_{L}^{\mathrm{T}}(x)\omega =0.0467x_{1}^2 -1.1023x_{2}^{2}-0.2016x_{1}x_{2}\). Moreover, in Fig. 3, the initial weights of the CNN are all set to zero, which means that the implementation of the control strategy does not require the initial stabilizing control. Figure 4 shows the intersample times \(h_{k}\), and the minimum \(h_{k}\) is 0.02 s. Moreover, simulation results about \(t\in [0,30]\) incidents that only 36 state samples applied to execute the ETOC approach, which takes about 0.036% of the whole state samples. Thus, the use of communication resources can be promoted and the computational complexity is greatly decrease.

Example 2

Consider the power system with stochastic disturbance as

$$\begin{aligned} dx={\mathcal {A}}xdt+{\mathcal {B}}(x)u(x)dt+{\mathcal {C}}(x)dw, \end{aligned}$$
(36)

where the system matrices as

$$\begin{aligned} {\mathcal {A}}= & {} \left[ \begin{array}{ccc} -\frac{1}{P_{t}} &{} \frac{P_{k}}{P_{t}} &{} 0 \\ 0 &{} -\frac{1}{T_{t}} &{} \frac{1}{T_{t}} \\ -\frac{1}{R_{g} G_{t}} &{} 0 &{} -\frac{1}{G_{t}} \end{array}\right] , \\ {\mathcal {B}}(x)= & {} \left[ \begin{array}{c} \frac{1}{P_{t}} x_{1}\\ \frac{1}{T_{t}}x_{2} \\ \frac{1}{G_{t}}x_{3} \end{array}\right] ,~ {\mathcal {C}}(x)=\left[ \begin{array}{c} 0 \\ 0 \\ \frac{1}{G_{t}}x_{3} \end{array}\right] . \end{aligned}$$

where \(x=\left[ \varDelta P_{f}, \varDelta G_{p}, \varDelta V_{g}\right] ^{\top }\), \(\varDelta P_{f}\) represents the incremental frequency deviation, \(\varDelta G_{p}\) denotes the incremental change in generator output, and \(\varDelta V_{g}\) denotes the incremental change in governor valve position. By \(x_{1}\) denoting the \(\varDelta P_{f}\), \(x_{2}\) denoting the \(\varDelta G_{p}\), and \(x_{3}\) denoting the \(\varDelta V_{g}\). \(P_{t}=0.5\), \(R_{g}=0.1\), \(T_{t}=0.6\), \(G_{t}=0.5\), and \(P_{k}=0.6\) represent the plant model time constant, the feedback regulation constant, the turbine time constant, the governor time constant, and the plant gain, respectively.

Remark 10

Most works on the power systems are based on deterministic systems [38, 47]. However, in practical applications, stochastic perturbations will have an impact on all aspects of the power systems, such as the fluctuation of system frequency, node voltage, and generator speed. The existence of stochastic perturbations destroys the stability and reduces the control performance of the systems. Therefore, the ETOC problem of the power system with stochastic perturbations is studied in this paper.

Fig. 5
figure 5

The state response x(t) and \(\bar{x}(t)\)

Full size image
Fig. 6
figure 6

The response of ETOC \(\mu (t)\) and TTOC u(x)

Full size image
Fig. 7
figure 7

The trajectories of \(\omega \)

Full size image
Fig. 8
figure 8

Sampling period \(h_{k}\)

Full size image

The cost function is given in (2), let \({\mathcal {Q}}(x)=x^{\mathrm{T}} I x\) with an identity matrix I and \({\mathcal {R}}=1\). Select the critic NN activation function vector is \(M_{L}(x)=[x_{1}^2,~x_{1}x_{2},~x_{2}^2, x_{1}x_{3},~x_{2}x_{3},~x_{3}^2]^{\mathrm{T}}\). The Lyapunov function candidate \({\mathcal {P}}(x)=\frac{1}{2}(x_{1}^2+x_{2}^2+x_{3}^2)\) and the initial condition \(x(t)=[1,-1,0.5]^{\mathrm{T}}\). Choosing the parameter c of triggering scheme (18) as 0.06.

Simulation figures are shown in Figs. 5, 6, 7, and 8. Figure 5 shows the response of the state x and \(\bar{x}\), one can find that the ETOC can guarantee system (36) is asymptotically stable in probability. Figure 6 shows the trajectories of ETOC \(\mu (t)\) and TTOC u(t), which reveals that the frequency of control updating of ETOC is greatly reduced. As reflected in Fig. 7, the CNN weight converges to \([0.334, -0.3568, 0.4211, -0.3813, 0.4064, 0.407]^{\mathrm{T}}\). Thus, the approximate value function as \(\hat{{\mathcal {V}}}(x) =M_{L}^{\mathrm{T}}(x)\omega =0.334x_{1}^2-0.3568x_{1}x_{2} +0.4211x_{2}^{2}-0.3813x_{1}x_{3}+0.4064x_{2}x_{3}+0.407x_{3}^{2}\). As illustrated in Fig. 8, the minimum interexecution times are 0.06 s. Moreover, simulation results about \(t\in [0,10]\) incidents that only 11 state samples applied to accomplish the ETOC algorithm, which takes about 0.03% of the whole state samples. In that sense, the ETOC used in this paper can maintain the control performance while effectively reducing the number of sampling and control tasks.

7 Conclusion

In this paper, we study the ETOC problem for nonlinear Itô-type stochastic systems based on ADP method. A new event-triggering scheme is proposed, which can be used to design ETOC directly via the solution of HJB equation. Furthermore, the stability of nonlinear Itô-type stochastic system is analyzed, and the given ETOC scheme can give an upper bound for predetermined C-F. In particular, the ADP approach is firstly applied to study nonlinear Itô-type stochastic systems with ETOC, which can achieve the numerical solution of the HJB equation.

There are some meaningful topics that can be investigated in the future. Since the practical systems are inevitably impacted by time-delay, stochastic perturbations, and unknown dynamics. Therefore, it is of great significance to study the ETOC for stochastic systems with time-delay and unknown dynamics. In addition, it is also a very promising topic to study the ETOC for nonlinear stochastic multi-agent systems.