Leader-following consensus of fractional-order multi-agent systems based on event-triggered control

Abstract

In this paper, an efficient event-triggered control is designed to address the leader-following consensus problem for the fractional-order multi-agent systems. First, in order to reduce the conservation of consensus criteria, a novel Wirtinger-based fractional-order integral inequality is proposed. Second, an adaptive control is designed by using a new event-triggered scheme without Zeno behavior, which can effectively reduce the communication cost in network. Later in order to analyze the consensus of the fraction-order leader-following systems, we employ a new approach based on fractional Lyapunov direct method. Finally, combining Wirtinger-based fractional-order integral inequality, the event-triggered adaptive control as well as the proposed consensus method, the consensus criteria of the leader-following fractional-order multi-agent systems are obtained. Two numerical examples are used to test the effectiveness and feasibility of the results presented in this study.

1 Introduction

The coordination of multi-agent systems (MASs) has attracted increasingly attention over the past decades due to its popularity in many practical applications such as leader–follower formation of the nonholonomic mobile robots [1], distributed formation of multi-robot systems with nonholonomic constraint [2], distributed consensus behavior in sensor networks [3], coordinated target of unmanned air vehicle formations and underwater vehicles [4] and [5]. As a critical issue in coordination of MASs, the consensus problems of first-order, second-order, and high-order systems have been extensively studied [6, 7]. According to the definition of fractional calculus, the fractional-order systems can accurately describe the memory and heredity properties [8,9,10,11,12,13,14]. Therefore, for more complicated dynamic phenomena, fractional calculus instead of integer one has been employed to describe them more accurately, such as the lubricating bacteria model for branching growth of bacterial colonies, biofluid dynamic model for lubricating bacteria, submarines and underwater robots that explores the seabed with large amounts of microorganisms and sticky substances, consensus behavior for unmanned aerial vehicles operating in complex weather (e.g., high-speed flight in dust storm, rain, or snow), and dynamic behavior of viscoelastic materials during vehicle movement [15,16,17,18,19,20].

Since Cao et al. first proposed the fractional-order multi-agent systems (FOMASs) in [21], some sufficient criteria have been proposed to achieve the consensus of the considered networks. Later the coordination, consensus and stability problems of FOMASs have been explored [22,23,24,25,26,27,28,29]. For instance, in [23] and [24], necessary and sufficient criteria for consensus of FOMASs are proposed by designing the distributed control protocols; by employing adaptive pinning control approach, the leader-following consensus of FOMASs is discussed in [25]; the distributed formation control in [26,27,28] is designed to obtain the consensus behavior of FOMASs; the sliding mode control method is introduced to ensure the distributed consensus tracking for FOMASs in [29] and [30].

It is worth noting that all these aforementioned works study the consensus problem of FOMASs by using continuous control, in which the input controlling signals have to be updated continuously. However, from economics perspective, these continuous protocols will spend a lot of time and money, leading to inefficiency in real application. Therefore, how to design a more efficient and practical controller for the consensus of FOMASs has become a challenge faced by scholars. Indeed, the controller can be divided into two types: continuous time controller [23,24,25,26,27,28,29,30,31,32] and discrete sampled-data one [33,34,35,36,37,38,39,40,41]. Compared with the widely application of continuous time controller [23,24,25,26,27,28,29,30,31,32], the discrete sampled-data controller, as a more economical one, is still in emergent stage for the consistency of FOMASs with only several event-triggered sampling techniques being proposed [34,35,36,37,38,39,40,41]. In [38], the event-triggered strategy for the consensus of FOMASs is designed, but it does not consider neighboring agent information. In [39,40,41], the event-triggered strategies are designed to solve the channel congestion caused by simultaneous information transferring. Thus to deal with these problems, in this study, we design a corresponding event-triggered mechanism for each agent by using information from the neighboring agents.

Inspired by the above discussion, this paper addresses the consensus problem of FOMASs by designing event-triggered control which only depends on the local information. The main contributions of this study include: (1) a novel Wirtinger-based fractional-order integral inequality (WBFOII) is introduced to estimate Lyapunov–Krasovskii functions, which can obtain much tighter bounds than fractional-order Jensen-like integral inequality; (2) new event-triggered control strategies without Zeno behavior are produced to monitor the dynamic behavior of each agent, which can reduce communication traffic; (3) by using the proposed WBFOII, the consensus criteria depending on $\alpha$-order are also suggested to analyze the dynamical behaviors of FOMASs with event-triggered control; (4) compared with the previous works [25] and [27,28,29], the proposed consensus criteria depending on $\alpha$-order can analyze the effect of $\alpha$-order on the dynamic behaviors of FOMASs more accurately; (5) the simulation results of the event-triggering numbers also verify the effectiveness of our approach as well as its advantage in comparison with the method in [41].

The rest of this paper is organized as follows. In Sect. 2, some related definitions and properties of fractional calculus are introduced and a network with FOMASs is described. Then, an adaptive controller for the consensus of FOMASs is designed based on WBFOII and the proposed event-triggered strategies in Sect. 3. Section 4 provides two numerical examples to demonstrate the validity and efficiency of the proposed controller. Finally, some conclusions are summarized in Sect. 5.

Notations: in this paper, ${\mathbb {N}}$ denotes the positive integer. ${\mathbb {R}}^n$ and ${\mathbb {R}}^{n\times {m}}$, respectively, represent the n-dimensional Euclidean space and the set of $n\times {m}$ real matrices. ${\mathbb {R}}$ is a real number set. ${\mathbf {C}}^m([0,+\infty ), {\mathbb {R}})$ denotes Banach space of all continuous and m-order differentiable functions. T stands for the transpose of matrix. $I_n$ denotes an n-dimensional identity matrix. The notation $diag(\ldots )$ stands for a block-diagonal matrix. $\lambda _\mathrm{{max}}(A)$ ($\lambda _\mathrm{{min}}(A)$) denotes the maximum (minimum) eigenvalues of A. The notation $A>0$ represents that A is a real symmetric and positive definite matrix. If $x\in {{\mathbb {R}}^n}$, we have $|x|=(|x_1|, |x_2|, \ldots , |x_n|)^T$ and $\Vert x\Vert =\left( \sum \nolimits _{k=1}^{n}\mid {x_k}\mid ^2\right) ^\frac{1}{2}$. If $a\in {\mathbb {R}}^n$, then $\mathrm{sgn}(a)$ denotes the symbol of scalar a.

2 Preliminaries and problem statement

In this section, some definitions and property of fractional calculus are introduced and then a FOMAS model with one leader and several followers is suggested to standardize the consensus problem in this study.

2.1 Fractional calculus

Definition 1

[42] The Caputo derivative of $\alpha$-order for function f(t) is defined as

$$\begin{aligned} {}_{t_{0}}D^{\alpha }_tf(t)=\frac{1}{\varGamma (m-\alpha )}\int _{t_0}^t (t-u)^{m-\alpha -1}f^{(m)}(u)\mathrm{d}u \end{aligned}$$

where $m-1\le \alpha <m$, $m\in {\mathbb {N}}$, $f\in {{\mathbf {C}}^m([t_0,+\infty ),{\mathbb {R}})}$, $t_0$ is the initial time, and $\varGamma (\cdot )$ is Gamma function. When $0<\alpha <1$, ${}_{t_{0}}D^{\alpha }_tf(t)=\frac{1}{\varGamma (1-\alpha )}\int _{t_0}^t (t-u)^{-\alpha }f'(u)\mathrm{d}u$.

Definition 2

[42] The integration of $\alpha$-order for function f(t) is defined as

$$\begin{aligned} {}_{t_{0}}I^{\alpha }_t f(t)=\frac{1}{\varGamma (\alpha )}\int _{t_{0}}^t (t-u)^{\alpha -1}f(u)\mathrm{d}u \end{aligned}$$

where $\alpha >0$ and f(u) is integrable in $[t_0, t]$.

Definition 3

[42] The Riemann–Liouville derivative of $\alpha$-order for function f(t) is defined as

$$\begin{aligned} {}_{t_{0}}^RD^{\alpha }_tf(t)=\frac{1}{\varGamma (m-\alpha )}\frac{\mathrm{d}^m}{\mathrm{d}t^m}\int _{t_0}^t (t-u)^{m-\alpha -1}f^{(m)}(u)\mathrm{d}u. \end{aligned}$$

The following property of the fractional calculus is necessary in proof of our main results.

Property 1

[42] Assume that f(t) is a continuous function, then ${}_{t_{0}}I^{\alpha }_t{}_{t_{0}} D^{\alpha }_tf(t)=f(t)-f(t_0)$, where $0<\alpha \le {1}$.

2.2 Problem statement

This paper studies the consensus of a multi-agent network with one leader and N followers. For more accuracy, the behavior of the leader and followers can be described as the fractional-order nonlinear dynamics. Without loss of generality, let $x_0$ be the leader. Then the dynamic behavior of the leader can be described by

$$\begin{aligned} {}_{t_0}D^\alpha _tx_0(t)=Ax_0(t)+f(x_0(t))+\varDelta _0(t) \end{aligned}$$

(1)

where $0<\alpha <1$, $x_0(t)=(x_{01}(t),x_{02}(t),\ldots ,x_{0n}(t))^T$ is the state of the leader; $A\in {{\mathbb {R}}^{n\times {n}}}$ is a constant matrix; $f(x_0(t))=(f_1(x_{0}(t)),f_2(x_{0}(t)),\ldots ,f_n(x_{0}(t)))^T\in {{\mathbb {R}}^n}$ is a nonlinear function; $\varDelta _0(t)=(\varDelta _{01}(t), \varDelta _{02}(t), \ldots ,$$\varDelta _{0n}(t))^T\in {\mathbb {R}}^n$ is the external disturbance in some special environment. The behavior of N followers is described by

$$\begin{aligned} {}_{t_0}D^\alpha _tx_i(t)=Ax_i(t)+f(x_i(t))+\varDelta _i(t)+u_i(t) \end{aligned}$$

(2)

where $x_i(t)=(x_{i1}(t),x_{i2}(t),\ldots ,x_{in}(t))^T$ is the state of follower i; $f(x_i(t))=(f_1(x_{i}(t)), f_2(x_{i}(t)),\ldots ,f_n(x_{i}$$(t)))^T\in {{\mathbb {R}}^n}$ is a nonlinear function; $\varDelta _i(t)=(\varDelta _{i1}(t),$$\varDelta _{i2}(t), \ldots ,\varDelta _{in}(t))^T$$\in {\mathbb {R}}^n$ is the external disturbance in some special environment; $u_i(t)$ represents a vector of control input.

Remark 1

In a real complicated environment, external disturbances are inevitable. For example, complex weather such as rain and snow storms, and a series of external noises will affect the communication of FOMASs. Therefore, it is necessary to consider the impact of external disturbances on the dynamic behavior of FOMASs.

Before proceeding further, it is necessary to make the following assumptions.

Assumption 1

 

• (1) The function f(x) of multi-agent systems is continuous, and there exists a constant matrix $Q>0$ such that $(x-y)^T(f(x)-f(y))\le (x-y)^TQ(x-y)$ for all $x,y\in {\mathbb {R}}^n$.

• (2) The unknown disturbance $\varDelta _i(t)$ is bounded, namely $|\varDelta _{ij}(t)|<\varDelta _{ij}$, $i=0,1,2,\ldots , N$, where $\varDelta _{ij}$ is a positive constant denoting $\varDelta _{i}=(\varDelta _{i1},\varDelta _{i2},\ldots ,\varDelta _{in})^T$.

Assumption 2

Assume that there is at least one communication path between the leader and each follower in the argued multi-agent network.

Definition 4

[43] The leader-following consensus of FOMASs is said to be achieved if, for any $x_i(0)$, $i\in \{0,1,2,\ldots ,N\}$, it satisfies

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }\Vert x_i(t)-x_0(t)\Vert =0. \end{aligned}$$

To study the consensus problem, the error vector $e_i(t)$ between the leader $x_0(t)$ and any follower $x_i(t)$ is defined as $e_i(t)=x_i(t)-x_0(t)$. Then the error system can be obtained as follows

$$\begin{aligned} {}_{t_0}D^\alpha _te_i(t)=Ae_i(t)+{\tilde{f}}(e_i(t))+{\tilde{\varDelta }}_i(t)+u_i(t) \end{aligned}$$

(3)

where ${\tilde{f}}(e_i(t))=f(x_i(t))-f(x_0(t))$, ${\tilde{\varDelta }}_i(t)=\varDelta _i(t)-\varDelta _0(t)$ and $i\in \{1,2,\ldots ,N\}$.

The purpose of this study is to design a more efficient and economical event-triggered mechanism to achieve the consensus problem of the above leader-following FOMASs.

3 Main results

In this section, first a new WBFOII is proposed to deal with Lyapunov–Krasovskii functions, then a novel event-triggered adaptive control is proposed to ensure the N followers states to be consistent with the leader’s behavior rapidly and economically.

3.1 Wirtinger-based fractional-order integral inequality

Lemma 1

Let x(t) be an arbitrary integrable function in [a, b]. Then, for any $n\times n$ matrix $Q>0$, the following inequality holds:

$$\begin{aligned} \begin{aligned}&{}_aI^{\alpha }_b(x^T(b)Qx(b)) \ge \frac{3}{\varGamma (\alpha +1)(b-a)^\alpha }\varOmega ^TQ\varOmega \\&\quad \quad +\frac{\varGamma (\alpha +1)}{(b-a)^\alpha }\left( {}_aI^{\alpha }_bx(b)\right) ^TQ \left( {}_aI^{\alpha }_bx(b)\right) \end{aligned} \end{aligned}$$

(4)

where $\varOmega =\frac{\varGamma (2\alpha +1)}{(b-a)^\alpha }{}_aI^{2\alpha }_bx(b)-\varGamma (\alpha +1){}_a I^{\alpha }_bx(b)$.

Proof

For any integrable function x(t), definition of the function z(t) is given for $\forall t\in [a,b]$,

$$\begin{aligned} \begin{aligned} z(t)=\,&x(t)-\frac{\varGamma (\alpha +1)}{(b-a)^\alpha }{}_aI^{\alpha }_bx(b)\\&-\left( \frac{6(b-t)^\alpha }{(b-a)^{2\alpha }}-\frac{3}{(b-a)^{\alpha }}\right) \varOmega . \end{aligned} \end{aligned}$$

(5)

According to Definition 2, we can obtain

$$\begin{aligned}&{}_a I^\alpha _b(z^T(t)Qz(t))\nonumber \\&\quad =\frac{1}{\varGamma (\alpha )}\int ^b_a(b-t)^{\alpha -1}z^T(t)Qz(t)\mathrm{d}t\nonumber \\&\quad =\frac{1}{\varGamma (\alpha )}\int ^b_a(b-t)^{\alpha -1}\left\{ x^T(t)Qx(t)\right. -2\frac{\varGamma (\alpha +1)}{(b-a)^\alpha }x^T(t)\nonumber \\&\qquad \times Q{}_aI^{\alpha }_bx(b)-2\left( \frac{6(b-t)^\alpha }{(b-a)^{2\alpha }} -\frac{3}{(b-a)^{\alpha }}\right) x^T(t)Q\varOmega \nonumber \\&\qquad +\left( \frac{\varGamma (\alpha +1)}{(b-a)^\alpha }\right) ^2({}_aI^{\alpha }_bx(b))^TQ({}_aI^{\alpha }_bx(b))\nonumber \\&\qquad +2\left( \frac{\varGamma (\alpha +1)}{(b-a)^\alpha }\right) \left( \frac{6(b-t)^\alpha }{(b-a)^{2\alpha }}-\frac{3}{(b-a)^{\alpha }}\right) ({}_aI^{\alpha }_bx(b))^T\nonumber \\&\qquad \times Q\varOmega \left. +\left( \frac{6(b-t)^\alpha }{(b-a)^{2\alpha }}-\frac{3}{(b-a)^{\alpha }}\right) ^2\varOmega ^TQ\varOmega \right\} \mathrm{d}t. \end{aligned}$$

(6)

Notice that

$$\begin{aligned}&\frac{1}{\varGamma (\alpha )}\int ^b_a(b-t)^{\alpha -1}\times \left( \frac{6(b-t)^\alpha }{(b-a)^{2\alpha }}-\frac{3}{(b-a)^{\alpha }}\right) \mathrm{d}t=0,\nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned}&\frac{1}{\varGamma (\alpha )}\int ^b_a(b-t)^{\alpha -1}\left( \frac{6(b-t)^\alpha }{(b-a)^{2\alpha }}-\frac{3}{(b-a)^{\alpha }}\right) x(t)\mathrm{d}t\nonumber \\&\quad =\frac{6}{\varGamma (\alpha )(b-a)^{2\alpha }}\int ^b_a(b-t)^{2\alpha -1}x(t)\mathrm{d}t\nonumber \\&\qquad -\frac{3}{(b-a)^{\alpha }}{}_aI^{\alpha }_bx(b) \nonumber \\&\quad =\frac{6\varGamma (2\alpha )}{\varGamma (\alpha )(b-a)^{2\alpha }}{}_aI^{2\alpha }_bx(b) -\frac{3}{(b-a)^{\alpha }}{}_aI^{\alpha }_bx(b) \nonumber \\&\quad =\frac{3}{\varGamma (\alpha +1)(b-a)^{\alpha }}\varOmega , \end{aligned}$$

(8)

$$\begin{aligned}&\frac{1}{\varGamma (\alpha )}\int ^b_a(b-t)^{\alpha -1}\left( \frac{6(b-t)^\alpha }{(b-a)^{2\alpha }}-\frac{3}{(b-a)^{\alpha }}\right) ^2\mathrm{d}t\nonumber \\&\quad =\frac{9}{\varGamma (\alpha )(b-a)^{4\alpha }}\int ^b_a\left( 4(b-t)^{3\alpha -1}\right. \nonumber \\&\qquad \left. -2(b-t)^{2\alpha -1}(b-a)^\alpha \right) \mathrm{d}t\nonumber \\&\quad =\frac{3}{\varGamma (\alpha +1)(b-a)^{\alpha }}. \end{aligned}$$

(9)

Therefore, substituting (7)–(9) into (6), it could be derived

$$\begin{aligned} \begin{aligned} {}_aI^{\alpha }_b(z^T (b)Qz(b))&={}_aI^{\alpha }_b(x^T(b)Qx(b))\\&\quad -\frac{\varGamma (\alpha +1)}{(b-a)^\alpha }\left( {}_aI^{\alpha }_bx(b)\right) ^TQ \left( {}_aI^{\alpha }_bx(b)\right) \\&\quad -\frac{3}{\varGamma (\alpha +1)(b-a)^\alpha }\varOmega ^TQ\varOmega . \end{aligned} \end{aligned}$$

(10)

Accordingly, $z^T(t)Qz(t)$ is always nonnegative since $Q>0$. Thus, we have

$$\begin{aligned} \begin{aligned}&{}_aI^{\alpha }_b(x^T(b)Qx(b))&\\&\quad \ge \frac{\varGamma (\alpha +1)}{(b-a)^\alpha }\left( {}_aI^{\alpha }_bx(b)\right) ^TQ \left( {}_aI^{\alpha }_bx(b)\right) \\&\qquad +\frac{3}{\varGamma (\alpha +1)(b-a)^\alpha }\varOmega ^TQ\varOmega . \end{aligned} \end{aligned}$$

(11)

$\square$

Remark 2

Notice that when $\alpha =1$, according to Lemma 1, we can obtain

$$\begin{aligned} \begin{aligned} \int ^b_ax^T(t)Qx(t)\mathrm{d}t\ge&\frac{1}{b-a}\int ^b_ax^T(t)\mathrm{d}tQ\int ^b_ax(t)\mathrm{d}t\\&+\frac{3}{b-a}\varOmega _1^TQ\varOmega _1 \end{aligned} \end{aligned}$$

(12)

where $\varOmega _1=\frac{2}{b-a}\int ^b_a\int ^s_ax(u)\mathrm{d}u\mathrm{d}s-\int ^b_ax(s)\mathrm{d}s$. Obviously, (12) is the same as Eq. (5) in [44], implying Lemma 1 is an extension of Corollary 5 in [44].

Remark 3

Compared with fractional-order Jensen-like integral inequality, the proposed WBFOII has an additional positive term. Therefore, using WBFOII to estimate Lyapunov–Krasovskii functions can obtain much tighter bounds.

Corollary 1

Let x(t) be an arbitrary continuously differentiable function in [a, b]. Then, for any $n\times n$ matrix $Q>0$, the following inequality holds:

$$\begin{aligned} \begin{aligned}&{}_aI^{\alpha }_b \left( \left( {}_aD^{\alpha }_b x(b)\right) ^TQ \left( {}_aD^{\alpha }_b x(b)\right) \right) \\&\quad \ge \frac{\varGamma (\alpha +1)}{(b-a)^\alpha }\varOmega _2^TQ\varOmega _2\\&\quad \quad +\frac{3}{\varGamma (\alpha +1)(b- a)^\alpha }\varOmega _3^TQ\varOmega _3 \end{aligned} \end{aligned}$$

(13)

where $\varOmega _2=x(b)-x(a)$,

$$\begin{aligned} \varOmega _3= & {} \frac{\varGamma (2\alpha +1)}{(b-a)^\alpha }{}_aI^{\alpha }_bx(b)-\frac{\varGamma (2 \alpha +1)}{\varGamma (\alpha +1)}x(a)\\&-\varGamma (\alpha +1)\varOmega _2. \end{aligned}$$

Corollary 2

Let x(t) be an arbitrary continuously differentiable function in [a, b]. Then, for any $n\times n$ matrix $Q>0$, the following inequality holds:

$$\begin{aligned} \begin{aligned}&{}_aI^{\alpha }_b\left( \left( {}_a^RD^{\alpha }_b x(b)\right) ^TQ \left( {}_a^RD^{\alpha }_b x(b)\right) \right) \\&\quad \ge \frac{\varGamma (\alpha +1)}{(b-a)^\alpha }x^T(b)Qx(b)\\&\qquad +\frac{3}{\varGamma (\alpha +1)(b- a)^\alpha }\varOmega _4^TQ\varOmega _4 \end{aligned} \end{aligned}$$

(14)

where $\varOmega _4=\frac{\varGamma (2\alpha +1)}{(b-a)^\alpha }{}_aI^{\alpha }_bx(b)-\varGamma (\alpha +1)x(b)$.

3.2 Design of the event-triggered scheme

The FOMAS with one decision-making leader and N followers can be simplified as a control system. In practice, the leader might be a large firm or the local government, whose decisions or policies are periodical, rather than continuous ones as discussed in [23,24,25,26,27,28,29]. Thus the event-triggered strategy in the control theory can describe their behaviors or activities better. Therefore, in this section, we try to design an event-triggered mechanism to reduce the control frequency. Let

$$\begin{aligned} \begin{aligned}&t_{k+1}=t_k+min\{\tau , T^i_k| i=1,2,\ldots , N\}\\&T^i_k=inf\{l|\digamma _i(t_k+l)\ge \varrho e^{-\varepsilon t_k}\}, k=0,1,2,\ldots \end{aligned} \end{aligned}$$

(15)

where l, $\varepsilon$ and $\tau$ are the positive constants, $t_0$ is the first trigged time, $t_k$ stands for the latest transmission instant, $t_{k+1}$ denotes the next transmission instant; $\digamma _i(t)=(\sum _{j=1}^NL_{ij}(x_j(t)-x_j(t_k)))^T R_i(\sum _{j=1}^NL_{ij}(x_j(t)-x_j(t_k))) -\rho (\sum _{j=1}^Nd_{ij}(x_i(t_k)-x_j(t_k)))^T R_i(\sum _{j=1}^Nd_{ij}($$x_i(t_k)-x_j(t_k)))$ where the matrix $R_i>0$, the scalars $\rho$ and $\varrho$, which are parameters of event-triggered scheme, will be designed later. $D=(d_{ij})_{N\times N}$ denotes a weighted adjacency matrix of the follower’s system, where $d_{ij}>0$ indicates that the follower agents i and j can exchange information with each other, otherwise $d_{ij}=0$; $L_{ij}=-d_{ij}$ when $i\ne j$, otherwise $L_{ii}=\sum \nolimits _{j=1}^Nd_{ij}$. We denote sampling interval $\tau _k=t_{k+1}-t_k$, namely $\tau _k\le \tau$.

Remark 4

This study designs the following event-triggered condition

$$\begin{aligned} \begin{aligned}&\left( \sum _{j=1}^NL_{ij}(x_j(t)-x_j(t_k))\right) ^TR_i\\&\qquad \times \left( \sum _{j=1}^NL_{ij}(x_j(t)-x_j(t_k))\right) \\&\quad \le \rho \left( \sum _{j=1}^Nd_{ij}(x_i(t_k)-x_j(t_k))\right) ^T\\&\qquad \times R_i\left( \sum _{j=1}^Nd_{ij}(x_i(t_k)-x_j(t_k))\right) +\varrho e^{-\varepsilon t_k}. \end{aligned} \end{aligned}$$

(16)

When the event-triggered scheme is violated, the leader will update control state to make the consensus of a leader and N followers. Otherwise, the control inputs of the N follower systems (2) are kept in holding time $[t_k, t_{k+1})$.

Remark 5

The interval $[t_0, +\infty )$ is divided into ${\mathbb {T}}=\{[t_k,t_{k+1})\mid k\in {\mathbb {N}}\}$ by using the event-triggered sample-data. Then the error system with $t\in [t_k, t_{k+1})$ can be obtained as follows:

$$\begin{aligned} {}_{t_k}D^\alpha _te_i(t)=Ae_i(t)+{\tilde{f}}(e_i(t))+{\tilde{\varDelta }}_i(t)+u_i(t). \end{aligned}$$

(17)

Then, in order to analyze the consensus of FOMASs, we propose the following lemmas.

Lemma 2

For system (17), let $\nu (t)$ be a positive definite function, $\vartheta (t)$ be an arbitrary function satisfying $\vartheta (t_k)=0$, and there exists a scalar $\sigma$ such that $t_{k+1}-t_k\ge \sigma >0$. If

$$\begin{aligned} {}_{t_k}D^\alpha _tV(t)\le -\kappa (\Vert e(t_k)\Vert ), t\in [t_k, t_{k+1}) \end{aligned}$$

(18)

where $\kappa (\cdot )$ is a K-class function and $V(t)=\nu (t)+\vartheta (t)$, then $\lim \limits _{t\rightarrow +\infty }\Vert e(t)\Vert =0$.

Proof

Applying the fractional-order integration on both sides, ${}_{t_k}D^\alpha _tV(t)\le -\kappa (\Vert e(t)\Vert )$ can be derived to

$$\begin{aligned} V(t_{t_{k+1}})-V(t_k)\le -\frac{(t_{k+1}-t_k)^\alpha }{\varGamma (1+\alpha )}\kappa (\Vert e(t_k)\Vert ). \end{aligned}$$

(19)

Further, we can obtain

$$\begin{aligned} \nu (t_{t_{k+1}})-\nu (t_k)\le -\frac{\sigma ^\alpha }{\varGamma (1+\alpha )}\kappa (\Vert e(t_k)\Vert ). \end{aligned}$$

(20)

Thereby, the following inequality holds

$$\begin{aligned} \sum \limits _{k=0}^{n}\kappa (\Vert e(t_k)\Vert )\le \frac{\varGamma (1+\alpha )}{\sigma ^\alpha }\nu (t_0). \end{aligned}$$

(21)

From the above inequality, the series $\sum \nolimits _{k=0}^{+\infty }\kappa (\Vert e(t_k)\Vert )$ is obviously converged, showing that $\lim \nolimits _{k\rightarrow +\infty }\kappa (\Vert e(t_k)\Vert )=0$, i.e., $\lim \nolimits _{k\rightarrow +\infty }\Vert e(t_k)\Vert =0$.

According to the designed event-triggered scheme, the following inequality holds with $\forall t\in [t_k, t_{k+1})$

$$\begin{aligned} \begin{aligned} \digamma _i(t)=&-\rho \left( \sum _{j=1}^NL_{ij}e_j(t_k)\right) ^T R_i\left( \sum _{j=1}^NL_{ij}e_j(t_k)\right) \\&+\left( \sum _{j=1}^NL_{ij}(e_j(t)-e_j(t_k))\right) ^T\\&\times R_i\left( \sum _{j=1}^NL_{ij}(e_j(t)-e_j(t_k))\right) \\ \le&\, \varrho e^{-\varepsilon t} \end{aligned} \end{aligned}$$

(22)

Thus, we have $\lim \limits _{t\rightarrow +\infty }\Vert e(t)\Vert =0$. $\square$

Lemma 3

For system (17), let $\nu (t)$ be a positive definite function, $\vartheta (t)$ be an arbitrary function satisfying $\vartheta (t_k)=0$, and there exists a scalar $\sigma$ such that $t_{k+1}-t_k\ge \sigma >0$. If

$$\begin{aligned}&{}_{t_k}D^\alpha _t(\nu (t)+\vartheta (t))\le -\kappa (\Vert e(t_k)\Vert )+\varrho e^{-\varepsilon t_k},\nonumber \\&\quad t\in [t_k, t_{k+1}), \end{aligned}$$

(23)

then $\lim \limits _{t\rightarrow +\infty }\Vert e(t)\Vert =0$.

Proof

The proof of this lemma is similar to that of Lemma 2. Thus, Lemma 3 can be obtained.

Remark 6

When $\alpha =1$, the asymptotic stability result of Lemma 2 is still valid. It is obvious that Lemma 2 in [45] is a special case of Lemma 2 in our study. Compared to Lemma 2 in our study, the asymptotic stability criteria of Lemma 3 are weaker.

3.3 Leader-following consensus criteria

Considering the consensus of FOMASs, each follower’s state of system (2) should converge to the leader’s state of system (1). Therefore, the consensus problem of FOMASs is equivalent to the stability of each error system (17). In this section, a novel adaptive controller will be designed to guarantee the stability of the trajectories of system (17). Furthermore, the controller gain matrices are derived by solving liner matrix inequalities (LMIs) constraints.

The adaptive control $u_i(t)$ is designed as

$$\begin{aligned} \begin{aligned} u_i(t)=&-k_{i1}\sum \limits ^N_{j=1}d_{ij}(x_i(t_k)-x_j(t_k))\\&-k_{i2}c_i(x_i(t_k)-x_0(t_k)) -{\hat{\varDelta }}^*_i(t) \end{aligned} \end{aligned}$$

(24)

where $i\in \{1,2,\ldots ,N\}$, $k_{ij}$ ($j=1,2$) is the controller parameter to be designed and there exists a positive constant k such that $k_{ij}\le k$. Throughout this paper, we assume $d_{ii}=0$. $C=diag(c_1,c_2,\ldots ,c_N)$ stands for the weighted adjacency matrix with one leader and N followers, where $c_i>0$ implies that the ith follower can obtain information from the leader, otherwise $c_i=0$. ${\hat{\varDelta }}^*_i(t)=({\hat{\varDelta }}_{i1}(t) \mathrm{sgn}(e_{i1}(t)),$${\hat{\varDelta }}_{i2}(t) \mathrm{sgn}(e_{i2}(t)),\ldots ,$${\hat{\varDelta }}_{in}(t) \mathrm{sgn}(e_{in}(t)))^T$, where ${\hat{\varDelta }}_i(t)=({\hat{\varDelta }}_{i1}(t),{\hat{\varDelta }}_{i2}(t),\ldots ,$${\hat{\varDelta }}_{in}(t))^T$ is the external disturbance estimation vector, which is updated with the following adaptive control law:

$$\begin{aligned} \left\{ \begin{aligned}&{}_{t_k}D^\alpha _t{\hat{\varDelta }}_i(t)=\theta _i\left( |e_i(t)| +\mu (t){\bar{\varDelta }}_i(t)\right) \\&\mu (t)=\frac{\delta \tau ^{1-2\alpha }}{nN\varGamma (2-\alpha )}\int ^t_{t_k}\Vert {}_{t_k}D^{1-\alpha }_se(s)\Vert ^2\mathrm{d}s\\&\quad +\frac{\delta \tau ^{1-\alpha }}{nN}{}_{t_k}I^{1-\alpha }_t \Vert {}_{t_k}D^{1-\alpha }_t e(t)\Vert ^2 \end{aligned} \right. \end{aligned}$$

(25)

where $\theta _i$ and $\delta$ are positive constants, and ${\bar{\varDelta }}_i(t)=(\frac{1}{2\varDelta _{i1}-{\hat{\varDelta }}_{i1}(t)}, \frac{1}{2\varDelta _{i2}-{\hat{\varDelta }}_{i2}(t)},$$\ldots , \frac{1}{2\varDelta _{in}-{\hat{\varDelta }}_{in}(t)})^T$.

For the convenience, the controller (24) is simplified to the following form

$$\begin{aligned} u_i(t)=-k_{i1}\sum \limits ^N_{j=1}L_{ij}e_j(t_k)-k_{i2}c_ie_i(t_k) -{\hat{\varDelta }}^*_i(t)\nonumber \\ \end{aligned}$$

(26)

Remark 7

From the controller (24), we may find that the sign function is introduced to deal with the unknown external disturbance. This also implies that the undesired chattering phenomenon is unavoidable. Thus, to avoid this problem, the controller (24) is improved to

$$\begin{aligned} \begin{aligned} u_i(t)=&-k_{i1}\sum \limits ^N_{j=1}d_{ij}(x_i(t_k)-x_j(t_k))\\&-k_{i2}c_i(x_i(t_k)-x_0(t_k)) -{\hat{\varDelta }}_i(t) \end{aligned} \end{aligned}$$

(27)

which is updated with the adaptive control law (25) and the following equation:

$$\begin{aligned} \begin{aligned} {}_{t_k}D^\alpha _t{\tilde{\varDelta }}_i(t)=&\theta _i\left( |e_i(t)| +\delta (2\varDelta _i-{\tilde{\varDelta }}_i(t))\right) . \end{aligned} \end{aligned}$$

(28)

Theorem 1

Under Assumptions 1 and 2, for any given scalars $0<\alpha , \rho <1$, the consensus of FOMASs can be achieved by using the controller (24) with adaptive law (25) if there exist scalar k and appropriate dimension matrices $R>0$, $Q>0$, $P>0$, $K_1$ and $K_2$ such that $\delta \ge \lambda _\mathrm{{max}}(P)$ and

$$\begin{aligned} \varXi =\begin{bmatrix}\varXi _{11}&\quad \varXi _{12}&\quad 3\varGamma (3-2\alpha )P \\ *&\quad \varXi _{22}&\quad \varXi _{23} \\ *&\quad *&\quad -\frac{\varGamma ^2(3-2\alpha )}{\varGamma (2-\alpha )}P\quad \end{bmatrix}<0 \end{aligned}$$

where $K_1=diag(k_{11}, k_{21},\ldots , k_{N1}), K_2=diag(k_{12}, k_{22}, \ldots , k_{N2}), {\tilde{L}}=diag(L_{11},$$L_{22},$$\ldots , L_{NN}),$$C=diag(c_1,$$c_2, \ldots , c_N),$

$$\begin{aligned} \varXi _{11}=&I_N\otimes \left( \frac{A+A^T}{2}+Q\right) +\frac{1}{2}(k^2{\tilde{L}})\otimes I_n\\&-4\varGamma (2-\alpha )P-R,\\ \varXi _{12}=&-\frac{1}{2}(K_1{\tilde{L}}+K_2C)\otimes I_n\\&-\left( \frac{\varGamma (3-2\alpha )}{\varGamma (2-\alpha )}-4\varGamma (2-\alpha )\right) P+R,\\ \varXi _{22}=&\frac{1}{2}{\tilde{L}}\otimes I_n-\left( \frac{3\varGamma ^2(3-2\alpha )}{\varGamma ^3(2-\alpha )}-\frac{6\varGamma (3-2\alpha )}{\varGamma (2-\alpha )}\right. \\&\left. -3\varGamma (2-\alpha )\right) P+(\rho -1)R,\\ \varXi _{23}=&\left( \frac{3\varGamma ^2(3-2\alpha )}{\varGamma ^2(2-\alpha )}-3\varGamma (3-2\alpha )\right) P\\ R=&\sum _{i=1}^N\left[ \begin{array}{*{20}{c}}I_N\otimes L_{i1}\\ \vdots \\ I_N\otimes L_{iN}\end{array}\right] R_i\left[ \begin{array}{*{20}{c}}I_N\otimes L_{i1}&\ldots&I_N\otimes L_{iN}\end{array}\right] . \end{aligned}$$

Proof

We consider the following Lyapunov–Krasovskii function

$$\begin{aligned} V(t)=V_1(t)+V_2(t)+V_3(t), \quad \forall t\in [t_k, t_{k+1}) \end{aligned}$$

(29)

where

$$\begin{aligned} V_1(t)= & {} \frac{1}{2}\sum \limits _{i=1}^Ne^T_i(t)e_i(t), \end{aligned}$$

(30)

$$\begin{aligned} V_2(t)= & {} \frac{1}{2}\sum \limits _{i=1}^N\frac{1}{\theta _i}(2\varDelta _i-{\hat{\varDelta }}_i (t))^T(2\varDelta _i-{\hat{\varDelta }}_i(t)), \end{aligned}$$

(31)

$$\begin{aligned} V_3(t)= & {} -\tau _k^{-\alpha }(t_{k+1}-t)\int ^t_{t_k}\left( {}_{t_k}D^{1-\alpha }_se(s)\right) ^T\nonumber \\&\times P\left( {}_{t_k}D^{1-\alpha }_se(s)\right) \mathrm{d}s. \end{aligned}$$

(32)

The time derivative of $V_1(t)$ along the solution $e_i(t)$ of system (17) can be calculated by

$$\begin{aligned} \begin{aligned}&{}_{t_k}D^\alpha _tV_1(t)\le \sum \limits _{i=1}^Ne^T_i(t){}_{t_k}D^\alpha _te_i(t)\\&\quad =\sum \limits _{i=1}^Ne^T_i(t)(Ae_i(t)+{\tilde{f}}(e_i(t))\\&\qquad +{\tilde{\varDelta }}_i(t)+u_i(t))\\&\quad \le \sum \limits _{i=1}^Ne^T_i(t)\left( (A+Q)e_i(t)+{\tilde{\varDelta }}_i(t)+u_i(t)\right) . \end{aligned} \end{aligned}$$

(33)

According to the adaptive controller (24), we have

$$\begin{aligned} \begin{aligned}&\sum \limits _{i=1}^N e^T_i(t)u_i(t)=\sum \limits _{i=1}^Ne^T_i(t)(-k_{i1} \sum \limits ^N_{j=1}L_{ij}e_j(t_k)\\&\qquad -k_{i2}c_ie_i(t_k)-{\hat{\varDelta }}^*_i(t))\\&\quad =-\sum \limits _{i=1}^Nk_{i1}e^T_i(t)(L_{ii}e_i(t_k)- \sum \limits ^N_{j=1,j\ne i}|L_{ij}|e_j(t_k))\\&\qquad -\sum \limits _{i=1}^N(k_{i2}c_ie^T_i(t)e_i(t_k)+|e_i(t)|^T{\hat{\varDelta }}_i(t))\\&\quad \le -\sum \limits _{i=1}^N(k_{i1}L_{ii}+k_{i2}c_i)e^T_i(t)e_i(t_k)\\&\qquad -\sum \limits _{i=1}^N|e_i(t)|^T{\hat{\varDelta }}_i(t)\\&\qquad +\sum \limits _{i=1}^N\frac{L_{ii}}{2}(k^2\Vert e_i(t)\Vert ^2+\Vert e_i(t_k)\Vert ^2). \end{aligned} \end{aligned}$$

(34)

By substituting (34) into (33), we have

$$\begin{aligned}&{}_{t_k}D^\alpha _t V_1(t)\le \sum \limits _{i=1}^N[e^T_i(t)(A+Q+\frac{1}{2}k^2L_{ii}I_n)e_i(t)\nonumber \\&\qquad +|e_i(t)|^T(2\varDelta _i-{\hat{\varDelta }}_i(t))]+\sum \limits _{i=1}^N\frac{L_{ii}}{2}\Vert e_i(t_k)\Vert ^2\nonumber \\&\qquad -\sum \limits _{i=1}^N(k_{i1}L_{ii}+k_{i2}c_i)e^T_i(t)e_i(t_k). \end{aligned}$$

(35)

According to Assumption 1, the $\alpha$-order derivative of $V_2(t)$ can be calculated by

$$\begin{aligned} {}_{t_k}D^\alpha _tV_2(t)\le -\sum \limits _{i=1}^N\frac{1}{\theta _i}(2\varDelta _i -{\hat{\varDelta }}_i(t))^T{}_{t_k}D^\alpha _t{\hat{\varDelta }}_i(t)\nonumber \\ \end{aligned}$$

(36)

By substituting (25) into (36), we get

$$\begin{aligned} {}_{t_k}D^\alpha _tV_2(t)\le&-\sum \limits _{i=1}^N(2\varDelta _i -{\hat{\varDelta }}_i(t))^T\left( |e_i(t)| +\mu (t){\bar{\varDelta }}_i(t)\right) \nonumber \\ \le&-\sum \limits _{i=1}^N|e_i(t)|^T(2\varDelta _i -{\hat{\varDelta }}_i(t))-nN\mu (t). \end{aligned}$$

(37)

From (35) and (37), we have

$$\begin{aligned} \begin{aligned}&{}_{t_k}D^\alpha _t(V_1(t)+V_2(t))\\&\quad \le e^T(t)(I_N\otimes \left( \frac{A+A^T}{2}+Q\right) \\&\qquad +\frac{1}{2}(k^2{\tilde{L}})\otimes I_n)e(t)\\&\quad \quad +e^T(t)(-(K_1{\tilde{L}}+K_2C)\otimes I_n)e(t_k)\\&\quad \quad + \frac{1}{2}e^T(t_k)({\tilde{L}}\otimes I_n)e(t_k)-nN\mu (t). \end{aligned} \end{aligned}$$

(38)

Taking the $\alpha$-order derivative of $V_3(t)$, the following inequality holds

$$\begin{aligned}&{}_{t_k}D^\alpha _t V_3(t)= \tau _k^{-\alpha } \int ^t_{t_k}\frac{(t-\tau )^{-\alpha }}{\varGamma (1-\alpha )}\nonumber \\&\qquad \times \int _{t_k}^\tau \left( {}_{t_k}D^{1-\alpha }_se(s)\right) ^TP\left( {}_{t_k}D^{1-\alpha }_se(s)\right) \mathrm{d}s\mathrm{d}\tau \nonumber \\&\qquad -\tau _k^{-\alpha } \int ^t_{t_k}\frac{(t_{k+1}-\tau )}{\varGamma (1-\alpha )(t-\tau )^{\alpha }} \left( {}_{t_k}D^{1-\alpha }_\tau e(\tau )\right) ^T\nonumber \\&\qquad \times P\left( {}_{t_k}D^{1-\alpha }_\tau e(\tau )\right) \mathrm{d}\tau \nonumber \\&\quad \le \tau _k^{-\alpha } \int ^t_{t_k}\frac{(t-\tau )^{-\alpha }}{\varGamma (1-\alpha )}\mathrm{d}\tau \\&\qquad \times \int _{t_k}^t\left( {}_{t_k}D^{1-\alpha }_se(s)\right) ^TP\left( {}_{t_k}D^{1-\alpha }_se(s)\right) \mathrm{d}s\nonumber \\&\quad \le \frac{\tau _k^{1-2\alpha }}{\varGamma (2-\alpha )} \int ^t_{t_k}\left( {}_{t_k}D^{1-\alpha }_se(s)\right) ^TP\left( {}_{t_k}D^{1-\alpha }_se(s)\right) \mathrm{d}s\nonumber \\&\qquad +\left( \tau _k^{1-\alpha } -(t-t_k)^{1-\alpha }\right) \nonumber \\&\qquad \times {}_{t_k}I^{1-\alpha }_t \left\{ \left( {}_{t_k}D^{1-\alpha }_t e(t)\right) ^TP\left( {}_{t_k}D^{1-\alpha }_t e(t)\right) \right\} .\nonumber \end{aligned}$$

(39)

According to Corollary 1, the following inequality holds

$$\begin{aligned}&-{}_{t_k}I^{1-\alpha }_t\left\{ \left( {}_{t_k}D^{1-\alpha }_t e(t)\right) ^TP\left( {}_{t_k}D^{1-\alpha }_t e(t)\right) \right\} \nonumber \\&\quad \le -\frac{\varGamma (2-\alpha )}{(t-t_k)^{1-\alpha }}\omega _{1}^TP\omega _{1}\nonumber \\&\qquad -\frac{3}{\varGamma (2-\alpha ) (t-t_k)^{1-\alpha }}\omega _{2}^TP\omega _{2} \end{aligned}$$

(40)

where $\omega _{1}=e(t)-e(t_k)$, $\omega _{2}=\frac{\varGamma (3-2\alpha )}{(t-t_k)^{1-\alpha }}{}_{t_k}I^{1-\alpha }_te(t) -\frac{\varGamma (3-2\alpha )}{\varGamma (2-\alpha )}e(t_k)-\varGamma (2-\alpha )\omega _{1}$. Combining (39) and (40), it could be derived

$$\begin{aligned} \begin{aligned}&{}_{t_k}D^\alpha _t V_3(t)\le nN\mu (t)\\&\quad -\left\{ \varGamma (2-\alpha )\omega _{1}^TP\omega _{1}+\frac{3}{\varGamma (2-\alpha )} \omega _{2}^TP\omega _{2}\right\} . \end{aligned} \end{aligned}$$

(41)

According to the event-trigger condition (16), the following inequality holds

$$\begin{aligned}&(e(t)-e(t_k))^TR(e(t)-e(t_k))\nonumber \\&\quad <\rho e(t_k)^TRe(t_k)+N\varrho e^{-\varepsilon t_k}. \end{aligned}$$

(42)

Then combining all the results from (33) to (42), we have

$$\begin{aligned} {}_{t_k}D^\alpha _tV(t)\le \zeta ^T(t)\varXi \zeta (t)+N\varrho e^{-\varepsilon t_k} \end{aligned}$$

(43)

where $\zeta (t)=(e^T(t), e^T(t_k), \frac{1}{(t-t_k)^{1-\alpha }}{}_{t_k}I^{1-\alpha }_te^T(t))^T$. According to the criteria of Theorem 1, we can get

$$\begin{aligned} {}_{t_k}D^\alpha _tV(t)\le \lambda _\mathrm{{max}}(\varXi )\Vert e(t_k)\Vert ^2+N\varrho e^{-\varepsilon t_k}. \end{aligned}$$

(44)

By using Lemma 3, we can derive the following result

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }\Vert e(t)\Vert =0. \end{aligned}$$

(45)

Therefore, the consensus of FOMASs is achieved. This completes the proof. $\square$

Remark 8

As a free variable, $\alpha$-order helps to regulate the dynamic behavior of FOMASs. In [25] and [27,28,29], the consensus criteria do not take into account the effect of the $\alpha$-order on the dynamic behavior of FOMASs. However, by using the proposed WBFOII, the sufficient criteria in Theorem 1 depending on the $\alpha$-order are obtained. Therefore, the proposed consensus criteria and method in this paper are less conservative than those in [25] and [27,28,29] for analyzing FOMASs.

Below we turn to prove Zeno behavior is excluded in the proposed combination event-triggered consensus scheme.

Theorem 2

Consider the leader–follower systems (1) and (2) with $0<\alpha <1$, if the controller (24) with adaptive law (25) is executed by the event-trigger scheme (15), then Zeno behavior will not happen, implying that there exists a minimum sample-data interval $\sigma$, viz, $\sigma =\min \limits _{k=0,1,\ldots }{\tau _k}$.

Proof

From the sample-data scheme (15), we can obtain that if the event-triggered function $\digamma _i(t)<0$ holds for all $t\in R$, then $\tau _k=\tau$. Thus, it is obvious that Zeno behavior can be excluded, namely $\sigma =\tau$. Next, we prove that Zeno behavior will not happen if there exists $k_1$ such that

$$\begin{aligned} \begin{aligned}&\lim \limits _{t\rightarrow t_{k_1+1}}(e(t)-e(t_{k_1}))^TR(e(t)-e(t_{k_1}))\\&\quad =\rho e(t_{k_1})^TRe(t_{k_1})+N\varrho e^{-\varepsilon t_{k_1}}. \end{aligned} \end{aligned}$$

(46)

$\square$

According to the proof of Theorem 1, ${}_{t_{k_1}}D^\alpha _t e(t)$ is bounded. Then, there exists a positive constant Z such that $\Vert {}_{t_{k_1}}D^\alpha _t e(t)\Vert \le \Vert K_1{\tilde{L}}+K_2C\Vert \Vert e(t_{k_1})\Vert +Z$ for all $t\in [t_{k_1}, t_{k_1+1})$. Denote $\psi (t)=e(t)-e(t_k)$, then, we have

$$\begin{aligned} \begin{aligned} {}_{t_{k_1}}D^\alpha _t \Vert \psi (t)\Vert&\le \Vert {}_{t_{k_1}}D^\alpha _te(t)\Vert \\&\le \Vert K_1{\tilde{L}}+K_2C\Vert \Vert e(t_{k_1})\Vert +Z \end{aligned} \end{aligned}$$

(47)

By using Property 1 (Fractional-order Newton–Leibniz formula), the following equation holds

$$\begin{aligned} \begin{aligned}&\Vert \psi (t)\Vert -\Vert \psi (t_{k_1})\Vert ={}_{t_{k_1}}I^\alpha _t{}_{t_{k_1}}D^\alpha _t \Vert \psi (t)\Vert \\&\quad \le \left( \Vert K_1{\tilde{L}}+K_2C\Vert \Vert e(t_{k_1})\Vert +Z\right) \frac{(t-t_{k_1})^\alpha }{\varGamma (\alpha +1)} \end{aligned} \end{aligned}$$

(48)

From (46), we have

$$\begin{aligned}&\lim \limits _{t\rightarrow t_{k_1+1}}\Vert \psi (t)\Vert ^2\ge \frac{1}{\lambda _\mathrm{{max}}(R)}\lim \limits _{t\rightarrow t_{k_1+1}}\psi (t)^TR\psi (t)\nonumber \\&\quad =\frac{1}{\lambda _\mathrm{{max}}(R)}\left( \rho e(t_{k_1})^TRe(t_{k_1})+N\varrho e^{-\varepsilon t_{k_1}}\right) . \end{aligned}$$

(49)

Combining (48) with (49), we may deduce

$$\begin{aligned} \begin{aligned}&\left( \frac{\rho \lambda _\mathrm{{min}}(R)}{\lambda _\mathrm{{max}}(R)}\right) ^\frac{1}{2}\Vert e(t_{k_1})\Vert \le \lim \limits _{t\rightarrow t_{k_1+1}}\Vert \psi (t)\Vert \\&\quad \le \left( \Vert K_1{\tilde{L}}+K_2C\Vert \Vert e(t_{k_1})\Vert +Z\right) \frac{(\tau _{k_1})^\alpha }{\varGamma (\alpha +1)}. \end{aligned} \end{aligned}$$

(50)

Therefore, the following equation is obtained

$$\begin{aligned} \begin{aligned} \tau _{k_1}\ge \frac{\left( \frac{\rho \lambda _\mathrm{{min}}(R)}{\lambda _\mathrm{{max}}(R)}\right) ^\frac{1}{2\alpha }(\varGamma (\alpha +1)\Vert e(t_{k_1})\Vert )^{\frac{1}{\alpha }}}{\left( \Vert K_1{\tilde{L}}+K_2C\Vert \Vert e(t_{k_1})\Vert +Z\right) ^{\frac{1}{\alpha }}}>0. \end{aligned} \end{aligned}$$

(51)

It is obvious that $\tau _{k_1}$ is strictly positive, viz, $\tau _{k_1}>0$. Thus there exists the minimum sample-data interval. This completes the proof.

Remark 9

From [46], $\alpha \in {(0,1)}$ is a necessary condition for ${}_{t_{0}}D^{\alpha }_t(f^T(t)Pf(t))\le 2{f^T(t)}P{}_{t_{0}}D^{\alpha }_tf(t)$ where $P>0$. Thus, in [8,9,10,11], $\alpha$-order always satisfies $\alpha \in (0,1)$. Further, when $\alpha =1$, we have ${}_{t_{0}}D^{\alpha }_t(f^T(t)Pf(t))=2{f^T(t)}P{}_{t_{0}}D^{\alpha }_tf(t)$. According to their proofs, Theorems 1 and 2 are valid for all $\alpha \in (0,1]$. Therefore, the results of Theorems 1 and 2 are still valid for integer-order MASs, meaning that the results in this study are more general than those in [7, 47,48,49,50,51,52,53].

Remark 10

In the consistency analysis of FOMASs, the $\alpha$-order differential plays a crucial role. [15, 22] and [29] investigated the consensus of leader-following FOMASs, but they did not consider the importance of $\alpha$-order differential in consensus criteria. However, by using the method presented in this paper, the $\alpha$-order differential of system is highlighted.

4 Numerical simulations

In this section, two examples are used to test the feasibility as well as effectiveness of the proposed adaptive controller for the consensus problem of the leader-following FOMASs.

4.1 Example 1

Consider a network with 5 agents: one leader and 4 followers. First, the dynamic behaviors of the leader and followers are described by

$$\begin{aligned} \left\{ \begin{aligned} {}_{t_k}D^\alpha _tx_0(t)&=Ax_0(t)+f(x_0(t))+\varDelta _0(t)\\ {}_{t_k}D^\alpha _tx_i(t)&=Ax_i(t)+f(x_i(t))+\varDelta _i(t)+u_i(t) \end{aligned} \right. \nonumber \\ \end{aligned}$$

(52)

where $f(x_i(t))=(0.1sin(x_{i1}(t)), 0.1sin(x_{i2}(t)), 0.1sin(x_{i3}(t)))^T$, $\varDelta _i(t)=0.01(cos(x_{i1}(t)), cos(x_{i2}(t)),$$cos(x_{i3}(t)))^T$, $i=0,1,\ldots ,4$,

$$\begin{aligned}&A=\left[ {\begin{array}{*{20}{c}} -1.56&{}\quad 0.5&{}\quad 0\\ -1&{}\quad -2&{}\quad 0.5\\ 0.5&{}\quad -1.2&{}\quad -1.5\\ \end{array}} \right] . \end{aligned}$$

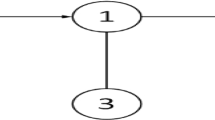
This example considers the network with fixed topological structure as shown in Fig. 1. From Fig. 1, we can obtain $C=diag(1,0,0,1)$,

$$\begin{aligned} D=\left[ {\begin{array}{*{20}{c}} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 1 &{}\quad 0&{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ \end{array}} \right] ,\quad L=\left[ {\begin{array}{*{20}{c}} 1 &{}\quad -1 &{}\quad 0 &{}\quad 0\\ -1 &{}\quad 1&{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad -1\\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 1\\ \end{array}} \right] . \end{aligned}$$

The feasible solutions of LMIs in Theorem 1 are solved by using MATLAB software. Due to the limitation of the length of this paper, we only give the parameters of the designed event-trigged scheme and the adaptive controller by solving LMIs of Theorem 1,

$$\begin{aligned} K_1&=diag(0.0099, 0.0194, 0.0194, 0.0099),\\ K_2&=diag(0.0281, 0, 0, 0.0281). \end{aligned}$$

Fig. 1

The topological structure of the network in Example 1

Figure 2 shows the operating states of the adaptive control $u_i(t)$ ($i=1,2,3,4$). From Figs. 3, 4, 5 and 6, we may find that these leader-following systems are convergent quickly by using the adaptive control $u_i(t)$. As shown in Fig. 7, Zeno behavior is excluded and there exists a minimum sample-data interval $\sigma =0.1$. From Fig. 8 which exhibits the error states of system (52), we may find that the consensus behavior does not change with $\alpha$. Thus, the numerical simulation proves that the results of this paper can be generalized to integer-order MASs, implying that the consensus criteria in this paper are more general than the obtained works in [7, 47,48,49,50,51,52,53]. In the case of $\alpha =0.9$ or $\alpha =1$, the consensus of FOMASs is not achieved for $t\in [0, 10]$. Therefore, in the comparative analysis, we only consider $\alpha \le 0.8$. From the comparison in Table 1, we can find the event-triggering numbers are much less than those in [41], indicating that the designed event-trigged scheme in this study is much more effective and economical.

Fig. 2

State trajectory of the adaptive control $u_i(t)$$(i=1,2,3,4)$ with $\alpha =0.8$

Fig. 3

State error trajectory $e_1$ of the leader-following systems (52) with $\alpha =0.8$

Fig. 4

State error trajectory $e_2$ of the leader-following systems (52) with $\alpha =0.8$

Fig. 5

State error trajectory $e_3$ of the leader-following systems (52) with $\alpha =0.8$

Fig. 6

State error trajectory $e_4$ of the leader-following systems (52) with $\alpha =0.8$

Fig. 7

Relationship between the event-trigged number k and the sample-data interval length $\tau _k$ with $\alpha =0.8$

Fig. 8

The maximum state error $E_\alpha =\Vert e(t)\Vert$ with different orders ($\alpha$)

4.2 Example 2

Consider a leader-following network with 7 agents: one leader and 6 followers, in which dynamic behaviors of the leader and followers are described by

$$\begin{aligned} \left\{ \begin{aligned} {}_{t_k}D^\alpha _tx_0(t)&=Ax_0(t)+f(x_0(t))+\varDelta _0(t)\\ {}_{t_k}D^\alpha _tx_i(t)&=Ax_i(t)+f(x_i(t))+\varDelta _i(t)+u_i(t) \end{aligned} \right. \nonumber \\ \end{aligned}$$

(53)

where $\alpha =0.8$, $f(x_i(t)){=}(0.11cos(x_{i1}(t)){-}0.1x_{i1}(t),$$0.11 cos(x_{i2}(t))-0.1x_{i2}(t), 0.11cos(x_{i3}(t))-0.1x_{i3}(t))^T$, $\varDelta _i(t)=(-0.01cos(x_{i1}(t)), -0.01cos(x_{i2}(t)), -0.01cos($$x_{i3}(t)))^T$, $i=0,1,2,\ldots ,6$,

$$\begin{aligned}&A=\left[ {\begin{array}{*{20}{c}} -1.7&{}\quad 0&{}\quad 0\\ -1.5&{}\quad -1.75&{}\quad 0.5\\ 0.8&{}\quad 0&{}\quad -1.5\\ \end{array}} \right] . \end{aligned}$$

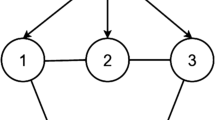
Figure 9 illustrates the topological structure of FOMASs (53). From Fig. 9, we can obtain $C=diag(1,0,0,$ 0, 0, 0),

$$\begin{aligned}&D=\left[ {\begin{array}{*{20}{c}} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ 1 &{}\quad 0&{} \quad 1 &{} \quad 1 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 1\\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0\\ \end{array}} \right] \end{aligned}$$

Table 1 Event-triggering numbers compared to methods [41] with different $\alpha$: $\epsilon =2$

By calculating the feasible solutions of LMIs in Theorem 1, we can get the parameters of the event-trigger scheme and the adaptive controller.

$$\begin{aligned} K_2&=diag(0.0723, 0, 0, 0, 0, 0),\\ K_1&=diag(0.0100,0.0199 ,0.0198, 0.0199, 0.0198, 0.0199). \end{aligned}$$

From Figs. 10, 11 and 12, the states of the leader-following systems (53) are consistent. Thus, the designed event-triggered adaptive control is effective to achieve the consensus of leader-following systems more economically and rapidly. As illustrated in Fig. 13, the event-trigger condition not only avoids the Zeno behavior, but also reduces the communication traffic.

Fig. 9

Topological structure of Example 2

Fig. 10

State error trajectory $e_1$ of the leader-following systems (53) with $\alpha =0.8$

Fig. 11

State error trajectory $e_2$ of the leader-following systems (53) with $\alpha =0.8$

Fig. 12

State error trajectory $e_3$ of the leader-following systems (53) with $\alpha =0.8$

Fig. 13

Relationship between the event-trigged number k and the sample-data interval length $\tau _k$ with $\alpha =0.8$

5 Conclusion

In this paper, the consensus of the fraction-order leader-following systems was studied. In order to obtain much tighter bounds for the estimated Lyapunov–Krasovskii function, a novel WBFOII was proposed. To reduce the frequency of network governance, an event-triggered scheme without Zeno behavior was produced. Furthermore, an event-triggered adaptive control was designed to ensure that the N followers’ behavior can converge to the leader’s state much faster and more economically than previous methods. Then, the sufficient criteria depending on the $\alpha$-order were obtained to achieve the consensus of the fraction-order leader-following systems. Finally, two examples were given to test the feasibility as well as effectiveness of the proposed results.