1 Introduction

In 1971, by deducing from the perspective of logic, Chua pointed out that there should be a circuit element linking magnetic flux and electric charge and enriches the relationships among the electric quantities [1]. Later, based on the theory, the first entity of TiO2 memristor was developed by HP laboratory, and it is becoming more and more interesting in lots of engineering areas such as non-volatile memories, nonlinear circuit designs, and so on [2,3,4]. So far, the characteristics of memristor have been explored extensively, such as input frequency, input amplitude and initial value-dependent dynamics behaviors [5, 6], and the local activity was considered as the origin of complexity [7]. In 2014, the first locally active memristor was proposed and verified physically by Chua [8]. The locally active memristor has intense nonlinear and complicated dynamics, and its mathematical modeling and physical implementation have widely aroused the researchers’ interests [9]. In recent years, some locally active memristors with different stable pinched hysteresis loops under different initial conditions have been reported, which are considered as multi-stable memristors [10]. Furthermore, diverse locally active characteristic curves indicate the complex polymorphic of locally active memristors. Liang et al. [11] proposed an S-type locally active memristor and then constructed an equivalent analog circuit, and a small signal equivalent analog circuit that was used to reveal the influence of the memristor on the amplification of extremely small energy fluctuation in the locally active region. By introducing an inductor and a capacitor to the memristor circuit, a third-order chaotic oscillator was found and analyzed in [11]. In addition, a bi-stable non-volatile locally active memristor with complex dynamics was proposed and analyzed in [12]. Then, a tri-stable locally active memristor with wide large active region was constructed and introduced in a Chua system, which has been implemented successfully by commercial analog elements [13], whereas there are few results reported about the effect of parameters on the local activity. Inspired by these considerations, a bi-stable locally active memristor is proposed, and the effect of different parameters on the local activity is investigated based on this new memristor. It is found that the variation of the memristive parameters not only causes the change of locally active region, but also determines the existence of local activity, which is an interesting phenomenon, and may be helpful to construct different type locally active memristors, such as N-type [14] and M-type locally active memristors.

The non-volatile property of memristor is worth exploring since this property can be used to determine the memristive state with power-off. Motivated by the multiple stable states of non-volatile memristor, Ying and Wang analyzed the switching mechanism of states using pulse excitation in order to verify the non-volatility. With the excitation of pulse voltage, the non-volatile memductance can be switched from one stable state to another state [15]. Some published papers have pointed out memristors can be utilized to describe external electromagnetic induction or as neural synapses. When the neurons are exposed to the electric field, considering the electromagnetic induction (MEI) theorem, the induced current will be added on the neurons resulting from the fluctuation of magnetic-flux, and the induced current can be described by a flux-controlled memristor [16,17,18,19]. Lin and Wang tried to put one neuron of Hopfield neural network (HNN) [20] to electromagnetic radiation and found the hidden extreme multi-stability and rich transient chaotic phenomena [21]. Besides, the locally active memristor can be used to simulate autapse [22]. By introducing hyperbolic tangent function, Wang et al. presented a bi-stable scissors-type locally active memristor which was utilized as an autapse in two Hindmarsh–Rose neural network [23]. Then, a tri-stable locally active memristor was proposed and introduced to emulate the autapse in 2D Hindmarsh–Rose neuron. Four coexisting firing activities were found, and physical circuit implementation results were then presented to demonstrate the validity of simulation results and theoretical analyses [24]. Furthermore, because of the potential difference among neurons in the nervous system, the complex electromagnetic field induced by electromagnetic induction can be detected, similarly, and the flux-controlled memristor can be utilized as the coupled synapse to represent the coupling relationships among neurons based on the MEI theorem [25,26,27,28]. A new memristor-coupled neuron model was proposed in [29], and the synchronization behavior between two neurons was investigated in detail. It was found that the phase synchronization can be achieved by field coupling. Moreover, the effect of magnetic field coupling intensity on phase synchronization of neurons was investigated and the stability of synchronization of the network was explored under noise in [30]. With the construction of a threshold memristor, Bao proposed a memristor synapse-coupled neuron network and discovered abundant firing phenomena and then achieved the complete exponential synchronization between two identical HR neurons [31]. In order to investigate the characteristics of the new proposed bi-stable threshold locally active memristor based neuron network, this new memristor is introduced to the modified FitzHugh–Nagumo (FHN) nervous system, which was proposed by [32], as a coupled synapse.

It is reported that the external electrical stimuli, such as random noise and electromagnetic radiation, are relevant to real electrophysiological environment, which influence the dynamics behaviors of the neural systems [33]. Besides, firing activities can be induced by external stimuli, which can help researchers better understand the abnormal firing behaviors of biological cells and has great medical significance. Bao et al. discovered the coexistence of periodic bursting firing and chaotic bursting firing by injecting a sinusoidal AC current to HR neuron [34]. In addition, under the excitation of bi-polar pulse signal, coexisting firing patterns were explored [35]. Similarly, in the memristive HNN, bursting phenomenon induced by external current was explained by analyzing the AC equilibrium points [36]. Moreover, Wang et al. introduced a multi-level pulse signal and a memristor to the HNN to imitate the external stimuli and magnetic field, then, multi-scroll phenomenon was found [37]. In this paper, a kind of multi-level current is introduced to the proposed nervous system, then, periodic burster and multi-scroll chaotic burster are found.

In recent years, some researchers have pointed out that the firing activities of nervous systems can be analyzed by energy supply and consumption. According to Helmholtz’s theorem, Yang et al. calculated the neuron Hamiltonian energy of Izhikevich neuron driven by external stimulus under electromagnetic induction and found that the transition of Hamiltonian energy is mainly dependent on the firing behaviors [38]. Based on the Hindmarsh–Rose neuron model, Wang et.al found that the change of Hamilton energy depends on the discharge mode and external currents [39]. Hence, the Hamiltonian energy is useful to better understand the relationship between firing behaviors and energy coding, and this paper uses the Hamiltonian-energy-function-based method to explore the energy changes of the coupled neuron model.

The rest of this paper is arranged as follows. In Sect. 2, a novel locally active memristor is designed, and its characteristics including non-volatility, local activity versus memristive parameters and switching mechanism are revealed by numerical analyses. In Sect. 3, a memristive synapse-coupled nervous system is modeled and analyzed. Section 4 presents the designed circuit and hardware experiments. Finally, conclusions are given in Sect. 5.

2 A threshold locally active memristor model

There is a definition about generic memristor proposed by Chua [40], which can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {v(t) = G(x)u(t)}\\ {\frac{{dx}}{{dt}} = H(x,u)} \end{array}} \right. \end{aligned}$$
(1)

where u(t), v(t) and x represent the input, output and state variable, respectively. The specific functions G(x) and H(x, u) determine the memductance (memristance) and some specific properties such as non-volatile memory and local activity. Locally active memristor can imitate neural synapse, but there are few threshold locally active memristors proposed in the literature. Considering the memductance induced by the electromagnetic induction will not be infinite [16], by introducing the hyperbolic tangent function, a threshold locally active memristor is proposed, and the mathematical model can be described as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{i_M} = G(x){v_M}}\\ {G(x) = a + b\tanh (x)}\\ {\frac{{dx}}{{dt}} = - {x^3} + x - {v_M}} \end{array},} \right. \end{aligned}$$
(2)

where a and b are memristive parameters, and \({v_M}\) and \({i_M}\) are the input voltage and output current, respectively. The remarkable characteristics of the presented memristive mathematical model including frequency-dependent and amplitude-dependent pinched hysteresis loops, non-volatile memory and local activity are deduced and verified using abundant numerical simulations in the following subsections.

Fig. 1
figure 1

Amplitude- and frequency-dependent pinched hysteresis loops. a \(F = 0.75{\;\text {Hz}}\) and \(x(0)= 0\) with different amplitudes. b \(A = 2{\;\text {V}}\) and \(x(0) = 0\) with different frequencies

Full size image

2.1 Pinched hysteresis loops dependent on amplitude and frequency

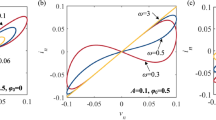
Letting the memristive parameters \(a= 0\) and \(b = 1\), the dynamics behaviors of the proposed memristor are analyzed under different input signal amplitudes and frequencies when a sinusoidal voltage source with variable voltage amplitude A and voltage frequency F is the input signal. With the initial state \(x(0)= 0\), it can be seen from Fig. 1 that there are six different pinched hysteresis loops in the \({v_M} - {i_M}\) plane when the memristor is driven by an external excitation. Fig. 1(a) illustrates that, with the frequency \(F = 0.75{\;\text {Hz}}\) fixed, as the external excitation amplitude increases from 1 to 2, the hysteresis lobe area will be magnified along \({v_M}{-}\text {axis}\) and \({i_M}{-}\text {axis}\). Choosing the amplitude \(A = 2{\;\text {V}}\), the frequency-dependent pinched hysteresis loops are presented in Fig. 1(b). Obviously, with the increase of frequency, the hysteresis lobe area gradually decreases and tends to be a single-valued function.

Fig. 2
figure 2

Pinched hysteresis loops with initial values \(x(0) = 0\) and \(x(0) = 8\). a \(A = 2{\;\text {V}}\),\(F = 0.5{\;\text {Hz}}\). b \(A = 2{\;\text {V}}\), \(F = 0.2{\;\text {Hz}}\)

Full size image

2.2 Pinched hysteresis loops with respect to bi-stable characteristics

For a bi-stable memristor, there are two coexisting stable pinched hysteresis loops under proper amplitudes, frequencies and initial values [23]. When the amplitude \(A = 2{\;\text {V}}\) and the frequency \(F = 0.5{\;\text {Hz}}\) are fixed, two totally diverse stable pinched hysteresis loops are depicted for \(x(0) = 0\) and \(x(0) = 8\), as shown in Fig. 2(a). It should be noted that the critical initial value \(x(0) = 0.0619\) splits the two pinched hysteresis loops. However, with the amplitude \(A = 2{\;\text {V}}\) and the frequency \(F = 0.2{\;\text {Hz}}\), two identical stable pinched hysteresis loops under two different initial values \(x(0) = 0\) and \(x(0) = 8\) are depicted in Fig. 2(b). As the input frequency decreases, two diverse pinched hysteresis loops tend to converge to a stable pinched hysteresis loop. It is obvious that both the frequency and initial value can affect the bi-stability.

2.3 Non-volatility

The non-volatile theorem [40] points out the power-off plot (POP) of the non-volatile memristor has two or more negative slopes that intersect the \(x{-}\text {axis}\) in the \(x{-} {{{\text {d}}x} / {{\text {d}}t}}\) plane. The memristance or memductance of the non-volatile memristor will retain a constant when power is off. Let \({v_M}= 0\), one can obtain the state equation below.

$$\begin{aligned} \frac{{{\text {d}}x}}{{dt}}|_{{v_M} = 0} = - {x^3} + x \end{aligned}$$
(3)

The dynamic route of the state equation can be shown in Fig. 3(a), which can be named as POP. Denote that the attached arrowheads on the POP illustrate the evolutionary direction of state x alongside the curve. For any initial point on the curve above the \(x{-}\text {axis}\), where \({{dx} / {dt}} > 0\), it must evolve to the right alongside the POP. On the contrary, while any initial point on the curve lies the lower half-plane, it must evolve to the left along the POP. This phenomenon is named as the no backtracking rule of dynamical route of non-volatile memristor. The intersection points \({Q_0}({x_0} = - 1)\), \({Q_1}({x_1} = 0)\) and \({Q_2}({x_2} = 1)\) are considered as the equilibrium points of the proposed memristor. One can observe that the equilibrium points \({Q_0}\) and \({Q_2}\) both have negative slopes and are asymptotically stable, while \({Q_1}\) is unstable. It indicates two stable equilibrium states in the non-volatile memristor under different initial values, namely

$$\begin{aligned} x(\infty ) = \left\{ {\begin{array}{*{20}{c}} { - 1,x(0) < 0}\\ {0, \, x(0) = 0}\\ {1, \, x(0) > 0} \end{array}} \right. , \end{aligned}$$
(4)
Fig. 3
figure 3

POP and asymptotically stable processes of the memristor. a POP. b asymptotically stable processes

Full size image

which indicates two stable memductances

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {G({x_0}) = - \tanh (1) \approx - 0.726\;{\text {S}},x(0) < 0}\\ {G({x_2}) = \tanh (1) \approx 0.726\;{\text {S}},x(0) > 0} \end{array}} \right. . \end{aligned}$$
(5)

When the memristor is powered off, in order to more intuitively show the asymptotically stable processes of the initial state x(0), the time series of x are shown in Fig. 3(b). It can be seen that, if the state \(x(0) > 0\), it finally converges to the state \(x(\infty )= 1\) with the corresponding memductance \(G = 0.726\;{\text {S}}\), while the state \(x(0) < 0\), it converges to \(x(\infty )= - 1\) with the corresponding memductance \(G = -0.726\;{\text {S}}\). Therefore, the memristor can be considered as a bi-stable memristor.

Fig. 4
figure 4

Five dynamic routes of DRM

Full size image

2.4 State switching mechanism of the non-volatile memristor

It should be noted that dynamic route map (DRM) is the collection of the dynamic routes with constant voltages [41]. Fig. 4 presents the DRM for five dynamic routes, which correspond to the constant voltages \({v_M} = -2\;{\text {V}}, \, -1\;{\text {V}}, \, 0\;{\text {V}}, 1\;{\text {V}}, \, 2\;{\text {V}}\), respectively. On the basis of no backtracking rule, by injecting a single pulse excitation on the memristor with suitable voltage amplitude v and pulse width w, one can switch from the stable state \({x_0}\) to the stable state \({x_2}\) alongside a suitable dynamic route.

Figs. 5(a), 5(c) and 5(e) present two different dynamic routes, where the red curve is the POP with constant voltage \({v_M}= 0\;{\text {V}}\) and the blue curve is the dynamic route with the constant voltage \({v_M}= - 2\;{\text {V}}\). If the amplitude \(v= - 2\;{\text {V}}\), different switching dynamic routes from state \({x_0}\) to \({x_2}\) are related to pulse width w. In Fig. 5(a), the initial state is \(x(0) = {x_0}\) corresponding to memductance \(G({x_0}) = - 0.726\; {\text {S}}\). When the pulse width \(w = 0.8\; {\text {s}}\), the initial state x(0) rises instantaneously to the blue dynamic route and ,then, traverses to the right alongside it. As the pulse ends, the state x(t) immediately drops to red curve and, then, asymptotically converges to the stable state \({x_2}\). Fig. 5(b) shows the memductance variation.

Fig. 5
figure 5

Switching mechanism of the non-volatile memristor from the state \({x_0}\) to \({x_2}\) under pulse excitations with different pulse widths. a stable state transition with \(w = 0.8\). b memductance variation with \(w = 0.8\).c stable state transition with \(w = 1\). d memductance variation with \(w = 1\). e stable state transition with \(w = 1.2\). f memductance variation with \(w = 1.2\)

Full size image

As shown in Fig. 5(c), when the pulse width satisfies

$$\begin{aligned} w = \int _{{x_0}}^{{x_2}} {\frac{1}{{f(x,v){|_{v = - 2{\text {V}}}}}}} {\text {d}}x = 1.0196\; {\text {s}}, \end{aligned}$$
(6)

one can switch directly from the initial state \({x_0}\) to the final state \({x_2}\) without the asymptotical process on the red curve. The evolutionary process of memductance can be visualized in Fig. 5(d).

When the pulse width \(w = 1.2\; {\text {s}}\), the circuitous evolutionary process and the change of memductance are shown in Fig. 5(e) and Fig. 5(f), respectively. It can be seen that, as the pulse peak appears at \(t = 1\; {\text {s}}\), the initial state instantly jumps to the blue curve and traverses to the left along the dynamic route. When the pulse peak disappears at \(t = 2.2 \;{\text {s}}\), the state \(x\;(t = 2.2 \;{\text {s}})\) drops vertically to the red POP. Based on the no backtracking rule, the state will finally evolve to the stable state \({x_2}\) along the red curve.

2.5 Local activity

Generally, locally active characteristic can be judged by performing the DC \(V-I\) plot [40]. It should be pointed out that not all of non-volatile memristors are locally active. To depict the DC \(V-I\) plot of the proposed memristor, by setting \({{dx} / {dt}} = 0\), one can obtain the equilibrium state equation as follows:

$$\begin{aligned} V = X - {X^3} \end{aligned}$$
(7)

Here, V represents DC voltage, and X represents a variable equilibrium state that always satisfies \({{dx} / {dt}}(x = X) = 0\). Furthermore, referring to (2) and (7), the DC current I can be expressed as

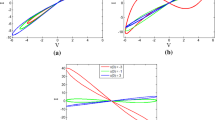
$$\begin{aligned} I = (a + b\tanh (X))V = (a + b\tanh (X))(X - {X^3}). \end{aligned}$$
(8)

If \(X \in [ - 1.2,1.2]\) and the memristive parameters \(a= 0\) and \(b = 1\), the \(X-V\) plot and the \(V-I\) plot are depicted in Fig. 6. If there are one or more negative slopes in DC \(V-I\) plot, the memristor is locally active. As can be seen from Fig. 6(b), the red loci are negative, and one can obtain the locally active region, namely \(X < 0\).

Specially, when \(a = 1.2\) and \(b = 1\), the corresponding characteristic loci of DC \(V-I\) plot change and are plotted in Fig. 7(a). It can be observed that the local activity of the proposed memristor disappears and the memristor is completely passive. Furthermore, with the memristive parameters \(a= - 1.2\) and \(b = 1\), the memristor is completely positive. Fig. 7(b) illustrates the positive characteristics. The phenomenon has not been reported so far and is worth exploring. By mathematical analysis, one can explain the influence of the memristive parameters on the local activity of the memristor.

Fig. 6
figure 6

Characteristics curves. a \(X-V\) curve. b \(V-I\) curve

Full size image
Fig. 7
figure 7

DC V-I loci with a \(a= 1.2\) and \(b = 1\). b \(a= -1.2\) and \(b = 1\)

Full size image

From (8), one can obtain the relationship between DC voltage V and DC current I as

$$\begin{aligned} \frac{{{\text {d}}I}}{{{\text {d}}V}} = (a + b\tanh (X)) \end{aligned}$$
(9)

which determines the slope of any point in the DC \(V-I\) plot.

Fig. 8
figure 8

The effect of memristive parameters on the local activity. a effect of single parameter. b effect of two-parameter

Full size image

Obviously, when \({{{\text {d}}I} / {{\text {d}}V}} < 0\), the locally active region can be obtained. Letting the parameter \(b = 1\), the variation of the locally active region with the change of parameter a can be computed as shown in Fig. 8(a). It can be seen that the dotted lines represent the slope of the locus in DC \(V-I\) plot and the slope is negative. With the increase of the parameter a, the locally active region is getting smaller and smaller. One can deduce that, when \(\left| a \right| > \left| b \right| \), the local activity disappears. Based on this, Fig. 8(b) shows the two-parameter effect on the local activity intuitively. It should be pointed out that b must not be equal to zero.

Fig. 9
figure 9

Memristive synapse-coupled nervous system

Full size image

3 Memristive synapse-coupled neural system

To fully explore the dynamic characteristic of memristor synapse-coupled neuron model, the proposed memristor is introduced into a two-neuron system as shown in Fig. 9. According to the MEI theorem, the current \({i_M}\) induced by the potential difference \({v_M}\) between two neurons can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{i_M} = W(\varphi ){v_M}= k(a + b\tanh (\varphi )){v_M}}\\ {{{{\text {d}}\varphi } / {\text {d}}}t = - {\varphi ^3} + \varphi - {v_M}} \end{array}} \right. \end{aligned}$$
(10)

where \(\varphi \) represents the magnetic-flux of the memristive synapse, and \(W(\varphi )\) indicates the memductance with the coupling weight k.

The modified FitzHugh–Nagumo (FHN) model is selected, which can be utilized to describe the firing activity of FHN neuron, and the corresponding mathematical model is

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\dot{v} = v(v - 1)(1 - {a_1}v) - w + {I_{ext}}}\\ {\dot{w} = {b_1}v} \end{array},} \right. \end{aligned}$$
(11)

where v represents the membrane potential, w represents the recovery potential, \({a_1}\) and \({b_1}\) are control parameters, and \({I_{{\text {ext}}}}\) is external stimulus current.

By introducing the memristive synapse into the neural system, the memristive synapse-coupled neuron model can be obtained and the mathematical model is

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\dot{x} = x(x - 1)(1 - {a_1}x) - y + {i_M} + {I_{ext}}}\\ {\dot{y} = {b_1}x}\\ {\dot{u} = u(u - 1)(1 - {a_2}u) - v - {i_M} + {I_{ext}}}\\ {\dot{v} = {b_2}u}\\ {{\dot{\varphi }} = - {\varphi ^3} + \varphi - (x - u)}\\ {{i_M}= k(a + b\tanh (\varphi ))(x - u)} \end{array}} \right. \end{aligned}$$
(12)

It is significant to note that all the internal control parameters are positive with \({a_1} = 6.5\), \({b_1} = 4.25\), \({a_2} = 6.75\) and \({b_2} = 3.5\) for the coupled neuron model. In this work, by using the coupling weight k, the memristive parameters a and b as well as the external stimulus \({I_{ext}}\) as control parameters, we study the dynamics characteristics of this model under fixed initial value \((0,0.51,0, - 0.5,0.8)\) and (0.1, 0, 0, 0, 0).

3.1 Equilibrium points and stability analysis

When \({I_{ext}}= 0\), let the left side of the system (12) be zero, three equilibrium points can be obtained: \({E_1} = (0,0,0,0,0)\), \({E_2} = (0,0,0,0, - 1)\) and \({E_3} = (0,0,0,0,1)\), which are also the equilibrium points of the proposed memristor. For the point \({E_1}\), the corresponding Jacobian matrix can be calculated as

$$\begin{aligned} {J_{{E_1}}} = \left[ {\begin{array}{*{20}{l}} {a \cdot k - 1}&{}{ - 1}&{}{ - a \cdot k}&{}0&{}0\\ {{b_1}}&{}0&{}0&{}0&{}0\\ { - a \cdot k}&{}0&{}{a \cdot k - 1}&{}{ - 1}&{}0\\ 0&{}0&{}{{b_2}}&{}0&{}0\\ { - 1}&{}0&{}1&{}0&{}1 \end{array}} \right] \end{aligned}$$
(13)

The corresponding characteristic equation below can be obtained by solving \(P(\lambda ) = (\lambda I - {J_{{E_0}}})\), where I is a \(5 \times 5\) identity matrix.

$$\begin{aligned} \begin{aligned} P(\lambda )&= {\lambda ^5} + (1 - 2ak){\lambda ^4} + ({b_1} + {b_2} - 1){\lambda ^3}\\&\quad + (2ak - a{b_1}k - a{b_2}k - 1){\lambda ^2}\\&\quad + ({b_1}{b_2} - {b_2} - {b_1} + a{b_1}k + a{b_2}k)\lambda - {b_1}{b_2} \end{aligned} \end{aligned}$$
(14)

According to the Routh–Hurwitz criterion, if all the principal minors are positive, the equilibrium point is stable. Assuming \({b_1} + {b_2} > 2\) and \(k,a \in (0,1)\), one can obtain

$$\begin{aligned} \begin{aligned} {{\varDelta }_3}&< [{a^2}{({b_1} + {b_2})^2} - 2{a^2}({b_1} + {b_2})]k\\&\quad + [ - a{({b_1} + {b_2})^2} + 3a({b_1} + {b_2})]k\\&\quad - ({b_1} + {b_2})k< ({{\text {b}}_1}+ {{\text {b}}_2})(a - 1) \\&\quad [({{\text {b}}_1}+ {{\text {b}}_2} - 2)a + 1]\\&< 0 \end{aligned} \end{aligned}$$
(15)

which indicates \({E_1}\) is always unstable. For example, when \(a = 0\), the equilibrium point \({E_1}\) is also unstable. As a result, the unstable equilibrium point may lead to the occurrence of chaos or periodic oscillations in the coupled FHN model.

3.2 Dynamical characteristics analysis

3.2.1 Bifurcation behavior with respect to the coupling weight k

Coupling weight plays an important role in multi-neuron systems and has a great influence on the neurodynamics. To explore the influence of the coupling weight on the dynamics of the proposed system, the memristive parameters \(a = 0\) and \(b = 1\) and two sets of initial conditions \((0,0.51,0, - 0.5,0.8)\) and (0.1, 0, 0, 0, 0) are chosen, and the maximum Lyapunov exponent spectrum and bifurcation diagram with k in the range [0.7, 1] are shown in Figs. 10(a) and 10(b), respectively. It can be observed from Fig. 10(b) that, when the initial condition is (0.1, 0, 0, 0, 0), the coupled neuron model is always stable. On the contrary, with the initial condition \((0,0.51,0, - 0.5,0.8)\), the system (12) presents the periodic-doubling bifurcation route to chaos for \(k \in [0.7,0.825]\). Afterwards, the system evolves into periodic-3. When k is greater than 0.923, the system enters into chaos again. Accordingly, with different coupling weights k, the coexisting behaviors can be illustrated by phase plane plots as shown in Fig. 11.

Fig. 10
figure 10

Bifurcation behaviors with the increase of coupling weight k under different initial values. a Maximum Lyapunov exponent spectrum. b Bifurcation diagram of state y

Full size image
Fig. 11
figure 11

Phase portraits of coexisting attractors in \(x-y\) plane. a \(k=0.7\). b \(k=0.98\)

Full size image

When \(b = 1\) and the memristive parameter a varies from 0 to 1, the locally active region gradually decreases although the local activity still exists. In order to investigate the influence of both a and k on the dynamical behaviors of the coupled neuron model, Fig. 12 shows dynamical evolution map and two-parameter bifurcation diagram in the \(a-k\) plane, respectively. As shown in Fig. 12(a), the right color bar indicates the value of the maximum Lyapunov exponent. One can conclude the blue and green regions mark non-oscillation, yellow shading denotes chaos, while other colors represent periodic oscillations. In order to further intuitively show the dynamics behavior proceeding of the coupled neuron model, two-parameter bifurcation diagram is shown in Fig. 12(b), which is consistent with the two-parameter maximum Lyapunov exponent diagram. Here, the white region represents point attractor, the yellow region is the periodic-1, the black region is the periodic-2, the magenta region is the periodic-3, the cyan region is the periodic-4, and the blue region is the chaotic behavior.

Fig. 12
figure 12

Dynamics analysis by increasing the values of both a and k from 0 to 1. a Dynamical evolution map. b Two-parameter bifurcation diagram in \(a-k\) plane

Full size image
Fig. 13
figure 13

Dynamics analysis by increasing the values of both a and b from \(-1\) to 1. a Dynamical evolution map. b Two-parameter bifurcation diagram in \(a-b\) plane

Full size image

3.2.2 Dynamics analysis about memristive parameters a and b

As discussed in Fig. 8(b), when the memristive parameters a and b vary simultaneously, the locally active region changes, which has an important influence on the dynamical behaviors of the memristor. Therefore, it is worth exploring the effect of the parameters a and b on the dynamical behaviors of the nervous system. With coupling weight \(k=0.98\), by scanning upward the values of a and b, the corresponding two-parameter bifurcation diagram and dynamical evolution map in the \(a-b\) plane are obtained by numerical simulations. As shown in Fig. 13(b), different colors stand for completely different oscillation states. The white area represents stable equilibrium point, the blue area represents chaos, the green area stands for quasi-periodic state, and others represent periodicities. The numerical simulation results demonstrate that the oscillation states mainly appear in the region of \(a > 0\).

3.3 Bi-stability depicted by local basins of attraction

For typical coupling weight \(k= 0.7\) and \(k= 0.98\) in the memristive synapse-coupled FHN model, the local attraction basins in the \(x(0) - y(0)\) plane with \(u(0) = 0\), \(v(0) = 0\) and \(\varphi (0) = 1e-6\) are shown in Fig. 14, where different colored regions represent different attractors. In Fig. 14(a), the yellow region represents periodic-1, and the white region represents the stable point. In Fig. 14(b), the blue region indicates chaotic attractor. It can be seen that the numerical simulation results indicate the bi-stability phenomenon. Bi-stability, exactly as multi-stability, means the coexistence of two different types of attractors. Moreover, it can be seen that the change of coupling weight k does not affect the local attraction basin of the stable point.

Fig. 14
figure 14

Local attraction basins versus coupling weight k. a \(k=0.7\). b \(k=0.98\)

Full size image

3.4 Periodic burster and multi-scroll chaotic burster induced by multi-level pulse excitation

In this paper, a multi-level pulse current \({I_{{\text {ext}}}}\) is introduced to the proposed system to mimic a periodic stimulus effect on the neurons, which can be described mathematically as [42]

$$\begin{aligned} {I_{{\text {ext}}}}= \sum \limits _{k = 1}^M {I{\mathrm{sgn}} (\sin (wt - {\phi _i}))} ,{\phi _i} = (i - 1)\pi /M\nonumber \\ \end{aligned}$$
(16)

where M is a control parameter for the number of levels, the amplitude I and frequency w are utilized to control the amplitude and pulse width of a single level, respectively. When \(M = 1\), a bi-polar pulse current can be generated.

Here, the amplitude \(I= 1\) and the frequency \(w= 0.045\) are chosen. Under the excitation of a bipolar pulse signal, when the initial value is \((0,0.51,0, - 0.5,0.8)\) and the coupling weight \(k = 0.7\), the coupled FHN model is in periodic bursting firing pattern, whereas when \(k = 0.98\), the model operates in chaotic bursting firing pattern. Moreover, from the perspective of phase space trajectory, multi-scroll chaotic attractor appears.

Fig. 15
figure 15

Periodic burster and double-scroll chaotic burster. a Phase diagram of periodic burster with \(k=0.7\). b Time domain waveforms of x and y with \(k=0.7\). c Phase diagram of chaotic burster with \(k=0.98\). d Oscillation waveforms of x and y with \(k=0.98\)

Full size image
Fig. 16
figure 16

Four-scroll chaotic burster. a Phase diagram in the \(x-y\) plane. b Time domain waveforms of x and y with \(k=0.98\)

Full size image

Fig. 15 describes the phase diagrams in \(x - y\) plane and the corresponding time domain waveforms with regard to \(k = 0.7\) and \(k = 0.98\). For Fig. 15(a), the marked points are AC equilibrium points. It is obvious that the state x(t) oscillates around the equilibrium point \(x = 0\) and y(t) oscillates around the equilibrium points \(y = -1\) and \(y = 1\) as shown in Fig. 15(b).

When \(M = 3\), a four-scroll chaotic burster can be generated around the marked AC equilibrium points \(y = - 3\), \(y = - 1\), \(y = 1\), \(y = 3\), as shown in Fig. 16(a). Fig. 16(b) depicts the oscillation waveforms of x and y. With the increase of parameter M, more and more scrolls can be generated along \(y-{\text {direction}}\). One can conclude the quantitative relationship between the number of scrolls and the number of equilibrium points:

$$\begin{aligned} N = M + 1, \end{aligned}$$
(17)

in which N represents the number of scrolls and M represents the control parameter.

3.5 Energy analysis

The Hamiltonian-energy-function-based method is widely utilized to analyze diverse dynamics systems including neural network, which is useful to explore energy release and supply of neurons. Some references have also mentioned that the Hamiltonian energy is an important index of chaos [43, 44].

According to the Helmholtz’s theorem [45], the vector field F(X) of the coupled neuron model can be divided into two categories: the conservative field \({F_{\text {c}}}(X)\) and the diverging field \({F_{\text {d}}}(X)\), which can be expressed mathematically as:

$$\begin{aligned} F(X)= & {} {F_{\text {c}}}(X) + {F_{\text {d}}}(X) \nonumber \\= & {} \left[ {\begin{array}{*{20}{c}} { - y - k(a + b\tanh (\varphi ))u}\\ {{b_1}x}\\ { - v - k(a + b\tanh (\varphi ))x}\\ \begin{array}{l} {b_2}u\\ - (x - u) \end{array} \end{array}} \right] \nonumber \\&+ \left[ {\begin{array}{*{20}{c}} {x(x - 1)(1 - {a_1}x) + k(a + b\tanh (\varphi ))x}\\ 0\\ {u(u - 1)(1 - {a_2}u) + k(a + b\tanh (\varphi ))u}\\ 0\\ { - {\varphi ^3} + \varphi } \end{array}} \right] \end{aligned}$$
(18)

Accordingly, Hamiltonian energy function is just related to conservative form \({F_{\text {c}}}(X)\) and has nothing to do with the external forcing term \({F_{\text {d}}}(X)\). By solving the equation \(\nabla {H^T}(X){F_c}(X) = 0\), the Hamiltonian energy function H(X) can be derived as

$$\begin{aligned} H(X) = \frac{1}{2}{x^2} + \frac{1}{{2{b_1}}}{y^2} - \frac{1}{2}{u^2} - \frac{1}{{2{b_2}}}{v^2} \end{aligned}$$
(19)

Moreover, the derivative of the Hamiltonian energy function with respect to time can be obtained as follows.

$$\begin{aligned} \begin{aligned} \dot{H}(X)&= x(x(x - 1)(1 - {a_1}x)\\&\qquad + k(a + b\tanh (\varphi ))x) \\&\quad - u(u(u - 1)(1 - {a_1}u)\\&\quad + k(a + b\tanh (\varphi ))u) \\&= \nabla {H^T}(X){F_d}(X) \end{aligned} \end{aligned}$$
(20)
Fig. 17
figure 17

Evolution of energy of different firing patterns. a 2D view of energy of the periodicity. b Energy and energy derivative of periodicity. c 2D view of energy of chaotic firing. d Energy and energy derivative of chaotic firing. e 2D view of energy of multi-scroll burster. f Energy and energy derivative of multi-scroll burster

Full size image

Obviously, according to (19), the Hamiltonian energy is directly related to the membrane potential and recovery potential of two neurons instead of external stimuli. The evolution of Hamiltonian energy of different attractors is described in detail in Fig. 17. Fig. 17(a) illustrates how the energy of periodic attractor alters along the orbit, and Fig. 17(b) shows that the Hamiltonian energy evolves in regular versus time. Fig. 17(c) indicates the energy distribution of chaotic attractor

Fig. 18
figure 18

Circuit schematic structure. a The schematic of circuit emulator. b tanh function circuit schematic

Full size image

with coupling weight \(k= 0.98\), and Fig. 17(d) shows the evolution of the energy with respect to time. With coupling weight unchanged, under external multi-level logic pulse excitation, the energy evolution of the double-scroll attractor in the model is explored and presented in Figs. 17(e)-(f). It can be seen from Fig. 17 that the coupling weight k not only affects the dynamical behaviors of the coupled neuron model, but also affects the fluctuation of Hamiltonian energy. Furthermore, for the double-scroll attractor, the energy distribution of two scrolls is extremely unequal as shown in Fig. 17(e), and the fluctuation of Hamiltonian energy between the scrolls is quite different. In other words, external stimulus influences the energy distribution indirectly and greatly.

4 Circuit implementation

Hardware implementation is necessary for practical engineering applications. Some analog electrical elements, such as capacitors, inductances, resistors and operational amplifiers, can be utilized to physically realize nonlinear systems. The memristor synapse-coupled neuron model can be designed and realized by commercial electric elements, which is helpful for the development of neuromorphic circuits.

4.1 Circuit emulator of the proposed memristor

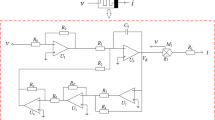
In order to physically verify the presented memristor, the circuit is designed and the corresponding schematic is given in Fig. 18(a), which involves one capacitor, one function operation unit, three amplifiers LM358, three multipliers AD633JN and some resistors. To realize the hyperbolic tangent function [34], one operation module is utilized as shown in Fig. 18(b), and this module includes four transistors \({T_i}(i = 1,2,3,4)\), three amplifiers and some resistors.

The multipliers use the default set as \({A_i}= 1(i = 1,2,3)\), and the circuit parameters are selected as \({R_0} = 10\;{\text {k}}\Omega \), \({R} = 1 \;\Omega \), \({R_s} = 9.8\; {\text {k}} \Omega \), \({R_{\text {f}}} = 520\;\Omega \), \({C_0} = 100{\;\text {nF}}\), \({R_{\text {m}}} = 1 {\;\text {k}\Omega }\) and \({R_T} = 2 {\;\text {k}\Omega }\). One can obtain the time constant \({\tau _0} = {R_0}{C_0} = 1 \;{\text {ms}}\) and the circuit equations are

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {i = {A_0}\tanh (x)v/R}\\ {\frac{{dx}}{{d\tau }} = - \frac{1}{{{R_0}{C_0}}}{x^3} + \frac{1}{{{R_0}{C_0}}}x - \frac{1}{{{R_0}{C_0}}}v} \end{array}} \right. \end{aligned}$$
(21)

where the input sinusoidal source voltage v is chosen as \(v(t)= {\text {sin}}(2\pi ft)\) with variable frequency f, and i is the current through the memristor. Furthermore, the circuit model corresponds to the simulation model (2). Let \(f= 500{\;\text {Hz}}\) and \(f= 750\;{\text {Hz}}\) the breadboard experimental results are shown in Figs. 19(a) and (b), respectively, which are consistent with the simulation results versus \(F = 0.5{\;\text {Hz}}\) and \(F = 0.75{\;\text {Hz}}\) as shown in Fig. 1(b).

Fig. 19
figure 19

Experimental pinched hysteresis loops with \(v(t)= {\text {sin}}(2\pi ft)\) obtained on the breadboard. a \(f= 500\;{\text {Hz}}\). b \(f= 750\;{\text {Hz}}\)

Full size image
Fig. 20
figure 20

Main circuit structure

Full size image

4.2 Experimental circuit of the coupled neuron model

Based on the proposed locally active memristor emulator in Fig. 18, the equivalent analog circuit schematic of the memristive synapse-coupled neuron model is designed and presented, as shown in Fig. 20, which has been implemented physically. The experimental circuits on the breadboard are shown in Fig. 21. The circuit state equations, which correspond to (12), can be found as follows:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\frac{{{\text {d}}{v_1}}}{{{\text {d}}\tau /{\tau _0}}} = - [{v_1}( - {v_1} + 1)(1 - \frac{{{R_0}}}{{{R_1}}}{v_1}) + {v_2} - {I_m} - {I_{ext}}]}\\ {\frac{{{\text {d}}{v_2}}}{{{\text {d}}\tau /{\tau _0}}} = - \frac{{{R_0}}}{{{R_2}}}( - {v_1})}\\ {\frac{{{\text {d}}{v_3}}}{{{\text {d}}\tau /{\tau _0}}} = - [{v_3}( - {v_3} + 1)(1 - \frac{{{R_0}}}{{{R_3}}}{v_3}) + {v_4} + {I_m} - {I_{ext}}]}\\ {\frac{{{\text {d}}{v_4}}}{{{\text {d}}\tau /{\tau _0}}} = - \frac{{{R_0}}}{{{R_4}}}( - {v_3})}\\ {\frac{{{\text {d}}{v_5}}}{{{\text {d}}\tau /{\tau _0}}} = - {v_5}^3 + {v_5} - ({v_1} - {v_3})}\\ {\;\;{I_m} = - (\frac{{{R_0}}}{{{R_a}}} + \frac{{{g_1}{R_0}}}{{{R_b}}}\tanh ({v_5}))({v_3} - {v_1})} \end{array}} \right. \end{aligned}$$
(22)
Fig. 21
figure 21

The photograph of the hardware circuit of the coupled neuron model

Full size image
Fig. 22
figure 22

Experimental portraits of the chaotic attractor. a Time-domain waveforms of \({v_1},\;{v_2},\;{v_3}\) and \({v_4}\). b Phase plane projection on the \({v_1} - {v_2}\) plane. c Phase plane projection on the \({v_2} - {v_5}\) plane. d Phase plane projection on the \({v_3} - {v_5}\) plane

Full size image
Fig. 23
figure 23

Experimental results of the double-scroll chaotic burster. a Time-domain waveforms of \({v_1},{v_2},{v_3}\) and \({v_4}\). b Phase plane projection on the \({v_1} - {v_2}\) plane

Full size image

Assume that \({\tau _0} = {R_0}{C_0} = 0.1\;{\text {ms}}\); then the resistance \({R_0}= 10{\;\text {k}}\Omega \) and the capacitor \({C_i} = 10\;{\text {nF}}(i = 1,2,3,4,5)\) are chosen. According to (12), the circuits parameters in Fig. 20 are derived as \({R_1} = 1.53\;{\text {k}} \Omega \), \({R_2} = 2.35\;{\text {k}\Omega }\), \({R_3} = 1.48{\;\text {k}}\Omega \) and \({R_4} = 2.35{\;\text {k}\Omega }\). Denote that \({g_1}= 1\); the resistances of \({R_a}\), \({R_b}\) are determined by \({R_a}= {{{R_0}} /{(ak)}}\) and \({R_b}= {{{R_0}} /{(bk)}}\), respectively. For example, when \(a= 0\), the switch \({S_1}\) is open. If the switch \({S_1}\) is open and \({R_b} = 10.2 \;{\text {k}}\Omega \), the chaotic dynamics appears as shown in Fig. 22. The time series of the voltages \({v_1},\;{v_2},\;{v_3},\;{v_4}\) are depicted in Fig. 22(a). The phase plane projections on the \({v_1} - {v_2},\;{v_2} - {v_5} \) and \({v_3} - {v_5}\) planes are experimentally captured, as shown in Figs. 22(b)-(d). Finally, the effect of multi-level-pulse excitation on the system dynamics is observed. The time series of the voltages \({v_1},\;{v_2},\;{v_3},\;{v_4}\) and experimental results are shown in Fig. 23.

5 Conclusion

In this paper, a new bi-stable and non-volatile memristor with locally activity was presented. The switching mechanism and memristive parameter-associated dynamics characteristics were numerically and experimentally explored. Based on the proposed memristor, a novel locally active memristive synapse-coupled neuron model was constructed. The dynamics of the coupled neuron model was investigated by bifurcation plots, dynamical evolution maps and so on. The new neuron model exhibits the characteristic of bi-stability under different coupling weights, which was numerically revealed by local attraction basins. Moreover, the periodic burster and multi-scroll chaotic burster were found under external stimuli. Furthermore, the Hamiltonian energy function was deduced and the energy distribution was analyzed to explore the energy changes of the coupled neuron model. Hardware experimental results further verify the numerical results, which have applications value. In the future, new types of locally active memristors with better characteristics may be designed, based on which novel neurodynamic behaviors in neural models may be explored.