Global dynamics of Chua Corsage Memristor circuit family: fixed-point loci, Hopf bifurcation, and coexisting dynamic attractors

Abstract

This paper presents an in-depth and rigorous mathematical analysis of a family of nonlinear dynamical circuits whose only nonlinear component is a Chua Corsage Memristor (CCM) characterized by an explicit seven-segment piecewise-linear equation. When connected across an external circuit powered by a DC battery, or a sinusoidal voltage source, the resulting circuits are shown to exhibit four asymptotically stable equilibrium points, a unique stable limit cycle spawn from a supercritical Hopf bifurcation along with three static attractors, four coexisting dynamic attractors of an associated non-autonomous nonlinear differential equation, and four corresponding coexistingpinched hysteresis loops. Thebasin of attractions of the above static and dynamic attractors is derived numerically via global nonlinear analysis. When driven by a battery, the resulting CCM circuit exhibits a contiguous fixed-point loci, along with its DC V–I curve described analytically by two explicit parametric equations. We also proved the fundamental feature of theedge of chaos property; namely, it is possible to destabilize a stable circuit (i.e., without oscillation) and make it oscillate, by merely adding a passive circuit element, namely $L >0$. The CCM circuit family is one of the few known example of a strongly nonlinear dynamical system that is endowed with numerous coexisting static and dynamic attractors that can be studied both experimentally, and mathematically, via exact formulas.

1 Introduction

Nonlinear dynamical systems are of interest in scientific research field as most of the systems in nature are inherently nonlinear [1,2,3]. Various nonlinear dynamical systems have multiple coexisting attractors, and the properties (such as fixed points, limit cycles, toruses, and chaotic) of these attractors depend upon the embedded parameters and initial conditions. Starting from a set of initial conditions, the basin of attraction of each such attractor exhibits a long-time transitional behavior approaching toward the attractors. Thus, the qualitative behavior of the long-time motion of a given nonlinear dynamical system depends upon the initial conditions [4, 5]. The dynamic behavior of a nonlinear system can be verified by analyzing its behavior based on the theorem of bifurcation and chaos which is highly dependent on initial conditions of the systems. Moreover, complex phenomena and information processing tend to emerge over the parameter ranges of a system, operating on, or near the neighborhood of its edge of chaos domain [6, 7]. Memristor is regarded as one of the most prominent element to exhibit both complex phenomena (such as oscillation and chaos [4,5,6,7,8,9]) and information processing (such application in neural network [10,11,12], resistive switching memory [13], and artificial intelligence [14]). Recently, numerous research activities have been conducted to exploit the nonlinear dynamical attributes of memristive systems in electronic circuits.

This paper presents an in-depth and rigorous nonlinear analysis of the Chua Corsage Memristor¹ (CCM). The versatile CCM is a piecewise-linear (PWL) multi-state memory device with the following state-dependent Ohm’s law and state equation [15]:

State-Dependent Ohm’s Law

$$\begin{aligned}&i=G(x)\,\,v, \end{aligned}$$

(1)

$$\begin{aligned}&\hbox { where } G(x)=G_{0} \,x^{2}, \end{aligned}$$

(2)

State Equation

$$\begin{aligned} \text {d}x/\text {d}t=\,\,f(x,\,\,v)=f(x)+\,\,v, \end{aligned}$$

(3)

where

$$\begin{aligned} f(x)= & {} 33-x+\left| {x-6} \right| -\left| {x-12} \right| \nonumber \\&+\left| {x-20} \right| \,-\left| {x-30} \right| \nonumber \\&+\left| {x-42} \right| -\left| {x-56} \right| , \end{aligned}$$

(4)

and x, v, and i denote the memristor state, voltage, and current, respectively, as shown in Fig. 1. The intrinsic memductance scale of the memristor is fitted with scaling constant ${G}_{0}$. In this paper, we choose $G_{0} =1$ so that the parameters of the small-signal equivalent circuit of the CCM will not be excessive.

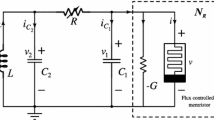
This paper presents an in-depth and rigorous nonlinear analysis of three members of the Chua Corsage Memristor (CCM) circuit family, where the CCM is driven by the external active circuits shown in Fig. 2:

External Circuit 1 A DC voltage source (battery) whose voltage $v = E$ is tuned over the entire real line, i.e., $-\infty<v<\infty .$

The resulting loci of the steady state (after the transient tends to zero) $x = X$, plotted as a function of constant voltage $v = V$ (dubbed the fixed-point loci), is proved in Sect. 2.3 to cover the entire real line—$\infty<X<\infty$, as the DC (constant) voltage is tuned from $V = -\infty$ to $V = +\infty$. The corresponding steady-state current I can be calculated from the state-dependent Ohm’s law of the CCM. When plotted in the I vs. V plane, the fixed-point loci is proved in Sect. 2.3 to be a multi-valued but contiguous curve—called the DC V–I curve of the CCM.

Fig. 1

Definition of the Chua Corsage Memristor (CCM) with ${G}_{0} =1$

External Circuit 2 A DC voltage source (with fixed voltage $v = V_\mathrm{DC})$ in series with an inductor whose inductance $L = L^{*}$ (derived via Chua’s oscillation formula) gives rise to a stable oscillation via Hopf bifurcation.

Fig. 2

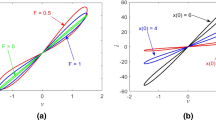
Three Chua Corsage Memristor (CCM) circuits. aCCM Circuit 1: The loci of (I, V) in i  vs. v plane, as the DC voltage E is tuned from $E =-\infty$ to $E =+\infty$, is called the DC V–I curve of the CCM. bCCM Circuit 2: With $E = -2.25\,\text {V}$ and $L= L^{{*}} = 355.5\,\hbox {mH}$, the CCM Circuit 2 is described by an autonomous system of two nonlinear ordinary differential equations, whose phase portrait shows an unique stable limit cycle along with three asymptotically stable equilibrium points in the $i_{{L}}\,\text {vs.} x$ phase plane. cCCM Circuit 3: The CCM is driven by a periodic sinusoidal voltage source $v_{{s}}(t) = A \,\sin (\omega t)$, where $A =\{1\,\text {V}, 3\,\text {V}\},$$\omega = \{0.02\pi \, \mathrm{rad/s}, 0.1\pi \, \mathrm{rad/s}, 0.2\pi \,\mathrm{rad/s}, \pi \,\mathrm{rad/s}, 2\pi \,\mathrm{rad/s}, 10\pi \,\mathrm{rad/s}, 20\pi \,\mathrm{rad/s}$}. The CCM Circuit 3 is described by a non-autonomous nonlinear differential equation. The steady-state response of the state variable x(t) is calculated with four initial states $x_{{a}}(0)$, $x_{{b}}(0)$, $x_{{c}}(0)$, and $x_{{d}}(0)$, each giving rise to a distinct periodic steady-state response, dubbed a dynamic attractor

A rigorous phase plane analysis supported by a detailed phase portrait is presented in Sect. 5 along with a unique stable limit cycle and its basin of attraction.

External Circuit 3 An AC sinusoidal voltage source $v_{s}(t) = A \sin (\omega t)$ is applied across the CCM. Over a wide range of amplitude A and frequency $\omega$, we show that, depending on the initial statex(0), the CCM circuits exhibit four distinct stable periodic steady-state response $x_{a}(t)$, $x_{b}(t)$, $x_{c}(t)$, and $x_{d}(t)$. The range of the initial state x(0) which converges to a particular periodic steady-state response $x_{j}(t)$, $j \in \{a, b, c, d\}$, is called the basin of attraction$B_{j} (0)$ of the dynamic attractor²$x_{j}(t)$. It is called an attractor because any trajectory with an initial state originating from inside the basin of attraction$B_{j} {(0)}$ converges to, or is attracted by, the periodic steady-state response $x_{j}(t)$, $j \in \{ a, b, c, d\}$.

The existence of the above four coexisting dynamic attractors$x_{a}(t)$, $x_{b}(t)$, $x_{c}(t)$, and $x_{d}(t)$ with explicit formulas, along with their basins of attraction, is destined to be a textbook example for future researchers on non-autonomous systems.

For each attractor $x_{j}(t), j \in \{a, b, c, d\}$, one can trivially calculate via Eq. (1) the corresponding steady-state current $i_{j}(t)$ of the CCM. When plotted in the i vs. v plane, with time t as parameter, the corresponding loci are proved to be a contiguous pinched hysteresis loop, as illustrated in Table 1. The fourcoexisting pinched hysteresis loops of the CCM, along with their basins of attraction, are a surprising new result of this paper.

Table 1 shows four steady-state (after the transient tends to zero) pinched hysteresis loops of the CCM Circuit 3 for amplitude $A = 3\,\hbox {V}$ and frequency $\omega = 0.2\pi \,\hbox {rad/s}$. Figure 3a shows an evolution toward the steady-state, and Fig. 3b shows the pinched hysteresis loops when the CCM Circuit 3 is driven by $v_{s}(t) =A\, \sin (\omega t)$, where $A =3\,\hbox {V}$ and $\omega = \{1\,\hbox {rad/s}, 10 \,\hbox {rad/s}, 20 \,\hbox {rad/s}, \text {and}\, 100\,\hbox {rad/s}\}$.

Table 1 Basins of attraction of the four dynamic attractors of the CCM Circuit 3, along with their associated coexisting pinched hysteresis loops with sinusoidal excitation $v_{{s}}(t) = A\, \sin (\omega t),$ where $A = 3 \,\hbox {V}$ and $\omega = 0.2\pi \, \text {rad/s}$. The steady-state response $x_{{j}}(t)$, $j \in \{a, b, c, d\},$ of CCM Circuit 3 for four initial states $x_{{j}}(0)$ and its associated steady-state current $i_{{j}}(t)$, when plotted in the $i_{{j}}(t)-v(t)$ plane, are pinched hysteresis loops

The main contributions of this paper are as follows:

• We present an in-depth and rigorous mathematical analysis of a family of nonlinear dynamical circuits whose only nonlinear component is a Chua Corsage Memristor (CCM) characterized by an explicit seven-segment piecewise-linear equation. Unlike most of the existing various nonlinear systems with disconnected DC V–I curves, the CCM (CCM Circuit 1) exhibits a complicated but contiguous DC V–I loci induced by the seven equilibrium states which can be expressed analytically by two exact explicit parametric equations.

• We proved the fundamental feature of the edge of chaos property³ by connecting the CCM in series with an appropriate choice of battery voltage $V = V^{*}$, and inductance $L = L^{*}$ (i.e., CCM Circuit 2) which exhibits a unique stable limit cycle spawn from a supercritical Hopf bifurcation along with three static attractors in phase plane.

• Another exciting discovery in this paper is that, when driven by $v =A \,\sin (2\pi \,{f t}),$ the non-autonomous ODE of CCM (CCM Circuit 3) exhibits four distinct periodic solutions (namely, $x_{a}(t)$, $x_{b}(t)$, $x_{c}(t)$, and $x_{d}(t))$ along with four distinct coexisting pinched hysteresis loops, whose corresponding basins of attraction were precisely calculated.

The rest of the paper is organized as follows: Various attributes of the CCM circuits are introduced in Sect. 2. In Sect. 3, the design and in-depth analysis of a CCM oscillator circuit are presented. The Hopf bifurcation analysis, which gives rise to a unique stable limit cycle, is given in Sect. 4. Section 5 presents a detailed analysis of the phase portrait of the CCM oscillator, including the location of limit cycle and three asymptotically stable equilibrium points $Q_{3}$, $Q_{5}$, and $Q_{7}$ (attractors) and four unstable equilibrium points $Q_{1}$, $Q_{2}$, $Q_{4}$, and $Q_{6}$ (repellers). The basins of attraction of the limit cycle and three attractors are clearly shown in the phase portrait. Section 6 shows four coexisting pinched hysteresis loops induced by the four coexisting dynamic attractors shown in Table 1, along with their basins of attraction. The final Sect. 7 is devoted to some concluding remarks.

Fig. 3

Signature of the CCM when driven by a sinusoidal input voltage $v_{{s}}(t) = A\, \sin (\omega t)$, where $A = 3\,\hbox {V}$ and initial state $x(0) = 1$. a Illustration of the identical zero-crossing phenomenon with frequency $\omega = 10 \,\hbox {rad/s}$. Observe each lobe of the hysteresis loop always passes through the origin whenever $v_{{s}}(t) = 0$, as the transient component decreases over time. bFour frequency-dependent steady-state pinched hysteresis loops computed with frequencies $\omega = \{ 1 \,\hbox {rad/s}, 10 \,\hbox {rad/s}, 20\,\text {rad/s}, \hbox {and } 100 \,\hbox {rad/s}\}$

2 Dynamic route map, parametric representation of contiguous multi-valued DC V–I curve of the CCM, fixed-point loci, and small-signal model

2.1 Dynamic route map of the CCM

In the parlance of nonlinear circuit theory, any curve f(x, v) plotted in the phase plane, e.g., (dx/dt vs. x) plane, along with the direction of motion from the representative points is called a dynamic route where it prescribes the dynamics of the defining scalar nonlinear differential equation [16, 17]. In spite of its simplicity, the dynamic route map (DRM) is the most powerful and ideal tool for analyzing the dynamics of any first-order differential equation $\text {d}x/\text {d}t = f(x, v)$ because of its predictability regarding the evolution of any initial state with increasing time [18]. The dynamic route map of the CCM Circuit 1 is shown in Fig. 4 for input voltages$v = V {=} \{-9\,\mathrm{V}, -7\,\mathrm{V}, -5\,\mathrm{V}, -3\,\mathrm{V}, 0\,\mathrm{V}, 3\,\mathrm{V}, 5\,\mathrm{V}, 7\,\mathrm{V}, 9\,\mathrm{V}\}.$ Observe that for any applied nonzero positive voltage ($v = +V_{A})$, the red curve f(x, 0) is translated upward by $V_{A}$ units. Conversely, for any nonzero negative voltage ($v = -V_{A})$, the red curve f(x, 0) is translated downwards by $V_{A}$ units, as shown in Fig. 4. As an example, for $v = +3\,\hbox {V}$ the corresponding DRM for f(x, 3) (blue curve) is obtained by translating the red curve (parameterized by $v = 0$) upward by three units. In contrast, for $v = -7\,\hbox {V}$, the DRM for $f(x, -7)$(burgundy curve) is obtained by translating the red curve f(x, 0) downward by seven units, as shown in Fig. 4.

Fig. 4

Dynamic route map (DRM) of the CCM. Each curve is analogous to a street whose street name is the value of the parameter v and whose direction is indicated by an arrowhead, which follows the traffic rule: move right (resp., move left) if the street is located above (resp., below) the horizontal axis$x = 0$

Fig. 5

Power-off plot (POP) of the CCM

2.2 Power-off plot (POP) of the CCM

The short-circuited ($v = 0$) dynamic route, also known as Power-off plot (POP) [17] of the CCM, is the street in Fig. 4 with the street name $v =0$. It is a plot of $\text {d}x/\text {d}t|_{v=0}$ vs. x, where

$$\begin{aligned} \left. \text {d}x/\text {d}t\right| _{v=0}= & {} f\left( {x,\,0} \right) =33-x+\left| {x-6} \right| \nonumber \\&-\left| {x-12} \right| +\left| {x-20} \right| \nonumber \\&-\left| {x-30} \right| +\left| {x-42} \right| -\left| {x-56} \right| . \end{aligned}$$

(5)

Figure 5 shows that every intersection between the POP and x-axis, where $\text {d}x/\text {d}t =0$, is an equilibrium point of the CCM Circuit 1 with $E =0$. The four equilibrium points $Q_{1}$, $Q_{3}$,$Q_{5}$, and $Q_{7}$ are asymptotically stable, whereas the three equilibrium points $Q_{2}$, $Q_{4}$, and $Q_{6}$ are unstable, since the state variable x(t) diverges away from $Q_{2}$, $Q_{4}$, and $Q_{6}$. Any initial point $x(0)>X_{Q}+ \delta x$, where $X_{Q} \in \{X_{Q2}$, $X_{Q4}$, $X_{Q6}\}$ and $\text {d}x/\text {d}t>0$, located near an unstable equilibrium points $Q_{2}$, $Q_{4}$, and $Q_{6}$ must converge to an adjacent stable equilibrium points $Q_{3}$, $Q_{5}$, and $Q_{7}$ on its right, as indicated by purple arrowheads in Fig. 5. Conversely, any initial point $x(0)<X_{Q}- \delta x$, where $\text {d}x/\text {d}t <0$, near the unstable equilibrium points $Q_{2}$, $Q_{4}$, and $Q_{6}$ must converge to an adjacent stable equilibrium points $Q_{1}$, $Q_{3}$, and $Q_{5}$ on its left, as indicated by black arrowheads in Fig. 5. Moreover, the calculated eigenvalues of the stable equilibrium points are found to be negative, whereas the calculated eigenvalues of the unstable equilibrium points are found to be positive, as predicted by theory in [19, 20].

2.3 Explicit parametric equations of DC V–I curve of the CCM

In circuit theory, the DC V–I curve of a two-terminal electronic device is defined as the set of all measurable or calculated points (V, I) upon application of a DC voltage V, DC current I, across the device. In general, the DC V–I curves of commercial two-terminal nonlinear resistive, or memristive, devices are generally described by a loci of points in the I vs. V plane because no analytical equations exist that would reproduce the measured loci of points. Moreover, for devices exhibiting strong nonlinearities, the DC V–I curve usually consist of two or more disconnected branches. As an example, consider the memristor [16] described by

Ohm’s Law

$$\begin{aligned} v=R\left( {x,\,\,i} \right) \,\,i=\left( {0.01\,x^{2}i^{2}} \right) \,\,i, \end{aligned}$$

(6)

State Equation

$$\begin{aligned} \text {d}x/\text {d}t=f\left( {x,\,\,i} \right) =-x^{3}-2\,x^{2}+\left( {3+\,i^{2}} \right) x. \end{aligned}$$

(7)

Equating (7) to zero, with constant (DC) current $i = I$, and solving for x, we obtain the exact equation of the following three equilibrium points

$$\begin{aligned}&\text {Equilibrium Point 1: } x=X_{0} =0, \end{aligned}$$

(8a)

$$\begin{aligned}&\text {Equilibrium Point 2: } x=X_{1} =-1+\sqrt{4+I^{2}} , \end{aligned}$$

(8b)

and

$$\begin{aligned}&\text {Equilibrium Point 3: } x=X_{2} =-1-\sqrt{4+I^{2}} . \end{aligned}$$

(8c)

Substituting Eqs. 8(a), (b), and (c) into the state-dependent Ohm’s law (6), we obtain the following three disconnected branches of the DC V–I curve of the above memristor:

$$\begin{aligned}&\textit{DC V--I Curve Branch } 1 : V\,=\,\,0, \end{aligned}$$

(9a)

$$\begin{aligned}&\textit{DC V--I Curve Branch } 2 : V=0.01\left[ {-1+\sqrt{4+I^{2}} } \right] I^{3}, \end{aligned}$$

(9b)

$$\begin{aligned}&\textit{DC V--I Curve Branch }3 : V=0.01\left[ {-1-\sqrt{4+I^{2}} } \right] I^{3}. \end{aligned}$$

(9c)

Thus, the DC V–I curve of the above memristor consists of three separated branches, as shown in Fig. 6.

We will now derive the exact analytical equation defining the DC V–I curve of the CCM defined in Fig. 1. In particular, we will derive two formulas which together gives the exactparametric equations of the DC V–I curves, with the equilibriumstate$x = X (-\infty<X <\infty )$, as an independent parameter.

Fig. 6

A memristor and its DC V–I curve, which consists of three disconnected branches described by the unstable branch $V = 0$ (dotted red loci), and two asymptotically stable branches (for each fixed value of I) defined analytically by a blue equation for $x(0) >0$, and by a magenta equation for $x(0)< 0$ [16]

Table 2 Coordinates of (V, I) for a sample set of X calculated from the two parametric equations, $V={\hat{v}}(x)$ and $I={\hat{i}}(x)$ in (10a) and (10b)

Let us assume that for each DC voltage $v = V$, the CCM has at least one equilibrium state $x = X$, namely ${\text {d}x/\text {d}t\vert }_{(v=V,\, x=X)}=0$. In particular, substituting $v = V$, $x = X$, and $\text {d}x/\text {d}t=0$ in (3), and solving for V, we obtain

$$\begin{aligned} V&=\,\,-\,\left[ {\begin{array}{l} 33-X+\left| {X-6} \right| -\left| {X-12} \right| +\left| {X-20} \right| \\ \,\,\,\,\,\,\,\,\,\,\,-\left| {X-30} \right| +\left| {X-42} \right| -\left| {X-56} \right| \\ \end{array}} \right] \nonumber \\&\triangleq \,\,{\hat{v}}\left( X \right) . \end{aligned}$$

(10a)

The plot of $V=\hat{v}(X)$ in the V vs. X plane is shown in Fig. 7a. Next, substituting (10a) into (1), with $v = V$, $i = I$, and $x = X$, we obtain

$$\begin{aligned} I&=\,\,-X^{2}\left[ {\begin{array}{l} 33-X+\left| {X-6} \right| -\left| {X-12} \right| +\left| {X-20} \right| \\ -\left| {X-30} \right| +\left| {X-42} \right| -\left| {X-56} \right| \, \\ \end{array}} \right] \,\nonumber \\&\triangleq \,\,{\hat{i}}\left( X \right) . \end{aligned}$$

(10b)

The plot of $I={\hat{i}}(X)$ in the I vs. X plane is shown in Fig. 7b.

Note that the equilibrium state X in Fig. 7a, b spans the entire horizontal axis, namely $-\infty< X <\infty$. Observe that for any value $X \in (-\infty , \infty )$, we can calculate the corresponding DC voltage V, and DC current I using the exact formulas (10a) and (10b), respectively. Table 2 shows the values of V and I for $-12< X <78$, which covers the region shown in Fig. 7.

Plotting the points (V, I) from Table 2 for $-7< X <73$, we obtain the DC V–I curve of the CCM (defined in Fig. 1) shown in Fig. 7c. Observe that unlike the examples shown in Fig. 6, this DC V–I curve is a contiguous curve. Each point on this curve corresponds to an equilibrium state X, which may be stable (solid line) or unstable (dotted line).

Moreover, substituting the value of the state variable $x=X_{Q_{i}}$ into (10a) at the seven equilibrium states $Q_{i}$ identified in Fig. 5, where $i =1,2,\ldots ,7$, we obtain $V\left( X_{Q_{i}} \right) =0$, at each of the seven equilibrium points $Q_{i}$ (listed in the upper left box in Fig. 7c). It follows from the state-dependent Ohm’s law in (10b) that $I\left( X_{Q_{i}} \right) =0$ at all seven equilibrium states. In other words, in the DC V–I plane in Fig. 7c, the loci of the state variable x pass through the origin $(V, I) = (0, 0)\, 7$ times.

It is important to observe that the DC V–I curve in Fig. 7c is obtained without solving any algebraic, or differential equations! Indeed, it is obtained by substituting any desired value of X, where $-\infty< X <\infty$, into the explicit analytical Eq. (10a) for $V=\hat{v}(x)$ and (10b) for $I=\hat{i}(x)$. This derivation of a memristor DC V–I curve by direct substitution into the explicit state-dependent Ohm’s law, and state equation is a truly remarkable example for future researchers.

Observe that the inset in the lower-right corner reveals a short piece of the DC V–I curve that exhibits a negative slope, over $-3 V< V < -1 V$. This implies the Chua Corsage Memristor is locally active [21] and can be used to design an oscillator, which is presented in Sect. 3.

Fig. 7

Exact parametric equation of the Chua Corsage Memristor. a$V=\hat{v}(X)$ vs. X , and b$I={\hat{i}}(x)$ vs. X, for each values of ${\chi =\{X:-12\le X \le 78\}}$. c DC V–I plot, where the coordinates (V, I) of each point are extracted from (a) and (b), for each values of X, where $\chi =\{X:-7\le X\le 73\}$. The lower-right inset shows the zoomed portion of red DC V–I curve over the voltage range $-5\,\hbox {V} \le V \le 2\,\hbox {V}$. The upper left inset shows the state variable X values at $V = 0\,\hbox {V}$

2.4 Explicit parametric equations of the fixed-point loci of CCM

The fixed-point loci of the CCM is defined to be the set of steady-state (constant) response of the state variable$x = X(V)$, calculated from the CCM Circuit 1 in Fig. 2a upon applying a constant DC voltage $v = V$, $-\infty<V <\infty$, across the CCM.

Observe that the above definition assumes the CCM circuit in Fig. 2a is in equilibrium, namely ${\text {d}x/\text {d}t\vert }_{v = V}=0$. The fixed-point loci of the CCM can be calculated by setting $\text {d}x/\text {d}t=0$ in (3) and solving for X for each constant $v = V$; namely, the fixed-point loci of the CCM is the set of all solutions of $x = X$ of the equilibrium equation

$$\begin{aligned}&f(X)+V\nonumber \\&\quad =\,\,\,\left[ {\begin{array}{l} 33-X+\left| {X-6} \right| -\left| {X-12} \right| +\left| {X-20} \right| \\ \,\,\,-\left| {X-30} \right| +\left| {X-42} \right| -\left| {X-56} \right| +V \\ \end{array}} \right] \nonumber \\&\quad =0. \end{aligned}$$

(11)

Using the notation in (10a), the fixed-point loci of the CCM is obtained by solving the voltage parametric equation (10a) for X, namely

$$\begin{aligned} X={\hat{v}}^{-1}\left( V \right) , \end{aligned}$$

(12)

where ${\hat{v}}^{-1}(\bullet )$ denotes the inverse of the single-valued function $V=\hat{v}(X)$ given in Fig. 7a, which is obtained by replotting Fig. 7a with V as the abscissa and X as the ordinate, as shown in Fig. 8. Observe that ${\hat{v}}^{-1}(V)$ in (12) is a multi-valued function of V. In particular, for each V value, where $-3 V< V < 3 V$, X has seven fixed points. Moreover, if we substitute (12) for X in (10b), we would obtain the equation of the DC V–I curve of the CCM; namely,

$$\begin{aligned} I={\hat{i}}\left( X \right) ={\hat{i}}\left( {\hat{v}^{-1}\left( V \right) } \right) \triangleq g\left( V \right) . \end{aligned}$$

(13)

The above equation is called a composition in mathematics and is denoted by ${\hat{i}}\,{\circ }\,{\hat{v}}^{-1}$. Hence, we have proved the DC V–I curve of the CCM is just the mathematical composition between the parametric equation for the current $I={\hat{i}}\mathrm {(X)}$ and the inverse voltage parametric equation $X={\hat{v}}^{-1}(V)$.

Fig. 8

Fixed-Point loci of the CCM

2.5 Small-signal equivalent circuit model of the CCM

Small-signal device modeling is the standard nonlinear circuit analysis technique for predicting the behavior of a nonlinear device via its linearized equation about an operating point on its DC V–I curve. The small-signal equivalent circuit of the CCM is derived about an equilibrium point (V, I), utilizing the circuit shown in Fig. 9a. Applying the Taylor series and the Laplace transform, presented in [5], the small-signal admittance function Y(s, Q) of the CCM about an equilibrium point Q is obtained as,

$$\begin{aligned} Y(s,Q)\triangleq \frac{\hat{{i}}(s)}{\hat{{v}}\,(s)}=\frac{a_{11} (Q)\,b_{12} (Q)}{s-b_{11} (Q)}+a_{12} (Q) \end{aligned}$$

(14)

where

$$\begin{aligned} a_{11} (Q)= & {} \left. {v\frac{\partial G(x)}{\partial x}} \right| _{Q} =2XV, \end{aligned}$$

(15a)

$$\begin{aligned} a_{12} (Q)= & {} \left. {G(x)\frac{\partial v}{\partial v}} \right| _{Q} =\left. {G(X)} \right| _{Q} =X^{2}, \end{aligned}$$

(15b)

$$\begin{aligned} b_{11} (Q)= & {} \left. {\frac{\partial }{\partial x}g(x,v)} \right| _{Q} =-1\,, \end{aligned}$$

(15c)

and

$$\begin{aligned} b_{12} (Q)= & {} \left. {\frac{\partial }{\partial v}g\,(x,v)} \right| _{Q} =1. \end{aligned}$$

(15d)

The small-signal parameters of the CCM can be extracted from (14) as:

$$\begin{aligned} Y(s,\,\,V)=Y_{x} (s,\,\,V){+}Y_{y} (s,\,\,V)=\frac{1}{s\,L_{x} +R_{x} }{+}\frac{1}{R_{y} }\,\, \end{aligned}$$

(16a)

where,

$$\begin{aligned}&{L_{x} (V)=\frac{1}{a_{11} (Q)\,b_{12} (Q)}=\frac{1}{2XV}}, \end{aligned}$$

(16b)

$$\begin{aligned}&{R_{x} (V)=\frac{-b_{11} (Q)}{a_{11} (Q)\,b_{12} (Q)}=\frac{1}{2XV}} , \end{aligned}$$

(16c)

and

$$\begin{aligned} {R_{y} (V)=\frac{1}{a_{12} (Q)}=\frac{1}{X^{2}}}. \end{aligned}$$

(16d)

Fig. 9

a Chua Corsage Memristor driven by $v = V +\delta v$, where $V = -2.25\,\text {V}$. b Small-signal equivalent circuit of the CCM at $V = -2.25\,\text {V}$. c Pole–zero diagram of the admittance function Y(s, V) of the CCM over the range $-10\,\text {V} \le V \le 3\,\text {V}$

Fig. 10

Frequency response of the admittance function $Y(i\omega , V)$ of the CCM parameterized by the input voltage V. a$\hbox {Re} [Y(i\omega , V)]\, \hbox {vs.} \omega$ for equilibrium point $Q_{{1}}$. The left inset shows the logarithmic plot of $\hbox {Re} [Y(i\omega , V)]$ over the input voltage $V \in (-0.05\,\hbox {V}, 0.05 \,V)$, and the right inset shows the zoomed-in view near the origin of (a). b$\hbox {Re} [Y(i\omega , V)]\, \hbox {vs.} \omega$ for equilibrium point $Q_{{2}}$, c$\hbox {Re} [Y(i\omega , V)] \,\hbox {vs.} \omega$ for equilibrium point $Q_{{5}}$, d$\hbox {Re} [Y(i\omega , V)] \,\hbox {vs.} \omega$ for equilibrium point $Q_{{7}}$. e Frequency response $[\hbox {Re} [Y(i\omega , V)] +i\, \mathrm{Im} [Y(i\omega , V)]]$ of the admittance function $Y(i\omega , V)$ of the CCM at $V = -2.25\,\hbox {V} (for\, Q_{{1}}$) over the frequency range $-10 \,\hbox {rad/s} \le \omega \le 10 \,\hbox {rad/s}$

The small-signal equivalent circuit of the CCM computed at $V =-2.25\,\,\text {V}$ is shown in Fig. 9b. Observe that both $L_{x}$ and $R_{x}$ are negative, whereas $R_{y}$ is positive.

The pole$s = p$ and the zero$s = z$ of the small-signal admittance Y(s, V) of the CCM Circuit 1, shown in Fig. 9c, can be obtained from (14) as :

$$\begin{aligned} Y(s,V)= & {} \frac{a_{12} (Q)s+\left( {a_{11} (Q)\,b_{12} (Q)-a_{12} (Q)\,b_{11} (Q)} \right) }{s-b_{11} (Q)} \nonumber \\= & {} \frac{b_{1} (V)s+b_{0} (V)}{a_{1} (V)s+a_{0} (V)}=\frac{K\left( {s-z} \right) }{\left( {s-p} \right) } , \end{aligned}$$

(17a)

where

$$\begin{aligned} K= & {} \frac{b_{1} (V)}{a_{1} (V)}=a_{12} (Q), \end{aligned}$$

(17b)

$$\begin{aligned} p= & {} -\frac{a_{0} (V)}{a_{1} (V)}=b_{11} (Q)=-1, \end{aligned}$$

(17c)

$$\begin{aligned} z= & {} -\frac{b_{0} (V)}{b_{1} (V)}=-\frac{[a_{11} (Q)b_{12} (Q)-a_{12} (Q)b_{11} (Q)]}{a_{12} (Q)}\,\nonumber \\= & {} -\frac{[2XV+X^{2}]}{X^{2}}. \end{aligned}$$

(17d)

Observe from Fig. 9c that the pole p is constant $(\hbox {Re}\, [p] = -1)$, whereas the zero z varies as a function of voltage, V.

It is well known that in order for a linear time-invariant circuit to oscillate, its admittance must have at least two poles. Hence, in order to design an oscillator using the locally active CCM, it is necessary to add at least one positive capacitor, or one positive inductor, to the CCM Circuit 1. This additional energy storage element can force the poles of the composite admittance $Y_{C}(s, V)$ of the CCM to move and cross the imaginary axis of the complex plane [5, 6]. The type and value of the energy storage element can be determined from the frequency response of the CCM Circuit 1. The frequency response $Y(i\omega , V)$ of the CCM at the applied DC voltage V is obtained by substituting $s = i\omega$ in (17a):

$$\begin{aligned} Y(i\omega ,\,\,V)= & {} \frac{a_{0} (V)\,b_{0} (V)+\omega ^{2}a_{1} (V)\,b_{1} (V)}{a_{0}^{2}(V)+\omega ^{2}a_{1}^{2}(V)}\, \nonumber \\&+i\frac{\omega \,\,\left( {a_{0} (V)\,b_{1} (V)-a_{1} (V)\,b_{0} (V)} \right) }{a_{0}^{2}(V)+\omega ^{2}a_{1}^{2}(V)},\nonumber \\ \end{aligned}$$

(18a)

where

$$\begin{aligned} {{\varvec{Re}}}\,{{\varvec{Y}}}\left( {{\varvec{i}}}{\varvec{\omega }} ,\,\,{{\varvec{V}}}\right)= & {} \frac{a_{0} (V)b_{0} (V)+\omega ^{2}a_{1} (V)b_{1} (V)}{a_{0} ^{2}(V)+\omega ^{2}a_{1}^{2}(V)} \nonumber \\= & {} \frac{\left( {2XV+X^{2}} \right) +\omega ^{2}X^{2}}{1+\omega ^{2}} , \end{aligned}$$

(18b)

$$\begin{aligned} {{\varvec{Im}}}\, {{\varvec{Y}}}\left( {{\varvec{i}}}{\varvec{\omega }} ,\,\,{{\varvec{V}}} \right)= & {} \frac{\omega \left( {a_{0} (V)b_{1} (V)-a_{1} (V)b_{0} (V)} \right) }{a_{0}^{2}(V)+\omega ^{2}a_{1}^{2}(V)} \nonumber \\= & {} \frac{\omega \left[ {X^{2}-\left( {2XV+X^{2}} \right) } \right] }{1+\omega ^{2}} . \end{aligned}$$

(18c)

The frequency responses $\hbox {Re} [Y(i\omega , V)]$ of the CCM, parameterized by the input voltage V, at the equilibrium points $Q_{1}$,$Q_{3}$, $Q_{5}$, and $Q_{7}$ over the frequency range $-10 \,\hbox {rad/s} \le \omega \le 10\, \text {rad/s}$ are shown in Fig. 10a–d, respectively. Observe from Fig. 10a–d that $\hbox {Re} [Y(i\omega , V)]$ is constant for all values of $\omega$ at $V =0,$ i.e., $\hbox {Re} [Y(i\omega , V)]$ is independent of $\omega$. At $V =0$, the inductance $L_{x}$ and the resistance $R_{x}$ of the small-signal equivalent circuit in Fig. 9b tend to infinity, i.e., $Y_{x}(s, V)=1/(sL_{x}+R_{x})\rightarrow 0$ [see Eq. (16a)] and the corresponding impedance $Z_{x}(s, V)=1/Y_{x}(s, V)\rightarrow \infty$ (open circuit). Hence, the admittance $Y\left( s, V \right) =Y_{y}\left( s, V \right) =X^{2}$, where the state variable X depends on the input voltage V at the equilibrium point $Q_{n}$, i.e., $X=F\left( V, X_{Q_{n}} \right)$ where $n \in \{ 1, 3, 5, 7\}$ . For example, the frequency response $Y(i\omega$, V) at $V = 0$ is equal to a constant ${Y\left( i\omega , 0 \right) \vert }_{Q_{1}}={\hbox {Re} [Y\left( i\omega , 0 \right) ]\vert }_{Q_{1}}=X_{Q_{1}}^{2}=9$ (see Fig. 7) over the frequency range $-10 \,\hbox {rad/s}\le \omega \le$$10\, rad/s$, as shown in the right inset of Fig. 10a. Similarly, Fig. 10b–d shows that the frequency response ${Y\left( i\omega , 0 \right) \vert }_{Q_{n}}=\hbox {Re} {[Y\left( i\omega , 0 \right) ]\vert }_{Q_{n}}={X^{2}\vert }_{Q_{n}}$, at $V = { 0}$, depends only on the value of the state variable $X_{Q_{n}}$ listed in Fig. 7, for n $=$ [3, 5, 7], despite the frequency($\omega )$ variation over the range $\omega \in (-\infty$, $\infty )$. The curve of $\hbox {Re} [Y(i\omega , V)]$ shown in the left inset (with logarithmic scale in $\hbox {Re} [Y(i\omega , V)])$ of Fig. 10a affirms that for nonzero voltage ($V \ne 0$) $\hbox {Re} [Y(i\omega , V)]$ is varying as a function of $\omega$ over the range $-3 \,\hbox {rad/s} \le \omega \le 3 \,\hbox {rad/s}$, whereas $\hbox {Re} [Y(i\omega , V)]$ is constant at $V = 0$. Moreover, at $V =0$, the value of $\hbox {Re} [Y(i\omega , V)]$ at the equilibrium points $Q_{1}$,$Q_{3}$, $Q_{5}$, and $Q_{7}$, shown in Fig. 10a–d, is equal to the corresponding slopes of the DC V–I curve shown in Fig. 7.

The frequency response $Y(i\omega$, V) of the CCM calculated at $V =-2.25\,\,\text {V}$ (for $Q_{1})$ is shown in Fig. 10e over the range $-10 \,\hbox {rad/s} \le \omega \le 10 \,\hbox {rad/s}$. Figure 10e shows that the real and imaginary parts of the frequency response $Y(i\omega )$ at $V =-2.25\,\text {V}$ are equal to $\hbox {Re} [Y(i\omega ^{*})] = 0$ and $\mathrm{Im} [Y(i\omega ^{*})] = \pm 1.258 S$, respectively, at $\omega ^{*} = \pm 2.236\,\hbox {rad/s}$. Since $\hbox {Re} [Y(i\omega ^{*})] =0$ and $\mathrm{Im} [Y(i\omega ^{*})] \ne 0$, the CCM requires a positive inductance with value $L = L^{*} H$ to be connected in series with the CCM in Fig. 9a to satisfy the main condition for oscillation to emerge; namely, the small-signal impedance must be zero at $V = -2.25\,\text {V}$ [5]. The value of the inductance $L^{*}$ is calculated from the following Chua oscillation formula:

$$\begin{aligned} {\,{L^{*} }\,\,{=}\,\,\frac{1}{\omega ^{*} \,\,\hbox {Im }Y(i\omega ^{*} )}\,\,=355.5\,\text {mH}}. \end{aligned}$$

(19)

Figure 10e shows that at $\omega = 0$ the admittance $Y(i\omega ) =-2.813\, S$ at $V = -2.25\,\hbox {V}$. This admittance is equal to the admittance of the small-signal equivalent circuit of the CCM, shown in Fig. 9b, but with the inductor $L_{x}$ replaced by a short circuit because the impedance of an inductor at DC ($\omega = 0$) is equal to zero. In particular, $Y\left( 0 \right) = \left[ \frac{1}{R_{x}}+\frac{1}{R_{y}} \right] =\left[ \frac{-1}{296.3\times {10}^{-3}}+\frac{1}{1.78} \right] =-2.813 S$.

3 Chua Corsage Memristor (CCM) oscillator circuit

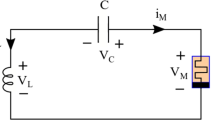
The composite one-port oscillator circuit, as shown in Fig. 11a, is designed based on the CCM Circuit 2 with an external inductance value ($L = L^{*} = 355.5\,\text {mH}$) and a battery ($E = -V = 2.25\,\text {V}$) connected in series with the CCM, where the input port current, $i = i_{L} = i_{M}$, input voltage $v = v_{L} + v_{M}$, and the memristor voltage $v_{M} = i_{M }/ G(x)$. The state-dependent Ohm’s law of the CCM and the two nonlinear differential equations of the Chua Corsage Memristor oscillator (CCM oscillator) circuit⁴ are defined as follows:

State-Dependent Ohm’s Law of CCM

$$\begin{aligned} i_{M} =G(x)\,v_{M}. \end{aligned}$$

(20)

Second-order autonomous differential equations of CCM oscillator circuit

$$\begin{aligned} \text {d}x/\text {d}t&{=} \,\,\left[ \begin{array}{l} 33 - x + \left| {x - 6} \right| - \left| {x - 12} \right| + \left| {x - 20} \right| \\ - \left| {x - 30} \right| + \left| {x - 42} \right| - \left| {x - 56} \right| + \,\,i_{L}/x^{2} \end{array} \right] \nonumber \\&\triangleq \,f\left( {x,\,\,{i_L}} \right) , \end{aligned}$$

(21a)

$$\begin{aligned} {\text {d}{i_L}} /{\text {d}t}&=1/L^{*}\left( V - \,\,i_{L}/x^{2}\right) \triangleq g\left( {x,\,\,{i_L}} \right) . \end{aligned}$$

(21b)

A typical trajectory of (21a)–(21b) starting from initial state (x(0), $i_{L}(0)) = (0.84, -1.767)$ is shown in Fig. 11b converging to a limit cycle. The corresponding periodic waveforms (x(t), $i_{L}(t))$ are shown in Fig. 11c, d, respectively.

To verify the oscillation conditions, we compute the admittance⁵$Y_{C}(s, Q)$ of the composite one-port ${{\varvec{\mathcal {N}}}}$ consisting of the inductor $L^{*}$ in series with the CCM in Fig. 11a. The small-signal admittance $Y_{C} (s, Q)$ of the composite one-port can be computed by adding the impedance 1/Y(s, Q) of the CCM and the impedance $1/ Y_{L^*}$ of the external inductor [5]:

$$\begin{aligned} \frac{1}{{{Y_C}(s,\,\,Q)}} = \frac{1}{{{Y_{{L^*}}}}} + \frac{1}{{Y(s,\,\,Q)}}, \end{aligned}$$

(22)

$$\begin{aligned} {Y_C}(s,\,\,V)= & {} \frac{{\hat{i}(s)}}{{\hat{v}(s)}} = \frac{{s\,{a_{12}}(Q) + \left( {{a_{11}}(Q)\,\,{b_{12}}(Q) - {a_{12}}(Q)\,\,{b_{11}}(Q)} \right) }}{{{s^2}{a_{12}}(Q){L^*} + s\left( {{L^*}{a_{11}}(Q)\,\,{b_{12}}(Q) - {L^*}{a_{12}}(Q)\,\,{b_{11}}(Q) + 1} \right) + \left( { - {b_{11}}(Q)} \right) }}\nonumber \\= & {} \frac{{{b_1}s + {b_0}}}{{{a_2}{s^2} + {a_1}s + {a_0}}}, \end{aligned}$$

(23a)

where

$$\begin{aligned}&\left. \begin{array}{l} {a_2} = {a_{12}}(Q)\,{L^*} = {L^*}{X^2}\\ {a_1} = \left( {{L^*}\left[ {{a_{11}}(Q)\,\,{b_{12}}(Q) - {a_{12}}(Q)\,\,{b_{11}}(Q)} \right] + 1} \right) \\ = \left( {{L^*}\left[ {2XV\,\, + {X^2}} \right] + 1} \right) \\ {a_0} = - {b_{11}}(Q) = 1 \end{array} \right\} , \end{aligned}$$

(23b)

$$\begin{aligned}&\left. \begin{array}{l} {b_1} = a{}_{12}(Q) = {X^2}\\ {b_0} = {a_{11}}(Q)\,\,{b_{12}}(Q) {-} {a_{12}}(Q)\,\,{b_{11}}(Q) {=} 2XV {+} {X^2} \end{array} \right\} .\nonumber \\ \end{aligned}$$

(23c)

The frequency response defined by ($\hbox {Re} [Z_{C}(i\omega ,\,\hbox {V})$] $+ i$$\mathrm{Im} [Z_{C}(i\omega ,\,\hbox {V})$]) of the composite impedance function $Z_{C }(s, V)$ of the one-port ${\varvec{\mathcal {N}}}$ in Fig. 11a at an applied voltage $v = V$ is computed by substituting $s = i\omega$ in (23a) [6] and then taking its inverse:

$$\begin{aligned} {Z_C}(i\omega ,\,\,V)= & {} \,\,\,\frac{1}{{{Y_C}(i\omega ,\,\,V)}}\nonumber \\= & {} \underbrace{\frac{{{a_0}{b_0} + {\omega ^2}\left( {{a_1}{b_1} - {a_2}{b_0}} \right) }}{{b_0^2 + b_1^2\,{\omega ^2}}}}_{{{\hbox {Re}}}\,\left[ {{{{Z}}_{{C}}}{{(i\omega ,}}\,\,{{V)}}} \right] } \nonumber \\&+ \,\,i\,\left[ {\underbrace{\frac{{\omega \left( {{a_2}{b_1}{\omega ^2} + {a_1}{b_0} - {a_0}{b_1}} \right) }}{{b_0^2 + b_1^2\,{\omega ^2}}}}_{{{Im}}\,\left[ {{{{Z}}_{{C}}}{{(i\omega ,}}\,\,{{V)}}} \right] }} \right] .\nonumber \\ \end{aligned}$$

(24)

Figure 12 shows the real and imaginary part of the composite impedance function $Z_{C }(i\omega , V)$ at $V = -2.25\,\text {V}$ over the range $-10 \,\hbox {rad/s} \le \omega \le 10 \,\hbox {rad/s}$. Observe from Fig. 12 that $Z_{C}(i\omega ^{*}, V= -2.25\,\hbox {V}) \rightarrow 0$ at $\omega = \omega ^{*} = \pm 2.236 \,\hbox {rad/s}$ which satisfies the prime condition of the CCM oscillator circuit; namely, the small-signal impedance of the composite one-port ${{\varvec{\mathcal {N}}}}$ must be equal to zero at $v = V = -2.25\,\hbox {V}$ Observe that at $V =-2.25\,\hbox {V}$ and $\omega = 0$, the value of the composite impedance function $Z_{C}(i\omega$,$V) = -355.5 \hbox { m}\Omega$, in Fig. 12, must be equal to the reciprocal of the admittance $Y(i\omega , V) = -2.813\, S$ at $\omega =0$ in Fig. 10e, because the impedance of the inductor $L^{*}$ is zero Ohms at $\omega =0$, so that $Z_{C}(i\omega , V) = 1/ Y_{C}(i\omega , V) = 1/-2.813 S =-355.5\,\text {m}\Omega$.

Fig. 11

Circuit diagram of CCM oscillator circuit with $E = 2.25\,\text {V}$, b a trajectory with initial state (x(0), $i_{{L}}(0))= (0.84, -1.767)$ in the phase plane. c Periodic waveforms of x(t) with $\hbox {T} = 2.81\hbox { s}$, and d corresponding periodic waveforms of $i_{{L}}(t)$

Fig. 12

Frequency response $\hbox {Re} [Z_{{C }}(i\omega , V)]$ and $\mathfrak {I}[Z_{{C }}(i\omega , V)]$ of the composite impedance function $Z_{{C }}(i\omega , V)$, plotted as a function of frequency $\omega$ , with $V = -2.25\,\hbox {V}$ and $L = L^{*} = 355.5\,\hbox {mH}$

The poles ${{\varvec{s}}} = \{{{\varvec{p}}}_{{{\varvec{1}}}}, {{\varvec{p}}}_{{{\varvec{2}}}}\}$ and zero ${{\varvec{s}}} = {{\varvec{z}}}_{{{\varvec{1}}}}$ of the composite admittance $Y_{C} (s$,V) in Fig. 11a are computed using (23a):

$$\begin{aligned} Y_{C} (s,\,\,V)= & {} \frac{b_{1} s+b_{0} }{a_{2} s^{2}+a_{1} s+a_{0} }=\frac{\left( {s-{z}_{{1}} } \right) }{\left( {s-{p}_{{1}} } \right) \left( {s-{p}_{{2}} } \right) },\nonumber \\ \end{aligned}$$

(25a)

where

$$\begin{aligned} z_{{1}}= & {} -\frac{b_{0} }{b_{1} }, \end{aligned}$$

(25b)

$$\begin{aligned} p_{{1}}= & {} \frac{-a_{1} +\sqrt{a_{1}^{2} -4a_{2} a_{0} } }{2a_{2}}, \end{aligned}$$

(25c)

$$\begin{aligned} {p}_{{2}}= & {} \frac{-a_{1} -\sqrt{a_{1}^{2} -4a_{2} a_{0} } }{2a_{2}}. \end{aligned}$$

(25d)

The loci of the real vs. imaginary parts of the poles $p_{i} =\hbox {Re} [p_{i}(V)] + i \,\mathrm{Im} [p_{i} (V)$] of the composite admittance $Y_{C}(s, V)$ of the composite one-port ${{\varvec{\mathcal {N}}}}$ in Fig. 11a, parameterized by the input voltage V over the range $-3\,\hbox {V} \le V \le 3\,\hbox {V}$, are shown in Fig. 13. The arrowheads indicate the direction of the movement of the poles. Observe the complex conjugate poles of $Y_{C}(s, V)$ in Fig. 13 lie in both the left-hand side and the right-hand side of the imaginary axis. Observe also that there are two pairs of complex conjugate poles on the imaginary axis at $V = -2.25\,\hbox {V}$ and $V = -1.75\,\hbox {V}$, respectively. The inset of Fig. 13 shows that $\hbox {Re} [p1] > 0$ and $\hbox {Re} [p2] > 0$ for input voltages $-2.25\,\text {V}< V < -1.75\,\hbox {V}$.

Figure 14 shows the loci of the $\mathrm{Im} [p1]$and$\mathrm{Im} [p2]$of the poles vs. $\hbox {Re} [p1]$ and $\hbox {Re}[p2]$of the poles$p_{1}$ and $p_{2 }$ of $Y_{C }(s, V)$, parameterized by the value of inductance L at DC input voltage $V = -2.25\,\hbox {V}$, where the arrowheads indicate the direction of movement of the poles. The pole diagram in Fig. 14 contains a pair of complex conjugate poles located at $\mathrm{Im} [p1] =2.236$ and $\mathrm{Im} [p2] = -2.236$ at the inductance value of $L = L^{*} =355.5\,\hbox {mH}$. Observe also when the inductance $L \rightarrow 0$, $\hbox {Re} [p1] \rightarrow -1$ and $\hbox {Re} [p2] \rightarrow -\infty$ and when $L \rightarrow \infty$, $\hbox {Re} [p1]_{ }\rightarrow 5$ and ${\hbox {Re} [p2]} \rightarrow 0$, respectively.

Fig. 13

Loci of the real and imaginary parts of the poles $p_{{1}}$ and $p_{{2}}$ of the admittance $Y_{{C}}\, (s,\,\hbox {V})$ of the composite one-port ${\varvec{\mathcal {N}}}$ of the CCM oscillator as a function of input voltage V, where the inductance $L = L^{*} = 355.5\,\text {mH}$

Fig. 14

Loci of the real and imaginary parts of poles of the composite admittance $Y_{{C}} (s, V)$ of the CCM oscillator, plotted as a function of the external inductance L, at the applied battery voltage $V =-2.25\,\text {V}$. To avoid clutter, we choose an uneven horizontal scaling between 2 and 5 in the horizontal axis

Figure 13 shows that the external inductance $L^{*}$ in the CCM oscillator circuit compels the constant poles of CCM [shown in Fig. 9c] to cross the imaginary axis of the complex plane. The right-hand side poles and the complex conjugate poles on the imaginary axis of the complex plane, in Fig. 13, might give rise to bifurcation. Moreover, Fig. 14 shows that the complex conjugate poles $(\mathrm{Im} [p1] =2.236$ and $\mathrm{Im} [p2] = -2.236)$ on the imaginary axis for an inductance $L = L^{*} = 355.5\,\hbox {mH}$ are equal to the operating frequency $\omega = \omega ^{*} =\pm 2.236\,\hbox {rad/s}$ (in Fig. 12). Thus, Figs. 13 and 14 affirm that the Hopf bifurcation points at $V = -2.25\,\hbox {V}$ and $V =-1.75\,\hbox {V}$ or a small neighborhood of these two points on the open right-half plane, in Fig. 13, might give rise to stable oscillation by exploiting the Hopf bifurcation.

4 Bifurcation analysis

The presence of complex phenomena in a nonlinear dynamical system is predicted by the local activity principle [21]. In particular, it asserts that a nonlinear circuit made of two-terminal circuit elements, and/or more complicated two-terminal devices, or one-ports [22], can exhibit complex bifurcation phenomena, such as oscillation and chaosonly if the circuit contains at least one nonlinear locally active element. There is a fundamental deep mathematical theorem given in [21] which allows one to test whether a two-terminal element, or one-port⁶, is locally active about some equilibrium point, aka a DC operating point. While a rigorous proof of this theorem is couched in abstruse mathematics, testing whether a two-terminal element, or one-port, is locally active involves only standard sophomore-level mathematics. In particular, the test is couched in terms of the small-signal impedanceZ(s), or admittance $Y(s) \triangleq 1/Z(s)$, derived from an equilibrium point (or DC operating point) Q of the two-terminal element, or one-port ${{\varvec{\mathcal {N}}}}$.

4.1 Simple test for local activity

A two-terminal element or one-port ${\varvec{\mathcal {N}}}$ is locally active at an equilibrium point (or a point on its associated DC V–I curve) Q if at least one of the following two criteria is satisfied:

Local Activity Criterion 1 Either Z(s), or Y(s), has a pole $s = p$ located in the open right-half s-plane, i.e., $\hbox {Re} [s] > 0$.

Local Activity Criterion 2 Either Re [$Z(i\omega )]<0$, or Re [$Y(i\omega )]< 0$, for at least one frequency $\omega$.

Here, Z(s) (resp., Y(s)) denotes the small-signal impedance (resp., admittance) about Q.

Example 1

Local Activity regime of the CCM

Consider the DC V–I curve of the CCM in Fig. 7c. Observe that the slope at any point on the DC V–I curve over $-3 V< V <-1 V$ (see the enlarge inset in lower-right corner) is negative. It follows from the derivations in Sect. 2.5 that the slope at DC operating point Q is equal to the $\hbox {Re} [Y(i\omega )]$ calculated at Q.

Since the slope at any point Q over the interval $-3\,\hbox {V}< V <-1\,\hbox {V}$ in Fig. 7c is negative, $\hbox {Re} [Y(i\omega )]< 0$ at Q and $\omega = 0$. Here, $\omega = 0$ because the testing signal is a DC battery.

It follows from the Local Activity Criterion 2 that the CCM is locally active at any DC operating point over the range $-3 V<V < -1 V$.

4.2 Edge of chaos

The preceding subsection shows that there are at least two avenues for a two-terminal element, or one-port ${{\varvec{\mathcal {N}}}}$, to be locally active. Example 1 is locally active at Q because the CCM satisfies the Local Activity Criterion 2. There are other examples where a two-terminal element, or one-port, is locally active because it satisfies the Local Activity Criterion 1. In fact, there are many examples of locally active elements which satisfies both criterion 1 and criterion 2.

However, there exists a much smaller subset of locally active two-terminal elements, or one-ports, which satisfies only Criterion 2, in the sense that all poles $p_{i}$ of its impedanceZ(s) (resp., admittance Y(s)) are located in the open left-half plane; namely, $\hbox {Re}\, p_{i}< 0, i = 1, 2, \ldots , n$, assuming Z(s) (resp., Y(s)) has “n” poles.

This relatively small subclass of locally activeimpedancesZ(s) (resp., admittances Y(s)) which satisfies only Local Activity Criterion 2, but not Criterion 1, is said to be operating in the edge of chaos [21].

Since there are two independent chances for an impedance Z(s) (resp., admittance Y(s)) of a two-terminal element, or one-port, to be locally active, but only one chance for it to be on the edge of chaos, it is much harder to earn the accolade of belonging to the edge of chaos club.

The reason why elements belonging to the edge of chaos club are superior over those that are only locally active is the following fundamental hypothesis in [21, 23].

Complexity Hypothesis Complex phenomena such as power amplification, oscillation, chaos, catastrophic events, and artificial intelligence tend to emerge over parameter ranges of a device or system, operating on, or near the neighborhood of the system’s edge of chaos domain.

Example 2

Edge of chaos domain of the CCM

Let us derive the parameter domain where the CCM defined in Fig. 9a is operating on the edge of chaos.

Figure 9c shows the admittance Y(s) of the CCM has only one pole $p = -1$ for $-\infty< V < \infty$. Hence, the Local Activity Criterion 1 cannot be satisfied by the admittance Y(s, V) of the CCM over all DC battery voltage $-\infty< V <\infty$. However, observe from Fig. 10a that $\hbox {Re} [Y(i\omega , V)]< 0$ over the open interval $-3\,V< V < -1\,\hbox {V}$. It follows from the Local Activity Criterion 2 that an edge of chaos domain of the CCM exists over ${{-3 \mathbf{V }}}< \mathbf{V } < \mathbf{-1 V }$.

4.3 Hopf bifurcation

Nonlinear dynamical systems satisfying the edge of chaos criterion can exhibit bifurcation from a stable equilibrium point regime to a chaotic regime by forced excitation [24]. In a local bifurcation, called the Hopf bifurcation, an equilibrium point of the system’s differential equations loses its stability as a pair of complex conjugate eigenvalues, or equivalently poles of its associated admittance Y(s, V) or impedance Z(s, I) if the CCM is driven by a DC voltage source V or current source I, cross the imaginary axis of the complex plane at some critical parameter value $\mu _{c}$ [25]. The Hopf bifurcation theorem asserts that under a relatively general situation, a small-amplitude sinusoidal oscillation will emerge for the control parameter $\mu >\mu _{c}$, and its amplitude A increases proportional to $\sqrt{\mu -\mu _{c}}$, for $\mu$ close to $\mu _{c}$ [25, 26]. The CCMoscillator circuit exhibits Hopf bifurcation as it is endowed with critical  Hopf bifurcation points, namely two pairs of complex conjugate poles at $V =-2.25\,\hbox {V}$ and $V =-1.75\,\hbox {V}$ on the imaginary axis of the complex plane shown in Fig. 13.

The Hopf bifurcation exhibited in the CCM oscillator circuit is classified as supercritical because the typical supercritical amplitude function $A_{v}(V)=\sqrt{\bar{x}^{2}+\bar{i}_{L}^{2}}$ (where $\bar{x}$ and $\bar{i}_{L}$ denote the amplitude of the small sinusoidal x(t) and $i_{L}(t))$ at $V = 2.25\,\text {V}$ and $V = -1.75\,\hbox {V}$ shown in Fig. 15a, b as a function of V is quite similar to the curve computed from the analytical formulas⁷$A_{m1}(V)=k_{1}[\sqrt{\left| V+2.25 \right| } ]$ and $A_{m2}\left( V \right) =k_{2} [\sqrt{\left| V+1.75 \right| } ]$ with control parameter ${\mu }= V$, critical parameter values $\mu _{c1} = -2.25$ and $\mu _{c2} = -1.75$, and constants $k_{1} = 2.65$ and $k_{2} = 8.75$, respectively. For further assurance of a supercritical Hopf bifurcation, we plotted the amplitude $A_{L}(L)=\sqrt{\bar{x}^{2}+\bar{i}_{L}^{2}}$ of the CCM Oscillator circuit with the inductance L as a bifurcation parameter in Fig. 15c.

Fig. 15

Numerical verification of supercritical Hopf bifurcation of the CCM oscillator circuit as a parameter of V, near a first Hopf bifurcation point $V = -2.25\,\text {V}$, and b second Hopf bifurcation point $V = -1.75 V$. c Verification of supercritical Hopf bifurcation of the CCM oscillator with the inductance L as the bifurcation parameter

According to the supercritical Hopf bifurcation theorem [26,27,28], the CCMoscillator circuit must exhibit a small stable near-sinusoidal oscillation, i.e., a limit cycle, over a small range of V beyond the critical parameter value $\mu _{c} = V = -2.25\,\hbox {V}$. Figure 16a, d shows that the transient waveforms converge to two asymptotically stable equilibrium points $Q_{0}^{1}(0.7, -1.127)$ for the parameter value $V = -2.3\,\hbox {V}$ [which is near but to the left of the first Hopf bifurcation point $V = -2.25\,\text {V}$(see inset of Fig. 13)], and $Q_{0}^{2}(1.3, -2.873)$ for $V = -1.7\,\hbox {V}$ (which is near but to the left of the second Hopf bifurcation point $V = -1.75\,\hbox {V}$), respectively. Observe, however, that the transient waveforms generated from two different initial states $(x(0) = 0.95$, $i_{L}(0) = -2.031)$ and $(x(0) =0.8$, $i_{L} (0) = -1.43$) in Fig. 16b converge to the yellow stable limit cycle for $V = -2.23\,\hbox {V}$ (which is near but to the right of the first Hopf bifurcation point $V = -2.25\,\text {V}$). Moreover, transient waveforms generated from two different initial states $(x(0) =1.1$, $i_{L}(0) =-2.431)$ and $(x(0) = 1.2$, $i_{L} (0) = -3.53$) for $V =-1.77$ [which is near but to the right of the second Hopf bifurcation point $V = -1.75\,\hbox {V}$ (see inset of Fig. 13)] converge to a larger yellow limit cycle shown in Fig. 16c. The numerical simulation results shown in Fig. 16 confirm that the CCMoscillator circuit exhibits a stable limit cycle when the bifurcation parameter $\mu = V$ is chosen between the Hopf bifurcation points at $V = -2.25\,\hbox {V}$ and $V = -1.75\,\hbox {V}$, as predicted by the supercritical Hopf bifurcation theorem.

In addition, the supercritical Hopf bifurcation phenomenon of the composite CCM oscillator circuit in Fig. 11a is also verified by choosing the external inductance L as the bifurcation parameter $\mu = L$, (with the input voltage $V = -2.25\,\text {V})$ as shown in Fig. 17. Observe that for the parameter value $\mu = L = 350.5\,\hbox {mH} < L^{*} = 355.5\,\hbox {mH}$, the transient waveforms in Fig. 17a converge to a stable equilibrium point $Q_{0} (0.75, -1.27)$, whereas for $\mu = L^{ }=356\,\hbox {mH}$ the transient waveforms converge to a very small stable limit cycle, as shown in Fig. 17b. Figure 17c shows that the transient waveforms generated from the two different initial states $(x(0), i_{L} (0)) = (0.95, -2.031)$ and $(x(0), i_{L}(0)) = (0.75, -1.27)$ converge to the green limit cycle for the parameter value $\mu = L = 370.5\,\hbox {mH}$, where $L = 370.5\,\hbox {mH} > L^{*} =355.5 \,\hbox {mH}$. It follows from Fig. 17 that the CCM oscillator circuit exhibits a supercritical Hopf bifurcation at $\mu = L \ge \quad L^{*} = 355.5\,\hbox {mH}$ resulting in a limit cycle, whereas at $\mu = L < L^{*} = 355.5\,\hbox {mH}$ it converges to a stable equilibrium point, as predicted by supercritical Hopf bifurcation theorem.

It is very interesting to observe that the numerical simulation results in Figs. 16 and 17 show that although $Q_{1}$ is stable in the CCM Circuit 1, it has become unstable in the composite CCM Circuit 2, by merely adding a passive circuit element, namely $L > 0$. This phenomenon is a fundamental feature of the edge of chaos property; namely, it is possible to destabilize a stable circuit (i.e., without oscillation) and make it oscillate, by adding only passive circuit elements.

5 Phase portrait

A phase portrait consists of a family of trajectories corresponding to differential initial conditions of a dynamical system in the phase plane. It is an invaluable graphical tool to visualize the qualitative behavior of the solutions of a second-order autonomous system of two ordinary differential equations. The phase portrait of a dynamical system reveals information about the presence of an attractor, a repeller, or a limit cycle for the chosen parameter values [26, 29]. The stable and unstable equilibrium points in a phase portrait are called an attractor or sink, and a repeller or source, respectively. The Cartesian plane where the family of solution curves reside is called the phase plane and the curves traced by the solutions, with the time t as hidden parameter, are called trajectories [26, 29]. Since every initial state of the CCM Circuit 1 (with only one state variable x) converges to one of four stable equilibrium points ($Q_{1}\, ,Q_{3}, \,Q_{5}$, and $Q_{7})$ and diverges from three unstable equilibrium points ($Q_{2}\, ,Q_{4}$, and $Q_{6})$ at $V = 0$, one might conjecture that the phase portrait of the second-order CCM oscillator, based on the CCM Circuit 2 (with two state variables x and $i_{L})$, could also exhibit four attractors and three repellers in the phase plane. But this conjecture is false as already shown in Figs. 16 and 17.

Fig. 16

Numerical simulation results of the supercritical Hopf bifurcation theorem with $L = L^{*} = 355.5\,\hbox {mH}$. a Transient waveform converges to $Q_{\mathrm {0}}^{\mathrm {1}}\mathrm {(0.7, -1.127)}$ for $V = -2.3 V$ with initial condition $(x(0), i_{\mathrm {L}}(0)) = (0.95, -2.031)$, b transient waveforms generated from two different initial states $(x(0), i_{{L}} (0)) = (0.95, -2.031) \hbox { and } (x(0), i_{{L}} (0)) = (0.8, -1.43)$ converge to a yellow limit cycle for $V = -2.23 V$, c transient waveforms generated from two different initial states $(x(0), i_{{L}} (0)) = (1.1, -2.431)$ and $(x(0), i_{{L}} (0)) = (1.2, -3.53)$ converge to a large yellow limit cycle for $V = -1.77\,\text {V}$, and d transient waveform converges to $Q_{{0}}^{{2}}{(1.3, -2.873)}$ for $V = -1.7\,\text {V}$ with initial condition $(x(0), i_{{L}}(0)) = (0.95, -2.031)$

Fig. 17

Simulation results illustrating supercritical Hopf bifurcation at $V = -2.25\,\text {V}$. a Transient waveform from initial condition $(x(0), i_{{L}}(0))= (0.95, -2.031$) converges to the asymptotically stable equilibrium point $Q_{{0}} (0.75, -1.27)$ for $L = 350.5\,\hbox {mH}$. b Transient waveform from initial condition $(x(0), i_{{L}}(0))= (0.95, -2.031)$ converges to a stable limit cycle for $L = 356\,\hbox {mH}$. c Transient waveforms generated from two different initial states $(x(0), i_{{L}} (0)) = (0.95, -2.031)$ and $(x(0), i_{{L}} (0)) = (0.75, -1.27)$ converge to a relatively large green limit cycle for $L = 370.5\,\hbox {mH}$

The phase portrait of the CCM oscillator circuit is shown in Fig. 18 with DC battery voltage $V = -2.23\,\hbox {V}$ and inductance $L = L^{*} = 355.5\,\hbox {mH}$. In Fig. 18, the arrowheads attached to the red, blue, cyan, and green trajectories indicate the direction of motion of the composite oscillator state (x, $i_{L})$ from the initial state $(x(0), i_{L}(0)$) (marked in black dots). Figures 18 and 19a show that the red trajectories converge to a small limit cycle surrounding the unstable equilibrium point $Q_{1}(x_{Q1} = 0.77, i_{L_{Q1}} = -1.32)$. All blue, cyan, and green trajectories, in Figs. 18 and 19b–d, converge to the stable equilibrium points $Q_{3}(x_{Q3}=12.77, i_{L_{Q3}}=-363.65)$, $Q_{5}(x_{Q5}=32.77, i_{L_{Q5}}=-2394.73)$, and $Q_{7}(x_{Q7}=60.77, i_{L_{Q7}}=-8235.37)$, respectively. Observe, however, the trajectories in a small neighborhood of the three unstable equilibrium points $Q_{2}(x_{Q2}=11.23, i_{L_{Q2}}=-281.23)$$Q_{4}(x_{Q4}=27.23, i_{L_{Q4}}=-1653.48)$, and $Q_{6}(x_{Q6}=51.23, i_{L_{Q6}}=-5852.66)$ diverge from them as shown in green dashes passing through $Q_{2}$ and $Q_{3}$ in Fig. 19e and in magenta and brown curves in Fig. 18. Each of these dash curves is called a separatrix. Since each trajectory can converge either to the limit cycle surrounding the unstable equilibrium point $Q_{1}$, or to one of the three stable equilibrium points $Q_{3}$, $Q_{5}$, and $Q_{7}$, or can diverge from $Q_{2}$, $Q_{4}$, and $Q_{6}$, it follows that the phase portrait of the CCM Circuit 2 has three attractors ($Q_{3}$, $Q_{5}$, and $Q_{7})$ and four repellers ($Q_{1}, Q_{2}$, $Q_{4}$, and $Q_{6})$. Observe that although the equilibrium point $Q_{1}$ is stable in the CCM Circuit 1, it has become unstable and diverges from $Q_{1}$ while converging to a limit cycle in the composite CCM Circuit 2 when $V = -2.23\,\hbox {V}$, as shown in Figs. 16b and 19a.

Fig. 18

Phase portrait of the CCM oscillator circuit for DC battery voltage $V = -2.23\,\text {V}$ with external inductor $L = L^{*} = 355.5\,\hbox {mH}$. The separatrix emerging from the unstable equilibrium points $Q_{{4}}$ and $Q_{{6}}$ is drawn as magenta and brown dashes loci, respectively

Fig. 19

Zoom view of the phase portrait in Fig. 18. a All red trajectories converge to the stable limit cycle corresponding to the repeller$Q_{{1}}$, b all blue trajectories converge to the stable equilibrium point$Q_{{3}}$, c all cyan trajectories converge to the stable equilibrium point$Q_{{5}}$, d all green trajectories converge to the stable equilibrium point$Q_{{7}}$. e Zoom view of the basins of attraction of the tiny stable limit cycle and stable equilibrium point$Q_{{3}}$, respectively. The separatrix (passing through $Q_{{2}}$) of the basins of attraction of the small stable limit cycle surrounding the repeller $Q_{{1}}$ and the stable equilibrium point $Q_{{3}}$ is shown in green dashes

Fig. 20

The steady-state pinched hysteresis loop response (i(t), v(t)) of the CCM Circuit 3 on the $i-v$ plane under AC periodic excitation $v_{{s}}(t) = A \sin (2\pi ft)$ where $A = 1\; V$ and frequencies: a$f = 0.01\,\text {Hz}$, b$f = 0.1\,\text {Hz}$, c$f = 0.5\,\text {Hz}$, and d$f = 1\,\text {Hz}$. For each frequency f, there exist four distinct basins of attraction, labeled as $B_{{a}}(0)$, $B_{{b}}(0)$, $B_{{c}}(0)$ and $B_{{d}}(0)$, for the corresponding four periodic steady-state state variable responses$x_{{a}}(t)$, $x_{{b}}(t)$, $x_{{c}}(t)$, and $x_{\mathrm {d}}(t)$, respectively

Fig. 21

The steady-state pinched hysteresis loop response (i(t), v(t)) of the CCM Circuit 3on the $i-v$ plane under AC periodic excitation $v(t) = A \,\sin (\omega t)$ with $A = 3\, V$ and frequencies: a$f = 0.01\,\text {Hz}$, b$f = 0.1\,\text {Hz}$, c$f = 0.5\,\hbox {Hz}$, and d$f = 1\,\text {Hz}$. Four distinct basins of attraction$B_{{j}}(0)$ of the state variables x(t) and their corresponding initial states $x_{{j}}(0)$, $j \in \{a, b, c, d\}$, are listed in the inset of each figure

Observe from Fig. 19e that all the trajectories starting from initial states to the left of the $Q_{2}$ separatrix converge to a small stable limit cycle surrounding repeller $Q_{1}$, whereas trajectories starting from initial states to the right of the $Q_{2}$ separatrix converge to the stable equilibrium point $Q_{{3}}$. The region on the left side of the $Q_{2}$ separatrix is called the basin of attraction of the stable limit cycle, and the region on the right side of the $Q_{2}$ separatrix is called the basin of attraction of the stable equilibrium point $Q_{3}$. Similarly, trajectories starting from any initial state to the left of the $Q_{4}$ separatrix converge to either the basin of attraction of the stable equilibrium point $Q_{{3}}$ or to the basin of attraction of the stable limit cycle, as shown in Fig. 18. In contrast, trajectories starting from initial states to the right of the $Q_{4}$ separatrix belong to the basin of attraction of the stable equilibrium point $Q_{{5}}$ and would converge to $Q_{5}$, as shown in Fig. 18. Similar dynamics also happens for initial states starting from either sides of the $Q_{6}$ separatrix, as shown in Fig. 18.

6 Basins of attractions of coexisting pinched hysteresis loops

The steady-state dynamics of a memristor or memristive system depends on the initial condition of the state variables. Under a periodic bipolar excitation, a memristor circuit can exhibit different asymptotic behaviors for different initial states [30, 31]. For such systems, the state space contains multiple attractors where each one has its own basin of attraction. A state-space trajectory would converge to an attractor whose basin of attraction contains the initial state x(0) [26]. The steady-state behavior of the dynamic attractors of the CCM Circuit 3, driven by a sinusoidal excitation $v_{s}(t) = A \,\sin (\omega t)$, where $\omega = 2\,\pi f$, with different amplitudes A, frequencies f, and initial states x(0) is shown in Figs. 20 and 21. For simplicity, let us fix the amplitude A of the input voltage and consider four frequencies $\{f_{{1}}$, $f_{{2}}$, $f_{{3}}$, $f_{\mathrm {4}}\}=\{ 0.01, 0.1, 0.5, 1\}$ Hz. For amplitude $A = 1\,\hbox {V}$ and $A = 3\,\hbox {V}$ of the sinusoidal excitation, the corresponding four distinct stable periodic steady-state responses $x_{j}(t)$ of the CCM Circuit 3 are shown in Figs. 20 and 21, respectively. The corresponding basins of attraction $B_{j}(0)$ of the $x_{j}(t)$, $j \in \{a, b, c, d\}$, are listed in their corresponding insets.

The four periodic steady-state responses of the state variable x, dubbed $x_{a}(t)$, $x_{b}(t)$, $x_{c}(t)$ and $x_{d}(t)$, of the CCM Circuit 3 in Figs. 20 and 21 exhibit four distinct types of stable pinched hysteresis loops. As an example, the blue pinched hysteresis loop for amplitude $A =1\,\hbox {V}$, initial state $x(0)= 15.12$, and $f = 0.1\,\text {Hz}$ in Fig. 20b is spawn from the stable periodic steady-state response $x_{b}(t)$ of the state variable x, because the initial state $x(0) = 15.12$ falls within the basin of attraction $B_{b}(0) \,(8.55 <x(0) \le 24.55$), as specified in the inset in Fig. 20b. However, for any initial states $x(0) \le 8.55$, or $x(0) > 24.55$, the state variable x(t) of the CCM Circuit 3 converges to the stable periodic steady-state response $x_{a}(t)$, or $x_{c}(t)$, respectively, in Fig. 20b, because $x(0) \le 8.55$ belongs to the basin of attraction $B_{a} (0)$, whereas $x(0) > 24.55$ falls in the $\textit{basin of attraction}\, B_{c}(0)$. In contrast, any initial state $x(0) > 48.55$ belongs to the basin of attraction$B_{d}(0)$, which spawns the corresponding green pinched hysteresis loop in the $i-v$ plane shown in Fig. 20b.

Fig. 22

The pinched hysteresis loop bifurcation points defining the basins of attraction of the dynamic attractors$x_{{a}}(t)$, $x_{{b}}(t)$, $x_{{c}}(t)$ and $x_{{d}}(t)$ of the CCM Circuit 3 for an input excitation $v(t) = A \,\sin (2\pi ft)$ in the amplitude–frequency plane. The heatmaps show a the bifurcation point $x^{\prime } (0)$ specifying the basins of attraction of the dynamic attractors $x_{{a}}(t)$, b the bifurcation point $x^{\prime \prime }(0)$ specifying the basins of attraction of the dynamic attractors $x_{{b}}$(t), and c the bifurcation point $x^{\prime \prime \prime }(0)$ specifying the basins of attraction of dynamic attractors $x_{{c}}(t)$

Similarly, Fig. 21a–d shows four pinched hysteresis loops in the $i-v$ plane, spawn by four corresponding stable periodic steady-state responses $x_{j}(t)$ of the CCM Circuit 3. Their basins of attraction$B_{j}(0)$ are determined by the corresponding initial states $x_{j}(0)$, where $j \in \{a, b, c, d\}$.

All steady-state responses in Figs. 20 and 21 are pinched hysteresis loopspassing through the origin, including those drawn as single-valued curves (in Figs. 20a and 21a) when their lobe areas are too small to discern. Moreover, observe that there exist four distinct stable steady-state responses ($x_{a}(t)$, $x_{b}(t)$, $x_{c}(t)$ and $x_{d}(t))$ for sinusoidal excitation just like the existence of four distinct equilibrium points ($Q_{{1}}, Q_{{3}}$, $Q_{{5}}$ and $Q_{{7}})$ under DC excitation⁸ (in Figs. 9a and 11a)

Since any initial state $x_{j}(0)$ originating from inside the basin of attraction$B_{j}(0)$ is attracted by a corresponding periodic steady-state response $x_{j}(t)$, the stable periodic steady-state responses $x_{j}(t)$ of the CCM Circuit 3 are called dynamic attractors in this paper. For each sinusoidal excitation, the one-dimensional basin of attraction $B_{j}(0)$ of the four distinct dynamic attractors $x_{j}(t)$ is separated by three real numbers $x^{\prime } (0)$, $x^{\prime \prime }(0)$, and $x^{\prime \prime \prime }(0)$, henceforth called pinched hysteresis loopbifurcation points. Each of the three bifurcation points depends on both the amplitude A, and the frequency f of the sinusoidal excitations, namely $x^{\prime } (0) = F^\prime (A, f)$, $x^{\prime \prime }(0) = F^{\prime \prime }(A, f)$, and $x^{\prime \prime \prime }(0) = F^{\prime \prime \prime }(A, f)$. For the convenience of readers, we include the heatmap, in Fig. 22, for specifying the bifurcation points (boundary points) separating the basins of attraction of the four dynamic attractors, $x_{a}(t)$, $x_{b}(t)$, $x_{c}(t)$, and $x_{d}(t)$, of the CCM Circuit 3, for amplitudes$A \in \{-3, -2, -1, 1, 2, 3\}$ and frequencies$f \in \{ 0.01, 0.05, 0.1, 0.5, 1, 5, 10\}$ . For example, the boundary points listed in the inset of Fig. 21 for $A = 3\,\hbox {V}$ are listed in Row 1 ($\hbox {A} = 3$) of Fig. 22a for $x_{a}(t)$, Fig. 22b for $x_{b}(t)$, and Fig. 22c for $x_{c}(t)$.

Fig. 23

Loci of the inverted DC V–I curve of the CCM, described analytically by two parametric equations $V=\hat{v}(x)$ and $I=\hat{i}(x)$ (Eqs. 10a and 10b). When the op-amp-based circuit realization of the CCM is measured experimentally using an oscilloscope, the dotted portion of the computed DC V–I curve in Fig. 7c cannot be seen without additional instrumentation because it represents unstable equilibrium points of the CCM circuit 1 in Fig. 2a, where the battery voltage is slowly tuned to cover the range $-10 V< V < 10 V$

For example, Fig. 22a shows the periodic steady-state response x(t) for a sinusoidal excitation⁹ with $A = -3 \,\text {V}$ and $f = 0.1\,\text {Hz}$ converges to the dynamic attractor $x_{a}(t)$ for any initial states $x(0) \le$ ($x^{\prime } (0) = F^{\prime } (-3, 0.1)= 10.35)$ whereas for $x(0) > (x^{\prime } (0) = 10.35)$, x(t) converges to the dynamic attractor $x_{b}(t)$. In contrast, any initial state ($x^{\prime } (0) = 10.35) < x(0) \le (x^{\prime \prime }(0) = F^{\prime \prime }(-3,0.1)= 26.35)$, the steady-state response x(t) of the CCM Circuit 3 exhibits the basin of attraction $B_{b}(0)$ corresponding to the dynamic attractor $x_{b}(t)$ shown in Fig. 22b, whereas for ($x^{\prime \prime }(0) = 26.35) < x(0) \le (x^{\prime \prime \prime }(0) = F^{\prime \prime \prime }({-3}, {0.1})= 50.35), x(t)$ converges to the dynamic attractor $x_{c}(t)$ with corresponding basin of attraction $B_{c}{(0)}$ as shown in Fig. 22c. However, any initial states greater than the pinched hysteresis loop bifurcation points $x^{\prime \prime \prime }{(0)}$, i.e., ${x(0) >}$($x^{\prime \prime \prime }{(0)} = F^{\prime \prime \prime }(A, f))$, the steady-state response x(t) of the CCM Circuit 3 converges to the dynamic attractor $x_{d}(t)$ and exhibits the basin of attraction $B_{d}{(0)}$.

7 Conclusion

This paper presents an in-depth global analysis of a three-element electronic oscillator circuit made of a Chua Corsage Memristor (CCM) connected in series with an inductor and a battery. The CCM can be built via a simple operational amplifier (op amp) circuit.

The CCM is a two-terminal electric device described by $i = x^{2} v$, where v and i denote the voltage and current of the device, respectively, and x is a state variable described by $\text {d}x/\text {d}t = f(x) + v$ where $f(x) = 33-x+| x-6| - |x-12|+|x-20|-| x-30|+|x-42|+|x-56|$.

When connected in series with an inductor L with current $i_{L}$ and a battery with voltage v, the Chua Corsage Memristor Oscillator is described by an autonomous system of two nonlinear ordinary differential equations (ODE)

$$\begin{aligned} \begin{array}{l} \text {d}x/\text {d}t{=} \left[ \begin{array}{l} 33 - x + \left| {x - 6} \right| - \left| {x - 12} \right| + \left| {x - 20} \right| \\ - \left| {x - 30} \right| + \left| {x - 42} \right| - \left| {x - 56} \right| + i_{L}/x^{2} \end{array} \right] \,\,\, \\ \quad \triangleq \,\,f\left( {x,\,\,{i_L}} \right) \\ \text {d}i_{L}/\text {d}t\,\, = \,\,1/L^{*}\left( {V - \,\,i_{L}/x^{2}} \right) \triangleq g\left( {x,\,\,{i_L}} \right) . \end{array}. \end{aligned}$$

When the CCM is connected directly (without the inductor) across a battery with voltage $v = V$, the resulting CCMcircuit exhibits four stable equilibrium states $X(Q_{1})$, $X(Q_{3})$, $X(Q_{5})$, and $X(Q_{7})$ and three unstable equilibrium states $X(Q_{2})$, $X(Q_{4})$, and $X(Q_{6})$, located at the equilibrium points $Q_{1}$, $Q_{3}$, $Q_{5}$, and $Q_{7}$, and $Q_{2}$, $Q_{4}$, and $Q_{6}$, in the (x, $\dot{x})$-plane, respectively.

Our first remarkable new results in this paper is to show that the DC V–I curve induced by the seven equilibrium states form a complicated but contiguous loci which can be expressed analytically by two exact explicit formulas $V = \hat{v}(X)$ and $I = \hat{i}(X)$, for $-\infty< X <\infty$.

Our next major result is to show that the second-order autonomous ODE can be designed into an oscillator with an appropriate choice of battery voltage $V = V^{*}$, and inductance $L = L^{*}$, by invoking the local activity principle. In particular, we derive a small subset of the two parameters (V, L), dubbed the edge of chaos, via explicit analytical formulas. We analyze the edge of chaos domain and found systematically a parameter set ($V^{*}$, $L^{*})$ satisfying the supercritical Hopf bifurcation theorem, leading automatically to an electronic oscillator circuit, dubbed the CCMoscillator.

But the most exciting discovery of this paper is that when driven by $v =A \sin (2\pi ft)$, instead of the constant battery voltage $v = V$, the resulting non-autonomous ODE exhibits four distinct periodic solutions $x = \hat{x}(t)$, which induces four corresponding periodic currents $i = \hat{i} (t)$. When plotted in the current-vs.-voltage plane, the four periodic attractors induced four distinct coexisting pinched hysteresis loops, whose corresponding basins of attraction were precisely calculated.

The nonlinear dynamical theory presented in this paper can be easily generalized to design other second-order non-autonomous system of ODE with any finite number of coexisting attractors and their corresponding coexisting set of pinched hysteresis loops, which are the fingerprints of memristive systems endowed with memory, which are essential for designing learning machines.

We end this manuscript with the pinup portrait of a contiguous DC V–I Curve, redrawn in the -I vs. V plane (shown in Fig. 23) of the Chua Corsage Memristor, which resembles a multi-lobe corsage ribbon.