1 Introduction

Without doubt, the asymptotic or finite-time stabilization for high-order nonlinear systems has been extensively known as a challenging problem in the nonlinear control field, primarily due to the system inherent nonlinearities as well as the lack of controllability/observability or the non-existence of the Jacobian linearization around the origin [1, 2]. A technological breakthrough was made by Qian and Lin in [1, 3] where the celebrated strategy named adding a power integrator technique was developed to derive solutions to the stabilization issue for high-order nonlinear systems. The underlying philosophy behind the adding a power integrator technique is the mechanism of feedback domination, which not only contributes to a distinctive perspective in dealing with the deep-seated obstacles stemming from system inherent nonlinearities but also potentially provides insights, for output feedback design, into constructing a state observer without relying on the separation principle, thereby stimulating considerable elegant results dedicated to the stabilization problem of high-order nonlinear systems; see, e.g., [4,5,6,7,8,9,10,11,12,13,14,15,16,17] and the references therein.

When a more ambitious objective, namely the stabilization subjected to some pre-specified output constraints, is pursued further for safety reasons and/or performance specifications [18,19,20,21,22,23,24], in the literature relatively less progress has been made toward high-order nonlinear systems [25,26,27,28,29,30], where [28,29,30] are particularly concerned with finite-time stabilization. The major remedy proposed in [28,29,30] for coping with the finite-time stabilization problem of high-order nonlinear systems subjected to output constraints is to introduce/employ a proper barrier Lyapunov function (BLF) (for the definition, see [30, 31]) together with the decisive requirement of full-state availability. When full-state measurements are unavailable, the schemes in [28,29,30] are no longer applicable, and a new method using output feedback design surely deserves further investigation/development. Notably, tackling this issue is a nontrivial and challenging task essentially due to the deficiency of constructive/explicit designs of BLFs and state observers in handling competently the output feedback finite-time stabilization subjected to asymmetric output constraints. As a matter of fact, even for a two-dimensional case, the problem of how to synthesize an output feedback finite-time stabilizer for high-order nonlinear systems subjected to asymmetric output constraints remains unknown and largely open in the literature.

Motivated by the results reviewed above, in this paper we focus our attention on the problem of finite-time stabilization via output feedback for high-order planar systems subjected to an asymmetric output constraint described by

$$\begin{aligned} {\dot{x}}_1&=x_2^p+\phi _1(x_1,t)\nonumber \\ {\dot{x}}_2&=\theta (x,t)u+\phi _2(x,t)\nonumber \\ y&=x_1 \end{aligned}$$
(1)

where \(x=(x_1,x_2)^T\in {\mathbb {R}}^2\), \(u\in {\mathbb {R}}\) and \(y\in {\mathbb {R}}\) denote the system state, control input, and output, respectively, and \(p\in {\mathbb {R}}_{odd}^+:=\{r\in {\mathbb {R}}~|~r=r_1/r_2~\text {with}~r_1~\text {and}~r_2~\text {being}\) \(\text {positive odd integers}\}\). For \(i=1,2\), the nonlinearity \(\phi _i:{\mathbb {R}}^i\times {\mathbb {R}}^+\) and unknown parameter \(\theta :{\mathbb {R}}^2\times {\mathbb {R}}^+\rightarrow {\mathbb {R}}\) are continuous. The initial state is represented by \(x(t_0)\in {\mathbb {R}}^2\) with \(t_0\in {\mathbb {R}}^+\) being the initial time, and the asymmetric output constraint is formulated as \(-\kappa _l<y(t)<\kappa _u\) for all \(t\ge t_0\) where \(\kappa _l\) and \(\kappa _u\) are pre-specified positive real constants. Because appropriate conditions on system uncertainties and nonlinearities are essentially necessary for output feedback stabilization [4, 9, 14], we impose the assumptions below on system (1).

Assumption 1

The unknown parameter \(\theta (x,t)\) is uniformly bounded in the sense that there exist two positive smooth functions \({\underline{\theta }}:{\mathbb {R}}\rightarrow (0,\infty )\) and \({\overline{\theta }}:{\mathbb {R}}\rightarrow (0,\infty )\) such that

$$\begin{aligned} {\underline{\theta }}(x_1)\le \theta (x,t)\le {\overline{\theta }}(x_1) \end{aligned}$$

for all \((x,t)\in {\mathbb {R}}^2\times {\mathbb {R}}^+\).

Assumption 2

The nonlinearities \(\phi _1(x_1,t)\) and \(\phi _2(x,t)\) satisfy locally homogeneous growth conditions; i.e., there exist a negative real constant \(\sigma \) and two nonnegative smooth functions \({\overline{\phi }}_i:{\mathbb {R}}\rightarrow {\mathbb {R}}^+\) for \(i=1,2\) such that

$$\begin{aligned} \left| \phi _1(x_1,t)\right|&\le {\overline{\phi }}_1(x_1)|x_1|^{\frac{m_1+\sigma }{m_1}}\\ \left| \phi _2(x,t)\right|&\le {\overline{\phi }}_2(x_1)\left( |x_1|^{\frac{m_2+\sigma }{m_1}}+|x_2|^{\frac{m_2+\sigma }{m_2}}\right) \end{aligned}$$

for all \((x,t)\in {\mathbb {R}}^2\times {\mathbb {R}}^+\), where \(m_1=1\), \(m_2=(m_1+\sigma )/p>0\) and \(m_2+\sigma >0\).

Based on the above assumptions, a new fraction-type asymmetric BLF acting a delicate treatment of asymmetric constraints is first designed by exploiting and using the intrinsic characteristics of the system nonlinearities \(\phi _i(\cdot )\)’s. Next, a continuous state feedback controller working as an intermediate design is synthesized by elaborately renovating the adding a power integrator technique through an artful implantation of the developed fraction-type asymmetric BLF together with exquisite manipulations of signum functions. Furthermore, a one-dimensional non-smooth state observer furnished with a state-dependent gain is organized by carefully pondering the nonlinearities inherent in system (1). By skillfully integrating the observer with the state feedback controller and befittingly setting the observer gain, a continuous output feedback finite-time stabilizer can be explicitly constructed for system (1), thereby fulfilling the finite-time stabilization task and meanwhile preventing the violation of the constraint on the output.

As the first work successfully achieving the finite-time stabilization via output feedback for high-order planar nonlinear systems subjected to asymmetric output constraints, this paper offers the following appealing novelties/innovations. First, the proposed fraction-type asymmetric BLF is significantly distinguished from the common tangent-type [19, 20, 22, 23] and logarithm-type [21, 28, 29, 31] BLFs in the aspect that the construction of the fraction-type asymmetric BLF in this paper fully takes into account and elegantly subsumes the intrinsic characteristics of the system nonlinearities \(\phi _i(\cdot )\)’s, thus offering the feasibility/utility of the designed fraction-type BLF to system (1) and some remarkable features (also, see Remark 4). Second, the presented scheme is a unification methodology by which one is able to achieve simultaneously the finite-time stabilization by output feedback for system (1) subjected to or free from asymmetric output constraints, without needing to change the controller and observer structures. That is to say, when the output constraint is purposely assigned to be infinity (i.e., considering the scenario of no constraint), the proposed strategy will directly evolve into the one applicable to dealing with the pure task of output feedback stabilization for system (1) without output constraints (also, refer to Remark 5).

Notation: The notations utilized in this paper are listed below. \({\mathbb {R}}\) denotes the set of real numbers, \({\mathbb {R}}^n\) represents the n-dimensional Euclidean space, \({\mathbb {R}}^+\) is the set of nonnegative real numbers, and \({\mathbb {R}}_{odd}^+=\{r\in {\mathbb {R}}~|~r=r_1/r_2~\text {with}~r_1~\text {and}~r_2~\text {being positive odd integers}\}\). Suppose that \(c_1\) is a nonnegative real constant, \(c_i\) for \(i=2,3\) are two positive real constants, and \({\mathbb {U}}\subset {\mathbb {R}}^n\) is an open connected set (i.e., a domain); we let \(\lceil z\rceil ^{c_1}=|z|^{c_1}sign(z)\) for all \(z\in {\mathbb {R}}\) with \(\lceil z\rceil ^{0}=1\) if \(z=0\), where \(sign(\cdot )\) being the standard signum function, \({\mathbb {M}}_i(c_2,c_3)=\{(z_1,\ldots ,z_i)^T\) \(\in {\mathbb {R}}^i~|~-c_2< z_1< c_3\}\subset {\mathbb {R}}^i\) for \(i=1,\ldots ,n\), and \(\partial {\mathbb {U}}\) be the boundary of \({\mathbb {U}}\).

2 Preliminaries and technical lemmas

Because the finite-time convergence can be secured only by non-Lipschitz continuous systems [13, 32], we first recall the definition and relevant lemma of a BLF in regard to a continuous time-varying nonlinear system.

Definition 1

([25]) Consider a time-varying nonlinear system described by

$$\begin{aligned} {\dot{\eta }}=f(\eta ,t),~~~\eta (t_0)\in {\mathbb {R}}^n,~~~t_0\in {\mathbb {R}}^+ \end{aligned}$$
(2)

where \(\eta =(\eta _1,\ldots ,\eta _n)^T\in {\mathbb {R}}^n\) and \(f:{\mathbb {R}}^n\times {\mathbb {R}}^+\rightarrow {\mathbb {R}}\) is continuous. Suppose that \({\mathbb {U}}\subset {\mathbb {R}}^n\) satisfying \(0\in {\mathbb {U}}\) is open connected (i.e., \({\mathbb {U}}\subset {\mathbb {R}}^n\) is a domain), and \(W:{\mathbb {U}}\rightarrow {\mathbb {R}}\) is positive definite and continuously differentiable. If \(W(\eta )\) satisfies the two conditions:

  1. (i)

    \(W(\eta )\rightarrow \infty \) as \(\eta \rightarrow \partial {\mathbb {U}}\)

  2. (ii)

    \(W(\eta (t))\le l\) for all \(t\ge t_0\) with \(l\in {\mathbb {R}}^+\) and for every complete solutionFootnote 1\(\eta (t)\) of system (2) starting from the initial state \(\eta (t_0)\in {\mathbb {U}}\)

then \(W(\eta )\) is called a BLF of system (2).

Remark 1

Definition 1 is an extension of the one in [21, 31]. In fact, the definition of a BLF presented in [21, 31] is with respect to time-invariant (autonomous) systems. In accordance with similar notions, Definition 1 is established here so as to provide a comprehensive/self-contained definition of a BLF when considering a general time-varying (non-autonomous) nonlinear system (2) which is continuous and not necessary to satisfy the Lipschitz condition.

Remark 2

Suppose that in the design process later there exists a continuously differentiable and positive definite function \(W:{\mathbb {D}}\subset {\mathbb {R}}^i\rightarrow {\mathbb {R}}\) with \(i<n\) and \({\mathbb {D}}\) being an open connected set, which exactly fulfills (i) of Definition 1 but depends only on partial states of system (1). Then, according to Definition 1, such a function \(W(\cdot )\) will be referred to, with an abuse of terminology, as a BLF of system (1).

Lemma 1

([25]) Consider system (2) and two positive real constants \(\kappa _l\) and \(\kappa _u\). If there exist two continuously differentiable functions \(W_1:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}\) and \(W_2:{\mathbb {M}}_n(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}\), where \(W_1(\eta _1)\) is positive definite and \(W_2(\eta )\) is nonnegative, such that

  1. (i)

    \(W_1(\eta _1)\rightarrow \infty \) as \(\eta _1\rightarrow \partial {\mathbb {M}}_1(\kappa _l,\kappa _u)\)

  2. (ii)

    When setting \(W(\eta )=W_1(\eta _1)+W_2(\eta )\), there hold \(W(\eta )\rightarrow \infty \) as \(\Vert (\eta _2,\ldots ,\eta _n)\Vert \rightarrow \infty \) with any fixed \(\eta _1\in {\mathbb {M}}_1(\kappa _l,\kappa _u)\), and

    $$\begin{aligned} \frac{\partial W(\eta )}{\partial \eta }f(\eta ,t)\le 0 \end{aligned}$$

    for all \((\eta ,t)\in {\mathbb {M}}_n(\kappa _l,\kappa _u) \times {\mathbb {R}}^+\)

then every solutionFootnote 2\(\eta (t)\) of system (2) starting from \(\eta (t_0)\in {\mathbb {M}}_n(\kappa _l,\kappa _u)\) is defined on \([t_0,\infty )\) and fulfills \(\eta (t)\in {\mathbb {M}}_n(\kappa _l,\kappa _u)\) for all \(t\ge t_0\).

We next introduce five lemmas, which play a crucial role in deriving the main results. The proof of the first three lemmas can be found in [2, 5, 17], whereas the last two lemmas are new and proved correspondingly.

Lemma 2

([2]) Let \(c_1\ge 0\) and \(c_i>0\) for \(i=2,3,4\) be real constants. For any \(z_1,z_2\in {\mathbb {R}}\), there holds

$$\begin{aligned}&c_1|z_1|^{c_3}|z_2|^{c_4}\\&\quad \le c_2|z_1|^{c_3+c_4}+\frac{c_4}{(c_3+c_4)}\left( \frac{c_3}{c_3+c_4}\right) ^{\frac{c_3}{c_4}}\\&\qquad \times c_2^{-\frac{c_3}{c_4}} c_1^{\frac{(c_3+c_4)}{c_4}}|z_2|^{c_3+c_4}. \end{aligned}$$

Lemma 3

([5, 17]) Let \(c>0\) be a real constant. For any \(z_i\in {\mathbb {R}}\) with \(i=1,\ldots ,n\), there holds

$$\begin{aligned} \left( |z_1|+\cdots +|z_n|\right) ^{c}\le \alpha \left( |z_1|^{c}+\cdots +|z_n|^{c}\right) \end{aligned}$$

where \(\alpha =n^{c-1}\) if \(c\ge 1\) and \(\alpha =1\) if \(c<1\).

Lemma 4

([17]) Let \(c_1\ge 1\) and \(c_2>0\) be real constants. For any \(z_1,z_2\in {\mathbb {R}}\), there holds

$$\begin{aligned} \left| \lceil z_1\rceil ^{\frac{c_2}{c_1}}-\lceil z_2\rceil ^{\frac{c_2}{c_1}}\right| \le 2^{1-\frac{1}{c_1}}\left| \lceil z_1\rceil ^{c_2}-\lceil z_2\rceil ^{c_2}\right| ^{\frac{1}{c_1}}. \end{aligned}$$

Lemma 5

Let \(c_1\in (0,1)\) and \(c_2\in [0,1]\). For any \(z\in {\mathbb {R}}\), there holds

$$\begin{aligned} \lceil z\rceil ^{c_1}+\lceil 1-z\rceil ^{c_1}+c_2^2|z|^{1+c_1}\ge (2^{c_1}-1)c_2^{1-c_1}. \end{aligned}$$

Proof

Let \(\varrho _i:{\mathbb {R}}\rightarrow {\mathbb {R}}\) for \(i=1,2,3\) be three functions respectively defined as

$$\begin{aligned} \varrho _1(z)&=\lceil z\rceil ^{c_1}+\lceil 1-z\rceil ^{c_1}+c_2^2|z|^{1+c_1}\\ \varrho _2(z)&=\varrho _1(z) -c_2^2|z|^{1+c_1}\\ \varrho _3(z)&=\left( \varrho _2(z) -\lceil z\rceil ^{c_1}\right) |z|^{1-c_1}+z. \end{aligned}$$

Because \(\varrho _2(z)\) is differentiable on \((-1,0)\cup (0,1)\) with

$$\begin{aligned} \frac{d\varrho _2(z)}{dz}=c_1|z|^{c_1-1}-c_1|1-z|^{c_1-1} \end{aligned}$$

for all \(z\in (-1,0)\cup (0,1)\), using the mean value theorem and the relation \(\varrho _1(z)\ge \varrho _2(z)\) for all \(z\in {\mathbb {R}}\), one has

$$\begin{aligned} \varrho _1(z)\ge \min \left\{ \varrho _2(-1),\varrho _2(1)\right\} \ge \left( 2^{c_1}-1\right) c_2^{1-c_1} \end{aligned}$$
(3)

for all \(z\in [-1,1]\). Next, it follows from Lemma 2 that

$$\begin{aligned} \varrho _1(z)\ge \varrho _3^{\frac{1+c_1}{2}}(z)c_2^{1-c_1} \end{aligned}$$
(4)

for all \(z\in (-\infty ,-1)\cup (1,\infty )\). Based on the fact that \(z^{c_1}-1<(z-1)c_1\) for all \(z\in (0,1)\cup (1,\infty )\) [34], one can easily show that

$$\begin{aligned} \frac{d\varrho _3(z)}{dz}=1+\left( 1-\frac{1}{z}\right) ^{c_1-1}\left( \frac{1}{z}-1-\frac{c_1}{z}\right) <0 \end{aligned}$$

for all \(z\in (-\infty ,-1)\cup (1,\infty )\). This together with (4) leads to

$$\begin{aligned} \varrho _1(z)&\ge \left( \min \left\{ \varrho _3(-1),\lim _{z\rightarrow \infty }\varrho _3(z)\right\} \right) ^{\frac{1+c_1}{2}}c_2^{1-c_1}\nonumber \\&\ge \left( 2^{c_1}-1\right) c_2^{1-c_1} \end{aligned}$$
(5)

for all \(z\in (-\infty ,-1)\cup (1,\infty )\). Combining (3) and (5) completes the proof. \(\square \)

Lemma 6

Let \(c_1\in (0,1)\), \(c_2\in (0,\infty )\) and \(t_0\in [0,\infty )\). If \(\varphi :[t_0,\infty )\rightarrow [0,\infty )\) is a continuous function satisfying \(\varphi (t_0)>0\) such that

$$\begin{aligned} \varphi (t) - \varphi (t_0)\le -c_2\int _{t_0}^t\varphi ^{c_1}(s)~\mathrm{{d}}s \end{aligned}$$
(6)

for all \(t\in [t_0,\infty )\), then there holds

$$\begin{aligned} \varphi (t)\le \left[ \varphi ^{1-c_1}(t_0)-c_2(1-c_1) (t-t_0)\right] ^{\frac{1}{1-c_1}} \end{aligned}$$

for all \(t\in [t_0,T)\) with

$$\begin{aligned} T=t_0+\frac{\varphi ^{1-c_1}(t_0)}{c_2(1-c_1)}. \end{aligned}$$

Proof

Define the set

$$\begin{aligned}&{\mathbb {H}}=\left\{ t~|~t\in (t_0,T]~\text {such that}~\varpi (t)<\varphi (t)\right\} \\&\quad \subseteq (t_0,T] \end{aligned}$$

and let \(\varpi :[t_0,T]\rightarrow {\mathbb {R}}\) be of the form

$$\begin{aligned} \varpi (t)=\left( \varphi ^{1-c_1}(t_0)-c_2(1-c_1) (t-t_0)\right) ^{\frac{1}{1-c_1}} \end{aligned}$$

which is clearly continuous. Because \(\varpi (t_0)=\varphi (t_0)>0\), \(\varpi (T)=0\) and \(\varpi (t)>0\) for all \(t\in [t_0,T)\), it suffices to prove that \({\mathbb {H}}\) is empty. To this end, assume that there exists \(t_1\in {\mathbb {H}}\) (i.e., \(\varpi (t_1)<\varphi (t_1)\)) and consider the set

$$\begin{aligned} {\mathbb {K}}=&\left\{ t~|~t\in (t_0,t_1)~\text {such that}~\varpi (s)<\varphi (s)\right. \\&\left. ~\text {for all}~s\in (t,t_1]\right\} \subseteq (t_0,t_1). \end{aligned}$$

Letting \(t_2=\inf ({\mathbb {K}})\), one has \(\varpi (t_2)=\varphi (t_2)\) and \(0< \varpi (t)<\varphi (t)\) for all \(t\in (t_2,t_1]\) due to the continuity of \(\varphi (\cdot )\) and \(\varpi (\cdot )\); this implies that

$$\begin{aligned} 0< \varpi (t)\le \varphi (t) \end{aligned}$$
(7)

for all \(t\in [t_2,t_1]\). Now, since

$$\begin{aligned} \varpi (t)-\varpi (t_0)=-c_2\int _{t_0}^t\varpi ^{c_1}(s)~\mathrm{{d}}s \end{aligned}$$

for all \(t\in [t_0,T]\), it is easy to derive from (6) that

$$\begin{aligned} \int _{t_0}^t\varphi ^{c_1}(s)~\mathrm{{d}}s<\int _{t_0}^t\varpi ^{c_1}(s)~\mathrm{{d}}s<0 \end{aligned}$$

for all \(t\in [t_2+\varepsilon ,t_1]\) with \(\varepsilon >0\); this also implies that there exists \(t_3\in [t_2+\varepsilon ,t_1]\subset [t_2,t_1]\) such that \(\varphi (t_3)<\varpi (t_3)\) and therefore leads to a contradiction to (7). The proof is completed. \(\square \)

Remark 3

It is worth pointing out that if \(c_2\in (-\infty ,0)\), Lemma 6 is exactly a special case of the so-called Bihari’s inequality [35]. Due to the generalization of the condition (6) with including a positive real constant \(c_2\in (0,\infty )\), Lemma 6 can be technically viewed as an extension or counterpart of the Bihari’s inequality. Notably, from Lemma 6 we have \(\varphi (T)=0\); if, in addition, \(\varphi (t)\) is non-increasing, one further has \(\varphi (t)=0\) for all \(t\in [T,\infty )\). Such an important consequence will be utilized in proving finite-time convergence in consideration of an asymmetric output constraint.

3 Main results

This section is dedicated to designing a continuous output feedback finite-time controller that stabilizes system (1) while guaranteeing the fulfillment of the asymmetric output constraint \(-\kappa _l<y(t)<\kappa _u\) for all \(t\ge t_0\) where \(\kappa _l\) and \(\kappa _u\) are pre-specified positive real constants. Specifically, the design begins with organizing a fraction-type asymmetric BLF by exploiting and using the intrinsic characteristics of the nonlinearities \(\phi _i(\cdot )\)’s. The synthesis of a continuous state feedback controller is then performed by elegantly renovating the adding a power integrator technique through an artful implantation of the designed BLF together with subtle manipulations of signum functions. Further, by elaborately pondering the nonlinearities inherent in system (1), the construction of a one-dimensional non-smooth state observer furnished with a state-dependent gain is presented so as to achieve output feedback design. Derived by a delicate integration of the non-smooth observer and the state feedback controller, along with a suitable choice of the observer gain, a continuous output feedback stabilizer is finally proposed for system (1) which is able to effectively ensure the fulfillment of the asymmetric output constraint.

3.1 Design of a new fraction-type asymmetric BLF

Considering the asymmetric output constraint \(-\kappa _l<y(t)<\kappa _u\) for all \(t\ge t_0\) with two pre-specified positive real constants \(\kappa _l\) and \(\kappa _u\), and taking the intrinsic characteristics of the system nonlinearities \(\phi _i(\cdot )\)’s depicted by Assumption 2, we pick

$$\begin{aligned} \omega \ge \mu \ge \max \{m_1,m_2\} \end{aligned}$$
(8)

with \(\mu \) being an auxiliary factor, and design a fraction-type function \(V_{F}:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}\) as follows

$$\begin{aligned} V_F(x_1)=\frac{\kappa _u^{2\omega -\sigma }\kappa _l^{2\omega -\sigma }|x_1|^{2\omega -\sigma }}{\left( 2\omega -\sigma \right) (\kappa _u-x_1)^{2\omega -\sigma }(\kappa _l+x_1)^{2\omega -\sigma }} \end{aligned}$$
(9)

which is obviously positive definite on \({\mathbb {M}}_1(\kappa _l,\kappa _u)\) and fulfills \(V_F(x_1)\rightarrow \infty \) as \(x_1\rightarrow \partial {\mathbb {M}}_1(\kappa _l,\kappa _u)\). By a direct calculation, it is easy to verify that

$$\begin{aligned} \frac{\partial V_F(x_1)}{\partial x_1}=\lambda (x_1)\lceil x_1\rceil ^{2\omega -\sigma -1} \end{aligned}$$
(10)

for all \(x_1\in {\mathbb {M}}_1(\kappa _l,\kappa _u)\), where \(\lceil x_1\rceil ^{2\omega -\sigma -1}\) is continuous on \({\mathbb {M}}_1(\kappa _l,\kappa _u)\) and \(\lambda :{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow (0,\infty )\) is of the form

$$\begin{aligned} \lambda (x_1) = \frac{\kappa _u^{2\omega -\sigma }\kappa _l^{2\omega -\sigma }\left( x_1^2+\kappa _u\kappa _l\right) }{(\kappa _u-x_1)^{2\omega -\sigma +1}(\kappa _l+x_1)^{2\omega -\sigma +1}} \end{aligned}$$
(11)

which is smooth on \({\mathbb {M}}_1(\kappa _l,\kappa _u)\); thus, \(V_F(x_1)\) is continuously differentiable on \({\mathbb {M}}_1(\kappa _l,\kappa _u)\) and forms a fraction-type asymmetric BLF of system (1) according to Definition 1 (also Remark 2). We call \(V_F(x_1)\) an asymmetric BLF due to the asymmetry of \(V_F(x_1)\) arising from the difference between \(\kappa _l\) and \(\kappa _u\). As we shall show later, \(V_F(x_1)\) acts as a key constituent/brick in renovating the adding a power integrator technique for coping with the output constraints.

Remark 4

Two distinctive traits of the designed fraction-type asymmetric BLF \(V_F(x_1)\) are emphasized as follows.

  1. (i)

    The design of the presented \(V_F(x_1)\) is directly related to the system nonlinearities \(\phi _i(\cdot )\)’s, thereby providing the applicability to system (1), when considering asymmetric output constraints. Specifically, with the help of Assumption 2, the intrinsic characteristics of system nonlinearities \(\phi _i(\cdot )\)’s is subtly extracted and equivalently kept in the parameters \(m_1\), \(m_2\), p and \(\sigma \). By fully taking into account \(m_1\), \(m_2\), p and \(\sigma \) (i.e., the feature of the nonlinearities \(\phi _i(\cdot )\)’s) in constructing of \(V_F(x_1)\), the resultant \(V_F(x_1)\) has the specific fraction structure, which drastically differs from the common logarithm-type [21, 28, 29, 31] and tangent-type [19, 20, 22, 23] BLFs, and offers for system (1) a delicate treatment of asymmetric constraints.

  2. (ii)

    The designed \(V_F(x_1)\) is a powerful tool making our scheme capable of simultaneously dealing with constrained and unconstrained cases. More precisely, considering \(\kappa _l=\kappa _u=\kappa \) with \(\kappa \rightarrow \infty \) (i.e., the circumstance of no constraint requirement on the output), one has

    $$\begin{aligned} \lim _{\kappa \rightarrow \infty }V_F(x_1)&=\lim _{\kappa \rightarrow \infty }\frac{\kappa ^{4\omega -2\sigma }|x_1|^{2\omega -\sigma }}{\left( 2\omega -\sigma \right) (\kappa ^2-x_1^2)^{2\omega -\sigma }}\\&=\frac{1}{\left( 2\omega -\sigma \right) }|x_1|^{2\omega -\sigma } \end{aligned}$$

    which is exactly the regular function used in [2, 6, 7, 17] for tackling the pure state or output feedback stabilization of high-order nonlinear systems without output constraints. In other words, the designed \(V_F(x_1)\) enjoys the appealing property that when there is no constraint on the output, that is, \(\kappa _l=\kappa _u=\kappa \rightarrow \infty \), it will molt into the one widely adopted for pure stabilization without constraint requirements; hence, \(V_F(x_1)\) can be thought of as a technical lever assisting us in unifying and achieving simultaneously the design of continuous output feedback finite-time stabilizers for system (1) subjected to or free from output constraints, without needing to change the resultant controller and observer structures.

3.2 Design of a continuous output feedback finite-time stabilizer

On the basis of the designed \( V_F(x_1)\), we are now ready to present the design of a continuous output feedback finite-time stabilizer for system (1), which also ensures the achievement of the asymmetric output constraint specified in advance.

Theorem 1

Suppose that Assumptions 1 and 2 hold. Then, there exists a continuous output feedback finite-time stabilizer of the following form

$$\begin{aligned} {\dot{\nu }}&=-G(x_1)\left( \left\lceil \nu +L(x_1)\right\rceil ^{\frac{m_1+\sigma }{\mu }} +\phi _1(x_1,t) \right) \nonumber \\ u(x)&=u(x_1,{\hat{x}}_2)~~\text {with}~~{\hat{x}}_2=\left\lceil \nu +L(x_1)\right\rceil ^{\frac{m_2}{\mu }} \end{aligned}$$
(12)

where \(L:{\mathbb {R}}\rightarrow {\mathbb {R}}\) is a continuously differentiable observer gain satisfying \(L(0)=0\) and \(\partial L(x_1)/\partial x_1=G(x_1)\ge 1\) for all \(x_1\in {\mathbb {M}}_1(\kappa _l,\kappa _u)\) under which every trajectory \((x(t),\nu (t))\) of system (1) starting from \((x(t_0),\nu (t_0))\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\) is defined on \([t_0,\infty )\), converges to the origin in finite time, and fulfills the constraint \(-\kappa _l<y(t)=x_1(t)<\kappa _u\) for all \(t\ge t_0\) where \(\kappa _l\) and \(\kappa _u\) are pre-specified positive real constants.

Proof

The proof as well as the design methodology is divided into four parts as follows.

Part I—Design of a state feedback controller

For a start, define \(\xi _1(x_1)=\lceil x_1 \rceil ^{\mu }\) and \(V_1:{\mathbb {M}}_1(\kappa _l,\kappa _u)\) \(\rightarrow {\mathbb {R}}\) to be in the form of \(V_1(x_1)=V_F(x_1)\) where \(\mu \) and \(V_F(x_1)\) are described by (8) and (9), respectively. Obviously, \(V_1(x_1)\) is positive definite and continuously differentiable on \({\mathbb {M}}_1(\kappa _l,\kappa _u)\), and by (10) and Assumption 2 one has

$$\begin{aligned} {\dot{V}}_1(x_1)&:=\frac{\partial V_1(x_1)}{\partial x_1}{\dot{x}}_1\nonumber \\&\le \lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{2\omega -\sigma -1}{\mu }}x_2^{*p}(x_1)\nonumber \\&\quad +\lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{2\omega -\sigma -1}{\mu }} \left( x_2^p-x_2^{*p}(x_1)\right) \nonumber \\&\quad +\lambda (x_1){\overline{\phi }}_1(x_1)|\xi _1(x_1)|^{\frac{2\omega }{\mu }} \end{aligned}$$
(13)

for allFootnote 3\((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\), where \(x_2^{*}:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}\) is a continuous virtual controller and \(\lambda (x_1)>0\) for all \(x_1\in {\mathbb {M}}_1(\kappa _l,\kappa _u)\) is given by (11). By selecting the virtual controller

$$\begin{aligned} x_2^{*}(x_1)=-\beta _1(x_1)\lceil \xi _1(x_1)\rceil ^{\frac{m_2}{\mu }} \end{aligned}$$
(14)

with \(\beta _1:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow (0,\infty )\) being a smooth function of the form

$$\begin{aligned} \beta _1(x_1)=\left( \frac{2+\lambda (x_1){\overline{\phi }}_1(x_1)}{\lambda (x_1)}\right) ^{\frac{1}{p}} \end{aligned}$$

it follows from (13) that

$$\begin{aligned} {\dot{V}}_1(x_1)&\le -\lambda (x_1)\left( \beta _1^p(x_1) + {\overline{\phi }}_1(x_1)\right) |\xi _1(x_1)|^{\frac{2\omega }{\mu }}\nonumber \\&\quad +\lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{2\omega -\sigma -1}{\mu }} \left( x_2^p-x_2^{*p}(x_1)\right) \nonumber \\&= -2|\xi _1(x_1)|^{\frac{2\omega }{\mu }}+\lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{2\omega -\sigma -1}{\mu }} \nonumber \\&\quad \times \left( x_2^p-x_2^{*p}(x_1)\right) \end{aligned}$$
(15)

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\).

To continue with the design, let \(\xi _2(x)=\lceil x_2\rceil ^{\mu /m_2}-\lceil x_2^*(x_1)\rceil ^{\mu /m_2}\) and \(V_2:{\mathbb {M}}_2(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}\) be defined as \(V_2(x)=V_1(x_1)+W(x)\) where \(x_2^*(x_1)\) is given by (14) and \(W:{\mathbb {M}}_2(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}\) has the following form

$$\begin{aligned} W(x)=\int _{x_2^*(x_1)}^{x_2}\left\lceil \lceil s\rceil ^{\frac{\mu }{m_2}}-\left\lceil x_2^*(x_1)\right\rceil ^{\frac{\mu }{m_2}} \right\rceil ^{\frac{2\omega -\sigma -m_2}{\mu }}\mathrm{{d}}s. \end{aligned}$$

Using an almost same argument stated in [7, 17], one can deduce that \(V_2(x)\) is positive definite and continuously differentiable on \({\mathbb {M}}_2(\kappa _l,\kappa _u)\), and W(x) satisfies

$$\begin{aligned}&\frac{\partial W(x)}{\partial x_1}\\&\quad =- \left( \frac{2\omega -\sigma -m_2}{\mu }\right) \frac{\partial \left\lceil x_2^*(x_1)\right\rceil ^{\frac{\mu }{m_2}}}{\partial x_1}\\&\qquad \times \int _{x_2^*(x_1)}^{x_2}\left| \lceil s\rceil ^{\frac{\mu }{m_2}}-\left\lceil x_2^*(x_1)\right\rceil ^{\frac{\mu }{m_2}} \right| ^{\frac{2\omega -\sigma -m_2-\mu }{\mu }}\mathrm{{d}}s\\&\frac{\partial W(x)}{\partial x_2}\\&\quad =\left\lceil \lceil x_2\rceil ^{\frac{\mu }{m_2}}-\left\lceil x_2^*(x_1)\right\rceil ^{\frac{\mu }{m_2}} \right\rceil ^{\frac{2\omega -\sigma -m_2}{\mu }}\\&\quad =\left\lceil \xi _2(x) \right\rceil ^{\frac{2\omega -\sigma -m_2}{\mu }} \end{aligned}$$

for all \(x\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\), where \({\partial W(x)}/{\partial x_1}\) has the property below

$$\begin{aligned} \left| \frac{\partial W(x)}{\partial x_1}\right|&\le \left( \frac{2\omega -\sigma -m_2}{\mu }\right) \left| \frac{\partial \left\lceil x_2^*(x_1)\right\rceil ^{\frac{\mu }{m_2}}}{\partial x_1}\right| \\&\quad \times 2^{\frac{\mu -m_2}{\mu }}\left| \xi _2(x) \right| ^{\frac{2\omega -\sigma -\mu }{\mu }}\\&\le \psi _1(x_1) \left| \xi _1(x_1) \right| ^{\frac{\mu -m_1}{\mu }}\left| \xi _2(x) \right| ^{\frac{2\omega -\sigma -\mu }{\mu }} \end{aligned}$$

for all \(x\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\) with \(\psi _1:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}^+\) being a smooth functionFootnote 4. By these relations, the inequality (15) and Assumption 2, the time derivative of \(V_2(x_1)\) along system (1) is

$$\begin{aligned}&{\dot{V}}_2(x)\nonumber \\&\quad :=\frac{\partial V_1(x_1)}{\partial x_1}{\dot{x}}_1 +\frac{\partial W(x)}{\partial x_1}{\dot{x}}_1+\frac{\partial W(x)}{\partial x_2}{\dot{x}}_2\nonumber \\&\quad \le -2|\xi _1(x_1)|^{\frac{2\omega }{\mu }}+\theta (x,t)\lceil \xi _2(x)\rceil ^{\frac{2\omega -\sigma -m_2}{\mu }}u \nonumber \\&\qquad +\lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{2\omega -\sigma -1}{\mu }}\left( x_2^p-x_2^{*p}(x_1)\right) \nonumber \\&\qquad +| \xi _2(x)|^{\frac{2\omega -\sigma -m_2}{\mu }} {\overline{\phi }}_2(x_1)\left( |x_1|^{\frac{m_2+\sigma }{m_1}} + |x_2|^{\frac{m_2+\sigma }{m2}}\right) \nonumber \\&\qquad +\psi _1(x_1) \left| \xi _1(x_1) \right| ^{\frac{\mu -m_1}{\mu }}\left| \xi _2(x) \right| ^{\frac{2\omega -\sigma -\mu }{\mu }}\nonumber \\&\qquad \times \left( |x_2|^p+ {\overline{\phi }}_1(x_1)|x_1|^{\frac{m_1+\sigma }{m_1}} \right) \end{aligned}$$
(16)

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\). Before moving on to designing the controller u, we estimate the last three terms on the right-hand side of (16).

First, owing to the inequality

$$\begin{aligned}&\left( x_2^p-x_2^{*p}(x_1)\right) \\&\quad \le \left| \left\lceil \lceil x_2\rceil ^{\frac{\mu }{m_2}}\right\rceil ^{\frac{m_1+\sigma }{\mu }}-\left\lceil \lceil x_2^*(x_1)\rceil ^{\frac{\mu }{m_2}}\right\rceil ^{\frac{m_1+\sigma }{\mu }}\right| \end{aligned}$$

for all \(x\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\) and \((m_1+\sigma )/\mu <1\), it follows from Lemmas 2 and 4 that

$$\begin{aligned}&\lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{2\omega -\sigma -1}{\mu }}\left( x_2^p-x_2^{*p}(x_1)\right) \nonumber \\&\quad \le \lambda (x_1)| \xi _1(x_1)|^{\frac{2\omega -\sigma -1}{\mu }}2^{1-\frac{m_1+\sigma }{\mu }}|\xi _2(x)|^{\frac{m_1+\sigma }{\mu }}\nonumber \\&\quad \le \frac{1}{3}|\xi _1(x_1)|^{\frac{2\omega }{\mu }}+\psi _2(x_1)|\xi _2(x)|^{\frac{2\omega }{\mu }} \end{aligned}$$
(17)

for all \(x\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\) where \(\psi _2:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}^+\) is a smooth function.

Second, using the fact \(m_2/\mu \le 1\) and Lemma 4, one has the inequality

$$\begin{aligned} |x_2|\le 2^{1-\frac{m_2}{\mu }}|\xi _2(x)|^{\frac{m_2}{\mu }}+\beta _1(x_1)|\xi _1(x_1)|^{\frac{m_2}{\mu }} \end{aligned}$$
(18)

for all \(x\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\). With this in mind, one can verify by using Lemmas 2 and 3 that there exists a smooth function \({\hat{\psi }}_2:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}^+\) such that

$$\begin{aligned}&|\xi _2(x)|^{\frac{2\omega -\sigma -m_2}{\mu }} {\overline{\phi }}_2(x_1)\left( |x_1|^{\frac{m_2+\sigma }{m_1}}+|x_2|^{\frac{m_2+\sigma }{m_2}}\right) \nonumber \\&\quad \le {\overline{\phi }}_2(x_1)\left| \xi _1(x_1) \right| ^{\frac{m_2+\sigma }{\mu }}|\xi _2(x)|^{\frac{2\omega -\sigma -m_2}{\mu }}\nonumber \\&\qquad +2^{\frac{(\mu -m_2)(m_2+\sigma )}{\mu m_2}}\left( 2^{\frac{m_2+\sigma }{m_2}-1}+1\right) {\overline{\phi }}_2(x_1)|\xi _2(x)|^{\frac{2\omega }{\mu }}\nonumber \\&\qquad +\left( 2^{\frac{m_2+\sigma }{m_2}-1}+1\right) {\overline{\phi }}_2(x_1)\beta _1^{\frac{m_2+\sigma }{m_2}}(x_1)\nonumber \\&\qquad \times \left| \xi _1(x_1) \right| ^{\frac{m_2+\sigma }{\mu }}|\xi _2(x)|^{\frac{2\omega -\sigma -m_2}{\mu }}\nonumber \\&\quad \le \frac{1}{3}|\xi _1(x_1)|^{\frac{2\omega }{\mu }}+{\hat{\psi }}_2(x_1)|\xi _2(x)|^{\frac{2\omega }{\mu }} \end{aligned}$$
(19)

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\).

Similarly to deriving (19), using Lemma 2–4 one can obtain the following

$$\begin{aligned}&\psi _1(x_1) \left| \xi _1(x_1) \right| ^{\frac{\mu -m_1}{\mu }}\left| \xi _2(x) \right| ^{\frac{2\omega -\sigma -\mu }{\mu }}\nonumber \\&\qquad \times \left( |x_2|^p+ {\overline{\phi }}_1(x_1)|x_1|^{\frac{m_1+\sigma }{m_1}} \right) \nonumber \\&\quad \le \left( 2^{p-1}+1\right) 2^{p-\frac{m_2p}{\mu }}\psi _1(x_1) \left| \xi _1(x_1) \right| ^{\frac{\mu -m_1}{\mu }}\nonumber \\&\qquad \left| \xi _2(x) \right| ^{\frac{2\omega +1-\mu }{\mu }}\nonumber \\&\qquad +\left( 2^{p-1}+1\right) \beta _1^p(x_1)\psi _1(x_1) \left| \xi _1(x_1) \right| ^{\frac{\mu +\sigma }{\mu }}\nonumber \\&\qquad \left| \xi _2(x) \right| ^{\frac{2\omega -\sigma -\mu }{\mu }}\nonumber \\&\qquad +\psi _1(x_1) {\overline{\phi }}_1(x_1)\left| \xi _1(x_1) \right| ^{\frac{\mu +\sigma }{\mu }}\nonumber \\&\qquad \left| \xi _2(x) \right| ^{\frac{2\omega -\sigma -\mu }{\mu }}\nonumber \\&\quad \le \frac{1}{3}|\xi _1(x_1)|^{\frac{2\omega }{\mu }}+{\tilde{\psi }}_2(x_1)|\xi _2(x)|^{\frac{2\omega }{\mu }} \end{aligned}$$
(20)

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\) where \({\tilde{\psi }}_2:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}^+\) is a smooth function.

Applying these estimations (17), (19) and (20) to (16) gives

$$\begin{aligned} {\dot{V}}_2(x)&\le -|\xi _1(x_1)|^{\frac{2\omega }{\mu }}+\theta (x,t)\lceil \xi _2(x)\rceil ^{\frac{2\omega -\sigma -m_2}{\mu }}u\nonumber \\&\quad +\left( \psi _2(x_1)+{\hat{\psi }}_2(x_1)+{\tilde{\psi }}_2(x_1)\right) |\xi _2(x)|^{\frac{2\omega }{\mu }} \end{aligned}$$
(21)

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\). Clearly, designing the continuous state feedback controller

$$\begin{aligned} u(x)=-\beta _2(x_1)\lceil \xi _2(x)\rceil ^{\frac{m_2+\sigma }{\mu }} \end{aligned}$$
(22)

with \(\beta _2:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow (0,\infty )\) being a smooth function taking the form

$$\begin{aligned} \beta _2(x_1)=\frac{1+\psi _2(x_1)+{\hat{\psi }}_2(x_1)+{\tilde{\psi }}_2(x_1)}{{\underline{\theta }}(x_1)} \end{aligned}$$

and using Assumption 1, one readily obtains

$$\begin{aligned} {\dot{V}}_2(x)&\le -|\xi _1(x_1)|^{\frac{2\omega }{\mu }}-\theta (x,t)\beta _2(x_1)| \xi _2(x)|^{\frac{2\omega }{\mu }}\nonumber \\&\quad {+}\left( \psi _2(x_1){+}{\hat{\psi }}_2(x_1)+{\tilde{\psi }}_2(x_1)\right) |\xi _2(x)|^{\frac{2\omega }{\mu }}\nonumber \\&=-|\xi _1(x_1)|^{\frac{2\omega }{\mu }}-| \xi _2(x)|^{\frac{2\omega }{\mu }} \end{aligned}$$
(23)

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\). Note that, with the help of Lemma 4 it is not difficult to see that

$$\begin{aligned}&V_2(x) \nonumber \\&\quad { =} V_1(x_1){+}\int _{x_2^*(x_1)}^{x_2}\left\lceil \lceil s\rceil ^{\frac{\mu }{m_2}}{-}\left\lceil x_2^*(x_1)\right\rceil ^{\frac{\mu }{m_2}} \right\rceil ^{\frac{2\omega -\sigma -m_2}{\mu }}\quad \mathrm{{d}}s\nonumber \\&\quad \ge V_1(x_1) +\varepsilon _1\left| x_2-x_2^*(x_1)\right| ^{\frac{2\omega -\sigma }{m_2}} \end{aligned}$$
(24)

for all \(x\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\) with \(\varepsilon _1\) being a positive real constant; this implies that, with any fixed \(x_1\in {\mathbb {M}}_1(\kappa _l,\kappa _u)\), \(V_2(x)\rightarrow \infty \) as \(|x_2|\rightarrow \infty \). Hence, if \(x=(x_1,x_2)^T\in {\mathbb {R}}^2\) are completely available, by Lemma 1 one knows that when \(x(t_0)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\), the continuous state feedback controller (22) successfully achieves the requirement of the asymmetric output constraint \(-\kappa _l<y(t)<\kappa _u\) for all \(t\ge t_0\). Because of the infeasibility/limitation on the full state measurement, a state observer is quite imperative for feedback design, as depicted in the next part.

Part II—Design of a one-dimensional observer

In order to efficiently perform the output feedback design, a one-dimensional non-smooth state observer is constructed as follows

$$\begin{aligned} {\dot{\nu }}&=-G(x_1)\left( \left\lceil \nu +L(x_1)\right\rceil ^{\frac{m_1+\sigma }{\mu }} +\phi _1(x_1,t) \right) \end{aligned}$$
(25)

where \(L:{\mathbb {R}}\rightarrow {\mathbb {R}}\) is a continuously differentiable observer gain function with \(L(0)=0\) and \(\partial L(x_1)/\partial x_1=G(x_1)\ge 1\) for all \(x_1\in {\mathbb {M}}_1(\kappa _l,\kappa _u)\); this gain function will be appropriately assigned later. Having the state variable \(\nu \), the observer (25) is devoted to estimating the unmeasurable state \(x_2\) by providing \({\hat{x}}_2=\left\lceil \nu +L(x_1)\right\rceil ^{m_2/\mu }\). Consider the estimation error \(e=\left\lceil x_2\right\rceil ^{\mu /m_2} - \left\lceil {\hat{x}}_2\right\rceil ^{\mu /m_2}\). It follows from (25) that

$$\begin{aligned} {\dot{e}}(x,\nu )&=\frac{\mu }{m_2}|x_2|^{\frac{\mu }{m_2}-1}\left( \theta (x,t)u+\phi _2(x,t)\right) \\&\quad -G(x_1)\left( x_2^p - \left\lceil \left\lceil x_2\right\rceil ^{\frac{\mu }{m_2}} - e\right\rceil ^{\frac{m_1+\sigma }{\mu }}\right) \end{aligned}$$

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\). Choosing \(V_3:{\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) as

$$\begin{aligned} V_3(x,\nu )=\left( \frac{\mu }{2\omega -\sigma -m_1+\mu }\right) |e(x,\nu )|^{\frac{2\omega -\sigma -m_1+\mu }{\mu }} \end{aligned}$$

which is nonnegative and continuously differentiable on \({\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\), we have

$$\begin{aligned}&{\dot{V}}_3(x,\nu )\\&\quad =\frac{\mu }{m_2}\lceil e(x,\nu )\rceil ^{\frac{2\omega -\sigma -m_1}{\mu }}\\&\qquad |x_2|^{\frac{\mu }{m_2}-1}\left( \theta (x,t)u+\phi _2(x,t)\right) \\&\qquad -\lceil e(x,\nu )\rceil ^{\frac{2\omega -\sigma -m_1}{\mu }}G(x_1)\\&\qquad \times \left( x_2^p - \left\lceil \left\lceil x_2\right\rceil ^{\frac{\mu }{m_2}} - e(x,\nu )\right\rceil ^{\frac{m_1+\sigma }{\mu }}\right) \end{aligned}$$

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\). Because \((m_1+\sigma )/\mu <1\) and \(G(x_1)\ge 1\), by Lemma 5 one can derive

$$\begin{aligned}&\lceil e(x,\nu )\rceil ^{\frac{2\omega -\sigma -m_1}{\mu }}\left( x_2^p - \left\lceil \left\lceil x_2\right\rceil ^{\frac{\mu }{m_2}} - e(x,\nu )\right\rceil ^{\frac{m_1+\sigma }{\mu }}\right) \nonumber \\&\quad \ge -G^{-\frac{3}{2}}(x_1)|e(x,\nu )|^{\frac{2\omega -\sigma -m_1-\mu }{\mu }}|x_2|^{\frac{m_1+\sigma +\mu }{m_2}}\nonumber \\&\qquad +\psi _3G^{-\frac{3}{4}}(x_1)|e(x,\nu )|^{\frac{2\omega }{\mu }} \end{aligned}$$
(26)

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\), in which \(\psi _3=2^{(m_1+\sigma )/\mu }-1>0\). Using (26), we further have

$$\begin{aligned}&{\dot{V}}_3(x,\nu )\nonumber \\&\quad \le G^{-\frac{1}{2}}(x_1)|e(x,\nu )|^{\frac{2\omega -\sigma -m_1-\mu }{\mu }}|x_2|^{\frac{m_1+\sigma +\mu }{m_2}}\nonumber \\&\qquad -\psi _3G^{\frac{1}{4}}(x_1)|e(x,\nu )|^{\frac{2\omega }{\mu }}+\frac{\mu }{m_2}\lceil e(x,\nu )\rceil ^{\frac{2\omega -\sigma -m_1}{\mu }}\nonumber \\&\qquad \times |x_2|^{\frac{\mu }{m_2}-1}\left( \theta (x,t)u+\phi _2(x,t)\right) \end{aligned}$$
(27)

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\). Remarkably, applying Lemma (3) to (18) yields

$$\begin{aligned} |x_2|^{\frac{\tau }{m_2}}&\le \varepsilon _2\left( 2^{\frac{(\mu -m_2)\tau }{\mu m_2}}|\xi _2(x)|^{\frac{\tau }{\mu }}+\beta _1^{\frac{\tau }{m_2}}(x_1)|\xi _1(x_1)|^{\frac{\tau }{\mu }}\right) \end{aligned}$$

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\) and \(\tau \in \{\mu +\sigma ,m_1+\mu +\sigma \}\) with \(\varepsilon _2=2^{\tau /m_2-1}+1\). Keeping this in mind and using Lemma 2 along with Assumptions 1 and 2 , one obtains

$$\begin{aligned}&\frac{\mu }{m_2}\lceil e(x,\nu )\rceil ^{\frac{2\omega -\sigma -m_1}{\mu }}|x_2|^{\frac{\mu }{m_ 2}-1}\left( \theta (x,t)u+\phi _2(x,t)\right) \nonumber \\&\quad \le \frac{\mu }{m_2}\left( {\overline{d}}(x_1)+2{\overline{\phi }}_2(x_1)\right) |e(x,\nu )|^{\frac{2\omega -\sigma -m_1}{\mu }}\nonumber \\&\qquad \times \left( |u|^{\frac{\mu +\sigma }{m_2+\sigma }}+|\xi _1(x_1)|^{\frac{\mu +\sigma }{\mu }}+|x_2|^{\frac{\mu +\sigma }{m_2}} \right) \nonumber \\&\quad \le \psi _4(x_1)|e(x,\nu )|^{\frac{2\omega }{\mu }} \nonumber \\&\qquad +{\hat{\psi }}_4(x_1)|e(x,\nu )|^{\frac{2\omega -\sigma -\mu }{\mu }}|u|^{\frac{\mu +\sigma }{m_2+\sigma }}\nonumber \\&\qquad +\frac{1}{2}|\xi _1(x_1)|^{\frac{2\omega }{\mu }}+\frac{1}{6}|\xi _2(x)|^{\frac{2\omega }{\mu }} \end{aligned}$$
(28)

and

$$\begin{aligned}&|e(x,\nu )|^{\frac{2\omega -\sigma -m_1-\mu }{\mu }}|x_2|^{\frac{m_1+\sigma +\mu }{m_2}}\nonumber \\&\quad \le |e(x,\nu )|^{\frac{2\omega }{\mu }}+\psi _5(x_1)|\xi _1(x_1)|^{\frac{2\omega }{\mu }} +{\hat{\psi }}_5|\xi _2(x)|^{\frac{2\omega }{\mu }} \end{aligned}$$
(29)

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\), where \(\psi _4,{\hat{\psi }}_4,\psi _5:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}^+\) are smooth functions and \({\hat{\psi }}_5\) is a positive real constant. Using (28) and (29), we obtain from (27) that

$$\begin{aligned} {\dot{V}}_3(x,\nu )\le&-\psi _3G^{\frac{1}{4}}(x_1)|e(x,\nu )|^{\frac{2\omega }{\mu }}\nonumber \\&+\left( \frac{1}{2}+G^{-\frac{1}{2}}(x_1)\psi _5(x_1)\right) |\xi _1(x_1)|^{\frac{2\omega }{\mu }} \nonumber \\&+\left( \frac{1}{6}+G^{-\frac{1}{2}}(x_1){\hat{\psi }}_5\right) |\xi _2(x)|^{\frac{2\omega }{\mu }}\nonumber \\&+\left( \psi _4(x_1) + G^{-\frac{1}{2}}(x_1)\right) |e(x,\nu )|^{\frac{2\omega }{\mu }}\nonumber \\&+{\hat{\psi }}_4(x_1)|e(x,\nu )|^{\frac{2\omega -\sigma -\mu }{\mu }}|u|^{\frac{\mu +\sigma }{m_2+\sigma }} \end{aligned}$$
(30)

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\).

\({{{\textit{Part III---Selection of the observer gain }} L(x_1)}}\)

In the spirit of the certainty equivalence principle, we replace the unmeasurable state \(x_2\) by the estimation \({\hat{x}}_2=\left\lceil \nu +L(x_1)\right\rceil ^{m_2/\mu }\) generated by the observer (25) so that the implementable continuous output feedback controller can be obtained as below

$$\begin{aligned} u(x_1,{\hat{x}}_2)&=-\beta _2(x_1)\lceil \xi _2(x_1,{\hat{x}}_2)\rceil ^{\frac{m_2+\sigma }{\mu }}\nonumber \\&=-\beta _2(x_1)\left\lceil \lceil {\hat{x}}_2\rceil ^{\frac{\mu }{m_2}}-\lceil x_2^*(x_1)\rceil ^{\frac{\mu }{m_2}}\right\rceil ^{\frac{m_2+\sigma }{\mu }}. \end{aligned}$$
(31)

With this controller, it can be verified by using Lemmas 2 and 3 that the last term on the right-hand side of (30) satisfies

$$\begin{aligned}&{\hat{\psi }}_4(x_1)|e(x,\nu )|^{\frac{2\omega -\sigma -\mu }{\mu }}|u(x_1,{\hat{x}}_2)|^{\frac{\mu +\sigma }{m_2+\sigma }}\\&\quad \le {\hat{\psi }}_4(x_1)|e(x,\nu )|^{\frac{2\omega -\sigma -\mu }{\mu }} \beta _2^{\frac{\mu +\sigma }{m_2+\sigma }}(x_1)\\&\qquad \times \left( 2^{\frac{\mu +\sigma }{\mu }-1}+1 \right) \left( |\xi _2(x)|^{\frac{\mu +\sigma }{\mu }}+|e(x,\nu )|^{\frac{\mu +\sigma }{\mu }}\right) \\&\quad \le \frac{1}{6}|\xi _2(x)|^{\frac{2\omega }{\mu }} +\psi _{6}(x_1)|e(x,\nu )|^{\frac{2\omega }{\mu }} \end{aligned}$$

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\), in which \(\psi _6:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}^+\) is a smooth function. Thus, (30) becomes

$$\begin{aligned}&{\dot{V}}_3(x,\nu )\le \left( \frac{1}{2}+G^{-\frac{1}{2}}(x_1)\psi _5(x_1)\right) |\xi _1(x_1)|^{\frac{2\omega }{\mu }} \nonumber \\&\quad +\left( \frac{1}{3}+G^{-\frac{1}{2}}(x_1){\hat{\psi }}_5\right) |\xi _2(x)|^{\frac{2\omega }{\mu }}\nonumber \\&\quad +\left( \psi _4(x_1) +\psi _{6}(x_1)+ G^{-\frac{1}{2}}(x_1)\right) |e(x,\nu )|^{\frac{2\omega }{\mu }}\nonumber \\&\quad -\psi _3G^{\frac{1}{4}}(x_1)|e(x,\nu )|^{\frac{2\omega }{\mu }} \end{aligned}$$
(32)

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\). Additionally, applying the controller (31) to (21), instead of u(x) defined by (22), and utilizing a similar analysis in deriving (17), we obtain

$$\begin{aligned}&{\dot{V}}_2(x)\nonumber \\&\quad \le -|\xi _1(x_1)|^{\frac{2\omega }{\mu }} - |\xi _2(x)|^{\frac{2\omega }{\mu }}+{\overline{\theta }}(x_1)\beta _2(x_1)|\xi _2|^{\frac{2\omega -\sigma -m_2}{\mu }}\nonumber \\&\qquad \times \left| \lceil \xi _2(x)\rceil ^{\frac{m_2+\sigma }{\mu }}-\left\lceil \xi _2(x)-e(x,\nu )\right\rceil ^{\frac{m_2+\sigma }{\mu }}\right| \nonumber \\&\quad \le -|\xi _1(x_1)|^{\frac{2\omega }{\mu }} - \frac{5}{6}|\xi _2(x)|^{\frac{2\omega }{\mu }}+\psi _7(x_1)|e(x,\nu )|^{\frac{2\omega }{\mu }} \end{aligned}$$
(33)

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\), where \(\psi _7:{\mathbb {M}}_1(\kappa _l,\kappa _u)\rightarrow {\mathbb {R}}^+\) is a smooth function. At present, we choose \(V:{\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) as \(V(x,\nu )=V_2(x)+V_3(x,\mu )\) which is surely continuously differentiable and positive definite on \({\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\). From (32) and (33), it is clear that

$$\begin{aligned} {\dot{V}}(x,\nu )\le&-\left( \frac{1}{2}-G^{-\frac{1}{2}}(x_1)\psi _5(x_1)\right) |\xi _1(x_1)|^{\frac{2\omega }{\mu }} \nonumber \\&-\left( \frac{1}{2}-G^{-\frac{1}{2}}(x_1){\hat{\psi }}_5\right) |\xi _2(x)|^{\frac{2\omega }{\mu }}\nonumber \\&-\left( \psi _3G^{\frac{1}{4}}(x_1)-\psi _4(x_1) -\psi _{6}(x_1)\right. \nonumber \\&\left. -\psi _7(x_1)-1 \right) |e(x,\nu )|^{\frac{2\omega }{\mu }} \end{aligned}$$
(34)

for all \((x,\nu ,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}\times {\mathbb {R}}^+\). Observing (34) and letting \({\mathcal {X}}=(x,\nu )\in {\mathbb {R}}^3\), one can directly verify that the selection of the observer gain \(L(x_1)\) with \(G(x_1)=\partial L(x_1)/\partial x_1\) complying with

$$\begin{aligned} G^{\frac{1}{2}}(x_1)&\ge \max \left\{ 1,4\psi _5(x_1),4{\hat{\psi }}_5\right\} \\ \psi _3G^{\frac{1}{4}}(x_1)&\ge \psi _4(x_1) +\psi _{6}(x_1) +\psi _7(x_1)+\frac{5}{4} \end{aligned}$$

results in

$$\begin{aligned} {\dot{V}}({\mathcal {X}})&\le -\frac{1}{4}\left( |\xi _1(x_1)|^{\frac{2\omega }{\mu }} + |\xi _2(x)|^{\frac{2\omega }{\mu }} + |e({\mathcal {X}})|^{\frac{2\omega }{\mu }} \right) \nonumber \\&=:-U({\mathcal {X}}) \end{aligned}$$
(35)

for all \(({\mathcal {X}},t)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\), in which \(U({\mathcal {X}}):=1/4(|\xi _1(x_1)|^{2\omega /\mu }+|\xi _2(x)|^{2\omega /\mu }+|e({\mathcal {X}})|^{2\omega /\mu }\). Remarkably, \(U({\mathcal {X}})\) is positive definite and continuous on \({\mathbb {M}}_3(\kappa _l,\kappa _u)\). In addition, from (24), we also have

$$\begin{aligned}&V({\mathcal {X}})= V_1(x_1){+}\int _{x_2^*(x_1)}^{x_2}\left\lceil \lceil s\rceil ^{\frac{\mu }{m_2}}{-}\left\lceil x_2^*(x_1)\right\rceil ^{\frac{\mu }{m_2}} \right\rceil ^{\frac{2\omega -\sigma -m_2}{\mu }}\quad \mathrm{{d}}s\nonumber \\&\qquad +\left( \frac{\mu }{2\omega -\sigma -m_1+\mu }\right) |e({\mathcal {X}})|^{\frac{2\omega -\sigma -m_1+\mu }{\mu }}\nonumber \\&\quad \ge V_1(x_1) +\varepsilon _1\left| x_2-x_2^*(x_1)\right| ^{\frac{2\omega -\sigma }{m_2}}\nonumber \\&\qquad +\left( \frac{\mu }{2\omega -\sigma -m_1+\mu }\right) \nonumber \\&\qquad \times \left| \left\lceil x_2\right\rceil ^{\frac{\mu }{m_2}}-\nu -L(x_1)\right| ^{\frac{2\omega -\sigma -m_1+\mu }{\mu }} \end{aligned}$$
(36)

for all \({\mathcal {X}}\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\); this directly gives, with any fixed \(x_1\in {\mathbb {M}}_1(\kappa _l,\kappa _u)\), \(V({\mathcal {X}})\rightarrow \infty \) as \(\Vert (x_2,\nu )\Vert \rightarrow \infty \). Hence, according to (35) and Lemma 1, one knows that when \({\mathcal {X}}(t_0)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\), every solution \({\mathcal {X}}(t)=(x(t),\nu (t))\) of system (1) under the controller (31) is defined on \([t_0,\infty )\) and fulfills \(-\kappa _l<y(t)=x_1(t)<\kappa _u\) for all \(t\ge t_0\).

Part IV—Analysis of the finite-time convergence

In what follows, we shall prove the finite-time convergence of system (1) under the controller (31). For this purpose, we consider the circumstance with \({\mathcal {X}}(t_0)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\). From (35) and (36), it follows readily that \(V({\mathcal {X}}(t))\) is non-increasing on \([t_0,\infty )\) and one also has

$$\begin{aligned}&0\le V_1(x_1(t)) +\varepsilon _1\left| x_2(t)-x_2^*(x_1(t))\right| ^{\frac{2\omega -\sigma }{m_2}}\\&\qquad +\left( \frac{\mu }{2\omega -\sigma -m_1+\mu }\right) \\&\qquad \times \left| \left\lceil x_2(t)\right\rceil ^{\frac{\mu }{m_2}}-\nu (t)-L(x_1(t))\right| ^{\frac{2\omega -\sigma -m_1+\mu }{\mu }}\\&\quad \le V({\mathcal {X}}(t_0))<\infty \end{aligned}$$

for all \(t\in [t_0,\infty )\), and thus \({\mathcal {X}}(t)\) is uniformly bounded on \([t_0,\infty )\). With these in mind, a tedious but straightforward analysis verifies directly that \(|\xi _1(x_1(t))|^{2\omega /\mu }\), \(|\xi _2(x(t))|^{2\omega /\mu }\) and \(|e({\mathcal {X}}(t))|^{2\omega /\mu }\) are uniformly continuous on \([t_0,\infty )\), and the fact \(\lim _{t\rightarrow \infty }V({\mathcal {X}}(t))=\varepsilon _2\le V({\mathcal {X}}(t_0))\) for some real constant \(\varepsilon _2\ge 0\); this leads to

$$\begin{aligned}&\lim _{t\rightarrow \infty }\int _{t_0}^t |\xi _1(x_1(s))|^{\frac{2\omega }{\mu }}~\mathrm{{d}}s<\infty \\&\lim _{t\rightarrow \infty }\int _{t_0}^t |\xi _2(x(s))|^{\frac{2\omega }{\mu }}~\mathrm{{d}}s<\infty \\&\lim _{t\rightarrow \infty }\int _{t_0}^t |e({\mathcal {X}}(s))|^{\frac{2\omega }{\mu }}~\mathrm{{d}}s<\infty . \end{aligned}$$

Consequently, using Barbalat’s lemma, one can conclude that when \({\mathcal {X}}(t_0)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\), \(|\xi _1(x_1(t))|\rightarrow 0\), \(|\xi _2(x(t))|\) \(\rightarrow 0\) and \(|e({\mathcal {X}}(t))|\rightarrow 0\) as \(t\rightarrow \infty \); thus, by the fact \(L(0)=0\) and the definitions of \(\xi _1(x_1(t))\), \(\xi _2(x(t))\) and \(e({\mathcal {X}}(t))\), it follows immediately that \({\mathcal {X}}(t)\rightarrow 0\) as \(t\rightarrow 0\). Now, in view of the continuity and positiveness of \(V({\mathcal {X}})\), there exists an open connected set \({\mathbb {S}}=\{{\mathcal {X}}\in {\mathbb {M}}_3(\kappa _l,\kappa _u)~|~V({\mathcal {X}})\le \varepsilon _3\}\subseteq {\mathbb {M}}_3(\kappa _l,\kappa _u)\) for some real constant \(\varepsilon _3>0\) such that \(-\kappa _l/2<x_1<\kappa _u/2\) and \(-1<e({\mathcal {X}})<1\) for all \({\mathcal {X}}\in {\mathbb {S}}\), which as well as Lemma 3 gives

$$\begin{aligned}&{\dot{V}}({\mathcal {X}}) + 2^{4\omega -3}V^{\frac{2\omega }{2\omega -\sigma }}({\mathcal {X}})\nonumber \\&\quad \le -\frac{1}{8}\left( |\xi _1(x_1)|^{\frac{2\omega }{\mu }} + |\xi _2(x)|^{\frac{2\omega }{\mu }} + |e({\mathcal {X}})|^{\frac{2\omega }{\mu }} \right) \le 0 \end{aligned}$$
(37)

for all \(({\mathcal {X}},t)\in {\mathbb {S}}\times {\mathbb {R}}^+\). In light of the construction of \({\mathbb {S}}\), there exists \(T^*\in [t_0,\infty )\) such that \({\mathcal {X}}(t)\in {\mathbb {S}}\) for all \(t\ge T^*\) whenever \({\mathcal {X}}(t_0)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\); hence, from (37) we have

$$\begin{aligned} {\dot{V}}({\mathcal {X}}(t))\le -2^{4\omega -3}V^{\frac{2\omega }{2\omega -\sigma }}({\mathcal {X}}(t)) \end{aligned}$$
(38)

for all \(t\ge T^*\). If \(V({\mathcal {X}} (T^*))=0\), observing (38) and noting the positiveness of \(V({\mathcal {X}})\), one obtains \({\mathcal {X}}(t)=0\) for all \(t\ge T^*\). In the case when \(V({\mathcal {X}} (T^*))\ne 0\), it can deduced from (38) that

$$\begin{aligned}&V({\mathcal {X}}(t)) - V({\mathcal {X}}(T^*))\\&\quad \le \int _{T^*}^t -2^{4\omega -3}V^{\frac{2\omega }{2\omega -\sigma }}({\mathcal {X}}(s))~\mathrm{{d}}s \end{aligned}$$

for all \(t\ge T^*\), which by Lemma 6 also results in \({\mathcal {X}}(t)=0\) for all \(t\ge T^{**}\) for some \(T^{**}\in (T^*,\infty )\). Combining these two case, one can conclude that when \({\mathcal {X}}(t_0)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\), every trajectory \({\mathcal {X}}(t)=(x(t),\nu (t))\) of system (1) under the controller (31) converges to the origin in finite time. \(\square \)

Remark 5

The proof of Theorem 1 explicitly presents a constructive approach to synthesizing a continuous output feedback finite-time stabilizer for system (1) and fulfilling the requirement of the asymmetric output constraint specified in advance. The philosophy and idea behind the development of this approach is to skillfully renovate the adding a power integrator technique based upon the interactive collaboration of the presented fraction-type asymmetric BLF (9) and the reduced-order non-smooth observer (25). An attractive trait of the proposed approach is the capability/feasibility of simultaneously coping with, in a unification fashion, the problem of output feedback finite-time stabilization for system (1) subjected to or free from output constraints. More precisely, when the output constraint is deliberately assigned to be infinity, i.e., \(\kappa _l=\kappa _u=\kappa \) with \(\kappa \rightarrow \infty \) (considering the scenario of no constraint), it follows immediately from Remark 5 that \(V({\mathcal {X}})=V_2(x)+V_3({\mathcal {X}})\) naturally molts into \(V_\infty ({\mathcal {X}})\) having the following structure

$$\begin{aligned} V_\infty ({\mathcal {X}})&=\frac{1}{\left( 2\omega -\sigma \right) }|x_1|^{2\omega -\sigma }\\&\quad +\int _{x_2^*(x_1)}^{x_2}\left\lceil \lceil s\rceil ^{\frac{\mu }{m_2}}-\left\lceil x_2^*(x_1)\right\rceil ^{\frac{\mu }{m_2}} \right\rceil ^{\frac{2\omega -\sigma -m_2}{\mu }}\mathrm{{d}}s\\&\quad +\left( \frac{\mu }{2\omega -\sigma -m_1+\mu }\right) |e({\mathcal {X}})|^{\frac{2\omega -\sigma -m_1+\mu }{\mu }} \end{aligned}$$

which is defined on \({\mathbb {R}}^3\) and is obviously continuously differentiable and positive definite on \({\mathbb {R}}^3\). Moreover, by using the schemes almost similar to those mentioned in [7, 17], it can be further verified that \(V_\infty ({\mathcal {X}})\) is proper; that is, the preimage of any compact set in \({\mathbb {R}}^+\) under \(V_\infty ({\mathcal {X}})\) is compact. When there is no constraint requirement, adopting \(V_\infty ({\mathcal {X}})\) in the convergence analysis one can immediately show by following the same procedure described in the proof of Theorem 1 that the output feedback controller (12) remains usable and straightly acts a global finite-time stabilizer for system (1), without needing of changing the controller and observer structures. Hence, when the asymmetric output constraint is intentionally assigned to be infinity so as to take into account the scenario of no constraint imposed on the output, the presented method will directly become a pure stabilization scheme under which the synthesized output feedback controller as well as the corresponding state observer secures the same structures as (12) and behaves effectively as a global finite-time stabilizer for system (1). This discloses explicitly that the presented approach is a unification methodology by which one is capable of performing simultaneously the design of a continuous output feedback finite-time stabilizer for system (1) subjected to or free from output constraints.

4 An illustrative example

In order to demonstrate the superiority and effectiveness of the proposed scheme, now we consider a planar system as below

$$\begin{aligned} {\dot{x}}_1&=x_2^3+\sin (2t)\cos (6x_1)\ln (1+x_1^2)\nonumber \\ {\dot{x}}_2&=\theta (x,t)u+\cos (5x_2+t)\sin (x_1) \end{aligned}$$
(39)

where \(\theta (x,t)=1+0.3\cos (2x_1x_2+0.5t)\). System (39) is structurally identical to system (1) with \(p=3\), \(\phi _1(x_1,t)\) \(=\sin (2t)\cos (6x_1)\ln (1+x_1^2)\) and \(\phi _2(x,t)=\cos (5x_2+t)\sin (x_1)\). It is clear that Assumption 1 is fulfilled with \({\underline{\theta }}(x_1)=0.7\) and \({\overline{\theta }}(x_1)=1.3\). Simply choosing \(m_1=1\) and \(\sigma =-1/5\), one has \(m_2=4/15\) and \(\omega =\mu =1\). By using the mean value theorem, it is easy to verify that

$$\begin{aligned}&\sin (2t)\cos (6x_1)\ln (1+x_1^2)\le 1.5|x_1|^{\frac{4}{5}}\\&\cos (5x_2+t)\sin (x_1)\le |x_1|^{\frac{1}{15}} \end{aligned}$$

for all \((x,t)\in {\mathbb {R}}^2\times {\mathbb {R}}^+\); hence, Assumption 2 is satisfied with \({\overline{\phi }}_1(x_1) =1.5\) and \({\overline{\phi }}_2(x_1)=1\). Following the procedure given by the proof of Theorem  1 we now consider

$$\begin{aligned} V_1(x_1)=\frac{5\kappa _u^{\frac{11}{5}}\kappa _l^{\frac{11}{5}}|x_1|^{\frac{11}{5}}}{11(\kappa _u-x_1)^{\frac{11}{5}}(\kappa _l+x_1)^{\frac{11}{5}}} \end{aligned}$$

and select \(x_2^*(x_1)=-\beta _1(x_1)\lceil \xi _1(x_1)\rceil ^{4/15}\) with \(\beta _1(x_1)=\left( 1.5 +2\lambda ^{-1}(x_1)\right) ^{1/3}\). A simple calculation leads to

$$\begin{aligned} {\dot{V}}_1(x_1) \le -2\xi _1^2(x_1)+\lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{6}{5}}\left( x_2^3-x_2^{*3}(x_1)\right) \end{aligned}$$

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\), where the function \(\lambda (x_1)\) takes the form below

$$\begin{aligned} \lambda (x_1) = \frac{\kappa _u^{\frac{11}{5}}\kappa _l^{\frac{11}{5}}\left( x_1^2+\kappa _u\kappa _l\right) }{(\kappa _u-x_1)^{\frac{16}{5}}(\kappa _l+x_1)^{\frac{16}{5}}}. \end{aligned}$$

To proceed with the controller synthesis, we next take

$$\begin{aligned}&V_2(x) = V_1(x_1)\\&\quad +\int _{x_2^*(x_1)}^{x_2}\left\lceil \lceil s\rceil ^{\frac{15}{4}}-\left\lceil x_2^*(x_1)\right\rceil ^{\frac{15}{4}} \right\rceil ^{\frac{29}{15}}\mathrm{{d}}s \end{aligned}$$

for which the time derivative along system (39) is

$$\begin{aligned}&{\dot{V}}_2(x)\le -2\xi _1^2(x_1)+\theta (x,t)\lceil \xi _2(x)\rceil ^{\frac{29}{15}}u\\&\quad +\lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{6}{5}}\left( x_2^3-x_2^{*3}(x_1)\right) \\&\quad +|\xi _1(x_1)|^{\frac{1}{15}}| \xi _2(x)|^{\frac{29}{15}}-1.94\varUpsilon (x_1){\dot{x}}_1\\&\quad \times \int _{x_2^*(x_1)}^{x_2}\left| \lceil s\rceil ^{\frac{15}{4}}-\left\lceil x_2^*(x_1)\right\rceil ^{\frac{15}{4}} \right| ^{\frac{14}{15}}\mathrm{{d}}s \end{aligned}$$

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\), where \(\varUpsilon (x_1) =- (1.5+2\lambda ^{-1}(x_1))^{1/4}(1.5\lambda ^2(x_1)+2\lambda (x_1)-2.5x_1(\partial \lambda (x_1) /\partial x_1))\) \(\lambda ^{-2}(x_1)\). Similarly to deducing (17), (19) and (20), we employ Lemmas 2–4 to deduce the following two estimations

$$\begin{aligned}&\lambda (x_1)\lceil \xi _1(x_1)\rceil ^{\frac{6}{5}}\left( x_2^3-x_2^{*3}(x_1)\right) +|\xi _1(x_1)|^{\frac{1}{15}}| \xi _2(x)|^{\frac{29}{15}}\\&\quad \le \frac{2}{3}\xi _1^2(x_1)+\left( \psi _2(x_1)+ {\hat{\psi }}_2(x_1)\right) \xi _2^2(x)\\&\qquad -1.94\varUpsilon (x_1){\dot{x}}_1 \int _{x_2^*(x_1)}^{x_2}\left| \lceil s\rceil ^{\frac{15}{4}}-\left\lceil x_2^*(x_1)\right\rceil ^{\frac{15}{4}} \right| ^{\frac{14}{15}}\mathrm{{d}}s\\&\quad \le \frac{1}{3}\xi _1^2(x_1)+ {\tilde{\psi }}_2(x_1)\xi _2^2(x) \end{aligned}$$

for all \((x,t)\in {\mathbb {M}}_2(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\), where \(\psi _2(x_1) =1.37\) \(\lambda ^{5/2}(x_1)\), \({\hat{\psi }}_2(x_1)=0.89\) and \({\tilde{\psi }}_2(x_1)= ((2.51\beta _1^3(x_1)+3.76)^{5/3} +3.22)(1+\varUpsilon ^2(x_1))^{5/6}\). In addition, considering \(V_3({\mathcal {X}})=5/11|e({\mathcal {X}})|^{11/5}\), one has

$$\begin{aligned} {\dot{V}}_3({\mathcal {X}})&\le -0.74G^{\frac{1}{4}}(x_1)|e({\mathcal {X}})|^{2}+G^{-\frac{1}{2}}(x_1)|e({\mathcal {X}})|^{\frac{1}{5}}|x_2|^{\frac{27}{4}}\\&\quad +3.75 \lceil e({\mathcal {X}})\rceil ^{\frac{6}{5}}|x_2|^{\frac{11}{4}}\left( \theta (x,t)u+\phi _2(x,t)\right) \end{aligned}$$

for all \(({\mathcal {X}},t)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\). Again, using Lemmas 2 and 3 , one can easily obtain

$$\begin{aligned}&G^{-\frac{1}{2}}(x_1)|e({\mathcal {X}})|^{\frac{1}{5}}|x_2|^{\frac{27}{4}}\\&\quad \le \psi _5(x_1)\xi _1^2(x_1) + {\hat{\psi }}_5 \xi _2^2(x) + e^2({\mathcal {X}}) \\&3.75 \lceil e({\mathcal {X}})\rceil ^{\frac{6}{5}}|x_2|^{\frac{11}{4}}\left( \theta (x,t)u+\phi _2(x,t)\right) \\&\quad \le \frac{1}{2}\xi _1^2(x_1) +\frac{1}{3}\xi _2^2(x)+\left( \psi _4(x_1)+\psi _6(x_1)\right) e^2({\mathcal {X}}) \end{aligned}$$

for all \(({\mathcal {X}},t)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\), in which \(\psi _5(x_1) = 1.97\beta _1^{15/2}(x_1)\), \({\hat{\psi }}_5 =1.97\), and \(\psi _4(x_1)+\psi _6(x_1) = 7.234 + 2\beta _1^{3}(x_1)\); moreover, using Lemmas 2 and 4 , one also has

$$\begin{aligned}&\theta (x,t)\beta _2(x_1)\lceil \xi _2(x)\rceil ^{\frac{29}{15}}\left| \lceil \xi _2(x)\rceil ^{\frac{1}{15}}-\left\lceil \xi _2(x)\right. \right. \\&\qquad \left. \left. -e({\mathcal {X}})\right\rceil ^{\frac{1}{15}}\right| \\&\quad \le \frac{1}{6}\xi _2^2(x) +\psi _7(x_1) e^2({\mathcal {X}}) \end{aligned}$$

for all \(({\mathcal {X}},t)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\), where \(\psi _7(x_1)=3.132\) \(\beta _2^{2}(x_1)\) with \(\beta _2(x_1)=(1+\psi _2(x_1)+{\hat{\psi }}_2(x_1)+{\tilde{\psi }}_2(x_1))/0.7\). Therefore, we choose \(L(x_1)=671.28x_1\) and directly design the output feedback finite-time controller and the observer as described by (31) and (25), respectively, such that

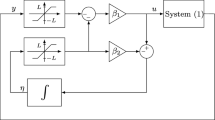
$$\begin{aligned} {\dot{V}}({\mathcal {X}})&={\dot{V}}_2(x)+{\dot{V}}_3({\mathcal {X}})\\&\le -\frac{1}{4}\left( \xi _1^2(x_1) +\xi _2^2(x)+ e^2({\mathcal {X}}) \right) \end{aligned}$$

for all \(({\mathcal {X}},t)\in {\mathbb {M}}_3(\kappa _l,\kappa _u)\times {\mathbb {R}}^+\). For demonstration, the initial time and the initial state in the simulations are set to be \(t_0=0\) and \((x_1(0),x_2(0),\) \(\nu (0))=(-1,-2.2,0)\), respectively.

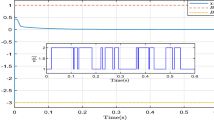
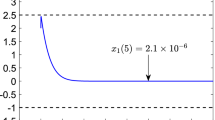
From the simulation results shown in Figs. 1, 2 and 3, it can be found that the designed output feedback controller not only finite-time stabilizes system (39) but also successfully ensures the fulfillment of the asymmetric output constraint \(-1.5=-\kappa _l<y(t)=x_1(t)<\kappa _u=1\) for all \(t\ge 0\). Furthermore, in the scenario when the output constraint is purposely assigned to be quite large (e.g., \(\kappa _u=\kappa _l=100\)) in order to simulate the scenario of almost no constraint on the output \(y(t)=x_1(t)\), the designed output feedback controller as well as the associated observer is still valid for finite-time stabilizing system (39), without needing to change the controller and observer structures; this also demonstrates the unification of our approach in performing simultaneously the construction of a continuous output feedback finite-time stabilizer subjected to or free from output constraints.

Fig. 1
figure 1

Timing responses of \(x_1\) with two different \(\kappa _l\) and \(\kappa _u\)

Full size image
Fig. 2
figure 2

Timing responses of \(x_2\) with two different \(\kappa _l\) and \(\kappa _u\)

Full size image
Fig. 3
figure 3

Timing responses of \(\nu \) with two different \(\kappa _l\) and \(\kappa _u\)

Full size image

5 Conclusion

We have presented a solution to the problem of output feedback finite-time stabilization for a significant class of high-order planar systems subjected to asymmetric output constraints. A novel design methodology was proposed by skillfully renovating the technique of adding a power integrator with the subtle implantation of a new developing fraction-type asymmetric barrier Lyapunov function as well as a delicate non-smooth state observer. With full extraction and utilization of the characteristics of system nonlinearities, the proposed scheme enjoys an appealing and attractive property that it enables us to straightly unify and achieve simultaneously the design of a continuous output feedback finite-time stabilizer for systems subjected to or free from asymmetric output constraints, without needing to change the controller and observer structures.