Fixed-time stabilization of high-order nonlinear systems with an asymmetric output constraint

Abstract

This article studies the problem of fixed-time stabilization for a class of uncertain high-order nonlinear systems subjected to an asymmetric output constraint. A tangent-type barrier function is first developed as an intermediate design ingredient by subtly extracting and utilizing the inherent features of system nonlinearities. Next, the proposed barrier function along with the intrinsic attributes of signum functions is exploited to elegantly renovate the celebrated technique of adding a power integrator, thereby establishing a unified approach by which a tangent-type asymmetric barrier Lyapunov function together with a continuous state feedback fixed-time stabilizer can be constructed systematically while guaranteeing the achievement of pre-specified output constraints successfully. A technical novelty of the presented scheme is ascribed to the unified nature enabling us to design a fixed-time stabilizer simultaneously workable for the system subjected to or free from output constraints without needing to revamp the controller structure. A numerical example is provided to show the effectiveness and superiority of the developed method.

1 Introduction

Without any doubt, the stabilization task of high-order nonlinear systems [1] (also known as p-normal form systems [2]) has been fairly recognized as a significantly formidable and challenging problem in the field of nonlinear control. The primary difficulty of this issue is the inherent nonlinearities of the system together with the uncontrollability and potential nonexistence of Jacobian linearization at the origin, which prevents the applicability of various existing nonlinear feedback design methods, including backstepping strategy [3] (also called adding an integrator [4]). Such a critical obstruction was conquered with a technological breakthrough achieved by Qian and Lin in seminal papers [5, 6], where a renowned scheme named adding a power integrator was proposed. The cardinal philosophy underlying the technique of adding a power integrator is the maneuvering of feedback domination, which not only provides distinctive insights into overcoming the ingrained obstacles originating in system inherent nonlinearities but also contributes to a revolutionary perspective on constructing a feedback stabilizer defeating the uncontrollability and nonexistence of Jacobian linearization and thereby invigorating a series of elegant works dedicated to the stabilization problem of high-order nonlinear systems in the past two decades; see, for instance, [7,8,9,10,11,12,13,14,15,16,17,18,19] and the references therein.

In addition to the pure stabilization mission, a more aspiring goal is to stabilize nonlinear systems in consideration of a pre-specified output constraint since system operation safety and/or performance specifications are crucial and critical to be pursued in practice. For example, the constraints on the joint angles of a robot manipulator during stabilization/tracking operation are imperative for preventing potential structural damage or injury to the persons nearby [20]; some practical examples can be also found in [21,22,23,24,25,26,27]. For high-order nonlinear systems (i.e., p-normal form systems), compared with the great advances in the pure stabilization issue (e.g., [7, 9,10,11,12,13,14,15,16,17,18, 28,29,30]), much less progress has been achieved toward investigating the problem of stabilization subjected to a pre-specified output constraint [31,32,33,34,35,36,37,38]. Specifically, the standard barrier Lyapunov function (BLF) (for the definition, see [39]), the tangent-type symmetric BLF¹, and the nonlinear transformation methods were adopted in the works [31,32,33,34,35], and [36], respectively, to deal with output constraints in the stabilization task; however, the schemes proposed in [31,32,33,34,35] only consider symmetric output constraints and the strategies in [31,32,33,34,35,36] are merely applicable to a rather limited class of high-order nonlinear systems because they essentially suffer from restrictive structural assumptions that either system powers must obey a monotone inequality relation or system nonlinear terms are forced necessarily to comply with several complicated growth conditions. By fully exploring the characteristics of system structures and inherent nonlinearities, a fraction-type BLF along with an explicit stabilizer design was presented in our recent results [37] and [38], where the structural restrictions in [31,32,33,34] were relatively lifted; thus, the methods in [37] and [38] are applicable to a broader class of high-order nonlinear systems, and in particular, the strategy in [38] further secures finite-time state convergence in the stabilization mission without violating output constraints.

Although stabilization can be successfully realized in a finite time horizon by the designs in [33, 34] and our previous study [38], an apparent defect included in [33, 34, 38] is the dependence between initial states and the estimation of the settling (convergence) time, which restrains to some extent the application scope of the manners in [33, 34, 38] due to the unavailability of precise initial states. Additionally, the main treatment/idea taken in [33, 34, 38] for rendering finite-time state convergence is asymptotic state convergence plus local finite-time stability [13, 40], which potentially prohibits analytically estimating the settling time, even when exact information on the initial states is available, and therefore leads to technical shortcomings. Interestingly, a notion named fixed-time state convergence (stability) was recently studied in [41, 42], depicting the property of finite-time state convergence with a guaranteed upper bound of the settling time independent of initial states and stimulating numerous studies devoted to the fixed-time stabilization² issue of various nonlinear systems (see, for example, [43, 44]). However, in the literature of which we are aware, the stabilization problem of high-order nonlinear systems (i.e., p-normal form systems) has never been exhaustively advanced with ensuring the property of fixed-time state convergence as well as the fulfillment of output constraints, that is, a fundamental question of how to construct a stabilizer for high-order nonlinear systems, achieving simultaneously the requirement of output constraints and the performance of fixed-time state convergence, remains largely open until now and deserves an in-depth investigation.

In this article, we concentrate on the problem of fixed-time stabilization for a class of uncertain high-order nonlinear systems subjected to a pre-specified asymmetric output constraint³ described by the equations of the form

$$\begin{aligned}&\dot{x}_1 =d_1(t,x)x_2^{p_1}+f_1(t,x,u)\nonumber \\&\dot{x}_2=d_2(t,x)x_3^{p_2}+f_2(t,x,u)\nonumber \\&\vdots \nonumber \\&\dot{x}_{n-1} =d_{n-1}(t,x)x_n^{p_{n-1}}+f_{n-1}(t,x,u)\nonumber \\&\dot{x}_n =d_n(t,x)u^{p_n}+f_n(t,x,u) y=x_1 \end{aligned}$$

(1)

where $x=(x_1,x_2,\ldots ,x_n)^T\in \mathbb {R}^n$, $u\in \mathbb {R}$, and $y\in \mathbb {R}$ are the system state, control input, and system output, respectively; with $t_0\in \mathbb {R}_+$ being the initial time instant, the initial state is represented by $x(t_0)\in \mathbb {R}^n$. For each $i=1,\ldots ,n$, the system power $p_i\in \mathbb {R}_{+}^{\text {odd}}=\{s\in \mathbb {R}_{+}|s=s_1/s_2~\text {with}~s_1~\text {and}~s_2~\text {being two positive odd}$ $\text {integers}\}$ with $p_n=1$, and the nonlinear term $f_i:\mathbb {R}_+\times \mathbb {R}^n\times \mathbb {R}\rightarrow \mathbb {R}$ and parameter $d_i:\mathbb {R}_+\times \mathbb {R}^n\rightarrow \mathbb {R}$ are uncertain (unknown) continuous functions. The primary objective is to develop a methodology effectively addressing and guiding the design of a state feedback controller u under which each trajectory x(t) of the closed-loop system (1) converges to the origin in fixed time, that is, $x(t)\rightarrow 0$ in finite time and $x(t)=0$ for all $t\ge T_r$ for some $T_r\in (t_0,\infty )$ being an upper bound of the settling (convergence) time, which is independent of the initial state $x(t_0)$ but related to certain design parameters. Meanwhile, the system output $y(t)=x_1(t)$ fulfills the pre-specified asymmetric constraint $-\varepsilon _L<y(t)=x_1(t)<\varepsilon _U$ for all $t\ge t_0$ with $\varepsilon _L$ and $\varepsilon _U$ being positive real constants. Notably, pursuing this problem is nontrivial and quite challenging. A key obstruction inhibiting us from seeking a solution is essentially the privation of constructive designs of BLFs and controllers (stabilizers) in efficiently performing the fixed-time stabilization as well as achieving the demand of asymmetric output constraints. Another difficult impediment is the lack of explicit methods for analyzing fixed-time state convergence involving pre-specified output constraints because, in the presence of output constraints imposed on the closed-loop system, the Lyapunov-like criterion presented in [41] is no longer applicable. Being aware of the aforementioned difficulties, in this article, we first design a new tangent-type barrier function⁴ as an intermediate/unformed design ingredient by artfully extracting and exploiting the inherent characteristics of system nonlinearities. Based on a skillful implantation of the presented barrier function and a delicate utilization of the intrinsic traits of signum functions, the technique of adding a power integrator is elegantly renovated to subtly establish a novel approach that, in a systematic fashion, guides us in constructing a tangent-type asymmetric BLF together with a continuous state feedback stabilizer (controller) and thereby fulfilling simultaneously the fixed-time stabilization task and the requirement of the pre-specified constraint on the system output.

To the best of our knowledge, this article is the first work in the literature coping with and offering an affirmative solution to the problem of fixed-time stabilization for uncertain high-order nonlinear systems (e.g., system (1)) subjected to asymmetric output constraints. Technically, the appealing innovations and contributions of this article can be summarized in the following three aspects.

• (i) The constructed tangent-type asymmetric BLF acting as a subtle leverage equipped in the proposed method in dealing with asymmetric output constraints differs significantly from the commonly utilized tangent-type [20, 21, 24, 25, 35] and logarithm-type [23, 33, 34, 39] BLFs; specifically, the inherent features of system nonlinearities $f_i(t,x,u)$’s are comprehensively taken into account and skillfully assimilated in the construction of a tangent-type barrier function as an intermediate/unformed design ingredient so that the resultant tangent-type asymmetric BLF under the presented approach inherits the dynamic characteristics of system (1), thereby providing the feasibility of achieving fixed-time stabilization for system (1).

• (ii) A new tool (i.e., Lemma 6) with the inspiration of modifying the so-called Bihari-type inequality [45] is introduced to facilitate the analysis of fixed-time state convergence; to be more specific, on the basis of the developed tool, the property of fixed-time state convergence can be evaluated/scrutinized directly and analytically without relying on the idea of asymptotic convergence plus local finite-time stability employed in [33, 34, 38], and an upper bound of the settling (convergence) time independent of initial states $x(t_0)$ can be acquired explicitly.

• (iii) The proposed approach offers and enjoys a unified nature that enables one to synthesize a fixed-time stabilizer simultaneously workable for system (1) subjected to or free from asymmetric output constraints, without needing to revamp the controller structure; in other words, when the output constraints are intentionally set to be infinity (or equivalently a very large value) so as to correspond to the scenario where the output constraints are no longer obligatory/imperative for system (1), the presented strategy will directly evolve into the design procedure applicable to tackling the pure mission of fixed-time stabilization for system (1) without output constraints.

Notation: All notations throughout this article are listed below. $\mathbb {R}$ and $\mathbb {R}_+$ represent the set of real numbers and the set of nonnegative real numbers, respectively. $\mathbb {R}^n$ is the standard n-dimensional Euclidean space and $\mathbb {R}_{+}^{\text {odd}}:=\{s\in \mathbb {R}_{+}|s=s_1/s_2~\text {with}~s_1~\text {and}~s_2~\text {being two}$ $\text {positive odd integers}\}$. Suppose that $x=(x_1,x_2,\ldots ,$ $x_n)^T\in \mathbb {R}^n$ and $\mathbb {B}\subset \mathbb {R}^n$ is an open connected set (i.e., a domain); for the sake of simplicity, we let $\overline{x}_i:=(x_1,x_2,\ldots ,x_i)^T\in \mathbb {R}^i$ for all $i=1,\ldots ,n$ with $\overline{x}_1=x_1$ and $\overline{x}_n=x$, and $\partial \mathbb {B}$ be the boundary of $\mathbb {B}\subset \mathbb {R}^n$. Given $\beta _i\in (0,\infty )$ with $i=1,2,3$, we also define $\left\lceil s \right\rceil ^{\beta _1}:=|s|^{\beta _1}sign(s)$ for all $s\in \mathbb {R}$, where $sign(\cdot )$ is the signum function, and $\mathbb {M}_i(\beta _2,\beta _3):=\{\overline{x}_i\in \mathbb {R}^i| -\beta _2<x_1<\beta _3\}\subset \mathbb {R}^i$ for all $i=1,\ldots ,n$.

2 Technical preliminaries and assumptions

First, we introduce an important lemma that contributes to handling an asymmetric output constraint imposed on a continuous non-autonomous (time-varying) nonlinear system, which can be non-Lipschitz continuous particularly; the detailed proof is referred to our previous work [38].

Lemma 1

([38]) Consider a non-autonomous nonlinear system

$$\begin{aligned} \dot{z}&=\phi (t,z),~~y=x_1 \end{aligned}$$

(2)

where $z=(z_1,z_2,\ldots ,z_n)^T\in \mathbb {R}^n$ and $\phi :\mathbb {R}_+\times \mathbb {R}^n\rightarrow \mathbb {R}^n$ is a continuous function and may not be Lipschitz. Let $-\varepsilon _L<y(t)=x_1(t)<\varepsilon _U$ for all $t\ge t_0$ be the asymmetric constraint imposed on the output $y=x_1$, where $\varepsilon _L,\varepsilon _U\in (0,\infty )$ are two pre-specified constants. Suppose that $V_1:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ and $V_2:\mathbb {M}_n(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ are two continuously differentiable functions, where $V_1(z_1)$ is positive definite while meeting the property $V_1(z_1)\rightarrow \infty$ as $z_1\rightarrow \partial \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$, and $V_2(z)$ is nonnegative. If $V(z):=V_1(z_1)+V_2(z)$ fulfills the following two conditions:

• (i) V(z) is radially unbounded with respect to $(z_2,z_3,\ldots ,$ $z_n)$; in other words, there holds

  $$\begin{aligned} V(z) \rightarrow \infty ~~\text {as}~~\Vert (z_2,z_3,\ldots ,z_n)\Vert \rightarrow \infty \end{aligned}$$

  for any fixed $z_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$

• (ii) the derivative of V(z) along system (2) is nonpositive; i.e., there holds⁵

  $$\begin{aligned} \frac{\partial V(z)}{\partial z}\phi (t,z)\le 0 \end{aligned}$$

  for all $(t,z)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$

then every solution⁶z(t) of system (2) starting at any initial state $z(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ is defined on $[t_0,\infty )$ (i.e., z(t) is forward complete⁷) and satisfies $z(t)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ for all $t\ge t_0$, thereby fulfilling the output constraint $-\varepsilon _L<y(t)=x_1(t)<\varepsilon _U$ for all $t\ge t_0$.

Remark 1

Remarkably, system (2) involved in Lemma 1 is continuous only (i.e., $\phi (t,z)$ is merely set as a continuous function); thus, Lemma 1 can be utilized to tackle non-autonomous nonlinear systems without needing both the Lipschitz continuity of $\phi (t,z)$ and the uniqueness of solutions corresponding to a given initial state. In fact, since fixed-time (or finite-time) state convergence would take place only in non-Lipschitz continuous systems [17, 41], Lemma 1 goes beyond Lemma 1 of the work [39], in which the systems are strictly restricted to be Lipschitz continuous, and further provides the technical possibility of investigating fixed-time state convergence in consideration of asymmetric output constraints.

Remark 2

It can be observed from Lemma 1 that a function V(z) (or equivalently $V_1(z_1)$ and $V_2(z)$) satisfying the differentiability, the positive definiteness and the conditions (i) and (ii) of Lemma 1 definitely induces the properties $V(z)\rightarrow \infty$ as $z\rightarrow \partial \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ and $V(z(t))\le B<\infty$ for all $t\ge t_0$ with $B\in \mathbb {R}_+$ and z(t) being an arbitrary solution of system (2) starting at the initial state $z(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$; these two induced properties are generally adopted in defining the so-called BLF [38, 39]. In other words, with the implication of Lemma 1 in mind, the organization of an asymmetric BLF V(z) for a continuous non-autonomous nonlinear system can be performed via designing $V_1(z_1)$ and $V_2(z)$ by fitting the conditions of Lemma 1. Based on this reason, in the design processes later, a positive definite and continuously differentiable function $V_1:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ satisfying $V_1(z_1)\rightarrow \infty$ as $z_1\rightarrow \partial \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$ will be specifically referred to as a barrier function.

We next present four lemmas in aid of deriving our main results; the proofs of the first three can be readily found in the literature (e.g., [5, 14, 18, 37]), and the last one is proven accordingly.

Lemma 2

([5]) Let $m_1>0$ and $m_2\ge 1$ be real constants. For any $s_1,s_2\in \mathbb {R}$, one has

$$\begin{aligned} \left| \left\lceil s_1 \right\rceil ^{\frac{m_1}{m_2}}-\left\lceil s_2\right\rceil ^{\frac{m_1}{m_2}}\right| \le 2^{1-\frac{1}{m_2}}\left| \left\lceil s_1 \right\rceil ^{m_1}-\left\lceil s_2\right\rceil ^{m_1}\right| ^{\frac{1}{m_2}}. \end{aligned}$$

Lemma 3

([14, 18]) Let $m_1,m_2>0$ be real constants and $\gamma :\mathbb {R}^2\rightarrow (0,\infty )$ be a function. For any $s_1,s_2\in \mathbb {R}$, there holds

$$\begin{aligned} |s_1|^{m_1}|s_2|^{m_2}&\le \frac{m_1}{m_1+m_2}\gamma (s_1,s_2) |s_1|^{m_1+m_2}\\&\quad + \frac{m_2}{m_1+m_2}\gamma ^{-\frac{m_1}{m_2}}(s_1,s_2) |s_1|^{m_1+m_2}. \end{aligned}$$

Lemma 4

([18, 37]) Let $m>0$ be a real constant. For any $s_i\in \mathbb {R}$ with $i=1,\ldots ,n$, one has

$$\begin{aligned} \left( |s_1|+\cdots +|s_n|\right) ^m\le \max (1,n^{m-1})\left( |s_1|^m+\cdots +|s_n|^m\right) . \end{aligned}$$

Lemma 5

For any $s\in [0,\pi /2)$, there holds $\tan \left( s\right) \le s\sec \left( s\right)$.

Proof

It suffices to prove the case where $s\in (0,\pi /2)$; to this end, one can deduce by the mean value theorem that for all $s\in (0,\pi /2)$ there always exists $s^*\in (0,s)$ such that $\cos (s^*)=\sin (s)/s$, which implies $\sin (s)\in (0,s]$ for all $s\in (0,\pi /2)$. This readily gives $\tan (s)\le s/\cos (s)=s\sec (s)$ for all $s\in (0,\pi /2)$. $\square$

The lemma below is newly developed; in this article, it will work as a new tool in helping and facilitating the analysis of fixed-time state convergence for nonlinear systems.

Lemma 6

Let $s_0\in \mathbb {R}_+$, $c_1,c_2>0$, $k> 1$, and $0<m_i<1$ for all $i=1,\ldots ,n$ be real constants. Suppose that $\Phi :[s_0,\infty )\rightarrow \mathbb {R}_+$ is a decreasing function of the form $\Phi (s):=\sum _{i=1}^n\Phi _i(s)$ with $\Phi _i:[s_0,\infty )\rightarrow \mathbb {R}_+$ being continuous for all $i=1,\ldots ,n$, and $m=\max _{i=1,\ldots ,n}\{m_i\}$. If $\Phi (s_0)>0$ and there holds

$$\begin{aligned} \Phi (s)\le \Phi (s_0)- \int _{s_0}^s\left[ c_1\left( \sum _{i=1}^n\Phi _i^{m_i}(\tau ) \right) + c_2\Phi ^k(\tau )\right] \mathrm{{d}}\tau \end{aligned}$$

(3)

for all $s\in [s_0,\infty )$, then $\Phi (s)=0$ for all $s \in [s_r,\infty )$ with

$$\begin{aligned} s_r=s_0 + \frac{1}{c_1(1-m)} + \frac{1}{c_2 (k-1)}. \end{aligned}$$

Proof

Two cases are considered as follows.

Case 1: When $\Phi (s_0)>1$, we shall show that $\Phi (s) \le 1$ for all $s\in [s^*_1,\infty )$ and for some $s^*_1\in (s_0,\infty )$; this is, instead, carried out by proving that $\Phi (s)\le \Theta (s)$ for all $s\in [s_0,\bar{s}^*_1]$ with $\Theta :[s_0,\bar{s}^*_1]\rightarrow \mathbb {R}$ being a continuous function of the form

$$\begin{aligned} \Theta (s) =\left[ \Phi ^{1-k}(s_0)+c_2(k-1) (s-s_0) \right] ^{\frac{1}{1-k}} \end{aligned}$$

and

$$\begin{aligned} \bar{s}^*_1=s_0+\frac{\Phi ^{(1-k)}(s_0) -1}{c_2(1-k)}. \end{aligned}$$

Toward this end, we assume that there exists $s_1\in (s_0,\bar{s}^*_1]$ such that $\Phi (s_1)>\Theta (s_1)$. Define

$$\begin{aligned} \Omega&= \left\{ s~|~s\in (s_0,s_1)~\text {such that}\right. \\&~~~~~~~~~~~~\left. ~\Phi (\tau )>\Theta (\tau )~\text {for all}~\tau \in (s,s_1]\right\} \subseteq (s_0,s_1) \end{aligned}$$

and $s_2=\inf \Omega$. From the continuity of $\Phi (\cdot )$ and $\Theta (\cdot )$, it follows that $\Phi ^k(s)\ge \Theta ^k(s)>0$ for all $s\in [s_2,s_1]$; in addition, it is direct to see that for all $s\in [s_0, \bar{s}^*_1]$

$$\begin{aligned} -c_2\int _{s_0}^s \Theta ^k(\tau )~\mathrm{{d}}\tau =\Theta (s)-\Theta (s_0). \end{aligned}$$

Using these two results, we can directly verify that

$$\begin{aligned}&\Phi (s_0) -c_2\int _{s_0}^s \Phi ^k(\tau )~\mathrm{{d}}\tau \\&\quad \ge \Phi (s) >\Theta (s) =\Theta (s_0)-c_2\int _{s_0}^s \Theta ^k(\tau )~\mathrm{{d}}\tau \ge 0 \end{aligned}$$

for all $s\in [s_2+\delta ,s_1]$ and for a real constant $\delta >0$ satisfying $s_2+\delta <s_1$. Since $\Phi (s_0)=\Theta (s_0)>0$ and $c_2>0$, it further gives

$$\begin{aligned} \int _{s_0}^s \Phi ^k(\tau )~\mathrm{{d}}\tau <\int _{s_0}^s \Theta ^k(\tau )~\mathrm{{d}}\tau \end{aligned}$$

for all $s\in [s_2+\delta ,s_1]$, which implies that there exists $s_3\in [s_2+\delta ,s_1]$ such that $\Phi ^k(s_3)<\Theta ^k(s_3)$ and thus leads to a contradiction. Hence, $\Phi (s)\le \Theta (s)$ for all $s\in [s_0,\bar{s}^*_1]$. Observing $\Theta (\bar{s}^*) =1$ and noticing that $\Phi (\cdot )$ is continuous and decreasing, one has $\Phi (s)\le 1$ for all $s\in [s_1^*,\infty )$ with $s^*_1$ being larger than $\bar{s}^*_1$ and, in point of fact, having the form

$$\begin{aligned} s^*_1 =s_0+\frac{1}{c_2(k-1)}. \end{aligned}$$

Case 2: In the case of $0<\Phi (s_0)\le 1$, one has $\Phi (s)\le 1$ for all $s\in [s_0,\infty )$ since $\Phi (\cdot )$ is continuous and decreasing. Moreover, it follows from Lemma 4 that

$$\begin{aligned} \Phi (s)-\Phi (s_0)\le -c_1 \int _{s_0}^s\Phi _i^{m_i}(\tau )~\mathrm{{d}}\tau \le -c_1 \int _{s_0}^s\Phi ^{m}(\tau )~\mathrm{{d}}\tau \end{aligned}$$

for all $s\in [s_0,\infty )$. Using this inequality and an almost identical argument in Case 1, we can easily show that there exists $s^*_2\in (s_0,\infty )$ taking the following form

$$\begin{aligned} s^*_2 = s_0 + \frac{1}{c_1(1-m)} \end{aligned}$$

such that $\Phi (s^*_2)=0$, which together with the fact that $\Phi (\cdot )$ is continuous and decreasing gives $\Phi (s)=0$ for all $s\in [s^*_2,\infty )$.

Combining the two cases one immediately obtains $\Phi (s)=0$ for all $s\in [s_r,\infty )$ with

$$\begin{aligned} s_r= s_0 + \frac{1}{c_1(1-m)} + \frac{1}{c_2 (k-1)} \end{aligned}$$

and therefore completes the proof. $\square$

Remark 3

It is worth pointing out that establishing Lemma 6 is inspired by modifying the so-called Bihari-type inequality [45]. As a matter of fact, in the case when $c_1<0$ and $c_2=0$, the condition (3) is exactly a special case of the Bihari-type inequality. Because Lemma 6 is truly developed with involving the positive real constants $c_1$ and $c_2$, the condition (3) is in a Bihari-like form with enlarged applicability, and thus, Lemma 6 can be technically thought of as a counterpart of the Bihari-type inequality. A crucial benefit supplied by Lemma 6 is the facile utility of investigating the convergence of a continuous and decreasing function $\Phi (\cdot )$ within a fixed time (i.e., $s_r$ in Lemma 6), without demanding its differentiability; such a benefit also purifies Lemma 6 to a new tool able to verify analytically the property of fixed-time state convergence of nonlinear systems that are continuous and probably not Lipschitz, and acquire explicitly an upper bound of the settling (convergence) time independent of initial states without relying on the idea of asymptotic convergence plus local finite-time stability [33, 34, 38].

Noting that appropriate conditions restricting the growth rates of both system nonlinearities and uncertainties are essentially imperative even for the task of purely stabilizing system (1) without any constraint on the output [1, 5, 6], we impose the following two assumptions on the uncertain parameters $d_i(t,x)$’s and the nonlinearities $f_i(t,x,u)$’s, respectively, before starting the development of the primary approach.

Assumption 1

There exist smooth functions $\underline{d}_i:\mathbb {R}^i\rightarrow (0,\infty )$ and $\overline{d}_i:\mathbb {R}^i\rightarrow (0,\infty )$ such that

$$\begin{aligned} \underline{d}_i(\overline{x}_i)\le d_i(t,x)\le \overline{d}_i(\overline{x}_i) \end{aligned}$$

for all $(t,x)\in \mathbb {R}_+\times \mathbb {R}^n$ and for all $i=1,\ldots ,n$.

Assumption 2

There exist real constants $\omega _n\le \cdots \le \omega _2\le \omega _1<0$ and a smooth function $\overline{f}_i:\mathbb {R}^i\rightarrow \mathbb {R}_+$ such that

$$\begin{aligned} \left| f_i(t,x,u)\right| \le \overline{f}_i(\overline{x}_i)\left( |x_1|^{\frac{\sigma _i+\omega _i}{\sigma _1}}+\cdots +|x_i|^{\frac{\sigma _i+\omega _i}{\sigma _i}}\right) \end{aligned}$$

(4)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {R}^n\times \mathbb {R}$ and for all $i=1,\ldots ,n$, where $\sigma _1, \sigma _2, \ldots ,\sigma _n$ are real constants defined by, for all $j=1,\ldots ,n,$

$$\begin{aligned} \sigma _1=1~~~~\text {and}~~~~\sigma _{j+1}=\frac{\sigma _j+\omega _j}{p_j}>0. \end{aligned}$$

(5)

Remark 4

Obviously, the inequality (4) in Assumption 2 means that $f_i(t,x,u)$, for $i=1,\ldots ,n$, has an upper bounded function (i.e., the right-hand side of (4)) depending only on $\overline{x}_i\in \mathbb {R}^i$ though $f_i(t,x,u)$ is related to $(t,x,u)\in \mathbb {R}_+\times \mathbb {R}^n\times \mathbb {R}$. Besides, as a clever appliance assisting in dipping up the intrinsic characteristics of system nonlinearities $f_i(t,x,u)$’s, Assumption 2 additionally includes several properties as follows.

• (i) Assumption 2 can be in reality treated as a locally homogeneous-like growth condition of system nonlinearities $f_i(t,x,u)$’s. Precisely, in the case when $\omega _i=\omega$ for all $i=1,\ldots ,n$, it is easy to derive that, on any compact set $\mathbb {U}\subset \mathbb {R}^n$, the right-hand side of (4) degenerates into a (weighted) homogeneous function in regard to the dilation weight $(\sigma _1,\ldots ,\sigma _i)$, thereby working as a homogeneous upper bound of the nonlinearities $f_i(t,x,u)$; i.e., on any compact set $\mathbb {U}\subset \mathbb {R}^n$, the relation (4) along with with $c=\sup _{(\overline{x}_i,x_{i+1},\ldots ,x_n)\in \mathbb {U}}\overline{f}_i(\overline{x}_i)$ becomes

  $$\begin{aligned} \left| f_i(t,x,u)\right| \le c\left( |x_1|^{\frac{\sigma _i+\omega }{\sigma _1}}+\cdots +|x_i|^{\frac{\sigma _i+\omega }{\sigma _i}}\right) \end{aligned}$$

  (6)

  for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {U}\times \mathbb {R}$, where the right-hand side of (6) forms a homogeneous function with respect to the dilation weight $(\sigma _1,\ldots ,\sigma _i)$; such a degenerated relation (6) has been widely stated/used in the literature [7, 9, 13, 16, 30]. Including the homogeneous one as a special case, the relation (4) not only retains genetically the spirit of weighted homogeneity in depicting the upper bounds of nonlinearities $f_i(t,x,u)$’s but also widens the applicability of Assumption 2 to more general circumstances.

• (ii) Assumption 2 holds the flexibility arising from the degree of freedom in selecting the monotone parameters $\omega _n\le \cdots \le \omega _2\le \omega _1$ so that it broadly encompasses diverse assumptions stated in existing studies. For example, if the system power $p_i$’s are all larger than one, that is, $p_i\ge 1$ for all $i=1,\ldots ,n$, Assumption 2 boils down to Assumption 2.1 in [7] when letting $\omega _i=\omega$ (a fixed real constant) for all $i=1,\ldots ,n$; in addition, if an extra monotone relation $p_1\ge p_2\ge \cdots \ge p_n\ge 1$ is satisfied, Assumption 2 becomes exactly Assumption 1 in [6] by choosing $\omega _i=p_i-1$. In the case where the system power $p_i$’s are identical to one and $\omega _i$’s are all set to be zero, i.e., $p_i=1$ and $\omega _i=0$ for all $i=1,\ldots ,n$, Assumption 2 directly reduces to the one used in Theorem 1 of the study [8].

• (iii) Assumption 2 can be fulfilled by $f_i(t,x,u)$’s with certain smoothness properties and structural conditions. More specifically, when the system nonlinearities $f_i(t,x,u)$’s depend only on $\overline{x}_i\in \mathbb {R}^i$ and are continuously differentiable with $f_i(0)=0$ for all $i=1,\ldots ,n$, such as the nonlinearities included in the under-actuated, weakly coupled, unstable mechanical system [5] and the liquid-level system [47], one can always find, in virtue of the Taylor expansion theorem [48], a smooth function $\hat{f}_i:\mathbb {R}^i\rightarrow \mathbb {R}_+$ such that

  $$\begin{aligned} \left| f_i(t,x,u)\right| \le \hat{f}_i(\overline{x}_i)\left( |x_1|+\cdots +|x_i|\right) \end{aligned}$$

  (7)

  for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {R}^n\times \mathbb {R}$; this inequality is involved in the formulation of (4) with $({\sigma _i+\omega _i})/{\sigma _j}=1$ for all $i=1,\ldots ,n$ and $j=1,\ldots ,i$. If, in addition, there holds $(\sigma _i+\omega _i)/\sigma _j\le 1$ for all $i=1,\ldots ,n$ and $j=1,\ldots ,i$, one can also verify that the relation $|x_j|\le \tilde{f}_{ij}(x_j)|x_j|^{(\sigma _i+\omega _i)/\sigma _j}$ is true for all $x_j\in \mathbb {R}$ and for all $i=1,\ldots ,n$ and $j=1,\ldots ,i$, where $\tilde{f}_{ij}:\mathbb {R}\rightarrow \mathbb {R}_+$ is a smooth function; with this fact in mind, the inequality (7) readily becomes (4).

3 Main results

With the aid of Assumptions 1 and 2, this section is dedicated to developing and presenting a new approach by which a continuous state feedback fixed-time stabilizer along with a tangent-type asymmetric BLF can be systematically constructed, thereby successfully guaranteeing the achievement of a pre-specified output constraint $-\varepsilon _L<y(t)=x_1(t)<\varepsilon _U$ for all $t\ge t_0$ with $\varepsilon _L$ and $\varepsilon _U$ being positive real constants. To be more specific, the development procedure is divided into two phases. It begins with organizing a new tangent-type barrier function as an intermediate/unformed design ingredient by delicately extracting and using the inherent characteristics of system nonlinearities. In the second phase, with an artful implantation of the presented barrier function along with an exquisite utilization of the intrinsic features of signum functions, the adding a power integrator technique is skillfully renovated to establish a novel approach that guides us, in a systematic fashion, in constructing a tangent-type asymmetric BLF together with a continuous state feedback controller capable of fulfilling simultaneously the fixed-time stabilization task and the requirement of the pre-specified asymmetric constraint on the system output.

3.1 Design of a tangent-type barrier function

Taking into consideration the pre-specified asymmetric output constraint $-\varepsilon _L<y(t)=x_1(t)<\varepsilon _U$ for all $t\ge t_0$ with two positive real constants $\varepsilon _L$ and $\varepsilon _U$, and exploiting the intrinsic feature of system nonlinearities characterized by Assumption 2, we set $\eta \ge \mu \ge \max _{1\le i\le n}\{\sigma _i\}\ge 1$ and design $V_T:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ as

$$\begin{aligned} V_T(x_1)&=\gamma (x_1)\frac{2 \varepsilon _U^{2\eta -\omega _1}}{(2\eta -\omega _1)\pi }\tan \left( \frac{|x_1|^{2\eta -\omega _1}\pi }{2 \varepsilon _U^{2\eta -\omega _1}}\right) \nonumber \\&+\left( 1-\gamma (x_1)\right) \frac{2 \varepsilon _L^{2\eta -\omega _1}}{(2\eta -\omega _1)\pi }\tan \left( \frac{|x_1|^{2\eta -\omega _1}\pi }{2 \varepsilon _L^{2\eta -\omega _1}}\right) \end{aligned}$$

(8)

where $\gamma :\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ is of the form

$$\begin{aligned} \gamma (x_1)=\left\{ \begin{array}{ll} 1 &{} \text {if}~~~x_1>0 \\ 0 &{} \text {if}~~~x_1\le 0 \\ \end{array}\right. . \end{aligned}$$

By the structure of $V_T(x_1)$, it is clear that $V_T(x_1)$ is positive definite on $\mathbb {M}_1(\varepsilon _L,\varepsilon _U)$ and meets $V_T(x_1)\rightarrow \infty$ as $x_1\rightarrow \partial \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$. Additionally, a straightforward calculation shows that the derivative of $V_T(x_1)$ with respect to $x_1$ is

$$\begin{aligned} \frac{\partial V_T(x_1)}{\partial x_1} = \Upsilon (x_1)\lceil x_1\rceil ^{2\eta -\omega _1-1} \end{aligned}$$

(9)

for all $x_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$, where $\Upsilon :\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow [1,\infty )$ is continuous and has the following form

$$\begin{aligned} \Upsilon (x_1)&=\gamma (x_1)\sec ^2\left( \frac{|x_1|^{2\eta -\omega _1}\pi }{2 \varepsilon _U^{2\eta -\omega _1}}\right) \nonumber \\&+\left( 1-\gamma (x_1)\right) \sec ^2\left( \frac{|x_1|^{2\eta -\omega _1}\pi }{2 \varepsilon _L^{2\eta -\omega _1}}\right) . \end{aligned}$$

(10)

Because of the continuity of $\Upsilon (x_1)$ and $\lceil x_1\rceil ^{2\eta -\omega _1-1}$ on $\mathbb {M}_1(\varepsilon _L,\varepsilon _U)$, the function $V_T(x_1)$ described in (8) is continuously differentiable and, according to Remark 2, is indeed a tangent-type barrier function with the asymmetry coming from the possible deviation between $\varepsilon _L$ and $\varepsilon _U$. As will be explicitly performed later, $V_T(x_1)$ serves as an intermediate design ingredient and also a key role for deriving the tangent-type asymmetric BLF and renovating the adding a power integrator technique with a view to achieving both the fixed-time stabilization and the demand of the pre-specified asymmetric output constraints.

Remark 5

Some distinctive traits/merits behind the presented tangent-type barrier function $V_T(x_1)$ are revealed as follows.

• (i) The design and construction of $V_T(x_1)$ are fundamentally in connection with the innate essence of system nonlinearities $f_i(t,x,u)$’s. More specifically, with the help of Assumption 2, the intrinsic attributes of system nonlinearities $f_i(t,x,u)$’s are skillfully dipped up and deposited/stored potentially in the parameters $\sigma _i$’s and $\omega _i$’s. By completely taking into account those parameters $\sigma _i$’s and $\omega _i$’s, the tangent-type barrier function $V_T(x_1)$ is constructed as an unformed design ingredient fully absorbing the inherent features of $f_i(t,x,u)$’s so that the subsequent tangent-type asymmetric BLF induced by the proposed approach later, which includes as a built-in core the tangent-type barrier function $V_T(x_1)$, attains and inherits the dynamic characteristics of system (1) while offering the feasibility of achieving fixed-time stabilization for system (1).

• (ii) Because of the elaborate absorption of the intrinsic essence of system nonlinearities $f_i(t,x,u)$’s, the tangent-type barrier function $V_T(x_1)$ acquires a particular structure such that the barrier nature of $V_T(x_1)$ will diminish spontaneously and dwindle away when the constraints on the output tend to infinity. To be more specific, if the pre-specified output constraints are deliberately assigned to be infinity, that is, $\varepsilon _L=\varepsilon _U=\varepsilon$ with $\varepsilon \rightarrow \infty$, in order to reflect correspondingly the circumstance that the constraints are no longer necessary/imperative, then one obtains

  $$\begin{aligned} \lim _{\varepsilon \rightarrow \infty } V_T(x_1)&=\frac{1}{(2\eta -\omega _1)}|x_1|^{2\eta -\omega _1}=:V_c(x_1) \end{aligned}$$

  which is clearly a continuously differentiable function without any barrier (namely, $V_c(x_1)\rightarrow \infty$ only if $|x_1|\rightarrow \infty$). As will be shown later, this property of $V_T(x_1)$ further endows, under the presented approach, the resultant tangent-type asymmetric BLF with the usability in unconstrained cases (also, see Remark 8).

3.2 Design of a fixed-time stabilizing controller

After completing the design of $V_T(x_1)$ as an intermediate ingredient, we are now in a position to show the development of our main approach which guides one in constructing a fixed-time stabilizer able to ensure the fulfillment of pre-specified output constraints. Details are presented in the theorem below and its proof.

Theorem 1

Under Assumptions 1 and 2, there exists a continuous state feedback stabilizer for system (1) such that for any $x(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$, every trajectory (solution) x(t) of system (1) starting at $x(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ satisfies the following

• (i) x(t) is forward complete; that is, x(t) is defined on $[t_0,\infty )$

• (ii) the output constraint is fulfilled; i.e., $-\varepsilon _L<y(t)=x_1(t)<\varepsilon _U$ for all $t\ge t_0$ where $\varepsilon _L$ and $\varepsilon _U$ are pre-specified positive real constants

• (iii) x(t) converges to the origin in fixed time; namely, $x(t)\rightarrow 0$ in finite time and $x(t)=0$ for all $t\ge T_r$ with $T_r\in ( t_0,\infty )$ being an upper bound of the settling (convergence) time and independent of $x(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ and $t_0\in \mathbb {R}_+$.

Proof

The proof inclusive of the methodology of designing a stabilizer is separated into two parts. With a skillful implantation of the presented barrier function $V_T(x_1)$ as well as a delicate utilization of the intrinsic traits of signum functions, a recursive (systematic) approach is explicitly presented in the first part to exhibit the construction of a continuous state feedback controller and validate the requirement of output constraints. Under the presented controller, the second part is concerned with the verification of the fixed-time state convergence of the closed-loop system and therefore confirms the validity of our approach.

Part I—Construction of a continuous state feedback fixed-time stabilizing controller

Step 1: To begin with, we let $\xi _1(x_1)=\lceil x_1\rceil ^{\mu /\sigma _1}$ and define $V_1:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ as $V_1(x_1)=V_T(x_1)$ with $V_T(x_1)$ being exactly the tangent-type barrier function given by (8); thus, $V_1(x_1)$ is positive definite and continuously differentiable on $\mathbb {M}_1(\varepsilon _L,\varepsilon _U)$. By virtue of Assumption 2 and (9), it follows from system (1) that

$$\begin{aligned} \dot{V}_1(x_1)&=\frac{\partial V_1(x_1)}{\partial x_1}\dot{x}_1\nonumber \\&=\Upsilon (x_1)\lceil x_1\rceil ^{2\eta -\omega _1-1}\left( d_1(t,x) x_2^{p_1}+f_1(t,x,u) \right) \nonumber \\&\le d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{2\eta -\omega _1-1}{\mu }} x_2^{p_1}\nonumber \\&\quad +\Upsilon (x_1)\overline{f}_1({x}_1)|\xi _1(x_1)|^{{\frac{2\eta }{\mu }}} \end{aligned}$$

(11)

for all⁸$(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$, where $\Upsilon (x_1)\ge 1$ for all $x_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$ is defined by (10). Let $\beta >0$ and $1<\theta <2$ be two real constants that are free adjustable design parameters. Then, by choosing $x_2^*:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ as a continuous virtual controller below

$$\begin{aligned} x_2^*(x_1) = -g_1(x_1)\lceil \xi _1(x_1) \rceil ^{\frac{\sigma _2}{\mu }} \end{aligned}$$

(12)

with

$$\begin{aligned} g_1^{p_1}(x_1)=\frac{ n\beta +\psi _1(x_1)\beta +\overline{f}_1({x}_1) }{\underline{d}_1(x_1)} \end{aligned}$$

where $g_1:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow (0,\infty )$ and $\psi _1:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ are both smooth functions, and $\psi _1(x_1)$ additionally suits the relation⁹

$$\begin{aligned} |\xi _1(x_1)|^{\frac{2\eta (\theta -1) - \omega _1\theta }{\mu }}\le \psi _1(x_1) \end{aligned}$$

for all $x_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$, it can be derived from Assumption 1 and (11) that

$$\begin{aligned}&\dot{V}_1(x_1)\nonumber \\&\quad \le d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{2\eta -\omega _1-1}{\mu }} x_2^{*p_1}(x_1)\nonumber \\&\qquad +\Upsilon (x_1)\overline{f}_1({x}_1)|\xi _1(x_1)|^{{\frac{2\eta }{\mu }}}\nonumber \\&\qquad +d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{2\eta -\omega _1-1}{\mu }} \left( x_2^{p_1}- x_2^{*p_1}(x_1)\right) \nonumber \\&\quad \le -\Upsilon (x_1)n\beta |\xi _1(x_1)|^{\frac{2\eta }{\mu }} -\Upsilon (x_1)\beta |\xi _1(x_1)|^{\frac{2\eta \theta - \omega _1\theta }{\mu }}\nonumber \\&\qquad +d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{2\eta -\omega _1-1}{\mu }} \left( x_2^{p_1}- x_2^{*p_1}(x_1)\right) \end{aligned}$$

(13)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. Interestingly, if $n=1$ and $x_2=u$ for system (1), the controller $u=x_2^*(x_1)$ being unrelated to the function $\Upsilon (x_1)$ is such that the inequality (13) turns into $\dot{V}_1(x_1)\le -\Upsilon (x_1)\beta$ $|\xi _1(x_1)|^{2\eta /\mu } -\Upsilon (x_1)\beta |\xi _1(x_1)|^{(2\eta \theta - \omega _1\theta )/\mu }\le 0$ for all (t, x,  $u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$, which by Lemma 1 indicates that the output constraint $-\varepsilon _L<y(t)=x_1(t)<\varepsilon _U$ is surely achieved for all $t\ge t_0$. This also discloses the fact that when system (1) is a scalar system (i.e., $n=1$), the stabilization in view of output constraints is always achievable by a simple controller $u=x_2^*(x_1)$ which is exclusive of the extra control effort produced by the function $\Upsilon (x_1)$. In contrast, in the case where $n\ge 2$, as described later, the term $\Upsilon (x_1)$ is necessarily contained somehow in controller gains for responding to the domination of output constraints.

Step 2: To continue the design for $n\ge 2$, here we pick the case $n=2$ and let $\xi _2(\overline{x}_2)=\lceil x_2\rceil ^{\mu /\sigma _2}-\lceil x_2^*(x_1)\rceil ^{\mu /\sigma _2}$ where $x_2^*(x_1)$ is presented in Step 1. We also consider $V_2:\mathbb {M}_2(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ defined as $V_2(\overline{x}_2)= V_1(x_1)+W_2(\overline{x}_2)$ with $W_2:\mathbb {M}_2(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ being of the following form

$$\begin{aligned} W_2(\overline{x}_2) = \int _{x_2^*(x_1)}^{x_2}\left\lceil \lceil s\rceil ^{\frac{\mu }{\sigma _2}}-\lceil x_2^*(x_1)\rceil ^{\frac{\mu }{\sigma _2}} \right\rceil ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}~ds. \end{aligned}$$

By the definitions of $V_1(x_1)$ and $W_2(\overline{x}_2)$, it is clear that $V_2(\overline{x}_2)$ is positive definite. In addition, a simple derivation according to the standard formulas of the partial derivatives $\partial W_2(\overline{x}_2)/\partial x_1$ and $\partial W_2(\overline{x}_2)/\partial x_2$ affirms that $V_2(\overline{x}_2)$ is continuously differentiable on $\mathbb {M}_2(\varepsilon _L,\varepsilon _U)$; specifically, it confirms for all $\overline{x}_2\in \mathbb {M}_2(\varepsilon _L,\varepsilon _U)$

$$\begin{aligned} \frac{\partial W_2(\overline{x}_2)}{\partial x_1}&=\frac{\partial \lceil x_2^*(x_1)\rceil ^{\frac{\mu }{\sigma _2}}}{\partial x_1}\left( \frac{\omega _2+\sigma _2-2\eta }{\mu }\right) \times \\&\quad \int _{x_2^*(x_1)}^{x_2}\left| \lceil s\rceil ^{\frac{\mu }{\sigma _2}}-\lceil x_2^*(x_1)\rceil ^{\frac{\mu }{\sigma _2}} \right| ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }-1}~ds\\ \frac{\partial W_2(\overline{x}_2)}{\partial x_2}&=\left\lceil \lceil x_2\rceil ^{\frac{\mu }{\sigma _2}}-\lceil x_2^*(x_1)\rceil ^{\frac{\mu }{\sigma _2}}\right\rceil ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}\\&\quad =\left\lceil \xi _2(\overline{x}_2)\right\rceil ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }} \end{aligned}$$

where $\partial W_2(\overline{x}_2)/\partial x_1$ is bounded by the following

$$\begin{aligned} \left| \frac{\partial W_2(\overline{x}_2)}{\partial x_1}\right| \le \rho _1(x_1)|\xi _1(x_1)|^{\frac{\mu -\sigma _1}{\mu }}|\xi _2(\overline{x}_2)|^{\frac{2\eta -\omega _2-\mu }{\mu }} \end{aligned}$$

for all $x_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$, with $\rho _1:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ being a smooth function.

Based on these facts and Assumptions 1 and 2, one can derive from system (1) and (13) that

$$\begin{aligned}&\dot{V}_2(\overline{x}_2)=\frac{\partial V_2(\overline{x}_2)}{\partial x_1}\dot{x}_1 +\frac{\partial V_2(\overline{x}_2)}{\partial x_2}\dot{x}_2\nonumber \\&\quad =\dot{V}_1(x_1)+\frac{\partial W_2(\overline{x}_2)}{\partial x_1}\dot{x}_1 +\frac{\partial W_2(\overline{x}_2)}{\partial x_2}\dot{x}_2\nonumber \\&\quad \le -\Upsilon (x_1)n\beta |\xi _1(x_1)|^{\frac{2\eta }{\mu }} -\Upsilon (x_1)\beta |\xi _1(x_1)|^{\frac{2\eta \theta - \omega _1\theta }{\mu }}\nonumber \\&\qquad +d_2(t,x)\left\lceil \xi _2(\overline{x}_2)\right\rceil ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}x_3^{p_2} \nonumber \\&\qquad +d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{2\eta -\omega _1-1}{\mu }} \left( x_2^{p_1}- x_2^{*p_1}(x_1)\right) \nonumber \\&\qquad +\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}\overline{f}_2(\overline{x}_2)\left( |x_1|^{\frac{\sigma _2+\omega _2}{\sigma _1}}+|x_2|^{\frac{\sigma _2+\omega _2}{\sigma _2}}\right) \nonumber \\&\qquad +\rho _1(x_1)|\xi _1(x_1)|^{\frac{\mu -\sigma _1}{\mu }}|\xi _2(\overline{x}_2)|^{\frac{2\eta -\omega _2-\mu }{\mu }}\nonumber \\&\qquad \times \left( \overline{d}_1(x_1) |x_2|^{p_1}+\overline{f}_1({x}_1)|x_1|^{\frac{\sigma _1+\omega _1}{\sigma _1}} \right) \end{aligned}$$

(14)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. To proceed forward, it is necessary to pursue the estimations of the last three terms on the right-hand side of (14); this can be performed as follows.

Noticing $(\sigma _1+\omega _1)/\mu <1$ and Lemma 2, we first have

$$\begin{aligned} \left( x_2^{p_1} - x_2^{*p_1}(x_1) \right) \le 2^{1-\frac{\sigma _1+\omega _1}{\mu }}\left| \xi _2(\overline{x}_2)\right| ^{\frac{\sigma _1+\omega _1}{\mu }} \end{aligned}$$

for all $\overline{x}_2\in \mathbb {M}_2(\varepsilon _L,\varepsilon _U)$. Additionally, the continuity of $\Upsilon (x_1)$ with regard to $x_1$ implies that there exists a smooth function $\hat{\Upsilon }:\mathbb {M}_1(\varepsilon _L,\varepsilon _U)\rightarrow [2,\infty )$ such that $\Upsilon (x_1)\le \hat{\Upsilon }(x_1)$ for all $x_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$. These two facts together with Assumption 1 and Lemma 3 yield

$$\begin{aligned}&d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{2\eta -\omega _1-1}{\mu }} \left( x_2^{p_1}- x_2^{*p_1}(x_1)\right) \nonumber \\&\quad \le 2^{1-\frac{\sigma _1+\omega _1}{\mu }}\Upsilon (x_1) \overline{d}_1({x}_1)\left| \xi _1(x_1)\right| ^{\frac{2\eta -\omega _1-1}{\mu }}\left| \xi _2(\overline{x}_2)\right| ^{\frac{\sigma _1+\omega _1}{\mu }}\nonumber \\&\quad \le \frac{1}{3}\beta \Upsilon (x_1)\left| \xi _1(x_1)\right| ^{\frac{2\eta }{\mu }} +\alpha _2(\overline{x}_2)\hat{\Upsilon }(x_1)\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta }{\mu }} \end{aligned}$$

(15)

for all $(t,x)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ where $\alpha _2:\mathbb {M}_2(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ is a smooth function.

Next, by Lemma 2 and the definitions of $\xi _1(x_1)$ and $\xi _2(\overline{x}_2)$, one has the relations $|x_1| =|\xi _1(x_1)|^{\sigma _1/\mu }$ and

$$\begin{aligned} |x_2|\le g_1(x_1)|\xi _1(x_1)|^{\frac{\sigma _2}{\mu }}+2^{1-\frac{\sigma _2}{\mu }} |\xi _2(\overline{x}_2)|^{\frac{\sigma _2}{\mu }} \end{aligned}$$

for all $\overline{x}_2\in \mathbb {M}_2(\varepsilon _L,\varepsilon _U)$. It further follows from Lemma 4 that $|x_1|^{(\sigma _1+\omega _1)/\sigma _1} =|\xi _1(x_1)|^{(\sigma _1+\omega _1)/\mu }$ and

$$\begin{aligned} |x_2|^{p_1}&\le \left( 2^{p_1 -1}+1\right) g_1^{p_1}(x_1)\left| \xi _1(x_1)\right| ^{\frac{\sigma _1+\omega _1}{\mu }}\\&\quad +\left( 2^{p_1 -1}+1\right) 2^{{p_1 -\frac{ p_1\sigma _2}{\mu }}} \left| \xi _2(\overline{x}_2)\right| ^{\frac{\sigma _1+\omega _1}{\mu }} \end{aligned}$$

for all $\overline{x}_2\in \mathbb {M}_2(\varepsilon _L,\varepsilon _U)$. Keeping these in mind and utilizing Lemma 3, we further obtain

$$\begin{aligned}&\rho _1(x_1)|\xi _1(x_1)|^{\frac{\mu -\sigma _1}{\mu }}|\xi _2(\overline{x}_2)|^{\frac{2\eta -\omega _2-\mu }{\mu }}\nonumber \\&\qquad \times \left( \overline{d}_1(x_1) |x_2|^{p_1}+\overline{f}_1({x}_1)|x_1|^{\frac{\sigma _1+\omega _1}{\sigma _1}} \right) \nonumber \\&\quad \le 2^{p_1 -\frac{ p_1\sigma _2}{\mu }}\left( 2^{p_1 -1} +1\right) \overline{d}_1({x}_1)\rho _1(x_1) \nonumber \\&\qquad \times |\xi _1(x_1)|^{\frac{\mu -\sigma _1}{\mu }}|\xi _2(\overline{x}_2)|^{\frac{2\eta -\mu +\sigma _1+\omega _1-\omega _2}{\mu }}\nonumber \\&\qquad +\left( 2^{p_1 -1} +1\right) \overline{d}_1({x}_1)\rho _1(x_1)g_1^{p_1}(x_1) \nonumber \\&\qquad \times |\xi _1(x_1)|^{\frac{\mu +\omega _1}{\mu }}|\xi _2(\overline{x}_2)|^{\frac{2\eta -\omega _2-\mu }{\mu }}\nonumber \\&\qquad +\rho _1(x_1)\overline{f}_1({x}_1)|\xi _1(x_1)|^{\frac{\mu +\omega _1}{\mu }}|\xi _2(\overline{x}_2)|^{\frac{2\eta -\omega _2-\mu }{\mu }}\nonumber \\&\quad \le \frac{1}{3}\beta \Upsilon (x_1)|\xi _1(x_1)|^{\frac{2\eta }{\mu }} +\tilde{\alpha }_2(\overline{x}_2)\hat{\Upsilon }(x_1)\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta }{\mu }} \end{aligned}$$

(16)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$, where $\tilde{\alpha }_2:\mathbb {M}_2(\varepsilon _l,\varepsilon _u)\rightarrow \mathbb {R}_+$ is a smooth function.

Under the same line of argument, it is easy to see that $|x_1|^{(\sigma _2+\omega _2)/\sigma _1} =|\xi _1(x_1)|^{(\sigma _2+\omega _2)/\mu }$ and

$$\begin{aligned} |x_2|^{\frac{\sigma _2+\omega _2}{\sigma _2}}&\le g_1^{\frac{\sigma _2+\omega _2}{\sigma _2}}(x_1)\left| \xi _1(x_1)\right| ^{\frac{\sigma _2+\omega _2}{\mu }}\\&\quad + 2^{{\frac{(\mu - \sigma _2)(\sigma _2+\omega _2)}{\mu \sigma _2}}} \left| \xi _2(\overline{x}_2)\right| ^{\frac{\sigma _2+\omega _2}{\mu }} \end{aligned}$$

for all $\overline{x}_2\in \mathbb {M}_2(\varepsilon _L,\varepsilon _U)$. By employing these relations and Lemma 3, it is not difficult to derive

$$\begin{aligned}&\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}\overline{f}_2(\overline{x}_2)\left( |x_1|^{\frac{\sigma _2+\omega _2}{\sigma _1}}+|x_2|^{\frac{\sigma _2+\omega _2}{\sigma _2}}\right) \nonumber \\&\quad \le \overline{f}_2(\overline{x}_2)|\xi _1(x_1)|^{\frac{\sigma _2+\omega _2}{\mu }}\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}\nonumber \\&\qquad +2^{{\frac{(\mu - \sigma _2)(\sigma _2+\omega _2)}{\mu \sigma _2}}}\overline{f}_2(\overline{x}_2)\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta }{\mu }}\nonumber \\&\qquad + \overline{f}_2(\overline{x}_2)g_1^{\frac{\sigma _2+\omega _2}{\sigma _2}}(x_1)\left| \xi _1(x_1)\right| ^{\frac{\sigma _2+\omega _2}{\mu }}\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}\nonumber \\&\quad \le \frac{1}{3}\beta \Upsilon (x_1)\left| \xi _1(x_1)\right| ^{\frac{2\eta }{\mu }} +\hat{\alpha }_2(\overline{x}_2)\hat{\Upsilon }(x_1)\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta }{\mu }} \end{aligned}$$

(17)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$, where $\hat{\alpha }_2:\mathbb {M}_2(\varepsilon _l,\varepsilon _u)\rightarrow \mathbb {R}_+$ is a smooth function.

Substituting the estimations provided by (15)–(17) into (14) yields

$$\begin{aligned}&\dot{V}_2(\overline{x}_2)\nonumber \\&\quad \le -\Upsilon (x_1)(n-1)\beta |\xi _1(x_1)|^{\frac{2\eta }{\mu }}-\Upsilon (x_1)\beta |\xi _1(x_1)|^{\frac{2\eta \theta - \omega _1\theta }{\mu }}\nonumber \\&\qquad +\left( \alpha _2(\overline{x}_2) +\tilde{\alpha }_2(\overline{x}_2) +\hat{\alpha }_2(\overline{x}_2)\right) \hat{\Upsilon }(x_1)\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta }{\mu }}\nonumber \\&\qquad +d_2(t,x)\left\lceil \xi _2(\overline{x}_2)\right\rceil ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}x_3^{p_2} \end{aligned}$$

(18)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. A continuous virtual controller $x_3^*:\mathbb {M}_2(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ being composed of

$$\begin{aligned} x_3^*(\overline{x}_2) = -g_2(\overline{x}_2)\hat{\Upsilon }^{\frac{1}{p_2}}(x_1)\lceil \xi _2(\overline{x}_2)\rceil ^{\frac{\sigma _3}{\mu }} \end{aligned}$$

with a smooth gain function $g_2:\mathbb {M}_2(\varepsilon _L,\varepsilon _U)\rightarrow (0,\infty )$ as below

$$\begin{aligned} g_2^{p_2}(\overline{x}_2) =\frac{ (n-1)\beta +\psi _2(\overline{x}_2)\beta +\alpha _2(\overline{x}_2) + \tilde{\alpha }_2(\overline{x}_2) +\hat{\alpha }_2(\overline{x}_2) }{\underline{d}_2(\overline{x}_2)} \end{aligned}$$

in which $\psi _2:\mathbb {M}_2(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ is a smooth function satisfying

$$\begin{aligned} |\xi _2(\overline{x}_2)|^{\frac{2\eta (\theta -1) - \omega _2\theta }{\mu }}\le \psi _2(\overline{x}_2) \end{aligned}$$

for all $\overline{x}_2\in \mathbb {M}_2(\varepsilon _L,\varepsilon _U)$, along with Assumption 1 is such that (18) becomes

$$\begin{aligned}&\dot{V}_2(\overline{x}_2)\nonumber \\&\quad \le -\Upsilon (x_1)(n-1)\beta |\xi _1(x_1)|^{\frac{2\eta }{\mu }} -\Upsilon (x_1)\beta |\xi _1(x_1)|^{\frac{2\eta \theta - \omega _1\theta }{\mu }}\nonumber \\&\qquad +d_2(t,x)\left\lceil \xi _2(\overline{x}_2)\right\rceil ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}x_3^{*p_2}(\overline{x}_2)\nonumber \\&\qquad +d_2(t,x)\left\lceil \xi _2(\overline{x}_2)\right\rceil ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}\left( x_3^{p_2}-x_3^{*p_2}(\overline{x}_2)\right) \nonumber \\&\qquad +\left( \alpha _2(\overline{x}_2)+\tilde{\alpha }_2(\overline{x}_2)+\hat{\alpha }_2(\overline{x}_2)\right) \hat{\Upsilon }(x_1)\left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta }{\mu }}\nonumber \\&\quad \le -\Upsilon (x_1)(n-1)\beta \left( |\xi _1(x_1)|^{\frac{2\eta }{\mu }} + \left| \xi _2(\overline{x}_2)\right| ^{\frac{2\eta }{\mu }}\right) \nonumber \\&\qquad -\Upsilon (x_1)\beta \left( |\xi _1(x_1)|^{\frac{2\eta \theta - \omega _1\theta }{\mu }} + |\xi _2(\overline{x}_2)|^{\frac{2\eta \theta - \omega _2\theta }{\mu }}\right) \nonumber \\&\qquad +d_2(t,x)\left\lceil \xi _2(\overline{x}_2)\right\rceil ^{\frac{2\eta -\omega _2-\sigma _2}{\mu }}\left( x_3^{p_2}-x_3^{*p_2}(\overline{x}_2)\right) \end{aligned}$$

(19)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. It can be observed that compared to $x_2^*(x_1)$ described by (12) the virtual controller $x_3^*(\overline{x}_2)$ clearly contains an extra term $\hat{\Upsilon }^{{1}/{p_2}}(x_1)$ that assures $\Upsilon (x_1)\le \hat{\Upsilon }(x_1)$ for all $x_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$ so as to produce/activate adequate control effort in dominating output constraints.

Inductive Step: At step $k-1$ with $k=3,\ldots ,n$, we suppose that there exist a positive definite and continuously differentiable function $V_{k-1}:\mathbb {M}_{k-1}(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ and a set of continuous virtual controllers $x_1^*=0$ and $x_i^*:\mathbb {M}_{i-1}(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ with $i=2,\ldots ,k$ defined as

$$\begin{aligned} x_2^*(x_1)= -g_1(x_1)\lceil \xi _1(x_1) \rceil ^{\frac{\sigma _2}{\mu }}~~~ \end{aligned}$$

and

$$\begin{aligned} x_i^*(\overline{x}_{i-1})=-g_{i-1}(\overline{x}_{i-1})\hat{\Upsilon }^{\frac{1}{p_{i-1}}}(x_1)\lceil \xi _{i-1}(\overline{x}_{i-1})\rceil ^{\frac{\sigma _i}{\mu }} \end{aligned}$$

for all $i=3,\ldots ,k$, where $g_i:\mathbb {M}_{i}(\varepsilon _L,\varepsilon _U)\rightarrow (0,\infty )$ are smooth gain functions and

$$\begin{aligned} \xi _{i}(\overline{x}_{i})=\lceil x_{i}\rceil ^{\frac{\mu }{\sigma _{i}}}-\lceil x_{i}^*(\overline{x}_{i-1})\rceil ^{\frac{\mu }{\sigma _{i}}} \end{aligned}$$

for all $i=1,\ldots ,k-1$, such that the derivative of $V_{k-1}(\overline{x}_{k-1})$ along system (1) is

$$\begin{aligned}&\dot{V}_{k-1}(\overline{x}_{k-1})= \sum _{i=1}^{k-1}\frac{\partial V_{k-1}(\overline{x}_{k-1})}{\partial x_i}\dot{x}_i\nonumber \\&\quad \le -\Upsilon (x_1)(n+2-k)\beta \sum _{i=1}^{k-1}\left| \xi _i(\overline{x}_i)\right| ^{\frac{2\eta }{\mu }}\nonumber \\&\qquad -\Upsilon (x_1) \beta \sum _{i=1}^{k-1} |\xi _i(\overline{x}_i)|^{\frac{2\eta \theta - \omega _i\theta }{\mu }}\nonumber \\&\qquad +d_{k-1}(t,x)\left\lceil \xi _{k-1}(\overline{x}_{k-1})\right\rceil ^{\frac{2\eta -\omega _{k-1}-\sigma _{k-1}}{\mu }}\nonumber \\&\qquad \times \left( x_k^{p_{k-1}}-x_k^{*p_{k-1}}(\overline{x}_{k-1})\right) \end{aligned}$$

(20)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. Obviously, the inequality (20) is precisely identical to (19) in the situation $k=3$. Subsequently, we shall verify that at step k with $k=3,\ldots ,n$, there also exists a continuous virtual controller $x_{k+1}^*:\mathbb {M}_{k}(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ such that (20) is valid as well for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$ and for a function $V_{k}:\mathbb {M}_{k}(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ being positive definite and continuously differentiable. For this purpose, we consider $V_k(\overline{x}_k)=V_{k-1}(\overline{x}_{k-1}) + W_k(\overline{x}_k)$ with $W:\mathbb {M}_k(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ defined as

$$\begin{aligned} W_k(\overline{x}_k)=\int _{x_k^*(\overline{x}_{k-1})}^{x_k}\left\lceil \lceil s\rceil ^{\frac{\mu }{\sigma _k}}-\lceil x_k^*(\overline{x}_{k-1})\rceil ^{\frac{\mu }{\sigma _k}}\right\rceil ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}ds. \end{aligned}$$

By letting $\xi _{k}(\overline{x}_{k})=\lceil x_k\rceil ^{{\mu }/{\sigma _{k}}}-\lceil x_{k}^*(\overline{x}_{k-1})\rceil ^{{\mu }/{\sigma _{k}}}$ similarly, the partial derivatives of $W_k(\overline{x}_k)$ in respect of $x_i$ for all $i=1,\ldots , k$ can be obtained through a simple verification as below

$$\begin{aligned} \frac{\partial W_k(\overline{x}_k)}{\partial x_i}&=\frac{\partial \lceil x_k^*(\overline{x}_{k-1})\rceil ^{\frac{\mu }{\sigma _k}}}{\partial x_i}\left( \frac{\omega _k+\sigma _k-2\eta }{\mu }\right) \\&\quad \times \int _{x_k^*(\overline{x}_{k-1})}^{x_k}\left| \lceil s\rceil ^{\frac{\mu }{\sigma _k}}-\lceil x_k^*(\overline{x}_{k-1})\rceil ^{\frac{\mu }{\sigma _k}}\right| ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }-1}ds\\ \frac{\partial W_k(\overline{x}_k)}{\partial x_k}&=\left\lceil \lceil x_k\rceil ^{\frac{\mu }{\sigma _k}}-\lceil x_k^*(\overline{x}_{k-1})\rceil ^{\frac{\mu }{\sigma _k}}\right\rceil ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}\\&=\left\lceil \xi _k(\overline{x}_k)\right\rceil ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }} \end{aligned}$$

for all $\overline{x}_k\in \mathbb {M}_{k}(\varepsilon _L,\varepsilon _U)$ and for all $i=1,\ldots ,k-1$; moreover, $\partial W_k(\overline{x}_k)/\partial x_i$ is indeed bounded in the sense that

$$\begin{aligned} \left| \frac{\partial W_k(\overline{x}_k)}{\partial x_i}\right|&\le \left( \sum _{j=1}^{k-1}|\xi _j(\overline{x}_j)|^{\frac{\mu -\sigma _i}{\mu }}\right) \\&\quad \times \rho _{k-1}(\overline{x}_{k-1})|\xi _k(\overline{x}_k)|^{\frac{2\eta -\omega _k-\mu }{\mu }} \end{aligned}$$

for all $\overline{x}_k\in \mathbb {M}_{k}(\varepsilon _L,\varepsilon _U)$ and for all $i=1,\ldots ,k-1$, where $\rho _{k-1}:\mathbb {M}_{k-1}(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ is a smooth function. Then, from (20) one knows that the derivative of $V_{k}(\overline{x}_{k})$ along system (1) is

$$\begin{aligned}&\dot{V}_k(\overline{x}_k)=\sum _{i=1}^{k}\frac{\partial V_{k}(\overline{x}_{k})}{\partial x_i}\dot{x}_i\nonumber \\&\quad =\dot{V}_{k-1}(\overline{x}_{k-1}) +\sum _{i=1}^{k-1}\frac{\partial W_k(\overline{x}_k)}{\partial x_i}\dot{x}_i+\frac{\partial W_k(\overline{x}_k)}{\partial x_k}\dot{x}_k\nonumber \\&\quad \le -\Upsilon (x_1)(n+2-k)\beta \sum _{i=1}^{k-1}\left| \xi _i(\overline{x}_i)\right| ^{\frac{2\eta }{\mu }}\nonumber \\&\qquad -\Upsilon (x_1) \beta \sum _{i=1}^{k-1} |\xi _i(\overline{x}_i)|^{\frac{2\eta \theta - \omega _i\theta }{\mu }}\nonumber \\&\qquad +d_k(t,x)\lceil \xi _k(\overline{x}_k)\rceil ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}x_{k+1}^{p_k}\nonumber \\&\qquad + \left| \xi _k(\overline{x}_k)\right| ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}\overline{f}_k(\overline{x}_k)\sum _{i=1}^k|x_i|^{\frac{\sigma _k+\omega _k}{\sigma _i}} \nonumber \\&\qquad +d_{k-1}(t,x)\left\lceil \xi _{k-1}(\overline{x}_{k-1})\right\rceil ^{\frac{2\eta -\omega _{k-1}-\sigma _{k-1}}{\mu }}\nonumber \\&\qquad \times \left( x_k^{p_{k-1}}-x_k^{*p_{k-1}}(\overline{x}_{k-1})\right) \nonumber \\&\qquad +\sum _{i=1}^{k-1}\frac{\partial W_k(\overline{x}_k)}{\partial x_i} \left( d_i(t,x)x_{i+1}^{p_i}+f_i(t,x,u) \right) \end{aligned}$$

(21)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. Following a similar line of argument in deducing (15)–(17), we can derive, respectively, the estimations of the last three terms on the right-hand side of (21) as follows

$$\begin{aligned}&d_{k-1}(t,x)\left\lceil \xi _{k-1}(\overline{x}_{k-1})\right\rceil ^{\frac{2\eta -\omega _{k-1}-\sigma _{k-1}}{\mu }}\nonumber \\&\qquad \times \left( x_k^{p_{k-1}}-x_k^{*p_{k-1}}(\overline{x}_{k-1})\right) \nonumber \\&\quad \le \frac{1}{3}\beta \Upsilon (x_1)|\xi _{k-1}(\overline{x}_{k-1})|^{\frac{2\eta }{\mu }}+\alpha _k(\overline{x}_{k})\hat{\Upsilon }(x_1)|\xi _{k}(\overline{x}_{k})|^{\frac{2\eta }{\mu }} \end{aligned}$$

(22)

$$\begin{aligned}&\sum _{i=1}^{k-1}\frac{\partial W_k(\overline{x}_k)}{\partial x_i} \left( d_i(t,x)x_{i+1}^{p_i}+f_i(t,x,u) \right) \nonumber \\&\quad \le \frac{1}{3}\beta \Upsilon (x_1)|\xi _{k-1}(\overline{x}_{k-1})|^{\frac{2\eta }{\mu }}+\frac{1}{2}\beta \Upsilon (x_1)\sum _{i=1}^{k-2}|\xi _i(\overline{x}_{i})|^{\frac{2\eta }{\mu }}\nonumber \\&\qquad +\tilde{\alpha }_k(\overline{x}_{k})\hat{\Upsilon }(x_1)|\xi _{k}(\overline{x}_{k})|^{\frac{2\eta }{\mu }} \end{aligned}$$

(23)

$$\begin{aligned}&\left| \xi _k(\overline{x}_k)\right| ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}\overline{f}_k(\overline{x}_k)\sum _{i=1}^k|x_i|^{\frac{\sigma _k+\omega _k}{\sigma _i}}\nonumber \\&\quad \le \frac{1}{3}\beta \Upsilon (x_1)|\xi _{k-1}(\overline{x}_{k-1})|^{\frac{2\eta }{\mu }}+\frac{1}{2}\beta \Upsilon (x_1)\sum _{i=1}^{k-2}|\xi _i(\overline{x}_{i})|^{\frac{2\eta }{\mu }}\nonumber \\&\qquad +\hat{\alpha }_k(\overline{x}_{k})\hat{\Upsilon }(x_1)|\xi _{k}(\overline{x}_{k})|^{\frac{2\eta }{\mu }} \end{aligned}$$

(24)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$, where $\alpha _k, \tilde{\alpha }_k, \hat{\alpha }_k:\mathbb {M}_{k}(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ are smooth functions. Substituting the three estimations (22)–(24) into (21) leads to

$$\begin{aligned} \dot{V}_k(\overline{x}_k)&\le -\Upsilon (x_1)(n+1-k)\beta \sum _{i=1}^{k-1}\left| \xi _i(\overline{x}_i)\right| ^{\frac{2\eta }{\mu }}\\&\quad -\Upsilon (x_1) \beta \sum _{i=1}^{k-1} |\xi _i(\overline{x}_i)|^{\frac{2\eta \theta - \omega _i\theta }{\mu }}\\&\quad +d_k(t,x)\lceil \xi _k(\overline{x}_k)\rceil ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}x_{k+1}^{p_k}\\&\quad +\left( \alpha _k(\overline{x}_{k}) + \tilde{\alpha }_k(\overline{x}_{k}) +\hat{\alpha }_k(\overline{x}_{k})\right) \hat{\Upsilon }(x_1)|\xi _{k}(\overline{x}_{k})|^{\frac{2\eta }{\mu }} \end{aligned}$$

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. Under Assumption 1, selecting a continuous virtual controller $x_{k+1}^*:\mathbb {M}_k(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ taking the form

$$\begin{aligned} x_{k+1}^*(\overline{x}_k)= -g_k(\overline{x}_k)\hat{\Upsilon }^{\frac{1}{p_k}}(x_1)\lceil \xi _{k}(\overline{x}_{k})\rceil ^{\frac{\sigma _{k+1}}{\mu }} \end{aligned}$$

(25)

with a smooth gain function $g_k:\mathbb {M}_k(\varepsilon _L,\varepsilon _U)\rightarrow (0,\infty )$ described as

$$\begin{aligned} g_k^{p_k}(\overline{x}_k)&=\frac{1}{\underline{d}_k(\overline{x}_k)}\left( (n-k+1)\beta +\psi _k(\overline{x}_k)\beta +\alpha _k(\overline{x}_{k}) \right. \\&\quad \left. + \tilde{\alpha }_k(\overline{x}_{k})+\hat{\alpha }_k(\overline{x}_{k})\right) \end{aligned}$$

where $\psi _k:\mathbb {M}_k(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ is a smooth function fulfilling

$$\begin{aligned} |\xi _k(\overline{x}_k)|^{\frac{2\eta (\theta -1)-\omega _k\theta }{\mu }}\le \psi _k(\overline{x}_k) \end{aligned}$$

for all $\overline{x}_k\in \mathbb {M}_k(\varepsilon _L,\varepsilon _U),$ implies that

$$\begin{aligned}&\dot{V}_k(\overline{x}_k)\nonumber \\&\quad \le -\Upsilon (x_1)(n+1-k)\beta \sum _{i=1}^{k-1}\left| \xi _i(\overline{x}_i)\right| ^{\frac{2\eta }{\mu }}\nonumber \\&\qquad -\Upsilon (x_1) \beta \sum _{i=1}^{k-1} |\xi _i(\overline{x}_i)|^{\frac{2\eta \theta - \omega _i\theta }{\mu }}\nonumber \\&\qquad +d_k(t,x)\lceil \xi _k(\overline{x}_k)\rceil ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}x_{k+1}^{*p_k} (\overline{x}_{k})\nonumber \\&\qquad + d_k(t,x)\lceil \xi _k(\overline{x}_k)\rceil ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}\left( x_{k+1}^{p_k}-x_{k+1}^{*p_k}(\overline{x}_{k})\right) \nonumber \\&\qquad +\left( \alpha _k(\overline{x}_{k}) + \tilde{\alpha }_k(\overline{x}_{k}) +\hat{\alpha }_k(\overline{x}_{k})\right) \hat{\Upsilon }(x_1)|\xi _{k}(\overline{x}_{k})|^{\frac{2\eta }{\mu }}\nonumber \\&\quad \le -\Upsilon (x_1)(n+1-k)\beta \sum _{i=1}^{k}\left| \xi _i(\overline{x}_i)\right| ^{\frac{2\eta }{\mu }}\nonumber \\&\qquad -\Upsilon (x_1) \beta \sum _{i=1}^{k} |\xi _i(\overline{x}_i)|^{\frac{2\eta \theta - \omega _i\theta }{\mu }}\nonumber \\&\qquad +d_k(t,x)\lceil \xi _k(\overline{x}_k)\rceil ^{\frac{2\eta -\omega _k-\sigma _k}{\mu }}\left( x_{k+1}^{p_k}-x_{k+1}^{*p_k}(\overline{x}_{k})\right) \end{aligned}$$

(26)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. Notably, the derivation so far solidly completes the inductive proof and validates that, under the continuous virtual controller $x_{k+1}^*(\overline{x}_k)$ shown in (25), the formula (20) still holds at step k with $k=3,\ldots ,n$ for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$; this therefore allows us to conclude that the inequality (26) is true for all $k=3,\ldots ,n$ and for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$.

Final Step: In accordance with the inductive proof, at step n where system (1) has $p_n=1$ and $x_{n+1}=u$, we can find, respectively, a continuous virtual controller $x_{n+1}^*:\mathbb {M}_{n}(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ and a positive definite and continuously differentiable function $V_n:\mathbb {M}_n(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ as below

$$\begin{aligned} x_{n+1}^*(x)= -g_n(x)\hat{\Upsilon }(x_1)\lceil \xi _{n}(x)\rceil ^{\frac{\sigma _{n+1}}{\mu }} \end{aligned}$$

and

$$\begin{aligned} V_n({x}_n)=V_{n-1}(\overline{x}_{n-1})+W_n({x}_n) \end{aligned}$$

where

$$\begin{aligned} \xi _{n}(x)=\lceil x_n\rceil ^{\mu /\sigma _n}-\lceil x_n^*(\overline{x}_{n-1})\rceil ^{\mu /\sigma _n} \end{aligned}$$

and $g_n:\mathbb {M}_n(\varepsilon _L,\varepsilon _U)\rightarrow (0,\infty )$ is a smooth function designed as

$$\begin{aligned} g_n(x) =\frac{\beta +\psi _n(x)\beta +\alpha _n(x) + \tilde{\alpha }_n(x)+\hat{\alpha }_n(x)}{\underline{d}_n(x)} \end{aligned}$$

with $\psi _n:\mathbb {M}_n(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}_+$ being a smooth function satisfying

$$\begin{aligned} |\xi _n(x)|^{\frac{2\eta (\theta -1)-\omega _n\theta }{\mu }}\le \psi _n(x) \end{aligned}$$

for all $x\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$, and $W_n:\mathbb {M}_n(\varepsilon _L,\varepsilon _U)\rightarrow \mathbb {R}$ is a function set to be

$$\begin{aligned} W_n(x)=\int _{x_n^*(\overline{x}_{n-1})}^{x_n}\left\lceil \lceil s\rceil ^{\frac{\mu }{\sigma _n}}-\lceil x_n^*(\overline{x}_{n-1})\rceil ^{\frac{\mu }{\sigma _n}}\right\rceil ^{\frac{2\eta -\omega _n-\sigma _n}{\mu }}ds \end{aligned}$$

such that the derivative of $V_n(x)$ along system (1) is

$$\begin{aligned}&\dot{V}_n(x)=\sum _{i=1}^{n}\frac{\partial V_{n}(x)}{\partial x_i}\dot{x}_i\nonumber \\&\quad =\dot{V}_{n-1}(\overline{x}_{n-1}) +\sum _{i=1}^{n-1}\frac{\partial W_n(x)}{\partial x_i}\dot{x}_i+\frac{\partial W_n(x)}{\partial x_n}\dot{x}_n\nonumber \\&\quad \le -\Upsilon (x_1)\beta \sum _{i=1}^{n}\left| \xi _i(\overline{x}_i)\right| ^{\frac{2\eta }{\mu }} -\Upsilon (x_1) \beta \sum _{i=1}^{n} |\xi _i(\overline{x}_i)|^{\frac{2\eta \theta - \omega _i\theta }{\mu }}\nonumber \\&\qquad +d_n(t,x)\lceil \xi _n(x)\rceil ^{\frac{2\eta -\omega _n-\sigma _n}{\mu }}\left( u-x_{n+1}^{*}(x)\right) \end{aligned}$$

(27)

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. By observing (27) and simply constructing a continuous state feedback stabilizer of the following form

$$\begin{aligned}&u(x)\nonumber \\&\quad =x_{n+1}^*(x)\nonumber \\&\quad =-g_n(x)\hat{\Upsilon }(x_1)\lceil \xi _{n}(x)\rceil ^{\frac{\sigma _{n+1}}{\mu }}\nonumber \\&\quad =-g_n(x)\hat{\Upsilon }(x_1)\left\lceil \lceil x_n\rceil ^{\frac{\mu }{\sigma _n}}+g_{n-1}^{\frac{\mu }{\sigma _n}}(\overline{x}_{n-1})\right. \nonumber \\&\qquad \times \hat{\Upsilon }^{\frac{\mu }{\sigma _{n}p_{n-1}}}(x_1)\lceil x_{n-1}\rceil ^{\frac{\mu }{\sigma _{n-1}}}\nonumber \\&\qquad +g_{n-1}^{\frac{\mu }{\sigma _n}}(\overline{x}_{n-1})g_{n-2}^{\frac{\mu }{\sigma _{n-1}}}(\overline{x}_{n-2})\hat{\Upsilon }^{\frac{\mu }{\sigma _{n}p_{n-1}} + \frac{\mu }{\sigma _{n-1}p_{n-2}}}(x_1)\nonumber \\&\qquad \times \lceil x_{n-2}\rceil ^{\frac{\mu }{\sigma _{n-2}}}+\cdots \nonumber \\&\qquad +\cdots +g_{n-1}^{\frac{\mu }{\sigma _n}}(\overline{x}_{n-1})g_{n-2}^{\frac{\mu }{\sigma _{n-1}}}(\overline{x}_{n-2})\cdots g_1^{\frac{\mu }{\sigma _2}}(x_{1})\nonumber \\&\qquad \times \left. \hat{\Upsilon }^{\frac{\mu }{\sigma _{n}p_{n-1}} + \frac{\mu }{\sigma _{n-1}p_{n-2}}+ \cdots +\frac{\mu }{ \sigma _3 p_2}}(x_1)\lceil x_1\rceil ^{\frac{\mu }{\sigma _{1}}}\right\rceil ^{\frac{\sigma _n+\omega _n}{\mu }} \end{aligned}$$

(28)

one immediately has

$$\begin{aligned} \dot{V}_n(x)&\le -\Upsilon (x_1)\beta \sum _{i=1}^{n}\left| \xi _i(\overline{x}_i)\right| ^{\frac{2\eta }{\mu }}\nonumber \\&\quad -\Upsilon (x_1) \beta \sum _{i=1}^{n} |\xi _i(\overline{x}_i)|^{\frac{2\eta \theta - \omega _i\theta }{\mu }} \end{aligned}$$

(29)

for all $(t,x)\in \mathbb {R}_+\times \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$. In addition, from the definition and structure of $V_n(x)$, it is not hard to verify that

$$\begin{aligned} V_n(x)&=V_1(x_1)+\sum _{i=2}^nW_i(\overline{x}_i)\nonumber \\&\ge V_1(x_1) +\sum _{i=2}^n \hat{c}\left| x_i-x_i^*(\overline{x}_{i-1})\right| ^{\frac{2\eta -\omega _i}{\sigma _i}} \end{aligned}$$

(30)

for all $x\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ and for a real constant $\hat{c}>0$; this as well as the definitions of $x_i^*(\overline{x}_{i-1})$’s in turn implies that $V_n(x)\rightarrow \infty$ as $\Vert (x_2,\ldots ,x_n)\Vert \rightarrow \infty$ for any fixed $x_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$. Based on this fact and the inequality (29), it follows from Lemma 1 that with the initial state $x(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$, every trajectory x(t) of system (1) under the controller (28) is defined on $[t_0,\infty )$ (that is, x(t) is forward complete) and certainly fulfills the output constraint $-\varepsilon _L<y(t)=x_1(t)<\varepsilon _U$ for all $t\ge t_0$ with $\varepsilon _L$ and $\varepsilon _U$ being pre-specified positive real constants.

Part II—Verification of the fixed-time state convergence of the closed-loop system

The remaining part of the proof is devoted to corroborating the fixed-time state convergence of system (1) under the controller (28). To this end, we consider the scenario where the initial state $x(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$; then, every trajectory (solution) x(t) of the closed-loop system (1) under the controller (28) is defined on $[t_0,\infty )$ and carries out $x(t)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ for all $t\ge t_0$. In what follows we shall show that $x(t)\rightarrow 0$ in finite time and $x(t)=0$ for all $t\ge T_r$ for some $T_r\in (t_0,\infty )$. Now, applying Lemmas 4 and 5 to $V_1(x_1)$ readily yields

$$\begin{aligned} V_1(x_1)&\le \frac{|x_1|^{2\eta -\omega _1}}{(2\eta -\omega _1)}\gamma (x_1)\sec \left( \frac{|x_1|^{2\eta -\omega _1}\pi }{2 \varepsilon _U^{2\eta -\omega _1}}\right) \\&\qquad +\frac{|x_1|^{2\eta -\omega _1}}{(2\eta -\omega _1)}\left( 1-\gamma (x_1)\right) \sec \left( \frac{|x_1|^{2\eta -\omega _1}\pi }{2 \varepsilon _L^{2\eta -\omega _1}}\right) \nonumber \\&\le |\xi _1(x_1)|^{\frac{2\eta -\omega _1}{\mu }}\Upsilon ^{\frac{1}{2}}(x_1) \end{aligned}$$

for all $x_1\in \mathbb {M}_1(\varepsilon _L,\varepsilon _U)$; besides, by using Lemma 2, it also follows that

$$\begin{aligned} W_i(\overline{x}_i)&\le \left| \int _{x_i^*(\overline{x}_{i-1})}^{x_i}\left\lceil \lceil s\rceil ^{\frac{\mu }{\sigma _i}}-\lceil x_i^*(\overline{x}_{i-1})\rceil ^{\frac{\mu }{\sigma _i}}\right\rceil ^{\frac{2\eta -\omega _i-\sigma _i}{\mu }}ds\right| \\&\le 2|\xi _i(\overline{x}_i)|^{\frac{2\eta -\omega _i}{\mu }} \end{aligned}$$

for all $x\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ and for all $i=2,\ldots ,n$. Considering these facts and utilizing Lemma 4, one further obtains

$$\begin{aligned} V_1^{\frac{2\eta }{2\eta -\omega _1}}(x_{1})&\le 2 |\xi _1(x_1)|^{\frac{2\eta }{\mu }}\Upsilon (x_1) \end{aligned}$$

and

$$\begin{aligned} W_i^{\frac{2\eta }{2\eta -\omega _i}}(\overline{x}_i)\le 2 |\xi _i(\overline{x}_i)|^{\frac{2\eta }{\mu }} \end{aligned}$$

for all $x\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ and for all $i=2,\ldots ,n$, which in turn make (29) become

$$\begin{aligned}&\dot{V}_n(x(t)) +\frac{\beta }{2}\left( V_1^{\frac{2\eta }{2\eta -\omega _1}}(x_1(t))+\sum _{i=2}^nW_i^{\frac{2\eta }{2\eta -\omega _i}}(\overline{x}_i(t))\right) \nonumber \\&\quad + \frac{\beta }{4n} V_n^{\theta }(x(t))\le 0 \end{aligned}$$

(31)

for all $t\in [t_0,\infty )$. Observing the inequality above, one knows that $V_{n}(x(t))$ is of course continuous and decreasing on $[t_0,\infty )$; this also means that if $V_n(x(t_0))=0$, the positive definiteness and continuity of $V_{n}(x)$ easily lead to $x(t)=0$ for all $t\in [t_0,\infty )$. In the case when $V_n(x(t_0))\ne 0$, it can be deduced from (31) that

$$\begin{aligned}&V_{n}(x(t)) - V_{n}(x(t_0))\\&\quad \le \int _{t_0}^t -\frac{\beta }{2}\left( V_1^{\frac{2\eta }{2\eta -\omega _1}}(x_{1}(s))+\sum _{i=2}^nW_i^{\frac{2\eta }{2\eta -\omega _i}}(\overline{x}_i(s))\right) \\&\qquad - \frac{\beta }{4n} V_n^{\theta }(x(s))~ds \end{aligned}$$

for all $t\in [t_0,\infty )$, which by Lemma 6 renders $V_{n}(x(t))=0$ for all $t\in [T_r,\infty )$ where

$$\begin{aligned} T_r=t_0+\frac{2}{\beta }\left( \frac{2n}{\theta -1} - \frac{2\eta -\omega _1}{\omega _1}\right) \in (t_0,\infty ) \end{aligned}$$

(32)

and thus $x(t)=0$ for all $t\in [T_r,\infty )$. Therefore, a direct combination of both cases implies that when $x(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$, every trajectory x(t) converges to the origin in fixed time; that is to say, $x(t)\rightarrow 0$ in finite time and $x(t)=0$ for all $t\ge T_r$ where $T_r\in (t_0,\infty )$ given by (32) is an upper bound of the settling (convergence) time and is clearly independent of both $x(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ and $t_0\in \mathbb {R}_+$. The proof is completed. $\square$

Remark 6

It is worthwhile noting from (32) that the upper bound $T_r\in (t_0,\infty )$ of the settling (convergence) time given by (32) is related to several tunable parameters. Specifically, when $\eta$ and $\omega _1$ are explicitly determined and fixed in accordance with the selection rule $\eta \ge \mu \ge \max _{1\le i\le n}\{\sigma _i\}$ and Assumption 2 which definitely depicts the innate features of system nonlinearities $f_i(t,x,u)$’s, the upper bound $T_r$ can be adjusted facilely by tuning the parameters $\beta >0$ and $1<\theta <2$, which are involved in the gain functions $g_i(\overline{x}_i)$’s and of course the resultant stabilizer (28). For example, the upper bound $T_r$ can be reduced by enlarging the value(s) of $\beta$ and/or $\theta$; in this situation, a smaller settling (convergence) time of the closed-loop system may be obtained at the expense of increased control efforts.

Remark 7

It can be observed from (29) and (30) that the positive definite and continuously differentiable function $V_n(x)=V_1(x_1)+\sum _{i=2}^nW_i(\overline{x}_i)$ constructed in Final Step and used for validating the fixed-time state convergence and the fulfillment of output constraints clearly satisfies the conditions (i) and (ii) of Lemma 1 and directly induces the properties $V_n(x)\rightarrow \infty$ as $x\rightarrow \partial \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$ and $V_n(x(t))\le V_n(x(t_0))<\infty$ for all $t\ge t_0$ with x(t) being any solution of the closed-loop system starting at $x(t_0)\in \mathbb {M}_n(\varepsilon _L,\varepsilon _U)$; therefore, by Remark 2, $V_n(x)$ is indeed a BLF. Furthermore, since the BLF $V_n(x)$ includes as a built-in core the tangent-type (asymmetric) barrier function $V_1(x_1)=V_T(x_1)$ described by (8), it is particularly called the tangent-type asymmetric BLF for system (1), and the intrinsic features of system nonlinearities $f_i(t,x,u)$’s absorbed into the barrier function $V_T(x_1)$ are entirely retained in $V_n(x)$ so that $V_n(x)$ inherits the dynamic characteristics of system (1) and technically provides the feasibility of performing fixed-time stabilization for system (1) in consideration of output constraints concurrently.

Remark 8

From the definition of $\Upsilon (x_1)$ given by (10), it is easy to see that if the pre-specified output constraints are purposefully set to be infinity, namely, $\varepsilon _L=\varepsilon _U=\varepsilon \rightarrow \infty$, for reflecting the situation of no constraint required on the output, there holds

$$\begin{aligned} \lim _{\varepsilon \rightarrow \infty } \Upsilon (x_1)&=\lim _{\varepsilon \rightarrow \infty }\sec ^2\left( \frac{|x_1|^{2\eta -\omega _1}\pi }{2 \varepsilon ^{2\eta -\omega _1}}\right) =1. \end{aligned}$$

Keeping this in mind, the smooth function $\hat{\Upsilon }(x_1)$ required to satisfy the requisite relation $\Upsilon (x_1)\le \hat{\Upsilon }(x_1)$ for all $x_1\in \mathbb {R}$ (noting that $\mathbb {M}_1(\varepsilon _L,\varepsilon _U)$ is replaced by $\mathbb {R}$) in designing the virtual controllers $x_i^*(\overline{x}_{i-1})$’s and the continuous state feedback stabilizer u(x) can be simply/directly assigned as $\hat{\Upsilon }(x_1)=1$ without destroying the effectiveness/validity of the design; thus, under the proposed scheme, the resultant continuous state feedback stabilizer u(x) becomes

$$\begin{aligned} u(x)&=-g_n(x)\left\lceil \lceil x_n\rceil ^{\frac{\mu }{\sigma _n}}+g_{n-1}^{\frac{\mu }{\sigma _n}}(\overline{x}_{n-1})\lceil x_{n-1}\rceil ^{\frac{\mu }{\sigma _{n-1}}}\right. \nonumber \\&\quad +g_{n-1}^{\frac{\mu }{\sigma _n}}(\overline{x}_{n-1})g_{n-2}^{\frac{\mu }{\sigma _{n-1}}}(\overline{x}_{n-2})\lceil x_{n-2}\rceil ^{\frac{\mu }{\sigma _{n-2}}}+\cdots \nonumber \\&\quad +\cdots +g_{n-1}^{\frac{\mu }{\sigma _n}}(\overline{x}_{n-1})g_{n-2}^{\frac{\mu }{\sigma _{n-1}}}(\overline{x}_{n-2})\cdots \nonumber \\&\quad \left. \times g_1^{\frac{\mu }{\sigma _{2}}}(\overline{x}_{1})\lceil x_1\rceil ^{\frac{\mu }{\sigma _{1}}}\right\rceil ^{\frac{\sigma _n+\omega _n}{\mu }} \end{aligned}$$

(33)

which surely has the same structure as (28) with only the gain function $\hat{\Upsilon }(x_1)$ changing into $\hat{\Upsilon }(x_1)=1$. Besides, from Remark 5 and the definition of $V_n(x)$, it is also simple to verify that under the same scenario $\varepsilon _L=\varepsilon _U=\varepsilon \rightarrow \infty$, the following is true

$$\begin{aligned}&\lim _{\varepsilon \rightarrow \infty }V_n(x)\nonumber \\&\quad =\frac{1}{(2\eta -\omega _1)}|x_1|^{2\eta -\omega _1}\nonumber \\&\qquad +\sum _{i=2}^n \int _{x_i^*(\overline{x}_{i-1})}^{x_i}\left\lceil \lceil s\rceil ^{\frac{\mu }{\sigma _i}}-\lceil x_i^*(\overline{x}_{i-1})\rceil ^{\frac{\mu }{\sigma _i}}\right\rceil ^{\frac{2\eta -\omega _i-\sigma _i}{\mu }}ds\nonumber \\&\quad =:V_{U}(x) \end{aligned}$$

(34)

where $V_U(x)$ is well defined on $\mathbb {R}^n$, positive definite, continuously differentiable and proper (i.e., the pre-image of any compact set under $V_{U}(x)$ is also compact). Taking u(x) and $V_U(x)$ given by (33) and (34), respectively, and using the similar argument of the proof of Theorem 1, one can validate straightforward that the continuous state feedback controller (33) remains valid while indeed being a pure global fixed-time stabilizer for system (1). That is, in the circumstance that there has no constraint required on the output or equivalently output constraints are no longer necessary, by letting the pre-specified asymmetric output constraint turn to infinity, i.e., $\varepsilon _L=\varepsilon _U=\varepsilon \rightarrow \infty$, the proposed approach will evolve automatically into the design technique under which the resultant continuous state feedback controller possesses the same structure as the one organized in view of output constraints and is capable of performing the pure fixed-time stabilization task of system (1) without output constraints. This in turn discloses that the presented approach enjoys and offers a unified nature that enables one to synthesize a fixed-time stabilizer simultaneously workable for system (1) subjected to or free from asymmetric output constraints without needing to revamp the controller structure.

Remark 9

Compared with our previous work [38] concerning the finite-time stabilization issue of high-order nonlinear systems with asymmetric output constraints, the main difficulties encountered here are basically the compound tasks arising from the composite demands of handling output constraints and achieving the fixed-time state convergence, which hinder possible utilization or direct parallel extensions of the method in [38] due to the instinctive capability and feasibility limitations on both the designed BLF and controllers, and thus deserve further developments of new design and analysis methodologies. In this article, under the proposed approach, the gain functions as well as structures of both the corresponding stabilizer (28) and BLF $V_n(x)$ (including the built-in tangent-type barrier function $V_1(x_1)=V_T(x_1)$) are constructed based on new synthesis strategies along with mild Assumptions 1 and 2, which not only substantially weaken the parameters restrictions of Assumptions 1 and 2 in [38] but also help with comprehensively extracting and exploiting the inherent characteristics of system nonlinearities in design; thus, both the BLF $V_n(x)$ and the stabilizer (28) are granted the ability in advancing and enhancing the state convergence without violating pre-specified output constraints. Moreover, in order to fill the gap regarding the lack of explicit methods in the literature for analyzing and assuring the fixed-time state convergence in connection with output constraints, a new tool (i.e., Lemma 6) is also developed by which the resultant stabilizer (28) collaborating with the BLF $V_n(x)$ can be easily verified to be capable of performing simultaneously the fixed-time stabilization task of system (1) and the requirement of the pre-specified asymmetric output constraint.

4 An illustrative example

To illustrate how the proposed approach can be utilized, we now consider a planar system as below

$$\begin{aligned} \dot{x}_1&=d_1(t,x)x_2^3+\sin (x_1)\cos (t+x_2+3u)\nonumber \\ \dot{x}_2&=d_2(t,x)u+\cos (x_2+u)\ln (1+x_1^2)\nonumber \\ y&=x_1 \end{aligned}$$

(35)

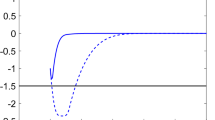
where $d_1(t,x)=1+0.2\cos (2t+x_2^3)$ and $d_2(t,x)=1+0.4\sin (3t+x_1)$. Note that, system (35) has the same structure as system (1) with $p_1=3$, $p_2=1$, $f_1(t,x,u)=\sin (x_1)\cos (t+x_2+3u)$ and $f_2(t,x,u)=\cos (x_2 + u)\ln (1+x_1^2)$. Assumption 1 is obviously fulfilled with $\underline{d}_1(x_1)=0.8$, $\overline{d}_1(x_1)=1.2$, $\underline{d}_2(x)=0.6$ and $\overline{d}_2(x)=1.4$. In light of the selection $\sigma _1=1$, $\omega _1=-1/10$ and $\omega _2=-1/5$, which lead to $\sigma _2=3/10$ and $\eta =\mu =1$, and the facts $|\sin (x_1)\cos (t+x_2+3u)|\le |x_1|^{{9}/{10}}$ and $|\cos (x_2 +u)\ln (1+x_1^2)|\le 19|x_1|^{{1}/{10}}$ for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {R}^2\times \mathbb {R}$, Assumption 2 is satisfied with $\overline{f}_1(x_1)=1$ and $\overline{f}_2(x)=19$, respectively. Based on Theorem 1, we first pick $\theta =1.5$ and $\beta =8$, which gives $T_r=t_0 +7.25$, and let

$$\begin{aligned} V_1(x_1)&=\gamma (x_1)\frac{20 \varepsilon _U^{\frac{21}{10}}}{21\pi }\tan \left( \frac{|x_1|^{\frac{21}{10}}\pi }{2\varepsilon _U^{^{\frac{21}{10}}}}\right) \\&\quad +\left( 1-\gamma (x_1)\right) \frac{20 \varepsilon _L^{\frac{21}{10}}}{21\pi }\tan \left( \frac{|x_1|^{\frac{21}{10}}\pi }{2\varepsilon _L^{^{\frac{21}{10}}}}\right) \end{aligned}$$

and the continuous virtual controller

$$\begin{aligned} x_2^*(x_1)=-\left( 31.25+10x_1^2\right) ^{\frac{1}{3}}\lceil x_1\rceil ^{\frac{3}{10}}. \end{aligned}$$

Then, one has

$$\begin{aligned} \dot{V}_1(x_1)&\le -16\Upsilon (x_1)|\xi _1(x_1)|^{2} -8\Upsilon (x_1)|\xi _1(x_1)|^{\frac{63}{20}}\\&\quad +d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{11}{10}} \left( x_2^{3}- x_2^{*3}(x_1)\right) \end{aligned}$$

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_2(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$, where $\Upsilon (x_1)$ is of the form

$$\begin{aligned} \Upsilon (x_1)&=\gamma (x_1)\sec ^2\left( \frac{|x_1|^{\frac{21}{10}}\pi }{2\varepsilon _U^{^{\frac{21}{10}}}}\right) \\&\quad +\left( 1-\gamma (x_1)\right) \sec ^2\left( \frac{|x_1|^{^{\frac{21}{10}}}\pi }{2\varepsilon _L^{^{\frac{21}{10}}}}\right) . \end{aligned}$$

Next, we choose

$$\begin{aligned} V_2(x)=V_1(x_1)+\int _{x_2^*(x_1)}^{x_2}\left\lceil \lceil s\rceil ^{\frac{10}{3}}-\lceil x_2^*(x_1)\rceil ^{\frac{10}{3}} \right\rceil ^{\frac{19}{10}}ds \end{aligned}$$

and calculate the derivative of $V_2(x)$ along system (35) as follows

$$\begin{aligned} \dot{V}_2(x)&\le -16\Upsilon (x_1)|\xi _1(x_1)|^{2} -8\Upsilon (x_1)|\xi _1(x_1)|^{\frac{63}{20}}\\&\quad +d_2(t,x)\left\lceil \xi _2(x)\right\rceil ^{\frac{19}{10}}u\\&\quad +d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{11}{10}} \left( x_2^{3}- x_2^{*3}(x_1)\right) \\&\quad +\rho _1(x_1)|\xi _2(x)|^{\frac{6}{5}}\left( |x_1|^{\frac{9}{10}}+1.2 |x_2|^{3} \right) \\&\quad +19\left| \xi _2(x)\right| ^{\frac{19}{10}}\left( |x_1|^{\frac{1}{10}}+|x_2|^{\frac{1}{3}}\right) \end{aligned}$$

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_2(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$, in which $\rho _1(x_1)$ is a smooth function directly calculated as $\rho _1(x_1)=-(31.25+10x_1^2 )^{{10}/{9}}-22.22$ $(31.25+10x_1^2)^{1/9}x_1^2$. By employing Lemmas 1–3, the estimations of the last three terms on the right-hand side of the above inequality can be easily found as below

$$\begin{aligned}&d_1(t,x)\Upsilon (x_1)\lceil \xi _1(x_1) \rceil ^{\frac{11}{10}}\left( x_2^{3}- x_2^{*3}(x_1)\right) \\&\quad \le \frac{8}{3}\Upsilon (x_1)\left| \xi _1(x_1)\right| ^{2} +\alpha _2(x) \hat{\Upsilon }(x_1)\left| \xi _2(x)\right| ^{2}\\&\rho _1(x_1)|\xi _2(x)|^{\frac{6}{5}}\left( |x_1|^{\frac{9}{10}}+1.2 |x_2|^{3} \right) \\&\quad \le \frac{8}{3}\Upsilon (x_1)\left| \xi _1(x_1)\right| ^{2} +\tilde{\alpha }_2(x) \hat{\Upsilon }(x_1)\left| \xi _2(x)\right| ^{2}\\&19\left| \xi _2(x)\right| ^{\frac{19}{10}}\left( |x_1|^{\frac{1}{10}}+|x_2|^{\frac{1}{3}}\right) \\&\quad \le \frac{8}{3}\Upsilon (x_1)\left| \xi _1(x_1)\right| ^{2} +\hat{\alpha }_2(x) \hat{\Upsilon }(x_1)\left| \xi _2(x)\right| ^{2} \end{aligned}$$

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_2(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$, where $\alpha _2(x) =0.1143$, $\tilde{\alpha }_2(x) =0.1694(38.5+12x_1^2)^{{5}/{3}}\rho _1^{{5}/{3}}(x_1)$, $\hat{\alpha }_2(x)$ $= 17.0956(1+(31.25+10x_1^2)^{{1}/{9}})^{{20}/{19}}$ and

$$\begin{aligned} \hat{\Upsilon }(x_1) =\gamma (x_1)\sec ^2\left( \frac{x_1^2\pi }{2\varepsilon _U^2}\right)&+\left( 1-\gamma (x_1)\right) \sec ^2\left( \frac{x_1^2\pi }{2\varepsilon _L^2}\right) . \end{aligned}$$

Hence, constructing the continuous state feedback controller

Fig. 1

Responses of $x_1$ with $\varepsilon _L=1$ and $\varepsilon _U=2.5$

Fig. 2

Responses of $x_2$ with $\varepsilon _L=1$ and $\varepsilon _U=2.5$

$$\begin{aligned} u(x)&=-g_2(x)\hat{\Upsilon }(x_1)\nonumber \\&~~~~\times \left\lceil \left\lceil x_2 \right\rceil ^{\frac{10}{3}}+\left( 31.25+10x_1^2\right) ^{\frac{10}{9}}x_1 \right\rceil ^{\frac{1}{10}} \end{aligned}$$

(36)

with $g_2(x)=13.52 + 13.33(1+x_2^2)^{{13}/{6}} +1.67(\alpha _2(x) +\tilde{\alpha }_2(x) +\hat{\alpha }_2(x))$, one simply obtains

$$\begin{aligned} \dot{V}_2(x)&\le -8\Upsilon (x_1)\left( |\xi _1(x_1)|^{2} +\left| \xi _2(x)\right| ^{2}\right) \\&\quad -8\Upsilon (x_1)\left( |\xi _1(x_1)|^{\frac{63}{20}}+\left| \xi _2(x)\right| ^{\frac{63}{20}}\right) \end{aligned}$$

Fig. 3

Responses of $x_1$ with $\varepsilon _L=\varepsilon _U=100$

Fig. 4

Responses of $x_2$ with $\varepsilon _L=\varepsilon _U=100$

for all $(t,x,u)\in \mathbb {R}_+\times \mathbb {M}_2(\varepsilon _L,\varepsilon _U)\times \mathbb {R}$. By letting the initial time $t_0 = 0$ and the initial state $(x_1(0), x_2(0))^T = (2,6)^T$, it can be clearly seen from the simulation results depicted in Fig.1–4 that the continuous state feedback controller (36) successfully stabilizes system (35) in fixed time, i.e., $x(t)\rightarrow 0$ in finite time and $x(t)=0$ for all $t\ge T_r=7.25$, while fulfilling the requirement of the asymmetric constraint $-1=-\varepsilon _L<y_1(t)=x_1(t)<\varepsilon _U=2.5$ for all $t\ge 0$. Furthermore, in the circumstance that the constraint is fairly large, e.g., $\varepsilon _L=\varepsilon _U=100$, which corresponds to the scenario where the output constraint is no longer imperative, the controller (36) with the same structure remains valid and serves as a pure global fixed-time stabilizer for system (35), almost without limiting/restricting the amplitude of the output $y_1(t)=x_1(t)$. Notably, this example explicitly demonstrates that the proposed approach provides a unified nature enabling us to perform the design of a fixed-time stabilizer for the system simultaneously with and without (asymmetric) output constraints.

5 Conclusion

This article has provided a solution to the problem of fixed-time stabilization for a class of uncertain high-order nonlinear systems subjected to an asymmetric output constraint. A new design methodology was established by subtly renovating the technique of adding a power integrator along with the subtle utilization of the intrinsic attributes of signum functions as well as a novel tangent-type barrier function designed with fully absorbing the inherent feature of system nonlinearities. Under the developed approach, a tangent-type asymmetric barrier Lyapunov function that helps with the convergence analysis, and a continuous state feedback fixed-time stabilizer that ensures both the fixed-time state convergence and the fulfillment of pre-specified output constraints can be constructed, respectively, in a systematic fashion. A distinctive technical novelty of the presented method is the unified nature that enables one to synthesize a fixed-time stabilizer simultaneously workable for the system subjected to or free from asymmetric output constraints, without needing to change the controller structure.