Reynolds number effect on in-line vortex-induced vibration (VIVx) of a circular cylinder for wider reduced velocity range

Abstract

Pure in-line vortex-induced vibrations (VIVx) of a circular cylinder are studied experimentally for different Reynolds number ranges. The experiments were performed in the current channel of LOC-COPPE/UFRJ for reduced velocity up to 10. The response amplitude and frequency are obtained by conducting a series of tests. The study is mainly aimed to investigate the oscillation of the circular cylinder in the first and second instability regions. This paper also provides the analysis of the response of a circular cylinder and flow characteristics for a reduced velocity range with the maximum value larger than five. The non-dimensional parameter, effective stiffness, is introduced, and the amplitude ratio is plotted as its function. The graphs of effective stiffness indicated that the maximum peak amplitudes in first and second instability regions do not occur because of lock-in. Although the response amplitude in pure in-line vortex-induced vibration (VIVx) for a reduced velocity larger than five is gradually increasing while there is a lock-in phenomenon. The existence of two distinct and separated instability regions was observed in VIVx for ${V}_{R}<5$. However, there is no zero amplitude in the valley between the two branches, which has been observed by some previous researchers.

1 Introduction

Vortex-induced vibration (VIV) is the oscillation induced on bluff bodies when interacting with an external flow, produced by almost periodical vortex shedding of this flow. [1] & [2] Vortex-induced vibration (VIV) occurs throughout nature and industry and can cause significant damage in many industrial applications, such as bridges, chimneys, marine structures, riser cables, and heat-exchangers. VIV has also been proposed as a possible source of renewable energy [3]. Due to the extensive application in oil extraction projects in deep water, a sector that has benefited from these studies is the oil and gas industry. This activity uses several underwater structures, in most cases cylindrical, such as umbilical cables for control of subsea equipment and oil extraction risers. The complete understanding of the dynamic behavior of this equipment is vital to the success of offshore production and operation because of the large amount of economic and human resources involved and the environmental impact issues from a possible accident.

The VIV has been investigated by many researchers experimentally [2] & [4] and numerically [5]. Hereafter, the 1-DOF vortex-induced vibration in the cross-flow and in-line is referred to as VIVy and VIVx, respectively. The VIV in cross-flow direction has drawn more attention to the researchers. One of the reasons the cross-flow vortex-induced vibration has been studied extensively is its higher amplitude of oscillation [6]. However, some studies have indicated that in free-spanning pipelines and jumpers, fatigue damage due to VIVx may become significant and even more critical than VIVy [7]. The principal reason for this importance is the VIVx initiates at a lower current velocity than VIVy [8]. Hence, it will occur more often. Another reason is that in 2-DOF vortex-induced vibration, VIVx response will happen at two times the frequency of VIVy [9]. It means that the number of stress cycles due to VIVx will become two times the number of VIVy cycles.

Auger was the first who reported the in-line vibrations caused by a steady wind in the aluminum cylinders of space-frame built for “Expo 1968” in San Antonio (TX, USA) [10]. The structure had been designed to avoid only cross-flow vibration. He concluded that the vibrations absorbers had to be mounted on all aluminum cylinders of the structure. However, King was the first researcher who emphasized the paramount importance of considering VIV in a streamwise direction [11]. During the installation of a jetty at Immingham, he observed intense in-line vibrations in circular piles caused by tidal currents. He stated that the oscillation could be excited at velocities one-quarter of those required for cross-flow VIV. Another example is the damage that occurred in 1995 to a thermocouple in the fast breeder reactor “Monju” of JNCD (Japan Nuclear Cycle Development Institute) caused principally by an in-line vortex-induced vibration [12].

The variation of amplitude and frequency is usually expressed as a function of flow velocity. The flow velocity is generally non-dimensionalized as the reduced velocity, ${V}_{R}=U/{(f}_{N}D)$, where $\mathrm{U}$ is the freestream velocity, ${f}_{N}$ is the natural frequency of the cylinder in the still fluid, and $D$ is the cylinder’s diameter. Sumer [13] has classified in-line vortex-induced vibration (VIVx) into three types by their reduced velocity range as follow:

• $1\le {V}_{R}\le 2.5$: is called the first instability region.

• $2.7\le {V}_{R}\le 4$: is called the second instability region.

• $4<{V}_{R}$: It happens where the cross-flow vibration occurs as well.

The last type of in-line vibration has usually been investigated along with cross-flow vibration within the 2-DOF system. However, the response oscillation in 1-DOF (VIVx) has dissimilar features from 2-DOF. The in-line vibration of a structure is caused by the oscillating drag force and can be led to make fatigue damage due to a higher frequency of occurrence.

Aguirre has demonstrated that the first kind of in-line vibrations (first instability region) is caused by the symmetric vortex shedding behind the cylinder due to in-line relative motion of the body concerning the fluid [14]. This vortex shedding produces a drag force that oscillates with a frequency three times the vortex frequency (${f}_{v})$. As a result, when this frequency is equal or close to the system’s natural frequency, the body starts to oscillate.

The second instability region will happen when the vortex shedding alters due to increasing velocity. The frequency of drag force oscillation in this region is two times the Strouhal frequency. The large amplitude in-line vibrations will occur again when the in-line frequency becomes equal to the natural frequency of the system$,{f}_{N}$. [15]

When the velocity increases further, the vortex shedding pattern is changed. The response amplitude then is increased concerning vortex shedding formation. Some research demonstrated that the current speed is up to 0.5 [m/s] near a sea bed [16]. But there are still no data about pure in-line vibration response in higher reduced velocity $5<{\mathrm{V}}_{\mathrm{R}}$ occurs in some cases in oil and gas fields such as jumpers and pipelines.

King [11] conducted a series of experiments for the full and model scales. He demonstrates that the maximum amplitude response for the model and full scales occurs in different reduced velocities. He also showed the trend of model oscillation is discrete and has two distinct instability regions, while the full-scale trend is continuous within the range.

The maximum amplitude in 1st and 2nd instability regions and the range of reduced velocity in which VIVx occurs strongly depend on the mass-damping parameter, ${C}_{n}=2{m}^{*}\delta$, where ${m}^{*}$ is the mass ratio, and $\delta$ is the logarithmic decrement of the system’s damping [12]. Most of the previous studies of VIVx have concentrated on relatively low $Re$. The conducted experiments mainly lie in the subcritical regime.

Okajima et al. have studied in-line vibration (VIVx) of a circular cylinder experimentally by two types of free-oscillation tests in a water tunnel at subcritical Reynolds numbers [17]. The rigid cylinder models were either elastically supported or cantilevered. They have concluded that for circular cylinder elastically supported, two kinds of excitation appear as observed in earlier research. The response amplitudes also are sensitive to the mass-damping parameter ${C}_{n}=2{m}^{*}\delta$. In contrast, two distinct regions were not observed in the cantilevered circular cylinder, and the trend is continuing in range.

They recorded two distinct instability regions in 1.2 < V_R < 3.8, which are characterized by two different types of vortex shedding as below:

• 1.2 < V_R < 2.5: shed symmetrically

• 2.7 < V_R < 3.8: shed alternately

They also expressed that VIVx occurs on ${C}_{n}$<1.2 and V_R > 1.2, while VIVy happens on ${C}_{n}$ <17 and V_R > 4.5. The amplitude of VIVy is up to an order of magnitude larger than VIVx.

The regime of the streamwise response of a cylinder was characterized by Aguirre [14]. He reported that at the 1st instability region, there is shedding of pairs of simultaneous eddies. In contrast, in the 2nd region, there is alternating shedding in which a pair of eddies is being shed. The mode competition has been investigated in VIVx by Cagney and Balabani [18]. They observed two branches in the cylinder response regime. Their findings demonstrated in the 1st branch, the wake mode S-I and A-II have occurred. Based on their study, the A-II mode is dominant for over 90% of the cylinder examined, while the S-II mode is more unstable. They described the response of a cylinder in streamwise VIV in terms of “true reduced velocity” ${V}_{R}St/{f}^{*}$, where $St$ is Strouhal number, and ${f}^{*}$ is the frequency ratio of VIV response. This term was proposed to account for the variations in the actual cylinder response frequency due to the added mass.

Okajima et al. [12] studied the sensitivity of the amplitude response of in-line VIV to the mass-damping parameter. They also confirmed there are two distinct excitation regions. They found the amplitude of VIVx response is very sensitive to ${C}_{n}$ (mass-damping ratio), especially in the 1st region in which the symmetric vortices appear. They also observed the symmetric vortex shedding and alternate vortex in the 1st and 2nd excitation regions, respectively.

Nishihara et al. [19] measured the fluid forces on a cylinder in a current water channel at subcritical $Re$ by forced oscillation experiments in the streamwise direction. Their study confirmed the existence of two distinct instability regions, which he described as negative added damping. The flow visualization also showed that the wake breathing and typical symmetric vortex shedding appear in the 1st excitation region. He observed asymmetric vortex shedding in the 2nd excitation region.

Although several researchers have investigated VIVx, their studies have been limited to the reduced velocity lower than 5 in 1-DOF. Some researchers have studied VIVx in 2-DOF and reported that the response amplitude of VIVx is increasing in higher reduced velocity [20] & [21]. The literature review regarding 1-DOF and 2-DOF of VIVx for free vibration is summarized in Table 1.

Table 1 Summary of the findings from previous researches

From Table 1, it is apparent that all experiments have been performed in subcritical regime flow. The stability parameter (${C}_{n}$) was also kept less than 1, which the VIVx is likely to occur. The aspect ratio among the literature review is around ten except King [11] who studied the full model. Table 1 also indicates that the maximum response amplitude among both instability regions may occur either in the 1st or 2nd region.

The effect of Reynolds number on the response amplitude and frequency of a circular cylinder undergoing cross-flow VIV has been investigated extensively by previous researchers [6, 20], and [22]. However, $Re$ effect has not been studied so far in the case of pure in-line vortex-induced vibration.

This paper provides an experimental study of the structural response of a circular cylinder to move freely in the streamwise direction in different Reynolds number regimes. The paper aims to introduce a non-dimensional parameter (effective stiffness) to analyze VIV response by eliminating the mass ratio (${m}^{*}$) and stiffness ($k$) effects and apply it to different Reynolds number ranges in the subcritical flow regime. Moreover, the findings demonstrate that Reynolds number has an impact on the maximum amplitude, frequency response and the range of the reduced velocity where 1^st and 2^nd instability regions occur. This study also examined the VIVx response of 1-DOF for reduced velocities larger than 5 which has not yet received much attention.

2 Physics of problem

Vortex-induced vibration occurs when a fluid passes over a body. In viscous fluid flows, there is a boundary layer on the body’s surface. For Reynolds number higher than 40, separation of the boundary layer occurs. The separated layer will cause rotation in fluid flow, which then leads to the formation of vortices that are shed from behind the body and travel downstream in the fluid. As a result of this process, vortices are formed and shed on the downstream side of bluff bodies in a current, inducing periodic forces on the body. [23]

The equation of motion that is generally used to characterize a circular cylinder oscillating in the streamwise direction is as below:

$$M\ddot{x} + c\dot{x} + kx = F_{x} \left( t \right)$$

(1)

where $M$ is the total mass of the system ($M = m + \Delta m$, where m and $\Delta m$ are the circular cylinder mass and added masses, respectively), c is the total damping coefficient of the system (structural and hydrodynamic), $k$ is the stiffness of the system, and ${F}_{x}\left(t\right)$ is the fluid force in the streamwise direction. The natural frequency of system (${f}_{N}$) is a function of system stiffness and the total mass. Therefore, by measuring the natural frequency from the decay test in the water, the hydrodynamic effect is considered directly in the calculation.

An approximation for cylinder oscillation and force can be presented as harmonic response:

$$x\left( t \right) = A\sin \left( {\omega t} \right)$$

(2)

$$F\left( t \right) = F_{0} \sin \left( {\omega t + \phi } \right)$$

(3)

where $A$ is maximum oscillation amplitude, ${F}_{0}$ is maximum force response, $\omega$ is angular frequency, and $\phi$ is the phase angle.

3 Dimensionless parameters

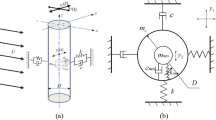
To analyze the VIV phenomenon, it needs to classify all cases of VIV problems with some tools. The best tool that shall be used is called dimensional analysis [24] and [25] have presented that the VIV problem is related to a series of physical parameters as follow:

• Geometry of body: diameter (D), length (L)

• Structural parameter: stiffness (k), damping constant (c), mass (m)

• Fluid flow: free stream velocity (U), fluid viscosity ($\mu$), fluid density ($\rho$)

Figure 1 briefly shows the parameters as mentioned above in VIVx problems.

Fig. 1

Physical parameters in VIVx

The amplitude, A, and the frequency, f, of VIV response are functions of the above-mentioned parameters as follow:

$$A = F\left( {D,\; L, \;k, \;c,\; m,\; U,\; \mu ,\; \rho } \right)$$

(4)

$$f = F\left( {D, \;L,\; k,\; c,\; m, \;U,\; \mu ,\; \rho } \right)$$

(5)

We can re-state the above-mentioned dimensionless groups into the following expressions:

$$\frac{A}{D} = F\left( {{\text{aspect ratio}}, {\text{Re}} ,\; m^{*} , \zeta , V_{R} } \right)$$

(6)

$$\frac{f}{{f_{n} }} = F\left( {{\text{aspect ratio}}, {\text{Re}} , \;m^{*} , \zeta , V_{R} } \right)$$

(7)

The experiments in the present work were performed in the water where the value of fluid density $\rho$ and viscosity $\mu$ is constant and fixed. The aspect ratio is also constant when the experiments are conducted on the same cylinder shape.

Some researchers such as Griffin [26] have considered that $\mathrm{A}/\mathrm{D}$ is dependent on a single parameter ${S}_{G}=2\pi {m}^{*}\zeta$ which he called the mass-damping ratio or the Scruton number. Some other researchers such as King [11] and Okajima [12] have introduced another non-dimensional parameter ${C}_{n}=2{m}^{*}\delta$ called the stability parameter which has the same character as ${S}_{G}$.

In our investigation $\mathrm{A}/\mathrm{D}, f/{f}_{n}$ are evaluated over varying reduced velocity ${V}_{R}$ in constant damping ratio $\zeta$. So instead of altering the mass ratio ${m}^{*}$, current velocity changed. The important non-dimensional parameters in the VIVx investigation are listed in Table 2.

Table 2 Non-dimensional parameters

Gharib [25] has introduced a non-dimensional parameter to investigate the response amplitude and frequency of a cylinder exposed to VIV. This parameter aims to eliminate the structural parameters ($k$ and $m$) from VIV analysis and isolate the contribution of the fluid force, structural forces, inertia, stiffness, and damping [25]. He non-dimensionalized the time and other parameters using the cylinder diameter, $D$, and the flow velocity, $U$. This resulted in development of a new non-dimensional parameter as it is called effective stiffness. Effective stiffness ${k}_{eff}^{*}$ relates the lift coefficient ${C}_{L}$ to the oscillation amplitude $A/D$ (${C}_{L}={k}_{eff}^{*}.A/D$), in the same way that a spring stiffness relates a force $F$ to the spring displacement $y$ ($F=-ky$). He applied this concept to investigate VIVy in 1-DOF. Since this study aims to analyze the VIVx in 1-DOF, the effective stiffness shall be defined for the oscillation in the flow direction.

By considering the general equation of motion for a fluid–structure system, the system can be treated as a mechanical system (left side of equation) with a fluid forcing function (right side of equation):

$$m\ddot{x} + c\dot{x} + kx = 0.5\rho U^{2} C_{{\text{D}}} \left( t \right)L{\text{D}}$$

(8)

where ${C}_{D}$ is the drag coefficient.

Using $U/D$ and $D$ to non-dimensionalize time and space, respectively, one can consider $x=DX, {t}^{*}=tU/D, \partial /\partial t=(\partial {t}^{*}/\partial t)(\partial /\partial {t}^{*})=(U/D)(\partial /\partial {t}^{*})$. Through substitution, one obtains:

$$\frac{{mU^{2} }}{{{\text{D}}^{2} }}{\text{D}}X\prime \prime + \frac{cU}{{\text{D}}}{\text{D}}X\prime + k{\text{D}}X = 0.5\;\rho U^{2} \;C_{{\text{D}}} \left( t \right)\;L{\text{D}}$$

(9)

simplifying and dividing by the right-hand side terms,

$$\frac{{{{2m} \mathord{\left/ {\vphantom {{2m} L}} \right. \kern-0pt} L}}}{{\rho {\text{D}}^{2} }}X\prime \prime + \frac{{{{2c} \mathord{\left/ {\vphantom {{2c} L}} \right. \kern-0pt} L}}}{{\rho U{\text{D}}}}X\prime + \frac{{{{2k} \mathord{\left/ {\vphantom {{2k} L}} \right. \kern-0pt} L}}}{{\rho U^{2} }}X = C_{{\text{D}}} \left( t \right)$$

(10)

renaming terms

$$m^{*} X\prime \prime + c^{*} X\prime + k^{*} X = C_{{\text{D}}}$$

(11)

where

$$m^{*} = \frac{{{{2m} \mathord{\left/ {\vphantom {{2m} L}} \right. \kern-0pt} L}}}{{\rho {\text{D}}^{2} }}, c^{*} = \frac{{{{2c} \mathord{\left/ {\vphantom {{2c} L}} \right. \kern-0pt} L}}}{{\rho U{\text{D}}}}, k^{*} = 0\frac{{{{2k} \mathord{\left/ {\vphantom {{2k} L}} \right. \kern-0pt} L}}}{{\rho U^{2} }}$$

(12)

Comparing identities in the above equations:

$$m^{*} = \frac{{{{2m} \mathord{\left/ {\vphantom {{2m} L}} \right. \kern-0pt} L}}}{{\rho {\text{D}}^{2} }}, \;c^{*} = \frac{{2m^{*} \zeta }}{{U^{*} }},\; k^{*} = \frac{{m^{*} }}{{U^{*2} }},\; f^{*} = \frac{f}{{f_{N} }} = ,\; A^{*} = \frac{A}{{\text{D}}},\; U^{*} = \frac{U}{{\omega_{n} {\text{D}}}}$$

(13)

Assuming a sinusoidal oscillation, $X\left({t}^{*}\right)={A}^{*}\mathrm{sin}\left({\omega }^{*}{t}^{*}\right)$ and fluid force with a phase $\phi$, ${C}_{D}\left({t}^{*}\right)={C}_{D0}\mathrm{sin}\left({\omega }^{*}{t}^{*}+\phi \right)$, we proceed with Eq. (11) by substitution:

$$- \omega^{*2} m^{*} A^{*} \sin \left( {\omega^{*} t^{*} } \right) + c^{*} \omega^{*} A^{*} \cos \left( {\omega^{*} t^{*} } \right) + k^{*} A^{*} \sin \left( {\omega^{*} t^{*} } \right) = C_{{{\text{D}}0}} \sin \left( {\omega^{*} t^{*} } \right)\cos \left( \phi \right) + C_{{{\text{D}}0}} \cos \left( {\omega^{*} t^{*} } \right)\sin \left( \phi \right)$$

(14)

Since the above equation is valid for all values of ${t}^{*}$, the coefficients in front of $\mathrm{sin}\left({\omega }^{*}{t}^{*}\right)$ and $\mathrm{cos}\left({\omega }^{*}{t}^{*}\right)$ should be equal:

$$\sin \left( {\omega^{*} t^{*} } \right): \left( { - \omega^{*2} m^{*} + k^{*} } \right)A^{*} = C_{{{\text{D}}0}} \cos \left( \phi \right)$$

(15)

$$\cos \left( {\omega^{*} t^{*} } \right):\quad \quad \quad c^{*} \omega^{*} A^{*} = C_{{{\text{D}}0}} \sin \left( \phi \right)$$

(16)

The term $\left(-{{\omega }^{*}}^{2}{m}^{*}+{k}^{*}\right)$ is called the effective stiffness (${k}_{eff}^{*}$). Since ${k}^{*}=\frac{{m}^{*}}{{{U}^{*}}^{2}}$ and ${\omega }^{*}=\omega D/U=f/{f}_{N}(1/{U}^{*})$, the effective stiffness may be related to the classical parameters in the following manner:

$$k_{{{\text{eff}}}}^{*} = - \omega^{*2} m^{*} + k^{*} = \frac{{m^{*} }}{{U^{*2} }}\left( {1 - \left( {\frac{f}{{f_{N} }}} \right)^{2} } \right)$$

(17)

A series of computational experiments [25] showed that at vanishing values of ${c}^{*}$, the fluid may respond through a single frequency ${f}^{*}$ (pure sine wave response) making ${k}_{eff}^{*}$ the fluid-structural parameter through ${k}_{eff}^{*}.{A}^{*}={C}_{D}$. Varying the values of ${m}^{*}$ and ${k}^{*}$ independently while keeping ${k}_{eff}^{*}=-{{\omega }^{*}}^{2}{m}^{*}+{k}^{*}$ constant resulted in the same flow field, oscillation amplitudes, and frequencies. The ${C}_{D}$ behavior as reported by Gharib [25] and Cagney, et al. [27] was found quite unpredictable.

In the presence of damping, ${c}^{*}$, Eq. (16) gives

$$\left( {k_{{{\text{eff}}}}^{{{*}2}} + \left( {c^{*} \omega^{*} } \right)^{2} } \right)A^{{{*}2}} = C_{{\text{D}}}^{2}$$

(18)

It is also noted that ${c}^{*}=2\zeta {m}^{*}/{U}^{*}$ has similarities with the mass-damping parameter, ${S}_{G}=2\pi {m}^{*}\zeta$, despite ${c}^{*}$ being dependent on ${U}^{*}.$

4 General description of the experimental setup

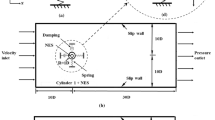
The experimental investigation in this study is based upon the tests conducted in the water current channel of LOC (Laboratório de Ondas e Correntes- Laboratory of Waves and Currents), housed at COPPE/UFRJ’s facility in Rio de Janeiro, Brazil. The current has a closed-circuit circulation system. The water stream passing through the working section is confined at the sidewalls and the bottom. Dimensions of the channel are 22 m × 1.4 m × 1 m (length × breadth × depth). Figure 2 gives an overview of the current channel.

Fig. 2

Overview of the current channel in LOC (Laboratório de Ondas e Correntes- Laboratory of Waves and Currents)

The cylinder was free to move only in the streamwise x. Two rollers and two steel braces were used on each side of the cylinder to reduce the system’s damping and confine the cylinder to oscillate in the x-direction only.

The pendulum setup was used for the VIVx investigation. This setup is advantageous for low-mass ratio experiments [9]. However, the most crucial challenge is to keep the damping ratio of the apparatus very low. The experiment was carried out when the cylinder was initially held at its neutral position, the current velocity increased in small steps, and then, the cylinder was released. The vortex shedding excited the cylinder, and the response amplitude increased till a linear amplitude was reached. The decay tests were performed by first holding the cylinder at an offset position larger than the expected response amplitude at still water. Figure 3 shows a brief schematic diagram of the experimental setup. The length of pendulum bar which connects the cylinder to upper joint is 2.8 m. Fernandes et al. [28] compared two different experimental setups (translational and pivoted) to analyze the VIV. They found there is no significant difference between the results extracted from these setups. The motion trace marker has been placed at the upper cylinder body.

Fig. 3

Schematic experiment setup

Various cylinders were designed to achieve different possible diameters, mass ratios, and Reynolds numbers. All cylinder models were made of polyvinyl chloride (PVC), and diameters ranged from 40 to 75 mm. All cylinder models were 80 cm long. The length L used to calculate the mass ratios ${m}^{*}$ was 49 cm, which is the length of the cylinder submerged in water.

The springs with an elastic stiffness of 50 N/m were used in all experiments. The springs were 20 cm long and 1.2 cm in diameter before loading. It must be noted that attention was paid to assure the springs were in a linear range. However, some small non-linearities were observed as expected.

The system’s damping was kept minimum by using rollers at all times to increase the possibility of in-line vortex-induced vibration (VIVx). No artificial damping was used in the tests. The damping ratio values reported in each case are based on the linear theory.

The experiments were focused on a single degree of freedom only, i.e., along the in-line direction of the fluid flow. Hence, the cylinder’s motion in the in-line direction was restrained by installing braces on the pendulum arms in the parallel direction. The experiments were conducted in the subcritical flow regime (900 < Re < 33,000), corresponding to a range of reduced velocity ${V}_{R}$, from 1 to 11. Two linear springs were connected to the cylinder in the in-line direction, and they were preloaded to obtain the linear translations over an entire cycle of oscillation. The time-series data were processed in a MATLAB environment to get the amplitudes of motion and their dominant frequencies.

5 Experimental procedure

The experiments consisted of three different cylinder diameters with different mass ratios and natural frequencies. The bottom end of the cylinders was fitted with a cap to ensure water tightness. In all tests, it is considered that the flow conditions are constant over the length of the cylinder (2D flow). Based on the finding of [29] and for this purpose, the lower end of the cylinder is kept $10 mm$ away from the bottom wall of the channel with no end plates to assure that there is no 3D effect at both ends of the cylinder.

The cylinder models were made from PVC, designed as a smooth cylinder, so no roughness effects were considered.  The channel’s draft was fixed at 0.5 m, exposing it to a free surface effect. The cylinders’ structural damping and natural frequency were evaluated by free decay tests conducted before each cylinder experiment. The free decay test for each corresponding cylinder was repeated four times, and the average value was calculated. The damping ratio ($\zeta$) values (%) were observed to vary between 0.45 and 0.57%, and the natural frequencies from 0.5 to 0.9 Hz.

A vertical cylinder of diameter D and length L was elastically mounted along z in a water channel with the free stream velocity $\mathrm{U}$ in the x-direction. The cylinder was attached to a carbon fiber (low mass) tube, installed vertically, and free to move. The motion of the cylinder was restricted to the streamwise direction by mounting two horizontal L bars in the x-direction and two rollers to reduce the friction between the cylinder and the L bars.

The guide frame and pendulum are connected by a universal joint that allows the cylinder’s motion in the streamwise direction. Since the aspect ratio of length to diameter is between 6.5 and 12.5, which is relatively small, the test cylinder is assumed to be rigid [30].

5.1 Water current channel

The current channel section was 1.4 m wide and 1 m depth. The water draft was kept at 50 cm during all tests to reduce the free surface effect. The test section was 24 m long and bounded on two sides by Plexiglas walls and the bottom by a steel wall. The current channel is equipped with four centrifugal pumps to obtain the water flow velocities with circulating water. The pumps’ RPM (Revolutions per Minute) is adjusted by the control board of pumps mounted at the working cabin. Thus, flow velocity could be varied from zero to $0.5 m/s$ at a water level around 0.5 m. The flow velocity in the channel could be regulated from zero to $0. 55 m/s$. The turbulence intensity is less than 5% RMS at the position of the cylinder’s body.

5.2 Motion trace

The Qualisys system was used to capture the oscillation of the cylinders. The Oqus platform (Qualisys) provides motion capture cameras suitable for all possible indoor and outdoor applications. The Oqus cameras are designed to capture accurate motion data with very low latency and work with passive and active markers.

The main feature of the Oqus cameras is the ability to calculate marker positions with accuracy and speed. The markers can be measured at thousands of frames per second, and everything runs off an ordinary laptop. The system becomes truly mobile and straightforward to set up. An efficient processing and rapid marker calculations allow the Oqus system to achieve a total approach to processing 3D/6-DOF reconstruction.

A Qualisys motion capture system (2 Oqus cameras and the QTM software version 2.9) was set up to trace the oscillation of the cylindrical body at 50 frames per second. The setup of the Oqus system is shown schematically in Fig. 4.

Fig. 4

Schematic diagram of QUALISYS setup for experiments

5.3 Flow velocity measurement

An acoustic Doppler velocimetry (ADV) system upstream of water flow was used to record the flow velocity in the flume. An average value and a deviation were recorded for every flume speed. The ADV device used in the experiment has been ADCP (Acoustic Doppler Current Profiler) type, see Fig. 5.

Fig. 5

ADV was installed upstream during the experiments

Acoustic Doppler current profiler (ADCP) measures the flow velocities over a depth range using the Doppler effect of sound waves reflected from particles within the water. The ADCPs utilize the traveling time of the sound to distinguish the position of the moving particles. Doppler current sensor (DCS) is another kind of Doppler type. It also uses the Doppler but ignores the traveling times. DCS typically has a velocity range from 0 to 3 m/s.

On the other hand, travel time devices determine flow velocity by two or more acoustic signals, at least one upstream and one downstream. By measuring the time to travel from the emitter to the receiver, the average water speed can be determined between the two points in both directions. The flow velocity can be measured in three dimensions by using multiple paths. Doppler meters have the advantage that they can determine the water velocity at a considerable range, and in the case of an ADCP, at various ranges.

The software “Vector” was set up to get flow velocity data during all tests. The ADV is suitable for real-time operation or self-contained deployments. According to the manufacturer manual to continuous sampling, the “Vector” also supports deployment planning, real-time data collection, and retrieval. All other sensors are sampled at 1 Hz. As an option, the post-processing program “ExploreV” is also available to review the process and interpret the “Vector” data.

5.4 Experimental procedure

Before each case, the following procedure was followed:

• The moving system and the ADV were checked for alignment.

• The QUALISYS setup was calibrated and tested for alignment.

• The rollers were tested for friction.

• According to the channel walls, the moving system was positioned to move exactly just along flow direction x.

• The system parameters: mass, natural frequency, and damping, were recorded before each case. This procedure was repeated after each set of experiments to ensure the values of mentioned parameters.

• The mass of the structure was measured within 10 g of accuracy.

• The free decay test of the system was carried out before and after each case.

• The Oqus setup and the ADV were calibrated as one system before every set of experiments.

A total number of three cases were examined in this study. The experiment cases would commence from the slowest channel velocity with small increments to obtain as many points as possible within the reduced velocity range. The vibration resulted in a few unsteady oscillations at higher flow velocities close to 0.5 m/s.

The data analysis process was sensitive due to the quasi-periodic nature of the oscillation. Most cases showed non-linearity and time-dependent frequencies in the signals. It was principally due to the lack of perfect synchronization between the oscillation and the vortex shedding. The data were reduced in two manners; the first one using an FFT over the entire signal, since FFT routines proved to be beneficial for linear time series. The second one using the manual procedure to explore extra elements such as noise, time-dependent frequencies, and amplitudes. The other benefit of a manual frequency analysis was focusing on areas where a relatively steady oscillation occurred. The non-dimensional amplitude $A/D$ and frequency, ${f}^{*}$, are plotted as a function of ${V}_{R}$ according to other researchers [11, 17] and [27].

A time period of about three to five minutes was devoted to every reduced velocity point to allow the flow to stabilize in the channel. Qualisys and ADV signals were sampled simultaneously for 120 s with 50 Hz sampling rates directly into the specified computer. The channel pumps’ RPM and the flow condition were recorded manually for redundancy. Table 3 shows the cases considered and corresponding structural parameters ordered in decreasing mass ratio values.

Table 3 List of the cases considered with decreasing diameter

The system parameters: mass, natural frequency, and damping, were recorded before or after each case. The mass of the structure was measured within 10 g of accuracy. The natural frequency of the structure and a first-order approximation to the structural damping using linear theory were deduced. A great effort was made to obtain as many points as possible within the VIV window of $U$.

6 Experimental results

In this section, the experimental results for the VIVx in 1-DOF cases are presented with increasing diameter values and then the Reynolds numbers. The damping ratio, $\zeta$, is slightly different in these cases. However, the detailed behavior observed is quite different. A small number of representative displacement traces are presented along with their corresponding Fourier spectra for every case. The amplitude for each path is based on an equivalent sine wave, i.e., the root mean square of the signal portion ($rms\times \sqrt{2}$) and the frequency is based on the FFT peak. The frequencies and amplitudes were computed only for the traces that were stable throughout their segments. A transient interval was chosen for a qualitative presentation when steady portions were too small. Due to this freedom in selecting the quantity of signal for amplitude and frequency analysis, there may be slight variations between values shown on a given trace and the reduced plots in a few cases. In reduced plots of amplitude and frequency, however, every trace was considered manually. Frequencies were obtained using a combination of FFT and peak counting and the amplitudes large oscillatory segments as explained above.

The data sets are non-dimensionalized in the classical manner as used by [31] and [12] ($A/D$ and ${f}^{*}$ vs. ${V}_{R}$). Also the graph is plotted according to the new non-dimensional parameter, effective stiffness, ($A/D$ and ${f}^{*}$ vs. $-{k}_{eff}^{*}$), discussed in previous sections. As [25] explained, the minus sign in $-{k}_{eff}^{*}$ is chosen to let $-{k}_{eff}^{*}$ increases with increasing $U$. The value of effective stiffness is calculated by (17) and other non-dimensional parameters ($A/D$ and ${f}^{*}$) are measured from experiment results.

6.1 1-DOF oscillation with a diameter of 40 mm

Case	$D \left[mm\right]$	$m [kg]$	$k [N/m]$	${m}^{*}$	$Cn$	${F}_{n} [Hz]$	$Re [{10}^{3}]$
P1	40	3	50	4.88	1.92	0.9	0.9 ~ 18

P1 was the smallest diameter case studied. Its structural parameters are listed above, and it involved a Reynolds number range of 0.9 × 10³ < Re < 1.8 × 10⁴. The free decay test for the cylinder was repeated four times, and the average value was calculated. Figure 6 demonstrates the decay test time series and the natural frequency FFT calculated. The time series of the amplitude ratio (A/D) and the power spectrums are shown in Fig. 7.

Fig. 6

Free decay test for case P1, D = 40 mm, m* = 4.88, Cn = 1.92

Fig. 7

Oscillation traces and frequency spectrum for case P1, D = 40 mm, m* = 4.88, Cn = 1.92 at various reduced velocities

Figure 8 shows the amplitude ratio as a function of reduced velocity in P1. The response amplitude of the first instability region strats at ${V}_{R}=1$ and increases significantly untill it reaches ${V}_{R}=1.4$. The amplitude declines sharply after the maximum peak in the first branch till the end of this region at ${V}_{R}=1.8$.

Fig. 8

Oscillation amplitude ratio vs. Reduced velocity, P1, D = 40 mm, m* = 4.88, Cn = 1.92

The second instability branch has the same trend, and just the maximum amplitude ratio occurs at ${V}_{R}=2.4$ and continues to end of the second branch at ${V}_{R}=3.2$. The maximum peak amplitude ratio in the first and second instability regions is 0.07 and 0.075, respectively. The response amplitude after the second branch increases steadily by increasing the reduced velocity.

The response frequency graph, in this case, shows a steady increase with the reduced velocity ${V}_{R}$ in the first and second instability regions (Fig. 9). The frequency ratio reaches a value of 1 (lock-in) at ${V}_{R}=6.5$ and remains constant till achieving maximum reduced velocity. The frequency response of the cylinder shows there are no signs of lock-in in the first and second instability regions. Although for ${V}_{R}>6.5$, the frequency ratio is close to one, which means, lock-in phenomenon occurs in this reduced velocity range. Unlike VIVy, the amplitude in VIVx during the lock-in phenomenon does not jump to the maximum amplitude, and it increases steadily.

Fig. 9

Oscillation amplitude ratio vs. Reduced velocity, P1, D = 40 mm, m* = 4.88, Cn = 1.92

The general shape of the A/D curve is consistent with other researchers. However, the reduced velocity range and maximum amplitude response are different. Other researchers for the 1-DOF system have not investigated the response amplitude and frequency.

Figure 10 displays the amplitude ratio as a function of the ${-k}_{eff}^{*}$ parameter. As discussed in Sect. 3, this non-dimensional parameter is called effective stiffness, which the structural parameters are vanished to obtain a parameter independent on $k$ and $m$. The effective stiffness parameter includes the effects of structural mass and stiffness, eliminating the need to define specific values for these structural parameters. The non-dimensional damping, ${c}^{*}$, and $Re$, however, do not remain constant in any of the cases presented.

Fig. 10

Amplitude ratio vs. effective stiffness, P1, D = 40 mm, m* = 4.88, Cn = 1.92

The figure is noteworthy for the significant variation in ${k}_{eff}^{*}$ resulting from the wide range of frequency ratio and reduced velocity. As [25] explained, mainly this is because of the ${k}_{eff}^{*}$ parameter was derived for a single frequency oscillation and the non-dimensional damping, ${c}^{*}$, varies during the experiment.

The clustering of amplitude ratio points around $-10<-{k}_{eff}^{*}<0$ in Fig. 10 serves to show the utility of $-{k}_{eff}^{*}$ as a tool of predicting VIV. The value close to zero for the effective stiffness means the frequency ratio is close to one. In other words, when the effective stiffness is zero, the lock-in phenomenon occurs. It is important to note that while $-{k}_{eff}^{*}$ remains around zero and if the damping parameter ${c}^{*}$ declines, it may affect the response amplitude. It explains the different response amplitudes around ${k}_{eff}^{*}$ values of around zero. In other words, while ${k}_{eff}^{*}$ is constant, ${c}^{*}$ causes a decline in A/D. Figure 10 also clarifies that the maximum amplitude does not occur due to the lock-in.

6.2 1-DOF oscillation with a diameter of 50 mm

Case	$D\left[mm\right]$	$m[kg]$	$k[N/m]$	${m}^{*}$	$Cn$	${F}_{n}[Hz]$	$Re[{10}^{3}]$
P2	50	3	50	3.12	1.42	0.633	1.2 ~ 23

Figure 11 demonstrates the free decay test of P2 and the calculated FFT. The displacement signal shown in Fig. 12 is highly unsteady and shows a reduction in mean peak height. The reason for this unsteadiness is not apparent, as the periods in which the cylinder exhibits large or low amplitude vibrations do not correspond to changes in the shedding mode.

Fig. 11

Free decay test for case P2, D = 50 mm, m* = 3.12, Cn = 1.42

Fig. 12

Oscillation traces and frequency spectrum for P2, D = 50 mm, m* = 3.12, Cn = 1.42 at various reduced velocities

The plots of amplitude ratio (Fig. 13) resemble those obtained for P1 (${m}^{*}=1.38$) except for the larger range of ${V}_{R}$ and higher values of $A/D$ in 1^st and 2^nd instability regions. The drop in amplitude ratio at ${V}_{R}=3.5$ is relatively steep. There is no evidence of lock-in, and the amplitude response constantly rises in the range ${V}_{R}>5$.

Fig. 13

Oscillation amplitude ratio vs. Reduced velocity, P2, D = 50 mm, m* = 3.12, Cn = 1.42

As Fig. 14 shows, the frequency ratio tends to increase in the first and second instability regions with no signs of lock-in. The frequency ratio reaches value one (lock-in) at ${V}_{R}=4$ and remains constant till ${V}_{R}=5$. The amplitude response in this range tends to rise with increasing the reduced velocity. For ${V}_{R}>6.5$, the frequency ratio declines steadily with no sign of lock-in.

Fig. 14

Oscillation amplitude ratio vs. Reduced velocity, P2, D = 50 mm, m* = 3.12, Cn = 1.42

Figure 15 displays the amplitude ratio as a function of effective stiffness. If there is any lock-in phenomenon ($f={f}_{N}$), based on Eq. (17), the effective stiffness equals to zero. The graph shows that the maximum amplitude in both instability regions does not occur due to the lock-in phenomenon. The clustering of data points around zero (lock-in region) shows that most of oscillations in the reduced velocity range $4<{V}_{R}<5.5$ are close to the natural frequency.

Fig. 15

Oscillation amplitude ratio vs. Reduced velocity, P2, D = 50 mm, m* = 3.12, Cn = 1.42

6.3 P3: 1-DOF oscillation with a Diameter of 75 mm

Case	$D\left[mm\right]$	$m[kg]$	$k[N/m]$	${m}^{*}$	$Cn$	${F}_{n}[Hz]$	$Re[{10}^{3}]$
P3	75	3	50	1.38	1.11	0.5	1.7 ~ 33

P3 was the largest diameter case studied. Its structural parameters are listed above. The oscillations occurred over an extensive range of free stream velocities with 1.7 × 10³ < Re < 3.3 × 10⁴. The free decay test for the cylinder was repeated four times, and the average value was calculated. Figure 16 demonstrates the decay test time series and the natural frequency calculated by FFT. The time series of the amplitude ratio (A/D) and the power spectrums are shown in Fig. 17.

Fig. 16

Free decay test for case P3, D = 75 mm, m* = 1.38, Cn = 1.11

Fig. 17

Oscillation traces and frequency spectrum for case P3, D = 75 mm, m* = 1.38, Cn = 1.11, at various reduced velocities

Figure 18 shows the amplitude ratio as a function of the reduced velocity. The first and second response branches occur in the reduced velocity ranges $1.8<{V}_{R}<2.9$ and $3.2{<V}_{R}<4.5$, respectively, and beyond the second response branch, the amplitude ratio after reduced velocity 4.6 shows a steady increase with the current velocity till ${V}_{R}=9.5$. The amplitude of oscillation in the first instability region reaches a value of $A/D\approx 0.11$ at ${V}_{R}=2.4$. The cylinder vibration amplitude in the second branch is increased to $A/D\approx 0.12$ at ${V}_{R}=4$, almost similar to that seen before the onset of the first branch. The general shape of the $A/D$ curve is according to those reported by [11]. The graph does not indicate zero amplitude in the valley between the first and second instability regions, unlike those reported by [12].

Fig. 18

Oscillation amplitude ratio vs. Reduced velocity, P3, D = 75 mm, m* = 1.38, Cn = 1.11

Although this case has the least mass ratio among other cases, the oscillation begins in higher reduced velocity (${V}_{R}=1.7$). The maximum amplitude and the reduced velocity range in both instability regions are higher than in other cases. Despite the lower mass ratio, oscillations, in this case, are relatively less stable than others. This is in contrast with the findings of Stappenbelt et al. [21], which the oscillation of the cylinder in 2-DOF is more stable in the lower mass ratio.

The frequency ratio, as demonstrated in Fig. 19, slowly increases from beginning along the first and second branches and then quickly declining beyond ${V}_{R}=4$. The frequency response in both instability regions does not indicate any signs of lock-in. However, it continues constantly around one after ${V}_{R}=7$. The graph shows a sudden increase in frequency response related to the maximum amplitude in the first branch. The steady frequency ratio increases with the reduced velocity, evident in Fig. 19.

Fig. 19

Frequency response vs. Reduced velocity, P3, D = 75 mm, m* = 1.38, Cn = 1.11

The behavior of the effective stiffness in Fig. 20 is different from previous cases. The clustering of amplitude ratio points in range $0<-{k}_{eff}^{*}<20$ shows that most of oscillations occur with a frequency ratio of more than one. Whereas the zero value of $-{k}_{eff}^{*}$ is related to the lock-in phenomenon; in this case, the amplitude ratio of higher reduced velocities fits in the region.

Fig. 20

Effective stiffness, P3, D = 75 mm, m* = 1.38, Cn = 1.11

The 1-DOF oscillation experiments with a low mass ratio showed no signs of lock-in for the first and second stability regions. Despite that, the lock-in phenomenon was observed for higher reduced velocity (${V}_{R}>4$). A comparison of the experimental conditions to those of [17] would most likely attribute the lack of lock-in to the small values of mass ratio and damping (${m }^{*}=1.38$, $\zeta =0.004$). However, Aguirre [14] and Jauvits and Williamson [20] observed the lock-in in the first and second branches, respectively.

The experiments were designed to achieve a wide range of mass ratios and one-dimensionality to study the effects of each element. As seen in the experiments, many 1-DOF runs were exhibited no lock-in behavior. It was hence concluded that the number of degrees of freedom (1-DOF vs. 2-DOF motion) is not the reason behind the lock-in mystery. Furthermore, the variations in the mass ratio ${m }^{*}$ can play an important role.

To observe the wake of the models in pure in-line vortex-induced vibration (VIVx) in the lack of particle image velocimetry (PIV), the flow visualization was employed to study the vortex patterns. The flow visualization was performed using the reflection of light on the free surface of the current to observe the Von Karman vortex street in the wake of the oscillating cylinder in the flow direction. Images were captured using a camcorder, and finally, image processing filters were employed to get clear images.

Figure 21 (a), (b), and (c) shows the S-I wake mode for three different cylinders diameters, in which the vortices are being shed symmetrically from both sides of the cylinder. In Fig. 21 (d), (e), and (f), the cylinders are undergoing the SA wake mode. These wake modes occur in first and second instability regions, simultaneously, as expected and reported by other researchers [11, 12], and [32].

Fig. 21

Wake modes in the first and second instability regions

King has concluded that when a cylinder responds to vortex shedding, it affects the flow, the Strouhal number, and the steady drag forces [31].

7 Conclusion

The pure in-line vortex-induced vibrations (VIVx) of a rigid circular cylinder have been studied based on the free vibration cases. Several configurations were employed in experiments to study a circular cylinder immersed in a current channel and allowed to oscillate in the flow direction (VIVx).

The literature review indicated that despite VIVx has been studied by several researchers, the cylinder response was limited to the reduced velocity range ${V}_{R}<4.5$. No previous studies have performed the experiments for larger reduced velocities associated with an oscillating cylinder in free vibration.

The experiment configurations were designed, which let the cylinder move only in the flow direction. The response amplitude and frequency were measured using the Qualisys system, in the Reynolds number range 1000–28,000.

The response amplitude and frequency were examined for a wider range of reduced velocity and different cylinder diameters. The response amplitude was characterized by two instability regions, separated by a valley (low amplitude region), consistent with the previous literature experiments. The amplitude response after the second branch rises steadily by increasing the reduced velocity.

The first response branch for all configurations commenced at the range ${V}_{R}\sim 1$, but the reduced velocity range in 1^st and 2^nd instability regions was different in each case. The experiments indicated that increasing Re caused a wider range for both instability regions in subcritical flow regime. Although the wake modes in experiments were not captured due to the lack of PIV system, the wake formation in both branches was observed visually during the tests.

The non-dimensional parameter of effective stiffness (${k}_{eff}$) for VIVx was introduced in this investigation based on the previous studies of VIVy, and the graph of response amplitude was plotted as a function of ${k}_{eff}$. According to the equation, the effective stiffness is a combination of the reduced velocity and frequency ratio, and also the structural parameters such as ${m}^{*}$ and ${k}^{*}$ are vanished in the equation. So, the amplitude response may be examined by a unique non-dimensional parameter.

The graphs of effective stiffness indicated that the maximum peak amplitudes in first and second instability regions do not occur because of lock-in. Although the clustering of data points in zero value of effective stiffness demonstrated lock-in phenomenon in higher reduced velocity, the amplitude continues to rise slowly till maximum tested current velocity.

The experiment results support the existence of two distinct and separated instability regions in VIVx for ${V}_{R}<5$. However, there is no zero amplitude in the valley between the two branches, which has been observed by some previous researchers. The experiment’s findings also reveal the slightly increasing response amplitude for ${V}_{R}>5$. Other researchers have not studied this range for 1-DOF cases.