Abstract
A continuum-based approach for simultaneously controlling the motion and shape of soft robots and materials (SRM) is proposed. This approach allows for systematically computing the actuation forces for arbitrary desired SRM motion and geometry. In order to control both motion and shape, the position and position gradients of the absolute nodal coordinate formulation (ANCF) are used to formulate rheonomic specified trajectory and shape constraint equations, used in an inverse dynamics procedure to define the actuation control forces. Unlike control of rigid-body systems which requires a number of independent actuation forces equal to the number of the joint coordinates, the SRM motion/shape control leads to generalized control forces which need to be interpreted differently in order to properly define the actuation forces. While the definition of these motion/shape control forces is demonstrated using air pressure actuation commonly used in the SRM control, the proposed procedure can be applied to other SRM actuation types. The approaches for determining the actuation pressure in the two cases of space-dependent and constant pressures are outlined. Effect of the change in the surface geometry on the actuation pressure is accounted for using Nanson’s formula. The obtained numerical results demonstrate that the motion and shape can be simultaneously controlled using the new actuation force definitions.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Robots, which are among the most important, widely used, and versatile machines, are critical to the technological competitiveness in many industry sectors including aerospace, automotive, health care and rehabilitation, food, and construction and agricultural machine industries. Because these machines are made of compliant components with varying degrees of stiffness, design optimization and weight reduction are necessary for efficient and economic operations. Nonetheless, undesirable deviations can negatively impact the robot performance, precision and accuracy, and repeatability. These deviations characterize most robots including material handling, welding, assembly, and dispensing robots, which, respectively, account for 38%, 29%, 10%, and 4% of the robots used by the industry [1]. Because robots are designed to increase productivity, ensure safety, and extend capabilities beyond human limitations, accurate robot mathematical modeling and virtual prototyping is critical for advancing this technology.
More emphasis has been placed recently on using robots made of soft materials, which have complex geometries. Nonetheless, because the mathematical foundation of such soft-robot systems has not been adequately established, our knowledge of their mechanics remains incomplete, making it difficult to advance this technology at a faster pace. For example, there are no well-established continuum-based approaches for the motion/shape control (MSC) of soft robots and materials (SRM). New mathematical models are needed to correctly capture the effect of deformations, allow implementing nonlinear and nonconventional constitutive models, and accurately define the control actuation forces using both conventional and nonconventional methods. This is particularly true for soft robots whose stability due to the large deformation and use of unconventional actuations is a major concern. Furthermore, soft robots may be designed to squeeze through groves and gaps for painting, spraying, and debris cleaning, and therefore, may undergo significant change in geometry. Because of the lack of a systematic MSC approach, SRM actuation forces are determined, for the most part, based on experimentation, which can be time-consuming, costly, and less effective. This paper develops a new approach to address this serious limitation in the SRM design.
Most robot investigations have been concerned with rigid link or small-deformation problems [2,3,4,5,6,7,8,9,10,11,12]. In the case of small deformation, the most popular approach is the floating frame of reference (FFR) formulation [13, 14]. While use of the FFR formulation creates a local linear problem that can be exploited to reduce the number of coordinates, use of such an approach has been limited to small-deformation problems and is not suited for the SRM motion/shape control. Furthermore, conventional structural finite elements (FEs), such as beams and plates, are based on kinematic description that does not allow for describing the geometry accurately, is not invariant under an orthogonal rigid-body transformation, and is not related by a linear mapping to computational geometry methods such as B-splines and NURBS [15,16,17,18,19,20,21,22,23,24].
Unlike conventional robots, soft robots are designed with higher number of degrees of freedom to provide higher degree of mobility and flexibility, have lower weight, and provide safe interactions with environments and objects [25,26,27,28,29,30,31,32,33,34]. Conventional robots are made of materials that have high modulus of elasticity in the range of \(10^{9} - 10^{12}\) Pa, and their motion is controlled using linear actuators and motors. On the other hand, soft robots are made of soft materials that have low modulus of elasticity in the range of \(10^{4} - 10^{9}\) Pa [26].
2 Scope and contributions of this investigation
There is no, in existence today, an agreed-upon approach for the SRM modeling, design, and actuation, which are based, for the most part, on simplified, experimental, and/or trial-and-error procedures that require building costly prototypes. Unlike other robot types, SRM designs may require use of complex geometry to enhance performance and strength and to provide superior dexterity and access to gaps and grooves. It is the objective of this study to develop a new continuum-based approach that can be effectively used to simultaneously control the motion and shape of soft robots.
In the soft-robot design process, accurate prediction of the reference configuration geometry, change in the geometry during the robot functional operation, actuation control forces, and stresses due to elastic deformations contribute to ensuring precision, durability, proper load handling, and robustness of the control design. It is the goal of this study to develop a new approach for achieving this goal. The contributions of this investigation are summarized as follows:
-
1.
A new continuum-based approach for SRM motion and shape control is developed. A review of SRM literature revealed lack and need of such an approach to advance the SRM technology.
-
2.
A systematic procedure to determine the actuation control forces that achieve the desired motion trajectories and shapes is developed, and its use is demonstrated using air pressure actuation. A similar procedure can be used for other actuation types.
-
3.
The paper describes new inverse dynamics procedure for the SRM generalized control forces. Unlike rigid-body systems, the SRM inverse dynamics problem may require numerical integration of nonlinear equations in order to determine the actuation forces.
-
4.
Generalization of the SRM approach is made by introducing a procedure for the numerical reconstruction of the SRM geometry from discrete data points that can be obtained using measurements and imaging techniques.
-
5.
A new method for computation of the actual actuation forces from the generalized control forces predicted using the inverse dynamics solution is introduced. The procedure is demonstrated using air pressure actuation. The two cases of space-dependent and constant actuation pressures are considered. In the procedure used in this study, the effect of the change in the surface geometry on the actuation pressure is accounted for using Nanson’s formula.
-
6.
Several examples are presented to demonstrate the use of the new approach in the SRM motion/shape control. In these examples, different geometry configurations are considered.
This paper is organized as follows. In Sect. 3, the concept of motion/shape control is introduced. Section 4 explains the formulation of the rheonomic constraints of the inverse dynamics problem using the ANCF position gradients. Section 5 discusses the fully and partially constrained inverse dynamics problem, while Sect. 6 uses the concept of the equipollent system of forces to provide explanation of the generalized forces associated with the ANCF position gradients. In Sect. 7, numerical reconstruction of the SRM geometry is discussed, and Sect. 8 provides detailed discussion of the SRM actuation forces. Numerical examples are presented in Sect. 9, and summary and conclusions drawn from this investigation are provided in Sect. 10.
3 Motion and shape control
Development of a systematic procedure for simultaneously controlling the motion and geometry is particularly important for SRM systems, often designed to work within specified boundaries. Shape control allows avoiding undesirable contacts that can cause damage of the SRM surface.
3.1 Problem definition
Figure 1 shows a simple example that demonstrates the concept used in this study. In this figure, the stress-free reference configuration is represented by a tapered beam in the horizontal position. A simple scenario, considered for the purpose of demonstration, is to bend the beam centerline to a quarter circle while changing the tapered beam cross section from varying linearly along the length to a constant cross section as shown in the figure. In order to achieve this motion/shape control, a computational procedure that allows for local shape manipulations during the motion is required. Existing FE formulations do not lend themselves easily for solving this problem as will be clear from the discussion presented in this section.
3.2 Position gradients and reference configuration geometry
In the analysis presented in this paper, distinction is made between the stress-free reference configuration geometry, an example of which is defined in Fig. 1 by the initial tapered geometry, and the desired or undesired change in geometry during the motion. This distinction is important in developing a motion/shape control strategy. Accurate description of the stress-free reference configuration geometry is particularly important in the SRM systems with surfaces characterized by complex shapes. Furthermore, such a reference configuration geometry serves as the reference and basis for defining geometry changes that evolve during the robot functional operation.
To facilitate the development of the FE kinematics, for the most part, the displacement fields are defined in a straight configuration in terms of a set of coordinates or parameters \({\mathbf{x}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } \\ \end{array} } \right]^{T}\), as shown in Fig. 2. The global position of an arbitrary point on the element can be defined in terms of these parameters as \({\mathbf{r}}\left( {{\mathbf{x}},t} \right) = {\mathbf{S}}\left( {\mathbf{x}} \right){\mathbf{e}}\left( t \right)\), where \({\mathbf{S}}\) is the FE shape function matrix, \({\mathbf{e}}\) is the vector of element nodal coordinates, and \(t\) is time. Having the position gradients as nodal coordinates allows for conveniently defining the stress-free initial geometry as well as the geometry due to the deformation. To this end, the vector of nodal coordinates used in this investigation consists of position and position-gradient coordinates. For a node \(k\) of an element \(j\), the nodal coordinates are defined as
In this equation, \({\mathbf{r}}^{jk}\) is the global position vector of the node, and \({\mathbf{r}}_{{x_{l} }}^{jk} = {{\partial {\mathbf{r}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}} {\partial x_{l} ,\;l = 1,2,3}}} \right. \kern-\nulldelimiterspace} {\partial x_{l} ,\;l = 1,2,3}}\), are the position-gradient vectors defined at the node by differentiation with respect to the coordinates \(x_{l} ,\) using this vector of nodal coordinates, the stress-free reference configuration geometry can be systematically defined using the equation
In this equation, \({\mathbf{e}}_{o}\) is the vector of nodal coordinates that defines the desired stress-free reference configuration geometry. For example, the tapered geometry shown in Fig. 1 can be systematically obtained by using a stretch factor \(\alpha_{k}\) for the position-gradient vector \({\mathbf{r}}_{{x_{2} }}^{k} ,\;k = 1,2, \ldots ,n_{n}\), at the nodes such that \({\mathbf{r}}_{{x_{2} }}^{k} = \alpha_{k} \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right]^{T}\), where \(n_{n}\) is the number of nodes. The use of the straight configuration defined by the coordinates \({\mathbf{x}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } \\ \end{array} } \right]^{T}\) is convenient for carrying out the integrations and differentiations. In continuum mechanics, this is accomplished using the matrix of position-gradient vectors \({\mathbf{J}}_{o} = {{\partial {\mathbf{X}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{X}}} {\partial {\mathbf{x}}}}} \right. \kern-\nulldelimiterspace} {\partial {\mathbf{x}}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{X}}_{{x_{1} }} } & {{\mathbf{X}}_{{x_{2} }} } & {{\mathbf{X}}_{{x_{3} }} } \\ \end{array} } \right]\). Using this matrix, one can write \(dV_{o} = J_{o} dV_{s}\), where \(V_{s}\) and \(V_{o}\) are, respectively, the volumes in the straight and reference configurations, and \(J_{o} = \left| {{\mathbf{J}}_{o} } \right|\) is the determinant of the matrix of position-gradient vectors that accounts for the stress-free reference configuration. The relationship between the current and straight configurations is defined by the position-gradient matrix \({\mathbf{J}}_{e} = {{\partial {\mathbf{r}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}} {\partial {\mathbf{x}}}}} \right. \kern-\nulldelimiterspace} {\partial {\mathbf{x}}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{r}}_{{x_{1} }} } & {{\mathbf{r}}_{{x_{2} }} } & {{\mathbf{r}}_{{x_{3} }} } \\ \end{array} } \right] = \left( {{{\partial {\mathbf{r}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}} {\partial {\mathbf{X}}}}} \right. \kern-\nulldelimiterspace} {\partial {\mathbf{X}}}}} \right)\left( {{{\partial {\mathbf{X}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{X}}} {\partial {\mathbf{x}}}}} \right. \kern-\nulldelimiterspace} {\partial {\mathbf{x}}}}} \right) = {\mathbf{JJ}}_{o}\), where \({\mathbf{J}} = {{\partial {\mathbf{r}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}} {\partial {\mathbf{X}}}}} \right. \kern-\nulldelimiterspace} {\partial {\mathbf{X}}}}.\)
4 Shape control during functional operations
The multibody system (MBS) approach, used in this investigation to achieve the SRM motion/shape control, allows defining the desired motion trajectory and geometry using a set of algebraic rheonomic constraint equations. These rheonomic constraints are used in an inverse dynamics procedure to determine expressions for the actuation forces that can be used with both conventional and unconventional actuation methods. If the number of rheonomic constraint equations eliminate all the degrees of freedom, one obtains fully constrained inverse dynamics in which an algebraic system of equations at the acceleration level can be solved for the system accelerations and the constraint forces as explained in the following section. If the rheonomic constraint equations do not eliminate all the degrees of freedom of the model, one obtains partially constrained inverse dynamics in which the solution for the accelerations and constraint forces requires the numerical integration of the independent accelerations.
Motion and geometry control constraints can be defined by specifying positions and position gradients of arbitrary points. It is more convenient and straightforward to use the coordinates at the nodal points of the FE mesh. For example, one can specify the following or a subset of the following rheonomic constraints at a node \(k\) of the FE mesh:
where \({\mathbf{f}}_{p}\) and \({\mathbf{f}}_{g}\) are specified functions that define the desired SRM motion trajectories and geometry. In order to ensure accuracy of the inverse dynamics procedure, the algebraic equations must be satisfied at the position, velocity, and acceleration levels. That is, the following velocity and acceleration constraints must be imposed at the velocity and acceleration analysis steps:
In the case of articulated SRM systems that consist of components which may have different degrees of flexibility, it is convenient to distinguish between the constraint equations imposed on the motion and shape of the soft components and the constraint equations that describe other mechanical joints and motion trajectories of stiffer components [14]. The vector of constraint equations that describe the motion trajectories and shape of the soft components can be written in a vector form as \({\mathbf{C}}_{s} = \left[ {\begin{array}{*{20}c} {C_{s1} } & {C_{s2} } & \cdots & {C_{{sn_{cs} }} } \\ \end{array} } \right]^{T},\) where \(n_{cs}\) is the number of algebraic constraint equations imposed on the motion of the soft components in the system [14].
The position-gradient constraints, in particular, allow for the local shape manipulations and for effectively describing the rotations, stretches, and shears. Generalized actuation forces associated with these gradient constraints will be defined, and the concept of the equipollent system of forces is used to convert these constraint forces to actual actuation forces that can be used in practice as described in a later section of this paper. Furthermore, if \(n_{cs} = n_{d},\) where \(n_{d}\) is the number of system degrees of freedom, the motion/shape constraints can be determined efficiently by solving a sparse system of algebraic equations without the need for performing numerical integration. This is the case of fully constrained inverse dynamics. If on the other hand, \(n_{cs} < n_{d}\), which is the case of partially constrained inverse dynamics, numerical integration of the independent equations is necessary. More motion/shape constraints may require more actuation power to achieve the desired trajectories and geometries.
5 Fully and partially constrained inverse problems
The inverse dynamics problem is widely used for determining the actuation forces used to control rigid-body robot manipulators. In this case, the end-effector motion can be specified using six algebraic equations that define the kinematics of the six-degree-of-freedom robot system. The motion of a rigid-body robot can be completely controlled using a combination of six actuators or motors whose forces and moments are determined using the inverse dynamics problem. While a similar concept can be used for soft robots, the soft-robot geometry and actuation introduce new fundamental issues that need to be considered.
5.1 Specified motion trajectories and shapes
Because the deformable bodies of the SRM systems have an infinite number of degrees of freedom, the control and actuation approach used for rigid-body systems is no longer applicable. In this paper, an inverse dynamics approach is used in which the motion and geometry are prescribed using a set of algebraic constraint equations \({\mathbf{C}}_{s} \left( {{\mathbf{q}},t} \right) = {\mathbf{0}},\) where \({\mathbf{q}}\) is the vector of the system coordinates that may include the coordinate vector \({\mathbf{e}}\) that defines the configuration of the soft components. The constraint equations \({\mathbf{C}}_{s} \left( {{\mathbf{q}},t} \right) = {\mathbf{0}}\) can be of the rheonomic (explicit function of time) type and can describe the evolution of the shape of the soft component during the actuation process. Other constraint equations that define other specified motion trajectories and mechanical joints in the case of articulated robot systems are denoted as \({\mathbf{C}}_{m} \left( {{\mathbf{q}},t} \right) = {\mathbf{0}}\). Some of the constraint equations in the vector \({\mathbf{C}}_{m} \left( {{\mathbf{q}},t} \right) = {\mathbf{0}}\) can be of the scleronomic (not explicit function of time) type. Therefore, the total vector of algebraic equations can be written as \({\mathbf{C}}\left( {{\mathbf{q}},t} \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{s}^{T} } & {{\mathbf{C}}_{m}^{T} } \\ \end{array} } \right]^{T} = {\mathbf{0}}\).
5.2 Constrained dynamic equations
The system equations of motion can be written as \({\mathbf{M}}\ddot{\mathbf{q}} = {\mathbf{Q}}_{e} + {\mathbf{Q}}_{c},\) where \({\mathbf{M}}\) is the system mass matrix, \({\mathbf{Q}}_{e}\) is the vector of applied forces, and \({\mathbf{Q}}_{c}\) is the vector of constraint forces. The vector of constraint forces can be written as
In this equation, \({\mathbf{C}}_{{\mathbf{q}}} = {{\partial {\mathbf{C}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{C}}} {\partial {\mathbf{q}}}}} \right. \kern-\nulldelimiterspace} {\partial {\mathbf{q}}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{{s{\mathbf{q}}}}^{T} } & {{\mathbf{C}}_{{m{\mathbf{q}}}}^{T} } \\ \end{array} } \right]^{T}\) is the constraint Jacobian matrix, \({{\varvec{\uplambda}}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\uplambda}}}_{s}^{T} } & {{{\varvec{\uplambda}}}_{m}^{T} } \\ \end{array} } \right]^{T}\) is the vector of Lagrange multipliers, \({\mathbf{C}}_{{s{\mathbf{q}}}} = {{\partial {\mathbf{C}}_{s} } \mathord{\left/ {\vphantom {{\partial {\mathbf{C}}_{s} } {\partial {\mathbf{q}}}}} \right. \kern-\nulldelimiterspace} {\partial {\mathbf{q}}}}\) and \({\mathbf{C}}_{{m{\mathbf{q}}}} = {{\partial {\mathbf{C}}_{m} } \mathord{\left/ {\vphantom {{\partial {\mathbf{C}}_{m} } {\partial {\mathbf{q}}}}} \right. \kern-\nulldelimiterspace} {\partial {\mathbf{q}}}}\) are, respectively, the Jacobian matrices of the constraint equations \({\mathbf{C}}_{s}\) and \({\mathbf{C}}_{m}\); and \({{\varvec{\uplambda}}}_{s}\) and \({{\varvec{\uplambda}}}_{m}\) are Lagrange multipliers associated, respectively, with the constraint equations \({\mathbf{C}}_{s}\) and \({\mathbf{C}}_{m}\). Differentiation of the constraint equations twice with respect to time defines the constraint equations at the acceleration level as
where \({\mathbf{Q}}_{ds}\) and \({\mathbf{Q}}_{dm}\) are vectors that result from the differentiation of the constraint equations twice with respect to time and absorb terms which are not linear in the velocities. Using the equations of motion, \({\mathbf{M}\ddot{\mathbf{q}}} = {\mathbf{Q}}_{e} + {\mathbf{Q}}_{c}\) and the preceding two equations, one obtains the following augmented form of the equations of motion:
This equation can be solved for the acceleration vector \({\ddot{\mathbf{q}}}\) and the vectors of Lagrange multipliers \({{\varvec{\uplambda}}}_{s}\) and \({{\varvec{\uplambda}}}_{m}\).
5.3 Fully and partially constrained inverse dynamics
In the case of the inverse dynamics, there are two different situations which are encountered in the control of soft-robot systems. In the first situation, the number of algebraic constraint equations is equal to the number of coordinates. This is the case of fully constrained inverse dynamics, in which the preceding equation represents a system of algebraic equations which can be solved for the system accelerations and Lagrange multipliers. In this case, there is no need to perform numerical integration since the algebraic constraint equations and their time derivatives completely define the system coordinates, velocities, and accelerations. Because the coefficient matrix in the preceding equation is sparse, the solution of this system can be efficient regardless of the number of coordinates. When ANCF finite elements are used, as it is the case in this investigation, ANCF Cholesky coordinates can be used, leading to a generalized identity inertia matrix.
In the second scenario, the number of constraint equations is less than number of coordinates. This case of partially constrained inverse dynamics arises when all degrees of freedom are not specified. The preceding equation can still be solved using sparse matrix techniques to determine the accelerations and Lagrange multipliers. The independent accelerations can be identified and integrated using direct numerical integration methods to determine the independent coordinates and velocities. The dependent coordinates and velocities can be determined using the constraint equations to ensure that these constraint equations are satisfied at the position, velocity, and acceleration level, avoiding violation of the D’Alembert–Lagrange principle [14].
From the discussion presented above, it is clear that in the case of the fully constrained inverse dynamics, there is no need for the numerical integration and the inverse dynamics problem reduces to solving a system of algebraic equations for the driving constraint forces. In the partially constrained inverse dynamics problem, numerical integration is required in order to determine the constraint forces that define the actuation forces. Nonetheless, in both cases, the vectors of Lagrange multipliers \({{\varvec{\uplambda}}}_{s}\) and \({{\varvec{\uplambda}}}_{m}\) can be used to determine, respectively, the generalized constraint forces, including the generalized actuation forces \({\mathbf{Q}}_{ca} = - {\mathbf{C}}_{{s{\mathbf{q}}}}^{T} {{\varvec{\uplambda}}}_{s}\) associated with the system generalized coordinates. The generalized actuation forces can be used with concept of the equipollent system forces to define the actual actuation forces required to produce the desired SRM motion shape. The two cases of partially and fully constrained inverse dynamics are encountered in the SRM motion/shape control as demonstrated by the numerical examples.
6 Equipollent systems of forces
The concept of equipollent systems of forces is important in the definition of the SRM actuation forces. In rigid-body dynamics, a force that acts at a point is equipollent to another system defined at another point that consists of the same force and a moment. Furthermore, in rigid-body dynamics, the force is a sliding vector and the moment is a free vector. These rigid-body concepts are not applicable to flexible bodies, particularly when position gradients are used as coordinates as in the case of the absolute nodal coordinate formulation (ANCF) [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]. In this section and in the numerical examples, the fully parameterized ANCF planar beam element is considered. This element is used to explain the relationship between the Cartesian forces and the generalized forces associated with the ANCF gradient coordinates. The generalized forces associated with the gradient coordinates are obtained from the solution of the inverse dynamics problem, while the Cartesian force representation can be important in the definition of the actual control forces when certain actuation types are used.
6.1 Element displacement field
The ANCF planar element, shown in Fig. 3, has two nodes, and each node has six coordinates: two position coordinates and four position-gradient coordinates. For a node \(k\) of an element \(j\), the vector of nodal coordinates is defined as \({\mathbf{e}}^{jk} = \left[ {\begin{array}{*{20}c} {{\mathbf{r}}^{{jk^{T} }} } & {{\mathbf{r}}_{{x_{1} }}^{{jk^{T} }} } & {{\mathbf{r}}_{{x_{2} }}^{{jk^{T} }} } \\ \end{array} } \right]^{T} ,\;j = 1,2\), where \({\mathbf{r}}^{jk}\) is the global position of the node, \({\mathbf{r}}_{{x_{l} }}^{jk} = {{\partial {\mathbf{r}}^{jk} } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}^{jk} } {\partial x_{l} }}} \right. \kern-\nulldelimiterspace} {\partial x_{l} }},\;l = 1,2\), is the position-gradient vector evaluated at node \(k\), as shown in Fig. 3, and \({\mathbf{x}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } \\ \end{array} } \right]^{T}\) is the element spatial coordinates. The displacement field of the element is defined as \({\mathbf{r}}^{j} \left( {{\mathbf{x}},t} \right) = {\mathbf{S}}^{j} \left( {\mathbf{x}} \right){\mathbf{e}}^{j} \left( t \right)\), where \({\mathbf{r}}^{j}\) is the position of an arbitrary point on the element, \({\mathbf{S}}^{j}\) is the element shape function matrix, \({\mathbf{e}}^{j} = \left[ {\begin{array}{*{20}c} {{\mathbf{e}}^{{j1^{T} }} } & {{\mathbf{e}}^{{j2^{T} }} } \\ \end{array} } \right]^{T}\), and \(t\) is time. The shape function matrix can be written as \({\mathbf{S}}^{j} \left( {\mathbf{x}} \right) = \left[ {\begin{array}{*{20}c} {s_{1} {\mathbf{I}}} & {s_{2} {\mathbf{I}}} & {s_{3} {\mathbf{I}}} & {s_{4} {\mathbf{I}}} & {s_{5} {\mathbf{I}}} & {s_{6} {\mathbf{I}}} \\ \end{array} } \right]\), where the shape functions \(s_{i} ,\;i = 1,2, \ldots ,6\), are defined as [54]
where \(\xi = {{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } l}} \right. \kern-\nulldelimiterspace} l}\), \(\eta = {{x_{2} } \mathord{\left/ {\vphantom {{x_{2} } l}} \right. \kern-\nulldelimiterspace} l}\), and \(l\) is the length of the beam element.
6.2 Equipollent systems
The virtual work of a force vector \({\mathbf{F}}\) acting at an arbitrary point \(P\) of the element, as shown in Fig. 3, can be written as
where \({\mathbf{x}}_{P}\) is the vector that defines the coordinates of point \(P\) in the element coordinate system. Using the shape function matrix of the element, one can write
where in this equation the shape functions \(s_{i}\) are evaluated at the point of application of the force vector \({\mathbf{F}}\), that is, \(s_{i} = s_{i} \left( {\xi_{P} ,\eta_{P} } \right),\;i = 1,2, \ldots ,6\), and \(\xi_{P}\) and \(\eta_{P}\) are the dimensionless parameters defined at point \(P\). The preceding equation demonstrates that a force vector \({\mathbf{F}}\) acting at an arbitrary point on a flexible beam is equipollent to system forces associated with the position and gradient coordinates and defined as
The vectors \({\mathbf{Q}}_{t1}\) and \({\mathbf{Q}}_{t2}\) are associated with the translational coordinates \({\mathbf{r}}^{j1}\) and \({\mathbf{r}}^{j2}\) of the two nodes of the element, while the forces \({\mathbf{Q}}_{g11} ,\;{\mathbf{Q}}_{g12} ,\;{\mathbf{Q}}_{g21}\), and \({\mathbf{Q}}_{g22}\) are associated with the position-gradient coordinates at the two nodes. It is clear that the forces \({\mathbf{Q}}_{t1}\) and \({\mathbf{Q}}_{t2}\) have the unit of forces and \({\mathbf{Q}}_{t1} + {\mathbf{Q}}_{t2} = {\mathbf{F}}\), while \({\mathbf{Q}}_{g11} ,\;{\mathbf{Q}}_{g12} ,\;{\mathbf{Q}}_{g21}\), and \({\mathbf{Q}}_{g22}\) have the units of moments. One can always convert the forces of the preceding equations defined at a point to linear actuator force and motor moment. For example, if one selects coordinates defined by the translation \({\mathbf{R}} = \left[ {\begin{array}{*{20}c} {R_{1} } & {R_{2} } \\ \end{array} } \right]^{T}\) of the first node and the rotation \(\theta\) (rigid-body displacement), one has
The virtual change in these vectors leads to
Using these equations, one can show that in the case of rigid-body coordinates, one has
From the definitions of the shape functions, it is clear that \(s_{1} + s_{4} = 1\), \(s_{2} + s_{4} l + s_{5} = \xi l\), and \(s_{3} + s_{6} = \eta l\). With the use of these identities, the preceding equation reduces to
which shows that a force at a point is equipollent to a force and a moment at another point.
7 Numerical reconstruction of geometry
For the development of a systematic procedure for SRM actuations, it is important to describe accurately the desired SRM configurations and geometry during the functional operation. In applications, in which the SRM geometry at different configurations is specified, the ANCF nodal coordinates, including the position gradients, need to be determined in order to define the rheonomic motion/shape constraint equations required to obtain the desired motion trajectories and geometries. This section proposes a procedure for describing numerically the SRM geometry assuming that this geometry is defined in terms of discrete data points, which can be determined from assumed desired shapes or can be obtained using scanning, measurements, or imaging techniques. It is explained how to determine the ANCF nodal coordinates if a desired shape defined by discrete points is provided.
In order to ensure the existence of a solution to the computational geometry problem, the displacement field of the element \({\mathbf{r}}^{j} \left( {{\mathbf{x}},t} \right) = {\mathbf{S}}^{j} \left( {\mathbf{x}} \right){\mathbf{e}}^{j} \left( t \right)\) is multiplied by \({\mathbf{S}}^{{j^{T} }} \left( {\mathbf{x}} \right)\) and the result of the multiplication is integrated over the volume to yield
In this equation, \(\rho^{j}\) and \(V^{j}\) are, respectively, the mass density and volume of the element. The integral on the right-hand side of the preceding equation is recognized as the element mass matrix \({\mathbf{M}}^{j} = \int_{{V^{j} }} {\rho^{j} {\mathbf{S}}^{{j^{T} }} \left( {\mathbf{x}} \right){\mathbf{S}}^{j} \left( {\mathbf{x}} \right){\text{d}}V^{j} }\), which is a constant, symmetric, nonsingular matrix for all ANCF finite elements. Therefore, its inverse \(\left( {{\mathbf{M}}^{j} } \right)^{ - 1}\) exists, and Eq. 16 can be used to write
where \({\mathbf{H}}^{j} \left( {{\mathbf{x}},t} \right) = {\mathbf{S}}^{{j^{T} }} \left( {\mathbf{x}} \right){\mathbf{r}}^{j} \left( {{\mathbf{x}},t} \right)\). Given the coordinates of a set of \(p\) points, the integral on the right-hand side of the preceding equation can be approximated using a summation as
In this equation, \(m_{p}^{j}\) is a mass coefficient which can be the same for all the points in the case of even distributions, \({\mathbf{x}}_{p}\) is the vector of spatial coordinates of point \(p\), and \({\mathbf{H}}^{j} \left( {{\mathbf{x}}_{p} ,t} \right) = {\mathbf{S}}^{{j^{T} }} \left( {{\mathbf{x}}_{p} } \right){\mathbf{r}}^{j} \left( {{\mathbf{x}}_{p} ,t} \right),\;p = 1,2, \ldots ,m\). Because the mass matrix \({\mathbf{M}}^{j}\) is nonsingular, a solution of the preceding equation exists. The accuracy of this solution depends on the number of points used to approximate the integral \(\int_{{V^{j} }} {\rho^{j} {\mathbf{H}}^{j} \left( {{\mathbf{x}},t} \right){\text{d}}V^{j} }\). For the single planar beam element considered, full integration (exact) requires the use of six points. Using standard FE assembly, Eq. 18 can be used to define the nodal coordinates, including the position gradients, for a given geometry defined by discrete data points. These nodal coordinates can be used to define the element displacement field \({\mathbf{r}}^{j} \left( {{\mathbf{x}},t} \right) = {\mathbf{S}}^{j} \left( {\mathbf{x}} \right){\mathbf{e}}^{j} \left( t \right)\) at an arbitrary point \({\mathbf{x}}\), ensuring a continuum representation of the SRM kinematics and the position and position gradients that enter into the definition of the inverse dynamics rheonomic constraint equations.
8 Actuation forces
For SRM systems, unconventional actuation forces, such as pressurized air, are used to obtain the desired motion trajectories and geometry. The generalized actuation forces obtained from the solution of the inverse dynamics problem can be used to develop a systematic procedure for the evaluation of the actuation forces, including air pressure, required to achieve the specified motion trajectories and the desired geometry. In this section, a brief discussion of SRM actuation is first presented, the inverse dynamics generalized actuation forces associated with the degrees of freedom are defined, and the more general case of a space-dependent pressure is considered followed by the simpler case of a constant pressure.
8.1 SRM actuation: background
SRM actuation can be classified into three categories: variable length tendon, electroactive polymers (EAPs), and fluidic elastomer actuators (FEAs) [25, 26, 67]. The variable length tendon actuators can be divided into two groups: tension cables and shape memory alloy (SMA). Soft-robot arm inspired by an octopus is a common application in which tension cables are used [68, 69]. These cables are embedded inside the octopus silicon arm, and they are actuated by electric motors placed on an external platform. SMA actuators are used in the soft caterpillar and mesh worm robots [70,71,72,73,74,75]. They are actuated electrically, and they can return to their original undeformed shape at certain temperatures. SMA actuators have the advantage of applying large actuation forces in short time intervals.
Electroactive polymer (EAPs) actuators have the ionic and electronic forms, and their size and shape can be changed using electric field. The electronic EAP has the advantage of high energy density and can produce large actuation force in short time, while the ionic EAP has the advantage of low voltage actuation and large bending displacement [25]. New viscoelastic ANCF solid element was proposed recently for studying the dynamic behavior of dielectric elastomers [76].
Fluidic actuators (FEAs), which are highly deformable and adaptable, consist of synthetic elastomers layers. These actuators are deformed by applying pressurized fluid inside the embedded chambers or channels [32, 77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93]. They are commonly called PneuNet (PN) actuators, and they are actuated either hydraulically or pneumatically. Pneumatic actuators are preferred more than the hydraulic actuators because of the properties of air which is lighter, less inviscid, and omnipresence. However, hydraulic actuators can produce larger forces than the pneumatic actuators and they can be used in water soft robots [25, 84].
Few investigations have been devoted to developing analytical models for explaining the actuation theory of soft actuators. A rod-based model was used to develop constitutive relation that depends on five parameters for PneuNet soft actuators. This simple model is developed based on the assumption of the elastica Euler beam theory. The flexural rigidity and intrinsic curvature were found to depend linearly on the pressure and the actuator length [78, 79]. The bending angle of the soft pneumatic actuators was evaluated as a function of the pressure by other researchers who developed PneuNet analytical models with multiple soft pneumatic chambers separated by a distance to increase the bending angle. Because the nonlinear deflection cannot be evaluated accurately using the classical beam theory, the material behavior was assumed as a linear relationship between the tensile stress and strain [80]. A discrete elastic rod formulation was developed and used to study different models for soft-robot locomotion. The use of the formulation was demonstrated using a caterpillar-inspired soft robot that is actuated by SMA actuators [70].
The assumption of constant curvature has been used in some investigations to apply rigid-body modeling techniques to soft robotics. Computational methods have been also used to predict the soft-robot motion using finite element (FE) analysis. The soft-robot control is achieved using both model-based and model-free approaches. Two new algorithms were proposed for control of soft robotic arm by trajectory tracking and surface following. Using these algorithms, closed-loop controllers were developed [94]. Two models for actuators and continuum rods were recently proposed: general reduced-order model and discretized model with absolute states and Euler–Bernoulli beam segments. The two models were implemented in the MATLAB software and used to perform simulation and visualization of continuum manipulators [95]. Three-dimensional printed pneumatic toolkit was developed in another investigation, and its use was demonstrated by considering soft robotics examples for crawling and gripping [96]. Recently, different motion profiles were achieved using mechanically programed actuators, based on various textile combinations. Two main classes of versatile fabric-based soft pneumatic actuators were introduced. The simulation of various types of soft pneumatic actuators was performed using the FE method, and the results were verified experimentally [97].
8.2 Actuation forces and degrees of freedom
The solution of the inverse dynamics problem defines the generalized actuation forces associated with the system generalized coordinates \({\mathbf{q}}\). These forces are defined by the vector \({\mathbf{Q}}_{ca} = - {\mathbf{C}}_{{s{\mathbf{q}}}}^{T} {{\varvec{\uplambda}}}_{s}\) which has dimension \(n\) equal to the number of system generalized coordinates. In order to define the actuation forces and the pressure that produces these forces, it is necessary to determine the actuation forces associated with the system-controlled degrees of freedom whose number in the inverse problem is equal to the number of SRM control constraint equations. If \({\mathbf{q}}_{i}\) is the vector of the system degrees of freedom with dimension \(n_{d}\), one can write the virtual change in \({\mathbf{q}}\) in terms of the virtual change of \({\mathbf{q}}_{i}\) as \(\delta {\mathbf{q}} = {\mathbf{B}}_{di} \delta {\mathbf{q}}_{i}\), where \({\mathbf{B}}_{di}\) is a velocity transformation matrix [14]. Therefore, the virtual work of the actuation forces can be written as
In this equation, \({\mathbf{Q}}_{sd} = {\mathbf{B}}_{di}^{T} \left( { - {\mathbf{C}}_{{s{\mathbf{q}}}}^{T} {{\varvec{\uplambda}}}_{s} } \right)\) is the \(n_{d}\)-dimensional vector of actuation forces associated with the degrees of freedom specified in the inverse dynamics problem.
8.3 Actuation pressure
In the case of using pressurized air, the SRM actuation forces are the result of pressure distribution that requires integration over areas. The SRM actuation pressure, \(p_{s} = p_{s} \left( {{\mathbf{x}},t} \right)\), is assumed to depend on the spatial element coordinates \({\mathbf{x}}\) and time \(t\). Because the pressure is assumed to apply in the direction normal to the surface defined by the unit normal \({\mathbf{n}}\), a pressure vector \({\mathbf{p}}_{s} = {\mathbf{p}}_{s} \left( {{\mathbf{x}},t} \right) = p_{s} {\mathbf{n}}\) can be defined. In the case of three-dimensional surfaces, the position vector of the material points can be written as \({\mathbf{r}} = {\mathbf{r}}\left( {\alpha_{1} ,\alpha_{2} } \right)\), where \(\alpha_{1}\) and \(\alpha_{2}\) are the parameters that define the surface geometry.
The ANCF fully parameterized beam element considered in this investigation defines a planar surface; this is despite the fact that the nodal coordinates of the element are associated with the beam centerline, defined by the dimensionless coordinate \(\eta = 0\). In this case, the actuation force is assumed to apply at arbitrary points \(\xi\) and \(\eta\) along the normal to the curve, which can be defined using the curve curvature vector expressed in terms of the curve arc-length parameter \(s = s\left( {\alpha_{1} ,\alpha_{2} } \right)\) to allow using arbitrary direction for the actuation pressure. The curvature vector of the curve \({\mathbf{r}} = {\mathbf{r}}\left( {s\left( {\alpha_{1} ,\alpha_{2} } \right)} \right)\) can be written using the derivatives of the position gradients at a point as
The curve curvature \(\kappa\) is \(\kappa = \left| {{{d^{2} {\mathbf{r}}} \mathord{\left/ {\vphantom {{d^{2} {\mathbf{r}}} {ds^{2} }}} \right. \kern-\nulldelimiterspace} {ds^{2} }}} \right|\). The unit normal to the curve is then defined as \({\mathbf{n}} = \left( {{1 \mathord{\left/ {\vphantom {1 \kappa }} \right. \kern-\nulldelimiterspace} \kappa }} \right)\left( {{{d^{2} {\mathbf{r}}} \mathord{\left/ {\vphantom {{d^{2} {\mathbf{r}}} {ds^{2} }}} \right. \kern-\nulldelimiterspace} {ds^{2} }}} \right)\). Knowing the width of the beam,\(w\left( {\mathbf{x}} \right)\), at the area of the pressure application, one can write the virtual work of the pressure forces for an element \(j\) as
where \(dA^{j} = w^{j} \left( {\mathbf{x}} \right)ds^{j}\) is an infinitesimal area and superscript \(j\) refers to the element number. This equation can be written according to the definition of the pressure vector as
The goal is to use the actuation force vector \({\mathbf{Q}}_{sd} = {\mathbf{B}}_{di}^{T} \left( { - {\mathbf{C}}_{{s{\mathbf{q}}}}^{T} {{\varvec{\uplambda}}}_{s} } \right)\) associated with the \(n_{d}\) degrees of freedom of the system to determine the value of the pressure \(p_{s}^{j}\) on the surface. This allows for computing the desired actuation pressure distribution.
8.4 Element pressure equations
The vector \({\mathbf{Q}}_{sd} = {\mathbf{B}}_{di}^{T} \left( { - {\mathbf{C}}_{{s{\mathbf{q}}}}^{T} {{\varvec{\uplambda}}}_{s} } \right)\), which has dimension equal to the number of degrees of freedom \(n_{d}\), can be computed at different time points using the inverse dynamics problem previously described. In order to use this vector to determine the pressure \(p_{s}^{j}\), Eq. 22 can be written for each ANCF element \(j,\;j = 1,2, \ldots ,n_{e}\), where \(n_{e}\) is the total number of elements. Using the virtual displacement \(\delta {\mathbf{r}}^{j} = {\mathbf{S}}^{j} \left( {\mathbf{x}} \right)\delta {\mathbf{e}}^{j}\), one can write
Furthermore, the virtual change in the vector of element coordinates \({\mathbf{e}}^{j}\) can be expressed in terms of the virtual change in the system coordinates \({\mathbf{q}}\) as \(\delta {\mathbf{e}}^{j} = {\mathbf{B}}_{e}^{j} \delta {\mathbf{q}}\), where \({\mathbf{B}}_{e}^{j}\) is the matrix that maps the element coordinates \({\mathbf{e}}^{j}\) to the system coordinates \({\mathbf{q}}\). Furthermore, one can write the virtual change in the element coordinates in terms of the virtual change of the system degrees of freedom as \(\delta {\mathbf{e}}^{j} = {\mathbf{B}}_{e}^{j} {\mathbf{B}}_{di} \delta {\mathbf{q}}_{i} = {\mathbf{B}}^{j} \delta {\mathbf{q}}_{i}\), where \({\mathbf{B}}^{j} = {\mathbf{B}}_{e}^{j} {\mathbf{B}}_{di}\). Substituting the equation of the virtual change \(\delta {\mathbf{e}}^{j} = {\mathbf{B}}^{j} \delta {\mathbf{q}}_{i}\) in the preceding equation, one obtains
In this equation,
is a vector which has dimension \(n_{d}\), which is the same dimension as the dimension of the vector of the system degrees of freedom that need to be controlled.
8.5 Pressure distribution
The integral \({\mathbf{Q}}_{ca}^{j}\) of Eq. 25 can be converted to summation by considering discrete points \(k^{j} ,\;k^{j} = 1,2, \ldots ,m^{j}\), as
where \(dA^{j} \left( {{\mathbf{x}}_{{k^{j} }} } \right) = w^{j} \left( {{\mathbf{x}}_{{k^{j} }} } \right)ds^{j}\) is an area that depends on the number of points selected; \({{\varvec{\upbeta}}}_{s}^{j}\) is an \(n_{d} \times m^{j}\) matrix whose columns are the vectors \({{\varvec{\upbeta}}}_{{k^{j} }}^{j} \left( {{\mathbf{x}}_{{k^{j} }} ,t} \right) = {\mathbf{B}}^{{j^{T} }} {\mathbf{S}}^{{j^{T} }} \left( {{\mathbf{x}}_{{k^{j} }} } \right){\mathbf{n}}^{j} \left( {{\mathbf{x}}_{{k^{j} }} ,t} \right)dA^{j} \left( {{\mathbf{x}}_{{k^{j} }} } \right)\), where \(n_{d}\) is the dimension of the vector of system degrees of freedom \({\mathbf{q}}_{i}\); and \({\mathbf{p}}_{s}^{j}\) is the vector of the unknown pressures. The vector \({\mathbf{p}}_{s}^{j}\) and the matrix \({{\varvec{\upbeta}}}_{s}^{j}\) are defined as
The vector of the system pressure forces can be obtained by assembling the element vectors as
The dimension of the pressure vector \({\mathbf{p}}_{s}^{j}\) is the number of selected points \(m^{j}\), while the dimension of \({\mathbf{Q}}_{sd}\) is the number of degrees of freedom \(n_{d}\). The preceding equation can be written as
where \({{\varvec{\upbeta}}}_{s}\) is an \(n_{d} \times n_{p}\) matrix, \(n_{p} = \left( {n_{e} \times m^{j} } \right) \le n_{d}\), and \({\mathbf{p}}_{s} = \left[ {\begin{array}{*{20}c} {p_{s,1} } & {p_{s,2} } & \cdots & {p_{{s,n_{p} }} } \\ \end{array} } \right]^{T}\) is the vector of unknown pressures. If the number of pressure points is equal to the degrees of freedom, that is, \(n_{d} = n_{p}\), the preceding equation can be solved for the pressure vector \({\mathbf{p}}_{s}\) since the vector \({\mathbf{Q}}_{sd}\) is assumed to be known at different time points from the inverse dynamics solution. If, on the other hand, the number of pressure points is less than the number of degrees of freedom, that is, \(n_{d} > n_{p}\), the pressure vector \({\mathbf{p}}_{s}\) can be determined by multiplying Eq. 29 by the transpose of the matrix \({{\varvec{\upbeta}}}_{s}\) to obtain the system \({{\varvec{\upbeta}}}_{s}^{T} {\mathbf{Q}}_{sd} = \left( {{{\varvec{\upbeta}}}_{s}^{T} {{\varvec{\upbeta}}}_{s} } \right){\mathbf{p}}_{s}\). This set of equations can be solved for the vector \({\mathbf{p}}_{s}\)
8.6 Constant air pressure
The air pressure equations can be specialized to the case of constant pressure. The soft PneuNet actuator, shown in Fig. 4, consists of discrete pneumatic chambers with hollow sections as shown in Fig. 5. In general, the construction of each chamber is not regular shape such as circle, rectangular, or sphere centered around the neutral axis. If the shape of the chamber is symmetric around the neutral axis, the resultant of the pressure force will pass through the neutral axis, producing uniform expansion in all directions. Therefore, the chamber is designed to have an offset e between the pressure center and the neutral axis to create actuation forces that produce bending moment required to achieve the desired motion trajectories and shape. The distributed air pressure forces acting on the internal surfaces of the chambers can be used to determine the generalized control forces using Nanson’s formula. The vector of generalized continuum-based air pressure forces that is applied at the internal surfaces of the ANCF pressurized chambers j can be written as [54]
where \({\mathbf{S}}^{j}\) is the element shape function matrix, \(J^{j}\) is the determinant of the matrix of position-gradient vectors \({\mathbf{J}}^{j}\), \(p_{t}\) is the magnitude of the pressure that changes with time, \(S_{o}^{j}\) is the area of the chamber in the reference configuration, and \({\mathbf{n}}^{j}\) is the unit normal to the surface that can be evaluated using the equation \({\mathbf{n}} = {{{\mathbf{r}}_{{\alpha_{1} }} \times {\mathbf{r}}_{{\alpha_{2} }} } \mathord{\left/ {\vphantom {{{\mathbf{r}}_{{\alpha_{1} }} \times {\mathbf{r}}_{{\alpha_{2} }} } {\left| {{\mathbf{r}}_{{\alpha_{1} }} \times {\mathbf{r}}_{{\alpha_{2} }} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {{\mathbf{r}}_{{\alpha_{1} }} \times {\mathbf{r}}_{{\alpha_{2} }} } \right|}}\), where \(\alpha_{1} \,\,{\text{and}}\,\,\alpha_{2}\) are the variables that are used to define the surface as shown in Fig. 5a. In the case of planar problems, \({\mathbf{n}} = {{{\mathbf{r}}_{{\alpha_{2} }} \times {\mathbf{k}}} \mathord{\left/ {\vphantom {{{\mathbf{r}}_{{\alpha_{2} }} \times {\mathbf{k}}} {\left| {{\mathbf{r}}_{{\alpha_{2} }} \times {\mathbf{k}}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {{\mathbf{r}}_{{\alpha_{2} }} \times {\mathbf{k}}} \right|}}\), where \({\mathbf{k}} = [\begin{array}{*{20}c} 0 & 0 & {1]^{T} } \\ \end{array}\) is assumed to be perpendicular to the surface as shown in Fig. 5a. Assuming the pressure is constant, the vector of generalized air pressure forces can be written as
where \({\mathbf{C}}_{p}^{j} = \int_{{S_{o}^{j} }} {({\mathbf{S}}^{j} )^{T} \left( {{{J^{j} {\mathbf{n}}^{j} } \mathord{\left/ {\vphantom {{J^{j} {\mathbf{n}}^{j} } {\sqrt {({\mathbf{n}}^{j} )^{T} {\mathbf{J}}^{j} ({\mathbf{J}}^{j} )^{T} {\mathbf{n}}^{j} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {({\mathbf{n}}^{j} )^{T} {\mathbf{J}}^{j} ({\mathbf{J}}^{j} )^{T} {\mathbf{n}}^{j} } }}} \right)} {\text{d}}S_{o}^{j}\). The element force vector \({\mathbf{Q}}_{p}^{j} = p_{t} {\mathbf{C}}_{p}^{j}\) can be used to obtain the assembled ANCF mesh force vector \({\mathbf{Q}}_{p} = p_{t} {\mathbf{C}}_{p}\), where \({\mathbf{C}}_{p}\) is the vector resulting from the assembly of the vector \({\mathbf{C}}_{p}^{j}\).
By solving the inverse dynamics problem, the generalized constraint forces associated with each constrained node can be obtained and expressed in terms of the constraint Jacobian matrix and the vector of Lagrange multipliers when the augmented formulation is used. The virtual work of the generalized constraint forces acting on the ANCF chamber j is written as
where \({\mathbf{e}}^{j}\) is the vector of element nodal coordinates, \({{\varvec{\uplambda}}}^{j}\) is the vector of Lagrange multipliers, and \({\mathbf{C}}_{{\mathbf{e}}}^{j}\) is the Jacobian matrix of the driving constraints of the inverse dynamics problem. In order to write the preceding equation in terms of the vector of nodal coordinates \({\mathbf{e}}^{j}\). The element vectors \({\mathbf{Q}}_{c}^{j}\) can be assembled to obtain the mesh force vector \({\mathbf{Q}}_{c}\) associated with the element nodal coordinates. Equating the two vectors \({\mathbf{Q}}_{c}\) and \({\mathbf{Q}}_{p}\), the magnitude of the pressure required to control the SRM motion and shape can be written as \(p_{t} = {{{\mathbf{Q}}_{c} .{\mathbf{C}}_{p} } \mathord{\left/ {\vphantom {{{\mathbf{Q}}_{c} .{\mathbf{C}}_{p} } {{\mathbf{C}}_{p} .{\mathbf{C}}_{p} }}} \right. \kern-\nulldelimiterspace} {{\mathbf{C}}_{p} .{\mathbf{C}}_{p} }}\).
9 Numerical examples
To demonstrate the use of the proposed approach for the SRM motion and shape control, four numerical examples are considered. The first two examples show the differences between applying position and position-gradient constraints to SRM control of a cantilever beam. In these two examples, a planar cantilever beam with constant cross section is bent to a quarter circle using position constraints in the first example and position and position-gradient constraints in the second example. These constraints describe the desired motion trajectories at each node.
The third and the fourth examples demonstrate the feature of the new approach to accurately capture the effect of the stress-free initially curved geometry and control the shape during the SRM motion. In the first of these two examples, a tapered cantilever beam is bent to a quarter circle without altering the shape of the beam cross section. In the second of these two examples, the shape of the beam, which is bent also to a quarter circle, is changed during the motion to have a constant cross section throughout the beam at the final configuration. In both examples, the inverse dynamics position-gradient constraints play a significant role, distinguishing this proposed ANCF approach for the motion/shape control from other continuum-based approaches.
For the four examples considered in this section, comparison is made between the results obtained using the inverse dynamics model and the results of the forward dynamics model to which the control actuation forces are applied. Using the air pressure control law, the air pressure is determined for different cases. The computer simulation is performed using the general-purpose MBS software SIGMA/SAMS (Systematic Integration of Geometric Modeling and Analysis for the Simulation of Articulated Mechanical Systems). Eight fully parameterized planar shear-deformable ANCF beam elements are used in the FE discretization. Silicone rubber material, which is commonly used in the manufacturing of soft pneumatic actuators, is used in this investigation [78, 80, 86, 91, 92]. The cantilever beam has a length of 0.5 m, height 0.2 m, and width 0.015 m. The material Young's modulus is \(1.2 \times 10^{6}\) Pa, the mass density is 1130 kg/m3, and Poisson’s ratio is 0.495. The elastic forces are formulated using the general continuum mechanics approach (GCM); and the Navier–Stokes damping, recently proposed for ANCF solids, is used [98]. The coefficient of dynamic viscosity \(\mu\) that is used in the Navier–Stokes damping is determined according to \(\mu = G\gamma_{\nu 2}\), where \(G\) is the modulus of rigidity and \(\gamma_{\nu 2}\) is the dissipation factor [98]. In the current investigation, the dynamic viscosity coefficient \(\mu\) is assumed to be \(3 \times 10^{4} \,{\text{Pa}}{.}\,{\text{s}}\) in all examples in order to have an objective comparison of the results. However, in the first example, it was found that a dynamic viscosity coefficient less than 1000 Pa.s is sufficient to damp out the high-frequency modes because of small number of constraints. The value of the dynamic viscosity coefficient \(\mu\) can reach very high values for the rubber materials at small shear rates [99, 100]. Recent investigation developed a novel technique to change the damping properties of the soft PneuNet chambers by adding cavities that have viscous fluid and granular particles [101].
9.1 Use of imaging techniques
If imaging techniques or experimental measurements are used to obtain a point cloud that defines the SRM geometry, one can systematically use such data to determine the ANCF coordinates and define the inverse dynamics rheonomic constraints. By providing images to software, such as MATLAB, discrete-point data that define the SRM geometry for given desired configurations can be determined. Using these data points, the ANCF nodal coordinates associated with each node can be calculated as previously discussed. For example, the configurations of the cantilever beam bent to a quarter circle as shown in Fig. 6 can be provided to MATLAB to obtain the data at the 9 points as shown in Table 1. The nodal coordinates can be calculated using the extracted data points and the tangent and normal vectors that can be used to define the gradients. Considering that the beam is divided into eight elements with nine nodes, the nodal coordinates of each node can be calculated as shown in Table 2 which presents the results for the last node at different configurations. Based on the calculated nodal coordinates for each node, the rheonomic constraint equations used in the inverse dynamics problem can be formulated.
9.2 Planar straight cantilever beam
In the first two examples, the straight cantilever beam is bent to a quarter circle that has a radius \(R_{1} = 0.25\) m as shown in Fig. 6. In order to achieve this desired motion, each node is subjected to rheonomic constraints that are explicit functions of time. The initial position of each node \(i\) is defined in the global coordinate system \(XY\) by the coordinates \(x^{i}\) and \(y^{i}\), \(i = 1,2, \ldots ,9\), where \([\begin{array}{*{20}c} {x^{i} } & {y^{i} } \\ \end{array} ]^{T} = [\begin{array}{*{20}c} {x_{1}^{i} } & {x_{2}^{i} } \\ \end{array} ]^{T}\). The final position of each node is defined by \(x_{d}^{i}\) and \(y_{d}^{i}\) as well as the angle \(\theta_{d}^{i}\), where \(\theta_{d}^{i}\) is defined as shown in the figure. The desired motion trajectory is achieved in the inverse dynamics by applying the motion constraint equations \(x_{d}^{i} = \left( {{t \mathord{\left/ {\vphantom {t T}} \right. \kern-\nulldelimiterspace} T}} \right)^{2} R_{1} \sin \theta_{d}^{i}\) and \(y_{d}^{i} = - \left( {{t \mathord{\left/ {\vphantom {t T}} \right. \kern-\nulldelimiterspace} T}} \right)^{2} \left( {R_{1} - R_{1} \cos \theta_{d}^{i} } \right)\), where T is a constant and \(0 \le t \le T\).
The motion is controlled in the first example by applying two position-constraint equations \(x_{d}^{i}\) and \(y_{d}^{i}\) at each node, except for the first node, which is connected to the ground by a rigid joint and its position does not change [41]. Therefore, sixteen position-constraint equations are applied in the first example to control the position coordinates of eight nodes. In this first example, no position-gradient constraints are applied, and therefore, in the inverse dynamics problem, the number of constraint equations of the model is less than the number of model coordinates. Consequently, numerical integration of a number of differential equations equal to the number of degrees of freedom of the inverse dynamics model is necessary. The constraint forces determined from the solution of the inverse dynamics problems are used to define the pressure actuation and driving forces of the forward dynamics model. The obtained displacements of the straight cantilever beam at different time steps are shown in Fig. 7, which demonstrates that the desired motion is achieved using the proposed position-constraint equations. Figure 7 shows that there is no difference between the measured displacements of the forward and inverse dynamics at different time steps, demonstrating the effectiveness of the proposed approach. Because in this first example the positions of all the nodes are controlled to achieve the desired motion trajectory while the nodal position gradients are not specified, the nodal position gradients are not expected to remain unit vectors and stretch and shear can occur. Figures 8 and 9 show the norm of the gradient vectors \({\mathbf{r}}_{{\mathbf{x}}}\) and \({\mathbf{r}}_{{\mathbf{y}}}\), respectively, at Nodes 5 and 9. It is shown that, while the norms of the gradient vectors obtained using the inverse and forward dynamics are in a good agreement, the position-gradient vectors \({\mathbf{r}}_{{\mathbf{x}}}\) and \({\mathbf{r}}_{{\mathbf{y}}}\) deviate from a unit vector leading to longitudinal and transverse stretches.
The second example has the same data and position constraints as the first example, but the position gradients at each node are specified to control the shape and eliminate the longitudinal and transverse stretches to achieve the desired shape shown in Fig. 6. For the planar ANCF shear-deformable beam element, the vector of nodal coordinates of node \(i\) is defined by \({\mathbf{e}}^{i} = \left[ {\begin{array}{*{20}c} {x^{i} } & {y^{i} } & {r_{{x_{1} }}^{i} } & {r_{{x_{2} }}^{i} } & {r_{{y_{1} }}^{i} } & {r_{{y_{2} }}^{i} } \\ \end{array} } \right]^{T}\). To obtain the shape shown in Fig. 6, the following position-gradient constraint equations are applied at each node in addition to the position constraints:
That is, 48 constraints are used to control the motion and the shape of the beam in this example. By applying both the position and position-gradient constraints to each node of the cantilever beam, the measured beam displacements at different time steps were found to be the same as obtained in the first example and shown in Fig. 7. The main difference between the two examples is in the norm of the gradient vectors \({\mathbf{r}}_{{\mathbf{x}}}\) and \({\mathbf{r}}_{{\mathbf{y}}}\) as shown in Figs. 10 and 11 which demonstrate that the norm of the position-gradient vectors \({\mathbf{r}}_{{\mathbf{x}}}\) and \({\mathbf{r}}_{{\mathbf{y}}}\) follows the motion trajectory defined by the position-gradient constraints to keep a constant cross section throughout the beam at a given time step. A comparison between the final configurations obtained in the first two examples is shown in Fig. 12. While this figure shows that the same motion of the nodes can be obtained using the two different sets of constraints, applying only position constraints is not sufficient to control both the motion and the shape of the beam. Position and position-gradient constraints need to be applied at each node to obtain the desired motion and shape. Because in the second example, the number of constraint equations is equal to the number of degrees of freedom, the inverse dynamics problem requires the solution of algebraic equations only, and therefore, it is efficient since numerical integration of motion equations is not required.
9.3 Planar tapered cantilever beam
A planar tapered cantilever beam is considered for the third and fourth examples used in this investigation to demonstrate the use of the new approach to capture accurately the stress-free initially curved geometry. On the other hand, when using ANCF elements that employ position gradients as nodal coordinates, the tapered geometry can be described by changing the norm of the gradient vectors, as shown in Fig. 13 in which the height of the tapered beam at the right side is 0.1 m, while at left side is 0.2 m. Position and position-gradient constraints are applied in the third and fourth examples to control the motion and the shape of the tapered beam (fully constrained inverse dynamics). In the third example, the tapered cantilever beam is bent to a tapered quarter circle as shown in Fig. 14. The position-constraint equations at each node are the same as the position-constraint equations used in the previous examples. The main difference between the straight and tapered beams is the change of cross section defined by the gradient vector \({\mathbf{r}}_{{\mathbf{y}}}\). To preserve the tapered geometry of the beam during bending, the following position-gradient constraint equations are applied:
where\(\left( {r_{{y_{2} }}^{i} } \right)_{o}\) represents the initial stretch value of the cross section at each node \(i\). For instance, node 9 has initial stretch value \(\left( {r_{{y_{2} }}^{9} } \right)_{o}\) of 0.5, while node 8 has initial stretch value \(\left( {r_{{y_{2} }}^{8} } \right)_{o}\) of 0.5625. The displacement of the beam centerline was found to be the same as the displacement obtained in the first two examples shown in Fig. 7. The norm of the gradient vector \({\mathbf{r}}_{x}\) for the midpoint and the tip-point is also the same as the ones obtained in the second example shown in Fig. 10. In this example, the norm of the gradient vector \({\mathbf{r}}_{{\mathbf{y}}}\) is assumed to remain constant. This is achieved as shown in Fig. 15 for the midpoint and the tip point. The figure also shows that the same results were obtained using the inverse- and forward dynamics models. The initial and final configurations of the tapered beam, bent to a tapered quarter circle, are shown in Fig. 16.
In the fourth example considered, the tapered cantilever beam is bent and while moving is shaped to have a constant cross section; that is, the tapered geometry is eliminated, as shown in Fig. 17. The constraint equations used to control the position of each node are the same as the equations of the previous examples. The challenge in this example is to convert the initial tapered geometry to a straight geometry. In order to obtain the desired non-tapered geometry, the following position-gradient constraint equations are used:
The displacements of the beam centerline obtained using the forward and inverse dynamics were found to be the same (Fig. 7). The main goal of presenting this example is to demonstrate how the position-gradient constraint can be used to eliminate the tapered geometry and obtain a curved beam with constant cross section, as shown in Fig. 18. The results obtained using the forward dynamics model by applying the control forces were found to be the same as those predicted using the inverse dynamics model. The initial and final configurations of the tapered beam, which is bent with constant cross section, are shown in Fig. 19. Figures 20 and 21 show the change of the norm of the gradient vector \({\mathbf{r}}_{{\mathbf{y}}}\) at the nodes of the third and fourth examples, respectively.
9.4 Actuation forces and air pressure
As discussed before, the inverse dynamics forces are considered as actuation forces applied in the forward dynamics problem to obtain the desired motion trajectories and shapes. Each node has six generalized constraint forces associated with its six nodal coordinates; consequently, 48 generalized constraint forces can be obtained for each of the previous examples. As an example, the generalized constraint forces associated with the midpoint (Node 5) for the fourth example are shown in Fig. 22. By assuming that the air pressure is the same for all elements and by using the element connectivity conditions, the air pressure in the four examples required to obtain the desired motion and shape can be predicted as shown in Fig. 23. The results of this figure show that the maximum air pressure is in case of the fourth example because the geometry change from tapered to constant cross section requires larger force. Previous investigations showed that the operating range of the applied pressure inside the chambers of soft pneumatic actuators is usually below 0.5 MPa [27]. However, another investigation presented nine different pressure generation methods that can be used with soft pneumatic actuators, and the pressure can have higher values such as 10 MPa [102]. The required air pressure in the current investigation was found to be relatively high because of several reasons that include use of larger dimensions, viscoelastic model, short time used to achieve the desired trajectories, assumption of solid beam, and beam width [87, 93]. By using model dimensions as the ones used in the literature, the magnitude of the pressure is reduced. For example, using smaller length of 0.112 m, height of 0.015 m, and width of 0.015 m, and assuming actuation time and dynamic viscosity of 0.1 s and 1000 Pa.s, respectively, the maximum pressure was found to be 50 kPa, a value commonly applied in the case of smaller soft robots [27, 78].
Table 3 shows the CPU time when using different numbers of elements for the first two examples. The first example employs position constraints only, while the second example uses position and position-gradient constraints. The simulation time is 10 ms with 0.001 ms step size using an Intel(R) Xeon(R) CPU E5-1650 0@3.20 GHZ computer. In the case of the partially constrained inverse dynamics problem, the numerical integration is performed using the explicit Adams–Bashforth predictor–corrector method. Table 3 shows that the second example takes more computational time than the first example because of the large number of rheonomic constraints. Also, the CPU time increases by increasing the number of elements.
10 Conclusions
The development of a systematic numerical procedure for the computation of the SRM actuation forces is demonstrated in this study. The new continuum-based approach developed allows controlling simultaneously both SRM motion and shape. To this end, the ANCF position and position gradients are used in the formulation of the desired specified motion trajectory and shape. This is achieved through the formulation of rheonomic constraint equations, which are used in an inverse dynamics procedure to define the actuation control forces. In order to generalize the approach developed in this study, a procedure for the numerical reconstruction of the SRM geometry using point cloud data that can be created using measurement or imaging techniques is presented. These geometry data can be used to define the ANCF nodal coordinates that enter into the formulation of the inverse dynamics rheonomic constraints. As discussed in the paper, unlike the control of rigid-body systems which requires number of independent actuation forces equal to the number of joint coordinates, the SRM motion/shape control leads to generalized control forces associated with the ANCF position and position-gradient coordinates [103]. The definition of these motion/shape control forces is demonstrated in this study using air pressure actuation commonly used in the SRM control. Nonetheless, the proposed procedure can be applied to other SRM actuation types as will be demonstrated in future investigations. Several numerical examples were presented in order to demonstrate the motion/shape control using the new approach. While the motion/shape control approach and algorithm used in this investigation are based on MBS formulations, it is important to acknowledge that there are other SRM simulation tools such as SOFA framework and discrete differential geometry-based methods that are being developed and employ conventional FE methods [104].
References
Calderone, L.: Robots in manufacturing applications | manufacturing tomorrow, 2016. https://www.manufacturingtomorrow.com/article/2016/07/robots-in-manufacturing-applications/8333 (2016)
Book, W.J.: Recursive Lagrangian dynamics of flexible manipulator arms. Int. J. Robot. Res. 3(3), 87–101 (1984)
Jayaweera, N., Webb, P.: Metrology-assisted robotic processing of aerospace applications. Int. J. Comput. Integr. Manuf. 23(3), 283–296 (2010)
Jafari, J., Ghazal, M., Nazemizadeh, M.: Nonlinear formulation of flexible-link robots based on finite element approach. Int. J. Basic Sci. Appl. Res. 3(11), 831–834 (2014)
Korayem, M.H., Rahimi, H.N.: Nonlinear dynamic analysis for elastic robotic arms. Front. Mech. Eng. 6, 219–228 (2008)
Korayem, M.H., Rahimi, H.N., Nikoobin, A., Nazemizadeh, M.: Maximum allowable dynamic payload for flexible mobile robotic manipulators. Latin Am. Appl. Res. 43(1), 29–35 (2013)
Kumar, R., Berkelman, P., Gupta, P., Barnes, A., Jensen, P.S., Whitcomb, L.L., Taylor, R.: Preliminary experiments in cooperative human/robot force control for robot assisted micro-surgical manipulation. Proc. IEEE Int. Conf. Robot. Autom. 1, 610–617 (2000)
Megahed, S.M., Hamza, K.T.: Modeling and simulation of planar flexible link manipulators with rigid tip connections to revolute joints. Robotica 22(3), 285–300 (2004)
Meghdari, A., Fahimi, F.: On the first-order decoupling of dynamical equations of motion for elastic multibody systems as applied to a two-link flexible manipulator. Multibody Syst. Dyn. 5, 1–20 (2001)
Changizi, K., Shabana, A.A.: A recursive formulation for the dynamic analysis of open loop deformable multi-body systems. ASME J. Appl. Mech. 55, 687–693 (1988)
Gofron, M., Shabana, A.A.: Equivalence of driving forces in flexible multibody systems. Int. J. Numer. Methods Eng. 38, 2907–2928 (1995)
Shabana, A.A., Hwang, Y.L.: Dynamic coupling between the joint and elastic coordinates in flexible mechanism systems. Int. J. Robot. Res. 12(3), 299–306 (1993)
Sherif, K., Nachbagauer, K.: A detailed derivation of the velocity-dependent inertia forces in the floating frame of reference formulation. ASME J. Comput. Nonlinear Dyn. (2014). https://doi.org/10.1115/1.4026083
Shabana, A.A.: Dynamics of Multibody Systems, 5th edn. Cambridge University Press, New York (2020)
Cook, R.D.: Concepts and Applications of Finite Element Analysis. Wiley, New York (1981)
Logan, D.L.: A First Course in the Finite Element Method, 6th Edition, Chapter 15, Cengage Learning (2017)
Zienkiewicz, O.C.: The Finite Element Method, 3rd edn. McGraw Hill, New York (1977)
Zienkiewicz, O.C., Taylor, R.L.: The Finite Element Method, Vol 2: Solid Mechanics, vol. 5. Butterworth-Heinemann, Oxford (2000)
Farin, G.: Curves and Surfaces for CAGD, A Practical Guide, 5th edn. Morgan Kaufmann, Publishers, , San Francisco (1999)
Gallier, J.: Geometric Methods and Applications: For Computer Science and Engineering. Springer, New York (2011)
Goetz, A.: Introduction to Differential Geometry. Addison Wesley, Boston (1970)
Kreyszig, E.: Differential Geometry. Dover Publications, USA (1991)
Piegl, L., Tiller, W.: The NURBS Book, 2nd edn. Springer, Berlin (1997)
Rogers, D.F.: An Introduction to NURBS with Historical Perspective. Academic Press, San Diego, CA (2001)
Lee, C., Kim, M., Kim, Y.J., Hong, N., Ryu, S., Kim, J., Kim, S.: Soft robot review. Int. J. Control Autom. Syst. 15(1), 3–15 (2017)
Rus, D., Tolley, M.T.: Design, fabrication and control of soft robots. Nature 521, 467–475 (2015)
Boyraz, P., Runge, G., Raatz, A.: An overview of novel actuators for soft robotics. Actuators 7(3), 48–68 (2018)
Kim, S., Laschi, C., Trimmer, B.: Soft robotics: a bioinspired evolution in robotics. Trends Biotechnol. 31(5), 287–294 (2013)
Zolfagharian, A., Kouzani, A.Z., Khoo, S.Y., Moghadam, A.A.A., Gibson, I., Kaynak, A.: Evolution of 3D printed soft actuators. Sens. Actuators, A 250, 258–272 (2016)
Galloway, K.C., Becker, K.P., Phillips, B., Licht, S., Tchernov, D., Wood, R.J., Gruber, D.F.: Soft robotic grippers for biological sampling on deep reefs. Soft Robot. 3(1), 23–33 (2016). https://doi.org/10.1089/soro.2015.0019
Hod, L.: Challenges and opportunities for design, simulation, and fabrication of soft robots. Soft Robot. 1(1), 21–27 (2013)
Marchese, A.D., Onal, C.D., Rus, D.: Autonomous soft robotic fish capable of escape maneuvers using fluidic elastomer actuators. Soft Robot. 1(1), 75–87 (2014)
Stokes, A.A., Sheperd, R.F., Morin, S.A., Ilievski, F., Whitesides, G.M.: A hybrid combining hard and soft robots. Soft Robot. 1(1), 70–74 (2014). https://doi.org/10.1089/soro.2013.0002
Tolley, M.T., Shepherd, R.F., Mosadegh, B., Galloway, K.C., Wehner, M., Karpelson, M., Wood, R.J., Whitesides, G.M.: A resilient, untethered soft robot. Soft Robot. 1(3), 213–223 (2014). https://doi.org/10.1089/soro.2014.0008
Chen, Y., Zhang, D.G., Li, L.: Dynamic analysis of rotating curved beams by using absolute nodal coordinate formulation based on radial point interpolation method. J. Sound Vib. 441, 63–83 (2019)
Dmitrochenko, O.N., Pogorelov, D.Y.: Generalization of plate finite elements for absolute nodal coordinate formulation. Multibody Syst. Dyn. 10, 17–43 (2003)
Fotland, G., Haskins, C., Rølvåg, T.: Trade study to select best alternative for cable and pulley simulation for cranes on offshore vessels. Syst. Eng. 23, 177–188 (2019). https://doi.org/10.1002/sys.21503
Hewlett, J.: Methods for Real-Time Simulation of Systems of Rigid and Flexible Bodies with Unilateral Contact and Friction, Ph.D. Thesis, Department of Mechanical Engineering, McGill University (2019)
Hewlett, J., Arbatani, S., Kovecses, J.: A fast and stable first-order method for simulation of flexible beams and cables. Nonlinear Dyn. 99, 1211–1226 (2020)
Htun, T.Z., Suzuki, H., Garcia-Vallejo, D.: Dynamic modeling of a radially multilayered tether cable for a remotely-operated underwater vehicle (ROV) based on the absolute nodal coordinate formulation (ANCF). Mech. Mach. Theory 153, 103961 (2020). https://doi.org/10.1016/j.mechmachtheory.2020.103961
Shabana, A.A., Eldeeb, A.E.: Relative orientation constraints in the nonlinear large displacement analysis: application to soft materials. Nonlinear Dyn. 101, 2551–2575 (2020)
Kłodowski, A., Rantalainen, T., Mikkola, A., Heinonen, A., Sievänen, H.: Flexible multibody approach in forward dynamic simulation of locomotive strains in human skeleton with flexible lower body bones. Multibody Syst. Dyn. 25(4), 395–409 (2011)
Laflin, J.J., Anderson, K.S., Khan, I.M., Poursina, M.: New and extended applications of the divide-and-conquer algorithm for multibody dynamics. ASME J. Comput. Nonlinear Dyn. 9(4), 0410041–0410048 (2014)
Lee, J.H., Park, T.W.: Dynamic analysis model for the current collection performance of high-speed trains using the absolute nodal coordinate formulation. Trans. Kor. Soc. Mech. Eng. A 36, 339–346 (2012)
Li, S., Wang, Y., Ma, X., Wang, S.: Modeling and simulation of a moving yarn segment: based on the absolute nodal coordinate formulation. Math. Probl. Eng. 2019, 1–15 (2019). https://doi.org/10.1155/2019/6567802
Nachbagauer, K.: Development of shear and cross section deformable beam finite elements applied to large deformation and dynamics problems, Ph.D. dissertation, Johannes Kepler University, Linz, Austria (2013)
Nachbagauer, K.: State of the art of ANCF elements regarding geometric description, interpolation strategies, definition of elastic forces, validation and locking phenomenon in comparison with proposed beam finite elements. Arch. Comput. Methods Eng. 21(3), 293–319 (2014)
Nachbagauer, K., Pechstein, A.S., Irschik, H., Gerstmayr, J.: A new locking-free formulation for planar, shear deformable, linear and quadratic beam finite elements based on the absolute nodal coordinate formulation. Multibody Syst. Dyn. 26(3), 245–263 (2011)
Olshevskiy, A., Dmitrochenko, O., Kim, C.W.: Three-dimensional solid brick element using slopes in the absolute nodal coordinate formulation. ASME J. Comput. Nonlinear Dyn. 9(2), 021001-1-021001–10 (2014)
Orzechowski, G.: Analysis of beam elements of circular cross section using the absolute nodal coordinate formulation. Arch. Mech. Eng. 59(3), 283–296 (2012)
Orzechowski, G., Frączek, J.: Integration of the equations of motion of multibody systems using absolute nodal coordinate formulation. Acta Mech. Autom. 6(2), 75–83 (2012)
Orzechowski, G., Fraczek, J.: Nearly incompressible nonlinear material models in the large deformation analysis of beams using ANCF. Nonlinear Dyn. 82(1), 451–464 (2015)
Pan, K., Cao, D.: Absolute nodal coordinate finite element approach to the two-dimensional liquid sloshing problems. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 234(2), 322–346 (2020). https://doi.org/10.1177/1464419320907785
Shabana, A.A.: Computational Continuum Mechanics, 3rd edn. Wiley, Chichester, UK (2018)
Shen, Z., Liu, C., Li, H.: Viscoelastic analysis of bistable composite shells via absolute nodal coordinate formulation. Compos. Struct. (2020). https://doi.org/10.1016/j.compstruct.2020.112537
Shen, Z., Tian, Q., Liu, X., Hu, G.: Thermally induced vibrations of flexible beams using absolute nodal coordinate formulation. Aerosp. Sci. Technol. 29(1), 386–393 (2013)
Sheng, F., Zhong, Z., Wang, K.: Theory and model implementation for analyzing line structures subject to dynamic motions of large deformation and elongation using the absolute nodal coordinate formulation (ANCF) approach. Nonlinear Dyn. 101(1), 333–359 (2020). https://doi.org/10.1007/s11071-020-05783-4
Skrinjar, L., Slavic, J., Boltežar, M.: Absolute nodal coordinate formulation in a pre-stressed large-displacements dynamical system. J. Mech. Eng. 63, 417–425 (2017). https://doi.org/10.5545/sv-jme.2017.4561
Takahashi, Y., Shimizu, N., Suzuki, K.: Study on the frame structure modeling of the beam element formulated by absolute coordinate approach. J. Mech. Sci. Technol. 19, 283–291 (2005)
Tian, Q., Chen, L.P., Zhang, Y.Q., Yang, J.Z.: An efficient hybrid method for multibody dynamics simulation based on absolute nodal coordinate formulation. ASME J. Comput. Nonlinear Dyn. 4(2), 021009-1-021009–14 (2009)
Wang, J., Wang, T.: Buckling analysis of beam structure with absolute nodal coordinate formulation. IMechE J. Mech. Eng. Sci. (2020). https://doi.org/10.1177/0954406220947117
Yamano, A., Shintani, A., Ito, T., Nakagawa, C., Ijima, H.: Influence of boundary conditions on a flutter-mill. J. Sound Vib. 478, 115359 (2020)
Yoo, W.S., Lee, J.H., Park, S.J., Sohn, J.H., Pogolev, D., Dmitrochenko, O.: Large deflection analysis of a thin plate: computer simulation and experiment. Multibody Syst. Dyn. 11, 185–208 (2004)
Yu, L., Zhao, Z., Tang, J., Ren, G.: Integration of absolute nodal elements into multibody system. Nonlinear Dyn. 62, 931–943 (2010)
Yuan, T., Liu, Z., Zhou, Y., Liu, J.: Dynamic modeling for foldable origami space membrane structure with contact-impact during deployment. Multibody Syst. Dyn. 50, 1–24 (2020)
Zhang, W., Zhu, W., Zhang, S.: Deployment dynamics for a flexible solar array composed of composite-laminated plates. ASCE J. Aerosp. Eng. 33, 04020071-1-04020071–21 (2020)
Marchese, A.D, Katzshmann, R.K, Rus, D.: Whole arm planning for a soft and highly compliant 2d robotic manipulator. In: IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, pp. 554–560 (2014)
Calisti, M., Gioelli, M., Levy, G., Mazzolai, B., Hochner, B., Laschi, C., Dario, P.: An octopus-bioinspired solution to movement and manipulation for soft robots. Bioinsp. Biomimetics 6(3), 036002 (2011)
Laschi, C., Cianchetti, M., Mazzolai, B., Margheri, L., Follador, M., Dario, P.: Soft robot arm inspired by the octopus. Adv. Robot. 26(7), 709–727 (2012)
Goldberg, N.N., Huang, X., Majidi, C., Novelia, A., O’Reilly, O.M., Paley, D.A., Scott, W.L.: On planar discrete elastic rod models for the locomotion of soft robots. Soft Robot. 6(5), 595–610 (2019)
Guo, H., Zhang, J., Wang, T., Li, Y., Hong, J., Li, Y.: Design and control of an inchworm-inspired soft robot with omega-arching locomotion. In: 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, pp. 4154–4159 (2017)
Huang, W., Huang, X., Majidi, C., Jawed, M.K.: Dynamics simulation of articulated soft robots. Nat. Commun. 11(1), 2233 (2020)
Huang, X., Kumar, K., Jawed, M.K., Nasab, A.M., Ye, Z., Shan, W., Majidi, C.: Highly dynamic shape memory alloy actuator for fast moving soft robots. Adv. Mater. Technol. 4(4), 1–9 (2019)
Huang, X., Kumar, K., Jawed, M.K., Ye, Z., Majidi, C.: Soft electrically actuated quadruped (SESQ)—integrating a flex circuit board and elastomeric limbs for versatile mobility. IEEE Robot. Autom. Lett. 4(3), 2415–2422 (2019)
Lin, H., Leisk, G.G., Trimmer, B.: GoQBot: a caterpillar-inspired soft-bodied rolling robot. Bioinsp. Biomimetics 6(2), 026007 (2011)
Tian, Q., Zhang, P., Luo, K.: Dynamics of soft mechanical systems actuated by dielectric elastomers. Mech. Syst. Signal Process. 151, 107392 (2021)
Branyan, C., Fleming, C., Remaley, J., Kothari, A., Tumer, K., Hatton, R.L., Mengüç Y.: Soft snake robots: mechanical design and geometric gait implementation. In: IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, pp. 282–289 (2017)
De Payrebrune, K.M., O’Reilly, O.M.: On the development of rod-based models for pneumatically actuated soft robot arms: a five-parameter constitutive relation. Int. J. Solids Struct. 120, 1339–1351 (2017)
De Payrebrune, K.M., O’Reilly, O.M.: On constitutive relations for a rod-based model of a pneu-net bending actuator. Extreme Mech. Lett. 8, 38–46 (2016)
Alici, G., Canty, T., Mutlu, R., Hu, W., Sencadas, V.: Modeling and experimental evaluation of bending behavior of soft pneumatic actuators made of discrete actuation chambers’. Soft Robot. 5(1), 24–35 (2018)
Gasoto, R., Macklin, M., Liu, X., Sun, Y., Erleben, K., Onal, C., Fu, J.: A validated physical model for real-time simulation of soft robotic snakes. In: International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, pp. 6272–6279 (2019)
Homberg, B.S., Katzschmann, R.K., Dogar, M.R., Rus, D.: Haptic identification of object using a modular soft robotic gripper. In: IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, pp. 1698–1705 (2015)
Hu, W., Mutlu, R., Li, W., Alici, G.: A structural optimisation method for a soft pneumatic actuator. Robotics 7(2), 1–16 (2018)
Katzschmann, R.K., Marchese, A.D., Rus, D.: Hydraulic autonomous soft robotic fish for 3d swimming. Exp. Robot. 109, 405–420 (2016)
Luo, M., Yan, R., Wan, Z., Qin, Y., Santoso, J., Skorina, E.H., Onal, C.D.: OriSnake: design, fabrication and experimental analysis of a 3-d origami snake robot. IEEE Robot. Autom. Lett. 3(3), 1993–1999 (2018)
Manns, M., Morales, J., Frohn, P.: Additive manufacturing of silicon based pneunets as soft robotic actuators. Proc. CIRP 72, 328–333 (2018)
Mosadegh, B., Polygerinos, P., Keplinger, C., Wennstedt, S., Shepard, R.F., Gupta, U., Shim, J., Bertoldi, K., Walsh, C.J., Whitesides, G.M.: Pneumatic networks for soft robotics that actuate rapidly. Adv. Funct. Mater. 24(15), 2163–2170 (2014)
Onal, C.D., Rus, D.: Autonomous undulatory serpentine locomotion utilizing body dynamics of a fluidic soft robot. Bioinsp. Biomimetics 8(2), 1–10 (2013)
Polygerinos, P., Lyne, S., Wang, Z., Nicolini, L.F., Mosadegh, B., Whitesides, G.M., Walsh, C.J.: Towards a soft pneumatic glove for hand rehabilitation. In: IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, pp. 1512–1517 (2013)
Qin, Y., Wan, Z., Sun, Y., Skorina, E.H., Luo, M., Onal, C.D.: Design, fabrication and experimental analysis of a 3-D robotic snake. In: 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, pp. 77–82 (2018)
Souhail. A., Vessakosol, P.: PneuNets bending actuator design and fabrication using low cost silicones. In: The 9th TSME International Conference on Mechanical Engineering, pp. 1–7 (2018)
Sun, Y., Song, Y.S., Paik, J.: Characterization of silicone rubber based soft pneumatic actuators. In: IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, pp. 4446–4453 (2013)
Sun, Y., Zhang, Q., Chen, X., Chen, H.: An optimum design method of pneu-net actuators for trajectory matching utilizing a bending model and GA. Math. Probl. Eng. 2019, 1–12 (2019)
Della Santina, C., Katzschmann, R.K., Bicchi, A., Rus, D.: Model-based dynamic feedback control of a planar soft robot: Trajectory tracking and interaction with the environment. Int. J. Robot. Res. 39(4), 490–513 (2020)
Sadati, S.M.H., Naghibi, S.E., Shiva, A., Michael, B., Renson, L., Howard, M., Rucker, C.D., Althoefer, K., Nanayakkara, T., Zschaler, S., Bergeles, C.: TMTDyn: a matlab package for modeling and control of hybrid rigid-continuum robots based on discretized lumped systems and reduced-order models. Int. J. Robot. Res. (2019). https://doi.org/10.1177/0278364919881685
Du Pasquier, C., Chen, T., Tibbits, S., Shea, K.: Design and computational modeling of a 3D printed pneumatic toolkit for soft robotics’. Soft Robot. 6(5), 657–663 (2019)
Nguyen, P.H., Zhang, W.: Design and computational modeling of fabric soft pneumatic actuators for wearable assistive devices. Sci. Rep. 10(1), 1–13 (2020)
Grossi, E., Shabana, A.A.: ‘Analysis of high-frequency ANCF modes: Navier–Stokes physical damping and implicit numerical integration. Acta Mech. 230, 2581–2605 (2019)
Lipińska, M., Soszka, K.: Viscoelastic behavior, curing and reinforcement mechanism of various silica and POSS filled methyl-vinyl polysiloxane MVQ rubber. Silicon 11, 2293–2305 (2019)
Zhao, J., Jiang, N., Zhang, D., He, B., Chen, X.: Study on optimization of damping performance and damping temperature range of silicone rubber by polyborosiloxane gel. Polymers 12, 1196 (2020)
Di Lallo, A., Catalano, M.G., Garabini, M., Grioli, G., Gabiccini, M., Bicchi, A.: Dynamic morphological computation through damping design of soft continuum robots. Front. Robot. AI 6, 1–19 (2019)
Adami, M., Seibel, A.: On-board pneumatic pressure generation methods for soft robotics applications. Actuators, ol. 8(1) (2019)
Shabana, A.A.: Continuum-based geometry/analysis approach for flexible and soft robotic systems (FSRS). Soft Rob. 5(5), 613–621 (2018). https://doi.org/10.1089/soro.2018.0007
SOFA (Simulation Open Framework Architecture) Software, https://nam04.safelinks.protection.outlook.com/?url=https%3A%2F%2Fwww.sofa-framework.org%2F&data=04%7C01%7Cshabana%40uic.edu%7C79e4c8fb5bcd4c80af3208d8a88f9c14%7Ce202cd477a564baa99e3e3b71a7c77dd%7C0%7C0%7C637444682071332605%7CUnknown%7CTWFpbGZsb3d8eyJWIjoiMC4wLjAwMDAiLCJQIjoiV2luMzIiLCJBTiI6Ik1haWwiLCJXVCI6Mn0%3D%7C1000&sdata=t5fm2yU%2FqHfw39GtKbKI1fVKXwh%2BAOazmKMRoeKKXE0%3D&reserved=0
Acknowledgements
This research was supported by the National Science Foundation (Projects # 1852510).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Shabana, A.A., Eldeeb, A.E. Motion and shape control of soft robots and materials. Nonlinear Dyn 104, 165–189 (2021). https://doi.org/10.1007/s11071-021-06272-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-021-06272-y


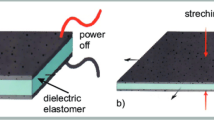









 inverse dynamics,
inverse dynamics,  forward dynamics). (Color figure online)
forward dynamics). (Color figure online)












 Node 3,
Node 3,  Node 4,
Node 4,  Node 5,
Node 5,  Node 6,
Node 6,  Node 7,
Node 7,  Node 8,
Node 8,  Node 9). (Color figure online)
Node 9). (Color figure online)




 fourth example). (Color figure online)
fourth example). (Color figure online)