Dynamic modeling for foldable origami space membrane structure with contact-impact during deployment

Abstract

The dynamic modeling for the foldable origami space membrane structure considering contact-impact during the deployment is studied in this paper. The membrane is discretized using the triangular elements of the Absolute Nodal Coordinate Formulation (ANCF), and the stress–strain relationship of the membrane is determined based on the Stiffness Reduction Model (SRM). A mixed method is proposed for the frictionless contact problem by combining the membrane surface-to-surface (STS) contact elements with the membrane node-to-surface (NTS) contact elements to improve precision. Compared with the traditional STS contact elements, the mixed method can effectively avoid mutual penetration of the element boundaries, especially for the foldable origami membrane structures undergoing overall motions. The penalty method is adopted to enforce the nonpenetration condition. Moreover, special constraints are built for the fold lines, and then the dynamic equations of the membrane multibody system considering the damping effect are formulated. The dynamic deployment procedure of a leaf-in origami membrane structure with contact-impact is performed employing this present mixed method. The results demonstrate the effectiveness and superiority of the presented mixed method in the solution of the complicated contact problem, and the influence of the contact-impact on the dynamic performance is analyzed.

1 Introduction

With the development of aerospace engineering in the direction of lightweight, large-scale and high precision, the membrane structure is attracting more and more attention due to the characteristics of being ultra-light, having small stowage volume, easy folding, and high stiffness-to-weight ratio [1, 2]. During the deployment of the membrane structure, the slacks and wrinkles exist on the surface of the large-area membrane structure, which is subjected to overall motion and large deformation. Thus, the study on the membrane is still considered as an enormous challenge.

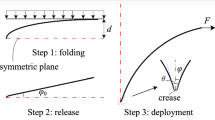
Since the foldable space membrane structures are stowed in a small volume during launch and flight, it is necessary to apply the new-type origami structures to the manufacturing and design of solar sail membranes. Indeed, origami structures have been widely used to develop foldable aerospace structures [3], such as frog-leg and Miura origami are used for the packaging of solar sail membranes [4, 5]. Miura origami is a relatively mature origami structure that has already been studied for several years, as shown in Fig. 1(a). In order to optimize the folding form of the membrane, De Focatiis and Guest [6] presented several folding patterns by developing the leaves, in which the leaf-in origami is one of the origami structures shown in Fig. 1(b). Relatively speaking, the investigation on the leaf-in origami is extremely rare and complicated, allowing for contact-impact, which is exactly what we are particularly interested in.

Fig. 1

Schematic of the origami membrane structures: (a) Miura origami; (b) leaf-in origami (Color figure online)

Due to the complexity of the deployment of membrane structures, the Multi-Particle Model (MPM) was used to simplify the analysis of the dynamics of the deployable membrane structures. Nakano [7] verified the stability criterion of spinning-deployable membrane by the MPM. Nishimaki [8] and Shirasawa [9] utilized the MPM to simulate the development of the “IKAROS” solar sail and it was compared with the experiment. Xu [10] described the behavior of the membrane during the deployment by a spring–mass model. However, the stress analysis of the membrane was not carried out.

Owing to the characteristics of large deformation of membrane structures, the geometric nonlinearity should be considered in the kinematic description. The Absolute Nodal Coordinate Formulation (ANCF) proposed by Prof. Shabana [11] has been widely used in the dynamic analysis of the flexible multibody systems undergoing overall motions, and it has been an important method for large deformation analysis in multibody systems for more than a decade [12]. Dmitrochenko and Mikkola [13] proposed an ANCF triangular plate element. Since the triangular elements can be applied to flexible bodies with arbitrary shapes, it is more convenient and effective to utilize the triangular elements for a membrane.

For membrane structures, wrinkles have an important influence on their mechanical behaviors. For example, wrinkles appear under a small amount of compressive stiffness [14] for extremely thin thickness of the membrane structure. According to the tension-field theory, Stein and Hedgepeth [15] introduced the variable Poisson’s ratio method to correct the constitutive relationship between the membrane wrinkles and the slacks region. Miyazaki [16] proposed a membrane model with small compressive stiffness, in which the stress along the wrinkling direction is reduced to a small value, but is not zero. Afterward, Miyazaki [17] reviewed the traditional wrinkle models and presented a Stiffness Reduction Model (SRM) with a wrinkle/slack criterion to describe the wrinkles.

Since contact-impact occurs in the process of membrane deployment, accurate models on membrane contacts play an important role in multibody systems. Cannella et al. [18] used flexible panels to model the origami carton, and the contact between actuators and panels was established according to Hertzian contact theory. Liu [19] proposed a computational algorithm to integrate the wrinkle/slack model into the ANCF thin shell elements for the flexible multibody dynamics. In the spinning deployment process of the sail, a simple contact model was applied to avoid penetration between the membrane and rigid hub. Based on the consideration of the contact between the cloths, Bernd et al. [20] proposed an internal friction model that reveals the hysteresis of force deformation in cloth. Zhu [21] utilized the segment-to-segment contact discretization to solve several contact/collision dynamic problems of space membrane structures. Although both methods can settle the contact problems of the spinning deployable membrane, the accuracy of the solution is insufficient for the complicated contact situations of foldable origami membranes. In addition, multiple-point contact is hardly taken into consideration in the deployment of the foldable origami space membrane structures. Thus, it is necessary to build an effective algorithm for complicated contact problems in foldable origami membrane systems.

The objective of this paper is to perform dynamic modeling for the contact problem of the foldable origami space membrane structures and analyze the influence of the contact-impact among the membrane elements during the deployment. The remaining of the paper is organized as follows: In Sect. 2, the kinematics of a triangle element is depicted using the ANCF triangular element, which is based on Specht’s shape functions, and then the stress–strain relationship of the membrane is derived by using the Stiffness Reduction Model (SRM). In the sequel, the element mass matrix and the vector of the element elastic force are obtained. In Sect. 3, a mixed method is proposed by combining the membrane STS contact elements with the NTS contact elements, and the normal contact force is formulated by the penalty method. In Sect. 4, the detailed description of the foldable origami membrane structure is introduced, including the special constraints built for the fold lines, and then the dynamic equations of the membrane multibody system considering the damping effect are obtained. In Sect. 5, the numerical simulation of the leaf-in origami membrane structure during the deployment is carried out to verify the proposed mixed method, and the influence of the contact on the membrane structure during the deployment is discussed. Finally, the main conclusions and the perspectives for future researches are summarized in Sect. 6.

2 ANCF membrane element

2.1 The discretization of the membrane element

In this section, the ANCF membrane element is presented using the thin plane element of ANCF [22]. Since triangular elements can be used to discretize arbitrary shapes, they are applied in this paper. As shown in Fig. 2, $\Pi _{0}$ is the mid-surface of the triangular membrane element. In the local Cartesian coordinate frame $O$–XYZ, the global position vector of an arbitrary point $P$ on the mid-surface can be expressed as

$$ \mathbf{r} = \mathbf{Sq}_{e}, $$

(1)

where $\mathbf{S}$ is the element shape function matrix of the membrane element, and $\mathbf{q}_{e}$ is the vector of element nodal coordinates. The details of $\mathbf{S}$ and $\mathbf{q}_{e}$ are given in the following.

Fig. 2

General motion of a triangular membrane element of ANCF (Color figure online)

In order to describe the finite elements of a triangle distinctly, the triangle area coordinates are used in this paper [13]. As shown in Fig. 3, the position coordinates of an arbitrary point $P$ of a triangle in the Cartesian coordinate system $O$–XY can be defined as follows:

$$ \textstyle\begin{array}{l} x_{P} = x_{1}\Delta _{1} + x_{2}\Delta _{2} + x_{3}\Delta _{3}, \\ y_{P} = y_{1}\Delta _{1} + y_{2}\Delta _{2} + y_{3}\Delta _{3}, \end{array} $$

(2)

where ($x_{i},y_{i}$), $i = 1$, 2, 3 represent the coordinates of three vertices, and $\Delta _{1},\Delta _{2},\Delta _{3}$ are triangular area coordinates, which are dimensionless areas of $\Delta _{1}^{*},\Delta _{2}^{*},\Delta _{3}^{*}$. The area coordinates are not independent, since $\Delta _{1} + \Delta _{2} + \Delta _{3} = 1$. According to Eq. (2), these area coordinates can be expressed as

$$ \Delta _{i} = \frac{\Delta _{i}^{*}}{\Delta } = \frac{1}{2\Delta } (c_{i 1}x_{P} + c_{i2}y_{P} + c_{i 3}),\quad i = 1, 2, 3, $$

(3)

where $\Delta = \left [ \left ( x_{1}y_{2} - x_{2}y_{1} \right ) + \left ( x_{2}y_{3} - x_{3}y_{2} \right ) + \left ( x_{3}y_{1} - x_{1}y_{3} \right ) \right ] / 2$ is the area of the triangle element, and $c_{ij}$, $j=1$, 2, 3 are area coefficients, and the detailed expressions of the area coefficients are written as follows:

$$ c_{i 1} = y_{j} - y_{k},\quad c_{i 2} = x_{k} - x_{j},\quad c_{i3} = x_{j}y_{k} - x_{k}y_{j}. $$

(4)

Fig. 3

The relationship of area coordinates and Cartesian coordinates (Color figure online)

The subscripts of the above and the latter equations obey a rule that $i, j$ and $k$ are a cyclic permutation with indices 1, 2 and 3. For the triangular element, the integral of triangular coordinates $\Delta _{1},\Delta _{2},\Delta _{3}$ can be approximated by a sum as follows:

$$ \iint _{\Delta } F\left ( \Delta _{1},\Delta _{2},\Delta _{3} \right ) \mathrm{d}\Delta = \Delta \sum _{i = 1}^{N} \omega _{i} F\left ( \lambda _{1i},\lambda _{2i},\lambda _{3i} \right ), $$

(5)

where $\omega _{i}$ is the weight coefficient, and $\lambda _{ 1 i}$, $\lambda _{2i}$, $\lambda _{ 3i}$ are the nodal coordinates of a quadrature rule [23].

The ANCF triangular plate element has nine degrees of freedom, and each node is defined by a position vector and two slope vectors. The vector of element nodal coordinates is

$$ \mathbf{q}_{e} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \mathbf{q}_{11}^{\mathrm{T}} & \mathbf{q}_{12}^{\mathrm{T}} & \mathbf{q}_{13}^{\mathrm{T}} & \mathbf{q}_{21}^{\mathrm{T}} & \mathbf{q}_{22}^{\mathrm{T}} & \mathbf{q}_{23}^{\mathrm{T}} & \mathbf{q}_{31}^{\mathrm{T}} & \mathbf{q}_{32}^{\mathrm{T}} & \mathbf{q}_{33}^{\mathrm{T}} \end{array}\displaystyle \right ]^{ \mathrm{T}}, $$

(6)

where $\mathbf{q}_{i 1} = \mathbf{r}_{i}$ is the nodal position vectors, and $\mathbf{q}_{i2} = \partial \mathbf{r}_{i} / \partial x_{P}$, $\mathbf{q}_{i3} = \partial \mathbf{r}_{i} / \partial y_{P}$ are the slope vectors.

Based on the Specht’s shape functions [24], the shape function matrix can be written as

$$ \mathbf{S} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} S_{11}\mathbf{I}_{3} & S_{12}\mathbf{I}_{3} & S_{13}\mathbf{I}_{3} & S_{21}\mathbf{I}_{3} & S_{22}\mathbf{I}_{3} & S_{23}\mathbf{I}_{3} & S_{31}\mathbf{I}_{3} & S_{32}\mathbf{I}_{3} & S_{33}\mathbf{I}_{3} \end{array}\displaystyle \right ], $$

(7)

where $\mathbf{I}_{3}$ is the identity matrix of three orders. $S_{i 1}$, $S_{i2}$ and $S_{i3}$ can be expressed in detail as follows [24, 25]:

$$ \textstyle\begin{array}{l} S_{i1} = \Delta _{i} - \Delta _{i}\Delta _{j} + \Delta _{k}\Delta _{i} + 2\left ( P_{i} - P_{k} \right ), \\ S_{i2} = c_{j2}\left ( P_{k} - \Delta _{k}\Delta _{i} \right ) + c_{k2}P_{i}, \\ S_{i3} = - c_{j1}\left ( P_{k} - \Delta _{k}\Delta _{i} \right ) - c_{k1}P_{i}, \end{array} $$

(8)

where $P_{i} = \Delta _{i}^{2}\Delta _{j} + \frac{1}{2}\Delta _{i}\Delta _{j}\Delta _{k}\left [ 3\left ( 1 - \mu _{k} \right )\Delta _{i} + \left ( 1 + 3\mu _{k} \right )\left ( \Delta _{k} - \Delta _{j} \right ) \right ]$, $\mu _{i} = \left ( l_{k}^{2} - l_{j}^{2} \right ) / l_{i}^{2}$, $l_{i}^{2} = c_{i1}^{2} + c_{i2}^{2}$.

2.2 Stress–strain relationship of the membrane

The membrane structures rely mainly on the forming and bearing of tensile stress, so there are inevitably states of slack and wrinkles on the surface. In order to sort the small compressive stiffness out in these regions of the membrane structure, Miyazaki [17] proposed a Stiffness Reduction Model (SRM). In this section, SRM was integrated into the ANCF membrane element. Since the membrane does not withstand the bending loads, the flexural rigidity can be ignored during the calculation of the membrane [19].

In the constitutive law of isotropic materials, the relationship between the principal stress $\boldsymbol{\tau }$ corresponding to the second Piola–Kirchhoff stress tensor and the principal strain $\boldsymbol{\gamma }$ corresponding to the Green–Lagrange strain tensor can be expressed as

$$ \boldsymbol{\tau } = \boldsymbol{\Gamma } \boldsymbol{\gamma },\quad \boldsymbol{\tau } = \left [ \textstyle\begin{array}{c} \sigma _{1} \\ \sigma _{2} \end{array}\displaystyle \right ],\quad \boldsymbol{\gamma } = \left [ \textstyle\begin{array}{c} \gamma _{1} \\ \gamma _{2} \end{array}\displaystyle \right ], $$

(9)

where $\sigma _{1}$ and $\sigma _{2}$ are the maximum principal stress and the minimum principal stress, respectively. Similarly, $\gamma _{1}$ and $\gamma _{2}$ correspond to the maximum principal strain and the minimum principal strain, respectively, and the detailed expressions of both are given as follows:

$$ \begin{aligned} &\gamma _{1} = \frac{\varepsilon _{11} + \varepsilon _{22}}{2} + \frac{1}{2}\sqrt{d}, \\ &\gamma _{2} = \frac{\varepsilon _{11} + \varepsilon _{22}}{2} - \frac{1}{2}\sqrt{d}, \end{aligned} $$

(10)

where $d = \left ( \varepsilon _{11} - \varepsilon _{22} \right )^{2} + 4\varepsilon _{12}^{2}$, and $\varepsilon _{11}$, $\varepsilon _{22}$, $\varepsilon _{12}$ are the components of the mid-surface strain tensor $\boldsymbol{\varepsilon }$, which is discussed in Sect. 2.3.

Since the direction of the principal stress is consistent with the principal strain, the elasticity matrix can be expressed as

$$ \boldsymbol{\Gamma } = \frac{E}{1 - \nu ^{2}}\left [ \textstyle\begin{array}{c@{\quad}c} 1 & \nu \\ \nu & 1 \end{array}\displaystyle \right ], $$

(11)

where $E$ and $\nu$ are the Young’s modulus and Poisson’s ratio of the material, respectively. According to the values of stress and strain, the membrane can be divided into three stress states: taut, wrinkle, and slack.

When the membrane is in taut state, the elasticity matrix for the taut membrane element $\boldsymbol{\Gamma }_{t}$ is equal to $\boldsymbol{\Gamma }$, which is expressed in Eq. (11).

For the wrinkle state, it is assumed that the Young’s modulus and Poisson’s ratio of the material in the direction of the minimum principal stress are small. In order to consider the compressive stiffness in the direction of wrinkles, the elasticity matrix of the wrinkled membrane element can be determined by

$$ \boldsymbol{\Gamma }_{w} = \frac{E}{1 - s_{1}\nu ^{2}}\left [ \textstyle\begin{array}{c@{\quad}c} 1 & s_{1}\nu \\ s_{1}\nu & s_{1} \end{array}\displaystyle \right ], $$

(12)

where $s_{1}$ is the stiffness reduction ratio in the minor principal strain direction.

For the last slack state, in addition to the minimum principal stress direction, the Young’s modulus and Poisson’s ratio of the material along the major principal strain direction are also small [19]. The elasticity matrix of the slack membrane element can be written as

$$ \boldsymbol{\Gamma }_{s} = \frac{E}{1 - s_{1}s_{2}\nu ^{2}}\left [ \textstyle\begin{array}{c@{\quad}c} s_{2} & s_{1}s_{2}\nu \\ s_{1}s_{2}\nu & s_{1} \end{array}\displaystyle \right ], $$

(13)

where $s_{2}$ is the stiffness reduction ratio in the major principal strain direction.

According to the modified wrinkle criterion [17], it can directly give a rule to determine the membrane states of taut, wrinkle, and slack. Two parameters $f_{1}$ and $f_{2}$ are introduced as follows:

$$ f_{1} = \gamma _{2} + \nu \gamma _{1},\quad f_{2} = \gamma _{1} + s_{1}\nu \gamma _{2}, $$

(14)

where the strain $\gamma _{1}$ and $\gamma _{2}$ can be obtained by Eq. (10). Based on the values of $f_{1}$ and $f_{2}$ in Eq. (14), the criterion of the elasticity matrix is given as

$$ \hat{\boldsymbol{\Gamma }} = \left \{ \textstyle\begin{array}{l@{\quad}l} \boldsymbol{\Gamma }_{t},& f_{1} \ge 0 \left ( \mathrm{taut} \right ), \\ \boldsymbol{\Gamma }_{w},& f_{1} < 0\ \mbox{and}\ f_{2} > 0 \left ( \textstyle\begin{array}{c} \mathrm{wrinkle} \end{array}\displaystyle \right ), \\ \boldsymbol{\Gamma }_{s}, &f_{2} \le 0 \left ( \mathrm{slack} \right ). \end{array}\displaystyle \right . $$

(15)

2.3 Mass matrix and elastic force vector

Based on the ANCF thin plane element [26], the energies of the membrane element are derived by neglecting the bending strain. It is assumed that the membrane is isotropic material with uniform thickness. As shown in Fig. 2, according to the continuum theory, the Green–Lagrange strain vector of an arbitrary point $P$ on the membrane mid-surface can be denoted as follows:

$$ \boldsymbol{\varepsilon } = \left [ \textstyle\begin{array}{c} \varepsilon _{11} \\ \varepsilon _{22} \\ 2\varepsilon _{12} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} \frac{1}{2}(\mathbf{r}_{x}^{\mathrm{T}}\mathbf{r}_{x} - 1) \\ \frac{1}{2}(\mathbf{r}_{y}^{\mathrm{T}}\mathbf{r}_{y} - 1) \\ \mathbf{r}_{x}^{\mathrm{T}}\mathbf{r}_{y} \end{array}\displaystyle \right ], $$

(16)

where $\mathbf{r}_{x} = \partial \mathbf{r}/\partial x$, $\mathbf{r}_{y} = \partial \mathbf{r}/\partial y$. Substituting Eq. (1) into Eq. (16), the Green–Lagrange strain vector $\boldsymbol{\epsilon }$ can be expressed as

$$ \boldsymbol{\varepsilon } = \left [ \textstyle\begin{array}{c} \frac{1}{2}(\mathbf{q}_{\mathrm{e}}^{\mathrm{T}}\mathbf{S}_{\mathrm{x}}^{\mathrm{T}}\mathbf{S}_{x} \mathbf{q}_{e} - 1) \\ \frac{1}{2}(\mathbf{q}_{\mathrm{e}}^{\mathrm{T}}\mathbf{S}_{\mathrm{y}}^{\mathrm{T}}\mathbf{S}_{y} \mathbf{q}_{e} - 1) \\ \mathbf{q}_{\mathrm{e}}^{\mathrm{T}}\mathbf{S}_{\mathrm{x}}^{\mathrm{T}}\mathbf{S}_{y} \mathbf{q}_{e} \end{array}\displaystyle \right ], $$

(17)

where $\mathbf{S}_{x} = \partial \mathbf{S}/\partial x$, $\mathbf{S}_{y} = \partial \mathbf{S}/\partial y$.

The virtual work of the inertia force of the membrane element can be written as

$$ \delta W_{i} = - \int _{V} \rho \delta \mathbf{r}^{\mathrm{T}} \ddot{\mathbf{r}}\, \mathrm{d}V = - \delta \mathbf{q}_{e}^{\mathrm{T}} \mathbf{M}_{e} \ddot{\mathbf{q}}_{e}, $$

(18)

where $\rho$ is the material density and $V$ is the volume of the membrane element. The element mass matrix $\mathbf{M}_{e}$ can be obtained by

$$ \mathbf{M}_{e} = h \int _{A} \rho \mathbf{S}^{\mathrm{T}}\mathbf{S} \,\mathrm{d}A, $$

(19)

where $h$ is the thickness of the membrane element, and $A$ is the area of the mid-surface of the membrane element.

The strain energy of the membrane element can be written as

$$ U_{se} = \frac{1}{2}h\int _{A} \left [ \textstyle\begin{array}{cc} \gamma _{1} & \gamma _{2} \end{array}\displaystyle \right ] \hat{\boldsymbol{\Gamma }} \left [ \textstyle\begin{array}{c} \gamma _{1} \\ \gamma _{2} \end{array}\displaystyle \right ] \mathrm{d}A, $$

(20)

where $\hat{\boldsymbol{\Gamma }}$ represents the symmetric elasticity matrix in different states, which is given in Eq. (15). Then the vector of the element elastic force can be obtained as

$$ \mathbf{Q}_{fe} = - \left ( \frac{\partial U_{se}}{\partial \mathbf{q}_{e}} \right )^{\mathrm{T}} = - h\int _{A} \left [ \textstyle\begin{array}{c@{\quad }c} \left ( \partial \gamma _{1}/\partial \mathbf{q}_{e} \right )^{\mathrm{T}} & \left ( \partial \gamma _{2}/\partial \mathbf{q}_{e} \right )^{\mathrm{T}} \end{array}\displaystyle \right ] \hat{\boldsymbol{\Gamma }} \left [ \textstyle\begin{array}{c} \gamma _{1} \\ \gamma _{2} \end{array}\displaystyle \right ] \mathrm{d}A. $$

(21)

Considering Eq. (19), the kinetic energy of the membrane element yields

$$ U_{te} = \frac{1}{2}\int _{V_{e}} \rho \dot{\mathbf{r}}^{\mathrm{T}}\dot{\mathbf{r}}\, \mathrm{d}V_{e} = \frac{1}{2}\dot{\mathbf{q}}_{e}^{\mathrm{T}} \mathbf{M}_{e} \dot{\mathbf{q}}_{e}. $$

(22)

3 Contact formulations for the membrane

Multiple-point contact is inevitable in the membrane multibody systems subjecting to overall motions and large deformations. Contact-impact leads to discontinuous features of the system, including the occurrence of state variables and high frequency oscillations. Therefore, it is critical to properly model the contact between structural parts.

The contact discretization type plays an important role in contact detection and contact force model. Two contact discretization types for the membrane triangle elements are derived in this section: one is the surface-to-surface (STS) contact element, and the other is the node-to-surface (NTS) contact element. In addition, a mixed method is proposed by combining the membrane STS contact elements with the NTS ones, which can avoid mutual penetration at the element boundaries in some complicated contact situations, as like the deployment of the foldable origami membrane structures.

For the frictionless contact problems, the normal contact force is formulated by the penalty method [27]. The virtual work of the contact force in the frictionless case is

$$ \delta W_{N}^{C} = \left \{ \textstyle\begin{array}{l@{\quad}l} - \int _{\Omega } \varepsilon _{N}g_{N}\delta g_{N}\,\mathrm{d} \Omega , & \mbox{if}\ g_{N} \le 0, \\ 0, & \mbox{otherwise}, \end{array}\displaystyle \right . $$

(23)

where $\varepsilon _{N}$ is the penalty parameter and $g_{N}$ is the normal penetration, and $\Omega$ is the contact area, which is defined on the slave body. Contact between elements occurs only if the value of the normal penetration is nonpositive.

3.1 Surface-to-surface (STS) contact element

In case of the surface-to-surface contact element, it is checked between each integration point of the slave surface and the master surface. As shown in Fig. 4, for an arbitrary slave point $S$, the corresponding closest point projection on the master surface is denoted as the point $C$.

Fig. 4

Geometry and kinematics of the STS contact element (Color figure online)

One STS contact element consists of $n$ nodes for the discretization of the master surface and of $m$ nodes for the slave surface. For the triangle element with linear approximation of master and slave surfaces, $n = 3$, $m = 3$. Thus, the nodal vector for the STS contact element can be stated as

$$ \mathbf{x} = \left [ \textstyle\begin{array}{c} \mathbf{x}_{M} \\ \mathbf{x}_{S} \end{array}\displaystyle \right ],\quad \mathbf{x}_{M} = \left [ \textstyle\begin{array}{c} \mathbf{x}_{M}^{(1)} \\ \mathbf{x}_{M}^{(2)} \\ \mathbf{x}_{M}^{(3)} \end{array}\displaystyle \right ],\quad \mathbf{x}_{S} = \left [ \textstyle\begin{array}{c} \mathbf{x}_{S}^{(4)} \\ \mathbf{x}_{S}^{(5)} \\ \mathbf{x}_{S}^{(7)} \end{array}\displaystyle \right ]. $$

(24)

The global position vectors of arbitrary point $P$ on the master surface and point $S$ on the slave surface are $\boldsymbol{\rho } = \mathbf{Nx}_{M}$ and $\mathbf{r}_{S} = \mathbf{Mx}_{S}$, respectively, where $\mathbf{N}$ and $\mathbf{M}$ are the corresponding shape function matrices of the master and slave elements, and the detailed expressions of $\mathbf{N}$ and $\mathbf{M}$ are given in Eq. (7).

In order to define the distance relationship between the master and slave surfaces, the relative displacement vector is defined as

$$ \mathbf{r}_{S} - \boldsymbol{\rho } = \mathbf{Ax}. $$

(25)

Considering $\Delta _{1}^{M} + \Delta _{2}^{M} + \Delta _{3}^{M} = 1$ and $\Delta _{1}^{S} + \Delta _{2}^{S} + \Delta _{3}^{S} = 1$, the matrix $\mathbf{A}$ can be written as

$$ \mathbf{A}(\boldsymbol{\Delta }^{M},\boldsymbol{\Delta }^{S}) = \left [ \textstyle\begin{array}{cc} - \mathbf{N}(\boldsymbol{\Delta }^{M}) & \mathbf{M}(\boldsymbol{\Delta }^{S}) \end{array}\displaystyle \right ], $$

(26)

where $\boldsymbol{\Delta }^{M} = \left [ \begin{array}{c@{\quad }c} \Delta _{1}^{M} & \Delta _{2}^{M} \end{array} \right ]^{\mathrm{T}}$ and $\boldsymbol{\Delta }^{S} = \left [ \begin{array}{c@{\quad }c} \Delta _{1}^{S} & \Delta _{2}^{S} \end{array} \right ]^{\mathrm{T}}$ are the vectors of convective coordinates, corresponding to the area coordinates of the master and slave elements, respectively.

Since contact between bodies is geometrical interaction between surfaces, the differential geometry of surface is required in contact mechanics [27]. By the principles of differential geometry in 3D space, the covariant tangent vectors $\boldsymbol{\rho }_{i}$ and $\mathbf{r}_{i}$, $i = 1, 2$ of the master and slave surfaces are computed as $\boldsymbol{\rho }_{i} = \partial \boldsymbol{\rho } / \partial \Delta _{i}^{M}$ and $\mathbf{r}_{i} = \partial \mathbf{r}_{S} / \partial \Delta _{i}^{S}$, respectively. The unit normal vector of the STS contact element is defined via the cross-product with the covariant tangent vectors $\boldsymbol{\rho }_{1}$ and $\boldsymbol{\rho }_{2}$, and its expression can be obtained as

$$ \mathbf{n} = \frac{\tilde{\boldsymbol{\rho }}_{1}\boldsymbol{\rho }_{2}}{\left \| \tilde{\boldsymbol{\rho }}_{1}\boldsymbol{\rho }_{2} \right \| }, $$

(27)

where $\tilde{\boldsymbol{\rho }}_{i}$ is the skew-symmetric matrix associated with $\boldsymbol{\rho }_{i} = \left [ \begin{array}{c@{\quad }c@{\quad }c} \rho _{1} & \rho _{2} & \rho _{3} \end{array} \right ]^{\mathrm{T}}$, which is defined as $\tilde{\boldsymbol{\rho }}_{i} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0 & - \rho _{3} & \rho _{2} \\ \rho _{3} & 0 & - \rho _{1} \\ - \rho _{2} & \rho _{1} & 0 \end{array} \right ]$. In addition, the direction of the normal vector is always outside the master body.

The premise of determining whether the slave point and master surface are in contact is to find the solution of the closest point projection (CPP) procedure. The CPP procedure is formulated directly as finding the minimum distance between the slave point and the master surface

$$ \bigl\| \mathbf{r}_{S} - \boldsymbol{\rho }_{C} \bigr\| = {\min} \bigl\| \mathbf{r}_{S} - \boldsymbol{\rho } (\boldsymbol{\Delta }^{M}) \bigr\| , $$

(28)

which is equivalent to the orthogonality conditions

$$ \left ( \mathbf{r}_{S} - \boldsymbol{\rho } \right )^{\mathrm{T}}\boldsymbol{\rho }_{i} = 0,\ i = 1, 2. $$

(29)

Equation (29) can be solved by the Newton–Raphson iteration method, if the closest point projection exists and is unique. Thus, each integration point of the allowable projection domain is projected uniquely onto the master surface, and these projection points are obtained by interpolation of shape function.

Considering the thickness in the STS contact element of the membrane, the normal penetration can be defined as

$$ g_{N} = \left ( \mathbf{r}_{S} - \boldsymbol{\rho } \right )^{\mathrm{T}}\mathbf{n} - \frac{th_{M} + th_{S}}{2}, $$

(30)

where $th_{M}$ and $th_{ S}$ are the thicknesses of the master and slave surfaces, respectively.

In the case of contact, the relative displacement vector can be expressed as

$$ \mathbf{r}_{S} - \boldsymbol{\rho } = \left ( g_{N} + \frac{th_{M} + th_{S}}{2} \right )\mathbf{n}. $$

(31)

Substituting Eq. (25) into Eq. (31), the variation of the normal penetration is given by

$$ \begin{aligned} \delta g_{N} &= \mathbf{n}^{\mathrm{T}}\delta \left ( \mathbf{r}_{S} - \boldsymbol{\rho } \right ) + \left ( \delta \mathbf{n} \right )^{\mathrm{T}}\left ( \mathbf{r}_{S} - \boldsymbol{\rho } \right ) \\ &= \mathbf{n}^{\mathrm{T}}\left ( \delta \mathbf{A} \right ) \mathbf{x} + \mathbf{n}^{\mathrm{T}}\mathbf{A} \delta \mathbf{x} + \left ( \delta \mathbf{n} \right )^{\mathrm{T}}\left ( \mathbf{r}_{S} - \boldsymbol{\rho } \right ). \end{aligned} $$

(32)

Since the relative displacement vector is parallel to the unit normal vector $\mathbf{n}$, which is orthogonal to $\delta \ \mathbf{n}$, one obtains that $(\delta \mathbf{n})^{\mathrm{T}}(\mathbf{r}_{S} - \boldsymbol{\rho } ) = 0$. In addition, considering Eq. (25), the first term of Eq. (32) is given by

$$ \mathbf{n}^{\mathrm{T}}\left ( \delta \mathbf{A} \right ) \mathbf{x} = \sum _{i = 1}^{2} \mathbf{n}^{\mathrm{T}}\frac{\partial \mathbf{A}}{\partial \Delta _{i}^{M}}\mathbf{x}\delta \Delta _{i}^{M} = \sum _{i = 1}^{2} \mathbf{n}^{\mathrm{T}}\frac{\partial \left ( \mathbf{Ax} \right )}{\partial \Delta _{i}^{M}}\delta \Delta _{i}^{M} = - \sum _{i = 1}^{2} \mathbf{n}^{\mathrm{T}}\boldsymbol{\rho }_{i}\delta \Delta _{i}^{M}. $$

(33)

Due to the orthogonality conditions in Eq. (29), it can be obtained that $\mathbf{n}^{\mathrm{T}}\delta \mathbf{Ax} = 0$. Thus, the variation of the normal penetration can be simplified as

$$ \delta g_{N} = \mathbf{n}^{\mathrm{T}}\mathbf{A}\delta \mathbf{x}. $$

(34)

Substituting Eq. (34) into Eq. (23), the virtual work of the contact force of the STS contact element can be expressed as

$$ \delta W_{N}^{C} = - \int _{\Omega } \varepsilon _{N}g_{N}\delta \mathbf{x}^{\mathrm{T}}\mathbf{A}^{\mathrm{T}}\mathbf{n}\,\mathrm{d}\Omega = \delta \mathbf{x}^{\mathrm{T}}\mathbf{Q}_{Ce}^{S}. $$

(35)

Then, the vector of the generalized contact force of the STS contact element is

$$ \mathbf{Q}_{Ce}^{S} = - \int _{\Omega } \varepsilon _{N}g_{N}\mathbf{A}^{\mathrm{T}}\mathbf{n}\,\mathrm{d}\Omega . $$

(36)

The contact tangential stiffness matrix can be obtained as

$$ \mathbf{K}_{teC}^{S} = \frac{\partial ( - \mathbf{Q}_{Ce}^{S})}{\partial \mathbf{x}} = \underbrace{\int _{\Omega } \varepsilon _{N}\mathbf{A}^{\mathrm{T}}\mathbf{nn}^{\mathrm{T}}\mathbf{A} \,\mathrm{d}\Omega }_{\mathrm{main}\; \mathrm{part}} + \underbrace{\int _{\Omega } \varepsilon _{N}g_{N}\partial (\mathbf{A}^{\mathrm{T}}\mathbf{n}) / \partial \mathbf{x}\, \mathrm{d}\Omega }_{\mathrm{curvature}\; \mathrm{part}}. $$

(37)

The full form of the contact tangential stiffness matrix is subdivided into the main and curvature parts, where the curvature part is usually much smaller compared with the main part [28]. Thus, the contact tangential stiffness matrix of the STS contact element is reduced to

$$ \mathbf{K}_{teC}^{S} = \int _{\Omega } \varepsilon _{N}\mathbf{A}^{\mathrm{T}}\mathbf{nn}^{\mathrm{T}}\mathbf{A} \,\mathrm{d}\Omega , $$

(38)

which is a symmetric matrix. Based on the numerical integration given in Eq. (5), the integral in Eq. (36) is calculated numerically as a sum over Gauss integration points positioned at the slave surface, which can be expressed as

$$ \mathbf{Q}_{Ce}^{S} = - \sum _{I = 1}^{ip} \varepsilon _{N}g_{N}\mathbf{A}^{\mathrm{T}}\mathbf{n}\sqrt{\left | \operatorname{det}\left ( b_{ij} \right ) \right |} w_{I} \Delta ^{S}, $$

(39)

where $\Delta ^{S}$ is the area of the slave surface, and $ip$, $w_{I}$ are the number and weight of Gauss integration points, respectively. The covariant components of the metric tensor of the slave surface are

$$ b_{ij} = \mathbf{r}_{i}^{\mathrm{T}}\mathbf{r}_{j},\quad i, j = 1, 2. $$

(40)

Similarly, the numerical integral for the contact tangential stiffness matrix is

$$ \mathbf{K}_{teC}^{S} = \sum _{I = 1}^{ip} \varepsilon _{N}\mathbf{A}^{\mathrm{T}}\mathbf{nn}^{\mathrm{T}}\mathbf{A}\sqrt{\left | \operatorname{det}\left ( b_{ij} \right ) \right |} w_{I} \Delta ^{S}. $$

(41)

3.2 Node-to-surface (NTS) contact element

The NTS contact element is the more widely used contact discretization type, which involves a slave node and a master surface. In comparison with the STS contact element, the solution process of the NTS contact element can be considered as part of the STS when replacing the slave integration point by a slave node $S$ as shown in Fig. 5.

Fig. 5

Geometry and kinematics of the NTS contact element (Color figure online)

For the triangle element, one NTS contact element consists of three nodes for the discretization of the master surface and a separated slave node for the slave surface. The nodal vector of the NTS contact element are given as

$$ \mathbf{x} = \left [ \textstyle\begin{array}{c} \mathbf{x}_{M} \\ \mathbf{x}_{S} \end{array}\displaystyle \right ],\quad \mathbf{x}_{M} = \left [ \textstyle\begin{array}{c} \mathbf{x}_{M}^{(1)} \\ \mathbf{x}_{M}^{(2)} \\ \mathbf{x}_{M}^{(3)} \end{array}\displaystyle \right ],\quad \mathbf{x}_{S} = \mathbf{x}_{S}^{(4)}. $$

(42)

The expression of the relative displacement vector is the same as in Eq. (26), but the approximation matrix $\mathbf{A}$ is rewritten as

$$ \mathbf{A}(\boldsymbol{\Delta }^{M}) = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} - \mathbf{N}(\boldsymbol{\Delta }^{M}) & \mathbf{I}_{3} & \mathbf{0}_{3 \times 6} \end{array}\displaystyle \right ], $$

(43)

where $\boldsymbol{\Delta }^{M} = \left [ \begin{array}{c@{\quad }c} \Delta _{1}^{M} & \Delta _{2}^{M} \end{array} \right ]^{\mathrm{T}}$ is the vector of convective coordinates, corresponding to the area coordinates of the master element. In addition, $\mathbf{I}_{3}$ is the $3 \times 3$ identity matrix and $\mathbf{0}_{3 \times 6}$ is the $3 \times 6$ zero matrix.

The unit normal vector for the NTS contact element is also obtained by Eq. (27). Additionally, Eqs. (28) and (29) are the solution of the CPP procedure, which involved an integration point and a master surface, so this procedure is applicable to the NTS one. As the slave node is defined on the mid-surface of the slave body, the normal penetration for the NTS contact element is also expressed by Eq. (30).

Since there is only one slave point on the slave surface, the generalized contact force vector and the contact tangential stiffness matrix of the NTS contact element can be directly expressed as

$$ \mathbf{Q}_{Ce}^{N} = - \varepsilon _{N}g_{N}\mathbf{A}^{\mathrm{T}}\mathbf{n}, $$

(44)

$$ \mathbf{K}_{teC}^{N} = \varepsilon _{N}\mathbf{A}^{\mathrm{T}}\mathbf{nn}^{\mathrm{T}}\mathbf{A}. $$

(45)

3.3 Mixed method for contact elements

Based on the formulations of the STS and NTS contact elements, the characteristics of these two contact discretizations can be summarized as follows. Since the surface regions are taken into account in the STS contact elements, penetration inside the element will not be easy, whereas the STS contact element only uses the integration points as the contact detection points, so there may be overpenetration on the boundaries and at the corners. On the contrary, the NTS contact element can avoid penetration in those regions. However, the NTS contact element is enforced only at individual nodes, hence penetration is easy in large area contact problems.

In some contact problems with well represented geometries, it is enough to only consider the STS contact element. However, in case that there are contacts at some sharp corners, such as the deployment of the foldable origami membrane structure, overpenetrations may occur at the corners and the fold lines, because the contact detection points of the STS contact element are all inside the element. Therefore, in order to improve the accuracy of the solution of the multiple-point contact problems, a mixed method is proposed in this section, which integrates the advantages of the STS contact elements with the NTS contact elements to avoid the mutual penetration of the element boundaries.

Figure 6 shows the flow chart for implementing the mixed method, and there are two kinds of slave points in the mixed method, integration points and nodes. The STS contact elements, which use the integration points as the contact detection points, can prevent penetration inside the element except for boundaries and corners. Meanwhile, the NTS contact elements can sort out the contact problem at the corners by detecting the nodes of the elements. Additionally, the implementation of the STS contact elements and the NTS contact elements are independent of each other, thus the contact calculation between them can be obtained in parallel. Consequently, the generalized contact force vector of the mixed method can be assembled by

$$ \mathbf{Q}_{C} = \sum _{n_{S}} \mathbf{B}_{Se}^{\mathrm{T}}\mathbf{Q}_{Ce}^{S} + \sum _{n_{N}} \mathbf{B}_{Ne}^{\mathrm{T}}\mathbf{Q}_{Ce}^{N}, $$

(46)

where $\mathbf{B}_{Se}$, $\mathbf{B}_{Ne}$ are the connectivity matrices of the STS and NTS contact elements, respectively, and $n_{S}$, $n_{N}$ are the numbers of the STS and NTS contact elements, respectively; $\mathbf{Q}_{Ce}^{S}$ and $\mathbf{Q}_{Ce}^{N}$ can be obtained from Eqs. (39) and (44), respectively.

Fig. 6

Flow chart for the implementing of a mixed method (Color figure online)

Owing to the advantages of the STS and NTS contact elements, the mixed method can avoid an overpenetration that may occur inside and on the boundaries of the elements. For the deployment of the foldable origami membrane, multiple-point contact is inevitable at the fold lines and corners, and it is necessary to utilize the mixed method to effectively avoid mutual penetration. Compared with the traditional STS contact elements, the mixed method has a higher accuracy and can better reveal the actual contact phenomenon.

4 The modeling of the foldable origami membrane structure

Due to the characteristics of being ultra-light and having small stowage volume, easy folding and high stiffness-to-weight ratio, the membrane structure has been widely used in aerospace engineering. Generally speaking, the foldable origami membrane structure is stowed in a small volume before launch, thus the deployment process is a key technique for the application of the membrane structure.

4.1 The detailed description of the foldable origami membrane structure

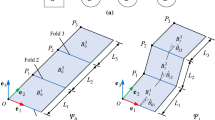
In order to achieve the dynamic modeling of the foldable origami membrane structure, it is first necessary to introduce the fundamental concepts of origami. We take the leaf-in origami membrane structure as an example to illustrate the characteristics of the foldable origami membrane structure.

The concepts of the folding pattern upon the fully deployed configuration of the leaf-in origami membrane are shown in Fig. 7, which is regarded as a bounded planar surface without overlap. It is observed that the membrane is folded along straight creases, and the line segments coincident with the creased folds are called fold lines, which are typically defined by their end points, formally called vertices. Then, the regions bounded by the fold lines and the boundaries are denoted as the faces, remaining the properties of the membrane during the deployment. In addition, the “mountain–valley” assignment are also indicted in Fig. 7, in which mountain folds are represented with solid red lines and valley folds are represented with dashed blue lines. For a mountain fold, the fold line is at the top and the face can be regarded as being rotated into the page, while a valley fold is at the bottom and can be considered as rotating out of it [3], and they are shaped as “$\Lambda$” and “$\mathrm{V}$”, respectively.

Fig. 7

Schematic of the leaf-in origami membrane (Color figure online)

4.2 Constraint equations of the fold line

In the modeling process of the foldable origami membrane structures, the connections between the membrane elements are implemented by the constraint equations on the boundaries. Since the membrane is a continuum, the establishment of the constraint equations is of great importance.

The space membrane is subdivided into various triangular faces that are connected at straight edges, and these edges include two kinds of boundaries. Two kinds of boundaries of membrane elements are shown in Fig. 8. For the folding boundary, it is required to impose the constraints of equal displacement gradients in the direction of fold line $\boldsymbol{\tau }_{\mathrm{f}}$ on the vertices of triangular membrane elements. For the nonfolding boundary, the constraints of equal displacement gradients in both directions $\boldsymbol{\tau }_{\mathrm{nf}}$ and $\mathbf{n}_{\mathrm{nf}}$ are applied on the vertices of triangular membrane elements.

Fig. 8

Constraints on the boundary of membrane elements: folding boundary represented by a dashed line; nonfolding boundary represented by straight lines (Color figure online)

For the folding boundary, the displacement constraint equation is

$$ \mathbf{r}_{Q} - \mathbf{r}_{R} = \mathbf{0}, $$

(47)

where $Q$ and $R$ are the vertices of different elements. The displacement gradient constraint equation is

$$ \frac{\partial \mathbf{r}_{Q}}{\partial \boldsymbol{\tau }_{\mathrm{f}Q}} - \frac{\partial \mathbf{r}_{R}}{\partial \boldsymbol{\tau }_{\mathrm{f}R}} = \mathbf{0}, $$

(48)

where $\boldsymbol{\tau }_{\mathrm{f}Q}$ and $\boldsymbol{\tau }_{\mathrm{f}R}$ are the coordinate vectors of $\boldsymbol{\tau }_{\mathrm{f}}$ defined in the element coordinate systems. To simplify the explanation of the displacement gradient constraint equation, defining the coordinate vector of the fold line as $\boldsymbol{\tau }_{\mathrm{f}} = \left [ \tau _{1},\tau _{2},\tau _{3} \right ]^{ \mathrm{T}}$, Eq. (48) can be written as

$$ \left ( \frac{\partial \mathbf{r}_{Q}}{\partial x_{Q}}\tau _{1} + \frac{\partial \mathbf{r}_{Q}}{\partial y_{Q}}\tau _{2} + \frac{\partial \mathbf{r}_{Q}}{\partial z_{Q}}\tau _{3} \right ) - \left ( \frac{\partial \mathbf{r}_{R}}{\partial x_{R}}\tau _{1} + \frac{\partial \mathbf{r}_{R}}{\partial y_{R}}\tau _{2} + \frac{\partial \mathbf{r}_{R}}{\partial z_{R}}\tau _{3} \right ) = \mathbf{0}. $$

(49)

In a similar manner, the constraint equations of the nonfolding boundary can be also expressed by Eqs. (47) and (49), where $P$ and $Q$ are the vertices of different elements. In addition to the constraints above, another constraint of equal displacement gradients in the vertical direction of the boundary is also essential in this case, which is given by

$$ \frac{\partial \mathbf{r}_{P}}{\partial \mathbf{n}_{\mathrm{nf}P}} - \frac{\partial \mathbf{r}_{Q}}{\partial \mathbf{n}_{\mathrm{nf}Q}} = \mathbf{0}, $$

(50)

where $\mathbf{n}_{\mathrm{nf}P}$ and $\mathbf{n}_{\mathrm{nf}Q}$ are the coordinate vectors of $\mathbf{n}_{\mathrm{nf}}$ in the element coordinate systems. Defining the coordinate vector of the boundary in the normal direction as $\mathbf{n}_{\mathrm{nf}} = \left [ n_{1},n_{2},n_{3} \right ]^{ \mathrm{T}}$, Eq. (50) can be written as

$$ \left ( \frac{\partial \mathbf{r}_{P}}{\partial x_{P}}n_{1} + \frac{\partial \mathbf{r}_{P}}{\partial y_{P}}n_{2} + \frac{\partial \mathbf{r}_{P}}{\partial z_{P}}n_{3} \right ) - \left ( \frac{\partial \mathbf{r}_{Q}}{\partial x_{Q}}n_{1} + \frac{\partial \mathbf{r}_{Q}}{\partial y_{Q}}n_{2} + \frac{\partial \mathbf{r}_{Q}}{\partial z_{Q}}n_{3} \right ) = \mathbf{0}. $$

(51)

Based on these constraint equations established on the boundaries, an arbitrary foldable origami membrane structure with complex fold lines can be modeled, including multiple interior fold intersections. Therefore, the key point of the constraint equations is to distinguish the boundary cases.

4.3 Dynamic equations

The vector of element nodal coordinates $\mathbf{q}_{e}$ is related to the vector of generalized coordinates of the membrane $\mathbf{q}$ by using the connectivity matrix $\mathbf{B}_{e}$, and the relationship is

$$ \mathbf{q}_{e} = \mathbf{B}_{e}\mathbf{q}. $$

(52)

The mass matrix of the membrane can be assembled as

$$ \mathbf{M} = \sum _{e} \mathbf{B}_{e}^{\mathrm{T}}\mathbf{M}_{e}\mathbf{B}_{e}. $$

(53)

Similarly, the vector of generalized forces of the membrane can be written as

$$ \mathbf{Q} = \mathbf{Q}_{f} + \mathbf{Q}_{C}, $$

(54)

where $\mathbf{Q}_{f} = \sum _{e} \mathbf{B}_{e}^{\mathrm{T}}\mathbf{Q}_{fe}$ is the vector of the generalized elastic force, and $\mathbf{Q}_{C}$ is given by Eq. (46).

In order to consider the effects of internal and external dissipation, the proportional damping model [29] is used in this membrane structure. Generally, the damping force vector is proportional to the velocity of the system,

$$ \mathbf{f}_{D} = \mathbf{C}\dot{\mathbf{q}}, $$

(55)

where $\mathbf{C} = \alpha \mathbf{M} + \beta \mathbf{K}$ is the damping matrix, and $\mathbf{K} = \partial \mathbf{Q} / \partial \mathbf{q}$ is the tangential stiffness matrix; $\alpha$ and $\beta$ are the coefficients of the mass matrix and the tangential stiffness matrix, respectively. Since the value of $\alpha$ was much greater than that of $\beta$ in large deformation analysis [30], the damping matrix can be reduced to

$$ \mathbf{C} = \alpha \mathbf{M}, $$

(56)

where $\alpha$ depends on the frequency and damping ratio of the system.

Based on the principle of virtual work, the variation of the equations of motion for the membrane structure is

$$ \delta \mathbf{q}^{\mathrm{T}}\left ( \mathbf{M} \ddot{\mathbf{q}} + \mathbf{f}_{D} - \mathbf{Q} \right ) = 0. $$

(57)

The dynamic equations of the constrained multibody system are obtained as

$$ \left \{ \textstyle\begin{array}{l} \mathbf{M}\ddot{\mathbf{q}} + \mathbf{f}_{D} - \mathbf{Q} + \boldsymbol{\Phi }_{\mathbf{q}}^{\mathrm{T}}\boldsymbol{\lambda } = \mathbf{0}, \\ \boldsymbol{\Phi } = \mathbf{0}, \end{array}\displaystyle \right . $$

(58)

where $\boldsymbol{\Phi }_{\mathbf{q}} = \partial \boldsymbol{\Phi } / \partial \mathbf{q}$ is the Jacobian matrix, and $\boldsymbol{\lambda }$ is the Lagrange multiplier vector corresponding to the constraint conditions $\boldsymbol{\Phi }$.

In this investigation, the generalized-$\alpha$ algorithm with variable step-size is used to solve the index-3 differential-algebraic equations (DAEs) in Eq. (58). In order to improve the efficiency of calculation, some constant matrices, including the mass matrix and the damping matrix, are calculated in the preprocessing part. Furthermore, the parallel computing technique is also utilized to accelerate the computation [31].

5 Numerical simulation and analysis

A solar sail can propel a spacecraft using the Sun’s energy for outer planetary exploration. However, considering its high risk, the development of the film solar sail has been slow. The successful launch of IKAROS in 2010 is a major step in the development of solar sails [32]. Thus, dynamic simulation of large membrane sails in space during the deployment is still a research hotspot in recent years.

5.1 Comparison of different contact models

The object of this study is a square leaf-in origami membrane structure, which can be seen as a simplified solar sail model. Different from the previous solar sails, this model uses a new type of leaf-in origami pattern, which is driven by relative translational drivers fixed in the four corners, and then the dynamic simulation of the membrane multibody system with large deformation and self-contact is carried out.

This square leaf-in origami membrane is made of polyimide material, which is widely used in aerospace because of its advantages such as excellent thermal stability, strong chemical resistance, and flexible mechanical properties. The geometric parameters of the square membrane structure are given in Fig. 9(a), in which the length and the thickness of the square membrane are $l = 0.6~\text{m}$ and $h = 0.5~\text{mm}$, respectively. The parameters of the polyimide membrane are as follows: mass density is $\rho = 1420~\text{kg} / \text{m}^{3}$, Young’s modulus is $E = 2.5~\text{GPa}$, Poisson’s ratio is $\nu = 0.34$, and the proportional damping coefficient is $\alpha = 1.5$.

Fig. 9

Leaf-in origami membrane structure: (a) geometric parameters of the fully deployed configuration; (b) one-eighth model (Color figure online)

The membrane structure is divided into 48 ANCF triangular membrane elements, and the mesh of one-eighth membrane structure is provided in Fig. 9(b). In this model, the stiffness reduction ratios of the membrane elements are set as $s_{1} = 1.0 \times 10^{ - 4}$ and $s_{2} = 1.0 \times 10^{ - 4}$, respectively. According to the classification of the boundaries in Sect. 4.2, the membrane elements are connected together by a series of constraint equations at the nodes on the fold lines.

As shown in Fig. 10(a), the nodes $P_{1} P_{2} P_{3} P_{4}$ on the outer corner are subjected to the relative translational drivers outward along the diagonal of the square fixed the global $\mathbf{Z}$ direction, respectively. The drive speed curves of these four drivers are the same as shown in Fig. 10(b), which ensures that the deployment of the membrane ends with a fully tense deployed configuration.

Fig. 10

Relative translational drivers: (a) distribution of the drivers; (b) the driving velocity profile (Color figure online)

During the deployment of the leaf-in origami membrane, multiple-point contact is inevitable in the membrane structure suffering from overall motion and large deformation. Therefore, it is particularly important to select an appropriate contact discretization type to avoid overpenetration, so the proposed mixed method is adopted to deal with such complicated contact problems.

In this study, we verify and compare the feasibility and accuracy of the proposed mixed method and other two contact models. The first one does not consider contact and is called Model 1. In Model 2, the contact model only considers the STS contact elements. For Model 3, the mixed method is used, which is combining the STS and NTS contact elements. It is necessary to notice that the friction between the contact elements is not taken into account, because they are quite small and can be ignored in general. The penalty parameters of the STS and NTS contact elements are $\varepsilon _{NS} = 10^{8}~\text{N} / \text{m}^{2}$ and $\varepsilon _{NN} = 3 \times 10^{6}~\text{N} / \text{m}^{2}$, respectively.

To visually compare differences between three different contact models, the configuration of the membrane at $t = 0.5$ s is selected as shown in Fig. 11(a). Subsequently, the region outlined by the rectangle in Fig. 11(a) is enlarged in Figs. 11(b), (c) and (d), corresponding to the results of the three contact models, respectively. It can be seen that overpenetration appears both on the boundary and inside the membrane elements in Model 1. In the case of Model 2, there exists a large penetration on the fold line. On the contrary, it is clearly observed that the membrane structure can deploy properly without overpenetration in Model 3. In summary, for the deployment of complicated foldable origami membrane structures, it is necessary to adopt the proposed mixed method to avoid mutual penetration, thereby improving the computational accuracy.

Fig. 11

(a) The configuration at 0.5 s; Locally enlarged figures for (b) Model 1: No contact; (c) Model 2: Only STS contact elements; and (d) Model 3: Mixed method (Color figure online)

5.2 Dynamic analysis for the membrane structure during the deployment

In order to analyze the mechanical properties of the leaf-in origami membrane during the deployment, the equivalent von Mises stress can be obtained based on the von Mises yield criterion as

$$ \sigma _{\upsilon } = \sqrt{\sigma _{1}^{2} - \sigma _{1}\sigma _{2} + \sigma _{2}^{2}}, $$

(59)

where $\sigma _{1}$ and $\sigma _{2}$ are the maximum and the minimum principal stress, respectively.

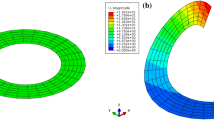
On the basis of the mixed method, the changing of configurations at different times is shown in Fig. 12, and the color maps represent the distribution of the von Mises stress. Here, the different colors represent the magnitude of the equivalent von Mises stress, and the red and blue regions indicate large stress and small stress, respectively. In the initial stowed configuration at $t = 0.0$ s as shown in Fig. 12(a), one-quarter of the square membrane has six overlapping submembranes, and the initial stress of membrane is set to zero. It can be found in Fig. 12(b) at $t = 1.0$ s that the stress concentration occurs in several regions, and the same phenomenon also can be observed in Figs. 12(c) and 12(d). In the configuration at $t = 3.0$ s as shown in Fig. 12(e), the membrane is fully deployed, while there are still wrinkles in some areas. Under further development, the membrane continues to be tightened until fully tensioned as shown in Fig. 12(f), which calls for the fully tense deployed configuration, and it marks the end of the dynamic development of the membrane.

Fig. 12

The configurations and the von Mises stress at different times (a) $t = 0.0$ s; (b) $t = 1.0$ s; (c) $t = 1.5$ s; (d) $t = 2.0$ s; (e) $t = 3.0$ s; (f) $t = 4.0$ s (Color figure online)

In engineering, it’s necessary to identify the vulnerable regions. To precisely analyze these regions, we select the von Mises stress contour at 1.0 and 4.0 s, as shown in Fig. 13. In Fig. 13(a), it can be observed that there are three types of stress concentration areas. Region A represents a multiple-point contact area. Regions B and C are located near the fold lines, and all fold lines have interior fold intersections. In Fig. 13(b), another stress concentration Region D is located near the corners of the square membrane where the drivers are applied. In conclusion, vulnerable regions of the leaf-in origami membrane are the stress concentration regions, to which attention should be paid.

Fig. 13

The von Mises stress of the membrane: (a) $t = 1.0$ s; (b) $t = 4.0$ s (Color figure online)

The impact of contact on multibody system is another important issue in engineering. Figure 14 gives the time histories of the energy of the membrane structure without contact and considering contact, corresponding to Model 1 and Model 3 above. The solid blue line indicates Model 3, and the red dotted line represents Model 1. To visibly reveal the impact of contact, the membrane deployment process from 0 to 2.4 s is selected in the plot of Fig. 14, because the contact-impact between membrane elements does not occur after 2.4 s.

Fig. 14

Variations of energy of the membrane during the deployment process (a) strain energy; (b) kinetic energy (Color figure online)

Figure 14(a) shows the time history of the strain energy, and the curve has two peaks. The first peak occurs around 1.2 s when the outermost submembranes squeeze the inner, then the strain energy of the membrane gradually decreases. The first valley occurs at about 1.4 s, when the outermost submembranes are separated from the second layer. The second peak occurs at around 2.0 s, when the innermost and the middle layers are almost fully deployed, but the outermost layer is still deploying. Then, the strain energy of the system gradually decreases as the membrane deploys. Comparing two curves of the different contact models, it can be obtained that the oscillation of the strain energy with contact is significantly greater than that of the strain energy without contact. When the contact no longer occurs, the strain energy of the system gradually stabilizes, and then the two curves are basically synchronized.

Figure 14(b) plots the kinetic energy of the membrane structure for Model 1 and Model 3. It clearly illustrates that the magnitude of the kinetic energy of the Model 3 considering contact is greater than that of Model 1 without considering contact. Nevertheless, by analyzing the kinetic energy curve of Model 1, the kinetic energy of the system curve oscillates at very high frequencies, which accounts for the significant flexibility of the membrane. Therefore, during the deployment simulation of the membrane structure with large deformation, it requires to set a sufficiently small step sizes to achieve numerical convergence.

For the purpose of analyzing the effect of contact on the stress distribution, Fig. 15 shows the equivalent stress of some points in the membrane for Models 1 and 3, respectively. Points $E$ and $F$ shown in Fig. 9(b) frequently experience contact-impact during deployment. As shown in Fig. 15(a), the equivalent stress of point $E$ in Model 3 appears to have two peaks at around 1.0 and 2.0 s. The first peak is higher than the second, and the peak stress of Model 3 considering contact is larger than that of Model 1. After 1.4 s, point $E$ is no longer in contact, and the two curves agree well. As shown in Fig. 15(b), the peak of the equivalent stress of point $F$ occurs later than for point $E$, and the influence of the contact-impact on the stress is also significant. Therefore, contact-impact has a great influence on the magnitudes of equivalent stress, and the proposed Model 3 can effectively simulate the deployment of the membrane.

Fig. 15

Equivalent stresses of some points in the membrane (a) point $E$; (b) point $F$ (depicted in Fig. 9(b)) (Color figure online)

Since the numerical oscillation of the membrane is obviously indicated from the above results, the $A$, $B$, $C$, and $D$ points of the one-eighth model in Fig. 9(b) are selected to analyze the vibration distribution of the membrane multibody system.

The dynamic responses of the membrane structure are depicted in Fig. 16. As for the displacement in the $Z$ direction in Fig. 16(a), there are two high-frequency vibrations during deployment. One occurs between 1.5 and 2.4 s, when the innermost and the middle layers are gradually completely unfolded, and it is consistent with the strain energy curve in Fig. 14(a). Another high-frequency vibration appears after 2.6 s, which is attributed to the transition of the membrane from slack to tense, where axial forces are generated, resulting in increased vibration. Subsequently, the oscillation of the system gradually slows down due to the decrease of driving speed and the effect of damping. Furthermore, it is observed that the vibration amplitude of point $A$ is the largest, and the order of the decrease is $B$, $C$, $D$. Point $D$ is a driving point whose $Z$ direction is constrained, and its displacement remains the same.

Fig. 16

Time history of points $A$, $B$, $C$, and $D$ in the membrane: (a) displacement in the $Z$ direction; (b) velocity in the $Z$ direction (Color figure online)

A more intuitive conclusion can be obtained about the velocity in the $Z$ direction shown in Fig. 16(b). During the deployment of the membrane, there are two peaks of the velocity, which occur at 2.0 and 2.7 s, respectively. Moreover, the maximum velocity at point $A$ can reach $7~\text{m} / \text{s}$ due to the axial forces in the tensioned configuration, to which attention should be paid in engineering. In summary, the amplitude of the vibration of the point near the membrane center is greater than that of the points far from the membrane center. Since the vibration problem of the membrane is significant, the vibration control in the membrane structure is required during the deployment.

6 Conclusion

In this investigation, the dynamic modeling for the deployment of the foldable origami space membrane structure considering contact-impact was executed. On the basis of Stiffness Reduction Model (SRM), the ANCF triangular membrane element was derived, which can settle the geometric nonlinearity and the wrinkles of the membrane. For the purpose of improving the accuracy in the contact-impact problem, a mixed method was proposed by combining the membrane STS contact elements with the NTS contact elements. Distinguished from the conventional STS contact elements, the presented method can effectively avoid mutual penetration of the element boundaries and better reveal the actual contact phenomenon. With respect to the frictionless contact problems, the normal contact force was calculated by using the penalty method. In the modeling process of the foldable origami membrane structure with fold lines between the membrane elements, the constraint equations were established. Subsequently, the dynamic equations of the membrane multibody system allowing for the damping effect were deduced. The generalized-$\alpha$ algorithm with variable step-size was adopted to solve the index-3 DAEs of the constrained multibody system.

To demonstrate the effectiveness of the proposed mixed method, the dynamic analysis of the leaf-in origami membrane structure with contact-impact was carried out. Comparison of three different contact models proved the superiority of the mixed method, in which the mutual penetration of the element boundaries can be successfully avoided. Meanwhile the membrane contact has a significant influence on the system energy and stress distribution. Furthermore, the results of the numerical example show that the vulnerable regions of the leaf-in origami membrane may suffer from the stress concentration, to which attention should especially be paid in the design of the membrane structures. Additionally, the research on membrane structure oscillations is valuable for the vibration control of membrane structures. The proposed modeling approach for the foldable origami membrane can be extended to formulate complicated origami membrane multibody systems with different topologies.