1 Introduction

Recently, the (3\(+\)1)-dimensional partial differential equations have been widely studied in the literature [1,2,3,4] since they are usually more accurate in describing nonlinear phenomena in the real space-time. Among these models, the (3 + 1)-dimensional nonlinear evolution equation

$$\begin{aligned} 3w_{xz}-(2w_t+w_{xxx}-2ww_x)_y+2(w_x\partial ^{-1}_{x}w_{y})_x=0 \end{aligned}$$
(1.1)

is a celebrated one, which was first derived in Ref. [5] to study the algebro-geometric solutions. Here, w is a real function of x, y, z, t. The symbol \(\partial ^{-1}_x\) is defined as \((\partial ^{-1}_xf)(x)=\int ^x_{-\infty }f(t)\mathrm{d}t\) under the decaying property at infinity. Up to date, Eq. (1.1) has been studied by many researchers from different aspects. For example, in Ref. [5], algebro-geometric solutions were explicitly obtained for it. In Ref. [6], N-soliton solutions and the Wronskian forms were constructed by using the Hirota method and the Wronskian technique. More results on soliton solutions, rogue waves, linear superposition principle, lump and higher-order lump solutions, interaction solutions, rational solutions, and others for Eq. (1.1) can be found in Refs. [7,8,9,10,11,12,13,14].

It is known that the Wronskian technique [15,16,17,18,19,20,21,22] is a fruitful method to derive multi-soliton solutions for soliton equations. In this method, the key process is a proper choice of the Wronskian condition, i.e., a system of linear partial differential equations that the generating functions satisfy. In the literature, Wronskian conditions have been given for many important soliton equations, such as the Korteweg-de Vries (KdV) equation [17], the Boussinesq equation [18], the (2+1)-dimensional extended shallow water wave equation [19], the (2+1)-dimensional breaking soliton equation [20], the generalized KP and BKP equations [21], and the AKNS equations [22], and so on. Additionally, there are some developments in the field of soliton solutions as well as its applications recently [23,24,25,26]. In this paper, our principle aim is to propose a new approach to investigate the nonlinear dynamics of Eq. (1.1) via Wronskian condition with a free function.

The present paper is organized as follows. In Sect. 2, we introduce a system of three linear partial differential equations with a free function q(y, z), and then, we verify that the system is a Wronskian condition for Eq. (1.1). In Sect. 3, with the aid of the bilinear transformation, some new exact solutions will be derived. Moreover, some novel dynamical behaviors will be analyzed and illustrated. The concluding remarks are given in Sect. 4.

2 Wronskian condition with a free function

We proceed by introducing the transformation [6]

$$\begin{aligned} w=-3{(\ln f)}_{xx}, \end{aligned}$$
(2.1)

from which Eq. (1.1) can be cast into the bilinear form

$$\begin{aligned} (D^3_xD_y+2D_yD_t-3D_xD_z)f\cdot f=0, \end{aligned}$$
(2.2)

where D is the known Hirota operator defined as [16]

$$\begin{aligned}&D^{m}_{x}D^{n}_{y}D^{l}_{z}D^{k}_{t}P(x,y,z,t)\cdot Q(x,y,z,t) \\&\quad \equiv \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^{m} \left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\right) ^{n} \left( \frac{\partial }{\partial z}-\frac{\partial }{\partial z'}\right) ^{l} \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\right) ^{k}\\&\qquad P(x,y,z,t) Q(x',y',z',t')|_{x'=x, y'=y,z'=z,t'=t}. \end{aligned}$$

In what follows, we shall propose a Wronskian condition involving a free function for the bilinear Eq. (2.2). For clarity, we give a proposition as follows.

Proposition 1

Suppose that the sufficiently smooth functions \(\phi _{i}=\phi _{i}(x,y,z,t)\ (1\le i\le N)\) satisfy the following linear partial differential equations

$$\begin{aligned}&\phi _{i,y}=q(y,z)\phi _{i,xx},\nonumber \\&\phi _{i,z}=q(y,z)\phi _{i,xxxx},\nonumber \\&\phi _{i,t}=\phi _{i,xxx}, \end{aligned}$$
(2.3)

where q(y, z) is a free function of y, z. Then, the Wronskian determinant

$$\begin{aligned}&f_N=\left| \begin{array}{cccc} \phi ^{(0)}_{1}&{}\phi ^{(1)}_{1}&{}\cdots &{}\phi ^{(N-1)}_{1}\\ \phi ^{(0)}_{2}&{}\phi ^{(1)}_{2}&{}\cdots &{}\phi ^{(N-1)}_{2}\\ \vdots &{}\vdots &{}\ddots &{} \vdots \\ \phi ^{(0)}_{N}&{}\phi ^{(1)}_{N}&{}\cdots &{}\phi ^{(N-1)}_{N} \end{array} \right| \ \mathrm{with} \ \phi ^{(j)}_{i}\nonumber \\&\quad =\frac{\partial ^{j}\phi _{i}}{\partial x^{j}} \ (1\le i\le N,0\le j\le N-1), \end{aligned}$$
(2.4)

under the bilinear transformation (2.1), gives a Wronskian solution for Eq. (1.1)

$$\begin{aligned} w=-3(\ln f_N)_{xx}. \end{aligned}$$
(2.5)

Proof

It suffices to verify that the Wronskian determinant \(f_N\) in (2.4), under the linear conditions in (2.3), satisfies Eq. (2.2), i.e.,

$$\begin{aligned}&(f_{N,xxx}f_{y}-3f_{N,xy}f_{N,xx}+2f_{N,y}f_{N,t})\nonumber \\&\quad -\, (f_{N,xxxy}+2f_{N,yt}-3f_{N,xz})f_N\nonumber \\&\quad +\, 3(f_{N,xxy}-f_{N,z})f_{N,x}=0. \end{aligned}$$
(2.6)

We use the method in Ref. [16] where the Wronskian determinant \(f_N\) is rewritten in a compact notation \(f=|\widehat{N-1}|\). In fact, using the linear conditions in (2.3), the corresponding derivatives of the Wronskian determinant \(f_N\) can be computed, respectively, which are

$$\begin{aligned} f_{N,x}= & {} |\widehat{N-2},N|,\end{aligned}$$
(2.7)
$$\begin{aligned} f_{N,y}= & {} q(y,z)(|\widehat{N-2},N+1|-\, |\widehat{N-3},N-1,N|),\end{aligned}$$
(2.8)
$$\begin{aligned} f_{N,z}= & {} q(y,z)(-|\widehat{N-5},N-3,N-2,N-1,N|\nonumber \\&\quad +\, |\widehat{N-4},N-2,N-1,N+1|),\nonumber \\ f_{N,t}= & {} |\widehat{N-4},N-2,N-1,N|\nonumber \\&\quad -\, |\widehat{N-3},N-1,N+1|\nonumber \\&\quad +\, |\widehat{N-2},N+2|\nonumber \\&\quad -\, |\widehat{N-3},N-1,N+2|\nonumber \\&\quad +\, |\widehat{N-2},N+3|,\end{aligned}$$
(2.9)
$$\begin{aligned} f_{N,xx}= & {} |\widehat{N-3},N-1,N|+|\widehat{N-2},N+1|,\end{aligned}$$
(2.10)
$$\begin{aligned} f_{N,xxx}= & {} |\widehat{N-4},N-2,N-1,N|\nonumber \\&\quad +\, 2|\widehat{N-3},N-1,N+1|\nonumber \\&\quad +\, |\widehat{N-2},N+2|,\end{aligned}$$
(2.11)
$$\begin{aligned} f_{N,xy}= & {} q(y,z)(|\widehat{N-2},N+2|\nonumber \\&\quad -\, |\widehat{N-4},N-2,N-1,N|),\end{aligned}$$
(2.12)
$$\begin{aligned} f_{N,xxy}= & {} q(y,z)(-|\widehat{N-5},N-3,N-2,N-1,N|\nonumber \\&\quad -\, |\widehat{N-4},N-2,N-1,N+1|\nonumber \\&\quad +\, |\widehat{N-3},N-1,N+2|\nonumber \\&\quad +\, |\widehat{N-2},N+3|),\end{aligned}$$
(2.13)
$$\begin{aligned} f_{N,xxxy}= & {} q(y,z)(-|\widehat{N-6},N-4,N-3,N-\, 2,N-1,N|\nonumber \\&\quad -\, |\widehat{N-4},N-2,N,N+1|\nonumber \\&\quad -\, 2|\widehat{N-5},N-3,N-2,N-1,N+1|\nonumber \\&\quad +\, |\widehat{N-3},N,N+2|\nonumber \\&\quad +\, |\widehat{N-2},N+4|+2|\widehat{N-3},N-1,N+3|),\end{aligned}$$
(2.14)
$$\begin{aligned} f_{N,yt}= & {} q(y,z)(|\widehat{N-5},N-3,N-2,N-1,N+1|\nonumber \\&\quad -\, |\widehat{N-6},N-4,N-3,N-2,N-1,N|\nonumber \\&\quad -\, |\widehat{N-4},N-2,N,N+1|\nonumber \\&\quad -\, |\widehat{N-3},N-1,N+3|\nonumber \\&\quad +\, |\widehat{N-3},N,N+2|+|\widehat{N-2},N+4|),\end{aligned}$$
(2.15)
$$\begin{aligned} f_{N,xz}= & {} q(y,z)(-|\widehat{N-6},N-4,N-3,N-\, 2,N-1,N|\nonumber \\&\quad +\, |\widehat{N-4},N-2,N,N+1|\nonumber \\&\quad +\, |\widehat{N-2},N+4|-|\widehat{N-3},N,N+2|), \end{aligned}$$
(2.16)

With these derivatives, we arrive at

$$\begin{aligned}&f_{N,xxx}f_{N,y}-3f_{N,xy}f_{N,xx}+2f_{N,y}f_{N,t}\nonumber \\&\quad =6q(y,z)(|\widehat{N-4},N-2,N-1,N|\nonumber \\&\qquad \times \, |\widehat{N-2},N+1| -\, |\widehat{N-3},N-1,N|\nonumber \\&\qquad \times \, |\widehat{N-2},N+2|), \end{aligned}$$
(2.17)
$$\begin{aligned}&f_{N,xxxy}+2f_{N,yt}-3f_{N,xz}\nonumber \\&\quad =-6q(y,z)(|\widehat{N-4},N-2,N,N+1|\nonumber \\&\qquad -\, |\widehat{N-3},N,N+2|), \end{aligned}$$
(2.18)
$$\begin{aligned}&f_{N,xxy}-f_{N,z}\nonumber \\&\quad =-2q(y,z)(|\widehat{N-4},N-2,N-1,N+1|\nonumber \\&\qquad -\, |\widehat{N-3},N-1,N+2|). \end{aligned}$$
(2.19)

Consequently, using the Plücker relation [16] for determinants, the left-hand side of (2.6) is nothing but zero. This completes the proof of the proposition. \(\square \)

Remark 1

Since the system (2.3) involves a free function q(y, z), the calculations of the derivatives require the consideration of the role of the function q(y, z). The free function q(y, z) gives us more freedom to derive novel exact solutions for Eq. (1.1). In fact, different functions q(y, z) will affect the generating functions \(\phi _i\) and thus affect the features of the Wronskian determinant \(f_N\).

3 Nonlinear dynamics

Due to the arbitrariness of the function q(y, z) in the Wronskian condition (2.3), abundant generating functions \(\phi _i\) formulating the Wronskian determinant \(f_N\) can be obtained in principle. Therefore, novel dynamical behaviors might be discovered by solving the Wronskian condition (2.3) with a specific function q(y, z). To achieve this goal, we shall consider the Wronskian condition (2.3) with

$$\begin{aligned} q(y,z)=\frac{m\psi '(my+mk^2z)}{k^2\psi (my+mk^2z)}. \end{aligned}$$

Here, m and \(k\ne 0\) are two real constants, \(\psi =\psi (\xi )\) is a smooth function of \(\xi \), and \(\psi '(my+mk^2z)=\tfrac{\mathrm{d}\psi }{\mathrm{d}\xi }|_{\xi =my+mk^2z}.\)

With q(y, z) above, it is not difficult to obtain a special solution for the Wronskian condition (2.3) with \(N=1\)

$$\begin{aligned} \phi _1=a+b\cosh (kx+k^3t)\psi (my+mk^2z), \end{aligned}$$
(3.1)

where a, b are real constants. Therefore, in view of (3.1), the Wronskian determinant in (2.4) can be determined. Then, using (2.5), we obtain a new Wronskian solution for Eq. (1.1)

$$\begin{aligned} w= & {} -3k^2b\nonumber \\&\times \frac{a\cosh (kx+k^3t)\psi (my+mk^2z)+b\psi ^2(my+mk^2z)}{\left[ a+b\cosh (kx+k^3t)\psi (my+mk^2z)\right] ^2}.\quad \end{aligned}$$
(3.2)

In what follows, we shall illustrate the novel dynamical behaviors described by the new Wronskian solution (3.2). For clarity, we focus on the situation that \(k>0,\ m>0,\ a=1\) and \( b=2\) in the following five cases.

Case 1 \(\psi (\xi )=e^{\mathrm{sin}\xi }\).

In this case, in the (x, y)-plane by setting \(t=z=0\), Eq. (3.2) can be rewritten as

$$\begin{aligned} w=-6k^2\frac{2e^{2\mathrm{sin}(my)}+\cosh (kx)e^{\mathrm{sin}(my)}}{\left[ 1+2\cosh (kx)e^{\mathrm{sin}(my)}\right] ^2}. \end{aligned}$$
(3.3)
Fig. 1
figure 1

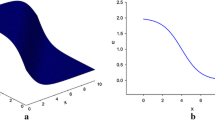
The stationary y-breather via (3.3) in the (x, y)-plane, where \(k=m=1\). a 3D plot, b density plot

Full size image
Fig. 2
figure 2

The bell-soliton behavior via (3.4) in the (x, t)-plane, where \(k=1\). a 3D plot, b density plot

Full size image
Fig. 3
figure 3

The periodic behavior via (3.5) in the (y, z)-plane, where \(k=m=1\). a 3D plot, b density plot

Full size image

From the expression (3.3), we know that it represents a breather wave which is localized along the direction of the x-axis and periodic along the direction of the y-axis with a period \(\frac{2\pi }{m}\). This solution is shown in Fig. 1. Obviously, the center of the breather is parallel to the y-axis. In other words, it is a stationary y-breather.

Moreover, setting \(y=z=0\) in the (x, t)-plane, we have from Eq. (3.2) that

$$\begin{aligned} w=-6k^2\frac{\cosh (kx+k^3t)+2}{[1+2\cosh (kx+k^3t)]^2}. \end{aligned}$$
(3.4)

In addition, in the (y, z)-plane by setting \(x=t=0\), Eq. (3.2) is turned into

$$\begin{aligned} w=-\dfrac{3k^2}{\sqrt{2}}e^{\dfrac{\mathrm{sin} (my+mk^2z)}{2}} \mathrm{sech}\left[ {\frac{\mathrm{sin} (my+mk^2z)}{2}}+\mathrm{\ln }\sqrt{2}\right] .\nonumber \\ \end{aligned}$$
(3.5)

Obviously, from the expression (3.4), we know that (3.2) gives a bell-soliton wave with an amplitude \(2k^2\) in the (x, t)-plane, while from the form of (3.5), we know that (3.2) gives a periodic wave with a period \(\frac{2\pi }{m}\) in the (y, z)-plane. These characteristics are demonstrated in Figs. 2 and 3. Moreover, we can see clearly from (3.2) that the solution dynamics in the (x, z)-plane, the (t, y)-plane and the (t, z)-plane are similar to that in the (x, y)-plane.

Case 2 \(\psi (\xi )=e^{\xi }\).

Fig. 4
figure 4

The line-soliton resonance via (3.2) with \(\psi (\xi )=e^{\xi }\) in the (x, y)-plane, where \(k=m=1\), \(t=z=0\). a 3D plot, b density plot

Full size image
Fig. 5
figure 5

The kink behavior via (3.9), where \(k=m=1\). a 3D plot, b density plot

Full size image

In this case, we use the coordinate frame \((kx+my,y)\) to perform the asymptotic analysis. On the one hand, keeping \(kx+my=X\) as constants, we find that the asymptotic form of (3.2) is

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} -\frac{3k^2}{4}\mathrm{sech}^2\frac{X}{2},&{}\quad \quad y\rightarrow -\infty ,\\ 0,&{}\quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.6)

On the other hand, using the coordinate frame \((kx-my,y)\) and keeping \(kx-my=X\) as constants, the asymptotic form of (3.2) is

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} -\frac{3k^2}{4}\mathrm{sech}^2\frac{X}{2},&{}\quad \quad y\rightarrow -\infty ,\\ 0,&{}\quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.7)

Moreover, using the coordinate frame (kx, y) and keeping \(kx=X\) as constants, the asymptotic form of (3.2) will be

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} 0,&{}\quad \quad y\rightarrow -\infty ,\\ -3k^2\mathrm{sech}^2X,&{}\quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.8)

The dynamical behaviors in this case are illustrated in Fig. 4 where a line-soliton resonance occurs during the interaction. There are two line-solitons before the collision. Far after the collision, a stationary line-soliton whose amplitude is four times of that before collision appears. In fact, this phenomenon can be clearly seen from (3.6) to (3.8).

Furthermore, in view of the form of (3.2), the nonlinear dynamics in the (x, t)-plane are similar to that shown in case 1. Additionally, in this case where \(\psi (\xi )=e^{\xi }\), the Wronskian solution (3.2) in the (y, z)-plane when \(x=t=0\) will be

$$\begin{aligned} w=-\frac{3k^2}{\sqrt{2}}e^{\frac{my+mk^2z}{2}}\mathrm{sech}\left( \frac{my+mk^2z}{2}+\mathrm{ln} \sqrt{2}\right) , \end{aligned}$$
(3.9)

which exhibits a kink behavior shown in Fig. 5.

Case 3 \(\psi (\xi )=e^{\xi ^2}\).

In this case, we introduce the coordinate frame (kx, y) and keep \(kx=X\) as constants. Then, the asymptotic form of (3.2) is found to be

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} -3k^2\mathrm{sech}^2X,&{}\quad \quad y\rightarrow -\infty ,\\ -3k^2\mathrm{sech}^2X,&{}\quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.10)

This means that whether y tends to the negative or the positive infinity, the Wronskian solution (3.2) approaches to the same stationary \(\mathrm{sech^2}\)-type of solitons. To see it more clearly, we give the corresponding three-dimensional plots in Fig. 6. To our knowledge, this type of line-soliton-like phenomenon has not been reported before for Eq. (1.1). Additionally, if restricted in the (y, z)-plane, the Wronskian solution (3.2) will exhibit a downward soliton-like behavior, which is shown in Fig. 7.

Fig. 6
figure 6

The line-soliton-like wave via (3.2) with \(\psi (\xi )=e^{\xi ^2}\) in the (x, y)-plane, where \(k=m=1\), \(t=z=0\). a 3D plot, b density plot

Full size image
Fig. 7
figure 7

The downward soliton-like behavior via (3.2) with \(\psi (\xi )=e^{\xi ^2}\) in the (y, z)-plane, where \(k=m=1\), \(x=t=0\). a 3D plot, b density plot

Full size image
Fig. 8
figure 8

The parabola–soliton interaction with four arms via (3.2) with \(\psi (\xi )=e^{-\xi ^2}\) in the (x, y)-plane, where \(k=m=1\), \(t=z=0\). a 3D plot, b density plot

Full size image

Case 4 \(\psi (\xi )=e^{-\xi ^2}\).

In this case, on the one hand, in the coordinate frame \((kx+my^2,y)\) and keeping \(kx+my^2=X\) as constants, the asymptotic form of (3.2) is

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} -\frac{3k^2}{4}\mathrm{sech}^2\frac{X}{2},&{}\quad \quad y\rightarrow -\infty ,\\ -\frac{3k^2}{4}\mathrm{sech}^2\frac{X}{2},&{}\quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.11)

On the other hand, in the coordinate frame \((kx-my^2,y)\) and keeping \(kx-my^2=X\) as constants, the asymptotic form of (3.2) is

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} -\frac{3k^2}{4}\mathrm{sech}^2\frac{X}{2},&{}\quad \quad y\rightarrow -\infty ,\\ -\frac{3k^2}{4}\mathrm{sech}^2\frac{X}{2},&{}\quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.12)
Fig. 9
figure 9

The upward soliton-like behavior via (3.2) with \(\psi (\xi )=e^{-\xi ^2}\) in the (y, z)-plane, where \(k=m=1\), \(t=z=0\). a 3D plot, b density plot

Full size image
Fig. 10
figure 10

The cubic–parabola–soliton resonance via (3.2) with \(\psi (\xi )=e^{\xi ^3}\) in the (x, y)-plane, where \(k=m=1\), \(t=z=0\). a 3D plot, b density plot

Full size image

We give these characteristics in Fig. 8, which shows that a parabola–soliton interaction with four arms occurs. Different from the usual two-soliton interaction with line behaviors, the four arms are all of the parabola types. Moreover, in this case, if restricted in the (y, z)-plane, the Wronskian solution (3.2) will exhibit a upward soliton-like behavior, which is shown in Fig. 9.

Case 5. \(\psi (\xi )=e^{\xi ^3}\).

In this case, on the one hand, under the moving frame \((kx+my^3,y)\) and keeping \(kx+my^3=X\) as constants, the asymptotic form of (3.2) is

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} -\frac{3k^2}{4}\mathrm{sech}^2\frac{X}{2},&{}\quad \quad y\rightarrow -\infty ,\\ 0,&{}\quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.13)

On the other hand, in the moving frame \((kx-my^3,y)\) and keeping \(kx-my^3=X\) as constants, the asymptotic form of (3.2) is

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} -\frac{3k^2}{4}\mathrm{sech}^2\frac{X}{2},&{} \quad \quad y\rightarrow -\infty ,\\ 0,&{} \quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.14)

Moreover, using the moving frame (kx, y) and keeping \(kx=X\) as constants, then the asymptotic form of (3.2) is

$$\begin{aligned} w\rightarrow \left\{ \begin{array}{ll} 0,&{} \quad \quad y\rightarrow -\infty ,\\ -3k^2\mathrm{sech}^2X,&{} \quad \quad y\rightarrow +\infty . \end{array} \right. \end{aligned}$$
(3.15)
Fig. 11
figure 11

The two-kink behavior via (3.2) with \(\psi (\xi )=e^{\xi ^3}\) in the (y, z)-plane, where \(k=m=1\), \(x=t=0\). a 3D plot, b density plot

Full size image

The plot is given in Fig. 10. This figure demonstrates that a cubic–parabola–soliton resonance occurs during the interaction. Before the collision, there are two cubic–parabola waves. After the collision, the two cubic–parabola waves disappear, while a line-soliton whose amplitude is four times of that before collision appears. On the other hand, if restricted in the (y, z)-plane, the Wronskian solution (3.2) will exhibit a two-kink behavior, which is shown in Fig. 11.

Fig. 12
figure 12

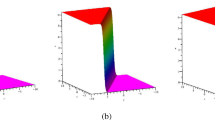
The singular localized waves via (3.17) in the (x, y)-plane at different times, where \(a=1,b=c=2,d=0,k=m=1,z=0\)

Full size image
Fig. 13
figure 13

The corresponding density plots of Fig. 12

Full size image

Furthermore, we consider the Wronskian condition (2.3) with \(N=2\) by choosing the function \(q(y,z)=-\frac{2 m^2}{k^2}(y+k^2z)\). In this case, the corresponding generating functions in the Wronskian determinant in (2.4) can be chosen as

$$\begin{aligned}&\phi _1=a+b\cosh (kx+k^3t)e^{-(my+mk^2z)^2},\quad \quad \nonumber \\&\phi _2=cx+d, \end{aligned}$$
(3.16)

where a, b, c, d, k, m are real constants. Utilizing (2.5) and (3.16), a new Wronskian solution for Eq. (1.1) is expressed as

$$\begin{aligned}&w=-3\left[ \ln \left( ac+b(c\cosh (kx+k^3t)\right. \right. \nonumber \\&\quad \left. \left. -k(cx+d)\sinh (kx+k^3t))e^{-(my+mk^2z)^2}\right) \right] _{xx}. \end{aligned}$$
(3.17)

To illustrate the dynamical behaviors via this solution, we give its solution characteristics in Figs. 12 and 13 in the (x, y)-plane by choosing suitable parameters. Interestingly, these figures show two singular waves. At \(t=0\), the two waves are symmetric with respect to \(x=0\). These two waves cannot interact with each other as shown in Fig. 12. Comparing the plots at \(t=\mp 5\), we observe that the left wave looks as if it changes to the right wave, while the right wave changes to the left one.

4 Concluding remarks

In this paper, a new method for deriving new exact solutions of Eq. (1.1) is proposed by introducing a Wronskian condition with a free function. The main feature of the Wronskian condition is that it involves a free function q(y, z). By choosing specific function q(y, z) and solving the system (2.3), some new Wronskian solutions are presented for Eq. (1.1). By choosing suitable parameters, some novel dynamical behaviors of Eq. (1.1) are graphically illustrated, including stationary y-breather behavior, line-soliton resonance, line-soliton-like phenomenon, parabola–soliton interaction, cubic–parabola–soliton resonance, kink-like behavior, and singular waves. These results not only illustrate the merits of the Wronskian condition in deriving exact solutions but also the novel dynamical behaviors in the equation. These dynamical behaviors may have applications for the description of nonlinear phenomena in the real space-time.

Before ending this paper, we further give two remarks about the Wronskian condition (2.3) that involves a free function. One is that Refs. [5,6,7,8,9,10,11,12,13,14] also presented various exact solutions for Eq. (1.1). Compared with these results, the method proposed in this paper has the merits that it is based on the Wronskian technique, which makes the construction of exact solutions more convenient. Moreover, the Wronskian condition (2.3) involves a free function. This free function gives us more freedom to derive novel exact solutions for Eq. (1.1). To our knowledge, these solutions and the corresponding nonlinear dynamics have not been reported before. Another remark we shall make is that the Wronskian condition (2.3) stems from the particular structure of Eq. (1.1). It is hoped that the method in this paper can work for other bilinear equations.