1 Introduction

Vibrational resonance (VR) is a phenomenon in which the amplification of a weak low-frequency signal can be enhanced by injecting a high-frequency periodic force [1]. This phenomenon shows many similarities to the phenomenon of stochastic resonance (SR), except that the high-frequency periodic force replaces random noise [2]. The mechanics of both VR and SR require noise injection rather than noise cancellation when detecting a weak low-frequency signal. Here, the high-frequency periodic force in VR can be regarded as special noise. Therefore, both VR and SR can be deemed noise utilization methods.

Traditional VR and SR perform well when detecting a weak signal whose frequency is lower than 1 Hz. However, if the frequency of a weak signal is much greater than 1 Hz, improvements are needed due to the restriction of adiabatic approximate theory. By using the scale transformation method, a high-frequency signal can be transformed into a low-frequency signal [2]. Based on the scale transformation method, Tan et al. [3] proposed a frequency-shifted and rescaling transfer method (FSRTM) and combined it with SR to detect bearing faults. This FSRTM is efficient if the fault characteristic frequency is known in advance. Wang et al. [4] developed an adaptive multiscale noise-tuning SR for diagnosing bearing faults.

An incipient fault in an operating rotating machine causes a typical weak high-frequency character signal with a frequency greater than 1 Hz. Detecting such a weak fault signal is an important issue in engineering applications. Researchers have shown great interest in producing different useful methods, such as spectral kurtosis [5, 6], empirical model decomposition (EDM) [7], wavelet transform [8] and S transform [9]. These methods are known as noise cancellation methods because their main goal is to extract fault-induced signatures by removing or suppressing background noises. Most noise utilization and noise cancellation methods can be regarded as frequency-based methods. In addition to these frequency-based methods, model-based methods are also important tools used in fault reconstruction [10,11,12].

Qiao et al. [13] stressed that weak fault characteristics can be weakened or even destroyed during the noise cancellation process; thus, they proposed an adaptive unsaturated bistable SR to detect bearing faults. Zhang et al. [14] proposed a nonlinear system resonance method to diagnose bearing faults. Li et al. [15] developed an adaptive SR method based on coupled bistable systems. Dong et al. [16] developed a second-order matched SR to improve the signal-to-noise ratio (SNR) of a weak period signal. Zhang et al. [17] constructed a new exponential bistable potential function in second-order underdamped SR to detect rolling bearing faults. Lai et al. [18] developed a multiparameter-adjusting SR in a standard tristable system. Additional works on SR applications in rotating machine fault detection are contained in Refs. [19, 20].

The above noise utilization methods for weak fault detection were mainly based on SR [13, 15,16,17,18,19,20]. Another noise utilization method, VR, is easier to control than SR [21]. The concerns related to added noise intensity, noise type and noise distribution that must be considered in SR need not be considered in VR [22]. Even though VR has been successfully applied to analogue electronic circuits [23, 24], excitable neurons [25, 26] and optical devices [27, 28], its application in weak fault detection on a rotating machine is relatively less common compared to SR. Here, only a limited number of recent and relevant publications are listed below. Gao et al. [29] proposed a VR-based weak fault detection method and compared the detection performance with envelope spectrum analysis. Liu et al. [29] proposed a step-varying VR based on a duffing oscillator nonlinear system to enhance the detection ability of bearing faults. In the methods proposed in Refs. [29, 30], only one nonlinear system was adopted. Xiao et al. [22] constructed an array of nonlinear systems for a VR-based weak fault detection method. In the above detection methods, the classic bistable state potential well function was adopted in nonlinear systems [22, 29, 30].

In addition to the above works, the classic bistable system (CBS) was commonly adopted in most fault detection methods that were based on VR [2, 4, 16, 22, 29, 30]. However, output saturation may occur when adopting a CBS. In addition, only one nonlinear system is adopted in most of the existing VR-based fault detection methods for rotating machines. Even though there are two or more nonlinear systems outlined in some publications, the nonlinear systems are presented in second-order, parallel or coupled formats [14, 17, 18].

Given the above analysis, an adaptive VR method for detecting a high-frequency character signal based on cascaded varying stable-state nonlinear systems (VSSNSs) is proposed for detecting a fault on a rotating machine. The proposed method integrates the following advantages:

  1. (1)

    The proposed detection method deploys the easy control advantage of VR compared with SR, since the concerns related to noise intensity, noise type and noise distribution need not be considered. Furthermore, the FSRTM proposed by Tan et al. [3] is introduced to overcome the restriction of adiabatic approximation theory when processing a high-frequency fault signal.

  2. (2)

    Cascaded nonlinear systems use background noise and manually injected high-frequency sinusoidal interference. Different from the existing noise cancellation methods, the background noise is used rather than filtered in our proposed method. Since the frequencies of background noises exist in a wide range, partial noises whose frequencies are very high can be regarded as special energy for resonance in a nonlinear system.

  3. (3)

    The potential well function in the nonlinear systems exists in a varying stable state rather than a fixed state; the nonlinear system can be transferred in different stable states by tuning system parameters. Therefore, there are more possibilities for a nonlinear system to achieve resonance.

The above aspects are considered in an integrated manner, which is the main contribution of this paper. The cascaded nonlinear systems that detect a high-frequency character signal are formulated using varying stable-state potential well functions and VR mechanisms. The proposed detection method is oriented to mechanical applications that have heavy strong background noise to enrich the limited number of VR-based fault detection methods in the existing publications.

The rest of the paper is organized as follows: Section 2 introduces the proposed method for detecting a high-frequency character signal. Validation of the proposed method is conducted on different faults of rotating machines in Sect. 3. The detection performance is assessed by using different nonlinear systems in Sect. 4, and the paper is concluded in Sect. 5.

2 Detection method for a high-frequency character signal based on VR

VR occurs when a high-frequency sinusoidal interference of appropriate amplitude can optimally amplify a weak low-frequency periodic signal in a nonlinear system. Let s(t) and I(t) represent the weak periodic signal and high-frequency sinusoidal interference, respectively. The frequency of the weak signal is usually lower than 1 Hz. The governing equation in VR is as follows:

$$ \frac{{\text{d}x}}{{\text{d}t}} = - \frac{{\text{d}U(x)}}{{\text{d}x}} + s(t) + I(t) $$
(1)

where s(t) = Acoswt, and the amplitude and frequency of the weak periodic signal are A and w/2π. I(t) = BcosΩt, the amplitude and frequency of the high-frequency sinusoidal interference are B and Ω/2π, respectively. Ω ≫ 2π. U(x) is the potential well function in the nonlinear system.

2.1 Saturation phenomenon in a CBS

In classic VR, the nonlinear system is a CBS. Its potential well function can be written as

$$ U(x) = - \frac{{a_{c} }}{2}x^{2} + \frac{{b_{c} }}{4}x^{4} ,\quad a_{{c}} ,b_{c} > 0 $$
(2)

where ac and bc are the system parameters in the CBS. Without external interference, the CBS has two potential wells with bottoms located at \( \pm x_{s} = \pm \sqrt {a_{c} /b_{c} } \) and one unstable point located at \( x_{u} = 0 \). The height of the barrier is \( \Delta U = a_{c}^{2} /4b_{c} \).

Assuming there is no input force in the CBS (i.e., A = 0 and B = 0), the output x can be calculated by substituting Eq. (2) into Eq. (1) according to the Bernoulli differential equation, and Eq. (3) is obtained. Considering two situations, t = 0 and t →+∞, the output x is given in Eq. (4).

$$ x = \pm \sqrt {\frac{{a_{c} \exp \left( {2a_{c} t} \right)}}{{1 + b_{c} \exp \left( {2a_{c} t} \right)}}} $$
(3)
$$ x = \left\{ {\begin{array}{*{20}l} { \pm \sqrt {a_{c} /\left( {1 + b_{c} } \right)} } \hfill & {t = 0} \hfill \\ { \pm \sqrt {a_{c} /b_{c} } } \hfill & {t \to + \infty } \hfill \\ \end{array} } \right. $$
(4)

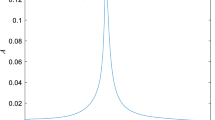
From Eqs. (3) and (4), the absolute values of the output x are limited in a range between \( \sqrt {a_{c} /\left( {1 + b_{c} } \right)} \) and \( \sqrt {a_{c} /b_{c} } \). A simplified illustration is given in Fig. 1, where different system parameters are considered. In Fig. 1, no matter what values these parameters are set to, abs(x) always asymptotically approaches a fixed value with the continuous increase in time t. For example, when ac= 1 and bc= 3, abs(x) approaches 0.57 as time t increases. This phenomenon is caused by the intrinsic characteristic of a CBS and is defined as output saturation. The output signal x varies with the input signals accordingly. Once the output signal x reaches a certain value, the output saturation phenomenon is about to occur.

Fig. 1
figure 1

Output saturation phenomenon in a CBS

Full size image

2.2 The construction of a VSSNS

Since a CBS may generate output saturation, the detection ability is thus restricted. In addition, the fixed stable state may need more time for system parameter adjustment to achieve resonance. Therefore, a reflection-symmetric sextic potential well function is adopted as

$$ U(x) = \frac{1}{6a}x^{6} - \frac{1 + b}{20}x^{4} + \frac{b}{2}x^{2} $$
(5)

where a and b are the system parameters in a VSSNS. We set a to a positive real value, but b can be an arbitrary real value.

If \( \frac{{{\text{d}}U(x)}}{{{\text{d}}x}} = 0 \), Eq. (5) can be rewritten as

$$ x\left( {\frac{1}{a}x^{4} - \frac{1 + b}{5}x^{2} + b} \right) = 0 $$
(6)

One of the real roots of Eq. (6) is x = 0.

\( \frac{1}{a}x^{4} - \frac{1 + b}{5}x^{2} + b = 0 \) can be rewritten as

$$ 5x^{4} + 0x^{3} - a(1 + b)x^{2} + 0x + 5ab = 0 $$
(7)

The root discriminant \( \Delta \) of Eq. (7) is calculated as

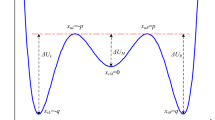
$$ \left\{ {\begin{array}{*{20}l} {{{a}}_{x} = 5,\;\;b_{x} = 0,\;\;c_{x} = - a(1 + b),\;\;d_{x} = 0,\;\;e_{x} = 5ab} \hfill \\ {E_{1} = 3b_{x}^{2} - 8a_{x} c_{x} } \hfill \\ {E_{2} = - b_{x}^{3} + 4a_{x} b_{x} c_{x} - 8a_{x}^{2} d_{x} } \hfill \\ {E_{3} = 3b_{x}^{4} + 16a_{x}^{2} c_{x}^{2} - 16a_{x} b_{x}^{2} c_{x} + 16a_{x}^{2} b_{x} d_{x} - 64a_{x}^{3} e_{x} } \hfill \\ {\Delta_{1} = E_{1}^{2} - 3E_{3} } \hfill \\ {\Delta_{2} = E_{1} E_{3} - 9E_{2}^{2} } \hfill \\ {\Delta_{3} = E_{3}^{2} - 3E_{1} E_{2}^{2} } \hfill \\ {\Delta = \Delta_{2}^{2} - 4\Delta_{1} \Delta_{3} } \hfill \\ \end{array} } \right. $$
(8)

Under the synergistic effects of the input signal, the outer force and the system parameters, the potential well function shows different stable states. Therefore, the resonance ability is enhanced by employing the VSSNS. Here, a simplified example is given in Fig. 2 with the following parameters: a = 20, b = − 4, b = 1, and b = 4. In Fig. 2, the stable-state types of the VSSNS are bistable (b = − 4), monostable (b = 1) and tristable (b = 4). Furthermore, if system parameter a is set to a constant (here a is set to 20) but b is changed from − 4 to 4, the potential well of the VSSNS is changed accordingly, and the stable-state types of the VSSNS are changed as follows: bistable → monostable → tristable.

Fig. 2
figure 2

Illustration of potential well functions with different system parameters

Full size image

If high-frequency interference is considered, let x(t) = X(t) + Ψ(τ, Ωt), where X(t) and Ψ(t) are slow and fast variables according to Ref. [31]. Assume that the mean value of Ψ, 〈Ψ〉, with respect to time τ = Ωt is

$$ \left\langle \psi \right\rangle { = }\frac{1}{2\pi }\int_{0}^{2\pi } {\psi \text{d}\tau } $$
(9)
$$ \left\langle {\psi^{m} } \right\rangle = \frac{1}{2\pi }\int_{0}^{2\pi } {\psi^{m} } \text{d}\tau $$
(10)

The equation for the slow motion can be regarded as the equation of the motion of a system with the effective potential well function as

$$ U_{\text{eff}} (X) = \frac{1}{2}R_{1} X^{2} + \frac{1}{4}R_{2} X^{4} + \frac{1}{6a}X^{6} $$
(11)

where

$$ \left\{ {\begin{array}{*{20}l} {R_{1} = b^{2} - \frac{{3(1 + b)B^{2} }}{{10\varOmega^{4} }} + \frac{{15B^{4} }}{{8a\varOmega^{4} }}} \hfill \\ {R_{2} { = } - \frac{1 + b}{5} + \frac{{5B^{2} }}{{a\varOmega^{4} }}} \hfill \\ \end{array} } \right. $$
(12)

The equilibrium points for the slow motion are given by

$$ \left\{ {\begin{array}{*{20}l} {X_{1}^{*} = 0} \hfill \\ {X_{2,3}^{*} = \pm \left( {\frac{{ - a^{2} R_{2} + \sqrt {a^{2} R_{2}^{2} - 4aR_{1} } }}{{2{{a}}}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \hfill \\ {X_{4,5}^{*} = \pm \left( {\frac{{ - a^{2} R_{2} - \sqrt {a^{2} R_{2}^{2} - 4aR_{1} } }}{{2{{a}}}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \hfill \\ \end{array} } \right. $$
(13)

When X* ≠ 0, let Y = X − X* where Y = ALcos(wt + Φ) in the limit t → ∞. If the nonlinear terms are neglected, AL and the response amplitude Q are obtained as

$$ A_{L} = \frac{A}{{\sqrt {w_{r}^{2} + w^{2} } }} $$
(14)
$$ w_{r}^{2} = R_{1} + 3R_{2} X^{*2} + \frac{5}{a}X^{*4} $$
(15)
$$ Q = \frac{{A_{L} }}{A} = \frac{1}{{\sqrt {w_{r}^{2} + w^{2} } }} $$
(16)

2.3 The detection method for a weak high-frequency character signal

The original VR method only focuses on the detection of a weak signal whose frequency is much lower than 1 Hz due to the restriction of the adiabatic approximation theory. However, the frequency of a weak target signal is usually greater than 1 Hz in engineering circumstances. Here, FSRTM is adopted to overcome the restriction of the adiabatic approximation theory.

The flowchart of the proposed VR-based detection method is illustrated in Fig. 3, where the raw data from a sensor contain the weak high-frequency character signal fT(t) and background noise D(t). Here, fT(t) is defined to distinguish the difference between a weak high-frequency character signal and a weak low-frequency input signal (s(t)). The weak high-frequency character signal fT(t) after processing by FSRTM can be regarded as a weak periodic signal s(t); however, the frequency of fT(t) before processing by FSRTM is much higher than that of s(t). The mixed signal y(t), which contains background noise, is processed by FSRTM and then imported into cascaded nonlinear systems with varying stable states. In this first VSSNS, the high-frequency background noise is regarded as the high-frequency interference for resonance. In the second VSSNS, manually injected high-frequency sinusoidal interference is used for resonance. In the two VSSNSs, particle swarm optimization (PSO) is adopted to optimize the system parameters along with the parameters of the injected high-frequency interference. The output from the second VSSNS is processed by fast Fourier transform (FFT); consequently, the frequency of the output signal can be obtained, and the high-frequency character signal can be detected by comparing the resonated frequency with the target frequency.

Fig. 3
figure 3

The procedure of the proposed VR-based detection method

Full size image

Note that the frequencies of the background noises usually exist in a wide range. Some of the frequencies are very high, but some are low. Even though FSRTM is conducted on the mixed signal that contains the target signal and the background noise, the frequencies of some noises are still very high after processing by FSRTM. Therefore, the noises whose frequencies are very high even after processing by FSRTM can be regarded as the high-frequency interference for resonance, and it is unnecessary to inject a high-frequency interference into the first VSSNS.

The fourth-order Runge–Kutta discretization method is used to calculate the discretized output from the two VSSNSs as Eq. (17), where h is the time calculation step, which is usually the reciprocal of the sampling frequency (fs). Note that h should be recalculated due to the rescaling process in the FSRTM. P[n] and O[n] are the discretization forms of P(t) and O(t). P(t) is the data before processing in a VSSNS, and O(t) is the output data from the VSSNS. n is the data series.

$$ \left\{ {\begin{array}{*{20}l} {k_{1} = h\left( { - \frac{1}{a}O[n]^{5} + \frac{(1 + b)}{5}O[n]^{3} - bO[n] + P[n]} \right)} \hfill \\ {k_{2} = h\left( {\left( { - \frac{1}{a}O[n] + \frac{{k_{1} }}{2}} \right)^{5} + \left( {\frac{1 + b}{5}O[n] + \frac{{k_{1} }}{2}} \right)^{3} - b\left( {O[n] + \frac{{k_{1} }}{2}} \right) + P[n]} \right)} \hfill \\ {k_{3} = h\left( {\left( { - \frac{1}{a}O[n] + \frac{{k_{2} }}{2}} \right)^{5} + \left( {\frac{1 + b}{5}O[n] + \frac{{k_{2} }}{2}} \right)^{3} - b\left( {O[n] + \frac{{k_{2} }}{2}} \right) + P[n]} \right)} \hfill \\ {k_{4} = h\left( {\left( { - \frac{1}{a}O[n] + k_{3} } \right)^{5} + \left( {\frac{1 + b}{5}O[n] + k_{3} } \right)^{3} - b\left( {O[n] + k_{3} } \right) + P[n]} \right)} \hfill \\ {O[n + 1] = O[n] + \frac{1}{6}\left( {k_{1} + k_{2} + k_{3} + k_{4} } \right)} \hfill \\ \end{array} } \right. $$
(17)

2.4 Parameter optimization by PSO

The resonance phenomenon and the stable type of a VSSNS are determined by the system parameters and the high-frequency interference. As shown in Fig. 3, PSO is adopted twice to optimize the system parameters in VSSNSs and the parameters of the injected high-frequency interference in the second VSSNS. PSO is a random searching algorithm and does not require the gradient information of an objective function. Here, the objective is to maximize the SNR of a target signal defined as

$$ {\text{SNR}} = 10\log_{10} \frac{{\eta_{T}^{2} }}{{\eta^{2} - \eta_{T}^{2} }} $$
(18)

where η is the FFT amplitude of the output from a nonlinear system; ηT is the FFT amplitude of the resonated frequency. Note that the definition of SNR is not standard in Eq. (18). To avoid the impact caused by the positive or negative values of the amplitudes of the target signal and noise, the square operator is utilized in Eq. (18).

Since there is no general guidance or theoretical standard about the parameter settings of a high-frequency interference in VR, the amplitude and frequency of a high-frequency interference signal is empirically set to be more than 100 times greater than the amplitude and frequency of the target signal according to Refs. [21, 22, 32, 33]. PSO is adopted to optimize the frequency and amplitude of an injected high-frequency interference.

When optimizing the system parameters in the first VSSNS, a particle is constructed with two dimensions that represent the calculation of parameters a and b. Some basic settings for PSO are given, including the positions and velocities of particles along with their associated maximum and minimum values, the population size of particles (Psize), terminal iteration epoch (Tgen) and learning factors C1 and C2.

The velocities and positions of particles are updated according to Eqs. (19–20).

$$ \left\{ {\begin{array}{*{20}c} {V_{a,i} = V_{a,i - 1} + C_{1} \times \sigma_{1,i} \times \left( {L_{a,i - 1} - P_{a,i - 1} } \right) + C_{2} \times \sigma_{2,i} \times \left( {G_{a,i - 1} - P_{a,i - 1} } \right)} \\ {V_{b,i} = V_{b,i - 1} + C_{1} \times \sigma_{1,i} \times \left( {L_{b,i - 1} - P_{b,i - 1} } \right) + C_{2} \times \sigma_{2,i} \times \left( {G_{b,i - 1} - P_{b,i - 1} } \right)} \\ \end{array} } \right. $$
(19)
$$ \left\{ {\begin{array}{*{20}l} {P_{a,i} = P_{a,i - 1} + V_{a,i} } \hfill \\ {P_{b,i} = P_{b,i - 1} + V_{b,i} } \hfill \\ \end{array} } \right. $$
(20)

In Eqs. (19–20), Va,i is the velocity of parameter a in the ith iteration; σ1 and σ2 are the random values in the interval of (0, 1); La,i is the local best parameter a in the ith iteration; Ga,i is the global best parameter a in the ith iteration; and Pa,i is the current position of parameter a in the ith iteration. Vb,i, Lb,i, Gb,i and Pb,i are the velocity of parameter b, the local best parameter b, the global best parameter b and the current position of parameter b in the ith iteration. If the position or velocity of a parameter exceeds its predetermined upper or lower bound, a new value is generated and replaces the unqualified value.

The terminal condition of optimization is that the optimal SNR is unchanged in the continued Tgen iterations. Once the terminal condition is met, the output from the first VSSNS is mixed with an injected high-frequency interference and then imported into the second VSSNS. During the optimization in the second VSSNS, a particle has four dimensions that represent the system parameters a and b and the amplitude B and frequency F of an injected high-frequency interference signal where 2πF = Ω. The velocities and positions of the particles in the second VSSNS are updated according to Eqs. (21–22).

$$ \left\{ {\begin{array}{*{20}l} {V_{a,i} = V_{a,i - 1} + C_{1} \times \sigma_{1,i} \times \left( {L_{a,i - 1} - P_{a,i - 1} } \right) + C_{2} \times \sigma_{2,i} \times \left( {G_{a,i - 1} - P_{a,i - 1} } \right)} \hfill \\ {V_{b,i} = V_{b,i - 1} + C_{1} \times \sigma_{1,i} \times \left( {L_{b,i - 1} - P_{b,i - 1} } \right) + C_{2} \times \sigma_{2,i} \times \left( {G_{b,i - 1} - P_{b,i - 1} } \right)} \hfill \\ {V_{B,i} = V_{B,i - 1} + C_{1} \times \sigma_{1,i} \times \left( {L_{B,i - 1} - P_{B,i - 1} } \right) + C_{2} \times \sigma_{2,i} \times \left( {G_{B,i - 1} - P_{B,i - 1} } \right)} \hfill \\ {V_{F,i} = V_{F,i - 1} + C_{1} \times \sigma_{1,i} \times \left( {L_{F,i - 1} - P_{F,i - 1} } \right) + C_{2} \times \sigma_{2,i} \times \left( {G_{F,i - 1} - P_{F,i - 1} } \right)} \hfill \\ \end{array} } \right. $$
(21)
$$ \left\{ {\begin{array}{*{20}l} {P_{a,i} = P_{a,i - 1} + V_{a,i} } \hfill \\ {P_{b,i} = P_{b,i - 1} + V_{b,i} } \hfill \\ {P_{B,i} = P_{B,i - 1} + V_{B,i} } \hfill \\ {P_{F,i} = P_{F,i - 1} + V_{F,i} } \hfill \\ \end{array} } \right. $$
(22)

In Eqs. (21–22), VB,i is the velocity of B in the ith iteration; σ1 and σ2 are the random values in the interval of (0, 1); LB,i is the local best B in the ith iteration; GB,i is the global best B in the ith iteration; and PB,i is the current position of B in the ith iteration. VF,i, LF,i, GF,i and PF,i are the velocity of parameter F, the local best parameter F, the global best parameter F and the current position of parameter F in the ith iteration, respectively. If the position or velocity of a parameter exceeds its upper or lower bound, a new value is generated and replaces the unqualified one. The optimization terminal condition in the second VSSNS is the same as that in the first VSSNS. After optimization, the optimal output signal from the second VSSNS is adapted by FFT to determine the resonated frequency.

3 Validation by a simulation dataset and faults on rotating machines

3.1 Validation by a simulation dataset

A simulation signal is generated, which is y(t) = 0.1 × sin(2π × 0.02t) + D(t), where D(t) is additive white Gaussian noise with an intensity of 1.5 V. The amplitude and frequency of the target signal are 0.1 V and 0.02 Hz, respectively. The sampling frequency fs is set to 20 Hz. The sampling lasts 250 s. The time-domain waveform and FFT frequency spectrum of y(t) are shown in Fig. 4, where the target frequency 0.02 Hz is submerged in the strong background noise. The frequency with the maximum FFT amplitude (AFFT), which is marked by fmax, is 6.32 Hz. The SNR of the target signal (SNRFFT), which is calculated according to Eq. (18) as − 27.30 dB.

Fig. 4
figure 4

a Time-domain waveform and b FFT frequency spectrum of y(t)

Full size image

Since the frequency of the target signal is lower than 1 Hz, FSRTM is unnecessary. However, PSO is adopted to optimize the system parameters and the amplitude and frequency of the injected high-frequency interference. The basic settings are given as follows: Psize = 30, Tgen = 20, and C1 = C2 = 1.5. The rest of the settings are listed in Table 1.

Table 1 Particle settings in the simulation dataset
Full size table

The output signal x(t) from the second VSSNS is shown in Fig. 5, where the target frequency 0.02 Hz is obvious from the perspective of the frequency spectrum. The AFFT of the target frequency is 0.92 V, and the SNRFFT is − 0.36 dB. The optimal parameters are as follows: a = 20.88, b = 0.67, B = 390 V and F = 789 Hz. According to parameters a and b, the VSSNS is monostable.

Fig. 5
figure 5

a Time-domain waveform and b FFT frequency spectrum of the output signal from our proposed method

Full size image

To compare the detection performance using the VSSNSs, each VSSNS in our proposed method is replaced by a CBS. After PSO optimization, the output signal from the second CBS is shown in Fig. 6, where the target frequency is detected with AFFT 0.43 V, and the SNRFFT is − 3.26 dB. The optimal parameters are ac= 0.66, bc= 0.93, B = 286 V and F = 767 Hz.

Fig. 6
figure 6

a Time-domain waveform and b FFT frequency spectrum of the output signal if the VSSNSs are replaced by the CBSs

Full size image

In the above comparison, two CBSs are adopted in cascaded format. As analyzed in the Introduction, some researchers have successfully detected target signals based on VR and only one CBS. To demonstrate the detection performance by using only one CBS and VR, another comparison example is given. After PSO optimization, the output signal is shown in Fig. 7. In Fig. 7, the target signal is detected. The AFFT and SNRFFT of the target frequency are 0.20 V and − 4.92 dB. The optimal parameters are ac= 1.79, bc= 8.69, B = 227 V and F = 809 Hz.

Fig. 7
figure 7

a Time-domain waveform and b FFT frequency spectrum of the output signal if only one CBS is adopted

Full size image

In the above comparison examples, the target frequency of 0.02 Hz is detected by adopting different nonlinear system(s), but by adopting our proposed method, the target frequency shows the highest AFFT along with the maximum SNRFFT. The detection results are compared in Table 2.

Table 2 Results from different nonlinear systems for the simulation dataset
Full size table

3.2 Validation by a gear fault on a planetary gearbox

A dataset for an implanted gear fault is used for validation. It is well known that the vibration sources in a planetary gearbox are very complex due to the meshing among different components. Therefore, the detection of a weak fault in a planetary gearbox is complex and difficult. The schematic of a planetary gearbox test rig is given in Fig. 8, which includes a single-stage planetary gearbox, a 4-kW three-phase asynchronous motor for driving the gearbox and a magnetic powder brake for loading. An NI data acquisition system is employed, including four IEPE accelerometers, a PXI-1031 mainframe, PXI-4472B data acquisition cards and LabVIEW software. In Fig. 8, S1, S2, S3 and S4 are the sensor locations for monitoring the gearbox condition. Additional information on the test rig is provided in Ref. [34].

Fig. 8
figure 8

Schematic of the planetary gearbox test rig

Full size image

The single-stage planetary gearbox consists of a sun gear with 13 teeth, 3 planet gears with 64 teeth and a fixed ring gear with 146 teeth. The sun gear, which is mounted on the input shaft and driven by an electric motor, rotates around its own center. The planet gears mesh with the sun gear and ring gear. In addition, the planet gears not only rotate around their own centers but also rotate around the center of the sun gear. A wear tooth fault is implanted on one sun gear tooth. The tooth wear fault is shown in Fig. 9. The fault characteristic frequency is 55.34 Hz, as calculated according to Ref. [34].

Fig. 9
figure 9

The implanted fault on the sun gear

Full size image

The time-domain waveforms, FFT spectra and zoomed spectra of the originally collected condition monitoring data from S1, S2, S3 and S4 are given in Fig. 10. The frequency that has the maximum FFT amplitude (AFFT) is marked by fmax. As shown in Fig. 10, the background noise is significant, and the frequencies exist in a wide range. The fault frequency of 55.34 Hz cannot be found directly from the frequency spectra.

Fig. 10
figure 10

The time-domain waveforms, FFT spectra and zoomed spectra of the sun gear data collected from a S1, b S2, c S3 and d S4

Full size image

The proposed method is used to detect the sun gear fault, and PSO is adopted to optimize the parameters. The basic settings for PSO, which are Psize, Tgen, C1 and C2, are the same as those in the simulation dataset validation. Other settings are given in Table 3. The stop-band cutoff frequency in the FSRTM is set to 52 Hz, and the rescaling ratio is 600.

Table 3 Partial PSO settings for detecting rotating machine faults
Full size table

The resonated signals from the second VSSNS are given in Fig. 11, where the detected frequencies are 54 Hz (from S1), 54.83 Hz (from S2), 54.83 Hz (from S3) and 55.83 Hz (from S4). These detected frequencies are close to the calculated fault characteristic frequency (55.34 Hz). In this paper, if the absolute frequency error between the fault characteristic frequency and detected frequency is lower than 2 Hz when considering the vibration impact caused by the operating environment and meshing among components, in addition, the output signal from the second VSSNS shows obvious periodicity. In such a case, the detected frequency is regarded as the frequency caused by a defective component, and the fault signal is detected. Otherwise, the fault signal is not detected. As shown in Fig. 11, the output signal shows obvious periodicity, and the frequency of the fault signal is exposed. The amplitude and SNR of the fault signal are listed in Table 4. In Table 4, the amplitudes and SNRs of the sun gear fault from our proposed method are derived by order of magnitude compared with the originally collected data.

Fig. 11
figure 11

The time-domain waveforms and FFT spectra of the output signals from the second VSSNS using the data from a S1, b S2, c S3 and d S4

Full size image
Table 4 The amplitudes and SNRs of the sun gear fault before and after processing by the proposed method
Full size table

3.3 Validation by a fixed-axis gearbox test rig

Bearings are typical components in rotating machines. A bearing with several naturally developed faults is used to validate our proposed method. The fault signal is collected from a fixed-axis gearbox test rig. It is widely accepted that a weak naturally developed fault is hard to detect because the characteristic fault frequencies related to the damage are usually submerged in heavy background noise due to the mashing gears. The background noise contains abundant disturbance frequencies that may be generated due to the faults on other components, the meshing among components, and the vibration of an input shaft or the operational conditions. The SNR of a weak naturally developed fault is usually very small.

The information for the fixed-axis gearbox test rig is referenced in Ref. [9]. The test rig shown in Fig. 12 includes a two-stage fixed-axis gearbox, a 4-kW three-phase asynchronous motor for driving the gearbox and adjusting different speeds and a magnetic powder brake for loading. In the gearbox, there are three shafts: a high-speed (HS), intermediate-speed (IS) and low-speed (LS) shaft. The gear, which has 81 teeth mounted on the LS shaft, is meshed with a gear with 18 teeth mounted on the IS shaft. Another gear with 64 teeth mounted on the IS shaft is meshed with a gear with 35 teeth mounted on the HS shaft. The HS and IS shafts are supported by SKF 6205 bearings, and the LS shaft is supported by SKF 6208 bearings.

Fig. 12
figure 12

Schematic of the fix-axis gearbox test rig

Full size image

The positions of the sensors are marked as S1, S2, S3 and S4. The NI data acquisition system is adopted, including four IEPE accelerometers, a PXI-1031 mainframe, PXI-4472B data acquisition cards and LabVIEW software. The experimental conditions are as follows: 20 Hz HS rotation, 20 kHz signal vibration sampling frequency, 12 s sampling duration with two different loads: 199 Nm and 405 Nm.

After the data acquisition, all the bearings and gears have faults at different levels. The bearings that are mounted on the HS shaft have many outer race damages. In addition, the inner race damages and ball damages presented simultaneously on the right-hand bearing. These damages are illustrated in Fig. 13. Due to the presence of three types of damage on different elements of a bearing simultaneously, the bearing mounted on the right-hand side of the HS shaft is selected. Therefore, the data collected from the S1 position are used to validate the proposed method. S1 is close to the source of the bearing faults.

Fig. 13
figure 13

The faults on the right-hand bearing mounted on the HS shaft: a the outer race faults, b the inner race faults and c the ball faults

Full size image

The characteristic frequencies of the bearing faults can be calculated according to Ref. [35]. The calculation of fault characteristic frequencies is given in Eq. (23), and the results are listed in Table 5. In Table 5, BPFO, BPFI, BSF and FTF represent the ball pass frequency outer race, ball pass frequency inner race, ball spin frequency and fundamental train frequency, respectively.

Table 5 The fault characteristic frequencies of bearings in the test rig
Full size table
$$ \left\{ {\begin{array}{*{20}l} {f_{\text{BPFO}} = \frac{{N_{\text{B}} }}{2}F_{\text{R}} \left( {1 - \frac{{D_{\text{B}} \cos (\theta )}}{{D_{\text{P}} }}} \right)} \hfill \\ {f_{\text{BPFI}} = \frac{{N_{\text{B}} }}{2}F_{\text{R}} \left( {1 + \frac{{D_{\text{B}} \cos (\theta )}}{{D_{\text{P}} }}} \right)} \hfill \\ {f_{\text{BSF}} = \frac{{D_{\text{P}} }}{{D_{\text{B}} }}F_{\text{R}} \left( {1 - \frac{{D_{\text{B}}^{2} \cos^{2} (\theta )}}{{D_{\text{P}}^{2} }}} \right)} \hfill \\ {f_{\text{FTF}} = \frac{1}{2}F_{\text{R}} \left( {1 - \frac{{D_{\text{B}} \cos (\theta )}}{{D_{\text{P}} }}} \right)} \hfill \\ \end{array} } \right. $$
(23)

In Eq. (23), NB is the number of rolling elements in a bearing, FR is the shaft speed, DB is the ball diameter, DP is the pitch diameter and θ is the ball contact angle.

The originally collected data from S1 are used for validation. The time-domain waveform and FFT spectrum of the collected data from S1 are shown in Fig. 14, where the fault characteristic frequencies are totally lost in the disturbance frequencies. However, the gear meshing frequency (Fmesh) and its harmonics are obvious. Fmesh refers to the meshing of gears mounted on the HS and IS shafts. This can be calculated according to the rotating speed of a gear (Rs) and its tooth number (NT) as Eq. (24). According to Eq. (24), Fmesh = 700 Hz.

Fig. 14
figure 14

a Time-domain waveform, b FFT spectrum and c zoomed spectrum of the collected data from S1 on a fixed-axis gearbox

Full size image
$$ F_{{\text{mesh}}} = R_{\text{s}} \times N_{\text{T}} $$
(24)

PSO is used to optimize the parameters. The settings for PSO are the same as those when using the planetary gearbox dataset for validation. When adopting FSRTM, the stop-band cutoff frequencies for the three types of faults are set as follows: 66 Hz (for BPFO), 104 Hz (for BPFI) and 43 Hz (for BSF). The rescaling ratio is 600. The detection results are given in Table 6.

Table 6 The FFT amplitudes and SNRs of the bearing faults before and after processing by the proposed method
Full size table

The detected frequencies are 72.33 Hz, 108.58 Hz and 46.25 Hz. These detected frequencies are close to the calculated fault characteristic frequencies when considering the vibrational circumstances; therefore, the detected frequencies are regarded as the fault frequencies.

The outputs from the second VSSNS are given in Fig. 15, where the output signal shows obvious periodicity compared with the originally collected data (in Fig. 14). In Fig. 14, no fault can be detected directly from the frequency spectrum, but the fault frequencies are obvious from the perspective of the frequency spectrum in Fig. 15. Therefore, the fault frequencies are exposed, and the amplitudes and SNRs are greatly improved.

Fig. 15
figure 15

The time-domain waveforms and frequency spectra of the detected signals for a BPFO, b BPFI and c BSF

Full size image

4 Comparison and discussion

In the proposed method, two VSSNSs are adopted. The background noise and manually injected high-frequency interferences are used to achieve resonance in the first and second VSSNSs, respectively. As analyzed before, some researchers have successfully detected a target signal using only one nonlinear system based on the VR mechanism. There is no general guidance or theoretical standard on how to determine the number of nonlinear systems. To demonstrate the impacts caused by the number of nonlinear systems on the detection performance, a series of scenarios are considered and compared as follows.

  • Scenario 1. Only one CBS is adopted, and high-frequency interference is injected.

  • Scenario 2. Only one VSSNS is adopted, and high-frequency interference is injected.

  • Scenario 3. Only one VSSNS is adopted, but high-frequency interference is not injected; only the background noise is used for achieving resonance.

  • Scenario 4. Two CBSs are used, and high-frequency interference is injected; the VSSNSs in our proposed method are replaced by CBSs.

  • Scenario 5. Our proposed method.

In the above five scenarios, datasets for the implanted sun gear fault in the planetary gearbox and the naturally developed bearing faults in the fixed-axis gearbox are used. PSO is adopted to optimize the related parameters. The detection results from the different scenarios are compared in Tables 7 and 8, where Fgear, FBPFO, FBPFI and FBSF denote the fault characteristic frequencies, which are calculated according to the operating and shape parameters of a component.

Table 7 Detection results of the implanted sun gear fault under different scenarios
Full size table
Table 8 Detection results of the naturally developed bearing faults under different scenarios
Full size table

In Tables 7 and 8, the gray color indicates an undetected fault in a scenario. In Tables 7 and 8, all the faults can be detected in Scenarios 4 and 5, which demonstrates that using two nonlinear systems is beneficial for fault detection. From the perspective of AFFT and SNRFFT, the detection results from our proposed method (Scenario 5) are better than those using the CBSs (Scenario 4).

If only one nonlinear system is used, the faults cannot always be detected (Scenarios 1–3 in Table 7 and Scenario 1 in Table 8). In particular, the faults cannot be detected by using only one CBS. The sun gear fault also cannot be detected by using only one VSSNS with or without injected high-frequency interference if the data collected from S4 are used (Scenarios 2 and 3 in Table 7). However, naturally developed bearing faults can be detected by using only one VSSNS with or without injected high-frequency interference (Scenarios 2–3 in Table 8). In Scenario 3 in Table 8, the effectiveness of the background noise on resonance is demonstrated. Even though some faults can be detected by using only one VSSNS with or without injected high-frequency interference, the detection performance is not as good as the performance of our proposed method (Scenario 5) from the perspective of AFFT and SNRFFT.

The positive effect on resonance caused by the background noise is illustrated by comparing Tables 5 and 6 with Tables 7 and 8. In Tables 5 and 6, the SNRs of naturally developed bearing faults are lower than the SNR of the implanted sun gear fault; the background noise in the fixed-axis gearbox is stronger than the noise in the planetary gearbox. However, the naturally developed bearing faults in the fixed-axis gearbox can be detected, and the SNRs are improved more (Scenario 3 in Table 8) than the SNR improvement of the implanted sun gear fault (Scenario 3 in Table 7). The output signals from the last nonlinear systems under different scenarios are given in Figs. 16, 17, 18, 19, 20, 21, 22, 23, 24 and 25, where the frequency with maximum amplitude in the zoomed frequency spectrum is marked by fmax. The output signals in Figs. 16, 17, 18, 19 and 20 focus on the detection of sun gear faults. The output signals in Figs. 21, 22, 23, 24 and 25 focus on the detection of naturally developed bearing faults.

Fig. 16
figure 16

The time-domain waveforms and zoomed FFT spectra of the output signals from Scenario 1 using the data collected from a S1, b S2, c S3 and d S4

Full size image
Fig. 17
figure 17

The time-domain waveforms and zoomed FFT spectra of the output signals from Scenario 2 using the data collected from a S1, b S2, c S3 and d S4

Full size image
Fig. 18
figure 18

The time-domain waveforms and zoomed FFT spectra of the output signals from Scenario 3 using the data collected from a S1, b S2, c S3 and d S4

Full size image
Fig. 19
figure 19

The time-domain waveforms and zoomed FFT spectra of the output signals from Scenario 4 using the data collected from a S1, b S2, c S3 and d S4

Full size image
Fig. 20
figure 20

The time-domain waveforms and zoomed FFT spectra of the output signals from Scenario 5 using the data collected from a S1, b S2, c S3 and d S4

Full size image
Fig. 21
figure 21

The time-domain waveforms and zoomed frequency spectra of the output signals from Scenario 1 for detecting a BPFO, b BPFI and c BSF

Full size image
Fig. 22
figure 22

The time-domain waveforms and zoomed frequency spectra of the output signals from Scenario 2 for detecting a BPFO, b BPFI and c BSF

Full size image
Fig. 23
figure 23

The time-domain waveforms and zoomed frequency spectra of the output signals from Scenario 3 for detecting a BPFO, b BPFI and c BSF

Full size image
Fig. 24
figure 24

The time-domain waveforms and zoomed frequency spectra of the output signals from Scenario 4 for detecting a BPFO, b BPFI and c BSF

Full size image
Fig. 25
figure 25

The time-domain waveforms and zoomed frequency spectra of the output signals from Scenario 5 for detecting a BPFO, b BPFI and c BSF

Full size image

In these zoomed frequency spectra, some faults are not detected under Scenarios 1–3. Even though all the faults can be detected under Scenarios 4 and 5, the amplitudes of these detected faults under Scenario 4 are lower than the values from our proposed method (Scenario 5). In view of the time-domain waveforms, the output signals still contain considerable background noise with high amplitudes even though the faults are detected under Scenarios 1–3. In addition, the output signals from our proposed method (Scenario 5) show more obvious periodicity in the view of time-domain waveforms than the output signals under Scenario 4.

The barrier height (BH) of a nonlinear system has an important impact on resonance. The BH, which is related to the stability type of a nonlinear system, is determined by the system parameters. Considering the above scenarios, all the faults can be detected in only Scenarios 4 and 5; therefore, the BHs of these nonlinear systems are listed in Tables 9 and 10, where BHs are calculated according to the system parameters of the second nonlinear system.

Table 9 The stability types and BHs of the second nonlinear system when detecting the sun gear fault in Scenarios 4–5
Full size table
Table 10 The stability types and BHs of the second nonlinear system when detecting the naturally developed bearing fault in Scenarios 4–5
Full size table

In Tables 9 and 10, “–” means that a BH is incalculable due to the stability type. MS, TS and BS stand for monostable, tristable and bistable. During detecting the sun gear fault and bearing faults, the stability type in the second VSSNS can be either MS, BS or TS in Table 9. If the stability type is MS, BH is not necessary for calculation. In Table 10, the second VSSNS can be TS or BS. If parameter b is negative, the stability type in the VSSNS is BS in both Tables 9 and 10. However, negative parameter b is meaningless from the physical view of a CBS. The BH is difficult to calculate if the VSSNS is transformed into BS or TS, but it can be obtained according to the output signal and potential well function. In Tables 9 and 10, even though the BHs in the CBSs are lower than those in the VSSNSs, the detection performance of our proposed method is better in view of the enhancement of AFFT and SNRFFT in a fault signal (regardless of whether the fault is an implanted gear fault or naturally developed bearing faults). Moreover, the adopted VSSNS provides more probability to achieve resonance by tuning system parameters.

Through all validations, the effectiveness of our proposed method, which focuses on the detection of a high-frequency character signal, is demonstrated. First, our proposed method shows better performance than the VR-based CBS(s) regardless of using only one CBS or cascade CBSs. This is demonstrated in Tables 7 and 8. Second, our proposed method is effectively employed to detect faults on rotating machines, including naturally developed bearing faults and an implanted gear fault. The frequencies of these faults are much greater than 1 Hz. Therefore, our proposed method can overcome the restriction of adiabatic approximation theory. Third, different rotating machines are considered: a fixed-axis gearbox and a planetary gearbox. Fourth, our proposed method shows improvements in amplitude, SNR and periodicity of the detected signals, which is demonstrated in Tables 7 and 8 and Figs. 16, 17, 18, 19, 20, 21, 22, 23, 24 and 25. Fifth, the VSSNS can be transferred into MS, BS or TS by tuning the system parameters; therefore, the possibility of resonance achievement is gained. Sixth, even though some faults can be detected by using only one nonlinear system, the detection performance is insufficient. There are still many disturbance frequencies with high FFT amplitudes, and the time-domain waveform of a resonated signal shows less periodicity than the one from our proposed method. Last, the background noises are not always undesirable; they are beneficial to resonance in the proposed method.

5 Conclusions

In this paper, a detection method for a high-frequency character signal is proposed based on the VR mechanism and cascaded VSSNSs. In this method, the background noise is used rather than suppressed, which is different from existing noise cancellation methods. The stability type of a VSSNS can be easily and adaptively changed into MS, BS or TS by tuning the system parameters. To deploy the VR mechanism, the background noise, which has been mixed when collecting data from the sensors, and the manually injected high-frequency interference are used to achieve resonance for the two cascaded VSSNSs. To achieve adaptive detection and optimization, the parameters related to the nonlinear systems and the injected high-frequency interferences are optimized by PSO. Through a validation conducted on the simulation dataset and rotating machines, the good performance of our proposed method is demonstrated in terms of the enhancement on FFT amplitude, SNR and periodicity of a resonated signal.

The main contribution of this paper is that a new VR configuration is constructed for detecting a high-frequency character signal, and its application is extended into mechanical industry. The classic VR is always restricted by the adiabatic approximation theory, which cannot be directly applied to weak fault detection because the fault character frequency of a rotating machine is always greater than 1 Hz, especially under operating conditions. In this paper, our proposed method has successfully detected faults on two typical rotating machines: a bearing and a gear. In addition, two common gearboxes, a planetary gearbox and a fixed-axis gearbox, are considered.

The frequency transform with respect to a high-frequency signal mainly depends on FSRTM, which is more effective if a fault characteristic frequency is known in advance. If the fault characteristic frequency is unknown in advance, the parameter related to the frequency shift in the FSRTM is hard to set, and the performance of the frequency transform may be impacted. In the future, we will adopt a more effective frequency transform method in which the characteristic frequency is not necessary.