1 Introduction

The external stimulus can be translated into electrical activities by neurons when the strength of the stimulus is sufficiently large, and the information of stimulus can be encoded into the spiking sequence. However, a weak signal is typically difficult to detect, because it is easily concealed by the troublesome noise. Interestingly, the detection of the weak signal can be enhanced by noise due to the contribution of stochastic resonance (SR), in which the response to the weak signal can be maximized by an optimal strength of noise [1, 2]. Due to the universality of noise, SR has been extensively investigated in engineering, chemistry, physics, and biology [3,4,5], especially in neuronal systems [6,7,8,9,10].

The constructive roles of noise on signal propagation have been studied widely in the neuronal networks. For example, transmission of the weak signal can be enhanced effectively by stochastic resonance in neural networks [11], and noise can optimize the propagation of weak periodic signals through a feedforward neuronal network [12,13,14,15]. Recently, a stochastic resonance-driven pacemaker has also been put forward to investigate the weak signal transmission [16, 17]. The pacemaker is an autonomous (or driven) rhythm neuron which can regulate the electrical activities of the whole neuronal network. It has been shown that the pacemakers have a significant impact on the cardiac function [18] and on the synchronization of ecosystems [19].

The phenomenon of vibrational resonance (VR), in which the detection of the low-frequency signal can be amplified and optimized by the moderate intensity of high-frequency force, shows that the high-frequency force has an effect similar to that of noise in signal detection [20,21,22]. The phenomenon of vibrational resonance has also attracted the interest of scientists [23,24,25,26,27,28,29,30] because multi-frequency signals are not only ubiquitous, but also play a significant role in biology [31,32,33,34]. For example, Gerhardt investigated the effect of two-frequency signals on vocal communication, which acts significantly on the reproduction of the green tree frog [35]. Notably, self-generated multi-frequency signals by weakly electric fishes play an important role in communication, hunting, location, and navigation [36]. The transmission of hybrid signals with a high-frequency force and a low-frequency envelope has also been investigated in an electrosensory system [37].

The synapse, as a major structure of information transmission in neuronal networks, is of significance in electrical activities. Van der Loos and Glaser originally found a special synapse in the neocortex which was termed autapse in 1972 [38]. Autapse is defined as a connection of the neuron with itself or a neuronal self-connection. Since its discovery, autapse has been investigated extensively in the brain and neuronal systems due to its significant roles in brain functions [39, 40]. For example, the autaptic currents are observed in hippocampal neurons of rat [41]. Bekkers found that the excitability of neuron can be regulated by inhibitory or excitatory autapses [42]. Experiments showed that the precision of spike timing can be increased by the dynamic clamp and artificial GABAergic autapses in principal cells [43]. Autapses can raise the threshold of action potentials and inhibit repetitive firing, demonstrating that the autapse is a forceful synapse [44]. Importantly, many numerical studies showed the significant impact of autapses on the rhythmic activity of neurons, generating rich dynamical phenomena [45,46,47,48,49,50,51,52,53,54,55].

In this paper, we study the effects of the autapse on signal transmission in neuronal networks, where an external two-frequency signal is introduced only to one neuron as a pacemaker. Our results reveal that the weak signal acting on the pacemaker can be propagated accurately to the whole network by vibrational resonance. Interestingly, the inhibitory autapse can effectively enhance signal transmission induced by vibrational resonance, while vibrational resonance is weakened by excitatory or electrical autapses. Thus, these results differ from the general view that inhibitory synapse plays an inactive role in neuronal dynamics [56, 57]. This paper is organized as follows. In Sect. 2, we present the coupled Hodgkin–Huxley neuronal network model with an autapse, and a factor for the measurement of signal transmission is provided. Section 3 shows the main numerical results. Finally, Sect. 4 is devoted to our conclusions.

2 Models and methods

To investigate the effect of autapses on signal transmission in neuronal networks, the coupled Hodgkin–Huxley neuron model is given by [58],

$$\begin{aligned}&C_m\frac{\mathrm{d}V_i}{\mathrm{d}t}=-(g_K n_i^4(V_i-V_K)+g_{Na} m_i^3h_i(V_i-V_{Na})\nonumber \\&\quad +\,g_l(V_i-V_l))+I_0+I^d_{aut}\nonumber \\&\quad +\,I^{d}_{stimu}+\frac{\epsilon }{k_i}\sum \limits _{j=1}^{N}g_{i,j}(V_{j}-V_i), \qquad i=1,\ldots ,N, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\mathrm{d}m_i}{\mathrm{d}t}=\frac{0.1(V_i+40)}{1-e^{\frac{-V_i-40}{10}}}(1-m_i)-4e^{\frac{-V_i-65}{18}} m_i, \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\mathrm{d}n_i}{\mathrm{d}t}=\frac{0.01(V_i+55)}{1-e^{\frac{-V_i-55}{10}}}(1-n_i)-0.125e^{\frac{-V_i-65}{80}} n_i, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\mathrm{d}h_i}{\mathrm{d}t}=0.07e^{\frac{-V_i-65}{20}}(1-h_i)- \frac{1}{1+e^{\frac{-V_i-35}{10}}} h_i, \end{aligned}$$
(4)

where \(V_i\) is the membrane potential, the sodium current is regulated by inactive gating variable \(h_i\) and active gating variable \(m_i\), and the gating variable \(n_i\) controls potassium current. \(I^d_{\mathrm{stimu}}=A\cos (\omega t)+B\cos (\varOmega t)\) is the two-frequency signal which is introduced to only one neuron as a pacemaker by setting \(i=d\). There exists a connection between the nodes j and i when \(g_{i,j}=1\), and otherwise \(g_{i,j}=0\). \(k_i=\sum \nolimits _{j=1}^{N} g_{i,j}\) is the degree of the node i. Table 1 shows the description and value of others parameters.

Table 1 Parameter values
Full size table

\(I^d_{aut}\) stands for the autaptic current. Three types of autapses are considered only for the pacemaker neuron in the network: electrical, excitatory, and inhibitory autapses. Experiments showed that the autapse is fitted well by monoexponential or biexponential functions [59]. In this work, the autaptic current is modeled by a monoexponential function, which is shown as,

$$\begin{aligned} I^d_{aut}= & {} g_{syn}\alpha (t-\tau -t_{fire})(V-V_{syn}), \end{aligned}$$
(5)
$$\begin{aligned} \alpha (t)= & {} \frac{t}{t_d}\mathrm{e}^{-\frac{t}{t_d}}, \end{aligned}$$
(6)

where \(t_{\mathrm{fire}}\) represents the spiking time, \(g_{\mathrm{syn}}\) is the synaptic weight, and \(\tau \) is the time delay in the self-feedback autapse, which is induced by the finite propagation speed and the time lapses in synaptic processing. In real neurons, delay time with tenths milliseconds can be observed [60]. We typically chose the autaptic reversal potential \(V_{\mathrm{syn}}=0.0\,\mathrm{mV}\) and \(V_{\mathrm{syn}}=-\,80.0 mV\) for the excitatory and inhibitory synapses, respectively [12, 61].

Although it remains unclear if there exists electrical autapse in neuronal system, we will still discuss it in our model as a numerical comparison. For the electrical autapse, we use the feedback scheme which is given by Pyragas [62], and we have

$$\begin{aligned} I^d_{\mathrm{aut}}=g_{\mathrm{syn}}(V(t-\tau )-V(t)), \end{aligned}$$
(7)

where \(g_{syn}\) and \(\tau \) correspond to synapse weight and time delay, respectively.

To quantify the detection and transmission of the low-frequency signal in the neuronal network, we calculate \(Q=\frac{1}{N}\sum \nolimits _{i=1}^{N}Q_{i}\) with \(Q_{i}\) defined by [20]

$$\begin{aligned} Q_i= & {} \sqrt{Q_{s_i}^{2}+Q_{c_i}^{2}}, \nonumber \\ Q_{s_i}= & {} \frac{2}{n T}\int _{T_{0}}^{T_{0}+n T}V_i\sin (\omega t)\mathrm{d}t,\ \nonumber \\ Q_{c_i}= & {} \frac{2}{n T}\int _{T_{0}}^{T_{0}+n T}V_i\cos (\omega t)\mathrm{d}t, \end{aligned}$$
(8)

where \(T=\frac{2 \pi }{\omega }\), \(n=100\) is selected. \(T_{0}\) is sufficiently large for deleting transient evolution. In neuron systems, the information of stimulus is encoded into time series of spikes, and we are interested in the frequency of spikes which could reflect the information of weak signal. Clearly, the factor Q can check the frequency of spikes, and the optimal signal transfer is represented by the synchronization between the weak signal and the output spiking.

Fig. 1
figure 1

The ascending \(Q_i\) at resonance window for \(\epsilon =0.5, 1.0\), 4.0, and 15.0, respectively. \(B=30\) (a), 30 (b), 60 (c), and 100 (d). Here, \(g_{syn}=3.0\) and \(\tau =5.0\)

Full size image

3 Observations and results

First, we investigate the pacemaker-driven signal transmission without the autapse in the Barab\(\acute{a}\)si–Albert (BA) scale-free neuronal network with average connection number \(\langle k\rangle =4\) and total number of neurons \(N=200\). The scale-free networks model starts with an all-to-all network with four nodes and grows by preferential attachment with a probability \(p_i=\frac{k_i}{\sum k_i}\) where \(k_i\) the degree of node [63]. We choose the pacemaker as the node with the maximal degree in the scale-free networks. Figure 1 gives the ascending \(Q_i\) for different values of the parameters \(\epsilon \) and B. The parameters in Fig. 1a–d correspond to \(\epsilon =0.5\) and \(B=30.0\), \(\epsilon =1.0\) and \(B=30.0\), \(\epsilon =4.0\) and \(B=60.0\), and \(\epsilon =15.0\) and \(B=100.0\), respectively. Our simulation data show that those neurons which are connected to hub have lower factor \(Q_i\). For the weak coupling strength, the signal transmission is local, \(Q_i\simeq 0\) for about two-thirds of the neurons, indicating that many neurons cannot receive the weak signal from the pacemaker (Fig. 1a), and the number of \(Q_i\simeq 0\) decreases with the increase in coupling strength (Fig. 1b). For medium coupling strength, the signal transmission can be global since there are two different values which are larger than zero (Fig. 1c). The weak signal can be transmitted to more neurons with the increase in coupling strength, indicating that the fine-tuning of a large enough coupling strength can facilitate the outreach of the weak signal of the pacemaker. The pacemaker activities induced by vibrational resonance with a very large \(\varOmega \) (\(\frac{\varOmega }{\omega }>20\)) have also been systematically tested, and vibrational resonance can be observed with a small Q. However, vibrational resonance can be observed with a very large Q for the high-frequency signal (\(\frac{\varOmega }{\omega }>20\)).

Figure 2 presents the spatiotemporal diagram of the membrane potential of the whole networks. The positions i in Fig. 2a–d have been reordered by the ascending \(Q_i\) in Fig. 1a–d. Figure 2a, b shows that many neurons do not spike at the weak coupling strength, while all neurons exhibit periodic spiking at medium coupling strength. However, there are two different frequencies corresponding to the two different values of \(Q_i\) in Fig.  1c (Fig. 2c). For sufficiently large coupling strength, all neurons emit periodic spikes with the frequency of the weak signal. The weak signal of the pacemaker can be accurately transmitted to every neuron of the neuronal network for sufficiently large coupling strengths (Fig. 2d).

In Fig. 3, we show the average response Q versus B without autapse, and with inhibitory, electrical, and excitatory autapses for \(\epsilon =0.5\), 1.0, 4.0, 15.0, respectively. From these figures, one can find that there is an optimal range of B corresponding to strong resonance response for different coupling strengths, and the usual vibrational resonance is clearly observed. We suggest that vibrational resonance can induce signal propagation from pacemaker to the network. Furthermore, we find that with increasing \(\epsilon \) the maximal value of Q increases and the width of the window of B gets wider for vibrational resonance. One may intuitively guess that the excitatory autapse should have an improved effect on signal transmission. However, compared to the neuron without autapse, the resonance range shrinks for the excitatory autapse, while the resonance region enlarges for electrical and inhibitory autapses, indicating that the inhibitory autapse can enhance signal propagation.

Fig. 2
figure 2

(Color online) Spatiotemporal evolutions of the membrane potential with the evolution time \(t= 10\,T\), where \(T=\frac{2\pi }{\omega }=12.56\). The positions i are reordered by the ascending \(Q_i\). \(B = 30\) (a), 30 (b), 60 (c), and 100 (d) respectively. The parameters are same as those in Fig. 1

Full size image
Fig. 3
figure 3

(Color online) The average response Q vs B without autapse with inhibitory, electrical, and excitatory autapses for \(\epsilon =0.5\) (a), 1.0 (b), 4.0 (c), and 15.0 (d), respectively. Here, \(g_{syn}=3.0\) and \(\tau =5.0\)

Full size image
Fig. 4
figure 4

(Color online) The maximal height of power spectrum (hollow circles), power spectrum at frequency \(\omega \) (solid points), and \(Q_i\) (pluses) with the inhibitory autapse for \(i=1\) (a), 6 (b), 9 (c), and 150 (d), respectively. Here, \(g_{\mathrm{syn}}=3.0, \epsilon =15.0\), and \(\tau =5.0\)

Full size image
Fig. 5
figure 5

(Color online) The bifurcation of \(\mathrm{\Delta t_i}\) (the interval time of successive spikes) of membrane potential \(V_9(t)\) for inhibitory (a–c), excitatory (d–f), and electrical (g–i) autapses, respectively. For left, middle, and right columns, \(g_{\mathrm{syn}}=1.2\), 3.0, and 4.8, respectively. Here, \(\epsilon =15.0\) and \(\tau =5.0\)

Full size image
Fig. 6
figure 6

(Color online) The phase diagrams for the frequency synchronization region for inhibitory autapse (a–c), excitatory autapse (d–f), and electrical autapse (g–i), respectively. \(g_{\mathrm{syn}}=1.2, 3.0\) and 4.8, respectively, for figure from left, middle, and right column, with \(\tau =5.0\). The frequency synchronization region is determined by \(\frac{\omega }{\omega _i^{'}}=1:1, i=1,\ldots ,N\), where \(\omega \) is the frequency of weak signal, \(\omega _i^{'}\) is the frequency of spiking

Full size image
Fig. 7
figure 7

The normalized scaling factor \(R=\frac{S_t}{S}\) in the \((\epsilon , B)\) plane as a function of \(g_{\mathrm{syn}}\) for \(\tau =2.0\) (a) and 5.0 (b), respectively, where \(S_t\) is the size of the frequency synchronization region in \((\epsilon , B)\) plane, and S is the size of the \((\epsilon , B)\) plane with \(0\le \epsilon \le 20\) and \(0\le B\le 240\)

Full size image
Fig. 8
figure 8

(a) Contour plot of the average response Q versus B and \(\epsilon \) for the small-world neuronal networks for \(p=0.3, N=200\) without autapse. (b) The \(Q_i\) in ascending order for \(\epsilon =1.0, B=30.0\) and \(\epsilon =4.0, B=80.0\). (c, d) Spatiotemporal evolutions of the membrane potential in the evolution time \(t= 10 T\), where \(T=\frac{2\pi }{\omega }\). The positions i are reordered by the ascending \(Q_i\). \(\epsilon =1.0, B=30.0\) (c), \(\epsilon =4.0, B=80.0\) (d). Here, \(g_{\mathrm{syn}}=0.9\) and \(\tau =5.0\)

Full size image
Fig. 9
figure 9

(Color online) The average response Q of the small-world neuronal networks as a function of B (a) without autapse and with (b) inhibitory, (c) electrical, and (d) excitatory autapses, respectively. Here, \(g_{\mathrm{syn}}=0.9, \epsilon =4.0\), and \(\tau =5.0\)

Full size image

To quantitatively discuss the transmission of the low-frequency signal in the neuronal network, we also compute power spectrum of membrane potential of all neurons. Figure 4a–d shows the maximal height of power spectrum, power spectrum at frequency \(\omega \), and \(Q_i\) with the inhibitory autapse for neuron \(i=1\), 6, 9, 150, respectively. From these figures, one could not find any significant difference between power spectra at \(\omega \) and \(Q_i\) for vibrational resonance. The maximal height of power spectrum overlaps with the power spectrum at \(\omega \) in the resonance interval, indicating that the frequency \(\omega \) is the most important component for the output signal of each neuron.

Fig. 10
figure 10

(Color online) The phase diagrams for the frequency synchronization region for inhibitory autapse (a–c), excitatory autapse (d–f), and electrical autapse (g–i), respectively. \(g_{\mathrm{syn}}=0.9, 2.1\), and 3.9 for the figures in left, middle, and right column, respectively with \(\tau =5.0\). The frequency synchronization region is determined by \(\frac{\omega }{\omega _i^{'}}=1:1, i=1,\ldots ,N\), where \(\omega \) is the frequency of weak signal, \(\omega _i^{'}\) is the frequency of spiking

Full size image

To understand better the inhibitory-autapse-enhanced signal transmission, Fig. 5 gives the bifurcation of \(\mathrm{\Delta t_i}\) (the interval time of successive spikes) of membrane potential \(V_9(t)\) for inhibitory (a–c), excitatory (d–f), and electrical autapses(g–i). Here, neuron \(i=9\) is chosen randomly. For left, middle, and right columns in Fig. 5, \(g_{syn}=1.2\), 3.0, and 4.8, respectively. There are some periodic windows for inhibitory, excitatory, and electrical autapses (i.e., \(\frac{\omega }{\omega ^{'}}=1:1\) or 2 : 1, where \(\omega ^{'}\) is the frequency of spiking) in these figures. Interestingly, comparing three subfigures in each row, one can find that the periodic windows for frequency synchronization with \(\frac{\omega }{\omega ^{'}}=1:1\) are prolonged for the electrical autapses with increasing \(g_{\mathrm{syn}}\). The excitatory autapse destroys these windows for sufficiently large autaptic weight. More surprisingly, the periodic windows for frequency synchronization can be kept with the inhibitory autapse.

Furthermore, the phase diagrams on the \((\epsilon , B)\) plane for frequency synchronization region with different types of autapse are shown in Fig. 6. From the left column to right column, \(g_{\mathrm{syn}} = 1.2, 3.0\), and 4.8, respectively. Figure  6 shows that frequency synchronization appears first at the optimal window of B as \(\epsilon \) is larger than a critical value, and the range of frequency synchronization enlarges when \(\epsilon \) further increases. Comparing two subfigures in each row on the first and second columns, one can observe clearly that the range of frequency synchronization is larger for network with inhibitory autapse than with the excitatory autapse. As a result, the inhibitory autapse has a stronger effect on the signal transmission. The subfigures in the last column indicate that the range of frequency synchronization increases first and then decreases with the increase in \(g_{syn}\) for the electrical autapse.

Fig. 11
figure 11

(Color online) The normalized scaling factor \(R=\frac{S_t}{S}\) in the \((\epsilon , B)\) plane versus \(g_{\mathrm{syn}}\) for \(\tau =2.0\) (a) and 5.0 (b), respectively, where \(S_t\) is the size of the frequency synchronization region in \((\epsilon , B)\) plane, and S is the size of the \((\epsilon , B)\) plane with \(0\le \epsilon \le 5\) and \(0\le B\le 160\)

Full size image
Fig. 12
figure 12

(Color online) The average response Q of the \(10\times 20\) lattice networks as a function of B (a) without autapse and with (b) inhibitory, (c) electrical, and (d) excitatory autapses, respectively. Here,\(g_{\mathrm{syn}}=5.0, \epsilon =10.0\), and \(\tau =5.0\)

Full size image

To quantify the change of synchronizing size, we also introduce a factor \(R=\frac{S_t}{S}\), where \(S_t\) is the size for frequency synchronization in the \((\epsilon , B)\) plane, and S is size of the \((\epsilon , B)\) plane discussed. The results are shown in Fig. 7. For the excitatory autapse, R decreases with increasing \(g_{\mathrm{syn}}\), while for the inhibitory autapse, R increases with increasing \(g_{syn}\). These results indicate that the inhibitory autapse plays an active role in the signal transmission, while the excitatory autapse does not favor the signal transmission. For the electrical autapse, there is an optimal synapse weight \(g_{syn}\) at which the size of the propagation region becomes maximal.

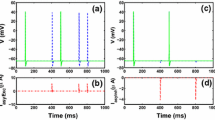
Next, we present the results obtained with the Watts–Strogatz small-world neuronal network (\(p=0.3, N=200\)). For the Watts–Strogatz small-world network, we start with a neighboring-connected ring with periodic boundary conditions. With the probability p, we disconnect an edge and reconnect this edge with a vertex which is chosen uniformly from the entire ring and then repeat this process for each nodes [64]. We examine first the pacemaker activity in such a network without autapse. Figure 8a shows the contour plots of Q as a function of B and \(\epsilon \). Clearly, the vibrational resonance occurs for a sufficiently large \(\epsilon \). Different from the scale-free neuronal network, the weak signal can be transmitted to others neurons only when the coupling strength is larger than a critical value. To show clearly the signal transmission, Fig. 8b presents the ascending \(Q_i\) for the parameters within and without the pink region. We also find that the weak signal can be transmitted accurately to every neuron in the small-world neuronal network. Figure 8c, d gives examples of inaccurate and accurate signal transmission, respectively.

To compare the effect of different types of autapses on signal propagation, Fig. 9a–d shows Q as a function of B without autapse and with inhibitory, electrical, and excitatory autapses, respectively. The vibrational-resonance-induced signal propagation can be observed in these four types of neuronal networks. However, compared to the system without autapse, the optimal range of B becomes narrower for networks with excitatory and electrical atlases, while the inhibitory autapse makes the optimal window wider.

The phase diagrams on the \((\epsilon , B)\) plane for frequency synchronization region for different types of autapses are shown in Fig. 10. From top row to bottom row, the phase diagrams correspond to the inhibitory, excitatory, and electrical autapses, respectively. From left column to right column, \(g_{\mathrm{syn}}=0.9\), 2.1, and 3.9, respectively. Comparing three figures in each row, we find that the inhibitory autapse is indeed advantageous for signal transmission, while the excitatory and electrical autapses do not favor signal propagation for the large autaptic weight \(g_{syn}\).

To show clearly the key role of the autaptic weight \(g_{syn}\), we also compute the factor \(R=\frac{S_t}{S}\), where \(S_t\) is the size of frequency synchronization region, and S is size of \((\epsilon , B)\) plane discussed. The results are shown in Fig. 11. The monotonic increase in the value R with increasing \(g_{\mathrm{syn}}\) for the inhibitory autapse indicates that the size of accurate signal transmission region increases with the increase in the autaptic weight, while the accurate signal transmission region disappears for the excitatory and electrical autapses when the autaptic weight is sufficiently large.

In fact, the cardiac myocytes architecture in the muscle fiber can be represented by a square or cubic lattice networks, and so the Barabasi–Albert and Watts–Strogatz complex networks are not suitable for the study of cardiac myocytes architecture. Finally, we are also interested in verifying the effects of autapse on the lattice networks. The results for a \(10\times 20\) grid networks with zero flux boundary conditions are shown in Fig. 12. Compared to neurons without autapse, we found that electrical and inhibitory autapses can enhance signal transmission, especially for electrical autapses, while excitatory autapse makes signal propagation weaken.

4 Conclusions

We investigated in detail the effects of different types of autapses on signal transmission in the scale-free and small-world neuronal networks, where only one pacemaker stimulated by an external two- frequency signal is introduced. Three types of autapses are considered only to the pacemaker neuron in the networks: electrical, excitatory, and inhibitory autapses. Without autapses, the weak signal stimulated on the pacemaker can be transmitted accurately to the whole networks by vibrational resonance for sufficiently large coupling strengths. We showed that the inhibitory autapse can enhance the pacemaker activity by vibrational resonance, while the electrical and excitatory autapses show a weakened effect on this behavior.

For the scale-free networks, compared to the no-autapse situation, the region of accurate signal transmission becomes large for the network with the inhibitory autapse, while it is reduced with the excitatory autapse and vanishes for sufficiently large autaptic weight. There exists an optimal autaptic weight of the electrical autapse with which the size of signal transmission is largest. In the small-world networks, we also found the strengthened effect of the inhibitory autapse on signal transmission. The size of transmission decreases with the increase in the autaptic weight of the electrical and excitatory autapses, indicating that electrical and excitatory autapses are not favor for signal propagation.

It has been reported that phase locking is of great importance in amplification of weak signal in the excitable system driven by two-frequency signal, called phase-locking modes induced vibrational resonance [28, 29]. We found in the paper that the 1 : 1 phase-locking mode (i.e., frequency synchronization) can be prolonged or kept by inhibitory and electrical autapses in neuronal networks, resulting in the strengthened signal propagation, while the strong excitatory autapse destroys the frequency synchronization, leading to the failure of signal propagation. The signal transmission enhanced by inhibitory self-feedback is unexpected and may contribute to expand our understanding of the dynamics of biological systems. The neuronal network may use the inhibitory self-feedback to amplify or detect the weak signal since the two-frequency signals are universal in nature for acoustics and communication [31,32,33].

The autapses exist widely in  80% cortical pyramidal neurons [65]. Different biological functions of autapse have been investigated. For example, the formation mechanism of atpase is associated with the injury of neuron, which can enhance self-adaptability to stimuli [66]. The autapse can suppress the bursting in neuronal behaviors and thus can regulate the collective behaviors of neural activities  [67]. Our study indicates that the inhibitory autapse may play an important role to detect weak signals in neuronal networks. The inhibitory self-feedback enhanced vibrational resonance is of great interest and may shed more light on our understanding of the dynamics of biological systems with self-feedback. We expect that these results will motivate the inspiration on the experimental studies of the biological systems in the future.