1 Introduction

Substitution box (S-box) is important nonlinear module in the design architecture of block ciphers which is used to confuse the relationship between cipher-text and secret key. In mathematical perspective, S-box can be regard as vectorial Boolean functions. S-box structures are generally based on mathematical structures and random methods. It is necessary to design a large number of robust S-boxes. The security of block ciphers is directly related to its S-boxes while the data encryption standard (DES) is the best example. There are 8 S-boxes in DES algorithm. Matsui pointed out that some S-boxes of DES have weak nonlinear characteristics, and proposed the linear cryptanalysis which trying to obtain the linear approximation of these S-boxes. Based on this method, Matsui successfully break the full 16-round of DES cipher with 247 known-plaintexts [1]. Afterward, differential attack to DES-like cipher is presented by Biham and Shamir [2]. The appearance of linear cryptanalysis and differential cryptanalysis require S-box contain good nonlinearity and differential uniformity. As a result, advanced encryption standard (AES) has been developed to replace DES [3]. Inversion mapping are used in AES S-boxes design which ensure constructed S-boxes have abilities to resist both linear and differential attacks. In terms of comprehensive performance, AES S-box structure is the best S-box structure that can be designed on GF (28). Particularly, differential probability and BIC-nonlinearity of AES S-box are the best in existing S-box structures, and the nonlinearity is almost best. Due to these excellent cryptography characteristics, AES S-box structure has stood the test in commercial practice for many years. However, the algebraic cryptanalysis [4] and side-channel cryptanalysis [5] researches developed recently showed that S-box base on algebraic structure remained weakness. The security of AES may also be challenged. For that reason, many researchers are working on new methods as an alternative to algebraic structures. Lately, many random methods are proposed to design S-box and chaotic systems are usually chosen to be randomness sources of these methods. Açikkapi et al. implemented side-channel attacks to AES algorithm before and after replacing the standard AES S-box to a best or worst chaotic S-box which presented in the last decade, found that the chaos-based random S-box have better performance than AES S-box in side-channel attacks resisting [6]. Therefore, chaotic S-box may be a good alternative choice to AES S-box structures especially in side-channel attacks prevention.

In the early days, discrete-time chaos was first used in S-box construction [7]. Since then, S-box design by different discrete chaos was proposed [8,9,10,11,12,13].After Özkaynak and Özer proposed a method base on Lorenz system [14], S-box construction methods based on continuous-time chaotic systems began to appear [15,16,17]. Some chaotic systems with more complex dynamic behaviors were used to S-box design to improve cryptography performance. Various S-box structures were presented based on time delay [18], fractional [19,20,21] and hyperchaotic systems [22, 23]. In order to obtain S-box structures with best performance criterion, researchers have combined chaotic systems with optimization algorithm [24,25,26,27,28]. Many approaches combined chaotic systems with mathematical structures which play a more important role than chaos were proposed [29,30,31,32,33,34,35].

Moreover, a universal method based on modulo operation to generate S-boxes for all chaotic maps was proposed in [36], in addition to suggest the standard of chaos-based S-box structure with best cryptographic properties. In order to analyze the role of chaotic system used in the S-box design process on S-box performance criteria, Özkaynak in [37] showed that strong S-box structures can be designed by the S-box design approach with modulo operation used in [36], using entropy source that do not display chaotic behavior. Which indicate that modulo operation play a more important role than entropy source in this case. Lately, the effects of pre and post some implements on design criteria were analyzed in [38, 39]. In [40], not only a successful design work be done, but also the effect of fixed point and reverse fixed point on cryptanalysis process was considered.

It has been proved that high-dimensional chaotic system has some advantages than low-dimensional chaotic map system, such as larger parameter range, more complex behavior and longer period [41]. For that reason, high-dimensional chaotic system is considered to be better choice in many cryptographic studies like image encryption and PRNG. On the other hand, there are few researches about the high-dimensional chaotic system, especially spatiotemporal chaotic system, in random S-box design. Therefore, it is necessary to investigate the performance of high-dimensional chaotic system in S-box generation compared with low-dimensional chaotic system. In this paper, spatiotemporal chaos was taken as a representation of high-dimensional chaotic system to investigate the above issue.

The coupled map lattice (CML) is a classical spatiotemporal chaos has been deeply studied and widely applied [42,43,44,45] in cryptography. Its adjacent couplings can describe by the following equation:

$$ X_{n + 1} \left( i \right) = \left( {1 - \varepsilon } \right)f\left[ {X_{n} \left( i \right)} \right] + \frac{\varepsilon }{2}\left\{ {f\left[ {X_{n} \left( {i - 1} \right)} \right] + f\left[ {X_{n} \left( {i + 1} \right)} \right]} \right\}; $$
(1)

where i = 1, 2,…, L is the lattice index, n is the time index, 0 < ε < 1 is the coupling coefficient, f(Xn) = ωXn(1 − Xn), (3.569946 ≤ ω ≤ 4) is logistic map. The periodic boundary condition Xn (0) = Xn (L) has been used in this system. But due to the periodic windows of CML, parameter u should be carefully selected. In recent years, many spatiotemporal chaos based on new coupling methods have been proposed to avoid the high correlation effect between adjacent lattices. Chen et al. investigated a novel spatiotemporal chaos which connections are rewired randomly with varying probability P and rewiring period T [46]. But the spatial connection pattern of this spatial random coupling method cannot be reproduced in same parameters, which limited its application in cryptography. Another direction is nonlinear coupling method. In [47], a novel dynamics base on nonlinear coupling method named Arnold coupled logistic map lattice (ACLML) was presented. Subsequently, a mixed linear–nonlinear coupled map lattices (MLNCML) was suggested in [48]. The nonlinear coupling method replaced the adjacent coupling with non-adjacent coupling, but the system base on it still retained property that one lattice is limited by another two fixed lattices in every iteration.

In other to avoid above disadvantages, we investigated a new spatiotemporal system with pseudo-random coupling strategy that we called 2DMCPML. The three coupling lattices selected by a novel 2D pseudo-random mixed coupling method, when two of them are neighbor lattices, and the last one decided by the pseudo-random sequence value of local lattice. The used of 2D pseudo-random mixed coupling method has following advantages: (1) make the dynamics behavior of local map more complex. (2) Accelerate the whole system into full spatial chaos. (3) Increase the number of coupling parameters. (4) Reduce the correlation effects of adjacent lattices, since every iterations are effected by a different lattice in random position. The local maps of many spatiotemporal chaos are classical Logistic map. The simple 1D map like Logistic map and Sin map has been proved that contain many disadvantages: blank windows, weak parameter space, low orbit complexity and uneven distribution of output chaotic sequence. Therefore, we designed a new 1D chaotic map named PS map to replace simple 1D map for local map. The PS map is constructed by PWLCM and Sin map base on nonlinear combination structure in [49]. Numerical simulation of PS map showed that it is more suitable for local map of spatiotemporal chaos than simple 1D map. Subsequently, we analyzed the dynamic properties of 2DMCPML. The experimental results of bifurcation diagrams, Kolmogorov–Sinai entropy density and spatiotemporal chaotic diagrams showed that 2DMCPML has advantages of larger parameter space, more complex chaotic behavior and more ergodic output sequence than CML. These new features ensure 2DMCPML more suitable in cryptography than CML. Moreover, the evolution of spatiotemporal chaotic diagrams from CML to 2DMCLML and then to 2DMCPML demonstrated the enhancement of chaotic behaviors which PS map and 2D mixed coupling method provided.

The purpose of our work is not only to present a new spatiotemporal system but also to investigate the availability of 2DMCPML in the generation of random S-box and the advantages of spatiotemporal system to low-dimensional chaos in S-box generation. Thus, we employed the spatial chaotic character of 2DMCPML to construct 1000 random S-boxes. The cryptographic performance of constructed S-boxes are tested. An example S-box with good cryptographic performance was selected to compare with the some representative S-box structures. Finally, four criteria bounds were set in this paper. The number of S-boxes satisfying these bounds generated by 2DMCPML and several 1D chaotic maps is calculated, respectively. The result showed that spatiotemporal chaos can generate more S-boxes with high cryptographic quality than low-dimensional chaos. This discovery may have important effect to the development of some cryptographic researches such as dynamic S-box algorithm.

The rest paper is organized in following way. In Sect. 2, the 1D PS map is presented. The 2D Mixed pseudo-random Coupling PS Map Lattices is proposed in Sect. 3. In Sect. 4, the details of S-box construction method based on 2DMCPML is given. The cryptographic performance of S-boxes constructed by 2DMCPML are analyzed in Sect. 5. In Sect. 6, the example S-box of our work is compared with some representative S-box structures, in addition, the advantage of spatiotemporal chaos to low-dimensional chaos in S-boxes generation is investigated. At last, a conclusion is drawn in Sect. 7.

2 The 1D PS map

Since the chaotic behavior of spatiotemporal chaos is mainly determined by local map, the local map should be selected carefully. Combining PWLCM map and Sin map, a new 1D PS map was proposed for the local map of 2DMCPML in this section.

The 1D PWLCM is a generalized form of tent map. It can describe by following function:

$$ X_{n + 1} = F_{p} \left( {X_{n} } \right) = \left\{ {\begin{array}{*{20}l} {X_{n} /p,} \hfill & {0 \le X_{n} < p,} \hfill \\ {\left( {X_{n} /p} \right)/\left( {0.5 - p} \right),} \hfill & {p \le X_{n} < 0.5,} \hfill \\ {F_{p} \left( {1 - X_{n} } \right),} \hfill & {0.5 \le X_{n} \le 1;} \hfill \\ \end{array} } \right. $$
(2)

where the parameter p should be selected from (0,0.5), and the status value Xn is in the range of [0,1]. The PWLCM is chaotic when p∈(0,0.5).

The Sin map is a well-known 1D chaos. It is widely used in study of cryptography. The Sin chaotic function is

$$ X_{n + 1} = \mu \sin \left( {\pi X_{n} } \right)/4; $$
(3)

where the parameter μ is in the interval (0,4], and the status value Xn is in the interval [0,1]. Sin map has chaotic behaviors, when μ∈[3.569946, 4].

The simple 1D map like PWLCM, Logistic and Sin map share some common disadvantages: blank windows, weak parameter space, low orbit complexity and uneven output sequences distribution. These problems limit their application in cryptography. Base on a modulo operation [49], we obtain the PWLCM-Sin map. The parameters of both seed maps are unified for convenience. The mathematical expression of PS map is

$$ \begin{aligned} & X_{n + 1} = F_{\omega } \left( {X_{n} } \right) \\ & \quad = \left\{ {\begin{array}{*{20}l} {\left( {\left( {4 - \omega } \right)\sin \left( {\pi X_{n} } \right)/4 + 8X_{n} /\omega } \right)\bmod 1,} \hfill & {0 \le X_{n} < 0.125\omega ,} \hfill \\ {\left( {\left( {4 - \omega } \right)\sin \left( {\pi X_{n} } \right)/4 + \left( {X_{n} - 0.125\omega } \right)/\left( {0.5 - 0.125\omega } \right)} \right)\bmod 1,} \hfill & {0.125\omega \le X_{n} < 0.5,} \hfill \\ {F_{\omega } \left( {1 - X_{n} } \right),} \hfill & {0.5 \le X_{n} \le 1;} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(4)

where the parameter ω is in the interval (0,4), the status value Xn also interval in [0,1]. The PS map has a more complex structure than a simple 1D map, which indicates that it may has more complex chaotic orbits. In order to get the quantified performance of PS map, Lyapunov exponent, bifurcation and distribution of output sequences are tested. Figure 1a shows that the Lyapunov exponents of PS system are positive in whole parameter space and significantly bigger than simple 1D map. Therefore, PS map has more complex orbits and chaotic sequences than simple 1D map. The bifurcation diagram of PS map is shown in Fig. 1b. It is clear that no blank windows and short-period phenomenon in appear the bifurcation which indicated PS map has a much larger available parameter space than simple 1D map. Figure 1c shows the relatively uniform output distribution of PS map. Above new features ensure PS map is suitable for cryptography.

Fig. 1
figure 1

The simulation of PS map. a Lyapunov exponents, b bifurcation diagram, c output distribution

Full size image

3 The proposed 2DMCPML system

Extending the spatial dimension to two-dimension, mixing the pseudo-random coupling component with adjacent coupling component, using PS map as local map, we proposed a novel spatiotemporal chaotic model 2DMCPML. It can describe by the following equation:

$$ \begin{aligned} & X_{n + 1} \left( {i,j} \right) = \left( {1 - \varepsilon } \right)f\left[ {X_{n} \left( {i,j} \right)} \right] + \frac{\varepsilon }{2}\left( {1 - \sigma } \right) \\ & \quad \left\{ {f\left[ {X_{n} \left( {i + 1,j} \right)} \right] + f\left[ {X_{n} \left( {i,j - 1} \right)} \right]} \right\} + \varepsilon \sigma f\left[ {X_{n} \left( {a,b} \right)} \right]; \\ \end{aligned} $$
(5)

where i, j, a, b are lattice indexes, n is time index. ε and σ are coupling coefficients in the range of [0,1]. Xn(i, j) is the state of local map in lattice (i, j) and the local dynamics f(X) define as PS map. The periodic boundary conditions Xn(i + L, j) = Xn(i, j) and Xn(i, j + L) = Xn(i, j) are used in 2DMCPML.

The coupling relationship in Eq. (5) is portrayed in Fig. 2. For any lattice (i, j), the state Xn+1(i, j) is influenced by following elements: (1) itself Xn(i, j), (2) adjacent lattice from two directions Xn(i + 1, j) and Xn(i, j −1), (3) non-adjacent lattice with random position Xn(a, b). Here, the value of a and b decided by the Xn(i, j) state value. Combining the first and second place in the decimal part of Xn(i, j) to get a two-digit number, mod this number with L then plus 1, one can get a. Similarly, combining the third and fourth place in the decimal part of Xn(i, j) to get another two-digit number, mod this number with L then plus 1, one can get b. For example, if Xn(i, j) = 0.40967142 and L = 16, the two-digit number is 40 and 96, respectively, so a = (40 mod 16) + 1=9 and b = (96 mod 16) + 1=1.

Fig. 2
figure 2

The coupling relationship of 2DMCPML

Full size image

For practicality and comparison purpose, CML assign L = 256, 2DMCPML assign L = 16. Here considered the spatiotemporal system under relatively weak coupling condition. The Bifurcation diagrams of CML and 2DMCPML with fixed ε are drawn in Fig. 3 to demonstrate the chaotic behavior in time dimension. Figure 3a–c indicate the bifurcations of CML with ε = 0.1, 0.3 and 0.5, respectively, when ω ∈ [3, 4]. Obviously, CML keeps some characters occur in Logistic map like forking behavior, blank Window and short periods which limits its application in cryptography.

Fig. 3
figure 3

The bifurcation diagrams of spatiotemporal chaos. a CML with ε = 0.1, b CML with ε = 0.3, c CML with ε = 0.5, d 2DMCPML with ε = 0.1, e 2DMCPML with ε = 0.3, f 2DMCPML with ε = 0.5

Full size image

The bifurcation diagrams of 2DMCPML with ε = 0.1, 0.3 and 0.5 where σ = 0.5 are shown in Fig. 3d–f, respectively. There are no forking behavior and blank window in these figures which is a new feature. Meanwhile the state values of 2DMCPML are distributed almost in entire space of [0,1]. The explanation of the difference in bifurcation is that the new PS map has better chaotic dynamics than logistic map and the 2D pseudo-random mixed coupling increases the instability of potential periodic orbits. CML systems are generally considered more suitable for cryptographic applications than ordinary low-dimensional maps for its less blank window. Similarly, 2DMCPML is more suitable for cryptographic applications than CML.

Lyapunov exponent measure the divergence of nearby orbits and provide a qualitative view to dynamic behavior of system. Generally, the larger Lyapunov exponent is, the more complex chaotic dynamical behavior is. The proposed spatiotemporal chaos 2DMCLML can be considered as L2 dimensions dynamics. Kolmogorov–Sinai (KS) entropy density is usually used to measure the chaotic property of multi-dimensions dynamics which is the average of all positive Lyapunov exponents [50].

The KS entropy density for different ε and ω of 2DMCLML and CML systems are shown in Fig. 4a, b, respectively. It is apparent that the KS entropy densities of CML are within [0, 0.5] in Fig. 4a while KS entropy densities of 2DMCPML are mostly higher than 0.5 in Fig. 4b. The proposed 2DMCPML have higher KS entropy densities than CML in almost entire parameter space. This characteristic indicates that 2DMCPML contains more intensive and extensive chaotic behaviors.

Fig. 4
figure 4

The KS entropy density for different ε and ω of spatiotemporal chaos. a CML, b 2DMCLML

Full size image

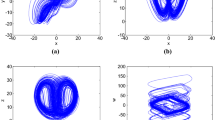
In order to analyze global chaotic properties of proposed system, the spatiotemporal chaotic diagrams with fixed local parameter and coupling strength is investigated. All spatiotemporal systems here consist of 256 lattices and iterate 500 times. Figure 5a illustrates the spatiotemporal chaotic diagrams of CML with ω = 3.9, ε = 0.1. As iteration progress, state values tend to converge slightly. The state values distribution is in small range and uneven.

Fig. 5
figure 5

The spatiotemporal chaotic diagrams of spatiotemporal chaos. a CML with ω = 3.9, ε = 0.1, b 2DMCLML with ω = 3.9, ε = 0.1 and σ = 0.5, c 2DMCPML with ω = 3.9, ε = 0.1 and σ = 0.5

Full size image

The spatiotemporal chaotic diagrams of 2D Mixed pseudo-random Coupling Logistic Map Lattices (2DMCLML) with ω = 3.9, ε = 0.1 and σ = 0.5 is drawn in Fig. 5b. Comparing Fig. 5a with Fig. 5b, it is clear that 2DMCLML have lager scope and more uniform distribution of state values. Bearing in mind that 2DMCLML and CML use a same local dynamics Logistic map, the only explanation of this difference is that the 2D Mixed pseudo-random Coupling method indeed benefit system chaotic property. Therefore, 2D Mixed pseudo-random Coupling method is more suitable in cryptography than adjacent coupling method.

Figure 5c shows the spatiotemporal chaotic diagrams of 2DMCPML with ω = 3.9, ε = 0.1 and σ = 0.5. Comparing Fig. 5b, c, one can found that the 2DMCPML have lager range and more uniform distribution of state values than 2DMCLML after replacing the local Logistic map with PS map. This new feature suggested again that PS map is a better choice for local map than Logistic map.

Above analysis indicated that 2DMCPML has advantages of large parameter space, more complex chaotic behavior and more ergodic output sequence than most chaotic system in terms of practical usability. According to the IEEE floating point standard, the computational precision of 64-bit double precision number is about 1016 [51]. In case of ω, ε and σ are chosen to be key, the key space of 2DMCPML is close to 4 × 1048 ≈ 2161which is a great number.

4 S-box construction method based on 2DMCPML

In this section, random S-box generation method using spatial chaotic property of 2DMCPML is provided which can construct robust S-box without significantly increase computation. In order to obtain n × n S-box, the size of 2DMCPML is set to L = 2n/2. Here take n = 8 for example. The detailed algorithm is described as follows:

  • Step 1: Determine the coupling parameters ε and σ, as well as the local map parameter ω. Set the initial values for all lattices of 2DMCPML that the initial values are not all the same.

  • Step 2: Iterate the spatiotemporal system 2DMCPML for k times to go into chaotic, where k > 200.

  • Step 3: Define a one-dimensional empty sequence with 256 elements: S = [S(0), S(1),…S(255)]. Save the lattices state value of 2DMCPML into S, row by row, starting from the first row, like this: S = [S(0) = X(1,1),…, S(15) = X(1,16),…, S(240) = X(16,1),…, S(255) = X(16,16)].

  • Step 4: Reorder all elements in S by ascending order of their values. The element with larger index put on the left, if values of two elements are equal. Translate the index of S to a 8 × 8 table, i.e., obtains an S-box. Afterward, iterate 2DMCPML one time to prepare for constructing next S-box.

Repeat the Steps 3–4, one can generate S-boxes as many as desired.

There are total 256! ≈ 21684 different bijective S-boxes on GF (28). The number of different bijective S-boxes indicated that there is a great space for exploration in the research of constructing 8 × 8 S-box. The proposed method used lots of long period orbits of spatiotemporal chaos to generate large numbers of S-boxes.

5 S-box performance analyze

Generating 1000 8 × 8 S-boxes by the method of last section with ε = 0.1, σ = 0.5, and ω = 2.1. Five basic requirements are used to evaluate the performance of the constructed S-boxes. Including bijective property, nonlinearity, strict avalanche criterion (SAC), outputs bit independence criterion (BIC) and equiprobable input/output XOR distribution. These criteria are widely used to assess S-box.

A Boolean function fi is bijective if it satisfies the following equation:

$$ {\text{wt}}\left( {\mathop \sum \limits_{i = 1}^{n} a_{i} f_{i} } \right) = 2^{n - 1} ; $$
(6)

where ai∈{0,1}, (a1, a2,…, an) ≠ (0, 0,…, 0) and wt() is the hamming weight. The proposed method in last section guarantees each element in the S-box are unique number between 0 and 255, so that each Boolean function satisfies Eq. (6), and all constructed S-boxes are bijective.

The nonlinearity measures the hamming distance between N-bit Boolean function and N-bit affine function [52]. If the nonlinearity of Boolean function is low, its linear approximation is easy to obtain and the S-box cryptographic performance is weak. For the convenience of calculation, the nonlinearity value of n-bit Boolean function f(x) is usually represented by the following formula:

$$ N_{f} = 2^{n - 1} \left( {1 - 2^{ - n} \mathop {\hbox{max} }\limits_{{\omega \in {\text{GF}}\left( {2^{n} } \right)}} \left| {S_{\left( f \right)} \left( \omega \right)} \right|} \right); $$
(7)

where S(f)(w) is the Walsh spectrum of f(x), it can describe by the following equation:

$$ S_{\left( f \right)} \left( \omega \right) = \mathop \sum \limits_{{x \in {\text{GF}}\left( {2^{n} } \right)}} \left( { - 1} \right)^{f\left( x \right) \oplus x \cdot \omega } ; $$
(8)

where ω∈GF(2n), and x·w denotes the dot product of x with w.

Here, we measure the nonlinearity property of S-box structure by the average nonlinearity values of N-bit Boolean function. Although, in recent study [53], the author claimed that this measurement was incorrect because it consider the average nonlinearity of N-bit Boolean function only, ignoring the rest of the linear combinations of N-bit Boolean function in the process. He suggested that the nonlinearity property should be measured as the minimum nonlinearity value of all linear combinations of N-bit Boolean function. However, whether the rest of linear combinations of N-bit Boolean function (such as f1 ⊕ f3 ⊕ f4 ⊕ f6) can be used in linear cryptanalysis is a question without certain answer at present. Thus, the measurement here is still correct.

Figure 6 shows the average nonlinearity values of S-boxes constructed by 2DMCPML. The lower bound of average nonlinearity values is 100, S-box with very poor nonlinearity property did not appear. The best and mean values of average nonlinearity are 107 and 103.54, respectively. Therefore, constructed S-boxes have good nonlinear properties.

Fig. 6
figure 6

Average nonlinearity values of S-boxes constructed by 2DMCPML

Full size image

Webster and Tavares proposed strict avalanche criterion (SAC) combining completeness and the avalanche effect [54]. An S-box satisfies the strict avalanche criterion, which means each output bit will change with a probability of 0.5, if changing one bit of the input. Constructing dependence matrix is usually used to verify SAC, and the optimum value is 0.5. The average value of dependence matrix and average offset of dependence matrix elements from 0.5 are both ordinarily used to measure SAC.

Figure 7 shows the average values of dependence matrix of S-boxes constructed by 2DMCPML. Constructed S-boxes have close property to SAC since all values are within the interval [0.485, 0.52].

Fig. 7
figure 7

Average values of dependence matrix of S-boxes constructed by 2DMCPML

Full size image

The outputs bit independence criterion (BIC) is another essential analysis criterion for the design of S-box. In this paper, the measurement proposed by Adams and Tavares is used to test the BIC of S-box which analyzes the effect of the two previous criteria on the output bits [55]. The 8 Boolean functions of 8 × 8 S-box are denoted as f1, f2,…, f8. If fv⊕ fw has high nonlinearity property and is quite close to SAC for any v and w (v, w∈{1, 2,…, 8}, and v ≠ w), we can believe that every pair of output bits have a very small correlation and the S-box has a good BIC property.

The average values of nonlinearity and dependence matrix of fv⊕ fw are shown in Figs. 8 and 9, respectively. In terms of nonlinearity, the Average nonlinearity values for BIC is greater than 101. In terms of SAC, the Average values of dependence matrix for BIC is very close to 0.5. Therefore, constructed S-boxes have good BIC property.

Fig. 8
figure 8

Average nonlinearity values for BIC of s-boxes constructed by 2DMCPML

Full size image
Fig. 9
figure 9

Average values of dependence matrix for BIC of s-boxes constructed by 2DMCPML

Full size image

The last measurement is equiprobable input/output XOR distribution which also known as maximum expected differential probability (MEDP) [2]. It is directly related to differential cryptanalysis. The maximum value in the input/output XOR distribution table should be as small as possible. Differential probability for a given function f can be calculated by:

$$ {\text{DP}}_{f} = \mathop {\hbox{max} }\limits_{\Delta x \ne 0,\Delta y} \left( {\# \left\{ {x \in X\left| {f\left( x \right) \oplus f\left( {x \oplus \Delta x} \right)} \right. = \Delta y} \right\}} \right); $$
(9)

where X is the set of all possible input values.

Figure 10 displays the max values of equiprobable input/output XOR distribution table of S-boxes constructed by 2DMCPML. The max values mostly concentrate in 10 and 12; meanwhile all max values are not greater than 14. This result indicated that constructed s-boxes can resist differential attacks well.

Fig. 10
figure 10

Max values of equiprobable input/output XOR distribution table of S-boxes constructed by 2DMCPML

Full size image

Above simulation results shows that the 1000 S-boxes generated by 2DMCPML have good overall cryptography performance and without very weak S-box. This is a good property to dynamic S-box algorithms. Moreover, the chaotic system 2DMCPML of proposed method has a big parameter space. These properties ensure the proposed method well suited for dynamic S-box algorithms.

6 Performance comparison

6.1 Example S-box comparison

An example S-box with good cryptographic performance of S-boxes generated by proposed method is selected and shown in Table 1. The nonlinearities of eight output bits of example S-box are 110, 104, 106, 106, 106, 108, 108, 108 and the average value is 107. The dependence matrix, nonlinearity of fv⊕ fw and equiprobable input/output XOR distribution of example S-box are shown in Tables 2, 3 and 4, respectively.

Table 1 The example of S-box constructed by proposed method
Full size table
Table 2 The dependence matrix of example S-box
Full size table
Table 3 The nonlinearity for fv⊕ fw of example S-box
Full size table
Table 4 Equiprobable input/output XOR distribution table of example S-box
Full size table

The example S-box is compared with some representative S-box structures in Table 5. The results showed that cryptographic performance of example S-box is stronger than most chaos-based random S-boxes but weaker than some S-box structures use mathematical structure or optimization algorithms.

Table 5 Comparison of example S-box and different S-box structures
Full size table

6.2 Different chaos comparison

Four criteria bounds are set as following way. (1) Bound 1: NL ≥ 104, (2) Bound 2: NL ≥ 104 && |SAC-0.5| ≤ 0.005, (3) Bound 3: NL ≥ 104 && |SAC-0.5| ≤ 0.005 && |BIC_SAC| ≤ 0.005, (4) Bound 4: NL ≥ 104 && |SAC-0.5| ≤ 0.005 && |BIC_SAC| ≤ 0.005 && DP ≤ 10. Where NL is the average nonlinearity value of S-box, SAC is the average value of dependence matrix of S-box, BIC_SAC is the average value of dependence matrix of S-box output pair fv⊕ fw and DP is the max values of equiprobable input/output XOR distribution table of S-box.

For comparison purpose, we use the output chaotic sequence of three different one-dimensional chaos: Logistic map, Sin map and PS map to generate 1000 8 × 8 random S-boxes, respectively. The numbers of S-boxes satisfying above four bounds generated by 2DMCPML and three different 1D chaos is calculated. The result is shown in Table 6. It is clear that the numbers of S-boxes satisfying the four bounds generated by 2DMCPML are all more than three 1D chaotic maps which mean the spatiotemporal chaos can indeed generate more S-boxes with strong cryptographic feature. This new discovery is significant to the development of some cryptographic researches such as dynamic S-box algorithm.

Table 6 The numbers of S-boxes satisfying one of four bounds generated by 2DMCPML and different 1D chaos
Full size table

7 Conclusion

In this paper, firstly, we design a new 1D PS map which derived from PWLCM and Sin map by modulo operation. Experimental results show that PS map overcomes many shortcomings such as blank windows, weak parameter space and bad ergodicity which widely occur in simple 1D map. Since the chaotic behavior of spatiotemporal chaos is mainly determined by its local map, the PS map is more suitable for local map of spatiotemporal dynamics. Secondly, with the novel 2D pseudo-random mixed coupling method we present a spatiotemporal chaos used PS map as local map f(x). The experimental results of bifurcation diagrams, Kolmogorov–Sinai entropy density and spatiotemporal chaotic diagrams showed that 2DMCPML has advantages of larger parameter space, more complex chaotic behavior and more ergodic output sequence than CML. Moreover, the evolutions of spatiotemporal chaotic diagrams from CML to 2DMCLML and then to 2DMCPML demonstrate the enhancement of chaotic behaviors which PS map and 2D mixed coupling method provided. Above new features ensure 2DMCPML more suitable in cryptography than CML. Subsequently, we employed the spatial chaotic character of 2DMCPML to generate a large number of S-boxes. The cryptographic performance indicated that generated S-boxes can resist cryptanalysis attack well. Finally, four criteria bounds are set. The numbers of S-boxes satisfying these bounds generated by 2DMCPML and three 1D chaotic maps is calculated, respectively. The result showed that spatiotemporal chaos can indeed generate more S-boxes with strong cryptographic features than low-dimensional chaos. This new discovery is significant to the development of some cryptographic researches such as dynamic S-box algorithm.

In terms of practical usability, the advantages and disadvantages of proposed method can be summarized as follow.

  1. (1)

    Considering chaos-based random S-box has better performance in side-channel attacks resisting [6], S-box constructed by proposed method can be used as masks to prevent side-channel attacks of symmetric cryptography.

  2. (2)

    The proposed method is well suited for dynamic S-box algorithms due to big parameter space and good overall S-box cryptography performance. Such as, the parameter space of proposed method is about 2161, much greater than dynamic AES S-box algorithms such as [56], which has 256 different dynamic AES S-boxes.

  3. (3)

    The large parameter space, more complex chaotic behavior and more ergodic output sequence of the entropy source 2DMCPML ensure it can well apply not only in S-box construction, but also in other cryptography like image encryption [48] and pseudo-random number generator [57].

  4. (4)

    The comprehensive performance of example S-box is stronger than most chaos-based S-boxes but weaker than some S-box structures used mathematical structure or optimization algorithms, which means that example S-box is weaker than some S-box structures used mathematical structure or optimization algorithms in linear cryptanalysis or differential cryptanalysis resisting.