1 Introduction

Chaos, primarily observed in the meteorology, is complex and irregular [23], it possesses some outstanding characteristics, e.g. randomness, extreme sensitivity to initial values and the unpredictable orbit. Since those special properties are essentially similar to those of cryptography [7], chaos has been widely used as a core component for designing chaos-based cryptographic schemes [4, 9, 21, 25,26,27, 30, 37]. Besides those application schemes, chaos theory is also an essential foundation for leading to the growing development of chaos cryptography [2, 3, 20]. Many researchers have explored chaos theory in the domain of chaos-based cipher [8, 11].

The chaotic system used in chaos cryptography is commonly simplified into two categories. One is the simple chaotic system, since having a simple structure, high efficiency and mature theoretical foundation [14], they are prevalent in those chaos-based cryptographic schemes. Another is the higher-dimensional chaotic system, compared with a simple one, it has more complicated chaotic dynamic behavior and unique advantages to be the core component for confusing information in a secure scheme. Among those higher-dimensional chaotic models, coupled map lattice (CML) is one of the most classic model [12], which has those highlights of the parallel structure and high computational efficiency, as well as keeping chaos both at time and space. Based on the above-mentioned highlights, CML has been universally used as a core component to design cryptographic primitives in those sub-fields, such as stream cipher [15, 18], Hash function [32, 34] and multimedia encryption [31, 33]. Combining two-dimensional (2D) CML and partitioned cellular automation, a novel and excellent stream cipher algorithm is proposed in [18]. In  [32], a new hash function is designed via an improved CML, which combines floating-point chaotic computations and algebraic operations, as well as local and global couplings, and finally achieves high bit confusion and diffusion. The 2D CML owns good statistical properties, and it is used for constructing the one-way hash function algorithm [34]. The bit-level image encryption scheme is designed based on an enhanced cross CML in [31], which has high effectiveness and safety against the common attacks. A new encryption scheme via the wide-range system mixed CML model is proposed [33], which is effective for securing both grayscale and color images.

Meanwhile, the pseudo-random number generator (PRNG) is commonly considered as a core component of chaos-based cryptography schemes. For enhancing security, the higher-dimensional chaotic system is popularly used to construct amounts of PRNG schemes[16, 31]. However, for the higher-dimensional chaotic system, it is important to obtain a better trade-off between security and efficiency. For instance, in [28], a novel dynamical 4-D chaotic circuit is designed, and then generates PRNG sequences by construction of chaotic circuits with competent S-Box parameters. However, its efficiency needs further improvement. Furthermore, combining three different fractional chaotic systems, a novel structure for the PRNG scheme is proposed as a keystream to encrypt the image. For this scheme, both security and efficiency are weak. During our previous research work [36], the 2D CML model is analyzed and designed for the PRNG scheme, the relation between chaos and the pseudo-random number is established, and our scheme has high security and efficiency. However, it is well acknowledged that in such chaos-based cryptography applications, more complexity underlying a chaotic system indicates much security. Therefore, suppose using the 3D CML model to design the PRNG scheme, and it is coupled by those adjacent six nodes from there dimensional. Under the premise of considering security, the security of 3D CML-based cryptography scheme will be probably improved, this point needs further verification in this paper.

The above-mentioned existing research shows that ensuring the complex dynamic behavior of CML by reasonably configuring its structure and parameters is of great significant and timely to the security schemes. From this perspective, extending 2D CML into 3D CML is a promising approach to obtaining more complicated dynamic behavior. However, to the best of our knowledge, there are only a few scientific theoretical studies on the behavior of 3D CML. From the view of using it for confusing or encrypting information, in this paper, two core metrics: Lyapunov exponent (LE) and synchronization stability are chosen and analyzed, because, from the view of cryptography, LE is usually used to measure the diffusion performance of a chaotic system, synchronization stability is closely related to the complexity of a system. To design security schemes based on 3D CML, we definitely expect this model to be in the asynchronous state, which is the opposite side of synchronization stability.

Motivated by this, the 3D CML model is taken for a case study, its LE and synchronization stability are theoretically derived, which provides important theoretical guidelines for cryptographic application. Bifurcation, ergodicity and probability density distribution (PDD) of the 3D CML model are simulated to show it has outstanding chaotic performance. Based on the above-mentioned theoretical outcome, our PRNG scheme is designed, and experimental simulations illustrate our scheme possesses outstanding performance.

To summarise, among others, the main objectives of our study include:

  1. 1.

    The mathematical expression of LE in the 3D CML model is given theoretically, according to the accurate LE values, it is easy to judge whether the 3D CML model is in a chaotic state or not, as well as providing important theoretical guidelines for ensuring the model in the fully developed chaotic state of cryptographic application.

  2. 2.

    The mathematical formula of synchronization stability in the 3D CML model is derived, according to theoretical results, the parameters are set reasonably to avoid synchronization phenomenon, and it improves the security of the chaos-based cryptographic application.

  3. 3.

    Finally, all experiment simulations of LE and synchronization stability align perfectly with the theoretic formulas, those conclusions greatly enrich and support the development of chaos cryptography. Also, bifurcation, ergodicity and PDD of the 3D CML model are analyzed. Compared with one-dimensional (1D) CML and two-dimensional (2D) CML, 3D CML has more complicated chaotic behavior for designing the chaos-based cryptographic scheme.

  4. 4.

    According to the 3D CML model, based on those theoretical results, a novel PRNG scheme is constructed with safety assurance, and all simulation results verify that our scheme is both secure and efficient.

  5. 5.

    Some important conclusion of LE in the ND CML model is derived, it can provide some theoretical guidance for application of the CML model.

The rest of this paper is written as follows. Section 2 shows some preliminary knowledge. Theoretical analysis of LE and synchronization stability in 3D CML is presented in Sect. 3, meanwhile, bifurcation,ergodicity and PDD of the 3D CML model are simulated in this section. In Sect. 4, our PRNG scheme is proposed via the 3D CML model. Some numerical tests are presented to further verify those theoretical results are correct, and our scheme has excellent performance via extensive simulation analyse in Sect. 5. Furthermore, some important conclusion of the ND CML model is shown in Sect. 6. Finally, the conclusion is drawn in Sect. 7.

2 Preliminaries

2.1 The 3D CML model

It is well known that the 2D CML model has outstanding chaotic dynamic behavior performance [31], in which, the current node value is decided by those adjacent four nodes. To further enhance the chaotic dynamic behavior, the 2D CML model is extended into a three-dimensional one, as depicted in Fig. 1, the current node value of 3D CML is calculated by those adjacent six nodes, and its mathematical definition is described as

Fig. 1
figure 1

The 3D CML model

Full size image

Definition 1

The three-dimensional CML model is defined as

$$\begin{aligned} \begin{aligned}&x_{n+1}^{s,t,u}=(1-\varepsilon )\text {F}(x_{n}^{s,t,u})+\frac{\varepsilon }{6}\left[ \text {F}(x_{n}^{s+1,t,u})+\text {F}(x_{n}^{s-1,t,u})\right. \\&\left. \!+\text {F}(x_{n}^{s,t+1,u})\!+\!\text {F}(x_{n}^{s,t-1,u}) \!+\!\text {F}(x_{n}^{s,t,u-1})\!+\!\text {F}(x_{n}^{s,t,u+1})\right] , \end{aligned} \end{aligned}$$
(1)

where \(s=1,2,\cdots ,R\), \(t=1,2,\cdots ,L\) and \(u=1,2,\cdots ,U\). And R, L and U are the row, column and height indexes of the 3D CML model, respectively.

And its periodic boundary conditions are \(x_{n}^{s+R,t,u}=x_{n}^{s,t,u}\), \(x_{n}^{s,t+L,u}=x_{n}^{s,t,u}\) and \(x_{n}^{s,t,u+U}=x_{n}^{s,t,u}\).

2.2 Lyapunov exponent

LE is significantly important in judging the chaotic behavior of a dynamic system quantitatively. In a system of \(x_{n+1}=\text {F}(x_{n})\), \(\text {LE}\ge 0\) indicates the system is chaotic, \(\text {LE}<0\) shows the system is regular, which is shown as

$$\begin{aligned} \text {LE}=\mathop {\lim }\limits _{n \rightarrow \infty }\dfrac{1}{n}\ln \left| \mathop {\prod }\limits _{m=1}^{n}\text {F}^{'}(x_{m})\right| . \end{aligned}$$
(2)

For a higher-dimensional chaotic system, according to the order from large to small, it has multiple LEs shown as \( \left\{ \text {LE}_{1},\text {LE}_{2},\cdots ,\text {LE}_{n}\right\} \), where \(\text {LE}_{1}\) is the maximum LE (MLE).

2.3 Pseudo-randomness

For a floating number x, it exists the following important theoretical results, and Theorem 1 is decipted and proven in [36].

Theorem 1

For a random (or pseudo-random) distribution in [0, 1], assume that the density function has a bounded first-order derivative.For any sample \(x=0.w_1w_2\cdots w_{z-1} w_{z}\) (\(w_i \in \{0,1\}\) and \(i \in [1, z]\)) from this distribution, one has

$$\begin{aligned} \lim _{z \rightarrow \infty } P(w_{z}=0) = \lim _{z \rightarrow \infty } P(w_{z}=1). \end{aligned}$$
(3)

According to Theorem 1, it is clear that \(z \rightarrow +\infty \) indicates \(P(w_{z}=0)=P(w_{z}=1)=\dfrac{1}{2}\).

3 The performace analyses of the 3D CML model

3.1 Lyapunov exponent analysis

In this section, we mathematically derive the LE expression of the 3D CML model. According to the theoretical formula, the parameters are properly set and its LEs are calculated accurately for evaluating its chaotic performance, which makes sure the model in the most complicated chaotic state and avoids it in the synchronization state. The details of derivation are described in the appendix A.

Proof

See the appendix A. \(\square \)

According to the appendix A, it is easy to obtain the mathematical expression in LE of the 3D CML model, which is shown as

$$\begin{aligned} & \text {LE}\!=\!\text {LE}_{\text {F}}\!+\!\ln \left| 1\!-\!\varepsilon \right. \nonumber \\ & \left. +\!\dfrac{\varepsilon }{3}(\cos \dfrac{2 \pi k}{U}\!+\!\cos \dfrac{2 \pi r}{R}\!+\!\cos \dfrac{2 \pi l}{L})\right| , \end{aligned}$$
(4)

In Eq. (4), for \(k=0,1,\cdots ,U-1\), \(r=0,1,\cdots ,R-1\) and \(l=0,1,\cdots ,L-1\), it is evident that we can accurately calculate the LEs of the 3D CML model for different sizes and the coupling parameters. In addition, when \(k=0, r=0\) and \(l=0\), it is immediate that we can obtain Theorem 2 about MLE of the 3D CML model, which provides the theoretical foundation for engineering application.

Theorem 2

The maximum Lyapunov exponent (MLE) of the 3D CML model is solely determined by the local chaotic map.

Proof

For Eq. (4), satisfying \(k=0, r=0\) and \(l=0\), the MLE of the 3D CML model is calculated as

$$\begin{aligned} \begin{aligned} \text {LE}_{\text {MLE}}&=\text {LE}_{\text {F}}+\ln \left| 1-\varepsilon +\dfrac{\varepsilon }{3}(\cos 0+\cos 0+\cos 0)\right| \\&=\text {LE}_{\text {F}}. \end{aligned} \end{aligned}$$
(5)

\(\square \)

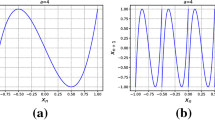
\(\text {LE}_{\text {MLE}}=\text {LE}_{\text {F}}\) implied Theorem 2 is correct, it provides theoretical guidelines for 3D CML’s application. For different parameters, one can easily calculate LEs, take the Logistic map \(x_{n+1}=4x_{n}(1-x_{n})\) as the local map, according to Theorem 2, it is clear that MLE of 3D CML is \(\ln ^{2}\). Furthermore, the Piece-Wise Logistic map (PLM) defined in Eq. (6) is an enhanced version of well-known Logistic map with much larger LE and more complex chaotic characteristics than the Logistic map [35].

$$\begin{aligned} \begin{aligned}&x_{m+1} = \text {PLM}(x_{m})\\&\quad = {\left\{ \begin{array}{ll} \mu N^{2} (x_{m}\!-\!\frac{i-1}{N})(\frac{i}{\!}-\!x_{m}),& \frac{i-1}{N} \!<\!x_{m}\!<\!\frac{i}{N},\\ \cdots \\ 1\!-\!N^{2}\mu (x_{m}\!-\!\frac{i-1}{N})(\frac{i+1}{N}\!-\!x_{m}),& \frac{i}{N}\!<\!x_{m}\!<\!\frac{i+1}{N},\\ \end{array}\right. } \end{aligned}\nonumber \\ \end{aligned}$$
(6)

where \(x_m\in (0,1)\) is the state value, \(\mu \in (0,4]\) is the control parameter, and N is the segment number of PLM. For comparison, PLM is selected as the local map, its MLE is 4.574594. When the 3D CML model is used for designing the chaos-based cryptography scheme, PLM is a better choice than the Logistic map. Consequently, for numerous of chaos-based cryptography schemes, Theorem 2 is a theoretical foundation for judging the chaotic dynamic behavior of the 3D CML model. Meanwhile, it is easy to get the following corollaries via Theorem 2.

Corollary 1

The MLE is independent of the size of the 3D CML model.

Corollary 2

In the 3D CML model, increasing LE of the local chaotic map \(\text {F}\) leads to an increase in the MLE of the model.

From the view of cryptography, the 3D CML model used in the encryption applications should own good chaotic performance. Corollaries 1 and 2 show that the local chaotic map is all-important for the 3D CML model, which directly determines its chaotic dynamic behavior. The larger the MLE of the local chaotic map is, the more complex the 3D CML model will be. Therefore, when designing those encryption schemes based on the 3D CML model, we should choose the local chaotic map \(\text {F}\) with a large MLE.

Here, to further verify those theoretical results, we select the classical Logistic map \(x_{n+1}=4x_{n}(1-x_{n})\) and PLM with \(\mu =4\) and \(N=64\) as the local map, denoted as L-3D CML and PLM-3D CML, respectively. Figure 2 illustrates the LEs of them via the simulation method and formula method. As can be seen from the figure, those simulation LEs and theoretical LEs are almost the same, which fully verifies the theoretical results in LE are correct.

Fig. 2
figure 2

LEs of the \(4\times 4\times 4\) 3D CML model with the Logistic map and PLM

Full size image
Fig. 3
figure 3

LE values of the 3D CML model with different parameters

Full size image

According to theoretical results, it is easy to get the different parameter changes on the chaotic behavior, since we can accurately compute the LE values via Eq. (4). Take PLM with \(\mu =4, N=64\) and Logistic with \(\mu =4\) as the local map for example, for PLM, set \(\varepsilon =0.1, U=R=L=4\); \(\varepsilon =0.8, U=R=L=4\); while in Logistics map, make \(\varepsilon =0.1, U=R=L=6\) and \(\varepsilon =0.8, U=R=L=6\). Calculate their LE values and show their LE values as following in Fig. 3. According to this figure, it is clear that the local map decides MLE of the 3D CML model, we choose the local map with larger LE. So, PLE is selected for display better chaotic performance. And also \(\varepsilon \) effect the other LE values, to demonstrate this point theoretically, take the derivative of Eq. (4) with respect to \(\varepsilon \),then \(\text {LE}^{'}\) is expressed as

$$\begin{aligned} \text {LE}^{'}=\frac{\cos \dfrac{2 \pi k}{U}+\cos \dfrac{2 \pi r}{R}+\cos \dfrac{2 \pi l}{L}-3}{3+\varepsilon (\cos \dfrac{2 \pi k}{U}+\cos \dfrac{2 \pi r}{R}+\cos \dfrac{2 \pi l}{L}-3)}.\nonumber \\ \end{aligned}$$
(7)

To select the coupling parameter \(\varepsilon \) with better chaotic property, we first consider the case that the denominator \(3+\varepsilon (\cos \dfrac{2 \pi k}{U}+\cos \dfrac{2 \pi r}{R}+\cos \dfrac{2 \pi l}{L}-3)\) of Eq. (7) is 0. In this case, \(k = r = l = 4\) and \(\varepsilon =0.5\), so \(\varepsilon =0.5\) should be avoided. We then investigate the value of \(\text {LE}'\) by enumerating all the possibilities of k, l and r. It turns out that when \(\varepsilon \in (0,0.5)\), \(\text {LE}' < 0 \) regardless the choices of k, l and r. And depending on specific choices of k, l and r, \(\text {LE}'\) can be either positive and negative for \(\varepsilon \in (0.5, 1)\). That said, the value of LE monotonically decreases for \(\varepsilon \in (0,0.5)\) and fluctuates for \(\varepsilon \in (0.5, 1)\) and smaller \(\varepsilon \) achieves better chaotic property.

To sum up, the mathematical formula of LE in the 3D CML model is essential for the application research in chaos cryptography, which guides the setting of parameters to remain the 3D CML model keep in a fully chaotic state.

3.2 Synchronization stability analysis

For the higher-dimensional chaotic system, the stability of periodic orbit and synchronization chaos are substantially more complicated than the simple chaotic system. From the standpoint of cryptography application, as appropriate parameter tuning is critical for applications based on chaotic systems, the parameter settings should ensure that the chaotic model keeps in a fully developed chaotic state with asynchronous.

In the 3D CML model, the indicator \(\{\text {LE}_{2},\cdots ,\text {LE}_{n}\}\) should be discussed, with \(\text {LE}_{2}>0\) meaning in an asynchronous state and \(\text {LE}_{2}<0\) meaning in a synchronous state. Thus, the theoretical investigation of the synchronization stability of the model is presented as follows:

To begin with, let \(k=R\), \(l=L-1\) and \(r=U\), according to Eq. (4), we can get the second maximum LE value \(\text {LE}_{2}\) as

$$\begin{aligned} \text {LE}_{2}=\text {LE}_{\text {F}}+\ln \left| 1-\varepsilon +\frac{\varepsilon }{3}\left( 2 +\cos \frac{2\pi (L-1)}{L}\right) \right| . \end{aligned}$$
(8)

Then, set \(\text {LE}_{2}=0\), the critical value of L is calculated as

$$\begin{aligned} L_{c} = \left\lfloor \dfrac{2\pi }{\arccos \frac{3e^{-\text {LE}_{\text {F}}}-3+\varepsilon }{\varepsilon }} \right\rfloor . \end{aligned}$$
(9)

Here, \(L_{c}\) represents the minimum number of nodes that can ensure the system keeps in an asynchronous state, i.e., \(L>L_{c}\) should be used to make \(\text {LE}_{2}>0\). According to Eq. (9), one can get the following theorem.

Theorem 3

In the 3D CML model, the critical value \(L_{c}\) of the synchronization stability is only related to \(\text {LE}_{\text {F}}\) and \(\varepsilon \).

Fig. 4
figure 4

The state values of the \(2\times 2\times 2\) L-3D CML

Full size image

For those chaos-based cryptographic schemes, according to Eq. (9) and Theorem 3, one can choose the suitable parameters and effectively avoid the chaotic iteration values appearing in the synchronous phenomenon in the 3D CML model, and it can guarantee the security of those chaos-based cryptographic schemes theoretically.

Fig. 5
figure 5

The state values of the \(2\times 2\times 4\) L-3D CML

Full size image
Fig. 6
figure 6

Bifurcation of the 3D CML model

Full size image

Furthermore, take the Logistic map and PLM as the local map to verify the synchronization stability. For the Logistic map, according to Eq. (9), set \(\varepsilon =0.9\), and \(L_{c} =2\) is obtained. So, initialize the 3D CML model with size \(2\times 2\times 2\). Then, iterate 3D CML for 100 times and 1000 times denoted as \(x_{100}^{u,v,w}\) and \(x_{1000}^{u,v,w}\), respectively. we plot them in Fig. 4. From this figure, we can observe the 3D CML model is not in a fully developed chaotic pattern. To make \(\text {LE}_{2}>0\), select the \(2\times 2\times 4\) 3D CML model, other parameters remain unchanged, simulation results are depicted in Fig. 5. As can be seen from the table, no stable synchronous chaos can be observed in the 3D CML model here. At the same time, based on Eq. (9), whatever the parameters are, PLM-3D CML is still in the asynchronous state.

This once again illustrates that PLM-3D CML model’s performance is better than L-3D CML model’s. With this consideration and to maintain a certain level of coupling effect, we take the empirical value \(\varepsilon = 0.1\) for 3D CML instantiated with PLM in the rest of this paper.

3.3 Bifurcation analysis

For the dynamic system, bifurcation intuitively displays the sudden change process near the critical point, it is used to effectively observe and analyze the dynamic behavior under different parameters. In the 3D CML model, choose PLM with \(\mu =4,N=64\) as the local map, set \(R=L=U=4\) and \(\varepsilon =0.1\). According to extensive experiments of all 64 nodes in the 3D CML model, it is observed that the bifurcation of all the nodes is basically the same, so, take the first node as an example for analyzing the bifurcation. The results are shown in Fig. 6. From the figure, it can be seen that the change of \(\varepsilon \) has a significant impact on the bifurcation of the model, with the increasing of \(\varepsilon \), bifurcation becomes more and more sufficient. When \(\mu =4\), LE of PLM is maximum, and bifurcation of the 3D CML is the most comprehensive. Therefore, when \(\mu =4\), chaotic dynamics behavior is the most complex, and cryptography applications have the best performance.

Fig. 7
figure 7

Ergodicity of the 3D CML model with different parameters \(\mu \)

Full size image

3.4 Ergodicity analysis

Ergodicity is that chaotic motion orbit would pass through the state point in the phase space in the finite time. It is closely related to randomness, the wider ergodicity indicates its randomness is difficult to predict. So, selecting a chaotic system with a wider and more uniform traversal interval is a better choice for designing kinds of chaos-based cryptography systems.

In the 3D CML model, choose PLM with \(N=64\) as the local map, and set \(R=L=U=4\) and \(\varepsilon =0.1\). For different \(\mu \) with 0.1, 0.5, 1.0,1.5,2.0,3.0, 3.5, and 4.0, respectively, the interval is shown in Fig. 7. According to the figure, it is clear that the traversal interval becomes much wider along the change of \(\mu \). When \(\mu =0.1\), the interval lies in [0, 0.1] and [0.9, 0.1], when \(\mu =2\), the interval is [0, 1], and most of values are mainly concentrated in [0.4, 0.6], when \(\mu =4\), the state values of the 3D CML model are uniformly distributed throughout the traversal interval [0, 1]. At this point, the chaotic performance of model is best, and the randomness and uniformity of chaotic sequences are also perfect.

3.5 PDD analysis

PDD describes the probability and distribution of the output values of a random variable in a certain region. From the view of cryptography, when using a chaotic system as the core component of designing a cryptographic algorithm, the more uniform PDD of chaotic sequences means stronger security of the algorithm. In this section, choose PLM with \(N=64\) and \(\mu =0.1\) as the local map, and set \(R=L=U=4\) and \(\varepsilon =0.1\). Then, generate the 3D CML model for multiple iterations and count the distribution of chaotic sequences in intervals [0, 1], the details are shown in algorithm 1. The results of algorithm 1 are plotted in Fig. 8, and it is clear that PDD of 3D CML is uneven.

Algorithm 1
figure a

PDD of PLM-3D CML

Full size image

3.6 Comparative analysis

To verify the 3D CML model has better chaotic performance than 1D CML and 2D CML, we do the following analyses.

Kolmogorov entropy is an important index to depict the chaotic behavior of a dynamic system, it is calculated as Eq. (10). According to Eq. (10), it is clear that the K is the sum of all positive LEs. The larger the value of K is, the more complex the dynamic behavior becomes.

$$\begin{aligned} K=\lim _{\text {LE}_{n}>0}\text {LE}_{n}. \end{aligned}$$
(10)

Kolmogorov entropy values of the 64 1D CML, the \(8\times 8\) 2D CML and the \(4\times 4\times 4\) 3D CML are calculated as \(K_{1}=41.03428\), \(K_{2}=41.05647\) and \(K_{3}=41.06386\), respectively, it is easy to get

$$\begin{aligned} K_{3}>K_{2}>K_{1}. \end{aligned}$$

For the same 64 nodes in different CML models (i.e.1D CML, 2D CML and 3D CML), the 3D CML model owns the highest information loss rate, which indicates the 3D CML model holds the best chaotic performance.

Considering the synchronization stability of 1D CML, 2D CML and 3D CML, selecting the Logistic map \(x_{n+1}=4x_n(1-x_n)\) as the local map. According to the corresponding equations in [8], \(\text {LE}_{\text {F}}=\text {ln}^2\), it is easy to calculate the critical node number \(L_{c}\), those values of \(L_{c}\) are shown in Table 1. According to this table, it is clear that those three models can appear the synchronization under certain conditions. When \(\varepsilon = 0.5, 0.8, 0.9\) and 0.999999999, those three model appear the synchronization state. For instance, \(L_{c}\) of 1D CML, 2D CML and 3D CML are 7, 2 and 2, respectively, in this case, 1D CML and 2D CML appear synchronization state, but 3D CML don’t. Consequently, 1D CML and 2D CML are more likely in the synchronization state for the same parameters. Above all, it demonstrates the 3D CML model has better chaotic performance than others.

Fig. 8
figure 8

PDD of the 3D CML model

Full size image
Table 1 Critical node number of the 3D CML model with synchronization
Full size table

4 The proposed PRNG scheme

According to the above-mentioned analysis, the 3D CML model possesses remarkable chaotic performance. So, it is taken as a core component for constructing the PRNG scheme, the details are depicted in algorithm 2 and summarized in the following steps.

\({\textbf {Step 1}}\): Set \(R=L=U=4,\varepsilon =0.1\) in the 3D CML and select PLM with \(\mu =4,N=64\) as the local map. Iterate the model 1000 times and then give up to eliminate the influence of the initial values.

\({\textbf {Step 2}}\): Continue to iterate the model and obtain the z floating number for one iteration. For each number \(x_{k}\),\(k\in [1,z]\), it can be transformed into

$$\begin{aligned} x_{k}=0.w_{1}w_{2}\cdots w_{z-1}w_{z}, w_{z}\in \{0,1\}. \end{aligned}$$
(11)

\({\textbf {Step 3}}\): The pseudo-randomness chaotic sequences w with \((z-s+1)\)-bit can be intercepted via the following equation.

$$\begin{aligned} w=w_{s}w_{s+1}\cdots w_{z-1}w_{z}. \end{aligned}$$
(12)
Algorithm 2
figure b

Our proposed PRNG scheme

Full size image

Here, one can select \(z=64\) and \(s=33\), in order to further reducing computational complexity or memory usage, we perform algorithm optimization measure. For each \(x^{i}\), we do the operation of extracting bits firstly, then, itarate the model, this can effectively reduce memory space. Its pseudocode is shown as in algorithm 3, which is parameterized based on algorithm 2. According to this algorithm, clearly, for one iteration of model, 2048-bit sequences are generated, then, for n times, 2048n-bit sequences are obtained. The performance analyses of our proposed PRNG scheme are shown in the following section.

Algorithm 3
figure c

Our proposed PRNG scheme for parameter concretization

Full size image

5 Performance analysis of the proposed PRNG

According to the above-mentioned analyses, those theoretical results in LE and synchronization stability provide the critical theoretical foundation for chaos cryptography. To further verify those theoretical results, and also test the performance of the pseudo-random number generator, we have carried out the following experimental simulations.

Fig. 9
figure 9

The diagram of NIST testing in algorithm 3

Full size image

5.1 The advantage of our scheme

Our proposed PRNG scheme based on the 3D CML model has those following highlights.

  1. 1.

    The 3D CML model, as a higher-dimensional chaotic model, has pretty chaotic dynamic behavior. Considering the 3D CML model as the core component, it can greatly improve the security of our scheme. And also, mathematical expression of LE and synchronization stability are given, it provides important theoretical guidelines for ensuring the model in the fully developed chaotic state of cryptographic application.

  2. 2.

    In our scheme, 32-bit sequences are directly obtained by intercepting the state value, no additional computational operations are required. One iteration of the model can generate 2048-bit, and it can greatly improve the efficiency of our scheme.

  3. 3.

    Our scheme is designed according to Theorm 1, its uniformity is theoretically guaranteed. Meanwhile, one can ensure the 3D CML model possesses best performance theoretically.

5.2 Randomness tests

The statistical test package STS launched by NIST is currently the most authoritative tool for testing the pseudo-random sequences, and it contains 15 items. For each item, there exists P-\(\text {Value}\) for measuring whether the sequences can pass the random testing successfully. Suppose P- \(\text {Value} \ge \alpha \), it indicates the testing sequences pass the random testing successfully. Otherwise, it fails the random testing.

In our testing simulation, according to the algorithm 3, for each iteration of our algorithm, 2048-bit random sequences are obtained. For NIST testing, the dataset with 1 000 000 000 bit sequences is required. So, iterate algorithm 3 for 62036 times to have 1 000 000 000 bit sequences, the details are shown in Fig. 9. Moreover, set \(\alpha =0.01\) and test 1000 pairs with each length of 1000 000 bit, the NIST test results are listed in Table 2. According to Table 2, it is clear that all the \(\text {{ P}-Value}\) are greater than 0.01, the minimum pass rate and the maximum pass rate are 0.9863 and 0.9936, respectively. We can get all the pass rates in an acceptable interval. The testing results of \(\text {{ P}-Value}\) and pass rates show that all the chaotic sequences produced by the 3D CML model possess perfect random characteristics.

TestU01 test is a statistical random testing tool, offering a collection of utilities for the uniform random number generators. We have unitized the 3D CML model to produce the chaotic sequences with length of \(2^{20}\),\(2^{25}\) and \(2^{30}\), respectively. Considering the three indexes of Rabbit test, Alphabit test, and BlockAlphabit test, we test the chaotic sequences and show the testing results in Table 3. According to Table 3, the different chaotic sequences can all pass the TestU01 test successfully. The TestU01 test verifies that the chaotic sequences have excellent randomness.

Table 2 NIST 800-22 test results on the chaotic sequences of our proposed PRNG scheme
Full size table

Above all, the above-mentioned testing of NIST and TestU01 test both prove that the chaotic sequences have outstanding random performance and those sequences are proper for being applied as the core model in the cryptography system.

5.3 Correlation tests

Correlation coefficient is an indicator that measures the degree of linear relationship between two sequences, its interval is \([-1,1]\). The closer the value is to 0, the independence between these two sequences is much stronger. When it is equal to 0, two sequences are independent. When in the interval \((-0.3,0.3)\), it demonstrates those two sequences are independent. Correlation coefficient can be calculated as

$$\begin{aligned} & cov(x,y)=E(x-E(x))(y-E(y)), \end{aligned}$$
(13)
$$\begin{aligned} & r_{xy}=\frac{cov(x,y)}{\sqrt{D(x)}\sqrt{D(y)}}, \end{aligned}$$
(14)

where x and y are two sequences with the length of l, \(E(x)=\sum \nolimits _{i=1}^{l}\dfrac{x_{i}}{l}\), \(D(x)=\sum \nolimits _{i=1}^{l}\dfrac{(x_{i}-E(x))^2}{l}\), \(x_{i}\) and \(y_{j}\) are the \(i^{th}\) and \(j^{th}\) element of x and y, respectively.

In our test, select PLM with \(N=64\) and \(\mu =4\) as the local map. For the 3D CML model, choose \(\varepsilon =0.1\) and \(R=L=U=4\), according to our proposed PRNG scheme, set 1000 initial value vectors randomly, 1000 different sets of chaotic sequences with 66000-bit are generated, then utilize those 1000 different sets and calculate the correlation coefficient value \(r_{xy}\), the values are shown in the Fig. 10. According to the figure, it can be seen that \(r_{xy}\) lies in the interval \((-0.02,0.02)\), which fully indicates that those chaotic sequences are mutually independent.

5.4 Key space

From a security perspective, key space must be large enough to effectively resist violent attacks. In our proposed scheme, initial all 64 nodes of the 3D CML as \(X(0,0,0),X(0,1,0), \cdots ,X(3,3,3)\), and all those nodes are taken as the secret key. According to the IEEE 754 standard, a 64-bit floating-point precision degree is \(10^{-15}\), and each node of the \(4\times 4\times 4\) 3D CML model has \(10^{15}\) key space, 64 nodes totally own \(10^{15\times 64}=10^{960}\). Therefore, the time of cracking the key space is calculated as

$$\begin{aligned} 10^{960}/(2^{168}\times 5.9 \times 10^{30})=2.7\times 10^{953} year. \end{aligned}$$
(15)

The time of cracking the key space \(10^{960}\) is \(10^{953}\) year, it can effectively resist violent attack, and also verifies our proposed algorithm is pretty secure.

5.5 Key sensitivity

Key sensitivity is a considerable indicator for measuring the security of encryption algorithm, it measures the change in output ciphertext through small changes in initial parameters, so, set the following two situations:

  • Case 1: \(\varepsilon =0.1,\mu =4,x_{0}=0.7639248273644901\);

  • Case 2: \(\varepsilon =0.1,\mu =4,x_{0}=0.7639248373644901\).

According to the above-mentioned two cases, two different chaotic sequences are produced to encrypt the same image Airplane, adopt the XOR operation between 8-bit chaotic sequences and image grayscale values. The encrypted images are described as in Figs. 11b, c, differences of those encrypted images are shown in Fig. 11d, its value is 0.9961. Meanwhile, count the histograms of these two encrypted images, the results are depicted in Figs. 11f, g, it is clear that the histogram is uneven. It demonstrates that the 3D CML model possesses strong key sensitivity.

5.6 Differential attack analysis

When adversaries perform differential attack on the encryption algorithm, according to minor adjustments of the plaintext, then, compare the difference between the original plaintext ciphertext and the slightly adjusted plaintext ciphertext. In the 3D CML model, make small changes and verify the algorithm’s resistance to differential attack. The key parameters are set in the following four cases:

  • Case 1: \(\varepsilon =0.1,\mu =4,x_{0}=0.7639248273644901\);

  • Case 2: \(\varepsilon =0.1,\mu =4+\Delta t,x_{0}=0.7639248273644901\);

  • Case 3: \(\varepsilon =0.1,\mu =4,x_{0}=0.7639248273644901+\Delta t\);

  • Case 4: \(\varepsilon =0.1+\Delta t,\mu =4,x_{0}=0.7639248273644901\);

where \(\Delta t = 2^{-20}\). According to the above-mentioned cases, generate four pairs of chaotic sequence \(S_{1},S_{2},S_{3},S_{4}\) with 10000000-bit. Then, compute average absolute distance d of sequences \((S_{1},S_{2})\),\((S_{1},S_{3})\) and \((S_{1},S_{4})\) via the following Eq. (16).

$$\begin{aligned} d=\frac{1}{M}\sum _{i=1}^{M}\left| e_{i}-e_{i}^{'} \right| , \end{aligned}$$
(16)

where \(e_{i}\) and \(e_{i}^{'}\) are the original sequence and the new sequence, respectively. The ideal value of average absolute distance d is 85.333. According to Eq. (16), the results are depicted in the Table 4. From this table, it is clear that all the values are near 85.333, and it fully demonstrates that our proposed scheme owns strong resistance to differential attacks.

Table 3 TestU01 test results on the chaotic sequences of our proposed PRNG scheme
Full size table
Fig. 10
figure 10

Correlation coefficient values

Full size image
Fig. 11
figure 11

The results of Airplane and the encrypted Airplane a Airplane; b The encrytped Airplane with Case 1; c The encrytped Airplane with Case 2;  d The different image of Case 1 and Case 2; e The histogram result of Airplane; f The histogram result of encrytped Airplane with Case 1; g The histogram result of encrytped Airplane with Case 2

Full size image

5.7 Balanced analysis

We have plotted the number of 1 s with respect to different lengths of our PRNG outputs,shown in Fig. 12. According to this figure, it is easy to see that the bit sequences generated by our scheme have an approximately equal number of 0 s and 1 s, and almost coincide with the ideal line \(y=\dfrac{n}{2}\). This indicates that our PRNG scheme has good balanced performance.

5.8 Periodicity analysis

PRNGs are necessarily periodic, which is a serious problem when the generation of random numbers is in question. For that reason, cycles of PRNGs should have great length in order to enable the smooth functioning for a long period of time. Some of the previous chaos-based PRNGs were evaluated on the basis of non-periodicity, but on a relatively small amount of data (less than \(2^{40}\) bits). However, none of these PRNGs have estimated cycle length.

Period of sequence in our proposed PRNG scheme is \(2^{128}\), while the classical period of PRNG scheme is \(2^{40}\). Consequently, our proposed PRNG scheme has sufficient length.

5.9 Entropy analysis

The entropy is an key indicator for measuring state’s uncertainty. If an n-bit number sequence has a good disorder, it will be considerd as a random one. A good PRNG should generate unexpected sequence with high disorder. So, we use Eq. (17) to determine those properties of our PRNG scheme.

$$\begin{aligned} E_{m} = \sum _{i=0}^{2^{N}-1} p(m_{i})\log _{b} \frac{1}{p(m_{i})}, \end{aligned}$$
(17)

where N is the number of bits in each element of the sequence m, \(p(m_{i})\) is the chance that the element \(m_{i}\) will appear in the sequence, \(E_{m}\) is the entropy value, and b represents the radix value.

To fully verify the entropy value of our PRNG scheme, take the radix \(b=2\) and \(b=8\) for example, according to Eq. (17), we can caculate entropy values of our PRNG scheme, the results are plotted in Figs. 13 and 14. From those figures, we can see the numerical results are very close to the ideal value. It indicates that the generated binary sequences of our PRNG scheme have high complexity.

Table 4 The average absolute of chaotic sequences
Full size table
Fig. 12
figure 12

The ratio of 0/1 in the random sequences generated by our PRNG scheme

Full size image
Fig. 13
figure 13

Entropy values with radix=2

Full size image
Fig. 14
figure 14

Entropy values with radix=8

Full size image

5.10 Efficiency analysis

To further assess the performance of our proposed PRNG algorithm, it is evaluated through comparing with other chaotic PRNGs [1, 10, 17, 19, 36]. The methods in [1] and [19] are more recent heuristic proposals based on enhancing simple chaotic systems and using CML, respectively. By enhancing 1D chaotic systems, the work in [10] is a famous heuristic PRNG design due to its simplicity and thorough experimental evaluation. It is noted that the design in [17] is the only previously known method that provides theoretically guaranteed uniform randomness from chaotic systems. For the 2D CML mode used for PRNG in [36]. For PRNGs in [1, 10, 17, 19, 36], the same settings of the original works are used. All the algorithms are then implemented on a Laptop with the Core i7-10710U CPU and 16 G RAM.

Table 5 lists the running speed (averaged from 1, 000 tests) for generating 1 MByte binary stream from all these methods. With a running speed of 23.85 MByte/s, the proposed method is more efficient than the other theoretical sound RPNGs [17] and [36], and is also more efficient than the heuristic designs [1] (with running speed 0.3338 MByte/s), [13] (with running speed 22.84 MByte/s), [19] (with running speed 17.24 MByte/s) and [35] (with running speed 22.16 MByte/s), but inferior to the method in [10] (with running speed 62.50 MByte/s). However, looking further at the third and fourth column of Table 5, it is clear that the proposed method provides theoretical randomness guarantee while the method in [10] does not.

Table 5 Running speed comparison
Full size table
Table 6 Number of basic operations in schemes for generating 8-bit
Full size table
Table 7 Analysis of our PRNGs in comparison to other existing schemes
Full size table

To further verify the efficiency of our proposed scheme, other similar classical schemes are used to compare with ours. Basic operations for generating 8-bit are counted and presented in Table 6. According to this table, our scheme requires 27 basic operations. While basic operations of other schemes in [1, 6, 10, 13, 17, 19, 24, 35, 36] are 27 basic operations, 1628 basic operations, 24.88 basic operations, 13.33 basic operations, 35.13 basic operations, 40 basic operations, 42 basic operations, 18 basic operations, 56 basic operations and 51.50 basic operations, repectively. Therefore, our scheme possesses a significant advantage in efficiency, also with theoretical analysis and experimental analysis to make sure its security.

5.11 Comparison analysis

Some chaos-based PRNGs are currently being proposed in the cryptographic field. Even though those schemes can pass some randomness analysis such as NIST testing, some or no security analysis have been mentioned in those schemes. PRNG is an core component of constructing the cyrptographic scheme, a thorough security analysis should be carried out to show its good performance. So, we perform the cpmparison analysis of our scheme with others in [5, 22, 29, 38, 39].

The comparison results are shown in Table 7,this table shows the investigated aspects of several PRNGs. According to this table, it is clear that our proposed scheme has been tested the most. In addition, note that this linear complexity test is just the frequency sub-test of NIST SP800-22, where 1000 binary sequences with length \(10^{6}\)-bit (produced by our PRNG) have been already tested extensively with results summarized in Table 2.

6 Promotion of the 3D CML model

According to the performance analyses of the 3D CML model in section 3, it is well known as a higher-dimensional chaotic for constructing numerous cryptographic schemes. With the increasing demand for security, and also in order to apply to more application scenarios in the future, the 3D CML model can be extended into the ND CML one, which is shown in definition 2.

Definition 2

The N-dimensional CML model is defined as

$$\begin{aligned} \begin{aligned}&x_{n+1}^{l_{1},l_{2},\cdots ,l_{N-1},l_{N}}=(1-\varepsilon )\text {F}(x_{n}^{l_{1},l_{2},\cdots ,l_{N-1},l_{N}})\\&+\frac{\varepsilon }{2N}\left[ \text {F}(x_{n}^{l_{1}+1,l_{2},\cdots ,l_{N-1},l_{N}})+\text {F}(x_{n}^{l_{1}-1,l_{2},\cdots ,l_{N-1},l_{N}})\right. \\&\left. +\text {F}(x_{n}^{l_{1},l_{2}+1,\cdots ,l_{N-1},l_{N}})+\text {F}(x_{n}^{l_{1},l_{2}-1,\cdots ,l_{N-1},l_{N}})\right. \\&\left. +\cdots +\text {F}(x_{n}^{l_{1},l_{2},\cdots ,l_{N-1}+1,l_{N}})+\text {F}(x_{n}^{l_{1},l_{2},\cdots ,l_{N-1}-1,l_{N}})\right. \\&\left. +\text {F}(x_{n}^{l_{1},l_{2},\cdots ,l_{N-1},l_{N}+1})+\text {F}(x_{n}^{l_{1},l_{2},\cdots ,l_{N-1},l_{N}-1})\right] . \end{aligned} \end{aligned}$$
(18)

where \(l_{1}=1,2,\cdots ,L_{1}\), \(l_{2}=1,2,\cdots ,L_{2}\), \(\cdots \), \(l_{N-1}=1,2,\cdots ,L_{N-1}\) and \(l_{N}=1,2,\cdots ,L_{N}\) are the indexes of all the nodes, respectively.

According to LE results of the 3D CML model, the significant theoretical results for LE can be conjectured as the following equation.

$$\begin{aligned} \begin{aligned} \text {LE}=&\text {LE}_{\text {F}}+\ln \left| 1-\varepsilon +\dfrac{\varepsilon }{N}(\cos \dfrac{2 \pi k_{1}}{L_{1}}+\cos \dfrac{2 \pi k_{2}}{L_{2}}\right. \\&\left. +\cdots +\cos \dfrac{2 \pi k_{N-1}}{L_{N-1}}+\cos \dfrac{2 \pi k_{N}}{L_{N}})\right| . \end{aligned} \end{aligned}$$
(19)

To veridate the conclusion of Eq. (19) is correct, the details are represented as in the following proof.

Proof

See the appendix B. \(\square \)

According to the appendix B, it is clear Eq. (19) is correct, we can get the following important theorem.

Theorem 4

The maximum Lyapunov exponent (MLE) of the ND CML model is solely determined by the local chaotic map.

Proof

For Eq. (19), satisfying \(k_{1}=0, k_{2}=0,\cdots ,k_{N-1}=0,k_{N}=0\), the MLE of the ND CML model is calculated as

$$\begin{aligned} \begin{aligned} \text {LE}_{\text {MLE}}&=\text {LE}_{\text {F}}+\ln \left| 1-\varepsilon +\dfrac{\varepsilon }{N}(\cos 0+\cos 0\right. \\&\left. +\cdots +\cos 0+\cos 0\right| ,\\&=\text {LE}_{\text {F}}. \end{aligned} \end{aligned}$$
(20)

\(\square \)

This important conclusion for LE in the ND CML model is obtained according to the process of 3D CML model, the LE values of the ND CML model can be calculated accurately, the model parameters would be set reasonably to keep the model in the fully chaotic state. Furthermore, the dynamic performance of the ND CML model is related to the security of chaotic-based cyrptographic schemes. Therefore, it is greatly beneficial to the application of the ND CML model.

7 Conclusion

The 3D CML model, as a higher-dimensional chaotic system, owns some special chaotic dynamic behavior, as well as more complicated peformance than 1D CML and 2D CML. Its mathematical expression of LE is derived, which is significantly used to set the parameters of 3D CML and ensure the model is in a fully chaotic state. Meanwhile, the synchronization stability expression of the 3D CML is given, this devotes itself to the suitable parameters for avoiding the synchronous state. The LE and synchronization stability analyses in the 3D CML model give new insights, as well as provide a theoretical foundation in cryptographic application. Based on those theoretical results, our PRNG scheme is designed, the simulation demonstrates our scheme possesses outstanding performance. In our scheme, massive bits are produced efficiently, it is suitable for lightwight devices. In fact, in scenarios where security requirements are not too high, the 3D CML model with the local Logistic map is a good choice, since Logistic map is faster than PLM, but the security is lower than PLM’s. In the future, the cryptographic application of the 3D CML model with different local map will be the focus area via scenarios with different levels of security, especially, for the chaos-based encryption schemes of massive images. Furthermore, the 3D CML model is extended into a ND CML one, its LE expression is obtained, it is substantial helpful for theoretical research and application development of the higher-dimensional model.