1 Introduction

Nonlinear evolution equations (NLEEs) have been proposed in such fields as fluid mechanics, plasma physics, fiber optics and ocean dynamics, and analytic solutions for the NLEEs such as the solitons, lumps and breathers have received people’s attention [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Solitons have been seen to maintain their shapes and velocities unchanged during the propagation [19,20,21,22,23,24,25,26]. Lumps have been considered as the waves localized in all directions in the space [27,28,29]. Breathers, localized waves with oscillatory patterns, have been classified as three types, namely the Akhmediev breathers, Kuznetsov-Ma breathers and Peregrine solitons [30,31,32,33,34,35,36]. Interactions among those nonlinear waves have attracted the researchers’ attention [37,38,39].

Refs. [40, 41] have considered the (2 + 1)-dimensional generalized Konopelchenko–Dubrovsky–Kaup–Kupershmidt equation for certain nonlinear phenomena in fluid mechanics, which reads

$$\begin{aligned} \begin{aligned} u_{t}&+h_1u_{xxx}+h_2uu_{x}+h_3u_{xxxxx}+h_4\partial _{x}^{-1}u_{yy}\\&+h_5u_{xxy}+h_6(u_{x}\partial _{x}^{-1}u_{y}+uu_{y})+h_7(u_{x}u_{xx}\\&+uu_{xxx})+h_8u^2u_{x}=0, \end{aligned} \end{aligned}$$
(1)

where \(u=u(x,y,t)\) is the amplitude of the relevant wave, x and y are the running coordinates, t is the time, the subscripts represent the partial derivatives, \(\partial _{x}^{-1}\) represents the integral with respect to x, and the coefficients \(h_{\ell }\)’s (\(\ell \) = 1,2,...,8) are the real constants. Some special cases of Eq. (1) in fluid mechanics and plasma physics have been seen as follows:

  • When \(h_1=0,h_2=0,h_3=1,h_4=-5,h_5=-5,h_6=-15,h_7=15,h_8=45\), Eq. (1) has been reduced to the (2 + 1)-dimensional B-type Kadomtsev–Petviashvili equation which describes the shallow water waves in a fluid or electrostatic wave potential in a plasma, where u is a wave amplitude function of the scaled space coordinates x, y and time coordinate t [42,43,44,45,46,47].

  • When \(h_2=6h_1,\ h_6=4h_5,\ h_3=h_4=h_7=h_8=0\), Eq. (1) has been degenerated to the (2 + 1)-dimensional generalized breaking soliton equation which describes the interaction of a Riemann wave propagating along the y axis and a long wave propagating along the x axis, where u represents the amplitude or elevation of the Riemann wave [48,49,50].

  • When \(h_3=1,\ h_7=15,\ h_8=45,\ h_1=h_2=h_4=h_5=h_6=0\) and u is independent of y, Eq. (1) has been reduced to the fifth-order Sawada-Kotera equation which describes the long waves in the shallow water under the gravity and in a one-dimensional nonlinear lattice [51,52,53,54,55].

N-soliton solutions of Eq. (1) have been obtained via the Hirota bilinear method, where N is a positive integer, and periodic-wave solutions of Eq. (1) have also been constructed via the Riemann theta function [40]. Lump, lumpoff and rogue wave solutions for Eq. (1) have been derived [41].

However, to our knowledge, Eq. (1) is still worthy of further study. Firstly, the higher-order lump solutions of Eq. (1) have not been reported, and interaction between the lumps has not been investigated. Secondly, breather solutions of Eq. (1) have not been obtained. Thirdly, although Ref. [41] has obtained the lumpoff solutions of Eq. (1) which describe the inelastic interaction between the lumps and one solitons, elastic interactions there have not been investigated, between the first-order breathers and one solitons, the first-order lumps and one solitons, as well as the first-order breathers and first-order lumps. Motivated by those, we will present this paper.

Through the dependent variable transformation [40],

$$\begin{aligned} \begin{aligned} u=12h_1{h_2}^{-1}(\mathrm{ln}f)_{xx}, \end{aligned} \end{aligned}$$
(2)

Eq. (1) has been transformed into the following bilinear equation [40]:

$$\begin{aligned} \begin{aligned}&(D_{x}D_{t}+h_1D_{x}^{4}+h_3D_{x}^6+h_{4}D_{y}^{2}\\&\quad +h_{5}D_{x}^{3}D_{y})f\cdot f=0, \end{aligned} \end{aligned}$$
(3)

where \(2h_1h_2^{-1}=5h_{3}h_{7}^{-1}=h_{5}h_{6}^{-1}=h_{7}h_{8}^{-1},\ 5h_3h_4=-h_5^2\), \(f=f(x,y,t)\) is a real function, and D is the Hirota’s bilinear differential operator defined as [56]

$$\begin{aligned} \begin{aligned}&D_{x}^{m_{1}}D_{y}^{m_{2}}D_{t}^{m_{3}}f(x,y,t)\cdot g(x,y,t)\\&=\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^{m_{1}} \left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\right) ^{m_{2}} \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\right) ^{m_{3}}\\&\qquad \qquad \qquad \qquad f(x,y,t)g(x',y',t')|_{x=x',y=y',t=t'}, \end{aligned} \end{aligned}$$
(4)

with \(g(x',y',t')\) being a function of the formal variables \(x',y'\) and \(t'\), while \(m_1,m_2\) and \(m_3\) being the nonnegative integers. N-soliton solutions for Eq. (1) have been expressed as Expression (2) [40] with

$$\begin{aligned}&f=\sum _{\mu =0,1} \mathrm{exp}\left( \sum _{i=1}^{N}\mu _{i}\eta _{i}+\sum _{i<j}^{N}\mu _{i}\mu _{j}A_{ij}\right) ,\nonumber \\&\eta _{i}=p_{i}x+k_{i}y+\omega _{i}t+\phi _{i},\ (i=1,2,\ldots ,N)\nonumber \\&\omega _{i}=-h_1p_{i}^3-h_3p_{i}^5-h_5p_{i}^2k_{i}-h_4p_{i}^{-1}k_{i}^2,\nonumber \\&e^{A_{ij}}=-\frac{R_{ij}}{S_{ij}},\ (i<j,\ j=2,3,\ldots ,N)\nonumber \\&R_{ij}=h_3(p_{i}-p_{j})^6+h_1(p_{i}-p_{j})^4+h_4(k_{i}-k_{j})^2\nonumber \\&\ \ \ \ \ \ \ +(p_{i}-p_{j})(\omega _{i}-\omega _{j})+h_5(p_{i}-p_{j})^3(k_{i}-k_{j}),\nonumber \\&S_{ij}=h_3(p_{i}+p_{j})^6+h_1(p_{i}+p_{j})^4+h_4(k_{i}+k_{j})^2\nonumber \\&\ \ \ \ \ \ \ +(p_{i}+p_{j})(\omega _{i}+\omega _{j})+h_5(p_{i}+p_{j})^3(k_{i}+k_{j}), \end{aligned}$$
(5)

where \(p_{i}\)’s, \(k_{i}\)’s and \(\phi _{i}\)’s are the complex constants, \(\sum _{\mu =0,1}\) denotes a summation over all the possible combinations of \(\mu _{1}=0,1,\ \mu _{2}=0,1,\ldots ,\ \mu _{N}=0,1\), and the notation \(\sum _{i<j}^{N}\) indicates a summation over all the possible pairs (i, j) chosen from the set \(\{1,2,\ldots ,N\}\), with the condition \(i<j\).

To sum up, this paper will investigate the higher-order lump, breather and hybrid solutions for Eq. (1), and study the effects of \(h_{1},\ h_2,\ h_4\) and \(h_5\) on those solutions. In Sect. 2, employing the long-wave limit method [57, 58], we will construct the Lth-order lump solutions, where L is a positive integer, and analyze the effects of \(h_{1},\ h_2,\ h_4\) and \(h_5\) on the velocities and amplitudes of the first-order lumps. We will graphically discuss the interaction between the two first-order lumps, and the effects of \(h_2\) and \(h_4\) on the first-order lumps. In Sect. 3, we will construct the Mth-order breathers, where M is a positive integer. Effects of \(h_1\) and \(h_2\) on the second-order breathers will be discussed. Interaction between the two first-order breather waves will be graphically presented. In Sect. 4, hybrid solutions composed of the first-order breathers and one solitons, the first-order lumps and one solitons, as well as the first-order lumps and first-order breathers will be obtained. Elastic interactions of those three kinds of hybrid solutions will be graphically illustrated. We will also discuss the effects of the coefficients on those hybrid solutions. In Sect. 5, we will give our conclusions.

2 The higher-order lump solutions for Eq. (1)

In this part, we will construct the Lth-order lumps via the long-wave limit of the N-soliton solutions for Eq. (1).

To construct the Lth-order lumps for Eq. (1), setting

$$\begin{aligned} \begin{aligned} \phi _{i}=I\pi ,\ p_{i}=\sigma P_{i},\ k_{i}=\sigma K_{i},\ N=2L, \end{aligned} \end{aligned}$$
(6)

and then taking \(\sigma \rightarrow 0\), we can generalize the Lth-order lumps from Solutions (2) and (5) as

$$\begin{aligned} \begin{aligned} u=12h_1{h_2}^{-1}(\mathrm{ln}f)_{xx}, \end{aligned} \end{aligned}$$
(7)

where \(I=\sqrt{-1}\), \(\sigma \) is a real constant, \(P_{i}\)’s and \(K_{i}\)’s are the complex constants,

$$\begin{aligned}&f=\prod _{i=1}^{2L}\theta _{i}+ \frac{1}{2}\sum _{i,j}^{2L}B_{ij}\prod _{\Gamma \ne i,j}^{2L}\theta _{\Gamma }+\cdots + \frac{1}{L! 2^{L}}\nonumber \\&\quad \times \sum _{i,j,\ldots ,\kappa ,\upsilon }^{2L} \overbrace{B_{ij}B_{rs}\ldots B_{\kappa \upsilon }}^{L}\prod _{\Upsilon \ne i,j,\ldots ,\kappa ,\upsilon }^{2L}\theta _{\Upsilon }+\cdots ,\nonumber \\&\theta _{i}=P_{i} x+K_{i} y-h_4\frac{K_{i}^2}{P_{i}}t,\nonumber \\&B_{ij}=\frac{6P_{i}^2P_{j}^2\left[ 2h_1P_{i}P_{j}+h_5(P_{j}K_{i}+P_{i}K_{j})\right] }{h_4(P_{j}K_{i}-P_{i}K_{j})^2}, \end{aligned}$$
(8)

\(\sum _{i,j,\ldots ,\kappa ,\upsilon }^{2L}\) means the summation over all the possible combinations of \(i,j,\ldots ,\kappa ,\upsilon \), which are taken from \(1,2,\ldots ,2L\) and are all different from each other.

To obtain the nonsingular solutions, we set

$$\begin{aligned} \begin{aligned} P_{r}&=P_{L+r}^{*}=P_{r1}+I P_{r2},\\ K_{r}&=K_{L+r}^{*}=K_{r1}+I K_{r2},\ (r=1,2,\ldots ,L) \end{aligned} \end{aligned}$$
(9)

and substitute Eqs. (9) into Eqs. (7) and (8), where the superscript \(*\) represents the complex conjugation, \(P_{r1}\)’s, \(P_{r2}\)’s, \(K_{r1}\)’s and \(K_{r2}\)’s are the real constants. Thus, we obtain the nonsingular lump solutions for Eq. (1) under the condition \(B_{r,L+r}>0\).

When \(L=1\), the first-order lump solutions for Eq. (1) can be written as

$$\begin{aligned} \begin{aligned} u=12h_1{h_2}^{-1}(\mathrm{ln}f)_{xx}, \end{aligned} \end{aligned}$$
(10)

where

$$\begin{aligned}&f=\theta _{1}\theta _{2}+B_{12},\nonumber \\&\theta _{1}=P_{1} x+K_{1} y-h_4\frac{K_{1}^2}{P_{1}}t,\nonumber \\&\theta _{2}=P_{2} x+K_{2} y-h_4\frac{K_{2}^2}{P_{2}}t,\nonumber \\&B_{12}=\frac{6P_{1}^2P_{2}^2\left[ 2h_1P_{1}P_{2}+h_5(P_{2}K_{1}+P_{1}K_{2})\right] }{h_4(P_{2}K_{1}-P_{1}K_{2})^2}.\nonumber \\ \end{aligned}$$
(11)

When one takes

$$\begin{aligned} \begin{aligned}&P_{1}=P_{2}^{*}=P_{11}+I P_{12},\\&K_{1}=K_{2}^{*}=K_{11}+I K_{12} \end{aligned} \end{aligned}$$
(12)

in Solutions (10), the corresponding solutions are nonsingular under the condition \(B_{12}>0\). Solutions (10) can also be expressed as

$$\begin{aligned} \begin{aligned} u=\frac{24h_1}{h_2}\frac{\left[ -(X'+\Lambda _1Y')^2+\Lambda _2^2Y'^{2}+\Lambda _3\right] }{\left[ (X'+\Lambda _1Y')^2+\Lambda _2^2Y'^{2}+\Lambda _3\right] ^2}, \end{aligned} \end{aligned}$$
(13)

with

$$\begin{aligned} \begin{aligned} X'&=x+\frac{h_4(K_{11}^2+K_{12}^2)}{P_{11}^2+P_{12}^2}t, \\Y'&=y-\frac{2h_4(K_{11}P_{11}+K_{12}P_{12})}{P_{11}^2+P_{12}^2}t,\\ \Lambda _1&=\frac{K_{11}P_{11}+K_{12}P_{12}}{P_{11}^2+P_{12}^2},\ \Lambda _2=\frac{K_{12}P_{11}-K_{11}P_{12}}{P_{11}^2+P_{12}^2},\\ \Lambda _3&=\frac{-3[h_5(K_{11}P_{11}+K_{12}P_{12}) +h_1(P_{11}^2+P_{12}^2)]}{h_4(P_{11}^2+P_{12}^2)^{-1}(K_{12}P_{11}-K_{11}P_{12})^2},\\ \end{aligned} \end{aligned}$$
(14)

where \(\Lambda _3>0\) must be satisfied. We find that \(u\rightarrow 0\) when \(x\rightarrow \infty \) and \(y\rightarrow \infty \) from Expressions (13). Hence, Solutions (10) are the first-order lumps moving on the constant backgrounds along the line

$$\begin{aligned} \begin{aligned} (K_{11}^2+K_{12}^2)y-2(K_{11}P_{11}+K_{12}P_{12})x=0. \end{aligned} \end{aligned}$$
(15)

Velocity components of the first-order lumps along the x and y directions, \(V_{x}\) and \(V_{y}\), are obtained as

$$\begin{aligned} \begin{aligned} V_{x}&=-\frac{h_4(K_{11}^2+K_{12}^2)}{P_{11}^2+P_{12}^2},\\ V_{y}&=\frac{2h_4(K_{11}P_{11}+K_{12}P_{12})}{P_{11}^2+P_{12}^2}. \end{aligned} \end{aligned}$$
(16)

For Solutions (10), when \(t=0\), there are three extreme points at (0, 0), \((\sqrt{3\Lambda _3},0)\) and \((-\sqrt{3\Lambda _3},0)\) on the \(x-y\) plane. Amplitudes of the humps and valleys of the first-order lumps are derived as

$$\begin{aligned} \begin{aligned} \wp _1&=\left| \frac{-8h_1h_4(K_{12}P_{11}-K_{11}P_{12})^2(P_{11}^2+P_{12}^2)^{-1}}{h_2[h_5(K_{11}P_{11}+K_{12}P_{12})+h_1(P_{11}^2+P_{12}^2)]}\right| ,\\ \wp _2&=\left| \frac{h_1h_4(K_{12}P_{11}-K_{11}P_{12})^2(P_{11}^2+P_{12}^2)^{-1}}{h_2[h_5(K_{11}P_{11}+K_{12}P_{12})+h_1(P_{11}^2+P_{12}^2)]}\right| . \end{aligned} \end{aligned}$$
(17)
Fig. 1
figure 1

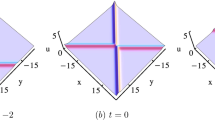
The second-order lump via Solutions (18) with \( P_1=P_3^{*}=-1-I,\ P_2=P_4^{*}=-I,\ K_1=K_3^{*}=2-I,\ K_2=K_4^{*}=2-I,\ h_1=1,\ h_2=2,\ h_4=-\frac{1}{5},\ h_5=1.\)

Full size image
Fig. 2
figure 2

The same as Fig. 1 except that \(h_2=4.\)

Full size image
Fig. 3
figure 3

The same as Fig. 1 except that \(h_4=-\frac{1}{10}.\)

Full size image

From Expressions (16) and (17), we find that the velocities of the first-order lumps are proportional to the coefficient \(h_4\). Amplitudes of the humps and valleys of the first-order lumps are related to the coefficients \(h_1\), \(h_2\), \(h_4\) and \(h_5\): both the amplitudes of the humps and valleys of the first-order lumps are proportional to \(h_4\), while inversely proportional to \(h_2\). Amplitudes of the humps of the first-order lumps are eight times as large as those of the valleys of the first-order lumps.

We need to point out that The First-Order Lump Solutions (10) are constructed via the long-wave limit method, which is different from the method adopted in Ref. [41]. Compared with those of the lump solutions obtained in Ref. [41], the trajectories of The First-Order Lump Solutions (10) always pass through the point (0, 0) on the \(x-y\) plane. The First-Order Lump Solutions (10) depend on four parameters, namely \(P_{11}\), \(P_{12}\), \(K_{11}\) and \(K_{12}\), while the first-order lump solutions obtained in Ref. [41] depend on more parameters.

When \(L=2\), the second-order lump solutions for Eq. (1) can be obtained via Solutions (7), as

$$\begin{aligned} \begin{aligned} u=12h_1{h_2}^{-1}(\mathrm{ln}f)_{xx}, \end{aligned} \end{aligned}$$
(18)

where

$$\begin{aligned} \begin{aligned} f&=\theta _{1}\theta _{2}\theta _{3}\theta _{4}+B_{12}\theta _{3}\theta _{4}+ B_{13}\theta _{2}\theta _{4}+B_{14}\theta _{2}\theta _{3}\\&\quad +B_{23}\theta _{1}\theta _{4}+B_{24}\theta _{1}\theta _{3}+ B_{34}\theta _{1}\theta _{2}\\&\quad +B_{12}B_{34}+B_{13}B_{24}+B_{14}B_{23}. \end{aligned} \end{aligned}$$
(19)

The second-order lumps describe the interaction between the two first-order lumps. As shown in Fig. 1, the two first-order lumps move along two lines

$$\begin{aligned} \begin{aligned}&(K_{11}^2+K_{12}^2)y-2(K_{11}P_{11}+K_{12}P_{12})x=0,\\&(K_{21}^2+K_{22}^2)y-2(K_{21}P_{21}+K_{22}P_{22})x=0, \end{aligned} \end{aligned}$$
(20)

on the \(x-y\) plane. It can be seen that the two first-order lumps have different shapes, velocities and amplitudes. They move close, and then interact with each other. When \(t=0\), due to the interaction, it can be seen that there are two humps with the same amplitude. Finally, the two first-order lumps separate and move further and further. We can find that the interaction between those two lumps is elastic since the shapes, velocities and amplitudes of those lumps have no changes the interaction. To investigate the effect of \(h_2\), based on the parameters in Fig. 1, we set \(h_2=4\) and fix the other parameters. Comparing Figs. 1 and 2, we find that the amplitudes of the two first-order lumps are inversely proportional to \(h_2\). When \(h_4=-\frac{1}{10}\) and the other parameters are the same as those in Fig. 1, a second-order lump is depicted in Fig. 3. Comparing Figs. 1 and 3, we find that both the velocities and amplitudes of those first-order lumps are proportional to \(h_4\).

3 The higher-order breather solutions for Eq. (1)

In this part, we will construct the Mth-order breathers under certain parameter constraints in the N-soliton solutions for Eq. (1).

Motivated by the procedure in Refs. [29, 37], we take

$$\begin{aligned} \begin{aligned}&N=2M,\ p_{\tau }=p_{M+\tau }^{*}=p_{\tau 1}+I p_{\tau 2},\\&k_{\tau }=k_{M+\tau }^{*}=k_{\tau 1}+I k_{\tau 2},\\&\phi _{\tau }=\phi _{M+\tau }^{*}=\phi _{\tau 1}+I\phi _{\tau 2},\ (\tau =1,2,\ldots ,M) \end{aligned} \end{aligned}$$
(21)

in Solutions (2) and (5), where \(p_{\tau 1}\)’s, \(p_{\tau 2}\)’s, \(k_{\tau 1}\)’s, \(k_{\tau 2}\)’s, \(\phi _{\tau 1}\)’s and \(\phi _{\tau 2}\)’s are the real constants. The Mth-order breather solutions of Eq. (1) are given as

$$\begin{aligned} \begin{aligned} u=12h_1{h_2}^{-1}(\mathrm{ln}f)_{xx}, \end{aligned} \end{aligned}$$
(22)

with

$$\begin{aligned}&f=\sum _{\mu =0,1} \mathrm{exp}\left( \sum _{i=1}^{2M}\mu _{i}\eta _{i}+\sum _{i<j}^{2M}\mu _{i}\mu _{j}A_{ij}\right) ,\nonumber \\&\eta _{\tau }=\eta _{M+\tau }^{*}=\eta _{\tau 1}+I\eta _{\tau 2},\nonumber \\&\eta _{\tau 1}=p_{\tau 1}x+k_{\tau 1}y-(p_{\tau 1}^2+p_{\tau 2}^2)^{-1}\nonumber \\&\ \ \ \ \ \times \big \{h_4\left[ \left( k_{\tau 1}^2-k_{\tau 2}^2\right) p_{\tau 1}+2k_{\tau 1}k_{\tau 2}p_{\tau 2} \right] \nonumber \\&\ \ \ \ \ +(p_{\tau 1}^2+p_{\tau 2}^2) \big [h_5((p_{\tau 1}^2-p_{\tau 2}^2)k_{\tau 1}-2k_{\tau 2}p_{\tau 1}p_{\tau 2})\nonumber \\&\ \ \ \ \ +h_1p_{\tau 1}(p_{\tau 1}^2-3p_{\tau 2}^2) +h_3p_{\tau 1}(p_{\tau 1}^4-10p_{\tau 1}^{2}p_{\tau 2}^{2}\nonumber \\&\ \ \ \ \ +5p_{\tau 2}^4)\big ]\big \}t +\phi _{\tau 1},\nonumber \\&\eta _{\tau 2}=p_{\tau 2}x+k_{\tau 2}y-(p_{\tau 1}^2+p_{\tau 2}^2)^{-1}\nonumber \\&\ \ \ \ \ \times \big \{h_4\big [(-k_{\tau 1}^2+k_{\tau 2}^2)p_{\tau 2}+2k_{\tau 1}k_{\tau 2}p_{\tau 1}\big ]\nonumber \\&\ \ \ \ \ +(p_{\tau 1}^2+p_{\tau 2}^2)\big [h_5((p_{\tau 1}^2-p_{\tau 2}^2)k_{\tau 2}+ 2k_{\tau 1}p_{\tau 1}p_{\tau 2})\nonumber \\&\ \ \ \ \ +h_1p_{\tau 2}(3p_{\tau 1}^2-p_{\tau 2}^2)+h_3p_{\tau 2}(5p_{\tau 1}^4-10p_{\tau 1}^{2}p_{\tau 2}^{2}\nonumber \\&\ \ \ \ \ +p_{\tau 2}^4)\big ]\big \}t +\phi _{\tau 2},\nonumber \\&e^{A_{ij}}=-\frac{R_{ij}}{S_{ij}},\nonumber \\&R_{ij}=h_3(p_{i}-p_{j})^6+h_1(p_{i}-p_{j})^4+h_4(k_{i}-k_{j})^2\nonumber \\&\ \ \ \ \ +(p_{i}-p_{j})(\omega _{i}-\omega _{j})+h_5(p_{i}-p_{j})^3(k_{i}-k_{j}),\nonumber \\&S_{ij}=h_3(p_{i}+p_{j})^6+h_1(p_{i}+p_{j})^4+h_4(k_{i}+k_{j})^2\nonumber \\&\ \ \ \ \ +(p_{i}+p_{j})(\omega _{i}+\omega _{j})+h_5(p_{i}+p_{j})^3(k_{i}+k_{j}), \end{aligned}$$
(23)

and \(e^{A_{\tau ,M+\tau }}>1\) to ensure that the solutions are nonsingular.

Fig. 4
figure 4

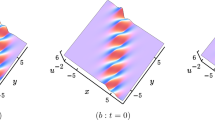
The second-order breather via Solutions (22) with \(M=2,\ p_1=p_3^{*}=\frac{3}{10}-\frac{1}{10}I,\ p_2=p_4^{*}=\frac{3}{5}I,\ k_1=k_3^{*}=\frac{3}{5}I,\ k_2=k_4^{*}=1+I,\ \phi _1=\phi _2=\phi _3=\phi _4=0,\ h_1=1,\ h_2=2,\ h_4=-\frac{1}{5},\ h_5=1.\)

Full size image
Fig. 5
figure 5

The same as Fig. 4 except that \(h_2=4.\)

Full size image
Fig. 6
figure 6

The same as Fig. 4 except that \(h_1=2.\)

Full size image

When \(M=1\), Solutions (22) reduce to the first-order breather solutions of Eq. (1),

$$\begin{aligned} \begin{aligned}&u=12h_1{h_2}^{-1}(\mathrm{ln}f)_{xx},\\ \end{aligned} \end{aligned}$$
(24)

with

$$\begin{aligned}&f=1+e^{\eta _1}+e^{\eta _1^{*}}+e^{\eta _1+\eta _1^{*}+A_{12}},\nonumber \\&\eta _{1}=\eta _{2}^{*}=\eta _{11}+I\eta _{12},\nonumber \\&\eta _{11}=p_{11}x+k_{11}y-(p_{11}^2+p_{12}^2)^{-1}\nonumber \\&\ \ \ \ \ \times \big \{h_4\left[ \left( k_{11}^2-k_{12}^2\right) p_{11}+2k_{11}k_{12}p_{12} \right] \nonumber \\&\ \ \ \ \ +\,(p_{11}^2+p_{12}^2) \big [h_5((p_{11}^2-p_{12}^2)k_{11}-2k_{12}p_{11}p_{12})\nonumber \\&\ \ \ \ \ +\,h_1p_{11}(p_{11}^2-3p_{12}^2)+h_3p_{11}(p_{11}^4-10p_{11}^{2}p_{12}^{2}\nonumber \\&\ \ \ \ \ +\,5p_{12}^4)\big ]\big \}t+\phi _{11},\nonumber \\&\eta _{12}=p_{12}x+k_{12}y-(p_{11}^2+p_{12}^2)^{-1}\nonumber \\&\ \ \ \ \ \times \big \{h_4\big [(-k_{11}^2+k_{12}^2)p_{12}+2k_{11}k_{12}p_{11}\big ]\nonumber \\&\ \ \ \ \ +\,(p_{11}^2+p_{12}^2)\big [h_5((p_{11}^2-p_{12}^2)k_{12}+ 2k_{11}p_{11}p_{12})\nonumber \\&\ \ \ \ \ +\,h_1p_{12}(3p_{11}^2-p_{12}^2)+h_3p_{12}(5p_{11}^4-10p_{11}^{2}p_{12}^{2}\nonumber \\&\ \ \ \ \ +\,p_{12}^4)\big ]\big \}t+\phi _{12},\nonumber \\&e^{A_{12}}=\,1-\frac{\mathfrak {R}}{\mathfrak {S}},\nonumber \\&\mathfrak {R}=\,3(p_{11}^2+p_{12}^2)^2\big \{h_5(k_{11}p_{11}+k_{12}p_{12})\nonumber \\&\ \ \ \ \ +\,(p_{11}^2+p_{12}^2)\big [h_1+5h_3(p_{11}^2-p_{12}^2)\big ]\big \},\nonumber \\&\mathfrak {S}=\,h_4(k_{12}p_{11}-k_{11}p_{12})^2+p_{11}^2(p_{11}^2+p_{12}^2)\nonumber \\&\ \ \ \ \ \times \big [3h_1+5h_3(3p_{11}^2-p_{12}^2)\big ]+h_5p_{11}(p_{11}^2+p_{12}^2)\nonumber \\&\ \ \ \ \ \times \big [2k_{12}p_{11}p_{12}+k_{11}(3p_{11}^2+p_{12}^2)\big ], \end{aligned}$$
(25)

and \(e^{A_{12}}>1\). The first-order breathers via Solutions (24) are localized along the direction of \(\eta _{11}=0\) and periodic along the direction of \(\eta _{12}=0\). Periods of those breathers are \(\frac{2\pi }{p_{12}}\) along the x direction and \(\frac{2\pi }{k_{12}}\) along the y direction. There are three kinds of the first-order breathers with different values of \(p_{11}\) and \(k_{11}\) in Solutions (24). When \(p_{11}=0\) and \(k_{11}\ne 0\), the first-order breathers are parallel to the x axis on the \(x-y\) plane; When \(p_{11}\ne 0\) and \(k_{11}=0\), the first-order breathers are parallel to the y axis on the \(x-y\) plane; More generally, when \(p_{11}\ne 0\) and \(k_{11}\ne 0\), the first-order breathers are parallel to the line \(y=-\frac{p_{11}}{k_{11}}x\) on the \(x-y\) plane. When \(p_{12}=k_{12}=\phi _{12}=0\), The First-Order Breather Solutions (24) reduce to the one-soliton solutions for Eq. (1). From Expressions (24) and (25), we also notice that the amplitudes of the first-order breathers are inversely proportional to \(h_2\).

Fig. 7
figure 7

Hybrid solution composed of a first-order breather and a single soliton via Solutions (2) and (5) with \(N=3,\ p_1=p_2^{*}=\frac{3}{10}-\frac{3}{10}I,\ p_3=\frac{1}{2},\ k_1=k_2^{*}=\frac{6}{5}+\frac{3}{5}I,\ k_3=2,\ \phi _1=\phi _2=\phi _3=0,\ h_1=1,\ h_2=2,\ h_4=-\frac{1}{5},\ h_5=1.\)

Full size image

Similarly, we can obtain the second-order breather solutions of Eq. (1) with \(M=2\) in Solutions (22). The second-order breathers describe the interaction between the two first-order breathers. As analyzed above, the second-order breathers can be composed of different kinds of the first-order breathers. For instance, we may construct a second-order breather which consists of two first-order breathers, one of which is parallel to the x axis, while the other is parallel to the y axis, as shown in Fig. 4. Those two first-order breathers keep interacting with each other on the \(x-y\) plane. As t goes on, the interaction region keeps moving. To investigate the effect of \(h_2\), based on the parameters in Fig. 4, we set \(h_2=4\) and fix the other parameters. Comparing Figs. 4 and 5, we find that the amplitudes of the two first-order breathers are inversely proportional to \(h_2\). When \(h_1=2\) and the other parameters are the same as those in Fig. 4, interaction between the two first-order breather is illustrated in Fig. 6. Effects of \(h_1\) on the amplitudes and shapes of the first-order breathers can be seen via comparing Figs. 4 with 6.

4 Hybrid solutions for Eq. (1)

In this section, we will focus on three types of hybrid solutions for Eq. (1). We will construct the hybrid solutions consisting of the first-order breathers and one solitons, of the first-order lumps and one solitons, and of the first-order lumps and first-order breathers.

4.1 Hybrid solutions consisting of the first-order breathers and one solitons for Eq. (1)

We take

$$\begin{aligned} \begin{aligned}&N=3,\ p_{1}\,=\,p_{2}^{*}=p_{11}+I p_{12},\ p_{3}=p_{31},\\&k_{1}\,=\,k_{2}^{*}=k_{11}+I k_{12},\ k_{3}=k_{31},\\&\phi _{1}\,=\,\phi _{2}^{*}=\phi _{11}+I \phi _{12},\ \phi _{3}\,=\,\phi _{31}, \end{aligned} \end{aligned}$$
(26)

in Solutions (2) and (5), and get the following:

Hybrid solutions composed of the first-order breathers and one solitons describe the interaction between the first-order breathers and one solitons, as shown in Figs. 7 and 8. When \(p_{11}k_{31}=p_{31}k_{11}\), the first-order breather is parallel to the one soliton on the \(x-y\) plane, as shown in Fig. 7. The first-order breather and one soliton move in opposite directions. As t goes on, they move close, interact with each other at \(t=0\), and finally become further and further. When \(t=0\), due to the interaction, each peak of the first-order breather is divided into two peaks, and amplitude of any peak is lower than that of the first-order breather. After the interaction, both the breather and soliton keep their shapes, velocities and amplitudes unchanged, which means that the interaction between the first-order breather and one soliton is elastic. When \(p_{11}k_{31}\ne p_{31}k_{11}\), the first-order breather and the one soliton are unparallel on the \(x-y\) plane, and keep interacting with each other as t goes on. To investigate the effect of \(h_2\), we take \(h_2=4\), and the other parameters are the same as those in Fig. 7. Comparing Figs. 7 and 8, we find that the amplitudes of both the first-order breathers and one solitons are inversely proportional to \(h_2\).

Fig. 8
figure 8

The same as Fig. 7 except that \(h_2=4\)

Full size image

4.2 Hybrid solutions consisting of the first-order lumps and one solitons for Eq. (1)

Via the long wave limit method [57, 58], hybrid solutions composed of the first-order lumps and one solitons for Eq. (1) can be derived via Solutions (2) and (5) with the parameters

$$\begin{aligned} \begin{aligned}&N=3,\ \phi _{1}=\phi _{2}=I \pi ,\ p_{1}=\sigma P_{1},\ \ p_{2}=\sigma P_{2},\\&k_{1}=\sigma K_{1},\ \ k_{2}=\sigma K_{2},\ \sigma \rightarrow 0. \end{aligned} \end{aligned}$$
(27)

Thus, we obtain the hybrid solutions composed of the first-order lumps and one solitons for Eq. (1) as

$$\begin{aligned} \begin{aligned} u=12h_1{h_2}^{-1}(\mathrm{ln}f)_{xx}, \end{aligned} \end{aligned}$$
(28)

where

$$\begin{aligned}&f=\theta _{1}\theta _{2}+B_{12}+(B_{12}+\xi _{13}\xi _{23}+\xi _{13}\theta _2 \nonumber \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\xi _{23}\theta _1+\theta _{1}\theta _{2})\mathrm{exp}(\eta _3),\nonumber \\&\xi _{13}=-\frac{\xi _{131}}{\xi _{132}},\nonumber \\&\xi _{131}=6P_1^2p_3^2[h_5(P_1k_3+K_1p_3)\nonumber \\&\qquad +2h_1P_1p_3+5h_3P_1p_3^3],\nonumber \\&\xi _{132}=h_5P_1p_3^3(2P_1k_3+K_1p_3)+3h_1P_1^2p_3^4\nonumber \\&\ \ \ \ \ \ \ \ +5h_3P_1^2p_3^6-h_4(P_1k_3-K_1p_3)^2,\nonumber \\&\xi _{23}=-\frac{\xi _{231}}{\xi _{232}},\nonumber \\&\xi _{231}=6P_2^2p_3^2[h_5(P_2k_3+K_2p_3)\nonumber \\&\quad +2h_1P_2p_3+5h_3P_2p_3^3],\nonumber \\&\xi _{232}=h_5P_2p_3^3(2P_2k_3+K_2p_3)+3h_1P_2^2p_3^4\nonumber \\&\ \ \ \ \ \ \ \ +5h_3P_2^2p_3^6-h_4(P_2k_3-K_2p_3)^2, \end{aligned}$$
(29)

and \(\theta _1\), \(\theta _2\), \(B_{12}\) and \(\eta _3\) are given by Expressions (5) and (11). In this case, we find that \(\xi _{13}=\xi _{23}^{*}\), which ensures that f be a real function. Velocities and amplitudes of the first-order lumps are given by Expressions (16) and (17). However, the velocity components of the one solitons along the x and y directions, \(V_{x-soliton}\) and \(V_{y-soliton}\), are obtained as

$$\begin{aligned} \begin{aligned}&V_{x-soliton}=\frac{h_1p_{3}^4+h_3p_{3}^6+h_5p_1^{3}k_{3}+h_4k_{3}^2}{p_3^2},\\&V_{y-soliton}=\frac{h_1p_{3}^4+h_3p_{3}^6+h_5p_1^{3}k_{3}+h_4k_{3}^2}{p_3k_3}, \end{aligned} \end{aligned}$$
(30)

and the amplitudes of the one solitons are \(\mid 3p_3^2h_1h_2^{-1}\mid \).

Fig. 9
figure 9

Hybrid solution composed of a first-order lump and a single soliton via Solutions (28) with \(P_1=P_2^{*}=-1-I,\ p_3=-\frac{1}{2},\ K_1=K_2^{*}=2-I,\ k_3=2,\ \phi _3=0,\ h_1=1,\ h_2=2,\ h_4=-\frac{1}{5},\ h_5=1.\)

Full size image
Fig. 10
figure 10

The same as Fig. 9 except that \(h_2=4\)

Full size image
Fig. 11
figure 11

The same as Fig. 9 except that \(h_4=-\frac{1}{10}\)

Full size image

Hybrid solutions composed of the first-order lumps and one solitons describe the interaction between the first-order lumps and one solitons, as shown in Figs. 9, 10 and 11. From Fig. 9, we can see that the velocities of the first-order lump and one soliton are different. At first, they move close, and then the first-order lump interacts with the one soliton at \(t=0\). When \(t=0\), due to the interaction, the maximum amplitude of u is lower than that of the first-order lump. Finally, they separate and the distance between them becomes further and further. After the interaction, no changes happen to the shapes, velocities, and amplitudes of the first-order lump and one soliton, which means that the interaction is elastic. Thus, properties of Hybrid Solutions (28) are different from those of the lumpoff solutions obtained in Ref. [41], which describe the inelastic interaction between the first-order lumps and one solitons.

To investigate the effect of \(h_2\), based on the parameters in Fig. 9, we set \(h_2=4\) and fix the other parameters. Comparing Figs. 9 and 10, we find that the amplitudes of this kind of hybrid solutions are inversely proportional to \(h_2\). When \(h_4=-\frac{1}{10}\) and the other parameters are the same as those in Fig. 9, interaction between a first-order lump and one soliton is illustrated in Fig. 11. Comparing Figs. 9 and 11, we find that the amplitude and velocity of the first-order lump are proportional to \(h_4\). However, amplitude of the one soliton does not depend on \(h_4\), and velocity of the one soliton is positively correlated to \(h_4\). In this case, we also notice that the first-order lump crosses over the one soliton and has two peaks due to the interaction when \(t=0\).

Fig. 12
figure 12

Hybrid solution composed of a first-order breather and a first-order lump via Solutions (32) with \(P_1=P_2^{*}=1-\frac{3}{4}I,\ p_3=p_4^{*}=\frac{3}{5}I,\ K_1=K_2^{*}=2+I,\ k_3=k_4^{*}=1+I,\ h_1=1,\ h_2=2,\ h_4=-\frac{1}{5},\ h_5=1.\)

Full size image
Fig. 13
figure 13

The same as Fig. 12 except that \(h_2=1\)

Full size image

4.3 Hybrid solutions consisting of the first-order breathers and first-order lumps for Eq. (1)

From Solutions (2) and (5) with

$$\begin{aligned}&N=4,\ \phi _{1}\,=\,\phi _{2}=I \pi ,\ p_{1}=\sigma P_{1},\ \ p_{2}=\sigma P_{2},\nonumber \\&k_{1}\,=\,\sigma K_{1},\ k_{2}=\sigma K_{2},\ \sigma \rightarrow 0, \end{aligned}$$
(31)

hybrid solutions composed of the first-order breathers and first-order lumps for Eq. (1) are obtained as

$$\begin{aligned} \begin{aligned} u&\,=\,12h_1{h_2}^{-1}(\mathrm{ln}f)_{xx}, \end{aligned} \end{aligned}$$
(32)

with

$$\begin{aligned}&f=\,\theta _{1}\theta _{2}+B_{12}+(B_{12}+\Delta _{13}\Delta _{23}+\Delta _{13}\theta _2\nonumber \\&\ \ \ \ \qquad +\Delta _{23}\theta _1+\theta _{1}\theta _{2})\mathrm{exp}(\eta _3)+(B_{12}\nonumber \\&\ \ \ \ \qquad +\Delta _{14}\Delta _{24}+\Delta _{14}\theta _2+\Delta _{24}\theta _1+\theta _{1}\theta _{2})\mathrm{exp}(\eta _4)\nonumber \\&\ \ \ \ \qquad +\big [\theta _{1}(\Delta _{23}+\Delta _{24})+\theta _{2}(\Delta _{13}+\Delta _{14})\nonumber \\&\ \ \ \ \qquad +B_{12}+\Delta _{13}\Delta _{23}+\Delta _{14}\Delta _{23}+\Delta _{13}\Delta _{24}\nonumber \\&\ \ \ \ \qquad +\Delta _{14}\Delta _{24}+\theta _{1}\theta _{2}\big ]\mathrm{exp}(\eta _3+\eta _4+A_{34}),\nonumber \\&\Delta _{\imath \jmath }=-\frac{\Delta _{\imath \jmath 1}}{\Delta _{\imath \jmath 2}},\ (\imath =1,2,\ \jmath =3,4)\nonumber \\&\Delta _{\imath \jmath 1}=6P_{\imath }^2p_\jmath ^2[h_5(P_{\imath }k_\jmath +K_{\imath }p_\jmath )\nonumber \\&\qquad +2h_1P_{\imath }p_\jmath +5h_3P_{\imath }p_\jmath ^3],\nonumber \\&\Delta _{\imath \jmath 2}=h_5P_{\imath }p_\jmath ^3(2P_{\imath }k_\jmath +K_{\imath }p_\jmath )+3h_1P_{\imath }^2p_\jmath ^4\nonumber \\&\ \ \ \ \ \ \ \ +5h_3P_{\imath }^2p_\jmath ^6-h_4(P_{\imath }k_\jmath -K_{\imath }p_\jmath )^2,\nonumber \\&p_3=p_4^{*}=p_{31}+I p_{32}, \end{aligned}$$
(33)

under the condition \(p_{31}=0\) or \(p_{32}=0\), where \(\eta _3\), \(\eta _4\), \(A_{34}\), \(\theta _1\), \(\theta _2\) and \(B_{12}\) are given by Expressions (5) and (11), \(p_{31}\) and \(p_{32}\) are the real constants. In this case, we find that \(\Delta _{13}=\Delta _{24}^{*}\) and \(\Delta _{14}=\Delta _{23}^{*}\), which ensure that f be a real function.

Hybrid solutions composed of the first-order breathers and first-order lumps describe the interaction between the first-order breathers and first-order lumps, as shown in Figs. 12 and 13. As t goes on, the breather and lump move close, interact with each other, and finally move further and further. It is found that the interaction is elastic since the shapes, velocities and amplitudes of the first-order breather and lump do not change after the interaction. To investigate the effect of \(h_2\), based on the parameters in Fig. 12, we set \(h_2=1\) and fix the other parameters. Comparing Figs. 12 and 13, we find that the amplitudes of this kind of hybrid solutions are inversely proportional to \(h_2\).

5 Conclusions

In this paper, we have studied the (2 + 1)-dimensional generalized Konopelchenko–Dubrovsky–Kaup–Kupershmidt equation, i.e., Eq. (1), which can be utilized to describe certain nonlinear phenomena in fluid mechanics. The Lth-Order Lump Solutions (7) have been constructed via the long-wave limit method. Based on Solutions (7), the first- and second-order lump solutions, i.e., Solutions (10) and (18), have been obtained. Via Expressions (16) and (17), it has been found that the velocities of the first-order lumps are proportional to the constant coefficient \(h_4\) in Eq. (1). We have also found that both the amplitudes of the humps and valleys of the first-order lumps are related to the constant coefficients \(h_1\), \(h_2\), \(h_4\) and \(h_5\) in Eq. (1), proportional to \(h_4\) while inversely proportional to \(h_2\). It has been found that the second-order lumps describe the interaction between two first-order lumps, which is elastic since those lumps keep their shapes, velocities and amplitudes unchanged after the interaction, as shown in Figs. 1, 2 and 3. Comparing Figs. 1 and 2, we have seen that the amplitudes of the second-order lumps are inversely proportional to \(h_2\). As shown in Figs. 1 and 3, we have seen that both the velocities and amplitudes of the first-order lumps are proportional to \(h_4\).

We have derived The Mth-Order Breather Solutions (22). The First-Order Breather Solutions (24) have been obtained from Solutions (22) with \(M=1\). Solutions (24) have indicated that the amplitudes of the first-order breathers are inversely proportional to \(h_2\). The second-order breather solutions have been obtained with \(M=2\) in Solutions (22). It has been found that the second-order breathers describe the interaction between two first-order breathers, as shown in Figs. 4, 5 and 6. Comparing Figs. 4 and 5, we have seen that the amplitudes of the second-order breathers are inversely proportional to \(h_2\). Effects of \(h_1\) on the amplitudes and shapes of the second-order breathers have been shown in Figs. 4 and 6.

Hybrid solutions consisting of the first-order breathers and one solitons have been constructed via the substitution of Expressions (26) into Solutions (2) and (5). Interaction between a first-order breather and one soliton has been found to be elastic as both the breather and soliton keep their shapes, velocities and amplitudes unchanged after the interaction, as shown in Figs. 7 and 8. Comparing Figs. 7 and 8, we have seen that the amplitudes of both the first-order breathers and one solitons are inversely proportional to \(h_2\). Via the long-wave limit method, hybrid solutions composed of the first-order lumps and one solitons, i.e., Solutions (28), have been obtained from Solutions (2) and (5) with the parameters given in Expression (27), and graphically analyzed, as shown in Figs. 9, 10 and 11. It has been found that the interaction between a first-order lump and one soliton is elastic. Comparing Figs. 9 and 10, we have found that the amplitudes of this kind of hybrid solutions are inversely proportional to \(h_2\). Comparing Figs. 9 and 11, we have seen that the amplitude and velocity of the first-order lump are proportional to \(h_4\). However, we have found that the amplitude of the one soliton does not depend on \(h_4\), and the velocity of the one soliton is positive correlated to \(h_4\). Hybrid solutions composed of the first-order breathers and first-order lumps, i.e., Solutions (32), have been obtained from Solutions (2) and (5) with the parameters given in Expressions (31). As shown in Figs. 12 and 13, the interaction between a first-order breather and a first-order lump has been found to be elastic. Comparing Figs. 12 and 13, we have found that the amplitudes of this kind of hybrid solutions are inversely proportional to \(h_2\).