1 Introduction

Fluid mechanics has been concerned with the behaviour of liquids and gases at rest and in motion [1, 2]. It has been reported that the nonlinear evolution equations (NLEEs) can be used to model some phenomena in fluid mechanics, optics, plasma physics and other fields [3,4,5,6].

The Korteweg-de Vries (KdV) equation has been developed to govern the long, one-dimensional, small-amplitude surface gravity waves in shallow water [7]. Later, it has been found that the KdV equation arises when the governing equation has the weak quadratic nonlinearity and weak dispersion [8]. The KdV equation has thus been considered to be a model for describing some other nonlinear phenomena, such as the internal waves in stratified fluids and ion-acoustic waves in plasmas [9]. The Kadomtsev-Petviashvili (KP) equation has been derived as a two-dimensional generalization of the KdV equation, with the KPI branch describing the water waves with weak surface tension and the KPII branch, with strong surface tension [8, 10,11,12]. The KP equation has also been applied in plasma physics, solid state physics, thin-plate dynamics and other fields [12].

There have been some other NLEEs such as a variable-coefficient modified KP system describing the electromagnetic waves in an isotropic charge-free infinite ferromagnetic thin film [13], a coupled mixed derivative nonlinear Schrödinger system describing the short pulses in the femtosecond or picosecond regime of a birefringent optical fiber [14], and a (3+1)-dimensional modified KdV-Zakharov-Kuznetsov equation in an electron-positron plasma [15]. Researchers have proposed several methods for studying those NLEEs, including the Hirota method [16,17,18,19,20], Pfaffian technique [21, 22], Riemann-Hilbert method [23], Darboux transformation [24,25,26,27,28,29,30], Lie symmetry approach [31], Bäcklund transformation [32,33,34] and similarity reduction [35,36,37].

Reference [38] has recently introduced an extended (2+1)-dimensional KP equation that reads

$$\begin{aligned} \left( u_t+6uu_x+u_{xxx}\right) _x - u_{yy} + \alpha _1 u_{xy} + \alpha _2 u_{tt} +\alpha _3 u_{yt}=0, \end{aligned}$$
(1)

where u(x, y, t) is a real differentiable function of the spatial variables x, y and temporal variable t, \(\alpha _1\), \(\alpha _2\) and \(\alpha _3\) are the constants, and the subscripts mean the partial derivatives. Equation (1), in comparison to the KPI equation, has three additional terms of the second-order derivatives and depicts more dispersion impact effect [38]. When \(\alpha _1=\alpha _2=\alpha _3=0\), Eq. (1) has been reduced to the KPI equation for the water waves with weak surface tension [11, 12]. Painlevé analysis, bilinear form, soliton, breather, periodic, rational, semi-rational and hybrid solutions of Eq. (1) have been derived [38].

However, for Eq. (1), bilinear form, N-soliton, M-breather, H-lump and hybrid solutions that differ from those in Ref. [38] have not been reported as yet, where N, M and H are the integers. In Sect. 2, we shall determine a bilinear form of Eq. (1) via the Hirota method. In Sect. 3, we shall work out the N-soliton solutions of Eq. (1) by virtue of that bilinear form. In Sect. 4, we shall derive the Mth-order breather solutions of Eq. (1) via the complex conjugated transformations. In Sect. 5, we shall obtain the Hth-order lump solutions of Eq. (1) by using the long-wave limit method. In Sect. 6, we shall derive some hybrid solutions of Eq. (1) based on the above results. In Sect. 7, our conclusions will be given.

2 Bilinear form of Eq. (1)

Under the coefficient constraint [38]

$$\begin{aligned} 4 \alpha _2= -\alpha _3^2, \end{aligned}$$
(2)

we take the dependent variable transformation

$$\begin{aligned} u=2 \left( \text {ln}{ f}\right) _{xx}+u_0, \end{aligned}$$
(3)

and then determine the following bilinear form of Eq. (1):

$$\begin{aligned} \begin{aligned} \left( D_xD_t + 6 u_0 D_x^2 + D_x^4 - D_y^2 + \alpha _1 D_xD_y - \frac{\alpha _3^2}{4} D_t^2 + \alpha _3 D_yD_t \right) f\cdot f =0, \end{aligned} \end{aligned}$$
(4)

where \(u_0\) is a real constant, f is a differentiable function of x, y and t, and \(D_x\), \(D_y\) and \(D_t\) are the bilinear operators defined by [39]

$$\begin{aligned} \begin{aligned}&D_x^{\beta _1} D_y^{\beta _2} D_t^{\beta _3} f \cdot g=\left( \frac{\partial }{\partial x} -\frac{\partial }{\partial x'}\right) ^{\beta _1} \left( \frac{\partial }{\partial y} -\frac{\partial }{\partial y'}\right) ^{\beta _2}\left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\right) ^{\beta _3} \! f\left( x,y,t\right) g\left( x',y',t'\right) \mid _{ x'=x,y'=y,t'=t}, \end{aligned} \end{aligned}$$

with \(g\left( x', y', t'\right) \) as a differentiable function of the formal variables \(x'\), \(y'\) and \(t'\), while \(\beta _1\), \(\beta _2\) and \(\beta _3\) as the non-negative integers.

3 N-soliton solutions of Eq. (1)

To construct some N-soliton solutions of Eq. (1), we begin by expanding f as

$$\begin{aligned} f=1+\varepsilon f_1+\varepsilon ^2 f_2+\varepsilon ^3 f_3+\cdots +\varepsilon ^N f_N, \end{aligned}$$
(5)

where \(\varepsilon \) is a formal expansion parameter, while \(f_{o}\)’s (\(o = 1, 2, \ldots , N\)) are the real differentiable functions of x, y and t.

Substituting Expression (5) into Bilinear Form (4) and balancing the coefficients of the same powers of \(\varepsilon \), we can derive the N-soliton solutions of Eq. (1) as

$$\begin{aligned}&u=2 \left( \text {ln}{ f}\right) _{xx} + u_0, \end{aligned}$$
(6a)
$$\begin{aligned}&f=\sum _{\mu =0,1} \text {exp} \left[ \sum _{\imath =1}^{N}\mu _{\imath }\xi _{\imath }+\sum _{1\le \imath <\jmath }^{(N)}\mu _{\imath }\mu _{\jmath }\,\text A_{\imath,\jmath} \right] , \end{aligned}$$
(6b)

under Coefficient Constraint (2), where

$$\begin{aligned} \begin{aligned}&\xi _{\imath }= k_{\imath } \left[ x+p_{\imath } y+ \frac{2\left( 1 + \alpha _3 p_{\imath } + q_{\imath } \right) }{\alpha _3^2} t \right] +\eta _{\imath },\\&{\rm e}^{A_{\imath,\jmath}}=\frac{2 + 2\alpha _3 \left( p_{\imath } + p_{\jmath } \right) + \alpha _3^2 \left[ \alpha _1 \left( p_{\imath } + p_{\jmath } \right) + 4k_{\imath }^2 -6 k_{\imath } k_{\jmath } +4 k_{\jmath }^2 +12 u_0 \right] - 2q_{\imath } q_{\jmath } }{2 + 2\alpha _3 \left( p_{\imath } + p_{\jmath } \right) + \alpha _3^2 \left[ \alpha _1 \left( p_{\imath } + p_{\jmath } \right) + 4k_{\imath }^2 + 6 k_{\imath } k_{\jmath } +4 k_{\jmath }^2 +12 u_0 \right] - 2q_{\imath } q_{\jmath }}, \\&q_{\imath } =\sqrt{ 1+ 2 \alpha _3 p_{\imath } + \alpha _3^2 \left( k_{\imath }^2 + 6 u_0 + \alpha _1 p_{\imath } \right) }, \end{aligned} \end{aligned}$$

\(\imath , \jmath = 1, 2, \ldots , N\), \(k_{\imath }\)’s, \(p_{\imath }\)’s and \(\eta _{\imath }\)’s are the complex constants, \(\sum _{\mu =0,1}\) denotes the summation over all possible combinations of \(\mu _{\imath }=0, 1\), and \(\sum _{1\le \imath <\jmath }^{(N)}\) implies the summation over all possible combinations of N elements with the condition \(1\le \imath <\jmath \).

Taking \(N=2\) and 3 in N-Soliton Solutions (6), we are able to obtain the two and three soliton solutions of Eq. (1), respectively. Figures 1 and 2 show the interaction between the two solitons and interaction among the three solitons, respectively. We can see that the interactions in Figs. 1 and 2 are elastic.

Fig. 1
figure 1

Interaction between the two solitons via Solutions (6) with \(N=2\), \(\alpha _1=\alpha _3=u_0=1\), \(k_1=\frac{6}{5}\), \(k_2=p_2=1\), \(p_1=-1\) and \(\eta _1=\eta _2=0\)

Full size image
Fig. 2
figure 2

Interaction among the three solitons via Solutions (6) with \(N=3\), \(\alpha _1=\alpha _3=u_0=1\), \(k_1=p_3=1\), \(k_2=-\frac{3}{2}\), \(k_3=p_1=-1\), \(p_2=\frac{1}{10}\) and \(\eta _1=\eta _2=\eta _3=0\)

Full size image

4 The Mth-order breather solutions of Eq. (1)

To obtain the Mth-order breather solutions of Eq. (1) via N-Soliton Solutions (6), we let \(N=2M\) and take the following complex conjugated transformations:

$$\begin{aligned} \begin{aligned}&k_r=k_{M+r}^{*}=k_{r,R}+ik_{r,I},~~p_r=p_{M+r}^{*}=p_{r,R}+ip_{r,I},~~\eta _r=\eta _{M+r}^{*}=\eta _{r,R}+i\eta _{r,I}, \end{aligned} \end{aligned}$$
(7)

where \(k_{r,R}\)’s, \(k_{r,I}\)’s, \(p_{r,R}\)’s, \(p_{r,I}\)’s, \(\eta _{r,R}\)’s and \(\eta _{r,I}\)’s are the real constants, M is a positive integer, \(r=1,2,\ldots ,M\), \(i=\sqrt{-1}\), the superscript “\(*\)” stands for the complex conjugation, and the subscripts “R” and “I” mean the real and imaginary parts, respectively.

Then, the Mth-order breather solutions of Eq. (1) under Coefficient Constraint (2) can be expressed as

$$\begin{aligned}&u=2 \left( \text {ln}{ f}\right) _{xx} + u_0, \end{aligned}$$
(8a)
$$\begin{aligned}&f=\sum _{\mu =0,1} \text {exp} \left[ \sum _{\imath =1}^{2M}\mu _{\imath }\xi _{\imath }+\sum _{1\le \imath <\jmath }^{(2M)}\mu _{\imath }\mu _{\jmath }\,A_{\imath,\jmath} \right] , \end{aligned}$$
(8b)

where

$$\begin{aligned}&\xi _r=\xi _{M+r}^{*}=\xi _{r,R} + i \xi _{r,I}, \\&\xi _{r,R}=k_{r,R} x + \left( k_{r,R} p_{r,R}\!-\!k_{r,I} p_{r,I} \right) y + \frac{2}{\alpha _3^2} \Bigg \{ k_{r,R} + \alpha _3 \left( k_{r,R}p_{r,R}\!-\!k_{r,I}p_{r,I} \right)\!+\!k_{r,R} h_r \text {cos} \left[ \frac{1}{2} \text {arg} \left( s_r \right) \right]\!-\!k_{r,I} h_r \text {sin} \left[ \frac{1}{2} \text {arg} \left( s_r \right) \right] \Bigg \} t + \eta _{r,R},\\&\xi _{r,I}=k_{r,I} x + \left( k_{r,R} p_{r,I} + k_{r,I} p_{r,R} \right) y + \frac{2}{\alpha _3^2} \Bigg \{ k_{r,I} + \alpha _3 \left( k_{r,R}p_{r,I} + k_{r,I}p_{r,R} \right) +k_{r,R} h_r \text {sin} \left[ \frac{1}{2} \text {arg} \left( s_r \right) \right] + k_{r,I} h_r \text {cos} \left[ \frac{1}{2} \text {arg} \left( s_r \right) \right] \Bigg \} t + \eta _{r,I},\\&h_r=\Bigg\{ \left[ 1+ 2\alpha _3 p_{r,R} + \alpha _3^2 \left( k_{r,R}^2-k_{r,I}^2 + 6 u_0 +\alpha _1 p_{r,R} \right) \right] ^2 + \alpha _3^2 \big[ 2\alpha _3 k_{r,R}k_{r,I} + \left( 2+ \alpha _1 \alpha _3 \right) p_{r,I} \big ]^2 \Bigg\}^{\frac{1}{4}}, \\&s_r=1+ 2 \alpha _3 \left( p_{r,R} + i p_{r,I} \right) + \alpha _3^2 \left[ \left( k_{r,R} + i k_{r,I} \right) ^2 + 6u_0 + \alpha _1\left( p_{r,R} + i p_{r,I} \right) \right] , \end{aligned}$$

\(A_{\imath ,\jmath }\)’s are defined in N-Soliton Solutions (6), while \({\rm e}^{A_{r,M+r}} > 1\) is required to ensure that these solutions are nonsingular.

When \(M=1\) and 2 in Solutions (8), we can determine the first- and second-order breather solutions of Eq. (1), respectively. Figures 3 and 4 display the one breather and elastic interaction between the two breathers, respectively. It can be observed that the amplitudes and shapes of the two breathers change nonlinearly in the interaction region, and then recover after the interaction.

Fig. 3
figure 3

One breather via Solutions (8) with \(M=1\), \(\alpha _1=\frac{1}{2}\), \(\alpha _3=u_0=1\), \(k_1=k_2^{*}=\frac{2}{5} + \frac{1}{5} i\), \(p_1=p_2^{*}=-\frac{1}{25}+2i\) and \(\eta _1=\eta _2^{*}=0\)

Full size image
Fig. 4
figure 4

Interaction between the two breathers via Solutions (8) with \(M=2\), \(\alpha _1=\frac{1}{2}\), \(\alpha _3=u_0=1\), \(k_1=k_3^{*}=\frac{2}{5} + \frac{1}{5} i\), \(k_2=k_4^{*}=\frac{1}{2} - \frac{1}{2} i\), \(p_1=p_3^{*}=-\frac{1}{25}+2i\), \(p_2=p_4^{*}=-1+2i\) and \(\eta _1=\eta _3^{*}=\eta _2=\eta _4^{*}=0\)

Full size image

5 The Hth-order lump solutions of Eq. (1)

To determine the Hth-order lump solutions of Eq. (1) via N-Soliton Solutions (6), we set \(N=2H\) and take the “long wave” limit as \(k_{\imath }\rightarrow 0\) under the following conditions:

$$\begin{aligned} \eta _{\imath }= i \pi , ~~~\frac{k_{\imath }}{k_{\jmath }}=O(1),~~~p_{\imath }=O(1), \end{aligned}$$
(9)

where H is a positive integer. Then the expression of f in N-Soliton Solutions (6) can be written as

$$\begin{aligned} f=\sum _{\mu =0,1} \prod \limits _{\imath =1}^{2H}\left( -1 \right) ^{\mu _{\imath }} \left( 1+\mu _{\imath } k_{\imath } \gamma _{\imath } \right) \prod \limits _{\imath <\jmath }^{(2H)} \left( 1+\mu _{\imath } \mu _{\jmath } k_{\imath } k_{\jmath } B_{\imath , \jmath } \right) + O(k^{2H+1}), \end{aligned}$$
(10)

where

$$\begin{aligned} & \gamma _{\imath } =x+p_{\imath }y+\frac{2 \left( 1+ \alpha _3 p_{\imath } +w_{\imath } \right) }{\alpha _3^2}t, \\ & B_{\imath , \jmath } =-\frac{12\alpha _3^2}{2+2\alpha _3\left( p_{\imath }+p_{\jmath } \right) + \alpha _3^2 \left[ 12 u_0 + \alpha _1 \left( p_{\imath }+p_{\jmath } \right) \right] - 2 w_{\imath } w_{\jmath }}, \\ & w_{\imath } =\sqrt{1+6u_0 \alpha _3^2 + \alpha _3 \left( 2+\alpha _1 \alpha _3 \right) p_{\imath }}. \end{aligned}$$

Following that, omitting the constant factor \(\prod _{\imath =1}^{2\,H} k_{\imath }\) in Expression (10) results in the Hth-order lump solutions of Eq. (1) as

$$\begin{aligned}&u=2 \left( \text {ln}{ f}\right) _{xx} + u_0, \end{aligned}$$
(11a)
$$\begin{aligned}&f=\prod \limits _{\imath =1}^{2H} \gamma _{\imath } + \frac{1}{2} \sum _{\imath , \jmath }^{(2H)} B_{\imath , \jmath } \prod \limits _{ \ell \ne \imath ,\jmath }^{2H} \gamma _{\ell } +\cdots +\frac{1}{H! 2^H}\nonumber \sum _{\imath , \jmath , \ldots , \kappa , \rho }^{(2H)} \overbrace{B_{\imath , \jmath } B_{\ell ,\nu } \cdots B_{\kappa , \rho }}^{H} \prod \limits _{ \varrho \ne \imath , \jmath , \ldots , \kappa , \rho }^{2H} \gamma _{\varrho } + \cdots , \end{aligned}$$
(11b)

under Coefficient Constraint (2) and the complex conjugated transformation

$$\begin{aligned} p_l=p_{H+l}^{*}=p_{l,R}+ip_{l,I}, \end{aligned}$$
(12)

where \(p_{l,R}\)’s and \(p_{l,I}\)’s are the real constants, \(l=1,2,\ldots ,H\) and \(B_{\imath , \jmath }>0\).

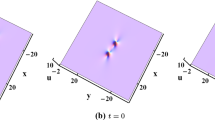
Choosing \(H=1\) and 2 in Solutions (11) yields the first- and second-order lump solutions of Eq. (1), respectively. Figure 5 shows the one lump. Figure 6 demonstrates the interaction between the two lumps with different shapes, velocities and amplitudes. The two lumps interact with each other around \(t = 0\), and then move apart. Amplitudes, velocities and shapes of the two lumps remain unchanged after the interaction, indicating that the interaction is elastic.

Fig. 5
figure 5

One lump via Solutions (11) with \(H=1\), \(\alpha _1=\alpha _3=u_0=1\) and \(p_1=p_2^{*}=-\frac{1}{5}+\frac{8}{5} i\)

Full size image
Fig. 6
figure 6

Interaction between the two lumps via Solutions (11) with \(H=2\), \(\alpha _1=\frac{1}{5}\), \(\alpha _3=\frac{4}{5}\), \(u_0=\frac{1}{10}\), \(p_1=p_3^{*}=-1+\frac{3}{5} i\) and \(p_2=p_4^{*}=\frac{2}{5}- \frac{4}{5} i\)

Full size image

6 Hybrid solutions of Eq. (1)

6.1 Hybrid solutions composed of the first-order breather and one soliton of Eq. (1)

To find out the hybrid solutions featuring the interactions between the one breather and one soliton of Eq. (1), we set \(N=3\) and take the following transformations for N-Soliton Solutions (6):

$$\begin{aligned} \begin{aligned}&k_1 =k_{2}^{*}=k_{1,R}+ik_{1,I},~~k_3=k_{3,R},~~ p_1=p_{2}^{*}=p_{1,R}+ip_{1,I},\\&p_3=p_{3,R},~~\eta _1=\eta _{2}^{*}=\eta _{1,R}+i\eta _{1,I},~~\eta _3=\eta _{3,R}. \end{aligned} \end{aligned}$$
(13)

Then, hybrid solutions composed of the first-order breather and one soliton of Eq. (1) are obtained as

$$\begin{aligned}&u=2 \left( \text {ln}{ f}\right) _{xx} + u_0, \end{aligned}$$
(14a)
$$\begin{aligned}f = 1+{\rm e}^{\xi_1}+{\rm e}^{\xi_2}+{\rm e}^{\xi_3}+{\rm e}^{\xi_1+\xi_2+A_{1,2}}+{\rm e}^{\xi_1+\xi_3+A_{1,3}}+{\rm e}^{\xi_2+\xi_3+A_{2,3}}+{\rm e}^{\xi_1+\xi_2+\xi_3+A_{1,2}+A_{1,3}+A_{2,3}}, \end{aligned}$$
(14b)

under Coefficient Constraint (2).

Figure 7 displays the interaction between the one breather and one soliton based on Hybrid Solutions (14). We observe that the amplitudes and shapes of the soliton and breather change nonlinearly in the interaction region and then recover after the interaction, thus the interaction is elastic.

Fig. 7
figure 7

Interaction between the one breather and one soliton via Solutions (14) with \(\alpha _1=\frac{3}{5}\), \(\alpha _3=u_0=1\), \(k_1=k_2^{*}=\frac{1}{2}-\frac{1}{2} i\), \(k_3=1\), \(p_1=p_2^{*}=-1+2 i\), \(p_3=-1\) and \(\eta _1=\eta _2^{*}=\eta _3=0\)

Full size image

6.2 Hybrid solutions composed of the first-order lump and one soliton of Eq. (1)

Setting \(N=3\) and considering the following conditions on N-Soliton Solutions (6):

$$\begin{aligned} \begin{aligned}&k_1\rightarrow 0,~~ k_{2}\rightarrow 0,~~k_3=k_{3,R},~~ p_1=p_{2}^{*}=p_{2,R}+ip_{2,I},\\&p_3=p_{3,R},~~\eta _1=\eta _{2}=i \pi ,~~\eta _3=\eta _{3,R}, \end{aligned} \end{aligned}$$
(15)

give rise to the hybrid solutions composed of the first-order lump and one soliton of Eq. (1) under Coefficient Constraint (2), i.e.,

$$\begin{aligned}&u=2 \left( \text {ln}{ f}\right) _{xx} + u_0, \end{aligned}$$
(16a)
$$\begin{aligned}&f=\gamma _1 \gamma _2 + B_{1,2} +\left[ \left( C_{1,3} + \gamma _1 \right) \left( C_{2,3} + \gamma _2 \right) + B_{1,2} \right] \textrm{e}^{\xi _3}, \end{aligned}$$
(16b)

where

$$\begin{aligned}&C_{1,3}=-\frac{12 \alpha _3^2 k_3}{2+2\alpha _3\left( p_1 + p_3\right) +\alpha _3^2 \left[ 4k_3^2 +12 u_0 +\alpha _1 \left( p_1 +p_3 \right) \right] - 2 w_1 q_3 },\\&C_{2,3}=-\frac{12 \alpha _3^2 k_3}{2+2\alpha _3\left( p_2 + p_3\right) +\alpha _3^2 \left[ 4k_3^2 +12 u_0 +\alpha _1 \left( p_2 +p_3 \right) \right] - 2 w_2 q_3 }. \end{aligned}$$

Figure 8 demonstrates the elastic interaction between the one lump and one soliton based on Hybrid Solutions (16). They interact with each other when \(t = 0\), resulting in the nonlinear changes in their amplitudes. Amplitudes and shapes of the lump and soliton keep unchanged after the interaction.

Fig. 8
figure 8

Interaction between the one lump and one soliton via Solutions (16) with \(\alpha _1=2\), \(\alpha _3=\frac{2}{5}\), \(u_0=\frac{1}{5}\), \(k_3=\frac{2}{5}\), \(p_1=p_2^{*}=\frac{1}{2}+\frac{4}{5} i\), \(p_3=-1\) and \(\eta _3=0\)

Full size image

6.3 Hybrid solutions composed of the first-order lump and first-order breather of Eq. (1)

When N-Soliton Solutions (6) with \(N=4\) satisfy the following conditions:

$$\begin{aligned} \begin{aligned}&k_1\rightarrow 0,~~ k_{2}\rightarrow 0,~~k_3=k_{4}^{*}=k_{3,R}+i k_{3,I},~~ p_1=p_{2}^{*}=p_{1,R}+ip_{1,I},\\&p_3=p_{4}^{*}=p_{3,R}+ip_{3,I},~~\eta _1=\eta _{2}=i \pi ,~~\eta _3=\eta _{4}^{*} = \eta _{3,R}+i \eta _{3,I}, \end{aligned} \end{aligned}$$
(17)

we obtain the hybrid solutions composed of the first-order lump and first-order breather of Eq. (1) as

$$\begin{aligned}&u=2 \left( \text {ln}{ f}\right) _{xx} + u_0, \end{aligned}$$
(18a)
$$\begin{aligned}&f=\gamma _1 \gamma _2 + B_{1,2} +\left[ \left( C_{1,3} + \gamma _1 \right) \left( C_{2,3} + \gamma _2 \right) + B_{1,2} \right] \textrm{e}^{\xi _3} \nonumber \\&~~~~~~+\left[ \left( C_{1,4} + \gamma _1 \right) \left( C_{2,4} + \gamma _2 \right) + B_{1,2} \right] \textrm{e}^{\xi _4} \nonumber \\&~~~~~~+ \left[ \left( C_{1,3} + C_{1,4} + \gamma _1 \right) \left( C_{2,3} +C_{2,4} + \gamma _2 \right) + B_{1,2} \right] {\rm e}^{\xi_3+\xi_4+A_{3,4}}, \end{aligned}$$
(18b)

under Coefficient Constraint (2), where

$$\begin{aligned}&C_{1,4}=-\frac{12 \alpha _3^2 k_4}{2+2\alpha _3\left( p_1 + p_4\right) +\alpha _3^2 \left[ 4k_4^2 +12 u_0 +\alpha _1 \left( p_1 +p_4 \right) \right] - 2 w_1 q_4 },\\&C_{2,4}=-\frac{12 \alpha _3^2 k_4}{2+2\alpha _3\left( p_2 + p_4\right) +\alpha _3^2 \left[ 4k_4^2 +12 u_0 +\alpha _1 \left( p_2 +p_4 \right) \right] - 2 w_2 q_4 }. \end{aligned}$$

Figure 9 exhibits the elastic interaction between the one lump and one breather based on Hybrid Solutions (18). We can see that as t progresses, they approach, interact with each other around \(t = 0\) and then separate.

Fig. 9
figure 9

Interaction between the one lump and one breather via Solutions (18) with \(\alpha _1=\frac{1}{2}\), \(\alpha _3=-1\), \(u_0=\frac{2}{5}\), \(k_3=k_4^{*}=\frac{1}{5} + \frac{1}{5} i\), \(p_1=p_2^{*}=\frac{7}{5}+\frac{4}{5} i\), \(p_3=p_4^{*}= i\) and \(\eta _3=\eta _4^{*}=0\)

Full size image

7 Conclusions

Investigations on the nonlinear phenomena in fluid mechanics have been active. In this paper, we have studied an extended (2+1)-dimensional KP equation in fluid mechanics, i.e., Eq. (1). Bilinear Form (4) and N-Soliton Solutions (6) have been constructed via the Hirota method. Based on N-Soliton Solutions (6), we have derived the Mth-order breather solutions as Solutions (8) via Complex Conjugated Transformations (7). We have also obtained the Hth-order lump solutions as Solutions (11) by virtue of the long-wave limit method. In addition, we have determined Hybrid Solutions (14) composed of the first-order breather and one soliton, Hybrid Solutions (16) composed of the first-order lump and one soliton, and Hybrid Solutions (18) composed of the first-order lump and first-order breather.

Based on N-Soliton Solutions (6) with \(N=2\) and 3, Figs. 1 and 2 have shown the elastic interaction between the two solitons and interaction among the three solitons, respectively. Via Solutions (8) with \(M=1\) and 2, one breather and elastic interaction between the two breathers have been exhibited in Figs. 3 and 4, respectively. Based on Solutions (11) with \(H=1\) and 2, Figs. 5 and 6 have displayed the one lump and elastic interaction between the two lumps, respectively. Elastic interaction between the one breather and one soliton has been described via Solutions (14), as shown in Fig. 7. Figure 8 has exhibited the elastic interaction between the one lump and one soliton via Solutions (16). Elastic interaction between the one lump and one breather via Solutions (18) has been demonstrated in Fig. 9.