Nonlinear model predictive position control for a tail-actuated robotic fish

Abstract

Position control is a significant technique for the underwater application of robotic fish; however, it is also very challenging due to the underactuated property and input coupling of system dynamics. In this article, a two-stage orientation–velocity nonlinear model predictive controller is proposed to solve this problem. A scaled averaging model of tail-actuated robotic fish is constructed at first. Then, the novel strategy based on orientation and velocity control is developed as well as proved to be equivalent with position control in the sense of Lyapunov. Furthermore, a nonlinear model predictive controller with a two-stage switching strategy is designed to regulate the orientation and velocity error. Finally, the simulation results demonstrate the superiority of the proposed control algorithm compared with other methods. Particularly, there exists an interesting twist-braking behavior in simulation, which indicates that the proposed method makes better use of the system dynamics. The proposed method is efficient for not only bionic robotic fish but also other aquatic underactuated robots, which offers new insight into the position control of underwater robots.

1 Introduction

The development of bionic robotic fish is an active area of underwater robotic research. Owing to its high maneuverability, high efficiency, and noiseless performance, bionic robotic fish is differentiated from the commercially developed autonomous underwater vehicles (AUVs) and holds tremendous promise for underwater applications undoubtedly [1, 2]. However, the prerequisite is the robust and precise control for carrying out the underwater mission efficiently and successfully. In particular, the precise position control is an essential technique for the large amounts of underwater applications, e.g., underwater salvage and rescue, underwater sensor network deployment. At present, the vast majority of existing studies about the control problem of robotic fish involve swimming control [3, 4], motion performance optimization [5, 6], target tracking [7,8,9], path following [10, 11], trajectory tracking [12,13,14,15], and formation control [16,17,18]. Nevertheless, the results on the position control of robotic fish are still limited, where one critical challenge of position control is the complex dynamic properties, e.g., underactuated characteristics and input coupling. The underactuated characteristics of robotic fish reflect in two aspects. Firstly, there are three degree-of-freedoms (DOFs) on the horizontal movement, but only two control inputs are available for robotic fish, which usually consist of the forward thrust and steering torque. Secondly, the forward thrust must be larger than or equal to zero, which indicates that the deceleration of robotic fish is difficult and mainly relies on the hydrodynamic force. Additionally, unlike the ordinary underactuated vessel or AUV, the input coupling property that the steering torque will induce the lateral acceleration, makes the position control more challenging for robotic fish.

In order to overcome the hurdles caused by the dynamic characteristics for the position control of robotic fish, the researchers have done a few works. Yang et al. transformed the nonholonomic fish robot system into the chained form at the kinematic level and applied the backstepping method to moor it to the desired docking position [19]. Yu et al. proposed the point-to-point (PTP) hybrid control scheme for a four-link robotic fish, which consists of the speed control based on the fuzzy logic algorithm and the proportional–integral–derivative (PID) orientation controller [20]. Kato et al. provided a fuzzy controller for the rendezvous and docking task of a fish robot equipped with a pair of two-motor-driven mechanical pectoral fins [21]. Except for the robotic fish, the other aquatic robots, e.g., underwater surface vessel and AUV, also face the same problem brought by the underactuated property [22, 23]. Mazenc et al. utilized coordinate transformation and backstepping technique for determining global uniform asymptotically stabilizing feedbacks for an underactuated vessel [24]. Sankaranarayanan et al. proposed a switched finite-time PTP control strategy for an underactuated AUV, which splits the system into several subsystems through state and input transformation and regulates them by finite-time controllers [25]. Yang et al. designed a backstepping-based dynamically mooring controller in terms of the kinematic model of underactuated AUV [26].

The above methods can be roughly divided into two categories. The first one is to circumvent the difficulty of underactuated dynamics and directly design the subtle rules to control robots, e.g., fuzzy controller [20, 21]. Although this method implements the position control without considering the dynamic model, it highly relies on the artificial experience so that it is easy to fail in some cases. The second one is to convert the kinematics [19, 26] or dynamics [24, 25] of robots into the amenable formulation by coordinate transformation and then design controller by means of the common nonlinear control techniques like backstepping. However, most of these works do not take into account the input coupling and the constraint of control input, e.g., thrust must be nonnegative, which are the core technical difficulties on the position control of robotic fish.

In this article, we propose a two-stage orientation–velocity nonlinear model predictive controller (TSOV-NMPC) to accomplish the position control of robotic fish, where the issues about underactuated characteristics and input coupling are addressed from three aspects. Firstly, the forward velocity constraint is derived to guarantee that the velocity is in a certain range and the robot is able to be braked by hydrodynamic force, which avoids the necessity of negative thrust. Secondly, in order to reduce the impact of input coupling, the heading and velocity orientation errors are defined as control goals, which is relatively easy to control compared with other error definitions. Lastly, the nonlinear model predictive control (NMPC) algorithm is utilized to address the underactuated issues. The NMPC algorithm can not only deal with the state and input constraints but also optimize the control value in maximum extent based dynamic characteristics even if the system is underactuated.

At present, there are many applications of the NMPC algorithm on AUV platforms [27, 28], while the use of the NMPC algorithm is limited for robotic fish due to the difficulty of dynamic modeling about fish-like propulsion [11, 13]. However, Wang et al. proposed a scaled averaging method to construct the dynamic model of a tail-actuated carangiform robotic fish, which is not only high-fidelity but also amenable to analysis and control design [29]. This article is on the basis of this averaging model and further utilize the NMPC algorithm to accomplish the position control of robotic fish.

The main purpose of this article is to develop a precise position controller for robotic fish, which lays the solid foundation for performing underwater missions. The main contributions are twofold. On the one hand, we propose a novel control strategy based on orientation and velocity control to replace the direct methods depending on the feedback of position or distance errors, which achieves better control precision and adaptability in the simulations. Besides, the equivalence between orientation–velocity control and position control is proved in the sense of Lyapunov, where the orientation control includes the heading orientation and velocity orientation control. On the other hand, a TSOV-NMPC algorithm is developed to accomplish position control of robotic fish, which combines the virtue of heading orientation and velocity orientation control as well as making better use of the robot’s dynamic property. Particularly, an interesting twist-braking mechanism is found in the deceleration process of robotic fish, which is not the pre-designed maneuver but automatically generated by the optimization algorithm. The proposed control algorithm offers new insight into the position control of underwater underactuated robots, which is not only efficient for robotic fish but also for other aquatic robots that possess similar dynamic properties.

The rest of this article is organized as follows. The dynamic modeling of tail-actuated robotic fish and the problem formulation of position control are provided in Sect. 2. Section 3 introduces the design of TSOV-NMPC in detail. The simulation setups and results are offered in Sect. 4. Finally, Sect. 5 concludes this article.

2 Problem formulation

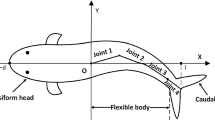
The planar motion model of the tail-actuated robotic fish shown in Fig. 1a is deduced in this section. In particular, the robot is assumed to be operated in an incompressible fluid within an infinite domain. The earth-fixed reference frame $C_w$ and body-fixed reference frame $C_b$ are displayed in Fig. 1b. The coordinate $C_b$ is located at the center of gravity (CG) of robotic fish, whose x axis is parallel with the anterior–posterior. The position X, Y, and orientation $\psi$ are defined in the frame $C_w$. The surge velocity u, sway velocity v, and yaw angular velocity $\omega$ are defined in the body frame. Obviously, the kinematic equations of the robot can be written as follows:

$$\begin{aligned} {\dot{X}}&= \cos \psi \cdot u - \sin \psi \cdot v\nonumber \\ {\dot{Y}}&= \sin \psi \cdot u + \cos \psi \cdot v \nonumber \\ {\dot{\psi }}&= \omega . \end{aligned}$$

(1)

Fig. 1

Tail-actuated robotic fish. a appearance rendering, b coordinate definition

As shown in Fig. 1a, the tail-actuated robotic fish consists of a rigid body and a rigid tail fin. Besides, the motion of tail fin follows the sinusoidal law

$$\begin{aligned} \alpha (t) = \alpha _0 + \alpha _a \sin (\omega _\alpha t) \end{aligned}$$

(2)

where $\alpha$ represents the tail deflection angle. $\alpha _0$, $\alpha _a$, and $\omega _\alpha$ denote the bias, amplitude, and frequency of tail beating, respectively. Particularly, considering the carangiform propulsion adopted, the hydrodynamic forces of tail fin are analyzed by the Lighthill’s large amplitude elongated body theory [30]. Besides, the hydrodynamic effects exerted on rigid body are considered to contain the viscous damping and additional mass. Eventually, the complete dynamic equations of the robotic fish are given by

$$\begin{aligned} {\dot{u}}= & {} v\omega -\frac{K_x}{M_x}|u|u-\frac{{K_t}}{M_x}{\ddot{\alpha }}\sin \alpha \nonumber \\ {\dot{v}}= & {} -u\omega -\frac{K_y}{M_y}|v|v+\frac{K_t}{M_y}{\ddot{\alpha }}\cos \alpha \nonumber \\ {\dot{\omega }}= & {} -\frac{M_x-M_y}{\varLambda _z}uv-\frac{K_{\tau }}{\varLambda _z}|\omega |\omega \nonumber \\&-\frac{{K_t}}{\varLambda _z}(-r_{bt}\ddot{\alpha }\cos \alpha +\frac{2}{3}L{{\ddot{\alpha }}}) \end{aligned}$$

(3)

where $M_x=m_b+m_{ax}$, $M_y=m_b+m_{ay}$, and$\varLambda _z=\varLambda _b+\varLambda _{az}$ denote the mass and moment of inertia of the body, respectively, which contain the added mass and inertia. $K_x$, $K_y$, and $K_{\tau }$ represent the damping coefficients. Besides, $K_t=\frac{1}{2}mL^2$, where $m=\frac{1}{4}\rho d^2$ is virtual mass for the per unit length of tail and L is tail length. $\rho$ is the density of water. d is the depth of the tail cross section.

Furthermore, the periodic model (3) is averaged for the convenience of practical control, and the scaled averaging method is applied as [29]

$$\begin{aligned} {\dot{u}}&= v\omega -\frac{K_x}{M_x}|u|u+\frac{K_{\mathrm{force}}{K_t}}{2M_x}u_1 \end{aligned}$$

(4a)

$$\begin{aligned} {\dot{v}}&= -u\omega -\frac{K_y}{M_y}|v|v+\frac{K_{\mathrm{force}}K_t}{2M_y}u_2 \end{aligned}$$

(4b)

$$\begin{aligned} {\dot{\omega }}&= -\frac{M_x-M_y}{\varLambda _z}uv-\frac{K_{\tau }}{\varLambda _z}|\omega |\omega -\frac{K_\mathrm{{moment}}{K_t}r_{bt}}{2\varLambda _z}u_2 \end{aligned}$$

(4c)

where $u_1=\alpha _A^2 \omega _\alpha ^2(1-\frac{1}{2}\alpha _0^2-\frac{1}{8}\alpha _A^2)$ and $u_2=\omega _\alpha ^2\alpha _A^2\alpha _0$. $K_{\mathrm{force}}$ and $K_\mathrm{{moment}}$ are scaling functions of tail force and torque. Generally, $K_{\mathrm{force}}$ is a constant and $K_\mathrm{{moment}}$ can be represented as the linear function of $\alpha _0$. $r_{bt}$ denotes the distance between CG and tail joint.

According to the above dynamic model, the underactuated property includes two aspects: the less number of independent control input and the limited range of $u_1$ that must be larger than zero. Besides, the input coupling refers that the same control input is utilized to control multiple states, e.g., the input $u_2$ is applied to control the lateral and turning acceleration simultaneously. It is worth noting that the dynamic model for most of the underwater surface vessel and AUV is input decoupling and there is usually no nonnegative limitation on the thrust. Therefore, the position control for robotic fish is relatively difficult than other underwater robots.

The target of position control is to drive the robot to arrive and stay at the desired point. Therefore, the control problem tackled in this paper can be formulated as follows:

Consider the robotic fish model in the horizontal plane described by (1) and (4a)–(4c). Derive a control law that generates the control input $u_1$ and $u_2$ to guarantee that the robotic fish arrives at the target position and its velocity decreases to zero at the same time.

3 Controller design

In this section, an NMPC-based controller is proposed to solve the above control problem, where the original position control is converted into a problem combining orientation and velocity control in a subtle manner.

3.1 Velocity constraint

Due to the underactuated property and input coupling, the direct method using the Cartesian coordinates of the desired point as feedback is hard to achieve satisfactory performances. Thus, the point tracking problem is converted into an angle tracking one in some works, which governs the heading of robotic fish to point to the target point. However, the controller based on angle tracking can only drive the robotic fish approaching target rather than stopping on it. In other words, the velocity control is essential for the position control of robotic fish, which indicates that the velocity should decrease as the robot approaches the target point. According to (4a), the forward velocity u mainly depends on the input $u_1$, but $u_1>0$ for most of cases. It means that the robotic fish cannot utilize negative thrust to brake itself and the viscous effect is the only source of deceleration forces. Therefore, if the velocity exceeds a certain range, the viscous force will be unable to brake the robotic fish and the robot will exceed the desired point. For the sake of further discussion, the constraint of velocity should be deduced at first.

Let us consider the free deceleration of the robotic fish, namely, $u>0$, $u_1=0$. Assuming lateral velocity is negligible, namely, $v=0$, Eq. (4a) can be written as

$$\begin{aligned} {\dot{u}} = -\frac{K_x}{M_x}|u|u= -\frac{K_x}{M_x}u^2,\ u(0)=V \end{aligned}$$

(5)

where V denotes the initial velocity of the free deceleration stage. Hence, the analytic solution of the above ordinary differential equation is given by

$$\begin{aligned} u=\frac{1}{\frac{1}{V}+\frac{K_x}{M_x}t}. \end{aligned}$$

(6)

In order to compute the free movement distance of the robot with initial velocity V, Eq. (6) is integrated over $[0,\tau ]$ as

$$\begin{aligned} d=\int _0^\tau u \ \mathrm{d}t=\frac{M_x}{K_x}\ln \left[ {1+\frac{K_x V}{M_x}\tau } \right] \end{aligned}$$

(7)

where $\tau$ is time constant that refers to the desired maximum time that the robotic fish does not exceed the target point. The larger $\tau$ means that the robotic fish will move a longer distance d, which indicates the stronger velocity constraint.

Furthermore, in order to ensure the robotic fish would not exceed the target point within time $\tau$, the movement distance d should be less than the current distance between robot and goal, which can be written as

$$\begin{aligned} d=\frac{M_x}{K_x}\ln \left[ {1+\frac{K_x V}{M_x}\tau }\right] < r \end{aligned}$$

(8)

where $r=\sqrt{(X_T-X)^2+(Y_T-Y)^2}$ denotes the distance from target point. $X_T$ and $Y_T$ represent the coordinates of target point in frame $C_w$.

According to (8), if the distance between robotic fish and target is r, the velocity constraint will be

$$\begin{aligned} V<V_{max} \end{aligned}$$

(9)

where the available maximum velocity is

$$\begin{aligned} V_{max}=\frac{M_x}{K_x \tau }\left[ \exp \left( \frac{K_x}{M_x}r \right) -1 \right] . \end{aligned}$$

3.2 Orientation–velocity control strategy

The single orientation control is unable to stop the robotic fish at the terminal position, thus the velocity control is essential. The idea of velocity control is intuitive, which requires that robot should track the velocity constraint $V_{max}$ as accurate as possible so that it approaches the target by a fast and stable manner. However, owing to the various orientation definitions, namely, heading orientation and velocity orientation, the orientation control of robotic fish can be divided into two types. The heading orientation control is to govern the robot’s head to point to the target, while the velocity orientation control is to coincide the velocity with the direction of the target. This subsection depicts these two control strategies in detail and demonstrates the equivalence between the orientation–velocity control and position control.

3.2.1 Heading–orientation–velocity (HOV) control strategy

As shown in Fig. 1b, the relative angle $\phi$ between the robotic fish and target can be represented as

$$\begin{aligned} \phi = \arctan {\frac{Y_e}{X_e}} \end{aligned}$$

(10)

where $X_e = X_T - X$ and $Y_e = Y_T - Y$ denote the position errors of x and y axis, respectively.

Define the heading angle error and velocity error as follows:

$$\begin{aligned} \alpha _e^h&= \phi - \psi \end{aligned}$$

(11)

$$\begin{aligned} V_e&= V_{max} - V_c \end{aligned}$$

(12)

where $V_c=\sqrt{u^2+v^2}$ is resultant velocity.

The objective of HOV control is to regulate the errors $\alpha _e^h$ and $V_e$ to zero. Furthermore, the equivalence between HOV control and position control can be deduced [31].

Assumption 1

The forward (surge) velocity is not less than zero, which means $u\ge 0$.

Theorem 1

Consider the system kinematics (1) satisfying Assumption 1. If there exists a control law letting $V_e=0$ and $\alpha _e^h=0$, $X_e$, $Y_e$, u, and v will asymptotically converge to zero as $t\rightarrow \infty$.

Proof

Let us define a Lyapunov function candidate

$$\begin{aligned} V=\frac{1}{2}X_e^2+\frac{1}{2}Y_e^2+\sqrt{u^2+v^2}. \end{aligned}$$

(13)

Owing to $V_e=0$ and $\alpha _e^h=0$, we have

$$\begin{aligned} \sqrt{u^2+v^2}=\frac{M_x}{K_x \tau }\left[ \exp \left( \frac{K_x}{M_x}\sqrt{X_e^2+Y_e^2} \right) -1 \right] \end{aligned}$$

(14)

$$\begin{aligned} \psi \!=\!\arctan {\frac{Y_e}{X_e}},\cos {\psi }\!=\!\frac{X_e}{\sqrt{X_e^2+Y_e^2}}, \sin {\psi } \!=\!\frac{Y_e}{\sqrt{X_e^2+Y_e^2}}.\nonumber \\ \end{aligned}$$

(15)

Taking the derivative of (13) and substituting (1), (14), and (15) into it, we have

$$\begin{aligned} {\dot{V}}&=X_e{\dot{X}}_e+Y_e{\dot{Y}}_e\nonumber \\&\ \ \ +\frac{\mathrm{d}}{\mathrm{d}t}\left\{ \frac{M_x}{K_x \tau }\left[ \exp \left( \frac{K_x}{M_x}\sqrt{X_e^2+Y_e^2} \right) -1 \right] \right\} \nonumber \\&=-X_e(\cos \psi \cdot u - \sin \psi \cdot v)-Y_e(\sin \psi \cdot u + \cos \psi \cdot v)\nonumber \\&\ \ \ +\frac{1}{\tau }\frac{X_e{\dot{X}}_e+Y{\dot{Y}}_e}{\sqrt{X_e^2+Y_e^2} }\exp \left( \frac{K_x}{M_x}\sqrt{X_e^2+Y_e^2} \right) \nonumber \\&=-\left[ \sqrt{X_e^2+Y_e^2}+\frac{1}{\tau }\exp \left( \frac{K_x}{M_x}\sqrt{X_e^2+Y_e^2} \right) \right] \cdot u\nonumber \\&\le 0. \end{aligned}$$

(16)

Let ${\mathscr {R}}$ be the set of all points in state space where ${\dot{V}}=0$, so ${\mathscr {R}}=\{x|u=0\}$. According to the dynamics of (4a) and (4b), the derivatives of all states can be zero only when $u=0$ and $v=0$. Then, the largest invariant set in ${\mathscr {R}}$ can be defined as ${\mathscr {M}}=\{x|u=0,v=0\}$. Furthermore, based on the (14), the $X_e$ and $Y_e$ must be zero when $u=0$ and $v=0$. Thus, the invariant set is equivalent with ${\mathscr {M}}=\{x|X_e=0,Y_e=0,u=0,v=0\}$.

Finally, according to the LaSalle’s invariance principle, the system states will asymptotically converge to ${\mathscr {M}}$ as $t\rightarrow \infty$. This completes the proof. $\square$

The HOV control strategy ensures the velocity of robotic fish converges to zero when it arrives at the target. However, the condition of Theorem 1 is hard to meet for the robotic fish, especially when it is close to the target. As the robot gets closer to the terminal point, the regulation of the heading angle would be more and more difficult owing to the input coupling between y axis acceleration and yaw angular acceleration. More specifically, the variation rate of relative angle $\phi$ will increase as the distance from the target is shorten, thus the heading of the robot needs to be adjusted frequently which induces the drifts on y axis and causes that the robot is hard to arrive at the goal accurately. Besides, since the control input $u_1$ is always nonnegative, the robotic fish can only rely on the fluid drag to decelerate, which causes that the forward velocity is hard to decrease to the desired range in a limited time.

3.2.2 Velocity–orientation–velocity (VOV) control strategy

As shown in Fig. 1b, the velocity orientation can be defined as below

$$\begin{aligned} \gamma = \arctan {\frac{v}{u}}. \end{aligned}$$

(17)

Define the velocity angle error $\alpha _e^v$ as

$$\begin{aligned} \alpha _e^v = \phi - \gamma - \psi . \end{aligned}$$

(18)

Similarly, the objective of VOV control is to regulate the errors $\alpha _e^v$ and $V_e$ to zero, and we can clarify the equivalence between VOV control and position control.

Theorem 2

Consider the system kinematics (1). If there exists a control law letting $V_e=0$ and $\alpha _e^v=0$, $X_e$, $Y_e$, u, and v will asymptotically converge to zero as $t\rightarrow \infty$.

Proof

Let us define a Lyapunov function candidate

$$\begin{aligned} V=\frac{1}{2}X_e^2+\frac{1}{2}Y_e^2+\sqrt{u^2+v^2}. \end{aligned}$$

(19)

Owing to $V_e=0$ and $\alpha _e^v=0$, we have Eq. (14) and

$$\begin{aligned}&\psi = \arctan {\frac{Y_e}{X_e}}-\arctan {\frac{v}{u}}\nonumber \\&\cos \psi = \frac{X_e\cdot u + Y_e\cdot v}{\sqrt{X_e^2+Y_e^2}\sqrt{u^2+v^2}} \nonumber \\&\sin \psi = \frac{Y_e\cdot u - X_e\cdot v}{\sqrt{X_e^2+Y_e^2}\sqrt{u^2+v^2}}. \end{aligned}$$

(20)

Taking the derivative of (19) and substituting (1), (14), and (20) into it, we have

$$\begin{aligned} {\dot{V}}&=X_e{\dot{X}}_e+Y_e{\dot{Y}}_e\nonumber \\&\ \ \ +\frac{\mathrm{d}}{\mathrm{d}t}\left\{ \frac{M_x}{K_x \tau }\left[ \exp \left( \frac{K_x}{M_x}\sqrt{X_e^2+Y_e^2} \right) -1 \right] \right\} \nonumber \\&=-\left[ 1+\frac{1}{\tau }\frac{1}{\sqrt{X_e^2+Y_e^2} }\exp \left( \frac{K_x}{M_x}\sqrt{X_e^2+Y_e^2} \right) \right] \nonumber \\&\ \ \ \ \cdot {\sqrt{X_e^2+Y_e^2}\sqrt{u^2+v^2}}. \end{aligned}$$

(21)

According to (14), $u^2+v^2$ will be not equal to zero when $X_e^2+Y_e^2\ne 0$. Thus, when $X_e\ne 0$, $Y_e\ne 0$, $u \ne 0$, and $v\ne 0$, there exists ${\dot{V}}<0$. It means that the system states will asymptotically converge to zero as $t \rightarrow \infty$. This completes the proof. $\square$

Since the VOV control scheme guarantees the resultant velocity of robotic fish to point to the goal, it can effectively solve the terminal drift issue caused by input coupling. However, the resultant velocity orientation depends on both surge velocity and sway velocity, which is relative with two control inputs of $u_1$ and $u_2$, so the allocation of control quantities is an issue. Besides, the controller based on the VOV strategy sometimes induces a few strange system behaviors, e.g., backward swimming, which will be discussed in simulation.

3.3 Two-stage orientation–velocity NMPC controller

The HOV and VOV control strategies each possess a few weaknesses, thus a novel control scheme combined the HOV and VOV is proposed to strike a sound balance, which is called the TSOV-NMPC algorithm. Particularly, there are three reasons for utilizing the NMPC algorithm, including 1) It allows explicit consideration of state and input constraints. 2) Through adjusting the weighting matrices of the cost function, the control strategies of HOV and VOV can be easily integrated into one framework. 3) NMPC can deal with the problem of control allocation in VOV control, which is difficult for the controller of single-input single-output, e.g., PID.

For formalizing this NMPC problem, the complete system state vector is defined as ${\mathbf {x}}=[V_e,\alpha _e^h,\alpha _e^v,X,Y,\psi ,u,v,\omega ]^T\in {\mathbb {R}}^9$. The control vector is defined as ${\mathbf {u}}=[u_1,u_2]^T\in {\mathbb {R}}^2$. The dynamic system can be written as follows [32]:

$$\begin{aligned} \dot{{\mathbf {x}}}=f({\mathbf {x}},{\mathbf {u}}) \end{aligned}$$

(22)

where

$$\begin{aligned}&{\dot{V}}_e=\frac{1}{\tau }\exp \left( \frac{K_x}{M_x}\sqrt{X_e^2+Y_e^2} \right) \frac{-X_e{\dot{X}} -Y_e{\dot{Y}}}{\sqrt{X_e^2+Y_e^2}}\\&-\frac{u{\dot{u}}+v{\dot{v}}}{\sqrt{u^2+v^2}}\\&{\dot{\alpha }}_e^h=\frac{-X_e{\dot{Y}}+Y_e{\dot{X}}}{X_e^2+Y_e^2}-\omega \\&{\dot{\alpha }}_e^v=\frac{-X_e{\dot{Y}}+Y_e{\dot{X}}}{X_e^2+Y_e^2}-\frac{{\dot{v}}u-{\dot{u}}v}{u^2+{v^2}}-\omega . \end{aligned}$$

The basic idea of NMPC is as follows: at each sampling instant we solve a finite horizon optimization problem that evaluates the cost of the predicted future behavior of the system, then apply the first element of optimized control sequences as feedback control for the next sampling interval. The optimization problem at time instant t can be formalized as below

$$\begin{aligned} \min _{{\mathbf {u}}(\cdot )} {J({\mathbf {x}}(t),{\mathbf {u}}(\cdot ))} \end{aligned}$$

(23)

subject to:

$$\begin{aligned}&\dot{\hat{{\mathbf {x}}}}(\tau ) = f(\hat{{\mathbf {x}}}(\tau ),{\mathbf {u}}(\tau )), \forall \tau \in [t,t+T_p]\\&{{\mathbf {u}}}(\tau ) = {{\mathbf {u}}}(t+T_c), \forall \tau \in [t+T_c,t+T_p]\\&\hat{{\mathbf {x}}}(\tau ) \in {\mathscr {X}},\ {\mathbf {u}}(\tau ) \in {\mathscr {U}}, \forall \tau \in [t,t+T_p] \end{aligned}$$

with

$$\begin{aligned} J({\mathbf {x}}(t),{\mathbf {u}}(\cdot ))&=\hat{{\mathbf {x}}}(t+T_p)^T{\mathbf {P}}\hat{{\mathbf {x}}}(t+T_p) \\&+\int _{t}^{t+T_p} \hat{{\mathbf {x}}}(\tau )^T{\mathbf {Q}}\hat{{\mathbf {x}}}(\tau )+{\mathbf {u}}(\tau ) ^T{\mathbf {R}}{\mathbf {u}}(\tau ) \ \mathrm{d}\tau \end{aligned}$$

where $J({\mathbf {x}},{\mathbf {u}})$ is the cost function. $\hat{{\mathbf {x}}}$ represents the predicted states based on (22) and ${\mathbf {u}}(\cdot )$ is the control sequence. $T_p$ and $T_c$ denote the prediction and control horizon, respectively, and $T_c\le T_p$. ${\mathscr {X}}$ and ${\mathscr {U}}$ are the sets of state constraints and input constraints. Besides, ${\mathbf {P}}$ and ${\mathbf {Q}}$ are positive semidefinite weighting matrices. ${\mathbf {R}}$ is positive definite weighting matrix. These matrices represent the coefficients of terminal penalty and running cost.

Based on the definition of the above optimization problem, the TSOV-NMPC algorithm can be listed as follows:

Note that the TSOV-NMPC algorithm can be regarded as that the HOV control and VOV control are automatically switched by a threshold condition. More specifically, the first stage of TSOV-NMPC is aimed to decrease the heading angle error $\alpha _e^h$. Once $\alpha _e^h$ is less than the predetermined threshold, the second stage is activated to govern velocity angle error. Besides, since the TSOV-NMPC algorithm is equivalent to a combination of two controllers, the feasibility and convergence of this controller can be divided into two individual parts to analyze. However, no matter for the separate HOV-based NMPC algorithm or the VOV-based one, they are classic applications of NMPC whose proofs of feasibility and convergence have been given by the literature [32]. Thus, the detailed explanations would not be explored in this article.

4 Simulation

In order to evaluate the effectiveness of the proposed position control scheme, the adequate simulations were conducted in Matlab environment. The parameters adopted are derived from the actual robot and are tabulated in Table 1. Additionally, the parameters applied to implement the NMPC algorithm are as follows:

• Simulation duration: 100 sec.

• Control period: 1 sec.

• Predicted and control horizon: $T_p=15$, $T_c=5$.

• State weighting matrix (TSOV first stage):

  ${\mathbf {Q}}=\text {diag}(100,100,10,0,0,0,0,0,0)$.

• State weighting matrix (TSOV second stage):

  ${\mathbf {Q}}=\text {diag}(100,0,10,0,0,0,0,0,0)$.

• Control weighting matrix: ${\mathbf {R}}=\text {diag}(0.01,0.01)$.

• Terminal penalty matrix: ${\mathbf {P}}=\text {diag}(0,0,0,0,0,0,0,0,0)$.

• Velocity constraint constant: $\tau =50$.

• State constraints: $V_e\ge 0$.

• Input constraints: $0 \le u_1 \le 0.5$, $-0.2 \le u_2 \le 0.2$.

Table 1 Simulation parameters of the robotic fish

Fig. 2

The motion trajectories of the robotic fish controlled by various controllers. The plots a–f depict the results of six kinds of controllers and the red pentagrams denote the target positions

4.1 Control strategy comparison

In this subsection, we primarily discuss the control performance for the robotic fish under the various error definitions. Based on the idea of feedback control, the definition of control error is the first thing that should be considered. There are several ways to define the error on position control, which brings completely different control performances. These error definitions can be divided into two categories. The first kind is directly related to the position, distance, and orientation, while the second one mainly depends on velocity and orientation. Here, five kinds of error definitions are given as below

Directed error

• Position error (PE): $X_e = X_T - X$, $Y_e = Y_T - Y$.

• Polar coordinate position error (PCPE): $\alpha _e^h$, $r_e=\sqrt{X_e^2+Y_e^2}$.

Velocity-based error

• HOV error: $V_e$, $\alpha _e^h$.

• VOV error: $V_e$, $\alpha _e^v$.

• TSOV error: $V_e$, $\alpha _e^h$, and $\alpha _e^v$.

Particularly, in order to evaluate the control effect of these error definitions, the NMPC algorithm was utilized as the unified controller to regulate the errors. Besides, a proportional–integral–derivative (PID) controller combined with the HOV error was applied to demonstrate the effectiveness of NMPC.

Without loss of generality, the robotic fish was commanded to start from the origin point and swim to eight positions, including the coordinates of (4, 0), $(4,-4)$, $(0,-4)$, $(-4,-4)$, $(-4,0)$, $(-4,4)$, (0, 4), and (4, 4). The initial states of robotic fish for simulation were set as zero.

The simulation results corresponding to six controllers are shown in Fig. 2. The first thing is to inspect the motion trajectories of every case. Obviously, the trajectories of TSOV-NMPC in Fig. 2a are far better than those in other cases. The robotic fish controlled by TSOV-NMPC successfully and precisely arrives at every position. Besides, it moves more efficiently compared with the case of HOV-PID in Fig. 2f, which can be inferred from the comparison of path length. For the case of HOV-NMPC (Fig. 2b), PCPE-NMPC (Fig. 2e), and HOV-PID (Fig. 2f), the robotic fish approaches the target point in the beginning but drifts off the course at the final stage. In addition, for the cases of VOV-NMPC (Fig. 2c) and PE-NMPC (Fig. 2d), the robotic fish fails to arrive at every target point and whether the position control is successful or not largely depends on the target position and its initial states. The further inspection of the robot velocities and cost function turns out that the optimization problem gets stuck at the local optimum and the robotic fish enters into a backward swimming mode, which is an abnormal motion and with very low velocity. Though the control input $u_1$ must be greater than zero, the Coriolis term $v\omega$ in (4a) makes ${\dot{u}}<0$ become possible. It should be noticed that backward swimming motion is easier to be activated in optimization-based methods, e.g., NMPC, since these methods leverage more dynamic characteristics compared with the modeless approach, e.g., PID. It reveals that a well-selected error definition and control algorithm will make a great impact on the success rate of position control and efficiency.

Fig. 3

The boxplot of the terminal error of various position controllers

The second thing is to observe the terminal performances of every case. Without regard to the failures, the robotic fish controlled by TSOV-NMPC and VOV-NMPC arrives at the target point with a smooth and precise way, which is benefit from the definition of velocity–orientation error $\alpha _e^v$. While for the case of HOV-NMPC, PCPE-NMPC, and HOV-PID, all of them utilize the heading angle error $\alpha _e^h$, the robotic fish will deviate the course whenever it approaches the terminal position. This is due to the input coupling of ${\dot{v}}$ and ${\dot{\omega }}$. When the robotic fish is close to the target, the change of $\alpha _e^h$ will increase. In order to adjust $\alpha _e^h$, the position error on the y axis will increase under the impact of input coupling. Besides, though the robot based on PE-NMPC reaches the target, the terminal path is relatively tortuous, which shows the deficiency of the definition of PE.

Furthermore, Fig. 3 shows the statistical results of terminal errors of various control strategies. The height of the box in the plot denotes the reliability of the control scheme. The shorter the box is, the better repeatability and success rate the controller possesses. The middle line represents the general control precision, namely, the lower middle line means smaller terminal error and higher precision. A careful inspection of Fig. 3 reveals that the TSOV-NMPC possesses the best control precision and the most reliable performance, whose terminal error is about 2 cm and success rate is $100\%$.

4.2 Terminal behavior analysis of TSOV-NMPC

There exists an interesting terminal behavior for the robotic fish controller by TSOV-NMPC. We name it as the twist-braking mechanism. As shown in Fig. 4, the forward velocity u, control inputs $u_1$ and $u_2$ for the case whose target is (4, 0) are displayed. It can be easily found that the thrust $u_1$ becomes zero after about 15 second and the velocity reaches the maximum value. Then, the deceleration process can be divided into two stages. The first stage is from 15 to 50 second, where the $u_1$ and $u_2$ are almost zero and the robotic fish is braked by hydrodynamic. The second stage begins at 50 second and the $u_2$ begins to exert influence on robotic fish, where the twist-braking mechanism is activated so that the velocity decreases rapidly to satisfy the velocity constraint.

Figure 5 displays the twist-braking mechanism visually. As shown in Fig. 5, the robotic fish controlled by TSOV-NMPC utilizes tail torque to twist its body and slide sideways, when it approaches the goal. Since the lateral resistance ($K_y=20$) is far larger than the forward one ($K_x=2$), the forward velocity decreases quickly so that the robotic fish is able to stay at the terminal point. However, in the reference case, the hydrodynamic force fails to brake the robotic fish, which slides away from the target eventually.

By careful inspection of the dynamic model (4a), we note that the velocity coupling term $v\omega$ provides the crucial deceleration force in the process of the twist-braking, since both the fluid drag and control input is quite small at that time. Furthermore, the deceleration effect of coupling term $v\omega$ is related to the two dynamic characteristics of robotic fish. The first one is the opposite sign of the control input for lateral acceleration (4b) and steering acceleration (4c). It causes that the lateral velocity $\omega$ and steering velocity v will increase along the opposite direction which makes the coupling term $v\omega$ easier to be negative. The second one is the large drag coefficient of y axis, which guarantees that the lateral velocity increases in a limited range. Besides, on the viewpoint of energy, the nature of the twist-braking mechanism is converting the forward velocity into the lateral velocity, then leveraging the larger lateral drag coefficient to achieve faster energy dissipation. In a word, the twist-braking mechanism fully reveals that the NMPC algorithm can leverage the dynamic characteristics of robotic fish to achieve a better control effect.

Fig. 4

The forward velocity curve and the corresponding control inputs of the robotic fish that controlled by TSOV-NMPC. The green dotted line denotes the velocity constraint calculated by (9). The blue dot-dash line denotes the velocity of the robotic fish that is without the twist-braking mechanism and only decelerated by viscous force

Fig. 5

Schematic of the twist-braking mechanism. The reference case means that the robotic fish can only decelerate itself by viscous force

Fig. 6

The simulation results of the underwater sensor network deployment by robotic fish. a motion trajectory, b x-direction displacement, c y-direction displacement, d resultant velocity

4.3 Underwater sensor network deployment

The motivation of the position control is to empower the robotic fish with the ability to arrive at the specified location and execute tasks. In this subsection, we assumed a mission that the robotic fish needs to automatically deploy an underwater sensor network consisted of six sensors. Then, the performances of TSOV-NMPC was evaluated. The locations of the six sensors were randomly generated. The robotic fish started from the origin, went to every target location to deploy sensors, and went back to origin eventually. Note that finding the optimal deploy order can be regarded as a traveling salesman problem, which was determined by the genetic algorithm in this article. Figure 6 shows the simulation results of robotic fish controlled by TSOV-NMPC. From the motion trajectories in Fig. 6a, it can be easily found that the robotic fish successfully arrives at every target position. As shown in Fig. 6b, the response curve of position control has no overshoot and the required time from one position to another is nearly the same. Besides, the velocity curve in Fig. 6c shows that the velocity will decrease to zero whenever the robot arrives at the target position, which creates the conditions for the sensor deployment.

However, the careful inspection reveals that the robotic fish sometimes does not take the direct route but makes a detour, which is due to the uncontrolled terminal orientation. Thus, our future work will focus on controlling the terminal position and orientation simultaneously.

5 Conclusion and future work

In this article, we have presented a TSOV-NMPC algorithm for the position control of bionic robotic fish, which creates a convenient condition for performing the underwater mission. At first, a scaled averaging model is constructed for tail-actuated robotic fish. By means of the dynamic model, the velocity constraint is derived. Besides, the HOV and VOV control strategies are proved to be equivalent with the position control in the sense of Lyapunov. Furthermore, the NMPC algorithm with a two-stage switching mechanism is designed to reduce the orientation and velocity error, which combines the virtue of HOV and VOV methods. Finally, the precision and adaptability of TSOV-NMPC are demonstrated by numerical simulation, and the twist-braking mechanism existing in simulation further reveals that the proposed method utilizes the dynamic characteristics of robotic fish to achieve better control performance.

The ongoing and future work will focus on the position control under external disturbance as well as the pose control of robotic fish that consists of position control and orientation control simultaneously.