Swimming on limit cycles with nonholonomic constraints

Abstract

The control and motion planning of bioinspired swimming robots is complicated by the fluid–robot interaction, which is governed by a very high (infinite)-dimensional nonlinear system. Many high-dimensional nonlinear systems, often have low-dimensional attractors. From the perspective of swimming robots, such low-dimensional attractors simplify the analysis of the mechanics of swimming and prove to be useful to design controllers. This paper describes such a low-dimensional model for the swimming of a class of robots that are propelled by the motion of an internal reaction wheel. The model of swimming on a low-dimensional attractor is itself motivated by recent work on the dissipative Chaplygin sleigh, a well-known nonholonomic system, that exhibits limit cycle dynamics. We show that the governing equations of the Chaplygin sleigh are a very useful surrogate model for the swimming robot. The Chaplygin sleigh model is used to demonstrate certain maneuvers by the robot through computations. Experiments with such a robot provide evidence of limit cycle dynamics. Computational models based on discrete-point vortex–body interaction confirm this behavior. Our work also suggests that there is a close phenomenological and mathematical similarity between the dynamics of swimming robots and those of ground-based nonholonomic robots, which could motivate the development of very low-dimensional mathematical models for the motion of other fish-like swimming robots.

1 Introduction

Natural swimmers like fish have many characteristics such as high propulsive efficiency, agility and stealth [1,2,3] that are highly desirable in a swimming robot. The last two decades have seen the development of several bioinspired swimming robots, perhaps the most famous of which is MIT’s robot-tuna [4, 5]. The locomotion of carangiform and sub-carangiform fish has inspired the design of robots with a compliant body or a compliant tail, see, for example, [6,7,8,9,10,11,12,13], as well as articulated joints to imitate fish vertebrae, [14,15,16]. Other multisegmented robots such as in [17,18,19,20] have been inspired by the motion of eels and snakes. In recent years, the authors and others investigated a class of swimming robots propelled by an internal reaction wheel [21, 22, 49] whose mathematical model was inspired by that of fish-like swimming [21, 23,24,25,26].

Besides the practical design of swimming robots, accompanying mathematical models of swimming dynamics and motion control are necessary. Here, one has to contend with the coupled robot-hydrodynamic interactions which are very challenging to model. Modeling the hydrodynamics by the Navier–Stokes equation is a significant challenge and can lead to intractable analytical models or purely numerical simulations that are computationally resource intensive. In such cases, the lack of simplified models makes the task of designing controllers for the robots challenging. The goal of this paper is to put forth a simplified model of fish-like swimming, based on the identification of limit cycles in the dynamics of robot–fluid interaction. The reduced order model is achieved in two steps: first by adopting a simplified model of the fluid flow and the interaction with the robot. In the second step, the dynamics of the swimming body is recognized to be similar to that of the Chaplygin sleigh, a nonholonomic system. It is shown through computations and experiments that a limit cycle exists in the velocity space of the swimmer. This identification is motivated by the previous work [21, 25] on the swimming of a fish-shaped body (a Joukowski foil), which showed that the vortex shedding past the sharp edge of the foil imposes a nonholonomic constraint on its motion that is similar to the constraint on a Chaplygin sleigh. The main contribution of the paper is showing the similarity of fish-like swimming to the dynamics of certain nonholonomic systems, in this paper specifically, the Chaplygin sleigh. In both the cases the dynamics are shown to converge to qualitatively similar limit cycles. Analytical approximations of these limit cycles are used to create a low dimensional surrogate model of the a rigid swimmer and this model is used to control its motion.

To obtain a simplified model of the fluid–swimmer interaction, the fluid is modeled to be ideal and the force on the body is computed through potential flow theory. The effects of viscosity which are important only in a thin boundary layer around the body are such that they lead to vortex shedding. This phenomenon is included in the inviscid models via the creation of singular distributions of vorticity at some point(s) close to the surface of the body of the robot. The Kutta–Joukowski condition [27] in one form or the other is often used to model this vortex shedding behavior. While the problem of dynamics of point vortices interacting with a body has a rich history, one of the early examples of this approach in the context of swimming can be found in [28,29,30]. More recently, it has been recognized that the interaction of point vortices with a rigid body has a Hamiltonian structure [31,32,33,34] and the associated conservation of linear and angular impulse has been used to model the propulsion of a fish-shaped body with prescribed deformations [35, 36]. The essential physics of these models is that a fish-shaped body (a Joukowski foil) with prescribed deformations can achieve propulsive motion through the vorticity that is created at the cusp of the Joukowski foil. While the changes in the inertia tensor of the body due to the shape deformations could result in small, perhaps reversible motion, vortex shedding is the more significant propulsive factor.

Inspired by this physics, it has been observed in [21, 23, 24] that vortex shedding can be induced at the cusp of a Joukowski foil through the motion of an internal reaction wheel. That this vortex shedding can be useful for propulsion was demonstrated in [22]. More interestingly, the simplicity of such swimming robot led to the identification of the vortex shedding condition in inviscid flow models as a nonholonomic constraint. An explicit calculation of this was shown in [21, 25] assuming the Kutta condition was in the steady state. The nonholonomic constraint on the motion of a Joukowski foil imposed by the Kutta condition was shown to be similar to the constraint on the Chaplygin sleigh, a well-known nonholonomic system [37,38,39,40,41]. The motion of the Chaplygin sleigh propelled by the rotation of an internal reaction wheel was investigated in [41,42,43]; however, the motion of the classical Chaplygin sleigh differs somewhat from that of the swimming robot with an internal reaction wheel, mainly due to the presence viscous dissipation in swimming. In [44], the dynamics of the Chaplygin sleigh in the presence of viscous dissipation were investigated and it was found that for periodic rotation of the reaction wheel, a globally stable limit cycle solution existed for the velocity of the sleigh.

In this paper, we first demonstrate the existence of limit cycle solutions for a Chaplygin sleigh with a prescribed periodic slip velocity, a so-called affine nonholonomic constraint. This is important because numerical simulations suggest that the transverse velocity of the fluid at the trailing edge of the Joukowski foil is not zero, but instead is periodic with a small magnitude. We then present experimental evidence that the velocity of a swimming robot with a reaction wheel has a limit cycle. This limit cycle is topologically similar to that of the dissipative Chaplygin sleigh. We also show through numerical simulations that the velocity dynamics of a Joukowski foil excited by periodic torque has a topologically similar limit cycle. An analytical approximation of the limit cycle is obtained by the harmonic balance approach for the swimming Joukowski foil based on a similar approximation for the Chaplygin sleigh in [44]. This approximation is used to simulate the controlled motion of the Joukowski foil. We essentially model the very complicated dynamics of the swimming robot by the equations of motion of the dissipative Chaplygin sleigh.

While the results presented here utilize a specific model of a swimming robot, they can be generalized to other fish-like robots with actuated or passive tail- or fin-like appendages. Within the framework of inviscid fluid flows, the Kutta–Joukowski condition that leads to vortex shedding at sharp edges is a nonholonomic constraint. Inspired by this, nonholonomic systems similar to a Chaplygin sleigh with appendages have been investigated in [45,46,47] and the equivalent swimming robots have been studied in [48], [?]. The motion of the swimming robots with tails in [?] demonstrates periodic limit cycle motion that is similar to the limit cycle dynamics discussed in this paper. It can therefore be expected that dissipative nonholonomic systems with appendages and multiple constraints can be computationally cheap and very useful control-oriented surrogate models of swimming robots.

The organization of the paper is as follows. In Sect. 2, we will first review the dynamics of the Chaplygin sleigh with a homogeneous nonholonomic constraint based on the work in [44, 50]. We will then extend this model to present new results on the dynamics of the Chaplygin sleigh with a periodic affine nonholonomic constraint in the form of a prescribed periodic slip velocity. The limit cycles of the Chaplygin sleigh with a homogeneous constraint and a periodic affine constraint are topologically similar, and an approximation is constructed based on the harmonic balance approach. The dynamics of the sleigh with the affine constraint are investigated and shown to be nearly identical to the dynamics of the Chaplygin sleigh with a zero slip velocity constraint. In Sect. 2.1, the limit cycle solutions are used to control the heading and the speed of the Chaplygin sleigh. In Sect. 3, we will present experimental evidence of limit cycles in the dynamics of a swimming robot. In Sect. 4, we will discuss the numerical simulations of a Joukowski foil whose hydrodynamic interactions are modeled by point vortex dynamics. The steady Kutta–Joukowski vortex shedding condition at the sharp edge of the foil is an affine nonholonomic constraint. Through simulations based on panel methods and point vortex dynamics, it will be shown that the unsteady Kutta condition is a periodic affine nonholonomic constraint. In Sect. 5, we show the utility of the sleigh-like surrogate models by applying the control algorithm developed for Chaplygin the sleigh, described in Sect. 2.1, to the swimming Joukowski foil, to steer it in a desired direction with a prescribed speed.

2 The dissipative Chaplygin sleigh

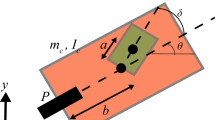
The Chaplygin sleigh is a well-known nonholonomic system. The system consists of a sleigh with a knife edge at the rear that is in contact with the ground at a single point. The sleigh is shown in Fig. 1. The axes denoted by X and Y in Fig. 1 correspond to a fixed inertial frame of reference. The axes denoted by $X_b$ and $Y_b$ correspond to a body frame. The point of contact of the knife edge with the ground is denoted by P. The position of the center of the sleigh measured in the inertial frame of reference is denoted by (x(t), y(t)) and its orientation by $\theta (t)$. The velocity of the point of contact P of the rear wheel with the ground is denoted by $(u_x, u_y)$ as measured in the body frame of reference. The sleigh can slip freely along the longitudinal axis, $X_b$, of the sleigh but the transverse velocity of the knife edge is constrained to be zero. This constraint is

$$\begin{aligned} -\dot{x}\sin {\theta } + \dot{y} \cos {\theta } - b\dot{\theta } = u_y = 0. \end{aligned}$$

(1)

Fig. 1

The Chaplygin sleigh—the body frame is denoted by the axes $X_b-Y_b$. The point P on the sleigh has zero velocity in the $Y_b$ direction

To propel the sleigh, a balanced momentum or reaction wheel is placed on top of it that can execute oscillatory motion. The relative angle of the reaction wheel with respect to the body frame is denoted by $\phi$. The configuration space of the system is $Q = SE2 \times S^1$. Because of the nonholonomic constraint, the motion of the sleigh can be described by a reduced number of equations, through the nonholonomic reduction. These reduced equations of motion of the sleigh with the nonholonomic constraint are well known, see for instance, [38] for a derivation using Newton’s laws of motion [41, 43] for a derivation using the Lagrange multiplier approach and [42, 51] for a derivation of the nonholonomic momentum equations using the reduced Lagrangian.

In this section, we derive the equations of motion of the Chaplygin sleigh with a more general nonholonomic constraint as well as a viscous friction force that acts in the allowable direction of motion. We will assume that the transverse velocity $u_y$ of the knife edge is prescribed. The case of $u_y=0$ can be obtained as a special case of the general equations. A possibly nonzero constraint velocity, $u_y$, that is prescribed generates a so-called affine nonholonomic constraint [52].

The velocity of the center of mass of the sleigh, $\mathbf {v}_c$, can be written as

$$\begin{aligned} \mathbf v _c=u_x\hat{i}_b+(u_y+b\omega )\hat{j}_b \end{aligned}$$

(2)

where $i_b$ and $j_b$ represent unit vectors aligned with the body axes. The acceleration of the center of mass of the sleigh is then

$$\begin{aligned} \dot{\mathbf{v }}_c=(\dot{u}_x-b\omega ^2-\omega u_y)\hat{i}_b+(\dot{u}_y+b\dot{\omega } +\omega u_x)\hat{j}_b. \end{aligned}$$

(3)

Suppose the constraint force at the point of contact of the knife edge P is $F_y\hat{j}_b$ and the viscous frictional force at the knife edge in the allowable direction of motion is $F_x = -c u_x$, then the equations of motion of the sleigh are

$$\begin{aligned}&m(\dot{u}_x-b\omega ^2-\omega u_y)=F_x \end{aligned}$$

(4)

$$\begin{aligned}&m(\dot{u}_y+b\dot{\omega }+\omega u_x)=F_y \end{aligned}$$

(5)

$$\begin{aligned}&I\dot{\omega }=\tau -b F_y. \end{aligned}$$

(6)

Here, $\tau$ is the torque acting on the sleigh and $\omega = \dot{\theta }$ is the angular velocity of the sleigh. Eliminating the constraint force $F_y$ by combining (5) and (6), the equations of motion become

$$\begin{aligned}&\dot{u}_x=b\omega ^2+\omega u_y-\frac{c}{m}u_x \end{aligned}$$

(7)

$$\begin{aligned}&\dot{\omega }=\frac{\tau -mb\omega u_x - mb\dot{u}_y}{I+mb^2} \end{aligned}$$

(8)

In the special case $u_y=0$ and $\dot{u}_y=0$, one obtains the standard nonholonomic equations of motion of the Chaplygin sleigh.

The motion of the sleigh in the plane is described by the equations

$$\begin{aligned} \dot{x}&= u_x\cos {\theta } - (u_y+\omega b)\sin {\theta } \end{aligned}$$

(9)

$$\begin{aligned} \dot{y}&= u_x\sin {\theta } + (u_y + \omega b)\cos {\theta } \end{aligned}$$

(10)

$$\begin{aligned} \dot{\theta }&= \omega . \end{aligned}$$

(11)

When a periodic torque $\tau = A\cos {\varOmega t}$ acts on the sleigh, the dynamical system described by (7) and (8) has a stable limit cycle [44, 50]. An approximation to the limit cycle can be obtained through the harmonic balance method. We extend these results to the general case where $u_y \ne 0$ is a prescribed periodic function

$$\begin{aligned} u_y=A_y\sin (\varOmega t)+B_y\cos (\varOmega t). \end{aligned}$$

(12)

Following the harmonic balance method, we assume a periodic solution to (7)–(8) of the form

$$\begin{aligned}&u_x=u_c+A_x \sin (2\varOmega t)+B_x \cos (2\varOmega t) \end{aligned}$$

(13)

$$\begin{aligned}&\omega = A_w \sin (\varOmega t)+B_w \cos (\varOmega t). \end{aligned}$$

(14)

Substituting the assumed periodic solutions into (7)–(8) and equating the coefficients of the sine and cosine functions up to the second order as well as the constant terms yield the following system of nonlinear equations:

$$\begin{aligned}&A_w^2bm+B_w^2bm-2cu_c+A_wA_ym+B_wB_ym = 0 \end{aligned}$$

(15a)

$$\begin{aligned}&2A_wB_wbm-2A_x c +4m\varOmega B_x\nonumber \\&\qquad +\,A_wB_ym+A_yB_wm = 0 \end{aligned}$$

(15b)

$$\begin{aligned}&-A_w^2bm+B_w^2bm-2B_xc-4m\varOmega A_x \nonumber \\&\qquad -A_wA_ym+B_wB_ym = 0 \end{aligned}$$

(15c)

$$\begin{aligned}&-A_xB_wbm+A_wB_xbm-2A_wbmu_c \nonumber \\&\qquad +2A+2\alpha \varOmega B_w+2B_y\varOmega bm = 0 \end{aligned}$$

(15d)

$$\begin{aligned}&-A_xA_wbm-B_xB_wbm-2B_wbmu_c \nonumber \\&\qquad -2\alpha \varOmega A_w-2A_y\varOmega bm = 0 \end{aligned}$$

(15e)

where $\alpha = I+mb^2$. Equations (15a)–(15e) can then be solved using a numerical technique such as the Newton–Raphson method.

A numerical solution of Eqs. (7) and (8) is shown in Fig. 2. The black dotted line in Fig. 2a shows the solution of the system for the nonholonomic constraint $u_y=0$. The solution converges to a periodic solution, the stable limit cycle, shown in blue. The trajectory of the sleigh in the plane obtained by integrating (9)–(11) is shown in Fig. 2b.

Fig. 2

Dynamics of the Chaplygin sleigh. The figures a and b in the top panel are for the case when $u_y=0$, and the figures c and d in the lower panel are for the case when $u_y$ is a small-amplitude periodic function ($A_y=0.03$, $B_y=0.03$). The solid blue line in a and c shows the predicted limit cycle in the velocity space, and the black dotted line shows the evolution of longitudinal and angular velocity of the sleigh and their convergence to the respective limit cycles. The path of sleigh in the plane is shown in b and d for the two cases of the transverse velocity $u_y$. (Color figure online)

A numerical solution of (7) and (8) for the case where a periodic transverse slip velocity is prescribed is shown in Fig. 2c and the corresponding trajectory of the sleigh in the plane is shown in Fig. 2d. The prescribed slip velocity has a small magnitude, with $\sqrt{A_y^2+B_y^2} = 0.03\sqrt{2}$. The approximate solution of the limit cycle given by (13) and (14), shown in blue, is a closed curve shaped as the number ‘8.’ In case of both the type of constraints, the equation of the limit cycles (13) and (14) is a close approximation of the numerical solution of the limit cycle. More importantly, the limit cycle solutions of the sleigh are nearly identical in the two cases with the constraint $u_y=0$ and $u_y = A_y\sin (\varOmega t)+B_y\cos (\varOmega t)$. The average value of the longitudinal velocity is $u_0 = 0.2533$ in the case of the no-slip constraint and $u_0 = 0.2545$ in the case of the periodic slip velocity. The limit cycle solutions show negligible differences in cases where the slip velocity has a small magnitude. A supplementary video of the motion of the sleigh with a periodic transverse slip velocity and the convergence of its longitudinal and angular velocity is available online.

2.1 Steering the sleigh and velocity tracking

The approximate solution to the limit cycle shows that the average angular velocity of the sleigh converges to zero, i.e., the change in the heading angle of the sleigh during one time period $T = \frac{2\pi }{\varOmega }$ is

$$\begin{aligned} \varDelta {\theta }= & {} \int _0^T \omega \mathrm{d}t \nonumber \\= & {} \int _0^T (A_w\sin {\varOmega t} + B_w\cos {\varOmega t}) \mathrm{d}t = 0\nonumber \\ \end{aligned}$$

(16)

The average longitudinal velocity of the sleigh $u_0$ is in general nonzero. This is also borne out in the simulated trajectories of the sleigh in Fig. 2b and d, where average heading of the sleigh becomes constant. On the velocity limit cycle, the average velocity of the sleigh can be defined as

$$\begin{aligned} \overline{\mathbf{v }}&= \frac{1}{T}\int _{t_1}^{t_1+T} (\dot{x} \hat{i} + \dot{y}\hat{j})\mathrm{d}t \end{aligned}$$

(17)

Since the average heading angle converges to a constant value, for the purpose of computing the average speed, one can assume that the average heading angle is $\overline{\theta } = 0$, i.e., $\frac{1}{T}\int _{t_1}^{t_1+T} \dot{y}\mathrm{d}t = 0$. The average speed of the sleigh is then

$$\begin{aligned} \overline{v}= & {} \frac{1}{T}\int _{t_1}^{t_1+T} \dot{x} \mathrm{d}t \nonumber \\= & {} \frac{1}{T}\int _{t_1}^{t_1+T} (u_x\cos {\theta } - (u_y+\omega b)\sin {\theta }) \mathrm{d}t \end{aligned}$$

(18)

where it should be noted that $\frac{1}{T}\int _{t_1}^{t_1+T} \omega b\sin {\theta } \mathrm{d}t = 0$.

Suppose the reference average speed of the sleigh is $\overline{v}_r$, the amplitude of the applied torque, $\tau = A \cos {\varOmega t}$, can be used as the control input to track this reference speed. The required amplitude A can be treated as an unknown. In this case, (15a)–(15e) together with (18) form six equations in the six unknowns, $(A_w, B_w, A_u, B_u, u_0, A)$. These unknowns can be found using a numerical method like the Newton–Raphson method. The velocity tracking control is illustrated for the case of the Chaplygin sleigh with a periodic affine constraint, for the specific case of the no-slip constraint, see [44].

When the solution to (7) and (8) converges to the limit cycle, the average heading angle of the sleigh converges to a constant value, as shown in Fig. 2b, d. This average heading angle can be controlled by a torque that is proportional to the error in average heading angle, i.e.,

$$\begin{aligned} \tau _I=-K_I\int _{t-T}^{t}(\theta (t)-\theta _r) \mathrm{d}t \end{aligned}$$

(19)

where $\theta _r$ is the reference average heading angle of the sleigh. Numerical simulations for a large range of sleigh parameters, reference angles and average velocities of the sleigh show that an input torque of the form

$$\begin{aligned} \tau =A\cos {\varOmega t}+\tau _I \end{aligned}$$

(20)

allows simultaneous control of the average speed of the sleigh and its heading. The first term $A\cos (\varOmega t)$ allows the sleigh to track reference average speed, and the second term $\tau _I$ allows the sleigh to track a desired average angle. A proof that the control input $\tau =A\cos (\varOmega t)+\tau _I$ can lead to tracking both average speed and heading is left for future work.

The utility of the limit cycle solutions can be demonstrated through a simulated maneuver of the sleigh, where it is required to first track an average heading of zero degrees and then make a $90^{\circ }$ turn while tracking an average speed of $\overline{v}=0.2$. The results of the simulation are shown in Fig. 3.

Fig. 3

Turning motion of the Chaplygin sleigh with periodic slip ($A_y=0.03$, $B_y=0.03$). a The average speed of the Chaplygin sleigh tracks the reference speed of $\bar{v}=0.2$. b The path of the sleigh in the plane. c Convergence of the velocity of the sleigh to a limit cycle. d Heading angle of the Chaplygin sleigh, with the average changing from zero to $90^{^{\circ }}$

Fig. 4

Experimental robot shaped as a Joukowski foil. The internal rotor (blue) is driven with a periodic angular velocity by a DC motor, which exerts a periodic torque on the torque on the robot. (Color figure online)

The sleigh’s average heading angle first converges toward zero and then to $90^{\circ }$ (Fig. 3b, d) while its average speed tracks the reference value (Fig. 3a). The sleigh’s velocity–angular velocity converge to the limit cycle, then experience a perturbation away from the limit cycle when the torque $\tau _I$ is added to the input and converge back to the limit cycle as $\tau _I$ converges to zero, see Fig. 3c. The control input for executing this maneuver is such that $\tau _I$ is much smaller in magnitude than A as shown in [44, 50].

$$\begin{aligned} \tau _I\rightarrow 0\quad \iff \frac{\int _{t-T}^{t}\theta (t)\mathrm{d}t}{T}\rightarrow \theta _r. \end{aligned}$$

The average heading angle approaches the desired average heading angle.

3 Swimming on limit cycles: experiments

The swimming robot used in the experimental investigation is shown in Fig. 4. The body of the robot is shaped as a Joukowski foil. The robot is propelled through the rotational oscillations of an internal reaction or momentum wheel attached to a right angle geared DC motor. The horizontal cross section of the robot was modeled after a NACA 0030 symmetric air foil, with total length of 36 cm and is 14 cm at its widest. The body was 3D printed from ABS plastic. The internal momentum wheel is the blue circular object in Fig. 4. The internal momentum wheel is a steal ring with an outer diameter of 13.2 cm and an inner diameter of 10.2 cm and is 0.95 cm thick. The moment of inertia of the momentum wheel about an axis passing through its center of rotation is approximately 14.6 kg cm. The DC motor is controlled by an Arduino Micro, both the motor and Micro were powered by a 7.4 V Lipo battery. The DC motor has a max angular velocity of 220 RPM and a maximum torque of 1.7 kg cm. The robot with all of its components weighs approximately 1100 g. During the experiments, the rotor is forced to turn by the motor with a periodic angular velocity $\dot{\phi }$,

$$\begin{aligned} \dot{\phi } = A\sin {\varOmega t}. \end{aligned}$$

The oscillations of the internal momentum wheel periodically change the heading angle of the robot so when we refer to straight-line swimming, we are referring to the motion on the average being in a straight-line and the periodic trajectory is demonstrated in Fig. 6. In Fig. 6, the solid red line represents the position of the approximate center of gravity (C.G.) of the robot during part of one experiment. The black circles represent the position of the C.G. at a time instant where we have included a blue line to give a visual representation of the robots angular orientation.

The amplitude A and frequency $\frac{\varOmega }{2 \pi }$ of the input function were changed to get results for 12 different input parameters with amplitude A varying between (255, 225, 200) and the input frequency varying between (0.5, 0.75, 1, 1.25) Hz. We have only included one representative result.

Fig. 5

Foil-shaped robot swimming in a pool. A whiteboard with two black filled circles is placed on top of the robot. The circles are detected in images to track the motion of the robot. The whiteboard is above the water level and does not contact the water surface

The experiments were performed in a pool that measures $4.87\,$m$\times$$2.43\,$m, with the depth of water being about $1.2\,$m. The position and the orientation of the robot are recorded by three cameras placed over the pool at a height of about $1.2\,$m from the surface of the water. The cameras recorded video at 1080p quality and a frame rate of 60 FPS. The robot is almost neutrally buoyant. When the robot is placed in water, the surface of the water reaches about 1 cm from the top face of the robot. A whiteboard is stuck on the top face of the robot. The white board has two filled circles drawn on it, as shown in Fig. 5. The circles lie on chord of the foil such that the center of mass of the robot is at the midpoint of the line joining these circles. The filled circles stand in contrast against the white background of the board. The image processing toolbox in MATLAB was used to track the positions of the circles in each image recorded by the cameras.

In each frame recorded by the cameras, the centers of the filled circles are identified. The center of the line joining these circle centers is the center of the robot. The slope of the line joining the centers of the circles identifies the orientation of the robot with respect to a fixed spatial frame of reference. Knowing the position of the center of the robot, $(x(t_k), y(t_k))$ and the orientation angle $\theta (t_k)$ at consecutive times $t_k$, the velocity $(V_x,V_y)$ and the angular velocity $\omega$ of the robot are calculated using Euler forward differences. A sample experimental trajectory obtained by tracking the filled circles is shown in Fig. 6, where the blue lines are the imaginary lines joining the filled circles and the midpoint of these blue lines tracks the position of the center of the robot along its trajectory (red curve).

Fig. 6

Trajectory during one experiment, with the bodies angular orientation shown by the solid blue lines. (Color figure online)

The velocities thus calculated are in the spatial reference frame. In the next step, the velocity of the body in a body frame is calculated. With the estimated global velocities, we apply a rotation matrix to determine the velocity in the body-fixed frame,

$$\begin{aligned} \begin{bmatrix} u_x(t_k)\\ u_y(t_k) \end{bmatrix} = \begin{bmatrix} \cos {\theta (t_k)}&\quad \sin {\theta (t_k)} \\ -\sin {\theta (t_k)}&\quad \cos {\theta (t_k)} \end{bmatrix} \begin{bmatrix} V_x(t_k)\\ V_y(t_k) \end{bmatrix}. \end{aligned}$$

(21)

Rather than plotting the velocity or angular velocity of the robot as functions of time, we instead plot the longitudinal velocity of the robot versus the angular velocity. This is inspired by the dynamics of the Chaplygin sleigh in the reduced velocity space. Figure 7 shows such a plot for one experiment, where the input torque parameters are $\varOmega = 2 \pi$, $A = 12$. Starting from $(u_x =0, \omega =0)$, the trajectory in the reduced velocity space converges to a limit cycle shaped as the number 8. A supplementary video of the motion of the robot and the convergence of its velocity to a limit cycle is available. One feature of the limit cycle is that the angular velocity is periodic with a frequency equal to that of the frequency of the torque applied via the internal rotor. The angular velocity of the robot on the limit cycle has zero mean. This is expected since the robot rotates in an opposite direction to that of the internal rotor. Furthermore, the robot’s heading angle converges to a constant value on the limit cycle. A more interesting feature of the limit cycle is that the velocity $u_x$ is periodic with a frequency that is twice that of the frequency of the forcing torque. The longitudinal velocity has a nonzero mean, which is the speed of the robot averaged over one time period. Across the range of frequencies and amplitudes we tested, the robot’s velocity converges to a limit cycles shaped as the Fig. 8, with the same features.

Fig. 7

Velocity (cm/s)–angular velocity ($^{\circ }$/s) of the robot. The trajectory in this reduced velocity space converges to the limit cycle shaped as ‘8.’ The convergent solution is shown by the black dashed line

Fig. 8

Representation of the foil broken into N panels. The body frame is denoted by the axes $x_b-y_b$. On each panel, the local normal and tangential directions are shown by the red lines. On a generic panel A, a source distribution of strength $\sigma$ is placed. A vortex wake panel of length $\varDelta$ is shown by the blue line at the trailing edge of the foil with a circulation $\varGamma$. The existing wake in the fluid is shown by the blue and red swirls behind the vortex wake panel. (Color figure online)

4 Numerical simulation of limit cycle dynamics of the swimming robot

A simplified computation of the robot–fluid interaction can be performed by assuming that the fluid is mostly inviscid except in a small region close to the boundary of the robot. This is justified, since the Reynolds number in our experiments varies between 5000 and 15,000. Such an assumption is common and standard in fluid mechanics [27, 53]. The viscous effects that dominate around the boundary of the robot lead to vortex shedding. Within an inviscid flow framework, this complex process is approximated by the creation of inviscid point vortices at the sharp edges of a body. This is achieved through the so-called Kutta condition [27]. There is no universal agreement on the exact statement of the Kutta condition, the interested reader is referred to [54] for a discussion on the Kutta condition. The steady Kutta condition states that the velocity of the fluid at the sharp edge of a body such as the Joukowski foil should be zero. In [21, 25], it was shown that the steady Kutta condition implies that

$$\begin{aligned} -2\dot{x}\sin {\theta } + 2\dot{y}\cos {\theta } - K \dot{\theta } = u_v. \end{aligned}$$

(22)

Here, $\dot{x}$ and $\dot{y}$ are the velocity of the center of mass of the Joukowski foil and $\dot{\theta }$ its angular velocity. The velocity of the fluid at trailing in a direction transverse to the trailing edge due to any existing wake is denoted by $u_v$. The term K is the numerical value of the Kirchhoff potential, associated with the spinning motion of the foil, evaluated at the trailing edge. This affine nonholonomic constraint is the same as the constraint on Chaplygin sleigh except for the nonhomogeneous part of the constraint, $u_v$. This nonhomogeneous component exists because the velocity of the foil at the trailing edge should not be zero, but rather equal to the velocity of the fluid, since the trailing edge is a stagnation point.

The drawback of the pure inviscid flow method using point vortex dynamics and the steady Kutta condition is that viscous drag like effects are entirely ignored. In fact, the motion of the Joukowski foil is computed using the conservation of linear and angular impulse. The second drawback is related to the validity of the application of the steady Kutta condition itself. To overcome these drawbacks, we adopt a numerical method that includes a drag force as well as incorporates an unsteady Kutta condition within a framework of an unsteady panel method, see, for example, [55, 56]. The unsteady Kutta condition states that there is no pressure gradient across the trailing edge. This version of the Kutta condition has been used to investigate the motion of fish-like bodies in other well-known work, see, for instance, [28, 30].

In the panel method simulation, the boundary of the two-dimensional cross section of the foil is broken up into N straight panels as shown in Fig. 8. On the ith panel at time step k, there are a continuous source distribution $\sigma _i$ and a constant circulation distribution $\gamma$ as shown in Fig. 8a. Additionally, there is a wake panel at the trailing edge of the foil, shown in Fig. 8b, with a circulation value equal to the change in circulation at the current time frame relative to the previous time frame. In the panel method, the boundary condition of no normal flow is only enforced at the center of each panel, known as the control point. The general outline of the panel method used for these simulations is shown in Fig. 9.

Fig. 9

Flowchart describing the panel code used

The simulation starts each new time frame by estimating the current parameters using extrapolation from previous time frames. It then uses these parameters to determine the $A^t$, $A^n$ matrices and the $B^n$, $B^t$, $C^n$, $C^t$, $W^t$ and $W^n$ vectors, where the superscripts n and t denote the normal and tangential components, respectively. The A matrices describe the affects of the N source distributions on the N panels, while the B, C and W vectors describe the affects of the circulation $\gamma$ on each panel, the affects of all point vortices previously shed and the affect of the circulation on the wake panel, respectively. The Neumann normal flow boundary condition can now be applied,

$$\begin{aligned}&\sum _{j=1}^{N} A^n_{i,j} (\sigma _j)_k + \gamma _k B^n_i + \sum _{d=1}^{k-1} C^n_{i,d} \frac{L}{\varDelta _k}(\gamma _{d-1}-\gamma _d) \nonumber \\&\quad \qquad +\,W_i^n \frac{L}{\varDelta _k}(\gamma _{k-1}-\gamma _k) = \mathbf V _i \cdot \mathbf n _i. \end{aligned}$$

(23)

In Eq. 23, L is the total perimeter of the foil and $\varDelta _k$ is the length of the current wake panel. The left-hand side of equation 23 describes the fluid velocity on the ith panels control point at time frame k, which equals the right-hand side describing the translational velocity of the ith control point. In Eq. 23, the only unknowns are the $\sigma$ vector and the scalar $\gamma$ and all other parameters are approximated from either the previous time frame or the previous iteration of the current time frame. Thus, $(\sigma )_k$ can be rewritten as a function of $\gamma _k$,

$$\begin{aligned} (\sigma )_k= & {} (A_{i,j}^t)^{-1} \gamma _k \left( -B_i^n + W_i^n \frac{L}{\varDelta } \right) \nonumber \\&+\,(A_{i,j}^t)^{-1} \left( \mathbf V \cdot \mathbf n - \sum _{d=1}^{k-1} C^n_{i,d} \frac{L}{\varDelta }(\gamma _{d-1}-\gamma _d) \right. \nonumber \\&\left. - W_i^n \frac{L}{\varDelta } \gamma _{k-1} \right) \end{aligned}$$

(24)

Equation 24 can be written in a more compact form by introducing variables $b1 \!=\! (A_{i,j}^t)^{-1} \left( -B_i^n + W_i^n \frac{L}{\varDelta } \right)$ and $b2 = + (A_{i,j}^t)^{-1} \big ( \mathbf V \cdot \mathbf n$$- \sum _{d=1}^{k-1} C^n_{i,d} \frac{L}{\varDelta }(\gamma _{d-1}-\gamma _d) - W_i^n \frac{L}{\varDelta } \gamma _{k-1} \big )$. So now Eq. 24 can be written as,

$$\begin{aligned} (\sigma )_k = b1 \gamma _k + b2. \end{aligned}$$

(25)

Recognizing that we have N equations and $N+1$ unknowns, we apply the Kutta condition on the trailing edge to solve for our current circulation strength $\gamma _k$. The Kutta condition sets the pressures on the first and last panel equal to each other. This is represented mathematically by altering the unsteady form of Bernoulli’s equation

$$\begin{aligned} \begin{aligned}&p + \frac{1}{2} ||\mathbf u ||^2 + \frac{\partial \phi }{\partial t} = \hbox {constant}\\&p_1 \!+ \!\frac{1}{2} ||\mathbf u _1||^2 \!+\! \frac{\partial \phi _1}{\partial t} = p_N + \frac{1}{2} ||\mathbf u _N||^2 \!+\! \frac{\partial \phi _N}{\partial t}\\&p_1 \!-\! p_N \!= \!0 \!=\! \frac{1}{2}(||\mathbf u _N||^2 \!-\! ||\mathbf u _1||^2) + \frac{\partial \phi _N}{\partial t} - \frac{\partial \phi _1}{\partial t}. \end{aligned} \end{aligned}$$

(26)

If two points $x_1$ and $x_2$ are connected by a path s, then the change in potential between the two points is given by

$$\begin{aligned} \varDelta \phi = \int _{x_1}^{x_2} \mathbf u \cdot \mathrm{d}s \end{aligned}$$

(27)

where $\mathbf u$ is the fluid velocity along the path s. Evaluating the integral along the surface of the foil in the clockwise direction can be defined as being equal to the circulation enclosed by the path:

$$\begin{aligned} \int _{1}^{N} \mathbf u \cdot \mathrm{d}s = \varGamma _b. \end{aligned}$$

(28)

So the change in $\varGamma _b$ can be written as

$$\begin{aligned} \frac{\varDelta \varGamma _b}{\varDelta t} = 2L \frac{(\gamma )_k - (\gamma )_{k-1}}{\varDelta t}, \end{aligned}$$

(29)

thus resulting in

$$\begin{aligned} \begin{aligned} ||\mathbf u _1||^2 - ||\mathbf u _N||^2 = 2L \frac{(\gamma )_k - (\gamma )_{k-1}}{\varDelta t}. \end{aligned} \end{aligned}$$

(30)

The fluid velocities tangential to the panels can be determined using an equation similar to Eq. 23 but the $A^t$, $B^t$, $C^t$ and $W^t$ matrix and vectors are used. The magnitude of the fluid velocities on panel 1 is expressed as a function of the scalar $\gamma _k$ value,

$$\begin{aligned} \begin{aligned}&||\mathbf u _1||^2 = (u_1^t)^2 + (u_1^n)^2\\&\quad =\left[ \gamma _k \left( \sum _{i=1}^N b1_i A^t_{1,i} + \sum _{i=1}^N B^t_{1,i} + W^t_1 \frac{L}{\varDelta _k} \right) \right. \\&\left. \qquad \times \left( \sum _{i=1}^N b2_i A^t_{1,i} + W^t_1 \frac{\gamma _{k-1} L}{\varDelta _k} + \sum _{d=1}^{k-1} C^t L (\gamma _{d-1} - \gamma _d) \right) \right] ^2\\&\qquad + (\mathbf V _1 \cdot \mathbf n _1)^2. \end{aligned}\nonumber \\ \end{aligned}$$

(31)

Equation 31 can be simplified by assigning variables to the product of the matrix and vector multiplications, similar to the process used to get Eq. 25, resulting in

$$\begin{aligned} ||\mathbf u _1||^2 = (\gamma _k d1_1 + d2_1)^2 + (\mathbf V _1 \cdot \mathbf n _1)^2. \end{aligned}$$

The same process is used to determine the magnitude of the fluid velocity on the Nth panel, and these velocity terms can be plugged back into Eq. 30,

$$\begin{aligned} \begin{aligned}&(\gamma _k d1_1 + d2_1)^2 + (\mathbf V _1 \cdot \mathbf n _1)^2 - (\gamma _k d1_1 + d2_1)^2 \\&\quad + (\mathbf V _1 \cdot \mathbf n _1)^2 = 2L \frac{(\gamma )_k - (\gamma )_{k-1}}{\varDelta t}. \end{aligned} \end{aligned}$$

(32)

Equation 32 is solved to determine the $\gamma _k$ value; note that the equation is quadratic which will result in two $\gamma _k$ values. We always select the value of $\gamma _k$ that results in the fluid flowing off of both the upper and lower trailing edge panels, meaning that $u_N^t > 0$ and $u_1^t < 0$.

The determined $\gamma _k$ value is then plugged into Eq. 25 to determine the source strengths on each panel. With the source strengths determined, the wake panel parameters can be updated based on the fluid velocity at the trailing edge,

$$\begin{aligned} \begin{aligned}&\varDelta _k = \varDelta t \sqrt{(u^x_{wp})^2+(u^y_{wp})^2}\\&\alpha _k = \hbox {arctan} \left( \frac{u^y_{wp}}{u^x_{wp}} \right) . \end{aligned} \end{aligned}$$

(33)

With the updated wake panel parameters, the code begins again solving for the new b1 and b2 vectors and then determining a new $\gamma _k$, $(\sigma )_k$ and wake panel parameters until these values converge to within a certain tolerance.

With the key foil parameters estimated, the unsteady Bernoulli’s equation is applied on each panel to determine the pressure forces. The method of solving the Bernoulli equation is similar to what was done in Eq. 26 except that here the pressure on the panels is found relative to the pressure infinitely far away, i.e., there is no fluid velocity or change in potential. This allows us to use,

$$\begin{aligned} p_i =-\frac{1}{2} ||\mathbf u _i||^2 - \frac{\partial \phi _i}{\partial t} \end{aligned}$$

(34)

Equation 34 can be rewritten in the body-fixed frame of reference eliminating the affects of shape changing in the potential function calculation. When changing the reference frame, the magnitude of the fluid velocities does not change but the $\frac{\partial \phi _i}{\partial t}$ does. It can be rewritten by

$$\begin{aligned} \begin{aligned} \left( \frac{\partial \phi }{\partial t} \right) _\mathrm{inertial}&= \left( \frac{\partial \phi }{\partial t} \right) _\mathrm{body} + \frac{\partial X}{\partial t} \frac{\partial \phi }{\partial x} + \frac{\partial Y}{\partial t} \frac{\partial \phi }{\partial y}\\&= \left( \frac{\partial \phi }{\partial t} \right) _\mathrm{body} + \mathbf V \cdot \nabla _{x,y} \phi \end{aligned} \end{aligned}$$

(35)

where $\mathbf V = -\mathbf V _0 - \varOmega \times r$. Or in other words, $\mathbf V$ is the velocity of the fluid due to the motion of the body relative to a body-fixed frame. The $\nabla _{x,y} \phi$ can be rewritten as

$$\begin{aligned} \begin{bmatrix} \frac{\partial \phi }{\partial x}\\ \frac{\partial \phi }{\partial y} \end{bmatrix} = \begin{bmatrix} \cos (\beta )&\quad \sin (\beta ) \\ -\sin (\beta )&\quad \cos (\beta ) \end{bmatrix} \begin{bmatrix} u^x\\ u^y \end{bmatrix} \end{aligned}$$

(36)

where $u^x$ and $u^y$ are the inertia fluid velocity components calculated on each panel by

$$\begin{aligned} \begin{bmatrix} u^x_i\\ u^y_i \end{bmatrix} = \begin{bmatrix} \cos (\theta _i)&-\sin (\theta _i) \\ \sin (\theta _i)&\cos (\theta _i) \end{bmatrix} \begin{bmatrix} u^t_i\\ u^n_i \end{bmatrix} \end{aligned}$$

(37)

where $\theta _i$ is the angle of the ith panel.

Now Eqs. 35–37 can be put back into Eq. 34,

$$\begin{aligned} \begin{aligned} p =&- \left( \frac{\partial \phi }{\partial t} \right) _\mathrm{body}-\frac{1}{2} \left( u'^2 + v'^2 \right) \\&-\frac{1}{2} \left[ (-V_b^x+\varOmega y)(u^x \cos (\theta ) + u^y \sin (\theta )) \right. \\&\left. + (-V_b^y - \varOmega x)(-u^x \sin (\theta ) + u^y \cos (\theta )) \right] . \end{aligned} \end{aligned}$$

(38)

The only term unknown in Eq. 38 is the $\left( \frac{\partial \phi }{\partial t} \right) _\mathrm{body}$, which is approximated using the backward finite difference method. With the pressures known, we know the forces on the body and thus we utilize $\sum F = m \dot{V}$ and $\sum M = I \dot{\omega }$ to determine translational and angular accelerations of the foil which are used to determine the velocity for the foil during the current time frame. The code then starts again, determining the foil parameters with the updated foil velocities. This process is repeated for each time frame until the foil parameters and velocities both converge.

Once the foil parameters and velocities both converge, the circulation of the wake panel is concentrated at its midpoint and represented by a point vortex, which is shed into the fluid. The positions of the foil and all previously shed point vortices are updated, and the code starts from the very beginning at a time $t_k = t_{k-1} + \varDelta t$.

In our simulations, the input to the body is a periodic torque $\tau = A\cos (\varOmega t)$. A simulation image of the wake formed behind a foil subjected to periodic torque is shown in Fig. 10.

Fig. 10

The foil and the point vortex wake from one of the simulations

When the foil is subjected to a periodic torque, the velocity of the foil and its angular velocity converge to a periodic function. A plot of the angular velocity of the foil versus the longitudinal velocity of the foil (in the body frame) is represented by the blue line in Fig. 12. In this velocity space, the trajectory of the state of system converges to a limit cycle that is shaped as the Fig. 8. The simulated motion of the foil and the associated wake, when the foil is subjected to a periodic torque, is shown in the supplementary video, along with the convergence of its longitudinal and angular velocity to the limit cycle.

We ran simulations for a range of forcing amplitudes and frequencies to find that such a limit cycle exists in all cases.

5 Chaplygin sleigh-like surrogate model for a swimming Joukowski foil

The dynamics of the swimming Joukowski foil are described by a high-dimensional dynamical system. However, the dynamics of the system are confined to a low-dimensional attractor that is topologically similar to the attractor of the velocity equations of the Chaplygin sleigh. The existence of such a low-dimensional attractor allows the Chaplygin sleigh to serve as a surrogate model for the swimming Joukowski foil. More formally, the unsteady Joukowski condition at the trailing edge ensures that the velocity of the fluid relative to the sharp edge is periodic with small amplitude. Figure 11 shows the transverse velocity (along the $Y_b$ axis in the body frame) of the trailing edge (red) and the transverse velocity of the fluid at the same point (blue). The difference between the two, which represents the slip velocity, is periodic with a small amplitude. The simulations of the foil–vortex interaction suggest that the foil’s motion is like that of a Chaplygin sleigh with a periodic affine nonholonomic constraint. We use the harmonic balance equations to define such a reduced order surrogate model of the foil. The Chaplygin sleigh with a no-slip constraint will be used as the surrogate model as opposed to the sleigh with an affine constraint, even though the unsteady Kutta condition could impose a small periodic affine constraint. As observed in Sect. 2, the limit cycles for both the types of sleigh are nearly identical when the prescribed slip velocity is small in magnitude. The analytical approximation of the limit cycles is, however, easier to compute if the surrogate model is the Chaplygin sleigh with the homogeneous constraint.

Fig. 11

Velocity of the foil’s trailing edge in red and the fluid velocity at the trailing edge from the vortex wake represented by the dashed blue line. (Color figure online)

A surrogate model for the swimming foil is constructed by first finding the amplitudes ($A_x$, $B_x$, $A_w$, $A_w$) of the harmonics of the limit cycle solution as well as the velocity constant $u_c$ from (13) and (14). With an approximate solution for the foil limit cycle known, the remaining problem is to determine the parameters of a Chaplygin sleigh that produce a limit cycle with the same solution. This requires the solution to an inverse problem where the parameters $(m, b,c, \alpha = I + mb^2 )$ are the unknowns and the parameters $(A_x,B_x,A_w,A_w, u_c)$ in (15) are known. The parameters $(A_x,B_x,A_w,A_w, u_c)$ are determined from the foil simulations by first assigning the cosine (A) amplitudes based on the foil velocities at the beginning of one input period. Next, an initial sine (B) amplitude is assigned and the error is summed between the estimated velocities and the simulation data for one complete time period. The (B) values are updated based on the error from the previous iteration, and the process is repeated until the errors converge. The same iterative process is then repeated to determine the $u_c$ value. This leaves the system of Eq. (15) overdetermined with five equations and four unknowns.

The overdetermined system of equations can be approximately solved through a constrained least squares method, the constraint being that all the four unknowns $(m, b,c, \alpha )$ should be nonnegative,

$$\begin{aligned} \begin{aligned} \min _x&\frac{1}{2} ||\mathbf C \mathbf {x}-\mathbf {d}||_2^2\\&s.t. \quad \mathbf A \mathbf {x} \le \mathbf {b}\\ \end{aligned} \end{aligned}$$

(39)

where

$$\begin{aligned} \begin{aligned}&\mathbf C = \begin{bmatrix} A_w^2 + B_w^2&\quad 0&\quad -2u_c&\quad 0\\ B_w^2-A_w^2&\quad -4 \varOmega A_x&\quad -2 B_x&\quad 0\\ A_w B_w&\quad 2B_x\varOmega&\quad -A_x&\quad 0\\ A_xA_w+B_xB_w+2u_cB_w&\quad 0&\quad 0&\quad 2 \varOmega A_w\\ B_xA_w-A_xB_w-2u_cA_w&\quad 0&\quad 0&\quad 2\varOmega B_w \end{bmatrix},\\&\mathbf {x} = \begin{bmatrix} \delta \\ m \\ c \\ \alpha \end{bmatrix}, \mathbf {d} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 2A \\ 0 \end{bmatrix},\quad \mathbf A = -\mathbf I _{4\times 4},\quad \mathbf {b} = \begin{bmatrix} 0\\0\\0\\0 \end{bmatrix}. \end{aligned} \end{aligned}$$

We used MATLAB’s lsqlin function to perform this calculation. As an example, using the limit cycle parameters $A_x = 0.001779$, $B_x = -0.000932$, $A_w = 0.115531$, $B_w = 0.699560$, and $u_c = 0.434879$ the least squares computation yielded the following surrogate sleigh parameters $m = 401.2119$, $b = 0.0959$, $c = 22.3925$, $\alpha = 0.4450$. These parameters were plugged into the sleigh equations (7)–(8) to simulate the dynamics of the surrogate sleigh. The solution of (7)–(8) is shown in (red) Fig. 12a. For comparison, the same trajectory for the swimming foil is shown in red. As the sleigh and foil approach their steady-state speeds, the dynamics converge to limit cycles as shown in Fig. 8. The trajectories of both the systems converge to limit cycles that are nearly identical. The limit cycles themselves obtained from the simulations are shown in Fig. 12b.

Fig. 12

a Foil and sleigh velocities as they converge to their respective limit cycles. b Foil and sleigh limit cycles. c The average velocities of the foil and the equivalent sleigh converge to nearly the same value

It should be noted from Fig. 12a that the transient trajectories of the foil do not match those of the sleigh very well. This is expected since only dynamics on the limit cycles have been modeled and matched with each other.

Beyond a qualitative match of the limit cycles, the average speeds of the sleigh and foil can be used as a quantitative measure of the accuracy of the sleigh as a surrogate model for the swimming foil. Their average speeds, $\overline{v}$, calculated using (18) are shown in Fig. 12c. In Fig. 12c, the blue dashed line is the average velocity for the foil, while the red solid line is the average velocity of the equivalent sleigh given the same periodic input. It is obvious that the transient dynamics of the two systems differ but both the foil and the sleigh’s average speeds converge to nearly the same value, with the difference in the two being $\approx 0.0006 \quad [BL/s]$ or $\approx 0.18 \%$. The small error arises due to the least squares approximation of the sleigh model, (39). The closeness of the average speeds is also seen in Fig. 12b. The point of intersection of the two branches of the limit cycle which also lies on the horizontal axis is the average speed. This is very close in magnitude for both the limit cycles shown in Fig. 12b.

Here, we remark once again that while Kutta condition could lead to an affine nonholonomic constraint, the limit cycle of the foil’s dynamics is close to that of the Chaplygin sleigh with a homogeneous nonholonomic constraint. Since it was shown that the limit cycle of the sleigh with an affine periodic constraint is nearly the same, it implies that the limit cycle of the foil’s dynamics is close to that of the sleigh with an affine periodic constraint.

6 Turning control

The utility of having a low-dimensional Chaplygin sleigh surrogate model for the swimming foil is that it can prove useful in controlling the dynamics of the swimming foil. Determining the control input that produces the desired motion and path of the swimming foil is greatly simplified by the very low-dimensional equivalent sleigh model. Essentially, a control input is designed to steer the surrogate Chaplygin sleigh with prescribed average speed. Such an input is given by (20) discussed in Sect. 2.1. The same control input is then applied to the swimming foil.

This control via the surrogate Chaplygin sleigh is demonstrated through a numerical simulation of the turning maneuver of the foil. The foil first starts from rest and tracks an average speed of $\mathbf {\overline{v}} = 0.385$ body lengths per second and an average heading angle $\theta = 0$. It is then required to make a $90^{\circ }$ turn while tracking the same speed. The necessary control inputs for the turning maneuver are the amplitude and frequency of oscillations of the applied torque via the internal reaction wheel. One can freely choose a frequency and determine the necessary amplitude of the torque to accomplish the prescribed maneuver. The frequency of the control torque is chosen to be the same as in the computations described earlier. The amplitude of the control torque is determined by first obtaining the equivalent sleigh parameters (m, b, I, c). These parameters of such an equivalent sleigh were computed in the previous section from the numerical simulations of the foil–vortex interactions and using (39), where the parameters are determined as described in the previous section. Once the equivalent sleigh parameters are determined using (39), the control torque (20) is applied on the foil to steer it to make a $90^{\circ }$ turn, while tracking the average speed of $\overline{v}= 0.385$.

The average heading angle from the simulation of the surrogate Chaplygin sleigh and the coupled fluid foil is shown in Fig. 13a, where the angle $(\bar{\theta })$ is the angular position of the body averaged over one time period of the forcing function. In Fig. 13a, the red dashed line is the average heading angle for the surrogate Chaplygin sleigh while the blue solid line is the average heading angle for the foil with the same torque input. The heading angle is originally 0 degrees with the foil swimming along a horizontal line. The foil begins its turning maneuver at $t=50$. At about $t= 70$, the difference in the final heading angle of the foil and the sleigh was $\approx 1^{^\circ }$. The average speed of the foil and the surrogate sleigh is shown in Fig. 13b, which converges to the desired speed and deviates only slightly during the turning maneuver. During the turning motion, the trajectory of the foil deviates from the limit cycle before converging back to it as shown in Fig. 13c. Here, we remark that the small differences between the average speed of the surrogate sleigh and the foil during the turning motion seen in Fig. 13b cannot be attributed solely to errors to the numerics. The Chaplygin sleigh is a good surrogate model for the swimming foil, only when the velocities of the two systems are close to their respective limit cycles. During the turning motion, when the trajectories in the velocity space deviate from the limit cycle, differences arise between the dynamics of the two systems.

Fig. 13

Turning maneuver of the foil by $90^{\circ }$ while tracking a specified average speed, with control torque computed from the surrogate sleigh model. a Average heading angle of the foil (blue solid line) and equivalent sleigh (red dashed line). b Average speed of the foil (blue solid line) and equivalent sleigh (red dashed line). c The sleigh’s velocity and angular velocity undergo a perturbation from the limit cycle during the turn, but converge back to the limit cycle. (Color figure online)

7 Conclusion

The dynamics of fish-like swimming robots have a close resemblance with the dynamics of terrestrial nonholonomic systems that are also subjected to a viscous ‘drag’-like force. The reason for this similarity is that the vortex shedding phenomenon at the sharp edge of a swimming body imposes a nonholonomic constraint on the swimmer. Specifically, we show that the system of the Chaplygin sleigh has limit cycle solutions when actuated by a periodic torque and a topologically similar limit cycle solution exists in the swimming motion of a Joukowski foil-shaped robot actuated by a periodic torque. We demonstrated this through both numerical simulations and experiments. This similarity in the limit cycle solutions for the two disparate systems allows the Chaplygin sleigh to serve as a simplified surrogate model for the dynamics of the swimming robot. Once such a simplified model is created, one can set aside the complicated coupled dynamics of the fluid–robot interaction. Such simplified models are extremely useful to control the dynamics of swimming robots. The utility of such a model is shown in this paper through the numerical simulation of a turning maneuver of a swimming robot while tracking a net speed. While we have only demonstrated the utility of the surrogate Chaplygin sleigh for controlling the motion of the foil, through numerical simulation, future work will address development of practical feedback control for a swimming robot based on this surrogate model.

A larger significance of this paper is that it advances a framework to model the dynamics of articulated multisegmented swimming robots. Terrestrial multiple segmented systems similar to the Chaplygin sleigh with possibly more than one physical nonholonomic constraint can allow one to model the dynamics of articulated fish-like robots.