1 Introduction

The inter-shaft bearings [1] play a crucial role in dual-rotor systems of the high-speed rotating machine, including generator, aircraft engine and electric motor. The radial cylindrical roller bearings are usually used as the inter-shaft bearings to optimize the structure and reduce the vibration of the dual-rotor system. Different from other bearings only for support, both outer and inner rings are rotating with higher pressure (HP) and lower pressure (LP) rotors at high speed, the thermal behaviours are more prominent. The friction heat generation and convergence will make the temperature rise, seriously, the scuffing [2] and biting may occur if at a very high temperature. Hence, the inter-shaft bearings’ thermal behaviours affected by dynamic properties of systems urgently need further investigations.

The thermal behaviours of rolling bearings have been studied by many researchers in the past decades. In 1945, an empirical formula about the friction heat generations of rolling bearings was pioneered by Palmgren [3] through a large number of experiments. Burton et al. [4] built a theoretical model for thermal failure in the case of dry or lightly-lubricated angular contact ball bearings to study the steady-state thermal behaviour rather than the transient behaviour. Sud et al. [5] studied the thermal behaviour of the angular contact ball bearings and thrust ball bearings under the preload experimentally. Harris [6] applied the basic laws of heat conduction and heat convection to the rolling bearing by lumped parameter method and predicted the steady-state temperatures of the rolling bearing main components, such as the inner ring, outer ring and rollers. Winer et al. [7] developed an analytical model of a tapered roller bearing and housing system, and calculated typical thermal resistances among the rotor parts. DeMul et al. [8, 9] presented a five-degree-of-freedom (5DOF) bearing model to analyze the load–deflection relationship in a matrix method. Based on which, Jorgensen and Shin [10] considered the thermal expansion to predict spindle/bearing performance at high speed and found the steady-state temperature distribution from a quasi-three-dimensional heat transfer model. Stein and Tu [11] utilized Palmgren’s empirical formula to estimate the friction torque and carried out a comprehensive thermal analysis of the angular contact ball bearing. Kim and Lee [12] investigated the thermal and dynamic behaviours of a rotor-bearing system considering tolerance, cooling conditions and thermal deformation. Sun et al. [13] offered an approach, named as modal truncation augmentation method, to simulate the blade loss considering the thermal expansion, to achieve this, they built the heat transfer network and listed the thermal resistances. Jiang and Mao [14] set up an experiment rig to comparative study a high-speed hybrid ceramic and steel ball bearings with oil-air lubrication. Ma et al. [15] established a mathematical model to accurately calculate the FHGs of spherical roller bearings based on the local analysis approach. Takabi and Khonsari [16] proposed a complex heat transfer network of the bearing assembly to study the unsteady-state temperature of a deep-groove ball bearing in an oil-bath lubrication system, and verified the validity through experimental tests. Ai et al. [17] established the thermal network model for the double-row tapered roller bearing according to the generalized Ohm’s law, and developed a static model to obtain force distribution and motion parameters of the roller bearing. Than and Huang [18] combined the static model with the finite element method as a unified method to predict nonlinear thermal behaviours of high-speed spindle bearings, and found that the temperature field of the spindle-bearing system was in good agreement with the experiment. Gao et al. [19] established a kinematic-Hertzian-thermo-hydro-dynamic (KH-THD) model to study the mechanism of the skid, over-skidding and negative-skidding phenomena, and found that there is a great temperature gradient inside the bearing. In all of the above works, they all focused on the supporting bearings rather than the inter-shaft bearings. It is essential to do some investigations on thermal behaviours of inter-shaft bearings because of their unique application.

Many researchers have studied the dynamics of a dual-rotor system with the inter-shaft bearing by far. Hibner [20] predicted the vibratory response of a two-shaft aircraft engine, with the aid of a unique transfer-matrix method, he illustrated the basic concepts of multi-shaft critical speeds and nonlinear viscous-damped response. Gupta et al. [21] built a dual-rotor test rig to investigate the dynamic properties of the dual-rotor system by simulating the two spool aircraft engine dynamically. A 2DOF simple but realistic model of the non-symmetric co-axial co-rotating or counter-rotating rotors was presented by Ferraris et al. [22] to study the critical speeds and the dynamic responses caused by the unbalance through hand calculations. Guskov et al. [23] studied the unbalanced responses of a dual-rotor system, which is consisted of one LP shaft, one HP shaft and an inter-shaft bearing between them. In the research of Sun et al. [24], the MHB-AFT (Multi-Harmonic Balance combined with the Alternating Frequency/Time domain) method is applied to compute the steady-state dynamic response of an 8DOF dual-rotor system caused by the rub-impact, but the inter-shaft bearing is simplified into a linear spring. Based on which, Gao et al. [25] considered the inter-shaft bearing’s nonlinear factors, such as the Hertzian contact and the clearance, and proposed a force model considering the local defect on outer and inner rings to investigate the dynamic behaviours of the simple 8DOF system. Unfortunately, in the above literature about the dual-rotor system, most of the inter-shaft bearings are simplified linearly, or even without considering the thermal effect of bearings.

This paper aims to investigate the effect of the dynamics of the dual-rotor system on the temperature of the inter-shaft bearing. Instead of the static load commonly used in previous literature, the dynamic load is employed to establish the unsteady-state heat balance equations of the inter-shaft bearing. Moreover, the dynamic load is able to mirror the dynamic properties of the system. Thus, the dynamics of the system is coupled with the heat transfer of the bearing. Furthermore, the viscosity-temperature relationship of the lubricant is considered in this model. Results show that the bearing’s temperatures form two “temperature peak” in the “resonance zone” of the system, which indicates the dynamic properties of the system make an important impact on the bearing’s temperatures.

2 Unsteady-state heat transfer model under the dynamic load

2.1 Dynamic load of the inter-shaft bearing

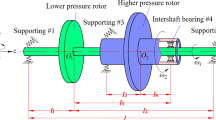
The structural diagram of a simple dual-rotor and an inter-shaft bearing system is shown in Fig. 1 [24, 25]. The LP and HP rotors are coupled by a radial cylindrical roller bearing, whose outer and inner rings whirl with HP and LP rotors. Where ω1 is the LP rotor’s rotation speed while ω2 is the HP rotor’s rotation speed. The rotation speed ratio \(\lambda = \frac{{\omega_{2} }}{{\omega_{1} }}\) is constant during operation, where \(\lambda > {1}\) for co-rotating while \(\lambda < - {1}\) for counter-rotating. Assume that the LP and HP rotors rotate at constant rotation speeds and the rotation speed ratio is constant, the DOFs of the rotational angles of LP and HP rotors around the z-axis can be ignored. Therefore, the simple dual-rotor system has 8DOFs, which are the vertical and horizontal displacements of LP and HP rotors x1, y1, x2, y2, and the rotational angles of LP and HP rotors around the vertical and horizontal axes θx, θy, φx, φy.

Fig. 1
figure 1

Structural diagram of a simple dual-rotor and an inter-shaft bearing system

Full size image

The structural diagram of a simple dual-rotor and an inter-shaft bearing system is shown in Fig. 1. The second kind of Lagrange’s equation is applied to establish the dynamic equations of the system. Both LP and HP rotors are assumed as rigid rotors, the energies of the system [24,25,26] are:

The kinetic energy of the system is

$$ T = \frac{1}{2}m_{1} \left( {\dot{x}_{1}^{2} + \dot{y}_{1}^{2} } \right) + \frac{1}{2}J_{{d_{1} }} \left( {\dot{\theta }_{x}^{2} + \dot{\theta }_{y}^{2} } \right) + \frac{1}{2}J_{{p_{1} }} \left( {\omega_{1}^{2} - 2\omega_{1} \theta_{x} \dot{\theta }_{y} } \right) + \frac{1}{2}m_{2} \left( {\dot{x}_{2}^{2} + \dot{y}_{2}^{2} } \right) + \frac{1}{2}J_{{d_{2} }} \left( {\dot{\varphi }_{x}^{2} + \dot{\varphi }_{y}^{2} } \right) + \frac{1}{2}J_{{p_{2} }} \left( {\omega_{2}^{2} - 2\omega_{2} \varphi_{x} \dot{\varphi }_{y} } \right), $$
(1a)

where m1, m2 are the mass of the LP and HP rotor; Jp1, Jp2 are the polar moment of inertia of the LP and HP rotor; Jd1, Jd2 are diameter moment of inertia of the LP and HP rotor.

The potential energy of the dual-rotor system is

$$ V = \frac{1}{2}k_{1} \left[ {\left( {x_{1} - \theta_{y} l_{1} } \right)^{2} + \left( {y_{1} + \theta_{x} l_{1} } \right)^{2} } \right] + \frac{1}{2}k_{2} \left[ {\left( {x_{1} + \theta_{y} l_{2} } \right)^{2} + \left( {y_{1} - \theta_{x} l_{2} } \right)^{2} } \right] + \frac{1}{2}k_{3} \left[ {\left( {x_{2} - \varphi_{y} l_{3} } \right)^{2} + \left( {y_{2} - \varphi_{x} l_{3} } \right)^{2} } \right] + m_{1} gx_{1} + m_{2} gx_{2} , $$
(1b)

where ki (i = 1, 2, 3) are stiffness of linear supports.

The dissipation energy of the dual-rotor system is

$$ D = \frac{1}{2}c_{1} \left[ {\left( {\dot{x}_{1} - \dot{\theta }_{y} l_{1} } \right)^{2} + \left( {\dot{y}_{1} + \dot{\theta }_{x} l_{1} } \right)^{2} } \right] + \frac{1}{2}c_{2} \left[ {\left( {\dot{x}_{1} + \dot{\theta }_{y} l_{2} } \right)^{2} + \left( {\dot{y}_{1} - \dot{\theta }_{x} l_{2} } \right)^{2} } \right] + \frac{1}{2}c_{3} \left[ {\left( {\dot{x}_{2} - \dot{\varphi }_{y} l_{3} } \right)^{2} + \left( {\dot{y}_{2} + \dot{\varphi }_{x} l_{3} } \right)^{2} } \right], $$
(1c)

where ci (i = 1, 2, 3) are damping of linear supports.

The virtual work of the dual-rotor system is

$$ \begin{gathered} \delta W = m_{1} \omega_{1}^{2} e_{1} \cos \left( {\omega_{1} t} \right)\delta x_{1} + m_{1} \omega_{1}^{2} e_{1} \sin \left( {\omega_{1} t} \right)\delta y_{1} + m_{2} \omega_{2}^{2} e_{2} \cos \left( {\omega_{2} t} \right)\delta x_{2} + m_{2} \omega_{2}^{2} e_{2} \sin \left( {\omega_{2} t} \right)\delta y_{2} \hfill \\ \, - F_{x} \left\{ {\delta x_{1} + \delta \theta_{y} \left( {l_{2} - l_{5} } \right) - \left( {\delta x_{2} + \delta \varphi_{y} l_{4} } \right)} \right\} - F_{y} \left\{ {\delta y_{1} - \delta \theta_{x} \left( {l_{2} - l_{5} } \right) - \left( {\delta y_{2} - \delta \varphi_{x} l_{4} } \right)} \right\}, \hfill \\ \end{gathered} $$
(1d)

where e1, e2 are unbalances of the LP rotor and the HP rotor; δx1, δy1, δx2, δy2, δθx, δθy, δφx, δφy are virtual displacements; Fx, Fy are the forces of the inter-shaft bearing along the vertical direction and horizontal direction.

Substitute Eqs. (1a–d) into the second kind Lagrange’s equation, the dynamic equations of the dual-rotor system are obtained as:

$$ m_{1} \ddot{x}{}_{1} + c_{1} \left( {\dot{x}_{1} - \dot{\theta }_{y} l_{1} } \right) + c_{2} \left( {\dot{x}_{1} + \dot{\theta }_{y} l_{2} } \right) + k_{1} \left( {x_{1} - \theta_{y} l_{1} } \right) + k_{2} \left( {x_{1} + \theta_{y} l_{2} } \right) = m_{1} \omega_{1}^{2} e_{1} \cos \left( {\omega_{1} t} \right) - F_{x} - m_{1} g, $$
(2a)
$$ m_{1} \ddot{y}_{1} + c_{1} \left( {\dot{y}_{1} + \dot{\theta }_{x} l_{1} } \right) + c_{2} \left( {\dot{y}_{1} - \dot{\theta }_{x} l_{2} } \right) + k_{1} \left( {y_{1} + \theta_{x} l_{1} } \right) + k_{2} \left( {y_{1} - \theta_{x} l_{2} } \right) = m_{1} \omega_{1}^{2} e_{1} \sin \left( {\omega_{1} t} \right) - F_{y} , $$
(2b)
$$ J_{{d_{1} }} \ddot{\theta }_{x} + \omega_{1} J_{{p_{1} }} \dot{\theta }_{y} + c_{1} l_{1} \left( {\dot{y}_{1} + \dot{\theta }_{x} l_{1} } \right) - c{}_{2}l_{2} \left( {\dot{y}_{1} - \dot{\theta }_{x} l_{2} } \right) + k_{1} l_{1} \left( {y_{1} + \theta_{x} l_{1} } \right) - k_{2} l_{2} \left( {y_{1} - \theta_{x} l_{2} } \right) = F_{y} \left( {l_{2} - l_{5} } \right), $$
(2c)
$$ J_{{{\text{d}}_{1} }} \ddot{\theta }_{y} - \omega_{1} J_{{{\text{p}}_{1} }} \dot{\theta }_{x} - c_{1} l_{1} \left( {\dot{x}_{1} - \dot{\theta }_{y} l_{1} } \right) + c{}_{2}l_{2} \left( {\dot{x}_{1} + \dot{\theta }_{y} l_{2} } \right) - k_{1} l_{1} \left( {x_{1} - \theta_{y} l_{1} } \right) + k{}_{2}l_{2} \left( {x_{1} + \theta_{y} l_{2} } \right) = - F_{x} \left( {l_{2} - l_{5} } \right), $$
(2d)
$$ m_{2} \ddot{x}{}_{2} + c_{3} \left( {\dot{x}_{2} - \dot{\varphi }_{y} l_{3} } \right) + k_{3} \left( {x_{2} - \varphi_{y} l_{3} } \right) = m_{2} \omega_{2}^{2} e_{2} \cos \left( {\omega_{2} t} \right) + F_{x} - m_{2} g, $$
(2e)
$$ m_{2} \ddot{y}{}_{2} + c_{3} \left( {\dot{y}_{2} + \dot{\varphi }_{x} l_{3} } \right) + k_{3} \left( {y_{2} + \varphi_{x} l_{3} } \right) = m_{2} \omega_{2}^{2} e_{2} \sin \left( {\omega_{2} t} \right) + F_{y} , $$
(2f)
$$ J_{{d_{2} }} \ddot{\varphi }_{x} + \omega_{2} J_{{p_{2} }} \dot{\varphi }_{y} + c_{3} l_{3} \left( {\dot{y}_{2} + \dot{\varphi }_{x} l_{3} } \right) + k_{3} l_{3} \left( {y_{2} + \varphi_{x} l_{3} } \right) = - F_{y} l_{4} , $$
(2g)
$$ J_{{{\text{d}}_{2} }} \ddot{\varphi }_{y} - \omega_{2} J_{{{\text{p}}_{2} }} \dot{\varphi }_{x} - c_{3} l_{3} \left( {\dot{x}_{2} - \dot{\varphi }_{y} l_{3} } \right) - k_{3} l_{3} \left( {x_{2} - \varphi_{y} l_{3} } \right) = F_{x} l_{4} , $$
(2h)

Equations (2a–h) in the matrix form is

$$ M\ddot{X} + C\dot{X} + KX = F, $$
(3)

where the variable vector \({\varvec{X}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {y_{1} } & {\theta_{x} } & {\theta_{y} } & {x_{2} } & {y_{2} } & {\varphi_{x} } & {\varphi_{y} } \\ \end{array} } \right]^{{\text{T}}}\); M, C, K, are the mass matrix, the damping matrix, the stiffness matrix; P is the external force vector.

The inter-shaft bearing is the nonlinear factors of the dynamic equations, such as the fractional exponential of Hertzian contact and the clearance. Figure 2 displays the inter-shaft bearing’s kinetic diagram.

Fig. 2
figure 2

The inter-shaft bearing’s kinetic diagram

Full size image

The angular position of the kth roller at any time t is expressed as

$$ \begin{array}{*{20}c} {\theta_{k} = \frac{2\pi }{{N_{b} }}\left( {k - 1} \right) + \omega_{c} t} & {\left( {k = 1, \, 2, \, \cdots , \, N_{b} } \right)} \\ \end{array} , $$
(4)

where \(\omega_{{\text{c}}} = \frac{{\omega_{{1}} r_{{\text{i}}} + \omega_{{2}} r_{{\text{o}}} }}{{r_{{\text{i}}} { + }r_{{\text{o}}} }}\) represents the cage’s rotation speed, where ri, ro represents the radiuses of the inner ring and the outer ring.

The relative deformation between kth roller and rings is

$$ \begin{aligned} \delta _{k} = &\ \left( {x_{i} - x_{o} } \right)\cos \theta _{k} + \left( {y_{i} - y_{o} } \right)\sin \theta _{k} - \delta _{0} \;\left( {k = 1,{\mkern 1mu} 2,{\mkern 1mu} \cdots ,{\mkern 1mu} N_{b} } \right),{\mkern 1mu} \\ =&\ \left\{ {\left[ {x_{1} + \theta _{y} \left( {l_{2} - l_{5} } \right)} \right] - \left( {x_{2} + \varphi _{y} l_{4} } \right)} \right\}\cos \theta _{k} + \left\{ {\left[ {y_{1} - \theta _{x} \left( {l_{2} - l_{5} } \right)} \right] - \left( {y_{2} - \varphi _{x} l_{4} } \right)} \right\}\sin \theta _{k} - \delta _{0} , \\ \end{aligned} $$
(5)

where 2δ0 is the radial clearance of the bearing; xi, yi, xo, yo are vertical displacement and horizontal displacement of the inner and outer rings.

The forces of the inter-shaft bearing [26] are

$$ \left[ {\begin{array}{*{20}c} {F_{x} } \\ {F_{y} } \\ \end{array} } \right] = K_{b} \sum\limits_{k = 1}^{{N_{b} }} {\delta_{k}^{10/9} H\left( {\delta_{k} } \right)} \left[ {\begin{array}{*{20}c} {\cos \theta_{k} } \\ {\sin \theta_{k} } \\ \end{array} } \right], $$
(6)

where \(H\left( \cdot \right) = \left\{ {\begin{array}{*{20}c} 1 & {\left( { \cdot > 0} \right)} \\ 0 & {\left( { \cdot \le 0} \right)} \\ \end{array} } \right.\) denotes the step function, Kb represents the stiffness and Nb represents the roller number of bearing.

The RMS, namely, root mean square [27, 28], is applied to compute the dynamic load of the bearing. The RMS can reflect the energy of the dynamic load, thus, RMS is more proper to compute the dynamic load than the P-P (peak-peak) value. The dynamic load can be expressed as

$$ F_{b} = \sqrt {\frac{{\int_{0}^{T} {\left( {\left( {F_{x} \left( t \right) - \overline{F}_{x} } \right)^{2} + \left( {F_{y} \left( t \right) - \overline{F}_{y} } \right)^{2} } \right)} dt}}{T}} = \sqrt {\frac{{\sum\limits_{i = 1}^{N} {\left( {\left( {F_{x} \left( i \right) - \overline{F}_{x} } \right)^{2} + \left( {F_{y} \left( i \right) - \overline{F}_{y} } \right)^{2} } \right)} }}{N}} , $$
(7)

where T denotes the period of forces; N denotes the discretization points number; \(\overline{F}_{x}\), \(\overline{F}_{y}\) are the averages of forces.

This research takes the NU1020 bearing for example to investigate the thermal behaviours of the inter-shaft bearing, and Table 1 lists the parameters of the NU1020 bearing.

Table 1 Parameters of the radial cylindrical roller bearing NU1020
Full size table

The dynamic parameters of the system are displayed below:

\(\begin{gathered} m_{1} = 97.37\,\text kg, \, J_{p1} = 3.6907\,\text kg \cdot m^{2} ,J_{d1} = 1.8454\,\text kg \cdot m^{2} ,m_{2} = 108.30\,\text kg, \, J_{p2} = 4.0119\,\text kg \cdot \text m^{2} , \, J_{d2} = 2.0060\, \text kg \cdot \text m^{2} , \hfill \\ k_{1} = k_{2} = k_{3} = 6 \times 10^{7} \text N/\text m, \, c_{1} = c_{2} = c_{3} = 655\,\text N \cdot \text s/m, \, l_{1} = 0.9188\,\text m, \, l_{2} = 1.1122\, \text m, \, l_{3} = 0.5120\,\text m, \, l_{4} = 0.6243\,\text m, \, l_{5} = 0.0995\,\text m, \hfill \\ \lambda = 1.2, \, e_{1} = 3\, \mu m, \, e_{2} = 2\, \mu m. \hfill \\ \end{gathered}\)

2.2 2.2 FHG under the dynamic load.

An empirical formula, presented by Palmgren [3], is utilized to compute the inter-shaft bearing’s friction torques. The total friction torque Mt (N•mm) is consisted of two portions, one is the friction torque due to load Mb and the other is the friction torque due to viscosity Mν, as

$$ M_{t} = M_{b} + M_{v} , $$
(8a)

Comparing with the static load [18] commonly used in previous literature, the dynamic load Fb is able to mirror the dynamic properties of the system, which enables the dynamic load more proper to depict the inter-shaft bearing’s practical load especially in the “resonance zone” of the system. Therefore, the dynamic load is applied to compute the friction torque due to load as

$$ M_{b} = f_{b} F_{b} D_{m} , $$
(8b)

where fb is a factor depended on bearing type and load, \(f_{{\text{b}}} = 0.0002 \sim 0.0004\) for the radial cylindrical roller bearings with cages [6]; Dm is the pitch diameter.

The friction torque due to viscosity is

$$ M_{v} = \left\{ {\begin{array}{*{20}c} {10^{ - 7} f_{v} \left( {\nu \cdot \Delta n} \right)^{2/3} D_{m}^{3} } & {\nu \cdot \Delta n \ge 2000} \\ {160 \times 10^{ - 7} f_{v} D_{m}^{3} } & {\nu \cdot \Delta n < 2000} \\ \end{array} } \right., $$
(8c)

where fν is a factor depended on bearing type and lubrication method, for radial cylindrical roller bearings with cages, \(f_{\nu } = 0.6 \sim 1\) for grease, \(f_{\nu } = 1.5 \sim 2.8\) for oil mist, and \(f_{\nu } = 2.2 \sim 4\) for oil bath [6]; ν is the kinematic viscosity of the lubricant (mm2/s), which is a function of the temperature; \(\Delta n = \frac{60}{{2\pi }}\left| {\omega_{2} - \omega_{1} } \right| = \frac{60}{{2\pi }}\left| {\lambda - 1} \right|\omega_{1}\) is the difference of rotation speeds (r/min), which is much more complex than the single rotor system.

The total FHG (W) under the dynamic load is

$$ Q_{t} = Q_{b} + Q_{v} , $$
(9a)

the load FHG under the dynamic load is

$$ Q_{b} = 10^{ - 3} \left| {\omega_{2} - \omega_{1} } \right|M_{b} = 10^{ - 3} \left| {\lambda - 1} \right|\omega_{1} M_{b} , $$
(9b)

the viscosity FHG is

$$ Q_{\nu } = 10^{ - 3} \left| {\omega_{2} - \omega_{1} } \right|M_{\nu } = 10^{ - 3} \left| {\lambda - 1} \right|\omega_{1} M_{\nu } , $$
(9c)

The viscosity of the lubricant is regarded as a function of temperature because the temperature makes an important impact on the viscosity. The viscosity-temperature relationship of the lubricant should be considered for the viscosity FHG. The experimental data of the kinematic viscosity at different temperatures [18] are shown in Table 2.

Table 2 The experimental data of the kinematic viscosity at different temperatures [18]
Full size table

The Reynolds’ model of viscosity-temperature relationship [29] is

$$ \nu = \nu_{0} e^{{ - \gamma \left( {T - T_{0} } \right)}} , $$
(10)

where γ is the viscosity-temperature coefficient, \(\gamma = 0.018 \sim 0.036 \, ^\circ \text C^{ - 1}\) for mineral oil; T0, ν0 are the initial temperature and the initial kinematic viscosity.

The Reynolds’ model is applied to fit the experimental data [18] in Table 2, the fitting curve is shown in Fig. 3. The viscosity-temperature coefficient is \(\gamma = 0.0256 \, ^\circ \text C^{ - 1}\), which indicates the Reynolds’ model is appropriate for the viscosity-temperature relationship of the lubricant. Moreover, the kinematic viscosity decreases greatly as the temperature rises, which further confirms the importance of the viscosity-temperature relationship.

Fig. 3
figure 3

The viscosity-temperature relationship of the lubricant

Full size image

2.3 Unsteady-state heat transfer model under the dynamic load

The material of bearings is bearing steel GCr15, thus, Biot numbers of the outer ring, the inner ring and cylindrical rollers, are small enough (\(Bi < 0.1\)). The lumped parameter method, i.e. lumped heat capacity method [30], can be used for the heat transfer modelling for the bearing. The structure size and the heat transfer network of the inter-shaft bearing are shown in Fig. 4, where dL, d, di, Dm, do, D, dH are the diameters; B, dr, ar are the width, the diameter of the roller, the length of the roller; Tr, Ti, To, TLP, THP, TL, T∞ are the temperatures; Rri, Rro, Ri, Ro are the heat conduction thermal resistances; RLr, RLi, RLo, RLP, RHP are the heat convection thermal resistances.

Fig. 4
figure 4

Inter-shaft bearing’s structure size and heat transfer network. a Structure size. b Heat transfer network

Full size image

Assume that the temperature of the lubricant is \(T_{{\text{L}}} = \frac{{T_{{\text{r}}} + T_{{\text{i}}} + T_{{\text{o}}} }}{3}\) [11], and an average partition coefficient [11] is applied as follows:

$$ Q_{t} = Q_{r} + Q_{i} + \, Q_{o} , $$
(11a)
$$ Q_{r} = 0.5 \, Q_{t} , $$
(11b)
$$ Q_{i} = 0.25 \, Q_{t} , $$
(11c)
$$ Q_{o} = 0.25 \, Q_{t} , $$
(11d)

where Qr is the FHG distributed to rollers, Qi is the FHG distributed to the inner ring and Qo is the FHG distributed to the outer ring.

According to the generalized Ohm's law [17], the unsteady-state heat balance equations are derived as

$$ \frac{{T_{i} - T_{r} }}{{R_{ri} }} + \frac{{T_{o} - T_{r} }}{{R_{ro} }} + \frac{{T_{L} - T_{r} }}{{R_{Lr} }} + Q_{r} = m_{r} c_{steel} \frac{{\partial T_{r} }}{\partial t}, $$
(12a)
$$ \frac{{T_{r} - T_{i} }}{{R_{ri} }} + \frac{{T_{LP} - T_{i} }}{{R_{i} }} + \frac{{T_{L} - T_{i} }}{{R_{Li} }} + Q_{i} = m_{i} c_{steel} \frac{{\partial T_{i} }}{\partial t}, $$
(12b)
$$ \frac{{T_{r} - T_{o} }}{{R_{ro} }} + \frac{{T_{HP} - T_{o} }}{{R_{o} }} + \frac{{T_{L} - T_{o} }}{{R_{Lo} }} + Q_{o} = m_{o} c_{steel} \frac{{\partial T_{o} }}{\partial t}, $$
(12c)
$$ \frac{{T_{i} - T_{LP} }}{{R_{i} }} + \frac{{T_{\infty } - T_{LP} }}{{R_{LP} }} = m_{LP} c_{steel} \frac{{\partial T_{LP} }}{\partial t}, $$
(12d)
$$ \frac{{T_{o} - T_{HP} }}{{R_{o} }} + \frac{{T_{\infty } - T_{HP} }}{{R_{HP} }} = m_{HP} c_{steel} \frac{{\partial T_{HP} }}{\partial t}, $$
(12e)

where t is time; csteel is the specific heat capacity of steel; mr, mi, mo are the mass of rollers, the inner ring, the outer ring; \(m_{{{\text{LP}}}} = \frac{\pi }{4}\rho_{{{\text{steel}}}} \left( {d^{2} - d_{{\text{L}}}^{2} } \right){\text{B}}\) is the mass of the part of LP rotor contact the inner ring, where \(\rho_{{{\text{steel}}}}\) is the density of the steel; \(m_{{{\text{HP}}}} = \frac{\pi }{4}\rho_{{{\text{steel}}}} \left( {d_{{\text{H}}}^{2} - D^{2} } \right){\text{B}}\) is the mass of the part of HP rotor contact the outer ring; the thermal resistance between the inner ring and the LP rotor \(R_{{\text{i}}} = \frac{{\ln \left( {{{d_{{\text{i}}} } \mathord{\left/ {\vphantom {{d_{{\text{i}}} } {d_{{\text{L}}} }}} \right. \kern-\nulldelimiterspace} {d_{{\text{L}}} }}} \right)}}{{2\pi k_{{{\text{steel}}}} {\text{B}}}}\), the thermal resistance between the outer ring and the HP rotor \(R_{{\text{o}}} = \frac{{\ln \left( {{{d_{{\text{H}}} } \mathord{\left/ {\vphantom {{d_{{\text{H}}} } {d_{{\text{o}}} }}} \right. \kern-\nulldelimiterspace} {d_{{\text{o}}} }}} \right)}}{{2\pi k_{{{\text{steel}}}} {\text{B}}}}\); the thermal resistance between rollers and the inner ring \(R_{{{\text{ri}}}} = \frac{{R_{{{\text{ri}}}}^{{{\text{one}}}} }}{{n_{{\text{b}}} }}\), the thermal resistance between rollers and the outer ring \(R_{{{\text{ro}}}} = \frac{{R_{{{\text{ro}}}}^{{{\text{one}}}} }}{{n_{{\text{b}}} }}\), herein nb is the average pressed roller number [31], \(R^{{{\text{one}}}} = \frac{1.13}{{k_{{{\text{steel}}}} \sqrt {A_{{\text{r}}} \cdot Pe^{*} } }}\) is the thermal resistance between one roller and the corresponding ring, Ar is the area of the interface between corresponding ring and roller, Pe* is the modified Peclet number [32].

The thermal resistance of heat convection can be derived by the Nusselt number Nu because of

$$ R_{\nu } = \frac{1}{{A_{\nu } h}} = \frac{1}{{A_{\nu } }} \cdot \frac{L}{k \cdot Nu}, $$
(13)

where Aν is the area of heat convection; h is the convective heat transfer coefficient; k is the thermal conductivity of the fluid; L is the characteristic length. The heat convection thermal resistances RLr, RLi, RLo, RLP, RHP can be calculated according to Eq. (13).

  • (1) The thermal resistance between the lubricant and the rollers \(R_{{{\text{Lr}}}}\).F and [33] offered a better correlation, instead of the McAdams correlation, to represent the experimental data for the forced convection from a cylinder to the liquid in crossflow, as

    $$ Nu = \left( {0.35 + 0.34 \, {\text{Re}}^{0.5} + 0.15 \, {\text{Re}}^{0.58} } \right)\Pr^{0.3} , $$
    (14)

    where \(Re = \frac{VL}{\nu }\) is the Reynolds number of the liquid; \(Pr = \frac{\nu }{\alpha }\) is the Prandtl number, herein α is the thermal diffusivity. The correlation is valid for \(10^{ - 1} < Re < 10^{5}\).

  • (2) The thermal resistance between the lubricant and the inner ring (the outer ring) \(R_{{{\text{Li}}}}\) (\(R_{{{\text{Lo}}}}\)) Gazley [34] and Bjorklund [35] studied the heat convection of two rotating concentric cylinders, which were separated by the mixture of grease-air. The inner race and the outer race can be seen as two rotating concentric cylinders separated by the lubricant, the correlation is

    $$ Nu = \left\{ {\begin{array}{*{20}c} 2 & {Ta < 41} \\ {0.167 \, Ta^{0.69} \Pr^{0.4} } & {41 \le Ta < 100} \\ {0.401 \, Ta^{0.5} \Pr^{0.4} } & {100 < Ta} \\ \end{array} } \right., $$
    (15)

    where \(Ta = Re\sqrt {\frac{{\delta_{{{\text{io}}}} }}{r}}\) is the Taylor number, in which \(\delta_{{{\text{io}}}} = \frac{{d_{{\text{o}}} - d_{{\text{i}}} }}{2}\) is the distance from the outer ring to the inner ring.

  • (3) The thermal resistance between the LP (HP) rotor and the ambient \(R_{{{\text{LP}}}}\) (\(R_{{{\text{HP}}}}\)) Yang [36] studied the heat convection between rotors and the ambient are forced convection due to the rotation of shafts, and offered the correlation as

    $$ Nu = \left\{ {\begin{array}{*{20}c} {0.00308 \, {\text{Re}} + 4.432} & {{\text{Re}} < 7300} \\ {{\text{Re}}^{0.37} } & {7300 \le {\text{Re}} < 9600} \\ {30.5 \, {\text{Re}}^{ - 0.0042} } & {9600 < {\text{Re}} } \\ \end{array} } \right., $$
    (16)

3 Results and discussions

3.1 Dynamic load

Dynamic responses of Eqs. (2a–h) and Eq. (6) can be easily obtained by fourth order Runge–Kutta method. The initial state for \(\omega_{1} = 500{\text{rad/s}}\) is \(\left[ {\begin{array}{*{20}c} {\varvec{X}} &\ & {\dot{\user2{X}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mathbf{0}} &\ & {\mathbf{0}} \\ \end{array} } \right]\), while for subsequent rotation speed, the initial state is the final state of the previous rotation speed. The calculation time is given as 10 s, which is long enough for the system to reach steady-state responses. The time step is given as 10–3 s, which is small enough to achieve accurate results. The errors are set as < 10–6. The RMS of the horizontal and vertical displacements in a period is utilized to represent the vibration amplitude of the numerical results. The amplitude frequency curves of the LP rotor and the HP rotor are shown in Fig. 5.

Fig. 5
figure 5

Amplitude frequency curve of the dual-rotor system. a The LP rotor. b The HP rotor

Full size image

Comparing Fig. 5a and Fig. 5b, it can be discovered that the two amplitude frequency curves are basically the same as each other, while the amplitude of the HP rotor is slightly greater than that of the LP rotor. Moreover, the amplitude increases so sharply in regions A and B that two peaks are formed here, while the amplitude is very small in other regions C, D and E. Thus, regions A and B are “resonance zone” and other regions C, D and E are “non-resonance zone”.

In order to analyze the mechanism of “resonance zone” A and B in detail, Fig. 6 and Fig. 7 are dynamic responses analysis for ω1 = 683 rad/s in A and ω1 = 821 rad/s in B, including the vertical displacement history, the horizontal displacement history, the orbit diagram of the LP rotor, the pressed roller number, the spectrum diagram of the LP rotor’s horizontal vibration signal and the Poincaré diagram. Herein, \(f_{{\text{L}}}\), \(f_{{\text{H}}}\) are the unbalance frequencies of LP and HP rotors.

Fig. 6
figure 6

Dynamic responses analysis for ω1 = 683 rad/s in A. a The vertical displacement history. b The horizontal displacement history. c The orbit of LP rotor. d The number of pressed rollers. e Spectrum diagram. f Poincaré diagram

Full size image
Fig. 7
figure 7

Dynamic responses analysis for ω1 = 821 rad/s in B. a The vertical displacement history. b The horizontal displacement history. c The orbit of LP rotor. d The number of pressed rollers. e Spectrum diagram. f Poincaré diagram

Full size image

For Fig. 6, the rotation speed ω1 = 683 rad/s is located in the “resonance zone” A, \(f_{{\text{H}}}\) is the dominant frequency of the dynamic responses, \(f_{{\text{L}}}\) is very small. The vertical signal and the horizontal signal seem like beat vibration, the orbit of the LP rotor looks almost circular and there is only one point in the Poincaré diagram. The number of pressed rollers is time-varying from 9 to 11. Thus, the “resonance zone” A is induced by the HP rotor’s unbalance.

For Fig. 7, the rotation speed ω1 = 821 rad/s is located in the “resonance zone” B, \(f_{{\text{L}}}\) is the dominant frequency of the dynamic responses, \(f_{{\text{H}}}\) is very small. The vertical signal and the horizontal signal seem like beat vibration, the orbit of the LP rotor looks almost circular and there is only one point in the Poincaré diagram. The number of pressed rollers is time-varying between 10 and 11. Thus, the “resonance zone” B is induced by the LP rotor’s unbalance.

Figures 8 and 9 are the inter-shaft bearing’s forces of for ω1 = 683 rad/s in A and for ω1 = 821 rad/s in B. It can be seen that the vertical and horizontal forces are time-varying just like sine curves. Therefore, it is very difficult to substitute the forces into Eq. (8b) to compute Mb.

Fig. 8
figure 8

Inter-shaft bearing’s forces for ω1 = 683 rad/s in A. a Vertical direction. b Horizontal direction

Full size image
Fig. 9
figure 9

Inter-shaft bearing’s forces for ω1 = 821 rad/s in B. a Vertical direction. b Horizontal direction

Full size image

Once the dynamic equations Eqs. (2a–h) are solved, the inter-shaft bearing’s forces along the vertical direction and horizontal direction are also attained at the same time. Based on Eq. (7), the dynamic load can be attained accordingly. Figure 10 displays the dynamic load varies with the LP rotor’s rotation speed.

Fig. 10
figure 10

The dynamic load of the inter-shaft bearing against the rotation speed

Full size image

In Fig. 10, the dynamic load increases so sharply in the “resonance zone” A and B that two peaks are formed here, while the dynamic load is very small in the “non-resonance zone” C, D and E. Comparing Figs. 5 and 10, the dynamic load curve are basically the same with the amplitude frequency curves.

All in all, the dynamic load is able to mirror the dynamic properties of the dual-rotor system. Comparing with the static load commonly used in previous literature, the dynamic load is more proper to depict the practical load of the inter-shaft bearing especially in the “resonance zone” of the system because it contains the dynamic properties of the system. Comparing with the time-varying forces of the bearing, the dynamic load is not time-varying but constant for any rotation speed, which enables it easier to compute the load FHG.

3.2 Thermal analysis

The unsteady-state heat balance equations Eq. (12) also can be solved by the Runge–Kutta method. The initial temperature is equal to the ambient temperature \(T_{\infty } = 20 \,^{{\text{o}}}{\text{C}}\); the calculation time is 10000 s, which is long enough for the inter-shaft bearing to reach steady-state temperatures; the time step is 10 s; the errors are < 10–6. The kinematic viscosity of the lubricant is changing as Fig. 3 during the temperature evolution. Figure 11 displays the steady-state temperature of rollers, inner ring and outer ring vary with the LP rotor’s rotation speed.

Fig. 11
figure 11

Steady-state temperature of the rollers, the inner ring and the outer ring against the LP rotor’s rotation speed

Full size image

In Fig. 11, it can be discovered that the rollers’ temperature Tr is highest and the outer ring’s temperature To is lowest. To is lower than the inner ring’s temperature Ti because the heat dissipation of the outer ring is stronger than that of the inner ring. Moreover, the variation for Tr, Ti and To with the rotation speed are the same with each other. In regions A and B, they all increase so sharply that two “temperature peak” are formed here. In regions C, D and E, they all increase gradually. Comparing Fig. 11 with Fig. 10, it can be discovered that A and B are exactly the “resonance zone” A and B of the dual-rotor system, while C, D and E are exactly the “non-resonance zone” C, D and E of the dual-rotor system.

In order to analyze the unsteady-state temperatures of rollers, the inner ring and outer ring in “resonance zone” and “non-resonance zone”, Fig. 12 displays the temperature evolutions of the rollers, the inner ring and the outer ring for five different rotation speeds in “resonance zone” A, B and “non-resonance zone” C, D, E. Herein, \(T^{{{\text{steady}}}}\) represents the ideal steady-state temperature, 0.99 \(T^{{{\text{steady}}}}\) is taken as the boundary between the unsteady-state heat transfer and the steady-state heat transfer.

Fig. 12
figure 12

Temperature evolutions of rollers, inner ring and outer ring. a For ω1 = 600 rad/s in C. b For ω1 = 683 rad/s in A. c For ω1 = 750 rad/s in D. d For ω1 = 821 rad/s in B. e For ω1 = 900 rad/s in E

Full size image

In Fig. 12, there is Tr > Ti > To during the entire evolution. Initially, the rate of temperature rise is the highest, and it decreases over time. Finally, the rate of temperature rise decreases to zero, which means that the temperature reaches a steady-state temperature and no longer changes. The temperature rises quickly from the ambient temperature to 0.8 \(T^{{{\text{steady}}}}\), but when the temperature further rises to 0.99 \(T^{{{\text{steady}}}}\), the time consumed will increase sharply. Comparing the rotation speeds and the temperature in “resonance zone” A, B and “non-resonance zone” C, D, E, there is \(\omega_{{\text{C}}} < \omega_{{\text{A}}} < \omega_{{\text{D}}} < \omega_{{\text{B}}} < \omega_{{\text{E}}}\) and \(T_{{\text{C}}} < T_{{\text{D}}} < T_{{\text{E}}} < T_{{\text{A}}} < T_{{\text{B}}}\). As the rotation speed increases, the temperature does not simply increase monotonically. It indicates the dynamic properties of the dual-rotor system make an important impact on the temperature of the inter-shaft bearing.

In short, the dynamic behaviours of the dual-rotor system are coupled with the thermal behaviours of the inter-shaft bearing. In the “resonance zone” of the system, the temperature of bearing increases so sharply that two “temperature peak” are formed just like “resonance peak”. In the “non-resonance zone” of the system, the temperature increases gradually.

3.3 FHG analysis

The effect of the rotation speed on the FHGs of the inter-shaft bearing is discussed in this section. The root cause of the temperature rise or fall is the accumulation or dispersion of heat. In order to find out the reason why the formation of temperature peaks in the “resonance zone” A and B, the FHG analysis is essential. Figure 13 displays the total FHG, the load FHG and the viscosity FHG vary with the LP rotor’s rotation speed.

Fig. 13
figure 13

FHGs against the LP rotor’s rotation speed

Full size image

In Fig. 13, it can be discovered that the load FHG Qb increases so sharply in “resonance zone” A and B that two peaks are formed here because the system resonates in A and B and the dynamic load is very large here; Qb is very small in the “non-resonance zone” C, D and E. The load FHG is basically the same as the dynamic load. The viscosity FHG Qν decreases so obviously in A and B that two valleys are formed here, because the temperature is higher and the lubricant viscosity is lower here; Qν increases gradually in C, D and E. Therefore, the total FHG Qt increases so sharply in “resonance zone” A and B that two peaks are formed here, while increases gradually in C, D and E.

It is worth noting that the total FHG shows the same behaviours with the inter-shaft bearing’s temperatures. In the “resonance zone” A and B, the load FHG plays a leading role because the dynamic load increases rapidly here. In the “non-resonance zone” C, D and E, the viscosity FHG plays a leading role because the dynamic load is very small here. In the “resonance zone” A and B, the load FHG forms two peaks while the viscosity FHG forms two valleys.

3.4 Influence of the ambient temperature

This section discussed the temperature and the FHGs affected by the ambient temperature, which are \(T_{\infty } = 0 \, ^{{\text{o}}}{\text{C}}\), \(T_{\infty } = 10 \, ^{{\text{o}}}{\text{C}}\), \(T_{\infty } = 20 \, ^{{\text{o}}}{\text{C}}\) and \(T_{\infty } = 30 \, ^{{\text{o}}}{\text{C}}\), respectively. Figure 14 displays the comparison of the steady-state temperature of rollers, the total FHG, the load FHG and the viscosity FHG at different ambient temperature. In Fig. 14a, it can be seen that as \(T_{\infty }\) increases, Tr in both “resonance zone” and “non-resonance zone” increases gradually, it looks like the curve moves upward. In Fig. 14b, as \(T_{\infty }\) increases, Qt in both “resonance zone” and “non-resonance zone” decreases gradually, it looks like the curve moves downward. In Fig. 14c, it can be discovered that \(T_{\infty }\) does not affect the Qb. In Fig. 14d, as \(T_{\infty }\) increases, Q decreases gradually, it looks like the curve moves downward.

Fig. 14
figure 14

Steady-state temperature and FHGs against the LP rotor’s rotation speed at different ambient temperature. a Steady-state temperature of rollers. b Total FHG. c Load FHG. d Viscosity FHG

Full size image

In a word, the ambient temperature has an opposite effect on the temperature and the total FHG. As the ambient temperature increase, the temperature-rotation speed curve moves upward, while the total FHG-rotation speed curve moves downward. The ambient temperature has little effect on the load FHG but makes an important impact on the viscosity FHG because the viscosity-temperature relationship of the lubricant is considered.

4 Conclusion

In this research, FHGs under the inter-shaft bearing’s dynamic load have been obtained by Palmgren’s empirical formula, subsequently, the unsteady-state heat balance equations under the dynamic load have been presented considering the viscosity-temperature relationship of the lubricant. Afterwards, the dynamic load analysis, the temperature analysis, the FHG analysis and the influence of the ambient temperature have been accomplished. Some new discovers are shown below:

  1. (1)

    The dynamic load of the inter-shaft bearing is able to mirror the dynamic properties of the dual-rotor system. It is more proper for the dynamic load to depict the practical load of the inter-shaft bearing especially in the “resonance zone” of the system, rather than the static load commonly used in the previous literature.

  2. (2)

    The dynamic behaviours of the dual-rotor system are coupled with the thermal behaviours of the inter-shaft bearing. In the “resonance zone” of the system, the temperature increases so sharply that two “temperature peak” are formed just like “resonance peak”. In the “non-resonance zone” of the system, the temperature increases gradually.

  3. (3)

    The total FHG shows the same behaviours with the inter-shaft bearing’s temperatures. In the “resonance zone” of the system, the load FHG plays a leading role because the dynamic load increases rapidly here. In the “non-resonance zone” of the system, the viscosity FHG plays a leading role because the dynamic load is very small here.

  4. (4)

    The ambient temperature has an opposite effect on the temperature and the total FHG. As the ambient temperature increase, the temperature-rotation speed curve moves upward, while the total FHG-rotation speed curve moves downward.

The future study will focus on the verification of the unsteady-state heat balance equations under the inter-shaft bearing’s dynamic load by experiment.