1 Introduction

Propagation of two or more components with different spectral peaks, modes, or polarization states in nonlinear media can be described by some coupled nonlinear Schrödinger (NLS) systems [1,2,3,4,5,6,7]. Such coupled NLS systems have been considered and investigated in multidisciplinary areas, e.g., nonlinear optics, plasma physics and Bose–Einstein condensates [1,2,3,4,5,6,7]. With the Ablowitz–Kaup–Newell–Segur (AKNS) method, the coupled NLS system with nonlinear coupling terms describing the potential dynamics of two orthogonally polarized modes in a nonlinear optical fiber has been proposed as [8]

$$\begin{aligned}&iQ_{1t}+Q_{1xx}+2(|Q_{1}|^2-2|Q_{2}|^2)Q_{1}-2Q^{*}_{1}Q^2_{2}=0, \end{aligned}$$
(1a)
$$\begin{aligned}&iQ_{2t}+Q_{2xx}+2(2|Q_{1}|^2-|Q_{2}|^2)Q_{2}+2Q^{*}_{2}Q^2_{1}=0, \end{aligned}$$
(1b)

where \(Q_{1}(x,t)\) and \(Q_{2}(x,t)\) are the slowly varying complex amplitudes in two interacting optical modes, the variables x and t, respectively, correspond to the space and time coordinates, and the asterisk denotes the complex conjugate. Equation (1) could also be rewritten as a matrix form

$$\begin{aligned} i\mathbf {Q }_{t}+\mathbf {Q}_{xx}+2\mathbf {Q}\mathbf {Q}^{*}\mathbf {Q}=0, \end{aligned}$$
(2)

with

$$\begin{aligned} \mathbf {Q}=\begin{pmatrix} Q_{1}&{}\quad Q_{2} \\ -Q_{2}&{}\quad Q_{1} \end{pmatrix}. \end{aligned}$$
(3)

Solitons of a class of matrix NLS equations have been investigated using the inverse scattering transform [9]. It is noted that Eq. (1) correspond to the case 3 in [9] with the identification \(q_{0}=iQ_{1}\) and \(q_{1}=-q_{-1}=Q_{2}\) and case 4 in [9] with the identification \(q_{0}=Q_{2}\) and \(q_{1}=-q_{-1}=Q_{1}\). Some other integrable matrix systems such as novel resonant wave interaction equations have been found in [10].

Besides, considering higher pulse input powers, one should include the higher-order effects in the basic NLS models [11,12,13,14,15,16,17]. Specifically, in optics, the third-order dispersion and self-steepening effects have been used to describe the propagation of ultrashort pulses along a fiber [11,12,13,14,15,16,17]. Motivated by the above reasons, we introduce the following matrix NLS equation with higher-order effects (i.e., the matrix form of Hirota equation [18]):

$$\begin{aligned} i\mathbf {Q}_{t}+\mathbf {Q}_{xx}+2\mathbf {Q}\mathbf {Q}^{*}\mathbf {Q}+i \alpha \mathbf {Q}_{xxx}+6i \alpha \mathbf {Q}\mathbf {Q}^{*}\mathbf {Q}_{x}=0, \end{aligned}$$
(4)

where \(\alpha \) denotes the perturbation strength of higher-order effects. With (3), we rewrite Eq. (4) as

$$\begin{aligned}&iQ_{1t}+Q_{1xx}+2(|Q_{1}|^2-2|Q_{2}|^2)Q_{1}-2Q^{*}_{1}Q^2_{2}+i\alpha Q_{1xxx}\nonumber \\&\quad +6i\alpha (|Q_{1}|^2-|Q_{2}|^2)Q_{1x}-6i\alpha (Q_{1}Q^*_{2}+Q_{2}Q^*_{1})Q_{2x}=0, \end{aligned}$$
(5a)
$$\begin{aligned}&iQ_{2t}+Q_{2xx}+2(2|Q_{1}|^2-|Q_{2}|^2)Q_{2}+2Q^{*}_{2}Q^2_{1}+i\alpha Q_{2xxx}\nonumber \\&\quad +6i\alpha (|Q_{1}|^2-|Q_{2}|^2)Q_{2x}+6i\alpha (Q_{2}Q^*_{1}+Q_{1}Q^*_{2})Q_{1x}=0, \end{aligned}$$
(5b)

where the coefficients of the self-phase modulation and cross-phase modulation still have the opposite signs. When \(\alpha \ne 0\), System (5) involves the third-order dispersion and self-steepening effects.

In this paper, we will show some dynamics of fundamental solitons and rogue waves of System (5). Firstly, we will obtain the vector breather solutions on the mixed (nonzero–zero) backgrounds. Here, the mixed background means that one component has nonzero background, while another one has zero background with \(x\rightarrow {\pm \infty }\). Since the breather-to-soliton conversion that could appear in scalar NLS equations with the presence of high-order effects [13,14,15], we could generate the vector solitons on the mixed backgrounds. Secondly, rogue waves are also the active multidisciplinary problems of research in the past ten years or more [14, 19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. Some analytical evidences show that fundamental rogue waves with ultra-high amplitude maybe appear in coupled systems [35,36,37,38]. The previous studies have shown such rogue waves on the vector nonzero backgrounds [35,36,37,38]. However, in this paper, the fundamental rogue waves of ultra-high peak amplitude on the mixed backgrounds are obtained.

The outline of this paper is as follows. In Sect. 2, we will construct the Lax pair and Darboux transformation (DT) of System (5). In Sect. 3, based on DT, we will study the vector breathers and solitons on the mixed backgrounds of System (5). Besides, we will study the fundamental rogue waves with ultra-high amplitude on the mixed backgrounds. Section 4 will be our conclusion.

2 Lax pair and DT

Using the AKNS formulation, the Lax pair associated with System (5) can be written in the \(4\times 4\) matrix form as

$$\begin{aligned}&\varPsi _{x}=\mathbf {U}\varPsi =\left[ \lambda U_{0}+U_{1}\right] \varPsi , \end{aligned}$$
(6a)
$$\begin{aligned}&\varPsi _{t}=\mathbf {V}\varPsi =\left[ \lambda ^3 V_{3}+ \lambda ^2V_{2}+\lambda V_{1}+V_{0}\right] \varPsi , \end{aligned}$$
(6b)

with

$$\begin{aligned}&U_{0}=i\begin{pmatrix} -\mathbf {I}_{2\times 2} &{}\quad \mathbf {O} \\ \mathbf {O}&{} \mathbf {I}_{2\times 2} \end{pmatrix}, \quad V_{2}=\begin{pmatrix} -2i\mathbf {I}_{2\times 2} &{}\quad 4\alpha \mathbf {Q} \\ -4\alpha \mathbf {Q}^*&{}\quad 2 i\mathbf {I}_{2\times 2} \end{pmatrix},\quad V_{3}=4i\alpha \begin{pmatrix} -\mathbf {I}_{2\times 2} &{}\quad \mathbf {O} \\ \mathbf {O}&{} \mathbf {I}_{2\times 2} \end{pmatrix},\nonumber \\&U_{1}=\begin{pmatrix} \mathbf {O} &{} \quad \mathbf {Q} \\ -\mathbf {Q}^* &{}\quad \mathbf {O} \end{pmatrix}, \quad \mathbf {Q}=\begin{pmatrix} Q_{1}&{}\quad Q_{2} \\ -Q_{2}&{}\quad Q_{1} \end{pmatrix},\quad V_{1}=\begin{pmatrix} 2i\alpha \mathbf {Q}\mathbf {Q}^* &{}\quad 2i\alpha \mathbf {Q}_{x} + 2\mathbf {Q} \\ 2i\alpha \mathbf {Q}^*_{x}-2\mathbf {Q}^* &{}\quad -2i\alpha \mathbf {Q}^*\mathbf {Q} \end{pmatrix},\nonumber \\&V_{0} = \begin{pmatrix} i \mathbf {Q}\mathbf {Q}^*+\alpha (\mathbf {Q}\mathbf {Q}^*_{x}-\mathbf {Q}_{x}\mathbf {Q}^*)&{}\quad i\mathbf {Q}_{x} -\alpha (\mathbf {Q}_{xx}+2\mathbf {Q}\mathbf {Q}^*\mathbf {Q}) \\ i\mathbf {Q}^*_{x}+\alpha (\mathbf {Q}^*_{xx}+2\mathbf {Q}^*\mathbf {Q}^*\mathbf {Q}) &{}\quad - i\mathbf {Q}^*\mathbf {Q} -\alpha (\mathbf {Q}^*_{x}\mathbf {Q}-\mathbf {Q}^*\mathbf {Q}_{x})\end{pmatrix}, \end{aligned}$$

where \(\varPsi \) is the vector eigenfunction and depends on the variables x and t, \(\lambda \) is the complex spectral parameter of Lax Pair (6), \(\mathbf {I}_{2\times 2}\) is the \(2 \times 2\) unit matrix, \(\mathbf {O}\) is the \(2 \times 2\) zero matrix. It can be verified that the zero-curvature equation \(\mathbf {U}_{t}-\mathbf {V}_{x}+[\mathbf {U},\mathbf {V}]=0\) yields System (5).

Introducing the gauge transformation

$$\begin{aligned} \varPsi [1]=\mathbf {D} \varPsi , \end{aligned}$$
(7)

and substituting it into Lax Pair (6), we obtain

$$\begin{aligned}&\mathbf {U}[1]\mathbf {D}=\mathbf {D}_{x}+\mathbf {D} \mathbf {U}, \end{aligned}$$
(8a)
$$\begin{aligned}&\mathbf {V}[1]\mathbf {D}=\mathbf {D}_{t}+\mathbf {D} \mathbf {V}, \end{aligned}$$
(8b)

where

$$\begin{aligned}&\mathbf {U}[1]=\lambda U_{0}[1]+U_{1}[1], \end{aligned}$$
(9a)
$$\begin{aligned}&\mathbf {V}[1]=\lambda ^3 V_{3}[1]+ \lambda ^2V_{2}[1]+\lambda V_{1}[1]+V_{0}[1], \end{aligned}$$
(9b)

which means they have the same forms as \(\mathbf {U}\) and \(\mathbf {V}\), except that the potentials \(Q_{1}\) and \(Q_{2}\) are replaced by \(Q_{1}[1]\) and \(Q_{2}[1]\). Motivated by [8], we note that if \(\begin{pmatrix} \psi _{1} &{}\quad -\psi _{2} \\ \psi _{2} &{}\quad \psi _{1} \\ \psi _{3} &{}\quad -\psi _{4} \\ \psi _{4} &{}\quad \psi _{3} \end{pmatrix}\) is a vector eigenfunction of Lax pair (6) with \(\lambda =\lambda _{1}\), then \(\begin{pmatrix} \psi ^*_{3} &{}\quad -\psi ^*_{4} \\ \psi ^*_{4} &{}\quad \psi ^*_{3} \\ -\psi ^*_{1} &{}\quad \psi ^*_{2} \\ -\psi ^*_{2} &{}\quad -\psi ^*_{1} \end{pmatrix}\) is a vector eigenfunction of Lax pair (6) with \(\lambda =\lambda ^*_{1}\). Therefore, the matrix \(\mathbf {D}\) is constructed as follows:

$$\begin{aligned} \mathbf {D}= & {} (\lambda \mathbf {I}_{4\times 4}-S), S=\begin{pmatrix} \psi _{1} &{}\quad -\psi _{2}&{}\quad \psi ^*_{3} &{}\quad -\psi ^*_{4} \\ \psi _{2} &{}\quad \psi _{1} &{}\quad \psi ^*_{4} &{}\quad \psi ^*_{3} \\ \psi _{3} &{}\quad -\psi _{4} &{}\quad -\psi ^*_{1} &{}\quad \psi ^*_{2} \\ \psi _{4} &{}\quad \psi _{3}&{}\quad -\psi ^*_{2} &{}\quad -\psi ^*_{1} \end{pmatrix}\begin{pmatrix} \lambda _{1} &{}\quad 0&{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \lambda _{1} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \lambda ^*_{1} &{}\quad 0 \\ 0 &{}\quad 0&{}\quad 0 &{}\quad \lambda ^*_{1} \end{pmatrix} \nonumber \\&\times \begin{pmatrix} \psi _{1} &{}\quad -\psi _{2}&{}\quad \psi ^*_{3} &{}\quad -\psi ^*_{4} \\ \psi _{2} &{}\quad \psi _{1} &{}\quad \psi ^*_{4} &{}\quad \psi ^*_{3} \\ \psi _{3} &{}\quad -\psi _{4} &{}\quad -\psi ^*_{1} &{}\quad \psi ^*_{2} \\ \psi _{4} &{}\quad \psi _{3}&{}\quad -\psi ^*_{2} &{}\quad -\psi ^*_{1} \end{pmatrix}^{-1}. \end{aligned}$$
(10)

It is noted that System (5) belongs to AKNS system. The Darboux matrix of scalar AKNS system is given in Section 1.3 of [39], and the Darboux matrix of matrix AKNS system is given in Theorem 3.1 of [40]. So we can know that the matrix (10) is the Darboux matrix of System (5).

Then, from (8) and (10), we have

$$\begin{aligned}&U_{0}[1]=U_{0},\quad V_{3}[1]=V_{3}, \end{aligned}$$
(11a)
$$\begin{aligned}&-U_{0}[1] S+U_{1}[1]=U_{1}-SU_{0}, \end{aligned}$$
(11b)
$$\begin{aligned}&-U_{1}[1]S=-S_{x}-SU_{1}, \end{aligned}$$
(11c)
$$\begin{aligned}&-V_{3}[1]S+V_{2}[1]=-SV_{3}+V_{2}, \end{aligned}$$
(11d)
$$\begin{aligned}&-V_{2}[1]S+V_{1}[1]=-SV_{2}+V_{1}, \end{aligned}$$
(11e)
$$\begin{aligned}&-V[1]S+V_{0}[1]=-SV_{1}+V_{0}, \end{aligned}$$
(11f)
$$\begin{aligned}&-V_{0}[1]S=-S_{t}-SV_{0}. \end{aligned}$$
(11g)

From (11b) to (11g), we can get the relation between \((Q_{1}[1],Q_{2}[1])\) and \((Q_{1},Q_{2})\) as

$$\begin{aligned} Q_{1}[1]=Q_{1}-2iS_{13},\quad Q_{2}[1]=Q_{2}-2iS_{14}, \end{aligned}$$
(12)

where \(S_{13}\) means the element in first row and third column of S and \(S_{14}\) means the element in first row and fourth column of S.

3 Dynamics of fundamental solitons and rogue waves on the mixed backgrounds

In this section, in order to derive the vector breather solutions on the mixed backgrounds, we start with the seed solutions of System (5) as

$$\begin{aligned}&Q_{10}=a_{1}e^{ i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) },\ Q_{20}=0. \end{aligned}$$
(13)

Firstly, we set

$$\begin{aligned} \varPsi _{0}=\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad e^{-i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad e^{- i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) } \end{pmatrix}\varPhi , \end{aligned}$$
(14)

from which, Lax Pair (6) reads

$$\begin{aligned} \varPhi _{x}=A(\lambda ) \varPhi , \quad \varPhi _{t}=B(\lambda )\varPhi , \quad A(\lambda )B(\lambda )-B(\lambda )A(\lambda )=0, \end{aligned}$$
(15)

where \(\varPhi \) is a \(4\times 4\) square matrix that depends on the variables x and t,

$$\begin{aligned}&A(\lambda )=\left( \begin{array}{cccc} -i \lambda &{}\quad 0 &{}\quad a_1 &{}\quad 0 \\ 0 &{}\quad -i \lambda &{}\quad 0 &{}\quad a_1 \\ -a_1 &{}\quad 0 &{}\quad i k+i \lambda &{}\quad 0 \\ 0 &{}\quad -a_1 &{}\quad 0 &{}\quad i k+i \lambda \\ \end{array} \right) ,\,\,\, B(\lambda )=\begin{pmatrix} \bigtriangleup _{11} &{}\quad 0 &{}\quad \bigtriangleup _{13}&{}\quad 0 \\ 0 &{}\quad \bigtriangleup _{22} &{}\quad 0 &{}\quad \bigtriangleup _{24} \\ \bigtriangleup _{31}&{}\quad 0 &{}\quad \bigtriangleup _{33} &{}\quad 0 \\ 0 &{}\quad \bigtriangleup _{42} &{}\quad 0 &{}\quad \bigtriangleup _{44} \end{pmatrix},\nonumber \\ \end{aligned}$$
(16)

with

$$\begin{aligned}&\bigtriangleup _{11}=-i \left( 2 \lambda ^2 (2 \alpha \lambda +1)+a_1^2 (-2 \alpha \lambda +2 \alpha k-1)\right) ,\\&\bigtriangleup _{13}=a_1 \left( -2 \alpha a_1^2+2 \lambda (2 \alpha \lambda +1)+\alpha k^2-k (2 \alpha \lambda +1)\right) ,\\&\bigtriangleup _{22}=-i \left( 2 \lambda ^2 (2 \alpha \lambda +1)+a_1^2 (-2 \alpha \lambda +2 \alpha k-1)\right) ,\\&\bigtriangleup _{24}=a_1 \left( -2 \alpha a_1^2+2 \lambda (2 \alpha \lambda +1)+\alpha k^2-k (2 \alpha \lambda +1)\right) ,\\&\bigtriangleup _{31}=a_1 \left( 2 \alpha a_1^2-2 \lambda (2 \alpha \lambda +1)-\alpha k^2+2 \alpha \lambda k+k\right) ,\\&\bigtriangleup _{33}=i \left( 2 \lambda ^2 (2 \alpha \lambda +1)+a_1^2 (-2 \alpha \lambda -4 \alpha k+1)+\alpha k^3-k^2\right) ,\\&\bigtriangleup _{42}=a_1 \left( 2 \alpha a_1^2-2 \lambda (2 \alpha \lambda +1)-\alpha k^2+2 \alpha \lambda k+k\right) ,\\&\bigtriangleup _{44}=i \left( 2 \lambda ^2 (2 \alpha \lambda +1)+a_1^2 (-2 \alpha \lambda -4 \alpha k+1)+\alpha k^3-k^2\right) . \end{aligned}$$

Then, \(\varPsi _{0}\) and \((\psi _{1}, \psi _{2}, \psi _{3}, \psi _{4} )^{T}\) can be written as

$$\begin{aligned}&\varPsi _{0}=\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad e^{-i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad e^{- i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) } \end{pmatrix} e^{A(\lambda ) x+ B(\lambda ) t}, \nonumber \\\end{aligned}$$
(17)
$$\begin{aligned}&(\psi _{1}, \psi _{2}, \psi _{3}, \psi _{4} )^{T} \nonumber \\&\qquad =\begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad e^{-i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad e^{- i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) } \end{pmatrix}\nonumber \\&\,\quad \times e^{A(\lambda ) x+ B(\lambda ) t} F_{0}, \nonumber \\ \end{aligned}$$
(18)

with \(F_{0}=(Z_{11}, Z_{21}, Z_{31}, Z_{41})^{T}\), where \(Z_{i1}\) \((i=1,2,3,4)\) are the arbitrary complex constants.

Using DT (12), we obtain the vector breather solutions on the mixed backgrounds as

$$\begin{aligned} Q_{1}=a_{1}e^{ i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) }-2iS_{13},\quad Q_{2}=-2iS_{14}, \end{aligned}$$
(19)

where \(S_{13}\) and \(S_{14}\) can be obtained in (10), \((\psi _{1}, \psi _{2}, \psi _{3}, \psi _{4} )^{T} \) is given in (18), \(a_{1}\) and k are the arbitrary real constants, \(\lambda \) is the arbitrary complex constant. In general, Solutions (19) represent the vector breathers except that some special constraints are satisfied (see the solitons or rogue waves in below).

Concretely, for the fixed parameters, we only need to derive \((\psi _{1}, \psi _{2}, \psi _{3}, \psi _{4} )^{T} \). For example, when \(\alpha =\frac{1}{3}\), \(a_{1}=1\), \(k=0\), \(\lambda =\frac{1}{2}+\frac{8}{9}i\), \(Z_{11}=0\), \(Z_{21}=Z_{31}=Z_{41}=1\), we have

$$\begin{aligned}&\psi _{1}=\frac{\tau _{1}}{\sqrt{((720+94 i) t-243 i x)^2}}, \quad \psi _{2}=\frac{\tau _{2}}{\sqrt{((720+94 i) t-243 i x)^2}},\\&\psi _{3}=\frac{\tau _{3}}{\sqrt{((720+94 i) t-243 i x)^2}}, \quad \psi _{4}=\frac{\tau _{4}}{\sqrt{((720+94 i) t-243 i x)^2}}\\&\tau _{1}=\left( \frac{2592}{105145}+\frac{1341 i}{105145}\right) \sqrt{149+288 i} \left( -1+e^{\varTheta }\right) ((720+94 i) t-243 i x)e^{i t-\frac{\varTheta }{2}},\\&\tau _{2}= \left( \frac{144}{105145}+\frac{149 i}{210290}\right) \sqrt{149+288 i} \left( (25326-3284 i) t \left( -1+e^{\varTheta }\right) \right. \\&\left. \qquad -(2187+8262 i) x \left( -1+e^{\varTheta }\right) -i \sqrt{149+288 i} \left( 1+e^{\varTheta }\right) \sqrt{((720+94 i) t-243 i x)^2}\right) \nonumber \\&\qquad \times e^{i t-\frac{\varTheta }{2}},\\&\tau _{3}=\left( \frac{144}{105145}+\frac{149 i}{210290}\right) \sqrt{149+288 i} \left( (-12366+4976 i) t \left( -1+e^{\varTheta }\right) \right. \\&\left. \qquad +(2187+3888 i) x \left( -1+e^{\varTheta }\right) -i \sqrt{149+288 i} \left( 1+e^{\varTheta }\right) \sqrt{((720+94 i) t-243 i x)^2}\right) \nonumber \\&\qquad \times e^ {-i t-\frac{\varTheta }{2}},\\&\tau _{4}=\left( \frac{144}{105145}+\frac{149 i}{210290}\right) \sqrt{149+288 i} \left( (-25326+3284 i) t \left( -1+e^{\varTheta }\right) \right. \\&\left. \qquad +(2187+8262 i) x \left( -1+e^{\varTheta }\right) -i \sqrt{149+288 i} \left( 1+e^{\varTheta }\right) \sqrt{((720+94 i) t-243 i x)^2}\right) \nonumber \\&\qquad \times e^{ -i t-\frac{\varTheta }{2}}, \end{aligned}$$

with

$$\begin{aligned} \varTheta ={\frac{\sqrt{149+288 i} \sqrt{((720+94 i) t-243 i x)^2}}{2187}}. \end{aligned}$$

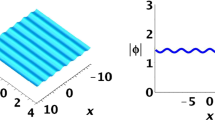
Such vector breather on the mixed backgrounds is shown in Fig. 1. In the \(Q_{1}\) component, the breather is located on the nonzero background, while in the \(Q_{2}\) component, the breather is located on the zero background. Such breathers with mixed backgrounds provide the possibility to generate the vector solitons on mixed backgrounds. We have known that the breather-to-soliton conversion could occur in Hirota equation [15]. For System (5), if taking the initial value \(Q_{1}\) as a plane-wave solution and \(Q_{2}\) as a zero solution, we will have the same eigenfunctions from the Lax pair as the Hirota equation, which means that we could use the same condition of breather-to-soliton conversion here as in Hirota equation. The conversion occurs when the lines of extrema of the hyperbolic and the trigonometric functions in breather solutions on the (x, t)-plane coincide (in other words, the group velocity is equal to the phase velocity) [15]. Via the breather-to-soliton conversion in Hirota equation [15], i.e., \(\alpha =\frac{1}{-4 Re(\lambda )}\), the vector breather on the mixed background is converted to the vector soliton on the mixed background, as shown in Fig. 2.

Fig. 1
figure 1

Vector breather envelope distributions \(|Q_{1}|\) and \(|Q_{2}|\) of Solutions (19) with \(\alpha =\frac{1}{3}\), \(a_{1}=1\), \(k=0\), \(\lambda =\frac{1}{2}+\frac{8}{9}i\), \(Z_{11}=0\), \(Z_{21}=Z_{31}=Z_{41}=1\)

Full size image
Fig. 2
figure 2

Vector breather to soliton conversions with the same parameters as Fig. 1 except \(\lambda =-\frac{3}{4}+\frac{8}{9}i\)

Full size image

To obtain the rogue-wave solutions, the two matrices \(A(\lambda )\) and \(B(\lambda )\) are not diagonalizable but are similar to a Jordan form, \((\psi _{1}, \psi _{2}, \psi _{3}, \psi _{4})\) is a linear combination of the polynomial functions, which means that we could generate rational solutions. Since \(A(\lambda )B(\lambda )=B(\lambda )A(\lambda )\), we just need check \(A(\lambda )\). We obtain the four roots of the characteristic polynomial of \(A(\lambda )\) as

$$\begin{aligned}&\varLambda _{1}=\varLambda _{2}=\frac{1}{2} \left( -\sqrt{-4 a_1^2-k^2-4 \lambda ^2-4 \lambda k}+i k\right) ,\nonumber \\&\varLambda _{3}=\varLambda _{4}=\frac{1}{2} \left( -\sqrt{-4 a_1^2-k^2-4 \lambda ^2-4 \lambda k}+i k\right) . \end{aligned}$$
(20)

If \(\varLambda _{1}=\varLambda _{2}\ne \varLambda _{3}=\varLambda _{4}\), \(A(\lambda )\) is diagonalizable as

$$\begin{aligned} \left( \begin{array}{cccc} \varLambda _{1} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \varLambda _{1} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \varLambda _{3} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \varLambda _{3} \\ \end{array} \right) . \end{aligned}$$

If \(\varLambda _{1}=\varLambda _{2}=\varLambda _{3}=\varLambda _{4}\), which means \(-4 a_1^2-k^2-4 \lambda ^2-4 \lambda k=0\) or \(\lambda =\frac{1}{2} \left( -k\pm 2 i a_1\right) \). Then \(A(\lambda )\) is similar to the following Jordan form

$$\begin{aligned} \left( \begin{array}{cccc} \frac{i k}{2} &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \frac{i k}{2} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \frac{i k}{2} &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{i k}{2} \\ \end{array} \right) . \end{aligned}$$

Therefore, using Expression (17) and DT (12), with \(\lambda =\frac{1}{2} \left( -k+2 i a_1\right) \), we obtain the rogue-wave solutions as follows:

$$\begin{aligned}&Q_{1}=a_{1}e^{ \left( i \left( k x-t \left( a_1^2 (6 \alpha k-2)-\alpha k^3+k^2\right) \right) \right) }-2iS_{13},\quad Q_{2}=-2iS_{14}, \end{aligned}$$
(21)

with

$$\begin{aligned} \psi _{1}= & {} e^{\frac{1}{2} i \left( a_1^2 t (2-6 \alpha k)+k \left( \alpha k^2 t-k t+x\right) \right) }[Z_{11} \left( a_1 \left( 3 \alpha k^2 t-2 k t+x\right) -2 i a_1^2 t (3 \alpha k-1)-6 \alpha a_1^3 t+1\right) \\&+a_1 Z_{31} \left( -2 i a_1 t (3 \alpha k-1)-6 \alpha a_1^2 t+3 \alpha k^2 t-2 k t+x\right) ],\\ \psi _{2}= & {} e^{\frac{1}{2} i \left( a_1^2 t (2-6 \alpha k)+k \left( \alpha k^2 t-k t+x\right) \right) } [Z_{21} \left( a_1 \left( 3 \alpha k^2 t-2 k t+x\right) -2 i a_1^2 t (3 \alpha k-1)-6 \alpha a_1^3 t+1\right) \\&+a_1 Z_{41} \left( -2 i a_1 t (3 \alpha k-1)-6 \alpha a_1^2 t+3 \alpha k^2 t-2 k t+x\right) ],\\ \psi _{3}= & {} e^{-\frac{1}{2} i \left( a_1^2 t (2-6 \alpha k)+k \left( \alpha k^2 t-k t+x\right) \right) }[-a_1 \left( Z_{11}+Z_{31}\right) \left( 3 \alpha k^2 t-2 k t+x\right) \\&+2 i a_1^2 t \left( Z_{11}+Z_{31}\right) (3 \alpha k-1)+6 \alpha a_1^3 t \left( Z_{11}+Z_{31}\right) +Z_{31}],\\ \psi _{4}= & {} e^{-\frac{1}{2} i \left( a_1^2 t (2-6 \alpha k)+k \left( \alpha k^2 t-k t+x\right) \right) }[-a_1 \left( Z_{21}+Z_{41}\right) \left( 3 \alpha k^2 t-2 k t+x\right) \\&+2 i a_1^2 t \left( Z_{21}+Z_{41}\right) (3 \alpha k-1)+6 \alpha a_1^3 t \left( Z_{21}+Z_{41}\right) +Z_{41}]. \end{aligned}$$

where \(a_{1}\) and k are the arbitrary real constants, \(Z_{i1}\) \((i=1,2,3,4)\) are the arbitrary complex constants.

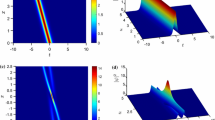
In Fig. 3, we show the fundamental rogue wave of ultra-high peak amplitude on the mixed background. It is noted that the value of the peak amplitude of \(|Q_{1}|\) is about 224 and the peak amplitude of \(|Q_{2}|\) is about 112. In the \(Q_{1}\) component, the rogue wave is located on the nonzero background and in the \(Q_{2}\) component, the rogue wave has double-peak profile and is located on the zero one.

Fig. 3
figure 3

Vector rogue wave envelope distributions \(|Q_{1}|\) and \(|Q_{2}|\) of Solutions (21) with \(\alpha =\frac{1}{20}\), \(a_{1}=1\), \(k=0\), \(Z_{11}=3+i\), \(Z_{21}=0.1\), \(Z_{31}=0\), \(Z_{41}=4\)

Full size image

The analytical forms corresponding to Fig. 3 can be expressed as

$$\begin{aligned} Q_{1}=e^{2it}\frac{A_{1}}{G}, \quad Q_{2}=80000 ie^{2it}\frac{A_{2}}{G}, \end{aligned}$$
(22)

where

$$\begin{aligned} A_{1}= & {} -1089896103441 t^4+24540 t^3 (13030722 x+(-14742319+43435740 i))\\&-100 t^2 \left( 5564118294 x^2-(1857780426-1563686640 i) x\right. \\&\left. +(-2125952711-2573990280 i)\right) \\&+2000 t \left( 39092166 x^3-(53960871-130307220 i) x^2+(1439763-38350380 i) x \right. \\&\left. +(19295880+11896810 i)\right) \\&-2500 \left( 26061444 x^4-12978552 x^3+(3199684-7872000 i)x^2 \right. \\&\left. +(255680-192000 i) x+(-748961-96000 i)\right) ,\\ G= & {} 1089896103441 t^4-24540 t^3 (13030722 x-14742319)\\&+200 t^2\left( 2782059147 x^2-928890213 x+269414969\right) \\&-3000 t \left( 26061444 x^3-35973914 x^2+13990564 x-1878399\right) \\&+2500 \left( 26061444 x^4-12978552 x^3+29261128 x^2-6233596 x+364801\right) ,\\ A_{2}= & {} 698889 t^2+t (-3258060 x+(437370-105090 i))+68100 x^2\\&-(259900-804300 i) x+(30050-89850 i). \end{aligned}$$

4 Conclusion

In this paper, on the mixed backgrounds, the vector solutions of the coupled higher-order NLS system with sign-alternating nonlinearity have been studied. We have constructed the Lax pair (6) and DT (12). Using the DT (12), we have obtained the vector breather solutions (19) and rogue-wave solutions (21). Based on such solutions, we have observed the vector solitons and fundamental rogue waves with ultra-high peak amplitude on the mixed backgrounds.