Periodic Orbits in the Muthuswamy-Chua Simplest Chaotic Circuit

Abstract

In 2010, Muthuswamy and Chua presented an autonomous chaotic circuit using only three elements in series: an inductor, a capacitor and a memristor. This circuit is known as the simplest chaotic circuit and it is determined by a three-dimensional differential system, which depends on the real parameters C, L, α and β. Although the Muthuswamy-Chua system is simpler in formulation than other chaotic systems, its dynamics has proven to be complicated. Here we analytically prove the existence of periodic orbits in this system for suitable choice of the parameter values α and β leading to interesting phenomena as multistability and formation of chaotic attractors. In order to do that, we consider the existence of first integrals, invariant algebraic surfaces and a result from averaging theory. In addition, we relate the obtained results to the memristance and to the physical characteristics of the memristor.

1 Introduction and Statement of the Main Results

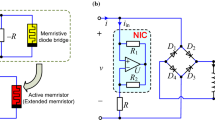
In [1], Muthuswamy and Chua proposed the memristor-based circuit shown in Fig. 1, composed of only three components in series: two energy storage elements (a linear passive inductor and a linear passive capacitor) and a nonlinear active memristor. They called it the simplest chaotic circuit, since it reduces the number of circuit elements required for chaotic dynamics and it is also the simplest possible circuit having only one locally-active element: the memristor. According to Muthuswamy and Chua, the memristor plays two important roles in the considered circuit: it provides the third essential state variable and the essential nonlinearity necessary for generating chaotic behavior.

Fig. 1

Schematic of the memristor-based circuit proposed by Muthuswamy and Chua in [1]

The memristor-based circuit proposed by Muthuswamy and Chua in [1] is described by the three-dimensional differential system

$$\begin{aligned} \dot{x}=\dfrac{y}{C}, \quad \quad \quad \dot{y}=-\dfrac{1}{L}\,[x+\beta (z^2-1)y], \quad \quad \quad \dot{z}=-y-\alpha z+yz, \end{aligned}$$

(1)

where $(x,y,z)\in \mathbb {R}^3$ are the state variables, C, L, α and β are real parameters and the dot denotes derivative with respect to the time t. The function $M(z)=\beta \,(z^2-1)$ is called memristance of the memristor device in Fig. 1. For more details on obtaining system (1) as the mathematical model of the circuit proposed by Muthuswamy and Chua and the physical meaning of parameters, see [1]. In such a paper, Muthuswamy and Chua fixed $C=1$, $L=3$, $\alpha =0.6$ and, by varying β, they empirically observed period-one and period-two oscillations for $\beta =1.2$ and $\beta =1.3$, respectively, and chaotic attractors for $\beta =1.5$ and $\beta =1.7$, which are reproduced in Fig. 2. Recent studies about the dynamics and integrability of system (1) can be found in [2,3,4,5,6,7,8,9].

Fig. 2

Chaotic attractors of system (1) for $C=1$, $L=3$, $\alpha =0.6$ and $\beta =1.5$ in (a) and $\beta =1.7$ in (b). The initial condition of the orbit is (0.1, 0, 0.1) in both cases

Here we consider the Muthuswamy-Chua system with $C=1$ and $L=3$, as the authors originally done in [1], that is,

$$\begin{aligned} \dot{x}=y, \quad \quad \quad \dot{y}=-\dfrac{1}{3}\,[x+\beta (z^2-1)y], \quad \quad \quad \dot{z}=-y-\alpha z+yz. \end{aligned}$$

(2)

We analytically prove the existence of periodic orbits in this system in three cases: for $\alpha =\beta =0$; for $\alpha =0$ and $\beta >0$ sufficiently small; and for $\alpha >0$ and $\beta >0$ sufficiently small.

For $\alpha =\beta =0$, the phase space of system (2) can be completely determined due to the existence of the functionally independent first integrals $H_1(x,y,z)=x-\ln (1-z)$, with $z<1$, $H_2(x,y,z)=-x+\ln (z-1)$, with $z>1$, and $H_3(x,y,z)=x^2+3y^2$. We recall that a first integral of system (2) is a non-constant differentiable function $H:U\subset \mathbb {R}^3\rightarrow \mathbb {R}$, which is constant on all solution curves (x(t), y(t), z(t)) of the system contained in U, that is

$$\begin{aligned} \dot{x}\,\dfrac{\partial H}{\partial x}+ \dot{y}\,\dfrac{\partial H}{\partial y}+ \dot{z}\,\dfrac{\partial H}{\partial z}\equiv 0, \end{aligned}$$

where $H=H(x(t),y(t),z(t))$. The existence of first integrals for the Muthuswamy-Chua system is treated, for instance, by Dias and Mello in [4] and by Llibre and Valls in [8]. A consequence from the existence of first integrals in system (2) for $\alpha =\beta =0$ is that its phase space is foliated by the cylinders $\mathcal {F}_c(x,y,z)=x^2+3y^2-c=0$, with $c\in \mathbb {R}_+$, and by the surfaces $\mathcal {G}_k(x,y,z)=-z+ke^x+1=0$, with $k\in \mathbb {R}$, which are invariant under the flow of the system.

For $\alpha =\beta =0$, the z-axis is formed by non-isolated zero-Hopf equilibrium points of system (2) as the eigenvalues of the Jacobian matrix of the system at these points are $\lambda _1=0$ and $\lambda _{2,3}=\pm i\sqrt{3}/3$. Moreover, these equilibrium points are nonlinear centers, since all orbits of the system are on the intersections of invariant cylinders $\mathcal {F}_c=0$ with invariant surfaces $\mathcal {G}_k=0$, as shown in Figs. 3 and 4.

Fig. 3

Case $\alpha =\beta =0$. The phase space of system (2) is foliated by the invariant surfaces $x^2+3y^2=c$ and $f_k=-z+ke^x+1=0$, with $c\in \mathbb {R}_+$ and $k\in \mathbb {R}$

Fig. 4

Case $\alpha =\beta =0$. (a) Periodic orbits in the phase space of system (2) and (b) their projection on the xz-plane

Note that system (2) presents a continuum of periodic orbits even when the memristance is turned off, that is, when $\beta =0$. Also, in this case, the z-coordinates of solutions on the invariant cylinders $\mathcal {F}_c=0$ are asymptotic to the plane $\mathcal {G}_0=-z+1=0$ when the voltage, represented by the x-axis, is more negative and they present spikes when the voltage is more positive, see Fig. 4. Although this case may seem trivial due to absence of memristor in the circuit modeled by system (2), it is interesting from dynamical point of view, since varying the parameter values α and β the Muthuswamy-Chua system can be seen as a perturbation of an integrable system and interesting phenomena can arise when the structure of invariant surfaces is broken. A similar approach was considered by Llibre et al. in [10] to study the Nosé-Hoover oscillator.

For $\alpha =0$ and $\beta >0$ sufficiently small, the phase space of system (2) is foliated by the invariant surfaces $\mathcal {G}_k=0$ and the z-axis is filled by equilibrium points of the system. In the next result, by using the existence of the invariant surfaces $\mathcal {G}_k=0$ and a result from the averaging theory, we prove the existence of a unique stable periodic orbit around each equilibrium point (0, 0, z), with $|z|<1$, see Fig. 5. These periodic orbits persist from the integrable structure observed in the phase space of system (2) when $\alpha =\beta =0$.

Theorem 1

For $\alpha =0$ and $\beta >0$ sufficiently small, there exists a unique stable periodic orbit around each equilibrium point (0, 0, z), with $|z|<1$, in the phase space of system (2).

Fig. 5

Case $\alpha =0$ and $\beta >0$. (a) Some periodic orbits on the invariant surfaces $f_k=0$, with $-2<k<0$, and (b) their projections on the xz-plane. Here $\beta =0.1$

Theorem 1 is proved in Section 2. Note that the periodic orbits obtained in Theorem 1 have different amplitudes, as can be observed in Fig. 5. Furthermore, the existence of such a periodic orbits is determined by the local activity of the memristor device of circuit in Fig. 1, since $M(z)=\beta \,(z^2-1)<0$ for $\beta >0$ and $|z|<1$.

As mentioned above, for $\alpha =0$ and $\beta >0$, (0, 0, z) are equilibrium points of system (2). The Jacobian matrix of the system at these equilibrium points are

$$\begin{aligned} \lambda _1=0, \quad \quad \quad \lambda _{2,3}=-\dfrac{1}{6}\left[ \beta (z^2-1)\pm \sqrt{\beta ^2(z^2-1)^2-12}\right] . \end{aligned}$$

(3)

Observe that the (normal) stability of each equilibrium point (0, 0, z) depends on the memristance $M(z)=\beta (z^2-1)$ of the memristive device of circuit in Fig. 1 and they are (normally) asymptotically stable if $|z|>1$ and unstable if $|z|<1$. The coexistence of distinct possible asymptotic stable states given by the equilibrium points (0, 0, z), with $|z|>1$, and by infinitely many stable periodic orbits leads to an interesting phenomenon known as multistability, in which the final state of orbits depends crucially on the initial conditions. For more details about this subject see [11] and references therein. This phenomenon often can creates inconveniences. In engineering systems, for instance, where a targeted dynamical behavior is often required, multistability creates dilemma to choose convenient initial conditions in order to obtain a desired final asymptotic state of the system. In this way, there are several papers, as [11, 12], that study the control of multistability. Furthermore, multistability was also reported in other memristive systems, as [13,14,15,16].

For $\alpha >0$ and $\beta >0$, the structure of invariant surfaces foliating the phase space of system (2), as observed for $\alpha =0$ or $\beta =0$, is broken, which makes the dynamics of the system much more difficult to be studied. In this case, by using the averaging theory, we analytically prove the existence of a stable periodic orbit, which persists from one of the periodic orbits on the invariant cylinder $\mathcal {F}_4=x^2+3y^2-4=0$ in the integrable case ($\alpha =\beta =0$). As far as we know, the existence of periodic orbits in system (2) for $\alpha >0$ and $\beta >0$ was verified only numerically until now, see [1, 5, 7]. The next theorem is proved in Section 3.

Theorem 2

For $\alpha >0$ and $\beta >0$ sufficiently small, there exists a stable periodic orbit in the phase space of system (2), which tends to an ellipse on the cylinder $\mathcal {F}_4=0$ when $\alpha \rightarrow 0$ and $\beta \rightarrow 0$.

Theorem 2 is proved in Section 3.

The stable periodic orbit obtained in Theorem 2 plays an important role in the formation of chaotic attractors in system (2). Indeed, we develop a numerical study on the continuation of this periodic orbit by using the software Maple, where differential equations were solved through a Fehlberg fourth-fifth order Runge-Kutta method with degree four interpolant (known as rk45 method), with step-size equals to 0.01. This method showed to be appropriate for the numerical study presented here. The files are available to the interested readers, under demand to the authors. We verify that, when we fix $\alpha =0.6$ and vary β from 0.01 to 1.7 into system (2), the periodic orbit initiates a cascade of period-doubling bifurcations from $\beta \approx 0.8$ until $\beta \approx 1.15$ and then it returns to a period-one periodic orbit for β near of 1.2, as can be seen in Figs. 6 (a) - (g). For $\beta >1.2$, the cascade of period-doubling bifurcations restarts giving rise to a strange attractor, see Figs. 6 (g) - (i) and Fig. 2, which was shown to be chaotic for $\beta =1.7$ by Muthuswamy and Chua in [1], through the study of Lyapunov exponents and simulations based on bifurcation analysis, and by Galias in [17] in a topological sense for $\beta =1.5$. This highlights the important role of periodic orbits in the occurrence of complex dynamics in system (2) as the parameter values are varied.

In order to corroborate the chaotic dynamics observed in system (2), we calculate the Lyapunov exponents using the time-series method [18] for a solution with initial conditions $(x_0,y_0,z_0)=(0.1,0,0.1)$, taking $\alpha =0.6$ and $\beta =1.5$. We obtained the values:

$$\begin{aligned} LE_1=0.0303, \quad LE_2=0., \quad LE_3=-0.5861, \end{aligned}$$

which characterize chaotic behavior. In [5], Galias computed bifurcation diagrams of system (2) with $\alpha =0.6$ and covering the extended interval $0.9\le \beta \le 2$, considering two independent ways and obtaining, visually, similar diagrams, which display an abundance of tunable ranges of periodic and chaotic self-oscillations, corroborating the results obtained here.

Fig. 6

Orbit of system (2) with $\alpha =0.6$ and initial condition (0.1, 0, 0.1) for different values of parameter β. Here $t\in [1000,1300]$

The next sections are devoted to prove the results presented above. In Section 2 we prove Theorem 1 and in Section 3 we prove Theorem 2.

2 Proof of Theorem 1

Before proving Theorems 1 and 2, for the sake of completeness and to fix the notation to be used, we present the following result from averaging theory. For a general introduction to this theory see [19, 20].

Theorem 3

Consider the initial value problems

$$\begin{aligned} \dot{\mathbf{x}}=\varepsilon \,F_1(t,\mathbf{x})+\varepsilon ^2\,F_2(t,\mathbf{x},\varepsilon ), \;\;\;\quad \;\;\; \mathbf{x}(0)=\mathbf{x}_0, \end{aligned}$$

(4)

and

$$\begin{aligned} \dot{\mathbf{y}}=\varepsilon \,g(\mathbf{y}), \;\;\;\quad \;\;\; \mathbf{y}(0)=\mathbf{x}_0, \end{aligned}$$

(5)

with x, y and x₀ in some open subset Ω of $\mathbb {R}^n$, $t\in [0,\infty )$ and $\varepsilon \in (0,\varepsilon _0]$, for some fixed $\varepsilon _0>0$ sufficiently small. Assume that $F_1$ and $F_2$ are periodic functions of period T in the variable t, and set

$$\begin{aligned} g(\mathbf{y})=\dfrac{1}{T}\,\int _0^T F_1(t,\mathbf{y}) dt. \end{aligned}$$

Assume that $F_1$, $D_{\mathbf{x}} F_1$, $D_\mathbf{xx} F_1$ and $D_\mathbf{x} F_2$ are continuous and bounded by a constant independent of ε in $[0,\infty )\times \Omega \times (0,\varepsilon _0]$, and that $\mathbf{y}(t)\in \Omega$ for $t\in [0,1/\varepsilon ]$, where $D_\mathbf{x} F$ and $D_\mathbf{xx} F$ are all the first and second derivatives of F. Then, the following statements hold.

• 1. For $t\in [0,1/\varepsilon ]$, we have ${ \mathbf{x}}(t)-{ \mathbf{y}}(t)=\mathcal {O}(\varepsilon )$ as $\varepsilon \rightarrow 0$.

• 2. If p is an equilibrium point of system (5) such that $\det [D_{ \mathbf{y}} g(p)]\ne 0$, then there exists a periodic solution $\phi (t,\varepsilon )$ of period T for system (4) which is close to p and such that $\phi (0,\varepsilon )-p=\mathcal {O}(\varepsilon )$ as $\varepsilon \rightarrow 0$.

• 3. The stability of the periodic solution $\phi (t,\varepsilon )$ is given by the stability of the equilibrium point p.

Theorem 3 was proved by Verhulst in [20].

Proof of Theorem 1

Suppose $\alpha =0$ and $\beta >0$ sufficiently small into system (2). In this case, the phase space of the system is foliated by the invariant surfaces $\mathcal {G}_k(x,y,z)=-z+k\,e^x+1=0$, with $k\in \mathbb {R}$, as $H_1(x,y,z)=x-\ln (1-z)$, with $z<1$, and $H_2(x,y,z)=-x+\ln (z-1)$, with $z>1$, are first integrals of the system for $\alpha =0$. The restriction of system (2) to the invariant surfaces $\mathcal {G}_k=0$ is given by the planar differential system

$$\begin{aligned} \dot{x}=y, \quad \quad \quad \dot{y}=-\dfrac{x}{3}-\dfrac{\beta }{3}\left[ (1+k\,e^x)^2-1\right] y. \end{aligned}$$

(6)

The origin is the only equilibrium point of system (6) and, for each $k\in \mathbb {R}$, it corresponds to the point (0, 0, z) of system (2) with $z=k+1$. In order to use Theorem 3, we write the linear part at the origin of system (6) into the real Jordan normal form through the change of coordinates

$$\begin{aligned} (x,y)\rightarrow (u,v), \quad \text{where} \,\, x=\sqrt{3}\,u \,\, \text{and}\,\, y=v, \end{aligned}$$

and the rescaling of time $t=\sqrt{3}\,\tau$, where τ is the new time. Then we obtain the differential system

$$\begin{aligned} \dot{u}=v, \quad \quad \quad \dot{v}=-u-\dfrac{\sqrt{3}}{3} \beta \left[ \left( 1+k\,e^{\sqrt{3}\,u}\right) ^2-1\right] v. \end{aligned}$$

(7)

Now, writing system (7) in polar coordinates $(r,\theta )$, where $u=r\cos \theta$ and $v=r\sin \theta$, and considering $\beta =\varepsilon >0$, it becomes

$$\begin{aligned} \begin{array}{l} \dot{r}=-\dfrac{\sqrt{3}}{3}\,\varepsilon \,k\,e^{\sqrt{3}\,r\cos \theta }\left( k\,e^{\sqrt{3}\,r\cos \theta }+2\right) \,r\sin ^2\theta , \\ \dot{\theta }=-1-\dfrac{\sqrt{3}}{3}\,\varepsilon \,k\,e^{\sqrt{3}\,r\cos \theta }\left( k\,e^{\sqrt{3}\,r\cos \theta }+2\right) \sin \theta \cos \theta . \end{array} \end{aligned}$$

(8)

Note that $\dot{\theta }\ne 0$ when $\varepsilon \rightarrow 0$. Then taking θ as the independent variable and doing the Taylor expansion of order 2 of the obtained equation at $\varepsilon =0$, we get

$$\begin{aligned} \dfrac{dr}{d\theta }=\left[ \dfrac{\sqrt{3}}{3}\,k\,e^{\sqrt{3}\,r\cos \theta }(k\,e^{\sqrt{3}\,r\cos \theta }+2)\,r\sin ^2\theta \right] \varepsilon +\mathcal {O}(\varepsilon ^2). \end{aligned}$$

(9)

Using the notation of Theorem 3, we have that if we take $t=\theta$, $T=2\pi$, $\mathbf{x}=r$,

$$\begin{aligned} F_1(t,\mathbf{x})=\dfrac{\sqrt{3}}{3}\,k\,e^{\sqrt{3}\,r\cos \theta }(k\,e^{\sqrt{3}\,r\cos \theta }+2)\,r\sin ^2\theta , \,\, \text {and} \,\, \varepsilon ^2F_2(t,\mathbf{x})=O(\varepsilon ^2) \end{aligned}$$

it is immediate to verify that system (9) can be written in the normal form (4) and it satisfies Theorem 3. Then, computing function g of Theorem 3, we obtain

$$\begin{aligned} g(r)=\dfrac{\sqrt{3}}{6\pi }\,k\,r\left( \int _0^{2\pi } (k\,e^{\sqrt{3}\,r\cos \theta }+2)\,e^{\sqrt{3}\,r\cos \theta }\,\sin ^2\theta \,d\theta \right) . \end{aligned}$$

(10)

Solving the integral in expression (10) using power series up to order three in the variable r, we get

$$\begin{aligned} g(r)=\dfrac{\sqrt{3}}{6}\,k\,r\,(k+2)+\dfrac{\sqrt{3}}{4}\,k\,r^3\,\left( k+\dfrac{1}{2}\right) . \end{aligned}$$

(11)

We have that, if $-2<k<k^*=-0.5$, then $g(r)=0$ has a unique real positive solution $r=r_0=\frac{\sqrt{-3(2k+1)(k+2)}}{3(2k+1)}$ with $g'(r_0)\ne 0$, since $g'(r_0)=0$ if, and only if, $k=-2$. We note that $k^*\rightarrow 0^-$ as we increase the order of the power series used to solve the integral in (11).

Going back the change of coordinates, for $\beta >0$ sufficiently small, system (6) has a unique periodic orbit if $-2<k<0$. Moreover, the obtained periodic orbit is stable. Indeed, writing system (2) in polar coordinates (see system (8) and remember that $\beta =\varepsilon >0$), we have that $\dot{r}>0$ for $-2<k<0$ and r sufficiently small, since

$$\left(k\,e^{\sqrt3\,r\,\cos\theta}+2\right)>0\quad\mathrm{when}\;r\rightarrow0,$$

and we have that $\dot{r}<0$ for $-2<k<0$ and r sufficiently large. Hence system (6) has a unique stable periodic orbit around the origin for each k with $-2<k<0$, see Fig. 7. As $z=k+1$, for $\alpha =0$ and $\beta >0$ sufficiently small, system (2) has a stable periodic orbit around each equilibrium point (0, 0, z) with $|z|<1$.

Fig. 7

Periodic orbit in the phase portrait of system (6) for $k=-1$. Here $\beta =0.1$

3 Proof of Theorem 2

Proof of Theorem 2

Suppose $\alpha >0$ and $\beta >0$ into system (2). First we write the linear part at the origin of system (2) into the real Jordan normal form. In order to do this, we consider the linear change of coordinates

$$\begin{aligned} (x,y,z)\mapsto (u,v,w), \quad \text{where} \;\;x=u, \; y=\dfrac{\sqrt{3}}{3}\,v \;\;and \;\;z=-u+w, \end{aligned}$$

and the rescaling of time $t=-\sqrt{3}\,\tau$, where $\tau$ is the new time. Then, we obtain the differential system

$$\begin{aligned} \begin{array}{l} \dot{u}=-v, \\ \dot{v}=u+\dfrac{\sqrt{3}}{3}\,\beta \,\left[ (u-w)^2-1\right] \,v, \\ \dot{w}=(v-\alpha \sqrt{3})\,(u-w). \end{array} \end{aligned}$$

(12)

As $\alpha >0$, there exists $m>0$ such that $m\,\alpha =1$. Then, system (12) can be rewritten as

$$\begin{aligned} \begin{array}{l} \dot{u}=-v, \\ \dot{v}=u+\dfrac{\sqrt{3}}{3}\,\beta \,\left[ (u-w)^2-1\right] \,v, \\ \dot{w}=\alpha \,(m\,v-\sqrt{3})\,(u-w). \end{array} \end{aligned}$$

(13)

Now, writing system (13) in cylindrical coordinates $(r,\theta ,w)$, where $u=r\cos \theta$ and $v=r\sin \theta$, and taking $\alpha =\varepsilon \,a$ and $\beta =\varepsilon \,b$, with $a>0$ and $b>0$, it becomes

$$\begin{aligned} \begin{array}{l} \dot{r}=\dfrac{\sqrt{3}}{3}\,\varepsilon \,b\,\left[ (r\cos \theta -w)^2-1\right] \,r\sin ^2\theta , \\ \dot{\theta }=1+\dfrac{\sqrt{3}}{3}\,\varepsilon \,b\,\left[ (r\cos \theta -w)^2-1\right] \cos \theta \sin \theta , \\ \dot{w}=\varepsilon \,a\,(m\,r\sin \theta -\sqrt{3})\,(r\cos \theta -w). \end{array} \end{aligned}$$

As $\dot{\theta }\ne 0$ when $\varepsilon \rightarrow 0$, we take θ as the new independent variable and do the Taylor expansion of order 2 of the obtained equations at $\varepsilon =0$. Then we get

$$\begin{aligned} \begin{array}{l} \dfrac{dr}{d\theta }=\left[ \dfrac{\sqrt{3}}{3}\,b\,[(r\cos \theta -w)^2-1]\,r\sin ^2\theta \right] \varepsilon +{O}(\varepsilon ^2), \\ \dfrac{dw}{d\theta }=\left[ -a\,(m\,r\sin \theta -\sqrt{3})\,(r\cos \theta -w)\right] \,\varepsilon +{O}(\varepsilon ^2). \end{array} \end{aligned}$$

(14)

Using the notation of Theorem 3 we have that if we take $t=\theta$, $T=2\pi$, $\mathbf{x}=(r,w)^T$,

$$\begin{aligned} F_1(t,\mathbf{x})=\left( \begin{array}{l} \dfrac{\sqrt{3}}{3}\,b\,[(r\cos \theta -w)^2-1]\,r\sin ^2\theta \\ -a\,(m\,r\sin \theta -\sqrt{3})\,(r\cos \theta -w) \end{array}\right) , \,\, \text {and} \,\, \varepsilon ^2F_2(t,\mathbf{x})={O}(\varepsilon ^2) \end{aligned}$$

it is immediate to verify that system (14) can be written in the normal form (4) and it satisfies the assumptions of Theorem 3. Then, computing function g of Theorem 3, it follows that

$$\begin{aligned} g(\mathbf{y})= g(r,w)=\dfrac{1}{2\pi }\,\int _0^{2\pi } F_1(\theta ,r,w) \,d\theta = \dfrac{\sqrt{3}}{24}\,\left( \begin{array}{c} b\,r\,(r^2+4w^2-4) \\ 24\,a\,w \end{array} \right) , \end{aligned}$$

which has a unique zero for $r>0$ at $(r,w)=(2,0)$. The determinant of the Jacobian matrix of g at (2, 0) is $a\,b\ne 0$ and the eigenvalues of the Jacobian matrix of g at this point are $\lambda _1=a\sqrt{3}>0$ and $\lambda _2=b\sqrt{3}/3>0$. Hence, for $\varepsilon >0$ sufficiently small, system (14) has an unstable periodic orbit $\varphi (\theta ,\varepsilon )=(r(\theta ,\varepsilon ),w(\theta ,\varepsilon ))$ such that $\varphi (0,\varepsilon )\rightarrow (2,0)$ when $\varepsilon \rightarrow 0$.

Going back the change of coordinates to system (12) we have that such a system has an unstable periodic orbit of period approximately $2\pi$ for $\alpha >0$ and $\beta >0$ sufficiently small given by

$$\begin{aligned} \begin{array}{l} u(\tau )=2\cos \tau +O(\alpha ,\beta ),\\ v(\tau )=2\sin \tau +O(\alpha ,\beta ),\\ w(\tau )=O(\alpha ,\beta ). \end{array} \end{aligned}$$

Finally, going back to the coordinates x, y, z and doing the rescaling of time $\tau =-(\sqrt{3}/3)\,t$, this periodic orbit become into a stable periodic orbit for system (2) of period also close to $2\pi$ for $\alpha >0$ and $\beta >0$ sufficiently small given by

$$\begin{aligned} \begin{array}{l} x(t)=2\cos t+O(\alpha ,\beta ), \\ y(t)=\dfrac{2\sqrt{3}}{3}\sin t+O(\alpha ,\beta ),\\ z(t)=-2\cos t+O(\alpha ,\beta ), \end{array} \end{aligned}$$

which tends to an ellipse on the cylinder $\mathcal {F}_4=0$ when $\alpha \rightarrow 0$ and $\beta \rightarrow 0$.