Leader-Following Consensus of Multi-order Fractional Multi-agent Systems

Abstract

The current study investigates the leader-following consensus problem for fractional-order multi-agent systems with different fractional orders under a fixed undirected graph. A virtual leader with the desired path is assumed, while the agents are chosen as fractional-order integrators with various orders. It is proved that the leader-following consensus problem for this multi-agent system is equivalent to the stability analysis of a multi-order fractional system. At first, the Laplace transform is employed to verify the asymptotic stability of a particular case of multi-order fractional systems. It is shown that if the state matrix is negative definite and a certain inequality between the fractional orders is met, the mentioned system is asymptotically stable. This inequality can be easily checked without any need for complex calculations. Accordingly, it is demonstrated that if a certain inequality is met among the fractional orders of a multi-order multi-agent system, the leader-following consensus of the mentioned heterogeneous multi-agent system can be realized. Numerical examples demonstrate the accuracy of the established leader-following consensus protocol.

1 Introduction

Nowadays, control engineers have been interested in different fields of distributed control of multi-agent systems (MAS). Mobile robots (Liu & Jiang, 2013), automatic vehicles (Yang et al., 2017), and sensor networks (Díaz-Ibarra et al., 2019) have been known as examples of MAS where distributed control has been employed therein. In distributed control, the interaction between each system (called an agent) with other agents and the leader is employed to obtain the control signals of agents. A variety of goals could be realized using distributed control of MAS, such as consensus (Ni & Cheng, 2010), flocking (Olfati-Saber, 2006), and containment control (Ji et al., 2008).

When the states of agents track the corresponding leader states, the leader-following consensus is realized. The leader-following consensus of MAS has been employed in various applications, such as mobile sensor networks (Safavi & Khan, 2015), ship course control systems (Wang et al., 2021), unmanned aerial vehicles (Trejo et al., 2021), and Pelican prototype robots (Cai et al., 2020). The leader-following consensus of MAS has been investigated in various works (Ni & Cheng, 2010). Matrix and algebraic graph theories have been employed to derive sufficient conditions for the leader-following consensus of MAS with directed switching graphs (Tang, 2015). Some conditions in linear matrix inequality (LMI) form have been found to ensure the leader-following consensus of MAS with a switching graph and communication delay (Guo, 2016; Liu & Liu, 2011). Sun and Guan (2013) studied the finite-time leader-following consensus issue for second-order MAS under fixed and switching graphs. Djaidja and Wu (2016) investigated the leader-following consensus issue for first-order MAS with communication delay and measurement noise. The leader‐following consensus problem of nonlinear singular MAS with intermittent communication under a fixed undirected graph has been studied (Xie & Mu, 2019). Girejko and Malinowska (2019) derived the necessary and sufficient conditions to attain the leader-following consensus for first- and second-order MAS on an arbitrary time model (called time scale). The leader-following consensus and formation control problems with velocity and input constraints have been solved for second-order MAS (Fu et al., 2019). Lu and Liu (2019) presented a novel distributed strategy to solve the leader-following consensus issue for heterogeneous second-order nonlinear MAS under external disturbances. Huang et al. (2022) verified the event-triggered leader-following consensus problem for nonlinear MAS under semi-Markov switching topology with partially unknown rates. Tan et al. (2020) studied the leader-following consensus problem of MAS under switching topologies and communication constraints. Zou et al. (2019) verified the mean square practical leader-following consensus of second-order nonlinear MAS with noises and unmodeled dynamics. However, this work and the above are only confined to integer-order systems.

Some physical plants could not be described entirely via ordinary differential equations. In this case, fractional calculus could be employed to describe them with non-integer differential equations (Monje et al., 2010). The leader-following consensus of fractional-order multi-agent systems (FOMAS) has been verified in previous studies. Liu et al. (2018) studied the distributed consensus problem for FOMAS with double-integrator agents containing different fractional orders and nonuniform delays. However, the same fractional orders have been considered for all the agents in the mentioned work. The Mittag–Leffler stability theory and low gain feedback method have been employed to ensure the robust consensus of FOMAS under input saturation and external disturbances (Chen et al., 2018). Adaptive leader-following consensus and neuro-adaptive leaderless consensus of FOMAS have been investigated by Ren and Yu (2017) and Mo et al. (2019), respectively. The leader-following consensus of second-order FOMAS without velocity information has been investigated (Yu et al., 2017). The Hermite–Biehler theorem has been employed to propose a sample-data-based consensus protocol for second-order FOMAS (Liu et al., 2019). Ye and Su (2019) solved the leader-following consensus problem for nonlinear FOMAS with fractional orders between zero and two. The even-triggered control has been utilized to study the consensus issue for FOMAS (Ren et al., 2019; Shi et al., 2019a, 2019b). The leader-following consensus of discrete-time FOMAS has been verified in the literature (Shahamatkhah & Tabatabaei, 2018; Wyrwas et al., 2018). Appropriate state observers for all agents have been designed to attain the output consensus for the leader-following issue for heterogeneous nonlinear FOMAS (Wen et al., 2020). An observer-based strategy has been employed to study the admissible leader-following consensus problem for FOMAS with singular agents (Pan et al., 2019). The consensus problem for input time-delay nonlinear FOMAS and a particular case of linear fractional-order agents have been studied by Yang et al. (2019) and Shi et al., (2019a, 2019b), respectively. Gong et al. (2019) verified the robust adaptive leaderless and leader-following consensus problems for heterogeneous FOMAS with different nonlinear dynamics. Ji et al. (2020) considered the leader-following consensus of FOMAS with adaptive rules for control gain. The leader-following consensus issue for heterogeneous FOMAS has been verified by Hu et al., (2020a, 2020b), in which the fractional order of the leader has been considered different from the corresponding one for the agents. The leader–follower consensus problem based on a time-varying gain approach has been investigated for nonlinear time-delay FOMAS under a fixed directed topology (Li et al., 2021). Hu et al. (2020a, 2020b) designed an event-triggered control to solve the leader-following consensus problem for the FOMAS. Leader-following non-fragile consensus of nonlinear time-delay FOMAS has been verified by Chen et al. (2022).

In all the published works concentrating on the leader-following consensus of FOMAS, the same fractional orders are considered for all the agents. A multi-order fractional-order system is obtained if different fractional orders are considered for the agents. This means that the leader-following consensus issue for this case of FOMAS leads to stability analysis of a multi-order fractional system. However, the stability analysis of multi-order fractional systems is difficult (Li & Zhang, 2011; Petras, 2009). Although there are few published studies about this issue in the literature (Buslowicz, 2012; Deng et al., 2007; Qian et al., 2010), there are no straightforward and simple criteria to verify the stability of these systems. Moreover, some works are confined to only a fractional-order system (FOS) with two different orders (Brandibur & Kaslik, 2018; Koksal, 2019). Badri and Sojoodi (2019) utilized the Linear Matrix Inequality (LMI) approach to study the stability of multi-order fractional systems. However, this method implies some numerical calculations and does not lead to any explicit criterion.

The current paper studies the stability of a multi-order fractional system. The idea proposed by Brandibur and Kaslik (2018) for a FOS with two non-identical orders is generalized to a multi-order fractional system. Accordingly, some sufficient explicit conditions are obtained in terms of fractional orders to ensure the stability of these systems. Based on this result, the leader-following consensus problem of FOMAS with different fractional orders is studied. A virtual leader is considered, and the agents are chosen as fractional-order integrators with different fractional orders in the range of (0,1]. It is demonstrated that the leader-following consensus issue for this kind of FOMAS under undirected topology is equivalent to the stability analysis of a multi-order fractional system. Then, it is shown that the leader-following consensus with positive feedback gains could be realized under a limitation on the fractional-order values. The performance of the presented distributed protocol is evaluated through numerical examples. This paper presents sufficient conditions to ensure the asymptotic stability of a particular multi-order FOS with an arbitrary number of different fractional orders. The multi-order FOS differs from that considered by Brandibur and Kaslik (2018), which employs a FOS with only two different fractional orders. Unlike the relevant literature (Buslowicz, 2012; Deng et al., 2007; Qian et al., 2010), the obtained conditions can be easily checked without complex numerical calculations. On the other hand, the obtained conditions are employed to solve the leader-following problem for multi-order FOMAS, in which the fractional orders of the agents are completely different. In the relevant literature for leader-following consensus of FOMAS, the fractional orders of all agents are the same. To the best of the authors’ knowledge, this paper is the first attempt to consider different fractional orders for the agents in a FOMAS.

Finally, the essential contributions of the present research are given as follows:

• The asymptotic stability of a particular kind of multi-order fractional system is studied. Although the stability of a FOS with two fractional orders has been verified by Brandibur and Kaslik (2018), the stability analysis of a FOS with an arbitrary number of different fractional orders is complicated. This paper presents a sufficient condition for the fractional orders to guarantee the asymptotic stability of a multi-order fractional system. To our knowledge, this kind of stability analysis has not been verified in the literature. Only some inexplicit conditions have been extracted in the previous studies to ensure the asymptotic stability of multi-order fractional systems that could not be employed in realistic situations (Buslowicz, 2012; Deng et al., 2007; Qian et al., 2010).

• Sufficient conditions are found to realize the leader-following consensus of heterogeneous FOMAS with different fractional orders. In the considered FOMAS, the dynamic of any agent is represented with a fractional-order integrator where its order is different from the others. This leads to a completely heterogeneous multi-order FOMAS. Although Hu et al. (2020a, 2020b) considered the fractional order of the leader different from those selected for the agents, all the agents have similar fractional orders. However, in the current work, all agents’ fractional orders could be different.

The current study is arranged as follows: The required mathematical principles of the graph theory are given in Sect. 2. The proposed theorem for stability analysis of multi-order fractional systems is provided in Sect. 3. Section 4 concerns the leader-following consensus issue of FOMAS with different fractional orders. Numerical simulations are presented in Sect. 5 to evaluate the accuracy of the presented distributed control strategy. Conclusions and future landscapes are discussed in Sect. 6.

2 A Brief Review of Graph Theory

The topology of MAS could be described via the graph theorem. In the following, the required definitions and principles of graph theory are presented. A set of nodes and edges is called a graph. A graph is described by $G = \left( {S,E} \right)$ where $S = \left\{ {s_{1} , \ldots ,s_{N} } \right\}$ indicates the set of nodes ($N$ nodes are considered) and $E \subseteq S \times S$ is the set of edges where its members are represented with $e_{ij} = \left( {s_{i} ,s_{j} } \right)$. The set of neighbors of node s_i is represented with $N_{i} = \left\{ {s_{j} \in S:\left( {s_{j} ,s_{i} } \right) \in E} \right\}$. The adjacency matrix for each graph describes the connection of edges and nodes. This is a $N \times N$ matrix where its non-negative elements are represented with $A = \left[ {a_{ij} } \right]$. The diagonal elements of $A$ are considered zero. If $\left( {s_{j} ,s_{i} } \right) \in E$, $i \ne j$, then $a_{ij} > 0$, else $a_{ij} = 0$. If $A$ is a symmetric matrix, then the graph is undirected. Otherwise, the graph is directed. The Laplacian matrix of a graph is defined as $L = \left[ {l_{ij} } \right]$ where $l_{ii} = \mathop \sum \limits_{j \ne i} a_{ij}$ and $l_{ij} = - a_{ij}$ for $i \ne j$. A directed graph with a directed path among any pair of its distinct nodes is called strongly connected. The word ‘strongly’ is deleted for undirected graphs. A spanning tree for a graph exists if at least one of its nodes has a path to all the other nodes. Thus, at least a spanning tree exists in the strongly connected (or connected) graphs. The Laplacian matrix of a directed graph contains at least a zero eigenvalue with the corresponding eigenvector $1 = \left( {1,1, \ldots ,1} \right)^{T}$.

Lemma 1

Lewis et al. (2014). The Laplacian matrix of a connected undirected graph has a zero eigenvalue with eigenvector 1, while the other eigenvalues are positive.

In the leader-following issue, the leader node is represented with $s_{0}$. To represent the relation among agents and the leader, the matrix $D = {\text{diag}}\left\{ {d_{1} , \ldots ,d_{n} } \right\}$ is defined. If agent $i$ is directly related to the leader, then $d_{i} = 1$, else $d_{i} = 0$.

Lemma 2

Ni and Cheng (2010). In connected undirected graphs with at least a single spanning tree, if there exists at least a single path connecting the leader to other agents, then each eigenvalue of the matrix $H = L + D$ is positive. This means that this matrix is positive-definite.

3 Stability Analysis of Multi-order Fractional Systems

The current section verifies the stability of a multi-order fractional system. To attain this goal, some mathematical preliminaries are introduced.

3.1 Fractional Calculus Preliminaries

The main idea in fractional calculus is to extend the ordinary derivative concept to its non-integer order. To achieve this, various definitions for the fractional-order derivative have been proposed. The Caputo definition is employed in the current work, which is more suitable for engineering applications.

Definition 1

Monje et al. (2010). The fractional-order derivative of an arbitrary function $f\left( t \right)$, or ${}_{0}^{ } D_{t}^{\alpha } f\left( t \right)$ is defined as

$$_{0} D_{t}^{\alpha } f(t) = \frac{1}{\Gamma (n - \alpha )}\int\limits_{0}^{t} {\frac{{f^{(n)} (\tau )}}{{(t - \tau )^{\alpha + 1 - n} }}{\text{d}}\tau ,} \quad \left( {n - 1 \le \alpha < n} \right),\quad n \in N $$

(1)

where $\alpha$ is the fractional order, and $\Gamma \left( . \right)$ is the popular Gamma function defined as $\Gamma \left( x \right) = \int_{0}^{\infty } {e^{ - z} z^{x - 1} {\text{d}}z}$.

The state-space equations of a multi-order fractional system (without input) could be represented as

$$ \left[ {\begin{array}{*{20}c} {D^{{\alpha_{1} }} x_{1} } \\ {D^{{\alpha_{2} }} x_{2} } \\ \vdots \\ {D^{{\alpha_{n} }} x_{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {F_{11} } & {F_{12} } & \cdots & {F_{1n} } \\ {F_{21} } & {F_{22} } & \cdots & {F_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {F_{n1} } & {F_{n2} } & \cdots & {F_{nn} } \\ \end{array} } \right]\underline {x} $$

(2)

where $\alpha_{i} \in \left( {0,1} \right)$, $i = 1, \ldots ,n$ denote the fractional orders $\left( {\alpha_{i} \ne \alpha_{j} ,i \ne j, i,j = 1, \ldots ,n} \right)$ and $\underline {x} \left( t \right) = \left[ {x_{1} \left( t \right), \ldots ,x_{n} \left( t \right)} \right].$ The corresponding state vector for fractional order $\alpha_{i}$ is represented with $x_{i} \in {\mathbb{R}}^{{n_{i} }} .$ Moreover, the state-space matrices are denoted by $F_{ij} \in {\mathbb{R}}^{{n_{i} \times n_{j} }} , i,j = 1, \ldots ,n$. In the current section, the asymptotic stability of system (2) is discussed. Thus, the system’s input is considered zero, and the initial state is considered an arbitrary nonzero vector $\underline {x} \left( 0 \right)$. In the particular case, if $\alpha_{i} = \alpha , i = 1, \ldots , n$, system (2) is called commensurate and $\alpha$ is called the commensurate order. The stability analysis of commensurate fractional-order systems has been discussed in the literature. However, the stability analysis of multi-order fractional systems is complicated. The stability of a multi-order fractional system has been verified in the literature. The proposed approaches require some numerical computations and could not give straightforward criteria for studying the stability of such systems. The following subsection verifies the stability of a particular case of system (2).

3.2 Stability Analysis of a Special Case of Multi-order Fractional Systems

Consider a special case of system (2) in which $n_{i} = 1, i = 1, \ldots ,n$. In this case, system (3) could be rewritten as

$$ \left[ {\begin{array}{*{20}c} {D^{{\alpha_{1} }} x_{1} } \\ {D^{{\alpha_{2} }} x_{2} } \\ \vdots \\ {D^{{\alpha_{n} }} x_{n} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {f_{11} } & {f_{12} } & \cdots & {f_{1n} } \\ {f_{21} } & {f_{22} } & \cdots & {f_{2n} } \\ \vdots & \vdots & \vdots & \vdots \\ {f_{n1} } & {f_{n2} } & \cdots & {f_{nn} } \\ \end{array} } \right]\underline {x} $$

(3)

where $f_{ij} ,i,j = 1, \ldots ,n$ are arbitrary real numbers and $0 < \alpha_{i} < 1, i = 1, \ldots ,n$. The negative sign in (3) simplifies the upcoming calculations. This could not be considered as a limitation. Applying Laplace transform to both sides of (3) yields

$$ X\left( s \right) = \left( {\Lambda + F} \right)^{ - 1} \Psi \underline {x} \left( 0 \right) $$

(4)

where

$$ {\varvec{F}} = \left[ {\begin{array}{*{20}c} {f_{11} } & {f_{12} } & \cdots & {f_{1n} } \\ {f_{21} } & {f_{22} } & \cdots & {f_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {f_{n1} } & {f_{n2} } & \cdots & {f_{nn} } \\ \end{array} } \right],{\varvec{\varLambda}}= \left[ {\begin{array}{*{20}c} {s^{{\alpha_{1} }} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {s^{{\alpha_{n} }} } \\ \end{array} } \right],{\varvec{\varPsi}}= \left[ {\begin{array}{*{20}c} {s^{{\alpha_{1} - 1}} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {s^{{\alpha_{n} - 1}} } \\ \end{array} } \right],{\varvec{X}}\left( s \right) = \left[ {\begin{array}{*{20}c} {X_{1} \left( s \right)} \\ \vdots \\ {X_{n} \left( s \right)} \\ \end{array} } \right] $$

(5)

This means that the characteristic equation of system (3) is

$$ \det \left( {{\Lambda } + F} \right) = 0 $$

(6)

It is evident that if each root of (6) lies in the left half-plane, system (3) is asymptotically stable (Li & Zhang, 2011; Petras, 2009). This means that real parts of the roots of (6) should be verified. A general form for (6) is obtained in the following lemma.

Lemma 3

The general form of the characteristic Eq. (6) could be obtained as

$$ \det \left( {{\Lambda } + F} \right) = \mathop \sum \limits_{{j_{1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{n} = 0}}^{1} F_{{j_{1} , \ldots ,j_{n} }} s^{{\mathop \sum \limits_{i = 1}^{n} \alpha_{i} j_{i} }} $$

(7)

where $F_{{j_{1, \cdots ,} j_{n} }}$ is the corresponding cofactor after omitting the rows and columns corresponding to $\alpha_{i} \left( {j_{i} \ne 0} \right)$. These cofactors are the principal minors of $F$. Furthermore, the coefficient $F_{1, \ldots ,1}$ is chosen as 1.

Proof

At first, let us verify (7) for $n = 2$. In this two-order case, (7) could be written as

$$ \det \left[ {\begin{array}{*{20}c} {s^{{\alpha_{1} }} + f_{11} } & {f_{12} } \\ {f_{21} } & {s^{{\alpha_{2} }} + f_{22} } \\ \end{array} } \right] = s^{{\alpha_{1} + \alpha_{2} }} + f_{22} s^{{\alpha_{1} }} + f_{11} s^{{\alpha_{2} }} + \det \left( F \right) $$

(8)

Now, (8) could be rewritten as

$$ \det \left[ {\begin{array}{*{20}c} {s^{{\alpha_{1} }} + f_{11} } & {f_{12} } \\ {f_{21} } & {s^{{\alpha_{2} }} + f_{22} } \\ \end{array} } \right] = F_{1,1} s^{{\alpha_{1} + \alpha_{2} }} + F_{1,0} s^{{\alpha_{1} }} + F_{0,1} s^{{\alpha_{2} }} + F_{0,0} $$

(9)

As could be seen from (9), (7) is valid for $n = 2$. Now, let to verify it for $n = 3$. In this case, (6) becomes

$$ \begin{aligned} &\det \left[ {\begin{array}{*{20}c} {s^{{\alpha_{1} }} + f_{11} } & {f_{12} } & {f_{13} } \\ {f_{21} } & {s^{{\alpha_{2} }} + f_{22} } & {f_{23} } \\ {f_{31} } & {f_{32 } } & {s^{{\alpha_{3} }} + f_{33} } \\ \end{array} } \right]\\ &\quad = s^{{\alpha_{1} + \alpha_{2} + \alpha_{3} }} + f_{33} s^{{\alpha_{1} + \alpha_{2} }} + f_{22} s^{{\alpha_{1} + \alpha_{3} }} + f_{11} s^{{\alpha_{2} + \alpha_{3} }} \\ & \qquad+ \left( {f_{22} f_{33} - f_{23} f_{32} } \right)s^{{\alpha_{1} }} + \left( {f_{11} f_{33} - f_{13} f_{31} } \right)s^{{\alpha_{2} }} \\ & \qquad+ \left( {f_{11} f_{22} - f_{12} f_{21} } \right)s^{{\alpha_{3} }} + \det \left( F \right) \\ \end{aligned} $$

(10)

(10) could be rewritten as the following form

$$ \begin{aligned} &\det \left[ {\begin{array}{*{20}c} {s^{{\alpha_{1} }} + f_{11} } & {f_{12} } & {f_{13} } \\ {f_{21} } & {s^{{\alpha_{2} }} + f_{22} } & {f_{23} } \\ {f_{31} } & {f_{32 } } & {s^{{\alpha_{3} }} + f_{33} } \\ \end{array} } \right]\\ &\quad = F_{1,1,1} s^{{\alpha_{1} + \alpha_{2} + \alpha_{3} }} + F_{1,1,0} s^{{\alpha_{1} + \alpha_{2} }} + F_{1,0,1} s^{{\alpha_{1} + \alpha_{3} }} \\ & \qquad + F_{0,1,1} s^{{\alpha_{2} + \alpha_{3} }} + F_{1,0,0} s^{{\alpha_{1} }} + F_{0,1,0} s^{{\alpha_{2} }} \\ & \qquad+ F_{0,0,1} s^{{\alpha_{3} }} + F_{0,0,0} \\ \end{aligned} $$

(11)

It is evident that (7) is valid for $n = 3$. Continuing this procedure, it could be easily verified that (7) is valid for any value of $n$. The proof is completed.□

Theorem 1

Gantmacher (1959). A symmetric matrix is positive-definite if and only if all of its principal minors are positive.

Corollary 1

All coefficients of (7) are positive if and only if $F$ is a symmetric positive-definite matrix.

Proof

The proof is trivial (considering Theorem 1 and Lemma 3).

Brandibur and Kaslik (2018) verified the asymptotic stability of a FOS with two different orders. The following theorem studies the asymptotic stability of system (3) (for any value of $n$).□

Theorem 2

Consider that the following conditions are fulfilled for system (3):

(a) $F$ is a symmetric positive-definite matrix.

(b) $\exists \alpha_{l} , \mathop \sum \limits_{i = 1, i \ne l}^{n} \alpha_{i} < 1, l = 1, \ldots ,n.$

Then, system (3) is asymptotically stable.

Proof

The theorem is proved based on contradiction. If system (3) is unstable, (7) has at least a root in the right half-plane. Therefore, there is a complex variable $s$ satisfying (7) and ${\text{Re}} \left( s \right) > 0$. Now, we have

$$ \left| {\arg \left( s \right)} \right| \le \frac{\pi }{2} \Rightarrow \left| {\arg \left( {s^{{\alpha_{l} }} } \right)} \right| = \alpha_{l} \cdot \left| {\arg \left( s \right)} \right| \le \alpha_{l} \frac{\pi }{2} < \frac{\pi }{2} $$

(12)

This means that ${\text{Re}} \left( {s^{{\alpha_{l} }} } \right) > 0$. By setting (7) to zero, we have

$$ s^{{\alpha_{l} }} = - \frac{p\left( s \right)}{{q\left( s \right)}} $$

(13)

where

$$ \begin{aligned} p\left( s \right) & = \mathop \sum \limits_{{j_{1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{l - 1} = 0}}^{1} \mathop \sum \limits_{{j_{l + 1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{n} = 0}}^{1} F_{{j_{1} , \ldots ,j_{l - 1} ,0,j_{l + 1} , \ldots j_{n} }} s^{{\mathop \sum \limits_{i = 1,i \ne l}^{n} j_{i} \alpha_{i} }} \\ q\left( s \right) & = \mathop \sum \limits_{{k_{1} = 0}}^{1} \cdots \mathop \sum \limits_{{k_{l - 1} = 0}}^{1} \mathop \sum \limits_{{k_{l + 1} = 0}}^{1} \cdots \mathop \sum \limits_{{k_{n} = 0}}^{1} F_{{k_{1} , \ldots ,k_{l - 1} ,1,k_{l + 1} , \ldots k_{n} }} s^{{\mathop \sum \limits_{i = 1,i \ne l}^{n} k_{i} \alpha_{i} }} \\ \end{aligned} $$

(14)

Now, the real part of (13) could be calculated by multiplying the numerator and denominator of the right-side of (13) by $q^{*} \left( s \right)$ where $q^{*} \left( s \right)$ indicates the complex conjugate of $q\left( s \right)$. This gives

$$ {\text{Re}} \left( {s^{{\alpha_{l} }} } \right) = \frac{{ - \left\{ {{\text{Re}} \left( {p\left( s \right)} \right){\text{Re}} \left( {q\left( s \right)} \right) + {\text{Im}} \left( {p\left( s \right)} \right){\text{Im}} \left( {q\left( s \right)} \right)} \right\}}}{{\left| {q\left( s \right)} \right|^{2} }} $$

(15)

Now, by considering $s = re^{j\theta }$, we have

$$ \begin{aligned}{\text{Re}}\left\{ {p\left( s \right)} \right\} = &\mathop \sum \limits_{{j_{1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{l - 1} = 0}}^{1} \mathop \sum \limits_{{j_{l + 1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{n} = 0}}^{1} F_{{j_{1} , \ldots ,j_{l - 1} ,0,j_{l + 1} , \ldots j_{n} }}\\ & r^{{\mathop \sum \limits_{i = 1,i \ne l}^{n} j_{i} \alpha_{i} }} \cos \left( {\theta \mathop \sum \limits_{i = 1,i \ne l}^{n} j_{i} \alpha_{i} } \right)\end{aligned} $$

(16)

$$\begin{aligned} {\text{Re}}\left\{ {q\left( s \right)} \right\} = &\mathop \sum \limits_{{k_{2} = 0}}^{1} \cdots \mathop \sum \limits_{{k_{l - 1} = 0}}^{1} \mathop \sum \limits_{{k_{l + 1} = 0}}^{1} \cdots \mathop \sum \limits_{{k_{n} = 0}}^{1} F_{{k_{1} , \ldots ,k_{l - 1} ,0,k_{l + 1} , \ldots ,k_{n} }} \\ &r^{{\mathop \sum \limits_{i = 1,i \ne l}^{n} k_{i} \alpha_{i} }} \cos \left( {\theta \mathop \sum \limits_{i = 1,i \ne l}^{n} k_{i} \alpha_{i} } \right)\end{aligned} $$

(17)

$$\begin{aligned} {\text{Im}}\left\{ {p\left( s \right)} \right\} = &\mathop \sum \limits_{{j_{1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{l - 1} = 0}}^{1} \mathop \sum \limits_{{j_{l + 1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{n} = 0}}^{1} F_{{j_{1} , \ldots ,j_{l - 1} ,0,j_{l + 1} , \ldots j_{n} }} \\ &r^{{\mathop \sum \limits_{i = 1,i \ne l}^{n} j_{i} \alpha_{i} }} \sin \left( {\theta \mathop \sum \limits_{i = 1,i \ne l}^{n} j_{i} \alpha_{i} } \right)\end{aligned} $$

(18)

$$\begin{aligned} {\text{Im}}\left\{ {q\left( s \right)} \right\} = &\mathop \sum \limits_{{k_{2} = 0}}^{1} \cdots \mathop \sum \limits_{{k_{l - 1} = 0}}^{1} \mathop \sum \limits_{{k_{l + 1} = 0}}^{1} \cdots \mathop \sum \limits_{{k_{n} = 0}}^{1} F_{{k_{1} , \ldots ,k_{l - 1} ,0,k_{l + 1} , \ldots ,k_{n} }} \\ &r^{{\mathop \sum \limits_{i = 1,i \ne l}^{n} k_{i} \alpha_{i} }} \sin \left( {\theta \mathop \sum \limits_{i = 1,i \ne l}^{n} k_{i} \alpha_{i} } \right)\end{aligned} $$

(19)

Replacing (16–19) in (15) gives

$$ {\text{Re}}\left( {s^{{\alpha_{l} }} } \right) = \frac{{ - M\cos \left( {\theta \mathop \sum \nolimits_{i = 1,i \ne l}^{n} \left( {j_{i} - k_{i} } \right)\alpha_{i} } \right)}}{{\left| {q\left( s \right)} \right|^{2} }} $$

(20)

where

$$ \begin{aligned} M & = \mathop \sum \limits_{{j_{1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{l - 1} = 0}}^{1} \mathop \sum \limits_{{j_{l + 1} = 0}}^{1} \cdots \mathop \sum \limits_{{j_{n} = 0}}^{1} F_{{j_{1} , \ldots ,j_{l - 1} ,0,j_{l + 1} , \ldots j_{n} }} r^{{\mathop \sum \limits_{i = 1,i \ne l}^{n} j_{i} \alpha_{i} }} \\ & \quad \mathop \sum \limits_{{k_{2} = 0}}^{1} \cdots \mathop \sum \limits_{{k_{l - 1} = 0}}^{1} \mathop \sum \limits_{{k_{l + 1} = 0}}^{1} \cdots \mathop \sum \limits_{{k_{n} = 0}}^{1} F_{{k_{1} , \ldots ,k_{l - 1} ,0,k_{l + 1} , \ldots ,k_{n} }} r^{{\mathop \sum \limits_{i = 1,i \ne l}^{n} k_{i} \alpha_{i} }} \\ \end{aligned} $$

(21)

Since matrix $F$ is positive-definite, all the coefficients $F_{{j_{1} , \ldots ,j_{l - 1} ,0,j_{l + 1} , \ldots j_{n} }}$ and $F_{{k_{1} , \ldots ,k_{l - 1} ,0,k_{l + 1} , \ldots ,k_{n} }}$ are positive according to Theorem 1, and $r$ is positive, too. Accordingly, $M > 0$. Moreover, the maximum value of $j_{i} - k_{i}$ in (20) is 1. Considering this fact and according to condition (b) and (12), we have

$$ \left| {\arg \left( {\theta \mathop \sum \limits_{i = 1,i \ne l}^{n} \left( {j_{i} - k_{i} } \right)\alpha_{i} } \right)} \right| \le \left| {\arg \left( {\theta \mathop \sum \limits_{i = 1,i \ne l}^{n} \alpha_{i} } \right)} \right| < \frac{\pi }{2} $$

(22)

This means that ${\text{Re}}\left( {s^{{\alpha_{l} }} } \right) < 0$, which contradicts our assumption. Thus, all roots of (7) must lie in the left half-plane. Then, system (3) is asymptotically stable.□

Remark 1

Theorem 2 only gives a sufficient condition for the asymptotic stability of system (3). This means that system (3) can be stable even if conditions (a) or (b) are not met.

Remark 2

According to condition (b), the only summation of a combination of $n - 1$ orders should be smaller than one. For instance, a system with three orders $0.9$, $0.7$, $0.2$ could be stable because of $0.7 + 0.2 < 1.$ Consider that $0.9 + 0.7 > 1$ and $0.9 + 0.2 > 1$.

Remark 3

In a particular case, for a two-order fractional system, it is enough that both of the fractional orders are smaller than one. It is compatible with the results obtained by Brandibur and Kaslik (2018).

4 The Leader-Following Consensus of Multi-order FOMAS

The leader-following problem for a multi-order FOMAS is studied in the current section. The fractional-order integrators with non-identical orders are selected as the agents. This means that the dynamics of agents can be described as

$$ D^{{\alpha_{i} }} x_{i} \left( t \right) = u_{i} \left( t \right), \quad i = 1, \ldots , N $$

(23)

where $\alpha_{i} \in \left( {0,1} \right), i = 1, \ldots ,N$ denote the fractional orders and $\alpha_{i} \ne \alpha_{j} , i \ne j$. This indicates that a heterogeneous FOMAS with different fractional orders is considered. The number of agents, the control signal and position for $i$-th the agent in time $t$ are indicated with $N$, $u_{i} \left( t \right)$, and $x_{i} \left( t \right)$, respectively. Besides, assume that condition (b) is satisfied with FOMAS (23). This paper considers a virtual leader with position $x_{d} \left( t \right)$ (Xie & Cheng, 2014).

Definition 2

Ni and Cheng (2010). The leader-following consensus of FOMAS (23) with a virtual leader position $x_{d} \left( t \right)$ will be realized if, for any agent $i, i = 1, \ldots ,N$, there exists a proper control signal $u_{i} \left( t \right)$ that

$$ \mathop {\lim }\limits_{t \to \infty } x_{i} \left( t \right) - x_{d} \left( t \right) = 0, i = 1, \ldots ,N $$

(24)

for each initial condition $x_{i} \left( 0 \right), i = 1, \ldots ,N$.

Theorem 3

Consider FOMAS (23) with connected undirected topology. Consider that the control signals for agents are defined as

$$ u_{i} \left( t \right) = k_{1} \mathop \sum \limits_{{j \in N_{i} }} a_{ij} \left( {x_{j} \left( t \right) - x_{i} \left( t \right)} \right) + k_{1} d_{i} \left( {x_{d} \left( t \right) - x_{i} \left( t \right)} \right) + D^{{\alpha_{i} }} x_{d} \left( t \right) $$

(25)

where $k_{1}$ is a positive feedback control gain. Moreover, consider that condition (b) is fulfilled. Now, the leader-following consensus for FOMAS (23) is attained.

Proof

Suppose that the position error between the i-th agent position and the virtual leader position (or the desired position) is represented with $\tilde{x}_{i} \left( t \right) = x_{i} \left( t \right) - x_{d} \left( t \right)$. Now, replacing (26) in (23) gives

$$ D^{{\alpha_{i} }} \tilde{x}_{i} \left( t \right) = k_{1} \mathop \sum \limits_{{j \in N_{i} }} a_{ij} \left( {\tilde{x}_{j} \left( t \right) - \tilde{x}_{i} \left( t \right)} \right) - k_{1} d_{i} \tilde{x}_{i} \left( t \right),i = 1, \ldots ,N $$

(26)

Based on the definition of matrices $D$, $L$ and $H$, (26) is converted to

$$ D^{{\overline{\alpha }}} \tilde{x}\left( t \right) = - k_{1} H\tilde{x}\left( t \right) $$

(27)

where $\tilde{x}\left( t \right) = \left[ {\tilde{x}_{1} \left( t \right), \ldots ,\tilde{x}_{N} \left( t \right)} \right]^{T}$, and $\overline{\alpha } = \left[ {\alpha_{1} , \ldots ,\alpha_{N} } \right]^{T}$.

Since a connected undirected graph is considered for FOMAS (23), based on Lemma 2, $H$ is a positive-definite matrix. Besides, $k_{1} > 0$. Thus, matrix $k_{1} H$ is also positive-definite. This implies that condition (a) in Theorem 2 is fulfilled. Moreover, condition (b) is also satisfied. Consequently, based on Theorem 2, system (27) is asymptotically stable. Thus, the agent’s position tends to the virtual leader’s position. This completes the proof.□

Remark 4

The control signal (25) has three terms. Implementing the first and second terms is straightforward (only multiplication and summation operators are needed). The third term includes a fractional-order derivative of the desired trajectory. When the desired trajectory is constant, its fractional-order derivative is zero (in the sense of Caputo). For a time-varying desired trajectory (such as the sinusoidal function), the fractional-order derivative of the desired trajectory should be calculated. This calculation can be performed using the FOTF toolbox (Chen et al., 2009).

Fig. 1

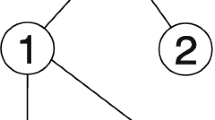
The topology structure for Example 1

Fig. 2

The positions of agents and the virtual leader in Example 1 for $k_{1} = 0.1$

Fig. 3

The positions of agents and the virtual leader in Example 1 for $k_{1} = 1$

Fig. 4

The control signals of the agents in Example 1 for $k_{1} = 0.1$

Fig. 5

The control signals of the agents in Example 1 for $k_{1} = 1$

5 Simulation Results

In the current section, three numerical examples are presented to demonstrate the accuracy of the established distributed control protocol.

Example 1

Assume a FOMAS where the dynamics of its agents are represented with (23). An undirected connected topology with three agents and a leader is considered, as presented in Fig. 1. The leader node is described with 0. The fractional orders of agents are addressed $\alpha_{1} = 0.5$, $\alpha_{2} = 0.6$, $\alpha_{3} = 0.4$. Consider that $\alpha_{1} + \alpha_{2} > 1$, $\alpha_{2} + \alpha_{3} = 1$ but $\alpha_{1} + \alpha_{3} < 1$. Thus, condition (b) is satisfied. The Laplacian matrix $\left( L \right)$ and matrices $D$ and $H$ are determined as

$$ L = \left[ {\begin{array}{*{20}c} 2 & { - 1} & { - 1} \\ { - 1} & 1 & 0 \\ { - 1} & 0 & 1 \\ \end{array} } \right], D = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right], H = \left[ {\begin{array}{*{20}c} 3 & { - 1} & { - 1} \\ { - 1} & 1 & 0 \\ { - 1} & 0 & 1 \\ \end{array} } \right] $$

(28)

It could be verified that $H$ is positive-definite. The initial positions of the agents are selected as $x_{1} \left( 0 \right) = 20$, $x_{2} \left( 0 \right) = 30$, $x_{3} \left( 0 \right) = - 20$. Considering $x_{d} = 10,$ Figs. 2 and 3 give the agent positions and the virtual leader positions for $k_{1} = 0.1$ and $k_{1} = 1,$ respectively. It is obvious that the agent positions converge to the desired position and the leader-following consensus is realized. Moreover, the convergence speed increases while decreasing the control gain $k_{1}$. Figures 4 and 5 show the control signals of the agents for $k_{1} = 0.1$ and $k_{1} = 1$, respectively. It can be concluded that the maximum value of the control signal increase while increasing the control gain.

Example 2

In this example, an undirected topology with six agents is considered (see Fig. 6). The dynamics of agents are compatible with (23) where $\alpha_{1} = 0.1$, $\alpha_{2} = 0.15$, $\alpha_{3} = 0.2$, $\alpha_{4} = 0.25$, $\alpha_{5} = 0.29$, $\alpha_{6} = 0.4$. It could be easily checked that condition (b) is fulfilled. In the following, the Laplacian matrix $\left( L \right)$ and matrices $D$ and $H$ for the graph are specified

$$\begin{aligned} L =& \left[ {\begin{array}{*{20}c} 2 & { - 1} & { - 1} & 0 & 0 & 0 \\ { - 1} & 4 & { - 1} & { - 1} & { - 1} & 0 \\ { - 1} & { - 1} & 3 & 0 & 0 & { - 1} \\ 0 & { - 1} & 0 & 2 & { - 1} & 0 \\ 0 & { - 1} & 0 & { - 1} & 3 & { - 1} \\ 0 & 0 & { - 1} & 0 & { - 1} & 2 \\ \end{array} } \right], \\ D =& \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right],H = \left[ {\begin{array}{*{20}c} 2 & { - 1} & { - 1} & 0 & 0 & 0 \\ { - 1} & 4 & { - 1} & { - 1} & { - 1} & 0 \\ { - 1} & { - 1} & 3 & 0 & 0 & { - 1} \\ 0 & { - 1} & 0 & 2 & { - 1} & 0 \\ 0 & { - 1} & 0 & { - 1} & 4 & { - 1} \\ 0 & 0 & { - 1} & 0 & { - 1} & 3 \\ \end{array} } \right]\end{aligned} $$

(29)

Example 3

This example considers an undirected topology with 10 agents (see Fig. 9). The dynamics of agents are compatible with (23) where $\alpha_{1} = 0.05$, $\alpha_{2} = 0.06$, $\alpha_{3} = 0.07$, $\alpha_{4} = 0.08$, $\alpha_{5} = 0.09$, $\alpha_{6} = 0.11$, $\alpha_{7} = 0.12$, $\alpha_{8} = 0.13$, $\alpha_{9} = 0.14$, and $\alpha_{10} = 0.2$. It could be easily checked that condition (b) is fulfilled. In the following, the Laplacian matrix $\left( L \right)$ and matrices $D$ and $H$ for the graph are specified.

Fig. 6

The topology structure for Example 2

Fig. 7

The positions of agents and the virtual leader in Example 2

Fig. 8

The control signals of the agents in Example 2

Fig. 9

The topology structure for Example 3

It could be easily checked that $H$ is positive-definite. The initial conditions for the agents are selected as $x_{1} \left( 0 \right) = 10$, $x_{2} \left( 0 \right) = 20$, $x_{3} \left( 0 \right) = 30$, $x_{4} \left( 0 \right) = - 10$, $x_{5} \left( 0 \right) = - 20$, $x_{6} \left( 0 \right) = - 30$. In this case, a sinusoidal path is considered for the virtual leader position as $x_{d} = 8\sin \left( {100\pi t} \right)$. The agent positions and the desired position are shown in Fig. 7 for $k_{1} = 0.1$. As shown in Fig. 7, the leader-following consensus is met, and all the agent positions tend to the virtual leader position. The control signals are shown in Fig. 8.

It could be easily checked that $H$ is positive-definite. The initial conditions for the agents are selected as $x_{1} \left( 0 \right) = 10$, $x_{2} \left( 0 \right) = 20$, $x_{3} \left( 0 \right) = 30$, $x_{4} \left( 0 \right) = 40$, $x_{5} \left( 0 \right) = 50$, $x_{6} \left( 0 \right) = - 10$, $x_{7} \left( 0 \right) = - 20$, $x_{8} \left( 0 \right) = - 30$, $x_{9} \left( 0 \right) = - 40$, $x_{10} \left( 0 \right) = - 50$. In this case, a sinusoidal path is considered for the virtual leader position as $x_{d} = 8\sin \left( {100\pi t} \right)$. The agent positions and the desired position are shown in Fig. 10 for $k_{1} = 0.1$. As shown in Fig. 10, the leader-following consensus is met, and all the agent positions tend to the virtual leader position.

6 Conclusion

The current paper extracts sufficient conditions to attain the leader-following consensus for a particular case of FOMAS with heterogeneous fractional-order integrator agents under fixed undirected topology. The simulation outcomes also clarify the efficiency of the presented distributed control strategy. Although the obtained constraint between the fractional orders could be considered a limitation for applying the proposed approach, the presented control protocol could be considered an initiation for future studies. Extracting conditions to realize the leader-following consensus for more generalized multi-order FOMAS without any limitation on the fractional orders could be considered a future research aspect. This idea could be generalized for FOMAS with double-integrator agents, too. This idea could be extended to FOMAS with double-integrator agents. The actuator saturation and the communication delay effects should be verified in future works. Extracting similar conditions for a switching topology could be chosen as another research field.

Fig. 10

The positions of agents and the virtual leader in Example 3