Distributed adaptive neural control for uncertain multi-agent systems with unknown actuator failures and unknown dead zones

Abstract

In actuality, the dead zones and failures often occur in actuators, but the existing algorithms have difficulty simultaneously tolerating dead zones and actuator failures in multi-agent systems. In this paper, the directed topology, uncertain dynamics, unknown dead zones and actuator failures are simultaneously taken into account for the multi-agent systems. By introducing distributed backstepping technique, the radial basis function neural networks and a bound estimation approach, the distributed fault-tolerant tracking controllers and relative adaptive laws for each follower are proposed, which guarantee all followers reach the synchronization and obtain the ideal tracking performance. Comparing with the existing results, it is a new attempt for strict-feedback multi-agent system to take unknown dead zones and unknown actuator failures into consideration. Moreover, the basis function vectors in RBF NNs are no longer required for controllers to decrease computational burden significantly. In the end, the efficiency of our proposed algorithm is verified by comparison simulation results.

1 Introduction

With the rapid development of computer technology, communication technology, sensors and actuators in the past two decades, it has been easier for multiple agents shown in [26, 41, 42] to work together to accomplish a group task in civil and military missions, such as formation cruise, transportation, logistics and geographic information acquisition. Compared with traditional work done by single agent, the cooperation of multiple agents can improve operational efficiency and reduce consumption significantly. Thus, the study of coordination control for multi-agent has grown rapidly. In the meanwhile, a lot of studies about coordinated control have been published. The objectives of these studies are to enable all agents to reach an agreement, including consensus [52], flocking [24], synchronization [9] and so on. In this paper, consensus is an significant performance index and research objective. As is well known, the strict-feedback form is a general form which can be used to describe many physical systems, including spring–mass–damper systems [25] and robotic systems [39]. By designing appropriate control strategies, agents can achieve synchronization of states. Therefore, many researchers have studied a lot of control strategies and tried to integrate neural networks (NNs) or fuzzy logic systems (FLS) and backstepping technique shown in [7, 21, 22, 33, 35, 36, 38, 46] so as to employ them in multi-agent systems (MASs) [32, 43]. However, in [2, 3, 8], the authors did not study high-order MASs and solve the calculations explosion problem noted in [18]. In addition, many results of consensus protocols require eigenvalue information of Laplacian matrix. It is challenging and momentous to take the directed graphs into consideration and design more general algorithms for high-order MASs.

There are many researches for strict-feedback MASs. At first, a definition of coordinated semi-global uniform ultimate bounded (CSUUB) was proposed in [47, 48]. In order to achieve formation control, based on backstepping technique, a distributed adaptive control protocol was proposed in [39]. Then, in [34], by introducing the RBF NNs, the distributed adaptive neural controllers were designed for each follower in nonlinear MASs under leader-following mode in order to track the output of leader. Further, the high-order leaders were taken into consideration in [18], whose states were estimated by distributed leader observers. However, in the above results, the unknown functions in design were approximated by the NNs or FLS, which cost a lot of time. In addition, many physical systems generally exist nonsmooth dead zones [10, 44], such as servo systems, medical systems, electric systems. It is well known that the presence of the dead zone phenomenon can result in systems instability. In order to guarantee system performance by completely eliminating or compensating for the effect of dead zones, many researchers had a deep research on systems with dead zones and put forward many adaptive control strategies shown in [4, 11, 13, 15, 16, 19, 27, 28, 37, 49]. In these results, there are few control strategies that can be employed in the MASs with dead zones [11, 34]. It can be observed that these systems studied in the above studies do not suffer unknown actuator failures. Nevertheless, actuator failures may degrade system performance and even cause safety problems, which is nonignorable.

With the development of industrial technology, it is significant for any MASs to ensure the reliability and robustness. In particular, system may lose control when actuators suffer stuck failures, resulting in huge industrial losses. An effective fault-tolerant control (FTC) algorithm can guarantee system reliability and improve efficiency. In order to protect system from the effect of actuator failures, some FTC algorithms have been proposed in [1, 50]. It can be observed that these algorithms either had a restriction on the number of failures or assumed failures happened after a finite time instant. Many researchers tried all kinds of methods to make a breakthrough. As for time-varying actuator failures, a FTC robust control protocol was proposed in [51]. So as to remove the restriction on the number of actuator failures, the FTC adaptive tracking control strategies were proposed in [20, 31, 40]. Moreover, by introducing a bound estimation method, the FTC algorithms for interconnected nonlinear systems were proposed in [29, 30] to completely compensate for the effect of unknown actuator failures. In [45], a distributed adaptive FTC algorithm for MASs was proposed. However, the above FTC results generally ignore the dead zone nonlinearities or actuator stuck failures. It is more meaningful and challenging to design appropriate controllers for MASs with unknown actuator failures and dead zones.

Motivated by the aforementioned observations, the first attempt is made to design distributed adaptive neural controllers for strict-feedback MASs with unknown actuator failures and unknown dead zones. The existence of actuator stuck failures can lead to a loss in single-input (SI) system; therefore, multiple actuators are employed in each follower to improve the robustness of systems. It is nonnegligible that the challenge of our control objective is the coexistence of unknown function, unknown actuator failures and unknown dead zones. To address it, the distributed backstepping technique, the RBF NNs and a bound estimation approach are introduced to design the distributed controllers. In final, the efficiency of our proposed algorithm can be verified by simulation results such that all signals in the result system are bounded, and the tracking errors for each follower are said to be CSUUB. In the meanwhile, for comparison, a simulation for the classical distributed algorithm is done. The main contributions are listed as follows.

• 1. As the authors acknowledge, so far, the existing studies about MASs do not simultaneously take the unknown actuator failures and unknown dead zones into consideration. They cannot guarantee the ideal tracking performance can be obtained as the presence of unknown actuator failures and unknown dead zones. It is the first time to propose the novel distributed neural control approach for a class of MASs with unknown actuator failures and unknown dead zones. Each follower is modeled by strict-feedback system with unknown actuator failures and unknown dead zones input as well as unknown nonlinear dynamics.

• 2. By introducing a bound estimation method, the estimates for the effects of unknown failures, unknown dead zones and unknown control gain are developed with only locally available information. Compared with the results on MASs by classical control, the failures and dead zones in the systems can be completely unknown. And the assumption that a known positive scalar exists and satisfies some restrictions for the slopes of dead zone, failure or control gain function is removed.

The remainder of this paper is organized as follows: The characteristics of the system and related knowledge are described in Sect. 1. Section 3 describes the design of distributed consensus protocol and stability analysis. The simulation results of spring–mass–damper control system are provided in Sect. 4. Section 5 describes the conclusion of this paper. In Table 1, the main notation used throughout this paper is stated.

Table 1 Notation

2 System formulation and preliminaries

2.1 Graph theory

It is supposed that there is a directed graph ${\mathbb {G}}=({\mathbb {V}},{\mathbb {E}})$ in this paper, where ${\mathbb {V}}=\{{1},\ldots ,{N}\}$ and ${\mathbb {E}}\subseteq {\mathbb {V}}\times {\mathbb {V}}$ denote the set of N nodes and the set of relative edges between N nodes, respectively. The edge is marked $({j},{i})\in {\mathbb {E}}$, representing the node j sends information to node i and then the node i obtains this information, but not vice versa. Moreover, ${N}_{i}=\{{j}\vert ({j},{i})\in {\mathbb {E}}\}$ denotes a set of neighbors j of node i. It is worth mentioning that the directed path (j, i) in directed graph is more than one. For example, it can be composed of a sequence of successive edges. In this paper, we consider leader-following mode. Therefore, it is critical that there exist at least one root node and some other nodes which can get information from the root nodes. In addition, the adjacent matrix ${A}=[a_{ij}]\in {R}^{N\times N}$ describes the topology of a weighted digraph ${\mathbb {G}}$, where $a_{ij}>0$ if $({j},{i})\in {\mathbb {E}}, j\ne i$, and $a_{ij}=0$ otherwise. Finally, ${D}=\mathrm{diag}[d_{1},\ldots , d_{N}]$ is defined as the in-degree matrix of directed graph, where $d_{i}=\sum _{j=1,j\ne i}^{N}a_{ij}$ is the weights of node $v_{i}$. $L = D - A$. Then, $b=[ b_{1},\ldots ,b_{N}] ^{\mathrm{T}}$ , with $b_{i}>0$ if the i th follower connects with the leader and $b_{i}=0$ otherwise. $B={\mathrm { diag}}[ b_{1},\ldots ,b_{N}]$.

2.2 System formulation

In this paper, the MASs adopt leader-following mode, including $N (N > 2)$ followers marked 1 to N and a leader marked 0. The dynamic of the ith follower is described as strict-feedback form with actuator failures and dead zones:

$$\begin{aligned} {\dot{x}}_{i,s}= & {} x_{i,s+1} +f_{i,s}\left( { {\bar{x}}_{i,s}}\right) ,~~s=1,\ldots ,n_{i}-1,\nonumber \\ {\dot{x}}_{i,n_{i}}= & {} \sum \limits _{q=1}^{M_i} \omega _{i,q}u_{i,q} + f_{i,n_{i}}\left( { {\bar{x}}_{i,n_{i}} }\right) , \nonumber \\ y_{i}= & {} x_{i,1}, \end{aligned}$$

(1)

where ${\bar{x}}_{i,s}=\left[ x_{i,1},x_{i,2},\ldots ,x_{i,s}\right] \in {R}^s$$(s=1,\ldots ,n_{i})$ is the state vector. The function $f_{i,s}({\bar{x}}_{i,s})~ (s=1,2,\ldots ,n_i)$ is continuous and unknown. The output $y_{i} \in {R}$ is from the ith follower. The input $u_{i}=\sum _{q=1}^{M_i}\omega _{i,q}u_{i,q} \in {R}$ is the sum of control input $u_{i,q}$. $\omega _{i,q}$ is a bounded control gain of (i, q)th actuators and unknown, while the sign of $\omega _{i,q}$ is known. $u_{i,q}$ denotes the output of the (i, q) th actuator. $n_i$ denotes the order of the ith follower’s system. $M_i$ denotes the number of actuators in the ith follower.

Remark 1

Many physical systems can be modeled by Eq. (1), such as spring–mass–damper systems [25], robotic systems [39], electromechanical system [13] and helicopter system [5]. The actuator failures and dead zones generally exist in the actuators. The actuator failure denotes that the actuator used to execute the control command in the control loop cannot execute the control command correctly due to the gain change or deviation. The dead zone of the actuator means that the actuator does not operate when the input signal of the actuator is small, and only when the input signal of the actuator reaches a certain value, the actuator acts. In addition, the combination of unknown failures and unknown dead zones is widely applied in practice. Therefore, system (1) takes the unknown function, multiple actuators, unknown dead zones and failures into account. So far, there has not been any result on adaptive neural control to be reported for this system.

According to the failure models shown in [29, 30] and the existence of actuator stuck failures, the following mathematic model (2) is employed to describe actuator failures in this paper:

$$\begin{aligned} \begin{array}{l} u_{i,q}(t)=\rho _{i,q,h}\nu _{i,q}(t)+{\bar{\nu }}_{i,q,h}(t), t\in \left[ {t_{i,q,h}^{\mathrm{st}},t_{i,q,h}^{\mathrm{en}}}\right] , \\ \rho _{i,q,h}{\bar{\nu }}_{i,q,h}(t)=0, \quad q=1,2,\ldots , M_i,h=1,2,\ldots , \end{array} \end{aligned}$$

(2)

where $\rho _{i,q,h}$ denotes actuator efficiency and $\rho _{i,q,h} \in [0,1]$. h denotes the number of actuator failures. ${\bar{\nu }}_{i,q,h}(t)$ is unknown but bounded. The time constants $t^{\mathrm{st}}_{i,q,h}$ represent the time instant of actuator failure starts. $t^{\mathrm{en}}_{i,q,h}$ represents the time instant of its ends. For convenience, in this paper, $0\le t^{\mathrm{st}}_{i,q,1}\le t^{\mathrm{en}}_{i,q,1}\le t^{\mathrm{st}}_{i,q,2}\le t^{\mathrm{en}}_{i,q,2}\le \cdots \le + \infty$ is defined. Moreover, $v_{i,q}(t)$ denotes the output of dead zones for (i, q)th actuator. According to model (2), there are three cases of actuator failures:

(1)$\rho _{i,q,h} \ne 0$ and ${\bar{\nu }}_{i,q,h} = 0$

In this case, actuator loses partial performance while operating. It is known as partial loss of effectiveness (PLOE).

(2) $\rho _{i,q,h} = 0$ and ${\bar{\nu }}_{i,q,h} \ne 0$

In this case, actuator loses total performance while operating. That is, $u_{i,q} = {\bar{\nu }}_{i,q,h}$ , and $u_{i,q}$ cannot be controlled by signal $\nu _{i,q}$. Thus, this case is total loss of effectiveness (TLOE).

(3) $\rho _{i,q,h} = 0$ and ${\bar{\nu }}_{i,q,h}(t) = 0$

It is a special example of TLOE, $u_{i,q}=0$.

By defining:

$$\begin{aligned} \rho _{i,q}(t)= & {} {\left\{ \begin{array}{ll} \rho _{i,q,h}, &{} \text{ if } ~t\in \left[ {t_{i,q,h}^{\mathrm{st}},t_{i,q,h}^{\mathrm{en}}}\right] \\ 1, &{} \text{ if } ~t\in \left[ {t_{i,q,h}^{\mathrm{en}},t_{i,q,h+1}^{\mathrm{st}}}\right] \end{array}\right. } \\ {\bar{\nu }}_{i,q}(t)= & {} {\left\{ \begin{array}{ll} {\bar{\nu }}_{i,q,h}(t), &{} \text{ if } ~t\in \left[ {t_{i,q,h}^{\mathrm{st}},t_{i,q,h}^{\mathrm{en}}}\right] \\ 0, &{} \text{ if } ~t\in \left[ {t_{i,q,h}^{\mathrm{en}},t_{i,q,h+1}^{\mathrm{st}}}\right] \end{array}\right. } \end{aligned}$$

model (2) is rewritten as

$$\begin{aligned} u_{i,q}(t)=\rho _{i,q}(t)\nu _{i,q}(t)+\bar{\nu }_{i,q}(t) , \end{aligned}$$

(3)

where $|{\bar{\nu }}_{i,q}(t)|\le \bar{{\bar{\nu }}} _{i,q}$, and $\bar{{\bar{\nu }}}_{i,q}$ is a positive constant. In addition, model (3) satisfies: the multi-agent system can still normally operate, even if the ith agent suffers $n_i-1$ actuator stuck failures.

In this paper, the dead zones are considered to occur in front of actuator failures. Therefore, the output of dead zones is defined as $\nu _{i,q}=D\left( {\tau _{i,q}}\right)$:

$$\begin{aligned} D\left( {\tau _{i,q}}\right)= & {} {\left\{ \begin{array}{ll} m_{i,q,r}\left( { \tau _{i,q}-\vartheta _{i,q,r}}\right) , &{} \tau _{i,q} \ge \vartheta _{i,q,r}, \\ 0,&{}-\vartheta _{i,q,l}< \tau _{i,q} <\vartheta _{i,q,r}, \\ m_{i,q,l}\left( { \tau _{i,q}+\vartheta _{i,q,l}}\right) , &{}\tau _{i,q} \le -\vartheta _{i,q,l}, \end{array}\right. }\nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned} D\left( {\tau _{i,q}}\right)= & {} k_{i,q}(t)\tau _{i,q}+h _{i,q}\left( t\right) , \end{aligned}$$

(5)

where $m_{i,q,r} \ne 0$ is the right slope of dead zones in the (i, q)th actuator. $m_{i,q,l} \ne 0$ is the left slope of dead zones in the (i, q)th actuator. $\vartheta _{i,q,r}\ge 0$ and $\vartheta _{i,q,l}\ge 0$ denote the breakpoint of dead zones. $\tau _{i,q} \in {R}$ is the (i, q)th control input to be designed.

$$\begin{aligned} k_{i,q}(t)= & {} {\left\{ \begin{array}{ll} m_{i,q,r}, &{} \tau _{i,q} >0 \\ m_{i,q,l}, &{} \tau _{i,q} \le 0 \end{array}\right. }, \end{aligned}$$

(6)

$$\begin{aligned} h _{i,q}\left( t\right)= & {} {\left\{ \begin{array}{ll} -m_{i,q,r}\vartheta _{i,q,r}, &{} \tau _{i,q} \ge \vartheta _{i,q,r} \\ -k_{i,q}(t)\tau _{i,q}, &{} -\vartheta _{i,q,l}<\tau _{i,q} < \vartheta _{i,q,r} \\ m_{i,q,l}\vartheta _{i,q,l}, &{} \tau _{i,q} \le -\vartheta _{i,q,l} \end{array}\right. }.\nonumber \\ \end{aligned}$$

(7)

In practice, $h _{i,q}\left( t\right)$ is a bounded function.

Compared with the results in [1, 50, 51], the failures here remove the restrictions on the number of failures and allow the existence of stuck failures. According to (1), (3), (5), the model of MASs (1) can be rewritten as

$$\begin{aligned} {\dot{x}}_{i,s}= & {} x_{i,s+1} +f_{i,s}\left( { {\bar{x}}_{i,s}}\right) ,~~s=1,2,\ldots ,n_{i}-1, \nonumber \\ {\dot{x}}_{i,n_{i}}= & {} u_i(t) + f_{i,n_{i}}\left( {\bar{x}}_{i,n_{i}}\right) ,\nonumber \\ y_{i}= & {} x_{i,1}. \end{aligned}$$

(8)

where the input of the ith agent is $u_i(t)$:

$$\begin{aligned} u_i(t)&=\sum _{q=1}^{M_{i}}\omega _{i,q}\left( \rho _{i,q}\left( t\right) \left( k_{i,q}(t)\tau _{i,q}(t)\right. \right. \nonumber \\&\quad +\left. \left. h _{i,q}\left( t\right) \right) +{\bar{\nu }}_{i,q}\left( t\right) \right) . \end{aligned}$$

(9)

In this paper, the leader node is in the form:

$$\begin{aligned} \begin{array}{l} {\dot{x}}_0=f_0\left( x_0,t\right) , \\ y_0=x_0, \end{array} \end{aligned}$$

(10)

where $f_0\left( x_0,t\right)$ is continuous, satisfying: (a) $|f_0\left( x_0,t\right) | \le g\left( x_0\right)$, (b) $|x_0\left( t\right) | \le X_M$, (c) $\Vert f_0(\breve{{x}}_{0}, t)-f_0({x}_{0},t)\Vert \le L_f \Vert \breve{{x}}_{0}- {x}_{0}\Vert$, $\forall \breve{ {x}}_{0}, {x}_{0} \in {R}$, $t \ge t_0$. $g(x_0)$ is a continuous function. $X_M$ is a positive constant. $L_f$ is the Lipschitz constant and independent of $x_0$ and t. For the leader-following mode in this paper, the leader should be the root of spanning trees in ${\mathbb {G}}$.

Remark 2

As stated in [34], if the leader is not the root of spanning trees, followers may not receive the signals from the leader such that they cannot track the leader. To achieve effective tracking, it is reasonable to require the leader which is the root of spanning tree. As shown later, the $g\left( x_0\right)$, $X_M$ are used to design controllers, but they do not have any effect on the final controllers, which means their true values do not require to be known.

Definition 1

[12] The distributed consensus tracking errors for nonlinear followers (1) under the communication graph are said to be CSUUB, if the positive constants $c_{1}$, $c_{2}$, $\beta _{1}$, $\beta _{2}$ and a time $T\ge 0$ are independent of $t_{0}$ for each $\alpha _{1}\in (0,c_{1})$ and $\alpha _{2}\in (0,c_{2})$ such that $\Vert y_{i}(t_{0})-r(t_{0})\Vert \le \alpha _{1}\Rightarrow \Vert y_{i}(t)-r(t)\Vert \le \beta _{1}$ and $\Vert y_{i}(t_{0})-y_{j}(t_{0})\Vert \le \alpha _{2}\Rightarrow \Vert y_{i}(t)-y_{j}(t)\Vert \le \beta _{2}$$\forall t\ge t_{0}+T$, $i,j=1,\ldots ,N$ and $i\ne j$.

The purpose of this paper is to design controllers for each follower with actuator failures and dead zones. The control protocol is to guarantee the followers can synchronize and track the leader, and all the signals in the closed-loop systems are bounded.

Lemma 1

[23] For $\forall {\bar{\epsilon }} > 0$ and $\varkappa {R}$, the following inequality holds;

$$\begin{aligned} 0 \le | \varkappa | - \varkappa ~ \mathrm{tan}h\left( \dfrac{\varkappa }{{\bar{\epsilon }}}\right) \le \varrho {\bar{\epsilon }}, \end{aligned}$$

(11)

where $\varrho =0.2785$.

2.3 RBF neural networks

As is well known, the advantage of neural networks is its uniform approximation ability, which can approximate any continuous unknown function in theory. Therefore, the following lemma holds:

Lemma 2

[6] There exists a neural network such that

$$\begin{aligned} \sup _{z\in \varOmega } \Bigg | f(z)-\xi ^{\mathrm{T}}\sigma (z) \Bigg | \le \bar{\varepsilon }, \forall {\bar{\varepsilon }}>0, \end{aligned}$$

(12)

where $f(z), z \in {R}^q$ is a continuous function defined on a compact set $\varPhi \subset R^q$. $\sigma (z)$ is the basis function vector, $\sigma (z)=[{{\bar{\sigma }}}_1(z),\ldots ,{{\bar{\sigma }}}_l(z)]^\mathrm{T} \in {R}^l$. ${\xi } = [{\bar{\xi }}_1, \ldots , {\bar{\xi }}_l]^\mathrm{T} \in {R}^l$ is the weight vector. l represents the number of neurons.

According to Lemma 2, there exists an approximation error $\varepsilon$ such that

$$\begin{aligned} {f}(z) = \xi ^{*T}\sigma (z) +\varepsilon ,~|\varepsilon | \le {\bar{\varepsilon }}, \end{aligned}$$

(13)

where $\xi ^{*} \in {R}^{l}$ denotes the ideal weight vector: $\xi ^{*T} := arg \min _{\xi {R}^l} \{\sup _{z\in \varOmega }|f(z)-\xi ^{\mathrm{T}}\sigma (z)|\};$ the radial basis function ${{\bar{\sigma }}}_i(z)$ commonly adopts Gaussian function (14):

$$\begin{aligned}&{{\bar{\sigma }}}_i(z)=\exp \Bigg [ -\frac{(z-\kappa _i)^{\mathrm{T}}(z-\kappa _i)}{\eta _i^2}\Bigg ],~ i=1\ldots , l, \end{aligned}$$

(14)

$$\begin{aligned}&\sigma ^{\mathrm{T}}(z)\sigma (z)\le l, \end{aligned}$$

(15)

where $\eta _i\in {R}$ is the width of the Gaussian function, $\kappa _i=[\kappa _{i1},\kappa _{i2},\ldots ,\kappa _{iq}]^{\mathrm{T}}$ is the center of receptive field. In [34], the efficiency of RBF neural networks has been proven. Hence, the RBF NNs are employed in designing this paper.

Remark 3

This paper focuses on semi-global adaptive RBF NNs coordination control for strict-feedback MASs. Note that the FLS can also obtain the similar results. If Gaussian function is selected as fuzzy membership function, inequality (15) holds for FLS, where l represents the total number of fuzzy rules. As shown later, the number of adaptive parameters for neural weights is independent of the neurons. Similarly, the number of adaptive parameters for fuzzy weights is independent of the fuzzy rules. Consequently, the true value of l does not affect the design of controllers, no matter what.

3 Distributed NN controllers design and stability analysis

The distributed adaptive consensus protocol for MASs with dead zones and actuator failures is designed in this section. In addition, the stability of the closed-loop system is also analyzed in this section.

At first, the synchronization error of the ith follower is defined as:

$$\begin{aligned} z_{i,1}=&\sum _{j=1}^{N}a_{ij}\left( { y_{i}-y_{j}}\right) +b_{i}\left( { y_{i}-y_{0}}\right) . \end{aligned}$$

(16)

Then, the following change of coordinates is made:

$$\begin{aligned} z_{i,s}=&x_{i,s} -\alpha _{i,s-1},~~ s=2,\ldots ,n_{i}, \end{aligned}$$

(17)

where the $z_{i,s}$ is the state error in the sth step for the ith follower. $\alpha _{i,s-1}$ denotes a visual control signal in the $(s-1)$th step for the ith follower. The virtual control signals are in the following form:

$$\begin{aligned} {\alpha }_{i,s}={\left\{ \begin{array}{ll} \dfrac{1}{d_i+b_i}\left[ -c_{i,1}z_{i,1}-\dfrac{z_{i,1}}{2} -\dfrac{1}{2a_{i,1}^{2}}z_{i,1}{\hat{\theta }}_{i}+\sum \limits _{j=1}^{N}a_{i,j}x_{j,2}+b_if_0\left( x_0,t\right) \right] , ~~ s=1 \\ -c_{i,2}z_{i,2}-\dfrac{z_{i,2}}{2}-\left( d_i+b_i\right) z_{i,1}-\dfrac{1}{2a_{i,2}^{2}}z_{i,2}{\hat{\theta }}_{i},~~ s=2 \\ -c_{i,s}z_{i,s}-\dfrac{z_{i,s}}{2}-z_{i,s-1}-\dfrac{1}{2a_{i,s}^{2}}z_{i,s}{\hat{\theta }}_{i},~~ s=3,\ldots ,n_{i}-1 \end{array}\right. } , \end{aligned}$$

(18)

where $c_{i,s}$ and $a_{i,s}$$(s=1, \ldots , n_i-1)$ are design positive constant, ${\hat{\theta }}_{i}$ is the estimation of the constants $\theta _i$:

$$\begin{aligned} \theta _{i}=\max \left\{ {l_{i,s}||\xi ^{*}_{i,s}||^{2}~,~~s=1,\ldots ,n_{i}}\right\} , \end{aligned}$$

(19)

${\hat{\beta }}_i$ and $\hat{{\bar{\lambda }}}_i$, respectively, represent the estimation of the unknown constants ${\beta }_i$ and ${\bar{\lambda }}_i$, as shown in (41). The estimation errors are $\tilde{{\theta }_{i}}= {\theta }_{i}- {\hat{\theta }}_{i}$, ${\tilde{\beta }}_{i}= \beta _{i}- {\hat{\beta }}_{i}$, $\tilde{{\bar{\lambda }}}_{i}={\bar{\lambda }}_{i} - \hat{\bar{\lambda }}_{i}$. Then, the adaptive laws are:

$$\begin{aligned} \dot{{\hat{\beta }}}_{i}&=\text{ z }_{i,n_i} {\alpha }_{i,n_i}, \end{aligned}$$

(20)

$$\begin{aligned} \dot{{\hat{\theta }}}_{i}&=\sum _{m=1}^{n_{i}}\frac{r_{i}}{2a_{i,m}^{2}}z_{i,m}^{2} - k_{i,0}{\hat{\theta }}_i, \end{aligned}$$

(21)

$$\begin{aligned} \dot{\hat{\bar{\lambda }}}_{i}&=z_{i,n_{i}}\tanh \left( {\frac{z_{i,n_{i}}}{\mu _{i}}}\right) , \end{aligned}$$

(22)

where $r_i$ and $\mu _{i}$ are design positive constants.

In addition, the actual controller $\tau _{i,q}$ is:

$$\begin{aligned} \tau _{i,q}=&{\mathrm {sgn}}\left( {\omega _{i,q}}\right) \tau _{i,0}, ~~ q=1,\ldots ,M_{i} , \nonumber \\ \tau _{i,0}=&-\frac{z_{i,n_{i}}{\hat{\beta }}_{i,n_{i}}^{2} {\alpha }_{i,n_{i}}^{2}}{\sqrt{z_{i,n_{i}}^{2}{\hat{\beta }}_{i,n_{i}}^{2} {\alpha }_{i,n_{i}}^{2}+\mu _{i}}}, \end{aligned}$$

(23)

where

$$\begin{aligned} {\alpha }_{i,n_{i}} = \frac{1}{2a_{i,n_{i}}^{2}}z_{i,n_{i}}\hat{\theta }_{i}+c_{i,n_{i}}z_{i,n_{i}} +\hat{{\bar{\lambda }}}_{i}\tanh \left( {\frac{z_{i,n_{i}}}{\mu _{i}}}\right) .\nonumber \\ \end{aligned}$$

(24)

Remark 4

The main results are shown in (18–23). Compared with the results in [34], it can be seen that the basis function of RBF NNs is ignored. As well known, the basis function of RBF NNs can be replaced with 1 by scaling. In the traditional adaptive neural control, the computational burden for estimation parameter about NNs usually is $\sum _{s=1}^{n_i}l_s$, while the computational burden decreases to ${n_i}$ in [17] or $l_s$ in [34]. By combining the pioneering works in [17, 34], the estimation parameter $\theta _i$ is defined in (19). Based on this definition, the computational burden reduces from $\sum _{s=1}^{n_i}l_s$ to 1, which is an improvement for the traditional adaptive control.

In the following, the designing of the virtual control signals, the final input signals of actuators and the adaptive laws will be described.

Step 1: Based on (19), consider the following Lyapunov function candidate:

$$\begin{aligned} V_{i,1} = \frac{1}{2}z_{i,1}^{2}+\frac{1}{2r_{i}}{\tilde{\theta }}_{i}^{2}. \end{aligned}$$

(25)

According to (16), we have the time derivative of $z_{i,1}$:

$$\begin{aligned} {\dot{z}}_{i,1}= & {} \left( d_i+b_i\right) \left( \alpha _{i,1} + z_{i,2}+f_{i,1}\left( {\bar{x}}_{i,1}\right) \right) -\sum \limits _{j=1}^{N}a_{ij}x_{j,2}\nonumber \\&-\sum \limits _{j=1}^{N}a_{ij}f_{j,1}\left( {\bar{x}}_{j,1}\right) -b_if_0\left( x_0,t\right) . \end{aligned}$$

(26)

Therefore, the time derivative of $V_{i,1}$ is:

$$\begin{aligned} {\dot{V}}_{i,1}=&z_{i,1}{\dot{z}}_{i,1}-\dfrac{1}{r_i}{\tilde{\theta }}_i \dot{{\hat{\theta }}}_i\nonumber \\ =&z_{i,1}\left[ \left( d_i+b_i\right) \alpha _{i,1}+{\bar{f}}_{i,1}-b_if_0 \left( x_0,t\right) \right. \nonumber \\&\left. -\sum \limits _{j=1}^{N}a_{ij}x_{j,2}\right] \nonumber \\&+\left( d_i+b_i\right) z_{i,1}z_{i,2}-\dfrac{1}{r_i}{\tilde{\theta }}_i \dot{{\hat{\theta }}}_i, \end{aligned}$$

(27)

where

$$\begin{aligned}&{\bar{f}}_{i,1}=\left( d_i+b_i\right) \left[ f_{i,1}\left( {\bar{x}}_{i,1}\right) \right. \\&\left. \quad -\dfrac{1}{\left( d_i+b_i\right) }\sum \limits _{j=1}^{N}a_{ij}f_{i,1}\left( {\bar{x}}_{j,1}\right) \right] . \end{aligned}$$

According to (1), $f_{i,1}$ is unknown. Thus, the virtual control input $\alpha _{i,1}$ cannot be designed by ${\bar{f}}_{i,1}$. As Lemma 2 shows, the RBF NNs can be utilized to describe ${\bar{f}}_{i,1}$ such that

$$\begin{aligned} {\bar{f}}_{i,1} = \xi _{i,1}^{*T}\sigma _{i,1}+\varepsilon _{i,1},~|\varepsilon _{i,1}| \le {\bar{\varepsilon }}_{i,1}. \end{aligned}$$

(28)

According to the fact $\sigma ^{\mathrm{T}} _{i,1}\sigma _{i,1} \le l_{i,1}$ and Young’s inequality, we get:

$$\begin{aligned} z_{i,1}{\bar{f}}_{i,1}\le \frac{1}{2a_{i,1}^{2}}z_{i,1}^{2}\theta _{i}+\frac{1}{2}a_{i,1}^{2}+\frac{1}{2}z_{i,1}^{2} +\dfrac{1}{2}\bar{\varepsilon }_{i,1}^{2} . \end{aligned}$$

(29)

Substituting (29) into (27) , we have:

$$\begin{aligned} {\dot{V}}_{i,1}&\le \dfrac{1}{2}a_{i,1}^{2}+\dfrac{1}{2}{\bar{\varepsilon }}_{i,1}^{2}+\left( d_i+b_i\right) z_{i,1}z_{i,2}\nonumber \\&\quad + \dfrac{1}{r_i}{\tilde{\theta }}_{i}\left( \dfrac{r_i}{2a_{i,1}^2}z_{i,1}^2- \dot{{\hat{\theta }}}_i\right) \nonumber \\&\quad + z_{i,1}\left[ \left( d_i+b_i\right) \alpha _{i,1} +\dfrac{1}{2}z_{i,1}-b_if_0\left( x_0,t\right) \right. \nonumber \\&\quad \left. -\sum \limits _{j=1}^{N}a_{ij}x_{j,2} +\frac{1}{2a_{i,1}^{2}}z_{i,1}{\hat{\theta }}_{i}\right] . \end{aligned}$$

(30)

Substituting (18) into (30) , we get:

$$\begin{aligned} {\dot{V}}_{i,1}&\le -\,c_{i,1}z^2_{i,1}-\dfrac{1}{r_i}\tilde{\theta }_{i}\left( \dot{{\hat{\theta }}}_i -\dfrac{r_i}{2a_{i,1}^2}z_{i,1}^2\right) \nonumber \\&\quad +\left( d_i+b_i\right) z_{i,1}z_{i,2} +\varphi _{i,1}, \end{aligned}$$

(31)

where $\varphi _{i,1}=\dfrac{1}{2}a_{i,1}^{2}+\dfrac{1}{2}\bar{\varepsilon }_{i,1}^{2}$.

Step s$\left( 2\le s \le n_{i}-1\right)$: Consider the following Lyapunov function candidate:

$$\begin{aligned} V_{i,s} =V_{i, s-1} +\frac{1}{2}z_{i,s}^{2} . \end{aligned}$$

(32)

According to (17), the time derivative of $V_{i,s}$ is:

$$\begin{aligned} {\dot{V}}_{i,s}=\,&{\dot{V}}_{i,s-1}+z_{i,s}\left( {\dot{x}}_{i,s}-{\dot{\alpha }}_{i,s-1}\right) \nonumber \\ =\,&{\dot{V}}_{i,s-1} +z_{i,s}\Biggl [z_{i,s+1}+\alpha _{i,s}+f_{i,s}\left( {\bar{x}}_{i,s}\right) \nonumber \\&\quad -\sum \limits _{m=1}^{s-1}\dfrac{\partial \alpha _{i,s-1}}{\partial x_{i,m}}\left( x_{i,m+1}+f_{i,m}\left( {\bar{x}}_{i,m}\right) \right) \nonumber \\&\quad -\dfrac{\partial \alpha _{i,s-1}}{\partial x_{0}}f_0\left( x_0,t\right) \nonumber \\&\quad -\sum \limits _{m=1}^{s}\sum _{j\in N_{i}}\dfrac{\partial \alpha _{i,s-1}}{\partial x_{j,m}}\left( x_{j,m+1} +f_{j,m}\left( {\bar{x}}_{j,m}\right) \right) \nonumber \\&\quad -\dfrac{\partial \alpha _{i,s-1}}{\partial {\hat{\theta }}_{i}}\dot{{\hat{\theta }}}_i\Biggr ]. \end{aligned}$$

(33)

By using Lemma1, we have:

$$\begin{aligned}&-z_{i,s}\dfrac{\partial \alpha _{i,s-1}}{\partial x_{0}}f_0\left( x_0,t\right) \nonumber \\&\le g\left( x_0\right) z_{i,s}\dfrac{\partial \alpha _{i,s-1}}{\partial x_{0}} \tanh \left( g\left( x_0\right) \dfrac{z_{i,s}\dfrac{\partial \alpha _{i,s-1}}{\partial x_{0}}}{{\bar{\varepsilon }}_{i,s}}\right) \nonumber \\&\quad +\varrho {\bar{\varepsilon }}_{i,s}. \end{aligned}$$

(34)

Substituting (34) into (33) , we have

$$\begin{aligned} {\dot{V}}_{i,s}&={\dot{V}}_{i,s-1}+z_{i,s}\left( z_{i,s+1}+\alpha _{i,s}+{\bar{f}}_{i,s}\right) +\varrho {\bar{\varepsilon }}_{i,s} \nonumber \\&\quad +z_{i,s}\left( \psi _{i,s}-\dfrac{\partial \alpha _{i,s-1}}{\partial {\hat{\theta }}_{i}}\dot{{\hat{\theta }}}_i\right) , \end{aligned}$$

(35)

where

$$\begin{aligned} {\bar{f}}_{i,s}&=f_{i,s}\left( {\bar{x}}_{i,s}\right) \\&\quad +g\left( x_0\right) \dfrac{\partial \alpha _{i,s-1}}{\partial x_{0}} \tanh \left( g\left( x_0\right) \dfrac{z_{i,s}\dfrac{\partial \alpha _{i,s-1}}{\partial x_{0}}}{{\bar{\varepsilon }}_{i,s}}\right) \\&\quad -\psi _{i,s}\\&\quad -\sum \limits _{m=1}^{s-1}\dfrac{\partial \alpha _{i,s-1}}{\partial x_{i,m}}\left( x_{i,m+1}+f_{i,m}\left( {\bar{x}}_{i,m}\right) \right) \\&\quad -\sum \limits _{m=1}^{s}\sum _{j\in N_{i}}\dfrac{\partial \alpha _{i,s-1}}{\partial x_{j,m}}\left( x_{j,m+1}+f_{j,m}\left( {\bar{x}}_{j,m}\right) \right) , \\ \psi _{i,s}&= -k_{i,0}{\hat{\theta }}_{i}\frac{\partial \alpha _{i,s-1}}{\partial {\hat{\theta }}_{i}}\\&\quad -\sum _{m=2}^{s}z_{i,s}\frac{r_{i}}{2a_{i,s}^{2}}\left| {z_{i,m}\frac{\partial \alpha _{i,m-1}}{\partial {\hat{\theta }}_{i}}}\right| \\&\quad +\sum _{m=1}^{s-1}\frac{\partial \alpha _{i,s-1}}{\partial \hat{\theta }_{i}}\frac{r_{i}}{2a_{i,m}^{2}}z_{i,m}^{2} . \end{aligned}$$

Similar to step 1, $f_{i,s}$ is unknown. Thus, the virtual control input $\alpha _{i,s}$ cannot be defined by ${\bar{f}}_{i,s}$. As Lemma 2 shows, the RBF NNs can be utilized to describe ${\bar{f}}_{i,s}$ such that

$$\begin{aligned} {\bar{f}}_{i,s} = \xi _{i,s}^{*T}\sigma _{i,s}+\varepsilon _{i,s},~|\varepsilon _{i,s}| \le {\bar{\varepsilon }}_{i,s} . \end{aligned}$$

(36)

According to the fact $\sigma ^{\mathrm{T}} _{i,s}\sigma _{i,s} \le l_{i,s}$ and Young’s inequality, we get:

$$\begin{aligned} z_{i,s}{\bar{f}}_{i,s}\le \frac{1}{2a_{i,s}^{2}}z_{i,s}^{2}\theta _{i} +\frac{1}{2}a_{i,s}^{2}+\frac{1}{2}z_{i,s}^{2} +\frac{1}{2}\bar{\varepsilon }_{i,s}^{2} . \end{aligned}$$

(37)

Substituting (37) into (35) , we get:

$$\begin{aligned} {\dot{V}}_{i,s}\le&{\dot{V}}_{i,s-1}+z_{i,s}\left( z_{i,s+1}+\alpha _{i,s}\right. \nonumber \\&\quad \left. +\frac{1}{2a_{i,s}^{2}}z_{i,s}\theta _{i}+\dfrac{1}{2}z_{i,s}\right) \nonumber \\&\quad +\dfrac{1}{2}a_{i,s}^{2} +\dfrac{1}{2}{\bar{\varepsilon }}_{i,s}^{2} +\varrho \bar{\varepsilon }_{i,s} \nonumber \\&\quad +z_{i,s}\left( \psi _{i,s}-\dfrac{\partial \alpha _{i,s-1}}{\partial {\hat{\theta }}_{i}}\dot{{\hat{\theta }}}_i\right) . \end{aligned}$$

(38)

Substituting (18) into (38) , we get:

$$\begin{aligned} {\dot{V}}_{i,s}\le&-\sum \limits _{m=1}^{s}c_{i,m}z_{i,m}^{2} -\dfrac{1}{r_i}{\tilde{\theta }}\left( \dot{{\hat{\theta }}} -\sum _{m=1}^{s}\dfrac{r_i}{2a_{i,m}^2}z_{i,m}^{2}\right) \nonumber \\&+\sum _{m=2}^{s}z_{i,m}\left( \psi _{i,s} -\dfrac{\partial \alpha _{i,m-1}}{\partial \hat{\theta _{i}}}\dot{{\hat{\theta }}}_i\right) \nonumber \\&+z_{i,s}z_{i,s+1} +\varphi _{i,s} , \end{aligned}$$

(39)

where

$$\begin{aligned} \varphi _{i,s}=\varphi _{i,s-1}+\dfrac{1}{2}a_{i,s}^2+\dfrac{1}{2}{ \bar{\varepsilon }}_{i,s}^{2}+\varrho {\bar{\varepsilon }}_{i,s} . \end{aligned}$$

Step $n_i$ : According to (9) and (17), the time derivative of $z_{i,n_i}$ is:

$$\begin{aligned} {\dot{z}}_{i,n_i}=&\sum _{q=1}^{M_i}\omega _{i,q}\rho _{i,q}\left( t\right) k_{i,q}(t)\tau _{i,q}(t)+\lambda _{i}+f_{i,n_i}\left( {\bar{x}}_{i,n_i}\right) \nonumber \\&-\sum _{m=1}^{n_i-1}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{i,1}}\left( x_{i,m+1}+f_{i,m}\left( {\bar{x}}_{i,m}\right) \right) \nonumber \\&-\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{0}}f_0\left( x_0,t\right) \nonumber \\&-\sum _{m=1}^{n_i}\sum _{j\in N_{i}}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{j,m}}\left( x_{j,m+1}+f_{j,m}\left( {\bar{x}}_{j,m}\right) \right) \nonumber \\&-\dfrac{\partial \alpha _{i,n_i-1}}{\partial {\hat{\theta }}_{i}} \dot{{\hat{\theta }}}_{i} , \end{aligned}$$

(40)

where $\lambda _{i}=\sum _{q=1}^{M_i}\omega _{i,q}\left( \rho _{i,q}(t)h_{i,q}(t)+{\bar{\nu }}_{i,q}(t)\right)$ .

As the fact $\sum _{q=1}^{M_i}\left| \omega _{i,q}\right| \rho _{i,q} \ge \max \left\{ \left| \omega _{i,1}\right| {\rho }_{i,1},\ldots ,\left| \omega _{i,M_i}\right| {{\rho }}_{i,M_i}\right\} > 0$, we have:

$$\begin{aligned} \inf _{t \ge 0}\sum _{q=1}^{M_i}\left| \omega _{i,q}\right| \rho _{i,q}(t) > 0 . \end{aligned}$$

Define:

$$\begin{aligned}&\eta _i=\inf _{t \ge 0}\sum _{q=1}^{M_i}\left| \omega _{i,q}\right| \rho _{i,q}(t)k_{i,q}(t)\nonumber \\&\quad \beta _i=\dfrac{1}{\eta _i}, ~~~{\bar{\lambda }}_{i}=\sup _{t \ge 0}\left| \lambda _{i}\right| . \end{aligned}$$

(41)

Remark 5

By introducing a bound estimation method, the estimates for the effects of unknown failures and unknown dead zones are developed with only locally available information. Compared with the results on MASs by classical control, the failures and dead zones in the systems can be completely unknown.

Remark 6

The unknown virtual control gain function $\omega _{i,q}$ is considered in (41); therefore, the effects of unknown control gain are also estimated. If $\rho _{i,q}(t) = k_{i,q}(t) = 1$ and $h_{i,q}(t) = {\bar{\nu }}_{i,q}(t) = 0$, the input $u_i$ is only affected by control gain $\omega _{i,q}$, i.e., $u_i(t)=\sum _{q=1}^{M_{i}}\omega _{i,q}\tau _{i,q}(t)$. It is worth noting that the inequality $0< \sum _{q=1}^{M_i}\left| \omega _{i,q}\right| < \infty$ is required to ensure the boundedness of $\eta _i$ and ${\bar{\lambda }}_{i}$ such that $0< \eta _i < \infty$, $0 \le {\bar{\lambda }}_{i} < \infty$.

Consider the following Lyapunov function candidate:

$$\begin{aligned} V_{i,n_i}=V_{i,n_i-1}+\dfrac{1}{2}z^2_{i,n_i}+\dfrac{1}{2}\tilde{{\bar{\lambda }}}_i^2+\dfrac{\eta _i}{2}{\tilde{\beta }}_i^2. \end{aligned}$$

(42)

Based on (40), the time derivative of $V_{i,n_i}$ is:

$$\begin{aligned} {\dot{V}}_{i,n_i}\le&{\dot{V}}_{i,n_i-1}+z_{i,n_i}\left[ \sum _{q=1}^{M_i}\omega _{i,q}\rho _{i,q}\left( t\right) k_{i,q}(t)\tau _{i,q}(t)\right. \nonumber \\&+\lambda _{i}+f_{i,n_i}\left( {\bar{x}}_{i,n_i}\right) \nonumber \\&-\sum _{m=1}^{n_i-1}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{i,1}}\left( x_{i,m+1}+f_{i,m}\left( {\bar{x}}_{i,m}\right) \right) \nonumber \\&-\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{0}}f_0\left( x_0,t\right) \nonumber \\&-\sum _{m=1}^{n_i}\sum _{j\in N_{i}}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{j,m}}\left( x_{j,m+1}+f_{j,m}\left( {\bar{x}}_{j,m}\right) \right) \nonumber \\&\left. -\dfrac{\partial \alpha _{i,n_i-1}}{\partial {\hat{\theta }}_{i}} \dot{{\hat{\theta }}}_{i}\right] -\tilde{{\bar{\lambda }}}_{i}\dot{\hat{{\bar{\lambda }}}}_i -\eta _i{\tilde{\beta }}_i\dot{{\hat{\beta }}}_i . \end{aligned}$$

(43)

By using Lemma1, we have

$$\begin{aligned}&\quad -z_{i,n_i}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{0}}f_0\left( x_0,t\right) \nonumber \\&\le g\left( x_0\right) z_{i,n_i}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{0}} \tanh \left( g\left( x_0\right) \dfrac{z_{i,n_i}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{0}}}{\bar{\varepsilon }_{i,n_i}}\right) \nonumber \\&\quad +\varrho {\bar{\varepsilon }}_{i,n_i} . \end{aligned}$$

(44)

Therefore,

$$\begin{aligned} {\dot{V}}_{i,n_i}&\le {\dot{V}}_{i,n_i-1}+z_{i,n_i}\left( \sum _{q=1}^{M_i}\omega _{i,q}\rho _{i,q}(t)k_{i,q}(t)\tau _{i,q}(t)+{\bar{f}}_{i,n_i}\right) \nonumber \\&\quad +\left| z_{i,n_i}\right| {\bar{\lambda }}_i -\dfrac{1}{2}z_{i,n_i}^2 +\varrho {\bar{\varepsilon }}_{i,n_i} +z_{i,n_i} \nonumber \\&\quad \times \left( \psi _{i,n_i} -\dfrac{\partial \alpha _{i,n_i-1}}{\partial {\hat{\theta }}_{i}} \dot{{\hat{\theta }}}_{i}\right) \nonumber \\&\quad -z_{i,n_i-1}z_{i,n_i} -\tilde{{\bar{\lambda }}}_{i}\dot{\hat{{\bar{\lambda }}}}_i -\eta _i{\tilde{\beta }}_i\dot{{\hat{\beta }}}_i , \end{aligned}$$

(45)

where

$$\begin{aligned} {\bar{f}}_{i,n_i}&=f_{i,n_i}\left( {\bar{x}}_{i,n_i}\right) \\&\quad +g\left( x_0\right) \dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{0}} \tanh \left( g\left( x_0\right) \dfrac{z_{i,n_i}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{0}}}{\bar{\varepsilon }_{i,n_i}}\right) \\&\quad +\dfrac{1}{2}z_{i,n_i}+z_{i,n_i-1}\\&\quad -\sum _{m=1}^{n_i-1}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{i,1}}\left( x_{i,m+1}\right. \\&\quad \left. +f_{i,m}\left( {\bar{x}}_{i,m}\right) \right) \\&\quad -\sum _{m=1}^{n_i}\sum _{j\in N_{i}}\dfrac{\partial \alpha _{i,n_i-1}}{\partial x_{j,m}}\left( x_{j,m+1}+f_{j,m}\left( {\bar{x}}_{j,m}\right) \right) -\psi _{i,n_i} ,\\ \psi _{i,n_i}&= -k_{i,0}{\hat{\theta }}_{i}\frac{\partial \alpha _{i,n_i-1}}{\partial {\hat{\theta }}_{i}}-\sum _{m=2}^{n_i}z_{i,n_i}\frac{r_{i}}{2a_{i,n_i}^{2}}\left| {z_{i,m}\frac{\partial \alpha _{i,m-1}}{\partial \hat{\theta }_{i}}}\right| \\&\quad +\sum _{m=1}^{n_i-1}\frac{\partial \alpha _{i,n_i-1}}{\partial {\hat{\theta }}_{i}}\frac{r_{i}}{2a_{i,m}^{2}}z_{i,m}^{2} . \end{aligned}$$

Similar to step 1, $f_{i,n_i}$ is unknown. Thus, the virtual control input $\alpha _{i,n_i}$ cannot be defined by ${\bar{f}}_{i,n_i}$. As Lemma 2 shows, the RBF NNs can be utilized to describe ${\bar{f}}_{i,n_i}$ such that

$$\begin{aligned} {\bar{f}}_{i,n_i} = \xi _{i,n_i}^{\mathrm{T}}\sigma _{i,n_i}+\varepsilon _{i,n_i},~|\varepsilon _{i,n_i}| \le {\bar{\varepsilon }}_{i,n_i} . \end{aligned}$$

(46)

According to the fact $\sigma ^{\mathrm{T}} _{i,n_i}\sigma _{i,n_i} \le l_{i,n_i}$ and Young’s inequality, we get:

$$\begin{aligned} z_{i,n_i}{\bar{f}}_{i,n_i}\le \frac{1}{2a_{i,n_i}^{2}}z_{i,n_i}^{2}\theta _{i} +\frac{1}{2}a_{i,n_i}^{2}+\frac{1}{2}z_{i,n_i}^{2} +\frac{1}{2}\bar{\varepsilon }_{i,n_i}^{2} . \end{aligned}$$

(47)

Thus,

$$\begin{aligned} {\dot{V}}_{i,n_i} \le&{\dot{V}}_{i,n_i-1}\nonumber \\&+z_{i,n_i}\sum _{q=1}^{M_i}\omega _{i,q}\rho _{i,q}(t)k_{i,q}(t)\tau _{i,q}(t) +z_{i,n_i}\alpha _{i,n_i} \nonumber \\&+\frac{1}{2a_{i,n_i}^{2}}z_{i,n_i}^{2}\theta _{i}\nonumber \\&+\frac{1}{2}a_{i,n_i}^{2} +\frac{1}{2}{\bar{\varepsilon }}_{i,n_i}^{2} +\left| z_{i,n_i}\right| {\bar{\lambda }}_i +\varrho {\bar{\varepsilon }}_{i,n_i} \nonumber \\&+z_{i,n_i}\left( \psi _{i,n_i} -\dfrac{\partial \alpha _{i,n_i-1}}{\partial {\hat{\theta }}_{i}} \dot{{\hat{\theta }}}_{i}\right) \nonumber \\&-z_{i,n_i-1}z_{i,n_i} -\tilde{{\bar{\lambda }}}_{i}\dot{\hat{{\bar{\lambda }}}}_i\nonumber \\&-\eta _i{\tilde{\beta }}_i\dot{{\hat{\beta }}}_i -z_{i,n_i}\alpha _{i,n_i} . \end{aligned}$$

(48)

Based on (24), we have:

$$\begin{aligned} -z_{i,n_{i}} {\alpha }_{i,n_{i}}&=-\frac{1}{2a_{i,n_{i}}^{2}}z_{i,n_{i}}^{2}\hat{\theta }_{i}-c_{i,n_{i}}z_{i,n_{i}}^{2} \nonumber \\&\quad -\hat{\bar{\lambda }}_{i}z_{i,n_{i}}\tanh \left( {\frac{z_{i,n_{i}}}{\mu _{i}}}\right) . \end{aligned}$$

(49)

By introducing (23), we have:

$$\begin{aligned}&z_{i,n_{i}}\sum _{q=1}^{M_{i}}\omega _{i,q}\rho _{i,q}\left( t\right) k_{i,q}(t)\tau _{i,q}(t)\nonumber \\&\quad =-\sum _{q=1}^{M_{i}}|\omega _{i,q}|\rho _{i,q}\left( t\right) k_{i,q}(t)\frac{z_{i,n_{i}}^{2}{\hat{\beta }}_{i,n_{i}}^{2} {\alpha }_{i,n_{i}}^{2}}{\sqrt{z_{i,n_{i}}^{2}\hat{\beta }_{i,n_{i}}^{2}{\alpha }_{i,n_{i}}^{2}+\mu _{i}}}\nonumber \\&\quad \le -\frac{\eta _{i}z_{i,n_{i}}^{2}{\hat{\beta }}_{i,n_{i}}^{2} {\alpha }_{i,n_{i}}^{2}}{\sqrt{z_{i,n_{i}}^{2} {\hat{\beta }}_{i,n_{i}}^{2} {\alpha }_{i,n_{i}}^{2}+\mu _{i}}}\nonumber \\&\quad \le \eta _{i}\mu _{i} -z_{i,n_{i}}\eta _{i} {\hat{\beta }}_{i,n_{i}}{\alpha }_{i,n_{i}} . \end{aligned}$$

(50)

$$\begin{aligned}&\qquad -z_{i,n_{i}}\eta _{i} {\hat{\beta }}_{i,n_{i}}{\alpha }_{i,n_{i}} +z_{i,n_i}\alpha _{i,n_{i}}=-z_{i,n_{i}}\eta _{i} {\hat{\beta }}_{i,n_{i}}{\alpha }_{i,n_{i}}\nonumber \\&\qquad + z_{i,n_{i}}\eta _{i}{\beta }_{i,n_{i}}{\alpha }_{i,n_{i}}\nonumber \\&\quad =z_{i,n_{i}}\eta _{i} {\tilde{\beta }}_{i,n_{i}}{\alpha }_{i,n_{i}} . \end{aligned}$$

(51)

Substituting (20), (21), (22), (39), (49), (50), (51) into (48), we have:

$$\begin{aligned} {\dot{V}}_{i,n_i}&\le -\sum _{m=1}^{n_i}c_{i,m}z_{i,m}^2 +\eta _{i}\mu _{i} -{\bar{\lambda }}_i\tanh \left( \dfrac{z_{i,n_i}}{\mu _{i}}\right) \nonumber \\&\quad +\left| z_{i,n_i}\right| {\bar{\lambda }}_i +\sum _{m=2}^{n_i}z_{i,m}\left( \psi _{i,m} -\dfrac{\partial \alpha _{i,m-1}}{\partial {\hat{\theta }}_{i}} \dot{{\hat{\theta }}}_{i}\right) \nonumber \\&\quad +\dfrac{k_{i,0}}{r_i}{\tilde{\theta }}_i{\hat{\theta }}_i +\varphi _{i,n_i} , \end{aligned}$$

(52)

where $\varphi _{i,n_i}=\varphi _{i,n_i-1} +\frac{1}{2}a_{i,n_i}^{2} +\frac{1}{2}{\bar{\varepsilon }}_{i,n_i}^{2} +\varrho {\bar{\varepsilon }}_{i,n_i} .$ From the work in [14], we have,

$$\begin{aligned} \sum _{m=2}^{n_i}z_{i,m}\left( \psi _{i,m} -\dfrac{\partial \alpha _{i,m-1}}{\partial {\hat{\theta }}_{i}} \dot{{\hat{\theta }}}_{i}\right) \le 0. \end{aligned}$$

(53)

Based on the Young’s inequality, we have:

$$\begin{aligned} {\tilde{\theta }}_i{\hat{\theta }}_i={\tilde{\theta }}_i(\theta _{i} - {\tilde{\theta }}_i) \le -\dfrac{1}{2}{\tilde{\theta }}_i^2 + \dfrac{1}{2}{\theta }_i^2 \end{aligned}$$

(54)

According to Lemma1, we have:

$$\begin{aligned} -{\bar{\lambda }}_{i}\tanh \left( {\frac{z_{i,n_{i}}}{\mu _{i}}}\right) +|z_{i,n_{i}}|\bar{\lambda }_{i}\le {\bar{\lambda }}_{i}\varrho \mu _{i} . \end{aligned}$$

(55)

Finally, substituting (53), (54) and (55) into (52) , we have

$$\begin{aligned} {\dot{V}}_{i,n_i} \le&-\sum _{m=1}^{n_i}c_{i,m}z_{i,m}^2 + \dfrac{k_{i,0}}{2r_i}{\theta }_i^2 \nonumber \\&\quad +{\bar{\lambda }}_{i}\varrho \mu _i +\eta _{i}\mu _{i} +\varphi _{i,n_i} . \end{aligned}$$

(56)

Through the above design procedure, the following theorem comes out:

Theorem 1

For the MASs (1) with unknown actuator failures (2) and unknown dead zones (4), adopting the adaptive laws (20), (21), (22) and controllers (23), the followers will synchronize and track the leader. The tracking errors $\left\| y-y_0\right\|$ in the total closed-loop system are CSUUB. By tuning the design parameters, the following inequality holds:

$$\begin{aligned} \lim _{t\rightarrow +\infty } \left\| y-y_0\right\| \le {\bar{\varepsilon }}, ~\forall {\bar{\varepsilon }} > 0, \end{aligned}$$

(57)

where $y = [y_1, y_2, \ldots , y_N]^{\mathrm{T}}$, ${\overline{y}}_0 = [y_0, y_0, \ldots , y_0]^{\mathrm{T}}$.

Proof

See Appendix. $\square$

Remark 7

As shown in (63), the smaller tracking error can be obtained by increasing the parameters $k_{i,0}$, $\mu _{i}$ and reducing the parameters $a_{i,m}$, $c_{i,m}$, $r_i ~(i=1, \ldots , N, ~m=1, \ldots , n_i)$. As a trade-off, such an operation may cause a relatively large amplitude of control signal. Note that it is difficult for the desired tracking errors to be designed only by tuning a design parameter. Thus, all these design parameters should be tuned properly according to the control constraint and requirement.

4 Simulation example

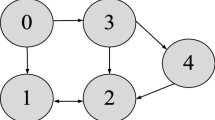
A practical example shown in [25] is given to verify the effectiveness of the proposed algorithm. As shown in Fig. 1, a six-node digraph ${\mathbb {G}}$ represents five followers marked i$(i=1,2,3,4,5)$ and a leader marked 0. Moreover, each follower adopts different spring–mass–damper control system, which is controlled by two torques $u_{i,1}$. The followers are modeled as:

$$\begin{aligned}&{\dot{x}}_{i,1}=x_{i,2} ,\nonumber \\&{\dot{x}}_{i,2}=\dfrac{1}{m_i}\sum _{q=1}^{2}u_{i,q} -\dfrac{k}{m_i}x_{i,1} -\dfrac{c}{m_i}x_{i,2} , \nonumber \\&y_i=x_{i,1} . \end{aligned}$$

(58)

where $m_i$ denotes mass of the ith follower. k denotes the stiffness of the spring. c denotes the damping coefficient. Moreover, $x_{i,1}$, $x_{i,2}$ and $y_{i}$ represent speed, acceleration and position, respectively. The parameters are chosen as Table 2.

Fig. 1

Directed graph of leader and followers

Table 2 Physical parameters of followers

As shown in Fig. 1, the edge weights $a_{ij}$ and the pinning gains $b_i$ are set to 1. Therefore, the adjacency matrix of followers is:

$$\begin{aligned} A=\begin{bmatrix} 0&0&0&0&1\\ 0&0&0&0&0\\ 0&1&0&0&0\\ 0&0&1&0&0\\ 0&0&0&1&0 \end{bmatrix}. \end{aligned}$$

(59)

In addition, the adjacency matrix of leader is $B=\mathrm{diag}\{1,1,0,0,0\}$.

The parameters of dead zones (2) are: $m_{1,1,r} = 1, m_{1,1,l} = 1.3, \vartheta _{1,1,r} = 0.3, {} \vartheta _{1,1,l} = 0.52, m_{1,2,r} = 0.7, m_{1,2,l} = 1.3, \vartheta _{1,2,r} = 0.7, {} \vartheta _{1,2,l} = 4, m_{i,q,r} = 0.8, m_{i,q,l} = 1.2, \vartheta _{i,q,r} = 4.8$ and $\vartheta _{i,q,l} = 1.8$, $i=2,3,4,5$, $q=1,2$.

The following failure models are considered:

$$\begin{aligned} \nu _{1,1}=&{\left\{ \begin{array}{ll} \tau _{1,1}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0.5 \tau _{1,1},&{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. },\\ ~~~~ \nu _{1,2}=&{\left\{ \begin{array}{ll} 0.3\tau _{1,2}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0.1\cos (t),&{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. }, \\ \nu _{2,1}=&{\left\{ \begin{array}{ll} \tau _{2,1}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0.6 \tau _{2,1}, &{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. },\\ \nu _{2,2}=&{\left\{ \begin{array}{ll} \tau _{2,2}, &{}~~~~~~\text{ if } ~t\in [t_1,t_2)\\ 0.3, &{}~~~~~~\text{ if }~t\in [t_2,t_3) \end{array}\right. }, \\ \nu _{3,1}=&{\left\{ \begin{array}{ll} \tau _{3,1}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0.5\tau _{3,1},&{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. },\\ \nu _{3,2}=&{\left\{ \begin{array}{ll} 0.1\tau _{3,2}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0.2 - 0.1\cos (t),&{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. }, \\ \nu _{4,1}=&{\left\{ \begin{array}{ll} \tau _{4,1}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0.6\tau _{4,1}, &{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. } ,\\ \nu _{4,2}=&{\left\{ \begin{array}{ll} 0.3\tau _{4,2}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0, &{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. }, \\ \nu _{5,1}=&{\left\{ \begin{array}{ll} \tau _{5,1}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0.5\tau _{5,1},&{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. } ,\\ \nu _{5,2}=&{\left\{ \begin{array}{ll} 0.3 \tau _{5,2}, &{}~~\text{ if } ~t\in [t_1,t_2)\\ 0.1\sin (t),&{}~~\text{ if }~t\in [t_2,t_3) \end{array}\right. }, \end{aligned}$$

where $t_1=2k$, $t_2=2k+1$, $t_3=2k+2$, $k=0,1,\ldots$.

According to (10), the dynamics of the leader is designed as

$$\begin{aligned} \begin{array}{l} {\dot{x}}_{0}=0.1 \sin \left( t\right) , \\ y_0=x_{0} . \end{array} \end{aligned}$$

Scenario 1—In this scenario, the design parameters are set to be $c_{1,1}=c_{2,1}=4.85,c_{3,1}=c_{4,1}=c_{5,1}=15, c_{i,2}=1, r_{i}=30, a_{i,1}=20, a_{i,2}=0.5, k_{i,0}=0.001$, and $\mu _{i}=0.001, i=1,2,3,4,5$. Then, the initial states of followers are set to be $x_{1}\left( 0\right) =[0.9, 0]^{\mathrm{T}}, x_{2}\left( 0\right) =[0.8, 0]^{\mathrm{T}}, x_{3}\left( 0\right) =[0.7, 0]^{\mathrm{T}}, x_{4}\left( 0\right) =[0.6, 0]^{\mathrm{T}}, x_{5}\left( 0\right) =[0.5, 0]^{\mathrm{T}}$. The initial states of adaptive parameters are: ${\hat{\beta }}_{i}\left( 0\right) =0, {\hat{\lambda }}_{i}\left( 0\right) =0$ and ${\hat{\theta }}_{i}\left( 0\right) =0,~i=1,2,3,4,5$.

Fig. 2

Tracking performance for systems without dead zones and failures

Fig. 3

Tracking performance for systems with dead zones and failures

Fig. 4

Tracking errors $e_{i,1}$ for systems without dead zones and failures

Fig. 5

Tracking errors $e_{i,1}$ for systems with dead zones and failures

Fig. 6

Trajectories of states $x_{i,2}$ for systems without dead zones and failures

Fig. 7

Trajectories of states $x_{i,2}$ for systems with dead zones and failures

Fig. 8

Adaptation parameters ${\hat{\theta }}_i$ for systems without dead zones and failures

Fig. 9

Adaptation parameters ${\hat{\theta }}_i$ for systems with dead zones and failures

Fig. 10

Adaptation parameters ${\hat{\beta }}_i$ for systems without dead zones and failures

Fig. 11

Adaptation parameters ${\hat{\beta }}_i$ for systems with dead zones and failures

Fig. 12

Adaptation parameters ${\hat{\lambda }}_i$ for systems without dead zones and failures

Fig. 13

Adaptation parameters ${\hat{\lambda }}_i$ for systems with dead zones and failures

The simulation results are shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14. The tracking performances for systems without dead zones and failures are shown in Fig. 2, while the tracking performances for systems with dead zones and failures are shown in Fig. 3. Meanwhile, the corresponding tracking errors $e_{i,1}=|y_{i}(t)-y_{0}(t)|$ are shown in Figs. 4 and 5, respectively. Figures 6 and 7 show the difference about the trajectories of state $x_{i,2}$ between the systems without dead zones and failures and systems with dead zones and failures. According to Figs. 2, 3, 4, 5, 6 and 7, it can be observed that actuator failures and dead zones have obvious effects on the system, but the effects are eliminated fleetly by the proposed controllers. The adaptive parameters are depicted in Figs. 8, 9, 10, 11, 12 and 13. Figure 14 demonstrates the boundedness of input$\tau _{i,j}$ and dead zone output $\nu _{i,j}$, $i=1, \ldots , 5,~ j=1,2$. It can be seen from Fig. 14 that the failures cause some jumps in the control inputs, but they are controllable. From all the above simulation results, we can know that all the followers reach the synchronization and obtain ideal tracking performance. Moreover, all the signals in the closed-loop system are bounded. Therefore, the effectiveness of the proposed algorithm has been validated.

Scenario 2—For comparison purposes, we have compared the proposed control method in this paper through simulation. Specifically, the following three control methods are considered.

Method I: the proposed distributed fault-tolerant control method (DFTCM);

Method II: the adaptive fuzzy control method;

Method III: the direct robust control method;

Fig. 14

Trajectories of control for systems with dead zones and failures:  a input$\tau _{1,1}$ and dead zone output $\nu _{1,1}$; b input$\tau _{1,2}$ and dead zone output $\nu _{1,2}$ ; c input$\tau _{2,1}$ and dead zone output $\nu _{2,1}$ ; d input$\tau _{2,2}$ and dead zone output $\nu _{2,2}$ ; e input$\tau _{3,1}$ and dead zone output $\nu _{3,1}$ ; f input$\tau _{3,2}$ and dead zone output $\nu _{3,2}$ ; g input$\tau _{4,1}$ and dead zone output $\nu _{4,1}$ ; h input$\tau _{4,2}$ and dead zone output $\nu _{4,2}$ ; i input$\tau _{5,1}$ and dead zone output $\nu _{5,1}$ ; j input$\tau _{5,2}$ and dead zone output $\nu _{5,2}$

Fig. 15

Tracking performance for comparison with our proposed method

Fig. 16

Tracking errors for comparison with our proposed method

For clarity, the comparative simulation results about one of the followers are presented in Figs. 15 and 16. It can be seen from the simulation result that, in terms of the tracking control performance, the proposed DFTCM is the best among the three tested control methods. This is mainly because the objective of Method II and Method III is to cope with the internal or external disturbances such that the insensitivity of result system is achieved. During control operation, the effect caused by the dead zones and actuator failures is regarded as the disturbance-like effect and not treated by any special treatment. Therefore, the obtained result is relatively conservative in the sense that the tracking performance is not very ideal. Different from Method II and Method III, the proposed DFTCM can be utilized to estimate the effect caused by unknown dead zones and unknown actuator failures by adaptive laws and compensate for it. As reflected in Figs. 15 and 16, the desired trajectory can be obtained for the MASs regardless of the existence of unknown actuator failures and unknown dead zones by our proposed Method I.

5 Conclusion

This paper mainly focuses on the MASs with unknown dead zones and unknown actuator failures. By introducing distributed backstepping technique, RBF NNs and a bound estimation approach, the proposed control protocol has been proposed to ensure that all followers reach an agreement and obtain the ideal tracking performance. It is the first time to design distributed adaptive neural control protocol for strict-feedback MASs with unknown actuator failures and unknown dead zones. In this paper, the effect of stuck failures and the restriction on the number of actuator failures have been taken into account. Note that the basis function of RBF NNs has been ignored by considering the definition of estimation parameter $\theta _i$ to reduce computational burden efficiently. In the end, the effectiveness of Theorem 1 has been illustrated by simulation results.

In this study, we have investigated the coordination control problem for MASs with unknown dead zones and unknown actuator failures. However, it is often required in practice that the consensus can be reached in finite time as such a feature offers numerous benefits including faster convergence rate, better disturbance rejection and robustness against uncertainties. Thus, our future work will focus on this topic.

Appendix: Proof of Theorem 1

The following overall Lyapunov function candidate function V is employed to analyze the stability in the total closed-loop system:

$$\begin{aligned} V = \sum _{i=1}^{N}V_{i,n_{i}}. \end{aligned}$$

(60)

Then, (56) is rewritten as

$$\begin{aligned}&{\dot{V}} \le -\sum _{i=1}^{N}\sum _{m=1}^{n_{i}}c_{i,m}z_{i,m}^{2} \nonumber \\&\quad +\sum _{i=1}^{N}\varphi _{i,n_i} +\sum _{i=1}^{N}\left( {\eta _{i} +{\bar{\lambda }}_{i}\varrho }\right) \mu _{i} \nonumber \\&\quad + \sum _{i=1}^{N}\dfrac{k_{i,0}}{2r_i}{\theta }_i^2. \end{aligned}$$

(61)

If the following compact set holds, ${\dot{V}} < 0$,

$$\begin{aligned} \varOmega= & {} \left\{ \sum _{i=1}^{N}\sum _{m=1}^{n_{i}}c_{i,m}{z_{i,m}^{2}}\right. \nonumber \\> & {} \left. \sum _{i=1}^{N}\varphi _{i,n_{i}} +\sum _{i=1}^{N}\left( {\eta _{i} +{\bar{\lambda }}_{i}\varrho }\right) \mu _{i}\right. \nonumber \\&\left. + \sum _{i=1}^{N}\dfrac{k_{i,0}}{2r_i}{\theta }_i^2\right\} , \end{aligned}$$

(62)

which implies that

$$\begin{aligned}&\lim _{t\rightarrow +\infty } \sum _{i=1}^{N}c_{i,1}{z_{i,1}^{2}}\le \sum _{i=1}^{N}\varphi _{i,n_{i}}\nonumber \\&+\sum _{i=1}^{N}\left( \eta _{i} +{\bar{\lambda }}_{i}\varrho \right) \mu _{i} \nonumber \\&+ \sum _{i=1}^{N}\dfrac{k_{i,0}}{2r_i}{\theta }_i^2. \end{aligned}$$

(63)

According to the similar results in [14], all the signals in the closed-loop system are bounded. Based on the work in [34], we have $\left\| y-y_0\right\| \le \Vert z_{.1}\Vert /\left( {\underline{\sigma }}\right. \left. (L + B)\right)$, where ${\underline{\sigma }}(L + B)$ is the minimum singular value of $L + B$, $z_{.1} = [z_{1,1}, z_{2,1}, \ldots , z_{N,1}]^{\mathrm{T}}$. It can be shown that, for $\forall {\bar{\varepsilon }} > 0$,

$$\begin{aligned} \left\| y-y_0\right\| \le {\bar{\varepsilon }},~~if ~ {z_{. 1}^{2}} \le {\bar{\varepsilon }}^2 \left( {\underline{\sigma }}(L + B)\right) \end{aligned}$$

(64)

It is worth mentioning that the desired tracking error $\left\| y-y_0\right\|$ can be controlled in a small neighborhood by tuning the parameters $k_{i,0}$, $r_i$, $a_{i,m}$, $c_{i,m}$$(i=1, \ldots , N, ~ m=1, \ldots , n_i)$. In order to obtain the desired tracking error, the parameters $k_{i,0}$, $r_i$, $a_{i,m}$, $c_{i,1}$, $\mu _{i}$, ${\bar{\varepsilon }}_{i,m}$ would be tuned in a appropriate set. According to Definition 1, the distributed consensus tracking error $\left\| y-y_0\right\|$ in the closed-loop system is CSUUB.

The proof is completed.