Theoretical and experimental investigations of the crossover phenomenon in micromachined arch resonator: part I—linear problem

Abstract

We investigate, experimentally and theoretically, the linear mode coupling between the first symmetric and antisymmetric modes of an electrothermally tuned and electrostatically actuated micromachined arch resonator. The arch is excited using an antisymmetric partial electrode to activate both modes of vibrations. Theoretically, we explore the static and dynamic behavior using the Galerkin method. When tuning the electrothermal voltage, the first symmetric frequency increases while the first antisymmetric frequency decreases until they cross. The results show linear coupling and hybridization of both modes near crossing only in the presence of the perturbation from the electrostatic force using the partial electrode. We show the linear merging of both modes at crossing. Also, the eigenfrequency variation around crossing shows a ratio of 2:1 between the second symmetric mode and the first symmetric/antisymmetric modes, which can lead to simultaneous 1:1 and 2:1 internal resonances.

1 Introduction

Mode coupling among various modes of vibration of micro- and nano-electromechanical systems (MEMS and NEMS) has been explored for several interesting capabilities and potential applications, such as mass sensing [1, 2], signals filtering [3] and timing/synchronization [4,5,6]. The wide implementation of mode coupling in N/MEMS in the past decade has been sparked by the exciting results demonstrated in the classical structure dynamics.

The coupling between different modes can be linear or nonlinear. The nonlinear coupling can be through a mechanical coupler within the involved structures [7, 8] or via internal resonance [1, 2, 4, 5, 9,10,11]. The majority of the reported nonlinear coupling studies are based on internal resonance [1, 2, 4, 5, 9,10,11].

The linear coupling between modes is mainly related to three well-known phenomena: crossover, veering [3, 12,13,14,15], and mode localization [16, 17]. These phenomena were demonstrated and investigated in both discrete and continuous systems. As two frequencies get close to each other while monitoring a control parameter, they either cross or veer away from each other.

The veering phenomenon (avoided crossing) has been reported between different modes: symmetric and/or antisymmetric. In the veering regime, both contributed modes affect each other (hybridized), and their nonlinearities interchange after veering. Veering was recently demonstrated in N/MEMS resonators, mostly in curved (arch) MEMS resonators [3, 15] and CNTs [18, 19].

Veering is also known to be associated with mode localization, which is defined as a strong localization and confinement of injected energy in a restricted region of a weakly coupled system influenced by a small perturbation. Inspired by the exciting results in the classical structural dynamics [16, 20], this phenomenon has been studied in recent decades using coupled MEMS resonators showing great capabilities in various potential applications [21, 22].

On the other hand, crossover typically occurs between symmetric and antisymmetric modes while changing a control parameter. Contrary to veering, modes at crossing are not known to hybridize or transfer energy. In the classical structural dynamics, crossover was primarily explored in cables and curved beams [13, 14, 23,24,25,26].

Since curved beams inherit cubic and quadratic nonlinearities, they have been widely reported to have different types of couplings either linear, via veering and crossover phenomena [3, 14, 15], or nonlinear through several types of internal resonances, 1:1, 2:1, 3:1 and 4:1 [10, 23, 24], resulting from interactions among different vibrational modes. With increasing their curvature, the fundamental frequency rises rapidly due to the stiffening stretching mechanism, while the antisymmetric frequency does not experience any alteration since it is not affected by stretching [27]. Hence, this leads to the crossing between both modes. Despite the extensive research on the static and dynamic behavior, particularly the nonlinear analysis of curved MEMS resonators [15, 28,29,30], there is little research, experimental and theoretical, on the linear coupling, unforced and forced, between the first symmetric and antisymmetric modes at the crossing zone while tuning their stiffness.

Here, we aim to study, experimentally and theoretically, the crossover phenomenon between the first symmetric and antisymmetric modes of an initially curved beam. The MEMS arch beam is electrothermally tuned and electrostatically driven. Also, to enhance the activation of different modes, we actuate the arch beam electrostatically using a partial electrode configuration [31]. In this paper, we focus on the linear coupling between modes at crossing, while the nonlinear coupling via internal resonance will be explored in the second part of this work [32].

The rest of the paper is organized as follows. The experimental setup is presented in Sect. 2. The modeling part is expanded in Sect. 3. A discussion of the static and dynamic results is presented in Sect. 4. Finally, the main conclusions are summarized in Sect. 5.

2 Experimental setup

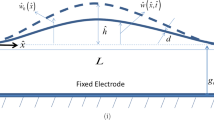
The initially curved beam of this work, in Fig. 1a, is fabricated from SOI wafer with highly conductive silicon device layer using a two-mask process. The curved beam is separated from a stationary electrode with a transduction gap of width d. In this work, we use the half-electrode configuration in order to actuate the symmetric and antisymmetric modes. The arch beam is actuated electrostatically by a DC bias voltage $V_\mathrm{DC}$ and an AC harmonic voltage of amplitude $V_\mathrm{AC}$ and frequency $\hat{{\Omega }}$. Also, we apply a DC voltage $V_\mathrm{Th}$ between the anchors of the arch beam leading to a DC current $I_\mathrm{Th}$ passing through it and heating it, which controls its induced axial load (i.e., stiffness). The initial shape $\hat{{w}}_0 (\hat{{x}})$ of the clamped–clamped arch beam (arc shape), in Fig. 1b, is governed by

$$\begin{aligned} \hat{{w}}_0 (\hat{{x}})=\left( {\hat{{b}}_0 -R+\sqrt{R^{2}-\left( {\hat{{x}}-l/2} \right) ^{2}}} \right) \end{aligned}$$

(1)

where $\hat{x}$ is the position along the arch length l, R represents the radius of the arch and $\hat{b}_0$ denotes the arch midpoint rise. The arch beam is of length $700\,{\upmu }\hbox {m}$, thickness 2 ${\upmu }\hbox {m} (h)$, depth $30\,{\upmu }\hbox {m}$ (b) and initial rise at the midpoint $2.6\,{\upmu }\hbox {m}$.

To measure the natural frequencies and to characterize the dynamic response of the arch beam, we use stroboscopic video microscopy (a high-speed camera) from Polytec [33], as shown in Fig. 1c. The natural frequencies of the curved beam are measured for different $V_\mathrm{Th}$ using ring-down tests and the fast Fourier transform (FFT). The dynamic response is measured by sweeping the frequency for various electrostatic loads.

Fig. 1

a An optical top-view image of the silicon clamped–clamped in-plane arch beam. b A schematic of the arch beam electrothermally tuned and electrostatically actuated. c A schematic of the experimental setup

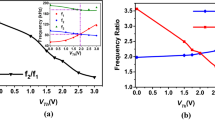
The stiffness of the arch beam is increased due to the compressive axial load induced by increasing the electrothermal voltage that heats the arch beam via Joules heating effect. Figure 2 shows the variation in the first three natural frequencies of the arch beam (first two symmetric modes ($f_{1}$ and $f_{3}$) and the first antisymmetric mode $(f_{2})$) while varying the electrothermal voltage. Initially, increasing the compressive load increases the first natural frequency, $f_{1}$, while the first antisymmetric, $f_{2}$, and the second symmetric, $f_{3}$, natural frequencies decrease. As we increase the electrothermal voltage further, the first symmetric frequency and first antisymmetric frequency cross and depart away from each other. This is known as the crossover phenomenon, which is a necessary condition to activate the 1:1 internal resonance between both modes as observed in the inset of Fig. 2. Besides, at crossing, the second symmetric mode has a ratio of 2 with the two first symmetric and antisymmetric modes that may lead to the possible activation of simultaneous 2:1 and 1:1 internal resonances. With increasing the electrothermal voltage beyond crossing, we notice that the first frequencies of the two modes, $f_{1}$ and $f_{2}$, depart away from each other while the third natural frequency increases, $f_{3}$, after crossing.

Fig. 2

Variation in the three lowest natural frequencies of the arch beam with the electrothermal voltage $V_\mathrm{Th}$. $f_{1}$ and $f_{3}$ denote the first and second symmetric modes, respectively. $f_{2}$ denotes the first antisymmetric mode. The inset shows the variation in the frequency ratios

3 Modeling

The governing equation of motion of the curved beam describing its transverse deflection $\hat{{w}}(\hat{{x}},\hat{{t}})$, where $\hat{{t}}$ is time, is written as [15, 34]

$$\begin{aligned}&\rho bh\frac{\partial ^{2}\hat{{w}}}{\partial \hat{{t}}^{2}}+EI\frac{\partial ^{4}\hat{{w}}}{\partial \hat{{x}}^{4}}+\hat{{c}}\frac{\partial \hat{{w}}}{\partial \hat{{t}}}=\left\{ \left( {\frac{\partial ^{2}\hat{{w}}}{\partial \hat{{x}}^{2}}+\frac{\mathrm{d}^{2}\hat{{w}}_{0} }{\mathrm{d}\hat{{x}}^{2}}} \right) \right. \nonumber \\&\quad \left. \times \left[ {\hat{{N}}+\frac{EA}{2l}\int \limits _0^l {\left( {\left( {\frac{\partial \hat{{w}}}{\partial \hat{{x}}}} \right) ^{2}+2\frac{\partial \hat{{w}}}{\partial \hat{{x}}}\frac{d\hat{{w}}_{0} }{d\hat{{x}}}} \right) \mathrm{d}\hat{{x}}} } \right] \right\} +\hat{{F}}_\mathrm{e}\nonumber \\ \end{aligned}$$

(2)

The beam is subjected to the below boundary conditions

$$\begin{aligned} \hat{{w}}(0,\hat{{t}})=\hat{{w}}(l,\hat{{t}})=0; \text{ and } \left. {\frac{\partial \hat{{w}}}{\partial \hat{{x}}}} \right| _{(0,\hat{{t}})} =\left. {\frac{\partial \hat{{w}}}{\partial \hat{{x}}}} \right| _{(l,\hat{{t}})} =0 \end{aligned}$$

(3)

The arch beam has Young’s modulus E,  material density $\rho$ and is subjected to viscous damping of coefficient ĉ. The    cross-sectional area is assumed to be rectangular, $A={bh}$, with a moment of inertia $I={ bh}^{3}/{12}$. $\hat{{F}}_\mathrm{e}$ denotes the electrostatic force induced by the half-electrode configuration and the arch beam, expressed as [31, 34]:

$$\begin{aligned} \hat{{F}}_\mathrm{e} =\frac{1}{2}\varepsilon b\frac{(V_\mathrm{DC} +V_\mathrm{AC} \cos (\hat{{\Omega }}\hat{{t}}))^{2}}{\left( {d-\hat{{w}}-\hat{{w}}_{0} } \right) ^{2}}u(\hat{{x}}-l /2) \end{aligned}$$

(4)

where $u\left( {\hat{x} -l/2} \right)$ denotes the unit step function and ${\upvarepsilon }$ represents the dielectric constant of the medium. The arch beam is subjected to an axial load $\hat{N} =\hat{N}_{0} -\hat{S} _\mathrm{Th}$ that designates the tensile axial load, where $\hat{N}_{0}$ arises from the fabrication process and $\hat{S}_\mathrm{Th}$ denotes the thermal compressive load given by

$$\begin{aligned} \hat{{S}}_\mathrm{Th} =\frac{EA}{l}\int \limits _0^l {\alpha (T)\left( {T(\hat{{x}})-T_\mathrm{a} } \right) \mathrm{d}\hat{{x}}} \end{aligned}$$

(5)

where $T\left( {\hat{x} } \right)$ denotes the temperature of the curved beam induced by the applied electrothermal voltage via Joules heating and $T_\mathrm{a}$ denotes the temperature at the ends of the arch beam assumed to be equal to the ambient temperature. Using Fourier’s law, $T\left( {\hat{x} } \right)$ is computed by the procedure described in [15]. The parameter $\alpha (T)$ is the thermal expansion coefficient of the silicon beam [35] and is expressed as:

$$\begin{aligned} \alpha (T)= & {} \left\langle 3.75\times \left( {1-\mathrm{e}^{\left\{ {-5.88\times 10^{-5}\left( {T-125} \right) } \right\} }} \right) \right. \nonumber \\&\left. +5.548\times 10^{-4}T \right\rangle \times 10^{-6} \end{aligned}$$

(6)

For convenience, we introduce the nondimensional variables:

$$\begin{aligned} w=\frac{\hat{{w}}}{d}{ ; }x=\frac{\hat{{x}}}{l}{ ; }t=\frac{\hat{{t}}}{T_{S} }\text{; } w_{0} =\frac{\hat{{w}}_{0} }{d}{; }\text{ and } b_{0} =\frac{\hat{{b}}_{0} }{d} \end{aligned}$$

(7)

where $T_{s} =\sqrt{{\rho bhl^{4}} / {EI}}$ is the timescale. Substituting Eq. (6) into Eqs. (1) and (2), we obtain the nondimensional equation of motion

$$\begin{aligned}&\frac{\partial ^{2}w}{\partial t^{2}}+\frac{\partial ^{4}w}{\partial x^{4}}+c\frac{\partial w}{\partial t} =\left( \left( {\frac{\partial ^{2}w}{\partial x^{2}}+\frac{\mathrm{d}^{2}w_{0} }{\mathrm{d}x^{2}}} \right) \right. \nonumber \\&\quad \left. \left[ {N+\alpha _{1} \int \limits _0^1 {\left[ {\frac{\partial w}{\partial x}^{2}+2\frac{\partial w}{\partial x}\frac{\mathrm{d}w_{0} }{\mathrm{d}x}} \right] \mathrm{d}x} } \right] \right) \nonumber \\&\qquad +\,\alpha _{2} \frac{(V_\mathrm{DC} +V_\mathrm{AC} \cos (\Omega t))^{2}}{\left( {1-w-w_{0} } \right) ^{2}}u(x-0.5) \end{aligned}$$

(8)

subjected to the nondimensional boundary conditions

$$\begin{aligned} w(0,t)=w(1,t)=0; \text{ and } \left. {\frac{\partial w}{\partial x}} \right| _{(0,t)} =\left. {\frac{\partial w}{\partial x}} \right| _{(1,t)} =0 \end{aligned}$$

(9)

The parameters appearing in Eq. (7) are defined as

$$\begin{aligned}&\alpha _{1} =6\frac{d^{2}}{h^{2}}\text{; }\quad N=N_{0} +S_\mathrm{Th} \text{; }\quad N_{0} =\frac{l^{2}}{EI}\hat{{N}}_{0} ;\nonumber \\&S_\mathrm{Th} =\frac{l^{2}}{EI}\hat{{S}}_\mathrm{Th} ;\alpha _{2} =\frac{6\varepsilon l^{4}}{Eh^{3}d^{3}}\text{; }c=\frac{l^{4}}{EIT}\hat{{c}}{ ;}\quad \Omega =T_{s} \hat{{\Omega }}\nonumber \\ \end{aligned}$$

(10)

To compute the variation in the natural frequencies, the eigenvalue problem and the mode shapes of the arch beam under electrothermal load and static electrostatic voltage are solved following the procedure described in “Appendix” [15]. Next, by fixing the electrothermal voltage near the crossing region, we simulate the dynamic response of the arch beam by discretizing Eq. (7) using a Galerkin procedure [15, 34], which yields a reduced order model (ROM). To do so, we express the arch deflection as follows [15, 34]:

$$\begin{aligned} w(x,t)=\sum \limits _{i=0}^n {q_{i} (t)\phi _{i} (x)} \end{aligned}$$

(11)

where $q_{i}(t)(i={0\ldots n})$ are the nondimensional modal coordinates and $\phi _{i} (x)$ ($i={0\ldots n}$) are the mode shapes of the arch beam at a constant electrothermal voltage and DC bias load $V_\mathrm{DC}$ (as described in “Appendix”) [15].

Next, we cross-multiply Eq. (7) by$\left( {1-w-w_{0} } \right) ^{2}$. Then, by substituting Eq. (10) into Eq. (7), multiplying by $\phi _{j}(x)$ and integrating along the arch beam, n equations governing $q_{i}(t)$ are obtained

$$\begin{aligned}&\sum \limits _{i=0}^n {M_{ij} (q)\ddot{{q}}_{i} (t)} +\sum \limits _{i=0}^n {C_{ij} (q)\dot{{q}}_{i} (t)} \nonumber \\&\quad +\sum \limits _{i=0}^n {K_{ij} (q)q_{i} (t)} =Fc_{j} (q)+Fe_{j} (t)\nonumber \\&\quad \quad \forall (j=0\ldots n) \end{aligned}$$

(12)

where

$$\begin{aligned}&M_{ij} (q)=\int \limits _0^1 \left[ \phi _{i} (x)\phi _{j} (x)\left( 1-\sum \limits _{i=0}^n {q_{i} (t)\phi _{i} (x)-w_{0}(x)} \right) ^{2} \right] \mathrm{d}x \nonumber \\&C_{ij} (q)=c\int \limits _0^1 \left[ \phi _{i} (x)\phi _{j} (x)\left( 1-\sum \limits _{i=0}^n {q_{i} (t)\phi _{i} (x)-w_{0}(x)} \right) ^{2} \right] \mathrm{d}x \nonumber \\&K_{ij} (q)=\int \limits _0^1 \left[ \phi _{i}^{(iv)}(x)\phi _{j} (x)\left( 1-\sum \limits _{i=0}^n {q_{i} (t)\phi _{i} (x)-w_{0}(x)} \right) ^{2} \right] \mathrm{d}x \nonumber \\&\hbox {Fe}_{j} (t)=\alpha _{\text{2 }} (V_\mathrm{DC} +V_\mathrm{AC} \cos (\Omega t))^{2}\nonumber \\&\quad \quad \int \limits _0^1 {\phi _{j} (x)u(x-0.5)\mathrm{d}x} \nonumber \\&\hbox {Fc}_{j} (q)=\alpha _{1} \Gamma (q)\int \limits _0^1 \left[ \phi _{j} (x)\left( {\sum \limits _{i=0}^n {q_{i} (t)\phi _{i} ''(x)+w_{0} ''(x)} } \right) \right. \nonumber \\&\quad \quad \left. \left( 1-\sum \limits _{i=0}^n {q_{i} (t)\phi _{i} (x)-w_{0}(x)} \right) ^{2} \right] \mathrm{d}x\nonumber \\&\Gamma (q)=N+\int \limits _0^1 {\left( {\sum \limits _{i=0}^n {q_{i} (t)\phi _{i} '(x)} } \right) ^{2}} \mathrm{d}x \nonumber \\&\qquad +2\int \limits _0^1 {\left( {\sum \limits _{i=0}^n {q_{i} (t)\phi _{i} '(x)} } \right) } w_{0} '(x)\mathrm{d}x \end{aligned}$$

(13)

The reduction procedure starts by computing the values of the integrals over the beam domain (x from 0 to 1) in Eq. (12) to solve the dynamic response of the arch beam described in Eq. (11). Then, a set of nonlinear differential equations of $q_{i}(t)(i={1\ldots n})$ is obtained and integrated in time using the Runge–Kutta technique and using four mode shapes (the first three symmetric modes and the first antisymmetric mode) [15]. Note here that the second antisymmetric mode (the fourth mode) does not get excited since it is orthogonal to the electrostatic force of a half electrode. The initial conditions for the time integration are updated for each frequency step as the solutions from the previous frequency step (continuation).

4 Results and discussions

First, we solve the associated eigenvalue problem [15] and simulate the variation in the lowest three natural frequencies of the arch beam with the electrothermal voltage and without including the effect of the electrostatic force. As revealed in Fig. 3a, good agreement is shown among the experimental and numerical results, capturing the frequency trends and the crossing phenomenon. Next, we compute the mode shape alteration of the first symmetric and antisymmetric modes around the crossing zone without including the electrostatic effect. Figure 3b shows that the two modes cross, from point A ($V_\mathrm{Th}=1.88\,\hbox {V}$) to point C ($V_\mathrm{Th}=1.98\,\hbox {V}$), without any hybridization of modes, contrary to that observed in the case of veering between the first two symmetric modes [15]. In addition, we note that the mode shapes orders interchange after crossing, from point B ($V_\mathrm{Th}=1.92\,\hbox {V}$) to point C.

Fig. 3

a Variation in the three lowest natural frequencies of the arch beam with $V_\mathrm{Th}$. The scattered points denote the experimental data, and the continuous lines represent the simulated results. $f_{1}$ and $f_{3}$ denote the first and second symmetric modes, respectively. $f_{2}$ denotes the first antisymmetric mode. b The first symmetric and antisymmetric mode shapes of the arch beam at different $V_\mathrm{Th}$ denoted as sections A ($V_\mathrm{Th}=1.88\,\hbox {V}$), B ($V_\mathrm{Th}=1.92\,\hbox {V}$) and C ($V_\mathrm{Th}=1.98\,\hbox {V}$) in a

Since commonly systems with repeated eigenvalues show high sensitivity to any perturbation, we next investigate this effect by introducing the DC electrostatic voltage. In Fig. 4, we plot the first symmetric and antisymmetric mode shapes of the arch beam for different DC voltages at different electrothermal voltages. For zero electrothermal voltage, in Fig. 4a, the two modes do not show any signs of hybridization or interchange even for high DC electrostatic voltage. A similar observation is shown in Fig. 4b when introducing an electrothermal voltage and being away from crossing, $V_\mathrm{Th}=1.2\,\hbox {V}$. Figure 4a, b demonstrates that the mode shapes show shifting of the position of the maximum peak of the symmetric mode and the nodal point of the antisymmetric mode at high values of electrostatic voltage caused by the antisymmetry of the driving electrode. When being closer to the crossing zone, in Fig. 4c and d, both mode shapes start to interact and hybridize at a critical DC electrostatic voltage. At crossing, the hybridization of both first symmetric and antisymmetric modes leads to the same out-of-phase mode shapes when passing the critical DC electrostatic force. The same observation as the case before crossing can be concluded about the mode shapes after crossing, as shown in Fig. 4e and f, but in this case the mode shapes have interchanged due to crossing.

Fig. 4

First symmetric and antisymmetric mode shapes of the arch beam at different $V_\mathrm{Th}$ and for various DC electrostatic voltages. a$V_\mathrm{Th}= 0\,\hbox {V}$. b$V_\mathrm{Th}= 1.2\,\hbox {V}$. c$V_\mathrm{Th}= 1.8\,\hbox {V}$. d$V_\mathrm{Th}= 1.92\,\hbox {V}$. e$V_\mathrm{Th}= 1.96\,\hbox {V}$. f$V_\mathrm{Th}= 2.4\,\hbox {V}$

Also, one can note that the critical electrostatic voltage decreases when getting closer to the crossing zone and then begins to increase again after crossing.

A further explanation of the influence of the DC electrostatic voltage on the mode contribution for different electrothermal voltages around the crossing zone is given in Fig. 5. Away from crossing, $V_\mathrm{Th}=1.2\,\hbox {V}$, we note the influence of the electrostatic voltage by shifting the nodal point of the second mode and the maximum peak of the first mode at $x=0.5$. However, no hybridization is observed. As we move closer to the crossing point at $V_\mathrm{Th}=1.88\,\hbox {V}$, the hybridization starts to appear which is indicated by the zero value of the first mode at $x=0.75$ at a critical electrostatic voltage of 42V. This critical value becomes the lowest at the crossing point, $V_\mathrm{Th}=1.92\,\hbox {V}$, where a small perturbation in the electrostatic voltage results into hybridization of the modes. Moving away from the crossing point, $V_\mathrm{Th}=2.4\,\hbox {V}$, the electrostatic voltage required to hybridize the modes reaches high values up to 130 V.

It is also noteworthy that exceeding the critical DC electrostatic voltage leads to the hybridization of both mode shapes that might strongly enhance the activation of a one-to-one internal resonance.

Fig. 5

Variation in the absolute amplitude of the first symmetric and antisymmetric normalized mode shapes at the midpoint, quarter and three-quarters of the arch beam for different $V_\mathrm{Th}$ values with the DC electrostatic voltages. ${\varphi }_{1 }$ and ${\varphi }_{2}$ denote the first symmetric and antisymmetric mode shapes before crossing ($V_\mathrm{Th}\le 1.92\,\hbox {V}$) and vice versa after crossing, respectively

Next, we study the linear vibration response of the first symmetric and antisymmetric modes around the crossing zone. The nonlinear interaction between these modes that might lead to simultaneous internal resonance of 1:1 and 2:1 with the second symmetric mode will be further studied in the second part of the paper [32].

We start by exciting the beam with low DC and AC electrostatic voltages in order to keep the linear motion of the arch beam by keeping $V_\mathrm{DC}=V_\mathrm{AC}= 15\,\hbox {V}$ leading to an effective static DC electrostatic voltage $V_\mathrm{eff} =\sqrt{V_\mathrm{DC} ^{2}+0.5V_\mathrm{AC}^{2}}=$ 18 V. Hence, the mode coupling (mode shape hybridization) is expected to occur at the crossing zone since the effective DC electrostatic voltage is higher than the critical voltage as described earlier in Fig. 5.

Fig. 6

Linear frequency response curves of the arch beam at the quarter point for different electrothermal voltages at fixed $V_\mathrm{DC}=V_\mathrm{AC}= 15\,\hbox {V}$. a Experimental. b The simulation results using the Galerkin procedure. c The contribution of the first symmetric and antisymmetric modes at the quarter point for $V_\mathrm{Th}= 1.8 \,\hbox {V}$, $V_\mathrm{Th}= 1.92\,\hbox {V}$, and $V_\mathrm{Th}= 2.5 \,\hbox {V}$. ${\varphi }_{1 }$ and ${\varphi }_{2}$ denote the first symmetric and antisymmetric mode shapes before crossing ($V_\mathrm{Th}\le$ 1.92 V) and vice versa after crossing, respectively

Experimentally, we swept the frequency around the first symmetric and antisymmetric modes around the crossing zone. Figure 6a shows that initially at $V_\mathrm{Th}=1.7\,\hbox {V}$ we have two peaks at the quarter point representing the contribution of the first symmetric and antisymmetric modes with a maximum amplitude close to $0.2\,{\upmu }$m. As getting closer to the crossing zone from $V_\mathrm{Th}= 1.7\,\hbox {V}$ to $V_\mathrm{Th}= 1.8\,\hbox {V}$, the linear amplitude of motion around the first symmetric mode uplifts the motion around the first antisymmetric modes. At crossing from $V_\mathrm{Th}= 1.85\,\hbox {V}$ to $V_\mathrm{Th}= 2\,\hbox {V}$, the motion of both modes merges into one synchronized mode showing steady amplitude of motion for a narrow range of electrothermal voltages near and at crossing. After crossing, from $V_\mathrm{Th}=2.1\,\hbox {V}$ to $V_\mathrm{Th}= 2.4\,\hbox {V}$, both modes interchange place and the first antisymmetric mode shows higher amplitude of motion than the first symmetric mode at the quarter point.

Fig. 7

a Simulated linear frequency response curves of the arch beam at the midpoint for different electrothermal voltages at fixed $V_\mathrm{DC}=V_\mathrm{AC}= 15\,\hbox {V}$. b The contribution of the first symmetric and antisymmetric modes at the midpoint for $V_\mathrm{Th}= 1.2\,\hbox {V}$, $V_\mathrm{Th}= 1.92\,\hbox {V}$, and $V_\mathrm{Th}= 2.5 \,\hbox {V}$. ${\phi }_{1}$ and ${\phi }_{2}$ denote the first symmetric and antisymmetric mode shapes before crossing ($V_\mathrm{Th} \le 1.92\,\hbox {V}$) and vice versa after crossing, respectively

Numerically, in Fig. 6b, a qualitative agreement is shown with the experimental data. However, the rise in of the amplitude of motion of the first symmetric mode is simulated at different electrothermal voltage values compared to the experimental data. This deviation can be explained by the fact that around crossing the amplitude of vibration of each mode becomes very sensitive to any small perturbation (mode localization behavior), which is due to the almost identical eigenvalues of the two modes in that zone. Hence, in the presence of the unavoidable fabrication imperfection, it is very hard for the model to predict the exact amplitude of motion near that regime. Essentially, the confinement of energy as the two modes cross is very sensitive to the applied voltage. Hence, it is very difficult to capture it exactly and numerically.

Also to better understand this change in amplitude at the quarter point, we draw the contribution of the first symmetric and antisymmetric modes at the quarter for different electrothermal voltages before, at and after crossing (Fig. 6c). The results show that the mode amplitude at the quarter of the first symmetric mode exceeds the amplitude of the first antisymmetric mode at crossing, $V_\mathrm{Th}= 1.92\,\hbox {V}$, contrary to the case away from crossing, $V_\mathrm{Th}=1.8\,\hbox {V}$. Hence, this explains the rise in amplitude of motion around the first symmetric mode around crossing. One should mention here that even slightly away from crossing, for example at $V_\mathrm{Th}=1.8\,\hbox {V}$, the amplitude of the first mode may surpass the one of the first antisymmetric at the beam quarter when exciting the beam with higher DC electrostatic voltage while tuning the damping to keep the linearity of the motion.

In contrary to the motion at the quarter point, the midpoint of the arch beam is usually maximum around the first symmetric mode. The midpoint is known in general as a nodal point of the antisymmetric modes. However, the presence of the half-electrode configuration slightly shifts this nodal point when increasing the DC effective electrostatic voltage. Figure 7 shows that away from crossing, $V_\mathrm{Th}= 1.2\,\hbox {V}$ to $V_\mathrm{Th}= 1.8\,\hbox {V}$, the amplitude of motion of the first antisymmetric mode at the midpoint is almost zero. However, at crossing, $V_\mathrm{Th}= 1.85\,\hbox {V}$ to $V_\mathrm{Th}= 1.96\,\hbox {V}$, it increases since the amplitudes of both modes are almost similar at midpoint for this specific $V_\mathrm{eff}$. After crossing, $V_\mathrm{Th}= 2.1\,\hbox {V}$ to $V_\mathrm{Th}= 2.5\,\hbox {V}$, the motion of the first antisymmetric mode vanishes again due to the interchange of the modes.

Also, we show the contribution of the first symmetric and antisymmetric modes at the midpoint for different electrothermal voltages before, at and after crossing in Fig. 7b. The results show that the mode amplitude at the midpoint of the first antisymmetric mode remains almost zero away from crossing for this range of DC electrostatic force, which explains the zero vibration around this mode away from crossing. Near crossing, the amplitude of the first antisymmetric mode at midpoint increases for low DC electrostatic voltages to approach the amplitude of the first symmetric mode, which demonstrates the detected motion at the midpoint of the first antisymmetric mode as shown in Fig. 7a.

5 Conclusions

In this paper, we investigated experimentally and theoretically the linear mode coupling between the first symmetric and antisymmetric modes of an electrothermally tuned and electrostatically actuated arch MEMS resonator. When tuning the stiffness of the arch beam electrothermally, the first symmetric and antisymmetric modes cross. The mode shapes of both modes showed hybridization around crossing only in the presence of perturbation originating from the electrostatic actuation by the half electrode. The linear modal interaction shown in this work seems to be different from veering and mode localization phenomena. The reported results motivate further research in this direction to exploit the linear coupling of both symmetric and antisymmetric modes at crossing for practical applications. On the other hand, the resonance frequencies alteration due to the electrothermal voltage showed that when experiencing crossing between the first symmetric and antisymmetric modes, they have a ratio of 2 with the second symmetric mode. This presents a strong condition to activate a simultaneous 2:1 internal resonance with the 1:1 internal resonance. A complex and rich dynamic behavior will be demonstrated for such a case in the second part of this work.

Appendix

Here, we present the procedure of solving the eigenvalue problem of the arch beam when varying the electrothermal and the DC bias voltages. The static deflection of the arch beam, due to $V_\mathrm{Th}$ and $V_\mathrm{DC}$, is governed by

$$\begin{aligned}&\frac{\mathrm{d}^{4}w_s }{\mathrm{d}x^{4}}=\left( \left( {\frac{\mathrm{d}^{2}w_s }{\mathrm{d}x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \right. \nonumber \\&\quad \left. \left[ {N+\alpha _1 \int _0^1 {\left[ {\left( {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right) ^{2}+2\frac{\mathrm{d}w_s }{\mathrm{d}x}\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right] \mathrm{d}x} } \right] \right) \nonumber \\&\quad +\,\alpha _2 \frac{V_\mathrm{DC} ^{2}}{\left( {1-w_s -w_0 } \right) ^{2}}u(x-0.5) \end{aligned}$$

(A.1)

with the associated boundary conditions

$$\begin{aligned} w_s (0)=w_s (1)=0\hbox { and }\left. {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right| _{x=0} =\left. {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right| _{x=1} =0\nonumber \\ \end{aligned}$$

(A.2)

To solve the eigenvalue problem, we drop the AC bias voltage and the damping terms from the equation of motion (Eq. (8)). Next, we assume that the total deflection is the sum of the static configuration, $w_{s}(x)$, and a small dynamic deflection of the arch beam, $w_{d}(x,t)$, around $w_{s}(x)$. The linearized equation of motion describing $w_{d}(x,t)$ is derived by substituting $w(x,t)=w_{d}(x,t)+w_{s}(x)$ into Eq. (8) and dropping the terms representing the equilibrium position and the nonlinear terms. This yields

$$\begin{aligned}&\frac{\partial ^{2}w_d }{\partial t^{2}}+\frac{\partial ^{4}w_d }{\partial x^{4}}\nonumber \\&\quad =\left[ {N+\alpha _1 \int _0^1 {\left[ {\left( {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right) ^{2}+2\frac{\mathrm{d}w_s }{\mathrm{d}x}\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right] dx} } \right] \frac{\partial ^{2}w_d }{\partial x^{2}} \nonumber \\&\quad \quad +\,2\alpha _1 \int _0^1 {\left[ {\left( {\frac{\mathrm{d}w_s }{\mathrm{d}x}+\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right) \frac{\partial w_d }{\partial x}} \right] \mathrm{d}x} \left( {\frac{\mathrm{d}^{2}w_s }{\mathrm{d}x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \nonumber \\&\quad \quad +\,2\alpha _2 \frac{V_\mathrm{DC} ^{2}}{\left( {1-w_s -w_0 } \right) ^{3}}u(x-0.5)w_d \end{aligned}$$

(A.3)

with the associated boundary conditions

$$\begin{aligned}&w_d (0,t)=w_d (1,t)=0\nonumber \\&\quad \hbox { and }\left. {\frac{\partial w_d }{\partial x}} \right| _{x=0,t} =\left. {\frac{\partial w_d }{\partial x}} \right| _{x=1,t} =0 \end{aligned}$$

(A.4)

We solve the eigenvalue problem of the arch beam under electrothermal voltage and electrostatic voltage [15, 34] by using the Galerkin discretization. Toward this, we let

$$\begin{aligned} w_d (x,t)=\sum _{i=0}^n {u_i (t)\varphi _i (x)} \end{aligned}$$

(A.5)

where $u_{i}{(t) (i=0,1,2\ldots n)}$ denotes the nondimensional modal coordinates and ${\varphi }_{i}(x) (i=0,1,2\ldots n)$ denotes the mode shape of the unactuated clamped–clamped arch beam. Next, we substitute Eq. (A.5) into Eq. (A.3), multiply the outcome by the mode shape ${\varphi }_{j}$ and integrate over the beam domain (from 0 to 1), which yield the below equation [15, 34]:

$$\begin{aligned} \ddot{u}_j= & {} -\int _0^1 {\varphi _j \left( {\sum _{i=0}^n {u_i \varphi _i ^{(iv)}} } \right) } \mathrm{d}x \nonumber \\&+\left[ N+\alpha _1 \int _0^1 \left[ \left( {\frac{\mathrm{d}w_s }{\mathrm{d}x}} \right) ^{2} \right. \right. \nonumber \\&+\,2\left. \left. \frac{\mathrm{d}w_s }{\mathrm{d}x}\frac{\mathrm{d}w_0 }{\mathrm{d}x} \right] \mathrm{d}x \right] \int _0^1 {\varphi _j \left( {\sum _{i=0}^n {u_i \varphi _i {\prime }{\prime }} } \right) } \mathrm{d}x \nonumber \\&+\,2\alpha _1 \int _0^1 {\left[ {\left( {\frac{dw_s }{\mathrm{d}x}+\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right) \sum _{i=0}^n {u_i \varphi _i {\prime }} } \right] \mathrm{d}x} \nonumber \\&\quad \quad \int _0^1 {\varphi _j \left( {\frac{\mathrm{d}^{2}w_s }{\mathrm{d}x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \mathrm{d}x} \nonumber \\&+\int _0^1 {\varphi _j \frac{2\alpha _2 V_\mathrm{DC} ^{2}}{\left( {1-w_s -w_0 } \right) ^{3}}\left( {\sum _{i=0}^n {u_i \varphi _i } } \right) u(x-0.5)\mathrm{d}x}\nonumber \\ \end{aligned}$$

(A.6)

Using four modes, we compute the Jacobian of the system of the four obtained equations, for each $V_\mathrm{Th}$ and $V_\mathrm{DC}$, and find the corresponding eigenvalues and eigenvectors (new mode shapes). Then, we compute the natural frequencies of the resonators, at constant $V_\mathrm{Th}$ and $V_\mathrm{DC}$, by taking the square root of these eigenvalues.