Introduction

Nonlinear Partial Differential Equations (NLPDE) has been widely used in the fields of science and engineering. The study of nonlinear phenomena involving in fluid dynamics, plasma physics, optical communication, quantum mechanics, etc. Soliton and exact solutions arising between the nonlinearity and dispersion relation of a NLPDE. There is no common method to solve all types of NLPDE in finding their possible closed form solutions.

In the past decades, various significant methods have been proposed, such as the inverse scattering transform [2, 6, 35], Bäcklund transformation [37, 41, 50], Lax pair [23, 61], Painlevé analysis [14, 58], Darboux transformation [38, 49], Bell polynomial [46, 53], Similarity transformation [11, 24, 33], tanh method [36], tanh-coth method [4, 55], Cole–Hope transformation [48], (\(G^\prime /G\)) expansion method [26], Sine–Gordon expansion method [5, 63], Modified \(exp(-\varOmega (\eta ))\)-expansion function method [64, 65], Function transformation method [42], Improved Bernoulli subequation function method [62] and so on. These methods are used to NLPDE and obtain different types of explicit exact solitary wave solutions. Additionally, Different types of NPLDE handled by some other methods (See, [10, 12, 19, 40, 52]).

In 1871 Boussinesq introduced a nonlinear evolution equation to describe the propagation of long waves and small amplitude in shallow water. Various types of Boussinesq equation [3, 16, 17, 22, 25, 45, 54, 56, 57, 59, 60, 66] with their exact solitary wave solutions and dynamic behaviors of interaction solutions of shallow water wave equation [7, 68] was extensively studied by many researchers. The (\(1+1\)) dimension of Boussinesq equation [32] solved by Wronskian formulation of the linear conditions to determined rational, Positons and complexiton solutions are explicitly. Lump and interaction solutions are computed for linear [29] and nonlinear partial differential equations [30, 31]. Furthermore, Cauchy problem of integrable Boussinesq and many other equations can be solved via the Riemann–Hilbert approach [1]. Recently, Zhu [71] introduced new generalized (\(2+1\)) dimensional Boussinesq equation to obtain line-soliton and rational solutions by Dbar-problem method. Cao et al. [8], Wang et al. [51] obtained exact solutions of extended (\(2+1\)) dimensional Boussinesq equation.

Here we consider the generalized (\(2+1\)) dimensional Boussinesq equation,

$$\begin{aligned} u_{tt}-4u_{yt}+4u_{yy}-3u_{xy}+\frac{3}{4}u_{xxxx}+\frac{3}{2}u^2_{xx}=0. \end{aligned}$$
(1)

Based on symbolic computation [18, 28, 43], we derive bilinear form and obtain single soliton, multi-soliton solutions by simplified Hirota method. In addition, we also derive rogue wave, periodic wave, multi-travelling wave and singular periodic wave solutions [9, 21, 27, 39, 69] by Extended Homoclinic Test Approach(EHTA) method via bilinear formalism.

The organizations of this paper is as follows. In “Multi-soliton Solution and Exact Solutions of Generalized (\(2+1\)) Dimensional Boussinesq Equation” section we derive the bilinear form to find single and multi-soliton solution. Further, the rogue wave, multi-travelling wave and singular periodic wave solutions are presented in “Soliton, Rogue Wave, Periodic and Singular Periodic Wave Solutions by EHTA” section. Finally, the results are discussed and summarised.

Multi-soliton Solution and Exact Solutions of Generalized (\(2+1\)) Dimensional Boussinesq Equation

The Hirota bilinear method [13, 20, 34, 44, 54,55,56,57, 67] is being studied by many researchers. We use this method to examine single and multi-soliton solutions of the generalized (\(2+1\)) dimensional Boussinesq equation by the dependent variable transformation

$$\begin{aligned} u(x,y,t)=3(\log (f))_{xx}, \end{aligned}$$
(2)

where f is a real function with respect to variables x, y and t. The dependent variable transformation (2) convert Eq. (1) into bilinear form as follows:

$$\begin{aligned} (4D^2_t-16D_yD_t+16D^2_x-12D_xD_y+3D^4_x)f\cdot f=0, \end{aligned}$$
(3)

where \(D_x\), \(D_y\), \(D_t\), \(D_xD_y\) and \(D_yD_t\) are all the Hirota bilinear derivative operator defined by

$$\begin{aligned} \begin{aligned} D^l_xD^m_yD^n_t(f\cdot g)&= \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^l \left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\right) ^m \\&\quad \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\right) ^n f(x,y,t)g(x,y,t)\mid _{x'=x,y'=y,t'=t}. \end{aligned} \end{aligned}$$
(4)

In order to determine the dispersion relation of Eq. (1), we assume that

$$\begin{aligned} u(x,y,t)=e^{\theta _i},\quad \theta _i=k_ix+l_iy-c_it,\quad i=1,2,\dots , \end{aligned}$$
(5)

where \(k_i\) and \(l_i\) are the real constants, substitute Eq. (5) into Eq. (1), we obtain the dispersion relation

$$\begin{aligned} c_i=-\frac{1}{2} \left( \sqrt{3} \sqrt{4 k_i l_i-k^4_i}+4 l_i\right) , \end{aligned}$$
(6)

where the auxiliary function f(x, y, t) for the one-soliton solution, we substitute

$$\begin{aligned}&f(x,y,t)= 1+\exp (\theta _1), \nonumber \\ \end{aligned}$$
(7)

where \(\theta _1=k_1 x+l_1 y+\frac{1}{2}(\sqrt{3} \sqrt{4 k_1 l_1-k^4_1}+4 l_1)t\), into Eq. (2) to obtain

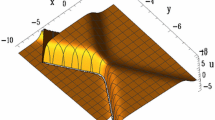
$$\begin{aligned} u(x,y,t)=\frac{3 k_1^2 \exp \left( k_1 x+l_1 y+\frac{1}{2} \left( \sqrt{3} \sqrt{4 k_1 l_1-k^4_1}+4 l_1 \right) t\right) }{\left( 1+\exp \left( k_1 x+l_1 y+\frac{1}{2} \left( \sqrt{3} \sqrt{4 k_1 l_1-k^4_1}+4 l_1 \right) t\right) \right) ^2}. \end{aligned}$$
(8)

Figure 1 shows graphically represent single line soliton and stationary hump soliton solution of u(x, y, t).

Fig. 1
figure 1

a–c represent 3D, contour, 2D plots for soliton solution of u(x, y, t) and d represents 3D plot for single stationary hump soliton solution of u(x, y, t)

Full size image

To determine the two soliton solution, we use the following auxiliary function f(x, y, t) of the form

$$\begin{aligned} f(x,y,t)=1+\exp (\theta _1)+\exp (\theta _2)+a_{12}\exp (\theta _1+\theta _2), \end{aligned}$$
(9)

where

$$\begin{aligned} \theta _i=k_ix+l_iy+\frac{1}{2} \left( \sqrt{3} \sqrt{4 k_i l_i-k^4_i}+4 l_i\right) t,\quad i=1,2, \end{aligned}$$

and the phase shift parameter is

$$\begin{aligned} a_{12}= \frac{2 k_1 \left( k_2^3-l_2\right) -2 k_2 l_1+2 k_2 k_1^3-3 k_2^2 k_1^2+\sqrt{4 k_1 l_1-k_1^4} \sqrt{4 k_2 l_2 -k_2^4}}{2 k_1 \left( k_2^3-l_2\right) -2 k_2 l_1+2 k_2 k_1^3+3 k_2^2 k_1^2+\sqrt{4 k_1 l_1-k_1^4} \sqrt{4 k_2 l_2-k_2^4}}. \end{aligned}$$
(10)

Substitute Eq. (9) with \(a_{12}\) and \(\theta _i (i=1,2)\) into Eq. (2), we obtain two-soliton solution explicitly. In the following part we present different characteristics of two-soliton solutions.

We formally choose the suitable values of the parameters \(k_1, k_2, l_1\) and \(l_2\) in Eq.(10), and observed the variety of dynamical behaviours of nonlinear waves.

Fig. 2
figure 2

a, b represent 3D and contour plots of two parallel soliton solution of u(x, y, t) with corresponding parameter values \(y=-7.7\), \(k_1=-1.34\), \(k_2=-1.257\), \(l_1=-0.62\) and \(l_2=-0.5\)

Full size image
Fig. 3
figure 3

a, b represent 3D and contour plots for collision of two-soliton solution of u(x, y, t) with corresponding parameter values \(y=0.5\), \(k_1=-0.55\), \(k_2=-0.4\), \(l_1=-0.1\) and \(l_2=-1\)

Full size image
Fig. 4
figure 4

a, b represent 3D, contour plots for elastic interaction of two-soliton solution of u(x, y, t) with corresponding parameter values \(y=-2\), \(k_1=-1\), \(k_2=-1.5\), \(l_1=-1\) and \(l_2=-2.5\) and c represents 3D plot for asymmetric collisions between two solitons with corresponding parameter values \(y=-4\), \(k_1=-1.3\), \(k_2=-1\), \(l_1=-0.6\) and \(l_2=-0.4\)

Full size image
Fig. 5
figure 5

2D plots for interaction of two-soliton solution of u(x, y, t) with corresponding parameter values \(k_1=-1\), \(k_2=-1.5\), \(l_1=-1\) and \(l_2=-2.5\)

Full size image

Figure 2 shows two parallel line soliton with out collision for the suitable parameter values. Figures 3 and 4 describes the interaction and elastic collision of the two solutions. The suitable parameter values of Fig. 3 present the elastic collision of two-solitons. Figure 4 describes the regular solitonic elastic interaction with suitable parameter values. Figure 5 shows the 2D represent of Fig. 4 for interaction, overlapping and retain their shapes, velocity of large amplitude soliton pulse elastically collied with small amplitude soliton pulse.

Soliton, Rogue Wave, Periodic and Singular Periodic Wave Solutions by EHTA

The extended homoclinic test approach method is being studied by many researchers, seen references [15, 47, 70] therein. Now, we assume the solution of Eq. (1) as

$$\begin{aligned} f(x,y,t)=\exp (-\xi _1)+\delta _1 \cos (\xi _2)+\delta _2\exp (\xi _1), \end{aligned}$$
(11)

where \(\xi _i=a_ix+b_iy+d_it\), \(a_i,b_i,d_i\) and \(\delta _i\), (\(i=1,2\)) are unknown constants to be determined later. Substituting the expression Eq. (11) into Eq. (3) and equating all the coefficients of \(\sin (\xi _2)\), \(\cos (\xi _2)\) and \(e^{j\xi _1}\), \(j=-1,0,1\) to zero, we can obtain the following set of algebraic equation for \(a_i, b_i, d_i\) and \(\delta _i\), (\(i=1, 2\)),

$$\begin{aligned}&3 a_2 b_2+3 a_2^4-\left( d_2-2 b_2\right) {}^2=0, \end{aligned}$$
(12)
$$\begin{aligned}&-\,48 a_1 b_1+48 a_1^4-64 b_1 d_1+64 b_1^2+16 d_1^2=0, \end{aligned}$$
(13)
$$\begin{aligned}&3 a_1 \left( a_2^3+b_2\right) +3 a_2 b_1-3 a_2 a_1^3-2 \left( 2 b_1-d_1\right) \left( 2 b_2-d_2\right) =0, \end{aligned}$$
(14)
$$\begin{aligned}&\left. \begin{array}{l} -\,12 a_1 b_1+12 a_2 b_2+3 a_1^4-18 a_2^2 a_1^2+3 a_2^4\\ +\,4 \left( -4 b_1 d_1+4 b_2 d_2+4 b_1^2-4 b_2^2+d_1^2-d_2^2\right) \end{array}\right\} =0. \end{aligned}$$
(15)

Solving the system of Eqs. (12–15) with the aid of symbolic computation such as Mathematica, we obtain the following sets of solutions.

$$\begin{aligned}&\text {set 1:}\quad a_2= i a_1,\;\; b_1= a_1^3,\;\; b_2= i a_1^3,\;\; d_1= 2 a_1^3,\;\; d_2= 2 i a_1^3. \end{aligned}$$
(16)
$$\begin{aligned}&\text {set 2:}\quad a_2= -i a_1,\;\; b_1= a_1^3,\;\; b_2= -i a_1^3,\;\; d_1= 2 a_1^3,\;\; d_2= -2 i a_1^3. \end{aligned}$$
(17)
$$\begin{aligned}&\text {set 3:}\quad a_2= i a_1,\;\; b_1= -i b_2,\;\; d_1= \sqrt{3} \sqrt{-a_1 \left( a_1^3+i b_2\right) }-2 i b_2, \nonumber \\&\qquad \qquad d_2= \frac{3 a_1 b_2+2 \sqrt{3} b_2 \sqrt{-a_1 \left( a_1^3+i b_2\right) }-3 i a_1^4}{\sqrt{3} \sqrt{-a_1 \left( a_1^3+i b_2\right) }}. \end{aligned}$$
(18)
$$\begin{aligned}&\text {set 4:}\quad a_2= i a_1,\;\; b_1= -i b_2,\;\; d_1= -\sqrt{3} \sqrt{-a_1 \left( a_1^3+i b_2\right) }-2 i b_2,\nonumber \\&\qquad \qquad d_2= \frac{-\sqrt{3} a_1 b_2+2 b_2 \sqrt{-a_1\left( a_1^3+i b_2\right) }+i \sqrt{3} a_1^4}{\sqrt{-a_1 \left( a_1^3+i b_2\right) }}. \end{aligned}$$
(19)
$$\begin{aligned}&\text {set 5:}\quad a_2= -i a_1,\;\; b_1= i b_2,\;\; d_1= 2 i b_2-\sqrt{-3 a_1^4+3 i a_1 b_2},\nonumber \\&\qquad \qquad d_2= -\frac{\sqrt{3} a_1 b_2-2 b_2 \sqrt{-a_1^4+i a_1 b_2}+i \sqrt{3}a_1^4}{\sqrt{-a_1^4+i a_1 b_2}}. \end{aligned}$$
(20)
$$\begin{aligned}&\text {set 6:}\quad a_2= -i a_1,\;\; b_1= i b_2,\;\; d_1= \sqrt{-3 a_1^4+3 i a_1 b_2}+2 i b_2, \nonumber \\&\qquad \qquad d_2= \frac{3 a_1 b_2+2 b_2 \sqrt{-3 a_1^4+3 i a_1 b_2}+3 i a_1^4}{\sqrt{-3a_1^4+3 i a_1 b_2}}. \end{aligned}$$
(21)
$$\begin{aligned}&\text {set 7:} \quad a_1= -i a_2,\;\; b_2= i b_1,\;\; d_1= 2 b_1+i \sqrt{3} \sqrt{a_2^4+i a_2 b_1}, \nonumber \\&\qquad \qquad d_2= 2 i b_1-\sqrt{3} \sqrt{a_2^4+i a_2 b_1}. \end{aligned}$$
(22)
$$\begin{aligned}&\text {set 8:}\quad a_1= -i a_2,\;\; b_2= i b_1,\;\; d_1= 2 b_1-i \sqrt{3} \sqrt{a_2^4+i a_2 b_1},\nonumber \\&\qquad \qquad d_2= \sqrt{3} \sqrt{a_2^4+i a_2 b_1}+2 i b_1. \end{aligned}$$
(23)
$$\begin{aligned}&\text {set 9:}\quad a_1= i a_2,\;\; b_2= -i b_1,\;\; d_1= 2 b_1-i \sqrt{3} \sqrt{a_2^4-i a_2 b_1}, \nonumber \\&\qquad \qquad d_2= -\sqrt{3} \sqrt{a_2^4-i a_2 b_1}-2 i b_1. \end{aligned}$$
(24)
$$\begin{aligned}&\text {set 10:}\quad a_1= i a_2,\;\; b_2= -i b_1,\;\; d_1= 2 b_1+i \sqrt{3} \sqrt{a_2^4-i a_2 b_1}, \nonumber \\&\qquad \qquad d_2= \sqrt{3} \sqrt{a_2^4-i a_2 b_1}-2 i b_1. \end{aligned}$$
(25)
$$\begin{aligned}&\text {set 11:}\quad a_1= -i a_2,\;\; b_2= i b_1,\;\; d_1= \frac{-3 a_2 b_1+2 \sqrt{3} b_1 \sqrt{a_2^4+i a_2 b_1}+3 i a_2^4}{\sqrt{3} \sqrt{a_2^4+i a_2 b_1}}, \nonumber \\&\qquad \qquad d_2= 2 i b_1-\sqrt{3} \sqrt{a_2^4+i a_2 b_1}. \end{aligned}$$
(26)
$$\begin{aligned}&\text {set 12:}\quad a_1= -i a_2,\;\; b_2= i b_1,\;\; d_1= \frac{3 a_2 b_1+2 \sqrt{3} b_1 \sqrt{a_2^4+i a_2 b_1}-3 i a_2^4}{\sqrt{3} \sqrt{a_2^4+i a_2 b_1}},\nonumber \\&\qquad \qquad d_2= \sqrt{3}\sqrt{a_2^4+i a_2 b_1}+2 i b_1. \end{aligned}$$
(27)
$$\begin{aligned}&\text {set 13:}\quad a_1= i a_2,\;\; b_2= -i b_1,\;\; d_1= \frac{-3 a_2 b_1+2 \sqrt{3} b_1 \sqrt{a_2^4-i a_2 b_1}-3 i a_2^4}{\sqrt{3} \sqrt{a_2^4-i a_2 b_1}}, \nonumber \\&\qquad \qquad d_2= -\sqrt{3}\sqrt{a_2^4-i a_2 b_1}-2 i b_1. \end{aligned}$$
(28)
$$\begin{aligned}&\text {set 14:}\quad a_1= i a_2,\;\; b_2= -i b_1,\;\; d_1= \frac{-3 a_2 b_1+2 \sqrt{3} b_1 \sqrt{a_2^4-i a_2 b_1}-3 i a_2^4}{\sqrt{3} \sqrt{a_2^4-i a_2 b_1}}, \nonumber \\&\qquad \qquad d_2= -\sqrt{3}\sqrt{a_2^4-i a_2 b_1}-2 i b_1. \end{aligned}$$
(29)

Substituting Eqs. (16–29) into (2), with Eq. (11), then we obtain the following sets of solutions

Case 1

$$\begin{aligned} \begin{aligned} u(x,y,t)&=3 \biggl (\frac{a_1^2 \delta _2 e^{\xi _1}+a_1^2 \delta _1 \cosh \left( \xi _2\right) +a_1^2 e^{-\xi _1}}{\delta _2 e^{\xi _1}+\delta _1 \cosh \left( \xi _2\right) +e^{-\xi _1}}\\&\quad -\,\frac{\left( a_1 \delta _2 e^{\xi _1}+a_1 \delta _1 \sinh \left( \xi _2\right) +a_1 \left( -e^{-\xi _1}\right) \right) {}^2}{\left( \delta _2 e^{\xi _1}+\delta _1 \cosh \left( \xi _2\right) +e^{-\xi _1}\right) {}^2}\biggr ). \end{aligned} \end{aligned}$$
(30)

If \(\delta _2>0\), then we obtain the exact solution

$$\begin{aligned} \begin{aligned} u(x,y,t)&=3 \biggl (\frac{a_1^2 \delta _1 \cosh \left( \xi _2\right) +2 a_1^2 \sqrt{\delta _2} \cosh \left( \xi _1-\theta \right) }{\delta _1 \cosh \left( \xi _2\right) +2 \sqrt{\delta _2} \cosh \left( \xi _1-\theta \right) }\\&\quad -\,\frac{\left( a_1 \delta _1 \sinh \left( \xi _2\right) -2 a_1 \sqrt{\delta _2} \sinh \left( \xi _1-\theta \right) \right) {}^2}{\left( \delta _1 \cosh \left( \xi _2\right) +2\sqrt{\delta _2} \cosh \left( \xi _1-\theta \right) \right) {}^2}\biggr ), \end{aligned} \end{aligned}$$
(31)

for \(\theta =\frac{1}{2}\log \left( \delta _2\right) \).

If \(\delta _2<0\), then we obtain the exact solution

$$\begin{aligned} \begin{aligned} u(x,y,t)&=3 \biggl (\frac{a_1^2 \delta _1 \cosh \left( \xi _2\right) +2 a_1^2 \sqrt{-\delta _2} \cosh \left( \xi _1-\theta \right) }{\delta _1 \cosh \left( \xi _2\right) +2 \sqrt{-\delta _2} \cosh \left( \xi _1-\theta \right) }\\&\quad -\,\frac{\left( a_1 \delta _1 \sinh \left( \xi _2\right) -2 a_1 \sqrt{-\delta _2} \sinh \left( \xi _1-\theta \right) \right) {}^2}{\left( \delta _1 \cosh \left( \xi _2\right) +2\sqrt{-\delta _2} \cosh \left( \xi _1-\theta \right) \right) {}^2}\biggr ), \end{aligned} \end{aligned}$$
(32)

for \(\theta =\frac{1}{2}\log \left( -\delta _2\right) \).

If the following \(\xi _1\), \(\xi _2\) indicate the exact solutions of Eq. (1)

$$\begin{aligned} \begin{aligned} \xi _1&=a_1 x+a_1^3 y+2 a_1^3 t,\\ \xi _2&=a_1 x+a_1^3 y+2 a_1^3 t. \end{aligned} \end{aligned}$$
(33)

Substitute (33) into (30–32), we get solution of \(u_1(x,y,t)\) and \(u_2(x,y,t)\). \(u_2(x,y,t)\) is same as \(u_1(x,y,t)\). Figure 6 depicts graphical representation of single soliton solution and singular periodic wave solutions by choosing the suitable parameter values of \(u_1\).

Fig. 6
figure 6

a represents soliton solution of \(u_1(x,y,t)\), b–d represent singular periodic wave solutions of \(u_1(x,y,t)\)

Full size image
$$\begin{aligned} \begin{aligned} \xi _1&=a_1 x-i b_2 y+\left( \sqrt{3} \sqrt{-a_1^4-i a_1 b_2}-2 i b_2 \right) t,\\ \xi _2&=a_1 x-i b_2y-\frac{i \left( 3 a_1 b_2+2 \sqrt{3} b_2 \sqrt{-a_1 \left( a_1^3+i b_2\right) }-3 i a_1^4\right) }{\sqrt{3} \sqrt{-a_1 \left( a_1^3+i b_2\right) }}t. \end{aligned} \end{aligned}$$
(34)

Substitute (34) into (30–32), we get solution of \(u_3(x,y,t)\).

$$\begin{aligned} \begin{aligned} \xi _1&=a_1 x-i b_2 y-\left( \sqrt{3} \sqrt{-a_1^4-i a_1 b_2}+2 i b_2\right) t,\\ \xi _2&=a_1 x-i b_2 y-\frac{i \left( -\sqrt{3} a_1 b_2+2 b_2 \sqrt{-a_1 \left( a_1^3+i b_2\right) }+i \sqrt{3} a_1^4\right) }{\sqrt{-a_1 \left( a_1^3+i b_2\right) }}t. \end{aligned} \end{aligned}$$
(35)

Substitute (35) into (30–32), we get solution of \(u_4(x,y,t)\).

$$\begin{aligned} \begin{aligned} \xi _1&=a_1 x+i b_2 y+\left( -\sqrt{-3 a_1^4+3 i a_1 b_2}+2 i b_2\right) t,\\ \xi _2&=a_1 x+i b_2 y-\frac{i \left( \sqrt{3} a_1 b_2-2 b_2 \sqrt{-a_1^4+i a_1 b_2}+i \sqrt{3} a_1^4\right) }{\sqrt{-a_1^4+i a_1 b_2}}t. \end{aligned} \end{aligned}$$
(36)

Substitute (36) into (30–32), we get solution of \(u_5(x,y,t)\).

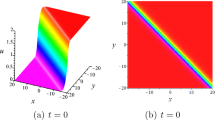
$$\begin{aligned} \begin{aligned} \xi _1&=a_1 x+i b_2 y+\left( \sqrt{-3 a_1^4+3 i a_1 b_2}+2 i b_2\right) t,\\ \xi _2&=a_1 x+i b_2 y+\frac{i \left( 3 a_1 b_2+2 b_2 \sqrt{-3 a_1^4+3 i a_1 b_2}+3 i a_1^4\right) }{\sqrt{-3 a_1^4+3 i a_1 b_2}}t. \end{aligned} \end{aligned}$$
(37)

Substitute (37) into (30–32), we get solution of \(u_6(x,y,t)\). The rogue wave solution depicted in Fig. 7, by the suitable parameter values of \(u_6\).

Fig. 7
figure 7

a–c represent 3D, contour and 2D plots for rogue wave solutions of \(u_6(x,y,t)\) with corresponding parameter values \(y=-2\), \(a_1=0.15\), \(b_2=-0.4\), \(\delta _1=1\), \(\delta _2=0.12\) and \(t=-1.5\)

Full size image

Case 2

$$\begin{aligned} u(x,y,t)&=3 \biggl (\frac{-a_2^2 \delta _2 e^{-\xi _1}-a_2^2 \delta _1 \cos \left( \xi _2\right) -a_2^2 e^{\xi _1}}{\delta _2 e^{-\xi _1}+\delta _1 \cos \left( \xi _2\right) +e^{\xi _1}}\nonumber \\&\quad -\,\frac{\left( -ia_2 \delta _2 e^{-\xi _1}-a_2 \delta _1 \sin \left( \xi _2\right) +ia_2 e^{\xi _1}\right) {}^2}{\left( \delta _2 e^{-\xi _1}+\delta _1 \cos \left( \xi _2\right) +e^{\xi _1}\right) {}^2}\biggr ). \end{aligned}$$
(38)
$$\begin{aligned} u(x,y,t)&=3 \biggl (\frac{-a_2^2 \delta _2 e^{\xi _1}-a_2^2 \delta _1 \cos \left( \xi _2\right) -a_2^2 e^{-\xi _1}}{\delta _2 e^{\xi _1}+\delta _1 \cos \left( \xi _2\right) +e^{-\xi _1}}\nonumber \\&\quad -\,\frac{\left( ia_2 \delta _2 e^{\xi _1}-a_2 \delta _1 \sin \left( \xi _2\right) -ia_2 e^{-\xi _1}\right) {}^2}{\left( \delta _2 e^{\xi _1}+\delta _1 \cos \left( \xi _2\right) +e^{-\xi _1}\right) {}^2}\biggr ). \end{aligned}$$
(39)

If \(\delta _2>0\), then we obtain the exact solution

$$\begin{aligned} \begin{aligned} u(x,y,t)&=3 \biggl (\frac{-a_2^2 \delta _1 \cos \left( \xi _2\right) -2 a_2^2 \sqrt{\delta _2} \cos \left( \xi _1-\theta \right) }{\delta _1 \cos \left( \xi _2\right) +2 \sqrt{\delta _2} \cos \left( \xi _1-\theta \right) }\\&\quad -\,\frac{\left( -a_2 \delta _1 \sin \left( \xi _2\right) -2 a_2 \sqrt{\delta _2} \sin \left( \xi _1-\theta \right) \right) {}^2}{\left( \delta _1 \cos \left( \xi _2\right) +2\sqrt{\delta _2} \cos \left( \xi _1-\theta \right) \right) {}^2}\biggr ), \end{aligned} \end{aligned}$$
(40)

for \(\theta =\frac{1}{2}\log \left( \delta _2\right) \).

If \(\delta _2<0\), then we obtain the exact solution

$$\begin{aligned} \begin{aligned} u(x,y,t)&=3 \biggl (\frac{-a_2^2 \delta _1 \cos \left( \xi _2\right) -2 a_2^2 \sqrt{-\delta _2} \cos \left( \xi _1-\theta \right) }{\delta _1 \cos \left( \xi _2\right) +2 \sqrt{-\delta _2} \cos \left( \xi _1-\theta \right) }\\&\quad -\,\frac{\left( -a_2 \delta _1 \sin \left( \xi _2\right) -2 a_2 \sqrt{-\delta _2} \sin \left( \xi _1-\theta \right) \right) {}^2}{\left( \delta _1 \cos \left( \xi _2\right) +2\sqrt{-\delta _2} \cos \left( \xi _1-\theta \right) \right) {}^2}\biggr ), \end{aligned} \end{aligned}$$
(41)

for \(\theta =\frac{1}{2}\log \left( -\delta _2\right) \).

If the following \(\xi _1\), \(\xi _2\) indicate the exact solutions of Eq. (1)

$$\begin{aligned} \begin{aligned} \xi _1&=a_2 x+i b_1 y+ \left( 2 i b_1-\sqrt{3} \sqrt{a_2^4+i a_2 b_1}\right) t,\\ \xi _2&=a_2 x+i b_1 y+ \left( 2 i b_1-\sqrt{3} \sqrt{a_2^4+i a_2 b_1}\right) t. \end{aligned} \end{aligned}$$
(42)

Substitute (42) into (38, 40 and 41), we get solution of \(u_7(x,y,t)\).

Fig. 8
figure 8

a–c represent 3D, contour and 2D plots for periodic travelling wave solution of \(u_7(x,y,t)\) with corresponding parameter values \(y=1\), \(a_2=-1.5\), \(b_1=-0.01\), \(\delta _1=-0.25\), \(\delta _2=-0.6\) and \(t=-1.5\)

Full size image

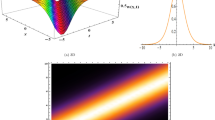
As shown in Fig. 8, the periodic wave solutions for choosing suitable parameter values of \(u_7\). When the parameter values of \(a_2\) decreased the periodic wave profile increased. If \(a_2\) increased then the wave profile decreased.

$$\begin{aligned} \begin{aligned} \xi _1&=a_2 x+i b_1 y+\left( \sqrt{3} \sqrt{a_2^4+i a_2 b_1}+2 i b_1\right) t,\\ \xi _2&=a_2 x+i b_1 y+ \left( \sqrt{3} \sqrt{a_2^4+i a_2 b_1}+2 i b_1\right) t. \end{aligned} \end{aligned}$$
(43)

Substitute (43) into (38, 40 and 41), we get solution of \(u_8(x,y,t)\) (see Fig. 9).

Fig. 9
figure 9

a, b represent 3D and 2D plots for second order periodic wave solutions of \(u_8(x,y,t)\) with corresponding parameter values \(y=-5\), \(a_2=-0.3\), \(b_1=0\), \(\delta _1=-2.1\), \(\delta _2=-1.5\). and \(y=-5\), \(a_2=-5.5\), \(b_1=0\), \(\delta _1=-2.1\), \(\delta _2=-1.5\) and \(t=-2\)

Full size image
$$\begin{aligned} \begin{aligned} \xi _1&=a_2 x-i b_1 y-\left( \sqrt{3} \sqrt{a_2^4-i a_2 b_1}+2 i b_1\right) t,\\ \xi _2&=a_2 x-i b_1 y- \left( \sqrt{3} \sqrt{a_2^4-i a_2 b_1}+2 i b_1\right) t. \end{aligned} \end{aligned}$$
(44)

Substitute (44) into (39, 40 and 41), we get solution of \(u_9(x,y,t)\).

$$\begin{aligned} \begin{aligned} \xi _1&=a_2 x-i b_1 y+\left( \sqrt{3} \sqrt{a_2^4-i a_2 b_1}-2 i b_1\right) t,\\ \xi _2&=a_2 x-i b_1 y+\left( \sqrt{3} \sqrt{a_2^4-i a_2 b_1}-2 i b_1\right) t. \end{aligned} \end{aligned}$$
(45)

Substitute (45) into (39, 40 and 41), we get solution of \(u_{10}(x,y,t)\).

$$\begin{aligned} \begin{aligned} \xi _1&=a_2 x+i b_1 y+\left( -\frac{\sqrt{3} a_2^4}{\sqrt{a_2^4+i a_2 b_1}}-\frac{i \sqrt{3} a_2 b_1}{\sqrt{a_2^4+i a_2 b_1}}+2 i b_1 \right) t,\\ \xi _2&=a_2 x+i b_1 y+ \left( 2 i b_1-\sqrt{3} \sqrt{a_2^4+i a_2 b_1}\right) t. \end{aligned} \end{aligned}$$
(46)

Substitute (46) into (38, 40 and 41), we get solution of \(u_{11}(x,y,t)\).

$$\begin{aligned} \begin{aligned} \xi _1&=a_2 x+i b_1 y+\left( \frac{\sqrt{3} a_2^4 }{\sqrt{a_2^4+i a_2 b_1}}+\frac{i \sqrt{3} a_2 b_1 }{\sqrt{a_2^4+i a_2 b_1}}+2 i b_1 \right) t,\\ \xi _2&=a_2 x+i b_1 y+ \left( \sqrt{3} \sqrt{a_2^4+i a_2 b_1}+2 i b_1\right) t. \end{aligned} \end{aligned}$$
(47)

Substitute (47) into (38, 40 and 41), we get solution of \(u_{12}(x,y,t)\).

$$\begin{aligned} \begin{aligned} \xi _1&=a_2 x-i b_1 y+\left( -\frac{\sqrt{3} a_2^4 }{\sqrt{a_2^4-i a_2 b_1}}+\frac{i \sqrt{3} a_2 b_1 }{\sqrt{a_2^4-i a_2 b_1}}-2 i b_1\right) t,\\ \xi _2&=a_2 x-i b_1 y-\left( \sqrt{3} \sqrt{a_2^4-i a_2 b_1}+2 i b_1\right) t. \end{aligned} \end{aligned}$$
(48)

Substitute (48) into (39, 40 and 41), we get solution of \(u_{13}(x,y,t)\).

$$\begin{aligned} \begin{aligned} \xi _1&=a_2 x-i b_1 y+\left( -\frac{\sqrt{3} a_2^4 }{\sqrt{a_2^4-i a_2 b_1}}+\frac{i \sqrt{3} a_2 b_1 }{\sqrt{a_2^4-i a_2 b_1}}-2 i b_1\right) t,\\ \xi _2&=a_2 x-i b_1 y- \left( \sqrt{3} \sqrt{a_2^4-i a_2 b_1}+2 i b_1\right) t. \end{aligned} \end{aligned}$$
(49)

Substitute (49) into (39, 40 and 41), we get solution of \(u_{14}(x,y,t)\).

The extended homoclinic test approach method enhanced enrich the variety of novel solutions. \(u_1\) and \(u_2\) are gives the soliton, singular periodic wave and travelling wave solutions. From \(u_3\) to \(u_6\) are gives rogue wave and exact solitary wave solutions. From \(u_7\) to \(u_{14}\) are gives the periodic wave and travelling wave solutions.

Conclusion

In this paper, we have studied generalized (\(2+1\)) dimensional Boussinesq equation by simplified Hirota method and extended homoclinic test approach method. Using the symbolic computation we have derived the bilinear form of Eq. (1). Based on the bilinear form we obtain one, two soliton solutions and interaction as well as collision of two solitons by the simplified Hirota bilinear method. We demonstrated these solutions by graphically which means of 2D, 3D and Contour plots. Equation (8) graphically represent single line soliton and stationary hump soliton (See Fig. 1). The dynamical behaviour of two soliton solutions have several physical phenomenon such as parallel of two line soliton without collision, interaction and collision of two soliton solutions. These are plotted with suitable parameter values are displayed in Figs. 2, 3, 4 and 5 respectively.

The single soliton, rogue wave, multi-travelling wave, periodic and singular periodic wave solutions employed by extended homoclinic test approach method. Case-I, presents single soliton, singular soliton and Rogue wave solutions analytically. These solutions are represented graphically in Figs. 6 and 7. Case-II, we analytically derived multi-travelling, periodic and second order periodic wave solutions. Figure 8 shows the multi-travelling wave solutions of wave profile increased when depending on the suitable parameter values of \(a_2\) decreased and Fig. 9 shows the second order periodic wave profile for suitable parameter values of the solution.

These two powerful methods to seek exact solitary wave solutions and some respective figures are plotted to describe the exact solitary wave solutions.