Dynamics of transitions from anti-phase to multiple in-phase synchronizations in inhibitory coupled bursting neurons

Abstract

Transition from anti-phase to in-phase synchronizations in inhibitory coupled bursting neurons is very important for locomotor rhythms of animals. Here, multiple in-phase (complete), anti-phase, and phase synchronous bursting patterns are simulated in inhibitory coupled map-based model neurons with bursting patterns, and synchronization transitions between these patterns are simulated in a two-dimensional parameter space of the coupling strength and time delay. Time delay-induced transition from anti-phase to in-phase synchronous bursting behaviors matches those observed in a biological experiment on the inhibitory coupled neurons in the stomatogastric ganglion of lobster. Furthermore, bursting patterns of the in-phase (complete) synchronous behaviors can be well interpreted with the dynamic responses of an isolated single neuron to a negative square current whose action time, duration, and strength are similar to those of the inhibitory coupling current modulated by the coupling strength and time delay. The burst of the synchronous behaviors manifests the same pattern as the square negative current-induced burst of the isolated single neuron, which is acquired with the fast–slow variable dissection method. The results not only present novel nonlinear phenomenon of the time delay-induced multiple synchronous behaviors and synchronization transitions, but also provide a reasonable interpretation with the different dynamic responses of map-based bursting model neuron to an external inhibitory stimulus applied at different phases.

1 Introduction

Synchronous behaviors [1] widely exist in the nervous systems and play important roles in the achievement of biological functions [2,3,4,5,6,7,8]. For example, synchronous behaviors are observed in the human cortex areas, the mammalian cortex, the thalamus, the cardiac tissues, as well as the lobster stomatogastric ganglion [2,3,4,5, 9, 10]. Synapse, which is a connection between neurons, can transmit information between neurons [11,12,13]. Electrical and excitatory chemical synapses are always suggested to enhance synchronous degree, and inhibitory chemical synapses are often thought to suppress the electronic activity and the synchronous behaviors. In addition to synapse, the dynamics of single neurons also influence the dynamics of synchronous behaviors. Bursting alternates between burst with fast spikes and quiescent state, exhibiting complex oscillatory activity than spiking which only contains fast spikes [14, 15]. Bursting can enhance reliability of synaptic transmission and give effective mechanism for selective communication between neurons [16, 17]. Dynamics of network composed of bursting neurons have attracted much attention in recent years [18,19,20,21,22,23,24,25,26,27,28,29,30].

Recently, inhibitory chemical synapses have been identified not suppress but enhance synchronization in some physiological conditions [31,32,33,34], for example, synchronous Gamma oscillations relying exclusive on inhibitory synapse [11, 13, 32], which is different from the traditional viewpoint that inhibitory synapses often help to form the anti-phase synchronous behaviors. Therefore, inhibitory chemical synapses have attracted much attention in recent years. The synchronization in inhibitory coupled neuronal networks has been studied in theoretical models, especially for the half-center oscillator [35], which is a pair of spiking or bursting neurons with reciprocally inhibitory couplings. As is well known, a half-center oscillator often exhibits alternating or anti-phase patterns if the synapse is fast [36,37,38,39]. However, in-phase synchronization can also be induced in some conditions such as non-instantaneous and slow decay inhibitory synapses [36,37,38,39,40,41,42] and even if fast reciprocal inhibitory synapses [25, 36, 37]. Furthermore, in-phase synchronization of bursting pattern was observed in the biological experiments on the inhibitory coupled neurons in the stomatogastric ganglion of lobster as the synaptic time constant was changed to a slow level [43]. However, anti-phase synchronization of bursting patterns was observed when the inhibitory synapse was fast [43]. The experimental result shows that transition from anti-phase to in-phase synchronizations was induced by the changes of the inhibitory synapse from fast to slow time constants.

It is well known that time delay exists in the real nervous systems due to the finite information transmission speed and synapse latency [13, 44]. The time delay of chemical synapse is often shorter than several milliseconds. And the conduction delay of axon can reach up to tens of milliseconds [13, 44, 45], which is dependent on the distance between neurons. Information transmission delays are an important factor affecting the synchronization in the nervous systems [44, 46,47,48,49,50,51]. When time delay is considered, complex dynamics including in-phase synchronization, anti-phase synchronization, coexistence of both [52,53,54,55], and phase synchronization are investigated in the inhibitory coupled neurons  [21, 24, 30, 56, 57]. For example, it is found that the coexistence of in-phase and anti-phase synchronizations appears at small time delays [54, 55], and in-phase synchronization at long time delays [54]. Transition from winner-less competition to synchronization induced by time delay is investigated in three coupled bursting neurons [58]. Time delay-induced transition from out-of-phase synchronization to in-phase synchronization via phase-flip bifurcation is simulated in the coupled bursting neurons [59].

Furthermore, multiple synchronization behaviors, each appearing at time delay being odd integer multiples of half-period of the spiking pattern of individual neurons, can be simulated [23]. More complicated, multiple synchronous behaviors appearing at time delays within one period of bursting pattern of a single neuron are simulated in recent investigations on the inhibitory coupled differential model neurons [24, 30]. It can be found that inhibitory coupled bursting neurons display more complex behaviors than spiking neurons. For example, two coupled bursting neurons exhibit coexistence of multiple phase-locking behaviors in addition to anti-phase and in-phase synchronizations [25, 60]. Moreover, the burst patterns of multiple synchronous behaviors can be well interpreted by the dynamics of the coupling or synaptic current and the bursting pattern of the isolated single neuron, which can be acquired by the fast–slow variable dissection method [24, 26, 30].

In the present paper, the transitions from anti-phase synchronization to multiple in-phase synchronization are investigated in inhibitory coupled bursting neurons. The Rulkov map-based model neurons rather than the differential equations-based model neurons and coupling with time delay are considered. Multiple bursting patterns of anti-phase synchronization, in-phase or complete synchronization, and phase synchronization are simulated when time delay and/or coupling strength are chosen as different values. With changing time delay or coupling strength, the transitions between anti-phase and multiple in-phase synchronizations can be simulated. Moreover, different bursting patterns of the in-phase synchronizations which appear at different time delay and coupling strength can also be well interpreted with the dynamic response of a single neuron to an external negative square current, which is applied at suitable phase of the bursting and has suitable strength. The negative square current is identified to play a role like the inhibitory coupling current, which can be acquired by using the fast–slow variable dissection method. The rest of the present paper is organized as follows. The model of neuron and synapse and the synchronization indexes are introduced in Sect. 2. In Sect. 3, main results are displayed. The conclusions are provided in Sect. 4.

2 Theoretical model

2.1 Non-chaotic Rulkov model of a single neuron

Rulkov model is a simply two-dimensional map model with two variables to describe neuronal dynamical behaviors including quiescent state, bursting, and spiking–bursting and is described as follows [61]

$$\begin{aligned} x_{n+1}= & {} f(x_{n}, y_{n}+{I}_{n}) \end{aligned}$$

(1)

$$\begin{aligned} y_{n+1}= & {} y_n-\mu (x_{n}+1)+\mu {\sigma }_{n} \end{aligned}$$

(2)

Here, $x_{n}$ is the fast dynamical variable and $y_{n}$ is the slow dynamical variable. Slow time evolution of $y_{n}$ is due to small value of the parameter $\mu = 0.001$. $I_{n}$ and $\sigma _{n}$ describe the external input or impact to the system. $\sigma _{n}$ can be chosen as a constant value $\sigma$, which is independent on n, and can be used as a control parameter to adjust the dynamic behavior of a single neuron. Note that $I_{n} = I$ is a constant and I can be removed from the equation by $y_{n}$ + $I = y_n^{new}$. For convenience, the symbol $y_{n}$ is used to replace $y_n^{new}$ and the mapping can be rewritten as follows

$$\begin{aligned} x_{n+1}= & {} f(x_{n}, y_{n}) \end{aligned}$$

(3)

$$\begin{aligned} y_{n+1}= & {} y_n-\mu (x_{n}+1)+\mu {\sigma } \end{aligned}$$

(4)

where $\sigma$ is a parameter associated with the dynamical behaviors of a single neuron. The function f(x, y) is discontinuous and its form is as follows

$$\begin{aligned} f(x,y)= & {} {\left\{ \begin{array}{ll}\frac{\alpha }{1-x}+y, &{}\quad x\le 0\\ \alpha +y, &{}\quad 0<{x}<{\alpha +y}\\ -1, &{} \quad {\alpha +y}\le x \end{array}\right. } \end{aligned}$$

(5)

where $\alpha$ is a control parameter of the map. As described in Ref. [61], for $\alpha >4$, the map model neuron manifests dynamical behaviors including quiescent state, bursting, and spiking, which are dependent on $\sigma$. In the present paper, $\alpha = 5$ and $\sigma = -\,0.18$ are chosen to ensure that the map model exhibits a period-4 bursting as representative.

2.2 Model of two inhibitory coupled non-chaotic Rulkov model neurons

The theoretical model of the two identical map-based neurons with reciprocally inhibitory synapses is described as follows

$$\begin{aligned} {\left\{ \begin{array}{ll}x_{i,n+1} = f(x_{i,n}, y_{i,n}+{I}_{i,n}^{\mathrm {syn}})\\ y_{i,n+1} = y_{i,n}-\mu (x_{i,n}+1)+\mu {\sigma } \end{array}\right. } \end{aligned}$$

(6)

Here, $x_{i,n} (i = 1, 2)$ represents the membrane potential of neuron i, and ${I}_{i,n}^{\mathrm {syn}}$ is the synaptic current received by the neuron $i (i = 1, 2)$ and is described as follows [62]

$$\begin{aligned} {I}_{i,n}^{\mathrm {syn}}=-(x_{i,n}-x_{\mathrm {syn}})\sum _{j=1}^2g \xi _{i,j}\varGamma (x_j) \end{aligned}$$

(7)

Here, $i,j = 1, 2$ and $j\not =i$ to avoid the self-coupling. g is the coupling strength. $\xi _{i,j} = 1$ if neuron i is coupled to neuron j and $\xi _{i,j} = 0$ otherwise. $x_{\mathrm {syn}}$ is the reversal potential of the synaptic current. In the present paper, $x_{\mathrm {syn}}= -\,2$ is chosen to ensure that the synapse is inhibitory.

The synaptic function is modeled by the sigmoidal function and is described as follows

$$\begin{aligned} \varGamma (x_j)=\frac{1}{1+\exp (-\lambda [x_{j,n-\tau }-\varTheta _{s}])} \end{aligned}$$

(8)

Here, $\varTheta _{s}$ is a synaptic threshold, $\lambda$ represents a constant rate for the onset of inhibition of the synapse, and $\tau$ is the time delay between two neurons. In the present paper, $\varTheta _{s} = -\,1$ and $\lambda = 30$.

2.3 The synchronization indexes

To be compared with the previous investigations of synchronization dynamics [23, 24, 30], the cross-correlation coefficient and the burst phase difference are employed in the present paper.

The cross-correlation coefficient $\rho$ of the membrane potential of the two coupled neurons is introduced as follows

$$\begin{aligned} \rho =\frac{\sum _{n=1}^N[(x_{1,n}-\langle x_{1,n} \rangle )(x_{2,n}-\langle x_{2,n} \rangle )]}{\sqrt{\sum _{n=1}^N(x_{1,n}-\langle x_{1,n} \rangle )^2(x_{2,n}-\langle x_{2,n} \rangle )^2}} \end{aligned}$$

(9)

Here, $\langle \rangle$ is the average of all N samples of $x_{i,n}(i=1,2, n=1,2,\ldots ,N)$. $N= 2000$ is used in the present paper. The larger cross-correlation coefficient $\rho$ is the higher correlation of the membrane potential between the two neurons will bring, which means the synchronization degree of the two coupled neurons is higher. In the present paper, $\rho = 1$ and $0.95\le \rho <1$ mean the achievement of the complete synchronization and nearly complete synchronization between two neurons, respectively. $\rho <0$ means a negative correlation.

Because coexistence of the synchronization behaviors, which leads to that $\rho$ value of the two coupled neurons, is dependent on the initial values, the probability of $\rho \ge 0.95$ for different initial values, which is labeled as R, is also used to characterize the synchronous dynamics. In the present paper, 100 randomly chosen initial values are used to calculate $\rho$ and R. A large R means that complete synchronization and nearly complete synchronization appear.

To further describe the synchronous degree of bursting patterns, the definition of burst phase has been stated in many previous investigations [21, 59]. For neuron i, the end time of kth burst is labeled as $M_{i,k}(i=1,2, k=1,2,\ldots ,K)$, where K is the number of burst used to calculate the phase of burst and $K=$ 101 is used in the present paper. $M_{i,k+1}-M_{i,k}$ is the period of kth burst of neuron i. The phase of burst at time m of neuron i is defined as follows

$$\begin{aligned} \varphi _i(m)=2\pi (k-1)+2\pi \frac{m-M_{i,k}}{M_{i,k+1}-M_{i,k}} \nonumber \\(M_{i,k}<m<M_{i,k+1},i=1,2) \end{aligned}$$

(10)

The synchronization of bursting patterns can be distinguished by averaging the absolute value of phase difference between neuron 1 and neuron 2 from $k = 2$ to K, which is described as follows

$$\begin{aligned} \Delta \varPhi =\frac{1}{M_{1,K}-M_{1,1}}\sum _{m=M_{1,1}}^{M_{1,K}} {|\varphi _1(m)-\varphi _2(m)|} \end{aligned}$$

(11)

Theoretically, $\Delta \varPhi = 0$ and $\Delta \varPhi =\pi$ means in-phase and anti-phase burst synchronizations of bursting patterns, respectively. In the present paper, $0<\Delta \varPhi <2\pi$ $(\Delta \varPhi \ne \pi )$ and $\Delta \varPhi >2\pi$ mean burst synchronization and non-burst phase synchronization, respectively. In practice, $\Delta \varPhi \approx 0$ and $\Delta \varPhi \approx \pi$, respectively, means in-phase and anti-phase synchronous of the bursting patterns. $\rho =1$ corresponds to in-phase synchronization of bursting pattern, and anti-phase synchronization exhibits a negative $\rho$ value.

3 Results

3.1 Dynamics of an isolated single neuron

3.1.1 Period-4 bursting pattern

Fig. 1

Dynamics of period-4 bursting of the Rulkov model when $\alpha =5$. a Spike trains; b trajectory of the bursting (the thin solid line) and bifurcations of the fast subsystem in-phase space. $N_\mathrm{s}$ (the bold solid line) and $N_\mathrm{u}$ (the dashed line) denote the stable and the unstable branches of the fixed points of the fast subsystem, respectively. The intersection point of $N_\mathrm{s}$ and $N_\mathrm{u}$ is a saddle-node bifurcation point (SN). The upper and lower dash-dot lines represent the maximal ($X_{\max }$) and minimal ($X_{\min }$, $x=-\,1$) values of the stable of fast subsystem, respectively. The intersection point between $X_{\min }$ and $N_\mathrm{u}$ is a homoclinic (H) bifurcation point.

When $\alpha = 5$ and $\sigma = -\,0.18$, the neuronal model exhibits a period-4 bursting, as shown in Fig. 1a. The period of period-4 bursting is $T = 267$. The peak of the first, second, third, and fourth spikes, respectively, appears at 121, 132, 144, and 159, and the cycle locates at 112, as shown in Fig. 1a. The first to fourth troughs appear at 122, 133, 145, and 160 after the cycle shown in Fig. 1a, respectively. The duration of the burst (from the first spike to the fourth spike) is about 39.

3.1.2 Dynamics of period-4 bursting pattern acquired through fast–slow dissection method

Since $\mu = 0.001$, the time process of $x_n$ is faster than $y_n$. $x_n$ is a fast variable and $y_n$ is a slow variable. The dynamics of single neuron model can be acquired through fast–slow dissection method.

When $y_n$ is set as the bifurcation parameter y, the bifurcation structures of the fast subsystem $x_{n+1} = f(x_n,y)$ are shown in Fig. 1b. The fast subsystem exhibits two fixed points (i.e., $x_n=x_{n+1}=x$), Fig. 1b which appear when $y<y_\mathrm{SN}\approx -3.47214$. One is a saddle corresponding to the upper branch (dashed line), which is labeled as $N_\mathrm{u}$, and the other is a stable node corresponding the lower branch (bold solid line), which is labeled as $N_\mathrm{s}$. The intersection point of $N_\mathrm{s}$ and $N_\mathrm{u}$ is a fold (labeled as SN in Fig. 1b bifurcation point of the fixed point appearing at $y=y_\mathrm{SN}\approx -3.47214$. When $y>y_\mathrm{SN}$, the fast subsystem also exhibits a stable periodic oscillation with minimal value (labeled as $X_{\min }$, the lower dash-dot line) being as $-1$ and the maximum values (labeled as $X_{\max }$, the upper dash-dot line). As y decreases to a value $y=y_\mathrm{H}=-\,3.5$, the periodic oscillation intersects with the $N_\mathrm{u}$ and the intersection point is a homoclinic bifurcation point (labeled as H in Fig. 1b).

The trajectory of the attractor of the period-4 bursting in (y, x) plane is illustrated by a thin line, as shown in Fig. 1b. The four spikes of the period-4 bursting run along $X_{\max }$ and $X_{\min }$ from right to left. After the fourth spike, the trajectory jumps down to the stable point $N_\mathrm{s}$ via the neighborhood of the H point to form the quiescent state of the period-4 bursting. After a long running time of the quiescent state on the $N_\mathrm{s}$, the trajectory transits from the quiescent state back to spike via the saddle-node bifurcation. According to Ref. [14], the bursting should be classified into fold/homoclinic bursting pattern. For the fold/homoclinic bursting pattern, the troughs locating between two neighboring spikes are close to the $N_\mathrm{u}$.

If a perturbation or current with suitable strength is applied at suitable phases such as the troughs, the trajectory will run across the $N_\mathrm{u}$ and jump down to $N_\mathrm{s}$ to terminate the expected period-4 burst and to form a novel bursting pattern. It can be speculated that if the suitable perturbation is applied at the kth trough, the novel burst should contain k spikes ($k = 1, 2, 3$, and 4).

3.1.3 Different responses to a negative impulse current

The response of the single neuronal model to a negative square impulse current and the negative current-induced bursting patterns is investigated. To be specific, the period-4 bursting shown in Fig. 1 is considered. The negative square impulse current is characterized by a fixed time width (labeled as $\Delta T$), strength (labeled as A), and action time (labeled as $\Delta t$), which is the application time of the negative square impulse current after the circle shown in Fig. 1a.

Fig. 2

The burst with k spikes induced by a negative impulse current applied around kth trough of the period-4 bursting. The strength, width, and action time of the pulse are labeled as A, $\Delta T$, and $\Delta t$, respectively. $A=-\,0.1$. a The burst with 1 spike when $\Delta T = 8$ and $\Delta t = 10$ (around the first trough); b the burst with 2 spikes when $\Delta T = 8$ and $\Delta t = 22$ (around the second trough); c the burst with 3 spikes when $\Delta T = 8$ and $\Delta t = 34$ (around the third trough); d the burst with 4 spikes when $\Delta T = 39$ and $\Delta t = 49$ (around the fourth trough)

For the period-4 bursting, if a negative square pulse current is introduced at a suitable phase between the kth peak and $(k+1)$th peak of the period-4 burst ($k = 1, 2, 3$), a burst with k spikes is induced when A is larger than a threshold. If A is smaller than the threshold, the firing pattern is still a burst with 4 spikes. For example, the threshold of a negative square impulse current (the dotted line) with $\Delta T = 8$ and $\Delta t = 10$ (between the first and second peaks) that can induce a burst with 1 spike (the solid line) is $A=-\,0.1$, as shown in Fig. 2a. The dashed line in Fig. 2a represents the period-4 bursting. Similarly, the negative square impulse current ($A=-\,0.1$, $\Delta T = 8$) is applied around the second ($\Delta t = 22$ chosen as an example) and third ($\Delta t = 34$ chosen as an example) troughs of the period-4 bursting, burst with 2 and 3 spikes can be induced, respectively, as shown in Fig. 2b, c. The cases with A weaker than the threshold are not shown here. When $\Delta t = 49$ ($\Delta T = 39$), the negative square impulse current is applied around the fourth trough, i.e., the beginning of the quiescent state after the period-4 burst, the firing pattern is still period-4 burst whether A is very strong or weak, as shown in Fig. 2d.

Fig. 3

The burst with different spikes induced by a strong negative impulse current applied within different phase of the quiescent state of the period-4 bursting. The strength, width, and action time of the pulse are labeled as A, $\Delta T$, and $\Delta t$, respectively. $A=-\,0.34$. a The burst with 5 spikes when $\Delta T = 49$ and $\Delta t = 55$; b The burst with 6 spikes when $\Delta T = 63$ and $\Delta t = 66$; c The burst with 7 spikes when $\Delta T = 71$ and $\Delta t = 76$; d The burst with 8 spikes when $\Delta T = 75$ and $\Delta t = 89$; e The burst with 9 spikes when $\Delta T = 80$ and $\Delta t = 108$; f The burst with 10 spikes when $\Delta T = 88$ and $\Delta t =111$.

When the amplitude of the negative pulse is large ($A=-\,0.34$ chosen as an example), novel bursts with 5, 6, 7, 8, 9, and 10 spikes can be induced at different $\Delta t$ values between 55 and 111, which corresponds to that the negative pulse is applied within the quiescent state of the period-4 bursting, and different $\Delta T$ values, which corresponds to the width of the novel burst, are shown in Fig. 3a–f, respectively. As $\Delta t$ becomes longer, the number of spikes within the negative pulse-induced novel burst becomes larger.

Being different from the results of the negative impulse current with large strength (Fig. 3), a negative pulse current with weak strength (A is weaker than 0.34) can induce burst with 5 spikes when $\Delta t$ is at different phase of the quiescent state (larger than 55) of the period-4 bursting, as shown in Fig. 4, for example, $A=-\,0.1$ and $\Delta t = 75$ (Fig. 4a), $A=-\,0.08$ and $\Delta t = 85$ (Fig. 4b), $A=-\,0.06$ and $\Delta t = 95$ (Fig. 4c), and $A=-\,0.04$ and $\Delta t= 116$ (Fig. 4d). And $\Delta T$ is 60 for Fig. 4a–d. From Fig. 4a–d, the strength decreases with increasing $\Delta t$.

Fig. 4

The burst with 5 spikes induced by a weak negative impulse current applied at different phase of the quiescent state of the period-4 bursting. $\Delta T = 60$. a $A=-\,0.1$ and $\Delta t = 75$; b $A=-\,0.08$ and $\Delta t = 85$; c $A=-\,0.06$ and $\Delta t = 96$; d $A=-\,0.04$ and $\Delta t = 116$

Fig. 5

The trajectory of period-4 bursting (the dotted line) and burst with different spikes (the thin solid line) caused by the negative pulse current corresponding to six figures of Figs. 2, 3, and 4, and bifurcations of the fast subsystem of the Rulkov model (the bold solid line and the dashed line denotes the stable and the unstable branches of the fixed points, respectively). a Burst with 1 spike (corresponding to Fig. 2a); b burst with 3 spikes (corresponding to Fig. 2c); c burst with 4 spikes (corresponding to Fig. 2d); d burst with 5 spikes (corresponding to Fig. 3a); e burst with 10 spikes (corresponding to Fig. 3f); f burst with 5 spikes (corresponding to Fig. 4d)

3.1.4 The trajectory of the burst induced by a negative impulse current

The trajectories of the bursts shown in Figs. 2a, c, d, 3a, f, and 4d and the bifurcations of the fast subsystem are illustrated in Fig. 5a–f, respectively. The trajectory of the period-4 bursting is depicted by the dotted line in Fig. 5. The burst with 1, 3, 4, 5, 10, and 5 spikes induced by the negative pulse current is illustrated by the thin solid line in Fig. 5a–f, respectively.

For Fig. 5a, the negative square pulse current takes action around the first trough (Fig. 2a), and the trajectory after the first spike runs across the $N_\mathrm{u}$ and jumps down to the $N_\mathrm{s}$ to form the quiescent state. The second to fourth spikes for the expected period-4 bursting (the dotted line) disappear and a novel burst with 1 spike (the solid line) appears. Therefore, the expected burst with 4 spikes (the dotted line) has been changed to the burst with 1 spike after the application of the negative square pulse current. Similarly, the trajectory of the burst with 3 or 4 spikes induced by a negative square pulse current applied around third or fourth troughs, respectively, is shown in Fig. 5b, c. When a negative square pulse current is applied at the quiescent state, x decreases and y increases to a large extent firstly, and then the trajectory of the first spike moves to right to a large extent, which leads to form a burst with many spikes (> 4), as shown in Fig. 5d–f.

3.2 Synchronous bursting patterns

3.2.1 In-phase or complete synchronizations and the relationships to the coupling current

Fig. 6

The spike trains of the synchronous bursting patterns (the solid line) and coupling currents (the dotted line) of the coupled neurons when $g = 1.46$. $\rho = 1$, and $\Delta \varPhi = 0$. a $\tau = 8$; b $\tau = 18$; c $\tau = 29$; d $\tau = 45$

Fig. 7

The spike trains of the synchronous bursting patterns (the solid line) and the coupling currents (the dotted line) of the coupled neurons with $g = 1.46$. a Period-5 bursting when $\tau = 55$; b period-6 bursting when $\tau = 66$; c period-7 bursting when $\tau = 76$; d period-8 bursting when $\tau = 89$; e period-9 bursting when $\tau = 108$; f period-10 bursting when $\tau = 111$

Fig. 8

The spike trains of the synchronous period-5 bursting patterns (the solid line) and the corresponding coupling currents (the dotted line). a $g = 0.4$ and $\tau = 75$; b $g = 0.3$ and $\tau = 85$; c $g = 0.2$ and $\tau = 96$; d $g = 0.1$ and $\tau = 116$

In the coupled neurons, various synchronous patterns can be simulated when g and $\tau$ are chosen as suitable values, as shown by the bold lines in Figs. 6, 7, and 8. The coupling currents of the two neurons manifest negative pulse-like behavior, as shown by the thin lines (upper) in Figs. 6, 7, and 8, which closely match the negative pulse current shown in Figs. 2, 3, and 4, respectively. The dash-dot and dot lines represent to neuron 1 and 2, respectively. The strength, width, and action time of the negative pulse of the coupling current, which corresponds to A, $\Delta T$, and $\Delta t$ of the negative pulse current applied to a single neuron are, respectively, related to the coupling strength, the burst width, and the time delay. The burst of the synchronous bursting pattern induced by the negative pulse of the coupling current exhibits the same pattern as the burst caused by the negative square current applied to a single neuron. The detailed relationships between the synchronous bursting patterns and the coupling current are introduced in the following paragraph.

For example, when $g = 1.46$ and $\tau = 8$, the spike trains of the synchronous period-1 bursting patterns are shown by the bold lines(lower)in Fig. 6a. It can be found that the coupling current exhibits a negative impulse applied near the trough after the first spike. It is the negative impulse of the coupling current that can induce the burst with 1 spike, which is similar to the condition of Fig. 2a. As $\tau$ becomes longer, the negative impulse of the coupling current can put inhibitory effect around the second, third, and fourth troughs, like the conditions shown in Fig. 2b–d, respectively, burst with 2, 3, and 4 spikes can be induced, as shown in Fig. 6b ($\tau = 18$), 6c ($\tau = 29$), and 6d ($\tau = 45$), respectively. The time delay is relative short and the coupling strength is relative large for these four synchronous bursting patterns. For the 4 synchronous bursting patterns, $\rho =1$ and $\Delta \varPhi =0$, which means in-phase and complete synchronous behaviors.

When the coupling strength remains at a strong level, burst with 5, 6, 7, 8, 9, and 10 spikes can be induced as time delay $\tau$ becomes much longer, and the coupling currents exhibit negative pulse current similar to those shown in Fig. 3a–f, respectively, as illustrated in Fig. 7a–f. The coupling strength is $g = 1.46$, and $\tau = 55$, 66, 76, 89, 108, and 111 for Fig. 7a–f, respectively. $\rho = 1$ and $\Delta \varPhi = 0$ for all of the 6 synchronous bursting patterns, which means in-phase and complete synchronous behaviors.

Fig. 9

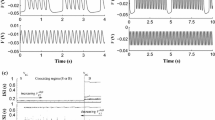
The spike trains of the bursting patterns with burst phase synchronization. The membrane potentials of the neuron 1 (the solid line) and neuron 2 (the dashed line). a $g = 1.28$, $\tau = 30$, $\rho = 0.59$, $\Delta \varPhi = 0.16$ ($0<\Delta \varPhi <\pi$); b $g = 0.03$, $\tau = 98$, $\rho = 0.14$, $\Delta \varPhi = 5.15$ ($\pi<\Delta \varPhi <2\pi$)

When time delay remains at a long level, synchronous period-5 bursting patterns can be induced at different $\tau$ values with different coupling strengths, for example, $g = 0.4$ and $\tau = 75$ (Fig. 8a), $g = 0.3$ and $\tau = 85$ (Fig. 8b), $g = 0.2$ and $\tau = 96$ (Fig. 8c), and $g = 0.1$ and $\tau = 116$ (Fig. 8d). The values of $\tau$ for Fig. 8a–d correspond to $\Delta t$ values for Fig. 4a–d, respectively. The duration of the negative impulse is about 63, nearly equaling $\Delta T$ (60) in Fig. 4. Being similarly to the conditions shown in Fig. 4, the synchronous period-5 bursting patterns (the bold line) can also be induced by the negative impulse of the coupling currents (the thin line). With increasing time delay $\tau$, the strength of coupling current and the coupling strength (g) that can induce the synchronous period-5 bursting patterns become weak, as shown in Fig. 8. This is also similar to that shown in Fig. 4. All of the 4 bursting patterns exhibit in-phase and complete synchronization ($\rho = 1$ and $\Delta \varPhi = 0$).

3.2.2 Burst phase synchronization

In addition, bursting patterns with phase synchronization can be simulated. For example, when $g = 1.28$ and $\tau = 30$, bursting pattern with $\Delta \varPhi = 0.16$ and $\rho = 0.59$ is simulated, as shown Fig. 9a. $\Delta \varPhi$ is much larger than 0 and is much lower than $\pi$. When $g = 0.03$ and $\tau = 98$, bursting pattern with $\Delta \varPhi = 5.15$ and $\rho = 0.14$ is simulated, as shown Fig. 9b. $\Delta \varPhi$ is larger than $\pi$ but lower than $2\pi$.

Fig. 10

The spike trains of different bursting patterns with anti-phase burst synchronization ($\Delta \varPhi \approx$ 3.1416). The membrane potentials of the neuron 1 (the solid line) and neuron 2 (the dashed line). a $g = 0.3$ and $\tau = 5$; b $g = 0.8$ and $\tau = 5$; c $g = 1.5$ and $\tau = 5$; d $g = 0.4$ and $\tau = 6$; e $g = 0.4$ and $\tau = 26$; f $g = 0.4$ and $\tau = 64$

3.2.3 Anti-phase synchronization

When time delay $\tau$ is very short, regardless of the coupling strength (g) is strong or weak, bursting patterns with anti-phase synchronization ($\Delta \varPhi \approx$ 3.1416) can be simulated. For example, when $\tau \approx$ 5, bursting patterns with 5, 8, and 10 spikes can be simulated when $g = 0.3$, $g = 0.8$, and $g = 1.5$, respectively, as shown in Fig. 10a–c. The results show that when $\tau$ is fixed, the number of spikes per burst for the anti-phase synchronous bursting patterns increases with the increase in g.

In addition, when the coupling strength is at a weak level, various bursting patterns with anti-phase synchronization ($\Delta \varPhi \approx$ 3.1416) can be simulated when $\tau$ is relative short. For example, when $g = 0.4$, bursting pattern with 6, 8, and 11 spikes per burst is simulated when $\tau = 6$, $\tau = 26$, and $\tau = 64$, respectively, as shown in Fig. 10d–f. It shows that when g is fixed, the number of spikes per burst increases with increasing $\tau$.

The value of $\rho$ is −0.52, −0.60, −0.62, −0.55, −0.42, and −0.23 for Fig. 10a–f, respectively.

3.2.4 Coexistence of synchronous behaviors

Fig. 11

Coexistence of synchronous behaviors. a The trajectories of attractors of uncoupled neuron 1 and neuron 2 for case-1 initial values ($x_{1,1} = 1.542$, $y_{1,1} = -\,3.459$, $x_{2,1} = -\,0.705$, $y_{2,1} =-\,3.455$); b the trajectories of attractors of uncoupled neuron 1 and neuron 2 for case-2 initial values ($x_{1,1} = -\,0.8$, $y_{1,1} = -\,3.4$, $x_{2,1} = -\,1.2$, $x_{2,1}=-\,3.4)$; c the non-complete synchronization for coupled neuron 1 and neuron 2 for case-1 initial values when $g=1.46$; d The complete synchronization for coupled neuron 1 and neuron 2 for case-2 initial values when $g=1.46$; e The changes of $\rho$ with respect to time delay $\tau$ for case-1 (dot) and case-2 (bold) initial values when $g=1.46$; f The changes of R with respect to time delay $\tau$ when $g=1.46$. The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 represent the synchronous bursting patterns with 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 spikes per burst, respectively

Two cases of randomly chosen initial values are considered as representative examples. For case-1, the initial values are $x_{1,1} = 1.542$ and $y_{1,1} =-\,3.459$ for neuron 1 and are $x_{2,1} = 0.705$ and $y_{2,1} =3.455$ for neuron 2. For case-2, the initial values for neuron 1 are $x_{1,1} = 0.8$ and $y_{1,1} = 3.4$ and for neuron 2 are $x_{2,1}=1.2$ and $x_{2,1} =3.4$. When uncoupled, the trajectories of neuron 1 and neuron 2 for the case-1 initial values are shown in Fig. 11a and for the case-2 are illustrated in Fig. 11b. For both cases, the trajectories for both neurons manifest different transient processes and at last evolve to the stable period-4 bursting.

For coupled neuron 1 and neuron 2, coexistence of synchronous behaviors appears at suitable g and $\tau$ values, for example, when $g = 1.46$ and $\tau = 8$, as shown in Fig. 11c–e. Non-complete synchronous behavior with negative value of $\rho =0.59$ appears for the case-1 initial values, as shown in Fig. 11c, and complete synchronous behavior with $\rho = 1$ appears for the case-2 initial values, as illustrated in Fig. 11d.

When $g = 1.46$, the changes of $\rho$ values with respect to $\tau$ for case-1 and case-2 initial values are shown by the solid and dot lines in Fig. 11e, respectively. The values of $\rho$ are different at the same $\tau$ values for the two cases of initial values, which appears at multiple ranges of $\tau$, showing that coexistence of the synchronous behaviors appears in the two coupled neurons and $\rho$ values are dependent on the initial values. This is similar to the results of Ref. [24], and the coexisting behaviors are due to spike interactions [60].

Therefore, it is necessary to calculate the probability of $\rho \ge 0.95$ for different initial values, labeled as R, to characterize the multiple synchronous behaviors. When $g = 1.46$, the changes of R for 100 initial values with respect to $\tau$ are shown in Fig. 11f.

Fig. 12

The distribution of $\rho$ and R on the plane $(\tau ,g)$. a $\rho$ for case-1 initial values; b $\rho$ for case-2 initial values; c difference of $\rho$ between (a, b); d R. The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 represent synchronous bursting pattern with 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 spikes per burst, respectively

Fig. 13

Changes of R with respect to time delay $\tau$ at different g levels when g is small. The number of 5 represents the synchronous bursting patterns with 5 spikes per burst. a $g = 0.4$; b $g = 0.3$; c $g = 0.2$; d $g = 0.1$

3.3 Synchronization transition processes

3.3.1 Multiple synchronous behaviors when the coupling strength is strong

The values of $\rho$ in the two-dimensional parameter space ($\tau$, g) for case-1 initial values and for case-2 initial values are shown in Fig. 12a, b, respectively. The difference of $\rho$ values between Fig. 12a, b is shown in Fig. 12c. It can be found that nonzero values exist in wide parameter region of the two-dimensional plane ($\tau$, g), which shows that coexistence of the synchronous behaviors appears in wide parameter region. The distribution of R values to characterize the probability of $\rho \ge 0.95$ for 100 cases of initial values in the ($\tau$, g) plane is shown in Fig. 12d.

Except the coexistence of synchronous behaviors, another important characteristic can be found from Fig. 12. It is that the complete (in-phase) synchronous behaviors ($\rho = 1$) appear in multiple ranges of $\tau$, which show that multiple synchronous behaviors are simulated at different $\tau$ values. The results are consistent with those shown in Figs. 6 and 7 and are similar to the results of Ref. [24].

The synchronous behaviors from period-1 to period-10 bursting patterns can be found at different $\tau$ values, which closely match those shown in Figs. 6 and 7. Being different from the present paper, only synchronous period-3, period-4, period-5, period-6, and period-7 bursting patterns are simulated in Ref. [24] when the uncoupled neuron exhibits period-6 bursting pattern. The dynamics of the period-3, period-4, period-5, and period-6 bursting patterns in the Ref. [24] are similar to period-1, period-2, period-3, and period-4 bursting patterns in the present paper. However, when the negative pulse of the coupling current put effect within the quiescent state, only a period-7 bursting pattern is simulated in Ref. [24], while period-5 to period-10 bursting patterns can be simulated in the present paper. The present paper presents more synchronous bursting patterns than the Ref. [24].

3.3.2 Various synchronous behaviors in the plane $(\tau ,g)$

The dependence of R on both g and $\tau$ is presented in Fig. 12d. Several obvious characteristics can be found.

Firstly, multiple synchronous periodic bursting patterns (from period-1 to period-10 bursting patterns) appear at suitable discrete ranges of $\tau$ when g is strong (> 0.6).

Secondly, when g is weak (< 0.6) and $\tau$ is long (> 70), synchronous period-5 bursting pattern appears, as shown by the arrow and the number “5” located at lower-right corner of Fig. 12d. The values of g for the synchronous period-5 bursting pattern decrease as $\tau$ values increase. For example, when $g = 0.4$, 0.3, 0.2, and 0.1, synchronous period-5 bursting pattern appears at different values, as shown in Fig. 13a, b, c, and d, respectively. The 4 cases for $g = 0.4, 0.3, 0.2$, and 0.1, respectively, correspond to those shown in Fig. 4a–d, and in Fig. 8a–d.

Thirdly, the $\tau$ values for synchronous period-k bursting pattern of the coupled neurons correspond to $\Delta t$ of the negative square pulse current that can induce burst with k spikes ($k= 19$) for the isolated single neurons. All of these characteristics of the synchronous patterns can be well understood with the dynamics of single neuron stimulated by a negative impulse.

Fourthly, the complete or nearly complete synchronous firing patterns cannot be found in the region within which time delay is short and coupling strength is weak, i.e., the lower-left corner of Fig. 12d [g is weak ($<0.6$) and $\tau$ is short ($<60$)].

Lastly, the synchronous bursting patterns with low probability R appear when $\tau$ is long ($110<\tau <140$) and coupling strength is not weak ($g>0.4$).

3.3.3 In-phase and anti-phase synchronous behaviors in the plane $(\tau , g)$

Furthermore, the distribution of the average burst phase difference between neuron 1 and neuron 2 ($\Delta \varPhi$) on the two-dimensional parameter space $(\tau ,g)$ is shown in Fig. 14.

Fig. 14

The distribution of the average burst phase difference ($\Delta \varPhi$) on the plane $(\tau , g)$.

Fig. 15

The transitions between anti-phase and in-phase synchronous patterns as $\tau$ is changed at different g levels. a $g = 1.46$; b $g = 0.2$

First, the anti-phase and nearly anti-phase burst synchronous patterns ($\Delta \varPhi =\pi$ theoretically, in the present paper $3.122<\Delta \varPhi <3.162$) locate at the region with very short $\tau$ ($\tau <6$) or at the lower-left corner (time delay is short and coupling strength is weak), which corresponds to the region of high negative R values shown in Fig. 12.

Second, the in-phase or nearly in-phase ($\Delta \varPhi = 0$, in the present paper $0\le \Delta \varPhi <0.02$) synchronous patterns correspond to the complete or nearly complete synchronous patterns, which locate within the regions corresponding to multiple synchronous patterns shown in Fig. 12.

Last, in the most regions of the remained parameter space of the plane $(\tau ,g)$, burst phase synchronous behaviors ($0.02\le \Delta \varPhi \le 3.122$ or $3.162\le \Delta \varPhi \le 6.283$) appear.

3.3.4 Transition from anti-phase or out-of-phase to in-phase synchronous behaviors

As can be found from Fig. 14, transition from anti-phase synchronous behaviors to multiple in-phase synchronous behaviors can be achieved through the modulation of g or the adjustment of $\tau$. For example, the changes of $\Delta \varPhi$ with respect to $\tau$ when $g=1.46$ and $g=0.2$ are shown in Fig. 15, and the changes of $\Delta \varPhi$ with respect to g when $\tau =7$ and $\tau =60$ are shown in Fig. 16. The transitions between anti-phase and in-phase synchronous behaviors are achieved.

The transition from anti-phase to in-phase synchronous behaviors happens 1, 2, 7, and 5 times in Figs. 15a, b, and 16a, b, respectively. More general, the transitions from in-phase to out-phase ($\Delta \varPhi \ne 0$) synchronous behaviors happen multiple times in both Fig. 15a, b. Compared with only one transition from out-of-phase to in-phase synchronous behaviors [59], the present paper presents more abundant and complex results. As reported in Ref. [59], the transition between in-phase and out-of-phase synchronous behaviors exhibits discontinuous changes, which are suggested to be caused by phase-slip bifurcation. The transitions in the present paper also exhibit discontinuous or nearly discontinuous changes.

Fig. 16

The transitions between anti-phase and in-phase synchronous patterns as g is changed at different $\tau$ levels. a $\tau = 7$; b $\tau = 60$

4 Conclusion

Time delay has been identified to induce or influence various dynamics of neuronal networks, for example, phase transition  [59], enhancement or suppression of synchronization, resonance-like phenomenon, and oscillation death  [59, 63,64,65,66,67]. Inhibitory coupling neurons have been shown to enhance or suppress the synchronizations. In the present paper, time delay-induced anti-phase or multiple in-phase (complete) synchronous bursting patterns are simulated at different parameter configurations in a map-based neuronal network with inhibitory chemical synapses. The anti-phase synchronous behaviors appear at short time delay and low coupling strength. Multiple in-phase synchronous behaviors appear at strong coupling strength and discrete ranges of time delay locating within a period of bursting pattern of an isolated single neuron. The results of the present paper are more complicated than the multiple synchronizations, each appearing at time delay being odd integer multiples of half-period of the bursting or spiking pattern of individual neurons [23]. Furthermore, the transitions between different bursting synchronous behaviors such as from in-phase to anti-phase or out-of-phase synchronizations are also simulated. The transitions between in-phase and out-of-phase happen one or multiple times, which is more complex than Ref. [30] wherein transition happened only one time. The present paper presents novel results in both synchronous patterns and synchronization transition in the inhibitory coupled neurons with time delay.

Phase synchronization of synchronous behaviors is the basis for various functions of the nervous system, such as motion, sensation, cognitive, attention, memory, and awareness. In a biological experiment on mutual inhibitory coupled bursting neurons of the pyloric circuit in the lobster stomatogastric ganglion [43], anti-phase synchronous bursting patterns were observed when the inhibitory synapse is fast (synaptic time constant < 100 ms). As inhibitory synapse was adjusted to a slow synapse (synaptic time constant > 400 ms) by using the dynamic clamp technique, the out-of-phase or anti-phase synchronous bursting patterns changed to in-phase synchronous bursting pattern. The synaptic time constant is larger, the delay of the coupling current to work is longer. To a high extent, a slow synapse is similar to a synapse with time delay. The experimental result of the transition from anti-phase to in-phase synchronous bursting patterns of the pyloric [43] matches the time delay-induced transition simulated in the present paper to a certain extent. The time delay-induced synchronization transition may be helpful for understanding the function modulation of lobster stomatogastric ganglion.

In Refs. [24, 26, 30], bursting patterns of multiple synchronous behaviors are well interpreted with dynamics of isolated single neurons and the coupling current, which are acquired through the fast–slow variable dissection method. In the present paper, bursting patterns of in-phase (complete) behaviors are also well interpreted with dynamic responses of an isolated single neuron to an inhibitory square impulse current. The generation of the burst of multiple synchronous behaviors in the present paper is consistent with those of the bursting patterns in Ref. [24]. It is suggested that the generation of these periodic bursting patterns in the present paper and in Ref. [24] should obey the same rules. In addition, the spatiotemporal patterns of the neuronal network are well explained with dynamics of isolated single neurons combined with the coupling currents [68]. The present paper and the Refs. [24, 26, 30, 68] present examples to identify network dynamics using dynamics of the isolated single units, which is the representative example to identify the dynamics across different levels.