Effects of damage parametric changes on the aeroelastic behaviors of a damaged panel

Abstract

In this study, the aeroelastic responses and stability boundaries of a simply supported supersonic plate with structural damage are investigated to assess the effects of damage parametric changes on the stability regions as well as to explore some potential tools for damage detection. In the modeling, structural damage is a local bending stiffness loss with various levels, extents and positions. The effects of damage level, extent and position are presented via exploiting nonlinear tools such as bifurcation diagrams, stability regions, Poincaré maps and Lyapunov exponents. Specially, the proper orthogonal decomposition (POD) method is applied to extract the POD modes to detect the damage parametric variations. It is determined that (1) structural damage has a notable influence on the aeroelastic stability of the panel; (2) the damage level and extent affect in a similar way that a larger damage level/extent tends to reduce the flutter boundary for a flat plate, but conversely increase the flutter boundary for a buckled plate; (3) the damage occurring around the leading of the panel corresponds to the least stable panel compared to the other positions along the chordwise; (4) the stability region as a novel way for damage detection is proved to be sensitive and effective, and the largest Lyapunov exponent as a quantitative measure is powerful to reveal the subtle differences in the chaos induced by damage changes; (5) the higher-order POD modes are more sensitive to the subtle damage than the primary POD modes.

1 Introduction

Considering the nonlinear in-plane stresses due to the large deflection, a long-term panel flutter exhibiting complex dynamic behaviors is very likely to result in a fatigue failure, prior to which structural damage such as cracking or hidden corrosion may occur. Damage can be defined as changes drawn into the system and will adversely affect the current or future performance of the system, which is thus very dangerous and of significant importance to predict the new stability boundaries induced by the structural damage, especially for aircraft and aerospace systems involved with human safety. Therefore, knowledge of the influence rules of damage changes to the aeroelastic behaviors and stability boundaries of a fluttering panel is of interest and will equip the safe flight with crucial information.

The investigations of aeroelastic behaviors and stabilities of a fluttering panel have been primarily focused on the perfect/healthy panel without damage. Dowell and his coworkers investigated the nonlinear limit cycle oscillations (LCOs) and chaos of a simply supported/cantilevered panel fluttering in supersonic flow using semi-analytical methodologies [10, 43, 47]. Considering more precise aerodynamic models, some relevant work were naturally followed [2, 4, 19, 39]. In addition to the simple rectangular panel, a trapezoidal wing-like panel was investigated [37]. To consider the complex geometries and constraint boundaries, some researches of supersonic and hypersonic panel flutter considering thermal effects or/and with laminated composite materials were done exploiting the finite element method [7, 20, 25, 33, 34]. For the sake of computational saving and physical insight of panel flutter, the reduced-order models (ROMs) using aeroelastic mode, proper orthogonal decomposition (POD) method were thus established for analysis of nonlinear aeroelastic behaviors [21, 28, 42, 45].

Whereas the study of aeroelastic characteristics of a damaged panel has seldom been presented. In Ref. [36], aeroelastic responses of damaged composite plates were analyzed. The linear flutter boundary evolving with damage was determined to be highly dependent with the damage growth. However, the nonlinear structural coupling between bending and stretching of the plate was not considered, and thus, the stability boundary was simply linear. It is well known that the nonlinear membrane force induced will limit the plate amplitude and the nonlinear flutter behavior has been observed in experiments [11, 23]. Therefore, a statistic study of the damage parametric changes to the nonlinear dynamics and nonlinear flutter boundaries is highly expected.

In order to discriminate the new aeroelastic responses and stability boundaries involved with the structural damage, powerful tools with high sensitivity for damage detection are of great necessity. Currently, extensive researches have been conducted in damage identification for a reliable and effective nondestructive technique to maintain safety and integrity of structures for a simple beam/plate or complex aircraft and aerospace system. In the literature, the most popular and effective damage identification methods belong to the field of signal processing, which can be mainly categorized as vibration-based methods, attractor-based methods and POD-based methods.

The physical idea of vibration-based damage identification method is that the damage-induced changes in the physical properties such as mass, damping and stiffness will cause detectable changes in modal parameters like natural frequencies, modal shapes and modal damping. Various kinds of vibration-based damage detection methods have been investigated for health monitoring. Wavelet transform and neural network identification based on vibration responses were used for simple plates and composite structures [31, 46]. Two vibration-based methods using time-series analysis of dynamic responses were explored for damage detection of a thin plate [38]. The categorization, merits/drawbacks and the choice of different vibration-based methods can be found in Refs. [9, 16]. The vibration-based methods discussed above are well developed for linear systems, however, are not sensitive in a nonlinear system for damage location and characterization.

The aeroelastic systems, however, are essentially nonlinear and their damage detections are very important since the structural failure once occurring will cause a great loss to both life and wealth. Due to the existence of nonlinearity, the additivity and homogeneity pertaining to the linear system become invalid [8, 40]. Thus, we have to resort to some nonlinear approaches. Therefore, attractor-based methods, extracting more information from the vibration data with signal processing, have been developed for nonlinear systems with higher sensitivity. As is known to all, a typical LCO occurs for an aeroelastic system when the flutter boundary is exceeded [1]. Therefore, the LCO shapes have been used as a feature to detect the damage position of the aeroelastic panel [13]. With more sensitivity for a nonlinear system, chaotic motions have been proved to be effective for identification of parametric variations in aeroelastic systems [14], and thus, the features of chaos such as Poincaré map [24], bifurcation [12], attractor dimension [26, 29, 30] and fractal dimension [22] have been exploited for damage identification by many researchers.

Generally speaking, attractor-based methods and vibration-based methods are both exploiting structural responses directly with signal processing technique, which however, pose two challenges: (1) the dynamic response of a system is not only based on geometric and material properties but also forces and environmental conditions, and thus, the variations of the latter may mask the changes of dynamic responses caused by the former, which is structural damage. Therefore, a methodology that can distinguish the changes of dynamic responses induced by both structural properties and environmental conditions is needed. (2) The damage is typically a local phenomenon and may not significantly influence the global response of a structure, which is usually measured and recorded as basis in vibration and attractor-based methods. To conquer the limitations of vibration/attractor-based methods, POD method as a reduced-order technique [5, 6, 45] has been applied for damage detection by using the system’s dynamical invariants to discriminate the changes of dynamic responses caused by structural damage [3, 17, 18, 32].

The present study aims to evaluate the effects of damage parametric changes to the aeroelastic responses and stability boundaries of a simple fluttering panel in supersonic flow. Structural damage alters the stiffness, mass or damping of a structure and in turn causes a change in its dynamic response and hence the stability boundary. Some nonlinear tools based on vibration/attractor of the system such as bifurcation diagram, Poincaré map, Lyapunov exponent [35, 41] and stability regions are exploited and proved to be sensitive to the structural damage, which will pave a way to the structural health monitoring of an aeroelastic system. Especially, the stability regions differentiating various types of dynamics are obtained for the first time for a damaged plate. Furthermore, the POD modes are exploited for detection of subtle structural damage.

This paper is organized as follows: in Sect. 2, aeroelastic equations of a damaged panel are constructed, and the damage is characterized as a local stiffness loss with three parameters. In Sect. 3, effects of damage parameters of damage level, extent and position are studied with bifurcation diagrams, stability regions, Poincaré maps and Lyapunov exponents. In addition, the POD method is exploited to extract POD modes for detection of damage parametric variations. The main conclusions are drawn in Sect. 4.

2 Modeling

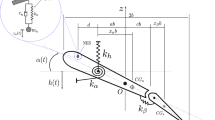
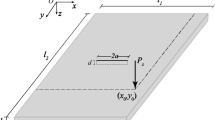
For a simply supported plate presented in Fig. 1, considering the coupling of out-of-plane bending and in-plane stretching, long-time of nonlinear dynamic behaviors like LCO and chaos may lead to fatigue failure, prior to which structural damage as a local stiffness loss is possible. Hence, as shown in Fig. 2, the bending stiffness and Young’s modulus due to a local damage are defined as ${\bar{D}}$ and ${\bar{E}}$, respectively, compared to D and E for a healthy panel. And thus a stiffness reduction factor is defined as $S_r={\bar{D}}/D~(\hbox {or} {\bar{E}}/E)$ quantifying the damage level. It should be noted that the smaller the $S_r$ is, the larger the damage is. Additionally, the possible damage is located at $x_d$ with a length of $l_d$, via which two more nondimensional damage parameters of $L_d=l_d/a$ and $\xi _d=x_d/a$ are defined to characterize the damage extent and position, respectively.

Fig. 1

Geometry of a fluttering panel undergoing supersonic flow

Fig. 2

Geometry of a two-dimensional panel with structural damage

For a simply supported panel [10], ignoring the spanwise bending and using the Kirchhoff–Love plate theory ignoring shearing stress and von Karman plate theory demonstrating nonlinear strain-displacement relation, the equation of motion for the damaged panel can be written as follows [15]:

$$\begin{aligned}&{\bar{D}}\left( \frac{\partial ^4w}{\partial x^4}\right) -\left[ \frac{{\bar{E}}h}{2a}\int _0^a\left( \frac{\partial w}{\partial x}\right) ^2\hbox {d}x+N_x^T\right] \left( \frac{\partial ^2w}{\partial x^2}\right) \nonumber \\&\quad +\,\rho _m h\left( \frac{\partial ^2w}{\partial t^2}\right) +(p-p_{\infty })=0, \end{aligned}$$

(1)

where the induced force from the coupling between the out-of-plane bending and in-plane stretching [10] is

$$\begin{aligned} N_x={\bar{E}}h/2a\int _0^a(\partial w/\partial x)^2 \hbox {d}x, \end{aligned}$$

(2)

and the externally applied in-plane thermal force, which is assumed uniform through the whole panel, is taking the form

$$\begin{aligned} N_x^T=-\frac{{\bar{E}}h\alpha T}{(1-\nu )}. \end{aligned}$$

(3)

Since the piston theory has been widely used in the range of $\sqrt{2}<M_a<5$ with good precise, the first-order piston theory is used for calculating the quasi-steady aerodynamic force [10]

$$\begin{aligned} p-p_{\infty }=\frac{2q}{\beta }\left[ \frac{\partial w}{\partial x}+\left( \frac{M_a^2-2}{M_a^2-1}\right) \frac{1}{U}\frac{\partial w}{\partial t}\right] . \end{aligned}$$

(4)

Substituting Eqs. (2)–(4) into Eq. (1) and using the following nondimensionalization,

$$\begin{aligned} \begin{aligned}&\xi \equiv x/a,~W \equiv w/h \\&\lambda \equiv 2qa^3/\beta D \\&\mu \equiv \rho a/\rho _mh \\&\tau \equiv t(D/\rho _mha^4)^{1/2} \\&R_{x}^T\equiv -12(1+\nu )(a/h)^2\alpha T \end{aligned} \end{aligned}$$

(5)

the nondimensional aeroelastic equation of a damaged panel is obtained:

$$\begin{aligned}&S_r\frac{\partial ^4W}{\partial \xi ^4}-6S_r(1-\nu ^2)\left[ \int _0^1\left( \frac{\partial W}{\partial \xi }\right) ^2\hbox {d}\xi \right] \frac{\partial ^2W}{\partial \xi ^2} \nonumber \\&\quad +\,\lambda \left\{ \frac{\partial W}{\partial \xi }+\left( \frac{M_a^2-2}{M_a^2-1}\right) \left( \frac{\mu }{\lambda M_a}\right) ^{\frac{1}{2}}\frac{\partial W}{\partial \tau }\right\} \nonumber \\&\quad -S_r R_x^T\frac{\partial ^2W}{\partial \xi ^2}+\frac{\partial ^2W}{\partial \tau ^2}=0. \end{aligned}$$

(6)

Using the Galerkin method with assumption of

$$\begin{aligned} W(\xi , \tau )=\sum _{m=1}^M a_m(\tau )\sin {(m\pi \xi )}, \end{aligned}$$

and then, the resulting ordinary differential equations (ODEs) are expressed as

$$\begin{aligned}&\frac{\hbox {d}^2a_n}{\hbox {d}\tau ^2}=-2\sum _{m=1}^M a_m(m\pi )^4\int _0^1 S_r(\xi )\sin (m\pi \xi )\sin (n\pi \xi )\hbox {d}\xi \nonumber \\&\quad -\,6(1-\nu ^2)\sum _{m=1}^M a_m^2(m\pi )^2\sum _{m=1}^M a_m(m\pi )^2\nonumber \\&\quad \times \int _0^1S_r(\xi )\sin (m\pi \xi )\sin (n\pi \xi )\hbox {d}\xi \nonumber \\&\quad -\,\lambda \left\{ \sum _{m=1, m\ne n}^M a_m\frac{2mn[1-(-1)^{m+n}]}{n^2-m^2}\right. \left. +\left( \frac{\mu }{\lambda M_a}\right) ^{\frac{1}{2}}\frac{\hbox {d}a_n}{\hbox {d}\tau }\right\} \nonumber \\&\quad -\,R_x^T\sum _{m=1}^M a_m(m\pi )^2\int _0^1S_r(\xi )\sin (m\pi \xi )\sin (n\pi \xi )\hbox {d}\xi ; \nonumber \\&\quad (n=1,~2,~\ldots ,~M). \end{aligned}$$

(7)

This is a set of M second-order, ordinary, coupled nonlinear differential equations for the unknown amplitudes $a_m(\tau )$, which can be solved by 4th Runge–Kutta (RK4) numerical integration method for the aeroelastic responses of the damaged panel.

3 Results and discussions

The panel material properties, geometrical dimensions and flow parameters are: $E=71\,\hbox {GPa},~\nu =0.3,~\alpha =2.34\times 10^{-6}/^{\circ }\hbox {C},~\rho _m=2750\,\hbox {kg}/\hbox {m}^3$; $h/a=1/300$; and $\rho =0.413\,\hbox {kg}/\hbox {m}^3,~Ma=4.5$, respectively. Effects of damage level, extent and position to the nonlinear dynamic behaviors and stability boundaries of the fluttering panel are discussed in detail. All figures are plots of a typical point at $\xi =0.75$. A critical temperature $T_\mathrm{cr}=\pi ^2h^2/[12(1+\nu )\alpha a^2]$ is defined for nondimensionalization of temperature differential T, and then $R_x^T=-\pi ^2(T/T_\mathrm{cr})$.

All the results of bifurcation diagrams, Poincaré maps and the largest Lyapunov exponent (LLE) are calculated and mapped out as follows:

(1) Bifurcation diagrams: sweep a damage parameter like $S_r$, $L_d$ or $\xi _d$, and then record the local deflection extrema of time response. It should be noted that the deflection extrema should be recorded after the transient response is damping out.

(2) Poincaré maps: first define an event point at $\xi =0.25$, and then record the deflection and velocity of the typical point when the event point reaches its zero deflection with a positive velocity.

(3) LLE: according to the procedure in Ref. [35], we calculate the LLE as follows:

• 1. Start with an orbit $\mathbf{a_0}$, and then iterate for a period of $t_0$ to make sure the orbit is on the attractor. Choosing $t_0=100$ in the present study is to drop the influence of transient responses.

• 2. Select another nearby orbit $\mathbf{b_0}$ satisfying $|\mathbf{b_0-a_0}|{=}d_0$ given $d_0=10^{-8}$. An easy way to choose $\mathbf{b_0}$ is as $\mathbf{b_0}(1)=\mathbf{a_0}(1)+d_0; \mathbf{b_0}(2:end)=\mathbf{a_0}(2:end)$.

• 3. Iterate both orbits a few steps, e.g., $N_1=10$ to obtain $\mathbf{a_1}$ and $\mathbf{b_1}$, and then calculate the new separation $d_1=|\mathbf{b_1-a_1}|$.

• 4. Calculate the largest Lyapunov exponent $\varLambda _1=log|\frac{\hbox {d}_1}{\hbox {d}_0}|\frac{1}{N_1 \hbox {d}t}$.

• 5. Readjust the second orbit to make its separation to the first orbit is $d_0$ in the same direction as $d_1$. Specifically, $\mathbf{a_0=a_1}$ and $\mathbf{b_0=a_1}+\frac{d_0}{d_1}(\mathbf{b_1-a_1})$.

• 6. Repeat steps 3–5 and then calculate the average of step 4.

Then, the criterion for chaos is obtained [27]:

$$\begin{aligned} \left\{ \begin{array}{ll} \varLambda >0 &{} \quad \hbox {chaotic} \\ \varLambda \leqq 0 &{} \quad \hbox {regular~motion} \\ \end{array} \right. \\ \end{aligned}$$

3.1 Effect of damage level

Effect of varying damage levels on the aeroelastic responses is first considered. Shown in Fig. 3 is a bifurcation diagram of deflection extrema versus damage level parameter $S_r$ by fixing the damage extent and position as $L_d=10\%,~\xi _d=0.75$ with fixed dynamic pressure and in-plane temperature stress as $\lambda =150,~T/T_\mathrm{cr}=4$. It should be noted that $S_r=1$ represents a healthy panel, and a smaller $S_r$ value indicates a larger damage level. The damage level is varying in a range $0 \rightarrow 1$ with a step increment of $\Delta S_r=0.01$. The results show that the panel exhibits complex dynamics as chaos, periodic and buckled motions for different damage levels. The robustness of the obtained bifurcation diagram has been conducted, and the initial conditions of $a_1=0.1$ and $a_1=0.01$ have been proved to obtain the identical bifurcation diagrams. So the initial condition of $a_1=0.01$ is used in all of the calculations in this study.

Fig. 3

Bifurcation diagram in terms of damage level $S_r$

Fig. 4

Bifurcation diagrams in terms of temperature $T/T_\mathrm{cr}$: a$S_r=1$; b$S_r=0.8$

Fig. 5

Panel responses for different $S_r$ at $T/T_\mathrm{cr}=4,~\lambda =150$: a Poincaré map for $S_r=1$; b LLE for $S_r=1$; c Poincaré map for $S_r=0.8$; d FFT for $S_r=0.8$; e Poincaré map for $S_r=0.6$; f LLE for $S_r=0.6$

Here, a possible suspicion may be proposed that one would be able to get a very similar result (perhaps even with similar chaotic and n-periodic windows) by maintaining the pristine structure, and instead gradually lowering the temperature (as the bifurcation parameter). For comparison, the resulting bifurcation diagrams with respect to temperature for $S_r=1$ and $S_r=0.8$ are presented in Fig. 4. First, the bifurcation diagram is changed noticeably with 20% stiffness reduced, which concludes that damage level affects the bifurcation diagram. Secondly, comparing with the bifurcation diagram of Fig. 3, we still can find the noticeable difference. Although they all show that the panel oscillates as chaos, periodic, buckled or stable, but still the boundaries between the complex behaviors are changed by the damage level.

Shown in Fig. 5 are the dynamic responses at typical damage levels of $S_r=1,~0.8$ and $S_r=0.6$. Poincaré plots and the largest Lyapunov exponent (LLE) indicate chaos for the healthy panel ($S_r=1$) and the damaged panel with 40% stiffness loss ($S_r=0.6$); in addition, a periodic-3 motion is obtained for the panel with 20% stiffness loss ($S_r=0.8$). For the chaotic motions, the Poincaré map as an attractor differs in the shapes for different damage levels, which however, is a qualitative feature without telling how the shapes deform with the damage level change. In contrast, the LLE as a quantitative measure to evaluate the complex dynamic behavior obtains the values of 2.52 and 3.98 for the chaos generated from $S_r=1$ and $S_r=0.6$, respectively. To understand better the dynamic response in the chaotic regions, the LLE is plotted in terms of the changing $S_r$ in Fig. 6. For buckled and periodic motions, LLE is negative or zero, in comparison, LLE is positive for the chaotic motion and sensitive to the changed damage levels.

To sum up, with the increase in damage level, as has been seen a healthy panel oscillating originally as chaos may oscillate as a periodic or buckled motion due to a local stiffness loss at a certain level. Therefore, as a preliminary supposition, the stability regions defining the boundaries of various complex dynamic behaviors will be affected by the changes of damage level.

A stability analysis is thus carried out for determining the boundaries separating different types of dynamics. Specifically, sweeps in $T/T_\mathrm{cr}=0:5$ and $\lambda =0:400$ are performed with fixing each $T/T_\mathrm{cr}$ and sweep of $\lambda$, and the local deflection extrema are recorded against $\lambda$ in a bifurcation diagram. Based on the points of distribution in bifurcation diagram, the boundaries of Stable flat, Stable buckled, LCO and Periodic/chaos are then recognized. Figure 7 spanned in the parameter space of $T/T_\mathrm{cr}$ and $\lambda$ is mapped out showing the stability regions at different damage levels: $S_r=1,~0.8,~0.6$ and $S_r=0.4$, and it is interesting to note that the difference observed is notable. As has been seen that with the increase in damage level, the flutter boundary for a flat panel is reached at lower dynamic pressure, which however, is increased for a buckled plate conversely. More complicated is that the boundary separating the regions of LCO and periodic/chaos increases notably and nonlinearly.

Fig. 6

LLE in terms of damage level $S_r$

Fig. 7

Stability regions with different damage levels: $S_r=1,~S_r=0.8,~0.6$ and $S_r=0.4$

Table 1 Definition of points A, B and C

Fig. 8

Panel buckled shapes for point A with different $S_r$

Fig. 9

Panel LCO shapes for point B with different $S_r$

Fig. 10

Panel responses for point C with lower damage levels: a Poincaré map for $S_r=1$; b LLE for $S_r=1$; c Poincaré map for $S_r=0.8$; d LLE for $S_r=0.8$

Fig. 11

Panel responses for point C with higher damage levels: a Poincaré map for $S_r=0.6$; b FFT for $S_r=0.6$; c Poincaré map for $S_r=0.4$; d LLE for $S_r=0.4$

Fig. 12

Bifurcation diagram in terms of damage extent $L_d$

Fig. 13

Panel responses for different $L_d$ at $T/T_\mathrm{cr}=4,~\lambda =150$: a Poincaré map for $L_d=1\%$; b LLE for $L_d=1\%$; c Poincaré map for $L_d=6\%$; d LLE for $L_d=6\%$

Three representative points marked as A,  B,  C in Fig. 7 are chosen for further discussions, the specific locations of which in the stability regions are defined in Table 1. At different damage levels, buckled shapes at point A and LCO shapes at point B are displayed in Figs. 8 and 9, respectively. The curves show that a higher damage level results in a larger buckled/LCO deflection, and the change is more obvious for buckled shapes. In contrast, as shown in Figs. 10 and 11, at point C the panel exhibits complex types of motion at different damage levels. The Poincaré maps indicate the panel oscillates as chaos except a periodic-3 motion for $S_r=0.6$ demonstrated in Figs. 11a, b. For the chaotic motions, LLEs are calculated and the values of 2.797,  0.294 and 4.035 are obtained as shown in Figs. 10b, d, and 11d corresponding to $S_r=1,~0.8$ and $S_r=0.4$, respectively. It will be noted that the LLE value is sensitive to the changes of damage level.

Based on the effect study of the damage level above, some concise conclusions can be drawn: (1) changes of damage level may differ the dynamic behaviors of the panel; (2) a higher damage level will tend to reduce the flutter boundary for a flat plate, but increase the one for a buckled plate and also the buckled/LCO deflections; (3) stability regions and Lyapunov exponent are both sensitive to reveal the changes of damage level.

Fig. 14

Stability regions with different damage extents: $L_d=0\%,~L_d=10\%$ and $L_d=20\%$

3.2 Effect of damage extent

Another parameter of interest is damage extent, which is characterized by $L_d$ representing a percentage of the damage length against panel length. For the sake of clarification, a possible damage extent is varying from 0 to 50% (larger than 50% of panel length with stiffness loss is hardly possible, which hence, is not discussed here). Figure 12 plots the bifurcation diagram of panel deflection extrema by varying the damage extent, and $T/T_\mathrm{cr}=4,~\lambda =150,~S_r=0.4,~\xi _d=0.75$ are fixed. It is demonstrated that with the increase in damage extent, the panel oscillates as chaos first and then changes to a dynamically stable buckled motion around $L_d=8\%$. In addition, it is worth noting that the damage extent larger than about $L_d=35\%$ obtains very close buckled deflections. In detail, the chaos induced by $L_d=1\%$ and $L_d=6\%$ are presented in Fig. 13. The Poincaré shapes are qualitatively different, and then, the LLE is calculated and the values of 3.148 and 3.943 for $L_d=1\%$ and $L_d=6\%$, respectively, indicate that a larger damage extent produces a larger LLE value representing a more nonlinear chaos, which is consistent with the effect of damage level.

Figure 14 displays the stability regions involving the boundaries between different types of motion in the parameter space of $T/T_\mathrm{cr}$ and $\lambda$. Typical damage extents of $L_d=0,10\%,~20\%$ and $L_d=40\%$ are considered, with $S_r=0.8,~\xi _d=0.75$ fixed. Compared to the curves in Fig. 7, it will be noted that the damage extent affects the stability regions in a similar way, except that the scale of boundary variations is smaller.

Fig. 15

Panel buckled shapes for point A with different $L_d$

Fig. 16

Panel LCO shapes for point B with different $L_d$

Fig. 17

Panel responses for point C with different $L_d$: a Poincaré map for $L_d=20\%$; b FFT for $L_d=20\%$; c Poincaré map for $L_d=40\%$; d FFT for $L_d=40\%$. Note For $L_d=0$ and $L_d=10\%$, readers are referred to Figs. 10a–d, respectively

Fig. 18

Bifurcation diagram in terms of damage position $\xi _d$

Again points of A,  B and C defined in Table 1 are taken as representatives for further comparisons. Figures 15 and 16 present the buckled and LCO deflection shapes at points A and B, respectively. The results conclude that a larger damage extent produces a larger deflection amplitude for both buckled and LCO motions, and the effect on the buckled motion is more notable. In Fig. 17 are displayed the dynamic responses at point C with different damage extents. It should be noted that the cases of $L_d=0$ and $L_d=10\%$ here are actually the same as the ones of $S_r=1$ and $S_r=0.8$, as shown in Fig. 10a–d, respectively. Only $L_d=20\%$ and $L_d=40\%$ are thus presented herein. The comparison indicates that with the increase in damage extent, the panel oscillates as chaos, a slight chaos, and two periodic-3 motions accordingly. It seems like a decrease in nonlinearity of the system with the increase in damage extent. Until the damage extent increases to a certain damage extent, the panel oscillation will not change anymore. This is peculiar but interesting, which may be discussed further in future work but is not under investigation here for the sake of brevity.

3.3 Effect of damage position

The damage position has been fixed at 75% of the panel length for the discussions above, one might hope, however, to explore the stability regions and nonlinear dynamics with a possible damage occurring at other positions. Figure 18 presents the bifurcation diagram in terms of deflection extrema against damage position varying along the panel length by fixing $T/T_\mathrm{cr}=4,~\lambda =150,~S_r=0.4,~L_d=10\%$. Compared to the bifurcation diagrams of damage level (Fig. 3) and damage extent (Fig. 12), this one is more complicated. It will be noted that the panel oscillates mainly as chaos with damage occurring from the leading to the trailing along the streamwise direction, and between $\xi _d=0.7\sim 0.9$, buckled motions are observed; additionally, periodic and LCO motions occur in the chaos region at some certain damage positions.

Fig. 19

Poincaré maps for different $\xi _d$ at $T/T_\mathrm{cr}=4,~\lambda =150$: a$\xi _d=0.25$; b$\xi _d=0.4$; c$\xi _d=0.6$; d$\xi _d=0.9$

Fig. 20

The largest Lyapunov exponents for different $\xi _d$ at $T/T_\mathrm{cr}=4,~\lambda =150$: a$\xi _d=0.25$; b$\xi _d=0.4$; c$\xi _d=0.6$; d$\xi _d=0.9$

Fig. 21

Stability regions at different damage positions: $\xi _d=0.75,~\xi _d=0.5$ and $\xi _d=0.25$

Take typical damage positions at $\xi _d=0.25,~0.4,~0.6$ and $\xi _d=0.9$ into account with $S_r=0.8,~L_d=10\%$ fixed. The shapes of Poincaré plots shown in Fig. 19 differ for the damage positions aforementioned, from which a qualitative conclusion is drawn that though the panel oscillates as chaos with damage at varying positions, still they are different chaos. Therefore, how on earth they differ from each other is further demonstrated quantitatively with LLE values in Fig. 20. It shows that from the leading to the trailing with the increase of $\xi _d$, the LLE values of 1.4,  2.73,  4.41 and 3.887 increase accordingly with a maximum at $\xi _d=0.6$ and then decreases slightly at $\xi _d=0.9$.

Table 2 Definition of points D, E and F

Fig. 22

Panel buckled shapes for point D with different $\xi _d$

Fig. 23

Panel LCO shapes for point E with different $\xi _d$ at $T/T_\mathrm{cr}=2,~\lambda =250$

Figure 21 plots the stability regions with damages occurring at $\xi _d=0.25,~0.5$ and $\xi _d=0.75$, which represent the leading, middle and trailing of the panel length, respectively. Interestingly, the damage at $\xi _d=0.25$ obtains the lowest flutter boundaries, and the largest boundaries are observed at $\xi _d=0.75$. Apparently, the panel with damage occurring at the leading is the least stable, the possible reason for which is that a disturbance to the supersonic flow only spreads backward rather than forward. The damage to the structure can be taken as a disturbance to the airflow, and the damage (disturbance) at the leading will affect the afterward airflow. With the move of the damage backward, the effect of the disturbance will decrease. So the damage at leading gets the panel the least stable.

Fig. 24

Panel responses for point F with different $\xi _d$: a Poincaré map for $\xi _d=0.75$; b FFT for $\xi _d=0.75$; c Poincaré map for $\xi _d=0.5$; d FFT for $\xi _d=0.5$; e Poincaré map for $\xi _d=0.25$; f LLE for $\xi _d=0.25$

Fig. 25

POMs for different damage levels with $L_d=10\%,~\xi _d=0.75$ fixed at $T/T_\mathrm{cr}=4,~\lambda =210$: a 1st–4th POMs for $S_r=1,~0.9,~0.8$ and $S_r=0.4$; b 5th–8th POMs for $S_r=1$ and $S_r=0.9$

Fig. 26

POMs for different damage extents with $S_r=0.8,~\xi _d=0.75$ fixed at $T/T_\mathrm{cr}=4,~\lambda =210$: a 1st–4th POMs for $L_d=0,~10\%,~20\%$ and $L_d=40\%$; b 5th–8th POMs for $L_d=8\%$ and $L_d=10\%$

Fig. 27

POMs for different damage positions with $S_r=0.8,~L_d=10\%$ fixed at $T/T_\mathrm{cr}=4,~\lambda =190$: a 1st–4th POMs for $\xi _d=0.75,~0.5$ and $\xi _d=0.25$; b 5th–8th POMs for $\xi _d=0.7$ and $\xi _d=0.75$

Specifically, three representative points of D,  E and F defined in Table 2 are selected for further discussions. Shown in Figs. 22 and 23 are the buckled and LCO defection shapes at points D and E, respectively. By contrast, the damages at different positions produce close buckled deflections, while for the LCO motions, the damage at $\xi _d=0.25$ results in the largest LCO deflection and the damage at $\xi _d=0.75$ obtains the smallest one. In an obvious way, the effect of damage position for buckled deflection shape is very tiny, which however, is more notable for LCO. This influence rule is different from the one of the damage level/extent, but still the damage around the leading edge corresponds to the least stable panel. In addition, the dynamic responses at point F are presented in Fig. 24, and the results show that a quasi-periodic, periodic-3 and a chaos are observed for the damage at $\xi _d=0.75,~0.5$ and $\xi _d=0.25$, respectively. As may be seen, the damage position changes the dynamic behaviors and the damage at the leading makes the panel more instable, which is consistent with Figs. 21 and 23.

3.4 Sensitivity of POD modes

Based on the discussions above, stability regions and Lyapunov exponent are sensitive to the damage parametric variations. In order to explore more effective tools for structural damage detection, proper orthogonal decomposition modes (POMs) are calculated and the primary modes and higher-order POMs are both selected for comparison between the healthy and damaged panels. POD method extracts the necessary spatial information to characterize the spatiotemporal complexity and reconstruct the dynamic systems with less dimensions, from a set of temporal snapshots gathered from either numerical simulations or experimental data. In this section, the snapshots are obtained from the Galerkin time responses. To avoid repetition, the definite procedure for POMs generation is omitted here, and for the readers interested, the previous work of authors [44, 45] is suggested for the POD method.

To evaluate the sensitivity of the POMs to the damage parametric variations, the damage level, damage extent and damage position are changed respectively, and the resulting POMs are compared in Figs. 25, 26 and 27 accordingly. Figure 25a demonstrates that the primary POD modes of the 1st–4th ones change dominantly for higher damage level, which however are close to each other for $S_r=1$ and $S_r=0.9$. What is more interesting, the deviation between the POMs for $S_r=1$ and $S_r=0.9$ is growing with the increase in the order of the POD modes. Thus, the higher-order POMs of 5th–8th are compared in Fig. 25b. Obviously, the higher the POM’s order is, the larger deviation between $S_r=1$ and $S_r=0.9$ is, which paves a way for detection of subtle structural damage. In order to further demonstrate the conclusions above, damage extent and damage position are changed and the POMs are compared in Figs. 26 and  27, respectively. A similar phenomenon can be observed that the higher-order POMs are much more sensitive to the structural damage, which will be effective to detect the subtle damage.

To sum up, the POD method is originally a mathematical statistical method for reconstruction of the high-order complex system with less dimensions, for which the primary POD modes are worth attention and the higher-order POMs are usually omitted. In this work however, the higher-order POMs are demonstrated to be much more sensitive to the subtle structural damage than the primary ones. The possible reason lies in that the subtle damage is a small scale of variation to the system, which hence cannot alter the global natural modes (primary POMs) but can change the modes with small scale (higher-order POMs). The higher-order POD modes will be effective for subtle damage detection in future work.

4 Concluding remarks

The objective of the present study is to obtain the influence rules of the damage parametric changes to the aeroelastic stabilities of a fluttering panel in supersonic flow, as well as to explore some effective nonlinear tools for structural health monitoring with high sensitivity. The structural damage is modeled as a local bending stiffness loss, which is quantified with nondimensional parameters of $S_r,~L_d$ and $\xi _d$ representing the damage level, extent and position, respectively. Bifurcation diagram, stability regions, Poincaré map and Lyapunov exponent are all exploited as nonlinear tools to provide an important insight into the effects of the damage parametric changes on the complex dynamic behaviors and flutter boundaries. Specially, POD modes are calculated and compared for damage parametric changes. Some main conclusions can be drawn from the numerical results:

• 1. Stability regions as a notable tool are mapped out in this study, which are demonstrated to be effective and sensitive to reveal the incipient damage parameter changes, whether for damage level, damage extent or damage position.

• 2. Damage level and extent affect in a qualitatively similar way that with the increase in damage level/extent, the flutter boundary for a flat panel is reduced subtly, but conversely the flutter boundary for a buckled plate and the deflection amplitude are both increased. Quantitatively, the damage level has a greater influence.

• 3. Comparison of damage positions at 1 / 4,  1 / 2 and 3 / 4 of the panel length demonstrates that the damage occurred around the leading edge makes the panel the most instable with minimum flutter boundaries and maximum deflection amplitudes.

• 4. For chaotic motions, the largest Lyapunov exponent is proved to be sensitive for identification of subtle damage changes. A larger damage level/extent tends to obtain a chaotic response with a larger LLE value, which can thus be used as an effective tool to detect structural damage.

• 5. Compared to the primary POD modes, the higher-order POD modes are demonstrated much more sensitive to subtle structural damage, which may provide another effective way for damage detection in future work.