Nonlinear aeroelastic behavior of a panel impinged by oscillating shock

Abstract

The aeroelastic responses and nonlinear behaviors of a two-dimensional panel impinged by an oscillating Mach stem shock are investigated through theoretical analysis. Through the nonlinear descriptors, such as Poincaré maps and Largest Lyapunov exponents, the panel with oscillating shock impingement is found to exhibit multiple responses, including single/multi-periodic limit cycle oscillation, quasi-periodic motion, and chaotic motion. Without altering the in-plane force, which is the principal source of structural nonlinearity, the shock oscillation complicates the nonlinear behaviors of the panel. With shock oscillation, the original divergence instability is transformed into post-divergence limit cycle oscillation, and the flutter response exhibits rich nonlinear characteristics. The effect of initial shock impingement location, shock oscillating amplitude, and shock oscillating frequency are disclosed through the bifurcation diagram, which significantly influences the nonlinear characteristics of the panel response. By reasonably adjusting the shock oscillating parameters, unpredictable nonlinear behaviors, especially chaotic motions, can be avoided.

1 Introduction

Panel aeroelastic instability, leading to undesirable structural fatigue and damage, is of great concern for supersonic/hypersonic vehicles, on which enormous investigations have been conducted [1, 2]. Shock waves are unavoidable when traveling at supersonic speed, which results in severe aerodynamic and thermal loads, aggravating the aeroelastic effects. Besides, as a primary source of aerodynamic nonlinearity, shock waves might have significant impacts on the nonlinear behaviors of panel responses [3]. In recent years, the panel aeroelasticity in shock-dominated flow, which can also be referred to as shock-induced panel aeroelasticity has aroused the interest of researchers [4, 5].

In most research on panel aeroelastic performance in shock-dominated flow, stationary shock impingement is widely considered. However, for high-speed vehicles, the aircraft maneuver, control surface operation, and aeroelastic behavior itself can form oscillating/moving shock waves on the fuselage panel [6]. Similarly, for the hypersonic inlet/isolator for scramjets, the shock oscillation is a prominent characteristic of the internal flow field [7]. The shock oscillation results in the non-stationary shock strengths and impingement, dispersing the aerodynamic pressure loads, which might have a significant effect on the aeroelastic behavior of the panel. Early in 1967, Croker [8] noticed the panel aeroelastic problem with oscillating and moving shock impingement and conducted a theoretical analysis. Recently, some research on panel aeroelasticity has taken the moving/oscillating shock impingement into consideration [9,10,11,12], which disclosed the unique impacts of shock motions on the panel aeroelastic response. However, the nonlinear characteristics of panel response with non-stationary shock impingement remain unexplored.

Due to the nonlinear elements contained in the panel aeroelastic system, the panel flutter exhibits complex dynamic behaviors[13]. Dowell [14, 15] revealed the nonlinear limit cycle oscillations (LCOs) and chaotic motions of a fluttering panel and summarized the helpful nonlinear descriptors, especially phase plane portraits and Poincaré maps, when detecting the essential structure of the panel response. With advanced methods introduced into the field, such as bifurcation diagram, largest Lyapunov exponent (LLE), and proper orthogonal decomposition (POD), the relevant research on the nonlinear behavior of panel response was then extended to different panels, such as damaged panel [16], viscoelastic panel [17], and cantilever panel [18], and different flow conditions, such as both-side flow [19], turbulent flow [20] and shock-dominated flow [21]. Usually, the complicated nonlinear behaviors of panel response are induced by the variation of in-plane force, which is the principal source of structural nonlinearity.

The existing studies regarding non-stationary shock have only taken the oblique shock impingement forming regular reflection into consideration. However, the situation in Mach reflection, as a main category of shock reflection [22], is worth further investigation. Compared with the regular reflection, the Mach reflection contains an additional Mach stem shock close to the panel, forming both supersonic regions and subsonic regions in the flowfield, which complicates the panel aeroelastic response and stability. Depending on the shock impingement location, the panel impinged by stationary Mach stem shock exhibits multiple aeroelastic instabilities, including divergence, flutter, and post-divergence flutter [23]. The post-divergence flutter is a unique instability situation, which indicates that the panel experiences flutter instability while retaining the static deflection due to divergence instability. With the non-stationary shock impingement location, the oscillating Mach stem shock might significantly change the aeroelastic instability and nonlinear behavior of the panel.

In this paper, the aeroelastic responses and nonlinear behaviors of a two-dimensional panel impinged by an oscillating Mach stem shock are investigated through theoretical analysis. The paper is organized as follows. Following the introduction, the aeroelastic theories, with which the panel aeroelastic model is established, and nonlinear descriptors are introduced in Sect. 2. The nonlinear characteristics of panel responses are analyzed with nonlinear descriptors in Sect. 3. In particular, the complicated nonlinear behaviors induced by shock oscillation are disclosed in Sect. 3.1. The effects of initial shock impingement location, shock oscillation amplitude, and shock oscillation frequency are revealed respectively in Sect. 3.2, 3.3, and 3.4. The main conclusions drawn from the present investigation are summarized in Sect. 4.

2 Modeling

2.1 Aeroelastic theory

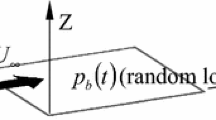
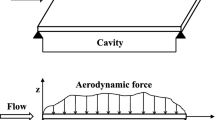
As shown in Fig. 1, a two-dimensional panel with both ends simply supported impinged by oscillating Mach stem shock is considered. For concision, the curvature of shock waves is ignored in the schematic. The three-shock theory is utilized to describe the flow structure of Mach reflection, where the Mach stem can be approximated as a normal shock.

Usually, the shock oscillations contain a limited number of frequencies, which stem from the motion of the shock generator. In the previous experimental and numerical research [6, 10], the shock generator experienced sinusoidal oscillations with a single frequency to induce shock oscillation. Thus, the Mach stem shock is also assumed to oscillate in the form of simple harmonic motion in the paper. The oscillating shock impingement location on the panel can be expressed as

$$\begin{aligned} x_T(t)=x_{T,0}+a\sin (\omega t) \end{aligned}$$

(1)

where $x_{T,0}$ represents the initial shock impingement location, which is the central position of the shock oscillation, a and $\omega$ represents shock oscillating amplitude and frequency respectively.

Fig. 1

Schematic of a two-dimensional panel impinged by oscillating Mach stem shock

Focusing on the nonlinear behavior of the panel response induced by oscillating shock impingement, the temperature of the whole panel and its supports are assumed to be the same, and the static pressure differential across the panel is ignored. According to the von Kármán large deflection plate theory, the coupled partial differential governing equation of motion for the panel is established as

$$\begin{aligned} D\frac{\partial ^{4} w}{\partial x^{4} } -N_{x} \frac{\partial ^{2} w}{\partial x^{2} }+c\frac{\partial w}{\partial t}+\rho h\frac{\partial ^{2} w}{\partial t^{2} }+q_a=0, \end{aligned}$$

(2)

where the in-plane force can be expressed as

$$\begin{aligned} \quad N_{x}=\frac{Eh}{2l\left( 1-v^{2} \right) } \int _{0}^{l} \left( \frac{\partial w}{\partial x} \right) ^{2}dx. \end{aligned}$$

(3)

The structural damping c is also included here, which is essential to correctly reflect the divergence instability [24].

The governing equation for the panel can be nondimensionalized as

$$\begin{aligned} \frac{\partial ^{4} W}{\partial \xi ^{4} } -R_{x} \frac{\partial ^{2} W}{\partial \xi ^{2} }+C\frac{\partial W}{\partial \tau }+\frac{\partial ^{2} W}{\partial \tau ^{2} }+\bar{q_a}=0. \end{aligned}$$

(4)

The shock impingement location in Eq. 1 can then be expressed in the nondimensional form:

$$\begin{aligned} \xi _T(t)=\xi _{T,0}+A\sin (\bar{\omega } t), \end{aligned}$$

(5)

where the dimensionless parameters are defined in Appendix A.

2.2 Aerodynamic pressure theory

The impingement of Mach stem shock forms a supersonic region and a subsonic region above the panel, where the unsteady pressure loads are calculated separately.

For the supersonic region ahead of the Mach stem shock, the quasi-steady first-order piston theory is employed to evaluate the unsteady aerodynamic pressure for its simplicity and accuracy, which can be expressed as

$$\begin{aligned} q_{a}=\frac{2 q_{\infty }}{\sqrt{M_{\infty }^{2}-1}}\left( \frac{\partial w}{\partial x}+\frac{M_{\infty }^{2}-2}{M_{\infty }^{2}-1} \frac{1}{U_{\infty }} \frac{\partial w}{\partial t}\right) . \end{aligned}$$

(6)

An additional discussion on the impacts of the order of piston theory is provided in Appendix B.

For the subsonic region behind the Mach stem shock, where the flow is compressible, the compressibility-corrected potential theory is applied to evaluate the unsteady aerodynamic pressure. The compressibility-corrected potential theory is a modification of classical potential theory by introducing a Prandtl-Glauert compressibility correction, which has been verified and proved to be valid and efficient [23]. The aerodynamic pressure can be expressed as

$$\begin{aligned} \begin{aligned}&q_{a}= \frac{1}{\sqrt{1-M^{2}_{\infty }}} \\ {}&\left[ \frac{\rho _{\infty } }{\pi }\int _{0}^{l}\left( \frac{\partial ^{2} w}{\partial t^{2} }+U^{2}\frac{\partial ^{2} w}{\partial t\partial x } \right) \ln _{}{\left| \frac{x-\xi }{l} \right| } d\xi \right. \\ {}&\left. +\frac{\rho _{\infty } }{\pi }\oint _{0}^{l} \left( U\frac{\partial w}{\partial t}+U^{2}\frac{\partial w}{\partial x} \right) \frac{1}{x-\xi }d\xi \right] , \end{aligned} \end{aligned}$$

(7)

where the integral symbol $\oint$ means Cauchy’s principal value to avoid an improper integral.

2.3 Galerkin approach

To solve the 4th-order partial differential equation, the Galerkin method is employed to discretize the continuous system into a multi-degree-of-freedom system. Considering the simply supported boundary conditions, the lateral displacement can be expressed as

$$\begin{aligned} W\left( \xi ,\tau \right) =\sum _{i=1}^{N}q_{i}\left( \tau \right) \sin \left( i\pi \xi \right) , \end{aligned}$$

(8)

where $q_{i}( \tau )$ are the generalized coordinates.

By substituting the expression into Eq. 4 and multiplying by another set of the primary spatial function and integrating from 0 to 1, the discrete motion equations are obtained.

$$\begin{aligned} \begin{aligned}&\frac{q_{j}\left( j\pi \right) ^4}{2}+3q_{j}\left( j\pi \right) ^2\left[ \sum _{r=1}^{N}\frac{{q_{r}}^{2}}{2}\left( r\pi \right) ^2 \right] \\ {}&\quad \quad +\frac{1}{2}\ddot{q_j}+Q+\frac{1}{2}C\dot{q_j}=0 \end{aligned} \end{aligned}$$

(9)

The equation above is a set of nondimensional ordinary differential equations, where the term Q represents the aerodynamic pressures terms with details given in Appendix C. By assuming that $\dot{q_i}=q_{i+N}$, the motion equations are converted into 1st-order ordinary differential equations, which are solved by the 4th-order Runge–Kutta direct numerical integration method.

2.4 Nonlinear descriptor

Although the observation of time history can provide intuitive results to identify the periodicity of the panel response, the potential long-periodic and quasi-periodic motion will lead to the mistaken identification of nonlinear behavior. Thus, nonlinear descriptors are essential to analyze the panel response, identifying the nonlinear behaviors [25].

In this paper, the bifurcation diagrams, Poincaré maps, frequency spectra, and largest Lyapunov exponent are calculated and plotted as follows:

• (1) Bifurcation diagrams: Usually, for the panel aeroelastic system, the bifurcation diagrams are plotted in terms of dynamic pressure $\lambda$ to observe the pre/post-chaotic behaviors. Recalling Eq. 5, the oscillating shock impingement introduces additional systemic parameters including $\xi _{T,0}$, A, and $\omega$, into the aeroelastic system. To investigate the potential effect of these parameters on the nonlinear behavior, the bifurcation diagrams are plotted by sweeping these parameters and recording the local deflection extrema of the panel response.

• (2) Poincaré maps: The Poincaré maps reduce the phase plane portraits into discrete points, which provide an intuitive way to qualitatively identify different motions. For the panel aeroelastic model, an autonomous system, the plots of Poincaré diagrams are based on the occurrence of an event. In this paper, $\xi =0.50$ is chosen as the identifying/event point. Considering the potential divergence instability, the event is defined as the deflection of $\xi =0.50$ reaching the post-divergence position with a positive velocity. The deflection and velocity of the typical point are recorded when the event occurs.

• (3) Frequency spectra: the Fast Fourier Transform (FFT) is utilized to obtain the frequency spectra of the panel response. The frequency spectra are characterized by sharp peaks for regular motions but by broadband behavior for chaotic motions.

• (4) Largest Lyapunov exponent (LLE): The largest Lyapunov exponent provides a quantitative measure to identify the chaotic motion: $LLE>0$, chaotic motion; $LLE \le 0$, regular motion. In this paper, the largest Lyapunov exponent is calculated according to the procedure indicated in [26], for which Xie et al. [16] provided a concise procedure description.

3 Results and discussions

The flow properties applied in this paper are listed in Table 1, in which the Mach number behind the Mach stem and the dynamic pressure ratio are calculated through normal shock theory. The panel response at $\xi =0.75$ as a typical location is analyzed, with which figures are plotted. Considering the sensitivity of chaotic motion and divergence instability to the initial condition, the initial condition of $q_1=0.1$ is applied.

Table 1 Flow properties

Fig. 2

Bifurcation diagram in terms of dynamic pressure $\lambda$ with a stationary shock impingement and b oscillating shock impingement

Fig. 3

Panel responses with different freesteam dynamic pressure $\lambda$: a $\lambda =345$; b $\lambda =370$; c $\lambda =480$; d $\lambda =500$

3.1 Nonlinear response induced by shock oscillation

To investigate the impact of shock oscillation on the nonlinear characteristics of panel response, the bifurcation diagrams in terms of freestream dynamic pressure are compared between stationary shock impingement and oscillating shock impingement as shown in Fig. 2, in which the freestream dynamic pressure increases from $\lambda =300$ to $\lambda =500$ with a step increment of $\Delta \lambda =1$. The shock impingement location is set as $\xi _{T,0}=0.70$. For the oscillating shock impingement, the nondimensional shock oscillating amplitude and frequency are $A=0.1$ and $\bar{\omega }=10$ respectively.

For the stationary shock impingement, the Hopf bifurcation occurs at $\lambda =339$, which represents that the panel experience flutter instability and forms limit cycle oscillation (LCO). For the oscillating shock impingement, the bifurcation diagram is relatively complicated. The onset of flutter instability occurs at $\lambda =343$, which has little change. However, the panel response contains potential quasi-periodic motions, multi-periodic LCOs, and chaotic motions. The shock oscillation significantly enrich the nonlinear characteristics of panel responses.

To further reveal the nonlinear characteristics of panel response with oscillating shock impingement, the time history, phase diagram, Poincaré map and frequency spectra are plotted for the panel response at typical dynamic pressure as shown in Fig. 3. The largest Lyapunov exponent is additionally plotted for the chaotic motion. For $\lambda =345$, the Poincaré map display a trajectory in the form of a torus, which indicates a quasi-periodic motion. For $\lambda =370$ and $\lambda =480$, a periodic-5 LCO and a periodic-6 LCO are observed, with the Poincaré map consisting of a set of five/six points. For $\lambda =500$, a positive value of $LLE=0.96$ is obtained, which demonstrates the panel response exhibits a chaotic motion. The cloud of unorganized points in the Poincaré map is consistent with the identification.

The shock oscillation significantly complicates the nonlinear behavior of the panel response without altering the in-plane force. With the introduction of shock oscillation, the flutter instability displays rich nonlinear characteristics, including single/multi-periodic LCOs, quasi-periodic motions, and chaotic motions, instead of simply single-periodic LCOs.

3.2 Effect of initial shock impingement location

In the previous research on the panel aeroelastic stability in Mach reflection, the shock impingement location is found to determine the panel instability types, including flutter, divergence, and post-divergence flutter. Considering the crucial effect of shock impingement location on the panel aeroelastic instability, the initial impingement location of oscillating shock is likely to have a significant impact on the nonlinear behaviors of the panel.

Fig. 4

Bifurcation diagram in terms of initial shock impingement location $\xi _{T,0}$

The bifurcation diagram is plotted in terms of initial shock impingement location $\xi _{T,0}$ at $\lambda =600$ as shown in Fig. 4, in which the initial shock impingement location increases from $\xi _{T,0}=0.10$ to $\xi _{T,0}=0.90$ with a step increment of $\Delta \xi _{T,0}=0.01$. The nondimensional shock oscillating amplitude and frequency are $A=0.1$ and $\omega =10$ respectively. With initial shock impingement location $\xi _{T,0}=0.10\sim 0.48$, the panel response exhibits post-divergence single-periodic LCO, whose amplitude increases with initial shock impingement location; With initial shock impingement location $\xi _{T,0}=0.49\sim 0.71$, the panel response exhibits periodic LCO and chaotic motion alternately; With initial shock impingement location $\xi _{T,0}=0.72\sim 0.90$, the panel response only exhibits quasi-periodic motion. As shown in Fig. 5, the largest Lyapunov exponents are plotted in terms of initial shock impingement location to show the nonlinear characteristics of the panel response. It can be seen the largest Lyapunov exponent is sensitive to the initial shock impingement location.

Fig. 5

Largest Lyapunov diagram in terms of initial shock impingement location $\xi _{T,0}$

Fig. 6

a Panel LCO shapes and b Panel divergence shapes with different initial shock impingement location

For the panel with stationary shock impingement at its leading portion, the panel exhibits divergence instability. With the introduction of shock oscillation, the divergence instability is transformed to the post-divergence single-periodic LCO, which is worth further discussion. The panel LCO shapes and divergence shapes with different initial shock impingement locations are plotted in Fig. 6. Usually, the peak of the LCO amplitude emerges near the 3/4 chord of the fluttering panel [27], which is also the situation for the panel with stationary shock impingement. However, the LCOs induced by oscillating shock exhibit distinct characteristics with the peak emerging at the leading portion of the panel, moving backward with the increase of initial shock impingement location. Similarly, the peak of divergence amplitude moves backward with increasing initial shock impingement location. The moving backward of initial shock impingement location results in the aggravation of oscillation but suppression of divergence.

Fig. 7

Panel responses with different initial shock impingement location $\xi _{T,0}$: a $\xi _{T,0}=0.40$; b $\xi _{T,0}=0.51$; c $\xi _{T,0}=0.70$; d $\xi _{T,0}=0.80$

To investigate the nonlinear behavior of the panel response, the time history, phase diagram, Poincaré map and frequency spectra are plotted for the panel response at typical initial shock impingement location as shown in Fig. 7. The largest Lyapunov exponent is additionally plotted for the chaotic motion. Despite multiple local amplitude extrema displayed in the bifurcation diagram, the panel response exhibits single-periodic LCO for $\xi _{T,0}=0.51$ with a single point displayed in the Poincaré map. The phase diagram shows there exist two twists for the limit cycle, which accounts for the extra local amplitude extrema. For $\xi _{T,0}=0.70$, a chaotic motion is observed with a positive value of $LLE=1.18$. For $\xi _{T,0}=0.40$ and $\xi _{T,0}=0.80$, a single-periodic LCO and a quasi-periodic motion are observed respectively.

In general, the initial shock impingement location significantly influences the nonlinear behaviors of panel responses. With oscillating Mach stem shock impinging at the leading portion, the panel tends to exhibit regular motions in the form of post-divergence LCOs, whose amplitude distribution is different from the classical fluttering panel. With oscillating Mach stem shock impinging at the trailing portion, the panel tends to exhibit complicated nonlinear behaviors, including chaotic motions and quasi-periodic motions. By reasonably arranging the initial shock impingement location, the complicated chaotic motion of the panel can be avoided.

3.3 Effect of shock oscillating amplitude

Fig. 8

Bifurcation diagram in term of shock oscillating amplitude A

Fig. 9

Largest Lyapunov diagram in terms of shock oscillating amplitude A

Fig. 10

a Panel LCO shapes and b Panel divergence shapes with different shock oscillating amplitude

The shock oscillation leads to the change of proportion of the supersonic region and subsonic region, which results in the variation in the aerodynamic load distribution, inducing complicated nonlinear behaviors. With the enlargement of the shock oscillating amplitude, the change becomes more intense, whose effects are of interest.

The bifurcation diagram is plotted in terms of nondimensional shock oscillating amplitude A at $\lambda =500$ as shown in Fig. 8, in which the oscillating amplitude increases from $A=0.0$ to $A=0.4$ with a step increment of $\Delta A=0.05$. It should be noticed that $A=0.0$ represents the stationary shock impingement. The initial shock impingement location is at $\xi _{T,0}=0.40$ and nondimensional shock oscillating frequency $\bar{\omega }=10$. With shock oscillating amplitude $A=0.000\sim 0.150$, the panel response exhibits post-divergence single-periodic LCO, whose amplitude increases with the shock oscillating amplitude; With shock oscillating amplitude $A=0.155\sim 0.315$, the panel response exhibits chaotic motions, multi-periodic LCOs, and post-divergence single-periodic LCOs alternately; With shock oscillating amplitude $A=0.320\sim 0.400$, the panel response exhibits only multi-periodic LCOs. As shown in Fig. 9, the largest Lyapunov exponents are plotted in terms of shock oscillating amplitude to show the nonlinear characteristics of the panel response. It can be seen the largest Lyapunov exponent is sensitive to the shock oscillating amplitude. The positive LLE representing chaotic motions are obtained with moderate shock oscillating amplitude.

Fig. 11

Panel responses with different nondimensional shock oscillating amplitude A: a $A=0.14$; b $A=0.27$; c $A=0.30$; d $A=0.35$

Similar to the effect of initial shock impingement location, the increase of shock oscillating amplitude results in the increases of LCO amplitude. The panel LCO shapes and divergence shapes with different shock oscillating amplitude are plotted in Fig. 10. The increase of shock oscillating amplitude leads to a larger LCO amplitude, but its impact on divergence amplitude is relatively limited, which decreases slightly. However, the shock oscillating amplitude has few effects on the distribution of the LCO and divergence amplitude, whose peaks remain unmoved. It seems that the initial shock impingement location is the only shock parameter having an obvious impact on the distribution of divergence and LCO amplitude.

The time history, phase diagram, Poincaré map and frequency spectra are plotted for the panel response at typical nondimensional shock oscillating amplitude as shown in Fig. 11. The largest Lyapunov exponent is additionally plotted for the chaotic motion. For $A=0.14$ and $A=0.27$, post-divergence single-periodic LCOs are observed with one-side twist formed for the limit cycle in the phase diagram. For $A=0.30$, a chaotic motion is observed with a positive value of $LLE=1.68$. For $A=0.35$, a 3-periodic LCO is observed.

Similar to the initial shock impingement location, the impact of shock oscillating amplitude on the nonlinear behavior of the panel is obvious. With small shock oscillating amplitude, the panel displays post-divergence LCOs; with moderate shock oscillating amplitude, the panel displays chaotic motions and single-periodic LCOs; with large shock oscillating amplitude, the panel displays multi-periodic LCOs.

3.4 Effect of shock oscillating frequency

The shock oscillating frequency also influence the intensity of shock oscillation, whose influence is worth discussion. Besides, the coupling between the natural frequency of the panel and the shock oscillating frequency is of interest.

The bifurcation diagram is plotted in terms of nondimensional shock oscillating frequency $\bar{\omega }$ at $\lambda =600$ as shown in Fig. 12, in which the oscillating frequency increases from $\bar{\omega }=0$ to $\bar{\omega }=80$ with a step increment of $\Delta \bar{\omega }=1$. It should be noticed that $\bar{\omega }=0$ represents the stationary shock impingement. The initial shock impingement location is at the midpoint of the panel $\xi _{T,0}=0.50$ and nondimensional shock oscillating amplitude $A=0.1$. With shock oscillating frequency $\bar{\omega }=0\sim 42$, the panel response exhibits post-divergence LCO and chaotic motion alternately, whose amplitude increases with the shock oscillating frequency; With shock oscillating frequency $\bar{\omega }=43\sim 47$, the panel response exhibits only periodic LCO without divergence instability; With shock oscillating frequency $\bar{\omega }=48\sim 67$, the panel response exhibits chaotic motions; With shock oscillating frequency further increases, the panel response exhibits post-divergence periodic LCO again. As shown in Fig. 13, the largest Lyapunov exponents are plotted in terms of shock oscillating frequency to show the nonlinear characteristics of the panel response. It can be seen the largest Lyapunov exponent is sensitive to the shock oscillating frequency. Compared with the other two shock oscillating parameters, the LLE distribution for shock oscillating frequency is more complicated, with two main regions of chaotic motions.

Fig. 12

Bifurcation diagram in term of shock impingement location $\xi _T$

Fig. 13

Largest Lyapunov diagram in terms of shock oscillating frequency $\bar{\omega }$

The shock oscillation introduces an additional frequency content into the aeroelastic system. It is wondered whether the relation between shock oscillating frequency and natural frequencies of the panel will have impacts on the nonlinear behaviors of the panel response. For an undamped panel aeroelastic system, the j-th order nondimensional natural frequency can be expressed as $(j\pi )^2$. Although a structural damping c is introduced into the present aeroelastic system to properly evaluate the divergence instability, the damping is too tiny to have an essential influence on the natural frequency.

To investigate the relation between the frequencies, the bifurcation diagram in terms of freestream dynamic pressure with shock oscillating frequency $\bar{\omega }=20$ is plotted as shown in Fig. 14, in which the freestream dynamic pressure increases from $\lambda =300$ to $\lambda =500$ with a step increment of $\Delta \lambda =1$. The initial shock impingement $\xi _{T,0}=0.7$ and shock oscillating amplitude $A=0.1$. Comparing Fig. 14 with Fig. 2(b), it can be seen that the nonlinear behaviors for $\bar{\omega }=20$ display more regular motions than that for $\bar{\omega }=10$, which is quite close to the first-order natural frequency of the panel. Besides, the chaotic motions display distinct characteristics for the two shock oscillating frequencies. The local amplitude extrema for chaotic motions fills the plane of the bifurcation diagram for $\bar{\omega }=20$ while forming a gap for $\bar{\omega }=10$. Recalling Fig. 3(d) for $\bar{\omega }=10$, the orbits in the phase diagram remain close to some periodic motion orbit and the frequency spectra show certain frequency spikes, which can be classified as limited or narrow-band chaos [25].

Fig. 14

Bifurcation diagram in term of dynamic pressure $\lambda$ with shock oscillating frequency $\bar{\omega }=20$

Fig. 15

Panel responses with different nondimensional shock oscillating frequency $\bar{\omega }$: a $\bar{\omega }=17$; b $\bar{\omega }=30$; c $\bar{\omega }=45$; d $\bar{\omega }=50$

The time history, phase diagram, Poincaré map and frequency spectra are plotted for the panel response at typical nondimensional shock oscillating frequency as shown in Fig. 15. For $\bar{\omega }=17$ and $\bar{\omega }=45$, a post-divergence single-periodic LCO and a normal single-periodic LCO are observed. For $\bar{\omega }=30$, a quasi-periodic motion is observed with the Poincaré map displaying the shape of a torus. For $\bar{\omega }=50$, a chaotic motion is observed with a positive value of $LLE=3.33$.

In the same way, the shock oscillating has an obvious impact on the nonlinear characteristics of the panel response. Differently, the relation between shock oscillating frequency and the natural frequency of the panel also plays an important role. With shock oscillating frequency close to the natural frequency, the panel is more likely to exhibit chaotic motions, which shows the characteristics of limited or narrow-band chaos.

3.5 Effect of multi-frequency shock oscillation

In the above-mentioned discussions, the shock oscillation is assumed as a simple harmonic motion with a single frequency. However, shock oscillation with a limited number of frequencies is also likely to be encountered, whose impacts are of concern. Thus, a preliminary exploration is conducted here to investigate the influence of an additional frequency. Here, a doubling frequency is introduced for the multi-frequency shock oscillation, which can be expressed as

$$\begin{aligned} \xi _T=\xi _{T,0}+A_1\sin (\bar{\omega }t)+A_2\sin (2\bar{\omega }t) \end{aligned}$$

(10)

where $A_1$ and $A_2$ are the amplitude of the basic and doubling frequency content.

The bifurcation diagram in terms of freestream dynamic pressure with multi-frequency oscillating shock impingement is plotted as shown in Fig. 16. The freestream dynamic pressure increases from $\lambda =300$ to $\lambda =500$ with a step increment of $\Delta \lambda =1$. The initial shock impingement $\xi _{T,0}=0.7$, shock oscillating amplitude $A_1=A_2=0.5A$ and basic shock oscillating frequency $\bar{\omega }=20$. Comparing Fig. 16 and Fig. 14, it can be seen that the introduction of an additional frequency significantly alters the bifurcation characteristics of the panel response. To further illustrate the impact of an additional frequency, the time history, phase diagram, Poincaré map, and frequency spectra of the panel response at $\lambda =380$ are plotted for single-frequency and multi-frequency shock impingement as shown in Fig. 17. For comparison, the coordinates are on the same scale. For $\lambda =380$, 3-periodic LCOs are observed for both two cases, exhibiting different characteristics. The additional frequency results in a higher flutter amplitude and a larger limit cycle in the phase diagram. Furthermore, from the frequency spectra, the introduction of a doubling frequency excites the panel response with more high-frequency contributions.

Fig. 16

Bifurcation diagram in term of dynamic pressure $\lambda$ with multiple shock oscillating frequency

Fig. 17

Panel responses at $\lambda =380$ with a single-frequency and b multi-frequency shock impingement

Fig. 18

Phase diagram with different frequency content proportion: a $A_1=0.2A$; b $A_1=0.4A$; c $A_1=0.6A$; d $A_1=0.8A$

To further disclose the interplay between frequency content in the shock and panel dynamics, the effects of the proportion of frequency content, namely the amplitude of each frequency content, are investigated. The phase diagrams of the aeroelastic response obtained with different frequency content proportions are plotted as shown in Fig. 18, in which the Poincáre points are also labeled. When the doubling frequency dominates the shock oscillation, the panel response exhibits a quasi-periodic motion. As the portion of basic frequency increases, the panel response transits to a 3-periodic LCO, whose shape in the phase diagram remains sensitive to the change in the portion of frequency content.

The nonlinear behaviors of the panel impinged by multi-frequency oscillating shock represent complicated dynamics, which may provide valuable insights into the chaotic motions induced by shock/boundary-layer interactions (SBLIs). In recent research [28, 29], potential chaotic motions were observed in the panel aeroelastic response induced by SBLIs. The SBLIs are believed to be the source of such complicated nonlinear behavior since the aperiodic motions do not exist for the steady inviscid shock impingement case. The sensitivity of nonlinear characteristics to the shock frequency content may provide a potential explanation for the complicated nonlinear behaviors of a panel subjected to SBLIs, where a wide range of frequencies dominates the spectrum. However, further evidence from numerical simulations and wind tunnel experiments is necessary to support the explanation in the future.

4 Conclusion

In this paper, the aeroelastic model of a two-dimensional simply supported panel impinged by oscillating Mach stem shock is established. With nonlinear descriptors, the nonlinear behaviors of the panel are investigated. The effect of initial shock impingement location, shock oscillating amplitude, and shock oscillating frequency are revealed through the bifurcation diagram. The main conclusions are drawn as follows:

(1) The shock oscillation induces complicated nonlinear behaviors of the panel without altering the in-plane force of the panel, which is the principal source of structural nonlinearity. With shock oscillation, the original divergence instability is transformed into post-divergence single-periodic LCO, and the original flutter instability is enriched with nonlinear characteristics. The panel impinged by oscillating Mach stem shock exhibits multiple responses, including (post-divergence) single/multi-periodic LCOs, quasi-periodic motions, and chaotic motions.

(2) Compared with classical panel flutter instability in supersonic flow, the LCO induced by oscillating Mach stem shock exhibits distinct characteristics, whose peak amplitude emerges at the leading portion of the panel. Both the initial shock impingement location and shock oscillating amplitude influence the LCO amplitude and divergence amplitude. However, only the initial shock impingement location has a significant impact on the distribution of LCO amplitude and divergence amplitude.

(3) The nonlinear behaviors of the panel are sensitive to the systemic parameters, including initial shock impingement location, shock oscillating amplitude, and shock oscillating frequency. By reasonably arranging the oscillating shock parameters, the large amplitude chaotic motions and quasi-periodic motions can be avoided and replaced with post-divergence LCOs.

(4) Depending on the relation between shock oscillating frequency and the natural frequency of the panel, it exhibits distinct nonlinear characteristics. With the shock oscillating frequency close to the natural frequency, the panel response tends to exhibits limited or narrow-band chaos.

Appendices

Nondimensional parameters

The nondimensional parameters utilized are listed as follow:

$$\begin{aligned} \begin{aligned}&\xi =\frac{x}{l},\quad W=\frac{w}{h},\quad A=\frac{a}{l}\\&\tau =t\sqrt{\frac{D}{\rho hl^4}},\quad \bar{\omega }=\omega \sqrt{\frac{\rho hl^4}{D}} \\&\mu =\frac{\rho l}{\rho _mh},\quad C=\frac{l^4}{Dh}c\\&\lambda _1=\frac{2q_1l^3}{\sqrt{{M_1}^2-1}D},\quad \lambda _2=\frac{2q_2l^3}{D},\\&R_x=\frac{N_xl^2}{D}=6\int _{0}^{1}(\frac{\partial W}{\partial \xi })^2d\xi . \end{aligned} \end{aligned}$$

Effect of the order of piston theory

To tell the effects of the order of piston theory, we compare the flutter amplitude obtained by the 1st-order and 3rd-order piston theories in the supersonic flow and steady Mach reflection as shown in Fig. 19. For the supersonic flow case, the adoption of the 3rd-order piston theory results in a larger flutters amplitude but does not influence the critical flutter dynamic pressure. However, for the Mach reflection case, the difference between the 1st-order and 3rd-order piston theory becomes smaller. This may be because the supersonic region, where the aerodynamic pressure is evaluated by the piston theory, is narrowed with the introduction of Mach reflection.

Fig. 19

Comparison in flutter amplitude between 1st-order and 3-order piston theory

To reveal the impact of the order of piston theory on the nonlinear behaviors of the panel, a comparison is also conducted on the bifurcation diagram obtained by the two theories. Figure 4 is recomputed through 3rd-order piston theory and plotted as shown in Fig. 20. Although the application of 3rd-order piston theory further complicates the bifurcation characteristics of the panel response, it still exhibits a similar distribution with the results computed through 1st-order piston theory and does not affect the relevant conclusions. The 1st-order piston theory is sufficient to provide crucial qualitative knowledge and insights into the nonlinear dynamics of the panel aeroelastic system with oscillating shock impingement. However, the enrichment of nonlinear characteristics induced by 3rd-order piston theory is worth further exploration in future work.

Fig. 20

Bifurcation diagram in terms of initial shock impingement location $\xi _T,0$ using 3rd-order piston theory

Aerodynamic terms

The aerodynamic pressure term Q can be expressed as follows.

$$\begin{aligned} Q=Q_1+Q_2+Q_3+Q_4+Q_5+Q_6+Q_7+Q_8 \end{aligned}$$

where $Q_1$ to $Q_4$ correspond to the aerodynamic terms in the supersonic region evaluated by the quasi-steady piston theory, and $Q_5$ to $Q_8$ correspond to the aerodynamic terms in the subsonic region evaluated by the compressibility-corrected potential theory:

$$\begin{aligned} Q_1&=\lambda _1\sum _{i=1}^{N}q_i(i\pi ) \times \\ {}&\quad \left\{ \frac{\cos [(i-j)k\pi ] }{2(i-j)\pi }-\frac{\cos [(i+j)k\pi ] }{2(i+j)\pi }-\frac{j }{(i^2-j^2)\pi } \right\} \\ Q_2&=\frac{1}{2}\lambda _1q_j\sin ^{2} (jk\pi )\\ Q_3&=\sqrt{\lambda _1R_{M1}}\sum _{i=1}^{N}\dot{q_i}\left[ \frac{\sin [(i-j)k\pi ]}{2(i-j)\pi }-\frac{\sin [(i+j)k\pi ] }{2(i+j)\pi } \right] \\ Q_4&=\frac{1}{2}\sqrt{\lambda _1R_{M1}}\dot{q_j}[k-\frac{\sin (2jk\pi )}{2j\pi }]\\ Q_5&=\frac{1}{\sqrt{1-M_{2}^2}} \sum _{i=1}^{N}\left[ -\frac{\mu h}{i\pi }\ddot{q_i}+\lambda _2(i\pi )q_i \right] \times \\ {}&\quad \left\{ \frac{\sin [(i+j)\pi k ] }{2\left( i+j \right) \pi }-\frac{\sin [(i-j)\pi k ] }{2\left( i-j \right) \pi } \right\} \\ Q_6&=\frac{1}{\sqrt{1-M_{2}^2} }\left[ -\frac{\mu h}{j\pi }\ddot{q_j}+\lambda _2(j\pi )q_j \right] \times \\ {}&\quad \left[ \frac{-2j\pi (k-1)+\sin (2jk\pi )}{4j\pi } \right] \\ Q_7&=-\frac{2\sqrt{\mu _2\lambda _2}}{\sqrt{1-M_{2}^2}} \sum _{i=1}^{N} \dot{q_i}\times \\ {}&\quad \left\{ \frac{j(-1)^{i+j}}{(i^2-j^2)\pi } +\frac{\cos [(i+j)k\pi ] }{2\left( i+j \right) \pi }-\frac{\cos [(i-j)k\pi ] }{2\left( i-j \right) \pi } \right\} \\ Q_8&=-\frac{2\sqrt{\mu _2\lambda _2}}{\sqrt{1-M_{2}^2} }\dot{q_j}\left[ \frac{\cos (2jk\pi )-1}{4j\pi } \right] \end{aligned}$$