Asymmetric effect of static radial eccentricity on the vibration characteristics of the rotor system of permanent magnet synchronous motors in electric vehicles

Abstract

Considering static radial eccentricity, a Jeffcott rotor model is established for the rotor system of the permanent magnet synchronous motors in electric vehicles. The system conservative force, including unbalanced magnetic pull, which results in nonlinearity is analyzed, and center manifold theorem and Lyapunov method are used to determine the stabilities of multiple equilibrium points. This analysis shows that static eccentricity spoils the symmetry of the equilibrium points, although they are distributed in the line along the direction of the static eccentricity. This asymmetry leads to the pitchfork bifurcation of equilibrium points to a generic bifurcation with a defect. This analysis provides two stability conditions for the rotor system. Furthermore, the effect of the asymmetry on the dynamic characteristics that can induce backward whirling motion coupled with forward whirling motion is quite different from the case without static eccentricity. These characteristics are investigated by multi-scale method. As a result, the analytical solution of the system at steady state is obtained. The frequency characteristics of the main resonance are analyzed, and the stability of the solution is determined using Routh–Hurwitz criterion and the geometric constraint of the rotor whirling motion. The characteristics reveal that a globally unstable frequency band appears due to the geometric constraint. However, this frequency band narrows and even vanishes with increases in damping and electromagnetic stiffness and decreases in mass imbalance, mechanical stiffness and static eccentricity. The analysis by multi-scale method is based on the assumption of the time invariance of the forward and backward whirling amplitudes, which is validated by the numerical method. The results of the two methods agree well, which indicates that this assumption and the analysis are reasonable.

1 Introduction

Permanent magnet synchronous motors (PMSMs) have many advantages and have been broadly applied to electric vehicles (EVs) and hybrid electric vehicles (HEVs). However, the dynamics problems of PMSMs in EVs and HEVs caused by rotor eccentricity have seriously affected machine performance. The transmission systems of the vehicles are susceptible to excessive vibration and noise. Therefore, these problems should be investigated for suppressing vibration and noise.

For the rotating electrical machines, the radial electromagnetic forces are balanced when the rotor is concentric with the stator. However, in a practical system, rotor eccentricity appears for several reasons, such as manufacturing error, assembly error and bearing wear [1,2,3]. This results in unbalanced magnetic pull (UMP), which compels the rotor to deviate from the stator and has the same direction that the eccentricity. Therefore, UMP reveals a negative stiffness effect, which causes problems of dynamics in the system. To date, investigations of rotor eccentricity can be classified into three areas: UMP, detection of rotor eccentricity, and vibration generation [4].

In the past several decades, many scholars have used finite element method (FEM) and analytical method for the calculation of UMP. The former [5,6,7,8,9,10,11,12] can offer accurate solutions but cannot provide an insight into the system parameters [2]. The analysis of the dynamic characteristics of the rotor system requires the analytical expression of UMP. Therefore, an extensive approach was widely applied to the analytical calculation of UMP, which used the air-gap permeance to modulate the magnetic motive force (MMF) to obtain the air-gap flux density, which includes the eccentricity information [13,14,15]. Then, UMP varying with pole-pair number can be analytically carried out by Maxwell tensor method [14]. This calculation reveals that UMP is a nonlinear function with respect to the eccentricity between the stator and rotor. However, we cannot recognize the type of rotor eccentricity according to UMP.

In fact, there exist three types of rotor eccentricity: dynamic eccentricity, static eccentricity and mixed eccentricity [16, 17]. The different types of rotor eccentricity result in different patterns of system parameters such as stator current, voltage and torque. According to these patterns, many scholars employed signal processing and mathematical algorithms to detect rotor eccentricities [18,19,20]. Roux et al. [21] investigated the experimental implementation and detection of rotor eccentricities in PMSMs by measuring only the stator current and voltage. Ebrahimi et al. [22,23,24,25] addressed an index of noninvasive diagnosis according to the sideband of the spectrum of the stator current, torque and magnetic field analysis for the three types of eccentricity in PMSMs. Akar et al. [26] proposed a spectral analysis method to detect static eccentricity fault for PMSMs and then considered the sideband effects in the vicinity of the fundamental frequency as the most important indicator of eccentricity. In reference [27], then they detected static eccentricity through a probability distribution based on equal width discretization and a neural network model. Mirimani et al. [28] used 3-D finite element analysis to study the detection of static eccentricity for permanent magnet machines, validated this numerical model by experimental measurements, presented an appropriate criterion for eccentricity detection by the back electromotive force and developed an online method for static eccentricity fault detection [29]. Hong et al. [30] presented a technique for automated monitoring of air-gap eccentricity, which was to use the inverter for testing of PMSMs at motor standstill. Da et al. [31] used direct flux measurement to develop an index of multifault detection in PMSMs that can determine the direction of static eccentricity. Karami et al. [32] employed an analysis of the performance of a line start PMSM with static eccentricity in steady state by FEM. Huang et al. [33] calculated the static eccentricity of a double rotor axial flux permanent magnet machine by an analytical model whose results were verified via experiment. Goktas et al. [34] addressed the discernment of static eccentricity and broken magnet faults in PMSMs through the stator phase current due to their strongly similar fault patterns in the back electromotive force and flux spectrum. Naderi et al. [35] studied the eccentricity fault by the current/torque signature and recognized the static and dynamic eccentricity faults by the power spectral density of the vibration signal and stator current. Naderi [36] further addressed a torque ripple analysis for four separate synchronous reluctance machines under health and eccentricity fault conditions considering slot opening and distributed winding effects. Oumaamar et al. [37] presented an alternative method based on the analysis of line neutral voltage for static eccentricity detection. Most of these references covered the detection of static eccentricity, which is a vital consideration for the fault diagnosis of electric machines. However, these papers did not focus on the dynamics mechanism caused by static eccentricity, which can provide the dynamical criterion of the detection. In fact, static eccentricity can also be susceptible to some dynamics problems such as excessive vibration and loss of stability, which are important considerations for the dynamic system. These dynamic effects can result in fault patterns that carry information about the type and degree of rotor eccentricity. Therefore, an investigation of the dynamic characteristics should be considered, which can provide insight to the eccentricity fault diagnosis and accurate detection.

UMP caused by rotor eccentricity exhibits a negative stiffness effect and nonlinearity, which play a key role in dynamic behaviors. Cylindrical and conical whirls induced by mass imbalance and external forces result in rotor eccentricity and hence UMP compelling the rotor to further move toward the stator and then distort the air-gap distribution [2]. This is a typical electromechanical coupling system [38] in which dynamic behaviors have been investigated in many papers. Pennacchi et al. [1] presented a vibration analysis for a generator considering the external exciting forces, including the mass imbalance of the rotor and the effect of UMP. He et al. [39] built up the finite element and boundary element models of a motor considering static eccentricity to predict the modal parameters, the dynamic vibrations, and the sound pressures. Shin et al. [40] employed the finite element analysis method to estimate the vibration characteristics of PMSMs. Xu et al. [41] took advantage of FEM to predict the vibration influenced by UMP. The results show that static eccentricity will lead to an offset in the axis center and give rise to the nonlinearity of the dynamic response. FEM can obtain accurate results but cannot provide insight into the dynamics mechanism of the rotor system. Kim et al. [38] analyzed the transient whirl response of a rotor system considering mass imbalance by a finite element-transfer matrix, and the computational efficiency is higher than that of FEM. This investigation shows that UMP reduces the system stiffness, which leads to more serious vibration compared with that of purely mechanical origins. The negative stiffness effect of UMP causes the stability problem, which has attracted the attention of scholars. Calleecharan et al. [16] applied the Jeffcott rotor model to the generator, performed a vibration analysis and noted the static eccentricity resulting in a decrease in the stability and even a loss of stability. Wu et al. [42] developed a four degrees of freedom rotor model considering the gyroscopic effect and investigated the dynamic behavior and stability of the generator. Lundström et al. [43] analyzed the dynamic response of the generator considering the shape deviations of the rotor and investigated the attraction basins for contact between the rotor and stator. Xiang et al. [44] investigated multiple equilibrium points and their stabilities by Lyapunov direct method and analyzed the free vibration and frequency characteristics of the rotor of the PMSMs used in EVs. This study discovered the coupling mechanism of the modulation effect of radial displacement components. However, the influence of static eccentricity was neglected in references [42,43,44]. Xu et al. [45] focused on the nonlinear vibration of a rotor with static and dynamic eccentricities. The vibration characteristics were discussed in detail for comparison. However, the analyses were performed by numerical method.

As mentioned above, the investigations of static eccentricity were mainly restricted to detection and diagnosis. In addition, a portion of the papers focusing on the rotor dynamics of electric machines neglected the static eccentricity, and the others considered it to study the vibration characteristics, usually paying attention to the dynamic response by numerical method. However, this method cannot offer insight into the vibration influenced by UMP. Furthermore, most of the electrical machines studied in these papers have a narrow speed range. However, the speed of PMSMs in HEVs and EVs varies with external loads in a large range. Due to static eccentricity, the complexity of dynamic behaviors further increases. The excitations deriving from road roughness and the internal combustion engine will impact on the rotor. These external loads with a wide frequency band may lead to the resonance of the rotor system, which decreases the performance of the rotor system. Therefore, the vibration characteristics of the PMSMs caused by static eccentricity and UMP should be scrutinized by an analytical method.

This paper focuses on the asymmetric effect of nonlinear vibration of the rotor system of PMSMs in HEVs and EVs caused by static eccentricity. In Sect. 2, the UMP model is selected, and the Jeffcott rotor model is applied to the rotor system. In Sect. 3, the influences of static eccentricity and UMP on the static characteristics of the rotor system are investigated, and stability analysis is performed. The corresponding bifurcation diagrams are plotted. In Sect. 4, the steady-state analytical solution and frequency characteristics of the main resonance are studied by multi-scale method. The stability of the solution is analyzed by Routh–Hurwitz criterion and the geometric constraint. The influences of the system parameters, such as the stiffness ratio, damping ratio, mass eccentricity ratio and static eccentricity ratio, on the frequency characteristics are analyzed. The results of the multi-scale method are validated by a numerical method. Conclusions are summarized in Sect. 5.

2 Mathematical model

In this paper, the following assumptions are adopted:

• (a) The rotor is mounted at the midspan of the two bearings supporting the rotor shaft, and the air gap is identical along the axial direction.

• (b) The vibration of the stator is neglected.

• (c) The mass eccentricity and static radial eccentricity of the rotor exist.

2.1 UMP model

In this paper, we adopt the model of UMP in reference [14]. Furthermore, the pole-pair number in the PMSMs of HEVs and EVs is usually more than 3, and the UMP expression is

$$\begin{aligned} f_{\mathrm{u}} =\frac{RL {\uppi } F_{\mathrm{m}}^2 }{4\mu _0 }(2{\varLambda }_0 {\varLambda }_1 +{\varLambda }_1 {\varLambda }_2 +{\varLambda }_2 {\varLambda }_3 ) \end{aligned}$$

(1)

where $\mu _{0}$ is the air permeability, R is the rotor core outer radius, L is the rotor core length, ${\varLambda }_{n}$ is the coefficient of the Fourier series of air-gap permeance and $F_{\mathrm{m}}$ is the fundamental MMF amplitude. ${\varLambda }_{n}$ and $F_{\mathrm{m}}$ can be determined by the following formulae:

$$\begin{aligned} {\varLambda }_n =\left\{ \begin{array}{ll} \quad \frac{\mu _0 }{\delta _0 }\frac{1}{\sqrt{1-\varepsilon ^{2}}} &{} n=0 \\ \frac{2\mu _0 }{\delta _0 }\frac{1}{\sqrt{1-\varepsilon ^{2}}} \left( {\frac{1-\sqrt{1-\varepsilon ^{2}}}{\varepsilon }}\right) ^{n} &{} n=1,2\ldots \\ \end{array} \right. \end{aligned}$$

(2)

where $\delta _{0}$ is the average air-gap length, the non-dimensional eccentricity $\varepsilon = r/\delta _{0}$ is also called non-dimensional radial displacement, and r is the eccentricity of the stator and rotor.

$$\begin{aligned} F_{\mathrm{m}} =\sqrt{F_{\mathrm{rm}}^2 +F_{\mathrm{sm}}^2 -2F_{\mathrm{rm}} F_{\mathrm{sm}} \sin {\varphi }_0} \end{aligned}$$

(3)

where $F_{\mathrm{rm}}$ is the fundamental MMF amplitude of the rotor, $F_{\mathrm{sm}}$ is the fundamental MMF amplitude of the three-phase winding and ${\varphi }_{0}$ is the inner power factor angle.

Fig. 1

Scheme of eccentricity between stator and rotor

2.2 Dynamic model

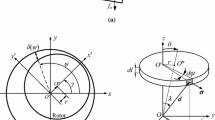
According to the above assumptions, an arbitrary cross section can reflect the eccentricity of the stator and rotor. For simplicity, we select the cross section at the middle of the span, as shown in Fig. 1a. The stator center O is fixed. Due to assembly error, the centerline of the rotor is not aligned with that of the stator. The rotor centerline deviates from but is parallel with the stator centerline. This deviation is the static radial eccentricity, which can be depicted by the stationary vector ${\textit{OO}}^{\prime \prime }$ with amplitude $e_{\mathrm{s}}$ and direction angle $\theta _{\mathrm{s}}$. Due to the mass eccentricity, the rotor center escapes from the point $O^{\prime \prime }$ when the rotor spins. Therefore, ${\textit{Ox}}^{\prime } y^{\prime }$ is a rotating coordinate system that has the same origin that the inertial coordinate system Oxy. At a general time instant t, the rotor center $O^{\prime }$ is shown in Fig. 1. The point C is the mass center of the rotor, and $O^{\prime }C$ is the mass eccentric distance of which the length is denoted by e. The radial eccentricity of the rotor center is ${\textit{OO}}^{\prime }$, whereas the deformation of the rotor shaft is $O^{\prime \prime } O^{\prime }$. Therefore, UMP always acts along the direction from the stator center O to the rotor center $O^{\prime }$, while the restoring force of the rotor shaft points to the point $O^{\prime \prime }$ from the rotor center $O^{\prime }$. The restoring force and UMP are generally not in the same direction.

The vibration system of the rotor is simplified to a Jeffcott rotor, and the corresponding motion equation can be written as:

$$\begin{aligned} \left\{ \begin{aligned}&m\ddot{x}+c {\dot{x}}+k(x-x_0 )-f_{\mathrm{u}} \cos \gamma =me\omega ^{2}\cos \omega t \\&m\ddot{y}+c {\dot{y}}+k(y-y_0 )-f_{\mathrm{u}} \sin \gamma =me\omega ^{2}\sin \omega t \end{aligned}\right. \nonumber \\ \end{aligned}$$

(4)

where m is the rotor mass, c is the damping coefficient, $x_{0}$ and $y_{0}$ are, respectively, the components of static eccentricity in the x- and y-directions, $\gamma$ is the direction angle of UMP, $\omega$ is the rotor angular speed, and k is the mechanical stiffness of the rotor shaft. According to Fig. 1, $x_{0}=e_{\mathrm{s}} \cos \theta _{s}, \, y_{0}=e_{\mathrm{s}} \sin \theta _{\mathrm{s}}$.

Let $\omega _0 =\sqrt{k/m}$ and $\tau =\omega _0 t$. The non-dimensional form of Eq. (4) is

$$\begin{aligned} \left\{ \begin{aligned}&{{\varepsilon }_x^{\prime \prime } +2\xi {\varepsilon }_x^{\prime } +\varepsilon _x -{\bar{f}}_{\mathrm{u}} (\varepsilon )\frac{\varepsilon _x }{\varepsilon }=\beta {{\bar{\omega }}}^{2}\cos {{\bar{\omega }}}\tau +\beta _{\mathrm{s}x} } \\&{{\varepsilon }_y^{\prime \prime } +2\xi {\varepsilon }_y^{\prime } +\varepsilon _y -{\bar{f}}_{\mathrm{u}} (\varepsilon )\frac{\varepsilon _y }{\varepsilon }=\beta {{\bar{\omega }}}^{2}\sin {{\bar{\omega }}}\tau +\beta _{\mathrm{s}y} } \end{aligned} \right. \nonumber \\ \end{aligned}$$

(5)

where $\xi =\frac{c}{2\sqrt{km}}$ is the damping ratio, $\beta =\frac{e}{\delta _0}$ is the mass eccentricity ratio, $\beta _{\mathrm{s}} =\frac{e_{\mathrm{s}}}{\delta _0}$ is the static eccentricity ratio (non-dimensional static eccentricity), ${{\bar{\omega }}} =\frac{\omega }{\omega _0}$ is the frequency ratio, ${\bar{f}}_{\mathrm{u}} (\varepsilon )=\frac{f_{\mathrm{u}} (\varepsilon )}{k\delta _0}$ is the non-dimensional UMP, $\varepsilon _x =x/{\delta _0}$ and $\varepsilon _y =y/{\delta _0}$ are the non-dimensional radial displacement components in the x- and y- directions, respectively, $\beta _{\mathrm{s}x} =\beta _{\mathrm{s}} \cos \theta _{\mathrm{s}}$ and $\beta _{\mathrm{s}y} =\beta _{\mathrm{s}} \sin \theta _{\mathrm{s}}$ are the non-dimensional static eccentricity components in the x- and y- directions, respectively, and $(\cdot )^{\prime }$ represents the differentiation with respect to the non-dimensional time $\tau$. It can be seen that the first and second terms on the right side in Eq. (5) are the external excitations caused by the mass imbalance and static eccentricity, respectively.

The complex form of Eq. (5) is

$$\begin{aligned} {z}^{\prime \prime } +2\xi {z}^{\prime } +z-{\bar{f}}_{\mathrm{u}} (\varepsilon )\frac{z}{|z|} = \beta {{\bar{\omega }}}^{2} \hbox {e}^{\mathrm{i}{{\bar{\omega }}}\tau }+z_{\mathrm{s}} \end{aligned}$$

(6)

where $z=\varepsilon _{x} + \hbox {i} \varepsilon _{y}$ is the non-dimensional radial displacement in complex form, $z_{\mathrm{s}} =\beta _{\mathrm{s}} \hbox {e}^{\mathrm{i}\theta _{\mathrm{s}}}$ is the non-dimensional static eccentricity in complex form, and i is the imaginary unit.

3 Static characteristics analysis considering static eccentricity

3.1 Characteristics of system conservative force

For the static characteristics of the rotor system, the angular speed is zero, that is, ${{\bar{\omega }}} =0$, yielding

$$\begin{aligned} {z}^{\prime \prime } +2\xi {z}^{\prime } +z-{\bar{f}}_{\mathrm{u}} (\varepsilon )\frac{z}{|z|}=z_{\mathrm{s}} \end{aligned}$$

(7)

As shown in Fig. 1, the non-dimensional form of the radial displacement ${\textit{OO}}^{\prime }$ can be expressed as $z=\varepsilon {\hbox {e}}^{\mathrm{i}\gamma }$. In Fig. 1b, the vector ${\textit{OO}}_{1}$ with amplitude $\varepsilon$ and direction angle ($\gamma \hbox {--} {\uppi }$) has the non-dimensional form $z=\varepsilon {\hbox {e}}^{\mathrm{i}(\gamma -{\uppi })}$. For simplicity, ${\textit{OO}}_{1}$ can be considered as a vector with direction angle $\gamma$. Thus, the corresponding amplitude is -$\varepsilon$ of which the sign denotes the opposite direction with respect to ${\textit{OO}}^{\prime }$. In this section, we specify that the amplitude of the relative radial displacement is permitted to be negative except for a special situation.

Fig. 2

Vector field of system conservative force

According to Eq. (6), for an arbitrary relative radial displacement, the non-dimensional system conservative force is:

$$\begin{aligned} {\bar{f}}(z)=z-z_{\mathrm{s}} -{\bar{f}}_{\mathrm{u}} (\varepsilon ) \frac{z}{|z|} \end{aligned}$$

(8)

It can be seen that ${\overline{f}} (z)$ is a vector function. Eq. (8) determines a steady planar vector field as shown in Fig. 2. The color and the streamline depict the magnitude and the direction of the force, respectively. For an arbitrary point in this vector field, the corresponding conservative force acts along the tangential direction of the streamline across the point. For simplicity, we decompose the conservative force into two components in the radial and tangential directions of the stator. The two non-dimensional components denoted by ${\overline{f}}_{\mathrm{r}} (\varepsilon )$ and ${\overline{f}}_{\mathrm{t}} (\varepsilon )$, respectively, are

$$\begin{aligned} \left\{ \begin{aligned}&{\bar{f}}_{\mathrm{r}} (\varepsilon )=\varepsilon -{\bar{f}}_{\mathrm{u}} (\varepsilon )-\beta _{\mathrm{s}} \cos \theta _{\mathrm{di}} =\varepsilon -{\bar{f}}_{\mathrm{u}} (\varepsilon )-\varepsilon _{\mathrm{r}} \\&{\bar{f}}_{\mathrm{t}} (\varepsilon )=\beta _{\mathrm{s}} \sin \theta _{\mathrm{di}} =\varepsilon _{\mathrm{t}} \end{aligned}\right. \end{aligned}$$

(9)

where $\theta _{\mathrm{di}} = \gamma - \theta _{\mathrm{s}}$ is the angle from the direction of the static eccentricity (${\textit{OO}}^{\prime \prime }$) to that of UMP (${\textit{OO}}^{\prime }$), and $\varepsilon _{\mathrm{r}} = \beta _{\mathrm{s}} \cos \theta _{\mathrm{di}}$ and $\varepsilon _{\mathrm{t}} = \beta _{\mathrm{s}} \sin \theta _{\mathrm{di}}$ are the non-dimensional additional forces in the radial and tangential directions of the stator caused by the static eccentricity, respectively. In addition to the static eccentricity, the two additional forces also depend on the angle $\theta _{\mathrm{di}}$, which varies in the range of [$-{\uppi }$, ${\uppi }$] according to Fig. 1.

The radial stiffness and the tangential stiffness denoted by ${\overline{k}}_{\mathrm{r}} (\varepsilon )$ and ${\overline{k}}_{\mathrm{t}} (\varepsilon )$ , respectively, are

$$\begin{aligned} \left\{ \begin{aligned}&{\bar{k}}_{\mathrm{r}} (\varepsilon )={\bar{k}}-{\bar{k}}_{\mathrm{u}} (\varepsilon )=1-{\bar{k}}_{\mathrm{u}} (\varepsilon ) \\&{\bar{k}}_{\mathrm{t}} (\varepsilon )=0 \end{aligned}\right. \end{aligned}$$

(10)

where $\bar{k}=1$ is the non-dimensional mechanical stiffness and ${\bar{k}}_{\mathrm{u}} (\varepsilon )$ is the non-dimensional electromagnetic stiffness of UMP.

$$\begin{aligned} {\bar{k}}_{\mathrm{u}} (\varepsilon )=\frac{\hbox {d}{\bar{f}}_{\mathrm{u}} (\varepsilon )}{\hbox {d}\varepsilon }=\frac{k_{\mathrm{u}} (\varepsilon )}{k} \end{aligned}$$

(11)

where $k_{\mathrm{u}} (\varepsilon )=\frac{\hbox {d}f_{\mathrm{u}} (\varepsilon )}{\hbox {d}r}$ is the dimensional electromagnetic stiffness. At $\varepsilon =0$, ${\overline{k}}_{\mathrm{u}} (\varepsilon )$ attains the minimum value, and thus, ${\overline{k}}_{\mathrm{r}} (\varepsilon )$ attains the maximum value. Let $\varepsilon =0$ which then yields

$$\begin{aligned} \left\{ \begin{aligned}&\alpha ={\bar{k}}_{\mathrm{u}} \left( 0 \right) =\frac{k_{\mathrm{u}} (0)}{k} \\&{\bar{k}}_{\mathrm{r0}} ={\bar{k}}_{\mathrm{r}} (0)=1-\alpha \end{aligned}\right. \end{aligned}$$

(12)

where, $k_{\mathrm{u}} (0) = \left( {\frac{\hbox {d}f_{\mathrm{u}} (\varepsilon )}{\hbox {d}r}} \right) _{r=0} =\frac{1}{2}\frac{\mu _0 RL {\uppi } F_{\mathrm{m}}^2}{\delta _0^3}$. The parameter $\alpha$ that represents the non-dimensional electromagnetic stiffness at $\varepsilon =0$ can be called the stiffness ratio according to the first formula in Eq. (12). Physically, the parameter $\alpha$ is the ratio of the electromagnetic stiffness at $\varepsilon =0$ to the mechanical stiffness, which gives a comparison of the two stiffnesses. $\alpha =1$ is a critical value that represents that the electromagnetic stiffness at $\varepsilon =0$ is equal to the mechanical stiffness. $\alpha < 1$ represents that the electromagnetic stiffness at $\varepsilon =0$ is less than the mechanical stiffness, and vice versa for $\alpha > 1$. According to the Taylor formula, we expand ${\overline{f}}_{\mathrm{u}} (\varepsilon )$ as a polynomial at $\varepsilon =0$, and keep the first three order terms, yielding

$$\begin{aligned} {\bar{f}}_{\mathrm{u}} (\varepsilon )\approx \alpha \varepsilon +\frac{3\alpha }{2}\varepsilon ^{3} \end{aligned}$$

(13)

Fig. 3

Force and stiffness characteristics

From Eq. (1), UMP is an odd function, and thus, the corresponding electromagnetic stiffness is an even function. UMP and its stiffness varying with $\alpha$ are shown in Fig. 3. Furthermore, UMP and its electromagnetic stiffness provide larger slopes as the magnitude of the radial displacement increases.

It can be seen that the system stiffness is independent of the static eccentricity that plays a significant role in the conservative force from Eqs. (9) and (10). The radial force ${\overline{f}}_{\mathrm{r}} (\varepsilon )$ influenced by the static eccentricity varies with the radial displacement as shown in Fig. 4. This discussion will be performed in the range of the angle from ${\textit{OO}}^{\prime \prime }$ (static eccentricity) to the line ${\textit{OO}}^{\prime }$, i.e., $\theta _{\mathrm{di}} \in [0, {\uppi }]$ due to the symmetry of the additional radial force $\varepsilon _{\mathrm{r}}$ with respect to the static eccentricity ${\textit{OO}}^{\prime \prime }$ according to Fig. 1 and Eq. (9). When the angle $\theta _{\mathrm{di}}$ is 0, the tangential force ${\bar{f}}_{\mathrm{t}}$ that is the additional tangential force $\varepsilon _{\mathrm{t}}$ vanishes, and therefore, the system conservative force is identical to the radial force ${\bar{f}}_{\mathrm{r}}$, and the additional radial force $\varepsilon _{\mathrm{r}}$ reaches the maximum value. Thus, the rotor center $O^{\prime }$ is located in the line ${\textit{OO}}^{\prime \prime }$, and the action line of UMP coincides with that of the restoring force. However, when $\theta _{\mathrm{di}}$ is ${\uppi }/2$, the additional tangential force $\varepsilon _{\mathrm{t}}$ reaches the maximum value, and the additional radial force $\varepsilon _{\mathrm{r}}$ is 0.

Fig. 4

Radial component of system conservative force

According to the above analysis, the equilibrium point of the system should be in the line ${\textit{OO}}^{\prime \prime }$, i.e., $\gamma = \theta _{\mathrm{s}}$. For the simplicity of the analysis of the equilibrium point, we only discuss the conservative force along the direction of the line ${\textit{OO}}^{\prime \prime }$. In this direction, the system conservative force is

$$\begin{aligned} {\bar{f}}(\varepsilon )=\varepsilon -\beta _{\mathrm{s}} -{\bar{f}}_{\mathrm{u}} (\varepsilon )={\bar{f}}_{\mathrm{k}} (\varepsilon )-{\bar{f}}_{\mathrm{u}} (\varepsilon ) \end{aligned}$$

(14)

where ${\overline{f}}_{\mathrm{k}} (\varepsilon )=\varepsilon -\beta _{\mathrm{s}}$ is the non-dimensional restoring force along the direction of the line ${\textit{OO}}^{\prime \prime }$.

Fig. 5

UMP, restoring force and system conservative force and their stiffnesses versus radial displacement. a Stiffness versus radial displacement $(\alpha <1)$: the line $\bar{k} = 1$ denotes the non-dimensional stiffness of the rotor shaft (mechanical stiffness); the curve $\bar{k}_\mathrm{u}$ (blue curve) that passes through the point $(0, \alpha )$ represents the non-dimensional UMP stiffness (electromagnetic stiffness); and the curve $\bar{k}_\mathrm{u}$ (red curve) that passes through the points $(0, 1-\alpha )$, $(-\epsilon _{1}, 0)$ and $(\epsilon _{1}, 0)$ denotes the non-dimensional system stiffness, where $\pm \epsilon _{1}$ are the zero points of the non-dimensional system stiffness. b Force versus radial displacement $(\alpha<1, -\beta _{s1}<\beta _{s}<\beta _{s1})$: the line $\bar{f}_\mathrm{k}$, the curve $\bar{f}_\mathrm{u}$ (blue curve) and the curve $\bar{f}$ (red curve) denote the non-dimensional restoring force, UMP and system conservative force, respectively. $\epsilon _\mathrm{s}, \epsilon _\mathrm{u1}$ and $\epsilon _\mathrm{u2}$ are the zero points of the non-dimensional system conservative force. $\beta _\mathrm{s1}$ is the critical static eccentricity ratio. The lines that pass through the points $(0, \beta _\mathrm{s1}) or (0, -\beta _\mathrm{s1})$ are tangential to the curve $\bar{f}_\mathrm{u}$ and parallel to the line $\bar{f}_\mathrm{k}$. $\pm \epsilon _{1}$ are the extreme points of the non-dimensional system conservative force.

According to Eqs. (13) and (14), UMP depends on the stiffness ratio $\alpha$, and the restoring force depends on the static eccentricity ratio $\beta _{\mathrm{s}}$. However, their stiffnesses are independent of $\beta _{\mathrm{s}}$. In light of Eqs. (10), (12) and the above analysis, for the case of $\alpha > 1$, the system stiffness, of which zero points do not exist, is always negative, and thus, the system undergoes the loss of stability. The system conservative force ${\bar{f}}(\varepsilon )$ has only one unstable zero point denoted by $\varepsilon _{\mathrm{s}}$. $\alpha < 1$ ensures that the rotor system has a positive stiffness interval ($-\varepsilon _{1}$, $\varepsilon _{1}$), of which the two endpoints are the zero points of the system stiffness and hence the extreme points of the force that are independent of the static eccentricity ratio $\beta _{\mathrm{s}}$, as shown in Fig. 5a. The smaller the stiffness ratio $\alpha$ is, the wider the interval. Assuming that $\beta _{\mathrm{s}}=0$ (without static eccentricity), the system conservative force ${\bar{f}}(\varepsilon )$ has three zero points denoted by $\varepsilon _{\mathrm{s}}$, $\varepsilon _{\mathrm{u1}}$ and $\varepsilon _{\mathrm{u2}}$. Furthermore, $\varepsilon _{\mathrm{s}}=0$ and $\varepsilon _{\mathrm{u1}} =- \varepsilon _{\mathrm{u2}}$ because ${\bar{f}} (\varepsilon )$ is an odd function for the case of $\beta _{\mathrm{s}}=0$. Therefore, for fixed $\beta _{\mathrm{s}}=0$, $\alpha = 1$ is a critical value. When the stiffness ratio $\alpha$ increases and passes through 1, the number of zero points of ${\bar{f}}(\varepsilon )$ increases from 1 to 3. As shown in Fig. 5b, for $\alpha <1$, when the static eccentricity ratio $\beta _{\mathrm{s}}$ increases from 0, the restoring force ${\overline{f}}_{\mathrm{k}} (\varepsilon )=\varepsilon -\beta _{\mathrm{s}}$ oves down and the zero points $\varepsilon _{\mathrm{u1}}$ and $\varepsilon _{\mathrm{u2}}$ are no longer symmetric with respect to $\varepsilon _{\mathrm{s}}$. Moreover, $\varepsilon _{\mathrm{s}} \ne 0$. The former two points are unstable, whereas the latter one is stable. As $\beta _{\mathrm{s}}$ increases to $\beta _{\mathrm{s1}}$, the restoring force ${\overline{f}}_{\mathrm{k}} (\varepsilon )$ is tangential to the UMP curve so that ${\bar{f}}(\varepsilon _1) =0$, and the zero points $\varepsilon _{\mathrm{s}}$ and $\varepsilon _{\mathrm{u1}}$, which coincide with the system stiffness zero point $\varepsilon _{1}$ together with $\varepsilon _{\mathrm{u2}}$, are unstable. The number of zero points decreases to 2, i.e., $\varepsilon _{1}$ and $\varepsilon _{\mathrm{u2}}$. Therefore, the parameter $\beta _{\mathrm{s1}}$ is critical to this number. With the increase in $\beta _{\mathrm{s}}$, $\beta _{\mathrm{s}} > \beta _{\mathrm{s1}}$ holds, and the zero point $\varepsilon _{1}$ disappears. The other zero point $\varepsilon _{\mathrm{u2}}$ is still unstable. For $\beta _{\mathrm{s}} <0$, when $\beta _{\mathrm{s}} =- \beta _{\mathrm{s1}}$, $\varepsilon _{\mathrm{s}}$ and $\varepsilon _{\mathrm{u2}}$ coincide with each other, and both are equal to $-\varepsilon _{1}$. At this time, both $-\varepsilon _{1}$ and $\varepsilon _{\mathrm{u1}}$ are unstable. The former zero point disappears for $\beta _{\mathrm{s}} < -\beta _{\mathrm{s1}}$. According to this analysis, we can yield

$$\begin{aligned} \pm \beta _{\mathrm{s}1} =\pm [\varepsilon _1 -{\bar{f}}_{\mathrm{u}} (\varepsilon _1 )] \end{aligned}$$

(15)

This parameter $\beta _{\mathrm{s1}}$ can be called the critical static eccentricity ratio, and the critical dimensional static eccentricities are

$$\begin{aligned} \pm e_{\mathrm{s}1} =\pm \beta _{\mathrm{s}1} \delta _0 =\pm [kr_1 -f_{\mathrm{u}} (\varepsilon _1 )]/k \end{aligned}$$

(16)

where, $r_{1}=\varepsilon _{1} \delta _{0}$. According to Eq. (16), $e_{\mathrm{s1}}$ is equal to the equivalent deformation produced by the extremum of the system conservative force without static eccentricity applying to the rotor shaft. Therefore, the analysis provides two stability conditions for a practical system: $\alpha <1$ and ${\vert } \beta _{\mathrm{s}} {\vert } < \beta _{\mathrm{s1}}$, as shown in Fig. 5b. The former is a stiffness condition that ensures that the rotor system has a positive stiffness interval ($-\varepsilon _{1}$, $\varepsilon _{1}$), of which the endpoints are independent of $\beta _{\mathrm{s}}$. Outside the interval [$-\varepsilon _{1}$, $\varepsilon _{1}$], the system stiffness is negative which leads to the contact of rotor and stator easily. The latter is an eccentricity condition. Under the prerequisite of the first condition, the latter ensures that the rotor system has at least one stable zero point (equilibrium point).

3.2 Stability analysis and bifurcation

The zero points of the conservative force correspond to the system equilibrium points. We can use Lyapunov method to determine their stabilities easily for the common equilibrium points. However, according to the analysis in Sect. 3.1, the equilibrium points $\varepsilon _{\mathrm{s}}=0 \, (\beta _{\mathrm{s}}=0, \alpha =1)$, $\varepsilon _{\mathrm{s}}=\varepsilon _{\mathrm{u1}}=\varepsilon _{1} \, (\beta _{\mathrm{s}} = \beta _{\mathrm{s1}}, \alpha < 1)$ and $\varepsilon _{\mathrm{s}}=\varepsilon _{\mathrm{u2}} =- \varepsilon _{1} \, (\beta _{\mathrm{s}} =- \beta _{\mathrm{s1}}, \alpha < 1)$ are the critical cases, and the corresponding Jacobi matrices all have zero eigenvalues, and the other eigenvalues all have negative real parts. The stabilities of these equilibrium points cannot be determined according to this method. Therefore, the center manifold theorem should be adopted. The analysis process for $\varepsilon _{\mathrm{s}} = \varepsilon _{\mathrm{u1}}=\varepsilon _{1} \, (\beta _{\mathrm{s}} = \beta _{\mathrm{s1}}, \alpha < 1)$ is given below.

For the case of $\varepsilon _{\mathrm{s}} = \varepsilon _{\mathrm{u1}} = \varepsilon _{1} \, (\beta _{\mathrm{s}} = \beta _{\mathrm{s1}}, \alpha < 1)$, the two equilibrium points coincide with the extreme point of the conservative force $\varepsilon _{1}$. To simplify the calculation, we assume that the rotor center only whirls along the direction of the static eccentricity (${\textit{OO}}^{\prime \prime }$). Therefore, Eq. (7) degrades into

$$\begin{aligned} {\varepsilon }^{\prime \prime } +2\xi {\varepsilon }^{\prime } +\varepsilon -\beta _{\mathrm{s1}} -{\bar{f}}_{\mathrm{u}} (\varepsilon )=0 \end{aligned}$$

(17)

To perform center manifold theorem, we select the equilibrium point as a new origin and then apply the translation transformation to Eq. (17). Thus, the corresponding state equation is

$$\begin{aligned} {{\varvec{y}}}^{\prime } = {{\varvec{G}}} ({{\varvec{y}}}) \end{aligned}$$

(18)

where ${{\varvec{y}}} =\left[ {\begin{array}{l} y_1 \\ y_2 \\ \end{array}} \right]$, ${{\varvec{y}}}^{\prime } =\left[ {\begin{array}{l} {y}_1^{\prime } \\ {y}_2^{\prime } \\ \end{array}} \right]$, and ${{\varvec{G}}} ({{\varvec{y}}})=\left[ {\begin{array}{c} y_2 \\ -2\xi y_2 -(y_1 +\varepsilon _1 )+{\bar{f}}_{\mathrm{u}} (y_1 +\varepsilon _1 )+\beta _{\mathrm{s1}} \\ \end{array}} \right]$.

The Taylor expansion of ${\bar{f}}_{\mathrm{u}} (y_1 +\varepsilon _1)$ is

$$\begin{aligned} {\bar{f}}_{\mathrm{u}} (y_1 +\varepsilon _1 )= & {} \varepsilon _1 -\beta _{\mathrm{s1}} +y_1 +\delta _2 y_1^2 \nonumber \\&+\delta _3 y_1^3 +\delta _4 y_1^4 +\cdots \end{aligned}$$

(19)

where, $\delta _i =\left. {\frac{\hbox {d}{\bar{f}}_{\mathrm{u}}^{(i)} (\varepsilon )}{2\hbox {d}\varepsilon ^{(i)}}} \right| _{\varepsilon =\varepsilon _1 } =\left. {\frac{\hbox {d}{\bar{f}}_{\mathrm{u}}^{(i)} (y_1 +\varepsilon _1 )}{2\hbox {d}\varepsilon ^{(i)}}} \right| _{y_1 =0}$. Clearly, $\delta _2 >0$ holds due to the stiffness of UMP being a convex function (Fig. 5b). The system determined by Eq. (18) has only one equilibrium point at $y_{1}= y_{2}=0$. The Jacobi matrix at this equilibrium point is

$$\begin{aligned} {{\varvec{J}}}=\left[ \begin{array}{cc} 0&{} 1 \\ 0&{} {-2\xi } \\ \end{array} \right] . \end{aligned}$$

The eigenvalues and eigenvectors of the matrix are, respectively,

$$\begin{aligned} \lambda _{1} = 0, \, {{\varvec{p}}}_{1} =[1, 0]^{\mathrm{T}}; \, \, \lambda _{2} = -2 \xi , \, {{\varvec{p}}}_{2}= [1, \, \lambda _{2}]^{\mathrm{T}}. \end{aligned}$$

We define a transformation as

$$\begin{aligned}{}[ {y_1 ,y_2 } ]^{\mathrm{T}}=[ {{{\varvec{p}}}_1, {{\varvec{p}}}_2}][{u,v} ]^{\mathrm{T}}=[ {u+v,-2\xi v} ]^{\mathrm{T}} \end{aligned}$$

(20)

Substituting Eq. (20) into Eq. (18) yields

$$\begin{aligned} \left\{ \begin{aligned}&{u}^{\prime } =-\frac{1}{2\xi }[(u+v+\varepsilon _1 -\beta _{\mathrm{s1}} )-{\bar{f}}_{\mathrm{u}} (u+v+\varepsilon _1 )] \\&{v}^{\prime } =-2\xi v+\frac{1}{2\xi }[(u+v+\varepsilon _1 -\beta _{\mathrm{s1}} )-{\bar{f}}_{\mathrm{u}} (u+v+\varepsilon _1 )] \\ \end{aligned} \right. \nonumber \\ \end{aligned}$$

(21)

Substituting Eq. (19) into Eq. (21), and combining Eq. (20), yields

$$\begin{aligned} \left\{ {\begin{array}{l} {u}^{\prime } =g(u,v) \\ {v}^{\prime } =-2\xi v-g(u,v) \\ \end{array}} \right. \end{aligned}$$

(22)

where, $g(u,v)=\frac{1}{2\xi }[\delta _2 (u+v)^{2}+\delta _3 (u+v)^{3}+\delta _4 (u+v)^{4}+\cdots ]$ is a nonlinear function excluding the linear term. According to Eq. (22), we can obtain

$$\begin{aligned}&g(0,0)=0, \quad \left. {\frac{\partial g}{\partial u}} \right| _{u=0,v=0} =0, \nonumber \\&\left. {\frac{\partial g}{\partial v}} \right| _{u=0,v=0} =0 \end{aligned}$$

(23)

According to the center manifold theorem, there exists a center manifold for Eq. (21), which can be expressed as the function $v=h(u)$, which then yields

$$\begin{aligned} h(0)=0, \, \left. {\frac{\partial h}{\partial u}} \right| _{u=0} =0 \end{aligned}$$

(24)

Substituting this function into Eq. (21), the equation of the center manifold is carried out as below.

$$\begin{aligned} \left( {\frac{\hbox {d}h}{\hbox {d}u}+1} \right) {u}^{\prime } +2\xi h=0 \end{aligned}$$

(25)

Assume that the Taylor expansion of h has the following form:

$$\begin{aligned} h=au^{2} \end{aligned}$$

(26)

Substituting Eq. (26) into Eq. (25) and using Eqs. (19) and (21) yields

$$\begin{aligned} a=-\frac{\delta _2 }{4\xi ^{2}} \end{aligned}$$

(27)

Thus, we can obtain the reduced system

$$\begin{aligned} {u}^{\prime } =\frac{\delta _2 }{2\xi }\left( {u-\frac{\delta _2}{4\xi ^{2}}u^{2}} \right) ^{2}. \end{aligned}$$

(28)

Due to $\delta _{2} >0$, the equilibrium point $u=0$ of the reduced system in Eq. (28). is unstable. Therefore, the equilibrium point of the original system in Eq. (18) is unstable, and hence, the equilibrium point $\varepsilon _{\mathrm{s}} = \varepsilon _{\mathrm{u1}}=\varepsilon _{1}$ according to center manifold theorem. For the equilibrium points $\varepsilon _{\mathrm{s}}=\varepsilon _{\mathrm{u2}} =- \varepsilon _{1} \, (\beta _{\mathrm{s}} =-\beta _{\mathrm{s1}}, \alpha < 1)$ and $\varepsilon _{\mathrm{s}}=0 \, (\beta _{\mathrm{s}}=0, \, \alpha =1)$, a similar procedure can also be performed by this method, and the results show that both equilibrium points are unstable. As the parameters $\alpha$ and $\beta _{\mathrm{s}}$ cross these critical values, the static bifurcation occurs as shown in Fig. 6. When the static eccentricity ratio $\beta _{\mathrm{s}}=0$ remains unchanged and the stiffness ratio $\alpha$ passes through 1, a pitchfork bifurcation occurs as shown in Fig. 6a. When the static eccentricity increases from 0, the pitchfork bifurcation is destroyed, and then a generic bifurcation with a defect occurs. Therefore, $\beta _{\mathrm{s}}$ is an unfolding parameter. For a comparatively large $\beta _{\mathrm{s}}$, the curve becomes single-valued. Therefore, a pair of saddle-node bifurcations occurs as $\beta _{\mathrm{s}}$ varies (Fig. 6b).

Fig. 6

Bifurcation diagrams

4 Forced response influenced by static eccentricity

The static eccentricity spoils the symmetry of the system conservative force and hence the equilibrium point. Moreover, this asymmetry has a dynamic effect on the rotor system. In this section, we will discuss this effect. For the simplicity of the analysis, substituting Eq. (13) into Eq. (6) yields

$$\begin{aligned} {z}^{\prime \prime } +2\xi {z}^{\prime } +\omega _{\mathrm{g}}^2 z-\varepsilon _{\mathrm{P}} z^{2}{\bar{z}}=\beta {\bar{\omega }}^{2}\hbox {e}^{\mathrm{i}{{\bar{\omega }}}\tau }+z_{\mathrm{s}} \end{aligned}$$

(29)

where $\omega _{\mathrm{g}} =\sqrt{1-\alpha }$ is the natural frequency of the generating system of Eq. (6), and $\varepsilon _{\mathrm{P}} =\frac{3\alpha }{2}$ is the nonlinear parameter. According to the static analysis in Sect. 3, the stiffness ratio $\alpha$ is a small parameter and hence $\varepsilon _{\mathrm{P}}$ for a practical system with adequate stability margin.

4.1 Vibration characteristics without static eccentricity

Considering the mass imbalance and neglecting the static eccentricity, the frequency characteristics can be obtained by using harmonic balance method.

$$\begin{aligned} \left\{ \begin{aligned}&\left( {\varepsilon ^{2}-\beta ^{2}} \right) {\bar{\omega }}^{4}+\left[ {4\xi ^{2}-2\left( {1-\alpha -\frac{3\alpha \varepsilon ^{2}}{2}} \right) } \right] \varepsilon ^{2}{{\bar{\omega }}}^{2} \\&\quad +\left( {1-\alpha -\frac{3\alpha \varepsilon ^{2}}{2}} \right) ^{2}\varepsilon ^{2}=0 \\&\tan {\varphi }=\frac{-2\xi {{\bar{\omega }}}}{1-\alpha -\frac{3\alpha \varepsilon ^{2}}{2}-{{\bar{\omega }}}^{2}} \end{aligned}\right. \end{aligned}$$

(30)

According to the analysis of harmonic balance method, only the fundamental harmonic component exists in the system response. Therefore, the steady-state periodic solution of Eq. (29) is

$$\begin{aligned} z=\varepsilon \hbox {e}^{\mathrm{i}({{\bar{\omega }}}\tau +{\varphi })} \end{aligned}$$

(31)

Substituting Eq. (31) into Eq. (29) and using averaging method, yields

$$\begin{aligned} \left\{ \begin{aligned}&{\varepsilon }^{\prime } =-2\xi \varepsilon -\beta {{\bar{\omega }}} \sin {\varphi }\\&{{\varphi }}^{\prime } =\frac{1-\alpha -\frac{3\alpha \varepsilon ^{2}}{2}}{{{\bar{\omega }}}}-\frac{\beta {{\bar{\omega }}} \cos {\varphi }}{\varepsilon }-{\bar{\omega }} \end{aligned}\right. \end{aligned}$$

(32)

For the steady state, we assume that both the amplitude and phase are time-invariant, i.e., $\varepsilon ^{\prime } =0$ and ${\varphi }^{\prime } =0$ . Substituting these two equations into Eqs. (32), (30) is obtained again, which denotes that this assumption is reasonable.

4.2 Vibration characteristics considering static eccentricity

In this section, we discuss the main resonance influenced by static eccentricity. For a system without static eccentricity, we can conveniently use harmonic balance method due to the symmetry of the system. However, for a system with static eccentricity, it is difficult to apply this method to such an asymmetric system. Here, multi-scale method is employed to determine a first-order approximation to the solution of Eq. (29) in the form

$$\begin{aligned} z=z_0 (T_0 ,T_1 )+\varepsilon _{\mathrm{P}} z_1 (T_0 ,T_1 ) \end{aligned}$$

(33)

where, $T_{0} = \tau$, $T_{1}=\varepsilon _{\mathrm{P}} \tau$. It follows that the derivatives of a function have the following forms:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\hbox {d}}{\hbox {d}\tau }=\hbox {D}_0 +\varepsilon _{\mathrm{P}} \hbox {D}_1 \\&\frac{\hbox {d}^{2}}{\hbox {d}\tau ^{2}}=\hbox {D}_0^2 +2\varepsilon _{\mathrm{P}} \hbox {D}_0 \hbox {D}_1 \end{aligned} \right. \end{aligned}$$

(34)

where $\hbox {D}_0 =\frac{\partial }{\partial T_0}$ and $\hbox {D}_1 =\frac{\partial }{\partial T_1}$.

4.2.1 Analytical solution

Considering that both the damping ratio $\xi$ and the amplitude of the dynamic excitation $\beta {\bar{\omega }}^{2}\hbox {e}^{\mathrm{i}{\bar{\omega }}\tau }$ are small and have an accuracy of $O (\varepsilon _{\mathrm{P}})$, let

$$\begin{aligned} \left\{ \begin{aligned}&\xi =\xi _1 \varepsilon _{\mathrm{P}} \\&\beta =\beta _1 \varepsilon _{\mathrm{P}} \end{aligned}\right. \end{aligned}$$

(35)

To investigate the main resonance, we introduce the detuning parameter $\sigma _{1,}$ which quantitatively describes the nearness of the excitation frequency ${\bar{\omega }}$ to the natural frequency of the generating system $\omega _{\mathrm{g}}$. Accordingly, we can write

$$\begin{aligned} {\bar{\omega }}^{2}=\omega _{\mathrm{g}}^2 +\sigma _{\mathrm{1}} \varepsilon _{\mathrm{P}} \end{aligned}$$

(36)

Substituting Eqs. (36) and (33) into Eq. (29) and then using Eq. (36) to eliminate the parameter $\omega _{\mathrm{g}}$ yields

order $\varepsilon _{\mathrm{P}}^0$:

$$\begin{aligned} \hbox {D}_0^2 z_0 +{\bar{\omega }}^{2}z_0 =z_{\mathrm{s}} \end{aligned}$$

(37)

and order $\varepsilon _{\mathrm{P}}^1$:

$$\begin{aligned} \hbox {D}_0^2 z_1 +{\bar{\omega }}^{2}z_1= & {} -2\hbox {D}_0 \hbox {D}_1 z_0 -2\xi _1 \hbox {D}_0 z_0 \nonumber \\&+\beta _1 {\bar{\omega }}^{2}\hbox {e}^{\mathrm{i}{\bar{\omega }}T_0} +\sigma _1 z_0 +z_0^2 {\bar{z}}_0 \end{aligned}$$

(38)

We can determine the free vibration solution of Eq. (37) in the form

$$\begin{aligned} z_{0\mathrm{F}} =A_1 (T_1 )\hbox {e}^{\mathrm{i}{\bar{\omega }}T_0 }+A_2 (T_1 )\hbox {e}^{\mathrm{-i}{\bar{\omega }}T_0 } \end{aligned}$$

(39)

where, $A_{1}(T_{1})$ and $A_{2}(T_{1})$ are the complex amplitudes of the forward and backward whirling motions, respectively. Both are functions with respect to the time scale $T_{1}$.

The forced response of the system of Eq. (37) caused by the static eccentricity is

$$\begin{aligned} z_{\mathrm{0S}} =\frac{z_{\mathrm{s}} }{{\bar{\omega }}^{2}}=\frac{\beta _{\mathrm{s}} \hbox {e}^{\mathrm{i}\theta _{\mathrm{s}} }}{{\bar{\omega }}^{2}} \end{aligned}$$

(40)

Therefore, the general solution of Eq. (37) is written as:

$$\begin{aligned} z_0 =z_{0 \mathrm{F}} +z_{0 \mathrm{S}} \end{aligned}$$

(41)

Substituting $z_{0}$ into Eq. (38), then yields

$$\begin{aligned} \hbox {D}_0^2 z_1 +{\bar{\omega }}^{2}z_1= & {} E_{{\bar{\omega }}} \hbox {e}^{\mathrm{i}{\bar{\omega }} T_0 }+E_{-{\bar{\omega }}} \hbox {e}^{\mathrm{-i}{\bar{\omega }}T_0 }+E_{2{\bar{\omega }}} \hbox {e}^{\mathrm{2i}{\bar{\omega }}T_0} \nonumber \\&+E_{-2{\bar{\omega }}} \hbox {e}^{\mathrm{-2i}{\bar{\omega }}T_0 }+E_{3{\bar{\omega }}} \hbox {e}^{\mathrm{3i}{\bar{\omega }}T_0} \nonumber \\&+E_{-3{\bar{\omega }}} \hbox {e}^{\mathrm{-3i}{\bar{\omega }}T_0 }+E_{\mathrm{S}} \end{aligned}$$

(42)

where,

$$\begin{aligned}&E_{{\bar{\omega }}} =-2\hbox {i}{\bar{\omega }}(D_1 A_1 +\xi _1 A_1 )+A_1 |{A_1}|^{2} \\&\qquad \quad +2A_1 |{A_2}|^{2}+2A_1 \left| {z_{0\mathrm{S}} } \right| ^{2}+{\bar{A}}_2 z_{0\mathrm{S}}^2 \\&\qquad \quad +\sigma _1 A_1 +\beta _1 {\bar{\omega }}^{2},\\&E_{-{\bar{\omega }}} =2\hbox {i}{\bar{\omega }}(D_1 A_2 +\xi _1 A_2 )+A_2 |{A_2}|^{2} \\&\qquad \quad +2A_2 |{A_1}|^{2} +2A_2 \left| {z_{0\mathrm{S}} } \right| ^{2}+{\bar{A}}_1 z_{0\mathrm{S}}^2 +\sigma _1 A_2, \\&E_{2{\bar{\omega }}} =A_1^2 {\bar{z}}_{0\mathrm{S}} +2A_1 {\bar{A}}_2 z_{0\mathrm{S}}, \\&E_{-2{\bar{\omega }}} =A_2^2 {\bar{z}}_{0\mathrm{S}} +2{\bar{A}}_1 A_2 z_{0\mathrm{S}} , \quad E_{3{\bar{\omega }}} =A_1^2 {\bar{A}}_2, \\&E_{-3{\bar{\omega }}} ={\bar{A}}_1 A_2^2, \end{aligned}$$

and

$$\begin{aligned} E_{\mathrm{S}}= & {} \sigma _1 z_{0\mathrm{S}} +2z_{0\mathrm{S}} ({|{A_1}|^{2}+ |{A_2}|^{2}}) \\&+2A_1 A_2 {\bar{z}}_{0\mathrm{S}} + |{z_{0\mathrm{S}}}|^{2} z_{0\mathrm{S}}. \end{aligned}$$

Both $E_{{\bar{\omega }}} \hbox {e}^{\mathrm{i}{\bar{\omega }} T_0}$ and $E_{-{\bar{\omega }}} \hbox {e}^{\mathrm{-i}{\bar{\omega }} T_0}$ are secular terms that should be avoided. Let

$$\begin{aligned} \left\{ \begin{aligned}&E_{{\bar{\omega }}} =0 \\&E_{-{\bar{\omega }}} =0 \\ \end{aligned} \right. \end{aligned}$$

(43)

After eliminating the secular terms, the right side of Eq. (42) has five residual terms, $E_{2{\bar{\omega }}} \hbox {e}^{\mathrm{2i}{\bar{\omega }}T_0}$, $E_{-2{\bar{\omega }}} \hbox {e}^{\mathrm{-2i}{\bar{\omega }}T_0}$, $E_{3{\bar{\omega }}} \hbox {e}^{\mathrm{3i}{\bar{\omega }}T_0}$, $E_{-3{\bar{\omega }}} \hbox {e}^{\mathrm{-3i}{\bar{\omega }}T_0}$ and $E_{\mathrm{S}}$. The responses of Eq. (42) caused by these terms are listed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&z_{2{\bar{\omega }}} =-\frac{E_{2{\bar{\omega }}} }{3{\bar{\omega }}^{2}}\hbox {e}^{\mathrm{2i}{\bar{\omega }}T_0 } \\&z_{-2{\bar{\omega }}} =-\frac{E_{-2{\bar{\omega }}} }{3{\bar{\omega }}^{2}}\hbox {e}^{\mathrm{-2i}{\bar{\omega }}T_0 } \\&z_{3{\bar{\omega }}} =-\frac{E_{3{\bar{\omega }}} }{8{\bar{\omega }}^{2}}\hbox {e}^{\mathrm{3i}{\bar{\omega }}T_0 } \\&z_{-3{\bar{\omega }}} =-\frac{E_{-3{\bar{\omega }}} }{8{\bar{\omega }}^{2}}\hbox {e}^{\mathrm{-3i}{\bar{\omega }}T_0 } \\&z_{\mathrm{ES}} =\frac{E_{\mathrm{S}} }{{\bar{\omega }}^{2}} \end{aligned} \right. \end{aligned}$$

(44)

The solution of the first-order approximate equation in Eq. (42) is

$$\begin{aligned} z_1 =z_{2{\bar{\omega }}} +z_{-2{\bar{\omega }}} +z_{3{\bar{\omega }}} +z_{-3{\bar{\omega }}} +z_{\mathrm{ES}} \end{aligned}$$

(45)

According to Eqs. (33), (41) and (45), the solution of the rotor system can be written as:

$$\begin{aligned} z= & {} z_{0\mathrm{F}} +z_{0\mathrm{S}} \nonumber \\&+\varepsilon _{\mathrm{P}} (z_{2{\bar{\omega }}} +z_{-2{\bar{\omega }}} +z_{3{\bar{\omega }}} +z_{-3{\bar{\omega }}} +z_{\mathrm{ES}} ) \end{aligned}$$

(46)

Compared with the case without static eccentricity, this response includes not only the higher harmonic components but also the backward whirling motion in addition to the forward whirling motion. From Eqs. (42), (44) and (46), we can observe the coupling of the forward and backward whirling motions.

4.2.2 Frequency characteristics of the main resonance

According to Eq. (43), we can obtain

$$\begin{aligned} \left\{ \begin{aligned} D_1 A_1&=-\xi _1 A_1 -\frac{\hbox {i}}{2{\bar{\omega }}} \\&\quad [A_1 |{A_1}|^{2}+2A_1 |{A_2}|^{2}+2A_1 |{z_{0\mathrm{S}}}|^{2} \\&\qquad +{\bar{A}}_2 z_{0\mathrm{S}}^2 +\sigma _1 A_1 +\beta _1 {\bar{\omega }}^{2} ] \\ D_1 A_2&=-\xi _1 A_2 +\frac{\hbox {i}}{2{\bar{\omega }}} \\&\quad [A_2 |{A_2}|^{2}+2A_2 |{A_1}|^{2}+2A_2 |{z_{0\mathrm{S}}}|^{2}\\&\qquad +{\bar{A}}_1 z_{0\mathrm{S}}^2 +\sigma _1 A_2] \end{aligned} \right. \end{aligned}$$

(47)

According to Eqs. (34) and (39), the derivatives of $A_{1}$ and $A_{2}$ with respect to $\tau$ are listed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\hbox {d}A_1 }{\hbox {d}\tau }=\varepsilon _{\mathrm{P}} D_1 A_1 \\&\frac{\hbox {d}A_2 }{\hbox {d}\tau }=\varepsilon _{\mathrm{P}} D_1 A_2 \\ \end{aligned} \right. \end{aligned}$$

(48)

Let $A_1 =r_1 \hbox {e}^{\mathrm{i}\theta _1 }$, $A_2 =r_2 \hbox {e}^{\mathrm{i} \theta _2}$, and $z_{0\mathrm{S}} =r_0 \hbox {e}^{\mathrm{i}\theta _{\mathrm{s}}}$, where $r_0 =\frac{\beta _{\mathrm{s}} }{{\bar{\omega }}^{2}}$. Substituting these expressions and Eq. (47) into Eq. (48) and then separating the real and imaginary parts yield

$$\begin{aligned} \left\{ \begin{aligned} {r}_1^{\prime }&=\varepsilon _{\mathrm{P}} \left[ -\xi _1 r_1 +\frac{r_0^2 r_2 }{2{\bar{\omega }}}\sin (2\theta _0 -\theta _1 -\theta _2) \right. \\&\quad \qquad \left. -\frac{{\bar{\omega }}\beta _1}{2}\sin \theta _1 \right] \\ r_1 {\theta }_1^{\prime }&=-\frac{\varepsilon _{\mathrm{P}} }{2{\bar{\omega }}} [r_1^3 +2r_1 r_2^2 +2r_0^2 r_1 \\&\qquad \qquad +r_0^2 r_2 \cos (2\theta _0 -\theta _1 -\theta _2) \\&\qquad \qquad +{\bar{\omega }}^{2}\beta _1\cos \theta _1 +\sigma _1 r_1 ] \\ {r}_2^{\prime }&=\varepsilon _{\mathrm{P}} \left[ {-\xi _1 r_2 -\frac{r_0^2 r_1 }{2{\bar{\omega }}}\sin (2\theta _0 -\theta _1 -\theta _2 )} \right] \\ r_2 {\theta }_2^{\prime }&=\frac{\varepsilon _{\mathrm{P}} }{2{\bar{\omega }}} [r_2^3 +2r_1^2 r_2 +2r_0^2 r_2 \\&\qquad \qquad +r_0^2 r_1 \cos (2\theta _0 -\theta _1 -\theta _2 )+\sigma _1 r_2] \end{aligned} \right. \end{aligned}$$

(49)

From Eq. (49), it can be seen that the amplitudes and phases are dependent on each other. For the steady state, we only assume that ${r}_1^{\prime } =0$ and ${r}_2^{\prime } =0$. From the third formula in Eq. (49), the phase ($2\theta _{0} - \theta _{1} - \theta _{2}$) should be time-invariant and hence phase $\theta _{1}$ according to the first formula in this equation yields

$$\begin{aligned} {\theta }_1^{\prime } ={\theta }_2^{\prime } =0 \end{aligned}$$

(50)

Unlike the case without static eccentricity, Eq. (50) is derived by analysis rather than assumption, although the phases are still time-invariant. Usually, in a single degree of freedom system, we assume that both the derivatives of the amplitude and phase with respect to time are equal to 0 for the steady state. This assumption can be further applied to the case without static eccentricity in which there only exists the forward whirling motion. However, for the case considering the static eccentricity, the backward whirling motion appears, and we only assume that the amplitudes of the two whirling motions are time-invariant, whereas the variations of the phases are carried out based on this assumption. As a result, Eq. (50) together with this assumption is validated in Sect. 4.2.4.

Substituting Eq. (50) into Eq. (49), we can get

$$\begin{aligned} \left\{ \begin{aligned}&-\xi _1 r_1 +\frac{r_0^2 r_2 }{2{\bar{\omega }}}\sin (2\theta _0 -\theta _1 -\theta _2 ) \\&\qquad -\frac{{\bar{\omega }}\beta _1 }{2}\sin \theta _1 =0 \\&r_1^3 +2r_1 r_2^2 +2r_0^2 r_1 +r_0^2 r_2 \cos (2\theta _0 -\theta _1 -\theta _2 ) \\&\qquad +{\bar{\omega }}^{2}\beta _1 \cos \theta _1 +\sigma _1 r_1 =0 \\&\xi _1 r_2 +\frac{r_0^2 r_1 }{2{\bar{\omega }}}\sin (2\theta _0 -\theta _1 -\theta _2 )=0 \\&r_2^3 +2r_1^2 r_2 +2r_0^2 r_2 +r_0^2 r_1 \cos (2\theta _0 -\theta _1 -\theta _2 ) \\&\qquad +\sigma _1 r_2 =0 \end{aligned} \right. \end{aligned}$$

(51)

Eliminating the trigonometric functions in Eq. (51), the frequency characteristics are obtained:

$$\begin{aligned} \left\{ \begin{aligned}&\left[ {(r_1^2 -r_2^2 )^{2}-\beta ^{2}r_1^2 } \right] {\bar{\omega }}^{4} \\&\quad +\left[ {4\xi ^{2}(r_1^2 +r_2^2 )^{2}+2a_{\mathrm{m}} (r_1^2 -r_2^2 )^{2}} \right] {\bar{\omega }}^{2} \\&\quad +a_{\mathrm{m}}^2 (r_1^2 -r_2^2)^{2}=0 \\&r_2^2 {\bar{\omega }}^{4}+r_2^2 (4\xi ^{2}+2b_{\mathrm{m}}){\bar{\omega }}^{2}+r_2^2 b_{\mathrm{m}}^2 -r_0^4 r_1^2 \varepsilon _{\mathrm{P}}^2 =0 \end{aligned} \right. \end{aligned}$$

(52)

where, $a_{\mathrm{m}} =\varepsilon _{\mathrm{P}} (r_1^2 +r_2^2 +2r_0^2) -\omega _{\mathrm{g}}^2$ and $b_{\mathrm{m}} =\varepsilon _{\mathrm{P}} (2r_1^2 +r_2^2 +2r_0^2 )-\omega _{\mathrm{g}}^2$ are the parameters defined for simplicity. We can use Routh–Hurwitz criterion to determine the stability of the solution. The Jacobi matrix corresponding to Eq. (49) is written as

$$\begin{aligned} J_{\mathrm{M}} =[a_{ij} ] \quad i=1, 2, 3, 4, \, j=1, 2, 3, 4 \end{aligned}$$

where,

$$\begin{aligned} a_{11}= & {} a_{22} =a_{33} =a_{44} =a_{42} =-\xi , \\ a_{12}= & {} \frac{\varepsilon _{\mathrm{P}} r_1 (2r_0^2 +r_1^2 +2r_2^2 +\sigma _1)}{2{\bar{\omega }}}, \, a_{13} =-\frac{\xi r_2 }{r_1}, \\ a_{14}= & {} \frac{\varepsilon _{\mathrm{P}} r_2^2 (2r_0^2 +2r_1^2 +r_2^2 +\sigma _1 )}{2{\bar{\omega }}r_1 }, \\ a_{21}= & {} -\frac{\varepsilon _{\mathrm{P}} (2r_0^2 +3r_1^2 +2r_2^2 +\sigma _1 )}{2{\bar{\omega }}r_1}, \\ a_{23}= & {} \frac{\varepsilon _{\mathrm{P}} r_2 (2r_0^2 -2r_1^2 +r_2^2 +\sigma _1 )}{2{\bar{\omega }}r_1^2 }, \\ a_{24}= & {} \xi \left( {\frac{r_2}{r_1}} \right) ^{2}, a_{31} =-a_{13}, \\ a_{32}= & {} -\frac{\varepsilon _{\mathrm{P}} r_2 (2r_0^2 +2r_1^2 +r_2^2 +\sigma _1 )}{2{\bar{\omega }}}, \\ a_{34}= & {} a_{32} , a_{41} =-\frac{\varepsilon _{\mathrm{P}} (2r_0^2 -2r_1^2 +r_2^2 +\sigma _1)}{2{\bar{\omega }}r_1 }, \end{aligned}$$

and

$$\begin{aligned} a_{43} =\frac{\varepsilon _{\mathrm{P}} (2r_0^2 +2r_1^2 +3r_2^2 +\sigma _1 )}{2{\bar{\omega }}r_2 }. \end{aligned}$$

The characteristic equation is

$$\begin{aligned} a_0 \lambda ^{4}+a_1 \lambda ^{3}+a_2 \lambda ^{2}+a_3 \lambda +a_4 =0 \end{aligned}$$

(53)

where $a_k =(-1)^{k}tr^{[k]}(J_{\mathrm{M}} )$ and $tr^{[k]}(J_{\mathrm{M}})$ is kth-order trace of matrix $J_{\mathrm{M}}$.

$$\begin{aligned}&tr^{[k]}(J_{\mathrm{M}} )=\sum _{1\le i_1<i_2<\cdots<i_k <4} \left| \begin{array}{lll} a_{i_{1} i_{1}} &{} \cdots &{} a_{i_{1} i_{k}} \\ \cdots &{} &{} \\ a_{i_{k} i_{1}} &{} \cdots &{} a_{i_{k} i_{k}} \\ \end{array} \right| \nonumber \\&\qquad k=0,1,2,3,4 \end{aligned}$$

(54)

Particularly, $a_0 =1$, $a_1 =-(a_{11} +a_{22} +a_{33} +a_{44} )$, and $a_4 =\det (J_{\mathrm{M}})$. According to Routh–Hurwitz criterion, the stable solution should satisfy the following relationship:

$$\begin{aligned} \left\{ \begin{aligned}&\xi>0, \, a_2>0, \, a_3>0, \, a_4>0 \\&a_3 (a_1 a_2 -a_3 )-a_1^2 a_4 >0 \\ \end{aligned} \right. \end{aligned}$$

(55)

In addition, due to the geometric constraint of the stator, the amplitude of the rotor whirling motion is limited in the range of 0 to the average air gap. ${\vert } z {\vert }=1$ denotes the contact of the rotor and stator. The stable solution should satisfy the geometric constraint

$$\begin{aligned} |z|\le 1 \end{aligned}$$

(56)

The solution with the non-dimensional amplitude larger than 1 cannot really occur; therefore, it can be included in the group of unstable solutions. As shown in Figs. 7 and 8a, both upper branches are stable according to Routh–Hurwitz criterion. However, in these branches, the solutions with amplitude ${\vert }z{\vert } > 1$ cannot be realized, so they are plotted with dashed lines that are shown in the curves of the forward whirling motion and the backward whirling motion (Figs. 7, 8). A similar situation can be observed in Figs. 9, 10, 11 and 12. Therefore, in this paper, the solutions with amplitudes larger than 1 are plotted with dashed lines.

Fig. 7

Amplitude–frequency curve without static eccentricity

Fig. 8

Amplitude–frequency curves of the forward whirling and backward whirling motions. To clearly show the results, c locally displays the curve of (b)

Fig. 9

Influence of the damping ratio $\xi$ on amplitude–frequency characteristics

Fig. 10

Influence of the nonlinear parameter $\varepsilon _{\mathrm{P}}$ on amplitude–frequency characteristics

Fig. 11

Influence of the mass eccentricity ratio $\beta$ on amplitude–frequency characteristics

Both Eqs. (55) and (56) form the stability condition. The former is obtained by Routh–Hurwitz criterion, and it depends on the natural characteristics and reflects the stability mechanism of the system, whereas the latter provides the geometric constraint that limits the region of the rotor whirl.

4.2.3 Comparison of the degenerate model and the model by harmonic balance method

Neglecting the static eccentricity, i.e., $r_{0}=0$, we can obtain $r_{2}=0$ from the third formula in Eq. (51) when the rotor system is in steady state. Therefore, at this time, the excitation that is only caused by mass imbalance which includes a single frequency (angular speed) leads to a synchronous whirling motion with the same frequency as that of the excitation, the backward whirling motion vanishes, and the degenerate form of Eq. (52) is

$$\begin{aligned}&(r_1^2 -\beta ^{2}){\bar{\omega }}^{4}+\left[ {4\xi ^{2}-2\left( {1-\alpha -\frac{3\alpha }{2}r_1^2 } \right) } \right] r_1^2 {\bar{\omega }}^{2} \nonumber \\&\quad +\left( {1-\alpha -\frac{3\alpha }{2}r_1^2 } \right) ^{2}r_1^2 =0 \end{aligned}$$

(57)

We can further derive the phase characteristics

$$\begin{aligned} \tan \theta _1 =\frac{-2\xi {\bar{\omega }}}{1-\alpha -\frac{3\alpha r_1^2 }{2}-{\bar{\omega }}^{2}} \end{aligned}$$

(58)

The results by multi-scale method coincide with those by harmonic balance method in comparisons of Eqs. (30) and (57)–(58). Therefore, the two methods have consistency. However, multi-scale method can simply address the common case of the combination of mass imbalance and static eccentricity.

4.2.4 Results and discussion

For a given frequency ratio, the solution of Eq. (52) can be obtained, and the amplitude–frequency characteristics are shown in Figs. 7 and 8. As shown in Fig. 7, the amplitude–frequency curve without static eccentricity bends to the left, and hence, the system reveals a soft type. From Eq. (30), the curve has the asymptote $\varepsilon =\beta$ as the frequency ratio ${\bar{\omega }}$ increases. This is the so-called self-centering. The jump phenomenon occurs when the frequency ratio slowly increases and passes through ${\bar{\omega }}_A$.

For the rotor system with static eccentricity, the characteristics of forward whirling motion, as well as those of the case without static eccentricity, also exhibit a softening type. However, a small branch grows from the lower branch, as shown in Fig. 8a, while the self-intersection phenomenon appears in the amplitude–frequency curve of the backward whirling motion. In general, this motion is weaker than that of the forward whirling motion, as shown in Fig. 8b, c.

According to Eq. (55), the upper branch of the amplitude–frequency curve of the forward whirling motion is stable. However, the geometric constraint in Eq. (56) results in the upper branch having one part that cannot occur (Fig. 8a). When the frequency ratio increases slowly and reaches ${\bar{\omega }}_A$, the system is in a critical state, and point A is a turning point. Any increment of the frequency ratio can lead to the jump phenomenon; however, the response cannot spontaneously jump from point A to point $A^{\prime }$ due to the geometric constraint of the rotor system. At this time, contact of the rotor and stator occurs, and thus, the system undergoes the loss of stability. Similarly, as the frequency ratio decreases slowly and passes through ${\bar{\omega }}_B$, the loss of stability occurs. Therefore, in the frequency band (${\bar{\omega }}_A$, ${\bar{\omega }}_B$), the response cannot be realized and is globally unstable.

Compared with the rotor system without static eccentricity, the response of the system with static eccentricity includes the backward whirling motion in addition to the forward whirling motion. When the parameters vary, the amplitude–frequency characteristics change dramatically, which are more complex than those of the system without static eccentricity. Here, we discuss the influences of four parameters, damping ratio $\xi$, nonlinear parameter $\varepsilon _{\mathrm{P}}$, mass eccentricity ratio $\beta$ and static eccentricity ratio $\beta _{\mathrm{s}}$, on these characteristics.

• (1) Damping ratio $\xi$

Fig. 12

Influence of the static eccentricity ratio $\beta _{\mathrm{s}}$ on amplitude–frequency characteristics

The amplitude–frequency characteristics vary with the parameter $\xi$, as shown in Fig. 9. When the damping ratio increases, both amplitude–frequency curves shorten, and the small branch growing from the lower branch of the amplitude–frequency curve of the forward whirling motion shrinks and then vanishes (Fig. 9, $\xi =0.01$ and $\xi =0.1$). At this time, the amplitude–frequency curve of the forward whirling motion is similar to that of the case without static eccentricity (Fig. 7). In this process, the globally unstable frequency band narrows and finally disappears. For a comparatively large damping ratio, even the amplitude–frequency curves of the two whirling motions are single-valued, and the solution becomes stable in the whole frequency domain (Fig. 9, $\xi =0.1$). However, the overlarge damping causes harm to the isolation of the vibration. In a practical system, appropriate damping is necessary for both stability and vibration isolation.

• (2) Nonlinear parameter $\varepsilon _{\mathrm{P}}$ (Stiffness ratio $\alpha =2 \varepsilon _{\mathrm{P}}/3$)

When the parameter $\varepsilon _{\mathrm{P}}$ increases, the system nonlinearity becomes stronger, and the bending deflection of the amplitude–frequency curve of the forward whirling motion increases (Fig. 10a) while that of the backward whirling motion lengthens and moves toward the left (Fig. 10b). The globally unstable frequency band becomes narrower and then disappears (Fig. 10, $\varepsilon _{\mathrm{P}}=1/10$ and $\varepsilon _{\mathrm{P}}=1/20$). Due to $\varepsilon _{\mathrm{P}} =3 \alpha /2$, the frequency band narrows with the increase in the stiffness ratio $\alpha$. Both the large electromagnetic stiffness and the small mechanical stiffness can increase $\alpha$. However, the stability margin becomes smaller simultaneously.

• (3) Mass eccentricity ratio $\beta$

The responses of the two whirling motions increase remarkably as the mass eccentricity ratio $\beta$ increases. For a comparatively small $\beta$ (Fig. 11a, $\beta =0.001$), there is no globally unstable frequency band. However, the frequency band begins to appear as $\beta$ increases. The larger the parameter $\beta$ is, the wider the frequency band. In the process of the increase in $\beta$, the amplitude–frequency curve of the backward whirling motion moves toward the left (Fig. 11b). Therefore, a decrease in the mass imbalance, which is feasible, can not only obtain a smooth and quiet operation of the rotor system but also narrow the globally unstable frequency band.

• (4) Static eccentricity ratio $\beta _{\mathrm{S}}$

Static eccentricity spoils the cyclic symmetry of the equilibrium point of the rotor system. The dynamic characteristics as well as the static characteristics exhibit complexity, such as the small branch produced in the amplitude–frequency curve of the forward whirling motion. However, for a comparatively small static eccentricity, this curve has no small branch despite the nonlinear parameter and mass eccentricity varying in large ranges, as shown in Figs. 10a and 11a. When the static eccentricity ratio varies at a low level (Fig. 12a, b), a slight increase in the response of the forward whirling motion can be observed, and the curves corresponding to $\beta _{\mathrm{s}}=0.01$ and $\beta _{\mathrm{s}} = 0.05$ almost coincide with each other (Fig. 12a). However, the curve of the backward whirling motion lengthens dramatically (Fig. 12b).

For a comparatively large static eccentricity ratio ($\beta _{\mathrm{s}}=0.2$, Fig. 12c, d and $\beta _{\mathrm{s}}=0.3$, Fig. 12e, f), not only the forward whirling motion but also the backward whirling motion changes substantially. The small branch in the curve of the backward whirling motion as well as that of the forward whirling motion begins to appear and grows further. The two curves become more complex as the parameter $\beta _{\mathrm{s}}$ increases. The self-intersection phenomenon can also be observed in the amplitude–frequency curve of the forward whirling motion. The order of magnitude of the backward whirling motion increases significantly and even matches that of the forward whirling motion. With the increase in $\beta _{\mathrm{s}}$, the globally unstable frequency band appears and becomes wider. Accordingly, a decrease in the static eccentricity is another option that can narrow and even eliminate the globally unstable frequency band. Furthermore, it can also reduce the vibration and noise of the rotor system.

Next, the approximate analytical solution in Eq. (46) obtained by multi-scale method is validated by numerical simulation. Using Runge–Kutta method to solve Eq. (5), the numerical solution is carried out and can be compared with the analysis by multi-scale method. The comparisons of the calculations using various combinations of the system parameters reveal that the results obtained by the two methods agree well in the vicinity of $\omega _{\mathrm{g}}$ (the natural frequency of the generating system). Here, we select the parameters $\varepsilon _{\mathrm{P}}=1/15$, $\xi =0.1$, $\beta =0.1$, $\beta _{\mathrm{s}} =0.1$ and $\theta _{\mathrm{s}}={\uppi }/4$ to illustrate the comparison of the analytical solution in Eq. (46) with the numerical results, as shown in Figs. 13 and 14. The orbits, amplitudes and initial phases of the two motions are plotted in (a), (b) and (c) of the two figures, respectively. For the different detuning parameters, the orbits of the analytical solution by multi-scale method are in good agreement with those by the numerical method. From (b–c) of Figs. 13 and 14, we can see that both the amplitudes and initial phases are time-invariant when the rotor system is in steady state. Note that the results coincide with not only the assumption of the time-invariant amplitudes but also the analysis result in Eq. (50). Compared with the forward whirling motion, the backward whirling motion is comparatively weak, and the corresponding amplitude curves almost coincide with each other in Figs. 13b and 14b.

From the results, the orbits obtained by the analytical solution match well with those obtained by the numerical simulation when the detuning parameter $\sigma _{1}$ is close to 0, which means that the frequency ratio is in the vicinity of $\omega _{\mathrm{g}}$. As $\sigma _{1}$ further deviates from 0, the error between the two results increases. Moreover, the error for lower frequency ($\sigma _{1} < 0$) is larger than that for higher frequency ($\sigma _{1} > 0$), as shown in Figs. 13a and 14a. From Eq. (40) obtained by multi-scale method, the response caused by static eccentricity is inversely proportional to ${\bar{\omega }}^{2}$. Therefore, as the frequency ratio decreases, the response becomes more substantial, which leads to deviations between the orbits obtained by the analytical solution and numerical solution. However, the shapes of the orbits obtained by the two methods are similar to each other. This result denotes that the direct component depends on the frequency ratio, and multi-scale method cannot predict the response for the case when the frequency ratio is close to 0. However, we can obtain a satisfying result in the vicinity of $\omega _{\mathrm{g}}$.

Fig. 13

Comparison of calculation results ($\sigma _{1} \ge 0$)

Fig. 14

Comparison of calculation results ($\sigma _{1} < 0$)

5 Conclusions

This paper mainly focuses on the nonlinear characteristics of the unbalanced rotor of PMSMs in EVs and HEVs influenced by static eccentricity. Based on the effect of static eccentricity on the conservative force, the equilibrium points are carried out, and their stabilities are determined. Then, the static bifurcation of the rotor system is investigated. The frequency characteristics are studied by multi-scale method and then validated by a numerical method. The conclusions are summarized as follows:

The static eccentricity spoils the symmetry of the system equilibrium points and results in a generic bifurcation with a defect that provides two stability conditions. One is the stiffness condition in which the electromagnetic stiffness without the relative eccentricity between the rotor and stator is less than the mechanical stiffness; the other is the eccentricity condition in which the static eccentricity of the system is less than the equivalent deformation produced by the extremum of the system conservative force without static eccentricity applied to the rotor shaft. However, this parameter has no influence on the system radial stiffness.

For the rotor system in steady state, an assumption of the time-invariant amplitudes of the forward and backward whirling motions is adopted, whereas that of the time-invariant phases is discarded. The analyses of the frequency characteristics of the main resonance by multi-scale method based on this assumption agree well with the results of the numerical method. This result shows that the assumption and the analysis are reasonable.

The response of the rotor system with mass imbalance without static eccentricity only includes the component of forward whirling motion. However, when static eccentricity is introduced, the backward whirling motion is induced in addition to the forward whirling motion. Furthermore, the two whirling modes are coupled with each other due to the nonlinearity of UMP. The backward whirling motion is comparatively weak. However, it is enhanced for comparatively large electromagnetic stiffness, large mass imbalance, large static eccentricity, small mechanical stiffness and small damping. In particular, some complex branches are induced in the amplitude–frequency curves of the two motions as static eccentricity increases.

Due to the geometric constraint of the stator, the amplitude of the rotor whirling motion is limited in the range of 0 to the average air gap. This result leads to the generation of a globally unstable frequency band. This band narrows and even disappears with increases in damping and electromagnetic stiffness and decreases in mass imbalance, mechanical stiffness and static eccentricity.