1 Introduction

In comparison with fixed-wing unmanned aircrafts, the UAHs have many advantages such as hovering, vertical take-off and landing, ultra-low-speed flight, ultra-low-altitude flight, etc., which can perform many flying missions in complex environments or narrow spaces. Then, in recent years, different scales of UAHs have been applied to practical fields including military attacks, photography, and investigation, which leads to the increasing demands for the UAHs. Yet, it is worth noting that owing to the characteristics of the UAHs, they are always sensitive to outside disturbances, which may lead to poor control performance or even aircraft crash. Therefore, it is significant to improve the anti-disturbance capability for the UAHs.

Currently, as for different UAHs, most existent control schemes were mainly established based on linear UAH systems or nonlinear ones. As for linear UAH systems, these proposed techniques include PID control [1, 2], LQR control [3], and \(\text {H}_{\infty }\) control [4, 5], in which the controllers were mainly designed based on the approximate linearization of nonlinear UAH systems. Yet, when the system state deviates from the set operating point, the linearized model cannot describe the accurate form and the control algorithms in [1,2,3,4,5] are not available, which might degrade control performance or even induce instability. Recently, some methods have been proposed to design the controllers for nonlinear UAH systems [6,7,8,9,10,11,12,13]. For instance, in [6,7,8,9,10], some prescribed performance-based robust adaptive nonlinear control schemes were developed for the UAH systems subject to output constraints. In [11,12,13], some sliding mode controllers were presented to tackle the position control for nonlinear UAH systems, in which parameter uncertainties and external disturbances were involved. Then, in this work, the nonlinear UAH system will be utilized to accomplish the controller design, which may exhibit theoretic and practical meanings.

In recent years, the feedback linearization method has been utilized to simplify the nonlinear systems [14,15,16,17]. Especially, owing to the coupling effects between translational dynamics and rotational dynamics, the UAH system always produces the unstable zero-dynamic subsystems. Then, it is always required to transform the UAH dynamic model into a minimum phase system by ignoring the body force. In [16, 17], by selecting the positions and yaw angle as system outputs, an approximate feedback linearization was utilized to simplify the UAH system. In [18], the feedback linearization of small-scale UAH system was proposed, and a tracking controller for position and yaw angle was designed. By comparing with traditional control, the feedback linearization does not depend on the solution or stability of the addressed system. On the other hand, in 1990s, the backstepping control was proposed to tackle the nonlinear control systems [19]. Then, as for the UAH systems, in [20], a backstepping controller based nonlinear model was proposed to complete the automatic hovering and maneuvering flight. In [21], a flight controller based an integral backstepping control was designed for the small-scale UAH. Especially, in [22,23,24,25], the combinations of the backstepping technique and performance function-based error transformation were employed to achieve the bounded transience and steady-state tracking errors. Yet, based on the above-mentioned literature, it worth noting that although the combination of the feedback linearization and backstepping control can facilitate the controller design, it still has not been utilized to investigate the tracking control for nonlinear UAH system, which constitutes the focus of this presented work.

Meanwhile, the UAHs might be unavoidably affected by outside disturbances such as the winds and modelling error. In recent years, the anti-disturbance control has become a heated topic in the control community and a large number of results have been reported [26,27,28]. Based on these existing methods, the disturbance observer-based control (DOBC) has been verified to be effective in tackling the disturbed UAH systems [29,30,31,32,33,34]. Normally, according to channel and mechanism, the disturbances are divided into matched disturbance and mismatched one. For matched disturbance, its estimation can be directly incorporated into the compound control strategy, that is to say, the controller design includes both feedback control and feedforward one [28, 29]. In [28], by designing the disturbance observer, the anti-saturation control for nonlinear systems was studied and the matched disturbance could be compensated directly. Yet, the model perturbation and unmodeled dynamics in a UMH system can be regarded as mismatched disturbance since they are difficult to be completely suppressed via a control channel. For instance, [30, 31] utilized an improved DOBC method to suppress mismatched disturbances, and [32, 33] exploited the fixed-time sliding mode DOBC to tackle the hover operations of the UAHs. It is worth noting that most DOBC methods rejected the disturbances thorugh output channels using the compensation, which means that the disturbances need to be eliminated by the input signal. Yet, in some cases, the disturbances can possess some positive effects on control performance [34]. Then, the influence of the disturbance needs to be redefined by using the disturbance characterization index (DCI), which can decide whether to retain the disturbances or not in controller design. Yet, to our best knowledge, few works have utilized the DCI concept to study the anti-disturbance control for the UAH systems, which remains important and challenging.

Motivated by the above discussions, this work will study the tracking control for the UAH system and a DCI-based anti-disturbance backstepping controller will be proposed, in which both matched disturbance and mismatched one are involved. The contributions of this work can be expressed as follows:

  1. 1.

    Based on the approximated feedback linearization and dynamic expansion technology, the nonlinear UAH system is simplified as an integral chain one. By combining the FTDOs and backstepping control, the virtual intermediate variables and control input are derived. Since the disturbances with successive derivatives are estimated, the repeated steps for calculating disturbance derivatives in the backstepping controller can be avoided, which can help reduce the complexity of controller design procedure.

  2. 2.

    Different from some existent methods that wholly eliminated the disturbances, an effective disturbance DCI-based backstepping controller scheme is developed for the UAH system under both matched disturbance and mismatched ones. For mismatched disturbance, it can be directly compensated in the backstepping controller. Yet, as for matched disturbances, a DCI definition is introduced and can determine whether the disturbance is harmful or not to the UAH system. Then, the harmful part is eliminated while the beneficial one is retained in the feedback controller, which can effectively improve the control performance.

Notations \({\mathbb {R}}^n\) denotes the set of n-dimensional Euclidean space, and \({\mathbb {R}}^{m\times n}\) means the set of all real \(m\times n\) matrices. \(e_3=[0~~0~~1]^{\textrm{T}}\) means a unitary vector. \(C_{\theta }\), \(S_{\theta }\), \(T_{\theta }\) denote the abbreviations of trigonometric functions \(\cos \theta \), \(\sin \theta \), \(\tan \theta \), respectively, and others are similarly abbreviated. \(\vert x\vert \) stands for the absolute value for each element of the vector x. The symbol \(\otimes \) represents the element-wise product.

1.1 Nonlinear dynamic model of unmanned aerial helicopter (UAH)

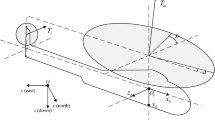
This subsection presents a nonlinear dynamic model for the UAH. The UAH system can be considered as a six-degree-of-freedom rigid body model with the simplified force and moment generation process, which further includes the disturbances and parameter uncertainties as the lumped disturbances. Then, this work focuses on the full-degree-of-freedom UAH system and studies the tracking control for the position and yaw angle under outside disturbances.

Based on [15], we consider the UAH attitude dynamic system as

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{P}}(t)=V(t),\\&\begin{array}{ll} {\dot{V}}(t)&{}=\,ge_3+R(t)e_3[-g+Z_{\omega }\omega (t)+Z_{\textrm{col}}\delta _{\textrm{col}}(t)]\\ &{}\quad +d_1(t), \end{array} \\&{\dot{\varTheta }}(t)=H(\varTheta )W(t),\\&\begin{array}{ll} {\dot{W}}(t)&{}=-JW(t)^\times JW(t)+AW(t)+Bu(t)\\ &{}\quad +d_2(t), \end{array} \end{aligned}\right. \end{aligned}$$
(1)

where \(P(t)=[x(t)\ y(t)\ z(t)]^{\textrm{T}} \in {\mathbb {R}}^3\) and \(V(t)=[u(t)\ v(t)\ w(t)]^{\textrm{T}} \in {\mathbb {R}}^3\) are the position vector and velocity vector in the inertial coordinate system, respectively; \(\varTheta (t)=[\phi (t)~\vartheta (t)~\psi (t)]^{\textrm{T}} \in {\mathbb {R}}^3\) and \(W(t)=[p(t)~q(t)~r(t)]^{\textrm{T}} \in {\mathbb {R}}^3\) are the Euler angle vector and angular rate vector in the body-fixed frame, respectively; \(\phi (t)\), \(\vartheta (t)\), and \(\psi (t)\) denote the roll, pitch, and yaw angles, respectively; p(t), q(t), and r(t) mean the angular rates; \(u(t)=[\delta _{\text{ col }}(t)~\delta _{\textrm{lon}}(t)~\delta _\textrm{lat}(t)~\delta _{\textrm{ped}}(t)]^{\textrm{T}}\in {\mathbb {R}}^4\) indicates the control input vector. The notations of \(d_1(t),d_2(t)\) are the lumped disturbance vectors, which contain the wind gusts, modeling error, and uncertainties. Moreover, the notation of g denotes the gravitational acceleration, and \(J=\textrm{diag}\{J_{xx}, J_{yy}, J_{zz}\}\) means the inertia matrix; \(Z_{\omega }\) and \(Z_{\textrm{col}}\) are the stability derivative and input derivative of the main rotor thrust \(T_m(t)=m[-\text {g}+Z_{\omega }\omega (t)+Z_{\textrm{col}}\delta _\textrm{col}(t)]\), respectively; \(A \in {\mathbb {R}}^{3 \times 3}\) and \(B \in {\mathbb {R}}^{3 \times 4}\) are the stability derivative matrix and input derivative matrix of the moment vector \(\tau (t)=AW(t)+Bu(t)\), respectively. The transformation matrix \(R(t) \in {\mathbb {R}}^{3}\) from the body coordinate system to the inertial coordinate one can be described as follows:

$$\begin{aligned} \begin{aligned} R(t)=\begin{bmatrix} C_{\theta } C_{\psi } &{}\quad ~S_{\theta } C_{\psi } S_{\phi }\!-\!S_{\psi } C_{\phi } &{}\quad ~S_{\theta } C_{\psi } C_{\phi }\!+\!S_{\psi } S_{\phi } \\ C_{\theta } S_{\psi } &{}\quad ~S_{\theta } S_{\psi } S_{\phi }\!+\!C_{\psi } C_{\phi } &{}\quad ~S_{\theta } S_{\psi } C_{\phi }\!-\!C_{\psi } S_{\phi } \\ -S_{\theta } &{}\quad ~C_{\theta } S_{\phi } &{}\quad ~C_{\theta } C_{\phi } \end{bmatrix}. \end{aligned}\nonumber \\ \end{aligned}$$
(2)

The attitude Kinematirc matrix \(H(\varTheta )\) in system (1) is defined as

$$\begin{aligned} \begin{aligned} H(\varTheta )=\begin{bmatrix} 1 &{}\quad S_{\phi } T_{\theta } &{}\quad C_{\phi } T_{\theta } \\ 0 &{}\quad C_{\phi } &{}\quad -S_{\phi } \\ 0 &{}\quad \dfrac{S_{\phi }}{C_{\theta }} &{}\quad \dfrac{C_{\phi }}{C_{\theta }}\end{bmatrix}, \end{aligned} \end{aligned}$$
(3)

and the derivative of R(t) is presented as

$$\begin{aligned} \begin{aligned} {\dot{R}}(t)=R(t)W^\times (t), \end{aligned}\end{aligned}$$
(4)

where \(W^{\times }(t)=\begin{bmatrix}0&{}\quad -r&{}\quad q\\ r&{}\quad 0&{}\quad -p\\ -q&{}\quad p&{}\quad 0\end{bmatrix}\).

1.2 Approximate feedback linearization model of UAH system

This subsection will utilize the input and output feedback linearization to simplify the system (1) for facilitating the controller design. Since the tracking target aims to make the UAH track the desired position \(P_d(t)=[x_d(t)\ y_d(t)\ z_d(t)]^{\textrm{T}}\) and yaw angle \(\psi _d(t)\), the control output can be selected as \(P_d(t)\) and \(\psi _d(t)\). However, the exact input–output linearization fails to linearize the complete system. Then in this work, an approximate feedback linearization technique will be developed for the UAH system [15].

It can be verified that the limped disturbances \(d_1(t),d_2(t)\) are the inherent components of the UAH system, which are independent of the control input. Then, to determine the relative order, we consider the system (1) without the disturbances, i.e., the lumped disturbances need to be set as \(d_1(t)=d_2(t)=0\). Moreover, to complete the feedback linearization procedure succinctly, the term \(-m[-g+Z_{\omega } \omega (t)+Z_{\textrm{col}} \delta _{\textrm{col}}(t)]\) should be replaced by the main rotor thrust \(T_m(t)\). For completing the linearization process of UAH input and output feedback, we define two variables as \(T_{1m}(t)={\dot{T}}_m(t), T_{2m}(t)={\dot{T}}_{1m}(t)\). Then, according to [15], the simplified model of the UAH system (1) can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{P}}(t)=V(t), \\&{\dot{V}}(t)=\text {g} e_{3}-\frac{1}{m} R(t) e_{3} T_{m}(t), \\&{\dot{\varTheta }}(t)=H(\varTheta ) W(t), \\&{\dot{W}}(t)=-J^{-1} W(t)^{\times } J W(t)+J^{-1}\tau (t),\\&{\dot{T}}_m(t)=T_{1m}(t),\\&{\dot{T}}_{1m}(t)=T_{2m}(t). \end{aligned}\right. \end{aligned}$$
(5)

Here, we define \({\tilde{u}}(t)=[{\tilde{\tau }}_{\phi }(t)\ {\tilde{\tau }}_{\theta }(t)\ {\tilde{\tau }}_{\psi }(t)\ {\tilde{T}}_{m}(t)]^{\textrm{T}}\) as the new control input, and \({\dot{W}}(t)={\tilde{\tau }}(t)=[{\tilde{\tau }}_{\phi }(t)~{\tilde{\tau }}_{\theta }(t)~{\tilde{\tau }}_{\psi }(t)]^\textrm{T}\). The transformation of the control signal is expressed as follows:

$$\begin{aligned} \begin{aligned} {\tilde{\tau }}(t)=-J^{-1} W^\times (t)J W(t)+\tau (t). \end{aligned}\end{aligned}$$
(6)

To utilize the input–output feedback linearization, one can differentiate the output variables P(t) and \(\psi (t)\) in (5). Moreover, by defining \(\zeta _1(t)=P(t),\) \( \zeta _2(t)={\dot{P}}(t),\) \( \zeta _3(t)={\ddot{P}}(t),\) and \(\zeta _4(t)=P^{(3)}(t)\), it follows from (5) that

$$\begin{aligned} {\dot{\zeta }}_1(t)&=V(t),\nonumber \\ {\dot{\zeta }}_2(t)&=\text {g}e_3-\frac{1}{m}R(t)e_3T_m(t),\nonumber \\ {\dot{\zeta }}_3(t)&=-\frac{1}{m}R(t)W^{\times }(t)e_3T_m(t)-\frac{1}{m}R(t)e_3{\dot{T}}_m(t),\nonumber \\ {\dot{\zeta }}_4(t)&=f_p(t)-\frac{1}{m}R(t)K(T_m)\tau _1(t), \end{aligned}$$
(7)

where \({f_p(t)}=-\frac{1}{m}R(t)W^{\times }(t)W^{\times }(t)e_3T_m(t)-\frac{2}{m}\times \) \(R(t)W^{\times }(t)e_3{\dot{T}}_m(t)\), \(\tau _1(t)=[{\tilde{\tau }}_{\phi }(t)\ {\tilde{\tau }}_{\theta }(t)\ {\tilde{T}}_m(t)]^{\textrm{T}}\), and

$$\begin{aligned} \begin{aligned} K(T_m)=\left[ \begin{array}{ccc} 0 &{} T_m &{} 0\\ -T_m &{} 0 &{} 0\\ 0 &{} 0 &{} 1 \end{array}\right] . \end{aligned}\end{aligned}$$
(8)

Now, by defining \(\zeta _5(t)=\psi (t)\) and \(\zeta _6(t)={{\dot{\psi }}}(t)\), we further obtain

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{\zeta }}_5(t)=\psi (t),\\&{\dot{\zeta }}_{6}(t)=f_\psi (t)+ \frac{S_\phi (t)}{C_\theta (t)}{\tilde{\tau }}_{\theta }(t) + \frac{C_\phi (t)}{C_\theta (t)}{\tilde{\tau }}_{\psi }(t),\\ \end{aligned}\right. \end{aligned}$$
(9)

where \(f_{\psi }(t)=[\frac{C_\phi (t)}{C_\theta (t)} {\dot{\phi }}(t)+\frac{S_\phi (t) T_\theta (t)}{C_\theta (t)} {\dot{\theta }}(t)] q(t)-[\frac{S_\phi (t)}{C_\theta (t)}\) \(\times {\dot{\phi }}(t)-\frac{C_\phi (t) T_\theta (t)}{C_\theta (t)} {\dot{\theta }}(t)] r(t)\).

Based on the above discussions, the dimension of the UAH system (1) amounts to \(n = 12\), and the total relative degree is \( r= 8\), which means that there must exist internal dynamics characterized via 4-D zero dynamics. Especially, by combining (7) and (9), we can obtain the relative order as \(R_t=14\). Since the dimensionality of the system (5) is \(R_n=14\), i.e., \(R_t=R_n\), it can be concluded that there exists no internal dynamics in the system (1). Then, as a conclusion, the system (1) can be wholly feedback linearized.

Now, by considering the disturbances, we can obtain the complete model of the UAH system as follows:

$$\begin{aligned}&S_{1}:\left\{ \begin{array}{l}{\dot{\zeta }}_{1}(t)=\zeta _{2}(t), \\ {\dot{\zeta }}_{2}(t)=\zeta _{3}(t)+d_{1}(t), \\ {\dot{\zeta }}_{3}(t)=\zeta _{4}(t), \\ {\dot{\zeta }}_{4}(t)=f_{p}(t)-\dfrac{1}{m} R(t) K(T_{m})\tau _1(t)+d_{2}(t), \end{array}\right. \end{aligned}$$
(10)
$$\begin{aligned}&S_{2}:\left\{ \begin{array}{l} {\dot{\zeta }}_{5}(t)=\zeta _{6}(t), \\ {\dot{\zeta }}_{6}(t)=f_{\psi }(t)+\dfrac{S_{\phi }}{C_{\theta }} {\tilde{\tau }}_{\theta }(t)+\dfrac{C_{\phi }}{C_{\theta }} {\tilde{\tau }}_{\psi }(t)+d_{3}(t), \end{array}\right. \end{aligned}$$
(11)

where \(d_1(t)=[d_{11}(t)~d_{12}(t)~d_{13}(t)]^{\textrm{T}} \in {\mathbb {R}}^3\), \(d_2(t)=[d_{21}(t)~d_{22}(t)~ d_{23}(t)]^{\textrm{T}} \in {\mathbb {R}}^3\), and \(d_3(t) \in {\mathbb {R}}\) represent the lumped disturbances. Especially, since \(d_2(t)\) and \(d_3(t)\) enter the helicopter system via the same channels together with the control inputs, they can be treated as the matched disturbance. However, \(d_1(t)\) does not satisfy the matching condition, and it can be called mismatched disturbance. Then, as for the position and yaw angle, we define their tracking errors and successive derivatives as

$$\begin{aligned} \left\{ \begin{array}{ll} x_n(t)=\zeta _n(t)-P_r^{(n-1)}(t),&{}n=1,2,3,4, \\ x_n(t)=\zeta _n(t)-\psi _r^{(n-5)}(t),&{}n=5,6,\\ \end{array}\right. \end{aligned}$$
(12)

where \(P_r^{(n-1)}(t)\) and \(\psi _r^{(n-1)}(t)\) denote the successive derivatives. Then, the tracking error system satisfies

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{x}}_1(t)=x_2(t),\\&{\dot{x}}_2(t)=x_3(t)+d_1(t),\\&{\dot{x}}_3(t)=x_4(t),\\&\begin{aligned} {\dot{x}}_4(t)&=f_p(t)-\frac{1}{m}R(t)K(T_m)u_1(t)\\&\quad -P_r^{(4)}(t)+d_2(t),\\ \end{aligned}\\&{\dot{x}}_5(t)=x_6(t),\\&\begin{aligned} {\dot{x}}_6(t)&=f_{\psi }(t)+\frac{S_\phi }{C_\theta }{\tilde{\tau }}_\theta (t)+\frac{C_\psi }{C_\theta }{\tilde{\tau }}_\psi (t)\\&\quad -\psi _r^{(2)}(t)+d_3(t). \end{aligned} \end{aligned}\right. \end{aligned}$$
(13)

Remark 1

It can be checked that the disturbances \(d_1(t)\), \(d_2(t), d_3(t)\) exist in \(x_2(t)\), \(x_4(t)\), and \(x_6(t)\), respectively. Then, we will combine the FTDO and backstepping control to tackle mismatched disturbance \(d_1(t)\), and the matched ones \(d_2(t),d_3(t)\) will be rejected via the DCI-based DOBC method.

2 Finite-time disturbance observer (FTDO)

First of all, a set of FTDOs are presented to estimate the disturbances with their successive derivatives in finite time. In order to develop the subsequent FTDOs, an assumption needs to be presented.

Assumption 1

The UAH model can be described as (13), where the mismatched disturbance \(d_1(t)\) satisfies at least 3-th order differentiability, and \(d^{(4)}_1(t)\) possesses the Lipschitz constant \(L_1\). The matched disturbances \(d_2(t),d_3(t)\) have at least 1-st order differentiability and their first derivatives \({\dot{d}}_i(t)~(i=2,3)\) have the Lipschitz constants \(L_2,L_3\), respectively.

Now, a third-order FTDO is developed to estimate the disturbance \(d_1(t)\) with its successive derivatives \(d^{(l)}(t)~(l=1,2,3)\), which can be expressed as

$$\begin{aligned}&{\dot{z}}^1_0(t)= \epsilon ^1_0(t)+x_3(t), \end{aligned}$$
(14)
$$\begin{aligned}&\begin{aligned} \epsilon ^1_0(t)&= -\lambda ^1_0L^{\frac{1}{4}}_1{\vert }z^1_0(t)-x_2(t){\vert }^{\frac{3}{4}}\textrm{sgn}{(}z^1_0(t)-x_2(t){)}\\&\quad +z^1_1(t), \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned}&{\dot{z}}^1_1(t)= \epsilon ^1_1(t), \end{aligned}$$
(16)
$$\begin{aligned}&\begin{aligned} \epsilon ^1_1(t)&= -\lambda ^1_1L^{\frac{1}{3}}_1{\vert }z^1_1(t)-\epsilon ^1_0(t){\vert }^{\frac{2}{3}}\textrm{sgn}(z^1_1(t)-\epsilon ^1_0(t))\\&\quad +z^1_2(t), \end{aligned} \end{aligned}$$
(17)
$$\begin{aligned}&{\dot{z}}^1_2(t)= \epsilon ^1_2(t), \end{aligned}$$
(18)
$$\begin{aligned}&\begin{aligned} \epsilon ^1_2(t)&= -\lambda ^1_2L^{\frac{1}{2}}_1{\vert }z^1_2(t)-\epsilon ^1_1(t){\vert }^{\frac{1}{2}}\textrm{sgn}(z^1_2(t)-\epsilon ^1_1(t))\\&\quad +z^1_3(t), \end{aligned} \end{aligned}$$
(19)
$$\begin{aligned}&{\dot{z}}^1_3(t)= \epsilon ^1_3(t), \end{aligned}$$
(20)
$$\begin{aligned}&\epsilon ^1_3(t) = -\lambda ^1_3L_1\textrm{sgn}(z^1_3(t)-\epsilon ^1_2(t)), \end{aligned}$$
(21)

where \(z^1_0(t)\) denotes the estimate of the state \(x_2(t)\); \(z^1_1(t)\), \(z^1_2(t),z^1_3(t)\) are the estimates of the disturbance \(d_1(t),d^{(1)}_1(t),d^{(2)}_1(t)\), respectively. Here, \(L_1>0\) and \(\lambda ^1_i>0~(i=0,1,2,3)\) denote the coefficients of the FTDO. In what follows, two first-order FTDOs are respectively proposed to estimate \(d_2(t),d_3(t)\)

$$\begin{aligned}&{\dot{z}}^2_0(t)= \epsilon ^2_0(t)+f_p(t)-\frac{1}{m}R(t)K(T_m)u_1(t), \end{aligned}$$
(22)
$$\begin{aligned}&\begin{aligned} \epsilon ^2_0(t)&= -\lambda ^2_0L^{\frac{1}{2}}_2{\vert } z^2_0(t)-x_4(t){\vert }^{\frac{1}{2}}\textrm{sgn}(z^2_0(t)-x_4(t))\\&\quad +z^2_1(t), \end{aligned} \end{aligned}$$
(23)
$$\begin{aligned}&{\dot{z}}^2_1(t)= \epsilon ^2_1(t), \end{aligned}$$
(24)
$$\begin{aligned}&\epsilon ^2_1(t) = -\lambda ^2_1L_2\textrm{sgn}(z^2_1(t)-\epsilon ^2_0(t)), \end{aligned}$$
(25)
$$\begin{aligned}&{\dot{z}}^3_0(t)= \epsilon ^3_0(t)+f_{\psi }(t)+\frac{S_\phi }{C_\theta }{\tilde{\tau }}_\theta (t)+\frac{C_\psi }{C_\theta }{\tilde{\tau }}_\psi (t), \end{aligned}$$
(26)
$$\begin{aligned}&\begin{aligned} \epsilon ^3_0(t)&= -\lambda ^3_0L^{\frac{1}{2}}_3{\vert } z^3_0(t)-x_6(t){\vert }^{\frac{1}{2}}\textrm{sgn}(z^3_0(t)-x_6(t))\\&\quad +z^3_1(t), \end{aligned} \end{aligned}$$
(27)
$$\begin{aligned}&{\dot{z}}^3_1(t)= \epsilon ^3_1(t), \end{aligned}$$
(28)
$$\begin{aligned}&\epsilon ^3_1(t) = -\lambda ^3_1L_3\textrm{sgn}(z^3_1(t)-\epsilon ^3_0(t)), \end{aligned}$$
(29)

where \(z^i_0(t)~(i=2,3)\) denote the estimates of the states \(x_{j}(t)~(j=4,6)\), and \(z^i_1(t)~(i=2,3)\) mean the estimates of the disturbances \(d_i(t)~(i=2,3)\). Moreover, \(L_j>0~(j=2,3)\) and \(\lambda ^j_i>0~(i=0,1;j=2,3)\) mean the coefficients of the proposed FTDOs.

Considering the tracking error system (13), the error dynamics of the FTDO (14) described in the Filippov sense can be presented as

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{e}}^1_0(t)=-\lambda ^1_0L^{\frac{1}{4}}_1\vert e^1_0(t)\vert ^{\frac{3}{4}}\textrm{sgn}(e^0_1)+e^1_1(t),\\&\begin{aligned} {\dot{e}}^1_1(t)&=-\lambda ^1_1L^{\frac{1}{3}}_1\vert e^1_1(t)-{\dot{e}}^1_0(t)\vert ^{\frac{2}{3}}\textrm{sgn}(e^1_1(t)-{\dot{e}}^0_1(t))\\&\quad +e^1_2(t), \end{aligned} \\&\begin{aligned} {\dot{e}}^1_2(t)&=-\lambda ^1_2L^{\frac{1}{2}}_1\vert e^1_2(t)-{\dot{e}}^1_1(t)\vert ^{\frac{1}{2}}\textrm{sgn}(e^1_2(t)-{\dot{e}}^1_1(t))\\&\quad +e^1_3(t), \end{aligned} \\&{\dot{e}}^1_3(t)=-\lambda ^1_3L_1\textrm{sgn}(e^1_3(t)-{\dot{e}}^1_2(t))+[-L_1,L_1], \end{aligned}\right. \end{aligned}$$
(30)

where the FTDO estimate errors are defined as \(e^1_0(t)=z^1_0(t)-x_2(t),e^1_1(t)=z^1_1(t)-d_1(t),e^1_2(t)=z^1_2(t)-d^{(1)}_1(t),\) and \(e^1_3(t)=z^1_3(t)-d^{(2)}_1(t)\). It follows from [15] that the estimate errors \(e^1_i(t)~(i=0,1,2,3)\) will converge to be convergent in finite time, which implies that there must exist a time second \(t_f\) such that \(e^1_i(t)=0\) for any \(t>t_f\). That is to say, \(z^1_i(t)=\epsilon ^1_{i-1}(t)~(i=1,2,3)\) hold for any \(t>t_f\). Similarly, we can derive the error dynamics of the FTDOs for (22) and (26) as follows:

$$\begin{aligned}&\left\{ \begin{aligned}&{\dot{e}}^2_0(t)=-\lambda ^2_0L^{\frac{1}{2}}_2\vert e^2_0(t)\vert ^{\frac{1}{2}}\textrm{sgn}(e^2_0)+e^2_1(t),\\&{\dot{e}}^2_1(t)=-\lambda ^2_1L_2\textrm{sgn}(e^2_1(t)-{\dot{e}}^2_1(t))+[-L_2,L_2], \end{aligned}\right. \end{aligned}$$
(31)
$$\begin{aligned}&\left\{ \begin{aligned}&{\dot{e}}^3_0(t)=-\lambda ^3_0L^{\frac{1}{2}}_3\vert e^3_0(t)\vert ^{\frac{1}{2}}\textrm{sgn}(e^3_0)+e^3_1(t),\\&{\dot{e}}^3_1(t)=-\lambda ^3_1L_3\textrm{sgn}(e^3_1(t)-{\dot{e}}^3_1(t))+[-L_3,L_3]. \end{aligned}\right. \end{aligned}$$
(32)

Based on [15], the stability of the error systems (31)–(32) can be guaranteed in finite time, which also implies that there must exist a time second \(t_f\) such that \(e^j_i(t)=0~(i=2,3;j=0,1)\) for any \(t>t_f\).

3 Tracking controller design

In this section, a DCI-based DOBC and backstepping control method will be presented to tackle the tracking control for the UAH system under external disturbances.

3.1 Backstepping controller

Defining the tracking variables \(\eta _1(t)\) and \(\eta _2(t)\) as

$$\begin{aligned} \begin{aligned} \eta _1(t)=x_1(t)-x_{1d}(t),~ \eta _2(t)=x_2(t)-x_{2d}(t), \end{aligned}\end{aligned}$$
(33)

where \(x_{1d}(t),x_{2d}(t)\) are the virtual control variables, they can be further designed as follows:

$$\begin{aligned} \begin{aligned} x_{1d}(t)=0, ~ x_{2d}(t)=-k_1\eta _1(t). \end{aligned}\end{aligned}$$
(34)

Then, the Lyapunov function of \(\eta _1(t)\) with its derivative can be derived as

$$\begin{aligned} \left\{ \begin{aligned}&V_1(t)=\frac{1}{2}\eta _1^{\textrm{T}}(t)\eta _1(t),\\&{\dot{V}}_1(t)=\eta _1^{\textrm{T}}(t)[-k_1\eta _1(t)+\eta _2(t)], \end{aligned}\right. \end{aligned}$$
(35)

where \(k_1\) denotes the controller parameter. Moreover, the Lyapunov function of \(\eta _2(t)\) with its derivative can be deduced as

$$\begin{aligned} \left\{ \begin{aligned}&V_2(t)=\frac{1}{2}\eta _2^{\textrm{T}}(t)\eta _2(t),\\&{\dot{V}}_2(t)=\eta _2^{\textrm{T}}(t)[x_3(t)+d_1(t)-{\dot{x}}_{2d}(t)]. \end{aligned}\right. \end{aligned}$$
(36)

Define \(\eta _3(t)=x_3(t)-x_{3d}(t)\) with \(x_{3d}(t)\) being expressed as

$$\begin{aligned} \begin{aligned} x_{3d}(t)=-k_2\eta _2(t)+{\dot{x}}_{2d}(t)-z^1_1(t). \end{aligned}\end{aligned}$$
(37)

Here, \(x_{3d}(t)\) can compensate for the disturbance \(d_1(t)\), and \(k_2\) denotes the controller parameter. Moreover, \({\dot{V}}_2(t)\) can be rewritten as

$$\begin{aligned} \begin{aligned} {\dot{V}}_2(t)&=\eta _2^{\textrm{T}}(t)[-k_2\eta _2(t)+\eta _3(t)]. \end{aligned}\end{aligned}$$
(38)

Then, the Lyapunov function of \(\eta _3(t)\) and its derivative can be obtained as

$$\begin{aligned} \left\{ \begin{aligned}&V_3(t)=\frac{1}{2}\eta _3^{\textrm{T}}(t)\eta _3(t),\\&{\dot{V}}_3(t)=\eta _3^{\textrm{T}}(t){\dot{\eta }}_3(t)=\eta _3^\textrm{T}(t)[x_4(t)-{\dot{x}}_{3d}(t)]. \end{aligned}\right. \end{aligned}$$
(39)

Now, we define \(\eta _4(t)=x_4(t)-x_{4d}(t)\), and \(x_{4d}(t)\) is expressed as

$$\begin{aligned} \begin{aligned} x_{4d}(t)=-k_3\eta _3(t)+{\dot{x}}_{3d}(t), \end{aligned}\end{aligned}$$
(40)

where \(k_3\) means the controller parameter. Then, \({\dot{V}}_3(t)\) can be written as

$$\begin{aligned} \begin{aligned} {\dot{V}}_3(t)&=\eta _3^{\textrm{T}}(t)[\eta _4(t)+x_{4d}(t)-{\dot{x}}_{3d}(t)]\\&=\eta _3^{\textrm{T}}(t)[-k_3\eta _3(t)+\eta _4(t)]. \end{aligned}\end{aligned}$$
(41)

The Lyapunov function of \(\eta _4(t)\) with its derivative can be obtained as \(V_4(t)=\frac{1}{2}\eta _4^{\textrm{T}}(t)\eta _4(t),\) and

$$\begin{aligned} \begin{aligned} {\dot{V}}_4(t)&=\eta _4^{\textrm{T}}(t)[f_p(t)-\frac{1}{m}R(t)K(T_m)u_1(t)\\&\quad -P_r^{(4)}(t)+d_2(t)-{\dot{x}}_{4d}(t)]. \end{aligned}\end{aligned}$$
(42)

Now, the control law \(u_1(t)\) can be designed as

$$\begin{aligned} \begin{aligned} u_1(t)&=mK^{-1}(T_m)R^{\textrm{T}}(t)[f_p(t)-P_r^{(4)}(t)\\&\quad +{\dot{x}}_{4d}(t)+k_4\eta _4(t)]. \end{aligned}\end{aligned}$$
(43)

Therefore, it follows from (42) and (43) that

$$\begin{aligned} \begin{aligned} {\dot{V}}_4(t)=-k_4\eta _4^{\textrm{T}}(t)\eta _4(t)+\eta _4^{\textrm{T}}(t)d_2(t), \end{aligned}\end{aligned}$$
(44)

where \(k_4\) denotes the controller parameter.

On the other hand, by defining the tracking variable \(\eta _5(t)=x_5(t)-x_{5d}(t)\), then the virtual control variable \(x_{5d}(t)\) can be designed as

$$\begin{aligned} \begin{aligned} x_{5d}(t)=0. \end{aligned}\end{aligned}$$
(45)

The Lyapunov function of \(\eta _5(t)\) with its derivative can be obtained as follows:

$$\begin{aligned} \begin{aligned} V_5(t)&=\frac{1}{2}\eta _5^{\textrm{T}}(t)\eta _5(t),~ {\dot{V}}_5(t)=\eta _5^{\textrm{T}}(t)x_6(t). \end{aligned}\end{aligned}$$
(46)

Defining \(\eta _6(t)=x_6(t)-x_{6d}(t)\), then \(x_{6d}(t)\) can be designed as

$$\begin{aligned} \begin{aligned} x_{6d}(t)=-k_5\eta _5(t), \end{aligned}\end{aligned}$$
(47)

where \(k_5\) is the controller parameter. Therefore, \({\dot{V}}_5(t)\) can be further written as

$$\begin{aligned} \begin{aligned} {\dot{V}}_5(t)&=\eta _5^{\textrm{T}}(t)[x_{6d}(t)+\eta _6(t)]\\&=\eta _5^{\textrm{T}}(t)[-k_5\eta _5(t)+\eta _6(t)]. \end{aligned}\end{aligned}$$
(48)

The Lyapunov function of \(\eta _6(t)\) and its derivative can be obtained as

$$\begin{aligned} \begin{aligned}&V_6(t)=\frac{1}{2}\eta _6^{\textrm{T}}(t)\eta _6(t),\\&\begin{aligned} {\dot{V}}_6(t)&=\eta _6^{\textrm{T}}(t)[f_{\psi }(t)+\frac{S_\phi }{C_\theta }{\tilde{\tau }}_\theta (t)+\frac{C_\phi }{C_\theta }{\tilde{\tau }}_\psi (t)\\&\quad -\psi _r^{(2)}(t)+d_3(t)-{\dot{x}}_{6d}(t)]. \end{aligned} \end{aligned}\end{aligned}$$
(49)

Thus, the control law \({\tilde{\tau }}_{\psi }(t)\) can be designed as

$$\begin{aligned} \begin{aligned} {\tilde{\tau }}_{\psi }(t)&=-\frac{C_\theta }{C_\phi }[k_6\eta _6(t)+f_\psi (t)+\frac{S_\phi }{C_\theta }{\tilde{\tau }}_\theta (t)\\&\quad -\psi _r^{(2)}(t) -{\dot{x}}_{6d}(t)], \end{aligned}\end{aligned}$$
(50)

where \(k_6\) means the controller parameter. Therefore, it follows from (50) that

$$\begin{aligned} \begin{aligned} {\dot{V}}_6(t)=\eta _6^{\textrm{T}}(t)[-k_6\eta _6(t)+d_3(t)]. \end{aligned}\end{aligned}$$
(51)

Since \(d_1(t)\) is the mismatched disturbance, it can be compensated during the design of the backstepping controller. Yet, as for the matched ones \(d_i(t)~(i=2,3)\), a new method based disturbance characterization index (DCI) is proposed to improve the tracking control performance, which can utilize the positive effects of the disturbances. Now, under the conventional backstepping control laws in the last section, we can select the Lyapunov function for the system (13) and compute out its time derivative as follows:

$$\begin{aligned} \left\{ \begin{aligned} V(t)&=V_1(t)+V_2(t)+V_3(t)+V_4(t)+V_5(t)+V_6(t),\\ {\dot{V}}(t)&=-k_1\eta _1^{\textrm{T}}(t)\eta _1(t)+\eta _1^{\textrm{T}}(t)\eta _2(t)-k_2\eta _2^{\textrm{T}}(t)\eta _2(t)\\&\quad +\eta _2^{\textrm{T}}(t)\eta _3(t)-k_3\eta _3^{\textrm{T}}(t)\eta _3(t)+\eta _3^{\textrm{T}}(t)\eta _4(t)\\&\quad -k_4\eta _4^{\textrm{T}}(t)\eta _4(t)+\eta _4^{\textrm{T}}(t)d_2(t)-k_5\eta _5^{\textrm{T}}(t)\eta _5(t)\\&\le +\eta _5^{\textrm{T}}(t)\eta _6(t)-k_6\eta _6^{\textrm{T}}(t)\eta _6(t)+\eta _6^{\textrm{T}}(t)d_3(t)\\&\quad -\left( k_1-\frac{1}{2}\right) \eta _1^{\textrm{T}}(t)\eta _1(t)-(k_2-1)\eta _2^{\textrm{T}}(t)\eta _2(t)\\&\quad -(k_3-1)\eta _3^{\textrm{T}}(t)\eta _3(t)-\left( k_4-\frac{1}{2}\right) \eta _4^{\textrm{T}}(t)\eta _4(t)\\&\quad -(k_5-\frac{1}{2})\eta _5^{\textrm{T}}(t)\eta _5(t)-\left( k_6-\frac{1}{2}\right) \eta _6^{\textrm{T}}(t)\eta _6(t)\\&\quad +\eta _4^{\textrm{T}}(t)d_2(t)+\eta _6^{\textrm{T}}(t)d_3(t). \end{aligned}\right. \end{aligned}$$
(52)

Based on the term (52), by choosing the suitable scalars \(k_i~(i=1,2,\ldots ,6)\), we can acquire that \(-(k_1-\frac{1}{2})\eta _1^{\textrm{T}}(t)\eta _1(t)-(k_2-1)\eta _2^\textrm{T}(t)\eta _2(t)-(k_3-1)\eta _3^\textrm{T}(t)\eta _3(t)-\left( k_4-\frac{1}{2}\right) \eta _4^\textrm{T}(t)\eta _4(t)-(k_5-\frac{1}{2})\eta _5^\textrm{T}(t)\eta _5(t)-\left( k_6-\frac{1}{2}\right) \eta _6^{\textrm{T}}(t)\eta _6(t)<0\) holds. Then, the derivative of V(t) satisfies \({\dot{V}}(t)<\eta _4^\textrm{T}(t)d_2(t)+\eta _6^{\textrm{T}}(t)d_3(t)\). Thus, it is worth noting whether \({\dot{V}}(t)\) to be negative or not depends on the term \(\eta _4^{\textrm{T}}(t)d_2(t)+\eta _6^{\textrm{T}}(t)d_3(t)\). Especially, when \(\eta _4^{\textrm{T}}(t)d_2(t)<0\) and \(\eta _6^{\textrm{T}}(t)d_3(t)<0\) hold, then \({\dot{V}}(t)<0\) holds and the stability of error system can be guaranteed, which shows that the disturbances \(d_2(t),d_3(t)\) are beneficial for the UAH system. Yet, if \(\eta _4^\textrm{T}(t)d_2(t)\ge 0\) and \(\eta _6^{\textrm{T}}(t)d_3(t)\ge 0\) hold, then \({\dot{V}}(t)<0\) cannot be true, which means that the disturbances \(d_i(t)~(i=2,3)\) are detrimental to the UAH system. Motivated by the above discussions, we introduce a DCI definition, which indicates the beneficial or harmful effects of the disturbances acting on the UAH system. Meanwhile, since the disturbances \(d_i(t)~(i=2,3)\) cannot be directly measured, the definition of the DCI will be presented by utilizing the estimations based on the FTDOs (14)–(26).

Definition 1

[34] Considering the Lyapunov functions (44) and (51), the DCI can be defined as

$$\begin{aligned} \left\{ \begin{aligned} J_{d_2}&=\textrm{sgn}(\eta _4) \otimes \textrm{sgn}(z_1^2),\\ J_{d_3}&=\textrm{sgn}(\eta _6) \otimes \textrm{sgn}(z_1^3). \end{aligned}\right. \end{aligned}$$
(53)

Remark 2

As illustrated in Definition 1, \(J_{d_2}=[J_{d_{21}}~J_{d_{22}}~J_{d_{23}}]^{\textrm{T}}\) denotes the \(3\times 1\) vector owing to that both \(\eta _4\) and \(z_1^2\) (estimation of \(d_2\)) are \(3 \times 1\) vectors, and \(J_{d_3}\) is a variable. Then, \(J_{d_2}\) and \(J_{d_3}\) can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned} J_{d_2}&=[J_{d_{21}}~J_{d_{22}}~J_{d_{23}}]^{\textrm{T}}, \\ J_{d_3}&= \textrm{sgn}(\eta _6)\textrm{sgn}(z_{1}^3) \end{aligned}\right. \end{aligned}$$
(54)

with \(J_{d_{2i}}=\textrm{sgn}(\eta _{4i})\textrm{sgn}(z_{1i}^2)~ (i=1,2,3)\).

3.2 Disturbance charaterization-based backstepping controller (DCBBC)

In this part, we will propose the design method for the disturbance charaterization-based backstepping controller (DCBBC). Based on the DCI definition, a switching control strategy will be developed for the control target of the UAH system, and the details will be described in the following theorem.

Theorem 1

Given the scalars \(k_i>\frac{1}{2}~(i=1,4,\) \(5,6),k_j>1~(j=2,3)\) in (38), the tracking errors \(\eta _i(t)~(i=1,2,3,4,5,6)\) can asymptotically converge to zero, if the DCBBC for the UAH system (13) is designed as

$$\begin{aligned} \left\{ \begin{aligned} u_1(t)&=mK^{-1}(T_m)R^{\textrm{T}}(t)[f_p(t)-P_r^{(4)}(t)\\&\quad +{\dot{x}}_{4d}(t)+k_4\eta _4(t)-\varXi (J_{d_2})z_1^2(t)],\\ {\tilde{\tau }}_\psi (t)&=-\frac{C_\theta }{C_\phi }[k_6\eta _6(t)+f_\psi (t)+\frac{S_\phi }{C_\theta }{\tilde{\tau }}_\theta (t)\\&\quad -\psi _r^{(2)}(t)-{\dot{x}}_{6d}(t)-\varXi (J_{d_3})z_1^3(t)], \end{aligned}\right. \end{aligned}$$
(55)

where the DCIs, \(J_{d_2},J_{d_3}\) are given in (54), the function \(\varXi (J_{d_2})\) is expressed as \(\varXi (J_{d_2})={\text {diag}}\{ \rho (\gamma _1)\) \(\rho (\gamma _2)~\rho (\gamma _3)\}\), \(\varXi (J_{d_3})\) is given as \(\varXi (J_{d_3})=\rho (\gamma _4)\), and the function \(\rho (\cdot )\) is selected as

$$\begin{aligned} \rho (\gamma _i)=\left\{ \begin{aligned} 1,~\gamma _i \le 0,\\ 0,~\gamma _i < 0. \end{aligned}\right. \end{aligned}$$
(56)

Proof

By substituting the control law (55) into the UAH system (13), we choose the Lyapunov function as the one in (52), i.e.,

$$\begin{aligned} \begin{aligned} V(t)&=\textstyle \sum \limits _{i=1}^{6}V_i(t), \end{aligned} \end{aligned}$$
(57)

where the terms \(V_i(t)~(i=1,2,3,4,5,6)\) are separately expressed in (35), (38), (41), (44), (48), and (51). Then, we compute out and estimate its derivative as

$$\begin{aligned} \begin{aligned} {\dot{V}}(t) \!&\le -\left( k_1-\frac{1}{2}\right) \eta _1^{\textrm{T}}(t)\eta _1(t)-(k_2-1)\eta _2^{\textrm{T}}(t)\eta _2(t)\\&\quad -(k_3-1)\eta _3^{\textrm{T}}(t)\eta _3(t)-\left( k_4-\frac{1}{2}\right) \eta _4^{\textrm{T}}(t)\eta _4(t) \\&\quad -(k_5-\frac{1}{2})\eta _5^{\textrm{T}}(t)\eta _5(t)-\left( k_6-\frac{1}{2}\right) \eta _6^{\textrm{T}}(t)\eta _6(t) \\&\quad +\eta _4^{\textrm{T}}(t)[d_2(t)-\varXi (J_{d_2})z^2_1(t)]+\eta _6^{\textrm{T}}(t)[d_3(t)\\&\quad -\varXi (J_{d_3})z^3_1(t)]. \end{aligned} \end{aligned}$$
(58)

Moreover, since \(k_i>\frac{1}{2}~(i=1,4,5,6)\) and \(k_j>1\) \((j=2,3)\) hold, we can further deduce

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)&\le \eta _4^{\textrm{T}}(t)[d_2(t)-\varXi (J_{d_2})z^2_1(t)]\\&\quad +\eta _6^{\textrm{T}}(t)[d_3(t) -\varXi (J_{d_3})z^3_1(t)]. \end{aligned}\end{aligned}$$
(59)

Meanwhile, since the function \(\varXi (\cdot )\) is symmetric, then \(\varXi (J_{d_2}),\varXi (J_{d_3})\) have the following expressions:

$$\begin{aligned} \left\{ \begin{aligned}&\varXi (J_{d_2})={\text {diag}}\{ \rho (\eta _{41}z_{11}^2),\rho (\eta _{42}z_{12}^2),\rho (\eta _{43}z_{13}^2) \},\\&\varXi (J_{d_3})=\rho (\eta _6z_1^3). \end{aligned}\right. \end{aligned}$$
(60)

Then, the item \(\eta _4^{\textrm{T}}(t)[d_2(t)-\varXi (J_{d_2})z^2_1(t)]\) can be rewritten as

$$\begin{aligned} \begin{aligned}&\eta _4^{\textrm{T}}(t)[d_2(t)-\varXi (J_{d_2})z^2_1(t)]\\&\quad =\eta _4^{\textrm{T}}(t)\{[d_2(t)-z^2_1(t)]+[z_1^2(t)-\varXi (J_{d_2})z^2_1(t)]\}\\&\quad =\eta _4^{\textrm{T}}(t)[d_2(t)\!-\!z^2_1(t)]\!+\!\eta _4^{\textrm{T}}(t)[z^2_1(t)\!-\!\varXi (J_{d_2})z^2_1(t)]\\&\quad =\eta _4^{\textrm{T}}(t)[d_2(t)-z^2_1(t)]\\&\quad \quad +\textstyle \sum \limits _{i=1}^3[1-\rho (\eta _{4i}z^2_{1i})]\eta _{4i}(t)z^2_{1i}(t). \end{aligned}\end{aligned}$$
(61)

Similarly, the term \(\eta _6^\textrm{T}(t)[d_3(t)-\varXi (J_{d_3})z_1^3(t)]\) can be also written as

$$\begin{aligned} \begin{aligned}&\eta _6^{\textrm{T}}(t)[d_3(t)-\varXi (J_{d_3})z_1^3(t)]\\&=\eta _6(t)[d_3(t)-z^3_1(t)]+[1-\rho (\eta _{6}z_1^3)]\eta _{6}(t)z_1^3(t). \end{aligned}\end{aligned}$$
(62)

Now, by considering \([1-\rho (\eta _{4i}z_{1i}^2)]\eta _{4i}(t)z_{1i}^2(t)<0\) and \([1-\rho (\eta _6z_{1}^3)]\eta _{6}(t)z_{1}^3(t)<0\), it follows from (59)–(62) that \({\dot{V}}(t)\) satisfies the following condition:

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)&\le \eta _4^{\textrm{T}}(t)[d_2(t)-z_1^2(t)]+\eta _6^{\textrm{T}}(t)[d_3(t)-z_1^3(t)]\\&= \eta _4^{\textrm{T}}(t)e_1^2(t)+\eta _6^{\textrm{T}}(t)e_1^3(t) \\&\le \frac{1}{2}\eta _4^{\textrm{T}}(t)\eta _4(t)+\frac{1}{2}\eta _6^{\textrm{T}}(t)\eta _6(t)\\&\quad +\frac{1}{2}({e_1^2}(t))^{\textrm{T}}e_1^2(t)+\frac{1}{2}({e_1^3}(t))^{\textrm{T}}e_1^3(t)\\&\le V(t)+\frac{1}{2}({e_1^2}(t))^\textrm{T}e_1^2(t)+\frac{1}{2}({e_1^3}(t))^{\textrm{T}}e_1^3(t). \end{aligned}\end{aligned}$$
(63)

Therefore, V(t) and \(\eta _i(t)~(i=1,2,\dots ,6)\) will not escape to infinity in the finite time.

Next, we will show that the tracking errors \(\eta _i(t)\) \((i=1,2,\dots ,6)\) will converge to zero in an asymptotic way. Based on the FTDOs in (14)–(26), we can obtain that the disturbance estimations \(z^1_1(t), z^2_1(t), z^3_1(t)\) will converge to real disturbances \(d_i(t)~(i=1,2,3)\) in the finite time, which illustrates that there must exist a time moment \(t_f>0\) ensuring \(z^i_1(t)=d_i(t)~(i=1,2,3)\) for \(t>f_f\). Therefore, as for \(t>t_f\), since \(\eta _4^{\textrm{T}}(t)e_1^2(t)+\eta _6^{\textrm{T}}(t)e_1^3(t)\) is converted to zero, then it follows from (58) that

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)&\le -\left( k_1-\frac{1}{2}\right) \eta _1^{\textrm{T}}(t)\eta _1(t)-(k_2-1)\eta _2^{\textrm{T}}(t)\eta _2(t)\\&\quad -(k_3-1)\eta _3^{\textrm{T}}(t)\eta _3(t)\\&\quad -\left( k_4-\frac{1}{2}\right) \eta _4^{\textrm{T}}(t)\eta _4(t)-(k_5-\frac{1}{2})\eta _5^{\textrm{T}}(t)\eta _5(t)\\&\quad -\left( k_6-\frac{1}{2}\right) \eta _6^{\textrm{T}}(t)\eta _6(t). \end{aligned}\end{aligned}$$
(64)

Moreover, by recalling \(k_i>\frac{1}{2}~(i=1,4,5,6)\) and \(k_j>1~(j=2,3)\), we can further deduce

$$\begin{aligned} \begin{aligned} {\dot{V}}(t) <&0,~\forall ~\eta _i(t)\ne 0~(i=1,2,\dots ,6). \end{aligned}\end{aligned}$$
(65)

In summary, the tracking errors converge to zero asymptotically, and the proof is completed. \(\square \)

Remark 3

In this work, the UAH system includes both matched disturbance and mismatch one, which are separately tackled in the procedures of controller design. As for the mismatched disturbance, it is directly compensated by using the backstepping control steps (37). Yet, as for the matched one, different from these existent works [35,36,37,38], we introduce the DCI concept to decide whether the disturbances are harmful or beneficial to the UAH system. Then, by applying the DCI to estimate the derivative of Lyapunov functional, our proposed methods keep the beneficial parts but remove the harmful ones, which can help improve the control performance in an effective way.

4 Simulated example

Based on [35], we assume that the disturbances \(d_i(t)~(i=1,2,3)\) are generated by the following exogenous systems:

$$\begin{aligned} \left\{ \begin{aligned} {\dot{\zeta }}_i(t)&=W_i\zeta _i(t),\\ d_i(t)&=V_i\zeta _i(t), \end{aligned}\right. \end{aligned}$$
(66)

where \(\zeta _i(t)\in {\mathbb {R}}^{n_{\zeta _i}}~(i=1,2,3)\) denote the states of the systems (66), and \(W_i\), \(V_i\) are expressed as follows:

$$\begin{aligned} W_1&=\!\left[ \!\begin{array}{cccc} 0 &{} 1.5 &{} 0 &{} 0\\ -1.5 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -1\\ 0 &{} 0 &{} 1 &{} 0 \end{array}\!\right] ,\quad W_2=\left[ \begin{array}{cccc} 0 &{} -2 &{} 0 &{} 0\\ 2 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -1\\ 0 &{} 0 &{} 1 &{} 0 \end{array}\right] ,\\ W_3&=\!\left[ \!\begin{array}{cccc} 0 &{} 1.5 &{} 0 &{} 0\\ -1.5 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -2\\ 0 &{} 0 &{} 2 &{} 0 \end{array}\!\right] , \quad V_1\!=\!\left[ \!\begin{array}{cccc} 1 &{} 1 &{} 0.5 &{} -0.7\\ 0.5 &{} 1 &{} 0 &{} 1\\ 1 &{} 0 &{} 1 &{} 0.5 \end{array}\!\right] ,\\ V_2&=\!\left[ \!\begin{array}{cccc} 1 &{} 0.2 &{} 0 &{} 1\\ -0.6 &{} 1 &{} 1 &{} 0\\ 1 &{} 0 &{} 1 &{} 0.5 \end{array}\!\right] ,\quad V_3=\left[ \begin{array}{cccc} 1&0.2&0&1 \end{array}\right] . \end{aligned}$$

In what follows, firstly, some numerical simulations are provided to demonstrate the effectiveness of our FTDO-based DCBBC methods. Secondly, some comparisons with existent DOBC methods are presented to evaluate the superiorities of our control scheme.

Based on [15], the parameters of the UAH system are given as \(m=8.2\,\text{ kg }\), \(\textrm{g}=9.81\) m s\(^{-2}\), \(Z_w=-0.76\,\text{ s}^{-1}\), \(Z_{\text{ col }}=-131.41\,\)m rad\(^{-1}\) s\(^{-2}\), \(J=\textrm{diag}\{0.18,0.34,0.28\}\) kg  m\(^2\), \(A=\textrm{diag}\{-48.1757,\) \(-25.5048,-0.9080\}\,\text{ s}^{-1}\), and

$$\begin{aligned} \begin{aligned} B=\left[ \begin{array}{cccc}0 &{} 0 &{} 1689.5 &{} 0 \\ 0 &{} 894.5 &{} 0 &{} 0 \\ -0.3705 &{} 0 &{} 0 &{} 135.8\end{array}\right] \text{ s}^{-2}. \end{aligned}\end{aligned}$$
(67)

Moreover, the coefficients of the FTDOs in (14)–(26) are selected as \(\lambda ^1_0=4\), \(\lambda ^1_1=3\), \(\lambda ^1_2=3\), \(\lambda ^1_3=4\), \(L_1=10\), \(\lambda ^2_0=4\), \(\lambda ^2_1=4\), \(L_2=15\), \(\lambda ^3_0=3\), \(\lambda ^3_1=3\), \(L_3=10\).

The control gains of the DCBBC in (55) are expressed as \(k_1=15\), \(k_2=18\), \(k_3=16\), \(k_4=18\), \(k_5=18\), \(k_6=10\). The desired reference trajectories of the position and yaw angle are set as follows:

$$\begin{aligned}\begin{aligned} \left[ \begin{array}{c}u_{d} \\ v_{d} \\ w_{d}\end{array}\right]&=\left[ \begin{array}{c}0 \\ 0 \\ 1.5\end{array}\right] +\left[ \begin{array}{c}0.8\cos t \\ 0.6\sin t\\ 2\cos (0.8t)\end{array}\right] , \psi _d=2\sin (0.5t). \end{aligned}\end{aligned}$$
Fig. 1
figure 1

The disturbances \(d_1(t)\) and its estimations

Full size image
Fig. 2
figure 2

The disturbances \(d_2(t)\) and its estimations

Full size image
Fig. 3
figure 3

The disturbances \(d_3(t)\) and its estimations

Full size image
Fig. 4
figure 4

The response curves of the position x(t)

Full size image
Fig. 5
figure 5

The response curves of the position y(t)

Full size image
Fig. 6
figure 6

The response curves of the position z(t)

Full size image
Fig. 7
figure 7

The response curves of the yaw angle \(\psi (t)\)

Full size image
Fig. 8
figure 8

The response curves of the position tracking error

Full size image
Fig. 9
figure 9

The response curves of the yaw angle \(\psi (t)\) tracking error

Full size image
Fig. 10
figure 10

The response curves of the control under the proposed FTDO-DCBBC method

Full size image
Fig. 11
figure 11

The response curves of the control under the DOBC method

Full size image

The simulation results are shown from Figs. 1, 2, 3, 4, 5, 6,7, 8, 9, 10 and 11. Figures 1, 2 and 3 depict the disturbance estimations by using the proposed FTDOs. It can be observed that the FTDOs can estimate the disturbances efficiently. Figures 4, 5, 6 and 7 illustrate the response curves of the position and yaw angle, respectively, which means that the reference trajectories can be tracked accurately under our proposed FTDO-DCBBC methods. Especially, the FTDO-DCBBC method in this work can be superior over some traditional DOBC ones. From Figs. 4, 5, 6 and 7, it can be seen that the overshoots by our FTDO-DCBBC method are smaller than the one by the DOBC method in some degree. Figures 8 and 9 show the tracking errors of the position and yaw angle, from which the tracking errors can converge to zero in a finite time.

Now, based on the tradition backstepping controller, we choose the similar parameters and further present some comparisons [35], which can be checked in Figs. 10 and 11. Then, based on the response curves of the control laws in Figs. 10 and 11, we can check that the control performance by our method is better than the one by the DOBC method since the trajectories fluctuates is much smaller in the early time interval. Moreover, to highlight the merits of our method, the root-mean-square (RMS) values of the tracking errors under the FTDO-DCBBC method and the DOBC are summarized in Table 1. As illustrated in Table 1, the proposed FTDO-DCBBC method achieves lower RMS values than the traditional DOBC, which reveals that our method can be superior over the existent ones.

Table 1 The RMS values of the tracking errors
Full size table

5 Conclusions

In this work, the trajectory tracking control for the UAH system under both matched disturbance and mismatched ones has been investigated. First, the input–output feedback linearization method was utilized to simplify the nonlinear UAH system, which could avoid the strong coupling. Then, some effective FTDOs were presented to estimate the disturbances with their successive derivatives. Thirdly, based on the backstepping control and proposed FTDOs, a tracking control scheme was offered and it could compensate for the mismatched disturbance directly. Moreover, by utilizing the DCI concept, an anti-disturbance backstepping controller was presented, and it could contain the beneficial effects of the matched disturbances, which might lead to better control performance. Finally, some simulations and comparisons have been exploited to demonstrate the effectiveness of the proposed control methods.