1 Introduction

In recent years, solitary wave solutions of nonlinear evolution equations have begun playing important roles in nonlinear science fields, especially in nonlinear physical science. The solitary wave solution can provide physical information and more insight into the physical aspects of the problem thus leading to further applications [1]. It is well known that there are many methods for finding special solutions of nonlinear partial differential equations, such as the inverse scattering method [1], the homogeneous balance method [2], the Darboux transformation method [3,4], the Hirota’s bilinear method [5,6], the improved tanh-method [7], the Lie group method [8], the extended homoclinic test approach [9–11], and so on.

In this work, we consider the (3 + 1)-dimensional B-type Kadomtsev–Petviashvili (BKP) equation

$$ u_{zt}-3(u_{x}u_{y})_{x}-u_{xxxy}+3u_{xx}=0, $$
(1)

where u :R x ×R y ×R z ×R t →R. The BKP equation was given this name because it is a B-type KP equation [12–14]. The well-known BKP equation possesses many integrable structures such as Lax formulation and the multiple soliton solutions. Exact solutions of the BKP equation have been studied by means of some effective approaches, such as the complex travelling wave solution [15], periodic solutions, multiple soliton solutions [16], Wronskian solution [17] and the Pfaffian solution [18]. However, to our best knowledge, the berather-type kink and rational breather solutions to the (3 + 1)-dimensional BKP equation (1) have not yet been studied. Therefore, in this paper, an approach of seeking rational breather-wave solution, called the homoclinic breather limit method [19,20], is proposed and applied. Exact breather kink wave and periodic breather solitary solutions are obtained, kink and periodic degeneracy are investigated, new rational breather solutions and rogue potential solution are constructed by homoclinic breather limit process or by Taylor expansion [21,22].

2 Homoclinic breather limit method

Consider a high-dimensional nonlinear evolution equation of the general form

$$ P(u,u_{t},u_{x},u_{y},u_{z},u_{xx},u_{yy},u_{zz},...)=0, $$
(2)

where u = u(x,y,z,t) and P is a polynomial of u and its derivatives. The basic idea of the homoclinic breather limit method can be expressed in the following five steps:

Step 1

By Painlevé analysis [10], a transformation

$$ u=T(f), $$
(3)

is made for some new unknown function f.

Step 2

By using the transformation in Step 1, the original equation can be converted into Hirota’s bilinear form

$$ G(D_{t},D_{x},D_{y},D_{z};f,f)=0, $$
(4)

where the D-operator [23] is defined by

$$\begin{array}{@{}rcl@{}} &&{}Q{}({}D_{x},D_{y},D_{z},D_{t},...{}){}F{}({}x,y,z,t,...{})\cdot G({}x,y,z,t,...{})\\&& {}=Q(\partial_{x}-\partial_{x^{\prime}},\partial_{y}-\partial_{y^{\prime}},\partial_{z}-\partial_{z^{\prime}},\partial_{t}-\partial_{t^{\prime}},...)\\ &&{}\times{}F{}({}x,y,z,t,...{})G({}x,y,z,t,...{})|_{x^{\prime}=x,y^{\prime}=y,z^{\prime}=z,t^{\prime}=t,...}, \end{array} $$
(5)

where Q is a polynomial of D x ,D y ,D t ,....

Step 3

As we know, the breather of integrable PDE is usually in the form of a rational function as the numerator and denominator are the combination of functions of cos, sin, cosh, sinh, and so f can be conjectured as a combination of cos and cosh (or sin and sinh). Then, substitute this trial form to the bilinear equation, eq. (5), to get a set of algebraic equation for some parameters, solve the above set of equation to obtain homoclinic breather wave solution, which was called the extended homoclinic test approach (EHTA)in [24].

Step 4

Let the period of periodic wave go to infinite in homoclinic breather wave solution. We can then obtain a rational breather wave solution.

Step 5

Solving the potential of breather wave solution in Step 3 and letting p tends to zero, we can obtain a rational homoclinic (heteroclinic) wave and this wave is just a rogue wave [25–47].

3 Applications

3.1 Kink degeneracy and new rational breather solution

By using Painlevé test, we can assume that

$$ u(x,y,z,t)=2(\ln f)_{x}, $$
(6)

where f(x,y,z,t) is an unknown real function. Substituting eq. (6) into eq. (1), we obtain the following bilinear form:

$$ (D_{z}D_{t}-{D_{x}^{3}}D_{y}+3{D_{x}^{2}})f\cdot f=0, $$
(7)

where

$$D_{z}D_{t}f\cdot f=2(f f_{zt}-f_{z} f_{t}) , $$
$${D_{x}^{3}}D_{y}f\cdot f=2(f_{xxxy}f -f_{xxx}f_{y}+3f_{xx}f_{xy}-3f_{x}f_{xxy}). $$

With regard to eq. (7), we can seek the solution in the form

$$ f=\mathrm{e}^{-p_{1}\xi}+\delta_{1}\cos(p\eta) +\delta_{2}\mathrm{e}^{p_{1}\xi}, $$
(8)

where ξ = x + a 1 y + b 1 z + c 1 t,η = x + a 2 y + b 2 z + c 2 t,a 1,b 1,c 1,a 2,b 2,c 2,p 1,p,δ 1,δ 2 are real constants to be determined. Substituting eq. (8) into eq. (7) and equating all the coefficients of different powers of eξ,e−ξ,sin(η),cos(η) and the constant term to zero, we can obtain a set of algebraic equations for p,p 1,a i ,b i ,c i ,δ i (i=1,2) as follows:

$$ \left\{ \begin{array}{l} -3a_{1}{p_{1}^{2}}-a_{2}{p_{1}^{2}}+3a_{2}p^{2}+c_{2}b_{1}+a_{1}p^{2}\\ +c_{1}b_{2}+6=0\\ -3a_{2}p^{2}{p_{1}^{2}}{}-{}3a_{1}p^{2}{p_{1}^{2}}{}+{}a_{1}{p_{1}^{4}}{}-{}3{p_{1}^{2}}{}+{}3p^{2}{}\\ +{}b_{2}c_{2}p^{2}{}-{}c_{1}b_{1}p^{2}{}+{}a_{2}p^{4}=0\\ 12\delta_{2}{p_{1}^{2}}-4a_{2}{\delta_{1}^{2}}p^{4}-b_{2}c_{2}{\delta_{1}^{2}}p^{2}-3{\delta_{1}^{2}}p^{2}\\ -16a_{1}\delta_{2}{p_{1}^{4}}+4b_{1}c_{1}\delta_{2}{p_{1}^{2}}=0. \end{array} \right. $$
(9)

Solving eq. (9) with the aid of Maple, we get the following results:

$$ \left\{ \begin{array}{l} \displaystyle a_{1}=-\frac{\begin{array}{l} p^{2}\left( a_{2}{\delta_{1}^{2}}p^{2}\left( p^{2}+2{p_{1}^{2}}\right)\right.\\ ~~~~~~\left.+{p_{1}^{2}}\left( a_{2}{\delta_{1}^{2}}{p_{1}^{2}}+4{\delta_{1}^{2}}-16\delta_{2}\right)\right) \end{array}} {4\delta_{2}{p_{1}^{2}}\left( p^{2}+{p_{1}^{2}}\right)^{2}},\\ \displaystyle c_{2}=-\frac{p^{2}\left( a_{2}p^{2}+3-2a_{2}{p_{1}^{2}}\right)-3{p_{1}^{2}}\left( 3+a_{2}{p_{1}^{2}}\right)}{b_{2}\left( p^{2}+{p_{1}^{2}}\right)},\\ \displaystyle b_{1}=-\frac{\begin{array}{l} b_{2}\left( a_{2}\delta_{1}p^{4}\left( p^{2}{\kern-1.2pt}+{\kern-1.2pt}2{p_{1}^{2}}\right){\kern-1.2pt}+{\kern-1.2pt}4p^{2}{p_{1}^{2}}\left( {\delta_{1}^{2}}{}-{}{\delta_{2}^{2}}\right)\right.\\ ~~~~~\left.+{\kern-1.2pt}{p_{1}^{4}}\left( a_{2}{\delta_{1}^{2}}p^{2}{\kern-1.2pt}+{\kern-1.2pt}12\delta_{2}\right)\right) \end{array}} {4\delta_{2}{p_{1}^{2}}\left( p^{2}{}+{}{p_{1}^{2}}\right)\left( a_{2}p^{2}{}+{}a_{2}{p_{1}^{2}}{}+{}3\right)},\\ \displaystyle c_{1}=-\frac{\left( 3p^{2}-{p_{1}^{2}}\right)\left( a_{2}p^{2}+a_{2}{p_{1}^{2}}+3\right)}{b_{2}\left( p^{2}+{p_{1}^{2}}\right)}, \end{array} \right. $$
(10)

where a 2,b 2,δ 1,δ 2,p,p 1 are some free real constants. There are different choices for δ 1,δ 2 and p in (10). Here, we specially take δ i ,i=1,2 and p such as \(\phantom {\dot {i}\!}\delta _{1}=-2\sqrt {p^{2}+1}, \delta _{2}=2p^{2}+1, p_{1}=p \) in eq. (10), so that it is more easy to get the form of 0/0 as p→0, in order to obtain rational breather solution. In this case, eq. (10) can be rewritten as

$$\begin{array}{@{}rcl@{}}\displaystyle a_{1}&=&-\frac{a_{2}p^{2}+a_{2}-1}{2p^{2}+1}, \\\displaystyle b_{1}&=&-\frac{a_{2}p^{2}(b_{2}p^{2}+3p^{2}+b_{2}+3)+8p^{2}+6}{2(2a_{2}p^{2}+3)(2p^{2}+1)},\\ \displaystyle c_{1}&=&-\frac{2a_{2}p^{2}+3}{b_{2}},\\ \displaystyle c_{2}&=&\frac{2a_{2}p^{2}+3}{b_{2}}. \end{array} $$
(11)

Substituting eq. (10) into eq. (8), we have

$$\begin{array}{@{}rcl@{}} f{}({}x,{}y{},{}z{},{} t{}){}&=&{} 2\sqrt {{}2p^{2}{}+{}1}{} \cosh(p(x+H_{1}y+K_{1}z+L_{1}t)\\ &&+\frac{1}{2}\ln(2p^{2}+1))-2\sqrt{p^{2}+1}\\ &&\times\cos(p(x+a_{2}y+b_{2}z-L_{1}t)), \end{array} $$
(12)

where

$$H_{1}=-\frac{a_{2}p^{2}+a_{2}-1}{2p^{2}+1}, $$
$$K_{1}=-\frac{b_{2}(2a_{2}p^{4}+2a_{2}p^{2}+4p^{2}+3)}{(2a_{2}p^{2}+3)(2p^{2}+1)}, $$
$$L_{1}=-\frac{2a_{2}p^{2}+3}{b_{2}}. $$

Substituting eq. (11) into eq. (6) yields the solution of the (3 + 1)-D BKP equation as follows:

$$ u(x,y,z,t)=\frac{\begin{array}{l} (2p\sqrt{2p^{2}+1}\sinh(p(x+H_{1}y+K_{1}z+L_{1}t)+\frac{1}{2}\ln(2p^{2}+1))\\ ~~+2\sqrt{p^{2}+1}\sin(p(x+a_{2}y+b_{2}z-L_{1}t)))\end{array}} {\begin{array}{l} \sqrt {2p^{2}+1}\cosh(p(x+H_{1}y+K_{1}z+L_{1}t)+\frac{1}{2}\ln(2p^{2}+1))\\ ~~-2\sqrt{p^{2}+1}\cos(p(x+a_{2}y+b_{2}z-L_{1}t))\end{array}}. $$
(13)

The solution u(x,y,z,t) represented by eq. (13) is a breather-type kink soliton. It is generated by the interaction between the soliton with variable X = p(x + H 1 y + K 1 z + L 1 t) + \(\phantom {\dot {i}\!}\frac {1}{2}\ln \)(2 p 2 + 1) and the periodic wave with variable Y = p(x + a 2 y + b 2 z − L 1 t).

If p→0 in eq. (13), we can get the rational breather solution as follows:

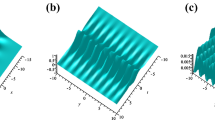
$$ u(x,y,z,t)=\frac{4{b_{2}^{2}}(2x+y-z+b_{2}z)}{(b_{2}(x+a_{2}y+b_{2}z)+3t)^{2}+(b_{2}(x+y-z)-(a_{2}b_{2}y+3t))^{2}+2{b_{2}^{2}}}. $$
(14)

The solution u(x,y,z,t) represented by eq. (14) is a new rational breather solution. Note that u tends to zero in eq. (15), when t→±∞, and so it is no longer kinky. Such a surprising feature of weakly dispersive long wave is first obtained. Meanwhile, this shows that kink is degenerated when the period of breather wave tends to infinity in the breather kink wave. Figures 1, 2, 3 and 4 exhibit the evolution breather kink wave and rational breather wave in the (x,t) and (x,y) planes, respectively. This is a new nonlinear phenomenon till now.

Figure 1
figure 1

The breather-type kink soliton solution when a 2=1,b 2=5,p=1,y = z=0.

Full size image
Figure 2
figure 2

The rational breather solution when a 2=1,b 2=5,y = z=0.

Full size image
Figure 3
figure 3

The breather-type kink soliton solution when a 2=1,b 2=5,p=1,t = z=0.

Full size image
Figure 4
figure 4

The rational breather solution when a 2=1,b 2=5,t = z=0.

Full size image

3.2 Kinky periodic degradation and new rational breather solution

In this section, we apply the homoclinic breather limit method to the (3 + 1)-dimensional BKP equation. By choosing the special test function, we obtained a kinky periodic-wave solution and a new rational breather solution.

Suppose that the solution of eq. (7) is

$$\begin{array}{@{}rcl@{}} f(x,y,z,t)&=&\mathrm{e}^{-p(x+b_{1}z+d_{1})}\\ &&+\,\delta_{1}\cos(p_{1}(y+b_{2}z+ct+d_{2})) \\ &&+\,\delta_{2}\mathrm{e}^{p(x+b_{1}z+d_{1})}, \end{array} $$
(15)

where b 1,b 2, c, d 1,d 2,δ 1,δ 2, p, p 1 are free real constants. Substituting eq. (15) into eqs (7), and equating all the coefficients of different powers of \(\phantom {\dot {i}\!}\mathrm {e}^{p(x+b_{1}z+d_{1})}, \mathrm {e}^{-p(x+b_{1}z+d_{1})}, \sin (p_{1}(y+b_{2}z+c_{2}t +d_{2})), \cos (p_{1}(y+b_{2}z+c_{2}t+d_{2}))\) and constant term to zero, we can obtain a set of algebraic equations for c,b i ,δ i (i=1,2). Solving the system with the aid of Maple, we get the following results:

$$ b_{1}=\frac{p^{2}}{c},\qquad p_{1}=\sqrt{\frac{3}{b_{2}c}}p,\quad \delta_{2}=\frac{1}{4}{\delta_{1}^{2}}. $$
(16)

Substituting eq. (16) into eq. (15) and taking b 2 c>0, we have

$$\begin{array}{@{}rcl@{}} f(x,y,z,t)\!&=&\!|\delta_{1}|\cosh\left( p\left( x+\displaystyle\frac{p^{2}}{c}z+d_{1}\right)\right.\\ && +\! \left. \ln\left( \displaystyle\frac{1}{2}|\delta_{1}|\right)\right)\\ && +\! \delta_{1}\cos\left( \sqrt{\displaystyle\frac{3}{b_{2}c}} p(y+b_{2}z+ct+d_{2})\vphantom{\sqrt{\frac{3}{1}}}\right).\\ \end{array} $$
(17)

Substituting eq. (17) into eq. (6) yields the kinky periodic soliton solution of the (3 + 1)-D BKP equation as follows:

$$ u(x,y,z,t)=\displaystyle\frac{2p|\delta_{1}|\sinh\big(p\big(x+\frac{p^{2}}{c}z+d_{1}\big)+\ln\big(\frac{1}{2}|\delta_{1}|\big)\big)}{|\delta_{1}|\cosh\big(p\big(x+\frac{p^{2}}{c}z+d_{1}\big)+\ln\big(\frac{1}{2}|\delta_{1}|\big)\big) +\delta_{1}\cos\big(\sqrt{\frac{3}{b_{2}c}}p(y+b_{2}z+ct+d_{2})\big)}. $$
(18)

The solution u(x, y, z, t) represented by eq. (18) can be considered as a kink soliton of the variable

$$X=p\left( x+\frac{p^{2}}{c}z+d_{1}\right)+\ln\left( \frac{1}{2}|\delta_{1}|\right) $$

spread along the direction of variable

$$Y=\sqrt{\frac{3}{b_{2}c}}p(y+b_{2}z+ct+d_{2}) $$

(see figure 5).

Figure 5
figure 5

The kinky periodic soliton solution when b 2=1/4,c=2,δ 1=1,p=1,d 1 = d 2 = y = z=0.

Full size image

Especially, for the same reason as dealing with eq. (10), we choose δ 1 = −2 in eq. (18), while p → 0, we can get the rational breather solution as follows:

$$\begin{array}{@{}rcl@{}} u(x,y,z,t)\,=\,\displaystyle\frac{4b_{2}c(x+d_{1})}{b_{2}c(x+d_{1})^{2}+3(y+b_{2}z+ct+d_{2})^{2}}.\\ \end{array} $$
(19)

The solution u(x,y,z,t) represented by eq. (19) is a breather wave which no longer has periodic kink feature. Here, periodic kink degeneracy occurs when the period of the periodic wave tends to infinity. It was observed that the periodic kink feature of the solution disappeared when p tends to zero. More importantly, we obtained a new rational breather wave solution (see figure 6).

Figure 6
figure 6

The rational breather solution when b 2=1/4,c=2,d 1 = d 2 = y = z=0.

Full size image

3.3 Periodic degeneracy and new rational breather solution

In this section, we obtained a breather-type periodic soliton solution and a rational breather solution by choosing another special test function. Suppose that the solution of eq. (7) is

$$\begin{array}{@{}rcl@{}} f(x,y,z,t)&=&\mathrm{e}^{-p(y+b_{1}z+ct+d_{1})}\\ &&+\delta_{1}\cos(p_{1}(x+b_{2}z+d_{2})) \\ &&+\delta_{2}\mathrm{e}^{p(y+b_{1}z+ct+d_{1})}, \end{array} $$
(20)

where b 1,b 2,c,δ 1,δ 2,p,p 1 are free real constants.

Substituting eq. (20) into eqs (7), and equating all the coefficients of different powers of \(\phantom {\dot {i}\!}\mathrm {e}^{p(y+b_{1}z+ct+d_{1})}, \mathrm {e}^{-p(y+b_{1}z+ct+d_{1})}, \sin (p_{1}(x+b_{2}z+d_{2})), \cos (p_{1}(x+b_{2}z+d_{2}))\) and constant term to zero, we can obtain a set of algebraic equations for c,b i ,δ i (i=1,2). Solving the system with the aid of Maple, we get the following results:

$$ b_{2}=-\frac{1}{3}b_{1}p^{2},\quad p_{1}=\sqrt{\frac{b_{1}c}{3}}p,\quad \delta_{2}=\frac{1}{4}{\delta_{1}^{2}}. $$
(21)

Substituting eq. (21) into eq. (20) and taking b 1 c>0, we have

$$\begin{array}{@{}rcl@{}} f(x,y,z,t)&=&|\delta_{1}|\cosh\!\left( \vphantom{\frac{1}{2}}\!p(y+b_{1}z+ct+d_{1})\right.\\ &&+\ln\left.\left( \displaystyle\frac{1}{2}|\delta_{1}|\right)\right)\\ &&+\delta_{1}\cos\left( {\kern-1.5pt}\sqrt{\displaystyle\frac{b_{1}c}{3}}p\left( {\kern-1.5pt}x-\frac{1}{3}b_{1}p^{2}z+d_{2}{}\right)\right),\\ \end{array} $$
(22)

Substituting eq. (22) into eq. (6), we obtain a breather-type periodic soliton solution of BKP equation as follows:

$$ u(x,y,z,t)=\displaystyle-\frac{2}{\sqrt{3}}\frac{\sqrt{b_{1}c}p\delta_{1}\sin\left( \sqrt{\frac{b_{1}c}{3}}p\left( x-\frac{1}{3}b_{1}p^{2}z+d_{2}\right)\right)}{|\delta_{1}|\cosh\!\big(p(y{}+{}b_{1}z{}+{}ct{}+{}d_{1}){}+{}\ln\big.\big({}\frac{1}{2}|\delta_{1}|{}\big)\big){}+{}\delta_{1}\cos\left( {}\sqrt{\frac{b_{1}c}{3}}p\left( x{}-{}\frac{1}{3}b_{1}p^{2}z{}+{}d_{2}{}\right){}\right)}. $$
(23)

The solution u(x,y,z,t) represented by eq. (23) can be considered as a soliton of variable

$$X=p(y+b_{1}z+ct+d_{1})+\ln\!\left( \frac{1}{2}|\delta_{1}|\right) $$

spread along the direction of variable

$$Y=\sqrt{\frac{b_{1}c}{3}}p\left( x-\frac{1}{3}b_{1}p^{2}z+d_{2}\right) $$

(see figure 7).

Figure 7
figure 7

The breather-type periodic soliton solution when b 1=1,p=2,c=4,δ 2=2,d 1 = d 2 = y = z=0.

Full size image

Similar to the way we deal with eq. (10), here we choose δ 1=−2 in eq. (23), when p→0, and we can get the rational breather solution as follows (figure 8):

$$\begin{array}{@{}rcl@{}} u(x,y,z,t) = \displaystyle\frac{4b_{1}c(x+d_{1})}{3(y+b_{1}z+ct+d_{2})^{2}+b_{1}c(x+d_{1})^{2}}.\\ \end{array} $$
(24)

Solution u(x,y,z,t) represented by eq. (24) is a breather wave which no longer has periodic feature. Here, periodic degeneracy occurs when the period of the periodic wave tends infinity. This is a strange and interesting physical phenomenon which causes the evolution of shallow water waves having small amplitudes. It is observed that the periodic feature of the solution disappeared when p tends to zero. More importantly, we obtained a new rational breather wave solution(see figure 10).

Figure 8
figure 8

The rational breather solution when b 1=1,c=4,d 1 = d 2 = y = z=0.

Full size image

3.4 Rogue potential solution

In this section, we solve the potential of eq. (13) and let p tend to zero. We then obtain a rational homoclinic (heteroclinic) wave and this wave is just a rogue wave.

Solving the potential of eq. (13), we have

$$\begin{array}{@{}rcl@{}} \phi&=&-(u(x,y,z,t))_{x}\\ &=&\frac{2p^{2}(-p^{2}+2\sqrt{2p^{2}+1}\sqrt{p^{2}+1}\sinh(p(x+H_{1}y+K_{1}z+L_{1}t)+\frac{1}{2}\ln(2p^{2}+1))\sin(p(x+a_{2}y+b_{2}z-L_{1}t)))}{(2\sqrt{2p^{2}+1}\cosh(p(x+H_{1}y+K_{1}z+L_{1}t)+\frac{1}{2}\ln(2p^{2}+1))-\sqrt{p^{2}+1}\cos(p(x+a_{2}y+b_{2}z-L_{1}t)))^{2}} \end{array} $$
(25)

where

$$H_{1}=-\frac{a_{2}p^{2}+a_{2}-1}{2p^{2}+1}, $$
$$K_{1}=-\frac{b_{2}(2a_{2}p^{4}+2a_{2}p^{2}+4p^{2}+3)}{(2a_{2}p^{2}+3)(2p^{2}+1)}, $$
$$L_{1}=-\frac{2a_{2}p^{2}+3}{b_{2}} $$

and ϕ is a breather-type periodic soliton (see figure 9).

Figure 9
figure 9

The breather-type periodic soliton ϕ when \(a_{2}=1, b_{2}=4, p=\frac {1}{2}, y=z=0\).

Full size image

Let p→0 and a 2=1 in eq. (25). By computing, we obtain the rational breather wave, and it is just a rogue wave as follows (see figure 10):

$$ U_{\text{rogue\; wave}}=\displaystyle\frac{-8{b_{2}^{2}}(6t(b_{2}z+3t-b_{2}x)+2b_{2}(x+y+b_{2}z)(3t-b_{2}x+b_{2}z)+{b_{2}^{2}})}{((b_{2}(x+y+b_{2}z)+3t)^{2}+(b_{2}(z-x)+3t)^{2}+{b_{2}^{2}})^{2}}. $$
(26)

U contains two waves with different velocities and directions. It is easy to verify that U rogue wave is a rational breather-type wave. In fact, U rogue wave contains two waves with different velocities and directions. From figure 10, we can see that U rogue wave has one upper dominant peak and two small holes. The spatial structure of the function U rogue wave is similar to the structure of the rogue waves which has been a point of hot discussion in recent years. In fact, U→0 for fixed x as y, z and t→±∞. So, U rogue wave is not only a rational breather wave but also a rogue wave solution, the amplitude of which is three times higher than its surrounding waves and U rogue wave generally forms in a short time.

Remark.

By using the same methodology as for eq. (13), we can solve the potential of solutions of eqs (18) and (23) in §3.2 and 3.3 respectively when p→0, to get rogue potential solutions.

Figure 10
figure 10

U rogue wave when b 2=4,y = z=0.

Full size image

4 Conclusion

In summary, by successfully applying the extended homoclinic test technique to the (3 + 1)-dimensional B-type Kadomtsev–Petviashvili equation, we obtained exact kink breather, kinky periodic and periodically breather solitary solutions. By using the homoclinic breather limit method proposed in this work, we obtained some new rational breather solutions. Furthermore, we investigated two new physical phenomena, kink and periodic degeneracy. Our results show different dynamics of high-dimensional systems. Meanwhile, we also obtained the rational potential solution which is just a rogue wave. This method is simple and straightforward. In the future, we shall investigate other types of nonlinear evolution equations and non-integrable systems.