A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials

Abstract

We present a general formulation of a class of uniaxial phenomenological models, able to accurately simulate hysteretic phenomena in rate-independent mechanical systems and materials, which requires only one history variable and leads to the solution of a scalar equation for the evaluation of the generalized force. Two specific instances of the class, denominated Bilinear and Exponential Models, are developed as an example to illustrate the peculiar features of the formulation. The Bilinear Model, that is one of the simplest hysteretic models which can be emanated from the proposed class, is first described to clarify the physical meaning of the quantities adopted in the formulation. Specifically, the potentiality of the proposed class is witnessed by the Exponential Model, able to simulate more complex hysteretic behaviors of rate-independent mechanical systems and materials exhibiting either kinematic hardening or softening. The accuracy and the computational efficiency of this last model are assessed by carrying out nonlinear time history analyses, for a single degree of freedom mechanical system having a rate-independent kinematic hardening behavior, subjected either to a harmonic or to a random force. The relevant results are compared with those obtained by exploiting the widely used Bouc–Wen Model.

1 Introduction

Hysteresis is a widespread phenomenon in science and engineering playing a significant role in industrial and technological applications.

Generally, the output of a hysteretic system depends on the past history of the input besides its current value, so that a number of state variables need to be known. Hysteresis is usually termed dynamic or static whether the rate of variation of the input does or does not influence the output [16]. Equivalent denominations are rate-dependent hysteresis in the former case and rate-independent in the latter.

Magnetics and mechanics are the two main areas of science and engineering where hysteresis phenomena are observed [64]. Hysteresis occurring in soft or hard magnetic systems and materials, such as soft iron, Si steel, permalloy, hexagonal ferrites, and Nd–Fe–B [6, 13], is referred to as magnetic hysteresis, whereas hysteresis occurring in mechanical systems and materials, such as ductile metals [67] and geomaterials [4], is referred to as mechanical hysteresis.

Hysteretic phenomena are so complex that they cannot be satisfactorily described by a single universal model. Indeed, the spectrum of their applications is so broad and their origin is due to such sophisticated and still unclear physical mechanisms that many phenomenological models have been proposed in the past.

Basically, phenomenological models are mathematical models that do not try to shed light on the physical origin of hysteresis but, rather, try to provide a suitable description and generalization of experimental findings [41]. Nevertheless, they have been resorted to, in the past as well as at present times, as powerful tools for design purposes.

As regards the hysteresis modeling of magnetic systems and materials, some of the widely used models are the Preisach model [41], the Jiles–Atherton model [31, 32], the Energetic Hauser model [26], and the Coleman–Hodgdon model [27]. As far as the hysteresis modeling of mechanical systems and materials is concerned, some of the widely used models are the bilinear model [1, 11, 19, 68], the Bouc–Wen model [8, 65, 66], the Ozdemir model [45], the Ramberg–Osgood model [49], the Giuffrè–Menegotto–Pinto model [23, 42], and plasticity-based models, such as multilayer models [7], single surface models [38], two-surface models [14, 15, 34], multi-surface models [29], and parallel elasto-plastic models [43].

Most of the existing phenomenological models, initially developed to describe a particular type of hysteresis, have been subsequently extended to describe other types of hysteretic phenomena, with their mathematical forms being suitable for multi-disciplinary extensions. For instance, hysteresis induced by friction occurring beetween several mechanical components of systems has been successfully described by the Preisach model [16].

A comprehensive classification of the hysteretic models is a rather hard task due to their large number. This is usually performed in the literature depending on the kind of equations that mathematically characterize the output variables. Actually, it is possible to distinguish:

• algebraic models, such as the bilinear, Ramberg–Osgood [49], and Giuffrè–Menegotto–Pinto [23, 42] models, in which an algebraic equation is solved to compute the output;

• transcendental models, in which the output is computed by solving transcendental equations, such as the Energetic Hauser model [26]. Transcendental equations involve functions such as trigonometric, inverse trigonometric, exponential, logarithmic, and hyperbolic functions [56];

• differential models, such as the Jiles–Atherton [31, 32], Coleman–Hodgdon [27], Bouc–Wen [8, 65, 66], and Ozdemir [45] models, in which first- or higher-order differential equations, either of ordinary or partial type, are solved to evaluate the output;

• integral models, such as the Preisach model [41], characterized by equations expressed in integral form.

The above-mentioned models can be broadly classified into two large categories. Actually, the current values of the input and output variables, as well as the direction of variation of the input variable, generally suffice to fully describe the behavior of hysteretic systems by exploiting differential models.

Conversely, the last reversal point of the hysteretic response, the direction along which input variation is considered, as well as additional information on the system history, is generally taken into account by algebraic, transcendental, and integral models.

This paper presents a class of uniaxial phenomenological models able to simulate hysteresis loops, limited by two parallel straight lines or curves, typical of rate-independent mechanical systems and materials with kinematic hardening or softening hysteretic behavior. The proposed class of models offers several important advantages over hysteretic models generally adopted to simulate the mechanical hysteresis phenomena. Actually, compared to differential models, the proposed class does not exploit the numerical solution of a differential equation, generally solved by adopting multi-steps [48] or Runge–Kutta methods [50], with the remarkable benefit of very significantly reducing the computational effort of finite element analyses. Compared to plasticity-based models, the proposed class of hysteretic models does not require the use of a return map algorithm [53] and can be easily implemented in a computer program.

The present paper is organized into three parts. In the first part (Sect. 2), the rate-independent hysteretic behavior of mechanical systems and materials, endowed with kinematic hardening or softening, is shortly described. In the second part (Sects. 3 and 4), the general formulation of the class of models is first presented. To better illustrate the features of the general formulation, always leading to the evaluation of the generalized force by solving a scalar equation, two specific instances of the proposed class, denominated Bilinear Model and Exponential Model, are presented. In particular, making reference to the classification alluded to above, the former is an algebraic model whereas the latter is a transcendental one since this characterizes, from a mathematical point of view, the nature of the scalar equation that provides the generalized force. The Bilinear Model is first illustrated to easily describe the meaning of the adopted quantities, since it represents one of the simplest models that can be emanated from the proposed class, whereas the Exponential Model is presented to illustrate the potentialities of the class, since it is able to accurately simulate a wide spectrum of rate-independent mechanical systems and materials.

In the third part (Sect. 5), the accuracy and the computational efficiency of the more elaborate Exponential Model are assessed by carrying out some nonlinear time history analyses performed on a rate-independent kinematic hardening post-yield single degree of freedom mechanical system. In particular, the results obtained for two different external forces, that is, a harmonic and a random force, have been compared with those obtained by using the celebrated Bouc–Wen Model [8, 65, 66], one of the most used differential models in the literature [2, 3, 17, 25, 33, 35, 36, 44].

2 Rate-independent mechanical systems and materials

Mechanical hysteresis is a rate-dependent or rate-independent process having a generalized displacement u, that is, displacement, rotation or strain as input, and a generalized force f, that is, force, moment or stress as output, or vice versa. In actual mechanical systems and materials, both types of hysteretic phenomena can be observed at the same time, although only rate-independent mechanical hysteresis is considered in this paper.

Fig. 1

An example of hysteresis loop limited by two straight lines typical of mechanical systems and materials exhibiting kinematic hardening (a) and softening (b) behavior

In rate-independent mechanical systems and materials, hysteresis is generally induced by plastic deformation mechanisms and/or friction forces [47]. If the generalized displacement cycles between two values, the generalized force traces a hysteresis loop in the input–output plane. This behavior is characterized by kinematic hardening (softening) when the generalized force increases (decreases) with generalized displacement and the hysteresis loops are limited by two bounds, i.e., two parallel limiting straight lines or curves, whose distance remains constant under repeated cycles. The increasing (decreasing) values of generalized forces as function of increasing values of generalized displacements, which typically characterizes hardening (softening), do not have to be confused with the behavior of the generalized tangent stiffness $\mathrm{d}f/\mathrm{d}u$ whose value is positive (negative) when hardening (softening) occurs.

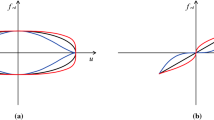
As an example of the aforementioned behaviors, Figs. 1a, 2a shows a hysteresis loop bounded by two straight lines (curves) typical of kinematic hardening mechanical systems and materials, whereas the hysteresis loop plotted in Figs. 1b, 2b is typical of kinematic softening behaviors.

Fig. 2

An example of hysteresis loop limited by two curves typical of mechanical systems and materials exhibiting kinematic hardening (a) and softening (b) behavior

In the field of structural, geotechnical, and seismic engineering, there are several examples of mechanical systems and materials having a rate-independent hysteretic behavior.

Hysteretic behavior characterized by hysteresis loops limited by two parallel straight lines is typical of many materials, such as ductile metals, e.g., steel [67], and geomaterials, e.g., soils [55] and concrete [4]. This hysteretic behavior is also typical of structural joints, such as steel [22], masonry [37], and wooden [52] joints, structural elements, e.g., steel braces [70], and seismic isolation bearings, such as wire rope isolators [60], steel dampers [30], and recycled rubber–fiber reinforced bearings [54].

Hysteretic behavior characterized by hysteresis loops limited by two parallel curves is typical of some structural joints [19], seismic devices, such as wire rope isolators [61], high damping rubber bearings [57], elastomeric seismic isolators [40], and recent hysteretic devices [9].

Generally, the above-described hysteretic behaviors are modeled in the literature [58, 59] using a uniaxial hysteretic spring parallel to a nonlinear elastic one, whose generalized tangent stiffnesses are $k_{h}$ and $k_{e}$, respectively. The former allows one to reproduce hysteresis loops limited by two straight lines, whereas the latter allows one to modify the shape of the straight lines to obtain two parallel limiting curves. This basic idea is generalized in the following section by assigning suitably defined functional forms to $k_{h}$ and $k_{e}$.

3 Proposed class of uniaxial phenomenological models

Mathematical modeling of hysteresis phenomena observed in mechanical systems and materials is very challenging, especially if the main aim is the development of accurate and computationally efficient models based on a small number of parameters having a clear mechanical significance.

In this section, a general formulation of a class of uniaxial phenomenological models, able to accurately simulate rate-independent mechanical hysteresis phenomena, is presented. More specifically, after some preliminaries about the adopted nomenclature, the proposed general form of the generalized tangent stiffness $k_{t}$, obtained by the sum of $k_{h}$ and $k_{e}$, is described; subsequently, the general expressions for the generalized force f and for the history variable $u_{j}$ are derived.

3.1 Preliminaries

Let $c_{u}$ and $c_{l}$ denote the upper and the lower limiting curves of a hysteresis loop, as shown in Fig. 3. The former intercepts the vertical axis at $f=\bar{f}$, whereas the latter at $f=-\bar{f}$. Assuming that cyclic loading phenomena do not modify the limiting curves, the distance between the two curves, along the vertical axis, is constant and equal to $2\bar{f}$.

Let $c^{+}$ denote the generic loading curve connecting points lying on the lower limiting curve $c_{l}$, having abscissa $u^{+}_{i}$, with points on the upper limiting curve $c_{u}$, having abscissa $u^{+}_{j}$, with $u^{+}_{i}=u^{+}_{j}-2u_{0}$. Furthermore, let $c^{-}$ denote the generic unloading curve connecting points lying on the upper limiting curve $c_{u}$, having abscissa $u^{-}_{i}$, with points on the lower limiting curve $c_{l}$, having abscissa $u^{-}_{j}$, with $u^{-}_{i}=u^{-}_{j}+2u_{0}$. The $+$ (−) sign used as superscript is reminiscent of loading (unloading) curves starting from the lower (upper) limiting curves. Furthermore, the subscript i (j) denotes the starting (ending) point of each curve.

The curves $c_{u}$, $c_{l}$, $c^{+}$, and $c^{-}$, in the case of a hysteresis loop limited by two parallel straight lines (curves), are shown in Fig. 3a, b. Notice that, for simplicity, the loading (unloading) curves have been further specified by means of arrows directly plotted on the curves. More specifically, a loading (unloading) curve is the one characterized by a positive (negative) sign of the velocity.

Fig. 3

Curves $c_{u}$, $c_{l}$, $c^{+}$, and $c^{-}$ in the case of a hysteresis loop limited by two parallel straight lines (a) or curves (b)

3.2 Generalized tangent stiffness

In the proposed formulation, the generalized tangent stiffness $k_{t}$ is given in the following general form:

$$\begin{aligned} k_{t}(u,u_{j})=k_{e}(u)+k_{h}(u,u_{j}), \end{aligned}$$

(1)

where $k_{h}(u,u_{j})$ is a function of a relative generalized displacement, obtained by relating the absolute displacement u to the history variable $u_{j}$; this last one is represented by $u^{+}_{j}$, when $\dot{u}>0$ (generic loading case), and by $u^{-}_{j}$, when $\dot{u}<0$ (generic unloading case), where $\dot{u}$ is the time derivative of the generalized displacement u.

As an example, assuming $k_{e}(u)=0$, Fig. 4a, b shows the graph of the function $k_{t}(u,u_{j})$ for the generic loading (unloading) curve $c^{+}$ ($c^{-}$) of Fig. 3a. In particular, the generalized tangent stiffness is a nonlinearly decreasing function, from $k_{a}$ to $k_{b}$, on $[u^{+}_{j}-2u_{0}, u^{+}_{j}]$ when $\dot{u}>0$, or on $[u^{-}_{j}, u^{-}_{j}+2u_{0}]$ when $\dot{u}<0$, being constant and equal to $k_{b}$ on $[u^{+}_{j},\infty )$ when $\dot{u}>0$, or on $(-\infty ,u^{-}_{j}]$ when $\dot{u}<0$.

Fig. 4

Graph of function $k_{t}(u,u_{j})$ for a generic loading (a) and unloading (b) case in Fig. 3a

The choice of a more elaborate analytical function to describe the generalized tangent stiffness may require the selection of an increasing number of model parameters. Such parameters are obtained by calibrating the curves of the hysteresis loop on the basis of the results of experimental tests.

3.3 Generalized force

According to Fig. 3, in the generic loading case, it turns out to be $f=c^{+}$ when $u^{+}_{i}<u<u^{+}_{j}$, and $f=c_{u}$ when $u>u^{+}_{j}$, whereas, in the generic unloading case, $f=c^{-}$ when $u^{-}_{j}<u<u^{-}_{i}$, and $f=c_{l}$ when $u<u^{-}_{j}$. Thus, in the sequel, the expressions for the upper ($c_{u}$) and lower ($c_{l}$) limiting curves as well as for the generic loading ($c^{+}$) and unloading ($c^{-}$) curves are derived by integrating the generalized tangent stiffness $k_{t}$ given by Eq. (1).

3.3.1 Upper limiting curve

The upper limiting curve $c_{u}$ can be obtained by integrating Eq. (1) as follows:

$$\begin{aligned} c_{u}\left( u,u^{+}_{j}\right) =\int k_{e}(u)\mathrm{d}u+\int k_{h}\left( u,u^{+}_{j}\right) \mathrm{d}u+C_{u}. \end{aligned}$$

(2)

Being interested in expressing the function $c_{u}$, we can assume that $u>u^{+}_{j}$ so that $k_{h}(u,u^{+}_{j})$ is constant and equal to $k_{b}$. Hence, Eq. (2) becomes:

$$\begin{aligned} c_{u}(u)=f_{e}(u)+k_{b}u+C_{u}, \end{aligned}$$

(3)

where

$$\begin{aligned} f_{e}(u)=\int k_{e}(u)\mathrm{d}u. \end{aligned}$$

(4)

The integration constant $C_{u}$ can be determined by imposing that the curve $c_{u}$ intercepts the vertical axis at $f=\bar{f}$:

$$\begin{aligned} f_{e}(0)+C_{u}=\bar{f}, \end{aligned}$$

(5)

from which, assuming $f_{e}(0)=0$:

$$\begin{aligned} C_{u}=\bar{f}. \end{aligned}$$

(6)

Thus, the general expression for the upper limiting curve is:

$$\begin{aligned} c_{u}(u)=f_{e}(u)+k_{b}u+\bar{f}. \end{aligned}$$

(7)

3.3.2 Lower limiting curve

The lower limiting curve $c_{l}$ can be obtained by integrating Eq. (1) as follows:

$$\begin{aligned} c_{l}\left( u,u^{-}_{j}\right) =\int k_{e}(u)\mathrm{d}u+\int k_{h}\left( u,u^{-}_{j}\right) \mathrm{d}u+C_{l}. \end{aligned}$$

(8)

As detailed for $c_{u}$, the function $c_{l}$ comes into play when $u<u^{-}_{j}$, a condition for which $k_{h}\left( u,u^{-}_{j}\right)$ is constant and equal to $k_{b}$. Hence, Eq. (8) becomes:

$$\begin{aligned} c_{l}(u)=f_{e}(u)+k_{b}u+C_{l}, \end{aligned}$$

(9)

where $f_{e}(u)$ is given by Eq. (4). The integration constant $C_{l}$ can be determined by imposing that the curve $c_{l}$ intercepts the vertical axis at $f=-\bar{f}$:

$$\begin{aligned} f_{e}(0)+C_{l}=-\bar{f}, \end{aligned}$$

(10)

from which, assuming $f_{e}(0)=0$, one infers:

$$\begin{aligned} C_{l}=-\bar{f}. \end{aligned}$$

(11)

Thus, the general expression for the lower limiting curve is:

$$\begin{aligned} c_{l}(u)=f_{e}(u)+k_{b}u-\bar{f}. \end{aligned}$$

(12)

It is apparent that the upper and lower limiting curves are parallel and that the distance between them, along the vertical axis, is equal to $2\bar{f}$.

3.3.3 Generic loading curve

The generic loading curve $c^{+}$ can be obtained by integrating Eq. (1) as follows:

$$\begin{aligned} c^{+}\left( u,u^{+}_{j}\right) =\int k_{e}(u)\mathrm{d}u+\int k_{h}\left( u,u^{+}_{j}\right) \mathrm{d}u+C^{+}, \end{aligned}$$

(13)

or, equivalently

$$\begin{aligned} c^{+}\left( u,u^{+}_{j}\right) =f_{e}(u)+f_{h}\left( u,u^{+}_{j}\right) +C^{+}, \end{aligned}$$

(14)

where $f_{e}(u)$ is given by Eq. (4), whereas $f_{h}(u,u^{+}_{j})$ is evaluated as:

$$\begin{aligned} f_{h}\left( u,u^{+}_{j}\right) =\int k_{h}\left( u,u^{+}_{j}\right) \mathrm{d}u. \end{aligned}$$

(15)

The integration constant $C^{+}$ can be determined by imposing that the generic loading curve $c^{+}$ intersects the upper limiting curve $c_{u}$ at $u=u^{+}_{j}$:

$$\begin{aligned} c^{+}\left( u^{+}_{j},u^{+}_{j}\right) =c_{u}\left( u^{+}_{j}\right) ; \end{aligned}$$

(16)

hence, on account of (7), one has:

$$\begin{aligned} f_{e}\left( u^{+}_{j}\right) +f_{h}\left( u^{+}_{j},u^{+}_{j}\right) +C^{+}=f_{e}\left( u^{+}_{j}\right) +k_{b}u^{+}_{j}+\bar{f}, \end{aligned}$$

(17)

from which one gets:

$$\begin{aligned} C^{+}=k_{b}u^{+}_{j}+\bar{f}-f_{h}\left( u^{+}_{j},u^{+}_{j}\right) . \end{aligned}$$

(18)

In conclusion, the general expression for the generic loading curve is:

$$\begin{aligned} c^{+}\left( u,u^{+}_{j}\right)= & {} f_{e}(u)+f_{h}\left( u,u^{+}_{j}\right) +k_{b}u^{+}_{j}\nonumber \\&+\quad \bar{f}-f_{h}\left( u^{+}_{j},u^{+}_{j}\right) . \end{aligned}$$

(19)

To show that the model parameters $\bar{f}$ and $u_{0}$ are related, we impose that the generic loading curve $c^{+}$ intersects the lower limiting curve at $u=u^{+}_{i}$. Thus, remembering that $u^{+}_{i}=u^{+}_{j}-2u_{0}$ and setting:

$$\begin{aligned} c^{+}\left( u^{+}_{j}-2u_{0},u^{+}_{j}\right) =c_{l}\left( u^{+}_{j}-2u_{0}\right) , \end{aligned}$$

(20)

the following equation is obtained, on account of (12):

$$\begin{aligned} \begin{aligned}&f_{e}\left( u^{+}_{j}-2u_{0}\right) +f_{h}\left( u^{+}_{j}-2u_{0},u^{+}_{j}\right) +k_{b}u^{+}_{j}+\bar{f}\\&-f_{h}\left( u^{+}_{j},u^{+}_{j}\right) =f_{e}\left( u^{+}_{j}-2u_{0}\right) +k_{b}\left( u^{+}_{j}-2u_{0}\right) -\bar{f}, \end{aligned} \end{aligned}$$

(21)

and the general expression relating $\bar{f}$ to $u_{0}$ is:

$$\begin{aligned} f_{h}\left( u^{+}_{j}-2u_{0},u^{+}_{j}\right) +2k_{b}u_{0}+2\bar{f}-f_{h}\left( u^{+}_{j},u^{+}_{j}\right) =0. \end{aligned}$$

(22)

As shown in Sect. 4, Eq. (22) can be solved for $\bar{f}$ or $u_{0}$ either in closed form or numerically depending on the type of function $f_{h}$ obtained by integrating the selected generalized tangent stiffness function $k_{h}$.

3.3.4 Generic unloading curve

The generic unloading curve $c^{-}$ can be obtained by integrating Eq. (1) as follows:

$$\begin{aligned} c^{-}\left( u,u^{-}_{j}\right) =\int k_{e}(u)\mathrm{d}u+\int k_{h}\left( u,u^{-}_{j}\right) \mathrm{d}u+C^{-}, \end{aligned}$$

(23)

or, equivalently

$$\begin{aligned} c^{-}\left( u,u^{-}_{j}\right) =f_{e}(u)+f_{h}\left( u,u^{-}_{j}\right) +C^{-}, \end{aligned}$$

(24)

where $f_{e}(u)$ is given by Eq. (4), whereas $f_{h}\left( u,u^{-}_{j}\right)$ is defined by:

$$\begin{aligned} f_{h}\left( u,u^{-}_{j}\right) =\int k_{h}\left( u,u^{-}_{j}\right) \mathrm{d}u. \end{aligned}$$

(25)

The integration constant $C^{-}$ can be determined by imposing that the generic unloading curve $c^{-}$ intersects the lower limiting curve $c_{l}$ at $u=u^{-}_{j}$:

$$\begin{aligned} c^{-}\left( u^{-}_{j},u^{-}_{j}\right) =c_{l}(u^{-}_{j}); \end{aligned}$$

(26)

hence, on account of (12), one has:

$$\begin{aligned} f_{e}(u^{-}_{j})+f_{h}\left( u^{-}_{j},u^{-}_{j}\right) +C^{-}=f_{e}(u^{-}_{j})+k_{b}u^{-}_{j}-\bar{f}, \end{aligned}$$

(27)

from which

$$\begin{aligned} C^{-}=k_{b}u^{-}_{j}-\bar{f}-f_{h}\left( u^{-}_{j},u^{-}_{j}\right) . \end{aligned}$$

(28)

Thus, the general expression for the generic unloading curve is:

$$\begin{aligned} c^{-}\left( u,u^{-}_{j}\right)= & {} f_{e}(u)+f_{h}\left( u,u^{-}_{j}\right) +k_{b}u^{-}_{j}\nonumber \\&-\bar{f}-f_{h}\left( u^{-}_{j},u^{-}_{j}\right) . \end{aligned}$$

(29)

By imposing that the generic unloading curve $c^{-}$ intersects the upper limiting curve at $u=u^{-}_{i}$, it is possible to derive a further general expression relating $\bar{f}$ to $u_{0}$. Thus, remembering that $u^{-}_{i}=u^{-}_{j}+2u_{0}$ and setting:

$$\begin{aligned} c^{-}\left( u^{-}_{j}+2u_{0},u^{-}_{j}\right) =c_{u}\left( u^{-}_{j}+2u_{0}\right) , \end{aligned}$$

(30)

the following equation is obtained on account of (7):

$$\begin{aligned} \begin{aligned}&f_{e}\left( u^{-}_{j}+2u_{0}\right) +f_{h}\left( u^{-}_{j}+2u_{0},u^{-}_{j}\right) +k_{b}u^{-}_{j}-\bar{f}\\&-f_{h}\left( u^{-}_{j},u^{-}_{j}\right) =f_{e}\left( u^{-}_{j}+2u_{0}\right) +k_{b}(u^{-}_{j}+2u_{0})+\bar{f}. \end{aligned} \end{aligned}$$

(31)

In conclusion, the general expression relating $\bar{f}$ to $u_{0}$ is:

$$\begin{aligned} f_{h}\left( u^{-}_{j}+2u_{0},u^{-}_{j}\right) -2k_{b}u_{0}-2\bar{f}-f_{h}\left( u^{-}_{j},u^{-}_{j}\right) =0, \end{aligned}$$

(32)

which complements the analogous relation (22).

3.4 History variable

Figure 5 shows a generic loading (unloading) curve having an initial point $P:(u_{P},f_{P})$ that lies between the two limiting curves. In this case, the distance, along the horizontal axis, required to reach the upper (lower) limiting curve, is equal to $u^{+}_{j}-u_{P}$ ($|u^{-}_{j}-u_{P} |$) and, therefore, it is smaller than $2u_{0}$. The generalized displacement $u^{+}_{j}$ ($u^{-}_{j}$), required to evaluate the generalized force f, has been previously presented as a history variable since it determines the current behavior of the system as a function of the previous states. However, we will show in the sequel that this variable can actually be computed for any starting point P; hence, there is no reason for storing its value, as it happens for classical history variables, if not for the pratical goal of enhancing the computational efficiency of the implementation.

Fig. 5

Evaluation of the history variable $u_{j}$

In the following, the general expressions for $u^{+}_{j}$ and $u^{-}_{j}$ are derived for any starting point P.

3.4.1 Evaluation of $u^{+}_{j}$

The generic loading curve $c^{+}$, shown in Fig. 5, is given by Eq. (19). By imposing that $c^{+}$ passes through the point $P:(u_{P},f_{P})$, the following equation is obtained:

$$\begin{aligned} c^{+}\left( u_{P},u^{+}_{j}\right) =f_{P}, \end{aligned}$$

(33)

which gives

$$\begin{aligned} f_{e}(u_{P})+f_{h}\left( u_{P},u^{+}_{j}\right) +k_{b}u^{+}_{j}+\bar{f}-f_{h}\left( u^{+}_{j},u^{+}_{j}\right) =f_{P}, \end{aligned}$$

(34)

from which $u^{+}_{j}$ can be evaluated.

3.4.2 Evaluation of $u^{-}_{j}$

The generic unloading curve $c^{-}$, shown in Fig. 5, is given by Eq. (29). By imposing that $c^{-}$ passes through the point $P:(u_{P},f_{P})$, the following equation is obtained:

$$\begin{aligned} c^{-}\left( u_{P},u^{-}_{j}\right) =f_{P}, \end{aligned}$$

(35)

which gives

$$\begin{aligned} f_{e}(u_{P})+f_{h}\left( u_{P},u^{-}_{j}\right) +k_{b}u^{-}_{j}-\bar{f}-f_{h}\left( u^{-}_{j},u^{-}_{j}\right) =f_{P}. \end{aligned}$$

(36)

Both $u^{+}_{j}$, by means of (34), and $u^{-}_{j}$, by means of the expression above, can be evaluated in closed form or numerically depending on the type of function $f_{h}$ obtained by integrating the selected generalized tangent stiffness function $k_{h}$. This will be addressed in the next section considering two hysteretic models.

4 Two instances of the presented class: the Bilinear and Exponential Models

In this section, two hysteretic models, namely Bilinear Model (BM) and Exponential Model (EM) that represent two specific instances of the proposed class are developed by using the general formulation described in Sect. 3.

The Bilinear Model, able to simulate hysteresis loops limited by two parallel straight lines, is one of the simplest hysteretic models that can be emanated from the presented class; thus, it is described to easily illustrate the meaning of the adopted quantities.

The Exponential Model, able to simulate the hysteresis loops limited by two parallel straight lines or curves, is presented to show the potentialities of the proposed class, since it can be adopted to accurately simulate more complex rate-independent hysteretic behaviors.

By selecting general tangent stiffness functions different from the ones adopted in the Bilinear and Exponential Models and by applying the general relations of Sect. 3, it is possible to derive new models characterized by hysteretic loops of different shapes and by different computational features in terms of numerical accuracy and efficiency.

4.1 Bilinear Model

4.1.1 Generalized tangent stiffness

The selected generalized tangent stiffness functions are:

$$\begin{aligned} k_{e}(u)=0\qquad \qquad \quad \;\,\,\,\,\,\,\mathrm {on}\;\left( -\infty ,\infty \right) , \end{aligned}$$

(37)

Thus, the model parameters to be calibrated from experimental tests are $k_{a}$, $k_{b}$, and $u_{0}$. We further assume that $k_{a}>k_{b}$, $k_{a}>0$, and that $u_{0}>0$.

Notice that the function $k_{h}$ is discontinuous at $u^{+}_{j}$ ($u^{-}_{j}$). This is due to the different value assumed by the tangents at $u^{+}_{j}$ for the two curves $c^{+}$ and $c_{u}$. The same property does hold at $u^{-}_{j}$ if one considers the curves $c^{-}$ and $c_{l}$. The graph of the function $k_{h}$ is plotted in Fig. 6 for the generic loading case.

Fig. 6

Graph of function $k_{h}$ for the generic loading case (Bilinear Model)

4.1.2 Generalized force

The expressions for the upper (lower) limiting curve $c_{u}$ ($c_{l}$) and for the generic loading (unloading) curve $c^{+}$ ($c^{-}$) are first derived; subsequently, the expression for $\bar{f}$, required for the evaluation of $c_{u}$, $c_{l}$, $c^{+}$, and $c^{-}$, is obtained.

Upper (lower) limiting curve

According to the definition (4) and to the assumption (37), it turns out to be:

$$\begin{aligned} f_{e}(u)=0. \end{aligned}$$

(40)

Hence, Eq. (7) yields:

$$\begin{aligned} c_{u}(u)=k_{b}u+\bar{f}, \end{aligned}$$

(41)

whereas Eq. (12) becomes:

$$\begin{aligned} c_{l}(u)=k_{b}u-\bar{f}. \end{aligned}$$

(42)

Generic loading (unloading) curve

On account of the assumption (38a), Eq. (15) specializes to:

$$\begin{aligned} f_{h}\left( u,u^{+}_{j}\right) =k_{a}u, \end{aligned}$$

(43)

so that Eq. (19) yields:

$$\begin{aligned} c^{+}\left( u,u^{+}_{j}\right) =k_{a}(u-u^{+}_{j})+k_{b}u^{+}_{j}+\bar{f}. \end{aligned}$$

(44)

Similarly, because of the assumption (39a), Eq. (25) becomes:

$$\begin{aligned} f_{h}\left( u,u^{-}_{j}\right) =k_{a}u. \end{aligned}$$

(45)

Hence, Eq. (29) yields:

$$\begin{aligned} c^{-}\left( u,u^{-}_{j}\right) =k_{a}\left( u-u^{-}_{j}\right) +k_{b}u^{-}_{j}-\bar{f}. \end{aligned}$$

(46)

Expression for $\bar{f}$

The expression for $\bar{f}$ can be obtained by using Eqs. (22) and (43) to get:

$$\begin{aligned} k_{a}\left( u^{+}_{j}-2u_{0}\right) +2k_{b}u_{0}+2\bar{f}-k_{a}u^{+}_{j}=0, \end{aligned}$$

(47)

from which we obtain:

$$\begin{aligned} \bar{f}=(k_{a}-k_{b})u_{0}, \end{aligned}$$

(48)

an expression providing a positive value of $\bar{f}$. The same result is arrived at by exploiting Eq. (32).

4.1.3 History variable

Involving (40) and (43), Eq. (34) specializes to:

$$\begin{aligned} k_{a}u_{P}+k_{b}u^{+}_{j}+\bar{f}-k_{a}u^{+}_{j}=f_{P}, \end{aligned}$$

(49)

from which the following expression of the history variable, holding for the loading case, is obtained:

$$\begin{aligned} u^{+}_{j}=\frac{k_{a}u_{P}+\bar{f}-f_{P}}{k_{a}-k_{b}}. \end{aligned}$$

(50)

Similarly, using (40) and (45), Eq. (36) becomes:

$$\begin{aligned} k_{a}u_{P}+k_{b}u^{-}_{j}-\bar{f}-k_{a}u^{-}_{j}=f_{P}, \end{aligned}$$

(51)

from which the following expression of the history variable, holding for the unloading case, is obtained:

$$\begin{aligned} u^{-}_{j}=\frac{k_{a}u_{P}-\bar{f}-f_{P}}{k_{a}-k_{b}}. \end{aligned}$$

(52)

Note that the history variable $u^{+}_{j}$ ($u^{-}_{j}$) may be positive or negative according to the coordinates of the initial point P of the generic loading (unloading) curve.

4.1.4 Hysteresis loop shape

Figure 7 shows two different shapes of the generalized force–displacement hysteresis loop obtained by applying a sinusoidal generalized displacement of unit amplitude and simulated by adopting the Bilinear Model parameters listed in Table 1. More specifically, Fig. 7a, b shows a hysteresis loop bounded by two straight lines typical of kinematic hardening (softening) mechanical systems and materials. Note that, although the hysteresis loop of Fig. 7b does not simulate a realistic softening behavior, it has been plotted to illustrate the properties of the Bilinear Model.

Fig. 7

Hysteresis loops simulated by adopting the Bilinear Model parameters given in Table 1

Table 1 Bilinear Model parameters

4.2 Exponential Model

4.2.1 Generalized tangent stiffness

The selected generalized tangent stiffness functions are:

$$\begin{aligned} k_{e}(u)=-2\beta +\beta \left( e^{\beta u}+e^{-\beta u}\right) \quad \quad \,\,\,\mathrm {on} \;\left( -\infty ,\infty \right) , \end{aligned}$$

(53)

where $k_{a}>k_{b}$, $k_{a}>0$, $u_{0}>0$, $\alpha >0$, and $\beta$ is real. They represent the model parameters to be calibrated from experimental tests. In particular, the parameter $\beta$ defines the shape of function $k_{e}$, a function that is convex on $(-\infty ,\infty )$, when $\beta >0$, whereas it is concave on $(-\infty ,\infty )$, when $\beta <0$.

Function $k_{h}$ is a nonlinearly decreasing function, from $k_{a}$ to $k_{b}+(k_{a}-k_{b})e^{-2\alpha u_{0}}$, on $[u^{+}_{j}-2 u_{0}, u^{+}_{j}[$, when $\dot{u}>0$, and on $]u^{-}_{j}, u^{-}_{j}+2 u_{0}]$, when $\dot{u}<0$; moreover, $k_{h}$ is equal to $k_{b}$ on $]u^{+}_{j},\infty )$, when $\dot{u}>0$, and on $(-\infty ,u^{-}_{j}[$, when $\dot{u}<0$. The positive parameter $\alpha$ rules the rate of variation of $k_{h}$ from $k_{a}$ to $k_{b}+(k_{a}-k_{b})e^{-2\alpha u_{0}}$. Figure 8 shows the graph of the function $k_{h}$ for the generic loading case.

Fig. 8

Graph of function $k_{h}$ for the generic loading case (Exponential Model)

Note that the function $k_{h}$ is discontinuous at $u^{+}_{j}$ ($u^{-}_{j}$). Denoting by $\delta _{k}$ the difference between the two different stiffness values at $u^{+}_{j}$ ($u^{-}_{j}$), as shown in Fig. 8 for the generic loading case, we can write:

$$\begin{aligned} (k_{a}-k_{b})e^{-2\alpha u_{0}}=\delta _{k}, \end{aligned}$$

(56)

from which we obtain:

$$\begin{aligned} u_{0}=-\dfrac{1}{2\alpha }ln\left( \frac{\delta _{k}}{k_{a}-k_{b}}\right) , \end{aligned}$$

(57)

an expression yielding positive values of $u_{0}$ for $\delta _{k}>0$. To have a generic loading (unloading) curve $c^{+}$ ($c^{-}$) that smoothly approaches the upper (lower) limiting curve $c_{u}$ ($c_{l}$), i.e., with a generalized tangent stiffness at $u^{+}_{j}$ ($u^{-}_{j}$) very close to the one of the upper (lower) limiting curve $c_{u}$ ($c_{l}$), one should set $\delta _{k}=0$ in (57), thus making $u_{0}$ indefined. However, the extensive numerical tests which have been carried out, only partially documented in the next section, have proved that a value $\delta _{k}=10^{-20}$ suffices for pratical purposes.

4.2.2 Generalized force

After deriving the expressions for the upper (lower) limiting curve $c_{u}$ ($c_{l}$) and for the generic loading (unloading) curve $c^{+}$ ($c^{-}$), we obtain the expression for $\bar{f}$ required for the evaluation of $c_{u}$, $c_{l}$, $c^{+}$, and $c^{-}$.

Upper (lower) limiting curve

According to the definition (4) and to the assumption (53), it turns out to be:

$$\begin{aligned} f_{e}(u)=-2\beta u+e^{\beta u}-e^{-\beta u}. \end{aligned}$$

(58)

Hence, Eq. (7) yields:

$$\begin{aligned} c_{u}(u)=-2\beta u+e^{\beta u}-e^{-\beta u}+k_{b}u+\bar{f}, \end{aligned}$$

(59)

whereas Eq. (12) becomes:

$$\begin{aligned} c_{l}(u)=-2\beta u+e^{\beta u}-e^{-\beta u}+k_{b}u-\bar{f}. \end{aligned}$$

(60)

Generic loading (unloading) curve

On account of the assumption (54a), Eq. (15) specializes to:

$$\begin{aligned} f_{h}\left( u,u^{+}_{j}\right) =k_{b}u-\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-\alpha \left( u-u^{+}_{j}+2u_{0}\right) }, \end{aligned}$$

(61)

so that, recalling (58), Eq. (19) yields:

$$\begin{aligned} \begin{aligned}&c^{+}\left( u,u^{+}_{j}\right) = -2\beta u+e^{\beta u}-e^{-\beta u}+k_{b}u\\&\quad -\frac{\left( k_{a}-k_{b}\right) }{\alpha }\left[ e^{-\alpha \left( u-u^{+}_{j}+2u_{0}\right) }-e^{-2\alpha u_{0}}\right] +\bar{f}. \end{aligned} \end{aligned}$$

(62)

Similarly, because of the assumption (55a), Eq. (25) becomes:

$$\begin{aligned} f_{h}\left( u,u^{-}_{j}\right) =k_{b}u+\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-\alpha \left( -u+u^{-}_{j}+2u_{0}\right) }. \end{aligned}$$

(63)

Substituting the previous expression in Eq. (29) and recalling (58), one obtains:

$$\begin{aligned} \begin{aligned}&c^{-}\left( u,u^{-}_{j}\right) = -2\beta u+e^{\beta u}-e^{-\beta u}+k_{b}u\\&\quad +\,\frac{\left( k_{a}-k_{b}\right) }{\alpha }\left[ e^{-\alpha \left( -u+u^{-}_{j}+2u_{0}\right) }-e^{-2\alpha u_{0}}\right] -\bar{f}. \end{aligned} \end{aligned}$$

(64)

Expression for $\bar{f}$

The expression for $\bar{f}$ can be obtained by using Eq. (22) or (32). Adopting (61), the former equation becomes:

$$\begin{aligned} \begin{aligned}&k_{b}\left( u^{+}_{j}-2u_{0}\right) -\frac{\left( k_{a}-k_{b}\right) }{\alpha }+2k_{b}u_{0}+2\bar{f}-k_{b}u^{+}_{j}\\&\quad +\,\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-2\alpha u_{0}}=0, \end{aligned} \end{aligned}$$

(65)

from which we obtain:

$$\begin{aligned} \bar{f}=\frac{\left( k_{a}-k_{b}\right) }{2\alpha }\left( 1-e^{-2\alpha u_{0}}\right) . \end{aligned}$$

(66)

Since $\alpha >0$ and $u_{0}>0$, the previous expression provides a positive value of $\bar{f}$.

4.2.3 History variable

Involving (58) and (61), Eq. (34) specializes to:

$$\begin{aligned} \begin{aligned}&-2\beta u_{P}+e^{\beta u_{P}}-e^{-\beta u_{P}}+k_{b}u_{P}\\&\quad -\,\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-\alpha \left( u_{P}-u^{+}_{j}+2u_{0}\right) }\\&\quad +\,k_{b}u^{+}_{j}+\bar{f}-k_{b}u^{+}_{j}+\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-2\alpha u_{0}} = f_{P}, \end{aligned} \end{aligned}$$

(67)

from which the following expression of the history variable, holding for the loading case, is obtained:

$$\begin{aligned} \begin{aligned} u^{+}_{j}&= u_{P}+2u_{0}+\frac{1}{\alpha }\ln \left[ \frac{\alpha }{\left( k_{a}-k_{b}\right) }\left( -2\beta u_{P}+e^{\beta u_{P}}-e^{-\beta u_{P}}\right. \right. \\&\quad \left. \left. +\,k_{b}u_{P}+\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-2\alpha u_{0}}+\bar{f}-f_{P}\right) \right] . \end{aligned} \end{aligned}$$

(68)

Similarly, using (58) and (63), Eq. (36) becomes:

$$\begin{aligned} \begin{aligned}&-2\beta u_{P}+e^{\beta u_{P}}-e^{-\beta u_{P}}+k_{b}u_{P}\\&\quad +\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-\alpha \left( -u_{P}+u^{-}_{j}+2u_{0}\right) }\\&\quad +k_{b}u^{-}_{j}-\bar{f}-k_{b}u^{-}_{j}-\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-2\alpha u_{0}} = f_{P}, \end{aligned} \end{aligned}$$

(69)

from which the following expression of the history variable, valid for the unloading case, is obtained:

$$\begin{aligned} \begin{aligned} u^{-}_{j}&= u_{P}-2u_{0}\\&-\frac{1}{\alpha }\ln \left[ -\frac{\alpha }{\left( k_{a}-k_{b}\right) }\left( -2\beta u_{P}+e^{\beta u_{P}}-e^{-\beta u_{P}}\right. \right. \\&\left. \left. +\,\,k_{b}u_{P}-\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-2\alpha u_{0}}-\bar{f}-f_{P}\right) \right] . \end{aligned} \end{aligned}$$

(70)

The history variable $u^{+}_{j}$ ($u^{-}_{j}$) may be positive or negative according to the coordinates of the initial point P of the generic loading (unloading) curve. In any case, the argument of the logarithm in Eqs. (68) and (70) is positive if $k_{a}>k_{b}$, $k_{a}>0$, $u_{0}>0$, and $\alpha >0$. To show this, we consider the argument of the logarithm in Eq. (68):

$$\begin{aligned} \begin{aligned} \arg =&\frac{\alpha }{\left( k_{a}-k_{b}\right) }\left( -2\beta u_{P}+e^{\beta u_{P}}-e^{-\beta u_{P}}+k_{b}u_{P}\right. \\&\left. +\,\frac{\left( k_{a}-k_{b}\right) }{\alpha }e^{-2\alpha u_{0}}+\bar{f}-f_{P}\right) , \end{aligned} \end{aligned}$$

(71)

and we show that its minimum value $\arg _{\min }$ is always positive. Making reference to Fig. 5, we remember that $u^{+}_{j}$ has two extreme values, which are $u_{P}+2u_{0}$, when P lies on the lower limiting curve $c_{l}$, and $u_{P}$, when P lies on the upper limiting curve $c_{u}$; hence, the argument of the logarithm in (68) has to be equal to 1 in the former case and equal to $\frac{\delta _{k}}{k_{a}-k_{b}}$ in the latter. Since $\delta _{k}=10^{-20}{\ll }$1, we have:

$$\begin{aligned} \mathrm{arg}_{\min }=\frac{\delta _{k}}{k_{a}-k_{b}}, \end{aligned}$$

(72)

a quantity that is always positive.

4.2.4 Hysteresis loop shape

Figure 9 shows four different shapes of the generalized force–displacement hysteresis loop obtained by applying a sinusoidal generalized displacement of unit amplitude and simulated by adopting the Exponential Model parameters listed in Table 2. More specifically, Fig. 9a, c shows a hysteresis loop bounded by two straight lines (curves) typical of kinematic hardening mechanical systems and materials, whereas the hystersis loop diagrammed in Fig. 9b, d is typical of kinematic softening behaviors. Note that, although the hysteresis loop of Fig. 9b does not simulate a realistic softening behavior, it has been plotted to illustrate the properties of the Exponential Model.

Fig. 9

Hysteresis loops simulated by adopting the Exponential Model parameters given in Table 2

Table 2 Exponential Model parameters

Figure 10 illustrates the influence of each EM parameter on the size and/or shape of hysteresis loops produced by imposing a sinusoidal generalized unit displacement. More specifically, the hysteresis loops in Fig. 10a have been obtained adopting $k_{b}=0.5$, $\alpha =5$, $\beta =0$, and three different values of $k_{a}$, that is 5, 10, and 15. It is evident that the increase of $k_{a}$ produces an increase of the size of the hysteresis loop without modifying its shape.

Figure 10b, c shows hysteresis loops simulated using $k_{a}=5$, $\alpha =5$, $\beta =0$, and three values of $k_{b}$, that is, 0, 0.5, and 1 (0, − 0.5, and − 1). It can be observed that the increase (decrease) of $k_{b}$ produces a counterclockwise (clockwise) rotation of the hysteresis loop and a slight decrease (increase) of its size.

The hysteresis loops in Fig. 10d have been obtained setting $k_{a}=5$, $k_{b}=0.5$, $\beta =0$, and adopting three different values of $\alpha$, that is, 5, 10, and 15. This figure reveals that the increase of $\alpha$ allows the reduction of the hysteresis loop size without modifying its shape.

Finally, Fig. 10e, f presents hysteresis loops simulated using $k_{a}=5$, $k_{b}=0.5$, $\alpha =5$, and three positive (negative) values of $\beta$, that is, 0, 1, and 1.5 (0, − 1, and − 1.5). It is evident that the parameter $\beta$ significantly affects the hysteresis loop shape.

Fig. 10

Influence of the EM parameters on the size and/or shape of the hysteresis loops

4.3 Computer implementation

For the reader’s convenience, a schematic flowchart of the Bilinear (Exponential) Model is presented in Tables 3 and 4. To this end, we suppose that a rate-independent mechanical system or material is subjected to a given time-dependent load and that a displacement-driven solution scheme has been adopted; hence, the generalized displacement history, in particular $u_{t-\Delta t}$ and $u_{t}$, is known over a time step $\Delta t$ and the generalized force $f_{t}$ has to be determined. Because of this assumption, the generalized velocity history, that is, $\dot{u}_{t-\Delta t}$ and $\dot{u}_{t}$, and the generalized force $f_{t-\Delta t}$ are also known.

Tables 3 and 4 summarize the implementation scheme for the Bilinear (Exponential) Model. The algorithm is composed of two parts. In the first one, called Initial settings, the model parameters are assigned and the associated internal ones are calculated. In the second one, called Calculations at each time step, the history variable $u^{+}_{j}$ ($u^{-}_{j}$) is updated if the sign of generalized velocity at time t, namely $s_{t}=sgn(\dot{u}_{t})$, changes with respect to the one at $t-\Delta t$ ; then, the generalized force $f_{t}$ is evaluated by adopting the expression of the generic loading (unloading) curve $c^{+}$ ($c^{-}$) if $u^{+}_{j}-2u_{0}<u_{t}<u^{+}_{j}$ ($u^{-}_{j}<u_{t}<u^{-}_{j}+2u_{0}$); otherwise it is evaluated by using the expression of the upper (lower) limiting curve $c_{u}$ ($c_{l}$).

Table 3 Bilinear Model algorithm

Table 4 Exponential Model algorithm

5 Numerical applications

In this section, the nonlinear dynamic response of a rate-independent kinematic hardening single degree of freedom mechanical system is simulated by modeling the generalized force of the system on the basis of the Exponential Model (EM) described in Sect. 4.

To demonstrate the accuracy of the EM and its capability to significantly decrease the computational burden of nonlinear time history analyses, the numerical results and the computational times are compared with those obtained by modeling the generalized force of the mechanical system with the Bouc–Wen Model (BWM) [8, 65, 66], which is one of the most used differential models in the literature [2, 3, 17, 25, 33, 36, 44]. Two different external forces, that is, a harmonic and a random force, are considered in the analysis.

5.1 Analyzed mechanical system

We first consider a nonlinear mechanical system characterized by a single degree of freedom; its motion is described by the equation:

$$\begin{aligned} m\ddot{u}+f_{d}(\dot{u})+f(u)=p(t), \end{aligned}$$

(73)

where m denotes the mass of the system, u the generalized displacement, $\dot{u}$ the generalized velocity, $\ddot{u}$ the generalized acceleration, $f_{d}(\dot{u})$ the generalized rate-dependent force, f(u) the generalized rate-independent force, and p the generalized external force depending upon time t. In rate-independent mechanical systems, the nonlinear ordinary differential equation given by Eq. (73) simplifies to:

$$\begin{aligned} m\ddot{u}+f(u)=p(t). \end{aligned}$$

(74)

The properties of the analyzed rate-independent kinematic hardening mechanical system are listed in Table 5, where $k_{ti}$ is the generalized pre-yield tangent stiffness, whereas $k_{ty}$ is the constant value assumed by the generalized post-yield tangent stiffness for generalized displacements greater than $2u_{y}$.

Table 5 Analyzed mechanical system properties

5.2 Applied generalized external forces

The nonlinear dynamic response of the rate-independent mechanical system is simulated for two different external generalized forces: a harmonic force and a random force.

The harmonic force, shown in Fig. 11a, is a sinusoidal force having an amplitude $p_{0}$ that increases linearly with time from 0 to 5 N, forcing frequency $\omega _{p}=2$ rad/s, and time duration $t_{d}=10$ s.

The random force, shown in Fig. 11b, is a Gaussian white noise having intensity $i{wn}=7.5$ N, and time duration $t_{d}=30$ s.

Fig. 11

Applied generalized external forces: a harmonic and b random force

5.3 Model parameters

The generalized force in (74), simulating a large variety of hysteretic behaviors, is usually assigned by means of the celebrated Bouc–Wen Model, a so-called differential model based on the Duhem hysteresis operator [18].

In particular, according to the Bouc–Wen Model, the generalized force of a mechanical system is given by:

$$\begin{aligned} f(u)= aku+\left( 1-a\right) kdz, \end{aligned}$$

(75)

where a is a dimensionless parameter, and k and d are parameters having dimension of stiffness and displacement, respectively. Finally, the adimensional variable z is obtained by solving the following first-order nonlinear ordinary differential equation:

$$\begin{aligned} \dot{z}=d^{-1}\left( A\dot{u}-b\left| \dot{u}\right| z \left| z\right| ^{n-1}-c\dot{u}\left| z\right| ^{n}\right) , \end{aligned}$$

(76)

where A, b, c, and n are dimensionless parameters that control the hysteresis loop shape.

To simulate the nonlinear behavior of the analyzed mechanical system and to compare the computational features of the EM with the ones of the classical BWM, the parameters listed in Tables 6 and 7 have been adopted.

In the Exponential Model, the parameter $\beta$ has been set equal to 0 to have two limiting straight lines; thus, being $k_{e}=0$, $k_{a}=k_{ti}$ and $k_{b}=k_{ty}$. The parameter $\alpha$ has been evaluated adopting (57) with $u_{0}=u_{y}$ and $\delta _{k}=10^{-20}$.

In the Bouc–Wen Model, the following parameters $n=1.5$, $A=1$, $b=1$, and $c=0$ have been used to obtain the desired hysteresis loop shape [28, 59]. Furthermore, the parameters k, a, and d have been selected so as to reproduce the hysteresis loops simulated with the Exponential Model.

A comparison between Tables 6 and 7 clearly shows that the EM requires a reduced number of parameters with respect to the celebrated BWM.

In addition, it has to be noted that an important benefit of the EM consists in the accurate determination of its parameters through an analytical fitting of the experimental hysteresis loops. Indeed, as it has been shown in 4.2.4, the EM parameters are directly associated with the graphical properties of the hysteresis loop. If more accurate identifications are required, usually of nonlinear nature, such computed parameters represent suitable first trial values for the iterations required to compute the optimal parameters, i.e., the ones that best fit the experimental curves according to the adopted criterion. Moreover, the peculiar analytical formulation of the proposed class permits a closed form computation of the response gradient, an issue of the outmost importance in identification procedures.

On the contrary, the interpretation of the BWM parameters is not straightforward and their identification from experimental data still remains an open issue which has been investigated over years by several approaches, depending on the peculiar formulation of the BWM [10, 12, 51, 69].

Table 6 EM parameters adopted in numerical simulations

Table 7 BWM parameters adopted in numerical simulations

5.4 Results of the nonlinear time history analyses

In the sequel, the accuracy and the computational efficiency of the Exponential Model are assessed by presenting the results of some numerical simulations.

The equation of motion, given by Eq. (74), has been numerically solved by adopting a conventional solution approach, that is the explicit time integration central difference method [5, 24], and using a time step of 0.005 s. Furthermore, in the Bouc–Wen Model, the first-order nonlinear ordinary differential equation, given by Eq. (76), has been numerically solved by using the unconditionally stable semi-implicit Runge–Kutta method [50] and considering 50 steps. The solution algorithm and the hysteretic models have been programmed in MATLAB and run on a computer equipped with an Intel$\circledR$Core$^\mathrm{TM}$ i7-4700MQ processor and a CPU at 2.40 GHz with 16 GB of RAM.

The results of the nonlinear time history analyses (NLTHAs), associated with harmonic and random forces, are shown in Tables 8 and 9, respectively.

The accuracy of the EM is very satisfactory since the maximum and minimum values of the generalized displacements, velocities, and accelerations are numerically quite close to those predicted by the BWM.

However, the computational burden of the EM, expressed by the total computational time tct, is significantly reduced with respect to that characterizing the BWM. Clearly, the parameter tct is not a fully objective measure of the algorithmic efficiency, since it depends upon the amount of the background process running on the computer, the relevant memory and CPU speed; for this reason, tct has been normalized as:

$$\begin{aligned} \mathrm {EM}\ tctp\ [\%]=\dfrac{\mathrm {EM}\ tct}{\mathrm {BWM}\ tct}\cdot 100\ , \end{aligned}$$

(77)

to get a more meaningful measure of the computational benefits associated with the use of the EM with respect to the BWM.

Table 8 NLTHAs results | Harmonic force

Table 9 NLTHAs results | Random force

Time histories of the mechanical system are illustrated in terms of generalized displacement, e.g., Fig. 12, generalized velocity, e.g., Fig. 13, and generalized acceleration, e.g., Fig. 14; generalized force–displacement hysteresis loops are shown in Fig. 15. Generally speaking, the comparison between the responses associated with the EM and the BWM shows a very good agreement.

Fig. 12

Generalized displacement time history obtained applying the a harmonic and b random force

Fig. 13

Generalized velocity time history obtained applying the a harmonic and b random force

Fig. 14

Generalized acceleration time history obtained applying the a harmonic and b random force

Fig. 15

Generalized force–displacement hysteresis loops obtained applying the a harmonic and b random force

6 Conclusions

We have presented a general formulation of a class of uniaxial phenomenological models, able to simulate hysteresis loops limited by two parallel straight lines or curves, typical of rate-independent mechanical systems and materials with kinematic hardening or softening hysteretic behavior. The proposed class of models requires only one history variable and leads to the solution of a scalar equation for the evaluation of the generalized force.

To illustrate the peculiar features of the proposed general formulation, two specific instances of the class, denominated Bilinear Model and Exponential Model, have been described. The Bilinear Model, able to simulate hysteresis loops limited by two parallel straight lines, is one of simplest models that can be emanated from the proposed class, whereas the Exponential Model, able to reproduce hysteresis loops limited by two parallel straight lines or curves, is a more elaborate model that can simulate the behavior of a wider spectrum of mechanical systems and materials.

To investigate the overall computational features of the EM, some nonlinear time history analyses have been carried out on a rate-independent SDOF mechanical system with kinematic hardening behavior.

Both a harmonic and a random force have been considered in the analyses and the results of the EM have been compared with those associated with the celebrated BWM. In this respect, the following conclusions can be drawn:

• the results of the EM closely match those predicted by the BWM, independently of the kind of external force;

• the total computational time associated with the EM is equal to 0.66% (0.69%), for the harmonic (random) force case, of the one required by the BWM;

• the BWM requires the calibration of seven parameters to simulate hysteresis loops limited by two parallel straight lines, whereas the EM needs only three model parameters having a clear mechanical significance.

Current research activities, which will be the topic of future contributions, are focused on the parameters identification performed by gradient-based least square optimization algorithms, previously employed by the authors for similar purposes [20, 62], and by static inverse identification [46]. Furthermore, current research is focusing on the extension of the proposed general formulation to the three-dimensional case through the definition of interaction domains involving loads and displacements. Such an approach has been successfully employed in characterizing nonlinear materials by means of uniaxial relationships typically obtained from experimental tests, e.g., concrete [63], composites [21] or alloys [39]. Thus, using suitably defined interaction domains, one can infer equivalent load–displacement quantities which are related by uniaxial relationships capable of determining equivalent flow rules.