1 Introduction

Viscoelastic materials that develop large strains, such as polymers or reinforced polymers, are widely used in today's industrial applications due to important mechanical properties as: noise reduction, damping of mechanical systems, protection against impact and vibration isolation. Soft living tissues are also considered to behave as viscoelastic materials at large strains. Thus, it is very important to know the mechanical behavior of these materials and to propose consistent theoretical and computational alternatives for their modeling.

A concise and didactic description of the existent theoretical and numerical strategies to model viscoelastic materials developing large strains can be seen in [1]. According to [1], in general, constitutive equations for viscoelastic materials developing large strains are based on two different approaches.

The first approach has its starting point on reference [2] which extends the Boltzmann's principle of linear superposition to finite strains [3]. In this case, the viscosity is modeled using convolutions or hereditary integrals involving the low strain rate response (instantaneous elastic part) and the viscous overstress. This strategy is widely used in rheology, see references [4,5,6], for instance. In solid mechanics, one may cite important works that use this approach, for example, references [7,8,9,10,11,12]. One may consult [13] for more specific information regarding hereditary integral models and their applications.

The second approach mentioned by [1] is based on the idea of [14] which has been written on more precise mathematical bases by [15] and [16]. These references use the multiplicative decomposition of Köner [17] and Lee [18], originally applied to solve elastoplastic problems. In this case, the viscous behavior is related to the time rate of the deformation gradient [16], leading to thermodynamically consistent expressions and the existence of intermediate configurations. It should be mentioned that the time rate of the deformation gradient is evaluated at the intermediate space in the sense of [19]. The modeling of a large variety of materials using this approach can be seen, for example, in references [20,21,22,23]. The Köner–Lee-based approach can be further divided according to whether the evolution of the viscous behavior is done by exponential mapping, see, for example, reference [24], or by finite differences, as made by reference [25]. A good understanding of the Köner–Lee-based approach can be seen in reference [26] that describes the existence and meaning of intermediate configurations. One may also consult references [27] and [28] that stress out the deviatory directions for plastic stresses and viscous stresses. Finally, references [29] and [30] also consider temperature.

Despite the good review presented by [1], a review associated with the study of living tissues [31] indicates a third viscoelastic approach that does not use the Köner–Lee decomposition but the Flory’s decomposition [32]. It should be mentioned that the Flory’s decomposition is well known and widely used to model hyperelastic solids. Regarding hyperelastic solids, the reader can see, among others, the classic following classic references [33, 34].

A widely used viscoelastic framework that applies the multiplicative Flory’s decomposition was proposed by [35, 36] in the context of the mechanical behavior of artery walls. This strategy follows some characteristics of inelastic processes such as those presented by [37,38,39]. In reference [35], the Flory’s decomposition was used together with an internal isochoric strain-like variable to describe the strain history and model the viscous dissipation in a thermodynamically consistent way [31]. The energetic conjugate of this strain-like variable is interpreted as non-equilibrated stress and constitutes a sum of several parallel Maxwell models [35]. The authors write a linear differential equation to formulate the evolution of this non-equilibrated stress.

Following the viscoelastic approach proposed by [35], we can mention some recent works as: the study presented in [40] concerned with the calibration of the model proposed by [35] for experiments on porcine arterial tissues, the work [41] that seeks efficient models to simulate living tissues and soft materials, the work [42] concerned with general constitutive models for continuous media including viscoelastodynamics, the study [43] interested in a thermodynamically consistent model for coupled thermo-viscoelastic elastomers; and finally, reference [44] that makes changes on the proposal of [35] to consider strain rate-dependent viscosity applied in soft tissue analysis. Although there are a very large number of works in the literature using the Flory’s decomposition—in elastic and viscoelastic analyses—as far as the authors' knowledge goes, there is no known formulation that follows the strategy proposed here.

In the present study, a simple alternative for viscoelastic analysis at large strains is presented; it uses the Flory´s decomposition [32]. It has two basic starting points: (a) the instantaneous relationship between viscous stresses and the time rate of isochoric strain invariants and (b) the instantaneous relationship between viscous stress and the time rate of the isochoric strain components. The absence of intermediate spaces, the absence of hereditary integrals and the presence of direct numerical derivatives of isochoric quantities indicate that the proposed models have originality and are interesting alternatives to be explored.

In order to provide a self-contained study, Sect. 2 describes the Flory´s decomposition, the employed elastic potentials and what is meant here by isochoric and volumetric strain components. Section 3 presents Kelvin–Voigt-like and Zener-like constitutive models based on the rate of isochoric strains invariants and rate of isochoric strain components including variable viscosity. Section 4 presents the weak form of the equilibrium equation and the finite element method implementation [45,46,47]. Finally, Sect. 5 presents three theoretical examples to show the ability of the proposed formulations to fulfill finite strain viscoelastic response requirements, two examples that compare our numerical results with literature’s experimental tests and classical models and a structural example that validates the FEM implementation. The last example also helps the understanding of a not obvious dynamic response of viscoelastic materials with instantaneous response. At the end of the study, conclusions and future perspectives are presented.

2 Preliminaries

In this section, some large strain basic concepts [48] are presented in order to simplify the description of the proposed models. The elastic part of our model is considered hyperelastic [34, 47], i.e., there is a specific strain energy potential \(W({\mathbf{C}})\) that is a function of the right Cauchy–Green stretch tensor \({\mathbf{C}} = {\mathbf{A}}^{T} \cdot {\mathbf{A}}\), in which \({\mathbf{A}}\) is the deformation gradient. The specific strain energy is decomposed in one volumetric and two isochoric parts. In order to do so, it is necessary to define the Flory’s multiplicative decomposition of the deformation gradient in its isochoric part,

$$\overline{{\mathbf{A}}} = J^{{ - 1/3}} {\mathbf{A}}\quad {\text{with}}\quad {\text{Det}}\left( {\overline{{\mathbf{A}}} } \right) = {\text{Det}}\left( {\mathbf{A}} \right)\left( {J^{{ - 1/3}} } \right)^{3} = 1$$
(1)

and its volumetric part

$${\hat{\mathbf{A}}} = J^{1/3} {\mathbf{I}}\quad {\text{with}}\quad {\text{Det}}\left( {{\hat{\mathbf{A}}}} \right) = {\text{Det}}\left( {\mathbf{I}} \right)\left( {J^{1/3} } \right)^{3} = J$$
(2)

in which \(J = {\text{Det}}({\mathbf{A}})\).

Thus, one recovers the deformation gradient by the product

$${\mathbf{A}} = {\hat{\mathbf{A}}} \cdot {\overline{\mathbf{A}}} = {\overline{\mathbf{A}}} \cdot {\hat{\mathbf{A}}}$$
(3)

Using Eqs. (1) and (2), one writes:

$${\overline{\mathbf{C}}} = {\overline{\mathbf{A}}}^{T} \cdot {\overline{\mathbf{A}}} = J^{ - 2/3} {\mathbf{C}}$$
(4)
$${\hat{\mathbf{C}}} = {\hat{\mathbf{A}}}^{T} \cdot {\hat{\mathbf{A}}} = J^{2/3} {\mathbf{I}}$$
(5)

and performing the following product one identifies the Flory’s decomposition of the right Cauchy–Green stretch as:

$${\mathbf{C}} = {\hat{\mathbf{C}}} \cdot {\overline{\mathbf{C}}} = {\overline{\mathbf{C}}} \cdot {\hat{\mathbf{C}}}$$
(6)

and verifies that

$${\text{Det}}\left( {{\overline{\mathbf{C}}}} \right) = \left( {J^{ - 2/3} } \right)^{3} J^{2} = 1\quad {\text{Det}}\left( {{\hat{\mathbf{C}}}} \right) = \left( {J^{2/3} } \right)^{3} = J^{2}$$
(7)

Thus, \({\overline{\mathbf{C}}}\) is the isochoric part of the Cauchy–Green stretch and \({\hat{\mathbf{C}}}\) is its volumetric part. From this decomposition—for a hyperelastic material—the strain energy density is written as a sum of volumetric and isochoric parts, as follows:

$$\psi = \psi^{{{\text{vol}}}} ({\hat{\mathbf{C}}}) + \psi^{{{\text{iso}}}} ({\overline{\mathbf{C}}})\quad {\text{or}}\quad \psi = \psi^{{{\text{vol}}}} (J) + \psi^{{{\text{iso}}}} ({\overline{\mathbf{C}}})$$
(8)

In this study, we adopt the Rivlin–Saunders [49, 50] isochoric energy density and the Hartmann–Neff [51] volumetric energy density to write the elastic parts of the proposed models, resulting:

$$\psi = \psi^{{{\text{vol}}}} (J) + \psi^{{{\text{iso}}1}} (\overline{I}_{1} ) + \psi^{{{\text{iso}}2}} (\overline{I}_{2} )$$
(9)

in which

$$\psi^{{{\text{vol}}}} (J) = \frac{K}{{8n^{2} }}\left( {J^{2n} + J^{ - 2n} - 2} \right),\,\psi^{{{\text{iso}}1}} = \frac{{G_{1} }}{4}(\overline{I}_{1} - 3),\,\psi^{{{\text{iso}}2}} = \frac{{G_{2} }}{4}(\overline{I}_{2} - 3)$$
(10)

in which \(\overline{I}_{1}\) and \(\overline{I}_{2}\) are the first and second invariants of \({\overline{\mathbf{C}}}\). In Eq. (10), \(K\) is the bulk modulus, \(G_{1} = G_{2} = G\) is the elastic shear modulus and \(n\) is an additional constant used by [51] to control the bulk modulus at large strains.

The adopted strain measure is the Green–Lagrange strain

$${\mathbf{E}} = \frac{1}{2}({\mathbf{C - I}})$$
(11)

and from Eq. (10) one calculates the second Piola–Kirchhoff stress as:

$${\mathbf{S}} = \frac{\partial \psi }{{\partial {\mathbf{E}}}} = \frac{{\partial \psi^{{{\text{vol}}}} }}{{\partial {\mathbf{E}}}} + \frac{{\partial \psi^{{{\text{iso}}1}} }}{{\partial {\mathbf{E}}}} + \frac{{\partial \psi^{{{\text{iso}}2}} }}{{\partial {\mathbf{E}}}}\,{\text{or}}\,{\text{ in}}\,{\text{ compact}}\,{\text{ form}}\quad {\mathbf{S}} = {\mathbf{S}}^{{{\text{vol}}}} + {\mathbf{S}}^{1} + {\mathbf{S}}^{2}$$
(12)

with

$${\mathbf{S}}^{{{\text{vol}}}} = \frac{{\partial \psi^{{{\text{vol}}}} }}{{\partial {\mathbf{E}}}} = \left\{ {\frac{K}{4n}\left( {J^{2n - 1} - J^{ - (2n + 1)} } \right)} \right\}\user2{\mathfrak{E}}^{{{\text{vol}}}} \quad {\text{and}}\quad \varvec{\mathfrak{E}}^{{{\text{vol}}}} = \frac{\partial J}{{\partial {\mathbf{E}}}} = J{\mathbf{C}}^{ - 1}$$
(13)
$${\mathbf{S}}^{1} = \frac{G}{4}\user2{\mathfrak{E}}^{1} \quad {\text{and}}\quad \user2{\mathfrak{E}}^{1} = \frac{{\partial \overline{I}_{1} }}{{\partial {\mathbf{E}}}} = - \frac{2}{3}J^{ - 2/3} {\text{Tr}}({\varvec{C}}){\varvec{C}}^{ - 1} + 2J^{ - 2/3} {\varvec{I}}$$
(14)
$${\mathbf{S}}^{2} = \frac{G}{4}\user2{\mathfrak{E}}^{2} \quad {\text{and}}\quad \user2{\mathfrak{E}}^{2} = \frac{{\partial \overline{I}_{2} }}{{\partial {\mathbf{E}}}} = 2J^{ - 4/3} \left( { - \frac{2}{3}{\varvec{C}}^{ - 1} I_{2} + \left\{ {{\text{Tr}}({\varvec{C}}){\varvec{I}} - {\varvec{C}}^{t} } \right\}} \right)$$
(15)

In Eqs. (14) and (15), tensors \(\user2{\mathfrak{E}}^{1}\) and \(\user2{\mathfrak{E}}^{2}\) are defined here as isochoric strains. When applying the pushing forward [52] on the Piola–Kirchhoff-like stresses \({\mathbf{S}}^{1}\) and \({\mathbf{S}}^{2}\) results the deviatory Cauchy stress components, see reference [46] for a straightforward operational demonstration, thus \(\user2{\mathfrak{E}}^{1}\) and \(\user2{\mathfrak{E}}^{2}\) are isochoric.

3 Viscoelastic models - isochoric space

As mentioned in the introduction, in this section we present two different phenomenological viscoelastic models (Kelvin–Voigt-like and Zener-like) following two different strategies for each one. Finally, we proposed a more general model that incorporates strain rate-dependent viscosity. Here, for all models, the viscous behavior is restricted to the isochoric strain space, i.e., the possibility of volumetric viscosity, usually present in foams or porous materials, is not considered.

It is interesting to stress that the Köner–Lee decomposition splits strains in elastic and viscous parts following a Maxwell arrangement from which it is not possible to represent Kelvin–Voigt-like models. Thus, the proposed Flory’s decomposition framework is a good alternative to represent this kind of model.

In this section, the basic equations are presented and do not offer difficulties, but more elaborated considerations are necessary and presented in the solution process of Sect. 4.3.

3.1 Kelvin–Voigt-like model - time rate of isochoric strain components

This strategy considers that viscous stresses are proportional to the time rate of isochoric strains, \(\user2{\dot{\mathfrak{E}}}^{1}\) and \(\user2{\dot{\mathfrak{E}}}^{2}\), see Eqs. (14) and (15), resulting:

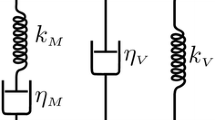
$${\mathbf{S}}_{v}^{1} = \frac{{\eta_{1} ( \bullet )}}{4}\user2{\dot{\mathfrak{E}}}^{1} \quad {\text{and}}\quad {\mathbf{S}}_{v}^{2} = \frac{{\eta_{2} ( \bullet )}}{4}\user2{\dot{\mathfrak{E}}}^{2}$$
(16)

in which \(\eta_{i} ( \bullet )\) are scalar viscous properties that may depend on the isochoric strain, its time derivative or isochoric strain invariants. For simplicity, we consider \(\eta_{1} ( \bullet ) = \eta_{2} ( \bullet ) = \eta ( \bullet )\) but maintain the dependence regarding other variables. The Kelvin–Voigt-like qualitative viscous arrangement is schematically presented in Fig. 1a.

Fig. 1
figure 1

Qualitative viscoelastic models arrangements

Full size image

The total deviatoric second Piola–Kirchhoff stress for this first model is the sum of the elastic \({\mathbf{S}}^{i}\) and viscous \({\mathbf{S}}_{v}^{i}\) parts, i.e.:

$${\mathbf{S}}_{T}^{i} = {\mathbf{S}}^{i} + {\mathbf{S}}_{v}^{i} \quad {\text{or}}\quad {\mathbf{S}}_{T}^{i} = \frac{G}{4}\user2{\mathfrak{E}}^{i} + \frac{\eta ( \bullet )}{4}\user2{\dot{\mathfrak{E}}}^{i}$$
(17)

in which \(i\) is the isochoric direction and \(T\) means total. To be concise, in the following equations the sign of dependence \(( \bullet )\), present in Eq. (17), is suppressed.

From Eqs. (14) and (15), one can see that the time rate of the isochoric strains falls in the same isochoric original space, i.e., the instantaneous time derivative only involves isochoric strains and time (a scalar quantity). As we are interested in a simple numerical solution, the time is discretized by \(t_{s + 1} = t_{s} + \Delta t\) and we calculate the isochoric strain rate by backward finite difference. Thus, Eq. (17) becomes simply:

$$\left( {{\mathbf{S}}_{T}^{i} } \right)_{s + 1} = \frac{G}{4}\user2{\mathfrak{E}}_{s + 1}^{i} + \frac{\eta }{4}\left[ {\user2{\mathfrak{E}}_{s + 1}^{i} - \user2{\mathfrak{E}}_{s}^{i} } \right]/\Delta t$$
(18)

A comment present in reference [47] regarding the possibility of losing the isochoric property of \(\user2{\mathfrak{E}}_{s}^{i}\) when measured at time \(t_{s + 1}\) is related to Zener-like models, in which sudden strain changes are possible. However, in the Kelvin–Voigt model only smooth strain transitions are present and this possible problem loses importance.

3.2 Kelvin–Voigt model - time rate of strain invariants

The second proposed model introduces viscous stresses as a function of the isochoric strain invariants. In order to do so, we propose the following version of second Piola–Kirchhoff viscous stress

$${\mathbf{S}}_{T}^{i} = {\mathbf{S}}_{{}}^{i} + {\mathbf{S}}_{v}^{i} \quad {\text{or}}\quad {\mathbf{S}}_{T}^{i} = \frac{G}{4}\user2{\mathfrak{E}}^{i} + \frac{{\overline{\eta }_{i} ( \bullet )}}{4}\dot{\overline{I}}_{i} \user2{\mathfrak{E}}^{i}$$
(19)

in which the new viscous parameters \(\overline{\eta }_{i} ( \bullet )\) are written using an upper bar. From the relation \(\dot{\overline{I}}_{i} = \user2{\mathfrak{E}}^{i} :\dot{E}\), one calculates the viscous dissipation as \(d_{v} = {\mathbf{S}}_{v}^{i} :{\dot{\mathbf{E}}} = \left( {\overline{\eta }_{i} ( \bullet )/4} \right)(\user2{\mathfrak{E}}^{i} :{\dot{\mathbf{E}}})^{2}\), i.e., \(\overline{\eta }\) should be positive in order to dissipation always be positive.

As one can see in Eq. (19), the viscous stress components follow isochoric directions and the numerical time derivative of the strain invariants (being scalars) do not involve direction. Thus, the total stress is numerically calculated as:

$$\left( {{\mathbf{S}}_{T}^{i} } \right)_{s + 1} = \frac{1}{4}\left[ {G + \overline{\eta }\left( {(\overline{I}_{i} )_{s + 1} - (\overline{I}_{i} )_{s} } \right)/\Delta t} \right]\user2{\mathfrak{E}}_{s + 1}^{i}$$
(20)

in which \(s + 1\) is the current instant and \(s\) is the previous one.

3.3 Zener-like model - time rate of isochoric strain components

Observing the qualitative representation of the Zener-like model at Fig. 1b, we assume that:

$${\mathbf{S}}_{T}^{i} = {\mathbf{S}}_{{}}^{i} + {\mathbf{S}}_{v}^{i}$$
(21)

with

$${\mathbf{S}}_{{}}^{i} = \frac{G}{4}\user2{\mathfrak{E}}_{{}}^{i} \quad {\mathbf{S}}_{v}^{i} = \frac{{\overline{G}}}{4}\user2{\mathfrak{E}}_{e}^{i} = \frac{\eta ( \bullet )}{4}\user2{\dot{\mathfrak{E}}}_{v}^{i}$$
(22)

in which \(\user2{\mathfrak{E}}_{e}^{i}\) is the isochoric strain component at the spring of the Maxwell branch of the model and \(\user2{\mathfrak{E}}_{v}^{i}\) is its viscous part.

Following comments after Eq. (17), time rates of the isochoric strains fall in the same isochoric original space, i.e., the instantaneous time derivative only involves isochoric strains and time (a scalar quantity). Thus, thanks to the Flory’s decomposition, \(\user2{\dot{\mathfrak{E}}}_{e}^{i}\) and \(\user2{\dot{\mathfrak{E}}}_{v}^{i}\) are in the same constrained direction and one can state that:

$$\user2{\dot{\mathfrak{E}}}_{{}}^{i} = \user2{\dot{\mathfrak{E}}}_{e}^{i} + \user2{\dot{\mathfrak{E}}}_{v}^{i}$$
(23)

From the second of Eq. (22), one writes:

$$\user2{\dot{\mathfrak{E}}}_{v}^{i} = \frac{{\overline{G}}}{\eta }\user2{\mathfrak{E}}_{e}^{i}$$
(24)

It is interesting to mention that Eq. (24) has the same format of, for example, Eq. (36) of reference [60], i.e., the linearization of a Köner–Lee representation of a viscoelastic Maxwell element. From this observation, we understand that splitting strain into its volumetric and isochoric parts by means of Flory’s decomposition (creating constrained spaces) enables us to propose this simple approach for the time evolution of pure isochoric strains.

Introducing Eqs. (24) into (23), one has:

$$\user2{\dot{\mathfrak{E}}}_{{}}^{i} = \user2{\dot{\mathfrak{E}}}_{e}^{i} + \frac{{\overline{G}}}{\eta }\user2{\mathfrak{E}}_{e}^{i}$$
(25)

Applying the backward finite difference on \(\user2{\dot{\mathfrak{E}}}_{e}^{i}\) results:

$$\left( {\user2{\mathfrak{E}}_{e}^{i} } \right)_{s + 1} = \left( {\left( {\user2{\dot{\mathfrak{E}}}^{i} } \right)_{s + 1} + \frac{{\left( {\user2{\mathfrak{E}}_{e}^{i} } \right)_{s} }}{\Delta t}} \right)/\left( {\frac{{\overline{G}}}{\eta } + \frac{1}{\Delta t}} \right)$$
(26)

Thus, one calculates the total deviatoric-like second Piola–Kirchhoff stress from Eqs. (21) and (22) as:

$$\left( {{\mathbf{S}}_{T}^{i} } \right)_{s + 1} = \frac{G}{4}\left( {\user2{\mathfrak{E}}_{{}}^{i} } \right)_{s + 1} + \frac{{\overline{G}}}{4}\left( {\user2{\mathfrak{E}}_{e}^{i} } \right)_{s + 1}$$
(27)

and using Eq. (26) results the complete viscoelastic stress equation:

$$\left( {{\mathbf{S}}_{T}^{i} } \right)_{s + 1} = \frac{G}{4}\left( {\user2{\mathfrak{E}}_{{}}^{i} } \right)_{s + 1} + \frac{{\overline{G}}}{4}\left( {\left( {\user2{\dot{\mathfrak{E}}}^{i} } \right)_{s + 1} + \frac{{\left( {\user2{\mathfrak{E}}_{e}^{i} } \right)_{s} }}{\Delta t}} \right)/\left( {\frac{{\overline{G}}}{\eta } + \frac{1}{\Delta t}} \right)$$
(28)

in which \(\left( {\user2{\dot{\mathfrak{E}}}^{i} } \right)_{s + 1}\) is also calculated by finite difference and \(\left( {\user2{\mathfrak{E}}_{e}^{i} } \right)_{s}\) is known at the current time step \(s + 1\).

It is well known that in formulations that use the Köner–Lee multiplicative decomposition to solve the Zener-like constitutive model, the viscous evolution law falls in equations like \({\dot{\mathbf{X}}} = B \cdot {\mathbf{X}}\) (in which \({\mathbf{X}}\) is the main tensor variable and \({\mathbf{B}}\) represents part of the viscous constitutive tensor) and the exponential map [23, 24] can be directly used. However, due to the Flory’s decomposition a mix among elastic and viscous terms appears in Eqs. (21) and (22) and the exponential map cannot be applied. In this context, a possible comment regarding the adopted time discretization [47] is the possibility of losing the isochoric property of \(\user2{\mathfrak{E}}_{s}^{i}\) and \(\left( {\user2{\dot{\mathfrak{E}}}_{e}^{i} } \right)_{s}\) when measured at time \(t_{s + 1}\). In Example 5.1, we show that volumetric loads do not promote shear strains, and in Example 5.3, we verify that shear loads do not promote volumetric strains. In addition, one can realize that sudden strain changes occur only in the instantaneous part of the model and strain rates are important during the smooth part of material behavior.

3.4 Zener-like model - time rate of strain invariants

In this item, we propose a viscous model that depends on scalar isochoric invariants. Following item 3.2, we propose the following version of second Piola–Kirchhoff stress for the Maxwell branch of the Zener-like model depicted in Fig. 1b:

$${\mathbf{S}}_{v}^{i} = \frac{{\overline{\eta }( \bullet )}}{4}\dot{\overline{I}}_{iv} \user2{\mathfrak{E}}^{i} \quad {\text{or}}\quad {\mathbf{S}}_{v}^{i} = \frac{{\overline{G}}}{4}\frac{{\partial \overline{I}_{ie}^{{}} }}{{\partial {\mathbf{E}}}}$$
(29)

in which \(\overline{I}_{iv}\) and \(\overline{I}_{ie}\) are parts of the total isochoric strain invariant \(\overline{I}_{i}\). Being the strain invariant a scalar value, it is fair to define its parts (not necessarily with real meaning) as:

$$\overline{I}_{i} = \overline{I}_{ie} + \overline{I}_{iv} = \alpha \overline{I}_{i} + (1 - \alpha )\overline{I}_{i}$$
(30)

in which \(\overline{I}_{ie} = \alpha \overline{I}_{i}\), \(\overline{I}_{iv} = (1 - \alpha )\overline{I}_{i}\) and \(\alpha\) is an auxiliary scalar to be eliminated.

Using the \(\alpha\) splitting, together with the adopted \(\overline{\eta }( \bullet )\) into Eq. (29), one writes:

$${\mathbf{S}}_{v}^{i} = (1 - \alpha )\frac{{\overline{\eta }}}{4}\dot{\overline{I}}_{i} \user2{\mathfrak{E}}^{i} \quad {\text{and}}\quad {\mathbf{S}}_{v}^{i} = \frac{{\overline{G}}}{4}\alpha \user2{\mathfrak{E}}^{i}$$
(31)

and, by equality, one achieves:

$$\alpha = {{\overline{\eta }\dot{\overline{I}}_{i} } \mathord{\left/ {\vphantom {{\overline{\eta }\dot{\overline{I}}_{i} } {\left( {\overline{G} + \overline{\eta }\dot{\overline{I}}_{i} } \right)}}} \right. \kern-0pt} {\left( {\overline{G} + \overline{\eta }\dot{\overline{I}}_{i} } \right)}}$$
(32)

Substituting Eqs. (32) into (31) results

$${\mathbf{S}}_{v}^{i} = \frac{{\overline{G}}}{4}\frac{{\overline{\eta }\dot{\overline{I}}_{i} }}{{\left( {\overline{G} + \overline{\eta }\dot{\overline{I}}_{i} } \right)}}\user2{\mathfrak{E}}^{i} = \frac{1}{4}\left[ {\frac{{\overline{\eta }\dot{\overline{I}}_{i} }}{{\left( {1 + \left( {\overline{\eta }\dot{\overline{I}}_{i} /\overline{G}} \right)} \right)}}} \right]\user2{\mathfrak{E}}^{i}$$
(33)

The total isochoric stress is achieved introducing Eq. (33) and the first of (22) into Eq. (21), i.e.,

$${\mathbf{S}}_{T}^{i} = \frac{1}{4}\left[ {G + \frac{{\overline{\eta }\dot{\overline{I}}_{i} }}{{\left( {1 + \left( {\overline{\eta }\dot{\overline{I}}_{i} /\overline{G}} \right)} \right)}}} \right]\user2{\mathfrak{E}}^{i}$$
(34)

in which \(\dot{\overline{I}}_{i}\) is calculated by finite difference.

When using this model for a simple ideal relaxation test, one should note that \(\dot{\overline{I}}_{i} = 0\) and \(\user2{\dot{\mathfrak{E}}}^{i} = {\mathbf{0}}\) and specific equations should be used. Observing Fig. 1b, rewriting Eq. (30) as \(\overline{I}_{i} = \overline{I}_{ie} + \overline{I}_{iv} = \alpha \overline{I}_{i} + (1 - \alpha )\overline{I}_{i} = \alpha \overline{I}_{i} + \overline{I}_{iv}\) and choosing \(\overline{I}_{iv}\) as the main variable, one rewrites Eq. (31) as:

$${\mathbf{S}}_{v}^{i} = \frac{{\overline{\eta }}}{4}\dot{\overline{I}}_{vi} \user2{\mathfrak{E}}^{i} = \frac{{\overline{G}}}{4}\alpha \user2{\mathfrak{E}}^{i} \quad {\text{from}}\,{\text{which}}\quad \alpha = \frac{{\overline{\eta }}}{{\overline{G}}}\dot{\overline{I}}_{iv}$$
(35)

Introducing this new value of \(\alpha\) into Eq. (30), one writes:

$$\overline{I}_{i} = \frac{{\overline{\eta }}}{{\overline{G}}}\dot{\overline{I}}_{iv} \overline{I}_{i} + \overline{I}_{iv}$$
(36)

also solved in this study by a simple finite difference, i.e.:

$$\overline{I}_{iv}^{s + 1} = \overline{I}_{i} \left( {1 + (\overline{\eta }/\overline{G})\overline{I}_{iv}^{s} /\Delta t} \right)/\left( {1 + (\overline{\eta }/\overline{G})\overline{I}_{i}^{{}} /\Delta t} \right)$$
(37)

Applying this result and \(\dot{\overline{I}}_{iv}^{s + 1} = (\overline{I}_{iv}^{s + 1} - \overline{I}_{iv}^{s} )/\Delta t\) in the first of Eq. (35) one calculates \({\mathbf{S}}_{v}^{i}\). At the beginning of an instantaneous ideal relaxation test (\(s = 0\)), one has \(\overline{I}_{iv}^{0} = (1 - \alpha_{0} )\overline{I}_{i}\), being \(\overline{I}_{i}^{{}}\) known and \(\alpha_{0}\) calculated by Eq. (32) as \(\dot{\overline{I}}_{i} \ne 0\) at instant zero.

3.5 Zener-like model - rate-dependent viscosity

From the above formulations, we identify that our model 3.3 is the more general. Thus, it has a good potential to be adapted to consider rate-dependent viscosity. In order to do so, we start defining our nonlinear viscosity by the following expression:

$$\eta = \eta^{*} + \upsilon \left( {\user2{\dot{\mathfrak{E}}}_{v}^{i} :\user2{\dot{\mathfrak{E}}}_{v}^{i} + rv} \right)^{\ell }$$
(38)

in which \(\eta^{*}\) is a reference constant viscosity, \(\upsilon\) indicates the participation of the isochoric strain rate into the model and \(rv\) is a regularization number with unity \(T^{ - 2}\). As our integration procedure is numeric, Eq. (28) is used to calculate the total isochoric stress, remembering that the viscosity (Eq. 38) is updated at iterations of the nonlinear solution process described in item 4.3.b5.

4 Finite element implementation

This section is divided into three items to briefly describe the adopted FEM procedure considering the proposed viscoelastic models. First we describe the weak equilibrium equation using the principle of virtual work, then we transform it into the approximate nonlinear equilibrium equation and, finally, we describe the solution process.

4.1 Weak equilibrium equation

We start from the six Eulerian local (strong) equilibrium equations, written as:

$$\nabla \cdot {\varvec{\sigma}}^{t} + \vec{b} = \rho \vec{\ddot{y}}\quad {\text{and}}\quad {\varvec{\sigma}}^{T} = {\varvec{\sigma}}$$
(39)

in which \(\sigma_{ij}\) is the Cauchy stress component acting on plane \(i\) and direction \(j\), \(\rho\) is the mass density, \(\ddot{y}_{i}\) is the acceleration of a particle following i-th direction and \(b_{i}\) is the i-th body force component. The second expression of Eq. (39) corresponds to the three moment equations, resulting in the symmetry of the Cauchy stress tensor.

The weak form of the first part of Eq. (39) is achieved here by applying the virtual work principle as:

$$\delta w = \left( {\nabla \cdot {\varvec{\sigma}}^{t} + \vec{b} - \rho \vec{\ddot{y}}} \right) \cdot \delta \vec{y} = 0$$
(40)

in which \(\delta\) means variation, \(w\) is work or energy by unit of volume and \(\vec{y}\) position. Integrating Eq. (40) over the current volume \(V\) and using the divergence theorem, one achieves:

$$\delta W = \int_{V}^{{}} {\rho \vec{\ddot{y}} \cdot \delta \vec{y}\,\,{\text{d}}V} - \int_{V}^{{}} {\vec{b} \cdot \delta \vec{y}\,{\text{d}}V} - \int_{S}^{{}} {\vec{h} \cdot \delta \vec{y}\,\,{\text{d}}S + \int_{V}^{{}} {{\varvec{\sigma}}:\delta {\varvec{\varepsilon}}\,\,{\text{d}}V} = 0}$$
(41)

in which \(\delta \varepsilon_{ij} = (\delta y_{i,j} + \delta y_{j,i} )/2\) is a variation of the true strain (measured in Eulerian reference), usually known in its rate form \(\dot{\varepsilon }_{ij} = (\dot{y}_{i,j} + \dot{y}_{j,i} )/2\) [52] and \(\vec{h}\) is the surface force. To transform Eq. (41) in its Lagrangian version, one uses the continuity theorem on the first term, considers body forces proportional to density, remembers Nanson’s formula for surface forces and uses the work conjugacy at the last term [47, 52], i.e.,

$$\int\limits_{V}^{{}} {{\varvec{\sigma}}:\delta {\varvec{\varepsilon}}} \,{\text{d}}V = \int\limits_{{V_{0} }}^{{}} {} {\mathbf{S}}:\delta {\mathbf{E}}\,{\text{d}}V_{0}$$
(42)

resulting

$$\delta W = \int_{{V_{0} }}^{{}} {\rho_{0} \vec{\ddot{y}} \cdot \delta \vec{y}\,{\text{d}}V_{0} } - \int_{{V_{0} }}^{{}} {\vec{b}_{{}}^{0} \cdot \delta \vec{y}\,{\text{d}}V_{0} } - \int_{{S_{0} }}^{{}} {\vec{h}_{0} \cdot \delta \vec{y}\,\,{\text{d}}S_{0} } + \int_{{V_{0} }}^{{}} {{\mathbf{S}}:\delta {\mathbf{E}}\,{\text{d}}V_{0} = 0}$$
(43)

in which \({\mathbf{S}} = {\mathbf{S}}_{T}^{1} + {\mathbf{S}}_{T}^{2} + {\mathbf{S}}^{vol}\), with \({\mathbf{S}}^{vol}\) being the elastic volumetric part of the second Piola–Kirchhoff stress, Eq. (13), and \({\mathbf{S}}_{T} = {\mathbf{S}}_{T}^{1} + {\mathbf{S}}_{T}^{2}\) the total isochoric second Piola–Kirchhoff stress—including both elastic and viscous parts—see Eqs. (34), (28), (20) and (18).

4.2 FEM approximate equilibrium equation

The adopted FEM is a variation of the classical FEM in which positions are taken as the main variables of the problem. So, the deformation function can be described as depicted in Fig. 2, in which a prismatic finite element with cubic approximation in the triangular base and linear approximation in its thickness is used for illustration (any approximation order can be used).

Fig. 2
figure 2

Approximated FEM deformation function using positions

Full size image

From Fig. 2, the initial and current mappings are given as:

$$\vec{f}_{{}}^{0} = \vec{x} = \phi_{\alpha } \left( {\vec{\xi }} \right)\vec{X}_{\alpha } \quad {\text{and}}\quad \vec{f}_{{}}^{1} = \vec{y} = \phi_{\alpha } \left( {\vec{\xi }} \right)Y_{\alpha }$$
(44)

in which \(\vec{x}\) are domain initial position and \(\vec{y}\) are current domain positions. \(\phi_{a}\) are shape functions related to node \(\alpha\) and \(\vec{X}_{\alpha }\) and \(\vec{Y}_{\alpha }\) are nodal initial and current positions, respectively. In Eq. (44), there is summation regarding \(\alpha\). Thus, the deformation function is written as:

$$\vec{y}(\vec{x}) = \vec{f}(\vec{x}) = \vec{f}^{1} (\vec{\xi }) \circ \left( {\vec{f}^{0} (\vec{\xi })} \right)^{ - 1}$$
(45)

and its gradient results:

$${\mathbf{A}} = {\mathbf{A}}^{1} \bullet \left( {{\mathbf{A}}^{0} } \right)^{ - 1}$$
(46)

with

$${\mathbf{A}}^{0} = \frac{{\partial \vec{f}^{0} }}{{\partial \vec{\xi }}}\quad {\text{and}}\quad {\mathbf{A}}^{1} = \frac{{\partial \vec{f}^{1} }}{{\partial \vec{\xi }}}$$
(47)

Equation (46) represents the chain rule and allows a simple modeling of distorted elements. As the gradient deformation \({\mathbf{A}}\) is a function of nodal positions, one may write the variation of the Green–Lagrange strain (see Eq. (43)) as:

$$\delta {\mathbf{E}} = \frac{{\partial {\mathbf{E}}}}{{\partial \vec{Y}}} \cdot \delta \vec{Y}$$
(48)

Using Eq. (48) and the approximations functions into Eq. (43) results the FEM weak equilibrium equation as:

$$\left( {\int_{{V_{0} }}^{{}} {\rho_{0} \,\vec{\phi } \otimes \vec{\phi }\,{\text{d}}V_{0} \cdot \vec{\ddot{Y}}} - \int_{{V_{0} }}^{{}} {\vec{\phi } \otimes \vec{\phi }\,{\text{d}}V_{0} \cdot \vec{B}^{0} } - \int_{{S_{0} }}^{{}} {\vec{\varphi } \otimes \vec{\varphi }\,\,{\text{d}}S_{0} \cdot \vec{P}} + \int_{{V_{0} }}^{{}} {\left( {{\mathbf{S}}_{T}^{1} + {\mathbf{S}}_{T}^{2} + {\mathbf{S}}^{{{\text{vol}}}} } \right):\frac{{\partial {\mathbf{E}}}}{{\partial \vec{Y}}}\,\,{\text{d}}V_{0} } } \right) \cdot \delta \vec{Y} = 0\\$$
(49)

in which domain forces are approximated by the same shape functions used for positions and surface forces are approximated by shape functions called \(\vec{\varphi }\). In Eq. (49), the nodal position variation \(\delta \vec{Y}\) is arbitrary. Thus, performing all integrals results the following FEM nonlinear dynamic equilibrium equation:

$${\mathbf{M}} \cdot \vec{\ddot{Y}} - \vec{F}^{{{\text{ext}}}} + \vec{F}^{{{\text{int}}}} (\vec{Y}) = \vec{0}$$
(50)

in which \({\mathbf{M}}\) is the constant mass matrix (total Lagrangian approach), \(\vec{F}^{{{\text{ext}}}}\) are conservative (in this study) external forces and \(\vec{F}^{{\text{int}}}\) are forces that depends on the proposed constitutive model and positions. More details regarding the adopted FEM framework can be seen in references [45,46,47] for instance.

4.3 Solution technique

Equation (50) is solved over time using the Newmark \(\beta\) method, which is well suited for constant mass matrix [53]. Thus, for a current instant \(t_{s + 1}\), the FEM dynamic equilibrium equation becomes:

$$\vec{g}\left( {\vec{Y}_{s + 1} } \right) = \vec{F}_{s + 1}^{{{\text{el}}.{\text{vol}}}} + \vec{F}_{s + 1}^{{{\text{v}}.{\text{iso}}}} + \frac{{\mathbf{M}}}{{\beta \Delta t^{2} }}\vec{Y}_{s + 1} - {\mathbf{M}} \cdot \vec{Q}_{s} { + }\frac{{\gamma {\mathbf{C}}}}{\beta \Delta t} \cdot \vec{Y}_{s + 1} + {\mathbf{C}} \cdot \vec{R}_{s} - \gamma \Delta t{\mathbf{C}} \cdot \vec{Q}_{s} - \vec{F}_{s + 1}^{{{\text{ext}}}} (t) = \vec{0}\\$$
(51)

in which \(\gamma\) and \(\beta\) are the Newmark’s parameters, \({\mathbf{C}}\) is a mass proportional viscous matrix (not related to the proposed viscous models) introduced for completeness, \(\vec{F}_{s + 1}^{{{\text{el}}.{\text{vol}}}}\) is the volumetric elastic internal force, \(\vec{F}_{s + 1}^{{{\text{v}}.{\text{iso}}}}\) is the isochoric viscoelastic internal force (resulting from the proposed models), and

$$\vec{Q}_{s} = \left( {\frac{{\vec{Y}_{s} }}{{\beta \Delta t^{2} }} + \frac{{\dot{\vec{Y}}_{s} }}{{\beta \Delta t^{{}} }} + \left( {\frac{1}{2\beta } - 1} \right)\vec{\ddot{Y}}_{s} } \right)\quad {\text{and}}\quad \vec{R}_{s} = \left[ {\dot{\vec{Y}}_{s} + \Delta t\left( {1 - \gamma } \right)\ddot{\vec{Y}}_{s} } \right]$$
(52)

are quantities of the previous time step.

If \(\vec{Y}_{s + 1}\) is not the correct current position in Eq. (51), the vector \(\vec{g}(\vec{Y}_{s + 1} )\) becomes a residuum of the equilibrium equation. In this sense, \(\vec{Y}_{s + 1}\) is understood as a trial solution and the following Taylor truncated expansion, i.e., the Newton–Raphson method takes place:

$$\vec{0} = \vec{g}(\vec{Y}_{s + 1}^{{}} ) \cong \vec{g}\left( {\vec{Y}_{s + 1}^{0} } \right) + \nabla \vec{g}\left( {\vec{Y}_{s + 1}^{0} } \right) \cdot \Delta \vec{Y}$$
(53)

in which

$${\mathbf{H}} = \nabla \vec{g}\left( {\vec{Y}_{s + 1} } \right) = \left. {\frac{{\partial \vec{F}^{el.vol} }}{{\partial \vec{Y}}}} \right|_{s + 1} + \left. {\frac{{\partial \vec{F}^{v.iso} }}{{\partial \vec{Y}}}} \right|_{s + 1} + \left( {\frac{{\mathbf{M}}}{{\beta \Delta t^{2} }} + \frac{{\gamma {\mathbf{C}}}}{\beta \Delta t}} \right) = {\mathbf{H}}^{{{\varvec{el}}\user2{.vol}}} + {\mathbf{H}}^{v.iso} + {\mathbf{H}}^{din}$$
(54)

is the Hessian matrix. From Eq. (53), one achieves the correction \(\Delta \vec{Y}\) to improve the trial solution by \(\vec{Y}_{s + 1} = \vec{Y}_{s + 1} + \Delta \vec{Y}\) until \(\left\| {\Delta \vec{Y}} \right\|/\left\| {\vec{X}} \right\| \le {\text{Tolerance}}\). More details can be seen in [45,46,47, 53] for instance.

The necessary Hessian matrix’s parts are calculated as:

$${\mathbf{H}}^{{{\text{el}}.{\text{vol}}}} = \int_{{V_{0} }}^{{}} {\frac{{\partial {\mathbf{E}}}}{{\partial \vec{Y}}}:\frac{{\partial {\mathbf{S}}^{{{\text{el}}.{\text{vol}}}} }}{{\partial {\mathbf{E}}}}:\frac{{\partial {\mathbf{E}}}}{{\partial \vec{Y}}} + {\mathbf{S}}^{{{\text{el}}.{\text{vol}}}} :\frac{{\partial^{2} {\mathbf{E}}}}{{\partial \vec{Y} \otimes \partial \vec{Y}}}\,\,{\text{d}}V_{0} }$$
(55)
$${\mathbf{H}}^{{{\text{v}}.{\text{iso}}}} = \int_{{V_{0} }}^{{}} {\frac{{\partial {\mathbf{E}}}}{{\partial \vec{Y}}}:\frac{{\partial {\mathbf{S}}_{T} }}{{\partial {\mathbf{E}}}}:\frac{{\partial {\mathbf{E}}}}{{\partial \vec{Y}}} + {\mathbf{S}}_{T} :\frac{{\partial^{2} {\mathbf{E}}}}{{\partial \vec{Y} \otimes \partial \vec{Y}}}\,\,{\text{d}}V_{0} }$$
(56)

The values \(\partial {\mathbf{E}}/\partial \vec{Y}\) and \(\partial^{2} {\mathbf{E}}/(\partial \vec{Y} \otimes \partial \vec{Y})\) are inherent to the positional FEM and can be consulted, for example in [54]. The other necessary quantities depend on the proposed constitutive model and are given as follows:

  • (a) Elastic Volumetric part

$$\frac{{\partial {\mathbf{S}}^{{{\text{el}}.{\text{vol}}}} }}{{\partial {\mathbf{E}}}} = \frac{K}{4n}\left\{ {\left( {(2n - 1)J^{2(n - 1)} + (2n + 1)J^{ - 2(n + 1)} } \right)\user2{\mathfrak{E}}^{{{\text{vol}}}} \otimes \user2{\mathfrak{E}}^{{{\text{vol}}}} + \left( {J^{2n - 1} - J^{ - (2n + 1)} } \right)\frac{{\partial \user2{\mathfrak{E}}^{{{\text{vol}}}} }}{{\partial {\mathbf{E}}}}} \right\}$$
(57)

with

$$\frac{{\partial \mathfrak{E}_{j\gamma }^{{{\text{vol}}}} }}{{\partial E_{oz} }} = J\left\{ {D_{j\gamma } D_{oz} - 2D_{jo} D_{z\gamma } } \right\}$$
(58)

In which \({\mathbf{D}} = {\mathbf{C}}^{ - 1}\).

  • (b) Viscoelastic isochoric parts

In Eqs. (59) through (63), we consider viscosity as a general function of the isochoric strain invariants. From Eqs. (64) through (71), we show a specific model for which viscosity depends on the time rate of isochoric strain components.

It is important to mention that \(\eta_{i}\) and \(\overline{\eta }_{i}\) are presented without indices and arguments.

  • (b1) For model 3.1, from Eq. (18):

$$\left. {\frac{{\partial {\mathbf{S}}_{T}^{i} }}{{\partial {\mathbf{E}}}}} \right|_{S + 1} = \frac{1}{4\Delta t}\left( {\frac{{{\text{d}}\eta }}{{{\text{d}}\overline{I}_{i} }}} \right)\user2{\mathfrak{E}}_{s + 1}^{i} \otimes \user2{\mathfrak{E}}_{s + 1}^{i} + \frac{1}{4}\left( {G + \frac{\eta }{\Delta t}} \right)\frac{{\partial \user2{\mathfrak{E}}_{s + 1}^{i} }}{{\partial {\mathbf{E}}}}$$
(59)

  • (b2) For model 3.2, from Eq. (20):

    $$\left. {\frac{{\partial {\mathbf{S}}_{T}^{i} }}{{\partial {\mathbf{E}}}}} \right|_{S + 1} = \frac{1}{4}\left\{ {\left( {\frac{{{\text{d}}\overline{\eta }}}{{{\text{d}}\overline{I}_{i} }}\dot{\overline{I}}_{i} + \overline{\eta }/\Delta t} \right)\user2{\mathfrak{E}}_{s + 1}^{i} \otimes \user2{\mathfrak{E}}_{s + 1}^{i} + \left( {G + \overline{\eta }\dot{\overline{I}}} \right)\frac{{\partial \user2{\mathfrak{E}}_{s + 1}^{i} }}{{\partial {\mathbf{E}}}}} \right\}$$
    (60)

  • (b3) For model 3.3, from Eq. (28):

    $$\frac{{\partial \left( {{\mathbf{S}}_{T}^{i} } \right)_{s + 1} }}{{\partial {\mathbf{E}}}} = \left( \frac{G}{4} \right)\left( {\frac{{\partial \user2{\mathfrak{E}}_{{}}^{i} }}{{\partial {\mathbf{E}}}}} \right)_{s + 1} + {{\left[ {\left( {\frac{{\overline{G}}}{4\Delta t}} \right)\left( {\frac{{\partial \user2{\mathfrak{E}}_{{}}^{i} }}{{\partial {\mathbf{E}}}}} \right)_{s + 1} + \frac{{{\text{d}}\eta }}{{{\text{d}}\overline{I}_{i} }}\frac{{\overline{G}}}{{\left( {\eta (\overline{I}_{i} )} \right)^{2} }}\user2{\mathfrak{E}}_{s + 1}^{i} \otimes \left( {{\mathbf{S}}_{v}^{i} } \right)_{s + 1} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {\frac{{\overline{G}}}{4\Delta t}} \right)\left( {\frac{{\partial \user2{\mathfrak{E}}_{{}}^{i} }}{{\partial {\mathbf{E}}}}} \right)_{s + 1} + \frac{{{\text{d}}\eta }}{{{\text{d}}\overline{I}_{i} }}\frac{{\overline{G}}}{{\left( {\eta (\overline{I}_{i} )} \right)^{2} }}\user2{\mathfrak{E}}_{s + 1}^{i} \otimes \left( {{\mathbf{S}}_{v}^{i} } \right)_{s + 1} } \right]} {\left( {\frac{{\overline{G}}}{\eta } + \frac{1}{\Delta t}} \right)}}} \right. \kern-0pt} {\left( {\frac{{\overline{G}}}{\eta } + \frac{1}{\Delta t}} \right)}}$$
    (61)

  • (b4) For model 3.4, from Eq. (33):

    $$\left. {\frac{{\partial {\mathbf{S}}_{T}^{i} }}{\partial E}} \right|_{s + 1} = {{\frac{G}{4}\frac{{\partial \user2{\mathfrak{E}}_{s + 1}^{i} }}{{\partial {\mathbf{E}}}} + \left\{ {\frac{{\overline{G}}}{4}\left[ {Q\,\user2{\mathfrak{E}}_{s + 1}^{i} \otimes \user2{\mathfrak{E}}_{s + 1}^{i} + Z\frac{{\partial \user2{\mathfrak{E}}_{s + 1}^{i} }}{{\partial {\mathbf{E}}}}} \right] - Q\,\user2{\mathfrak{E}}_{s + 1}^{i} \otimes \left( {{\mathbf{S}}_{v}^{i} } \right)_{s + 1} } \right\}} \mathord{\left/ {\vphantom {{\frac{G}{4}\frac{{\partial \user2{\mathfrak{E}}_{s + 1}^{i} }}{{\partial {\mathbf{E}}}} + \left\{ {\frac{{\overline{G}}}{4}\left[ {Q\,\user2{\mathfrak{E}}_{s + 1}^{i} \otimes \user2{\mathfrak{E}}_{s + 1}^{i} + Z\frac{{\partial \user2{\mathfrak{E}}_{s + 1}^{i} }}{{\partial {\mathbf{E}}}}} \right] - Q\,\user2{\mathfrak{E}}_{s + 1}^{i} \otimes \left( {{\mathbf{S}}_{v}^{i} } \right)_{s + 1} } \right\}} {\left( {1 + Z} \right)}}} \right. \kern-0pt} {\left( {1 + Z} \right)}}$$
    (62)

    with

    $$Z = \left( {\overline{\eta }\dot{\overline{I}}_{i} /\overline{G}} \right)\quad \frac{\partial Z}{{\partial {\mathbf{E}}}} = \frac{1}{{\overline{G}}}\left( {\frac{{{\text{d}}\overline{\eta }}}{{{\text{d}}\overline{I}_{i} }}\left( {\dot{\overline{I}}_{i} } \right)_{s + 1} + \frac{{\overline{\eta }}}{{\Delta t}}} \right)\user2{\mathfrak{E}}_{s + 1}^{i} = Q\,\user2{\mathfrak{E}}_{s + 1}^{i}$$
    (63)

  • (b5) For model 3.5, from Eqs. (28) and (38):

Here, it is necessary to recalculate Eq. (61) in order to consider the rate-dependent viscosity given by Eq. (38). In order to do so, we rewrite Eq. (28) as:

$$\left( {\frac{{\overline{G}}}{\eta } + \frac{1}{\Delta t}} \right)\left( {{\mathbf{S}}_{v}^{i} } \right)_{s + 1} = \frac{{\overline{G}}}{4}\left( {\left( {\user2{\dot{\mathfrak{E}}}^{i} } \right)_{s + 1} + \frac{{\left( {\user2{\mathfrak{E}}_{e}^{i} } \right)_{s} }}{\Delta t}} \right)$$
(64)

And proceed the derivative in both sides, i.e.:

$$\frac{\partial }{{\partial {\mathbf{E}}}}\left[ {\left( {\frac{{\overline{G}}}{\eta } + \frac{1}{\Delta t}} \right)\left( {{\mathbf{S}}_{v}^{i} } \right)_{s + 1} } \right] = \frac{{\overline{G}}}{4}\frac{\partial }{{\partial {\mathbf{E}}}}\left( {\left( {\user2{\dot{\mathfrak{E}}}^{i} } \right)_{s + 1} + \frac{{\left( {\user2{\mathfrak{E}}_{e}^{i} } \right)_{s} }}{\Delta t}} \right)$$
(65)

After some manipulations, one finds:

$$\left( {\frac{{\partial {\mathbf{S}}_{v}^{i} }}{{\partial {\mathbf{E}}}}} \right)_{s + 1} = \left\{ {\frac{{\overline{G}}}{4\Delta t}\left( {\frac{{\partial \user2{\mathfrak{E}}_{{}}^{i} }}{{\partial {\mathbf{E}}}}} \right)_{s + 1} + \overline{G}\left( {\left( \eta \right)^{ - 2} \frac{\partial \eta }{{\partial {\mathbf{E}}}}} \right) \otimes \left( {{\mathbf{S}}_{v}^{i} } \right)_{s + 1} } \right\}/\left( {\frac{{\overline{G}}}{\eta } + \frac{1}{\Delta t}} \right)$$
(66)

Now, using Eq. (38) one finds:

$$\frac{\partial \eta }{{\partial {\mathbf{E}}}} = 2\upsilon \ell \left( {\user2{\dot{\mathfrak{E}}}_{v}^{i} :\user2{\dot{\mathfrak{E}}}_{v}^{i} + rv} \right)^{\ell - 1} \left( {\frac{{\partial \user2{\dot{\mathfrak{E}}}_{v}^{i} }}{{\partial {\mathbf{E}}}}:\user2{\dot{\mathfrak{E}}}_{v}^{i} } \right)$$
(67)

In Eq. (67), one needs to calculate \(\partial \user2{\dot{\mathfrak{E}}}_{v}^{i} /\partial {\mathbf{E}}\). In order to do so, we use Eqs. (26) and (24) to write:

$$\user2{\dot{\mathfrak{E}}}_{v}^{i} \left( {1 + \frac{\eta }{{\overline{G}\Delta t}}} \right) = \left( {\user2{\dot{\mathfrak{E}}}^{i} + \frac{{\left( {\user2{\mathfrak{E}}_{e}^{i} } \right)_{s} }}{\Delta t}} \right)$$
(68)

and execute derivatives regarding the Green–Lagrange strain at both sides of Eq. (68), resulting:

$$\frac{{\partial \user2{\dot{\mathfrak{E}}}_{v}^{i} }}{{\partial {\mathbf{E}}}} = \left[ {\frac{1}{{\Delta t}}\frac{{\partial \user2{\mathfrak{E}}^{i} }}{{\partial {\mathbf{E}}}} - \frac{1}{{\overline{G}\Delta t}}\frac{\partial \eta }{{\partial {\mathbf{E}}}} \otimes \user2{\dot{\mathfrak{E}}}_{v}^{i} } \right]/\left( {1 + \frac{\eta }{{\overline{G}\Delta t}}} \right)$$
(69)

Substituting Eqs. (69) into (67) and making some algebraic arrangements, Eq. (67) becomes:

$$\frac{\partial \eta }{{\partial {\mathbf{E}}}} = \Xi \left( {\frac{{\partial \user2{\mathfrak{E}}^{i} }}{{\partial {\mathbf{E}}}}:\user2{\dot{\mathfrak{E}}}_{v}^{i} } \right)/\left( {\Delta t + \frac{\Xi }{{\overline{G}}}\user2{\dot{\mathfrak{E}}}_{v}^{i} :\user2{\dot{\mathfrak{E}}}_{v}^{i} } \right)$$
(70)

with

$$\Xi = \frac{{2\ell \upsilon \left( {\user2{\dot{\mathfrak{E}}}_{v}^{i} :\user2{\dot{\mathfrak{E}}}_{v}^{i} + rv} \right)^{\ell - 1} }}{{\left( {1 + \frac{{\eta^{*} }}{{\overline{G}\Delta t}}} \right)}}$$
(71)

Model 3.5 is summarized by Eqs. (38), (28), (66) and (70).

Finally, for all viscoelastic cases it is necessary to know the derivatives of the isochoric strains regarding the Green–Lagrange strain, i.e.:

$$\frac{{\partial \mathfrak{E}_{ij}^{{{\text{iso}}1}} }}{{\partial E_{k\ell } }} = \frac{4}{3}J^{ - 2/3} \left\{ {\frac{1}{3}\left\{ {D_{ij} D_{k\ell } + 3D_{ik} D_{\ell j} } \right\}I_{1} - D_{ij} \delta_{k\ell } - D_{k\ell } \delta_{ij} } \right\}$$
(72)
$$\frac{{\partial \mathfrak{E}_{ij}^{{{\text{iso}}2}} }}{{\partial E_{k\ell } }} = \frac{8}{3}J^{ - 4/3} \left\{ \begin{gathered} \left[ {\frac{2}{3}D_{ij} D_{k\ell } + D_{ik} D_{\ell j} } \right]I_{2} - \left[ {C_{zz} \left( {D_{ij} \delta_{k\ell } + D_{k\ell } \delta_{ij} } \right)} \right] \hfill \\ \qquad+ D_{ij} C_{k\ell } + D_{k\ell } C_{ij} + \frac{3}{2}\left[ {\delta_{ij} \delta_{k\ell } - \delta_{jk} \delta_{i\ell } } \right] \hfill \\ \end{gathered} \right\}$$
(73)

5 Examples

The first three examples are presented in order to show the proposed models behavior regarding the volumetric/isochoric split, pure creep and relaxation. Three other examples are presented to show the applicability of the proposed framework in rate-dependent viscoelasticity, comparing numerical and experimental results and solving structural problems.

5.1 Instantaneous volumetric change

In order to observe if the isochoric viscosity (proposed in the models) has some influence in the volume change, a unitary cube (\(1\,{\text{mm}}\, \times \,1\,{\text{mm}}\)) is discretized by two prismatic finite elements (linear approximation due to the simplicity of the test). Figure 3 shows the discretization and boundary conditions. The cube is subjected to an instantaneous hydrostatic stress. The hydrostatic stress is directly applied in Eq. (13) as follows:

$${\mathbf{S}}^{{{\text{vol}}}} = \left\{ {\frac{K}{4n}\left( {J^{2n - 1} - J^{ - (2n + 1)} } \right) - 1000\,{\text{MPa}}} \right\}\user2{\mathfrak{E}}^{vol}$$
Fig. 3
figure 3

Geometry and discretization

Full size image

The adopted elastic properties are: \(G = 10\,{\text{MPa}}\), \(\overline{G} = 8\,{\text{MPa}}\) and \(K = 1000\,{\text{MPa}}\). It is not necessary to plot any results as all models give instantaneous behavior with final volume of \(V = 4015\,{\text{mm}}^{3}\) and no viscosity appears, i.e., there is no shear stress or strain present from volumetric loading. We tested all viscous parameters and models explored in the other examples.

In Example 5.3, we show that when applying an instantaneous isochoric strain no volumetric (hydrostatic) stress appears.

5.2 Uniaxial tension tests

The same cube (\(1\,{\text{mm}}\, \times \,1\,{\text{mm}}\)) of the previous example is stretched following the third direction, see Fig. 3. We performed pure creep and relaxation tests as follows:

(a) Tension creep test:

To perform the creep test an instantaneous force of \(41.88N\) (corresponding to a nominal surface force of \(41.88\,{\text{MPa}}\)) is applied at the plane \(x_{3} = 1\,{\text{mm}}\) and maintained constant during all the analysis. It results in a total displacement of \(7\,{\text{mm}}\) (\(\lambda_{3} = 8\)) for both Kelvin–Voigt and Zener-like models. The Zener-like model has an instantaneous displacement of \(2.84\,{\text{mm}}\).

Different behaviors for same viscosity values are expected as \(\eta\) is related to \(\user2{\dot{\mathfrak{E}}}_{v}^{i}\) and \(\overline{\eta }\) is related to \(\dot{\overline{I}}_{i}\). In Fig. 4, we present the longitudinal displacement over time of the specimen for various viscosity values for both Zener-like models. In Fig. 5, we present the same displacements for the Kelvin–Voigt-like models. In Fig. 4, the large time range is used to stress the qualitative results of models and the small time range is used to detach the difference among models 3.3 and 3.4. The same caption is used for Figs. 4a and 4b. As one can see from Fig. 4, the creep phenomenon is properly represented, i.e., under a constant load an instantaneous stretch appears (Zener-like) and gradually evolves until a stabilized value that corresponds to the final elastic response.

Fig. 4
figure 4

Tension creep test for Zener-like models

Full size image
Fig. 5
figure 5

Tension test for Kelvin-like and Zener-like models \(\Delta t = 0.1s\)

Full size image

When solving the creep test for model 3.1 (Kelvin-like), we noted that the viscous part of the numerical constitutive tensor (Eq. 59) depends on \(\left( {\Delta t} \right)^{ - 1}\). In order to overcome this difficulty, we magnified the Hessian matrix volumetric part of model 3.1 multiplying it by \(\left[ {3 \cdot (\eta + G)/K} \right]/\Delta t^{2}\). Results for model 3.1 and 3.2 are presented in Fig. 5a. It is important to mention that only model 3.1 uses this magnifying factor.

When increasing the shear modulus \(\overline{G}\) of the Maxwell part of the Zener-like model (model 3.3, for example), the instantaneous material behavior is reduced and results a quasi-Kelvin-like model less sensitive to the time step size. In this example, we adopted \(\overline{G} = 50\,{\text{MPa}}\) to reduce the instantaneous behavior of model 3.3, and in Fig. 5b, we compare results of models 3.1 using the magnifying factor \(\left[ {3 \cdot (\eta + G)/K} \right]/\Delta t^{2}\) and model 3.3 without the use of this magnifying factor. As one can see, a small difference can be noted for viscosity values \(\eta = 12\,{\text{MPa}}.{\text{s}}\) and \(\eta = 60\,{\text{MPa}}.{\text{s}}\). For a large value, \(\eta = 160\,{\text{MPa}}.{\text{s}}\), for example, a sensible difference appears because the instantaneous response of model 3.3 becomes evident.

In the Kelvin–Voigt-like model, creep occurs without an instantaneous value, but a fast evolving of displacement occurs at the initial instants. As mentioned before, the viscous behavior and the viscous parameters of models 3.2 and 3.4 are different from models 3.1 and 3.3.

For both Zener-like models, in Fig. 6, we present the longitudinal total second Piola–Kirchhoff Stress \(S_{33}\). As one can see, at the beginning of the analyzed time, the total stress corresponds to the instantaneous strength of both springs of Fig. 1b, and, after stabilization, only the isolated spring works, mitigating the viscous overstress. In Fig. 6, models 3.2 and 3.4 are presented separately to show the qualitative behavior, as it is not expected same results.

  • (b) Tension relaxation test for Zener-like models

Fig. 6
figure 6

Piola Kirchhoff stress \(S_{33}\) for Zener-like models

Full size image

The same cube of Fig. 3 is now instantaneously stretched keeping the stretch constant over time. The applied stretch corresponds to \(\lambda_{3} = 8\). In Fig. 7, we show the Cauchy viscous stress for models 3.3 and 3.4.

Fig. 7
figure 7

Relaxation tests for Zener-like models

Full size image

Again, it is worth mentioning that responses have the same qualitative behavior for different rate models.

5.3 Shear relaxation test

In this example, the unitary cube (\(1\,{\text{mm}}\, \times \,1\,{\text{mm}}\)) is subjected to an instantaneous shear strain of \(\gamma_{12} = 3\), see Fig. 8. In Fig. 9, one can see the total Cauchy stress \(\sigma_{12}\) along time for Zener-like models 3.3 and 3.4. Both models achieved the final expected stress, i.e., \(\sigma_{12}^{{{\text{final}}}} = 30\,{\text{MPa}}\).

Fig. 8
figure 8

Discretization and imposed shear isochoric strain

Full size image
Fig. 9
figure 9

Total Cauchy stress for relaxation shear test

Full size image

All degrees of freedom are restricted and we calculate \(\sigma_{33} = 0\) over all analyzed time, i.e., for both models there is no influence of isochoric strains in the volumetric direction. Thus, considering this example and Example 1 we conclude that the proposed models (using the Flory’s decomposition) are capable of modeling viscoelastic problems in the large strain range.

5.4 Example 5.4 Rate-dependent response - validation with literature experiments

Reference [55] presents a very interesting study regarding high damping rubber (HDR) and natural rubber (NR). It presents an expressive review on the subject that reveals a significant viscous rate-dependence of some material and the necessity to develop proper viscous models to represent this class of material. Specifically, they identified a dependence of viscosity regarding isochoric strain time derivative (using Köner–Lee-based approach).

Now, we reproduce two experimental shear relaxation tests of reference [55] using the same discretization of previous examples and using model 3.5. The following parameters’ are adopted:

(a) For HDR: \(K = 1000\,{\text{MPa}}\), \(G = 0.5\,{\text{MPa}}\), \(\overline{G} = 0.6\,{\text{MPa}}\), \(\eta^{*} = 10.0\,{\text{MPa}} \times {\text{s}}\), \(\ell = - 0.5\), \(rv = 0.0004\,{\text{s}}^{ - 2}\) and \(\upsilon = 1.8\,{\text{MPa}} \times\,{\text{s}}^{2\ell + 1} = 1.8\,{\text{MPa}}\).

(b) For NR: \(K = 1000\,{\text{MPa}}\), \(G = 0.8\,{\text{MPa}}\), \(\overline{G} = 0.35\,{\text{MPa}}\), \(\eta^{*} = 10.0\,{\text{MPa}} \cdot {\text{s}}\), \(\ell = - 0.5\), \(rv = 0.0003\,{\text{s}}^{ - 2}\) and \(\upsilon = 2.25\,{\text{MPa}} \cdot {\text{s}}^{2\ell + 1} = 2.25\,{\text{MPa}}\).

It is worth noting that these parameters are not the same as the ones presented by [55] as the models are completely different.

Figure 10 compares the achieved Cauchy stress for three different imposed shear strains with the experimental results presented by [55]. The adopted time step is \(\Delta t = 1.0s\). In order to improve understanding of Fig. 10, the stress time histories are separated each other by \(200s\).

Fig. 10
figure 10

Numerical results for shear relaxation (values of \(\gamma\) in caption) and experimental data from [55]

Full size image

As one can see in Fig. 10a, the adopted constants are calibrated for the intermediate shear strain level and the achieved numerical results are almost the same as the experimental data. Regarding HDR, for the high strain level \(\gamma = 2.50\) results are very good at the beginning of the curve (high strain time rate) and for the low strain level \(\gamma = 1.00\) results are very good at the end of the curve (low strain time rate). However, results are very good considering the simplicity of the proposed model and the numerical results presented in reference [55].

Regarding NR, the overall behavior is the same of the HDR analysis, see Fig. 10b. However, it is important to mention that model 3.5 is calibrated for the intermediate strain level, but the final elastic response of the other strain levels is not achieved using the reference reported applied strains. As the final elastic stress results are obvious, we adopted for NR the strain levels depicted in Fig. 10b. For the HDR case, results are achieved using exactly the data of reference [55].

In Fig. 11, using HDR constants, we show for \(\gamma = 2.50\) the sensitivity of the model regarding parameter \(\upsilon\) keeping \(\eta^{*} = 10.0\,{\text{MPa}} \cdot {\text{s}}\) and regarding \(\eta^{*}\) imposing \(\upsilon = 0.0\). For both cases \(rv = 0.0003\,{\text{s}}^{ - 2}\).

Fig. 11
figure 11

Sensitivity of model 3.5 regarding parameters \(\upsilon\) and \(\eta^{*}\)

Full size image

It is important to mention that results of Fig. 11b correspond to model 3.3 when \(\eta = \eta^{*}\), see Eq. (38). Finally, when \(\ell < 0\) viscosity is low for high strain rates and high for low strain rates. For \(\ell > 0\), viscosity is high for high strain rates and low for low strain rates.

5.5 Example 5.5 Viscoelastic sandwich circular plate

In this analysis, we use a polypropylene [56] as the core filler of a structural element. A simple supported circular plate with radius \(R = 1{\text{m}}\) and thickness \(t = 3{\text{cm}}\) is subjected to a transverse uniform loading. Only \(1/4\) of the structure is modeled using 300 prismatic finite elements with cubic approximation parallel to the plate surface and linear along its thickness, totalizing 3 unitary layers, see Fig. 12. The simple support condition is applied at boundary nodes of the bottom face. The load is applied as a volume force on the superior layer of the plate. Three situations are considered (1) pure elastic, (2) sandwich viscous quasi-static and (3) sandwich viscous dynamic:

  • (i) Pure elastic:

Fig. 12
figure 12

Elastic case (steel): Discretization, boundary conditions and transverse displacement \((w_{\max } = 0.688\,{\text{cm}})\)

Full size image

Only to verify the discretization adequacy, the three layers are considered elastic (steel) with properties: \(K = 120\,{\text{GPa}}\) and \(G = 80\,{\text{GPa}}\). The adopted transverse load is \(b_{3} = 5000\,{\text{kN/m}}^{{3}}\) on the upper lamina, corresponding to a surface force of \(h_{3} = 50\,{\text{kN/m}}^{{2}}\). The achieved central transverse displacement is \(w = 0.688\,{\text{cm}}\), see Fig. 12, very near the linear Kirchhoff kinematics analytical solution that is \(w_{k} = 0.684\,{\text{cm}}\) given by [57], for instance. It is important to mention that this element has been validated for simple solid analysis by [58, 59].

  • (ii) Sandwich viscous quasi-static:

Keeping the loading of case (i), the material of the central layer is substituted by a polypropylene core [56] with the following properties: \(K = 100\,{\text{GPa}}\), \(G = 550\,{\text{MPa}}\), \(\overline{G} = 180\,{\text{MPa}}\), \(\eta^{*} = 200\,{\text{MPa}} \cdot {\text{s}}\), \(\ell = - 0.5\), \(\upsilon = 6.8\,{\text{MPa}}\) and \(rv = 1.0\, \times \,10^{ - 7} \,{\text{s}}^{ - 2}\). We validate the adopted parameters with experimental data [56] using a relaxation test (\(\varepsilon_{33} = 1\%\)), see Fig. 13a.

Fig. 13
figure 13

a Relaxation test for instantaneous strain \(\varepsilon_{33} = 1\%\). b Quasi-static Instantaneous loading

Full size image

The central displacement for the elastic (sandwich plate) and quasi-static viscoelastic cases are shown in Fig. 13b, being the maximum elastic displacement \(w_{\max } = 0.7504\,{\text{cm}}\), \(9.1\%\) larger than the steel case (i). We used \(1000\) time steps of \(\Delta t = 0.001\,{\text{s}}\) for the quasi-static viscoelastic analysis. As one can see, using the polymer actual constants, the analyzed time of Fig. 13b is large to show the viscous relaxation, thus we introduce two other viscosity values to see the sensitivity of parameters. One should note that the adopted analyzed time is based on the dynamic analysis performed as follows.

  • (iii) Sandwich dynamic

Considering the steel density \(\rho_{{{\text{steel}}}} = 7000\,{\text{kg/m}}^{{3}}\) and the polypropylene density \(\rho_{{{\text{pol}}}} = 910\,{\text{kg/m}}^{{3}}\), we perform a dynamic analysis considering the same instantaneous load of the previous cases. At Fig. 14, the central displacement along time is compared with the static elastic result of case (ii). We used 2000 time steps of \(\Delta t = 0.001\,{\text{s}}\). As one can see, the original value of the viscoelastic shear modulus (\(\overline{G} = 180\,{\text{MPa}}\)) prevents the viscous part of the model to be activated and damping does not occurs. It happens due to the high strain rate imposed in the polypropylene by the structural vibration. Making the viscoelastic shear modulus 100 times larger than the original value, i.e., \(\overline{G} = 18{,}000\,{\text{MPa}}\), we activate the structural damping, as one can see in Fig. 14.

Fig. 14
figure 14

Viscoelastodynamic central displacement for the sandwich plate-damping effect

Full size image

Using the Köner–Lee decomposition and hereditary integrals, reference [1] indicates the occurrence of this material behavior, but solving a quasi-static uniaxial test. An interesting discussion regarding the use of these techniques in dynamic problems is also presented without examples by reference [1]

The above structural behavior, modeled by the proposed formulation, validates the FEM implementation, indicating that the proposed strategy is a good alternative to assemble computational codes. Moreover, it indicates that the proposed framework can be used for further developments of general viscoelastic models.

5.6 Example 5.6 Proposed models verification regarding classical models

After analyzing multiple scenarios using the proposed formulation, it is important to show that results achieved with important classical models can be reproduced by our models. In order to do so, we reproduce the creep problem solved by [60] and [61]. It is the simulation of a cube with lateral length of \(0.1\,{\text{m}}\) subjected to a constant force \(F = 1.737 \times 10^{4} \,{\text{N}}\) suddenly applied in the third direction, see Fig. 3a, i.e., this example is similar to case (a) of Example 5.2.

The constitutive models of references [60] and [61] have different format when compared to our model. In order to be complete, the material constants adopted by reference [60] to solve this problem are: \(\mu_{1} = 0.63\,{\text{MPa}}\), \(\alpha_{1} = 1.3\), \(\mu_{2} = - 0.01\,{\text{MPa}}\), \(\alpha_{2} = - 2\), \(\mu_{3} = 0.0012\,{\text{MPa}}\), \(\alpha_{3} = 5\), \((\mu_{m} )_{1} = 0.63\,{\text{MPa}}\), \((\alpha_{m} )_{1} = 1.3\), \((\mu_{m} )_{2} = - 0.1\,{\text{MPa}}\), \((\alpha_{m} )_{2} = - 2\), \((\mu_{m} )_{3} = 0.0012\,{\text{MPa}}\), \((\alpha_{m} )_{3} = 5\), \(\tau_{1} = 30s\), \(\tau_{2} = 10s\), \(K = 2000\,{\text{MPa}}\) and \(\beta = 1\). Two ways (called FV - quadratic evolution and FLV - linearized evolution) to compute viscosity are used by reference [60]. Readers are invited to consult reference [60] to check the meaning of these elastic and viscous parameters.

To reproduce the results of FV, we adopted model 3.3 with: \(K = 1000\,{\text{MPa}}\), \(G = 0.{584}\,{\text{MPa}}\), \(\overline{G} = 0.8\,{\text{MPa}}\) and \(\eta = 1.9\,{\text{MPa}} \cdot {\text{s}}\). To reproduce the results of FLV, we adopted model 3.5 with: \(K = 1000\,{\text{MPa}}\), \(G = 0.{584}\,{\text{MPa}}\), \(\overline{G} = 0.8\,{\text{MPa}}\) and \(\eta = 1.9\,{\text{MPa}} \cdot {\text{s}}\), \(\upsilon = 1.9\,{\text{MPa}}\), \(\ell = 0.5\) and \(rv = 1.0\, \times \,10^{ - 7} \,{\text{s}}^{ - 2}\). In Fig. 15a, we reproduce the Cauchy stress behavior over time and one can see that results agree very well with reference [60]. In Fig. 15b, we compare the stretch behavior over time and also very good results are achieved. For all situations, we used a time step of \(\Delta t = 0.1s\) and the discretization presented in Fig. 3b.

Fig. 15
figure 15

Comparison of the proposed models results and classical formulationss

Full size image

6 Conclusions

In this study, we present some alternative large strain viscoelastic models with and without instantaneous response. These models are based on the Flory’s multiplicative decomposition that separates elastic volumetric and viscoelastic isochoric responses. The developed constitutive models are used in computational mechanics (finite elements) and finite differences are employed to calculate their time evolution. This approach simplifies the definition of the algorithmic tangent viscoelastic constitutive tensor. One of the models (Zener-like model that uses the time rate of isochoric strain components) is extended to consider strain rate-dependent viscosity. Specific numerical examples are used to show that the proposed framework prevents the manifestation of volumetric changes in purely distortional viscoelastic situations and vice versa. Calibration of real material with rate-dependent viscosity is successfully carried out demonstrating the practical possibilities of the proposed models. A simulation of a dynamic composite structure demonstrates that the computational implementations are correct and confirm how viscoelastic materials with instantaneous response (Zener-like model) may not be efficient to promote structural damping. For future developments, we intend to incorporate plasticity and fiber reinforcement into the presented viscoelastic models.