1 Introduction

Hysteretic mechanical systems typically exhibit a complex dynamic behavior characterized by a nonlinear relation between the generalized forces, namely forces, moments, and stress, and the generalized displacements, namely displacements, rotations, and strain. The dynamic behavior of such systems is referred to as rate-dependent (rate-independent) if the response does (not) depend upon the rate of variation, that is, the first time derivative, of the input quantity [22].

In particular, in rate-dependent hysteretic mechanical systems, such a complex dynamic behavior is generally due to viscoelastic and/or thermoelastic effects, whereas in rate-independent hysteretic mechanical systems, it is typically due to plastic deformation mechanisms and/or friction [37]. Experimental tests available in the literature reveal that several mechanical systems may also present both types of hysteretic behaviors [45, 46].

Nonlinear time history analysis is generally performed to accurately evaluate the dynamic response of hysteretic mechanical systems. The accuracy and the computational efficiency of such a structural analysis procedure strongly depend upon a suitable combination of the phenomenological models, adopted to describe the hysteretic behavior, and the time integration method, required to solve the nonlinear equilibrium equations.

For what concerns the modeling of the hysteretic behavior, it is possible to adopt rate-dependent and/or rate-independent phenomenological models. The former (latter) do (not) take into account the rate of variation of the input variable in time. In the literature, such models are classified into four main categories according to the type of equation that needs to be solved to evaluate the output variable: (i) algebraic models [25, 32, 39, 41, 48], (ii) transcendental models [47], (iii) differential models [5, 36, 49, 50], and (iv) integral models [31].

Algebraic rate-dependent models, such as the Seleemah and Constantinou model [41], and differential rate-independent models, such as the Bouc–Wen model [5, 49, 50] or its modified versions, are generally employed since they are accurate and adopt a relatively small number of parameters. Unfortunately, the latter are not computationally efficient since they require the numerical solution of a first-order nonlinear ordinary differential equation, typically solved by using multi-steps [38] or Runge–Kutta methods [40], for each time step of a nonlinear time history analysis; in addition, they usually adopt parameters having a not always clear mechanical significance, what prompts the use of sophisticated identification procedures for the parameter estimation [6, 10, 18, 44].

Regarding the numerical solution of the nonlinear equilibrium equations, several time integration methods are available in the literature. Such methods are usually classified into two categories according to the kind of coefficients that characterize the expressions employed for the evaluation of the unknown generalized displacement and velocity vectors at the generic time \(t+\varDelta t\) of the analysis. Specifically, it is possible to distinguish between conventional time integration methods, such as the Newmark’s family of methods [33], and structure-dependent time integration methods, such as the Chang’s families of methods [14, 15]. In the former, the coefficients that appear in the expressions of the generalized displacement and velocity vectors are scalar parameters, whereas, in the latter, the above-mentioned coefficients can be scalar parameters or matrices that may depend on the time step \(\varDelta t\) and on the initial properties of the hysteretic mechanical system, namely the generalized mass matrix and the initial generalized tangent damping and stiffness matrices [12, 19, 26, 27].

Implicit unconditionally stable conventional time integration methods, such as the Newmark’s constant average acceleration method [13], are currently the most widely used methods to perform nonlinear time history analyses of hysteretic mechanical systems since they allow for the use of a relatively large time step, the accuracy being the only requirement to fulfill [4]; unfortunately, such methods are not computationally efficient and may suffer from convergence issues since they need to be employed in conjunction with an iterative procedure, such as the Newton–Raphson method or the pseudo-force method [20].

Aim of this paper is to illustrate an accurate and computationally efficient procedure for carrying out nonlinear time history analyses of hysteretic mechanical systems that exhibit rate-dependent and kinematic hardening non-stiffening rate-independent hysteretic behavior. In particular, the proposed computational strategy combines a novel rate-independent phenomenological model and an explicit structure-dependent time integration method.

The developed rate-independent model, belonging to the class of uniaxial models recently formulated by Vaiana et al. [47], is able to simulate generalized rate-independent force–displacement hysteresis loops, bounded between two parallel straight lines, affected neither by cyclic loading phenomena, nor by stiffening behaviors [7, 24, 28, 35, 42, 43, 52].

The proposed model is of algebraic nature since the generalized rate-independent hysteretic force, representing the output variable of the model, is computed by solving an algebraic equation. Compared to differential models, typically employed for simulating the rate-independent behavior of hysteretic mechanical systems, the developed one does not need the numerical solution of a first-order nonlinear ordinary differential equation at each time step of the analysis for the evaluation of the generalized rate-independent hysteretic force; furthermore, it is based on a set of only three parameters having a clear mechanical significance, and it can be easily implemented in a computer program.

The selected time integration method suitably extends to hysteretic systems the Chang’s family of explicit structure-dependent methods, originally formulated for elastic systems [15]. The proposed method is shown to exhibit excellent accuracy and stability properties. Indeed, it is unconditionally stable for all non-stiffening hysteretic mechanical systems, has a second-order accuracy, does not suffer from numerical damping, and displays a small relative period error for small time step. Compared to implicit unconditionally stable conventional time integration methods, currently adopted for the analysis of hysteretic mechanical systems, the proposed one does not require iterative procedures and, consequently, does not suffer from convergence issues.

The present paper is organized into four parts. For the reader’s convenience, in the first part (Sect. 2), the nonlinear equilibrium equations of a hysteretic mechanical system are formulated; subsequently, a conventional computational strategy, combining some of the most employed phenomenological models with a widely used conventional time integration method, is briefly illustrated and the key issues affecting its efficiency are emphasized.

In the second part (Sect. 3), the class of uniaxial phenomenological models formulated by Vaiana et al. [47] is first summarized in order to develop the novel rate-independent model; then, the formulation as well as the implementation details of the proposed model are illustrated.

Similarly, in the third part (Sect. 4), the Chang’s family of explicit methods [15] is first summarized in order to select the most suitable explicit time integration method; then, the formulation as well as the implementation details of the proposed method are presented.

Finally, in the fourth part (Sect. 5), the results of several nonlinear time history analyses, carried out on different hysteretic mechanical systems, are illustrated in order to show the accuracy of the proposed procedure as well as its capability to significantly decrease the computational burden of the analyses.

For notational convenience, we shall make use of several acronyms that are summarized in “Appendix”.

2 A typical solution strategy for hysteretic systems

Hysteretic mechanical systems generally exhibit a dynamic behavior characterized by a nonlinear relation between the generalized forces and the generalized displacements. Specifically, hysteretic mechanical systems display a rate-dependent (rate-independent) hysteretic behavior if the response does (not) depend on the rate of variation, namely the first time derivative, of the input quantity [22].

Rate-dependent hysteretic behavior is typically due to viscoelastic and/or thermoelastic effects; on the contrary, rate-independent hysteretic behavior is generally associated with plastic deformation mechanisms and/or friction [37]. It is important to observe that several mechanical systems may present both types of hysteretic behaviors at the same time [45, 46].

For the reader’s convenience, the nonlinear equilibrium equations of a hysteretic mechanical system are first formulated. Subsequently, a typical solution strategy, frequently exploited to address the dynamic behavior of hysteretic mechanical systems, is presented; it combines some of the most diffused phenomenological models with a widely used time integration method that we shall refer to as conventional to distinguish it from the proposed one. In particular, for both of them we shall emphasize the key issues that strongly affect the efficiency of the overall computational strategy.

The proposed alternative to the existing approaches for the modeling of hysteretic behaviors, on one side, and for solving the nonlinear equilibrium equations, on the other one, will be discussed in Sects. 3 and 4, respectively.

2.1 Nonlinear equilibrium equations

Let us briefly introduce the equations of motion of a Multi-Degree-Of-Freedom (MDOF) hysteretic mechanical system, exhibiting both types of hysteretic behaviors. Denoting by \(\mathbf{u }\), \(\dot{\mathbf{u }}\), and \(\ddot{\mathbf{u }}\) the generalized displacement, velocity, and acceleration vectors, respectively, and by \(\mathbf{p }(t)\) the generalized external force vector depending on time t, the equations of motion can be defined by means of d’Alembert’s principle as the equilibrium between generalized forces vectors:

$$\begin{aligned} \mathbf{f }_\mathrm{i}(t)+\mathbf{f }_\mathrm{rd}(t)+\mathbf{f }_\mathrm{ri}(t)+\mathbf{f }_\mathrm{e}(t)=\mathbf{p }(t), \end{aligned}$$
(1)

in which \(\mathbf{f }_\mathrm{i}(t)\) represents the generalized inertia force, \(\mathbf{f }_\mathrm{rd}(t)\) the generalized rate-dependent hysteretic force, \(\mathbf{f }_\mathrm{ri}(t)\) the generalized rate-independent hysteretic force, and \(\mathbf{f }_\mathrm{e}(t)\) the generalized elastic force.

The generalized inertia force vector \(\mathbf{f }_\mathrm{i}(t)\) is related to the generalized acceleration vector \(\ddot{\mathbf{u }}\) by the following equation:

$$\begin{aligned} \mathbf{f }_\mathrm{i}(t)=\mathbf{M }\ddot{\mathbf{u }}(t), \end{aligned}$$
(2)

where \(\mathbf{M }\) is the mass matrix of the mechanical system, usually assumed to be constant.

The generalized rate-dependent hysteretic force \(\mathbf{f }_\mathrm{rd}(t)\) and elastic force \(\mathbf{f }_\mathrm{e}(t)\) vectors can be expressed as the sum of linear and nonlinear components:

$$\begin{aligned}&\mathbf{f }_\mathrm{rd}(t)=\mathbf{C }\dot{\mathbf{u }}(t)+\mathbf{f }_\mathrm{rdn}(t), \end{aligned}$$
(3)
$$\begin{aligned}&\mathbf{f }_\mathrm{e}(t)=\mathbf{K }\mathbf{u }(t)+\mathbf{f }_\mathrm{en}(t), \end{aligned}$$
(4)

where the matrices \(\mathbf{C }\) and \(\mathbf{K }\) are the generalized constant damping and elastic stiffness matrices, whereas \(\mathbf{f }_\mathrm{rdn}(t)\) and \(\mathbf{f }_\mathrm{en}(t)\) are the nonlinear components of the generalized rate-dependent hysteretic force \(\mathbf{f }_\mathrm{rd}(t)\) and elastic force \(\mathbf{f }_\mathrm{e}(t)\) vectors, respectively.

Thus, using Eqs. (2), (3), and (4), Eq. (1) becomes:

$$\begin{aligned} \mathbf{M }\ddot{\mathbf{u }}(t)+\mathbf{C }\dot{\mathbf{u }}(t)+\mathbf{K }\mathbf{u }(t)+\mathbf{f }_\mathrm{rdn}(t)+\mathbf{f }_\mathrm{ri}(t)+\mathbf{f }_\mathrm{en}(t)=\mathbf{p }(t). \end{aligned}$$
(5)

Mathematically, Eq. (5) represents a system of coupled nonlinear Ordinary Differential Equations (ODEs) of the second order in time that must be numerically solved by adopting a suitable time integration method. Actually, closed-form solutions are only possible for linear ODEs with analytically described external forces [51]. The initial conditions required to numerically integrate Eq. (5) are assumed to be \(\mathbf{u }(0)=\mathbf{d }_{0}\) and \(\dot{\mathbf{u }}(0)=\mathbf{v }_{0}\), where \(\mathbf{d }_{0}\) and \(\mathbf{v }_{0}\) are, respectively, the generalized displacement and velocity vectors of the hysteretic mechanical system defined at the beginning of the analysis.

Fig. 1
figure 1

An example of generalized rate-dependent hysteretic forces, plotted versus displacement (a) and velocity (b), generally modeled by employing the Seleemah and Constantinou model

Full size image
Fig. 2
figure 2

An example of generalized rate-independent hysteretic forces, plotted versus displacement, generally modeled by employing the BWM (a) and the MBWM (b)

Full size image

2.2 Phenomenological models

A large number of rate-dependent and rate-independent phenomenological models have been proposed in the literature to simulate the dynamic behavior of hysteretic mechanical systems [22].

According to the type of equation that needs to be solved to evaluate the output variable, existing rate-dependent and rate-independent phenomenological models can be classified into four main categories: (i) algebraic models, (ii) transcendental models, (iii) differential models, and (iv) integral models.

In the following, we briefly describe an algebraic rate-dependent model and two differential rate-independent models, widely used to simulate, respectively, the typical rate-dependent and kinematic hardening non-stiffening rate-independent hysteretic behaviors, that are of specific interest in this work.

2.2.1 Rate-dependent model

Let \(f_\mathrm{rd}(t)\) denote a generic component of the vector \(\mathbf{f }_\mathrm{rd}(t)\) in Eq. (3). An expression of its nonlinear part \(f_\mathrm{rdn}(t)\) can be obtained by adopting the widely used algebraic rate-dependent model proposed by Seleemah and Constantinou [41]:

$$\begin{aligned} f_\mathrm{rdn}(t)=c_{n}\left| {\dot{u}}(t)\right| ^{q}\mathrm{sgn}[{\dot{u}}(t)], \end{aligned}$$
(6)

where \(c_{n}\) is the generalized damping coefficient and q is an exponent whose value defines the shape of the generalized rate-dependent force–displacement hysteresis loop.

Figure 1a (b) presents an example of generalized rate-dependent hysteretic forces, plotted versus the generalized displacement (velocity), generally modeled by employing the above-described Seleemah and Constantinou model.

In particular, Fig. 1 shows that the shape of the generalized rate-dependent force–displacement hysteresis loop, obtained by applying a generalized harmonic displacement, is an ellipse if the relation between \(f_\mathrm{rd}\) and \({\dot{u}}\) is linear; on the contrary, the shape of the hysteresis loop becomes the blue (red) one if the relation between \(f_\mathrm{rd}\) and \({\dot{u}}\) is nonlinear and the first derivative of \(f_\mathrm{rd}\) with respect to \({\dot{u}}\) increases (decreases) with increasing generalized velocity.

2.2.2 Rate-independent models

One of the most widespread rate-independent models is the celebrated differential Bouc–Wen Model (BWM) [5, 49, 50] whose flexibility in modeling a large variety of hysteretic behaviors has fostered several improvements and extensions over years [1,2,3, 8, 9, 11, 23, 29, 30, 34].

Let \(f_\mathrm{ri}(t)\) denote a generic component of the vector \(\mathbf{f }_\mathrm{ri}(t)\). An expression of the generalized rate-independent hysteretic force \(f_\mathrm{ri}(t)\), for the case of hysteresis due to plastic deformation mechanisms, can be defined by employing the above-mentioned BWM:

$$\begin{aligned} f_{ri}(t)= aku(t)+\left( 1-a\right) kdz(t), \end{aligned}$$
(7)

where \(a\in \left( 0,1\right) \) is a dimensionless parameter, \(k>0\) and \(d>0\) are parameters having dimension of generalized stiffness and displacement, respectively, and z(t) is a dimensionless variable obtained by solving the following first-order nonlinear ODE:

$$\begin{aligned} {\dot{z}}(t)= & {} d^{-1}\left[ A{\dot{u}}(t)-b\left| {\dot{u}}(t)\right| z(t)\left| z(t)\right| ^{e-1}\right. \nonumber \\&\quad \left. -c{\dot{u}}(t)\left| z(t)\right| ^{e}\right] , \end{aligned}$$
(8)

where e is a positive number, and A, b, and c are scalars.

A Modified Bouc–Wen Model (MBWM), proposed by Constantinou et al. [21], is often used to express the generalized rate-independent hysteretic force \(f_\mathrm{ri}(t)\) for the case of friction-based hysteresis:

$$\begin{aligned} f_\mathrm{ri}(t)= \mu _{s}Nz(t), \end{aligned}$$
(9)

where \(\mu _{s}\) is the generalized friction coefficient, N is the generalized axial force, and z(t) is the dimensionless variable obtained by solving Eq. (8).

Figure 2a (b) presents an example of generalized rate-independent hysteretic force, plotted versus the generalized displacement, typical of mechanical systems with kinematic hardening non-stiffening rate-independent hysteretic behavior due to plastic deformation mechanisms (friction), generally modeled by employing the above-described BWM (MBWM).

In particular, Fig. 2 shows that the generalized rate-independent force–displacement hysteresis loops, obtained by applying a generalized harmonic displacement, are bounded between two parallel straight lines that are affected neither by cyclic loading phenomena, nor by stiffening behaviors.

It is important to note that the above-described differential models are not computationally efficient since they require the numerical solution of Eq. (8), typically solved by using multi-steps [38] or Runge–Kutta methods [40], for each time step of a nonlinear time history analysis.

2.3 Conventional time integration method

The system of coupled nonlinear ODEs, governing the dynamic response of a MDOF hysteretic mechanical system, can be conveniently expressed at the generic time \(t+\varDelta t\) as:

$$\begin{aligned} \begin{aligned}&\mathbf{M }\ddot{\mathbf{u }}(t+\varDelta t)+\mathbf{C }\dot{\mathbf{u }}(t+\varDelta t)+\mathbf{K }\mathbf{u }(t+\varDelta t)\\&\quad +\mathbf{f }_\mathrm{rdn}(t+\varDelta t)+\mathbf{f }_\mathrm{ri}(t+\varDelta t)\\&\quad +\mathbf{f }_\mathrm{en}(t+\varDelta t)=\mathbf{p }(t+\varDelta t), \end{aligned} \end{aligned}$$
(10)

where \(\varDelta t\) is the time step of a Nonlinear Time History Analysis (NLTHA).

Equation (10) can be numerically solved by adopting a time integration method, that is generally obtained by supplementing the equations of motion with two difference equations for the evaluation of the unknown generalized displacement and velocity vectors. Specifically, the general formulation of a family of time integration methods can be expressed as:

$$\begin{aligned}&\mathbf{M }\mathbf{a }_{i+1}{+}\mathbf{C }\mathbf{v }_{i+1}{+}\mathbf{K }\mathbf{d }_{i+1} {+}(\tilde{\mathbf{f }}_\mathrm{rdn})_{i+1}{+}(\tilde{\mathbf{f }}_\mathrm{ri})_{i+1}\nonumber \\&\quad +(\tilde{\mathbf{f }}_\mathrm{en})_{i+1}{=}\mathbf{p }_{i+1}, \end{aligned}$$
(11a)
$$\begin{aligned}&\mathbf{d }_{i+1}{=}\mathbf{d }_{i}{+}\mathbf{A }_{1}\varDelta t\mathbf{v }_{i}{+}\mathbf{A }_{2}(\varDelta t)^{2}\mathbf{a }_{i}{+}\mathbf{A }_{3}(\varDelta t)^{2}\mathbf{a }_{i+1}{+}\mathbf{q }_{i+1}, \end{aligned}$$
(11b)
$$\begin{aligned}&\mathbf{v }_{i+1}=\mathbf{v }_{i}+\mathbf{B }_{1}\varDelta t\mathbf{a }_{i}+\mathbf{B }_{2}\varDelta t\mathbf{a }_{i+1}+\mathbf{r }_{i+1}, \end{aligned}$$
(11c)

where \(\mathbf{d }_{i+1}\), \(\mathbf{v }_{i+1}\), and \(\mathbf{a }_{i+1}\) are approximate estimates of the generalized displacement \(\mathbf{u }(t+\varDelta t)\), velocity \(\dot{\mathbf{u }}(t+\varDelta t)\), and acceleration \(\ddot{\mathbf{u }}(t+\varDelta t)\) vectors at the \((i+1)\)th time step, respectively; \((\tilde{\mathbf{f }}_\mathrm{rdn})_{i+1}=\mathbf{f }_\mathrm{rdn}(\mathbf{v }_{i+1})\), \((\tilde{\mathbf{f }}_\mathrm{ri})_{i+1}=\mathbf{f }_\mathrm{ri}(\mathbf{d }_{i+1})\), \((\tilde{\mathbf{f }}_\mathrm{en})_{i+1}=\mathbf{f }_\mathrm{en}(\mathbf{d }_{i+1})\), and \(\mathbf{p }_{i+1}\) are approximate estimates of the generalized nonlinear rate-dependent hysteretic force \(\mathbf{f }_\mathrm{rdn}(t+\varDelta t)\), rate-independent hysteretic force \(\mathbf{f }_\mathrm{ri}(t+\varDelta t)\), nonlinear elastic force \(\mathbf{f }_\mathrm{en}(t+\varDelta t)\), and external force \(\mathbf{p }(t+\varDelta t)\) vectors at the \((i+1)\)th time step, respectively. The matrices \(\mathbf{A }_{1}\), \(\mathbf{A }_{2}\), \(\mathbf{A }_{3}\), as well as \(\mathbf{B }_{1}\), \(\mathbf{B }_{2}\) are coefficient matrices that define a specific family of time integration methods, whereas \(\mathbf{q }_{i+1}\) and \(\mathbf{r }_{i+1}\) are load-dependent vectors, namely vectors that are functions of the external force vector, introduced to eliminate the unusual amplitude growth that occurs in the steady-state response of a high frequency mode when structure-dependent methods are employed in forced vibration problems [16, 17].

In conventional time integration methods, such as the Newmark’s family of methods [33], all the coefficient matrices become scalar quantities, that is, \(A_{1}\), \(A_{2}\), \(A_{3}\), \(B_{1}\), and \(B_{2}\), and both the load-dependent vectors become zero vectors, that is, \(\mathbf{q }_{i+1}=\mathbf{r }_{i+1}=\mathbf{0 }\).

For the case of structure-dependent time integration methods, such as the Chang’s families of methods [14, 15], only some of the coefficient matrices become scalars; moreover, some of them are functions of the time step \(\varDelta t\) and of the initial properties of the system, namely the mass matrix \(\mathbf{M }\), and the initial generalized tangent damping \(\mathbf{C }_{0}\) and stiffness \(\mathbf{K }_{0}\) matrices.

One of the widely used methods employed to perform NLTHAs of hysteretic mechanical systems is the Newmark’s constant Average Acceleration Method (AAM) [13], whose formulation can be obtained by setting \(A_{1}=1\), \(A_{2}=A_{3}=1/4\), \(B_{1}=B_{2}=1/2\), and \(\mathbf{q }_{i+1}=\mathbf{r }_{i+1}=\mathbf{0 }\) in Eq. (11).

Such an implicit unconditionally stable conventional time integration method allows for the use of a relatively large time step, the accuracy being the only requirement to fulfill [4]; unfortunately, it is not computationally efficient and may suffer from convergence issues since it needs to be employed in conjunction with an iterative procedure, such as the Newton–Raphson method or the pseudo-force method [20].

3 Proposed rate-independent model

The computational efficiency of the solution strategy described in Sect. 2 is substantially hampered by the need of solving, at each time step, the first-order nonlinear ODE associated with the BWM or its modified version. For this reason, we develop a novel accurate and computationally efficient hysteretic model able to reproduce non-stiffening rate-independent hysteretic behaviors characterized by kinematic hardening. It represents a particular instance of the more general Class of Hysteretic Models (CHMs) recently proposed by Vaiana et al. [47]. Thus, after a brief review of this general class, the formulation and the implementation details of the Proposed Hysteretic Model (PHM) are illustrated.

3.1 Review of a class of hysteretic models

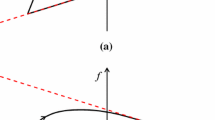
In the class of uniaxial phenomenological models developed by Vaiana et al. [47], the generalized displacement u (generalized rate-independent hysteretic force \(f_\mathrm{ri}\)) is assumed to be the input (output) variable, and a generalized rate-independent force–displacement hysteresis loop is described by means of four types of curves, that is, the upper \(c_\mathrm{u}\) and the lower \(c_\mathrm{l}\) limiting curves and the generic loading \(c^{+}\) and unloading \(c^{-}\) curves.

Figure 3 illustrates the four curves for a hysteresis loop bounded by two parallel straight lines, that is of particular interest in this work. The generic loading (unloading) curve, defined by a positive (negative) sign of the generalized velocity \({\dot{u}}\), is identified by an arrow plotted on the curve.

Fig. 3
figure 3

Curves \(c_\mathrm{u}\), \(c_\mathrm{l}\), \(c^{+}\), and \(c^{-}\) for a hysteresis loop bounded by two parallel straight lines

Full size image

As shown in Fig. 3, the upper (lower) limiting curve \(c_\mathrm{u}\) (\(c_\mathrm{l}\)) intercepts the vertical axis at \(f_\mathrm{ri}={\bar{f}}\) (\(f_\mathrm{ri}=-{\bar{f}}\)). Furthermore, the generic loading (unloading) curve has a starting point, lying on the lower (upper) limiting curve, having abscissa \(u^{+}_{i}\) (\(u^{-}_{i}\)) and an ending point, lying on the upper (lower) limiting curve, having abscissa \(u^{+}_{j}\) (\(u^{-}_{j}\)), being \(u^{+}_{i}=u^{+}_{j}-2u_{0}\) (\(u^{-}_{i}=u^{-}_{j}+2u_{0}\)).

The generalized tangent stiffness \(k_\mathrm{t}\) is described by means of a general expression that, for the generic loading case (\({\dot{u}}>0\)), is:

$$\begin{aligned} k_\mathrm{t}\left( u,u^{+}_{j}\right) =k_\mathrm{e}\left( u\right) +k_{h}\left( u,u^{+}_{j}\right) , \end{aligned}$$
(12)

whereas, for the generic unloading case (\({\dot{u}}<0\)), becomes:

$$\begin{aligned} k_\mathrm{t}\left( u,u^{-}_{j}\right) =k_\mathrm{e}\left( u\right) +k_{h}\left( u,u^{-}_{j}\right) . \end{aligned}$$
(13)

In the previous formulas, \(k_\mathrm{e}\) is a function of u, whereas \(k_{h}\) is a function of a relative generalized displacement evaluated by relating u to \(u^{+}_{j}\) (\(u^{-}_{j}\)).

Figure 4a (b) presents the graph of function \(k_\mathrm{t}(u,u^{+}_{j})\) (\(k_\mathrm{t}(u,u^{-}_{j})\)), namely the generalized tangent stiffness of the upper (lower) limiting curve \(c_\mathrm{u}\) (\(c_\mathrm{l}\)) and of the generic loading (unloading) curve \(c^{+}\) (\(c^{-}\)) of Fig. 3. It can be observed that, assuming \(k_\mathrm{e}(u)=0\), \(k_\mathrm{t}(u,u^{+}_{j})\) (\(k_\mathrm{t}(u,u^{-}_{j})\)) nonlinearly decreases from \(k_{a}\) to \(k_{b}\), on \([u^{+}_{j}-2u_{0}, u^{+}_{j}]\) (\([u^{-}_{j}, u^{-}_{j}+2u_{0}]\)), whereas it is constant and equal to \(k_{b}\) on \([u^{+}_{j},\infty )\) (\((-\infty ,u^{-}_{j}]\)).

Fig. 4
figure 4

Graph of \(k_\mathrm{t}\) for the generic loading (a) and unloading (b) cases in Fig. 3

Full size image

Similarly, the generalized rate-independent hysteretic force \(f_\mathrm{ri}\) is defined by a general expression that, for the generic loading case (\({\dot{u}}>0\)), is:

figure a

whereas, for a generic unloading case (\({\dot{u}}<0\)), becomes:

figure b

The general expressions of the upper (lower) limiting curve and of the generic loading (unloading) curve are derived by integrating the expression of the generalized tangent stiffness \(k_\mathrm{t}\), Eq. (12) (Eq. (13)). Specifically, as described in detail in [47], the general expressions of the upper and lower limiting curves are:

$$\begin{aligned}&c_\mathrm{u}\left( u\right) =f_\mathrm{e}\left( u\right) +k_{b}u+{\bar{f}}, \end{aligned}$$
(16)
$$\begin{aligned}&c_\mathrm{l}\left( u\right) =f_\mathrm{e}\left( u\right) +k_{b}u-{\bar{f}}, \end{aligned}$$
(17)

being:

$$\begin{aligned} f_\mathrm{e}\left( u\right) =\int k_\mathrm{e}\left( u\right) \mathrm{d}u, \end{aligned}$$
(18)

whereas the general expressions of the generic loading and unloading curves are:

$$\begin{aligned}&c^{+}\left( u,u^{+}_{j}\right) =f_\mathrm{e}\left( u\right) +f_{h}\left( u,u^{+}_{j}\right) +k_{b}u^{+}_{j}\nonumber \\&\quad +{\bar{f}}-f_{h}\left( u^{+}_{j},u^{+}_{j}\right) , \end{aligned}$$
(19)
$$\begin{aligned}&c^{-}\left( u,u^{-}_{j}\right) =f_\mathrm{e}\left( u\right) +f_{h}\left( u,u^{-}_{j}\right) +k_{b}u^{-}_{j}\nonumber \\&\quad -{\bar{f}}-f_{h}\left( u^{-}_{j},u^{-}_{j}\right) , \end{aligned}$$
(20)

being:

$$\begin{aligned} f_{h}\left( u,u^{+}_{j}\right) =\int k_{h}\left( u,u^{+}_{j}\right) \mathrm{d}u, \end{aligned}$$
(21)

and

$$\begin{aligned} f_{h}\left( u,u^{-}_{j}\right) =\int k_{h}\left( u,u^{-}_{j}\right) \mathrm{d}u. \end{aligned}$$
(22)

The model parameters \({\bar{f}}\) and \(u_{0}\) are related by the following general expression:

$$\begin{aligned} f_{h}\left( u^{+}_{j}-2u_{0},u^{+}_{j}\right) +2k_{b}u_{0}+2{\bar{f}}-f_{h}\left( u^{+}_{j},u^{+}_{j}\right) =0, \end{aligned}$$
(23)

that can be solved for \({\bar{f}}\) or \(u_{0}\), in closed form or numerically depending on the complexity of the function \(f_{h}\).

Finally, the history variable is evaluated by a general expression that, for the generic loading case (\({\dot{u}}>0\)), is:

$$\begin{aligned} f_\mathrm{e}\left( u_{P}\right) {+}f_{h}\left( u_{P},u^{+}_{j}\right) {+}k_{b}u^{+}_{j}{+}{\bar{f}}{-}f_{h}\left( u^{+}_{j},u^{+}_{j}\right) {=}f_{P}, \end{aligned}$$
(24)

whereas, for the generic unloading case (\({\dot{u}}<0\)), becomes:

$$\begin{aligned} f_\mathrm{e}\left( u_{P}\right) +f_{h}\left( u_{P},u^{-}_{j}\right) +k_{b}u^{-}_{j}-{\bar{f}}-f_{h}\left( u^{-}_{j},u^{-}_{j}\right) =f_{P}, \end{aligned}$$
(25)

where \(u_{P}\) and \(f_{P}\) are the coordinates of a generic point P that lies between the two limiting curves.

Equations (24) and (25) can be solved for \(u^{+}_{j}\) and \(u^{-}_{j}\), respectively, in closed form or numerically depending on the complexity of the function \(f_{h}\).

3.2 Proposed hysteretic model

In this subsection, we first develop the PHM, that is a specific instance of the above-described CHMs proposed by Vaiana et al. [47]. Subsequently, we demonstrate its ability to reproduce hysteresis loops limited by two parallel straight lines, typical of kinematic hardening non-stiffening rate-independent hysteretic behaviors, by employing a set of only three parameters and we examine the influence of each model parameter on the hysteresis loop size. Finally, we present the implementation scheme of the model, useful for computer implementation.

3.2.1 Development of the model

To develop the model, we first select the generalized tangent stiffness functions, that is, \(k_\mathrm{e}\) and \(k_{h}\); then, we analytically derive the expressions of the generalized rate-independent hysteretic force and of the history variable.

Generalized tangent stiffness

The proposed generalized tangent stiffness functions are:

$$\begin{aligned} k_\mathrm{e}\left( u\right) =0 \qquad \qquad \mathrm {on} \;\left( -\infty ,\infty \right) , \end{aligned}$$
(26)
figure c

where \(k_{a}>k_{b}\), \(k_{a}>0\), \(\gamma >0\), \(\gamma \ne 1\), \({\bar{u}}=1\), \(u_{0}>0\). In particular, \(k_{a}\), \(k_{b}\), and \(\gamma \) are model parameters to be calibrated by using experimental data, \({\bar{u}}\) is a model parameter adopted to non-dimensionalize the denominator in Eqs. (27a) and (28a), whereas \(u_{0}\) is a model parameter evaluated as a function of \(k_{a}\), \(k_{b}\), and \(\gamma \), as demonstrated in the following.

Fig. 5
figure 5

Graph of \(k_{h}\) for the generic loading case

Full size image

The selected \(k_{h}\) is a function that nonlinearly decreases, from \(k_{a}\) to \(k_{b}+(k_{a}-k_{b})\left( 1+2u_{0}\right) ^{-\gamma }\), on \([u^{+}_{j}-2 u_{0}, u^{+}_{j}[\), when \({\dot{u}}>0\), and on \(]u^{-}_{j}, u^{-}_{j}+2 u_{0}]\), when \({\dot{u}}<0\); moreover, \(k_{h}\) is constant and equal to \(k_{b}\) on \(]u^{+}_{j},\infty )\), when \({\dot{u}}>0\), and on \((-\infty ,u^{-}_{j}[\), when \({\dot{u}}<0\). The parameter \(\gamma \) rules the velocity of variation of \(k_{h}\), from \(k_{a}\) to \(k_{b}+(k_{a}-k_{b})\left( 1+2u_{0}\right) ^{-\gamma }\), as illustrated in Fig. 5 for the generic loading case (\({\dot{u}}>0\)). The graph of \(k_{h}\) for the generic unloading case (\({\dot{u}}<0\)) is not illustrated for brevity.

In order to derive the expression of the internal model parameter \(u_{0}\) and show that it can be evaluated as a function of the parameters \(k_{a}\), \(k_{b}\), and \(\gamma \), we observe that \(k_{h}\) is discontinuous at \(u^{+}_{j}\) (\(u^{-}_{j}\)), as shown in Fig. 5 for the generic loading case. Thus, if we denote by \(\delta _{k}\) the difference between the two different values of \(k_{h}\) at \(u^{+}_{j}\) (\(u^{-}_{j}\)), we can write:

$$\begin{aligned} \frac{k_{a}-k_{b}}{\left( 1+2u_{0}\right) ^{\gamma }}=\delta _{k}, \end{aligned}$$
(29)

from which we obtain:

$$\begin{aligned} u_{0}=\frac{1}{2}\left[ \left( \frac{k_{a}-k_{b}}{\delta _{k}}\right) ^{\frac{1}{\gamma }}-1\right] , \end{aligned}$$
(30)

that is an expression giving positive values of \(u_{0}\) for \(0<\delta _{k}<k_{a}-k_{b}\). In order to have a generic loading (unloading) curve \(c^{+}\) (\(c^{-}\)) that smoothly approaches the upper (lower) limiting curve \(c_\mathrm{u}\) (\(c_\mathrm{l}\)), that is, with a generalized tangent stiffness at \(u^{+}_{j}\) (\(u^{-}_{j}\)) very close to the one of the upper (lower) limiting curve \(c_\mathrm{u}\) (\(c_\mathrm{l}\)), we set \(\delta _{k}\) equal to \(10^{-20}\) in Eq. (30). The choice of such a value has been assumed for purely numerical reasons.

Generalized rate-independent hysteretic force

According to the general formulation described in 3.1, the evaluation of the generalized rate-independent hysteretic force \(f_\mathrm{ri}\), for the generic loading (unloading) case, requires the derivation of the expressions for the upper (lower) limiting curve \(c_\mathrm{u}\) (\(c_\mathrm{l}\)) and for the generic loading (unloading) curve \(c^{+}\) (\(c^{-}\)).

As regards the upper and lower limiting curves, on account of the definition (18) and of the assumption (26), we have:

$$\begin{aligned} f_\mathrm{e}\left( u\right) =0. \end{aligned}$$
(31)

Hence, Eq. (16) specializes to:

$$\begin{aligned} c_\mathrm{u}\left( u\right) =k_{b}u+{\bar{f}}, \end{aligned}$$
(32)

whereas Eq. (17) provides:

$$\begin{aligned} c_\mathrm{l}\left( u\right) =k_{b}u-{\bar{f}}. \end{aligned}$$
(33)

As far as the generic loading and unloading curves are concerned, on account of the assumption (27a), Eq. (21) specializes to:

$$\begin{aligned}&f_{h}\left( u,u^{+}_{j}\right) =k_{b}u+\left( k_{a}-k_{b}\right) \nonumber \\&\quad \times \frac{\left( 1+u-u^{+}_{j}+2u_{0}\right) ^{\left( 1-\gamma \right) }}{1-\gamma }, \end{aligned}$$
(34)

so that, recalling (31), Eq. (19) yields:

(35)

Similarly, on account of the assumption (28a), Eq. (22) specializes to:

$$\begin{aligned}&f_{h}\left( u,u^{-}_{j}\right) =k_{b}u+\left( k_{a}-k_{b}\right) \nonumber \\&\quad \times \frac{\left( 1-u+u^{-}_{j}+2u_{0}\right) ^{\left( 1-\gamma \right) }}{\gamma -1}, \end{aligned}$$
(36)

so that, recalling (31), Eq. (20) yields:

(37)

In order to derive the expression of the internal model parameter \({\bar{f}}\), required to compute \(c_\mathrm{u}\), \(c_\mathrm{l}\), \(c^{+}\), and \(c^{-}\), we exploit Eq. (23). Thus, adopting (34), the former equation becomes:

$$\begin{aligned} \begin{aligned}&k_{b}\left( u^{+}_{j}-2u_{0}\right) +\frac{\left( k_{a}-k_{b}\right) }{1-\gamma }+2k_{b}u_{0}+2{\bar{f}}-k_{b}u^{+}_{j}\\&\quad -\left( k_{a}-k_{b}\right) \frac{\left( 1+2u_{0}\right) ^{\left( 1-\gamma \right) }}{1-\gamma }=0, \end{aligned} \end{aligned}$$
(38)

from which we obtain:

$$\begin{aligned} {\bar{f}}=\frac{k_{a}-k_{b}}{2}\left[ \frac{\left( 1+2u_{0}\right) ^{\left( 1-\gamma \right) }-1}{1-\gamma }\right] . \end{aligned}$$
(39)

Since \(k_{a}>k_{b}\), \(\gamma \ne 1\), and \(u_{0}>0\), Eq. (39) gives a positive value of \({\bar{f}}\).

History variable

Fig. 6
figure 6

Hysteresis loops, simulated by using the PHM parameters listed in Table 1, typically due to plastic deformation mechanisms (a) and friction (b)

Full size image

The expression of the history variable, for the loading case, is derived by invoking (31) and (34), so that Eq. (24) specializes to:

$$\begin{aligned} \begin{aligned}&k_{b}u_{P}+\left( k_{a}-k_{b}\right) \frac{\left( 1+u_{P}-u^{+}_{j}+2u_{0}\right) ^{\left( 1-\gamma \right) }}{1-\gamma }\\&\quad +k_{b}u^{+}_{j}+{\bar{f}}-k_{b}u^{+}_{j}\\&\quad -\left( k_{a}-k_{b}\right) \frac{\left( 1+2u_{0}\right) ^{\left( 1-\gamma \right) }}{1-\gamma }=f_{P}, \end{aligned} \end{aligned}$$
(40)

from which we obtain:

(41)

Similarly, for the unloading case, the expression of the history variable is derived by invoking (31) and (36), so that Eq. (25) specializes to:

$$\begin{aligned} \begin{aligned}&k_{b}u_{P}+\left( k_{a}-k_{b}\right) \frac{\left( 1-u_{P}+u^{-}_{j}+2u_{0}\right) ^{\left( 1-\gamma \right) }}{\gamma -1}\\&\quad +k_{b}u^{-}_{j}-{\bar{f}}-k_{b}u^{-}_{j}\\&\quad -\left( k_{a}-k_{b}\right) \frac{\left( 1+2u_{0}\right) ^{\left( 1-\gamma \right) }}{\gamma -1}=f_{P}, \end{aligned} \end{aligned}$$
(42)

from which we obtain:

$$\begin{aligned} \begin{aligned}&u^{-}_{j}=-1+u_{P}-2u_{0}+\left\{ \frac{\gamma -1}{k_{a}-k_{b}}\left[ f_{P}-k_{b}u_{P}\right. \right. \\&\quad \left. \left. +{\bar{f}}+\left( k_{a}-k_{b}\right) \frac{\left( 1+2u_{0}\right) ^{\left( 1-\gamma \right) }}{\gamma -1}\right] \right\} ^{\left( \frac{1}{1-\gamma }\right) }. \end{aligned} \end{aligned}$$
(43)

3.2.2 Hysteresis loop shape

Figure 6 shows two different generalized rate-independent force–displacement hysteresis loops, bounded by two parallel straight lines, obtained by imposing a sinusoidal generalized displacement, having unit amplitude and frequency, and simulated by using the PHM parameters listed in Table 1. In particular, the hysteresis loop of Fig. 6a (b) is typical of mechanical systems having a kinematic hardening non-stiffening rate-independent hysteretic behavior induced by plastic deformation mechanisms (friction).

Table 1 PHM parameters
Full size table

Figure 7 shows the influence of each PHM parameter on the size of generalized force–displacement hysteresis loops simulated by applying a sinusoidal transverse displacement with unit amplitude and frequency. In particular, the hysteresis loops in Fig. 7a have been reproduced setting \(k_{b}=0.5\), \(\gamma =10\), and adopting three values of \(k_{a}\), that is, 5, 10, and 15. It is evident that the larger is \(k_{a}\), the larger is the size of the hysteresis loop.

Figure 7b (c) illustrates hysteresis loops obtained setting \(k_{a}=10\), \(\gamma =10\), and using three values of \(k_{b}\), that is, 0, 0.5, and 1 (0, \(-\,0.5\), and \(-\,1\)). It is clear that if \(k_{b}\) is increased (decreased), the hysteresis loop rotates counter-clockwise (clockwise) and its size slightly decreases (increases).

Finally, Fig. 7d presents hysteresis loops simulated setting \(k_{a}=10\), \(k_{b}=0.5\), and adopting three values of \(\gamma \), that is, 10, 15, and 20. It is evident that the larger is \(\gamma \), the smaller is the size of the hysteresis loop.

Fig. 7
figure 7

Influence of the PHM parameters on the size of the hysteresis loops

Full size image
Table 2 PHM Algorithm
Full size table

3.2.3 Computer implementation

The implementation scheme of the proposed model is presented in Table 2. Such a schematic flowchart,composed of two parts, called Initial settings and Calculations at each time step, respectively, is based on the assumptions that a hysteretic mechanical system is subjected to a given time-dependent generalized external force and that a displacement-driven solution scheme is employed. In particular, considering a generic time interval \(t_{i}\le t \le t_{i+1} \), the approximate estimates of the generalized displacement, velocity, and rate-independent hysteretic force at time step i, namely \(d_{i}\), \(v_{i}\), and \(({\tilde{f}}_\mathrm{ri})_{i}\), as well as the approximate estimates of the generalized displacement and velocity at time step \(i+1\), namely \(d_{i+1}\) and \(v_{i+1}\), are assumed to be known. On the contrary, the approximate estimate of the generalized rate-independent hysteretic force at time step \(i+1\), namely \(({\tilde{f}}_\mathrm{ri})_{i+1}\), has to be computed taking into account that the history variable \(u_{j}\) needs to be updated if the sign of the generalized velocity, \(s=\mathrm{sgn}(v)\), changes over the generic time interval, that is, if \(s_{i}s_{i+1}<0\).

4 Proposed explicit time integration method

It has been repeatedly emphasized that the phenomenological models and the time integration method are the key issues affecting the efficiency of the strategies typically employed to perform NLTHAs of hysteretic mechanical systems. The first issue has been addressed in the previous section by proposing a novel rate-independent model that avoids, within each time step, the solution of the first-order nonlinear ODE associated with the Bouc–Wen model or its modified version.

The second issue is addressed in this section by proposing an explicit structure-dependent time integration method that belongs to the more general Chang’s Family of Explicit Methods (CFEMs) [15] and extends its range of validity from elastic systems to the hysteretic ones. Thus, after a brief review of this general family, we present the formulation as well as the implementation details of the proposed Chang’s Explicit Method (CEM).

4.1 Review of the Chang’s family of explicit methods

The family of explicit structure-dependent time integration methods developed by Chang [15] can be obtained from Eq. (11) by assuming:

$$\begin{aligned} \mathbf{A }_{1}=\mathbf{1 },\quad \mathbf{A }_{3}=\mathbf{0 },\quad \mathrm {and}\quad \mathbf{B }_{2}=\mathbf{0 }. \end{aligned}$$
(44)

Hence, the formulation of the CFEMs is:

$$\begin{aligned}&\mathbf{M }\mathbf{a }_{i+1}+\mathbf{C }\mathbf{v }_{i+1}+\mathbf{K }\mathbf{d }_{i+1} +(\tilde{\mathbf{f }}_\mathrm{rdn})_{i+1}+(\tilde{\mathbf{f }}_\mathrm{ri})_{i+1}\nonumber \\ {}&+(\tilde{\mathbf{f }}_\mathrm{en})_{i+1}=\mathbf{p }_{i+1},\end{aligned}$$
(45a)
$$\begin{aligned}&\mathbf{d }_{i+1}=\mathbf{d }_{i}+\varDelta t\mathbf{v }_{i}+\mathbf{A }_{2}(\varDelta t)^{2}\mathbf{a }_{i}+\mathbf{q }_{i+1},\end{aligned}$$
(45b)
$$\begin{aligned}&\mathbf{v }_{i+1}=\mathbf{v }_{i}+\mathbf{B }_{1}\varDelta t\mathbf{a }_{i}+\mathbf{r }_{i+1}, \end{aligned}$$
(45c)

where the coefficient matrices \(\mathbf{A }_{2}\) and \(\mathbf{B }_{1}\), assumed to be constant during the complete numerical integration procedure, depend on the time step \(\varDelta t\) and on the initial properties of the analyzed hysteretic mechanical system, that is, \(\mathbf{M }\), \(\mathbf{C }_{0}\), and \(\mathbf{K }_{0}\). Specifically, \(\mathbf{A }_{2}\) and \(\mathbf{B }_{1}\) are evaluated as follows:

$$\begin{aligned}&\mathbf{A }_{2}=\left[ \mathbf{M }+\beta \varDelta t\mathbf{C }_{0}+\alpha (\varDelta t)^{2}\mathbf{K }_{0}\right] ^{-1} \mathbf{M }=\mathbf{S }_{0}^{-1}\mathbf{M }, \end{aligned}$$
(46)
$$\begin{aligned}&\mathbf{B }_{1}=\mathbf{A }_{2}, \end{aligned}$$
(47)

where the scalar parameters \(\alpha \) and \(\beta \) determine the numerical properties (i.e., accuracy and stability) of the algorithm under consideration. The load-dependent vectors \(\mathbf{q }\) and \(\mathbf{r }\) at the \((i+1)\)th time step are defined as:

$$\begin{aligned}&\mathbf{q }_{i+1}=\mathbf{S }_{0}^{-1}\left[ \alpha (\varDelta t)^{2}\left( \mathbf{p }_{i+1}-\mathbf{p }_{i}\right) \right] , \end{aligned}$$
(48)
$$\begin{aligned}&\mathbf{r }_{i+1}=\mathbf{0 }. \end{aligned}$$
(49)

Considering Eqs. (3) and (4), the initial generalized tangent damping \(\mathbf{C }_{0}\) and stiffness \(\mathbf{K }_{0}\) matrices of a hysteretic mechanical system can be computed as follows:

$$\begin{aligned}&\mathbf{C }_{0}=\left. \frac{\partial \mathbf{f }_\mathrm{rd}}{\partial \dot{\mathbf{u }}}\right| _{\mathbf{v }_{0}}=\mathbf{C }+\left. \frac{\partial \mathbf{f }_\mathrm{rdn}}{\partial \dot{\mathbf{u }}}\right| _{\mathbf{v }_{0}}, \end{aligned}$$
(50)
$$\begin{aligned}&\mathbf{K }_{0}=\left. \frac{\partial \mathbf{f }_\mathrm{ri}}{\partial \mathbf{u }}\right| _{\mathbf{d }_{0}}+\left. \frac{\partial \mathbf{f }_\mathrm{e}}{\partial \mathbf{u }}\right| _{\mathbf{d }_{0}}=\left. \frac{\partial \mathbf{f }_\mathrm{ri}}{\partial \mathbf{u }}\right| _{\mathbf{d }_{0}}+\mathbf{K }+\left. \frac{\partial \mathbf{f }_\mathrm{en}}{\partial \mathbf{u }}\right| _{\mathbf{d }_{0}}. \end{aligned}$$
(51)

For a MDOF hysteretic mechanical system, the critical time step \(\varDelta t_\mathrm{cr}\), that is, the maximum value of the time step that can be adopted to avoid stability problems, is different for each natural mode evaluated at the \((i+1)\)th time step of a NLTHA. Specifically, assuming a zero viscous damping ratio, the value of the critical time step of the jth mode at the \((i+1)\)th time step, that is, \((\varDelta t_\mathrm{cr})^{(j)}_{i+1}\), can be evaluated as [15]:

figure d

where \(T_{0}^{(j)}\) is the initial natural period, that is, the natural period at the beginning of the analysis, of the jth mode, whereas \(\kappa _{i+1}^{(j)}\) is the current degree of nonlinearity of the jth mode at the \((i+1)\)th time step:

$$\begin{aligned} \kappa _{i+1}^{(j)}=\left[ \frac{T_{0}^{(j)}}{T_{i+1}^{(j)}}\right] ^{2}, \end{aligned}$$
(53)

where \(T_{i+1}^{(j)}\) is the natural period of the jth mode evaluated by using the generalized tangent stiffness matrix \(\mathbf{K }_{i+1}\) at the \((i+1)\)th time step. It is worth being emphasized that \(\kappa _{i+1}^{(j)}\) turns out to be greater (smaller) than 1 in presence of (non-)stiffening rate-independent hysteretic behavior.

Table 3 Proposed CEM numerical properties
Full size table

4.2 Proposed Chang’s explicit method

The proposed CEM is obtained by setting \(\alpha =1/4\) and \(\beta =1/2\) in Eqs. (46) and (47). Such a method exhibits excellent accuracy and stability properties. Indeed, as shown in Table 3, CEM is unconditionally stable for all non-stiffening hysteretic mechanical systems that are of interest in this paper. Furthermore, belonging to the subfamily of methods for which \(\beta =1/2\), it has a second-order accuracy, does not suffer from numerical damping, and displays a small relative period error for \(\varDelta t\le 0.05\,T_{0}^{(j)}\).

4.2.1 CEM formulation

Let us consider a generic time interval \(t_{i}\le t \le t_{i+1}\) and let the generalized external force vector \(\mathbf{p }_{i}\) (\(\mathbf{p }_{i+1}\)) be assigned at the beginning (end) of the interval. We assume that the generalized displacement, velocity, and acceleration vectors at time step i, that is, \(\mathbf{d }_{i}\), \(\mathbf{v }_{i}\), and \(\mathbf{a }_{i}\), are known. Our aim is to evaluate such vectors at time step \(i+1\), that is, \(\mathbf{d }_{i+1}\), \(\mathbf{v }_{i+1}\), and \(\mathbf{a }_{i+1}\), by means of the proposed algorithm. To this end, we first observe that Eq. (45b) provides, on account of Eqs. (46) and (48), the expression for the evaluation of the unknown generalized displacement vector \(\mathbf{d }_{i+1}\):

$$\begin{aligned} \mathbf{d }_{i+1}= & {} \mathbf{d }_{i}+\varDelta t\mathbf{v }_{i}+\mathbf{S }_{0}^{-1}\nonumber \\&\times \left[ \mathbf{M }(\varDelta t)^{2}\mathbf{a }_{i}+\alpha (\varDelta t)^{2}\left( \mathbf{p }_{i+1}-\mathbf{p }_{i}\right) \right] . \end{aligned}$$
(54)
Table 4 Proposed CEM algorithm
Full size table

The unknown generalized velocity vector \(\mathbf{v }_{i+1}\) can be computed by using Eq. (45c) that, on account of Eqs. (47) and (49), can be also written as:

$$\begin{aligned} \mathbf{v }_{i+1}=\mathbf{v }_{i}+\mathbf{S }_{0}^{-1}\mathbf{M }\varDelta t\mathbf{a }_{i}. \end{aligned}$$
(55)

Once the generalized nonlinear forces vectors \((\tilde{\mathbf{f }}_\mathrm{rdn})_{i+1}=\mathbf{f }_\mathrm{rdn}(\mathbf{v }_{i+1})\), \((\tilde{\mathbf{f }}_\mathrm{ri})_{i+1}=\mathbf{f }_\mathrm{ri}(\mathbf{d }_{i+1})\), and \((\tilde{\mathbf{f }}_\mathrm{en})_{i+1}=\mathbf{f }_\mathrm{en}(\mathbf{d }_{i+1})\) have been evaluated by employing suitable phenomenological models, the unknown generalized acceleration vector \(\mathbf{a }_{i+1}\) can be computed by using the following expression derived from Eq. (45a):

$$\begin{aligned} \begin{aligned} \mathbf{a }_{i+1}&=\mathbf{M }^{-1}\left[ \mathbf{p }_{i+1}-\mathbf{C }\mathbf{v }_{i+1}-\mathbf{K }\mathbf{d }_{i+1}-(\tilde{\mathbf{f }}_\mathrm{rdn})_{i+1}\right. \\ {}&\left. -(\tilde{\mathbf{f }}_\mathrm{ri})_{i+1}-(\tilde{\mathbf{f }}_\mathrm{en})_{i+1}\right] . \end{aligned} \end{aligned}$$
(56)

4.2.2 CEM implementation details

Table 4 summarizes the implementation scheme of the proposed algorithm that is composed of two parts. In the first one, called Initial settings, the generalized constant mass \(\mathbf{M }\), damping \(\mathbf{C }\), and stiffness \(\mathbf{K }\) matrices as well as the initial generalized tangent damping \(\mathbf{C }_{0}\) and stiffness \(\mathbf{K }_{0}\) matrices, obtained from Eqs. (50) and (51), respectively, are first assembled. Then, the initial generalized displacement \(\mathbf{d }_{0}\) and velocity \(\mathbf{v }_{0}\) vectors are initialized and the initial generalized acceleration vector \(\mathbf{a }_{0}\) is evaluated using the following equation:

$$\begin{aligned} \mathbf{a }_{0}= & {} \mathbf{M }^{-1}\left[ \mathbf{p }_{0}-\mathbf{C }\mathbf{v }_{0}-\mathbf{K }\mathbf{d }_{0}-(\tilde{\mathbf{f }}_\mathrm{rdn})_{0}\right. \nonumber \\&\left. -(\tilde{\mathbf{f }}_\mathrm{ri})_{0}-(\tilde{\mathbf{f }}_\mathrm{en})_{0}\right] , \end{aligned}$$
(57)

that has been formally obtained by setting \(i = -1\) in Eq. (56).

Finally, after the selection of the time step \(\varDelta t\) and the definition of the two scalar parameters \(\alpha =1/4\) and \(\beta =1/2\), matrix \(\mathbf{S }_{0}=\mathbf{M }+\beta \varDelta t\mathbf{C }_{0}+\alpha (\varDelta t)^{2}\mathbf{K }_{0}\), appearing in Eqs. (54) and (55), is computed and the inverse of matrices \(\mathbf{M }\) and \(\mathbf{S }_{0}\), that is, \(\overline{\mathbf{M }}=\mathbf{M }^{-1}\) and \(\overline{\mathbf{S }}_{0}=\mathbf{S }_{0}^{-1}\), are evaluated. It is important to note that \(\mathbf{M }\) and \(\mathbf{S }_{0}\) need to be inverted only once during the NLTHA and have to be saved for the subsequent computations.

Fig. 8
figure 8

Schematic drawing of the adopted family of hysteretic mechanical systems

Full size image

In the second part of the proposed algorithm, called Calculations at each time step, the generalized displacement, velocity, and acceleration vectors are computed, at each time step of the analysis, by using Eqs. (54), (55), and (56), respectively.

5 Numerical experiments

This section presents the results of several analyses carried out on hysteretic mechanical systems presenting both types of hysteretic behaviors, namely rate-dependent and kinematic hardening non-stiffening rate-independent hysteretic behaviors, in order to investigate the accuracy and the computational efficiency of the proposed procedure.

Specifically, the family of hysteretic mechanical systems, selected to carry out the numerical experiments, is represented by a n-DOFs linear mass-spring-damper system with nonlinear hysteretic elements. Figure 8 illustrates a schematic drawing of such a family of systems where \(M_{i}\) is the ith generalized mass and \(u^{(i)}\) is its generalized displacement, \(C_{i}\) and \(K_{i}\) are the generalized viscous damping coefficient and stiffness of the ith linear viscous damper and linear elastic spring, respectively, whereas \(c_{i}\) and \(k_{i}\) are the initial generalized tangent damping coefficient and stiffness of the ith nonlinear rate-dependent and rate-independent hysteretic elements, respectively. For simplicity, a generic system belonging to such a family is denoted as System RdRiPn (RdRiFn), where Rd is reminiscent of its rate-dependent behavior, RiP (RiF) is reminiscent of its rate-independent behavior due to plastic deformation mechanisms (friction), and n specifies the number of DOFs.

Fig. 9
figure 9

Applied generalized external forces: harmonic force (a) and random force (b)

Full size image

To perform the analyses, the rate-dependent model proposed in [41], briefly illustrated in 2.2.1, is adopted to simulate the dynamic behavior of the nonlinear rate-dependent hysteretic elements, whereas the novel rate-independent model, developed in 3.2, is used to reproduce the dynamic behavior of the rate-independent hysteretic elements. Furthermore, the proposed explicit time integration method, described in 4.2, is employed to numerically integrate the nonlinear equilibrium equations.

In order to demonstrate the accuracy properties of the proposed procedure and its capability to significantly decrease the computational burden of the analyses, the numerical results and the computational times are compared with those obtained by employing the conventional solution strategy described in Sect. 2; such a strategy combines the celebrated Bouc–Wen model [5, 49, 50] or its modified version [21] with the well-known Newmark’s constant average acceleration method [13, 33].

In particular, the BWM (MBWM) is used to model the kinematic hardening non-stiffening behavior, due to plastic deformation mechanisms (friction), displayed by the rate-independent hysteretic elements. Note that, in this work, the first-order nonlinear ODE, given by Eq. (8), is numerically solved by using the unconditionally stable semi-implicit Runge–Kutta method [40] and considering 50 steps. Furthermore, the AAM is adopted in conjunction with the pseudo-force iterative procedure employed with a convergence tolerance value of \(10^{-8}\).

The hysteretic models and the solution algorithms have been programmed in MATLAB and run on a computer having an Intel\(\circledR \) Core\(^{\mathrm{TM}}\) i7-4700MQ processor and a CPU at 2.40 GHz with 16 GB of RAM.

5.1 Accuracy

To show the accuracy of the proposed procedure, we present the results of NLTHAs performed on two different hysteretic mechanical systems: Systems RdRiP1 and RdRiF1.

5.1.1 Mechanical systems properties

The initial properties of System RdRiP1 (RdRiF1) are \(M_{1}=1\)\(\hbox {Ns}^{2}\)/m, \(C_{1}=1\) Ns/m, \(K_{1}=1\) N/m, \(c_{1}=0\) Ns/m, and \(k_{1}=100\) N/m (\(M_{1}=1\)\(\hbox {Ns}^{2}\)/m, \(C_{1}=1\) Ns/m, \(K_{1}=1\) N/m, \(c_{1}=0\) Ns/m, and \(k_{1}=1000\) N/m). Thus, the initial natural period of System RdRiP1 (RdRiF1), evaluated as \(T=2\pi \sqrt{M_{1}/\left( K_{1}+k_{1}\right) }\), is 0.625 s (0.198 s).

5.1.2 Applied generalized external forces

The analyses are performed for two different generalized external forces, namely a harmonic force and a random force.

Figure 9a shows the applied harmonic force, that is, a sinusoidal force with an amplitude \(p_{0}\), that increases linearly with time from 0 to 4 N, a forcing frequency \(\omega _{p}\) = 2\(\pi \) rad/s, and a time duration \(t_{d}\) = 10 s.

Figure 9b shows the applied random force, that is, a Gaussian white noise with an intensity iwn = 9 N, and a time duration \(t_{d}\) = 10 s.

5.1.3 Hysteretic models parameters

The dynamic behavior of the nonlinear rate-dependent hysteretic element of Systems RdRiP1 and RdRiF1 is simulated, in both the proposed and conventional procedures, by adopting the rate-dependent model developed by Seleemah and Constantinou [41], illustrated in 2.2.1. Specifically, the two parameters used for the evaluation of the generalized nonlinear rate-dependent hysteretic force, given by Eq. (6), are \(c_{n}=1\) and \(q=1.5\).

The dynamic behavior of the rate-independent hysteretic element of Systems RdRiP1 and RdRiF1 is simulated adopting the novel rate-independent model, developed in 3.2, when the analyses are carried out by employing the proposed procedure; on the contrary, it is modeled by means of the Bouc–Wen model (modified Bouc–Wen model), described in 2.2.2, when the analysis of System RdRiP1 (RdRiF1) is performed by using the conventional procedure. Specifically, the parameters adopted in the PHM are listed in Table 5, whereas the ones used in the BWM (MBWM) are listed in Table 6a (b).

Table 5 PHM parameters
Full size table
Table 6 (a) BWM parameters and (b) MBWM parameters
Full size table
Table 7 NLTHAs results | (a) system RdRiP1 and (b) system RdRiF1
Full size table
Fig. 10
figure 10

Results of the analyses carried out on System RdRiP1 by applying the Harmonic Force

Full size image
Fig. 11
figure 11

Results of the analyses carried out on System RdRiF1 by applying the Random Force

Full size image

5.1.4 Numerical results

The selection of an appropriate time step \(\varDelta t\) is a crucial aspect to accurately analyze the above-described systems. As suggested in the literature [4, 20], time history analyses of linear elastic systems can be performed adopting \(\varDelta t=T/10\) or T / 20. Since for nonlinear systems a smaller time step is required to limit the detrimental effects due to factors that affect the accuracy of the adopted time integration method, such as the period distortion, the analyses of Systems RdRiP1 and RdRiF1 are performed adopting a time step \(\varDelta t\) = 0.001 s, that is smaller than T / 100.

The results of the analyses carried out on System RdRiP1 (RdRiF1) are shown in Table 7a (b). The accuracy of the proposed procedure is very satisfactory since the maximum and minimum values of the approximate estimates of the generalized displacement, velocity, and acceleration of the analyzed systems, namely \(d^{(1)}\), \(v^{(1)}\), and \(a^{(1)}\), respectively, are numerically quite close to those predicted by using the conventional procedure.

The response history of System RdRiP1 (RdRiF1), simulated by applying the harmonic force (random force), is illustrated in terms of generalized displacement, e.g., Fig. 10a (11a), generalized velocity, e.g., Fig. 10b (11b), and generalized acceleration, e.g., Fig. 10c (11c); generalized nonlinear rate dependent and rate-independent force–displacement hysteresis loops are shown in Figs. 10d (11d) and 10e (11e), respectively. The plots of the response history of System RdRiP1 (RdRiF1), obtained for the random force (harmonic force), are omitted for brevity. Generally speaking, the comparison between the responses of System RdRiP1 (RdRiF1) obtained with the PHM-CEM and the conventional BWM-AAM (MBWM-AAM) shows a very good agreement.

5.2 Computational efficiency

To show the computational efficiency of the proposed procedure, we present the results of NLTHAs performed on eight different hysteretic mechanical systems: Systems RdRiPn and RdRiFn, with n = 1, 10, 100, and 1000.

5.2.1 Mechanical systems properties

The initial properties of Systems RdRiPn (RdRiFn), with n = 1, 10, 100, and 1000, are \(M_{i}=1\)\(\hbox {Ns}^{2}\)/m, \(C_{i}=1\) Ns/m, \(K_{i}=1\) N/m, \(c_{i}=0\) Ns/m, and \(k_{i}=100\) N/m (\(M_{i}=1\)\(\hbox {Ns}^{2}\)/m, \(C_{i}=1\) Ns/m, \(K_{i}=1\) N/m, \(c_{i}=0\) Ns/m, and \(k_{i}=1000\) N/m), for \(i = 1,..., n\). The initial natural period of System RdRiP1 (RdRiF1), evaluated as \(T=2\pi \sqrt{M_{1}/\left( K_{1}+k_{1}\right) }\), is 0.625 s (0.198 s). As regards Systems RdRiPn (RdRiFn), with n = 10, 100, and 1000, the lowest initial natural period, evaluated solving the eigenvalue problem adopting the initial generalized tangent stiffness matrix \(\mathbf{K }_{0}\), is found to be 0.3126 s (0.0993 s) for all the three systems.

5.2.2 Applied generalized external forces

The analyses are performed by applying a harmonic force at the ith mass of each system.

Such a harmonic force is a sinusoidal force having a constant amplitude \(p_{0}\) = 4 N, a forcing frequency \(\omega _{p}\) = 2\(\pi \) rad/s, and a time duration \(t_{d}\) = 1 s.

5.2.3 Hysteretic models parameters

The dynamic behavior of the ith nonlinear rate-dependent hysteretic element of Systems RdRiPn and RdRiFn, with n = 1, 10, 100, and 1000, is simulated, in both the proposed and conventional procedures, by adopting the rate-dependent model developed by Seleemah and Constantinou [41], illustrated in 2.2.1. Specifically, the two parameters used for the evaluation of the ith generalized nonlinear rate-dependent hysteretic force, given by Eq. (6), are \(c_{n}=1\) and \(q=1.5\).

The dynamic behavior of the ith rate-independent hysteretic element of Systems RdRiPn and RdRiFn, with n = 1, 10, 100, and 1000, is simulated adopting the novel rate-independent model, developed in 3.2, when the analyses are carried out by employing the proposed procedure; on the contrary, it is modeled by means of the Bouc–Wen model (modified Bouc–Wen model), described in 2.2.2, when the analyses of Systems RdRiPn (RdRiFn) are performed by using the conventional procedure. Specifically, the three PHM parameters used for the evaluation of the ith generalized rate-independent hysteretic force of the analyzed mechanical systems are the same of the ones listed in Table 5, whereas the seven BWM (MBWM) parameters used for evaluating the ith generalized rate-independent hysteretic force of Systems RdRiPn (RdRiFn) are the same of the ones listed in Table 6a (b).

Table 8 NLTHAs results | (a) systems RdRiPn and (b) systems RdRiFn
Full size table
Fig. 12
figure 12

Average total computational times required for Systems RdRiPn (a) and RdRiFn (b)

Full size image

5.2.4 Numerical results

The analyses of the above-described systems are performed adopting a time step \(\varDelta t\) = 0.001 s that allows the proposed procedure to give enough accurate results as those obtained by employing the conventional one described in Sect. 2; these numerical results are omitted for brevity.

In order to show the computational efficiency of the proposed strategy, Table 8a (b) and Fig. 12a (b) present the average total computational time tct required to analyze Systems RdRiPn (RdRiFn), with n = 1, 10, 100, and 1000, by employing the PHM-CEM and the conventional BWM-AAM (MBWM-AAM). It is evident that the computational burden of the proposed procedure, expressed by tct, is significantly reduced with respect to that characterizing the conventional one.

We also report a second parameter, denominated tctp, since the parameter tct is not a fully objective measure of the PHM-CEM efficiency due to its dependency on the amount of the background process running on the computer, the relevant memory, as well as the CPU speed. In particular, the parameter tctp has been obtained by normalizing the tct parameter of the proposed approach with respect to that characterizing the conventional one. Hence, by defining:

$$\begin{aligned} \mathrm {PHM{-}CEM}\ tctp\ [\%]{=}\dfrac{\mathrm {PHM-CEM}\ tct}{\mathrm {(M)BWM-AAM}\ tct}\cdot 100\ , \end{aligned}$$
(58)

one obtains a more meaningful measure of the computational benefits related to the use of the proposed strategy.

6 Conclusions

We have presented an accurate and computationally efficient procedure to analyze non-stiffening hysteretic mechanical systems. Such a procedure combines a novel rate-independent model, belonging to the class of uniaxial phenomenological models recently formulated by Vaiana et al. [47], and an explicit structure-dependent time integration method, belonging to the Chang’s family of explicit methods [15].

To show the accuracy and the computational efficiency of the proposed approach, nonlinear time history analyses have been performed on several hysteretic mechanical systems. Specifically, the numerical results and the computational times obtained with the proposed strategy have been compared to those obtained by employing a conventional solution approach that combines the celebrated Bouc–Wen model, or its modified version, with the widely used Newmark’s constant average acceleration method.

In particular, the accuracy of the proposed procedure has been numerically confirmed by analyzing two single degree of freedom mechanical systems that display both rate-dependent and rate-independent hysteretic behaviors: Systems RdRiP1 and RdRiF1. The dynamic responses of such systems, obtained for two different external forces, that is, a harmonic force and a random force, reveal that the accuracy of the presented strategy is very satisfactory since the numerical results closely match those predicted by the conventional one, independently of the kind of external force.

The computational efficiency of the proposed procedure has been investigated by analyzing eight mechanical systems, displaying both rate-dependent and rate-independent hysteretic behaviors, that are characterized by an increasing number n of DOFs: Systems RdRiPn and RdRiFn, with n = 1, 10, 100, and 1000. The dynamic responses of such systems, obtained applying a harmonic force at each mass, reveal that the computational burden required by the proposed strategy is significantly reduced with respect to that characterizing the conventional one; in particular, the total computational time percentage, tctp, of proposed approach is always less than 0.50%.