Nonlinear vibrations of a piecewise-linear quarter-car truck model by incremental harmonic balance method

Abstract

A two-degree-of-freedom (2DOF) quarter-car model with a piecewise leaf spring for the rear suspension of a truck is presented. A leaf spring, which contains a main leaf and an auxiliary leaf, can be regarded as a model with piecewise-linear stiffness and damping, and the model is built with two load states according to whether the auxiliary leaf spring is at work at the static equilibrium. The incremental harmonic balance method is used to obtain the nonlinear dynamics of the presented quarter-car truck model. The accuracy of this method is verified by comparing the nonlinear responses, including the sub-harmonic resonance, with the Runge–Kutta method. Afterward, the effects of the auxiliary leaf spring’s stiffness, the sprung mass ratio and the main leaf spring’s damping on the dynamic responses of the system are investigated. It is found that the piecewise-linear system shares similar dynamic characteristics with a Duffing oscillator, and the proper design of the auxiliary leaf spring can contribute to the reduction in the fundamental resonance amplitudes of the system. The frequency response curve shows ‘snap-back’ features in the sub-harmonic resonance under a certain sprung mass and the leaf spring’s damping, which is due to the coupled nonlinearities of both DOFs. In addition, the increase of the main leaf spring’s damping can shrink or even eliminate the sub-harmonic or chaos resonances.

1 Introduction

Nowadays, with the development of lightweight technology on vehicles, there are many applications of leaf springs with variable stiffness on the design of suspensions. Compared with traditional leaf springs, these leaf springs have the advantages of lightness of weight, comfortability in riding, enhancement of carrying capacity, etc. In the vehicle design of a leaf spring suspension, the suspension that contains a main leaf spring and an auxiliary leaf spring has often been used, especially in trucks that carry a wide variety of loads. Usually, the design on the lightness of weight would cause a low performance on vibration; thus, the dynamics of the suspension are an essential part of suspension design and optimization [1]. Many scholars have proposed the quarter-car model to analyze the dynamics of the suspension system [2,3,4,5,6,7], which can be adopted to evaluate a piecewise-linear leaf spring suspension [8,9,10,11,12]. The perturbation methods seem to be a universal way to predict the responses of this type of vehicle suspension system. Zhong et al. [8] proposed a 2-DOF piecewise-linear leaf spring suspension model, and the average method was used to investigate the nonlinear dynamics of the system, and the transition sets; 40 groups of bifurcation curves were found with various system parameters. Li et al. [9] used the average method to study the effects of a mass variation of the dynamic response of the SDOF piecewise-linear suspension system. Silveira et al. [10] discussed the 2-DOF quarter-car model with piecewise-linear damping under harmonic excitation, and the results showed that the piecewise damping ratio directly influenced the maximum displacement, speed and acceleration of the sprung mass. Deshpande et al. [11] studied a more general piecewise-linear vibration isolation system with secondary suspension, the characteristic of the jump-free zones was investigated and a boundary surface between no-jump (unique response) and jump areas was established.

However, the perturbation methods are only suitable for weakly nonlinear problems. Bajkowski et al. [12] showed that amplitude–frequency response curves from the averaging method and the numerical method became different when there were strong nonlinearities in the system. Some piecewise-linear characteristics, such as super-harmonic and sub-harmonic resonance are difficult to obtain with these methods. The IHBM that was proposed by Cheung [13] is an effective method for solving both weakly and strongly nonlinear problems under periodic excitations [14,15,16]. Zhou [2] studied the vehicle suspension system with nonlinear stiffness and damping through IHBM and the numerical method, and the results of these methods showed good agreement. Regarding the piecewise-linear problems, IHBM also provided a systematic procedure by introducing the step functions [18, 19]. Various piecewise-linear system dynamics have been investigated with this method [17, 20,21,22,23,24,25,26,27,28]. The accuracy of the IHBM results of piecewise-linear systems has also been consistent with the accuracy of the numerical method, including super-harmonic and sub-harmonic resonance [24]. In addition, to track the unstable response or sub-harmonic resonance, many continuous methods have been used to acquire the frequency response curves including the incremental arc-length method combined with a cubic extrapolation technique [13]; Broyden’s method [16]; arc-length method [17, 24, 27], etc.

By using IHBM, the super-harmonic and sub-harmonic resonance of piecewise-linear systems can also be predicted. Wong et al. [18] showed that the bifurcation of the 1 / m sub-harmonic resonances can be found on the right side of the fundamental resonance’s peak and m super-harmonic resonances on the left side in the SDOF piecewise-linear system by using IHBM. Lau et al. [19] considered a SDOF system with symmetric piecewise stiffness, it was found that the sub-harmonic response shrinks into complicated closed curves in the presence of damping. Kim et al. [24] studied a reduced order torsional system with symmetric piecewise stiffness using IHBM with adaptive arc-length continuation, and the results showed that the appearance of sub-harmonic resonance depends on the frequency separation between the primary harmonic of the compliant side and the mean operating point crossover position to the stiffness transitions. Duan et al. [25] used multi-term IHBM to analyze a family of isolated sub-harmonic branches in the nonlinear frequency response of piecewise-linear systems and concluded that the relationship between the linear mean operating and transition points rather than asymmetric piecewise stiffness appeared to be the key factor that generated the isolated branches.

Although many articles have been devoted to SDOF piecewise systems that consider sub/super-harmonic resonances, the literature has reported few studies on multiple DOF piecewise systems, especially when the added DOFs could affect these resonances of the system. In the present paper, considering the piecewise-linear stiffness and damping of the suspension, the nonlinear responses, including the sub-harmonic response, of a 2-DOF piecewise-linear quarter-car model are studied with IHBM. Because of the different types of local dynamic behaviors, the piecewise-linear suspension model is built by two load states according to whether the auxiliary leaf spring is at work at the static equilibrium. This paper is organized as follows. Section 2 establishes a 2-DOF quarter-car model with a piecewise-linear leaf spring for the rear suspension of a truck. In Sect. 3, IHBM is derived to obtain the nonlinear motions of the present model subject to the external road profile. The results of IHBM are validated by the Runge–Kutta method, and the effect of some key system parameters on the dynamic response of the present models is studied in Sect. 4. Finally, Sect. 5 draws some conclusions from the present work.

Fig. 1

Schematic model of a piecewise-linear quarter-car model

2 The quarter-car system

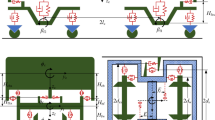
The dynamic system of a 2-DOF quarter-car truck model with a piecewise-linear leaf spring is shown in Fig. 1. When the sprung load on the leaf spring is small, only the main leaf spring works. The distance between the main leaf spring and the auxiliary leaf spring decreases as the load increases. On the critical sprung load where the distance becomes zero, the auxiliary leaf spring exactly begins to work. As the sprung load continues to increase, both leaf springs work. In this paper, the variable $z_{1}$ represents the unsprung mass vertical displacement, $z_{2}$ is the sprung mass vertical displacement, and $z_{0}$ is the road profile. The road profile is expressed by

$$\begin{aligned} z_0 =r\sin (\omega t) \end{aligned}$$

(1)

where r and $\omega$ are the amplitude and frequency, respectively, of the harmonic road profile.

Fig. 2

Load state definitions of the piecewise-linear spring leaf

Other parameters that are shown in Fig. 1 are defined as follows. $m_{1}$ and $m_{2}$ are the unsprung mass and the sprung mass, respectively, of the truck. $k_{1}$ and $k_1^{*}$ are the nonlinear coefficients of the tire stiffness, and the tire stiffness can be approximately regarded as a quadratic curve-fitting model. Equation (2) gives the curve-fitting form:

$$\begin{aligned} g_N (x)=k_1 x+k_1^*x^{2} \end{aligned}$$

(2)

where $c_{1}$ is the tire damping, $k_{2}$ and $k_{3 }$ are the stiffness of the main and auxiliary leaf springs, respectively, $c_{2}$ and $c_{3}$ are the damping of the main and auxiliary leaf springs, respectively, e represents the distance between the main leaf spring and the auxiliary leaf spring when the two leaf springs are at the no-load state, and $d_{1}$ and $d_{2}$ are the critical distances, namely, the distances between the position where the sprung mass is loaded at the state of static equilibrium and the critical position where the auxiliary leaf spring exactly does not work. $d_{1}$ and $d_{2}$ can be defined as

$$\begin{aligned} d_1 =e-\frac{m_2 g}{k_2 },d_2 =\frac{m_2 g-k_2 e}{k_2 +k_3 } \end{aligned}$$

(3)

To investigate the nonlinear motions of the 2-DOF system, the relative displacements are used as follows:

$$\begin{aligned} z_{21}= & {} z_2 -z_1 \nonumber \\ z_{10}= & {} z_1 -z_0 \end{aligned}$$

(4)

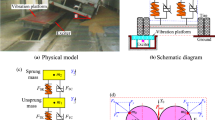
In this work, the origin coordinates are set to the static balance position to ignore the gravity of the system. As seen in Fig. 2, the static balance position of system is divided into two states because of the variation of the sprung mass: the light load state and the heavy load state. Additionally, the two different load states are also relevant to the local dynamic behaviors of the primary resonances, which are studied in Sect.  4.2. The critical sprung mass can be obtained with Eq. (5).

$$\begin{aligned} m_{2\mathrm{cr}} =\frac{k_2 e}{g} \end{aligned}$$

(5)

By applying the Newtonian law, the dynamic equations of the light load state and the heavy load state can be obtained.

For the light load state,

$$\begin{aligned}&m_2 ({\ddot{z}}_0 +{\ddot{z}}_{10} +{\ddot{z}}_{21} )+c_2 {\dot{z}}_{21} +k_2 z_{21} \nonumber \\&\quad +\,f_1 (z_{21} ,\dot{z}_{21} )=0 \nonumber \\&m_1 ({\ddot{z}}_0 +{\ddot{z}}_{10})-c_2 {\dot{z}}_{21} \nonumber \\&\quad -\,k_2 z_{21} -f_1 (z_{21} ,{\dot{z}}_{21} )+c_1 {\dot{z}}_{10} +g_N (z_{10} )=0\nonumber \\ \end{aligned}$$

(6)

For the heavy load state,

$$\begin{aligned}&m_2 ({\ddot{z}}_0 +{\ddot{z}}_{10} +{\ddot{z}}_{21} )+(c_2 +c_3 ){\dot{z}}_{21} \nonumber \\&\quad +\,(k_2 +k_3 )z_{21} +f_2 (z_{21} ,{\dot{z}}_{21} )=0 \nonumber \\&m_1 ({\ddot{z}}_0 +{\ddot{z}}_{10})-(c_2 +c_3 ){\dot{z}}_{21} -(k_2 +k_3 )z_{21} \nonumber \\&\quad -\,f_2 (z_{21} ,{\dot{z}}_{21} )+\hbox {c}_1 {\dot{z}}_{10} +g_N (z_{10} )=0 \end{aligned}$$

(7)

where the overhead dot represents the differentiation with respect to time t. $f_1 (z_{21} ,{\dot{z}}_{21} )$ and $f_2 (z_{21} ,{\dot{z}}_{21} )$ are the piecewise-linear functions that represent the auxiliary leaf spring forces:

$$\begin{aligned}&f_1 (z_{21} ,{\dot{z}}_{21} ){=}\left\{ {\begin{array}{ll} c_3 {\dot{z}}_{21} +k_3 (z_{21} +d_1 )&{}\quad z_{21} <-\,d_1 \\ 0,&{}\quad z_{21} \ge -\,d_1 \\ \end{array}} \right. \nonumber \\\end{aligned}$$

(8)

$$\begin{aligned}&f_2 (z_{21} ,{\dot{z}}_{21}){=}\left\{ {\begin{array}{ll} 0,&{}\quad z_{21} <d_2 \\ -\,c_3 {\dot{z}}_{21} -\,k_3 (z_{21} -\,d_2 ),&{} \quad z_{21} \ge d_2 \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(9)

To simplify the above equations, the following dimensionless quantities are introduced:

$$\begin{aligned} \omega _1= & {} \sqrt{\frac{k_1 }{m_1 }},\xi =\frac{c_1 }{2\sqrt{m_1 k_1 }},{t}'=\omega _1 t,\nu _2 \nonumber \\= & {} \frac{k_2 }{k_1 },\nu _3 =\frac{k_3 }{k_1 },\eta _2 =\frac{c_2 }{c_1 },\eta _3 =\frac{c_3 }{c_1 }, \nonumber \\ x_1= & {} \frac{z_{10} }{r},x_2 =\frac{z_{21} }{r},D=\frac{e}{r},\alpha =\frac{k_1^*}{k_1 }r,\nu \nonumber \\= & {} \frac{m_1 g}{k_1 r},\mu =\frac{m_2 }{m_1 },\varOmega =\frac{\omega }{\omega _1 }, \nonumber \\&\mu _{cr} =\frac{k_2 e}{m_1 g},\varDelta _1 =-\frac{d_1 }{r},\varDelta _2 =\frac{d_2 }{r} \end{aligned}$$

(10)

For the piecewise-linear equations, the step function is used to make the derivation simpler [18]:

$$\begin{aligned}&h_{\left( {x_2 -\Delta _1 } \right) } =\left\{ {\begin{array}{ll} 1&{}\quad x_2 <\varDelta _1 \\ 0&{}\quad x_2 \ge \varDelta _1 \\ \end{array}} \right. \end{aligned}$$

(11)

$$\begin{aligned}&h_{\left( {x_2 -\Delta _2 } \right) } =\left\{ {\begin{array}{ll} 0&{}\quad x_2 <\varDelta _2 \\ -\,1&{}\quad x_2 \ge \varDelta _2 \\ \end{array}} \right. \end{aligned}$$

(12)

Thus, the step functions have a unified form for both states:

$$\begin{aligned} h_{\left( {x_2 -\varDelta } \right) } =\left\{ {\begin{array}{ll} h_{\left( {x_2 -\varDelta _1 } \right) } \mu <\mu _{\mathrm{cr}} ,&{}\quad \varDelta =\varDelta _1 \\ h_{\left( {x_2 -\varDelta _2 } \right) } \mu \ge \mu _{\mathrm{cr}} ,&{}\quad \varDelta =\varDelta _2 \\ \end{array}} \right. \end{aligned}$$

(13)

Letting

$$\begin{aligned}&c=\left\{ {\begin{array}{ll} \eta _2 ,&{}\quad \mu <\mu _{\mathrm{cr}} \\ \eta _2 +\eta _3 ,&{}\quad \mu \ge \mu _{\mathrm{cr}} \\ \end{array}} \right. \end{aligned}$$

(14)

$$\begin{aligned}&k=\left\{ {\begin{array}{ll} \nu _2 ,&{}\quad \mu <\mu _{\mathrm{cr}} \\ \nu _2 +\nu _3 , &{}\quad \mu \ge \mu _{\mathrm{cr}} \\ \end{array}} \right. \end{aligned}$$

(15)

$$\begin{aligned}&G=h_{\left( {x_2 -\Delta } \right) } (\nu _3 (x_2 -\varDelta )+2\xi \eta _{3} \dot{x}_2 ) \end{aligned}$$

(16)

$$\begin{aligned}&{} \mathbf{q}=\left[ {{\begin{array}{ll} {x_1 }&{} \quad {x_2 } \\ \end{array} }} \right] ^{T}=\left[ {{\begin{array}{ll} {q_1 }&{} \quad {q_2 } \\ \end{array} }} \right] ^{T} \end{aligned}$$

(17)

$$\begin{aligned}&{\bar{{\mathbf{M}}}}=\left[ {{\begin{array}{ll} \mu &{}\quad \mu \\ 1&{}\quad 0 \\ \end{array} }} \right] \end{aligned}$$

(18)

$$\begin{aligned}&{\bar{{\mathbf{C}}}}_L =\left[ {{\begin{array}{cc} 0&{} {2\xi c} \\ {2\xi }&{} {-\,2\xi c} \\ \end{array} }} \right] \end{aligned}$$

(19)

$$\begin{aligned}&\bar{{\mathbf{K}}}_L =\left[ {{\begin{array}{cc} 0&{}\quad k \\ 1&{}\quad {-\,k} \\ \end{array} }} \right] \end{aligned}$$

(20)

$$\begin{aligned}&\bar{{\mathbf{G}}}_{\mathrm{NL}} =\left[ {{\begin{array}{c} G \\ {-G+\alpha x_1^2 } \\ \end{array} }} \right] \end{aligned}$$

(21)

$$\begin{aligned}&\bar{{\mathbf{F}}}=\left[ {{\begin{array}{c} \mu \\ 1 \\ \end{array} }} \right] \end{aligned}$$

(22)

By substituting Eqs. (13)–(22) into Eqs. (6)–(9), the dynamic equations can be rewritten with the matrix form:

$$\begin{aligned} \bar{{\mathbf{M}}}\ddot{\mathbf{q}}+\bar{{\mathbf{C}}}_L \dot{\mathbf{q}}+\bar{{\mathbf{K}}}_L \mathbf{q}+\bar{{\mathbf{G}}}_{\mathrm{NL}} =\varOmega ^{2}\sin (\varOmega {t}')\bar{{\mathbf{F}}} \end{aligned}$$

(23)

where the overhead dot represents the differentiation with respect to time $t'$.

3 IHBM for piecewise-linear system

3.1 IHBM scheme

In this section, the IHBM procedures are adopted to solve Eq. (23). Letting $\tau =\varOmega t'$, Eq. (23) can be rewritten as

$$\begin{aligned} \varOmega ^{2}\bar{{\mathbf{M}}}\ddot{\mathbf{q}}+\varOmega \bar{{\mathbf{C}}}_L \dot{\mathbf{q}}+\bar{{\mathbf{K}}}_L \mathbf{q}+\bar{{\mathbf{G}}}_{\mathrm{NL}} -\varOmega ^{2}\sin (\tau )\bar{{\mathbf{F}}}=\mathbf{0}\nonumber \\ \end{aligned}$$

(24)

where the overhead dot represents the differentiation with respect to time $\tau$, and $\varOmega$ is the non-dimensional excitation frequency of relevance. Let $\mathbf{q}_{\mathrm{i}0}$ and $\varOmega _{0}$ denote the state of vibration in hand, and the neighboring state can be expressed by adding the corresponding increments to them [13]:

$$\begin{aligned} \mathbf{q}=\mathbf{q}_0 +\Delta \mathbf{q},\varOmega =\varOmega _0 +\Delta \varOmega \end{aligned}$$

(25)

where $\mathbf{q}=[\mathbf{q}_{10}, \mathbf{q}_{20}]^{\mathrm{T}}$ and $\Delta \mathbf{q}=[\Delta \mathbf{q}_{1}, \Delta \mathbf{q}_{2}]^{\mathrm{T}}$.

By substituting Eq. (25) into Eq. (24), the following incremental equation can be obtained by neglecting the high-order incremental terms:

$$\begin{aligned}&\varOmega _0^2 \bar{{\mathbf{M}}}\Delta \ddot{\mathbf{q}}+\varOmega _0 (\bar{{\mathbf{C}}}_L +\bar{{\mathbf{C}}}_{\mathrm{NL}} )\Delta \dot{\mathbf{q}}\nonumber \\&\quad +\,(\bar{{\mathbf{K}}}_L +\bar{{\mathbf{K}}}_{\mathrm{NL}} )\Delta \mathbf{q}=\bar{{\mathbf{R}}}+\bar{{\mathbf{R}}}_{\mathrm{mc}} \Delta \varOmega \end{aligned}$$

(26)

Here, the unknown matrices can be expressed as follows:

$$\begin{aligned} \bar{\mathbf{C}}_{\mathrm{NL}}= & {} \left[ {{\begin{array}{cc} 0&{}\quad {2h_{\left( {q_{20} -\varDelta } \right) } \xi c} \\ 0&{} \quad {-\,2h_{\left( {q_{20} -\varDelta } \right) } \xi c} \\ \end{array} }} \right] \end{aligned}$$

(27)

$$\begin{aligned} \bar{\mathbf{K}}_{\mathrm{NL}}= & {} \left[ {{\begin{array}{cc} 0&{} {h_{\left( {q_{20} -\varDelta } \right) } k} \\ {2\alpha q_{10} }&{} {-\,h_{\left( {q_{20} -\varDelta } \right) } k} \\ \end{array} }} \right] \end{aligned}$$

(28)

$$\begin{aligned}&\bar{{\mathbf{E}}}_N =\left[ {{\begin{array}{c} {h_{\left( {q_{20} -\varDelta } \right) } k(q_{20} -\varDelta )} \\ {-\,h_{\left( {q_{20} -\varDelta } \right) } k(q_{20} -\varDelta )+\alpha q_{10}^2 } \\ \end{array} }} \right] \end{aligned}$$

(29)

$$\begin{aligned}&\bar{{\mathbf{R}}}=-\,(\varOmega _0^2 \bar{{\mathbf{M}}}\ddot{\mathbf{q}}_0 +\varOmega _0 (\bar{{\mathbf{C}}}_L +\bar{{\mathbf{C}}}_{\mathrm{NL}} )\dot{\mathbf{q}}_0 +\bar{{\mathbf{K}}}_L \mathbf{q}_0 ) \nonumber \\&-\,\bar{{\mathbf{E}}}_N +\varOmega _0^2 \sin (\tau )\bar{{\mathbf{F}}} \end{aligned}$$

(30)

$$\begin{aligned} \bar{{\mathbf{R}}}_{\mathrm{mc}}= & {} -\,2\varOmega _0 \bar{{\mathbf{M}}}\ddot{\mathbf{q}}_0 -(\bar{{\mathbf{C}}}_L +\bar{{\mathbf{C}}}_{\mathrm{NL}} )\dot{\mathbf{q}}_0 +2\varOmega _0 \sin (\tau )\bar{{\mathbf{F}}}\nonumber \\ \end{aligned}$$

(31)

Then, the harmonic balance procedure is adopted. Given the periodic solution with a truncated finite Fourier series,

$$\begin{aligned} q_{j0} (\tau )= & {} \frac{1}{2}a_{j0} +\sum _{i=1}^N {\left( a_{ji} \cos \frac{i\tau }{m}+b_{ji} \sin \frac{i\tau }{m}\right) } \nonumber \\&=\mathbf{C}_s \mathbf{A}_j \end{aligned}$$

(32)

$$\begin{aligned} \Delta q_j (\tau )= & {} \frac{1}{2}\Delta a_{j0} +\sum _{i=1}^N {\left( \Delta a_{ji} \cos \frac{i\tau }{m}+\Delta b_{ji} \sin \frac{i\tau }{m}\right) } \nonumber \\= & {} \mathbf{C}_s \Delta \mathbf{A}_j \end{aligned}$$

(33)

where N is the number of the harmonic terms used in the solution, and m is the order of the sub-harmonic solution. Other parameters are expressed below:

$$\begin{aligned}&{} \mathbf{C}_s =\left[ {\frac{1}{2},\cos \frac{\tau }{m},\ldots ,\cos \frac{N\tau }{m},\sin \frac{\tau }{m},\ldots ,\sin \frac{N\tau }{m}} \right] \end{aligned}$$

(34)

$$\begin{aligned}&{} \mathbf{S}=\mathrm{diag}\left[ {\mathbf{C}_s ,\mathbf{C}_s } \right] \end{aligned}$$

(35)

$$\begin{aligned}&{} \mathbf{A}_j =\left[ {a_{j0} ,a_{j1} ,\ldots ,a_{jN} ,b_{j1} ,\ldots ,b_{jN} } \right] ^{T},j=1,2 \nonumber \\\end{aligned}$$

(36)

$$\begin{aligned}&\Delta \mathbf{A}_j =\left[ {\Delta a_{j0} ,\Delta a_{j1} ,\ldots ,\Delta a_{jN} ,\Delta b_{j1} ,\ldots ,\Delta b_{jN} } \right] ^{T},\nonumber \\&\quad j=1,2 \end{aligned}$$

(37)

$$\begin{aligned}&{} \mathbf{A}=\left[ {\mathbf{A}_1 ,\mathbf{A}_2 } \right] ^{T},\Delta \mathbf{A}=\left[ {\Delta \mathbf{A}_1 ,\Delta \mathbf{A}_2 } \right] ^{T} \end{aligned}$$

(38)

According to the above equations, the vectors of the non-dimensional displacement unknowns and their increments can be expressed as

$$\begin{aligned} \mathbf{q}_0 =\mathbf{SA},\Delta \mathbf{q}=\mathbf{S}\Delta \mathbf{A} \end{aligned}$$

(39)

The positive integer m and N introduced in Eqs. (32) and (33) should be chosen according to the number of period-m bifurcations that the system has undergone [15]. $m = 1$ and $N=N_{\mathrm{m}}$ for the period-1 solution, and $m=p$ and $N = pN_{\mathrm{m}}$ for the period-p solution (where $p = 2, 3$,...). $N_{\mathrm{m}}$ is determined in terms of the required computing accuracy, which is studied in Sect. 4.1.

The Galerkin procedure is performed as follows:

$$\begin{aligned}&\int _0^{2m\pi } \left[ \varOmega _0^2 \bar{{\mathbf{M}}}\Delta \ddot{\mathbf{q}}+\varOmega _0 (\bar{{\mathbf{C}}}_L +\bar{{\mathbf{C}}}_{\mathrm{NL}} )\Delta \dot{\mathbf{q}}+(\bar{{\mathbf{K}}}_L \right. \nonumber \\&\left. \qquad +\,\bar{{\mathbf{K}}}_{\mathrm{NL}} )\Delta \mathbf{q} \right] \updelta \left( {\Delta \mathbf{q}} \right) \hbox {d}\tau \nonumber \\&\quad =\int _0^{2m\pi } {\left( {\bar{{\mathbf{R}}}+\bar{{\mathbf{R}}}_{\mathrm{mc}} \Delta \varOmega } \right) \updelta \left( {\Delta \mathbf{q}} \right) } \hbox {d}\tau \end{aligned}$$

(40)

By substituting Eqs. (32) and (33) into Eq. (40), the following $2N+1$ sets of linear equations with $2N+2$ unknowns can be obtained:

$$\begin{aligned} \mathbf{C}\Delta \mathbf{A}=\mathbf{R}+\Delta \varOmega \mathbf{R}_{\mathrm{mc}} \end{aligned}$$

(41)

where

$$\begin{aligned}&{} \mathbf{C}=\varOmega _0^2 \mathbf{M}+\varOmega _0 (\mathbf{C}_L +\mathbf{C}_{\mathrm{NL}} ) +(\mathbf{K}_L +\mathbf{K}_{\mathrm{NL}} ) \end{aligned}$$

(42)

$$\begin{aligned}&{} \mathbf{R}=-\left[ {\varOmega _0^2 \mathbf{M}+\varOmega _0 (\mathbf{C}_L +\mathbf{C}_{\mathrm{NL}} )+\mathbf{K}_L } \right] \mathbf{A}\nonumber \\&\quad -\,\mathbf{E}_N +\varOmega _0^2 \mathbf{F} \end{aligned}$$

(43)

$$\begin{aligned}&{} \mathbf{R}_{\mathrm{mc}} =-\,\left[ {2\varOmega _0 \mathbf{M}+(\mathbf{C}_L +\mathbf{C}_{\mathrm{NL}} )} \right] \mathbf{A}+\mathbf{2}\varOmega _0 \mathbf{F} \end{aligned}$$

(44)

The unknown matrices derived in Eqs. (42)–(44) can be expressed as follows:

$$\begin{aligned}&{} \mathbf{M}=\left[ {{\begin{array}{cc} {\mu \mathbf{M}_{1} }&{}\quad {\mu \mathbf{M}_{1} } \\ {\mathbf{M}_{1} }&{} \quad \mathbf{0} \\ \end{array} }} \right] , \quad \mathbf{C}_L =\left[ {{\begin{array}{cc} \mathbf{0}&{}\quad {2\xi c\mathbf{C}_{1} } \\ {2\xi \mathbf{C}_{1} }&{}\quad {-\,2\xi c\mathbf{C}_{1} } \\ \end{array} }} \right] ,\\&{} \mathbf{K}_L =\left[ {{\begin{array}{cc} \mathbf{0}&{}\quad {k\mathbf{K}_{1} } \\ {\mathbf{K}_{1} }&{}\quad {-\,k\mathbf{K}_{1} } \\ \end{array} }} \right] , \mathbf{F}=\left[ {{\begin{array}{c} {\mu \mathbf{F}_1 } \\ {\mathbf{F}_1 } \\ \end{array} }} \right] ,\nonumber \\&{} \mathbf{C}_{\mathrm{NL}} =\left[ {{\begin{array}{cc} \mathbf{0}&{}\quad {2\xi c\mathbf{C}_2 } \\ \mathbf{0}&{}\quad {-\,2\xi c\mathbf{C}_2 } \\ \end{array} }} \right] ,\nonumber \\&{} \mathbf{K}_{\mathrm{NL}} =\left[ {{\begin{array}{cc} \mathbf{0}&{} \quad {k\mathbf{K}_2 } \\ {2\alpha \mathbf{K}_3 }&{} \quad {-\,k\mathbf{K}_2 } \\ \end{array} }} \right] , \quad \mathbf{E}_N =\left[ {{\begin{array}{c} {k\mathbf{E}_1 } \\ {-\,k\mathbf{E}_1 +\alpha \mathbf{E}_2 } \\ \end{array} }} \right] \end{aligned}$$

where

$$\begin{aligned} \mathbf{M}_1= & {} \int _0^{2m\pi } {\mathbf{C}_S^T } {\mathbf{C}}''_S \hbox {d}\tau , \quad \mathbf{C}_1 =\int _0^{2m\pi } {\mathbf{C}_S^T } {\mathbf{C}}'_S \hbox {d}\tau ,\\ \mathbf{K}_1= & {} \int _0^{2m\pi } {\mathbf{C}_S^T } \mathbf{C}_S \hbox {d}\tau ,\\ \mathbf{F}_1= & {} \int _0^{2m\pi } {\mathbf{C}_S^T } \hbox {sin}(\tau )\hbox {d}\tau ,\\ \mathbf{C}_2= & {} \int _0^{2m\pi } {h_{\left( {x_{20} -\varDelta } \right) } \mathbf{C}_S^T } {\mathbf{C}}'_S \hbox {d}\tau ,\\ \mathbf{K}_2= & {} \int _0^{2m\pi } {h_{\left( {x_{20} -\varDelta } \right) } \mathbf{C}_S^T } \mathbf{C}_S \hbox {d}\tau ,\\ \mathbf{K}_3= & {} \int _0^{2m\pi } {x_{10} \mathbf{C}_S^T } \mathbf{C}_S \hbox {d}\tau ,\\ \mathbf{E}_1= & {} \int _0^{2m\pi } {h_{\left( {x_{20} -\varDelta } \right) } (x_{20} -\varDelta )\mathbf{C}_S^T } \hbox {d}\tau , \\ \mathbf{E}_2= & {} \int _0^{2m\pi } {x_{10}^2 \mathbf{C}_S^T } \hbox {d}\tau . \end{aligned}$$

The elements of the above integration matrices can be referred to Appendix.

Because the number of unknowns is greater than the equations, one unknown should be set in advance as the control increment. To obtain the amplitude–frequency curves of the system by solving Eq. (41), many methods have been proposed [13, 17,18,19] . The simplest way is to set $\Delta \varOmega =0$, and then, the Newton-Raphson interactions can be processed until the corrective vector norm $\left\| \mathbf{R}\right\|$ is smaller than a given convergence parameter. However, the unstable solutions cannot be obtained by this method. For a more universal approach, the arc-length method is adopted to track the unstable equilibrium paths that involve the “snap-backs” phenomena. In this paper, Crisfield’s procedure [29,30,31] is used to solve Eq. (41).

3.2 Stability of the periodic solution

Once the periodic solution is determined, the solution’s stability can be investigated by the Floquet theory [17]. First, the small perturbation ${\updelta \mathbf{q}}$ of $\mathbf q _{{0}}$ at $\varOmega _{0}$ can be expressed as

$$\begin{aligned} \mathbf {q}=\mathbf {q}_{0} +\updelta {\mathbf {q}} \end{aligned}$$

(45)

By substituting Eq. (1) into Eq. (26), the linearized equation can be obtained for the small perturbation ${\updelta \mathbf{q}}$ as follows:

$$\begin{aligned} \varOmega _{0}^{2} {\bar{\mathbf {M}}}\updelta {\ddot{\mathbf {q}}+}\varOmega _{0} ({\bar{\mathbf {C}}}_{L} +{\bar{\mathbf {C}}}_{\mathrm{NL}} )\updelta {\dot{\mathbf {q}}}+({\bar{\mathbf {K}}}_{L} {+}{\bar{\mathbf {K}}}_{\mathrm{NL}} )\delta \mathbf {q}=0\nonumber \\ \end{aligned}$$

(46)

Transforming above equations into linear ordinary differential equations,

$$\begin{aligned} {\dot{\mathbf {Z}}}=\mathbf {Q}(\tau )\mathbf {Z} \end{aligned}$$

(47)

where

$$\begin{aligned} \mathbf{Z}= & {} {\left[ {\updelta {\mathrm{q}_1},\updelta {\mathrm{q}_2}} \right] ^T},\mathbf{Q}(\tau ) \nonumber \\= & {} \left[ {\begin{array}{*{20}{c}} \mathbf{0}&{}\mathbf{I}\\ { - \,\frac{{{{\bar{\mathbf{K}}}_L} + {{\bar{\mathbf{K}}}_{\mathrm{NL}}}}}{{\varOmega _0^2\bar{\mathbf{M}}}}}&{}{ - \,\frac{{{{\bar{\mathbf{C}}}_L} + {{\bar{\mathbf{C}}}_{\mathrm{NL}}}}}{{{\varOmega _0}\bar{\mathbf{M}}}}} \end{array}} \right] \end{aligned}$$

(48)

$\mathbf{0}$ is the $2\times 2$ null matrix, and I is the $2\times 2$ unit matrix. It can be seen that matrix Q($\tau )$ has the same period with $\mathbf q _{0}$ [15]. Friedmann [32] proposed an efficient numerical approach to approximate the periodic matrix with a set of step functions, namely the matrix Q($\tau$) keeps the same figure in a relatively small range of time. In this case, period $2m\uppi$ is divided into $N_{\mathrm {k}}$ intervals for numerical computation, and the $k\hbox {th}$ interval is [$\tau _{\mathrm {k-1}}$, $\tau _{\mathrm {k}}$] with the interval length of $\varDelta _{\mathrm {k}}=\tau _{\mathrm {k}}-\tau _{\mathrm {k-1}}$. Thus, the constant matrix $\mathbf C _{\mathrm {k}}$ can be written as

$$\begin{aligned} \mathbf {C}_{{\mathrm{k}}} =\frac{1}{\Delta _{k} }\int _{\tau _{k-1} }^{\tau _{k} } {\mathbf {Q}\left( \tau \right) \hbox {d}\tau } \end{aligned}$$

(49)

After the constant matrix $\mathbf C _{\mathrm {k}}$ is obtained, the transition matrix or the monodromy matrix, which is used to decide the stability of the system, can be expressed:

$$\begin{aligned} \mathbf {P}\,{=}\,\prod \limits _{i=1}^{N_{k} } {\exp (\mathbf {C}_{{\mathrm{k}}} \Delta _{k} )} \end{aligned}$$

(50)

The terms $\hbox {exp}(\mathbf C _{\mathrm {k}}\Delta _{\mathrm {k}})$ are expanded with the Taylor formula for programming:

$$\begin{aligned} \mathbf{P} = \prod \limits _{i = 1}^{{N_k}} {\left( \mathbf{I} + \sum \limits _{j = 1}^M {\frac{{{{\left[ {{\varDelta _i}{\mathbf{C}_i}} \right] }^j}}}{{j!}}} \right) } \end{aligned}$$

(51)

where M is the number of terms in the approximation of the constant matrix exponential [18]. In this paper, M is set to 4. The stability of the solution can be decided by the eigenvalues of matrix P which are called Floquet multipliers [17]. If any of the Floquet multipliers has a module that is greater than one, then the solution is unstable. Namely [15],

• (1) A real Floquet multiplier moves out of the unit circle, and the remaining Floquet multipliers stay inside the unit circle; and

• (2) A pair of conjugate Floquet multipliers move out of the unit circle, and the remaining Floquet multipliers stay inside the unit circle.

For sub-harmonic resonances, a proper value of m can be set to acquire the 1/m sub-harmonic resonance of the system, and the stability of these responses can also be checked by the above procedure.

Table 1 System parameters

Table 2 Computation results of IHBM on different values of $N_\mathrm{m}$ for $\mu _{\mathrm{cr}} =2.0698$ and $\varOmega =0.36$

4 Numerical simulation and discussion

4.1 Numerical simulation and validation

To demonstrate the accuracy of IHBM, the amplitude–frequency curves and phase diagrams of the piecewise-linear quarter-car model are solved by both IHBM and the Runge–Kutta method (RKM). System parameters used in the simulation are given in Table 1.

Here, the simulations are presented with the sprung mass ratio of $\mu _{\mathrm{cr}}=2.0698 \,(m_{2}=m_{2\mathrm{cr}})$. First, the number of the harmonic terms $N_{\mathrm{m}}$ in the simulation is investigated. It can be seen from the Table 2 that the results of IHBM are close to the solution presented by RKM with increasing value of $N_{\mathrm{m}}$. When $N_{\mathrm{m}}=1$, the solution obtained with IHBM, which can be regarded as the solution obtained with the average method, does not match well with the result of RKM. To improve the accuracy of simulation and to save the computation consumption, $N_{\mathrm{m}}$ is set to 6 in this paper.

Fig. 3

Phase diagrams of the system DOFs at a $\varOmega =0.4$ and b $\varOmega =1.2$

Fig. 4

Response diagram for $\mu =2.0698$: a frequency response curve of the amplitude of $x_{1}$, b frequency response curve of the amplitude of $x_{2}$ and c the eigenvalues of the monodromy matrix compared with $\varOmega$

Then, Figs. 3 and 4 show the nonlinear dynamic responses of the quarter-car model by using both IHBM and RKM, and the results are in good agreement with one another. Figure 3 shows the phase diagrams of both DOFs at the non-dimensional frequencies $\varOmega =0.36$ and $\varOmega =1.20$, which indicate the two peaks of the frequency response curves. In Fig. 3, the solid line ‘-’ denotes the IHBM solutions, and the dot denotes the RKM solutions. In the primary resonance peak, more than one harmonic term contributes to the vibration of both DOFs under one external harmonic excitation, which shows nonlinear characteristics of the system. However, in the second resonance peak, only one harmonic term works which indicates that the nonlinearity is weak at the presented state.

An interesting phenomenon can be found when the sprung mass ratio is close to a certain value. In Fig. 4, the frequency response curves of both DOFs with a mass ratio of $\mu _{\mathrm{cr}} =2.0698$ are studied. The black circle represents the numerical results from RKM, and the solid line denotes the calculation solutions from IHBM. It can be observed from Fig. 4c that between $\varOmega =0.6803$ and $\varOmega =0.7457$, the fundamental solutions lose stabilities with one of their Floquet multipliers that leaves the unit circle. This finding is consistent with Fig. 4a, b, and the period-1 solutions of IHBM do not match with the period-1 solutions of RKM in this unstable region, which means that sub-harmonic or chaos resonances exist in this region. Figure 5 shows 1/2 sub-harmonic response of both DOFs at $\varOmega =0.70$, and it can be seen that the harmonic terms $0.5\varOmega$ and $1.5\varOmega$ play an important role in vibration responses. In Fig. 6, the sub-harmonic resonances of these unstable regions are investigated. The black solid and dashed lines denote the stable and unstable solutions, respectively, of the fundamental resonances with IHBM, and the red solid line represents the sub-harmonic resonances with IHBM. The 1/2 sub-harmonic resonances can be found with the “snap-back” phenomenon, which indicates the strong coupled nonlinearities of both DOFs in this region. This finding is different from the SDOF piecewise-linear system. Other 1 / m sub-harmonic resonances are not found in the frequency response curves, mainly because of the existence of the second order resonance of the system.

4.2 Effect of the auxiliary leaf spring’s stiffness on the dynamic response of the system

The auxiliary leaf spring’s stiffness that is discussed in this section is an essential parameter for suspension design. As seen in Fig. 4, two resonance peaks exist in the frequency response curves, and the primary resonance peak that represents the resonance of $x_{2}$ has a larger amplitude. To reduce the vibrations of the model, the effect of the auxiliary leaf spring’s stiffness ratio $\nu _{3}$ on the primary resonance peak is discussed in this section. The frequency response curves of the $x_{2 }$ of different load states with five different auxiliary leaf spring stiffness ratios, namely $\nu _{3}=0$. 184, 0.285, 0.368, 0.736 and 1.104, are shown in Figs. 7 and 8. The black solid line denotes the system in which the stiffnesses of the main and auxiliary leaf spring are the same, and the black dash dot line represents the absolute value of the critical distance of each case.

Usually, the stiffness of the auxiliary leaf spring is set a larger value than that of the main leaf spring. It can be seen from these figures that the existence of the auxiliary leaf spring with larger stiffness will decrease the maximum amplitude in both the light and heavy load states. Thus, a proper design of the auxiliary leaf spring can contribute to the reduction in the suspension vibration. In addition, at the light load state, when the displacement of $x_{2}$ increases, the spring of suspension becomes stiff as the stiffness changes from $k_{2}$ to $k_{2}\,+\,k_{3}$. As a result, the system shows a “harden” characteristic, which is similar to a “harden” Duffing oscillator [33]. It can be seen from Fig. 7 that the resonance peak of the frequency response curve moves to the right when the displacement of $x_{2}$ is greater than the absolute value of $\varDelta _{1}$. The similarity of the heavy load state system to the “soft” Duffing oscillator can also be concluded.

Fig. 5

Vibration of 1/2 sub-harmonic response for $\varOmega =0.7$: a time history of $x_{1}$, b time history of $x_{2}$, c Fourier spectrum of $x_{1}$ and d Fourier spectrum of $x_{2}$

4.3 Effect of the sprung mass ratio on the dynamic response of the system

In this section, the effect of the sprung mass ratio $\mu$ on the dynamic responses of the piecewise quarter-car model is investigated with IHBM, and the other parameters remain the same as in previous analyses. From Fig. 9, when the sprung mass ratio $\mu$ is larger, the amplitude of both $x_{1}$ and $x_{2}$ are larger for the primary resonance. It can be concluded that if the truck is overloaded, it will be very dangerous because the amplitude of the displacement can exceed the designed dynamic deflection of the suspension.

In addition, the sub-harmonic resonances can be found on some sprung mass ratios that are close to a certain value. The existence of an unstable region where the frequency varies from 0.6 to 0.9 can be determined by the Floquet multipliers for all of the possible sprung mass ratios of $\mu$ from 1.25 to 3.0. This unstable region that includes 1 / m sub-harmonic resonances or chaotic vibration will greatly increase the response amplitude in this frequency region, which is shown in Fig. 9.

From Fig. 10, the unstable region occurs when the sprung mass ratio $\mu$ changes from 1.508 to 2.767. The entire unstable region that comprises the frequency and the mass ratio presents a ‘gourd’ shape, and the boundary frequencies of the unstable region decrease with the mass ratio increases until $\mu \approx 2.40$ where the maximum difference between the upper and lower boundary frequencies occurs. Afterward, the difference begins to decrease and become zero when $\mu =2.767$.

4.4 Effect of the main leaf spring’s damping on the dynamic response of the system

In Sect. 4.3 the unstable region is discussed for various sprung mass ratios, and these regions should be avoided in engineering by changing the system parameters. The proper way to avoid these regions is to add a vibration isolation system to increase the main leaf spring’s damping of the suspension [19, 25].

Fig. 6

Partial enlarged plot of the unstable region of $\mu _{\mathrm{cr}} =2.0698$: a frequency response curve of the amplitude of $x_{1}$ and b Frequency response curve of the amplitude of $x_{2}$

In this section, the effect of the main leaf spring’s damping on the dynamic response of system is discussed, and other parameters remain the same. Figure 11 shows that with the increasing damping coefficient of the main leaf spring, the fundamental tendency of the frequency response curves remains unchanged, but the amplitudes of the primary resonance and the sub-harmonic resonance decrease markedly for both DOFs. Meanwhile, the frequency interval of the unstable region will be reduced with greater values of damping coefficients, and when the damping coefficients $\eta _{2}=1.6000 \,(\mu =\mu _{\mathrm{cr}})$, an unstable region is not detected.

Based on the above analysis, the main leaf spring’s damping will decrease the sub-harmonic resonance, Fig. 12 illustrates the unstable region that is calculated for different main leaf springs’ damping coefficients for all of the possible sprung masses of $m_{2}$ from 600 to 1400 kg ($\eta _{2}=0.3310$, $\eta _{2}=0.6628$, $\eta _{2}=0.9930$, and $\eta _{2}=1.6000$). According to Fig. 12, when the value of $\eta _{2}$ grows, the unstable region quickly diminishes. For $\eta _{2}\approx 1.617$, all of the Floquet multipliers are in the unit circle, which indicates that all of these solutions are stable. This results can be instructive for the design of a suspension vibration absorber.

Fig. 7

Partial enlarged plot of the frequency response curves of the amplitude of $x_{2}$ in the light load state case where $\mu =1.2698$

Fig. 8

Partial enlarged plot of the frequency response curves of the amplitude of $x_{2}$ in the heavy load state case where $\mu =5.2910$

Fig. 9

Frequency response curves for different unsprung mass ratios: a frequency response curve of the amplitude of $x_{1}$ and b frequency response curve of the amplitude of $x_{2}$

Fig. 10

Unstable region calculated by the Floquet theory for mass ratio from 1.25 to 3.0 and frequencies from 0.6 to 0.9 (the shadow region refers to the unstable region)

Fig. 11

Frequency response curves for $\mu =2.0698$: a frequency response curve of the amplitude of $x_{1}$ and b frequency response curve of the amplitude of $x_{2}$

Fig. 12

Unstable region calculated by the Floquet theory for different main leaf springs’ damping coefficients

5 Conclusion

In this study, the nonlinear dynamic behavior of a 2-DOF quarter-car truck model with a piecewise-linear leaf spring is studied with IHBM. The effect of the auxiliary leaf spring’s stiffness, the sprung mass ratio and the main leaf spring’s damping on the nonlinear dynamic responses are discussed. The results can be summarized as follows.

• 1. The periodic motion of the system is investigated with IHBM, and the results obtained by IHBM compare well with the results that are calculated by the RKM. The sub-harmonic resonance on the frequency response curve can be found with the ‘snap-back’ characteristic due to the coupled influence of both DOFs.

• 2. The effect of the auxiliary leaf spring’s stiffness on the dynamic response of the system is investigated. The piecewise-linear stiffness of a leaf spring shares similar characteristics with the stiffness of a Duffing oscillator. Additionally, the proper design of an auxiliary leaf spring contributes to the reduction in the suspension vibration.

• 3. The effect of the sprung mass ratio on the dynamic response of the system is investigated. The amplitudes of both $x_{1}$ and $x_{2}$ for the primary resonance are found to increase as the sprung mass increase. The unstable region will occur at certain sprung mass ratios.

• 4. The effect of the main leaf spring’s damping on the dynamic response of the system is investigated. It is found that when the damping coefficient increases, the amplitude of the response curve, as well as the unstable region, has a significance decline. When $\eta _{2}\approx 1.617$, the unstable region is diminished.

Appendix

The analytical expressions of the unknown matrices are listed below:

$$\begin{aligned}&[\mathbf {M}_{1} ]_{ij} =\left\{ {\begin{array}{lll} \frac{j^{2}\pi \delta _{ij} }{m},i=0,1,\ldots ,N;j=0,1,\ldots ,N \\ \frac{(j-N)^{2}\pi \delta _{ij} }{m},i=N+1,\ldots ,2N;\\ \quad j=N+1,\ldots ,2N \\ \end{array}} \right. \\&[\mathbf {C}_{1} ]_{ij} =\left\{ {\begin{array}{lll} j\pi \beta _{ij} ,i=0,1,\ldots ,N;j=0,1,\ldots ,N \\ (j-N)\pi \beta _{ij} ,i=N+1,\ldots ,2N;\\ \quad j=N+1,\ldots ,2N \\ \end{array}} \right. \\&[\mathbf {K}_{1} ]_{ij} =\alpha _{i} m\pi \delta _{ij} ,i=0,1,\ldots ,N;j=0,1,\ldots ,N\\&{\mathbf{C}_2} = \left[ {\begin{array}{*{20}{c}} {\mathbf{C}_2^{cc}}&{}\quad {\mathbf{C}_2^{cs}}\\ {\mathbf{C}_2^{sc}}&{}\quad {\mathbf{C}_2^{ss}} \end{array}} \right] , {\mathbf{K}_2} = \left[ {\begin{array}{*{20}{c}} {\mathbf{K}_2^{cc}}&{}\quad {\mathbf{K}_2^{cs}}\\ {\mathbf{K}_2^{sc}}&{}\quad {K_2^{ss}} \end{array}} \right] , {\mathbf{E}_1} = \left[ {\begin{array}{*{20}{c}} {\mathbf{E}_1^c}\\ {\mathbf{E}_1^s} \end{array}} \right] \end{aligned}$$

Consider a period $2\uppi$, where $\theta _{0} =0$ and $\theta _\mathrm{M+1}=2\uppi$. There are M zeros of $q_{20}= \quad \Delta$, denote as $\theta _{{1}}$, $\theta _{{2}},\ldots \theta _{{\mathrm{M}}}\,(\theta _{{1}}<\theta _{{2}}<\ldots <\theta _\mathrm{M})$.

$$\begin{aligned}&\left[ {\mathbf {C}_{2}^{cc} } \right] _{ij} =-\,\alpha _{i} j\sum \limits _{l=0}^M h_{(q_{20} -\varDelta )} (B_{ij} (\theta _{l+1} )\\&\quad \quad -\,B_{ij} (\theta _{l} )) ,i=0,1,\ldots ,N;j=0,1,\ldots ,N\\&\left[ {\mathbf {C}_{2}^{cs} } \right] _{ij} =\alpha _{i} j\sum \limits _{l=0}^M h_{(q_{20} -\varDelta )} (A_{ij} (\theta _{l+1} )\\&\quad \quad -\,A_{ij} (\theta _{l} )) ,i=0,1,\ldots ,N;j=1,\ldots ,N\\&\left[ {\mathbf {C}_{2}^{sc} } \right] _{ij} =-\,j\sum \limits _{l=0}^M h_{(q_{20} -\varDelta )} (D_{ij} (\theta _{l+1} )\\&\quad \quad -\,D_{ij} (\theta _{l} )) ,i=1,\ldots ,N;j=0,1,\ldots ,N\\&\left[ {\mathbf {C}_{2}^{ss} } \right] _{ij} =j\sum \limits _{l=0}^M h_{(q_{20} -\varDelta )} (C_{ij} (\theta _{l+1} )\\&\quad \quad -\,C_{ij} (\theta _{l} )) ,i=1,\ldots ,N;j=1,\ldots ,N\\&\left[ {\mathbf {K}_{2}^{cc} } \right] _{ij} =\alpha _{i} \alpha _{j} m\sum \limits _{l=0}^M h_{(q_{20} -\varDelta )} (A_{ij} (\theta _{l+1} )\\&\quad \quad -\,A_{ij} (\theta _{l} )) ,i=0,1,\ldots ,N;j=0,1,\ldots ,N\\&\left[ {\mathbf {K}_{2}^{cs} } \right] _{ij} =\alpha _{i} m\sum \limits _{l=0}^M h_{(q_{20} -\,\varDelta )} (B_{ij} (\theta _{l+1} )\\&\quad \quad -\,B_{ij} (\theta _{l} )) ,i=0,1,\ldots ,N;j=1,\ldots ,N\\&\left[ {\mathbf {K}_{2}^{sc} } \right] _{ij} =\alpha _{j} m\sum \limits _{l=0}^M h_{(q_{20} -\,\varDelta )} (C_{ij} (\theta _{l+1} )\\&\quad -\,C_{ij} (\theta _{l} )) ,i=1,\ldots ,N;j=0,1,\ldots ,N\end{aligned}$$

$$\begin{aligned}&\left[ {\mathbf {K}_{2}^{ss} } \right] _{ij} =m\sum \limits _{l=0}^M h_{(q_{20} -\varDelta )} (D_{ij} (\theta _{l+1} )\\&\quad -\,D_{ij} (\theta _{l} )) ,i=1,\ldots ,N;j=1,\ldots ,N\\&{\left[ {\mathbf{E}_1^c} \right] _i} = m\sum \limits _{l = 0}^M {h_{({q_{20}} -\, \Delta )}}\left\{ \sum \limits _{j = 0}^N {\alpha _j}\left[ {a_{1j}}({A_{ij}}({\theta _{l + 1}})\right. \right. \\&\left. \left. \quad -\, {A_{ij}}({\theta _l})) + {b_{1j}}({B_{ij}}({\theta _{l + 1}}) - {B_{ij}}({\theta _l})) \right] \right. \\&\left. \quad - \,\Delta ({E_{ij}}({\theta _{l + 1}}) - {E_{ij}}({\theta _l}))\right\} ,i = 0,\ldots ,N\\&{\left[ {\mathbf{E}_1^s} \right] _i} = m\sum \limits _{l = 0}^M {h_{({q_{20}} - \Delta )}}\left\{ \sum \limits _{j = 0}^N {\alpha _j}\left[ {a_{1j}}({C_{ij}}({\theta _{l + 1}}) \right. \right. \\&\left. \left. \quad -\, {C_{ij}}({\theta _l})) + {b_{1j}}({D_{ij}}({\theta _{l + 1}}) - {D_{ij}}({\theta _l})) \right] \right. \\&\left. \quad -\, \Delta ({F_{ij}}({\theta _{l + 1}}) - {F_{ij}}({\theta _l}))\right\} ,i = 1,\ldots ,N\\&[\mathbf {K}_{3} ]_{i,j} =\frac{m\pi }{4}\left\{ {\begin{array}{ll} a_{10},&{}\quad i=0;j=0 \\ 2a_{1i},&{}\quad i\ne 0;j=0 \\ 2a_{{1}j}, &{}\quad i=0;j\ne 0 \\ 2(a_{1(i+j)} +\varphi _{ij} a_{1\left| {i-j} \right| } ),&{}\quad \hbox { otherwise} \\ \end{array}} \right. \\&q_{20}^{2} =\left[ {\frac{1}{2}a_{{2}0} {+}\sum \limits _{i={1}}^N {\left( {a_{{2}i} \cos \frac{i\pi }{m}+b_{{2}i} \sin \frac{i\pi }{m}} \right) } } \right] ^{{2}}\\&\qquad =\text{ G }_{{0}} {+}\sum \limits _{i={1}}^{{2}N} {\left( {G_{i} \cos \frac{i\pi }{m}+H_{i} \sin \frac{i\pi }{m}} \right) }\\&[\mathbf {E}_{2} ]_{i} =m\pi \left\{ {\begin{array}{ll} G_{0}, &{}\quad i=0 \\ G_{i},&{}\quad i=1,\ldots ,N \\ H_{i-N},&{}\quad i=N+1,\ldots ,2N \\ \end{array}} \right. \end{aligned}$$

where $\delta _{ij} =\left\{ {\begin{array}{ll} 1,&{}\, i=j \\ 0,&{}\, i\ne j \\ \end{array}} \right.$, $\alpha _{i} =\left\{ {\begin{array}{ll} 0.5,&{}\, i=0 \\ 1,&{}\, i\ne 0 \\ \end{array}} \right.$ , $\beta _{ij} =\left\{ {\begin{array}{ll} -\,1,&{}\, i=j+N \\ 1,&{}\, j=i+N \\ 0,&{}\, \mathrm{otherwise} \\ \end{array}} \right.$ , $\varphi _{ij} =\left\{ {\begin{array}{ll} 2,&{}\, i=j \\ 1,&{}\, i\ne j \\ \end{array}} \right.$ . And expressions of $A_{ij} ,B_{ij} ,C_{ij} ,D_{ij} ,E_{i} ,F_{i}$ can be referred to Wong [18].