Nonlinear dynamic responses of high-speed railway vehicles under combined self-excitation and forced excitation considering the influence of unsteady aerodynamic loads

Abstract

The dynamic characteristics of a railway vehicle system under unsteady aerodynamic loads are examined in this study. A dynamic analysis model of the railway vehicle considering the influences of aerodynamic loads was established. The model not only considers the forced excitation effect of unsteady aerodynamic loads but also accounts for the effect of unsteady aerodynamic loads on the change of the wheel–rail contact normal forces as well as changes of the wheelset creep coefficients and creep forces/moments. Therefore, this model also considers the influences of unsteady aerodynamic loads on the self-excited vibration characteristics of the vehicle system. The time-history curves, phase trajectory diagrams, Poincaré sections, and Lyapunov exponents of the vehicle system running on a smooth straight track under unsteady aerodynamic loads were determined. The results show that when the critical speed is exceeded, the vehicle system usually performs quasi-periodic motion under unsteady aerodynamic loads, which is significantly different from the periodic motion under steady aerodynamic loads. In different cases, the amplitude and phase of motion are significantly different. The amplitude of the motions can be increased by more than 159%, and the difference of phase can be up to 173°. (The phase is almost reversed.) The dynamic responses of the vehicle system under unsteady aerodynamic loads contain abundant frequency components, including the frequency of the self-excited vibration, the frequency of the forced excitation, and combinations of their integer multiples. The vibration forms corresponding to the main harmonic components under unsteady and steady aerodynamic loads were compared, and the self-excited vibration component of the vehicle system under unsteady aerodynamic loads was identified. The variations in the critical speed with various parameter combinations were computed. The variation range of the critical velocity can reach 73%.

1 Introduction

The dynamic characteristics of railway vehicles are important to the train operation. The hunting stability and ride comfort of railway vehicles are related to the self-excited and forced vibrations, respectively. There have been many studies on vehicle self-excited and forced vibrations that did not consider the effects of aerodynamic loads.

Many studies related to the hunting stability and the critical speed in the self-excited vibrations of vehicles have been conducted. Some of this research focused on wheelsets and bogies [1,2,3,4]. To analyze the dynamics of railway vehicles more comprehensively and accurately, a complete dynamic analysis model including the wheelset, frame, and car body can be established. Kim and Seok [5] used the multiple scales method to conduct bifurcation analysis of a nonlinear railway vehicle with dual bogies to examine the coupling effect of bogies on the vehicle’s hunting behavior. Di Gialleonardo et al. [6] analyzed the effect of track modeling on railway vehicle stability. True [7] summarized the different methods that can be used to calculate the critical speed. He proposed that the nonlinear critical velocity of a vehicle system could be accurately calculated by the path following method or the ‘True Strategy.’ Iwnicki et al. [8] summarized the development history of railway freight vehicles, and they introduced the most common current train bogies in detail and new methods to simulate the dynamic performances of railway vehicles. Zboinski and Dusza [9] studied the nonlinear stability of railway vehicles on a curved track. They pointed out that this problem is a self-excited vibration problem in nature and studied its Hopf bifurcation characteristics. Zeng et al. [10] studied the influences of the wheelset gyroscopic action on the hunting stability of vehicle systems. Sun et al. [11] conducted observations and experiments on the hunting instability of an electric locomotive under the condition of low wheel–rail contact conicity and studied the optimization of the suspension parameters.

There have also been many studies on the forced vibrations of vehicles. Antolin et al. [12] established a vehicle–bridge coupled dynamics model considering nonlinear wheel–rail contact forces and analyzed the dynamic interactions between a high-speed train and a bridge. Xu and Zhai [13] proposed a stochastic analysis and reliability evaluation model for a vehicle–track coupled system considering earthquakes and random track irregularities to study the dynamic responses. Sadeghi et al. [14] studied the impact of ballast-less track irregularities on the ride performances of high-speed trains. Yang et al. [15] used three-dimensional modal theory to analyze the dynamics of a train–track coupled system. Cheng and Wu [16] studied the influences of the suspension parameters, wheel tread conicity, and wheel radius on the derailment safety and ride comfort of railway vehicles. Bokaeian et al. [17] applied the equivalent linearization method to analyze the ride comfort of a car body considering the traction rod. Dumitriu and Stănică [18] investigated the effects of an anti-yaw damper on the vertical vibrations and ride comfort of the car body. Ma et al. [19] analyzed the medium- and high-frequency dynamic resonance due to the interactions of multiple flexible wheels and rails of high-speed railways. Some other developments in structural dynamics response modeling and analysis can be found in studies by Keshtegar et al. [20], Fei et al. [21, 22], and Lu et al.[23].

For the most part, the above studies did not consider the influences of aerodynamic loads. The aerodynamic loads acting on a train are proportional to the square of the operating speed. With the continuous increase in the train running speed, the aerodynamic loads have more and more significant effects on the hunting stability and dynamic responses of high-speed railway vehicles. In recent years, more research has been conducted to study the effects of aerodynamic loads on the dynamic responses of high-speed trains.

Some research mainly focused on the flow field distributions around high-speed trains and the aerodynamic loads acting on the vehicles [24,25,26]. These studies did not involve the dynamic responses of the vehicle systems under aerodynamic loads. There have also been studies on the dynamic responses of vehicles under aerodynamic loads. Baker et al. [27] proposed a method to generate the aerodynamic load time histories acting on a train and then analyzed the dynamic responses of the vehicle. Thomas et al. [28] simulated the effects of crosswinds by applying lateral excitations on the car body and studied the dynamic responses of railway vehicles under aerodynamic loads experimentally and numerically. Xu and Zhai [29] investigated the dynamic behaviors and statistical responses of vehicle systems considering unsteady aerodynamics and track irregularities. Montenegro et al. [30] studied the influences of random turbulent wind on the dynamics of vehicle–bridge systems. Neto et al. [31] conducted a numerical study on the safety of train operation under crosswind conditions.

The above-mentioned research on the dynamic responses of high-speed trains under unsteady aerodynamic loads only used aerodynamic loads as a forced excitation and analyzed the forced vibration responses of the vehicles. The influences of aerodynamic loads on the inherent characteristics of vehicle systems were not considered. However, aerodynamic loads not only affect the forced vibration responses of the train through external forced excitations but also by changing the inherent characteristics of the dynamical system, such as its damping and stiffness, thus affecting the hunting stability of the train (self-excited vibration characteristics). The aerodynamic load components in various directions can change the creep coefficients by changing the normal force of the wheel–rail contact. The change of the normal force will also change the gravitational stiffness and the gravitational angular stiffness. Therefore, the existence of aerodynamic loads changes the damping and stiffness matrices on the left side of the vehicle system dynamics equation and changes the inherent characteristics of the high-speed train dynamical system. The quantitative analysis results of Zeng et al. [32,33,34] showed that these changes caused by steady aerodynamic loads have a significant influence on the hunting stability of high-speed trains. According to the mechanism described above, the unsteady aerodynamic loads will certainly affect the self-excited vibration characteristics of the vehicle. In addition, the unsteady aerodynamic loads also act as forced excitations to the vehicle dynamical system.

Steady aerodynamic loads are just a simplified case of unsteady aerodynamic loads. Not only is there a significant difference between the two cases in terms of the numerical values, but the combined action of the self-excited and forced vibrations under the action of unsteady aerodynamic loads will also lead to a dynamic response of the nonlinear vehicle system with richer harmonic components, where each harmonic component corresponds to a vibration form with a large difference in amplitude and phase. The internal mechanisms that create different harmonic components vary.

We briefly summarize the literature review above in Table 1. Many studies on the dynamic responses of railway vehicles did not consider the effects of aerodynamic loads. In other studies, the effect of aerodynamic loads was considered on either self-excited vibrations or only forced excitations. However, unsteady aerodynamic loads will lead to the combined action of both self-excitation and forced excitations, so it is prudent to consider this combined action during analysis. In the dynamics equations, the stiffness and damping matrices on the left side of the equation are changed by the aerodynamic loads, and the non-homogeneous terms caused by unsteady aerodynamic loads are added on the right side of the equation. This combined action will change not only the magnitude of the vehicle dynamic responses but also the inherent properties of the responses. However, there has been little research on the combined effect of self-excitation and forced excitations on railway vehicle systems, and this remains an open problem. In view of this, the present study examines these issues.

Table 1 Brief summary of literature review

In this paper, Sect. 2 explains the impacts of unsteady aerodynamic loads on the vehicle dynamics equations and presents the equations. In Sect. 3, we study the forced and self-excited vibration responses of a railway vehicle system running on a smooth straight track under unsteady aerodynamic loads in detail. Furthermore, we obtain the quasi-periodic solution, which is significantly different from the periodic solution under steady aerodynamic loads. We analyze and compare the vibration forms of the main harmonic components in the case of unsteady and steady aerodynamic loads and identify the self-excited vibration components of the vehicle system under unsteady aerodynamic loads. Finally, the conclusions are presented in Sect. 4.

2 Analysis model for railway vehicles under unsteady aerodynamic loads

2.1 Vehicle system

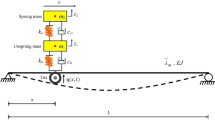
In this paper, a high-speed vehicle dynamics model considering aerodynamic loads was established. Figure 1 shows a schematic diagram of the vehicle dynamical system. The vehicle dynamical model is simplified into a multi-rigid-body dynamical system composed of wheelsets, frames, the car body, and the suspension systems. The vehicle system has 27 rigid-body degrees of freedom: the lateral displacement y_wi, pitch β_wi, and yaw ψ_wi of the wheelset (i = 1, 2, 3, 4); the lateral displacement y_fi, vertical displacement z_fi, roll ϕ_fi, pitch β_fi, and yaw ψ_fi of the frame (i = 1, 2); and the lateral displacement y_c, vertical displacement z_c, roll ϕ_c, pitch β_c, and yaw ψ_c of the car body. These are collectively expressed in the vector Y₁:

$$ {\mathbf{Y}}_{1} = \left[ \begin{gathered} y_{{{\text{w}}1}} \quad y_{{{\text{w2}}}} \quad y_{{{\text{w3}}}} \quad y_{{{\text{w4}}}} \quad \psi_{{{\text{w}}1}} \quad \psi_{{{\text{w2}}}} \quad \psi_{{{\text{w3}}}} \quad \psi_{{{\text{w4}}}} \quad \beta_{{{\text{w}}1}} \quad \beta_{{{\text{w2}}}} \quad \beta_{{{\text{w3}}}} \quad \beta_{{{\text{w4}}}} \hfill \\ y_{{{\text{f}}1}} \quad y_{{{\text{f2}}}} \quad z_{{{\text{f}}1}} \quad z_{{{\text{f2}}}} \quad \phi_{{{\text{f}}1}} \quad \phi_{{{\text{f}}2}} \quad \beta_{{{\text{f}}1}} \quad \beta_{{{\text{f2}}}} \quad \psi_{{{\text{f}}1}} \quad \psi_{{{\text{f}}2}} \quad y_{{\text{c}}} \quad z_{{\text{c}}} \quad \phi_{{\text{c}}} \quad \beta_{{\text{c}}} \quad \psi_{{\text{c}}} \hfill \\ \end{gathered} \right]^{{\text{T}}} . $$

(1)

Fig. 1

Schematic diagram of the railway vehicle dynamical system

The meanings of the other symbols in Fig. 1 are defined in “Appendix B”. It is assumed that the high-speed railway vehicle runs on a straight track without any irregularities at a constant speed V, and the track is set to be rigid. Assuming that there is no wheel lift and that the wheels are always in contact with the rails, the vertical displacement z_wi and roll ϕ_wi of the wheelset are determined by the wheel–rail geometry constraints. These are related to the vehicle lateral displacement and yaw and are not independent degrees of freedom.

The wheelsets and the frame are connected by the primary suspension, and the frames and the car body are connected by the secondary suspension. In addition, both the secondary lateral damping and the yaw damping are modeled by series-connected springs and dampers (Maxwell model). There are lateral displacements y_hx(L,R)i of the spring–damper connection point of the secondary lateral damper (i = 1, 2). There are longitudinal displacements y_sx(L,R)i of the spring–damper connection point of the secondary yaw damper (i = 1, 2). These degrees of freedom can be expressed collectively by the vector Y₂:

$$ {\mathbf{Y}}_{2} = \left[ {\begin{array}{*{20}c} {y_{{{\text{hxL}}1}} } & {y_{{{\text{hxR1}}}} } & {y_{{{\text{hxL2}}}} } & {\begin{array}{*{20}c} {y_{{{\text{hxR2}}}} } & {y_{{{\text{sxL1}}}} } & {y_{{{\text{sxR1}}}} } & {\begin{array}{*{20}c} {y_{{{\text{sxL2}}}} } & {y_{{{\text{sxR2}}}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{{\text{T}}} . $$

(2)

The dynamics equations of the vehicle system on a smooth straight track without any forced excitations can be expressed in matrix form as follows:

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{\ddot{Y}}}_{1} } \\ {\mathbf{0}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{1} \left( {{\dot{\mathbf{Y}}}_{1} ,{\mathbf{Y}}_{1} } \right)} & {\mathbf{0}} \\ {{\mathbf{C}}_{2} \left( {{\dot{\mathbf{Y}}}_{1} ,{\dot{\mathbf{Y}}}_{2} } \right)} & {{\mathbf{C}}_{3} \left( {{\dot{\mathbf{Y}}}_{1} ,{\dot{\mathbf{Y}}}_{2} } \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{Y}}}_{1} } \\ {{\dot{\mathbf{Y}}}_{2} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{1} \left( {{\dot{\mathbf{Y}}}_{1} ,{\mathbf{Y}}_{1} } \right)} & {{\mathbf{K}}_{2} } \\ {{\mathbf{K}}_{3} } & {{\mathbf{K}}_{4} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{Y}}_{1} } \\ {{\mathbf{Y}}_{2} } \\ \end{array} } \right\}\user2{ = }\left\{ \begin{gathered} {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill \\ \end{gathered} \right\}, $$

(3)

where M₁, C₁, and K₁ are the generalized inertia matrix, damping matrix, and stiffness matrix, respectively; C₂ and C₃ are the damping matrices of the lateral and yaw dampers, respectively; K₂, K₃, and K₄ are the supporting stiffness matrices of the spring–damper connection point of the lateral and yaw dampers. The detailed differential equations of motion for the vehicle system given by Eq. (3) are listed in “Appendix A”. The nomenclature used in the dynamics equations is given in “Appendix B”.

Equation (3) is the conventional vehicle dynamics equation that does not account for aerodynamic loads. The effects of unsteady aerodynamic loads are considered in this study, so Eq. (3) is modified. The influences of unsteady aerodynamic loads on the dynamics equations can be divided into two categories. The first is forced excitation forces added to the right side of Eq. (3), which make the dynamics equations of the vehicle system on a smooth straight track non-homogeneous. The second is that the aerodynamic loads change the wheel–rail normal forces, the geometric parameters (such as rolling circle radius of wheel–rail contact point), and the creep forces/moments, resulting in changes in the damping and stiffness matrices on the left side of Eq. (3). This will be explained in detail below.

2.2 Influences of aerodynamic loads

The distribution of the pressure and shear stress on the car body surface of a high-speed train in high-speed airflow can form resultant forces F_i (i = 1, 2, 3), called the aerodynamic drag force, aerodynamic lateral force, and aerodynamic lift force, which act in the longitudinal, lateral, and vertical directions, respectively. M_i (i = 1, 2, 3) represents the aerodynamic roll moment around the x-axis, the aerodynamic pitch moment around the y-axis, and the aerodynamic yaw moment around the z-axis, respectively. The forces and moments are expressed as follows:

$$ \begin{aligned} & F_{i} = \frac{1}{2}\rho AC_{i} \left| {{\mathbf{V}} + {\mathbf{U}}} \right|^{2} \quad C_{i} = C_{{{\text{s}}i}} + C_{{{\text{u}}i}} \cdot \sin \left( {2\pi f_{i} t + \varphi_{ci} } \right)\quad \left( {i = 1,2,3} \right) \\ & M_{i} = \frac{1}{2}\rho ALC_{Mi} \left| {{\mathbf{V}} + {\mathbf{U}}} \right|^{2} \quad C_{Mi} = C_{{M{\text{s}}i}} + C_{{M{\text{u}}i}} \cdot \sin \left( {2\pi f_{Mi} t + \varphi_{Mci} } \right)\quad \left( {i = 1,2,3} \right), \\ \end{aligned} $$

(4)

where ρ, A, and L are the air density, reference area, and reference length, respectively; V and U are the velocity vectors of the running speed of the vehicle and the crosswind, respectively; C_i (i = 1, 2, 3) represents the coefficients of the aerodynamic drag force, aerodynamic lateral force, aerodynamic lift force, respectively; C_Mi (i = 1, 2, 3) represents the coefficients of the aerodynamic roll moment, pitch moment, and yaw moment, respectively; C_si and C_Msi (i = 1, 2, 3) are the steady parts of the coefficients of the unsteady aerodynamic forces and moments, respectively; C_ui and C_Mui (i = 1, 2, 3) are the unsteady parts of the coefficients of the unsteady aerodynamic forces and moments, respectively; f_i and f_Mi (i = 1, 2, 3) are the excitation frequencies of the unsteady aerodynamic forces and moments, respectively; φ_c and φ_Mci (i = 1, 2, 3) represent the initial phase angles.

2.2.1 Wheel–rail contact geometry

The geometric relation of the wheel–rail contact is one of the most important nonlinear factors in railway vehicle systems. In this study, the wheel–rail contact point coordinates were calculated using three-dimensional space contact theory [35]. After obtaining the contact point coordinates, the corresponding vertical displacement z_w and roll ϕ_w of the wheelset as well as the geometric parameters, such as the rolling circle radius R_w, contact angle δ_w, wheel cross-sectional radius of curvature r_w, and track cross-section radius of curvature r_r at the contact point, were obtained. These geometric parameters were then used to calculate the creep forces/moments.

In conventional vehicle dynamics analysis, the influences of aerodynamic loads on the geometric parameters of the wheel–rail contact are not considered. In this study, the influences of aerodynamic loads on these geometric parameters are considered. The steady components of the aerodynamic loads change the static equilibrium position of the vehicle, causing the coordinates of the wheel–rail contact points in the static balance position to change, and then all the geometric parameters described above change due to the influences of the aerodynamic loads. The unsteady components in the aerodynamic loads make the vehicle vibrate around the new static equilibrium position. The coordinates of each instantaneous wheel–rail contact point and other wheel–rail contact geometry parameters are affected jointly by the steady and unsteady components. In this study, the influences of the aerodynamic loads mentioned above were taken into account when calculating the wheel–rail contact geometry parameters at each instant. In Sect. 2.2.3, it will be shown that the aerodynamic loads can further affect the creep forces by changing the wheel–rail contact geometry parameters.

2.2.2 Wheel/rail normal force

In conventional vehicle dynamics analysis, the influences of aerodynamic loads on the wheel–rail normal forces are not considered. Compared with the case where the aerodynamic loads are not considered, the normal wheel–rail contact forces change after considering the aerodynamic loads. The positive/negative aerodynamic lift force reduces/increases the axle load, the aerodynamic lateral force and aerodynamic roll moment cause the normal forces of the left and right wheel–rail contact points to be different, and the aerodynamic resistance and aerodynamic pitching moment cause the normal forces of the wheel–rail contact points of wheelsets in different longitudinal positions to be different. The aerodynamic loads change the restoring forces/moments of the vehicle system by changing the wheel–rail contact normal forces, thereby changing the gravitational stiffness/gravitational angular stiffness of the system. This will change the inherent characteristics of the system. In this study, we have considered the above-mentioned effects of unsteady aerodynamic loads when calculating the wheel–rail contact forces at each instant. In the next section, it will be shown that the aerodynamic loads can further affect the creep forces by changing the wheel–rail contact normal forces.

2.2.3 Wheel–rail creep force

In this study, Kalker’s linear creepage theory is used to calculate the creep forces/moments [36], and then a nonlinear creep model is used to modify the creep forces/moments [35]. The influences of unsteady aerodynamic loads on the creep forces/moments are not considered in conventional analysis. It will be shown in this section that the aerodynamic loads change the creep forces/moments in terms of both the creep coefficients and the correction factor.

According to Kalker's linear creepage theory, the wheel–rail contact creep forces/moment are as follows:

$$ \begin{aligned} & F_{x} = - f_{11} \xi_{x} \\ & F_{y} = - f_{22} \xi_{y} - f_{23} \xi_{\phi } \\ & M_{z} = - f_{32} \xi_{y} - f_{33} \xi_{\phi } , \\ \end{aligned} $$

(5)

where F_x, F_y, and F_z are the longitudinal creep force, lateral creep force, and spin creep moment in the wheel–rail contact plane, respectively; f_ij is the creep coefficient; ξ_x, ξ_y, and ξ_ϕ are longitudinal, lateral, and spin creepages, respectively.

The creep coefficient f_ij is related to the contact normal force and geometric parameters at the contact point, such as the rolling circle radius R_w, contact angle δ_w, wheel cross-sectional radius of curvature r_w, and track cross-sectional radius of curvature r_r at the contact points. As mentioned in Sect. 2.2.1, the above geometric parameters are all affected by aerodynamic loads, so the creep coefficients and creep forces/moment in Eq. (5) are also affected by aerodynamic loads.

Kalker's linear creepage theory is only applicable to the situation of a small linear creep and small spin. For this reason, a nonlinear correction can be used so that the calculation of the wheel–rail creep forces can be widely applied to the case of an arbitrary creepage value and small spin. We made the following corrections to the creep forces:

$$ F = \sqrt {F_{x}^{2} + F_{y}^{2} } , $$

(6)

$$ F^{\prime } = \left\{ {\begin{array}{*{20}l} {\mu N\left[ {\frac{F}{\mu N} - \frac{1}{3}\left( {\frac{F}{\mu N}} \right)^{2} + \frac{1}{27}\left( {\frac{F}{\mu N}} \right)^{3} } \right]} \hfill & {(F \le 3\mu N)} \hfill \\ {\mu N} \hfill & {(F > 3\mu N)} \hfill \\ \end{array} } \right., $$

(7)

where F, N, and F′ are the synthetic creep force, normal force, and modified synthetic creep force, respectively, and μ is the friction coefficient between the wheel and the rail. As mentioned in Sect. 2.2.2, the normal force N is also affected by unsteady aerodynamic loads.

The correction factor ε is introduced, which is defined as follows:

$$ \varepsilon = \frac{{F^{\prime } }}{F}. $$

(8)

Components of the modified creep forces/moment are obtained as follows:

$$ \begin{aligned} & F_{x}^{\prime } = \varepsilon \cdot F_{x} \\ & F_{x}^{\prime } = \varepsilon \cdot F_{y} \\ & M_{z}^{\prime } = \varepsilon \cdot M_{z} . \\ \end{aligned} $$

(9)

The above-mentioned creep forces/moment components are defined on the contact plane, and the dynamics equations in “Appendix A” are defined in the vehicle system coordinate system. Therefore, after calculating the above creep forces/moment components, a coordinate transformation is required to express the creep force/moment components as the components along the axes of the vehicle coordinate system.

In this study, we consider the unsteady aerodynamic loads described above when calculating the wheel–rail creep forces/moments at each instant. There are items related to the creep forces/moment in the damping and stiffness matrices of the vehicle dynamical system, so the change of the creep forces/moments will change the damping and stiffness matrices. This means that the unsteady aerodynamic loads will affect the inherent characteristics of the vehicle system by changing the creep forces/moments.

2.3 Equations of motion considering unsteady aerodynamic loads

In summary, the unsteady aerodynamic loads change the damping and stiffness matrices of the vehicle system dynamics equations by changing the wheel–rail contact geometry parameters, wheel–rail normal forces, and wheel–rail creep forces/moments. After considering the unsteady aerodynamic loads, Eq. (3) becomes the following:

$$ \begin{aligned} & \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{\ddot{Y}}}_{1} } \\ {\mathbf{0}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{1} \left( {C_{{{\text{s}}i}} ,C_{{{\text{u}}i}} ,C_{{M{\text{s}}i}} ,C_{{M{\text{u}}i}} ,{\mathbf{V}},{\mathbf{U}},{\dot{\mathbf{Y}}}_{1} ,{\mathbf{Y}}_{1} } \right)} & {\mathbf{0}} \\ {{\mathbf{C}}_{2} \left( {{\dot{\mathbf{Y}}}_{1} ,{\dot{\mathbf{Y}}}_{2} } \right)} & {{\mathbf{C}}_{3} \left( {{\dot{\mathbf{Y}}}_{1} ,{\dot{\mathbf{Y}}}_{2} } \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{Y}}}_{1} } \\ {{\dot{\mathbf{Y}}}_{2} } \\ \end{array} } \right\} \\ & \quad + \;\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{1} \left( {C_{{{\text{s}}i}} ,C_{{{\text{u}}i}} ,C_{{M{\text{s}}i}} ,C_{{M{\text{u}}i}} ,{\mathbf{V}},{\mathbf{U}},{\dot{\mathbf{Y}}}_{1} ,{\mathbf{Y}}_{1} } \right)} & {{\mathbf{K}}_{2} } \\ {{\mathbf{K}}_{3} } & {{\mathbf{K}}_{4} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{Y}}_{1} } \\ {{\mathbf{Y}}_{2} } \\ \end{array} } \right\}\user2{ = }\left\{ {\begin{array}{*{20}c} {{\mathbf{P}}_{{{\text{air}}}} \left( {C_{{{\text{s}}i}} ,C_{{{\text{u}}i}} ,C_{{M{\text{s}}i}} ,C_{{M{\text{u}}i}} ,{\mathbf{V}},{\mathbf{U}},t} \right)} \\ {\mathbf{0}} \\ \end{array} } \right\}, \\ \end{aligned} $$

(10)

where P_air is the vector of the aerodynamic loads, and ${\mathbf{C}}_{1} \left( {C_{{{\text{s}}i}} ,C_{{{\text{u}}i}} ,C_{{M{\text{s}}i}} ,C_{{M{\text{u}}i}} ,{\mathbf{V}},{\mathbf{U}},{\dot{\mathbf{Y}}}_{1} ,{\mathbf{Y}}_{1} } \right)$ and ${\mathbf{K}}_{1} \left( {C_{{{\text{s}}i}} ,C_{{{\text{u}}i}} ,C_{{M{\text{s}}i}} ,C_{{M{\text{u}}i}} ,{\mathbf{V}},{\mathbf{U}},{\dot{\mathbf{Y}}}_{1} ,{\mathbf{Y}}_{1} } \right)$ are the damping and stiffness matrices considering the effects of aerodynamic loads, respectively. The definitions of the other symbols are the same as those in Eq. (3).

A comparison of Eqs. (3) and (10) shows that after considering the unsteady aerodynamic loads, the forced excitation vector due to the aerodynamic loads is added to the right side of the vehicle system dynamics equations, and the damping and stiffness matrices on the left are affected by the unsteady aerodynamic loads. In other words, the unsteady aerodynamic loads not only add a forced excitation but also change the self-excited vibration characteristics of the vehicle system.

3 Numerical results and discussions

We have previously studied the influences of the steady aerodynamic loads on the stability of high-speed trains [32,33,34]. These studies showed that steady aerodynamic loads change the hunting stability of the train, causing significant changes in the critical speed. In the actual operation process, the aerodynamic loads acting on the railway vehicle are unsteady. Therefore, the influences of unsteady aerodynamic loads on the dynamic response of the vehicle system are analyzed in this study. The results showed that the vehicle dynamic response under unsteady aerodynamic loads includes both self-excited and forced vibration characteristics. This is fundamentally different from a vehicle under steady aerodynamic loads. The unsteady aerodynamic loads change the vehicle dynamic responses from periodic motion to quasi-periodic motion, increase the number of frequency components, change the vibration form, and change the critical velocity. This section presents these results in detail and analyzes the mechanism of the phenomena described above.

For verification, we compared the results with several published examples. The first two examples of the vehicle dynamic responses were taken from Refs. [37] and [38], which provided the time-history curves and phase trajectories of the wheelset at different speeds without aerodynamic loads. We recalculated the results for these two examples, and the results are shown in Figs. 2 and 3, where the solid line represents the results of this study and the triangular symbol represents the results from Refs. [37] and [38]. The results of the present study and Refs. [37] and [38] agree closely. The third example was from Ref. [39], which provided the bifurcation point of the vehicle system without aerodynamic loads. We recalculated this example, which is shown in Fig. 4. The comparison of the results showed good agreement. The fourth example was taken from Ref. [34], which considered the influences of steady aerodynamic loads and provided the time-history curves of the 1st wheelset and front frame in this case. We recalculated this example, which is shown in Fig. 5. The comparison of the results showed good agreement.

Fig. 2

Comparison of the results of this study and Ref. [37]: a V = 500 km/h and b V = 800 km/h

Fig. 3

Comparison of the results of this study and Ref. [38]: a time history at 322 km/h and b shift velocity versus displacement at 322 km/h

Fig. 4

Comparison of the results of this study and Ref. [39]. The effect of natural frequency and damping ratio on the bifurcation speed

Fig. 5

Comparison of the results of this study and Ref. [34]. Time history for a vehicle moving at a speed V = 280 km/h and under a centrifugal crosswind V_f = 10.7 m/s: a lateral displacement of the first wheelset and b lateral displacement of the front frame

We also made a comparison with experimental results. In Ref. [40], the critical speed of a vehicle with a new type of independently rotating wheelset with a negative tread conicity was studied experimentally using 1/10-scaled model roller rig. During the experiment, except for the rotation of the wheelset, the vehicle model had no forward speed, so it was hardly affected by aerodynamic loads. Ref. [40] showed the variation of critical speed with the suspension stiffness. We recalculated the results and compared them with the experimental results in Ref. [40], as shown in Fig. 6. Black solid points and error bars represent experimental values, and the blue solid line represents the results of the present study. Compared with Ref. [40], reasonably good agreement was obtained between our results and the experimental data.

Fig. 6

Variation of the critical speed with the longitudinal stiffness from the results of this study and Ref. [40]

The influences of unsteady aerodynamic loads on the dynamic responses of high-speed trains will be analyzed in detail. The fourth-order Runge–Kutta method was used to solve Eq. (10) during the computations. The details of Eq. (10) are given in “Appendix A”. The vehicle dynamics parameters are provided in “Appendix B”. The wheel–rail treads are LMA/CHN60, and the wheel–rail contact geometry parameters, such as the radius difference and contact angle difference associated with this type of tread, are shown in Fig. 7. The solid lines and the triangular symbols are the results of this study and Ref. [41], respectively, and they are in good agreement.

Fig. 7

Comparison of the results from our nonlinear wheel–rail subroutine with those from Ref. [41]: a radius difference and b contact angle difference of the wheels

The unsteady aerodynamic loads were computed by Eq. (4), where φ_ci = φ_Mci = 0 (i = 1, 2, 3). The frequency corresponding to the highest peak in the graph of the power spectral density versus frequency is between 0.5 and 4.0 Hz [42]. In this study, f_i = f_Mi = 1.0 Hz (i = 1, 2, 3) was taken as the representative frequency, and the analysis process is the same for other frequencies.

For a crosswind speed of 10 m/s and a wind direction perpendicular to the forward direction of the train, the aerodynamic force and moment coefficients, which were obtained based on the results given in Ref. [42], are shown in Table 2.

Table 2 Aerodynamic coefficients

3.1 Dynamic responses under steady aerodynamic loads

Before proceeding to the study of the vehicle dynamic responses under unsteady aerodynamic loads, we first analyze the dynamic responses under steady aerodynamic loads to serve as the basis for understanding the unsteady results. The comparison between the two can also clearly show new vehicle dynamic responses under unsteady aerodynamic loads and help to reveal the mechanism behind these responses in depth.

Based on the method presented in Ref. [34], we obtained the bifurcation diagram of the high-speed vehicle under steady aerodynamic loads, as shown in Fig. 8. The influences of the steady aerodynamic loads on the wheel–rail forces and creep coefficients were considered in the computations. Figure 8 shows the variation in the amplitude of the lateral displacement limit cycles of the wheelsets, frames, and car body with the running speed of the vehicle. The nonlinear critical speed of the vehicle was 524 km/h when considering the steady aerodynamic loads. We then examined the responses of the wheelsets, frames, and car body above the nonlinear critical speed. As expected, the computations showed that the response amplitudes are determined by the running speed, which reflects the self-excited vibration characteristics of the system. Figure 9 shows the time-history curves of the lateral displacement and the phase trajectories in phase plane of each component at a speed of 550 km/h.

Fig. 8

Bifurcation diagram under steady aerodynamic loads

Fig. 9

Time-history curves of the lateral displacement and phase trajectories in the phase plane for each part of the vehicle moving at a speed V = 550 km/h considering steady aerodynamic loads: a, b lateral displacements of the wheelsets, c, d lateral displacements of the frames, and e, f lateral displacement of the car body

The time-history curves and phase trajectories show that the lateral displacement amplitudes (that is, half the peak-to-peak values) of the 1st and 2nd wheelsets on the front frame are approximately the same, with values of 8.38 and 8.15 mm, respectively. The lateral displacement amplitudes of the 3rd and 4th wheelsets on the rear frame are about half the lateral displacement amplitudes of the 1st and 2nd wheelsets, with values of 3.80 and 4.56 mm, respectively. The lateral displacement amplitude of the front frame is 8.63 mm, and the amplitude of the rear frame is 4.70 mm, which is 54.46% of the amplitude of the front frame. The lateral amplitude of the car body is about half the lateral amplitude of the rear frame, which is 2.32 mm. In this case, each degree of freedom of the vehicle system forms an isolated closed-phase trajectory in the phase plane, namely a limit cycle.

We then investigated the Poincaré mapping of the vehicle dynamic responses under steady aerodynamic load conditions. The Poincaré section $\sigma = \left\{ {\left( {{\varvec{y}},V} \right) \in {\varvec{R}}^{54} \times {\varvec{R}}\left| {y_{w1} = 0,} \right.\dot{y}_{w1} < 0} \right\}$ was used to observe the projection of the intersection point of the motion trajectory and the hyperplane on the two-dimensional plane, as shown in Fig. 10. There is only one fixed point on each projection plane in this case, so the vehicle system is in periodic motion.

Fig. 10

Projections of the intersection points of the motion trajectory and the Poincaré section on several two-dimensional planes, under steady aerodynamic load conditions: a y_w1–y_w2 plane, b y_w1–y_w3 plane, c y_w1–y_w4 plane, d y_w1–y_f1 plane, e y_w1–y_f2 plane, and f y_w1–y_c plane

We now examine the frequency spectrum of the dynamic responses of the vehicle system. A fast Fourier transform (FFT) was applied to the time-history curve of the lateral displacement of the 1st wheelset to obtain its spectrum. In Fig. 11, the red line represents the spectrum of the lateral displacement of the 1st wheelset under steady aerodynamic load conditions; both the abscissa and ordinate are expressed in logarithmic coordinates. The red curve has multiple spikes, where the highest spike corresponds to the frequency f_s, indicating that the frequency of the harmonic component with the most significant amplitude is f_s. The amplitude of this harmonic component is more than 17 times those of the other harmonic components. The frequencies corresponding to other spikes are integer multiples of f_s. The reason for the appearance of these integer multiples of the harmonics is as follows: when the equilibrium position is in the center of the two tracks, nonlinear factors, such as the wheel–rail relationship, lead to the occurrence of odd multiples of the harmonics, and when the steady aerodynamic loads cause the equilibrium position to deviate from the center of the two tracks, both odd and even multiples appear [34]. A similar analysis can be performed on the other degrees of freedom to obtain the same result. Thus, the self-excited vibrations of the vehicle considering the influences of steady aerodynamic loads is a periodic solution with a frequency f_s.

Fig. 11

Frequency spectrum of lateral displacement of 1st wheelset under aerodynamic loads at a speed of 550 km/h

In summary, the time-history curve of the response for each degree of freedom of the wheelset, frame, and car body under steady aerodynamic loads is a periodic curve, and the phase trajectories in the phase plane form a limit cycle determined by the vehicle operating speed. This is shown as a single fixed point on the Poincaré section. The frequency spectrum is a discrete spectrum composed of a single peak with a frequency of f_s and small peaks at integer multiples of f_s. The dynamic response of the vehicle system considering the influences of the steady aerodynamic loads exceeding the nonlinear critical speed is a self-excited vibration with a period of 1/f_s, and its amplitude is determined by the running speed.

3.2 Dynamic responses under unsteady aerodynamic loads

The case with unsteady aerodynamic loads is significantly different from that with steady aerodynamic loads. In the case of unsteady aerodynamic loads, external excitations varying with time appear on the right side of the vehicle system dynamics equations, and the system dynamic responses become the dynamic responses under the combined action of the self-excited and forced excitations, which can also be said to be the forced vibration responses of the self-excited vibration system.

We next examine the time-history curves and phase trajectories in the phase plane of the response for each degree of freedom of the vehicle system under the action of unsteady aerodynamic loads. We performed simulations for many cases at different speeds, and the results show that although the numerical values of the responses of the vehicle system are different at different speeds, these results have similar dynamic characteristics. To facilitate the comparison with the case of steady aerodynamic loads in Sect. 3.1, the dynamic response of the vehicle system under unsteady aerodynamic loads at a speed of 550 km/h is specifically analyzed in this section.

Figure 12, like its counterpart from the case of steady aerodynamic loads (Fig. 9), shows the time-history curves and phase trajectories of the unsteady aerodynamic load case at a speed of 550 km/h. The phase trajectories in the phase plane shown in Fig. 12 (unsteady aerodynamic loads conditions) and Fig. 9 (steady aerodynamic loads conditions) are both projections of high-dimensional phase trajectories on a two-dimensional plane. The dynamical system under unsteady aerodynamic loads is a non-autonomous system. As is well known, a non-autonomous system can be turned into an autonomous system by adding additional dimensions. Therefore, the dynamical system under the unsteady aerodynamic loads can also be regarded as a higher-dimensional autonomous system than that under steady aerodynamic loads.

Fig. 12

Time-history curves and phase trajectories in the phase plane of the vehicle moving at a speed V = 550 km/h considering unsteady aerodynamic loads: lateral displacements of the a–e wheelsets, f–g frames, and h–i car body

The computations show that, different from the case of steady aerodynamic loads, the displacement time-history curves of the wheelsets, frames, and car body lose periodicity under unsteady aerodynamic loads. The corresponding phase trajectory projection curves are no longer closed curves but are entangled with a finite width. Figure 12 shows the time-history curves of the lateral displacement of each component and the corresponding phase trajectory projections. Because there is no periodicity, we use half the difference between the ordinates of the maximum and minimum extreme points of Fig. 12 as the nominal amplitude to measure the vibration magnitude of each component. The nominal amplitudes of the 1st and 2nd wheelsets on the front frame are 8.61 and 8.45 mm, respectively, and the nominal amplitudes of the 3rd and 4th wheelsets on the rear frame are 4.95 and 6.33 mm, respectively. The nominal amplitudes of the front and rear frames are 8.96 and 6.27 mm, respectively. The nominal amplitude of the car body is 3.31 mm. Compared with the case under steady aerodynamic loads, the lateral displacement amplitudes of the front frame and the 1st and 2nd wheelsets on it did not change significantly, increasing by 3.82%, 2.74%, and 3.68%, respectively. However, the lateral displacement amplitudes of the rear frame, the 3rd and 4th wheelsets on it, and the car body changed significantly, with increases of about 33.40%, 30.26%, 38.82%, and 42.67%, respectively. This indicates that the unsteady aerodynamic loads significantly increase the amplitudes of the components with smaller vibrations under steady loads. In fact, according to Fig. 7b, when the lateral displacement of the wheelset reaches 6.67 and 8.88 mm, the contact angle difference of the wheelset increases significantly. Once the lateral displacement of the wheelset exceeds these two values, the restoring force increases dramatically, which limits the increase in the lateral displacement of the wheelset. Therefore, the lateral displacements of the 1st and 2nd wheelsets do not increase much under unsteady aerodynamic loads, but the absolute value at the minimum point slightly exceeds 8.88 mm instantaneously. Although the lateral displacements of the 3rd and 4th wheelsets increase significantly, the lateral displacement of 3rd wheelset does not exceed 6.67 mm. The maximum value of the 4th wheelset exceeds 6.67 mm instantaneously, but does not exceed 8.88 mm.

The vehicle dynamical system under unsteady aerodynamic loads is a non-autonomous system. Thus, we can adopt the stroboscopic method [43], that is, sample the phase trajectory at a certain interval, to investigate the dynamic characteristics of the system. We performed a large number of computations in the frequency region where the values of the aerodynamic loads were large. The results showed that, overall, the dynamic response properties of the vehicle system caused by unsteady aerodynamic loads at different frequencies were similar. Therefore, the response of the vehicle system under unsteady aerodynamic loads with a period of 1 s is taken as a typical representative for analysis. We sampled every 1 s and projected the sampling points into the three-dimensional space, as shown in Fig. 13. The black points in Fig. 13 represent the sampling points projected into the three-dimensional space, and the red, blue, and green points represent the sampling points further projected on the two-dimensional planes. The sampling points on different two-dimensional planes are shown in Fig. 14 in more detail. The blue five-pointed stars, red circular dots, and black points in Fig. 14 represent the cases with 20, 60, and 10,000 sampling points, respectively. With the increase in the number of sampling points, projections of the intersections of the phase trajectory and the Poincaré section on a two-dimensional plane form a clearly defined closed curve, which is not blurred at all. This indicates that the dynamic response of the vehicle system under unsteady aerodynamic loads has a quasi-periodic solution.

Fig. 13

Distribution of the stroboscopic sampling points in three-dimensional space: a y_w1–y_w2–y_w3 and b ϕ _f2–ψ_f2–ψ_c

Fig. 14

Projection of stroboscopic sampling points on several two-dimensional planes: a y_w1–y_w2 plane, b y_w2–y_w3 plane, c y_w3–y_w4 plane, d y_w4–y_f1 plane, e ϕ _f2–ψ_f2 plane, and f ϕ_c–ψ_c plane

We can also determine the dynamic characteristics of the system by calculating the Lyapunov exponent spectrum of the vehicle dynamical system under unsteady aerodynamic loads. In this study, the BBA method [44] was used to determine the Lyapunov exponent spectrum of the reconstructed time series, and the first three largest Lyapunov exponents were obtained. The longer the time series used to calculate Lyapunov exponents is, the better the convergence of the obtained Lyapunov exponents to the true value becomes. Figure 15 shows the variations of the first three Lyapunov exponents with the length of the time series. The left ordinate indicates the values of the first three Lyapunov exponents with conventional Cartesian coordinates; the right ordinate has logarithmic coordinates to represent the maximum Lyapunov exponent, and the abscissa represents the length of the time series in logarithmic coordinates. When the length of time series increases, both the largest and the second largest Lyapunov exponents tend to zero, while the third largest Lyapunov exponent is always less than zero, which indicates that the response of the system is quasi-periodic.

Fig. 15

Convergence of the first three largest Lyapunov exponents λ₁, λ₂, and λ₃ with the length of the time series

3.3 Mechanism analysis

In this section, the mechanism of the quasi-periodic response under unsteady aerodynamic loads is analyzed. We investigate the amplitude frequency spectrum of the vehicle dynamic response. Figure 11 shows the spectrum of the lateral displacement of the 1st wheelset, in which the red line represents the spectrum under steady aerodynamic conditions and the black line represents the spectrum under unsteady aerodynamic conditions. Figure 11 shows that, in the case of steady aerodynamic loads, when the critical speed is exceeded, the vehicle system undergoes self-excited vibrations with f_s as the fundamental frequency, and the amplitude of the harmonic component of the frequency f_s is much larger than that of other frequencies nf_s (n = 2, 3, 4, …). Because the frequency of each harmonic component is commensurable, the vehicle system vibrates periodically under steady aerodynamic loads.

However, for a vehicle system under unsteady aerodynamic loads, the situation is completely different. Under this circumstance, not only have the inherent dynamic characteristics of the system changed, as mentioned above, but the system is also subjected to the external excitation of the unsteady aerodynamic loads with a frequency f_a. Figure 11 shows that the height and position of the highest peak of the black line are very close to the red line, and the highest peak of the black line is significantly higher than other peaks of the black line. This indicates that the vehicle system response under unsteady aerodynamic loads still has a harmonic component whose amplitude far exceeds those of other components, and the frequency f_u of this harmonic component is very close to the fundamental frequency f_s for the case of steady aerodynamic loads. This implies that the vibration forms corresponding to the above two frequencies will be the same, which is further analyzed below. The other lower peaks of the black line show that the corresponding frequencies of these peaks are integer multiples pf_u (p = 2, 3, 4, …) of f_u, integer multiples qf_a (q = 1, 2, 3, 4, …) of f_a, and combined frequencies of f_u, pf_u, and qf_a, such as f_u − 2f_a, f_u − f_a, 2f_u − f_a, f_u + f_a, f_u + 2f_a, and 2f_u + f_a. The above harmonic components are combined to form the vehicle dynamic responses under unsteady aerodynamic loads. The mutual coupling of each degree of freedom of the vehicle system and the existence of nonlinear terms leads to the appearance of the combined frequencies, which is a typical characteristic of multi-degree-of-freedom nonlinear systems.

Further analysis shows that the vibration form corresponding to the frequency f_u is closely related to the self-excited vibration of the homogeneous equation, and therefore, f_u is highly related to the inherent characteristics of the vehicle dynamical system. f_u is a real and usually an irrational number (e.g., f_u is proportional to the square root of the tread slope for a free wheelset with a cone-shaped tread). The frequency f_a is completely determined by the characteristics of the external flow field, and its value is independent of the inherent characteristics of the vehicle dynamics system. The value range of f_a is also a real number field. In this study, we do not consider the exceptional case in which f_u and f_a were commensurable or near-commensurable. f_u and f_a are independent of each other and can take values continuously within the real number range, so in general, the ratio of f_u to f_a is an irrational number. Therefore, the function composed of f_u, pf_u (p = 2, 3, 4, …), qf_a (q = 1, 2, 3, 4, …), and other frequency harmonic components must be quasi-periodic. This shows that the dynamic response of the vehicle system under the action of unsteady aerodynamic loads is a quasi-periodic solution, which is consistent with the previous results obtained by the Poincaré section and Lyapunov exponents.

The amplitude of the harmonic component of the frequency f_u is significantly higher than those of the other components, and thus, it is the most important component in the case of unsteady aerodynamic loads. We next analyze the vibration form corresponding to the frequency f_u. The values of f_u (≈ 2.29 Hz) and f_s (≈ 2.33 Hz) are very close, differing by only 1.75%, which indicates there is a close relationship between the vibration forms corresponding to these two frequencies. To facilitate the comparison of the vibration forms later, we introduce a vector diagram to represent the vibration form and illustrate it with Fig. 16. The time-history curves of the lateral displacements y_w1 and y_w3 of the 1st and 3rd wheelsets, respectively, under steady aerodynamic loads were filtered to obtain the time-history curves of a₁ and a₃ of the 1st and 3rd wheelsets, respectively, containing only frequency f_s. The black and red cosine curves in Fig. 16a correspond to $a_{{1}} = {\text{Re}} \left[ {A_{{1}} {\text{e}}^{{i\alpha_{1} }} {\text{e}}^{{i2\pi f_{{\text{s}}} t}} } \right]$ and $a_{{3}} = {\text{Re}} \left[ {A_{{3}} {\text{e}}^{{i\alpha_{3} }} {\text{e}}^{{i2\pi f_{{\text{s}}} t}} } \right]$, respectively. For simplicity, the two cosine curves in Fig. 16a are represented by two vectors in Fig. 16b, which represent the amplitude and phase difference of the lateral displacements of the 1st and 3rd wheelsets corresponding to the same frequency harmonic component, and thus, they reflect the vibration form at this frequency. Figure 16b shows that the 1st and 3rd wheelsets underwent periodic motions of frequency f_s. The amplitudes of these two motions are A₁ and A₃, respectively, and the corresponding phases are α₁ and α₃. The amplitude ratio of the 3rd wheelset to the 1st wheelset is A₃/A₁, and the phase of the 3rd wheelset is α₃ − α₁ ahead of the 1st wheelset. Thus, the two vectors in Fig. 16b can be used to represent the vibration forms of the harmonic components of the 1st and 3rd wheelsets corresponding to the frequency f_s. This representation is used in the following sections to compare the vibration forms by comparing vectors in different cases.

Fig. 16

a Time-history curves. b Vector diagram

The vibration forms of the dynamic responses of the vehicle system in the cases with unsteady and steady aerodynamic loads are represented by vector diagrams in Fig. 17. Figure 11 shows that the dominant components of the vehicle system's dynamic response under unsteady and steady aerodynamic loads were the components corresponding to two towering peaks at frequencies f_u and f_s, respectively. Therefore, Fig. 17 shows the vector diagrams corresponding to harmonic components of f_u and f_s, in which numbers 1–4 represent the lateral displacements of the four wheelsets and 5–7 represent the lateral displacements of the front and rear frames and the car body, respectively. The numbers 8–11 represent the yaw of the four wheelsets, 12 and 13 represent the roll of the front and rear frames, respectively, 14 and 15 represent the yaw of the front and rear frames, respectively, and 16 and 17 represent the roll and yaw of the car body, respectively. Figure 17a, b show vector graphs of the translational displacement and rotational displacement, respectively. When the vectors of the vibration forms of various degrees of freedom are drawn in Fig. 17, the phase of the lateral displacement of the 1st wheelset under steady aerodynamic loads (being set to zero without loss of generality) is used as a reference to determine the phase of each degree of freedom; the amplitudes of the lateral displacement and yaw angle of the 1st wheelset under steady aerodynamic loads are used as references to determine the amplitudes of each translational and rotational degree of freedom. The dominant components of each degree of freedom (that is, the harmonic component corresponding to f_u and f_s) are close to each other in both amplitude and phase in the cases of unsteady and steady aerodynamic loads.

Fig. 17

Vector diagrams for translational and rotational displacements corresponding to frequencies f_s (red) and f_u (black): a translational degrees of freedom and b rotational degrees of freedom

We further normalized the vibration form and used the degree of freedom with the maximum amplitude as the reference to obtain the normalized amplitude. For example, in the cases of steady and unsteady aerodynamic loads, the lateral displacement amplitude A₅ of the front frame is the maximum translation amplitude, so the normalized amplitudes of the other translational degrees of freedom are A_i/A₅ (i = 1, 2, 3, …, 7). The yaw angle amplitude A₉ of the 2nd wheelset is the largest rotation amplitude, so the normalized amplitude of the other rotational degrees of freedom is A_i/A₉ (i = 8, 9, 10, …, 17). The phase of the lateral displacement of the front frame is used as a reference to determine the phases of the translational and rotational degrees of freedom, so the phase of each degree of freedom is α_i − α₅ (i = 1, 2, 3, …, 17). In Fig. 18, the abscissa represents the sequence number of the degrees of freedom of the vehicle system, and the left and right ordinate axes, respectively, represent the normalized amplitude and the phase of each degree of freedom. Figure 18 shows that for the cases of unsteady and steady aerodynamic loads, the normalized amplitudes and phases of the harmonic vibrations corresponding to f_u and f_s are consistent. This indicates that the vibration forms corresponding to f_u and f_s are highly consistent. The values of f_u and f_s are very close, and their corresponding vibration forms are also very similar to each other, which indicates that they are vibrations of the same nature. Considering that the vibration of f_s corresponds to self-excited vibrations under steady aerodynamic loads, f_u and the vibration corresponding to f_u are referred to as the self-excited vibration frequency (i.e., the frequency of hunting) and the self-excited vibration component under unsteady aerodynamic loads, respectively.

Fig. 18

Normalized amplitude corresponding to f_u and f_s: a translational degrees of freedom and b rotational degrees of freedom

A significant difference between the vehicle dynamical system under unsteady aerodynamic loads and that under steady aerodynamic loads is that the former also includes a forced excitation of the aerodynamic loads with a frequency of f_a that appears as an inhomogeneous term in the dynamics equations. The vibration forms of the harmonic components corresponding to the forced excitation frequency f_a and the self-excited vibration frequency f_u are compared in Fig. 19. When the vectors of vibration forms of various degrees of freedom are drawn in Fig. 19, the phase of the self-excited vibration component of the lateral displacement of the 1st wheelset (being set to zero without loss of generality) was used as a reference to determine the phase of each degree of freedom; the amplitudes of the self-excited vibration component of the lateral displacement and yaw angle of the 1st wheelset were used as a reference to determine the amplitudes of each translational and rotational degree of freedom, respectively. Figure 19a, c shows the translational and rotational displacement vector diagrams, respectively, and Fig. 19b, d shows enlarged vectors obtained by magnifying Fig. 19a, c 10 and 5 times near the origin, respectively. Figure 19 shows that the amplitude and phase of the harmonic components corresponding to f_a and f_u of each degree of freedom are significantly different. More importantly, the proportional relationship between the amplitudes of each degree of freedom also changes essentially. For example, for the harmonic component of the self-excited vibration corresponding to f_u, the amplitudes of the lateral displacements of the 1st wheelset, 2nd wheelset, and front frame are much larger than those of the 3rd wheelset, 4th wheelset, and rear front (the former is about 58.63%–100.69% larger than the latter). However, for the harmonic components corresponding to f_a, the situation is reversed: the amplitudes of the lateral displacements of the 1st wheelset, 2nd wheelset, and front frame are smaller than those of the 3rd wheelset, 4th wheelset, and rear front (the former is about 64.36%–76.14% smaller than the latter). The same is true for the amplitudes of the other degrees of freedom. For the phase, there are significant differences in the rotational degrees of freedom, among which the phase difference of the roll of the frames can reach 77.46° and 173.27°. The phase differences of the yaw of the front frame and the roll of the car body are also significantly different.

Fig. 19

Vector diagrams for translational and rotational displacements corresponding to frequencies f_u (black) and f_a (blue): a translational degrees of freedom, b enlarged drawing of (a), c rotational degrees of freedom, and d enlarged drawing of (c)

Using the same normalization method of the vibration form described above, we can obtain harmonic vibration forms of each degree of freedom corresponding to frequencies f_a and f_u under unsteady aerodynamic loads, as shown in Fig. 20. For the self-excited vibration component corresponding to f_u, the lateral displacement amplitude A₅ of the front frame is the largest translational amplitude, and the normalized amplitudes of the other translational degrees of freedom are A_i/A₅ (i = 1, 2, 3, …, 7). The yaw angle amplitude A₉ of the 2nd wheelset is the largest rotational amplitude, and the normalized amplitudes of the other rotational degrees of freedom are A_i/A₉ (i = 8, 9, 10, …, 17). The phase of the lateral displacement of the front frame is used as a reference to determine the phase of each degree of freedom, which is α_i − α₅ (i = 1, 2, 3, …, 17). For the harmonic components corresponding to frequency f_a, the lateral displacement amplitude A₄ of the 4th wheelset is the largest translational amplitude, and the normalized amplitudes of other translational degrees of freedom are A_i/A₄ (i = 1, 2, 3, …, 7). The roll angle amplitude A₁₆ of the car body is the largest rotational amplitude, and the normalized amplitudes of the other rotational degrees of freedom are A_i/A₁₆ (i = 8, 9, 10, …, 17). The phase of the lateral displacement of the 4th wheelset is used as reference to determine the phase of each degree of freedom, which is α_i − α₄ (i = 1, 2, 3, …, 17). Figure 20 shows that the harmonic vibration forms corresponding to f_a and f_u are completely different. The values of f_a and f_u are different, and the corresponding vibration forms are different, which indicates that the harmonic components corresponding to f_a and f_u are two kinds of vibrations with completely different properties. This is evident because the harmonic component corresponding to f_a is the forced vibration response caused by the unsteady aerodynamic loads, while the harmonic component corresponding to f_u is the self-excited vibration response, as previously mentioned.

Fig. 20

Normalized amplitudes corresponding to f_u and f_a: a linear displacement and b angular displacement

3.4 Critical speed with unsteady aerodynamic loads

In the previous two sections, the difference between the dynamic response characteristics of the vehicle system at the same running speed when considering unsteady and steady aerodynamic loads was mainly investigated. In this section, the changes of dynamic responses of the vehicle system with speed when considering the influences of unsteady aerodynamic loads are investigated.

We computed the dynamic responses of the vehicle system at different running speeds. Figures 21 and 22 show the time-history curves of the wheelsets, frames, and car body and the Poincaré sections at the running speeds of 538 km/h (case 1) and 539 km/h (case 2). Figure 21 shows that the vibration amplitude and frequency of the vehicle system in case 2 are significantly larger than those in case 1. For example, the later displacement amplitude of the 2nd wheelset of case 2 is 158.62% larger than that of case 1. The frequency of each degree of freedom of Case 2 is about 2.22 Hz, while that of case 1 is 1.00 Hz. The blue five-pointed stars and black points in Fig. 22 represent the sampling points in cases 1 and 2, respectively. The projections of the intersection of the phase trajectories of cases 1 and 2 with the Poincaré section on the two-dimensional plane are an isolated point and a closed curve, respectively. This indicates that the system dynamic response in case 1 is a periodic solution, while the system dynamic response in case 2 is a quasi-periodic solution. Thus, there is a critical value between the two speeds of 538 and 539 km/h. When the speed exceeds this critical value, the dynamic response characteristics of the vehicle system under unsteady aerodynamic loads will change essentially, and the speed corresponding to this critical value is called the critical speed under unsteady aerodynamic loads in this study.

Fig. 21

Time-history curves of the vehicle moving at speeds V = 538 and 539 km/h: a 1st wheelset and 2nd wheelset, b 3rd wheelset and 4th wheelset, c front frame and rear frame, and d car body

Fig. 22

Projection of stroboscopic sampling points on several two-dimensional planes at speeds of 538 km/h (blue five-pointed stars) and 539 km/h (black points): a y_w1–y_w2 plane, b y_w2–y_w3 plane, c y_w3–y_w4 plane, d y_w4–y_f1 plane, e ϕ _f2–ψ_f2 plane, and f ϕ_c–ψ_c plane

The frequency spectra of the two cases were also investigated. Figure 23 shows the spectrum diagram of lateral displacement of the 1st wheelset, in which the blue and black lines correspond to cases 1 and 2, respectively. In the spectrum diagram of case 1, the highest peak, which is significantly higher than the other peaks, corresponds to the unsteady aerodynamic load frequency f_a, and the other low peaks correspond to the integer multiples qf_a (q = 2, 3, 4, …) of the frequency f_a. The vehicle's nonlinear factors, such as the wheel–rail contact of the system, lead to the appearance of these frequency components qf_a. The vehicle dynamic response in case 1 is the forced vibration caused by unsteady aerodynamic loads. Although the running speed of case 2 is only 1 km/h higher than that of case 1, the response spectrum is completely different. The black line corresponding to case 2 is similar to the black line in Fig. 11. The highest peak is much higher than the other peaks, corresponding to frequency f_u1; other lower peaks correspond to other frequencies, most of which are incommensurable with f_u1. Through the same analysis as that in Sect. 3.3, we can determine that the frequency corresponding to the highest peak in case 2 is the self-excited vibration frequency mentioned in Sect. 3.3. The frequencies corresponding to the other lower peaks in case 2 are integer multiples pf_u1 (p = 2, 3, 4, …) of frequency f_u1, integer multiples qf_a (q = 2, 3, 4, …) of frequency f_a, and the combined frequencies of f_u1, f_a, pf_u1, and qf_a, such as f_u1 − 2f_a, 2f_u1 − f_a, f_u1 + f_a, f_u1 + 2f_a, 2f_u1 + f_a…. For the same reason as that in Sect. 3.3, the vehicle system response in case 2 is quasi-periodic motion. The fundamental difference between cases 1 and 2 is that the vibration of the vehicle system at low speeds (such as in case 1) is a forced vibration, while the most important component of the vehicle system's dynamic response at high speeds is a self-excited vibration, whose amplitude is much larger than those of other components.

Fig. 23

Frequency spectrum of lateral displacement of 1st wheelset under unsteady aerodynamic loads at speeds of 538 and 539 km/h

Thus, for the vehicle running on a smooth straight track under unsteady aerodynamic loads, the variation behavior of the dynamic responses with the running speed is obtained as follows. When the running speed is lower than the critical speed, the vehicle system performs periodic forced vibrations, the vibration frequencies are integer multiples qf_a (q = 1, 2, 3, 4, …) of the aerodynamic load frequency f_a, and there are no other frequencies. The frequency corresponding to the harmonic component with the largest amplitude is the external excitation frequency f_a. When the running speed exceeds the critical speed, the vehicle system performs quasi-periodic motion, and the self-excited vibration is excited to become the dominant component of the vehicle system dynamic response, whereas the amplitudes of the external excitation frequency component and other combined frequency components are small. Therefore, the occurrence of self-excited vibrations can be used as the basis for judging whether the nature of the dynamic response of the vehicle system has changed (loss of motion stability), and the running speed of the vehicle system when a self-excited vibration occurs is the critical speed.

Figure 24 shows the bifurcation diagram of the lateral displacement amplitude of the wheelset, frame, and car body as the speed varies under unsteady aerodynamic loads. To create the bifurcation diagram, the amplitude of the self-excited vibration component of the vehicle system dynamic response is used as the ordinate of the bifurcation diagram. Figure 24 shows that the critical velocity under unsteady aerodynamic loads is 538 km/h, which changes compared with that under steady aerodynamic loads, as shown in Fig. 8.

Fig. 24

Bifurcation diagram under unsteady aerodynamic loads

3.5 Influences of variations of parameters on critical speed

In this sub-section, we examine the influences of the following typical parameters on the critical velocity: the excitation frequency of unsteady loads f_i, the fluctuation size of the unsteady aerodynamic loads C_u/C_s, the longitudinal and lateral stiffness of the primary suspension K_px and K_py, the stiffness of the spring–damper connecting point of the yaw damper K_sx1, and the lateral damping of the secondary suspension C_sy. To avoid high computation costs, the orthogonal test method is used to determine which parameter combinations need to be selected for the calculation. The orthogonal array L₂₅(5⁶) is adopted, as shown in Table 3, in which 25 is the number of parameter combinations to be calculated, and 5⁶ indicates that there are six factors and five levels per factor. The factors and their levels are shown in Table 4, in which the values of level 3 correspond to the values in “Appendix B”.

Table 3 L₂₅(5⁶) orthogonal array

Table 4 Factors and their levels

The calculation results of the above different parameter combinations are shown in the form of box-plots in Fig. 25. Figure 25a shows the maximum, minimum, median, and upper and lower quartiles of the critical velocity when the aerodynamic load frequency is taken as levels 1, 2,..., 5. The box-plot corresponding to each level is obtained from the statistics of the calculation results of all the parameter combinations when the aerodynamic load frequency is at that level. Similarly, Fig. 25b shows the box-plots corresponding to the fluctuation size of the unsteady aerodynamic loads. When the unsteady aerodynamic loads are considered, the critical speed of vehicle system has a large variation range, and the maximum variation range can reach 73.23% of the nominal value.

Fig. 25

Box-plots of a aerodynamic load frequency and b fluctuation size of unsteady aerodynamic loads

4 Conclusion

This study shows that the influences of unsteady aerodynamic loads on the dynamic responses of high-speed trains are different from those of steady aerodynamic load conditions. Based on the model established in the present study, the time-history curves, phase trajectories in the phase plane, Poincaré section, and Lyapunov exponents of the vehicle system running on an ideal straight track under the action of unsteady aerodynamic loads were computed. The vibration forms corresponding to the main harmonic components under unsteady and steady aerodynamic loads were compared, and the self-excited vibration components of the vehicle system under unsteady aerodynamic loads were identified.

The characteristics and numerical values of the dynamic responses of the vehicles change significantly when the combined action of self-excitation and forced excitations caused by unsteady aerodynamic loads are considered. In previous work, either the periodic solution of forced vibrations or the periodic solution of self-excited vibrations was given. However, the present study showed that this is not sufficient. The findings were as follows: (1) with the increase in the running speed, the vehicle response under unsteady aerodynamic loads changes from a forced vibration periodic solution to a quasi-periodic solution, in which a self-excited vibration is the main component; (2) the vibration amplitude increases significantly, and the vibration frequency changes considerably; (3) the responses of the vehicle system include self-excited vibrations, forced vibrations, and combined vibrations, and the frequencies of the combined vibrations are the combination of integer multiples of the frequencies of the first two kinds of vibrations. The mechanisms of these phenomena were also revealed.

Appendices

Appendix A: Details of equations of motion

The force diagrams and dynamics equations of each component of the vehicle system are listed in detail below [35].

For the i-th wheelset (i = 1–4) (Fig. 

Fig. 26

Schematic diagram of the force of the i-th wheelset

26).

For the front frame (n = 1) (Fig. 

Fig. 27

Schematic diagram of the force of the front frame

27).

The rear frame (n = 2) is similar to the front frame.

For the car body (Fig. 

Fig. 28

Schematic diagram of force of the car body

28).

The primary suspension longitudinal force is as follows (i = 1–4):

$$ F_{{x{\text{f}}\left( {{\text{L}},{\text{R}}} \right)i}} = K_{{{\text{p}}x}} \left( { \pm d_{{\text{w}}} \psi_{{{\text{f}}n}} + H_{{{\text{fw}}}} \beta_{{{\text{f}}n}} \mp d_{{\text{w}}} \psi_{{{\text{w}}i}} } \right) + C_{{{\text{p}}x}} \left( { \pm d_{{\text{w}}} \dot{\psi }_{{{\text{f}}n}} + H_{{{\text{fw}}}} \dot{\beta }_{{{\text{f}}n}} \mp d_{{\text{w}}} \dot{\psi }_{{{\text{w}}i}} } \right) $$

(A.1)

n = 1 when i = 1, 2 and n = 2 when i = 3, 4. The subscript i = 1–4 represents the i-th wheelset, and n = 1–2 represents the n-th frame, where the upper and lower sign (‘ + ’ or (‘ − ’) of ± and ∓ apply to the left and right wheel, respectively. This convention is also followed in similar cases later.

The primary suspension lateral force is as follows (i = 1–4):

$$ F_{{y{\text{f}}\left( {{\text{L}},{\text{R}}} \right)i}} = K_{{{\text{p}}y}} \left[ {y_{{{\text{w}}i}} - y_{{{\text{f}}n}} + H_{{{\text{fw}}}} \phi_{{{\text{f}}n}} + \left( { - 1} \right)^{i} l_{{\text{f}}} \psi_{{{\text{f}}n}} } \right] + C_{{{\text{p}}y}} \left[ {\dot{y}_{{{\text{w}}i}} - \dot{y}_{{{\text{f}}n}} + H_{{{\text{fw}}}} \dot{\phi }_{{{\text{f}}n}} + \left( { - 1} \right)^{i} l_{{\text{f}}} \dot{\psi }_{{{\text{f}}n}} } \right]. $$

(A.2)

The primary suspension vertical force is as follows (i = 1–4):

$$ \begin{aligned} F_{{z{\text{f}}\left( {{\text{L}},{\text{R}}} \right)i}} & = K_{{{\text{p}}z}} \left[ {z_{{{\text{f}}n}} - z_{{{\text{w}}i}} + \left( { - 1} \right)^{i} l_{{\text{f}}} \beta_{{{\text{f}}n}} \pm d_{{\text{w}}} \phi_{{{\text{w}}i}} \mp d_{{\text{w}}} \phi_{{{\text{f}}n}} } \right] \\ & \quad + \;C_{{{\text{p}}z}} \left[ {\dot{z}_{{{\text{f}}n}} - \dot{z}_{{{\text{w}}i}} + \left( { - 1} \right)^{i} l_{{\text{f}}} \dot{\beta }_{{{\text{f}}n}} \pm d_{{\text{w}}} \dot{\phi }_{{{\text{w}}i}} \mp d_{{\text{w}}} \dot{\phi }_{{{\text{f}}n}} } \right] + \frac{{\left( {2M_{{\text{f}}} + M_{{\text{c}}} } \right)g}}{8}. \\ \end{aligned} $$

(A.3)

The secondary suspension longitudinal force is as follows (i = 1, 2):

$$ F_{{x{\text{t}}\left( {{\text{L}},{\text{R}}} \right)i}} = K_{{{\text{s}}x}} \left( {H_{{{\text{cb}}}} \beta_{{\text{c}}} + H_{{{\text{bf}}}} \beta_{{{\text{f}}i}} \pm d_{{\text{s}}} \psi_{{\text{c}}} \mp d_{{\text{s}}} \psi_{{{\text{f}}i}} } \right) + C_{{{\text{s}}x}} \left( {H_{{{\text{cb}}}} \dot{\beta }_{{\text{c}}} + H_{{{\text{bf}}}} \dot{\beta }_{{{\text{f}}i}} \pm d_{{\text{s}}} \dot{\psi }_{{\text{c}}} \mp d_{{\text{s}}} \dot{\psi }_{{{\text{f}}i}} } \right). $$

(A.4)

The secondary suspension lateral force is as follows (i = 1, 2):

$$ \begin{aligned} F_{{y{\text{t}}\left( {{\text{L}},{\text{R}}} \right)i}} & = K_{{{\text{s}}y}} \left[ {y_{{{\text{f}}i}} - y_{{\text{c}}} + H_{{{\text{bf}}}} \phi_{{{\text{f}}i}} + H_{{{\text{cb}}}} \phi_{{\text{c}}} + \left( { - 1} \right)^{i} l_{{\text{c}}} \psi_{{\text{c}}} } \right] \\ & \quad + \;C_{{{\text{s}}y}} \left[ {\dot{y}_{{{\text{f}}i}} - \dot{y}_{{\text{c}}} + H_{{{\text{bf}}}} \dot{\phi }_{{{\text{f}}i}} + H_{{{\text{cb}}}} \dot{\phi }_{{\text{c}}} + \left( { - 1} \right)^{i} l_{{\text{c}}} \dot{\psi }_{{\text{c}}} } \right]. \\ \end{aligned} $$

(A.5)

The secondary suspension vertical force is as follows (i = 1, 2):

$$ \begin{aligned} F_{{z{\text{t}}\left( {{\text{L}},{\text{R}}} \right)i}} & = K_{{{\text{s}}z}} \left[ {z_{{\text{c}}} - z_{{{\text{f}}i}} \pm d_{{\text{s}}} \phi_{{{\text{f}}i}} \mp d_{{\text{s}}} \phi_{{\text{c}}} + \left( { - 1} \right)^{i} l_{{\text{c}}} \beta_{{\text{c}}} } \right] \\ & \quad + \;C_{{{\text{s}}z}} \left[ {\dot{z}_{{\text{c}}} - \dot{z}_{{{\text{f}}i}} \pm d_{{\text{s}}} \dot{\phi }_{{{\text{f}}i}} \mp d_{{\text{s}}} \dot{\phi }_{{\text{c}}} + \left( { - 1} \right)^{i} l_{{\text{c}}} \dot{\beta }_{{\text{c}}} } \right] + \frac{{M_{{\text{c}}} g}}{4}. \\ \end{aligned} $$

(A.6)

The secondary lateral damper force is as follows (i = 1, 2):

$$ F_{{y{\text{hx}}\left( {\text{L,R}} \right)i}} = K_{{{\text{hx}}}} \left( {y_{{{\text{f}}i}} + H_{{{\text{fhx}}}} \phi_{{{\text{f}}i}} - y_{{{\text{hx}}\left( {\text{L,R}} \right)i}} \pm E\psi_{{{\text{f}}i}} } \right). $$

(A.7)

The secondary yaw damper force is as follows (i = 1, 2):

$$ F_{{{\text{sx}}\left( {\text{L,R}} \right)i}} = K_{{{\text{sx}}1}} \left( { - y_{{{\text{sx}}\left( {\text{L,R}} \right)i}} \pm d_{{{\text{sx}}}} \psi_{{{\text{f}}i}} - H_{{{\text{fsx}}}} \beta_{{{\text{f}}i}} } \right). $$

(A.8)

The bump stop force is as follows (i = 1, 2):

$$ F_{{y{\text{zd}}i}} = K_{{{\text{zd}}}} \left( {y_{{{\text{f}}i}} - y_{{\text{c}}} + H_{{{\text{fzd}}}} \phi_{{{\text{f}}i}} + H_{{{\text{czd}}}} \phi_{{\text{c}}} + \left( { - 1} \right)^{i} l_{{{\text{zd}}}} \psi_{{\text{c}}} } \right). $$

(A.9)

For the wheelset (i = 1–4),

$$ M_{{\text{w}}} \ddot{y}_{{{\text{w}}i}} = - F_{{y{\text{fL}}i}} - F_{{y{\text{fR}}i}} + F_{{{\text{L}}yi}} + F_{{{\text{R}}yi}} + N_{{{\text{L}}yi}} + N_{{{\text{R}}yi}} $$

(A.10)

$$ \begin{gathered} I_{{{\text{w}}z}} \ddot{\psi }_{{{\text{w}}i}} + I_{{{\text{w}}y}} \dot{\phi }_{{{\text{w}}i}} \left( {\dot{\beta }_{{{\text{w}}i}} - \frac{V}{{r_{0} }}} \right) = a_{0} \left( {F_{{{\text{L}}xi}} - F_{{{\text{R}}xi}} } \right) + a_{0} \psi_{{{\text{w}}i}} \left( {F_{{{\text{L}}yi}} - F_{{{\text{R}}yi}} + N_{{{\text{L}}yi}} - N_{{{\text{R}}yi}} } \right) \\ + M_{{{\text{L}}zi}} + M_{{{\text{R}}zi}} + d_{{\text{w}}} \left( {F_{{x{\text{fL}}i}} - F_{{x{\text{fR}}i}} } \right) + a_{0} \left( {N_{{{\text{L}}xi}} - N_{{{\text{R}}xi}} } \right) \\ \end{gathered} $$

(A.11)

$$ \begin{aligned} I_{{{\text{w}}y}} \ddot{\beta }_{{{\text{w}}i}} & = r_{{{\text{L}}i}} F_{{{\text{L}}xi}} + r_{{{\text{L}}i}} \psi_{{{\text{w}}i}} \left( {F_{{{\text{L}}yi}} + N_{{{\text{L}}yi}} } \right) + r_{{{\text{R}}i}} F_{{{\text{R}}xi}} + r_{{{\text{R}}i}} \psi_{{{\text{w}}i}} \left( {F_{{{\text{R}}yi}} + N_{{{\text{R}}yi}} } \right) \\ & \quad + \;M_{{{\text{L}}yi}} + M_{{{\text{R}}yi}} + r_{{{\text{L}}i}} N_{{{\text{L}}xi}} + r_{{{\text{R}}i}} N_{{{\text{R}}xi}} . \\ \end{aligned} $$

(A.12)

For the frame (i = 1, 2),

$$ M_{{\text{f}}} \ddot{y}_{{{\text{f}}i}} = F_{{y{\text{fL}}\left( {2i - 1} \right)}} + F_{{y{\text{fL}}\left( {2i} \right)}} - F_{{y{\text{tL}}i}} + F_{{y{\text{fR}}\left( {2i - 1} \right)}} + F_{{y{\text{fR}}\left( {2i} \right)}} - F_{{y{\text{tR}}i}} - F_{{y{\text{hxL}}i}} - F_{{y{\text{hxR}}i}} $$

(A.13)

$$ M_{{\text{f}}} \ddot{z}_{{{\text{f}}i}} = F_{{z{\text{tL}}i}} - F_{{z{\text{fL}}\left( {2i - 1} \right)}} - F_{{z{\text{fL}}\left( {2i} \right)}} + F_{{z{\text{tR}}i}} - F_{{z{\text{fR}}\left( {2i - 1} \right)}} - F_{{z{\text{fR}}\left( {2i} \right)}} + M_{{\text{f}}} g $$

(A.14)

$$ \begin{aligned} I_{{{\text{f}}x}} \dot{\phi }_{{{\text{f}}i}} & = - \left[ {F_{{y{\text{fL}}\left( {2i - 1} \right)}} + F_{{y{\text{fL}}\left( {2i} \right)}} + F_{{y{\text{fR}}\left( {2i - 1} \right)}} + F_{{y{\text{fR}}\left( {2i} \right)}} } \right]H_{{{\text{fw}}}} \\ & \quad + \;\left[ {F_{{z{\text{fL}}\left( {2i - 1} \right)}} + F_{{z{\text{fL}}\left( {2i} \right)}} - F_{{z{\text{fR}}\left( {2i - 1} \right)}} - F_{{z{\text{fR}}\left( {2i} \right)}} } \right]d_{{\text{w}}} + \left( {F_{{z{\text{tR}}i}} - F_{{z{\text{tL}}i}} } \right)d_{{\text{s}}} \\ & \quad - \;\left( {F_{{y{\text{tL}}i}} + F_{{y{\text{tR}}i}} } \right)H_{{{\text{bf}}}} - \left( {F_{{y{\text{hxL}}i}} + F_{{y{\text{hxR}}i}} } \right)H_{{{\text{fhx}}}} - F_{{y{\text{zd}}i}} H_{{{\text{fzd}}}} + M_{{{\text{r}}i}} \\ \end{aligned} $$

(A.15)

$$ \begin{aligned} I_{{{\text{f}}y}} \ddot{\beta }_{{{\text{f}}i}} & = \left[ {F_{{z{\text{fL}}\left( {2i - 1} \right)}} - F_{{z{\text{fL}}\left( {2i} \right)}} + F_{{z{\text{fR}}\left( {2i - 1} \right)}} - F_{{z{\text{fR}}\left( {2i} \right)}} } \right]l_{{\text{f}}} - \left( {F_{{x{\text{tL}}i}} + F_{{x{\text{tR}}i}} } \right)H_{{{\text{bf}}}} \\ & \quad - \;\left[ {F_{{x{\text{fL}}\left( {2i - 1} \right)}} + F_{{x{\text{fL}}\left( {2i} \right)}} + F_{{x{\text{fR}}\left( {2i - 1} \right)}} + F_{{x{\text{fR}}\left( {2i} \right)}} } \right]H_{{{\text{fw}}}} + \left( {F_{{{\text{sxL}}i}} + F_{{{\text{sxR}}i}} } \right)H_{{{\text{fsx}}}} \\ \end{aligned} $$

(A.16)

$$ \begin{aligned} I_{{{\text{f}}z}} \ddot{\psi }_{{{\text{f}}i}} & = \left[ {F_{{y{\text{fL}}\left( {2i - 1} \right)}} - F_{{y{\text{fL}}\left( {2i} \right)}} + F_{{y{\text{fR}}\left( {2i - 1} \right)}} - F_{{y{\text{fR}}\left( {2i} \right)}} } \right]l_{{\text{f}}} + \left( {F_{{x{\text{tL}}i}} - F_{{x{\text{tR}}i}} } \right)d_{{\text{s}}} - \left( {F_{{{\text{sxL}}i}} - F_{{{\text{sxR}}i}} } \right)d_{{{\text{sx}}}} \\ & \quad + \;\left[ {F_{{x{\text{fR}}\left( {2i - 1} \right)}} + F_{{x{\text{fR}}\left( {2i} \right)}} - F_{{x{\text{fL}}\left( {2i - 1} \right)}} - F_{{x{\text{fL}}\left( {2i} \right)}} } \right]d_{{\text{w}}} + \left( {F_{{y{\text{hxR}}i}} - F_{{y{\text{hxL}}i}} } \right)E \\ \end{aligned} $$

(A.17)

For the car body,

$$ M_{{\text{c}}} \ddot{y}_{{\text{c}}} = F_{{y{\text{tL}}1}} + F_{{y{\text{tL}}2}} + F_{{y{\text{tR}}1}} + F_{{y{\text{tR}}2}} + F_{{y{\text{hxL}}1}} + F_{{y{\text{hxL}}2}} + F_{{y{\text{hxR}}1}} + F_{{y{\text{hxR}}2}} + F_{{y{\text{zd}}1}} + F_{{y{\text{zd}}2}} + F_{2} $$

(A.18)

$$ M_{{\text{c}}} \ddot{z}_{{\text{c}}} = - F_{{z{\text{tL}}1}} - F_{{z{\text{tL}}2}} - F_{{z{\text{tR}}1}} - F_{{z{\text{tR}}2}} + M_{{\text{c}}} g + F_{3} $$

(A.19)

$$ \begin{aligned} I_{{{\text{c}}x}} \ddot{\phi }_{{\text{c}}} & = - \left( {F_{{y{\text{tL}}1}} + F_{{y{\text{tL}}2}} + F_{{y{\text{tR}}1}} + F_{{y{\text{tR}}2}} } \right)H_{{{\text{cb}}}} - \left( {F_{{y{\text{hxL}}1}} + F_{{y{\text{hxL}}2}} + F_{{y{\text{hxR}}1}} + F_{{y{\text{hxR}}2}} } \right)H_{{{\text{chx}}}} \\ & \quad + \;\left( {F_{{z{\text{tL}}1}} + F_{{z{\text{tL}}2}} - F_{{z{\text{tR}}1}} - F_{{z{\text{tR}}2}} } \right)d_{{\text{s}}} - \left( {F_{{y{\text{zd}}1}} { + }F_{{y{\text{zd2}}}} } \right)H_{{{\text{czd}}}} - M_{{{\text{r1}}}} - M_{{{\text{r2}}}} + M_{1} \\ \end{aligned} $$

(A.20)

$$ \begin{aligned} I_{{{\text{c}}y}} \ddot{\beta }_{{\text{c}}} & = \left( {F_{{z{\text{tL}}1}} - F_{{z{\text{tL}}2}} + F_{{z{\text{tR}}1}} - F_{{z{\text{tR}}2}} } \right)l_{{\text{c}}} - \left( {F_{{x{\text{tL}}1}} { + }F_{{x{\text{tL2}}}} { + }F_{{x{\text{tR}}1}} { + }F_{{x{\text{tR}}2}} } \right)H_{{{\text{cb}}}} \\ & \quad \times \;\left( {F_{{x{\text{sL}}1}} + F_{{x{\text{sL}}2}} + F_{{x{\text{sR}}1}} + F_{{x{\text{sR}}2}} } \right)H_{{{\text{csx}}}} + M_{2} \\ \end{aligned} $$

(A.21)

$$ \begin{aligned} I_{{{\text{c}}z}} \ddot{\psi }_{{\text{c}}} & = \left( {F_{{y{\text{tL}}1}} - F_{{y{\text{tL}}2}} + F_{{y{\text{tR}}1}} - F_{{y{\text{tR}}2}} } \right)l_{{\text{c}}} + \left( {F_{{x{\text{tR}}1}} + F_{{x{\text{tR2}}}} - F_{{x{\text{tL}}1}} - F_{{x{\text{tL2}}}} } \right)d_{{\text{s}}} \\ & \quad - \;\left( {F_{{x{\text{sR}}1}} + F_{{x{\text{sR2}}}} - F_{{x{\text{sL}}1}} - F_{{x{\text{sL2}}}} } \right)d_{{{\text{sx}}}} + \left( {F_{{y{\text{hxL}}1}} - F_{{y{\text{hxL}}2}} + F_{{y{\text{hxR}}1}} - F_{{y{\text{hxR}}2}} } \right)l_{{\text{c}}} \\ & \quad + \;\left( {F_{{y{\text{hxL}}1}} + F_{{y{\text{hxL}}2}} - F_{{y{\text{hxR}}1}} - F_{{y{\text{hxR}}2}} } \right)E + \left( {F_{{y{\text{zd}}1}} - F_{{y{\text{zd}}2}} } \right)l_{{\text{c}}} + M_{3} . \\ \end{aligned} $$

(A.22)

For the connecting points of the lateral dampers (i = 1, 2),

$$ K_{{{\text{hx}}}} \left( {y_{{{\text{f}}i}} + H_{{{\text{fhx}}}} \phi_{{{\text{f}}i}} - y_{{{\text{hx}}\left( {\text{L,R}} \right)i}} \pm E\psi_{{{\text{f}}i}} } \right) = C_{{{\text{hx}}}} \left( {\dot{y}_{{{\text{hx}}\left( {\text{L,R}} \right)i}} - y_{{\text{c}}} + H_{{{\text{chx}}}} \dot{\phi }_{{\text{c}}} + \left( { - 1} \right)^{i} \left( {l_{{\text{c}}} \pm E} \right)\dot{\psi }_{{\text{c}}} } \right). $$

(A.23)

For the connecting points of the yaw dampers (i = 1, 2),

$$ K_{{{\text{sx1}}}} \left( { \pm d_{{{\text{sx}}}} \psi_{{{\text{f}}i}} - H_{{{\text{fsx}}}} \beta_{{{\text{f}}i}} - y_{{{\text{sx}}\left( {{\text{L}},{\text{R}}} \right)i}} } \right) = C_{{{\text{sx1}}}} \left( {\dot{y}_{{{\text{sx}}\left( {{\text{L}},{\text{R}}} \right)i}} \mp d_{{{\text{sx}}}} \dot{\psi }_{{\text{c}}} - H_{{{\text{csx}}}} \dot{\beta }_{{\text{c}}} } \right). $$

(A.24)

Appendix B: Nomenclature and vehicle parameters

The nomenclature used in the dynamics equations follows [45] (Tables

Table 5 Nominal values of vehicle parameters

5,

Table 6 Damping characteristics of yaw dampers

6,

Table 7 Damping characteristics of lateral dampers

7,

Table 8 Characteristics of bump stop forces

8).