Adaptive exponential cluster synchronization in colored community networks via aperiodically intermittent pinning control

Abstract

This paper investigates the problem of pinning cluster synchronization for colored community networks via adaptive aperiodically intermittent control. Firstly, a general colored community network model is proposed, where the isolated nodes can interact through different kinds of connections in different communities and the interactions between different pair of communities can also be different, and moreover, the nodes in different communities can have different state dimensions. Then, an adaptive aperiodically intermittent control strategy combined with pinning scheme is developed to realize cluster synchronization of such colored community network. By introducing a novel piecewise continuous auxiliary function, some globally exponential cluster synchronization criteria are rigorously derived according to Lyapunov stability theory and piecewise analysis approach. Based on the derived criteria, a guideline to illustrate which nodes in each community should be preferentially pinned is given. It is noted that the adaptive intermittent pinning control is aperiodic, in which both control width and control period are allowed to be variable. Finally, a numerical example is provided to show the effectiveness of the theoretical results obtained.

1 Introduction

Fig. 1

Sketch map of a colored community network consisting of 18 nodes and 3 communities, where nodes with different colors represent that they have different local dynamics and edges with different colors denote different interactions

Currently, community networks have attracted increasing attention from various research fields. In a community network, nodes in the same community are often densely connected, while the connections of the nodes belonging to different communities are lower density [1]. In fact, community structure has been revealed in many real-world networks, such as technological networks, social networks, biological networks and Congressional cosponsorship networks [1,2,3,4]. In general, nodes belonging to the same community have identical local dynamics and those in different communities have different local dynamics [5, 6]. Additionally, nodes in the same community interact through the same type of connection and those in different communities interact through different types of connections. Meanwhile, the interactions between the same pair of communities are usually identical and those between different pair of communities are different. In other words, there are diverse types of interactions in community networks [7, 8]. In order to better describe these phenomena, a community network model with colored nodes and edges, which is called colored community network [7], has been proposed. In this kind of community network, nodes with different colors represent that they have different local dynamics and edges with different colors denote different interactions. The sketch map of a colored community network consisting of 18 nodes and 3 communities is indicated in Fig. 1.

It is well known that synchronization can be observed in many application areas, including biology, sociology and technology [9, 10]. By general definition, synchronization is a process wherein two (or many) dynamical systems adjust a given property of their motion to a common behavior by virtue of coupling or forcing [9]. In the past two decades, synchronization in complex networks of coupled dynamical systems called complex dynamical networks has been extensively studied due to its broad potential applications [10, 11]. Hitherto, several types of synchronization features have been presented, such as complete synchronization [11], phase synchronization [12], lag synchronization [13], generalized synchronization [14], projective synchronization [15] and cluster synchronization [16]. As a particular type of synchronization pattern, cluster synchronization means that the set of nodes in a complex network split into a certain number of communities (clusters or groups), such that the nodes belonging to the same community are synchronized, but no synchronization occurs among different communities [6]. In the light of its significance in brain science [17], communication engineering [18] and biological science [19], cluster synchronization has received much attention in recent years. In [16], for connected chaotic networks, a coupling scheme with cooperative and competitive weight couplings was constructed to stabilize arbitrarily selected cluster synchronization patterns with several clusters. In [20], cluster synchronization in an array of delayed neural networks with hybrid coupling was studied. In [21], the problem of cluster synchronization for a class of hybrid-coupled impulsive delayed dynamical networks was considered.

In the real world, many complex networks cannot achieve synchronization by themselves or synchronize with desired orbits automatically [22]. Therefore, several control techniques have been proposed to drive complex networks to achieve synchronization, such as feedback control [13], pinning control [23,24,25,26,27,28], adaptive control [15, 29], impulsive control [30,31,32,33] and intermittent control [34,35,36]. Among these control strategies, pinning control is a powerful approach because it is effective and more conveniently realized by controlling only a small fraction of network nodes rather than all network nodes [23,24,25,26,27,28]. In recent years, many efforts have been devoted to the study of pinning synchronization problem for complex dynamical networks, and a lot of excellent works on cluster synchronization under pinning control scheme have been reported. For instance, Wang et al. [6] proposed an effective pinning control scheme to realize cluster synchronization of community networks with nonidentical nodes. Wu et al. [37] explored the problem of driving an undirected network to a selected cluster synchronization pattern by introducing a single controller for each cluster. In [38], by imposing two effective feedback control strategies on partial communities, cluster synchronization of directed community networks was considered. In [39], pinning cluster synchronization of directed networks with nonlinearly coupled nonidentical dynamical systems was discussed. In [40], cluster synchronization was concerned for undirected complex networks by means of a decentralized adaptive pinning strategy. In [41], by designing two effective strategies to enhance the coupling weights, edge-based adaptive pinning control problem for cluster synchronization of community networks with nonidentical nodes was investigated.

Besides, intermittent control is a discontinuous control scheme, which is activated during certain nonzero time intervals and off during other time intervals [35, 42]. Intermittent control has been widely adopted in engineering fields, such as transportation, manufacturing and communication, due to the fact that it is easy to be implemented in engineering control [34,35,36, 42,43,44]. Obviously, by combining intermittent control and pinning control, the amount of the transmitted information and the control cost can be greatly reduced. Therefore, it will be of great interest to investigate the intermittent pinning control problem for synchronization of complex dynamical networks. Up to now, there are many important results available for synchronization based on intermittent pinning control strategy; see [34, 35, 44,45,46,47,48,49,50,51,52] and the references therein. It should be pointed out that most of the previous studies on intermittent pinning control focused on periodically intermittent pinning control, which requires that the control width and the control period both should be fixed constants. Evidently, this requirement is quite restricted and limits application scopes of the intermittent control strategy. To deal with this constraint, a general intermittent control technique, namely aperiodically intermittent control [43, 48, 49], has recently been proposed. In this type of intermittent control, both control width and control period are allowed to be variable; hence, it is more practically applicable than the periodically intermittent control. Recently, aperiodically intermittent control has been applied successfully to study the pinning synchronization of complex dynamical networks with or without time delays [48,49,50,51,52,53]. In [48], the synchronization problem for complex dynamical networks with nonlinear coupling function was considered via aperiodically intermittent pinning control. In [49, 50], the exponential synchronization of delayed dynamical networks under aperiodically intermittent pinning control was investigated. In [51, 52], the problem of adaptive outer synchronization between two general delayed dynamical networks was discussed via aperiodically intermittent pinning control. However, to the best of our knowledge, there are few results about the cluster synchronization of colored community networks via aperiodically intermittent pinning control. Moreover, it is well known that adaptive strategy can effectively prevent the appearance of larger feedback control gains than those required in practice [26, 47, 52]. Therefore, in this paper we will focus on the cluster synchronization in colored community networks using adaptive aperiodically intermittent pinning control strategy.

Clearly, it can be observed that the state dimensions of nodes in complex dynamical networks discussed in [6, 8, 20,21,22,23,24,25,26,27, 29,30,31,32,33,34,35,36,37,38,39,40,41, 44,45,52] are assumed to be identical. For many realistic networks, however, this assumption may be unreasonable. Actually, synchronization can also appear in real-world interactive systems having different state dimensions [7, 54,55,56]. For instance, in the cardiorespiratory system, it has been shown that synchronization between the lung and the heart can occur, despite the dimensions of their dynamics are different [54]. In view of this, a general model of colored community network with nodes possessing different state dimensions will be considered in this paper.

Based on the above analysis, this paper is concerned with the cluster synchronization problem for colored community networks with nodes of different state dimensions via adaptive aperiodically intermittent pinning control. By constructing a novel piecewise auxiliary function, some globally exponential cluster synchronization criteria are established according to Lyapunov stability theory and piecewise analysis approach. A numerical example is finally given to show the validity of the derived theoretical results. The main contributions of this paper can be stated as follows: (1) a general community network model is proposed, where the isolated nodes can interact through different kinds of connections in different communities and the interactions between different pair of communities can also be different, and moreover, the nodes in different communities can have different state dimensions; (2) the adaptive intermittent pinning control is aperiodic, in which both control width and control period are allowed to be variable; (3) a novel piecewise continuous Lyapunov candidate function is established and then based on which some sufficient conditions to guarantee globally exponential cluster synchronization are presented; (4) a guideline is provided to illustrate which nodes in each community should be preferentially pinned.

Notations The following notations and definitions will be used throughout this paper. Let $\mathbb {R}=(-\,\infty , +\,\infty )$ be the set of real numbers, ${\mathbb {N}^+=\{1,2,\ldots \}}$ be the set of positive integer numbers, and $\mathfrak {R}=\big \{1,2,\ldots ,m \big \}$. $\mathbb {R}^{n}$ and $\mathbb {R}^{n\times n}$ represent, respectively, the n-dimensional Euclidean space and the set of $n\times n$ real matrices. The superscript $\top$ denotes the transpose of a vector or a matrix. $||\cdot ||$ stands for the standard Euclidean norm in $\mathbb {R}^{n}$. $I_n\in \mathbb {R}^{n\times n}$ is an n-dimensional identity matrix, $\mathbf{0}_{n} \in \mathbb {R}^n$ is an n-dimensional vector of zeros, $\mathrm{diag}(\gamma _1,\gamma _2,\ldots ,\gamma _n)\in \mathbb {R}^{n\times n}$ is the diagonal matrix with diagonal entries $\gamma _i(1\le i \le n)$. For a square matrix $A\in \mathbb {R}^{n\times n}$, $\lambda _{\min }(A)$ and $\lambda _{\max }(A)$ represent its minimum and maximum eigenvalue, respectively. For a real symmetric matrix $M\in \mathbb {R}^{n\times n}$, write $M<0 (M\le 0)$ if M is negative (semi-negative) definite. The Kronecker product of an $M_1\times N_1$ matrix $A=(a_{ij})$ and an $M_2\times N_2$ matrix B is the $M_1M_2\times N_1N_2$ matrix $A\otimes B$, defined as

$$\begin{aligned} A\otimes B= \left( {\begin{matrix} a_{11}B\,&{} \cdots \,&{} a_{1N_1}B \\ \vdots \,&{}\ddots \,&{} \vdots \\ a_{M_11}B \,&{} \cdots \,&{} a_{M_1N_1}B \end{matrix}} \right) \end{aligned}$$

and the Kronecker product has the following properties:

$$\begin{aligned}&(A\otimes B)^{\top }=A^{\top }\otimes B^{\top } \quad \hbox { and } \\&(A\otimes B)(C\otimes D)=(AC)\otimes (BD). \end{aligned}$$

2 Model description and preliminaries

In this paper, we consider a colored community network consisting of N nodes and m communities with $2\le m <N$, where each node in the kth community ($k \in \mathfrak {R}$) is an $n_k$-dimensional dynamical system. The state equations of the while network are described by:

$$\begin{aligned} {\dot{x}}_{i}(t)= & {} f_k\big (t,x_{i}(t)\big )+c_k\sum _{j\,\in \mathcal {C}_k, j\ne i } b_{ij}\,{\varGamma }_{kk} \big (x_j(t)-x_i(t)\big )\nonumber \\&+\sum _{p=1,p\ne k}^{m}\varepsilon _{kp} \sum _{j\,\in \mathcal {C}_p} b_{ij} \big ({\varGamma }_{kp}x_j(t)-{\varGamma }_{kk}^{p}x_i(t)\big ), \nonumber \\&\qquad \, i\in \mathcal {C}_k\,\, \mathrm{and} \,\,\ k\in \mathfrak {R} \end{aligned}$$

(1)

where $x_i(t) = (x_{i1}(t),x_{i2}(t),\ldots ,x_{in_k}(t))^{\top } \in \mathbb {R}^{n_k}$ is the $n_k$-dimensional state variable of node i in the kth community, $f_k :[0, +\infty )\times \mathbb {R}^{n_k} \rightarrow \mathbb {R}^{n_k}$ is a continuous vector-valued function representing the local dynamics of each individual node in the kth community, $c_k>0$ is the inner coupling strength of the kth community, $\varepsilon _{kp}>0$ is the external coupling strength between the kth and pth communities, and $\mathcal {C}_k$ denotes the set of all nodes belonging to the kth community. ${\varGamma }_{kk} = \mathrm{diag} \big (\gamma _{kk}^{(1)},\gamma _{kk}^{(2)},\dots , \gamma _{kk}^{(n_k)}\big )>0$ is the inner coupling matrix in the community $\mathcal {C}_k$, which is defined as follows: If the rth component of node $i\, (i \in \mathcal {C}_k )$ is affected by that of node $j\, (j \in \mathcal {C}_k )$, then $\gamma _{kk}^{(r)}\ne 0$; otherwise, $\gamma _{kk}^{(r)}= 0$. ${\varGamma }_{kp}=\big ( \gamma _{kp}^{(rs)}\big )\in \mathbb {R}^{n_k\times n_p}$ and ${\varGamma }_{kk}^{p} = \mathrm{diag} \big (\gamma _{kk}^{p(1)}, \gamma _{kk}^{p(2)},\dots , \gamma _{kk}^{p(n_k)}\big )$ are the inner coupling matrix between the kth and pth communities, which are defined as follows: If the rth component of node $i\, (i \in \mathcal {C}_k )$ is affected by the sth component of node $j\, (j \in \mathcal {C}_p )$, then $\gamma _{kp}^{(rs)}\ne 0$ and $\gamma _{kk}^{p(r)}\ne 0$; otherwise, $\gamma _{kp}^{(rs)}= 0$ and $\gamma _{kk}^{p(r)}=0$. This indicates that the interactions between different pair of communities can be nonidentical. $B=(b_{ij})_{N\times N}$ is the outer coupling matrix denoting the network topology, in which $b_{ij}$ is defined as follows: If there is a connection from node j to node $i \, (i\ne j)$, then $b_{ij}\ne 0$; otherwise, $b_{ij}=0$. This means that the network can be directed and the outer coupling matrix can be asymmetrical. Additionally, the diagonal entries of matrix B are given by $b_{ii}=-\,\sum _{j=1,j\,\ne i}^{N} b_{ij}$, and thus, $\sum _{j=1}^{N} b_{ij}=0$, $i=1,2,\ldots ,N$.

Remark 1

In network model (1), the individual nodes can interact through different kinds of connections in different communities and the interactions between different pair of communities can also be different; in addition, the nodes in different communities can have different state dimensions. Furthermore, the outer coupling matrix B is not restricted to be symmetric or irreducible. Obviously, network model (1) is a generalization of that considered in [6,7,8, 38, 41] and can describe many real-world networks better.

Without loss of generality, the sets of subscripts of m communities in network (1) are assumed to be $\mathcal {C}_1=\{1,2,\dots ,r_1\}$, $\mathcal {C}_2=\{r_1+1,r_1+2,\dots ,r_1+r_2\}$, $\dots$, $\mathcal {C}_m=\{r_1+r_2+\cdots +r_{m-1}+1,r_1+r_2+ \cdots +r_{m-1}+2,\dots ,r_1+r_2+\cdots +r_{m-1}+r_m\}$, where $1< r_k< N$, $k\in \mathfrak {R}$ and $\sum _{k=1}^{m} r_k =N$. Then, we can describe the outer coupling matrix B using the following block form

$$\begin{aligned} B=\left( {\begin{matrix} B_{11} &{} \,\,\, B_{12} &{} \,\,\, \cdots &{} \,\,\, B_{1m}\\ B_{21} &{} \,\,\, B_{22} &{} \,\,\, \cdots &{} \,\,\, B_{2m}\\ {\small \vdots } &{} \,\,\, {\small \vdots } &{} \,\,\, {\small \ddots } &{} \,\,\, {\small \vdots }\\ B_{m1} &{} \,\,\, B_{m2} &{} \,\,\, \cdots &{} \,\,\, B_{mm} \end{matrix}} \right) \end{aligned}$$

(2)

where each diagonal block $B_{uu}\in \mathbb {R}^{r_u\times \, r_u} (u\in \mathfrak {R})$ denotes the internal connections in the uth community, and each nondiagonal block $B_{u\upsilon }\in \mathbb {R}^{r_u\times \, r_{\upsilon }} (u,\upsilon \in \mathfrak {R}, u\ne \upsilon )$ denotes the external connections between the uth and $\upsilon$th communities.

In this paper, we focus on driving colored community network (1) to achieve globally exponential cluster synchronization by introducing some effective controllers. For this purpose, a mathematical definition of globally exponential cluster synchronization is given first.

Definition 1

Colored community network (1) is said to be globally exponentially cluster synchronized if there exist positive constants $M_0>0$ and $\lambda >0$, such that for any initial condition

$$\begin{aligned} ||x_i(t)-s_k(t)||\le M_0\, { {e}^{-\lambda t }}, \quad i\in \mathcal {C}_k \,\,\, \mathrm{and}\,\,\, k\in \mathfrak {R}, \end{aligned}$$

where $s_k(t)\in \mathbb {R}^{n_k}$ is a trajectory defined by ${\dot{s}}_k(t)=f_k\big (t,s_k(t)\big )$.

Fig. 2

Schematic diagram of the aperiodically intermittent control strategy

For achieving the globally exponential cluster synchronization of colored community network (1), appropriate controllers are needed. Here, the aim is realized by means of adaptive aperiodically intermittent pinning control scheme. For simplicity, suppose that the first $l_k \, (l_k<r_k)$ nodes in the community $\mathcal {C}_k$ are selected to be pinned, then we can obtain the following controlled colored community network:

$$\begin{aligned} {\dot{x}}_{i}(t)= & {} f_k\big (t,x_{i}(t)\big )+c_k\sum _{j\,\in \mathcal {C}_k, j\ne i } b_{ij}\,{\varGamma }_{kk} \big (x_j(t)-x_i(t)\big )\nonumber \\&+\sum _{p=1,p\ne k}^{m}\varepsilon _{kp}\sum _{j\,\in \mathcal {C}_p} b_{ij} \big ({\varGamma }_{kp}x_j(t)-{\varGamma }_{kk}^{p}x_i(t)\big ) \nonumber \\&+\,u_i(t), \quad \, i\in \mathcal {C}_k\,\, \mathrm{and} \,\,\ k\in \mathfrak {R} \end{aligned}$$

(3)

where $u_i(t)$ is an adaptive aperiodical intermittent controller given by

$$\begin{aligned} u_i(t)= & {} d_i(t){\varGamma }_{kk}\big (s_k(t)-x_i(t)\big ), \nonumber \\ L_{k-1} +1\le & {} i \le L_{k-1}+l_k,\,\,l_k<r_k, \end{aligned}$$

(4)

where $L_{k-1} = \sum _{j=0}^{k-1}r_j$ with $r_0 = 0$ and $d_i(t)$ is the adaptive intermittent feedback control gain designed as:

$$\begin{aligned} d_i(t)=\left\{ \begin{array}{ll} d_i(0),&{} \quad t=0,\\ d_i\big (t_\omega +\delta _\omega \big ),&{} \quad t=t_{\omega +1},\\ 0,&{} \quad t_\omega +\delta _\omega<t<t_{\omega +1}, \end{array} \right. \end{aligned}$$

(5)

with the updating law

$$\begin{aligned} {\dot{d}}_{i}(t)= & {} h_i \big (x_i(t)-s_k(t)\big )^{\top } {\varGamma }_{kk}\big (x_i(t)-s_k(t)\big ), \nonumber \\ t_\omega\le & {} t \le t_\omega +\delta _\omega , \end{aligned}$$

(6)

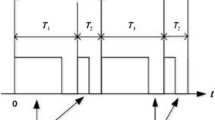
where $\omega \in {\mathbb {N}^+}$, $h_i>0$ and $d_i(0)> 0$ for $L_{k-1} +1 \le i \le L_{k-1}+l_k$. The time sequence $\{t_{\omega }\}_{\omega =1}^{+\infty }$ satisfies $0=t_1<t_2<\cdots<t_\omega <\cdots$ and $\lim _{\omega \rightarrow +\infty } t_\omega =+\infty$. For the $\omega$th time span $[t_\omega , t_{\omega +1})$, $\omega \in {\mathbb {N}^+}$, $[t_\omega , t_\omega +\delta _\omega ]$ is the $\omega$th work time span and $\delta _\omega$ is called the $\omega$th control width, while $\big (t_\omega +\delta _\omega , t_{\omega +1}\big )$ is the $\omega$th rest time span and $(t_{\omega +1}-t_\omega )-\delta _\omega$ is called the $\omega$th rest width; in addition, $(t_{\omega +1}-t_\omega )$ is called the $\omega$th control period. Figure 2 shows the schematic diagram of the aperiodically intermittent control strategy. Obviously, this control is more general than the periodically intermittent one, because its control periods as well as its control widths can be nonidentical. In particular, when $t_{\omega +1}-t_\omega \equiv {T}$ and $\delta _\omega \equiv \delta$, $\omega \in {\mathbb {N}^+}$, where T and $\delta$ are two positive constants; then, the intermittent control type turns into the periodic one.

In order to prove the main results, the following assumptions and lemmas are required.

Assumption 1

[38, 46] There exists a constant $\beta _k$ for each $k\in \mathfrak {R}$ such that the vector-valued function $f_k\big (t,x(t)\big )$ satisfies

$$\begin{aligned}&\big (x(t)-y(t)\big )^{\top }\big ( f_k(t,x(t))- f_k(t,y(t))\big ) \\&\quad \le \beta _k\,\big (x(t)-y(t)\big )^{\top }{\varGamma }_{kk}\big (x(t)-y(t)\big ). \end{aligned}$$

for any x(t), $y(t)\in \mathbb {R}^{\,n_k}$.

Assumption 2

[44, 46] Each block matrix $B_{u\upsilon } (u,\upsilon \in \mathfrak {R})$ in (2) is a zero-row-sum matrix, i.e., $\sum _{j\,\in \mathcal {C}_\upsilon }b_{ij}=0$ for any $i\in \mathcal {C}_u$ and $u,\upsilon \in \mathfrak {R}$, and each diagonal block $B_{uu}$ in (2) satisfies $b_{ij}\ge 0 (i\ne j)$ and $g_{ii}=-\sum _{j\in \mathcal {C}_u} b_{ij}$, $i,j\in \mathcal {C}_u$ and $u\in \mathfrak {R}$.

Remark 2

It has been verified in [6, 7, 24, 26, 29, 37] that many well-known chaotic (hyperchaotic) systems, such as chaotic (hyperchaotic) Lorenz system, chaotic (hyperchaotic) Chen system, Rössler system, Lü system, Chua’s circuit and cellular neural networks, satisfy Assumption 1. In general, $b_{ij}>0$ (or $<0$), $i \ne j$ can be viewed as the cooperative (or competitive) relationship between the node i and the node j, which will facilitate (or impede) synchronization between the nodes i and j [37, 40, 44, 46]. Hence, Assumption 2 implies that nodes belonging to the same community only have cooperative relationships, while nodes in different communities can have both competitive and cooperative relationships. Indeed, complex networks with both cooperative and competitive couplings are ubiquitous in reality, such as biological networks, social networks and technological networks [40].

Lemma 1

(Schur complement [34]) The following linear matrix inequality:

$$\begin{aligned} \left( {\begin{matrix} S_{11} &{} \quad S_{12} \\ S_{12}^{\top } &{} \quad S_{22} \end{matrix}} \right) <0 \end{aligned}$$

where $S_{11}=S_{11}^{\top }$, $S_{22}=S_{22}^{\top }$, and $S_{12}$ is a matrix with suitable dimensions, is equivalent to the following condition:

$$\begin{aligned} S_{22}<0, \quad S_{11}-S_{12}S_{22}^{-1}S_{12}^{\top }<0. \end{aligned}$$

Lemma 2

[26] Assume that ${\varOmega }_1$ and ${\varOmega }_2$ are two real symmetric matrices in $\mathbb {R}^{N\times N}$. Let $\alpha _1\ge \alpha _2\ge \cdots \ge \alpha _N$, $\gamma _1\ge \gamma _2\ge \cdots \ge \gamma _N$ and $\lambda _1\ge \lambda _2\ge \cdots \ge \lambda _N$ be eigenvalues of matrices ${\varOmega }_1$, ${\varOmega }_2$ and ${\varOmega }_1+{\varOmega }_2$, respectively. Then, one has $\alpha _i+\gamma _N\le \lambda _i \le \alpha _i+\gamma _1$, $i=1,2,\ldots ,N$.

3 Main results

In this section, some sufficient conditions will be established such that globally exponential cluster synchronization of the controlled colored community network (3) with the adaptive aperiodical intermittent controllers (4)–(6) can be achieved.

For convenience, let ${T}_\omega = t_{\omega +1}-t_\omega$ and $\theta _\omega =\delta _\omega /{T}_\omega$, $\omega \in {\mathbb {N}^+}$, where $\theta _\omega$ is called the control rate of the $\omega$th control period. Denote $B_{kk}^{\,s}=\frac{1}{2}\big (B_{kk}+B_{kk}^{\top }\big )$, ${\widetilde{{\varGamma }}}_{kp}= \varepsilon _{kp} {\varGamma }_{kp}$, $k,p\in \mathfrak {R}$ and $k\ne p$, and

$$\begin{aligned} G= & {} \left( {\begin{matrix} G_{11} &{} \,\,\, G_{12} &{} \,\,\, \ldots &{} \,\,\, G_{1m}\\ G_{21} &{} \,\,\, G_{22} &{} \,\,\, \ldots &{} \,\,\, G_{2m}\\ {\small \vdots } &{} \,\,\, {\small \vdots } &{} \,\,\, {\small \ddots } &{} \,\,\, {\small \vdots }\\ G_{m1} &{} \,\,\, G_{m2} &{} \,\,\, \ldots &{} \,\,\, G_{mm} \end{matrix}} \right) \\= & {} \left( {\begin{matrix} (c_1B_{11}+\beta _1I_{r_1}) \otimes {\varGamma }_{11} &{} \,\,\, B_{12}\otimes {\widetilde{{\varGamma }}}_{12} &{} \,\,\, \ldots &{} \,\,\, B_{1m}\otimes {\widetilde{{\varGamma }}}_{1m}\\ B_{21}\otimes {\widetilde{{\varGamma }}}_{21} &{} \,\,\, (c_2B_{22}+\beta _2I_{r_2})\otimes {\varGamma }_{22} &{} \,\,\, \ldots &{} \,\,\, B_{2m}\otimes {\widetilde{{\varGamma }}}_{2m}\\ {\small \vdots } &{} \,\,\, {\small \vdots } &{} \,\,\, {\small \ddots } &{} \,\,\, {\small \vdots }\\ B_{m1}\otimes {\widetilde{{\varGamma }}}_{m1} &{} \,\,\, B_{m2}\otimes {\widetilde{{\varGamma }}}_{m2} &{} \,\,\, \ldots &{} \,\,\, (c_mB_{mm}+\beta _mI_{r_m})\otimes {\varGamma }_{mm} \end{matrix}} \right) . \end{aligned}$$

Theorem 1

Suppose that Assumptions 1 and 2 hold and ${\inf }_{\omega \in Z^+} \{\theta _\omega \}=\theta _{\inf }>0$, by the adaptive aperiodical intermittent controllers (4)–(6), the globally exponential cluster synchronization of the controlled colored community network (3) can be achieved if there exist some positive constants $\xi _k$, $k\in \mathfrak {R}$ and $\rho _0$ such that

• (i) $\displaystyle c_k \big (B_{kk}^s\big )_{l_k}+ \big (\beta _k+\xi _k\big ) I_{r_k-l_k}<0$,

• (ii) $a_1 \theta _{\inf } -a_2^+(1-\theta _{\inf })>0$,

where $\pi _0=\displaystyle (m-1)\Big (\rho _0 \max _{1\le k, j\le m,\, k\ne j} \big (\lambda _{\max }(B_{kj}B_{kj}^{\top } ) \lambda _{\max }( {\widetilde{{\varGamma }}}_{kj}{\widetilde{{\varGamma }}}_{kj}^{\top })\big )+{1}/{\rho _0}\Big )$, $a_1 = \displaystyle 2\min _{1\le k \le m} \big (\xi _k \lambda _{\min }({\varGamma }_{kk})\big )-\pi _0$, $a_2^+=\max \{0,a_2\}$ with $a_2=\lambda _{\max } \big (G+G^{\top } \big )$, and $\big (B_{kk}^s\big )_{l_k}$ is the minor matrix of $B_{kk}^s$ by removing all the ith $\big (L_{k-1} + 1\le i \le L_{k-1} + l_{k}\big )$ row–column pairs of $B_{kk}^s$.

Proof

For $k\in \mathfrak {R}$, let the synchronous errors of the community $\mathcal {C}_k$ be $z_i(t) = x_i(t)-s_k(t)$, $i\in \mathcal {C}_k$, $Z_k(t)=\big (z_{L_{k-1} +1}^{\top }(t),\ldots ,z_{L_{k}}^{\top }(t) \big )^{\top }$, $F(Z_k(t))=\Big (\big (f_k\big (t,x_{L_{k-1} +1}(t)\big )-f_k\big (t,s_k(t) \big ) \big )^{\top },\ldots , \big (f_k\big (t,x_{L_{k}}(t)\big )-f_k\big (t,s_k(t) \big ) \big )^{\top }\Big )^{\top }$, and $Z(t)=\big (Z_1^{\top }(t),\ldots ,Z_m^{\top }(t) \big )^{\top }$. Under Assumption 2, one has $\sum _{j\,\in \mathcal {C}_p} b_{ij}{\widetilde{{\varGamma }}}_{kp} s_p(t)=\sum _{j\,\in \mathcal {C}_p} b_{ij}\varepsilon _{kp}{\varGamma }_{kk}^p x_i(t)=\mathbf{0}_{n_k}$, $i\in \mathcal {C}_k$ and $k,p\in \mathfrak {R} (p\ne k)$. Then, according to Eqs. (3)–(6), we can derive the following error system

$$\begin{aligned} \left\{ \begin{array}{lll} \displaystyle {\dot{Z}}_{k}(t)&{}=&{} \displaystyle F(Z_k(t))+c_k \big (B_{kk}\otimes {\varGamma }_{kk}\big ) Z_{k\,}(t) \\ &{}&{} + \sum _{j=1,j\ne k}^{m}\big (B_{kj}\otimes {\widetilde{{\varGamma }}}_{kj}\big ) Z_{j\,}(t)\\ &{}&{}-\big (D_{k}(t)\otimes {\varGamma }_{kk}\big )Z_k(t),\\ &{}&{} \quad t_\omega \le t \le t_\omega +\delta _\omega , \, L_{k-1}\\ &{}&{}\quad \quad +1 \le i \le L_{k-1}+l_k,\\ \displaystyle {\dot{Z}}_{k}(t)&{}=&{} \displaystyle F(Z_k(t))+c_k \big (B_{kk}\otimes {\varGamma }_{kk}\big ) Z_{k\,}(t) \\ &{}&{} + \sum _{j=1,j\ne k}^{m}\big (B_{kj}\otimes {\widetilde{{\varGamma }}}_{kj}\big ) Z_{j\,}(t),\\ &{}&{} \quad t_\omega +\delta _\omega<t<t_{\omega +1},\, L_{k-1}\\ &{}&{}\qquad +l_k+1 \le i \le L_{k}, \end{array} \right. \end{aligned}$$

(7)

where $\omega \in {\mathbb {N}^+}$, $D_k(t)=\mathrm{diag}\big (d_{L_{k-1} +1}(t),\dots ,d_{L_{k-1} +l_k}(t),0,\ldots ,0\big )\in \mathbb {R}^{r_k\times \, r_k}$, and $k\in \mathfrak {R}$.

Constructing a piecewise Lyapunov candidate function as follows

$$\begin{aligned} V(t)=V_1(t)+V_2(t), \end{aligned}$$

(8)

where

$$\begin{aligned} V_1(t)= & {} \frac{1}{2}\sum _{k=1}^{m}Z_{k}^{\top }(t)(I_{r_{k}}\otimes I_{n_k})Z_{k}(t) \nonumber \\= & {} \frac{1}{2}\sum _{k=1}^{m} \sum _{i\in \mathcal {C}_{k}} z_{i}^{\top }(t)z_{i}(t) \end{aligned}$$

(9)

and $V_2(t)=\displaystyle \frac{1}{2} {e}^{-a_1 t } {\varPhi }(t)$ with

$$\begin{aligned} {\varPhi }(t)= \left\{ \begin{array}{ll} \displaystyle \sum _{k=1}^{m}\, \sum _{i=L_{k-1}+1}^{L_{k-1}+l_k} \frac{1}{h_i}\Big (d_i(t)-d_i^*{e}^{a_1 (t_\omega +\delta _\omega ) } \Big )^2,\,\,\quad t_\omega \le t \le t_\omega +\delta _\omega ,\\ \displaystyle \sum _{k=1}^{m}\, \sum _{i=L_{k-1}+1}^{L_{k-1}+l_k} \frac{1}{h_i}\Big (d_i\big ( t_\omega +\delta _\omega \big )-d_i^* {e}^{a_1 (t_\omega +\delta _\omega ) } \Big )^2,\,\,\quad \quad t_\omega +\delta _\omega<t<t_{\omega +1}, \end{array} \right. \end{aligned}$$

(10)

where $\omega \in {\mathbb {N}^+}$ and each $d_i^*$ is a positive constant to be determined later. Evidently, $V_1(t)$ is continuous for all $t\ge 0$. In addition, it follows from (5) that $V_2(t)$ is also continuous for all $t\ge 0$. Hence, the piecewise Lyapunov function V(t) is continuous for all $t\ge 0$.

Since $0<\theta _{\inf }< 1$, condition (ii) implies that $a_1>0$. Consequently, for $t_\omega \le t \le t_\omega +\delta _\omega$, $\omega \in {\mathbb {N}^+}$, by Assumption 1, we can calculate the derivative of V(t) with respect to time t along the trajectories of (7) as follows

$$\begin{aligned} {\dot{V}}(t)= & {} \sum _{k=1}^{m}Z_{k}^{\top }(t)(I_{r_{k}}\otimes I_{n_k}){\dot{Z}}_{k}(t) \nonumber \\&-\frac{a_1}{2} {e}^{-a_1 t } {\varPhi }(t)+\frac{1}{2} {e}^{-a_1 t } {\dot{{\varPhi }}}(t)\nonumber \\= & {} \sum _{k=1}^{m}Z_{k}^{\top }(t)(I_{r_{k}}\otimes I_{n_k}) \nonumber \\&\bigg (F(Z_k(t))+c_k \big (B_{kk}\otimes {\varGamma }_{kk}\big ) Z_{k\,}(t) \nonumber \\&+ \sum _{j=1,j\ne k}^{m}\big (B_{kj}\otimes {\widetilde{{\varGamma }}}_{kj}\big ) Z_{j\,}(t)\nonumber \\&-\big (D_{k}(t)\otimes {\varGamma }_{kk}\big )Z_k(t) \bigg )-\,\frac{a_1}{2} {e}^{-a_1 t } {\varPhi }(t)\nonumber \\&+\, {e}^{-a_1 t }\sum _{k=1}^{m}\, \sum _{i=L_{k-1}+1}^{L_{k-1}+l_k} \nonumber \\&\Big (d_i(t)-d_i^*{e}^{a_1 (t_\omega +\delta _\omega ) } \Big )z_{i}^{\top }(t){\varGamma }_{kk} z_{i}(t)\nonumber \\= & {} \sum _{k=1}^{m}\sum _{i=L_{k-1}+1}^{L_{k-1}+r_k}z_{i}^{\top } (t)\Big (f_k\big (t,x_{i}(t)\big )-f_k\big (t,s_k(t) \big )\Big ) \nonumber \\&+\sum _{k=1}^{m}c_k Z_{k}^{\top }(t) \big (B_{kk}\otimes {\varGamma }_{kk}\big ) Z_{k\,}(t)\nonumber \\&+\sum _{k=1}^{m} \sum _{j=1, j \ne k}^{m} Z_{k}^{\top }(t)\big (B_{kj}\otimes {\widetilde{{\varGamma }}}_{kj}\big ) Z_{j\,}(t) \nonumber \\&-\sum _{k=1}^{m}\, \sum _{i=L_{k-1}+1}^{L_{k-1}+l_k} d_i(t)z_{i}^{\top }(t){\varGamma }_{kk} z_{i}(t)\nonumber \\&+\,{e}^{-a_1 t }\sum _{k=1}^{m}\, \sum _{i=L_{k-1}+1}^{L_{k-1}+l_k} d_i(t)z_{i}^{\top }(t){\varGamma }_{kk} z_{i}(t) \nonumber \\&-\frac{a_1}{2} {e}^{-a_1 t } {\varPhi }(t)\nonumber \\&-\sum _{k=1}^{m}\, \sum _{i=L_{k-1}+1}^{L_{k-1}+l_k} d_i^*{e}^{a_1 (t_\omega +\delta _\omega -t) }z_{i}^{\top }(t){\varGamma }_{kk} z_{i}(t)\nonumber \\\le & {} \sum _{k=1}^{m}\sum _{i=L_{k-1}+1}^{L_{k-1}+r_k} \beta _k z_{i}^{\top }(t) {\varGamma }_{kk} z_i(t) \nonumber \\&+\sum _{k=1}^{m}c_k Z_{k}^{\top }(t) \big (B_{kk}\otimes {\varGamma }_{kk}\big ) Z_{k\,}(t)\nonumber \\&+\sum _{k=1}^{m} \sum _{j=1, j \ne k}^{m} Z_{k}^{\top }(t)\big (B_{kj}\otimes {\widetilde{{\varGamma }}}_{kj}\big ) Z_{j\,}(t) \nonumber \\&-\sum _{k=1}^{m}\, \sum _{i=L_{k-1}+1}^{L_{k-1}+l_k} d_i^*z_{i}^{\top }(t){\varGamma }_{kk} z_{i}(t)-a_1V_2(t)\nonumber \\= & {} \sum _{k=1}^{m} Z_{k}^{\top }(t)\Big (\big (c_kB_{kk}^{\,s}+\beta _k I_{r_{k}}-D_k^*\big )\otimes {\varGamma }_{kk}\Big ) \nonumber \\&\times Z_{k}(t)-a_1V_2(t)\nonumber \\&+\sum _{k=1}^{m} \sum _{j=1,j\ne k}^{m} Z_{k}^{\top }(t)\big (B_{kj}\otimes {\widetilde{{\varGamma }}}_{kj}\big ) Z_{j\,}(t) \end{aligned}$$

(11)

where $D_k^*=\mathrm{diag}\Big \{d_{L_{k-1}+1}^*, d_{L_{k-1}+2}^*,\ldots ,d_{L_{k-1}+l_k}^*,0,\ldots ,0 \Big \} \in \mathbb {R}^{r_k\times \, r_k}$, $m\in \mathfrak {R}$.

On the other hand, using the properties of the Kronecker product of the matrices [35], we can derive the following inequality:

$$\begin{aligned}&\sum _{k=1}^{m} \sum _{j=1,j\ne k}^{m} Z_{k}^{\top }(t)\big (B_{kj}\otimes {\widetilde{{\varGamma }}}_{kj}\big ) Z_{j\,}(t)\nonumber \\&\quad \le \frac{1}{2} \sum _{k=1}^{m} \sum _{j=1,j\ne k}^{m} \nonumber \\&\qquad \times \bigg [\rho _0 Z_{k}^{\top }(t) \Big (B_{kj}B_{kj}^{\top }\otimes {\widetilde{{\varGamma }}}_{kj}{{\widetilde{{\varGamma }}}_{kj}}^{\top }\Big ) Z_{k}(t) \nonumber \\&\qquad \quad +\frac{1}{\rho _0} Z_{j\,}^{\top }(t) \big (I_{r_{j}}\otimes I_{n_j}\big ) Z_{j\,}(t)\bigg ]\nonumber \\&\quad \le \frac{1}{2}\bigg ({\rho _0} \max _{1\le k,j\le m,\, k\ne j} \nonumber \\&\qquad \qquad \Big (\lambda _{\max }\big (B_{kj}B_{kj}^{\top } \big ) \lambda _{\max }\big ({\widetilde{{\varGamma }}}_{kj} {\widetilde{{\varGamma }}}_{kj}^{\top }\big )\Big )+\frac{1}{\rho _0}\bigg ) \nonumber \\&\qquad \times \sum _{k=1}^{m} \sum _{j=1,j\ne k}^{m} Z_{k}^{\top }(t)\big (I_{r_{k}}\otimes I_{n_k}\big ) Z_{k\,}(t)\nonumber \\&\quad =(m-1)\bigg (\rho _0 \max _{1\le k,j\le m,\, k\ne j} \nonumber \\&\qquad \qquad \qquad \quad \Big (\lambda _{\max }\big (B_{kj}B_{kj}^{\top } \big ) \lambda _{\max }\big ( {\widetilde{{\varGamma }}}_{kj} {\widetilde{{\varGamma }}}_{kj}^{\top } \big )\Big ) + \frac{1}{\rho _0}\bigg ) \nonumber \\&V_1(t)=\pi _0 V_1(t). \end{aligned}$$

(12)

Substituting (12) into (11) gives

$$\begin{aligned} {\dot{V}}(t)\le & {} \sum _{k=1}^{m} Z_{k}^{\top }(t)\Big (\big (c_kB_{kk}^{\,s}+\beta _k I_{r_{k}}-D_k^*\big )\otimes {\varGamma }_{kk}\Big ) \nonumber \\&\times Z_{k}(t)+\pi _0V_1(t)-a_1V_2(t)\nonumber \\= & {} \sum _{k=1}^{m} Z_{k}^{\top }(t) \Big (\big (c_kB_{kk}^{\,s} +(\beta _k+\xi _k) I_{r_{k}}-D_k^*\big )\otimes {\varGamma }_{kk}\Big )\nonumber \\&\quad \times Z_{k}(t) - \sum _{k=1}^{m} Z_{k}^{\top }(t)\big (\xi _k I_{r_{k}}\otimes {\varGamma }_{kk} \big )Z_{k}(t)\nonumber \\&+\,\pi _0V_1(t)-a_1V_2(t). \end{aligned}$$

(13)

For $k\in \mathfrak {R}$, let $Q_k=c_k B_{kk}^s+\big (\beta _k+\xi _k\big )I_{r_k}$ and $Q_k-D_k^* = {\small \begin{pmatrix} E_k-{{\tilde{D}}_k^*} &{} S_k \\ S_k^{\top } &{} Q_{l_k} \end{pmatrix}}$, where ${\tilde{D}}_k^*=\mathrm{diag}\Big \{d_{L_{k-1}+1}^*, d_{L_{k-1}+2}^*,\ldots ,d_{L_{k-1}+l_k}^* \Big \}$ and $Q_{l_k}$ is the minor matrix of $Q_k$ by removing all the ith $(L_{k-1} + 1 \le i \le L_{k-1} + l_{k})$ row–column pairs of $Q_k$. Obviously, $Q_{l_k}=c_k\big (B_{kk}^s\big )_{l_k}+ \big (\beta _k+\xi _k\big )I_{r_k-l_k}$, $k\in \mathfrak {R}$. Hence, based on condition $(\mathrm{i})$ and Lemma 1, it can be concluded that when $d_i^*>0$, $L_{k-1}+1\le i \le L_{k-1}+l_{k}$, $k\in \mathfrak {R}$ are sufficiently large such that $d_i^*>\lambda _{\max }(E_k-S_kQ_{l_k}^{-1}S_k^{\top })$, $L_{k-1}+1\le i \le L_{k-1}+l_{k}$, $k\in \mathfrak {R}$, then $Q_k-D_k^*<0$, $k\in \mathfrak {R}$. This combines with (13), and we obtain

$$\begin{aligned} {\dot{V}}(t)\le & {} - 2\min _{1\le k \le m} \big (\xi _k \lambda _{\min }({\varGamma }_{kk})\big ) V_1(t) \nonumber \\&+\,\pi _0 V_1(t) -a_1 V_2(t)\nonumber \\= & {} - \Big (2\min _{1\le k \le m} \big (\xi _k \lambda _{\min }({\varGamma }_{kk})\big )-\pi _0 \Big )\nonumber \\&V_1(t)-a_1 V_2(t) \nonumber \\= & {} -a_1 V_1(t)-a_1 V_2(t)=-a_1 V(t), \nonumber \\&\quad t_\omega \le t \le t_\omega +\delta _\omega ,\,\, \omega \in {\mathbb {N}^+}, \end{aligned}$$

(14)

therefore,

$$\begin{aligned} V(t)\le & {} V(t_\omega ){e}^{-a_1(t-t_\omega )}, \nonumber \\ t_\omega\le & {} t \le t_\omega +\delta _\omega ,\,\, \omega \in {\mathbb {N}^+}. \end{aligned}$$

(15)

By the similar analysis, for $t_\omega +\delta _\omega<t<t_{\omega +1}$, $\omega \in {\mathbb {N}^+}$, we get

$$\begin{aligned} {\dot{V}}(t)= & {} \sum _{k=1}^{m}Z_{k}^{\top }(t)(I_{r_{k}}\otimes I_{n_k}){\dot{Z}}_{k}(t)-\frac{a_1}{2} {e}^{-a_1 t } {\varPhi }(t)\nonumber \\\le & {} \sum _{k=1}^{m} Z_{k}^{\top }(t)\Big (\big (c_kB_{kk}+\beta _k I_{r_{k}}\big )\otimes {\varGamma }_{kk}\Big ) Z_{k}(t) \nonumber \\&+\sum _{k=1}^{m} \sum _{j=1,j\ne k}^{m} Z_{k}^{\top }(t) \big (B_{kj}\otimes {\widetilde{{\varGamma }}}_{kj}\big ) Z_{j\,}(t)\nonumber \\= & {} Z^{\top }(t) G Z(t)=\frac{1}{2} Z^{\top }(t) \big (G+G^{\top }\big ) Z(t)\nonumber \\\le & {} \lambda _{\max } \big (G+G^{\top } \big ) V_1(t)=a_2 V_1(t) \le a_2^+ V(t),\nonumber \\ \end{aligned}$$

(16)

therefore,

$$\begin{aligned} V(t)\le & {} V(t_\omega +\delta _\omega ){e}^{a_2^+(t-t_\omega -\delta _\omega )}, \nonumber \\&t_\omega +\delta _\omega<t<t_{\omega +1},\,\, \omega \in {\mathbb {N}^+}. \end{aligned}$$

(17)

Let ${T}_0=0$ and $\theta _0=0$. Combining with (15) and (17), by mathematical induction, one has

$$\begin{aligned} V(t_{\omega +1})\le & {} V(t_\omega +\delta _\omega ) {e}^{a_2^+(t_{\omega +1}- t_\omega -\delta _\omega )}\nonumber \\\le & {} V(t_\omega ){e}^{a_2^+(t_{\omega +1}-t_\omega - \delta _\omega )-a_1 \delta _\omega }\nonumber \\= & {} V(t_\omega ){e}^{ [a_2^+(1-\theta _\omega )-a_1 \theta _\omega ] {T}_\omega }\nonumber \\\le & {} \cdots \le V(0){e}^{ \sum _{j=0}^{\omega } [a_2^+(1-\theta _j)-a_1 \theta _j] {T}_j},\quad \omega \in {\mathbb {N}^+}.\nonumber \\ \end{aligned}$$

(18)

Since for any $t\ge 0$, there exists a positive integer i such that $t_i\le t < t_{i+1}$. Consequently, by (15), (17), (18) and condition (ii), the following estimation of V(t) can be derived for any $t\ge 0$.

For $t_i\le t \le t_i+\delta _i$, $i\in {\mathbb {N}^+}$,

$$\begin{aligned} V(t)\le & {} V(t_i){e}^{-a_1(t-t_i)}\nonumber \\\le & {} V(0){e}^{ \sum _{j=0}^{i-1} [a_2^+(1-\theta _j)-a_1 \theta _j] {T}_j}{e}^{-a_1(t-t_i)}\nonumber \\\le & {} V(0){e}^{ [a_2^+(1-\theta _{\inf })-a_1 \theta _{\inf }]\sum _{j=0}^{i-1} {T}_j}{e}^{a_1t_i}{e}^{-a_1t}\nonumber \\= & {} V(0){e}^{(a_2^++a_1)(1-\theta _{\inf })t_i }{e}^{-a_1t}\nonumber \\\le & {} V(0){e}^{-[a_1\theta _{\inf } -a_2^+(1-\theta _{\inf }) ]t }. \end{aligned}$$

(19)

And for $t_i+\delta _i< t < t_{i+1}$, $i\in {\mathbb {N}^+}$,

$$\begin{aligned} V(t)\le & {} V(t_i+\delta _i){e}^{a_2^+(t-t_i-\delta _i)}\nonumber \\\le & {} V(t_i){e}^{-a_1\delta _i} {e}^{a_2^+(t_{i+1}-t_i-\delta _i)} \nonumber \\\le & {} V(0){e}^{ [a_2^+(1-\theta _{\inf })-a_1 \theta _{\inf }]\sum _{j=0}^{i} {T}_j}\nonumber \\\le & {} V(0){e}^{-[a_1\theta _{\inf } -a_2^+(1-\theta _{\inf })]t }. \end{aligned}$$

(20)

Combining (19) and (20) yields

$$\begin{aligned} V(t)\le V(0){e}^{-[a_1\theta _{\inf } -a_2^+(1-\theta _{\inf }) ]t },\quad t\ge 0. \end{aligned}$$

(21)

This means that the cluster synchronization can be globally exponentially achieved. The proof is thus completed. $\square$

For $k\in \mathfrak {R}$, let $\eta _k=\displaystyle \beta _k +\xi _k$. By virtue of Lemma 2, we can get that $\lambda _{\max }\big ( c_k (B_{kk}^s)_{l_k} + \eta _k I_{r_k-l_k} \big )\le c_k \lambda _{\max }\big ((B_{kk}^s)_{l_k}\big )+\eta _k$, $k\in \mathfrak {R}$. Then, from Theorem 1, the following result can obtained.

Corollary 1

Suppose that Assumptions 1 and 2 hold and ${\inf }_{\omega \in Z^+} \{\theta _\omega \}=\theta _{\inf }>0$, by the adaptive aperiodical intermittent controllers (4)–(6), the globally exponential cluster synchronization of the controlled colored community network (3) can be achieved if there exist some positive constants $\xi _k$, $k\in \mathfrak {R}$ and $\rho _0$ such that

• (i) $\displaystyle \lambda _{\max }\big ((B_{kk}^s)_{l_k}\big )<-\frac{\eta _k}{c_k}$,

• (ii) $\displaystyle \frac{a_2^+}{a_1+a_2^+}<\theta _{\inf }<1$,

where $\eta _k=\displaystyle \beta _k +\xi _k$, and $\pi _0$, $a_1$, $a_2^+$, $(B_{kk}^s)_{l_k}$ are defined in Theorem 1.

In the case that $t_{\omega +1}-t_\omega \equiv {T}$ and $\delta _\omega \equiv \delta$ for all $\omega \in {\mathbb {N}^+}$, where T and $\delta$ are both positive constants, the control turns to adaptive periodically intermittent pinning one. Denote $\theta =\delta /{T}$, according to Corollary 1, we can get the following result.

Corollary 2

Under Assumptions 1 and 2, the controlled colored community network (3) is globally exponentially cluster synchronized under the adaptive periodically intermittent pinning control if there exist some positive constants $\xi _k$, $k\in \mathfrak {R}$ and $\rho _0$ such that

• (i) $\displaystyle \lambda _{\max }\big ((B_{kk}^s)_{l_k}\big )<-\frac{\eta _k}{c_k}$,

• (ii) $\displaystyle \frac{a_2^+}{a_1+a_2^+}<\theta <1$,

where $\eta _k=\displaystyle \beta _k +\xi _k$, and $\pi _0$, $a_1$, $a_2^+$, $(B_{kk}^s)_{l_k}$ are defined in Theorem 1.

Remark 3

In [7], by means of periodically intermittent control scheme, cluster synchronization in colored community network with different order node dynamics was discussed. Unfortunately, it can be seen in [7] that the periodical intermittent controllers are required to be added to all network nodes. Since real-world complex networks usually contain a large set of nodes, it is practically impossible to apply control actions to all network nodes. In this paper, the intermittent controllers just apply on partial nodes in each community, and moreover, the intermittent control is aperiodic [see Eqs. (4)–(6)]. The results derived here are thus more practically applicable than those in [7].

Remark 4

In [45, 46], by constructing a piecewise auxiliary function and utilizing the theory of series with nonnegative terms, pinning synchronization for directed dynamical networks with node balance and pinning cluster synchronization for directed heterogeneous dynamical networks were investigated via adaptive periodically intermittent control, respectively. It should be noted that the piecewise auxiliary function given in [45, 46] is discontinuous at $t=t_{\omega +1}$, $\omega \in {\mathbb {N}^+}$; therefore, only asymptotical synchronization criteria were established in [45, 46]. In this paper, a novel piecewise auxiliary function ($V_2(t)$) is introduced [see Eq. (10)], which is continuous for all $t\ge 0$, and then, based on which and Lyapunov stability theory, we derive some globally exponential cluster synchronization criteria for a general colored community network with nodes of different state dimensions under adaptive aperiodically intermittent pinning control. Therefore, the approach developed in this work differs from that in [45, 46] and the theoretical results obtained generalize those in [45, 46].

Remark 5

It can be observed that our cluster synchronization criteria are dependent on the quantity $\theta _{\inf }$, but not the control widths $\delta _w (w\in {\mathbb {N}^+})$ or the control periods ${T}_w (w\in {\mathbb {N}^+})$. This means that, for achieving the globally exponential cluster synchronization, each control period ${T}_w$ can be arbitrarily selected. For practical problems, we can choose the control periods ${T}_\omega$, $\omega \in {\mathbb {N}^+}$ according to the actual requirement.

Remark 6

From Eqs. (5) and (6), it is obvious that the adaptive intermittent feedback control gains $d_i(t)$, $L_{k-1} +1 \le i \le L_{k-1}+l_k, k\in \mathfrak {R}$ are increasing during the work time span but identically equal to zeros during the rest time span. When the cluster synchronization is achieved, they tend to some positive constants during each work time span. This point will be verified via the numerical simulations in the next section.

Remark 7

Clearly, to make condition $(\mathrm{i})$ in Corollary 1 be satisfied, at least we need to pick $l_k$ pinned candidates in the community $\mathcal {C}_k$ for each $k\in \mathfrak {R}$ such that $\lambda _{\max }\big ((B_{kk}^s)_{l_k}\big )<0$. Let Intra-DegIn(i, k) be the intra-indegree of a node i in the community $\mathcal {C}_k$, i.e., the sum of the weights of directed edges e(i, j) with $j\in \mathcal {C}_k$ into $i\in \mathcal {C}_k$, and Intra-DegOut(i, k) be the intra-outdegree of a node i in the community $\mathcal {C}_k$, i.e., the sum of the weights of directed edges e(j, i) with $j\in \mathcal {C}_k$ emanating from $i\in \mathcal {C}_k$ [38, 47]. According to the definition of the outer coupling matrix B in (1) and noticing that the matrices $B_{kk}$ satisfy $b_{ij}\ge 0 (i\ne j)$ and $g_{ii}=-\,\sum _{j\in \mathcal {C}_k} b_{ij}$, $i,j\in \mathcal {C}_k$ and $k\in \mathfrak {R}$, it is easy to obtain that for any $i\in \mathcal {C}_k$ and $k\in \mathfrak {R}$

$$\begin{aligned} \hbox {Intra-DegIn} (i,k)= & {} \displaystyle \sum _{j\,\in \mathcal {C}_k,j\,\ne i} b_{ij} \, \hbox { and } \\ \hbox {Intra-DegOut} (i,k)= & {} \displaystyle \sum _{j\,\in \mathcal {C}_k,j\,\ne i} b_{j\,i}. \end{aligned}$$

For $k\in \mathfrak {R}$, define a intra-degree-difference vector for the community $\mathcal {C}_k$:

$$\begin{aligned} \hbox {Intra-DegDif} (i,k)= & {} \hbox {Intra-DegOut} (i,k) \\&- \hbox {Intra-DegIn} (i,k), \quad i\in \mathcal {C}_k. \end{aligned}$$

Then, similar to the discussion in [26], it can be concluded that the nodes in the community $\mathcal {C}_k$ whose intra-outdegrees are bigger than their intra-indegrees should be chosen as pinned candidates, which can lead to $\lambda _{\max }\big ((B_{kk}^s)_{l_k}\big )\le 0$. Inspired by this fact, for the kth community $\mathcal {C}_k$ in the controlled colored community network (3), we first apply adaptive aperiodical intermittent control to the nodes with zero intra-indegrees since their states are not influenced by others in the community $\mathcal {C}_k$. Then, we continue to select other nodes in descending order according to their intra-degree-difference as defined above (for those with the same intra-degree-difference, in ascending order according to their intra-outdegrees) until condition (i) in Corollary 1 is satisfied. Additionally, it can be deduced from condition (i) of Corollary 1 that, for each $k\in \mathfrak {R}$, the least number of pinned nodes $l_k$ for the community $\mathcal {C}_k$ should satisfy

$$\begin{aligned} \lambda _{\max }\big ((B_{kk}^s)_{l_k-1}\big )\ge -\displaystyle \frac{\eta _k}{c_k} \,\, \hbox { and } \,\, \lambda _{\max }\big ((B_{kk}^s)_{l_k}\big )<-\displaystyle \frac{\eta _k}{c_k}. \end{aligned}$$

Remark 8

It should be pointed out that, if we have picked $l_k$ pinned nodes in the community $\mathcal {C}_k$ for each $k \in \mathfrak {R}$ to satisfy condition (i) of Corollary 1. Then, the inner coupling strength $c_k$ for each $k \in \mathfrak {R}$ is required to satisfy $c_k>-\big ({\eta _k}/{\displaystyle \lambda _{\max }\big ((B_{kk}^s)_{l_k}\big )}\big )$. Usually, the theoretical value of $c_k$ is much larger than the needed values in reality [24, 26]. When $c_k$ is small, selecting a small fraction of network nodes in the community $\mathcal {C}_k$ such that condition (i) of Corollary 1 holds may be infeasible. To realize the cluster synchronization, one can use centralized or decentralized adaptive approaches to tune the inner coupling strengths automatically [24, 26, 40, 44, 48, 49, 58]. In this paper, we focus on the pinning cluster synchronization of a general colored community network with fixed inner and external coupling strengths via adaptive intermittent control.

Remark 9

By Corollary 1, one can estimate the value range of the quantity $\theta _{\inf }$ in a simple way; therefore, the adaptive aperiodical intermittent controllers can be designed conveniently. To shed light on how to design suitable adaptive aperiodical intermittent controllers in practical application for realizing cluster synchronization, the following steps are given:

Step 1 Given positive constants $\xi _k$, $k \in \mathfrak {R}$ and $\rho _0$, pick $l_k$ pinned candidates in the community $\mathcal {C}_k$ for each $k \in \mathfrak {R}$ by means of Remark 6, such that condition (i) of Corollary 1 is satisfied.

Step 2 For the given $\xi _k$, $k \in \mathfrak {R}$ and $\rho _0$, compute the value of ${a_2^+}/{(a_1+a_2^+)}$, and then, optionally select the control rates $\theta _\omega$, $\omega \in {\mathbb {N}^+}$, only if condition (ii) of Corollary 1 is satisfied.

Step 3 Choose the control periods ${T}_\omega$, $\omega \in {\mathbb {N}^+}$ according to the practical requirement.

Step 4 For $k\in \mathfrak {R}$, based on the above chosen $l_k$ pinned nodes, $\theta _\omega$ and ${T}_\omega$, $\omega \in {\mathbb {N}^+}$, design the adaptive aperiodical intermittent controllers (4)–(6).

4 Numerical examples

In order to illustrate the effectiveness of our theoretical results, in this section we consider the colored community network shown in Fig. 1 as an example. Choose the node dynamics of the first community as the following Chua’s circuit [26]:

$$\begin{aligned} \left\{ \begin{array}{lll} {\dot{x}}_{i1}=10 \big ( x_{i2}-x_{i1}- \varphi (x_{i1}) \big )\\ {\dot{x}}_{i2}= x_{i1}-x_{i2}+x_{i3}\\ {\dot{x}}_{i3}=-14.87 x_{i2} \end{array} \right. \end{aligned}$$

(22)

with $\varphi (x_{i1})=-\,0.68x_{i1}-0.295(|x_{i1}+1|-|x_{i1}-1|)$ and $i=1,\ldots ,5$, the node dynamics of the second community as cellular neural networks [44]:

$$\begin{aligned} \left\{ \begin{array}{lll} {\dot{x}}_{i1}=-\,x_{i1}+1.25 \psi (x_{i1}) -3.2\psi (x_{i2}) -3.2\psi (x_{i3}) \\ {\dot{x}}_{i2}= -\,x_{i2}-3.2 \psi (x_{i1}) +1.1\psi (x_{i2}) -4.4\psi (x_{i3})\\ {\dot{x}}_{i3}=-\,x_{i3}-3.2\psi (x_{i1}) + 4.4\psi (x_{i2})+ 1\psi (x_{i3}) \end{array} \right. \nonumber \\ \end{aligned}$$

(23)

with $\psi (s)=0.5(|s+1|-|s-1|)$ and $i=6,\ldots ,11$, the node dynamics of the third community as hyperchaotic Chen system [57]:

$$\begin{aligned} \left\{ \begin{array}{llll} {\dot{x}}_{i1}=35(x_{i2}-x_{i1})+x_{i4} \\ {\dot{x}}_{i2}= 7x_{i1}+12x_{i2}-x_{i1}x_{i3}\\ {\dot{x}}_{i3}=-3x_{i3}+x_{i1}x_{i2} \\ {\dot{x}}_{i4}=0.25x_{i4}+x_{i2}x_{i3} \end{array} \right. \end{aligned}$$

(24)

with $i = 12,\ldots ,18$. For simplicity, the inner and outer coupling matrices are given as follows:

• ${\textcircled {{\small 1}}}$ For the inner coupling matrices in each community

  $$\begin{aligned} {\varGamma }_{11}={\varGamma }_{22}=I_3, \, {\varGamma }_{33}=I_4. \end{aligned}$$

• ${\textcircled {{\small 2}}}$ For the inner coupling matrices between different communities

  $$\begin{aligned} {\varGamma }_{12}= & {} \left( {\begin{matrix} 1\,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 1 \,\,&{} 0 \end{matrix}} \right) , \quad {\varGamma }_{13} = \left( {\begin{matrix} 0\,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 1 \,\,&{} 0 \end{matrix}} \right) , \\ {\varGamma }_{11}^2= & {} \left( {\begin{matrix} 1\,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 1 \end{matrix}} \right) ,\quad {\varGamma }_{11}^3= \left( {\begin{matrix} 0\,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 1 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 1 \end{matrix}} \right) , \\ {\varGamma }_{21}= & {} {\varGamma }_{12}^{\top }, \quad {\varGamma }_{23}= \left( {\begin{matrix} 0\,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 1 \end{matrix}} \right) , \\ {\varGamma }_{22}^1= & {} \left( {\begin{matrix} 1\,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 1 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \end{matrix}} \right) ,\quad {\varGamma }_{22}^3= \left( {\begin{matrix} 1\,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 1 \\ 0 \,\,&{} 0 \,\,&{} 0 \end{matrix}} \right) , \\ {\varGamma }_{31}= & {} {\varGamma }_{13}^{\top }, \quad {\varGamma }_{32}={\varGamma }_{23}^{\top }, \quad {\varGamma }_{33}^1= \left( {\begin{matrix} 0\,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 1 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 1 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \end{matrix}} \right) , \\ {\varGamma }_{33}^2= & {} \left( {\begin{matrix} 0\,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 1 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \end{matrix}} \right) . \end{aligned}$$

• ${\textcircled {{\small 3}}}$ For the outer coupling matrices in each community

  $$\begin{aligned} B_{11}= & {} \left( {\begin{matrix} -\,4\,\,&{} 1 \,\,&{} 1 \,\,&{} 1 \,\,&{} 1 \\ 1 \,\,&{} -\,3 \,\,&{} 1 \,\,&{} 1 \,\,&{} 0\\ 1 \,\,&{} 1 \,\,&{} -\,4 \,\,&{} 1 \,\,&{} 1\\ 1 \,\,&{} 1 \,\,&{} 1 \,\,&{} -\,3 \,\,&{} 0 \\ 1 \,\,&{} 0 \,\,&{} 1 \,\,&{} 0 \,\,&{} -\,2 \end{matrix}} \right) , \\ B_{22}= & {} \left( {\begin{matrix} -\,4\,\,&{} 1 \,\,&{} 1 \,\,&{} 1 \,\,&{} 0 \,\,&{} 1 \\ 1 \,\,&{} -\,2 \,\,&{} 0 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0\\ 1 \,\,&{} 0 \,\,&{} -\,3 \,\,&{} 0 \,\,&{} 1 \,\,&{} 1 \\ 1 \,\,&{} 1 \,\,&{} 0 \,\,&{} -\,4 \,\,&{} 1 \,\,&{} 1\\ 0 \,\,&{} 0 \,\,&{} 1 \,\,&{} 1 \,\,&{} -\,3 \,\,&{} 1 \\ 1 \,\,&{} 0 \,\,&{} 1 \,\,&{} 1 \,\,&{} 1 \,\,&{} -\,4 \end{matrix}} \right) , \\ B_{33}= & {} \left( {\begin{matrix} -\,3\,\,&{} 1 \,\,&{} 0 \,\,&{} 1 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \\ 1 \,\,&{} -\,2 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 1 \,\,&{} -\,4 \,\,&{} 1 \,\,&{} 0 \,\,&{} 1 \,\,&{} 1 \\ 1 \,\,&{} 0 \,\,&{} 1 \,\,&{} -\,3 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \\ 1 \,\,&{} 0 \,\,&{} 0 \,\,&{} 1 \,\,&{} -\,2 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \,\,&{} -\,2 \,\,&{} 1 \\ 0 \,\,&{} 0 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \,\,&{} 1 \,\,&{} -\,2 \end{matrix}} \right) . \end{aligned}$$

• ${\textcircled {{\small 4}}}$ For the outer coupling matrices between different communities

  $$\begin{aligned} B_{12}= & {} B_{21}^{\top }= \left( {\begin{matrix} 0\,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0\,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ -\,1 \,\,&{} 1 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 1 \,\,&{} -\,1 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \end{matrix}} \right) , \\ B_{13}= & {} B_{31}^{\top }= \left( {\begin{matrix} 0\,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0\,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 1 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} -\,1 \\ -\,1 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 1 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \end{matrix}} \right) , \\ B_{23}= & {} B_{32}^{\top }= \left( {\begin{matrix} 0\,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0\,\,&{} 0 \,\,&{} 0 \,\,&{} -\,1 \,\,&{} 1 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 1 \,\,&{} -\,1 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \\ 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \,\,&{} 0 \end{matrix}} \right) . \end{aligned}$$

Fig. 3

Interactions between the nodes 4, 7 and 18, where the green, blue, red and yellow points represent the first, second, third and fourth components of each isolated node, respectively. (Color figure online)

For detailing the interactions between different communities, the nodes 4, 7 and 18 are chosen as the representative nodes in the three communities, and the interactions between these nodes are shown in Fig. 3. It can be seen that, for nodes in the first community having connections with nodes in the second community, their first component is affected only by the first component of those nodes in the second community, and their third component is affected only by the second component of those nodes in the second community; in addition, for nodes in the first community having connections with nodes in the third community, their second component are affected only by the second component of those nodes in the third community. By the method of analogy, other interactions between the three communities can be similarly analyzed.

For the first community, it is easy to verify that [46]

$$\begin{aligned}&\big (x_i(t)-s_1(t)\big )^{\top }\big ( f_1(t,x_i(t))-f_1(t,s_1(t)) \big )\nonumber \\&\quad =e_i^{\top }(t) \Big (10 \big (e_{i2}(t)- e_{i1}(t)-(\varphi (x_{i1}(t)) \nonumber \\&\qquad -\,\varphi (s_{11}(t))) \big ), e_{i1}(t)-e_{i2}(t)+e_{i3}(t), \nonumber \\&\qquad -\,14.87 e_{i2}(t)\Big )^{\top }\nonumber \\&\quad \le 2.7 e_{i1}^2(t)-e_{i2}^2(t)+11 e_{i1}(t)e_{i2}(t) \nonumber \\&\qquad -13.87 e_{i2}(t)e_{i3}(t)\nonumber \\&\quad \le 9.062 e_i^{\top }(t)e_i(t) \end{aligned}$$

(25)

where $i=1,2,\ldots ,5$. Hence, Assumption 1 is satisfied if we choose $\beta _1=9.062$. Similarly, for the second community, one has

$$\begin{aligned}&\big (x_i(t)-s_2(t)\big )^{\top }\big ( f_2(t,x_i(t))-f_2(t,s_2(t)) \big )\nonumber \\&\quad = -\,e_{i1}^2(t)-e_{i2}^2(t)-e_{i3}^2(t) \nonumber \\&\qquad +\, 1.25e_{i1}(t) \big (\psi (x_{i1}(t))-\psi (s_{21}(t)) \big ) \nonumber \\&\qquad -\,3.2e_{i1}(t)\big (\psi (x_{i2}(t))-\psi (s_{22}(t))\big )\nonumber \\&\qquad -\,3.2e_{i1}(t)\big (\psi (x_{i3}(t))-\psi (s_{23}(t)) \big ) \nonumber \\&\qquad -\,3.2e_{i2}(t)\big (\psi (x_{i1}(t))-\psi (s_{21}(t)) \big ) \nonumber \\&\qquad +\,1.1e_{i2}(t)\big (\psi (x_{i2}(t))-\psi (s_{22}(t))\big )\nonumber \\&\qquad -4.4 e_{i2}(t)\big (\psi (x_{i3}(t))-\psi (s_{23}(t))\big )\nonumber \\&\qquad -\,3.2e_{i3}(t)\big (\psi (x_{i1}(t))-\psi (s_{21}(t))\big )\nonumber \\&\qquad +\,4.4 e_{i3}(t)\big (\psi (x_{i2}(t))-\psi (s_{22}(t))\big )\nonumber \\&\qquad +\,e_{i3}(t)\big (\psi (x_{i3}(t))-\psi (s_{23}(t))\big )\nonumber \\&\quad \le 0.25 e_{i1}^2(t) +0.1 e_{i2}^2(t)+6.4 |e_{i1}(t)| |e_{i2}(t)|\nonumber \\&\qquad +\,6.4 |e_{i1}(t)| |e_{i3}(t)|+8.8 |e_{i2}(t)| |e_{i3}(t)|\nonumber \\&\quad \le 7.339 e_i^{\top }(t)e_i(t) \end{aligned}$$

(26)

where $i=6,7,\ldots ,11$. Therefore, if we choose $\beta _2=7.339$, then Assumption 1 holds.

It has been shown in [57] that the attractor of hyperchaotic Chen system is bounded. Here it is assumed that all nodes are running in the given bounded region. By computer simulations, we find that there are some constants $M_1 = 20$, $M_2 = 22$, $M_3 = 36$ and $M_4 = 110$, such that $|x_{ij}|,|s_{3j}(t)|\le M_j$ for $12\le i \le 18$ and $1\le j\le 4$. Then, for the third community, we have [7]

$$\begin{aligned}&\big (x_i(t)-s_3(t)\big )^{\top }\big ( f_3(t,x_i(t))-f_3(t,s_3(t)) \big )\nonumber \\&\quad \le e_{i1}(t) \big (-35 e_{i1}(t)+35e_{i2}(t)+e_{i4}(t) \big ) \nonumber \\&\qquad +e_{i2}(t) \big ( 7e_{i1}(t)+12e_{i2}(t)-s_{33}(t)e_{i1}(t)\nonumber \\&\qquad -\,s_{31}(t)e_{i3}(t)- e_{i1}(t)e_{i3}(t) \big )\nonumber \\&\qquad + e_{i3}(t) \big (-3 e_{i3}(t)+s_{32}(t)e_{i1}(t) \nonumber \\&\qquad +\,s_{31}(t)e_{i2}(t)+ e_{i1}(t)e_{i2}(t) \big ) \nonumber \\&\qquad +e_{i4}(t) \big (0.25 e_{i4}(t)+x_{i3}(t)e_{i2}(t)+s_{32}(t)e_{i3}(t) \big )\nonumber \\&\quad \le -35 e_{i1}^2(t)+12 e_{i2}^2(t)-3e_{i3}^2(t) +0.25e_{i4}^2(t)\nonumber \\&\qquad +\,(42+M_3)|e_{i1}(t)||e_{i2}(t)|\nonumber \\&\qquad +\,M_2|e_{i1}(t)||e_{i3}(t)|+|e_{i1}(t)||e_{i4}(t)|\nonumber \\&\qquad +\, M_3|e_{i2}(t)||e_{i4}(t)|+M_2|e_{i3}(t)||e_{i4}(t)|\nonumber \\&\quad \le \bigg (-34.5+\frac{(42+M_3)\kappa _1}{2}+ \frac{M_2 \kappa _2}{2} \bigg )e_{i1}^2(t)\nonumber \\&\qquad +\bigg (12+\frac{(42+M_3)}{2\kappa _1}+ \frac{M_3 \kappa _3}{2}\bigg ) e_{i2}^2(t)\nonumber \\&\qquad +\bigg (-3+\frac{M_2}{2\kappa _2}+ \frac{M_2 \kappa _4}{2}\bigg ) e_{i3}^2(t)\nonumber \\&\qquad +\bigg (0.75+\frac{M_3}{2\kappa _3}+ \frac{M_2}{2\kappa _4}\bigg ) e_{i4}^2(t) \end{aligned}$$

(27)

where $i=12,13,\ldots ,18$ and $\kappa _j > 0$, $1 \le j \le 4$ are arbitrary positive constants. Letting $\kappa _1=1.75$, $\kappa _2=0.75$, $\kappa _3=0.475$ and $\kappa _4=2.75$, then one can choose $\beta _3=42.84$ to satisfy Assumption 1.

For brevity, we select all the external coupling strengths $\varepsilon _{12}=\varepsilon _{13}=\varepsilon _{21}= \varepsilon _{23}=\varepsilon _{31}=\varepsilon _{32}=0.25$, the inner coupling strengths $c_1=c_2=12$, $c_3=35$ and $\rho _0=2$. By simple computation, we obtain $\pi _0=2$ and $a_2^+=85.68$. Choose $\xi _1=\xi _2=\xi _3=15$; then, we can get $a_1=28$, $\eta _1=24.062$, $\eta _2=22.339$ and $\eta _3=57.84$. Consequently, it can be obtained from conditions (i) and (ii) of Corollary 1 that

$$\begin{aligned}&\lambda _{\max }\big ((B_{11}^s)_{l_1}\big )<-\, 2.005, \nonumber \\&\lambda _{\max }\big ((B_{22}^s)_{l_2}\big )<-\,1.862 \nonumber \\&\lambda _{\max }\big ((B_{33}^s)_{l_3}\big )<-\,1.653, \end{aligned}$$

(28)

and

$$\begin{aligned} 0.7537<\theta _{\inf }<1. \end{aligned}$$

(29)

Fig. 4

Time evolutions of the synchronization errors under the adaptive aperiodically intermittent pinning control with $\theta _\omega =0.80$ and ${T}_{\omega }=0.3\omega$, $\omega \in \mathbb {N}^+$. a $e_{i1}(t)$, $e_{i2}(t)$, $e_{i3}(t) (1\le i\le 5)$ of the first community. b $e_{i1}(t)$, $e_{i2}(t)$, $e_{i3}(t) (6\le i\le 11)$ of the second community. c $e_{i1}(t)$, $e_{i2}(t)$, $e_{i3}(t)$, $e_{i4}(t) (12\le i\le 18)$ of the third community

According to Remark 7, we rearrange nodes of each community and then calculate $\lambda _{\max }\big ((B_{kk}^s)_{l_k}\big )$ for $1\le l_k< r_k$ and $k=1,2,3$ using MATLAB software, where $r_1=5$, $r_2=6$ and $r_3=7$. The computing results show

$$\begin{aligned}&\lambda _{\max }\big ((B_{11}^s)_{2}\big )=-\,1.585\quad \mathrm{and}\quad \lambda _{\max }\big ((B_{11}^s)_{3}\big )=-\,3,\nonumber \\&\lambda _{\max }\big ((B_{22}^s)_{2}\big )=-\,1.186\quad \mathrm{and}\quad \lambda _{\max }\big ((B_{22}^s)_{3}\big )=-\,2.0,\nonumber \\&\lambda _{\max }\big ((B_{33}^s)_{3}\big )=-\,1.382\quad \mathrm{and}\quad \lambda _{\max }\big ((B_{33}^s)_{4}\big )=-\,1.753. \end{aligned}$$

Therefore, based on Corollary 1, we only need to pick the first $l_1=3$ rearranged nodes of the first community (i.e., the nodes 5, 2 and 4), the first $l_2=3$ rearranged nodes of the second community (i.e., the nodes 7, 8 and 10), and the first $l_3=4$ rearranged nodes of the third community (i.e., the nodes 13, 16, 17 and 18) as pinned nodes; then, the globally exponentially cluster synchronization can be realized under the adaptive aperiodical intermittent controllers (4)–(6) with the control rates $\theta _k>0.7537$ ($k\in {\mathbb {N}^+}$).

Fig. 5

Time evolutions of the adaptive intermittent feedback control gains $d_i(t)$ ($i =$ 2,4,5,7,8,10,13,16,17,18) under the adaptive aperiodically intermittent pinning control with $\theta _\omega =0.80$ and ${T}_{\omega }=0.3\omega$, $\omega \in \mathbb {N}^+$

Fig. 6

Time evolutions of the community errors $E_1(t)$, $E_2(t)$ and $E_3(t)$ under the adaptive aperiodically intermittent pinning control with $\theta _\omega =0.80$ and ${T}_{\omega }=0.3\omega$, $\omega \in \mathbb {N}^+$

Fig. 7

Time evolutions of the community errors $E_1(t)$, $E_2(t)$ and $E_3(t)$ under the adaptive aperiodically intermittent pinning control with $\theta _\omega =0.80$, $\omega \in \mathbb {N}^+$ and the sequence of control periods given by (30)

In numerical simulations, taking $\theta _\omega =0.80$ and ${T}_{\omega }=t_{\omega +1}-t_{\omega }=0.3\omega$, $\omega \in {\mathbb {N}^+}$, Figs. 4 and 5 show, respectively, the time evolutions of the synchronization errors $e_{i}(t) (1\le i \le 18)$ and the adaptive intermittent feedback control gains $d_i(t)\,( i=2,4,5,7,8,10,13,16,17,18)$ under the adaptive aperiodically intermittent pinning control, where the initial conditions of the numerical simulations are $x_i(0)=(-\,3+0.5i,-\,2+0.3i,1+0.2i)^{\top }$ for $1\le i \le 11$, $x_i(0)=(2+0.3i,-\,3+0.4i,-\,1+0.6i,1+0.2i)^{\top }$ for $12\le i \le 18$, $s_1(0)=(1,2 ,3)^{\top }$, $s_2(0)=(-\,3,-\,1,2)^{\top }$, $s_3(0)=(1.5,2,2.5,3)^{\top }$, and $d_j(0)=0.1$, $h_j=0.1$, where $j=2,4,5,7,8,10,13,16,17,18$. It can be observed that the exponential cluster synchronization is realized and the adaptive intermittent feedback control gains $d_{i}(t) (i=2,4,5,7,8,10,13,16,17,18)$ approach to some positive constants intermittently. After the cluster synchronization is completed, the values of the adaptive intermittent feedback control gains satisfy $d_i(t)\le 10.5$ ($i =$ 2,4,5,7,8,10,13,16,17,18), which illustrates the adaptive intermittent pinning control approach can obtain feasible feedback control gains. Additionally, we can increase the number of pinned nodes in each community to avoid the appearance of high feedback control gains. Figure 6 depicts the community errors $E_1(t)=\sqrt{\sum _{i=1}^{5}\big |\big |x_i(t)-s_1(t) \big |\big |^2}$, $E_2(t)=\sqrt{\sum _{i=6}^{11}\big |\big |x_i(t)-s_2(t) \big |\big |^2}$ and $E_3(t)=\sqrt{\sum _{i=12}^{18}\big |\big |x_i(t)-s_3(t) \big |\big |^2}$ in the three communities. Figure 6 shows that the community errors approach to zero, which indicates clearly that the cluster synchronization is realized.

In order to illustrate that, for achieving the cluster synchronization, control periods can be arbitrarily selected, we choose each control period ${T}_{\omega }=t_{\omega +1}-t_{\omega }$, $\omega \in \mathbb {N}^+$ randomly from the interval [0.25, 6.25] (from any other interval can be analyzed similarly), and obtain the following sequence of control periods:

$$\begin{aligned} \big \{{T}_{\omega }\big \}_{\omega =1}^{+\infty }= & {} \big \{0.6,\, 4.34,\, 0.5,\, 0.68,\, 3.38,\, 0.83,\, 5.16, \nonumber \\&5.15,\, 4.58,\, 1.15,\, 4.2,\, 3.36,\, 6.09,\, \ldots \big \}.\nonumber \\ \end{aligned}$$

(30)

Taking $\theta _\omega =0.80$, $\omega \in \mathbb {N}^+$, Figs. 7 and 8 depict, respectively, the time evolutions of the community errors $E_i(t) (1\le i \le 3)$ and the adaptive intermittent feedback control gains $d_i(t)\,( i=2,4,5,7,8,10,13,16,17,18)$ under the adaptive aperiodically intermittent pinning control, where the initial conditions of this numerical simulations are $x_i(0)=(1+0.2i,-\,3+0.4i,2+0.6i)^{\top }$ for $1\le i \le 11$, $x_i(0)=(2+0.1i,-\,2+0.3i,-\,5+0.4i,1+0.7i)^{\top }$ for $12\le i \le 18$, $s_1(0)=(1,2 ,3)^{\top }$, $s_2(0)=(-\,3,-\,1,2)^{\top }$, $s_3(0)=(1.5,2,2.5,3)^{\top }$, and $d_j(0)=0.1$, $h_j=0.01$, where $j=2,4,5,7,8,10,13,16,17,18$. Obviously, these two figures show that the cluster synchronization can be achieved, which verifies the correctness of the theoretical results.

Fig. 8

Time evolutions of the adaptive intermittent feedback control gains $d_i(t)$ ($i =$ 2,4,5,7,8,10,13,16,17,18) under the adaptive aperiodically intermittent pinning control with $\theta _\omega =0.80$, $\omega \in \mathbb {N}^+$ and the sequence of control periods given by (30)

5 Conclusions

This paper discussed the cluster synchronization problem for a general colored community network with nodes of different state dimensions. An effective adaptive aperiodically intermittent pinning control scheme was developed to drive such colored community network to realize cluster synchronization. Based on a novel piecewise continuous Lyapunov candidate function, some sufficient conditions to guarantee globally exponential cluster synchronization were derived by means of the stability analysis method. According to the derived theoretical results, it was found that the nodes in each community whose intra-outdegrees are bigger than their intra-indegrees should be preferentially chosen as pinned nodes. It is noted that the adaptive intermittent pinning control is aperiodic, in which control periods as well as control widths are allowed to be different. Finally, the effectiveness of the proposed cluster synchronization criteria was illustrated by some numerical simulations. Our next goal is to extend the approach presented in this paper to the investigation of exponential cluster synchronization problem for more general colored community networks with time-varying delays or stochastic perturbation.

As we all know, convergence time is a key indicator for assessing the performance of the controller. In this paper, the proposed adaptive intermittent controllers for colored community networks can only make the networks be exponentially synchronized, which implies that the time required for realizing the cluster synchronization is infinite. In real-world applications, however, it is highly desirable that the networks can achieve synchronization in a finite time [36]. Therefore, it would be interesting to investigate the problem of finite time cluster synchronization for colored community networks by means of adaptive intermittent control technique. This important problem will be focused on in the future.