1 Introduction

1.1 Scope

Most of the phenomena in nature can be formulated mathematically by nonlinear partial differential equations. There are numerous examples on physical modeling in various fields of sciences and engineering, particularly in fluid mechanics, solid state physics, plasma physics and chemical science. Analysis of physical models allows us to predict and understand the possible behavior of the corresponding physical system. It is imperative to find out the exact solutions of the relevant nonlinear evolution equations to understand the dynamics of a system. Closed-form exact solutions of these equations are inherently complex.

The purpose of this article is to derive some closed-form exact solutions of the PKP equation. Hence, we consider the following form of the PKP equation

$$\begin{aligned} u_{xt}+\frac{3}{2}u_{x}u_{xx}+\frac{1}{4} u_{xxxx}+\frac{3}{4} u_{yy}=0. \end{aligned}$$

On application of the above form, various solutions of the PKP equation such as kink wave, multiple-front wave, waves interaction, multisoliton, parabolic and stationary wave are obtained. These solutions bear significance in the fields of plasma physics, adaptive optics and nonlinear mechanics. Kink wave is a sharp twist or curve in something that is otherwise straight. Kink wave or Alfv\(\acute{e}\)n wave is a transverse magnetohydrodynamics wave traveling in the direction of the magnetic field in a magnetized plasma. They have wide applications in the field of plasma physics. These waves are frequently observed in the solar atmosphere. Propagation of these waves may annihilate the dissipation of energy in the solar environment.

A wavefront is an imaginary surface joining all points in the space that are reached at the same instant by a wave propagating through a medium. The wavefront is described by the positions of various identical phases and can be modified with conventional optics. Wavefront phenomenon plays an important role in real-life problems. This phenomenon is used to construct wavefront sensors, which describe the instability in an optical system. Multiple wavefront phenomena are also used to develop the wavefront sensors and wavefront curvature sensing. Phase imaging or curvature sensing techniques are also suitable for wavefront estimations.

Solitary waves emerge due to nonlinear and dispersive effects. While a soliton is also a solitary wave that behaves like a group of particles. It conserves its shape, velocity and amplitude with the collision of other solitons. Solitons or solitary waves arise in most of the continuum systems explained by various nonlinear equations such as the KdV equation, KP equations and Schr\(\ddot{\text{ o }}\)dinger equations. Various physical systems can be modeled on the basis of soliton theory.

1.2 Related work

We consider a (2+1)-dimensional generalization of KdV equation [1]

$$\begin{aligned} \mathbf u_{t}+\frac{3}{4}u^2_{x}+\frac{1}{4} u_{xxx}+\frac{3}{4}\int ^x{ u_{yy}\,\hbox {d}x=0}, \end{aligned}$$
(1)

which describes the dynamics of a wave with small and finite amplitude in two dimensions. Equation (1) is derived in many physical contexts with the assumption that the wave is moving along the x-direction, and all changes in the y-direction are slower than in the direction of motion.

In the proposed research, we have considered the following form of the PKP equation

$$\begin{aligned} \mathbf u_{xt}+\frac{3}{2}u_{x}u_{xx}+\frac{1}{4} u_{xxxx}+\frac{3}{4} u_{yy}=0, \end{aligned}$$
(2)

which is known as potential Kadomtsev–Petviashvili equation.

In the last few decades, many effective methods have been used by various communities of researchers to derive exact solutions of the PKP equation. Li et al. [2] obtained soliton solutions of the PKP equation through the symbolic computation method proposed by Gao and Tian. Batiha et al. [3] obtained analytic solutions of the PKP equation by applying the variational iteration method and compared it with exact solutions. Inan [4] et al. used improved tanh function method and attained some exact solutions of the PKP equation. Dai et al. [5] found exact periodic kink wave solutions, periodic solitons and doubly periodic solutions of the PKP equation by using a homoclinic test technique and extended homoclinic test technique. Furthermore, they investigated that periodic soliton is degenerated into doubly periodic wave varying with direction of wave propagation. Rosenhaus [6] studied local conservation laws with non-vanishing conserved densities and corresponding boundary conditions for the PKP equation. Moreover, he analyzed an infinite symmetry group and generated a finite number of conserved densities corresponding to infinite symmetries through appropriate boundary conditions. Li et al. [7] obtained exact solutions containing soliton, multisoliton and rational solutions of the PKP equation through generalized tanh method. Jawad et al. [8] derived soliton solutions of the PKP equation by using the tanh–coth and the tan–cot methods. Pohajanpelto [9] described the variational bicomplex forms of the PKP equation under symmetry algebra. Moreover, he computed the cohomology of the associated Euler–Lagrange complex. Ren et al. [10] derived interaction and multiple-front wave solutions of the PKP equation through truncated Painlev\(\acute{e}\) analysis and consistent tanh expansion method. Furthermore, Wazwaz et al. studied various forms of the KP equation [11,12,13,14] and derived solutions like multiple-soliton solutions, multiple-front wave solutions and multiple singular soliton solutions by using simplified Hirota’s direct method. They investigated Painlev\(\acute{e}\) integrability of some generalized forms of the KP equation through MAPLE.

1.3 Motivation

Nature pays much attention to the nonlinearity requirement of classical mathematics. Exact solutions of nonlinear partial differential equations still pose a big challenge in the nonlinear world. Invariant results of the PKP equation have diversified applications in various fields of science and technology. Some direct applications can be seen in the fields of plasma physics, adaptive optics, nonlinear mechanics, wavefront sensor and phase imaging process. Various researchers are working on exact closed-form results of the PKP equation. Some of them have calculated numerical or approximate results. But closed-form exact solutions always have their own importance. Hence, to fill up the gap of the research [1,2,3,4,5,6,7,8,9,10,11,12,13,14], a serious effort has been made to get some new exact solutions of the PKP equation. Lie symmetry analysis has been used to get invariant results. Applications and theory of the method can be seen from literature [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The exact solutions of the equation are analyzed physically.

1.4 Outlines

The structure of the manuscript is organized in the following manner : Introductory part of Sect. 1 comprises with scope, related work and motivation. Section 2 includes a brief introduction of Lie symmetry method. In Sect. 3, infinitesimals are calculated via Lie symmetry analysis for the PKP equation. The invariant solutions of the PKP equation are obtained in Sect. 4. Analysis and discussions are covered by Sect. 5. Finally, Sect. 6 provides the conclusion of the manuscript.

2 Method of Lie symmetries

A brief introduction about the Lie symmetries of a system of PDEs has been stated in this section to make the work self-confined. Consider the following nth-order system of differential equations in a independent and b dependent variables as

$$\begin{aligned}&\triangle _\nu (\hat{x}, \hat{u}^{(n)})=0, ~~~~\nu =1,2,\ldots l, \end{aligned}$$
(3)

where \(\hat{x}=(x_1, x_2,x_3,\ldots x_a)\), \( \hat{u}=(u^1, u^2,\ldots ,u^b)\) and \(\hat{u}^{(n)}\) denotes the nth-order derivative of \(\hat{u}\). One can consider a one-parameter (\(\epsilon \)) Lie group of infinitesimal transformations acting on both variables of the system to keep system invariant, as

$$\begin{aligned}&x^*_i = x_i + \epsilon ~\xi _i (\hat{x}, \hat{u})+ O(\epsilon ^2),\nonumber [1]\\&u^*{^j} = u ^j+ \epsilon ~\eta ^{j} (\hat{x}, \hat{u})+ O(\epsilon ^2 ), \end{aligned}$$
(4)

where \(\epsilon \) is the parameter of the transformations and \(\xi _i\), \(\eta ^{j}\) are the infinitesimals of the transformations for the independent and dependent variables, respectively.

The infinitesimal generator \(\mathbf {v}\) associated with the above Lie group of transformations can be explored as

$$\begin{aligned}&\mathbf{v} = \sum _{i =1}^a \xi _i (\hat{x}, \hat{u}^{(n)})\, \frac{\partial }{\partial {x_i}}+ \sum _{\alpha =1}^b\,\eta ^{j} (\hat{x}, \hat{u}^{(n)})\,\frac{\partial }{\partial u^\alpha }. \end{aligned}$$
(5)

A symmetry of a differential equation is a transformation which keeps the solution invariant in the transformed space. The system of PDEs leads to the following invariance condition under the infinitesimal transformations

$$\begin{aligned}&Pr^{(n)}{} \mathbf{v}[\triangle _\nu (\hat{x}, \hat{u}^{(n)})] = 0, ~~~~\nu =1,2,\ldots l ~~~\nonumber [1]\\ {}&\text{ alongwith }~~\triangle (\hat{x},\hat{u}^{(n)})=0. \end{aligned}$$
(6)

In the above condition, \(Pr^{(n)}\) is termed as nth-order prolongation [16] of the infinitesimal generator \(\mathbf{v}\) which is given by

$$\begin{aligned}&Pr^{(n)}{} \mathbf{v}=\mathbf{v}+\sum _{\alpha =1}^b \sum _{J} \eta ^{J}_\alpha (\hat{x}, \hat{u}^{(n)})\,\frac{\partial }{\partial u^\alpha _J}, \end{aligned}$$
(7)

the second summation being over all (unordered) multi-indices \(J=j_1, j_2,j_3,\ldots ,j_k\), with \( 1\le j_k \le a, 1\le k \le n\). The coefficient functions \(\eta ^{J}_\alpha \) of \(Pr^{(n)}{} \mathbf{v}\) are given by the following expression

$$\begin{aligned} \eta ^{J}_\alpha (\hat{x}, \hat{u}^{(n)})=D_J\Bigr (\eta _\alpha -\sum _{i =1}^a \xi _i\, u_i^\alpha \Bigr ) +\sum _{i=1}^a \xi _i \,u_{J,i}^\alpha , \end{aligned}$$
(8)

where \(u_{i}^\alpha =\frac{\partial u^{\alpha }}{\partial x_i}\), \(u_{J,i}^\alpha =\frac{\partial u_J^{\alpha }}{\partial x_i}\) and \(D_J\) denotes total derivative.

3 Lie symmetry analysis for the PKP equation

Authors considered the following one-parameter Lie group of infinitesimals transformations for \(x_1= x\), \(x_2 = y\), \(x_3 = t\); \(\xi _1=\xi ^{(1)}\), \( \xi _2=\xi ^{(2)} \), \(\xi _3=\tau \); \(u^1 = u\) as

$$\begin{aligned} x^* = x+\epsilon ~ \xi ^{(1)}(x,y,t,u)+O(\epsilon ^2), \nonumber \\ y^* = y+\epsilon ~ \xi ^{(2)}(x,y,t,u)+O(\epsilon ^2), \nonumber \\ t^* = t+\epsilon \tau (x,y,t,u)+O(\epsilon ^2),~~~~ \nonumber \\ u^* = u+\epsilon ~ \eta (x,y,t,u)+O(\epsilon ^2),~~ \end{aligned}$$
(9)

where \(\epsilon \) is a small parameter and \( \xi ^{(1)}\), \(\xi ^{(2)}\), \( \tau \) and \( \eta \) are infinitesimals for the variable x, y, t and u, respectively.

The associated vector field takes the form :

$$\begin{aligned} \mathbf{v} = \xi ^{(1)}(x, y,t; u)\frac{\partial }{\partial x}+\xi ^{(2)}(x, y,t; u)\frac{\partial }{\partial y}\\\nonumber +\tau (x,y, t; u)\frac{\partial }{\partial t}\nonumber [1] +\eta (x,y, t; u)\frac{\partial }{\partial u}. \end{aligned}$$

Using the invariance condition \(Pr^{(4)}{} \mathbf{v}(\triangle ) = 0\); whenever \(\triangle = 0\) and \(Pr^{(4)}{} \mathbf{v}\) is fourth prolongation of \(\mathbf{v}\). Applying the fourth prolongation of \(\mathbf{v}\) to Eq. (2), we derive following system of equations:

$$\begin{aligned}&\xi _{xx}^{(1)}=0, \xi _u^{(1)}=0, \xi _{x}^{(2)}=0, \xi _{u}^{(2)}=0, \xi _{yy}^{(2)}=0, \tau _{x}=0,\nonumber \\&\tau _{y}=0, \tau _{u}=0, \eta _{ux}=0, \eta _{uy}=0, \eta _{uu}=0, \eta _{xxx}=0,\nonumber \\&3\, \xi _x^{(1)}-\tau _{t} =0,\, \xi _x^{(1)}-\frac{1}{2}\,\xi _y^{(2)} =0,\, \frac{3}{2}\,\xi _y^{(1)}+\xi _t^{(2)} =0,\,\nonumber \\&\frac{3}{2}\,\eta _x-\xi _t^{(1)},\,~~ \frac{3}{4}\,\eta _{yy}+\eta _{xt},\,~~ \eta _{ut}-\frac{3}{4}\,\xi _{yy}^{(1)}=0,\nonumber \\&\eta _u+\xi _x^{(1)}=0,\,~~~ \frac{3}{2}\,\eta _{xx}+\eta _{ut}-\xi _{xt}^{(1)}-\frac{3}{4}\,\xi _{yy}^{(1)}=0.\nonumber \\ \end{aligned}$$
(10)

Solving the above system of equations, we get following infinitesimals

$$\begin{aligned}&\xi ^{(1)} = \frac{x}{2}\bar{f_1}(t) -\frac{y^2}{3}\bar{\bar{f_1}}(t)-\frac{2y}{3}\bar{f_2}(t)+f_3(t),\nonumber \\&\xi ^{(2)} = y\bar{f_1}(t)+f_2(t), \tau =\frac{3}{2}f_1(t) +1,\nonumber \\&\eta = \Bigg [-\frac{u}{2}\bar{f_1}(t)+\frac{x^2}{6}\bar{\bar{f_1}}(t)+\frac{2}{81}y^4\bar{\bar{\bar{\bar{f_1}}}}(t) \nonumber \\&~~~~~~~+\frac{8}{81}y^3\bar{\bar{\bar{f_2}}}(t)-\frac{4}{9}y^2\bar{\bar{f_3}}(t)+yf_4(t)+f_5(t)\nonumber \\&~~~~~~~-\frac{2}{9}\left\{ y^2\bar{\bar{\bar{f_1}}}(t)+2y\bar{\bar{f_2}}(t)-3\bar{f_3}(t)\right\} x\Bigg ], \end{aligned}$$
(11)

where \(f_{i}'s\) \((1\le i \le 5)\) are arbitrary functions of time t and bar is used for the derivatives throughout the article. The choices of \(f_{i}'s\) may provide the rich physical structure to the solutions of (2).

The symmetry of Eq. (2) can be written as [30],

$$\begin{aligned} \mathbf{V}=\mathbf{V_1}(f_1)+ \mathbf{V_2}(f_2)+ \mathbf{V_3}(f_3)+\mathbf{V_4}(f_4)+\mathbf{V_5}(f_5)+\mathbf{V_6}, \end{aligned}$$
(12)

where

$$\begin{aligned} \mathbf{V_1}(f_1)= & {} \{\frac{x}{2}\bar{f_1} -\frac{y^2}{3}\bar{\bar{f_1}}\}\frac{\partial }{\partial x}+y\bar{f_1}\frac{\partial }{\partial y}+\frac{3}{2}f_1\frac{\partial }{\partial t}\\&+\,\{\frac{x^2}{6}\bar{\bar{f_1}}-\frac{u}{2}\bar{f_1}-\frac{2}{9}xy^2\bar{\bar{\bar{f_1}}}+\frac{2}{81}y^4\bar{\bar{\bar{\bar{f_1}}}}\}\frac{\partial }{\partial u}, \\ \mathbf{V_2}(f_2)= & {} -\frac{2y}{3}\bar{f_2}\frac{\partial }{\partial x}+f_2\frac{\partial }{\partial y}+\{\frac{8}{81}y^3\bar{\bar{\bar{f_2}}}-\frac{4}{9}xy\bar{\bar{f_2}}\}\\&\times \frac{\partial }{\partial u}, \\ \mathbf{V_3}(f_3)= & {} f_3 \frac{\partial }{\partial x}+\{\frac{2}{3}x\bar{f_3} -\frac{4}{9}y^2\bar{\bar{f_3}}\frac{\partial }{\partial u}\}, \\ \mathbf{V_4}(f_4)= & {} y\,f_4\frac{\partial }{\partial u},\quad \mathbf{V_5}(f_5)= f_5\frac{\partial }{\partial u},\quad \mathbf{V_6}=\frac{\partial }{\partial t}. \end{aligned}$$

The associated Lie algebra between these vector fields becomes:

$$\begin{aligned}&[\mathbf{V_i}, \mathbf{V_i}]=0,~~~i=1,2,3,4,5,6\\&[\mathbf{V_1}(f_1), \mathbf{V_2}(f_2)]=\mathbf{V_2}(\frac{3}{2}f_1\,\bar{f_{2}}-f_2\,\bar{f_{1}}),\\&[\mathbf{V_1}(f_1),\mathbf{V_3}(f_3)]= \mathbf{V_3}(\frac{3}{2}f_1\,\bar{f_{3}}-\frac{1}{2}\,f_3\,\bar{f_{1}}),\\&[\mathbf{V_1}(f_1),\mathbf{V_4}(f_4)]= \mathbf{V_4}(\frac{3}{2}f_1\,\bar{f_{4}}+\frac{3}{2}f_4\,\bar{f_{1}}),\\&[\mathbf{V_1}(f_1), \mathbf{V_5}(f_5)]= \mathbf{V_5}(\frac{3}{2}f_1\,\bar{f_{5}}+\frac{1}{2}\,f_5\,\bar{f_{1}}),\\&[\mathbf{V_1}(f_1),\mathbf{V_6}]= \mathbf{V_1}(-\bar{f_{1}}),\\&[\mathbf{V_2}(f_2),\mathbf{V_3}(f_3)]= \mathbf{V_4}(\frac{4}{9}f_3\,\bar{\bar{f_{2}}}-\frac{4}{9}\bar{f_{2}}\,\bar{f_{3}}-\frac{8}{9}f_2\,\bar{\bar{f_{3}}}),\\&[\mathbf{V_2}(f_2),\mathbf{V_4}(f_4)]= \mathbf{V_5}(f_2\,f_4),\,~ \\&[\mathbf{V_2}(f_2),\mathbf{V_5}(f_5)]= 0,\\&[\mathbf{V_2}(f_2),\mathbf{V_6}]= \mathbf{V_2}(-\bar{f_{2}}),\,~\\&[\mathbf{V_3}(f_3),\mathbf{V_4}(f_4)]= 0,\\&[\mathbf{V_3}(f_3),\mathbf{V_5}(f_5)]= 0,\,~ \\&[\mathbf{V_3}(f_3),\mathbf{V_6}]= \mathbf{V_3}(-\bar{f_{3}}),\\&[\mathbf{V_4}(f_4),\mathbf{V_5}(f_5)]= 0,\, ~\\&[\mathbf{V_4}(f_4),\mathbf{V_6}]= \mathbf{V_4}(-\bar{f_{4}}),\\&[\mathbf{V_5}(f_5),\mathbf{V_6}]= \mathbf{V_5}(-\bar{f_{5}})\\&[\mathbf{V_1}(g_1), \mathbf{V_1}(h_1)]= \mathbf{V_1}(\frac{3}{2}g_1\,\bar{h_{1}}-\frac{3}{2}h_1\,\bar{g_{1}}),\\&[\mathbf{V_2}(g_2), \mathbf{V_2}(h_2)]= \mathbf{V_3}(\frac{2}{3}h_2\,\bar{g_{2}}-\frac{2}{3}g_2\,\bar{h_{2}}),\\&[\mathbf{V_3}(g_3), \mathbf{V_3}(h_3)]= \mathbf{V_5}(\frac{2}{3}g_3\,\bar{h_{3}}-\frac{2}{3}h_3\,\bar{g_{3}}),\\&[\mathbf{V_4}(g_4), \mathbf{V_4}(h_4)]=0,\,\\&[\mathbf{V_5}(g_5), \mathbf{V_5}(h_5)]=0. \end{aligned}$$

4 Invariant solutions of the PKP equation

Further, we took the choice of arbitrary functions \(f_{2}(t)=a_0\bar{f_{1}}(t)\), \( f_{3}(t)=-\frac{a^2_0}{3}\bar{\bar{f_1}}(t)\), \( f_{4}(t)=\frac{8}{81}a^3_0\bar{\bar{\bar{\bar{f_1}}}}(t)\) and \( f_{5}(t)=\frac{2}{81}a^4_0\bar{\bar{\bar{\bar{f_1}}}}(t)\), where \(a_0\) is an arbitrary constant.

Thus, to get invariant solutions of Eq. (2), the corresponding Lagrange system is

$$\begin{aligned} \frac{\hbox {d}x}{\xi ^{(1)}(x,y, t, u)}= & {} \frac{\hbox {d}y}{\xi ^{(2)}(x,y,t,u)}=\frac{\hbox {d}t}{\tau (x,y,t,u)}\nonumber \\= & {} \frac{\hbox {d}u}{\eta (x,y,t,u)}. \end{aligned}$$
(13)

From Eqs. (11) and (13) we obtain

$$\begin{aligned}&\dfrac{\hbox {d}x}{\frac{x}{2}\bar{f_1}(t) -\frac{y^2}{3}\bar{\bar{f_1}}(t)-\frac{2y}{3}\bar{f_2}(t)+f_3(t)} =\dfrac{\hbox {d}y}{y\bar{f_1}(t)+f_2(t)} \\&\quad =\dfrac{\hbox {d}t}{\frac{3}{2}f_1(t) +1} \end{aligned}$$
$$\begin{aligned} =\frac{\hbox {d}u}{\begin{array}{l}\Big [-\frac{u}{2}\bar{f_1}(t)+ \frac{x^2}{6}\bar{\bar{f_1}}(t)-\frac{2}{9}\{y^2\bar{\bar{\bar{f_1}}}(t) +2y\bar{\bar{f_2}}(t)-3\bar{f_3}(t)\}x\\ +\frac{2}{81}y^4\bar{\bar{\bar{\bar{f_1}}}}(t)+ \frac{8}{81}y^3\bar{\bar{\bar{f_2}}}(t)-\frac{4}{9}y^2 \bar{\bar{f_3}}(t)+yf_4(t)+f_5(t) \Big ]\end{array}}. \end{aligned}$$
(14)

The similarity form of the solution of Eq. (2) can be written as

$$\begin{aligned} u(x,y,t)= & {} \frac{40(y+a_0)^4{\bar{f_1}}^3}{2187(f_1+\frac{2}{3})^3}+\frac{8x(y+a_0)^2\bar{f_1}^2}{81(f_1+\frac{2}{3})^2}\nonumber \\&+\,\frac{x^2\bar{f_1}}{9(f_1+\frac{2}{3})}+\frac{4(y+a_0)^4\bar{\bar{\bar{f_1}}}}{243(f_1+\frac{2}{3})}\nonumber \\&-\,\frac{4x(y+a_0)^2\bar{\bar{f_1}}}{27(f_1+\frac{2}{3})}-\frac{8(y+a_0)^4\bar{f_1}\bar{\bar{f_1}}}{243(f_1+\frac{2}{3})^2}\nonumber \\&+\,\frac{ U(X,Y)}{(f_1+\frac{2}{3})^{\frac{1}{3}}}, \end{aligned}$$
(15)

where U(X, Y) is a similarity function of similarity variables X and Y, which can be expressed as

$$\begin{aligned} X=\frac{x}{(f_1+\frac{2}{3})^{\frac{1}{3}}}+\frac{2(y+a_0)^2\bar{f_1}}{9(f_1+\frac{2}{3})^{\frac{4}{3}}} \text{ and }~Y=\frac{(y+a_0)}{(f_1+\frac{2}{3})^{\frac{2}{3}}}. \end{aligned}$$
(16)

Inserting the value of u from Eq. (15) into Eq. (2), we get the following partial differential equation

$$\begin{aligned} U_{XXXX}+6U_{X}U_{XX}+3U_{YY}=0. \end{aligned}$$
(17)

Since the PDE (17) is nonlinear and it has two independent variables and one dependent variable, applying STM on Eq. (17) as in Eq. (2) again will provide the following infinitesimals

$$\begin{aligned}&\bar{\xi }^{(1)} = a_1+\frac{a_5}{2}X,~ \bar{\xi }^{(2)} = a_2+a_5Y \nonumber \\&\bar{\eta }= a_3+a_4Y-\frac{a_5}{2} U, \end{aligned}$$
(18)

where \(a_1,a_2, a_3, a_4 \) and \(a_5\) are arbitrary constants.

Case(I): If \( a_5 \ne 0\) in Eq. (18), then corresponding Lagrange system for Eq. (17) is read as

$$\begin{aligned} \frac{\hbox {d}X}{A_1+\frac{1}{2}X}=\frac{\hbox {d}Y}{A_2+Y}= \frac{\hbox {d}U}{A_3+A_4Y-\frac{1}{2}U}, \end{aligned}$$
(19)

where \(A_1=\frac{a_1}{a_5}, A_2=\frac{a_2}{a_5},A_3=\frac{a_3}{a_5} \) and \(A_4=\frac{a_4}{a_5}\).

Therefore, similarity transformations predict the following form of unknown function U for the partial differential equation(17)

$$\begin{aligned} U=A_5+\frac{2}{3}A_4(A_2+Y)+\frac{U_1(X_1)}{(A_2+Y)^{\frac{1}{2}}}, \end{aligned}$$
(20)

where \( X_1=\frac{(2A_1+X)}{(A_2+Y)^{\frac{1}{2}}}\) and \(A_5=2(A_3-A_2A_4)\). From Eqs. (17) and (20), we obtain an ODE given by

$$\begin{aligned} ~~\bar{\bar{\bar{\bar{U_1}}}}+6\bar{U_1}\bar{\bar{U_1}}+\frac{3X^2_1}{4}\bar{\bar{U_1}}+\frac{15X_1}{4}\bar{U_1}+\frac{9}{4} U_1 =0, \end{aligned}$$
(21)

where bar denotes the derivative of \(U_1\) with respect to \(X_1\).

Integrating Eq. (21), we have

$$\begin{aligned} \bar{\bar{\bar{U_1}}}+3\bar{U_1}^2+\frac{3X^2_1}{4}\bar{U_1}+ \frac{9X_1}{4}{U_1}=c_1 , \end{aligned}$$
(22)

\(c_1\) is a constant of integration.

Equation (22) is a nonlinear differential equation. The authors could not find its general solution.

However, some particular solutions of Eq. (22) can be obtained as

Case I(a): The particular solution of Eq. (22) is given by

$$\begin{aligned} {U_1=-\frac{X^3_1}{6}+c_2\, X_1}, (c_1= 3\,c_2^2 -1). \end{aligned}$$
(23)

Ultimately, from Eqs. (15), (20) and (23), one can furnish the solution of potential Kadomtsev–Petviashvili in explicit form as

$$\begin{aligned} u(x,y,t)= & {} \frac{40(y+a_0)^4{\bar{f_1}}^3}{2187(f_1+\frac{2}{3})^3}+\frac{8x(y+a_0)^2\bar{f_1}^2}{81(f_1+\frac{2}{3})^2}\nonumber \\&+\frac{A_5+\frac{2}{3}A_4(A_2+Y)-\frac{(2A_1+X)^3}{6(A_2+Y)^2}+\frac{c_2\,(2A_1+X)}{(A_2+Y)}}{(f_1+\frac{2}{3})^{\frac{1}{3}}}\nonumber \\&+\frac{x^2\bar{f_1}}{9(f_1+\frac{2}{3})}+\frac{4(y+a_0)^4\bar{\bar{\bar{f_1}}}}{243(f_1+\frac{2}{3})}\nonumber \\&-\frac{4x(y+a_0)^2\bar{\bar{f_1}}}{27(f_1+\frac{2}{3})} -\frac{8(y+a_0)^4\bar{f_1}\bar{\bar{f_1}}}{243(f_1+\frac{2}{3})^2}, \end{aligned}$$
(24)

where X and Y are given by Eq. (16).

Case I(b): By setting \(c_1=3\) in Eq. (22), another particular solution of the PKP equation can be expressed as

$$\begin{aligned} {U_1=\frac{2}{X_1}}. \end{aligned}$$
(25)

Thus, from Eqs. (15), (20) and (25), we have explicit solution of the PKP equation as

$$\begin{aligned} u(x,y,t)= & {} \frac{40(y+a_0)^4{\bar{f_1}}^3}{2187(f_1+\frac{2}{3})^3}+\frac{8x(y+a_0)^2\bar{f_1}^2}{81(f_1+\frac{2}{3})^2}\nonumber \\&+\frac{x^2\bar{f_1}}{9(f_1+\frac{2}{3})}+\frac{4(y+a_0)^4\bar{\bar{\bar{f_1}}}}{243(f_1+\frac{2}{3})}\nonumber \\&-\frac{4x(y+a_0)^2\bar{\bar{f_1}}}{27(f_1+\frac{2}{3})} -\frac{8(y+a_0)^4\bar{f_1}\bar{\bar{f_1}}}{243(f_1+\frac{2}{3})^2}\nonumber \\&+\frac{A_5+\frac{2}{3}A_4(A_2+Y)+\frac{2}{(2A_1+X)} }{(f_1+\frac{2}{3})^{\frac{1}{3}}}, \end{aligned}$$
(26)

where X and Y can be taken from Eq. (16).

Case I(c): Moreover, one more solution of Eq. (22) can be obtained by assuming \(c_1=8\), as follows

$$\begin{aligned} {U_1=\frac{2}{X_1}}-\frac{X^3_1}{6}. \end{aligned}$$
(27)

Therefore, Eqs. (15), (20) and (27) may provide a new explicit solution of the PKP equation as

$$\begin{aligned} u(x,y,t)= & {} \frac{40(y+a_0)^4{\bar{f_1}}^3}{2187(f_1+\frac{2}{3})^3}+\frac{8x(y+a_0)^2\bar{f_1}^2}{81(f_1+\frac{2}{3})^2}\nonumber \\&+\frac{A_5+\frac{2}{3}A_4(A_2+Y)+\frac{2}{(2A_1+X)} -\frac{(2A_1+X)^3}{6(A_2+Y)^2}}{(f_1+\frac{2}{3})^{\frac{1}{3}}}\nonumber \\&+\frac{x^2\bar{f_1}}{9(f_1+\frac{2}{3})}+\frac{4(y+a_0)^4\bar{\bar{\bar{f_1}}}}{243(f_1+\frac{2}{3})}\nonumber \\&-\frac{4x(y+a_0)^2\bar{\bar{f_1}}}{27(f_1+\frac{2}{3})}-\frac{8(y+a_0)^4\bar{f_1}\bar{\bar{f_1}}}{243(f_1+\frac{2}{3})^2}, \end{aligned}$$
(28)

where X and Y can be viewed from Eq. (16).

Case(II): If \(a_5 =0\) and \(a_2 \ne 0\) in Eq. (18), the corresponding Lagrange system for Eq. (17) can be written as

$$\begin{aligned} \frac{\hbox {d}X}{A_6}=\frac{\hbox {d}Y}{1}= \frac{\hbox {d}U}{A_7+A_8Y}, \end{aligned}$$
(29)

where \(A_6=\frac{a_1}{a_2}, A_7=\frac{a_3}{a_2} \)and \(A_8=\frac{a_4}{a_2}\) are newly introduced arbitrary constants .

Therefore, for the similarity transformations for Eq. (17) predicts the following form of unknown function U

$$\begin{aligned} U=A_7Y+\frac{A_8Y^2}{2}+U_2(X_2), \end{aligned}$$
(30)

with similarity variable \( X_2=(X-A_6Y)\). From Eqs. (17) and (30), we obtain an ODE

$$\begin{aligned} \bar{\bar{\bar{\bar{U_2}}}}+6\bar{U_2}\bar{\bar{U_2}}+3(A_8+A^2_6\bar{\bar{U_2}})=0. \end{aligned}$$
(31)

Primitive of Eq. (31) is

$$\begin{aligned} \bar{\bar{\bar{U_2}}}+ 3 \bar{U_2}^2+ 3(A_8X_2+A^2_6\bar{U_2})=c_3. \end{aligned}$$
(32)

The general solution of Eq. (32) is quite complex due to its nonlinearity. However, the equation can be integrated once more by taking \(A_8=0\) as

$$\begin{aligned} {\bar{\bar{U_2}}}^2+ 2{\bar{U_2}}^3 +3A^2_6{\bar{U_2}}^2-2 c_3\bar{U_2}-c_4 = 0, \end{aligned}$$
(33)

where \(c_3,c_4\) are constants of integration. Equation (33) is still nonlinear and cannot be solve easily. By the way some particular results of the equation can be read as

Case II(a) : If \(c_3=0\) and \(c_4=0\), then the solution of Eq. (33) proceeds as

$$\begin{aligned} U_2= \pm ~\sqrt{3} A_6 \tan ( c_5 \mp \frac{\sqrt{3}A_6}{2} X_2)+c_6. \end{aligned}$$
(34)

Here \(c_5\) and \(c_6\) are constants of integration. Thus, from Eqs. (15), (30) and (34), the explicit solution of the PKP equation can be expressed as

$$\begin{aligned} u(x,y,t)= & {} \frac{40(y+a_0)^4{\bar{f_1}}^3}{2187(f_1+\frac{2}{3})^3}+\frac{x^2\bar{f_1}}{9(f_1+\frac{2}{3})} \nonumber \\&+\frac{A_7Y \pm ~ \sqrt{3}A_6 \tan ( c_5 \mp \frac{\sqrt{3}A_6}{2} (X-A_6Y))+c_6 }{(f_1+\frac{2}{3})^{\frac{1}{3}}}\nonumber \\&+\frac{8x(y+a_0)^2\bar{f_1}^2}{81(f_1+\frac{2}{3})^2}+\frac{4(y+a_0)^4\bar{\bar{\bar{f_1}}}}{243(f_1+ \frac{2}{3})}\nonumber \\&-\frac{4x(y+a_0)^2\bar{\bar{f_1}}}{27(f_1+\frac{2}{3})} -\frac{8(y+a_0)^4\bar{f_1}\bar{\bar{f_1}}}{243(f_1+\frac{2}{3})^2}. \end{aligned}$$
(35)

Case II(b): On choosing \(c_4=0\) and \(c_3=-\frac{9A^4_6}{16} \), then another solution of Eq. (33) reads as

$$\begin{aligned} U_2=\pm \frac{\sqrt{3}A_6}{\sqrt{2}}\tanh ( c_{7} \pm \frac{\sqrt{3}A_6}{2\sqrt{2}} X_2)-\frac{3A^2_6}{4} X_2+c_8, \end{aligned}$$
(36)

where \(c_{7}\) and \(c_{8}\) are constants of integration. Thus, from Eqs. (15), (30) and (36), the solution of the PKP equation can be given as

$$\begin{aligned} u(x,y,t)= & {} \frac{40(y+a_0)^4{\bar{f_1}}^3}{2187(f_1+\frac{2}{3})^3}+\frac{x^2\bar{f_1}}{9(f_1+\frac{2}{3})}+\frac{A_7 Y}{(f_1+\frac{2}{3})^{\frac{1}{3}}}\nonumber \\&+\frac{c_8-2k^2_{1}\, (X-A_6Y) \pm 2k_1\tanh ( c_{7} \pm k_1 (X-A_6Y))}{(f_1+\frac{2}{3})^{\frac{1}{3}}}\nonumber \\&+\frac{8x(y+a_0)^2\bar{f_1}^2}{81(f_1+\frac{2}{3})^2}+\frac{4(y+a_0)^4\bar{\bar{\bar{f_1}}}}{243(f_1+\frac{2}{3})}\nonumber \\&-\frac{4x(y+a_0)^2\bar{\bar{f_1}}}{27(f_1+\frac{2}{3})} -\frac{8(y+a_0)^4\bar{f_1}\bar{\bar{f_1}}}{243(f_1+\frac{2}{3})^2}, \end{aligned}$$
(37)

where \(k_1=\frac{\sqrt{3}A_6}{2\sqrt{2}}\).

Case II(c) : On setting \(A_6= \sqrt{2k_2}\), \(c_3=-3 k_2^2\) and \(c_4=- 2k^3\), with \(k_2 > 0\), the solution of Eq. (33) can be furnished as

$$\begin{aligned} U_2=-k_2 X_2 \pm \frac{2}{(c_{9}\pm X_2)}+c_{10}. \end{aligned}$$
(38)

Here \(c_{9}\) and \(c_{10}\) are constants of integration. Consequently the solution of Eq. (2) can be furnished as

$$\begin{aligned} u(x,y,t)= & {} \frac{40(y+a_0)^4{\bar{f_1}}^3}{2187(f_1+\frac{2}{3})^3}+\frac{8x(y+a_0)^2\bar{f_1}^2}{81(f_1+\frac{2}{3})^2}\nonumber \\&+\frac{A_7Y-k_2 (X-A_6Y) \pm \frac{2}{(c_{9}\pm (X-A_6Y))}+c_{10}}{(f_1+\frac{2}{3})^{\frac{1}{3}}}\nonumber \\&-\frac{8(y+a_0)^4\bar{f_1}\bar{\bar{f_1}}}{243(f_1+\frac{2}{3})^2}+\frac{4(y+a_0)^4\bar{\bar{\bar{f_1}}}}{243(f_1+\frac{2}{3})}\nonumber \\&+\frac{x^2\bar{f_1}}{9(f_1+\frac{2}{3})}-\frac{4x(y+a_0)^2\bar{\bar{f_1}}}{27(f_1+\frac{2}{3})},\nonumber \\ \end{aligned}$$
(39)

where X and Y can be read from Eq. (16).

Fig. 1
figure 1

Annihilation of doubly soliton profile of Eq. (24) with function \(f_1(t)=a_6\,exp(a_7\,t+a_8)\)

Full size image
Fig. 2
figure 2

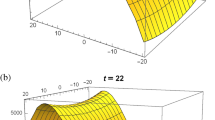
Annihilation of curve-shaped multisoliton profiles for Eq. (26) after \(t=6.12\)

Full size image
Fig. 3
figure 3

Waves interaction profiles of Eq. (28)

Full size image
Fig. 4
figure 4

Multiple-front wave profiles of Eq. (35) with variation of time

Full size image
Fig. 5
figure 5

Evolution profiles of Eq. (37). a Kink wave profiles of Eq. (37) with the variation of time and \(f_1(t)=a_6\,exp(a_7\,t+a_8)\) and b multiple-front wave profiles of Eq. (37) with the function \(f_1(t)=a_6\,\tan (a_7\,t+a_8)\). (c) Periodic solitons profiles of Eq. (37) with the function \(f_1(t)=a_6\,\sin (a_7\,t+a_8)\)

Full size image
Fig. 6
figure 6

Annihilation of curve-shaped multisoliton profile for Eq. (39) begin from \(t=55\)

Full size image

5 Analysis and discussion

In this manuscript six invariant solutions of the PKP equation have been presented via Eqs. (24), (26), (28), (35), (37) and (39). Numerical simulations have been performed to obtain the best view of graphical representations of the results. A diversified nature of the explicit results like doubly solitons, curve-shaped multisoliton, parabolic, waves interaction, multiple-front wave, kink wave and stationary wave can be seen via Figs. 1, 2, 3, 4, 5 and 6. Each derived result shows singularity at \( f_1(t)=-\frac{2}{3} \), while other singular points of the results and their nature have been discussed under the heading through Figs. 1, 2, 3, 4, 5 and 6. The results are useful in the various fields of science and technology. Solitons play a prevalent role in propagation of light in fibers, surface waves in nonlinear dielectrics, optical bistability, optical switching in slab wave guides, and many other phenomena in plasma and fluid dynamics [31]. Propagations of kink waves may annihilate the dissipation of energy in the solar environment. Wavefront phenomena have been used to design wavefront sensor which may deal with the variation in a coherent signal to describe the optical quality in an optical system. Wavefronts can also provide a variety of applications in adaptive optics, optical metrology and disorder in the retina of the eye. The results of the PKP equations presented in the manuscript have richer physical structure than results available in the literature [1,2,3,4,5,6,7,8,9,10]. The reported results are significant in the context of nonlinear dynamics. The results can illustrate various dynamic phenomena due to the existence of arbitrary functions of spatiotemporal variables. The dynamic behavior of the results are analyzed in the following manner:

Figure 1 This figure shows annihilation of doubly solitons profile of Eq. (24) with the variation of time. The graphical representation of Fig. 1. shows two solitons in opposite directions and consequently annihilate into single soliton. We have the taken arbitrary function \(f_1(t)=a_6\,exp(a_7\,t+a_8)\) to plot theses profiles. While value of constants are taken from MATLAB simulation as

\(a_0= 0.3899\), \(a_1= 0.5909\), \(a_2= 0.4594\), \(a_3= 0.0503\), \(a_4= 0.2287\), \(a_5= 0.8342\), \(a_6= 0.0156\), \(a_7= 0.8637\), \(a_8= 0.0781\), \(A_1=0.7083\), \(A_2= 0.5507\), \(A_3= 0.0603\), \(A_4=0.2742\), \(A_5=-0.1812\) and \(c_2 = 0.7060\).

Figure 2 Annihilation of curve-shaped multisoliton can be viewed after t = 6.12 corresponding to Eq. (26). Profiles are traced for the function \(f_1=(a_9\,t+a_{10})^2\). The singular points can be found by taking the roots of the polynomials \((a_9\,t+a_{10})^2+\frac{2}{3}=0\). For numerical simulation, values of constants are taken as \(a_9= 0.2287\), \(a_{10}= 0.8342\) and remaining constants are same as in Fig. 1.

Figure 3 The solution given by Eq. (28) is specified graphically in this figure. We have recorded the physical nature with variation of time. Initially, velocity profile shows interaction of waves and after sometime, it turns into single soliton nature. The profiles are traced for function \(f_1=(a_9\,t+a_{10})^2\) and constants kept same as in previous figures.

Figure 4 A graphical representation of Eq. (35) corresponding to case II(a) shows curve-shaped multiple-front wave nature with the variation of time. The Nature of the result has been investigated on the basis of various singular points of the tangent function corresponding to this case. Figures are traced by selecting the values of arbitrary constants as \(a_9= 0.2287\),

\(a_{10}= 0.8342\) , \(c_5= 0.3909\), \(c_6= 0.4168\), \(A_6=1.2862\), \(A_7=0.1094\), and remaining are same as in Fig. 1. Furthermore, arbitrary function \(f_1(t)\) is also same as in Fig. 2.

Figure 5a The profile of wave propagation initially rise asymptotically and then turns into stationary nature corresponding to Eq. (37). The phenomenon describes kink wave and ultimately annihilates into parabolic profile with the variation of time. The values of arbitrary constants to trace the profiles are taken from the numerical simulation as \(a_7= 0.8637\),

\(a_8= 0.0781\), \(c_7=0.7210\), \(c_8=0.5225\), \(A_6=1.2862\), \(A_7=0.1094\), and remaining constants are same as in previous profiles. While arbitrary function \(f_1(t)\) is considered equal to \(a_6\,exp(a_7\,t+a_8)\).

Figure 5b Corresponding to case II(b), Fig. 5b for Eq. (37) traced between the spatiotemporal (x-t) axes shows multiple-front wave with function \(f_1(t)=a_6\,\tan (a_7\,t+a_8)\). Initially, wave profile shows curve-front wave and then converts into plane-front wave with the increase in value of y. The values of constants are same as in previous figures.

Figure 5c This figure traced for Eq. (37) between the spatiotemporal (x-t) axes corresponding to case II(b). A graphical representation has been described for multiple-front wave with function \(f_1(t)=a_6\,\sin (a_7\,t+a_8)\). Initially, wave profile shows stationary wave and then converts into plane-front wave with the increase in value of y. The values of constants are same as in previous figures.

Figure 6 A graphical representation of Eq. (39) reveals annihilation of curve-shaped multisoliton after t = 55. These profiles are traced for \(f_1=(a_7\,t+a_8)\). The suitable values of constants are recorded to trace physically meaningful profiles from MATLAB simulation as \(a_7= 0.8637\), \(a_8= 0.0781\), \(c_9=0.0012\), \(c_{10}=0.4624\), \(A_6=1.2862\) and \(A_7=0.1094\). Other constants are same as in previous figures.

6 Conclusion

Invariant solutions of potential Kadomtsev–Petviashvili (PKP) equation have been obtained by using Lie symmetry analysis. The solutions derived through Eqs. (24), (26), (28), (35), (37) and (39) are obtained explicitly and represent doubly solitons, curve-shaped multisoliton, parabolic, waves interaction, multiple-front wave, kink wave and stationary wave profiles. The reported results have richer physical structure as compared to previously reported results available in the literature [1,2,3,4,5,6,7,8,9,10]. The results have direct relevance in various branches of science, such as adaptive optics, metrology and sensor technology. All the solutions are analyzed graphically through Figs. 1, 2, 3, 4, 5 and 6. Ultimately, Lie symmetry provides the exact solutions of the PKP equation in explicit form. The results of this investigation may provide a better platform for researchers working in the field of numerical techniques. These results can also be of use to validate newly developed numerical techniques along with their convergence.